Analisa Pelat Persegi Panjang Dengan Metode Hirzfeld Dan Metode M.Levy

ANALISA PELAT PERSEGI PANJANG DENGAN METODE

HIRZFELD DAN METODE M.LEVY

(STUDI LITERATUR)

TUGAS AKHIR

Diajukan untuk melengkapi tugas-tugas dan memenuhi syarat untuk menempuh ujian sarjana Teknik Sipil

Disusun oleh:

RICHARD A.SIHOMBING

03 0404 022

PROGRAM STUDI STRUKTUR

DEPARTEMEN TEKNIK SIPIL

FAKULTAS TEKNIK

ABSTRAK

Struktur bangunan memiliki beberapa bagian, salah satu adalah pelat yang

digunakan sebagai lantai tempat aktivitas berlangsung. Seperti bagian struktur yang

lain, analisa pelat juga harus dilakukan dalam perencanan untuk mendapatkan

dimensi yang kokoh, aman dan tentu saja ekonomis. Analisa yang dilakukan adalah

untuk mendapatkan besaran-besaran lendutan, momen lapangan dan momen

tumpuan yang akan digunakan dalam proses perencanaan. Diantara analisa pelat

yang biasa digunakan adalah analisa pelat Metode Hirzfeld (2001) dan metode

M.Levy (1985) .Pelat yang ditinjau adalah pelat persegi-panjang dua arah dengan

beban lateral terbagi merata dengan seluruh tepinya memiliki perletakan sederhana,

pelat persegi-panjang dengan dua tepi yang berhadapan ditumpu secara sederhana

dan dua sisi lainnya terjepit, pelat persegi-panjang yang ketiga tepinya ditumpu

sederhana dan satu tepinya terjepit, dan pelat persegi-panjang yang semua tepinya

terjepit.

Metode yang digunakan dalam penulisan ini adalah studi literatur dengan

terlebih dahulu mengumpulkan bahan - bahan yang berhubungan dengan

permasalahan, kemudian manganalisa teori – teori ( metode ) yang berhubungan

dengan tugas akhir tersebut. Setelah itu membandingkan kedua metode yaitu

Hirzfeld (2001) dan M.Levy (1985) lewat contoh – contoh kasus. Dan menarik

kesimpulan dari hasil analisa tersebut.

Hasil analisa dalam tulisan ini menunjukkan bahwa baik lendutan maupun

Momen yang dihasilkan dari analisa metode Hirzfeld lebih besar dibandingkan

dengan metode M.Levy, dan dari hasil analisa juga didapat bahwa metode Hirzfeld

Daftar

Isi

Abstrak__________________________________________________________ i

Kata Pengantar____________________________________________________ ii

Daftar Isi_________________________________________________________ iv

Daftar Notasi______________________________________________________vi

BAB I PENDAHULUAN__________________________________________ 1

1.1 Umum_______________________________________________________

1.2 Latar Belakang Masalah_________________________________________

1.3 Maksud dan Tujuan_____________________________________________

1.4 Pembatasan Masalah____________________________________________

1.5 Metode Pembahasan____________________________________________

BAB II DASAR TEORI

2.1 Umum________________________________________________________

2.2 Pengenalan Teori Elastisitas_______________________________________

2.3 Persamaan Differensial Pelat ______________________________________

2.4 Kondisi tepi Menurut Teori Lentur__________________________________

2.5 Deret Fourier dalam Penyelesaian Persamaan Differensial Pelat___________

BAB III ANALISA PELAT PERSEGI PANJANG

3.A Metode Hirzfeld______________________________________________

Sederhana pada Keempat Sisinya ( kasus 1 )________________________

3.a.2 Analisa Pelat Persegi-Panjang dengan Dua Tepi yang Berhadapan

Ditumpu Secara Sederhana dan Dua sisi Lainnya Dijepit ( kasus 2 )_____

3.a.3 Analisa Pelat Persegi-Panjang yang Ketiga Tepinya Ditumpu

Secara Sederhana dan Satu Tepinya Terjepit. ( kasus 3 )______________

3.a.4 Analisa Pelat Persegi-Panjang yang Semua Tepinya Terjepit ( kasus 4 )__

3.B Metode M.Levy

3.b.1 Analisa Pelat Persegi-Panjang yang Ditumpu Secara

Sederhana pada Keempat Sisinya ( kasus 1 )_______________________

3.b.2 Lenturan pelat persegi-panjang Akibat Momen

yang Terbagi Sepanjang Tepi-tepinya ____________________________

3.b.3 Analisa Pelat Persegi-Panjang dengan Dua Tepi yang Berhadapan

Ditumpu Secara Sederhana dan Dua sisi Lainnya Dijepit ( kasus 2 )_____

3.b.4 Analisa Pelat Persegi-Panjang yang Ketiga Tepinya Ditumpu

Secara Sederhana dan Satu Tepinya Terjepit. ( kasus 3 )_____________

3.b.5 Analisa Pelat Persegi-Panjang yang Semua Tepinya Terjepit ( kasus 4 )__

BAB IV PERBANDINGAN METODE HIRZFELD

DAN METODE M.LEVY

4.1 Analisa Pelat Persegi-Panjang yang Ditumpu Secara

Sederhana pada Keempat Sisinya ( kasus 1 )_______________________

4.2 Analisa Pelat Persegi-Panjang dengan Dua Tepi yang Berhadapan

Ditumpu Secara Sederhana dan Dua sisi Lainnya Dijepit ( kasus 2 )____

Secara Sederhana dan Satu Tepinya Terjepit. ( kasus 3 )______________

4.4 Analisa Pelat Persegi-Panjang yang Semua Tepinya Terjepit ( Kasus 4 )_

BAB V KESIMPULAN DAN SARAN

5.1 Kesimpulan________________________________________________

5.2 Saran______________________________________________________

DAFTAR PUSTAKA_______________________________________________

Daftar Notasi

b

a, Dimensi linear pelat dalam arah X dan Y

D,Dx,Dy Ketegaran lentur Pelat

E modulus Elastisitas

G Modulus geser

h Tebal Pelat

I Momen inersia

y x l

l , Dimensi linear pelat dalam arah X dan Y

i

m, Bilangan bulat positif ( 1,2,3,.. ) yanga menyatakan suku deret

0

M Momen lentur yang didistribusikan disepanjang tepi terjepit

y x M

M , Momen dalam arah X dan Y

y x Q

Q , Gaya geser

q Gaya lateral

y x p

p , Faktor beban

r ,ε Perbandingan rasio panjang/lebar

T Periode fungsi

) (x

f Lendutan balok

f Lendutan Pelat

v Rasio Poisson

z y

x, , Koordinat Kartesius

α Koefesien Lendutan

y x B B

B, , Koefesien momen lapangan

y x γ γ

γ, , Koefesien momen tumpuan

m m β

α , Konstanta

z y x ε ε

ε , , komponen regangan normal

xy γ

γ, Regangan geser

z y x σ σ

σ , , Komponen tegangan normal

xy τ

τ, Tegangan geser

k

ABSTRAK

Struktur bangunan memiliki beberapa bagian, salah satu adalah pelat yang

digunakan sebagai lantai tempat aktivitas berlangsung. Seperti bagian struktur yang

lain, analisa pelat juga harus dilakukan dalam perencanan untuk mendapatkan

dimensi yang kokoh, aman dan tentu saja ekonomis. Analisa yang dilakukan adalah

untuk mendapatkan besaran-besaran lendutan, momen lapangan dan momen

tumpuan yang akan digunakan dalam proses perencanaan. Diantara analisa pelat

yang biasa digunakan adalah analisa pelat Metode Hirzfeld (2001) dan metode

M.Levy (1985) .Pelat yang ditinjau adalah pelat persegi-panjang dua arah dengan

beban lateral terbagi merata dengan seluruh tepinya memiliki perletakan sederhana,

pelat persegi-panjang dengan dua tepi yang berhadapan ditumpu secara sederhana

dan dua sisi lainnya terjepit, pelat persegi-panjang yang ketiga tepinya ditumpu

sederhana dan satu tepinya terjepit, dan pelat persegi-panjang yang semua tepinya

terjepit.

Metode yang digunakan dalam penulisan ini adalah studi literatur dengan

terlebih dahulu mengumpulkan bahan - bahan yang berhubungan dengan

permasalahan, kemudian manganalisa teori – teori ( metode ) yang berhubungan

dengan tugas akhir tersebut. Setelah itu membandingkan kedua metode yaitu

Hirzfeld (2001) dan M.Levy (1985) lewat contoh – contoh kasus. Dan menarik

kesimpulan dari hasil analisa tersebut.

Hasil analisa dalam tulisan ini menunjukkan bahwa baik lendutan maupun

Momen yang dihasilkan dari analisa metode Hirzfeld lebih besar dibandingkan

dengan metode M.Levy, dan dari hasil analisa juga didapat bahwa metode Hirzfeld

BAB I PENDAHULUAN

1.1Latar Belakang

Perkembangan perencanaan konstruksi bangunan bertingkat beberapa tahun

belakangan ini cukup berkembang pesat, hal ini membuktikan bahwa manusia

sebagai pelaku utama berusaha mendapatkan konsep perencanaan lebih aman,

nyaman, praktis dan tentu saja ekonomis. Konstruksi bangunan bertingkat

merupakan satu kesatuan utuh yang terdiri dari beberapa bagian seperti pondasi,

balok, kolom, dinding bangunan, atap dan pelat harus direncanakan sedemikian rupa

agar kondisi kondisi ideal tersebut dapat terpenuhi.

Salah satu bagian dalam konstruksi bangunan bertingkat ialah pelat. Pelat

merupakan struktur bidang yang lurus ( datar atau tidak melengkung ) yang tebalnya

jauh lebih kecil di bandingkan dimensi lain. Geometri suatu pelat bisa di batasi oleh

garis lurus atau garis lengkung. Ditinjau dari segi statika, jenis tumpuan pelat bisa

bebas ( free ), bertumpuan sederhana ( simply supported ) dan jepit (clip ). Beban

statis dan dinamis yang di pikul pelat umumnya tegak lurus bidang permukaan pelat.

Keragaman dimensi pelat persegi yang merupakan besaran rasio antara panjang

dan lebar pelat( b/a atapun ly/lx ) dan kondisi kondisi tepi serta beban yang bekerja

memberikan pengaruh pada perilaku pelat persegi panjang.

Sumber : Teori dan Analisis Pelat (Szilard, 1989:14)

Gambar 1.1.Rasio panjang dan lebar pelat a

b ly

Keterangan

- Ly = b =Rasio panjang

- Lx = a =Rasio lebar

Y

X

Ada beberapa metode analisa yang dapat digunakan untuk menentukan besaran-

besaran yang di timbulkan seperti lendutan, momen, reaksi perletakan dan peralihan

untuk masing – masing kasus. Besaran – besaran tersebut akan sangat

mempengaruhi dalam merencanakan sehingga di perlukan analisa yang cukup akurat

agar struktur pelat yang akan di desain itu mampu memikul beban – beban yang

bekerja.

Sebagai perencana, mengetahui dan memahami pelbagai metode analisa

perencanaan pelat merupakan usaha untuk mendapatkan kondisi yang mampu

menghasilkan konstruksi bangunan bertingkat yang aman, nyaman dan ekonomis.

Dalam tugas akhir ini analisa yang dilakukan ialah membandingkan metode Hirzfeld

( 2001 ) dengan metode M.Levy ( 1992 ) untuk pelat persegi panjang dengan

berbagai kondisi perletakan. Kedua metode ini memiliki karakteristik tersendiri

dalam penentuan perilaku pelat yang terjadi akibat pembebanan. Metode yang akan

digunakan adalah metode yang memiliki kemudahan dalam penggunaan dengan

tetap mengedepankan prinsip keamanan struktur bangunan.

1.2Tujuan Penelitian

Adapun Tujuan dari pembahasan tugas ahkir ini adalah :

1. Membahas analisa pelat persegi panjang dengan metode Hirzfeld ( 2001 )

2. Menghitung besarnya perbedaan perilaku pelat persegi panjang yang di

hasilkan dari analisa kedua metode tersebut yang berupa koefisien lendutan

dan momen.

3. Membandingkan hasil analisa pelat persegi panjang metode Hirzfeld ( 2001 ) dengan M.Levy ( 1992 ) berdasarkan perbandingan dimensi panjang dan

lebar pelat (ly/lx atau b/a ) .

1.3 Pembatasan masalah

Dalam menganalisa dan membandingkan kedua metode perhitungan pelat

tersebut, penulis akan membatasi permasalahan dengan tujuan memfokuskan kepada

pokok pokok permasalahan dan penyederhanan perhitungan. Pembatasan masalah

adalah sebagai berikut :

1. Material yang di bahs dalam analisa ini adalah beton yang di anggap

homogen dan isotropis.

2. Beban yang digunakan adalah beban lateral terbagi merata dimana

merupakan beban total dari penjumlahan beban mati dan beban hidup.

3. Pelat yang di tinjau adalah pelat dua arah ( two way slab ) dengan bentuk

persegi panjang.Pelat dua arah ( two way slab ) adalah pelat dengan rasio

perbandingan ly/lx atau b/a < 3 sedangkan pelat satu arah ( one way slab )

adalah pelat dengan rasio perbandingan ly/lx atau b/a > 3 .

4. Perletakan yang di bahas berupa :

a. kasus 1 : Seluruh tepi memiliki perletakan sederhana

Ly b

Ly b

Lx a

Gambar 1.2.Perletakan sederhana

b. kasus 2 :Dua tepi yang berhadapan ditumpu secara sederhana dan dua sisi lainnya

( sisi lx atau a ) dijepit.

Ly

Lx a

Gambar 1.3.Perletakan dengan dua tepi yang berhadapan ditumpu secara sederhana

dan dua sisi lainnya ( sisi lx atau a ) dijepit.

c. kasus 3 :Ketiga tepinya ditumpu secara sederhana dan satu tepinya (sisi lx atau a )

terjepit.

Ly Ly Ly

Ly b

Gambar 1.4.Perletakan dengan ketiga tepinya ditumpu secara sederhana dan satu

tepinya (sisi lx atau a ) terjepit.

d. kasus 4 : semua tepinya terjepit sempurna

Lx a

Gambar 1.5.Perletakan dengan semua tepinya terjepit sempurna

Dimana kesepakatan jenis tumpuan adalah :

• Perletakan

Lx Lx Lx

1.Perletakan bebas 2.Perletakan sederhana 3.Perletakan terjepit

1.4 Metodologi

Metode yang digunakan dalam penulisan ini adalah studi literatur dengan terlebih

dahulu mengumpulkan bahan-bahan yang berhubungan dengan permasalahan,

kemudian menganalisa teori – teori ( metode ) yang berhubungan tugas akhir

tersebut, setelah itu membandingkan kedua metode yang ada yaitu Hirzfeld ( 2001 )

dan M.Levy ( 1992 ) lewat contoh-contoh kasus. Dari Perbandingan kedua metode

tersebut akan ditarik kesimpulan akurat yang bersesuaian dengan teori yang telah

BAB II DASAR TEORI

2.1 Umum

Pelat beton (slab) merupakan elemen struktur yang paling luas digunakan

dalam bentuk lantai dan atap bangunan untuk menompang beban normal pada

permukaannya. Pelat tersebut dapat ditopang pada dinding atau balok secara

langsung pada kolom. Balok yang menompang pelat dipertimbangkan (dianggap)

kaku dengan lendutan (deflection) relative sangat kecil jika dibandingkan lendutan

pelat. Pelat yang ditopang pada dinding atau balok diklasifikasikan sebagai pelat

dengan tumpuan tepi (edge supported slabs). Pelat yang ditopang secara langsung

pada kolom tanpa balok dikenal sebagai pelat cendawan (flat slabs).

Pelat tumpuan tepi secara umum berbentuk persegi, namun dapat juga dalam

berbagai bentuk seperti segitiga, trapesium, lingkaran dan lainnya. Beban

ditransfer dari pelat dalam bentuk momen lentur, geser dan torsi ketumpuan. Seperti

pelat yang ditumpu pada dua sisi yang sejajar (gambar 2.1a) yang memikul beban

lentur dalam arah sejajar memanjang pada tumpuannya. Hal ini dikenal sebagai pelat

satu arah dan sebenarnya merupakan suatu balok dengan dimensi lebar yang besar.

Pelat yang ditumpu pada keempat sisinya juga dapat merupakan pelat satu arah (one

way slab) jika dimensi sepanjangnya sangat besar dibandingkan dengan lebarnya.

Pelat persegi panjang dengan dimensi panjang tidak terlalu besar dibandingkan

dengan dimensi lebarnya atau pelat bujur sangkar yang didukung pada keempat

sebagai pelat dua arah (two way slab). Dan pada tulisan ini hanya akan dibahas pelat

dua arah (two way slab).

(b) Pelat satu arah tumpuan sederhana

(a) Pelat satu arah tumpuan sederhana

(c) pelat dua arah dengan

perletakan sederhana yang

ditumpu pada dinding

Gambar 2.1.Pelat satu arah dan dua arah

Pelat dua arah adalah struktur statis tak tentu tingkat tinggi. Analisanya harus

selalu memenuhi prinsip-prinsip dasar statika secara teoritis seharusnya

mempertimbangkan pengekangan terhadap rotasi dan translasi yang diakibatkan

sistem perletakan.

b

L

Masonry

support

b

L<2b

Masonry

support

b

2.2 Pengenalan Teori Elastisitas

Teori elastisitas merupakan cabang yang penting dari fisika matematis, yang

mengkaji hubungan antara gaya, perpindahan, tegangan, dan regangan dalam benda

elastis. Bila suatu benda pejal dibebani oleh gaya luar benda tersebut akan berubah

bentuk/berdeformasi (Gambar 2.2), sehingga timbul tegangan dan regangan dalam.

Perubahan bentuk ini tergantung pada konfigurasi geometris dari benda tersebut dan

pada sifat mekanis bahannya. Dalam teori elastisitas, pembahasan hanya dibatasi

hanya pada bahan elastis linear, yaitu keadaan dimana hubungan antara tegangan

dan regangan bersifat linear, dan perubahan bentuk serta tegangan akan hilang bila

gaya luar dihilangkan. Selain itu teori elastiitas klasik menganggap bahan bersifat

homogen dan isotropik, dengan demikian, sifat mekanis bahan sama dalam segala

arah. Walaupun bahan-bahan struktural tidak tepat memenuhi semua anggapan ini,

pengujian menunjukkan bahwa untuk sruktur baja, misalnya, teori elstisitas

memberikan hasil dengan ketetapan yang tinggi, asal tegangannya masih berada

dibawah titik leleh (yield point). Teori pelat klasik yang merumuskan dan

menyelesaikan masalah pelat berdasarkan analisis matematis yang eksak, merupakan

penerapan khusus yang penting dari elastis. Oleh karena itu, pengertian menyeluruh

tentang konsep dasarnya,notasi, denfinisi, dan lainnya, sangat penting. Tujuan dari

bagian ini ialah mengenalkan dasar dalam bentuk yang ringkas.

Sumber : Teori dan Analisis Pelat (Szilard, 1989:14)

a. Keadaan tegangan pada benda elastis

Dalam statika benda tegar (rigid body), disini akan dikaji gaya luar yang

bekerja pada suatu benda tidak meinjau perubahan bentuk yang timbul. Sebaliknya,

dalam teori elastisitas, ditinjau perubahan bentuk akibat gaya luar. Melalui

perubahan bentuk pada benda tersebut, gaya-gaya luar dikonversi menjadi gaya-gaya

dalam.

Kita mulai dengan meninjau suatu benda elsatis dengan bentuk sembarang

dalam system koordinat cartesius X, Y, Z, yang memikul gaya luar yang berada

dalam keseimbangan. Untuk menentukan gaya dalam yang timbul di antara

partikel-partikel benda tersebut, kita bayangkan benda tersebut dipenggal menjadi dua bagian

oleh suatu bidang, seperti pada Gambar 2.3a. Jika sekarang kita bayangkan bahwa

bagian B dihilangan, keseimbangan benda tersebut harus dipertahankan oleh

gaya-gaya luar yang bekerja pada permukaan penampangnya. Marilah kita ambil suatu

luas ∆A yang kecil pada penampang tersebut dan kita nyatakan gaya dalam yang

bekarja pada luas ini sebagai ∆ P (Gambar 2.3b). perbandingan ∆ P/∆A adalah

tegangan rata rata, yang didefinisikan sebagai limit dari perbandingan; jadi

Tegangan =

A P P

A ∆

∆

=_∆lim_→0 (gaya per satuan luas) (2.1)

Karena ∆P ummnya tidak tegak lurus penampang, kita lebih mudah menggunakan

komponen normal (tegak lurus) dan tangensialnya (sebidang). Dengan demikian

definisi tegangan normal (σ) dan tegangan geser (τ) (Gambar 2.3b) adalah

A P_n

A ∆

∆ =_∆lim_→0

σ dan

A P_t

A ∆

∆ =_∆lim_→0

Sumber : Teori dan Analisis Pelat (Szilard, 1989:14)

Gambar 2.3. Metode Irisan

Perlu diperhatikan bahwa tegangan pada suatu bidang adalah vektor tegangan.

Resultan tegangan dengan mudah dapat dicari dengan penjumlahan vektor dari

komponen-komponennya. Keadaan tegangan pada benda elastis biasanya bervariasi

dari satu titik ke titik lainnya; jadi, kita dapat tuliskan σ(x,y,z) dan τ(x,y,z).

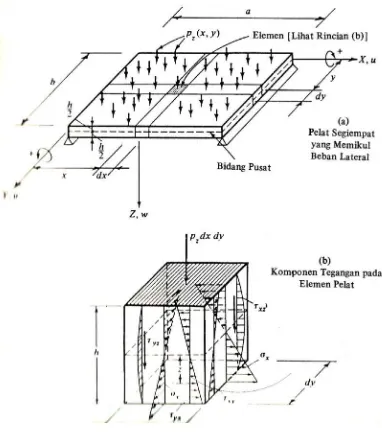
Untuk menggambarkan keadaan tegangan tiga-dimensi, kita ambil suatu

elemen yang kecil dalam bentuk kontak (dx dy dz) yang mukanya sejajar dengan

bidang koordinat, seperti yang ditunjukkan pada gambar 2.4. Komponen tegangan

normal X, Y, dan Z, masing-masing diberi notasi σx,σy, dan σz . Subskribnya(

subscript/huruf bawah) menunjukkan garis normal (tegak lurus) permukaan tempat

vector tegangan tersebut bekerja. Tegangan geser τ biasanya memiliki dua subskrib.

Subskrib pertama menunjukkan arah garis normal permukaan, sedang subskrib kedua

[ ]

  

 

  

  =

y zy zx

yz y yx

xz xy x

σ τ

τ σ τ

τσ τ τ σ

letaknya pada suatu benda, intensitasnya akan berubah bila bidang rujuknya

digerakkan sejauh dx, dy, dz. Pertambahan yang timbul dinyatakan oleh dua suku

pertama dari deret Taylor (Gambar 2.4)

Sumber : Teori dan Analisis Pelat (Szilard, 1989:15)

Gambar 2.4. Elemen tiga dimensi

Perjanjian tanda berikut akan digunakan dalam pembahasan berikutnya. Pada bidang

dekat suatu elemen (dipandang dari ujung-ujung sumbu koordinat positif dianggap

positif. Pada bidang jauh suatu elemen, semua tegangan yang bekerja pada arah

sumbuh koordinat negatif dianggap positif. Perjanjian tanda ini mengikuti aturan

umum yang dipakai dalam praktek bidang teknik; yakni, tarikan bertanda positif dan

tekanan bertanda negatif.

Keadaan tegangan tiga-dimensi di sembarang titik benda elastis ditentukan

oleh sembilan komponen tensor tegangan dengan matriks

(2.3)

yang simetris terhadap diagonal utama. Dimana Tensor adalah besaran yang

yx xy τ

τ = τxz =τzx τyz =τzy

ini dalam teori elastis adalah rotasi sumbu. Tensor orde dua dinyatakan dalam bentuk

(Szilard,1989:15). Karena sifat simetris ini,

dan (2.4)

Dalam beberapa literatur, Persaman (2.1) disebut hukum timbale-balik tegangan

geser dan mudah dibuktikan dengan mengambil momen dari tegangan-tegangan

terhadap sumbu koordinat. Sementara keadaan tegangan dalam pelat yang tebal

bersifat tiga-dimensi, pelat tipis yang memiliki ketegangan lentur yang mempunyai

keadaan tiga-dimensi yang tidak sempurna; yakni, semua komponen tegagan

permukaan yang sejajar bidang XY sama dengan nol.

Dalam analisis pelat elastis, keadaan tegangan dua-dimensi berperan penting.

Pada keadaan ini, σz = τyz = τxz = 0; dengan demikian, matriks tensor tegangan yang

bersangkutan menjadi

[ ]

  

 =

z x

σ τ τ σ

σ (2.5)

dimana τ = τxy = τyz.

Misalkan komponen tegangan σx, σy, dan τ = τxy = τyx pada suatu elemen dua

dimensi (Gambar 2.5) dalam system koordinat kartesius diketahui.

Sumber : Teori dan Analisis Pelat (Szilard, 1989:16)

Dengan demikian, kedua arah tegak lurus ([1], [2]) bidang-bidsang dimana tegangan

geser sama dengan nol (τ = 0) dan tegangan normal σ memiliki nilai ekstrim yang

dapat ditentukan dari

jadi (2.6)

Arah-arah ini disebut arah utama (principal direction). Tegangan normal maksimum

dan minimum yang bekerja pada bidang ini disebut tegangan utama (σ1, σ2) dan

dapat dihitung sebagai

(2.7a)

dengan cara yang sama, tegangan geser maksimum adalah

(2.7b)

Variasi komponen tegangan bila sudut α berubah-ubah dapat ditentukan dari

(2.8)

Persamaan untuk menentukan tegangan tegangan utama [Persamaan (2.6) dan (2.7)],

dan juga persamaan tranformasi tegangan dua-dimensi [Persamaan (2.8)] dapat

diturunkan dan dinyatakan secara grafis dalam lingkaran Mohr (Gambar 2.6).

Oleh karena momen dalam yang bekerja pada elemen pelat merupakan vector

momen yang diperoleh dari komponen tegangan σx, σy, dan τ, momen yang bekerja

pada bidang yang miring, dengan garis normal n (Gambar 2.7), dapat ditentukan

dengan cara yang sama. Jadi, kita dapat tuliskan ;

2 2

tan ₀

y x σ

σ τ

α = ₋

y x σ

σ τ α = _tan− 2₋

2

1 1

0

2 2 2

, 1

2

2 τ

σ σ σ

σ

σ = x + y + _ x − y _ +

2 2 2

1

2 )

( 2 1

τ σ

σ σ

σ

τ = − = _ x− y _ + maks

α τ α σ

σ σ σ

σ cos2 sin2

2 2

' = x+ y + x− y +

x

α σ

σ α τ

τ sin2

2 2 cos

' x− y

Sumber : Teori dan Analisis Pelat (Szilard, 1989:17)

Gambar 2.6 Lingkaran Mohr untuk tegangan

dan (2.9)

α α

α sin sin2

cos2 _y 2 _yx

x

n m m m

m = + +

α α sin2 2

cos 2

2 yx

y x y x

m m

m m m

+ −

+ + =

α

α sin2

2 2

cos x y

xy nt

m m m

Sumber : Teori dan Analisis Pelat (Szilard, 1989:17)

Gambar 2.7. Komponen-komponen momen pada bidang miring dalam suatu elemen pelat

Momen-momen utama yang menyatakan nilai ekstrim juga dapat ditentukan dari

lingkaran mohr,

(2.10)

Sudut α0 yang berkaitan dengan letak momen lentur maxmum dan minimum dapat

juga dihitug dari persamaan yang serupa dengan persamaan (2.6):

(2.11)

b. Regangan dan perpindahan

Benda elastis yang diprlihatkan pada Gambar 2.2 ditumpu sedemkian rupa

sehingga perpindahan benda tegar/rigid body (translasi dan rotasi) tidak terjadi.

Karena benda elastis tersebut berubah bentuk akibat gaya luar, setiap titik padanya

( )

(

)

( )

max

(

)

2 2

min

2 2 max

min

4 2

1

4 2

1 2

xy y

x nt

xy y

x y

x nt

m m

m m

m m

m m

m m

+ −

+ =

+ −

+ + =

y x

xy m m

m a

− = 2

mengalami perpindahan elastis yang kecil. Dengan menyatakan komponen

perpindahan translasiional dalam arah X, Y, Z sebagai u, v, w, dapat dituliskan

u= f1(x,y,z) v= f2(x,y,z) dan w= f3(x,y,z) (2.12)

yang menunjukkan bahwa komponen perpindahan juga merupakan fungsi dari

letaknya.

Untuk menghubungkan perpindahan dan berubah bentuk, kita tinjau

kembali kotang yang sangat kecil dengan sisi dx, dy, dan dz pada suatu benda elastis

(Gambar 2.4). Karena keseluruhan benda elastis ini berubah bentuk, elemen kecil

tersebut juga akan berubah bentuk, yakni panjang sisi dan sudut-sudut antara yang

semula siku-siku juga akan berubah (Gambar 2.8). Dengan membatasi pembatasan

kita pada perubahan bentuk yang kecil, kita definisikan regangan normal, ε , sebagai perubahan panjang satuan. Misalnya, regangan normal dalam arah X adalah

(2.13a)

Sumber : Teori dan Analisis Pelat (Szilard, 1989:18)

Gambar 2.8. Deformasi suatu elemen ,

dx dx x

∆ =

dimana pertambahan ∆dx dapat dinyatakan denga n suku kedua deret Taylor (∆dx=

(∂u / ∂x)dx); jadi, dapat ditulis

dan (2.13b)

Akibat pengaruh tegangan geser, permukaan elemen tersebut akan berputar (Gambar

2.8b). Sebagai contoh, dengan mengambil proyeksi elemen tersebut pada bidang XY

seperti yang ditunjukkan dalam Gambar 2.9, dapat didefinisikan regangan geser

sebagai distorsi sudut; jadi

(2.14)

Sumber : Teori dan Analisis Pelat (Szilard, 1989:19)

Gambar 2.9. Distorsi yang diproyeksikan

Dengan cara yang sama, kita peroleh

dan (2.15)

Sama halnya dengan tensor tegangan [Persamaan (2.3)] di suatu titik regangan tensor

dapat didefinisikan:

(2.16) ,

x u x

∂ ∂ =

ε ,

y u Y

∂ ∂ =

ε z u_z

∂ ∂ =

ε

.

'' '

yx xy

y u x v

γ γ

γ

γ =

∂ ∂ + ∂ ∂ = + =

zx xz

x w z u

γ

γ =

∂ ∂ + ∂ ∂

= yz zy.

y w z v

γ

γ =

∂ ∂ + ∂ ∂ =

[ ]

  

 

  

  =

z zy zx

yz y

yx

xz xy z

ε γ

γ ε γ

γ γ γ

ε ε

2 1 2

1

2 1 2

1

2 1 2

c. Hukum Hooke Umum

Untuk bahan struktur yang menunjukkan batas elastis linear yang jelas,

hokum hooke suatu dimensi menghubungkan tegangan dan regangan normal sebagai

,

ε

σ =E (2.17)

dimana E adalah modulus elastis young. Jika tegangan normal bekerja dalam arah X,

perpanjangan εx, diikuti oleh perpendekan lateral; jadi, regangan dalam arah X,Y, dan

Z adalah

dan ( 2.18 )

dengan ν adalah angka poisson yang bekisar antara 0.15 dan 0.35 untuk kebanyakan

bahan struktur. Untuk struktur linear yang mengikuti Hukum Hooke, prinsip

supeposisi dapat diterapkan; dengan demikian, jika tegangan σx, σy, dan σz bekerja

secara bersamaan pada elemen yang kecil tersebut, hukum Hooke diperluas menjadi

(2.19)

Dengan cara yang sama, hubungan antara tegangan dan regangan geser adalah

, G

τ

γ = (2.20)

dimana G adalah modulus elaslisitas geser atau modulus geser/gelincir. Jika

tegangan geser bekerja pada semua permukaan elemen, Persamaan (2.21) menjadi

, 1

xy xy

Gτ

γ = yz 1 yz, Gτ

γ = dan zx 1 zx, Gτ

γ = (2.21)

[

]

[

]

[

( )

]

1

) (

1

) (

1

y x z

z

z x y

y

z y x

x

E E E

σ σ ν σ ε

σ σ ν σ ε

σ σ ν σ ε

+ −

=

+ −

=

+ −

=

, E

x x

σ

ε = ,

E x y

σ

ε = ,

E x z

Hubungan antaara modulus elastisitas Young E dan mmodulus geser G adalah

) 1 ( 2 +ν

= G

E , atau .

) 1 ( 2 +ν

= E

G (2.22)

2.3 Persamaan Differensial Pelat dalam Sistem Koordinat Kartesius a. Sistem Koordinat dan Perjanjian Tanda.

Bentuk pelat cukup ditentukan dengan menunjukkan geometri bidang

pusatnya (middle surface), yang merupakan bidang /permukaan yang membagi dua

tebal pelat h setiap titik (Gambar 2.10). Szilard (1989:24) mengatakan teori pelat

dengan lendutan kecil. Yang sering kali disebut teori Kirchhoff dan Love, didasarkan

pada anggapan berikut:

1. Bahan pelat bersifat elastis, homogen, dan isotropis

2. Pelat pada mulanya datar

3. Tebal pelat relatif kecil dibandingkan dengan dimensi lainnya. Dimensi

lateral terkecil pada pelat paling sedikit sepuluh kali lebih besar daripada

ketebalannya

4. Lendutan sangat kecil dibandingkan dengan pelat. Lendutan maksimum

sebesar sepersepuluh sampai seperlima tebal pelat dianggap sebagai batasan

untuk teori lendutan yang kecil. Batasan ini juga dapat dinyatakan dalam

panjang pelat; misalnya, lendutan maksimum lebih kecil dari satu perlima

puluh panjang bentang yang terkecil

5. Kemiringan bidang pusat yang melendut jauh lebih kecil dari satu

6. Perubahan bentuk pelat bersifat sedemikian rupa sehingga garis lurus yang

semula tegak lurus bidang pusat pelat, tetap berupa garis lurus dan tetap tegak

7. Lendutan pelat diakibatkan oleh perpindahan titik-titik bidang pusat yang

tegak lurus awalnya

8. Besarnya tegangan yang lurus bidang pusat sangat kecil sehingga bias

diabaikan. Banyak dari anggapa ini terkenal karena sama seperti balok dasar.

Pengujian dengan skala kecil dan besar telah membuktikan berlakunya

anggapan-anggapan tersebut.

9. Pada kasus pelat yang memiliki daya tahan lentur, anggapan penyerdehanaan

tambahan dapat juga dibuat: regangan pada bidang pusat akibat gaya-gaya

sebidang biasanya dapat diabaikan jika dibandingkan dengan regangan akibat

lentur (teori pelat internasional)

Untuk pelat segiempat (persegi), pemakaian system koordinat kartesius

merupakan cara yang paling mudah (Gambar 2.10). Gaya luar dan dalam serta

komponen lendutan u, v, dan w dianggap positif bila searah dengan arah positif

sumbu koordinat X, Y, dan Z. Dalam praktik bidang teknik, momen positif

menimbulkan tarikan pada serat yang terletak dibagian bawah struktur. Perjanjian

tanda seperti ini juga berlaku untuk pelat.

Kita tinjau suatu kotak kecil yang dipotong dari sebuah pelat pada (Gambar

2.11). Kemudian kita berikan gaya dalam dan momen positif pada bidang-bidang

dekat (near face). Agar elemen tersebut seimbang, gaya dalam momen negatif harus

bekerja pada bidang jauhnya (far side). Subkrip pertama pada gaya dalam

menunjukkan arah garis normal (garis tegak lurus) permukaan penampang tempat

[image:30.595.136.518.111.559.2]

Sumber : Teori dan Analisis Pelat (Szilard, 1989:25)

[image:31.595.140.495.165.522.2]

Sumber : Teori dan Analisis Pelat (Szilard, 1989:26)

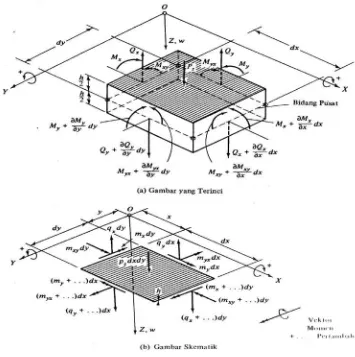
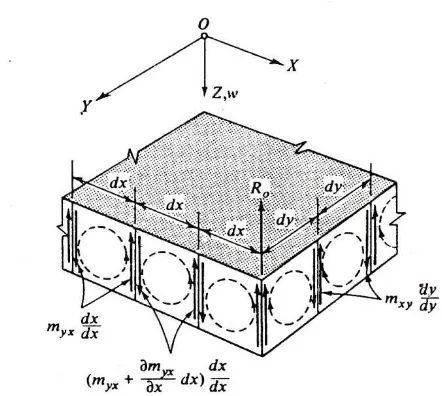
Gambar 2.11. Gaya dalam dan luar pada elemen bidang pusat

Sumber : Teori dan Analisis Pelat (Szilard, 1989:25)

b. Keseimbangan elemen pelat

Dengan menganggap pelat hanya memikul beban lateral, diantara keenam

persamaan keseimbangan dasar hanya tiga persamaan berikut yang digunakan:

dan (2.23)

Perilaku pelat dalam banyak hal analog dengan perilaku jaringan silang dua

dimensi. Jadi beban luar Pz dipikul oleh gaya transversal Qx dan Qy serta oleh momen

lentur Mx dan My. perbedaan yang jelas dengan aksi jaringan balok silang

dua-dimensi ialah adanya momen puntir Mxy dan Myx (Gambar 2.11a). Dalam teori pelat,

umumnya gaya dalam dan momen dinyatakan persatuan panjang bidang pusat

(Gambar 2.11b). Untuk membedakan gaya dalam ini dengan resultan yang disebut

diatas, notasi Qx, Qy, Mx, My, Mxy, dan Myx, akan digunakan disini.

Prosedur untuk menurunkan persamaan differensial keseimbangan adalah

sebagai berikut:

1. Pilih system koordinat yang memudahkan dan gambarkan suatu

elemen pelat (gambar 2.11)

2. Tinjaulah semua gaya dalam dan luar yang bekerja pada elemen

tersebut

3. Berikan gaya dalam positif dengan penambahannya

(qx+…qy+…dan seterusnya) pada bidang dekat

4. Beriakan gaya dalam negatif pada bidang jauh

5. Nyatakan pertambahan tersebut dalam deret Taylor yang

dipenggal:

. ,

, dy dst

y M M

dM M

dx x Q Q dQ

Q y y y y

x x x x

∂ ∂ + = +

∂ ∂ + =

6. Tuliskan keseimbangan gaya dalam dan luar yang bekerja pada

elemen tersebut.

Sebagai contoh, kita samakan jumlah momen semua gaya dalam terhadap sumbu Y

dengan nol (gambar 2.11b), sehingga diperoleh

dx M dy dy y M M

dy M dy dx x M

M yx

yx yx

x

x −

  



∂ ∂ + +

−    

 

∂ ∂

+

0 2

2 − =

   

 

∂ ∂ +

− dx dydx Q dydx x

Q

Q x _x

x (2.25)

Setelah disederhanakan, kita abaikan suku yang mengandung besaran

( )

dx dy x

q_x 2

2 1

     

δ

δ _{. Karena merupakan suku berorde tinggi yang sangat kecil. Dengan}

demikian, persamaan (2.25) menjadi

0 . .

. − =

∂ ∂ + ∂

∂

dx dy Q dx dy y M dy dx x M

x yx

x

(2.26)

Dan, setelah dibagi dengan dx dy, kita peroleh

x yx x

Q y M

x M

= ∂ ∂ + ∂

∂ _(2.27)

Dengan cara yang sama, perjumlahan momen-momen lterhadap sumbu X

menghasilkan

y xy y

Q x M

y M

= ∂ ∂ + ∂ ∂

(2.28)

Penjumlahan semua gaya dalam arah Z menghasilkan persamaan keseimbangan

ketiga:

0 . . .

. +∂ + =

∂

∂ _{dxdy qdxdy}

dy Q dy dx x

Qx y

Yang setelah dibagi oleh dx dy menjadi

q dy

Q

x

Qx +∂ y =− ∂

∂ _(2.30)

Dengan memasukkan persamaan (2.27) dan (2.28) ke persamaan (2.30) dan

memperhatikan bahwa M_xy =M_yx, kita peroleh

q y

M y

x M x

Mx xy y =−

∂ ∂ + ∂ ∂ ∂ + ∂ ∂

2 2 2

2 2

(2.31)

Momen lentur dan puntir dalam persamaan (2.31) tergntung pada regangan, sedang

regangan merupkan fungsi dari komponen perpindahan. Oleh karena itu, langkah

selanjutnya ialah mencari hubungan antara momen dalam dan komponen

perpindahan.

c. Hubungan Antara Tegangan, Regangan, dan Perpindahan

Anggapan bahwa bahan bersifat elastis memungkinkan pemakaian hukum

Hooke dua-dimensi (yang diperoleh dari persamaan (2.19) dengan σz =0),

y x x Eε vσ

σ = + (2.32a)

dan

x y y Eε vσ

σ = + (2.32b)

Yang menghubungkan tegangan dan regangan pada suatu elemen pelat. Subtitusi

persamaan (2.32b) ke persamaan (2.32a) menghasilkan

( )(

x y

)

x v

v E

ε ε

σ +

−

= 2

1 (2.33)

( )(

y x

)

y v

v E

ε ε

σ +

−

= 2

1 (2.34)

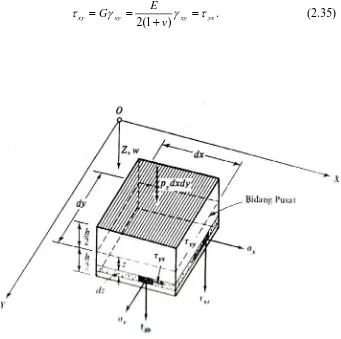
Momen puntir M_xydan M_yxmenimbulkan tegangan sebidang (in-plane shear)τ_xydan

yx

τ (Gambar 2.12), yang berhubungan dengan regangan geser γ melalui persamaan

yang sejenis dengan hukum Hooke Persamaan (2.21), yaitu

yx xy xy

xy

v E

Gγ γ τ

τ =

+ = =

) 1 (

2 . (2.35)

[image:35.595.187.528.228.567.2]

Sumber : Teori dan Analisis Pelat (Szilard, 1989:28)

Gambar 2.12. Tegangan pada suatu elemen pelat

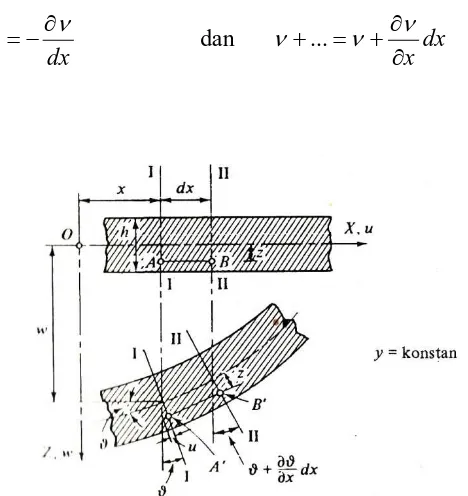
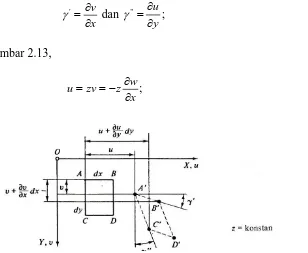
Selanjutnya, ditinjau geometri pelat yang melendut untuk menyatakan

regangan dalam koefesien perpindahan. Dengan mengambil sutu irisan pada nilai y

yang konstan, seperti yang ditunjukkan dalam Gambar 2.13, kita bandingkan

dan 6, yang disebutkan di muka bagian ini, kita bisa nyatakan sut rotasi garis I-I dan

II-II sebagai

dx

ν

ν =−∂ dan dx

x

∂ ∂ + = + ν ν

ν ... (2.36)

[image:36.595.193.427.136.384.2]

Sumber : Teori dan Analisis Pelat (Szilard, 1989:29)

Gambar 2.13. Penampang sebelum dan sesudah berubah bentuk.

Setelah berubah bentuk,panjang suatu deret AB yang terletak pada jarak z dari

bidang pusat menjadi A'B' ( gambar 2.13 ).dengan memakai defenisi regangan yang

diberikan dalam persamaan ( 2.13 ),dapat dituliskan

(

)

[

/

]

_.

' '

x v z dx

dx x v z dx AB

AB B A dx

dx x

∂ ∂ = ∂

∂ + = − = ∆ =

ε ( 2.37 )

Kemudian persamaan pertama disubtitusi dari persamaan ( 2.36 ) ke persamaan ini

akan menghasilkan

,

2 2

x w z x

∂ ∂ − =

ε

(2.38)

.

2 2

y w z y

∂ ∂ − =

ε

(2.39)

Selanjutnya ditentukan distorsi sudut γ_xy =γ'+γ '' dengan membandingkan

segiempat ABCD ( gambar 2.14 ) yang terletak pada suatu jarak konstan zdari

bidang pusat,dengan keadaannya setelah berubah bentuk ' ' ' '

D C B

A pada permukaan pelat yang melendut.Dari kedua segitiga kecil dalam gambar 2.14 dan dari

persamaan ( 2.14 ) jelas terlihat bahwa

x v

∂ ∂ =

'

γ dan

y u ∂ ∂ =

"

γ ; ( 2.40 )

Tetapi dari gambar 2.13,

; x w z zv u

∂ ∂ − =

= (2.41 )

[image:37.595.180.488.284.537.2]

Sumber : Teori dan Analisis Pelat (Szilard, 1989:30 )

Gambar 2.14. Distorsi Sudut.

Dengan cara yang sama,

, y w z v

∂ ∂ − =

y x

w z

xy ∂ ∂

∂ − = +

= ' '' 2

2

γ γ

γ ( 2.42 )

Perubahan kelengkungan pada bidang pusat yang melendut didefenisikan sebagai

,

2 2

x

w

k

_x

∂

∂

−

=

₂ ,

2

y w k_y

∂ ∂ −

= dan

y y

w ∂ ∂∂ = 2

χ ( 2.43 )

Dimana χmenyatakan pemilinan ( warping ) pelat.

d.Gaya dalam yang dinyatakan dalam w

Komponen tegangan σ_x dan σ_y ( gambar 2.12 ) menimbulkan momen lentur

pada elemen pelat dengan cara yang sama seperti pada teori balok dasar. Jadi, dengan

mengintegrasikan komponen tegangan normal, kita peroleh momen lentur yang

bekerja pada elemen pelat:

( )

∫

−+

= ( /2) 2 /

k

k x

x zdz

M σ dan ( 2.44 )

( )

∫

−+

= ( /2) 2 /

k

k y

y zdz

M σ ( 2.44 )

Demikian pula,momen puntir akibat tegangan geser τ = τ_xy = τ_yx dapat dihitung

dari

( ) ( )

∫

−+

= /2 2 /

k k xy

xy zdz

M τ dan

( ) ( )

∫

−+

= /2 2 /

k k yx

yx zdz

M τ ( 2.45 )

Namun τ_xy = τ_yx = τ sehingga M_xy = M_yx.

Jika persamaan ( 2.38 ) dan ( 2.39 ) disubtitusikan ke dalam persamaan ( 2.33 ) dan (

2.34 ),tegangan normal σ_x dan σ_y bisa dinyatakan dalam lendutan lateral

w .Jadi,dapat ditulis sebagai

  



∂ ∂ + ∂ ∂ − −

= 2

2 2

2 2

1 y

w v x

w v

Ez x

σ ( 2.46 )

    ∂ ∂ + ∂ ∂ − − = 2 2 2 2 2 1 x w v y w v Ez y

σ ( 2.47 )

Integrasi persamaan ( 2.44 ), setelah substitusi persamaan di atas σ_x dan σ_y,

menghasilkan

(

)

    ∂ ∂ + ∂ ∂ − − = 2 2 2 2 2 3 1 12 y w v x w v Eh M_x

(

kx vky

)

D y w v x w

D = +

    ∂ ∂ + ∂ ∂ − = 2 2 2 2 ( 2.48) Dan

(

y x

)

y D k vk

x w v y w D

M = +

    ∂ ∂ + ∂ ∂ − − = 2 2 2 2

( 2.49 )

Di mana

(

2

)

3 1 12 v Eh D −

= ( 2.50 )

Menyatakan ketegaran lentur/kekakuan pelat ( flextural rigidity ) pelat. Dengan cara

yang sama,kita peroleh persamaan momen puntir dalam lendutan lateral:

( ) ( ) ( ) ( )

dz

z

y

x

w

G

z

zd

M

M

h h h h yx xy 2 2 / 2 / 2 2 / 2

/

2

∫

∫

−+ + −

∂

∂

∂

−

=

=

=

τ

χ ) 1 ( ) 1 ( 2 v D y x w v

D = −

∂ ∂∂ − − = ( 2.51)

Jika persamaan ( 2.48 ),( 2.49 ) dan ( 2.51 ) disubstitusikan ke persamaan ( 2.31 )

akan menghasilkan persamaan differensial penentu untuk pelat yang memikul beban

D q y

w y

x w x

w

= ∂ ∂ + ∂ ∂∂ + ∂ ∂

4 4 2 2

4 4

4

2 ( 2.52 )

Persamaan ini merupakan persamaan differensial parsial

takhomogen,berorde-empat yang termasuk jenis eliptis dengan koefesien konstan,

yang sering kali disebut persamaan biharmonis takhalogen (szilard,

1989:31).Persamaan (2.52) bersifat linear karena turunan dari w tidak memiliki

eksponen yang lebih besar dari satu.

Selanjutnya, merumuskan gaya geser transversal dalam lendutan lateral. Persamaan (

2.48) dan, (2.49), dan (2.51) disubstitusi ke persamaan (2.27) dan (2.28)

menghasilkan

  



∂ ∂ + ∂ ∂ ∂∂ − = ∂ ∂ + ∂ ∂

= 2

2 2 2

y w x

w x D y

M x

M

Q x yx

x ( 2.53 )

  



∂ ∂ + ∂ ∂ ∂∂ − = ∂ ∂ + ∂ ∂

= 2

2 2 2

y w x

w y D x

M y

M

Q_y y xy ( 2.54 )

2.4 Kondisi Tepi Menurut Teori Lentur

Penyelesaian eksak untuk persamaan pelat ( persamaan 2.52 ) harus juga

memenuhi persamaan differensial tersebut dalam kondisi tepi ( syarat batas ) masalah

pelat tertentu.karena persamaan ( 2.52 ) merupakan persamaan differensial berorde –

empat, dua kondisi tepi, baik untuk perpindahan ataupun untuk gaya-gaya dalam,

diperlukan setiap tepi. Dalam teori lentur pelat, ada tiga komponen gaya dalam yang

harus ditinjau: momen lentur, momen puntir dan gaya geser transversal. Demikian

pula, komponen perpindahan yang harus dipakai dalam perumusan kondisi tepi

adalah lendutan lateral dan kemiringan ( putaran sudut ). Kondisi tepi pelat yang

tersebut. Adapun kondisi tepi yang digunakan dalam pembahasan tugas akhir ini

adalah sebagai berikut :

a. Kondisi tepi geometris ( jepit ). Kondisi geometris tertentu yang diperoleh

berdasarkan besarnya perpindahan ( translasi dan rotasi ) dapat digunakan

untuk merumuskan kondisi tepi dalan bentuk matematis.Misalnya, lendutan

dan kemiringan permukaan pelat yang melendut di tepi jepit( gambar 2.15a )

sama dengan nol, jadi, dapat dituliskan

( )

w _x = 0,  = 0

    

∂ ∂

x x w

( x = 0 atau x = a )

Dan ( 2.55 )

( )

w _y = 0, = 0

   

∂ ∂

y y w

( y = 0 atau y = b )

Kondisi tepi seperti ini disebut kondisi tepi geometris

b. Kondisi tepi statis ( tepi bebas ). Untuk kondisi tepi statis, gaya-gaya tepi

memberikan persamaan matematis yang diperlukan. Misalnya, di tepi bebas suatu pelat yang tidak dibebani ( gambar 2.15b ), kita dapat katakan bahwa momen dan gaya geser transversal ( V ) di tepi tersebut sama dengan nol; jadi,

Sumber : Teori dan Analisis Pelat (Szilard, 1989:33 )

( ) ( )

M_{x x} = V_{x x} = 0 di x = 0 a, ,

Atau ( 2.56 )

( ) ( )

= = 0

y y y

y V

M di x = 0 b, ,

Gaya geser di tepi pelat terdiri dari dua suku,yaitu gaya geser transversal dan

pengaruh momen puntir. Dengan memperhatikan tepi-tepi pelat yang memiliki garis

normal dalam arahX dan Y, gaya tepi per satuan panjang diperoleh sebagai

   

 

∂ ∂∂ − + ∂ ∂ − = ∂ ∂

= 2

3 3

3

) 2 (

y x

w v x

w D y

M Q

V_{x x} xy

( 2.57 )

   

 

∂ ∂∂ − + ∂ ∂ − = ∂ ∂ =

y x

w v y

w D y

M Q

Vy y yx 2

3 3

3

) 2 (

Dimana Q dan _x Qyadalah gaya geser lateral ( persamaan 2.53 dan 2.54 ).Suku kedua

y mxy ∂

∂ / dan ∂myx / ∂y dalam persamaan ( 2.57 ) menyatakan gaya geser

tambahan di tepi tersebut yang diakibatkan oleh momen puntir M_xy = M_yx.Dengan

mengganti momen puntir dengan kopel ekivalen secara statis M_xydy / dy dan

dx dx

M_yx / ( gambar 2.16 ),gaya-gaya ini saling menghapus di elemen elemen yang

bersebelahan,kecuali bagian pertambahannya:

dy y M_xy

∂ ∂

dan dx

x M_yx

∂ ∂

Dengan membagi persamaan ini masing-masing dengan dy dan dx ,kita peroleh

gaya geser tambahan persatuan panjang :

y M

Q_x xy

∂ ∂

= dan

x M

Q_y yx

∂ ∂ =

[image:43.595.227.448.84.282.2]

Sumber : Teori dan Analisis Pelat (Szilard, 1989:34 )

Gambar 2.16. Pengaruh tepi dari momen puntir

Dengan mengganti momen puntir dengan gaya geser ekivalen ini, Kirchhoff

mengurangi jumlah gaya dalam yang harus ditinjau,yakni dari tiga menjadi

dua.Dengan demikian,dari persamaan ( 2.48 ),dan ( 2.49 ), dan ( 2.56 , dan ( 2.57 )

Kondisi tepi bebas adalah :

0

2 2 2

2

=   



∂ ∂ + ∂ ∂

x y

w v x

w

,

(

2

)

₂ 0

3 3

3

=    

 

∂ ∂∂ − + ∂ ∂

x y x

w v x

w

( 2.58 )

Dan

, 0

2 2 2

2

=   



∂ ∂ + ∂ ∂

y x

w v y

w

(

2

)

₂ 0

3 3

3

=    

 

∂ ∂∂ − + ∂ ∂

y y x

w v y

w

(2.59 )

c. Kondisi tepi sederhana.Tepi yang bertumpuan sederhana (gambar 2.15c )

Menghasilkan kondisi tepi campuran. Karena lendutan dan momen lentur di

sepanjang tepi ini melibatkan persamaan yang berkaitan dengan perpindahan

dan gaya. Jadi,

( )

w _x = 0,

( )

₂ 0

2 2

2

=   



∂ ∂ + ∂ ∂ =

x x

x

y w v x

Dan ( 2.60 )

( )

w y = 0,

( )

2 0 2

2 2

=   



∂ ∂ + ∂ ∂ =

y y

y

x w v y

w M

2.5 Deret Fourier dalam Penyelesaian Persamaan Differensial Pelat

Deret Fourier merupakan alat yang ampuh untuk mendapatkan penyelesaian

analitis dari banyak masalah dalam bidang mekanika terapan (applied mechanics ),

seperti penyelesaian persamaan differensial parsial pada teori elastisitas, getaran,

liran panas, transmisi listrik, dan gelombang elektromagnetik. Begitu pula analisa

pelat yang akan dibahas kemudian, yaitu metode M.Levy. Perluasan deret Fourier

menghasilkan integral Fourier dan transformasi Fourier.Walaupun metode terahkir

dianggap alat yang canggih untuk analisis tingkat tinggi, kita tidak akan

menggunakannya disini untuk menyelesaikan masalah pelat agar tidak melampaui

tujuan tulisan ini sebagai pengenalan.

Untuk penyelesaian persamaan differensial dari persamaan yang digunakan

dalam penurunan rumus untuk metode M.Levy, disini hanya digunakan deret Fourier

tunggal untuk mendapatkan penyelesaian analitisnya.

Dalil fourier menyatakan bahwa suatu fungsi sembarang y = f(x)dapat

dinyatakan dengan deret tak-hingga yang terdiri dari suku sinus dan

kosinus.jadi,fungsi semula dapat diganti dengan superposisi sejumlah gelombang

sinus dan kosinus.Jika f(x)adalah fungsi periodik,dalil Fourier menyatakan bahwa

... 2

cos ... 4

cos 2

cos 2

1 )

( = ₀ + ₁ + ₂ + +

T x n A

T x A

T x A

A x

f π π _n π

... 2

sin ... 4

sin 2

sin ₂

1 + + +

+

T x n B

T x B

T x

B π π _n π ( 2.61 )

x n x

n A A

x

f _n cos ω sin ω

2 1 ) (

1 1

0

∑

∑

∞ ∞

+ +

= ( 2.62 )

Dimana A₀, A_n, dan B_n(n = 1,2,3,...)adalah koefesien ekspansi Fourier;ω adalah

T

π ω = 2

(2.63)

[image:45.595.159.475.254.349.2]

Serta Tadalah periode fungsi yang ditinjau ( gambar 2.17 )

Gambar 2.17. Fungsi periodik sembarang

Persamaan ( 2.62 ) berlaku untuk sembarang fungsi periodik beraturan yang

terdiri dari sejumlah segmen ( piecewise ), yang boleh memiliki

diskontinuitas.persamaan ini menyatakan fungsi periodic sembarang f(x) dalam

seluruh jangkauan dari x = −∞ sampai x = +∞ , sehingga disebut ekspansi dengan jangkauan penuh ( full-range expansion).

Koefesien A0, An,dan B dihitung sebagai n

( )

xdx f T A

T

∫

=

0 0

2

( 2.64 )

( )

∫

= T

n f x n x

T A

0

cos 2

ω dx ( 2.65 )

( )

∫

= T

n f x n x

T B

0

sin 2

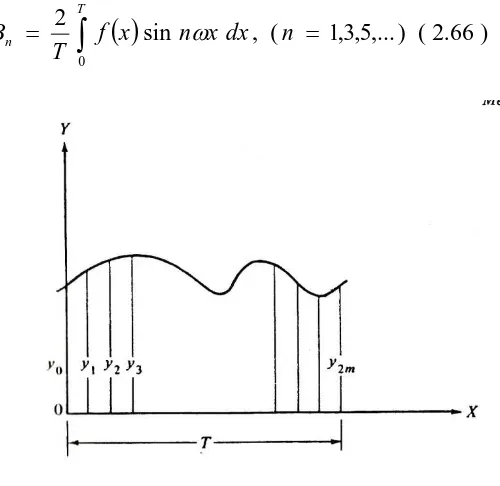
[image:46.595.192.442.87.330.2]

ω dx , (n = 1,3,5,...) ( 2.66 )

Gambar 2.18. Analisis Harmonis

Bila bentuk analitis dari fungsi f(x) tidak diketahui atau terlalu rumit untuk

diintegrasi,kita dapat memanfatkan analitis harmonis yang mengganti integral

dengan penjumlahan.dengan membagi periode T menjadi interval-interval yang

sama sebesar 2m ( lihat gambar 2.18 ),koefesien Fourier bisa ditentukan sebagai

∑

₌−

= 2 1

0 0

1 m

k k y m

A ( 2.67 )

∑

₌−

= 2 1

0

cos

1 m

k k n

m kn y

m

A π ( 2.68 )

Dan

, sin 1 2 1

0 m

kn y

m B

m k

k n

π

∑

₌−

= ( 2.69 )

(k = 0,1,2,...,2mdan n = 1,2,3,...,m )

Metode pendekatan lainnya untuk menghitung konstanta ekspansi Fourier

ialah dengan menggambarkan kurva f(x), f(x) cos

(

2πx /T

)

dan sin

(

2πx /T

)

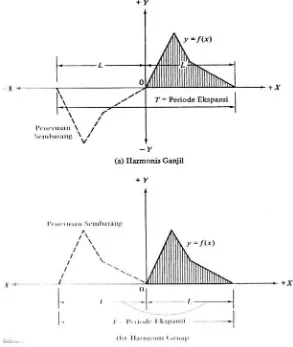
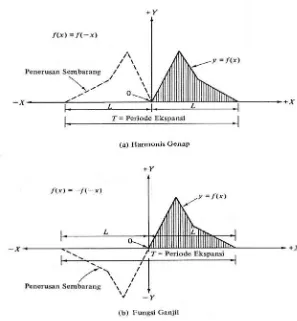
dan

Jika suatu fungsi periodic,fungsi tersebut dapat dibuat periodik dengan

meneruskan fungsi secara sembarang keluar intervalnya.penerusan sembarang ini

dapat berupa harmonis gelap, harmonis ganjil ( gambar 2.19 ), atau genap ganjil (

gambar 2.20). Karena dalam banyak hal tujuan kita adalah menyatakan fungsi

) (x

f hanya pada panjang tertentu L, kita lebih mudah memakai ekspansi

setengah-jangkauan( half-range expansion ) dengan pengulangan interval T=2L dan dengan

mengambail titik awal swbagai pusatnya, seperti diperlihatkan pada gambar 2.20.

Misalkan kita hendak menyatakan fungsi f(x)hanya dalam suku kosinus.

untuk itu, kita tambahkan secara sembarang suatu fugsi genap dalam x pada fugsi

[image:47.595.168.461.371.718.2]

tak- periodik semula ( gambar 2.20a ) , sehingga hubungan

) ( )

(x f x

f = − _(2.70)

berlaku;jadi suku sinus, dalam persamaan ( 2.62 ) menghilang selama

integrasi.demikian pula, dengan membuat fungsi ganjil ( gambar 2.20b ) sehingga

hubungan

) ( )

(x f x

f = − − ( 2.71 )

Berlaku,suku sinus akan hilang dalam integrasi dan akan diperoleh deret

trigonometris sinus dengan cara ekspansi deret Fourier setengah-jangkauan.car

terahkir, karena deret ini mengandung konstanta A₀

[

sebenarnya merupakan suku

kosinus menurut persamaan ( 2.64 ) dan ( 2.65 )

]

dan dapat menyatakan kondisi

tepi geometris bagi tumpuan sederhana, akan sering digunakan dalam penyelesaian

[image:48.595.166.463.399.720.2]

masalah nilai tepi yang sesuai.

Contoh ekspansi deret Tunggal ( Szilard,1989:47 ).

Kita dapat mengekspansikan fungsi pada gambar 2.21 menjadi deret Fourier

[image:49.595.206.430.171.273.2]

dengan tiga ( 3 ) cara :

Gambar 2.21. Fungsi yang akan diekspansikan menjadi deret Fourier

1. Ekspansi jangkauan-penuh,yang mengandung konstanta serta suku sinus dan

kosinus.

2. Ekspansi setengah-jangkauan,yang hanya mengandung suku sinus.

3. Ekspansi setengah-jangkauan,yang hanya mengandung suku kosinus

1 Untuk ekspansi jangkauan-penuh

Periode ekspansi adalah T = 2x₀. Suku konstan diperoleh dari persamaan(

2.64):

∫

=

= 2 0

0 0

0

0 ( )

1 x

f dx x f x

A ( 2.72 )

Dan persamaan( 2.65 )

, 0 cos

) ( 1 2 0

0

0

0

∫

= = x

n dx

x x n x f x

A π (n = 1,2,3...) ( 2.73 )

∫

= 2 0

0

0 0

sin ) (

1 x

n dx

x x n x f x

B π ( )sin 0 0 (cos 1)

0

0 0

0 0

− −

= +

=

∫

π _π nπ

n f dx

x x n x f x

f x

(2.74)

Sehingga diperoleh

π

n f B_n = 2 0

untuk n = 1,3,5,....

( 2.75 )

, 0

= n

B untuk n = 1,3,5,....

Nilai-nilai tersebut disubtitusikan ke persamaan ( 2.62 ), menghasilkan ekspansi

deret Fourier penuh

  

 _{+ + +}

+

= sin 5 ...

5 1 3

sin 3 1 sin

2 2

1 ) (

0 0

0 0

0

x x x

x x

x f

f x

f π π π

[image:50.595.165.493.397.709.2]

π ( 2.76 )

Gambar 2.22a menunjukan kurva tiga suku pertama dari persamaan ( 2.7.6 )

Sumber : Teori dan Analisis Pelat (Szilard, 1989:48 )

2. Berikutnya kita ubah fungsi yang sama ( gambar 2.21 ) menjadi deret

trigonometris yang hanya mengandung suku sinus.untuk itu, digunakan

ekspansi setengah-jangkauan dengan periode T = 4x₀. Kemudian, fungsi ini

secara sembarang diperpanjang melampaui titik pusat sehingga diperoleh

fungsi ganjil ( gambar 2.20b ). Karena fungsi dalam integral f(x) dan

x n x

f( ).cos ω merupakan fungsi ganjil,persamaan ( 2.64 ) dan ( 2.65 )

menghasilkan A₀ = A_n = 0.namun, f(x)sin nωx = F(x)adalah fungsi

genap, dan untuk fungsi genap.

∫

T =

∫

L

dx x F dx

x F

0 ( ) 2 0 ( ) , ( 2.77 )

Dimana T = 2L.Dengan demikian,persamaan ( 2.66 ) menjadi

∫

= L

n dx

L x n x f L B

0 ( )sin ,

2 π

( 2.78 )

Nilai-nilai untuk contoh ini kita subtitusikan ke persamaan ( 2.78 ),kita peroleh

0 2

sin 1

2 sin ) ( 2

2

0 2

0 0 0

0 0

0

0 0

+ =

=

∫

∫

dx

x x n f x dx x

x n x f x

Bn x x

π π

   



 ₋

− =    

  −

= 1

2 cos 2

2 cos

2 ₀

0 0 0

0 0

0

π π

π π

n n

f x

x n n

x x

f x

( 2.79 )

Untuk berbagai nilai n, kita peroleh

, 2 ₀

π

n f

B_n = untuk n= 1,3,5,...

, 4 0

π

n f

Bn = untuk n= 2,6,10,...

, 0

= n

  

  

 

= =

= =

= =

, 4,6,12,... n

untuk , 0 B

, 2,6,10,... n

untuk , n 4f B

1,3,5,..., n

untuk , n 2f B

n

0 n

0 n

π π

( 2.80 )

Dari nilai-nilai diatas dan persamaan ( 2.62 ),kita peroleh

∑

∞

=

1

sin )

(x B n x

f n ω

  

 _{+ + + +}

= ...

2 5 sin 5 1 2

3 sin 3 1 sin

2 sin 2

0 0

0 0

0

x x x

x x

x x

x

f π π π π

[image:52.595.166.522.82.317.2]

π ( 2.81 )

Grafik penjumlahan berbagai suku-suku ini ditunjukan pada gambar 2.22b.

3. Selanjutnya,kita ekspansikan fungsi yang sama ( gambar 2.21 ) ke deret

trigonometris yang hanya mengandung suku kosinus. Kembali, kita akan

gunakan ekspansi setengah-jangkauan dengan periode T = 2L = 4x0. Akan

tetapi, untuk kasus ini, perpanjangan sembarang yang melampaui titik awal

akan menghasilkan suatu fungsi genap seperti yang diperlihatkan pada

gambar 2.20b.

Sekarang, fungsi dalam integral f(x)dan f(x)cosnωxdalam

persamaan (2.64 ) dan ( 2.65 ) merupakan fungsi genap, sedang f(x)sin nωx

dalam persamaan ( 2.66 ) adalah fungsi ganjil. jadi, kita simpulkan bahwa

, 0

= n

B dan dari persamaan ( 2.64 ) dan ( 2.65 ), diperoleh

∫

= L

dx x f L A

0

0 ( )

2

dan 2 ( )cos .

0

∫

= L

n dx

L x n x

f L

A π ( 2.82 )

Dengan demikian,ekspansi Fourier untuk sembarang fungsi genap berperiose 2L

∑

∞

+ =

1

0 cos .

2 1 ) ( L x n A A x

f _n π ( 2.83 )

Penyelesaian untuk koefesien-koefesien menghasilkan

[ ]

∫

= =

= 0 ₀

0 0 0

0 0 0 0 0 x _x f x x f dx x f

A ( 2.84 )

Dan

∫

      = + = 0 0 0 0 0 0 0 0 0 0 0 2 sin 2 0 2 cos 1 x x n x x n n x x f dx x x n f x A π π π (2.85 )       ₋ = 0 2 sin

2 ₀ π

π

n n

f

,

Untuk berbagai nilai n,kita peroleh

       = − = = = = =