ABSTRACT
ON THE MOMENTS, CUMULANTS, AND CHARACTERISTIC FUNCTION OF LOG-LOGISTIC DISTRIBUTION
By
DIAN EKAWATI
The characteristic of a probability distribution such as moment, cumulants, skewness, kurtosis, characteristic function and other are helpful on statistic analysis. This research will examine about moment, cumulant, and characteristic function of log-logistic distribution. Log-log-logistic distribution has two parameters which are α as a shape parameter and β as a scale parameter. The moment of Log-logistic distribution was able to be determined by using moment generating function or definition of its expected value. The cumulants can be determined by moment that had been found before. Furthermore, we are able to determined skewness and kurtosis of log-logistic distribution. Although the characteristic function are retrieved from the expectation of , where i as a imaginary number. The norm value of characteristic function of log-logistic distribution is equal to 1, that means the characteristic function is a monoton function. To observe the curve of the probability density function, skewness, and kurtosis of log-logistic distribution by doing simulation using MATLAB.
MOMEN, KUMULAN, DAN FUNGSI KARAKTERISTIK DARI DISTRIBUSI LOG-LOGISTIK
Oleh
Dian Ekawati
Skripsi
Sebagai Salah Satu Syarat untuk Memperoleh Gelar SARJANA SAINS
Pada
Jurusan Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
MOMEN, KUMULAN, DAN FUNGSI KARAKTERISTIK DARI DISTRIBUSI LOG-LOGISTIK
(Skripsi)
Oleh DIAN EKAWATI
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
RIWAYAT HIDUP
Dian Ekawati, lahir di Bandar Lampung pada tanggal 6 Desember 1992, anak sulung dari tiga bersaudara pasangan Bapak Wardiman Iskandar dan Ibu Sukarsih, kakak dari Rezky Dwi Syaputra dan Nanda Triani Pratiwi
Pada tahun 1997 memulai pendidikan melalui TK Negeri Pembina dan lulus 1 tahun kemudian 1998. Pendidikan sekolah Dasar di SD Negeri 2 Tanjung Gading Bandar Lampung dan lulus pada tahun 2004. Pendidikan sekolah menengah pertama di SMP Negeri 4 Bandar Lampung tercatat lulus pada tahun 2007. Pendidikan sekolah menengah atas di SMA Negeri 3 Bandar Lampung dan lulus pada tahun 2010. Pada tahun 2010 penulis melanjutkan pendidikan ke perguruan tinggi dan terdaftar sebagai mahasiswi Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.
Penulis merupakan anggota Generasi Muda HIMATIKA Himpunan Mahasiswa Jurusan Matematika (HIMATIKA) FMIPA Unila periode 2010/2011, diamanatkan untuk menjadi anggota bidang kesekretariatan HIMATIKA FMIPA Unila periode 2011-2012, dan pada periode 2012-2013 menjadi Kepala Biro Kesekretariatan HIMATIKA FMIPA Unila.
Moto :
“Lakukan pekerjaanmu dengan jiwa yang tenang dan
bersungguh-sungguh
“
(Dian Ekawati)“Maka sesungguhnya setelah kesulitan itu ada kemudahan”
(Q.S. Al-Insyirah : 5)
“
Semua kejadian baik dan besar yang kita sebut keberhasilan itu,
dicapai dengan menaiki tangga yang dibangun dari
PERSEMBAHAN
Segala puji hanya milik Allah SWT atas rahmat, nikmat dan kasih-Nya yang tiada pernah berhenti diberikan kepadaku selama ini. Shalawat serta salam selalu tercurah
kepada Nabi besar Muhammad SAW.
Ku persembahkan karya ini sebagai tanda bakti kepada Ayah, Mama, Nenek dan kedua Adik tercinta. Terima kasih atas kasih sayang, doa, dan dukungannya yang
selalu mengiringi hariku.
Sahabat-sahabat terkasih yang canda dan tawanya selalu menemani, setia saat berkeluh kesah. Terima kasih untuk semua semangatnya.
Semua orang yang mengasihiku dimana pun.
SANWACANA
Alhamdulillahi robbil ‘alamin, puji dan syukur kepada Allah SWT yang telah memberikan ridho-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul
“Momen, Kumulan, dan Fungsi Karakteristik dari Distribusi Log-logistik”.
Shalawat beriring salam selalu tercurah kepada suri tauladan umat islam, Nabi Muhammad SAW
Pada proses penyusunan skripsi ini, penulis memperoleh banyak bimbingan, kritik, dan saran yang membangun sampai akhirnya skripsi ini selesai. Untuk itu penulis mengucapkan terima kasih kepada:
1. Bapak Warsono, Ph.D, selaku dosen pembimbing I telah membimbing dan memberikan masukkan kepada penulis dalam menyelesaikan skripsi ini. 2. Ibu Dian Kurniasari, S.Si, M.Sc., selaku dosen pembimbing II yang telah
banyak membantu, mengarahkan, dan selalu sabar dalam membimbing penulis sehingga skripsi ini dapat diselesaikan.
4. Ibu Dra. Dorrah Azis, sebagai pembimbing akademik yang telah mendampingi penulis selama menempuh pendidikan di Jurusan Matematika FMIPA Universitas Lampung..
5. Bapak Drs. Tiryono Ruby, M.sc, Ph.D, selaku Ketua Jurusan Matematika FMIPA Universitas Lampung.
6. Bapak Prof. Suharso, Ph.D, selaku Dekan FMIPA Universitas Lampung. 7. Seluruh dosen, staff, dan karyawan jurusan Matematika FMIPA Universitas
Lampung yang telah membantu dalam proses penyelesaian skripsi ini.
8. Bapak Wardiman dan Ibu Sukarsih sebagai orang tua yang tak pernah lelah mencurahkan kasih saying, doa, dan dukungannya kepada penulis hingga saat ini. Teruntuk Rezky dan Nanda sebagai adik yang telah memotivasi penulis selama ini.
9. Sahabat-sahabat tercinta, Ambar, Dinda, Engine, Tri, Miftah, Abang Karim, Sofyan, Edo, Rohandi, dan yang seperjuangan Indri, yang telah menghadirkan perjalanan hidup yang indah bagi penulis.
10.Teman-teman seperjuangan bimbingan bersama, Apit, Indri, Miranti, Tiara, Tiurma, dan Fransiska.
11.Sepupu, Om, Tante, dan Nenek atas dukungannya. Khusus untuk mbak Tika atas pengalaman dan bantuannya.
12.Teman-teman angkatan Matematika 2010 atas kebersamaannya selama menempuh pendidikan di Jurusan Matematika FMIPA Universitas Lampung. 13.Kakak tingkat dan Adik tingkat atas segala bentuk perhatiannya kepada
14.Teman-teman seperjuangan di HIMATIKA atas pengalaman hidup berharga bagi penulis.
15. Seluruh pihak yang telah membantu dalam penyusunan skripsi ini sehingga skripsi ini dapat diselesaikan dengan baik.
Bandar lampung, Juli 2014 Penulis
DAFTAR ISI
1.3 Tujuan Penelitian………...2
1.4 Manfaat Penelitian ………3
II. TINJAUAN PUSTAKA 2.1 Distribusi Log-logistik………...4
2.2 Fungsi Beta ………5
2.3 Ekspansi Deret Maclaurin ………6
2.4 Ekspektasi Dari Variabel Acak………..8
2.5 Fungsi Pembangkit Momen………...9
2.6 Momen……….10
2.7 Kumulan………...11
2.8 Kemiringan ………..12
2.10 Fungsi Karakteristik……….14
III. METODOLOGI PENELITIAN 3.1Waktu dan Tempat Penelitian……….16
3.2Metodologi Penelitian……….16
IV. HASIL DAN PEMBAHASAN 4.1Fungsi Pembangkit Momen dari Distribusi Log-logistik………17
4.2Momen Ke-R ………...21
4.3Ekspektasi dari Distribusi Log-logistik………...26
4.3.1 Ekspektasi Pertama………..27
4.3.2 Ekspektasi Kedua……….28
4.3.3 Ekspektasi Ketiga………29
4.3.4 Ekspektasi Keempat………30
4.3.5 Ekspektasi Ke-R………..32
4.4Kumulan ……….33
4.5Kemiringan……….35
4.6Kurtosis………...36
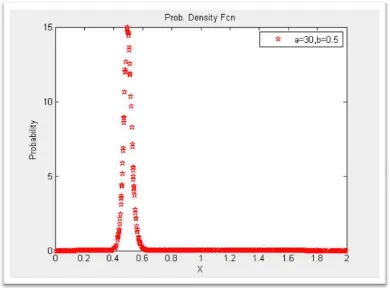
4.8Simulasi Grafik Fungsi Distribusi Log-logistik………..51
4.8.1 Fungsi Kepekatan Peluang………...51
4.8.2 Fungsi Kemiringan………...59
4.8.3 Fungsi Kurtosis ………...65
DAFTAR GAMBAR
Gambar Halaman
1. GrafiKFungsiKepekatanPeluangDistribusiLog-logistik………5 2. GrafiKFungsiKepekatanPeluangDistribusiLog-logistikDengan α Tetap
βMeningkat………..52 3. GrafiKFungsiKepekatanPeluangDistribusiLog-logistikDengan α Tetap
βMenurun……….53
4. GrafiKFungsiKepekatanPeluangDistribusiLog-logistikDengan α
Meningkat β Tetap………54 5. GrafiKFungsiKepekatanPeluangDistribusiLog-logistikDengan α
Menurun β Tetap ………..55 6. GrafiKFungsiKepekatanPeluangDistribusiLog-logistikDengan α
Meningkat β Meningkat ………..56 7. GrafiKFungsiKepekatanPeluangDistribusiLog-logistikDengan α
Meningkat β Menurun………...57 8. GrafiKFungsiKepekatanPeluangDistribusiLog-logistikDengan α
1
I. PENDAHULUAN
1.1 Latar Belakang
Distribusi log-logistik adalah distribusi peluang dari variabel acak yang logaritmanya memiliki distribusi logistik. Distribusi ini memiliki kesamaan bentuk dengan distribusi log-normal tetapi memiliki ekor yang lebih berat. Dalam statistik, distribusi log-logistik (dikenal sebagai distribusi risk dibidang ekonomi) merupakan distibusi peluang kontinu untuk variabel acak tak-negatif. Sebagai contoh angka kematian akibat diagnosis kanker atau perawatan, berikutnya juga telah digunakan dalam hidrologi untuk model debit air dan curah hujan dan dalam ekonomi sebagai model sederhana dari distribusi kekayaan atau pendapatan.
2
sering digunakan untuk menentukan karakteristik dari suatu distribusi peluang. Fungsi karaktersitik juga dapat digunakan untuk menentukan momen dan selanjutnya dengan momen dapat menentukan kumulan untuk suatu distribusi peluang.
Karakteristik dari suatu distribusi ini berguna untuk analisis selanjutnya. Berdasarkan latar belakang tersebut penulis tertarik untuk mengkaji tentang momen, kumulan, dan fungsi karakteristik dari distribusi log-logistik (α,β).
1.2 Batasan Masalah
Karakteristik populasi dari suatu distribusi yang memiliki fungsi kepekatan peluang dapat dicari melalui fungsi pembangkit momen distribusi tersebut. Sehingga tahap awal dalam penelitian ini adalah menentukan fungsi pembangkit momen dari distribusi log-logistik dan selanjutnya dari fungsi pembangkit momen itu ditentukan karakteristik dari distribusi log-logistik (α,β). Dalam penelitian ini penulis membatasi hanya mencari momen yang selanjutnya dapat menentukan rataan, varians, dll, kumulan, dan fungsi karakteristik dari distribusi log-logistik (α,β).
1.3 Tujuan Penelitian
Adapun tujuan dari penelitian ini adalah sebagai berikut:
3
2. Mencari kumulan dan fungsi karakteristik dari distribusi log-logistik (α,β).
1.4Manfaat Penelitian
Manfaat yang dapat diperoleh dari penelitian ini adalah sebagai berikut:
1. Memberikan panduan dan sumbangan pemikiran kepada peneliti lain tentang cara mencari momen dari distribusi log-logistik (α,β).
4
II. TINJAUAN PUSTAKA
Dalam bab ini akan dijelaskan mengenai teori-teori yang mendukung dalam menentukan momen, kumulan, dan fungsi karakteristik dari distribusi log-logistik (α,β).
2.1 Distribusi Log-Logistik
Distribusi log-logistik adalah distribusi peluang dari variabel acak yang logaritmanya memiliki distribusi logistik. Distribusi log logistik dengan 2 parameter yaitu α sebagai parameter bentuk dan β sebagai parameter skala
Definisi 2.1
Variabel acak X dikatakan mengikuti distribusi log-logistik dengan parameter bentuk α danparameter skala β, dilambangkan dengan X LL (α,β), jika fungsi
kepekatan peluang (fkp) diberikan sebagai berikut :
5
Gambar 1. Grafik Fungsi Kepekatan Peluang Distribusi Log-logistik
(Asha Dixit, 2008)
Sub-bab selanjutnya akan membahas tentang fungsi Beta yang akan digunakan dalam penelitian ini untuk menyelesaikan bentuk integral tertentu dalam mencari karakteristik dari distribusi log-logistik.
2.2 Fungsi Beta
Fungsi Beta digunakan untuk mengevaluasi integral tentu, sehingga dalam
penelitian ini sangat diperlukan untuk mengevaluasi integral tentu yang terbentuk dalam mencari momen. Fungsi Beta disimbolkan dengan .
6
Definisi 2.2
Fungsi Beta dengan parameter a dan b
Dengan .
(Milton Abramowitz dan Irene A. Stegun, 1972)
Selain fungsi Beta untuk mengevaluasi integral tentu yang terbentuk,
selanjutnya diperlukan ekspansi deret Maclaurin dalam menemukan momen dari distribusi log-logistik yang akan dibahas pada sub-bab selanjutnya.
2.3 Ekspansi Deret Maclaurin
Deret Maclaurin merupakan deret Taylor yang berpusat di titik nol. Deret ini digunakan untuk meleburkan bentuk dalam persamaan momen yang akan dicari dalam penelitian ini.
Teorema Deret Maclaurin
Misalkan f adalah fungsi di mana turunan ke (n+1). (x), ada untuk setiap x
pada suatu selang terbuka l yang mengandung Jadi, untuk setiap x di dalam l
berlaku : (2.1)
Persamaan (2.1) disebut sebagai ekspansi deret Taylor bagi fungsi Jika maka bentuk deret pada persamaan (2.1) menjadi :
7
Dan bentuk deret pada persamaan (2.2) disebut sebagai ekspansi deret Maclaurin bagi fungsi
Dengan mengandung persamaan (2.2) maka fungsi dapat diuraikan menjadi bentuk deret sebagai berikut:
=1
=
=
Sehigga diperoleh:
(2.3)
Fungsi dapat diuraikan menjadi bentuk deret sebagai berikut:
(2.4)
Fungsi dapat diuraikan menjadi bentuk deret seperti berikut:
(2.5)
(Leithold,1978)
8
2.4 Ekspektasi dari Variabel Acak
Sifat-sifat dari suatu distribusi dapat dikaji dengan bantuan ekspektasi matematika atau nilai harapan.
Definisi 2.3
Misal X variabel acak yang mempunyai fungsi kepekatan peluang sedemikian sehingga memiliki konvergensi mutlak tertentu, yaitu dalam kasus diskrit,
ada, Atau, dalam kasus kontinu,
ada,
Ekspektasi dari variabel acak adalah
, dalam kasus diskrit Atau
, dalam kasus kontinu
(Hogg and Craig, 1965)
9
2.5 Fungsi Pembangkit Momen
Fungsi pembangkit momen digunakan untuk menghitung momen dari variabel acak X. Fungsi pembangkit momen disimpulkan dengan , definisinya sebagai berikut:
Definisi 2.4
Misalkan ada sejumlah angka positif h sehingga untuk ekspektasi ada. Sehingga
Jika x merupakan variabel acak kontinu, atau
Jika x merupakan variabel acak diskrit. Ekspektasi ini disebut fungsi pembangkit momen (FPM) dari X (atau dari distribusi) dan dilambangkan dengan M(t), yaitu
(Hogg and Craig, 1965)
Selanjutnya dari fungsi pembangkit akan ditentukan momen-momen dari distribusi log logistik (α,β) dan pada sub-bab setelah ini akan dijelaskan tentang
10
2.6 Momen
Rataan dan varians sebenarnya merupakan hal istimewa dari kelompok ukuran lainnya yang disebut momen. Dari momen ini beberapa ukuran lain dapat diturunkan. Momen itu sendiri didefinisikan sebagai berikut:
Definisi 2.5
Momen ke-r tentang asal-usul dari suatu variabel acak X, dilambangkan dengan , adalah nilai harapan dari Xr dituliskan,
Untuk pada saat X diskrit
Pada saat X kontinu.
(Irwin Miller, Marrylees Miller, 1999)
Selain momen terdapat karakteristik lainnya dari suatu distribusi, dalam penelitian ini karakteristik lain yang akan dicari yaitu kumulan. Definisi dari kumulan akan di uraikan pada sub-bab selanjutnya.
2.7 Kumulan
11
ditentukan sebelumnya. Adapun definisi dari kumulan akan dijelaskan di bawah ini:
Definisi 2.6
Kumulan didefinisikan sebagai
ln
Dengan menggunakan deret Maclaurin maka didapat :
ln
+ )+
Dimana momen baku, maka dapat dituis kembali sebagai ;
. .
12
Rata-rata dan ukuran penyebaran dapat menggambarkan distribusi data tetapi tidak cukup untuk menggambarkan sifat distribusi. Untuk dapat menggambarkan karakteristik dari suatu distribusi data digunakan konsep lain yang dikenal sebagai kemiringan dan keruncingan. Dua sub-bab selanjutnya akan membahas tentang kemiringan dan keruncingan.
2.8 Kemiringan
Kemiringan atau kecondongan (skewness) adalah tingkat ketidaksimetrisan atau kejauhan simetri dari sebuah distribusi. Sebuah distribusi yang tidak simetris akan memiliki rata-rata, median, dan modus yang tidak sama besarnya.
Skewness dari suatu variabel random X yang dinotasikan dengan Skew[X] didefinisikan sebagai:
Skewness ini juga dinamakan skewness populasi. Skewness merupakan ukuran dari
kesimetrisan atau lebih tepatnya kekurang-simetrisan. Suatu distribusi dikatakan simetris jika distribusi tersebut nampak sama antara sebelah kanan dan sebelah kiri titik pusatnya. Distribusi yang simetris misalnya distribusi normal, distribusi t dan distribusi seragam. Distribusi yang mempunyai skewness positif misalnya distribusi eksponensial, distribusi Chi-kuadrat, distribusi Poisson dan distribusi Binomial dengan p > 0.5 sedangkan distribusi yang mempunyai skewness negatif misalnya distribusi Binomial dengan p < 0.5.
13
Selanjutnya akan dibahas mengenai keruncingan kurva yang nantinya akan dilakukan simulasi dengan aplikasi program Matlab terhadap formula keruncingan yang didapat.
2.9 Kurtosis
Kurtosis (keruncingan distribusi data) adalah ukuran tinggi rendahnya puncak dari suatu ditribusi.
Definisi 2.7
Momen keempat terhadap rataan, , bila dibagi dengan disebut kurtosis distribusi X dan sering dinyatakan dengan :
(Dudewicz, J. Edward, 1995)
Pada sub-bab terakhir akan dijelaskan tentang fungsi karakteristik dari suatu distribusi peluang.
2.10 Fungsi Karakteristik
14
distribusi dari suatu variabel acak yang dikenal sebagai teorema inversi fungsi karakteristik. Fungsi karakteristik merupakan salah satu sifat yang menjadi ciri khas dari suatu distribusi. Fungsi karakteristik dari suatu variabel acak X, dinotasikan dengan , didefinisikan sebagai berikut:
Diperkenalkan fungsi karakteristik
sebagai fungsi pembangkit momen.
Ingat, ditingkat pertama bahwa selalu ada, karena
Jadi, mendefinisikan terpisah konvergensi mutlak. Selanjutnya, F adalah kontinu seragam dalam t dan waktu j terdiferensialkan di bawah tanda integral jika ekspresi yang dihasilkan ada dan konvergen seragam, yang sudah cukup bahwa vj ada. Untuk itu,
adalah nyata jika dan hanya jika f simetris.
(Kendall M.G, 1977)
15
Definisi 2.7
Misalkan X variabel acak dan t sembarang bilangan asli. Maka,
Merupakan variabel acak kompleks.
Ekspektasi ada untuk setiap t dan untuk setiap variabel acak dan ini
III. METODOLOGI PENELITIAN
3.1 Waktu daan tempat Penelitian
Penelitian ini dilakukan di Jurusan Matematika Fakultas Matematiks dan Ilmu Pengetahuan Alam Universitas Lampung pada semester genap tahun akademik 2013-2014.
3.2 Metodologi Penelitian
Metode penelitian yang digunakan dalam penyusunan skripsi ini adalah studi kepustakaan yaitu dengan menggunakan buku-buku penunjang, skripsi, dan jurnal yang mendukung dengan skripsi ini. Adapun langkah-langkah dalam penelitian ini adalah sebagai berikut :
1. Mengumpulkan buku-buku penunjang, skripsi, dan jurnal tentang distribusi log logistik (α,β) serta materi pendukung lainnya.
2. Mencari fungsi pembangkit moment dari distribusi log-logistik (α,β). 3. Mencari moment dan ekspektasi dari distribusi log-logistik (α,β).
4. Mencari cumulans dan fungsi karakteristik dari distribusi log-logistik (α,β). 5. Melakukan simulasi bentuk kurva fungsi kepekatan peluang, kemiringan, dan
69
V. KESIMPULAN
Berdasarkan hasil penelitian yang telah dilakukan dapat diperoleh kesimpulan sebagai berikut:
1. Diperoleh momen ke-r dari distribusi log-logistik (β,α) adalah
2. Cumulans dari distribusi log-logistik (β,α) adalah
70
Keruncingan dari distribusi log-logistik (β,α) adalah
DAFTAR PUSTAKA
Abromowits,M. and Stegun, I.A.(Eds).1972.Handbook of Mathematical Functions with Formulas, Graps, and Mathematical Tables, 9th printing. New York:
Dover,p.928.
De Gunst, M. C. M. 1994. Statistische Data Analyse, Faculteit Wiskunde en Informatica. Amsterdam: Vrije Universiteit.
Dixit, Asha. 2008. Exact Comparison of Hazard Rate Functions of Log-Logistic Survival Distributions. Alabama: Auburn University.
Dudewicz, J Edward and Mishra, N. Satya. 1995. Statistika Matematika Modern. Bandung: ITB Bandung.
Hogg, V Robert. and Craig, T Allen. 1965. Introduction to Mathematical Statistic Fifth Sdition. New Jersey: The United States of America.
Kendall, M.G, and Stuart, A. 1977. The Advanced Theory of Statistics (Vol I). New York: MacMillan.
Leithold. 1978. The Calculus. New York: Harper and Row.
Lukacs, E and Laha, R.G.1964. Applications of characteristic Functions. New York: Hafner Publishing Company.