ABSTRAK
REPRESENTASI DAN PENENTUAN BANYAKNYA GRAF BERLABEL TANPA SISI PARALEL
BERORDE MAKSIMAL EMPAT
Suatu graf G (V,E) adalah suatu struktur yang terdiri dari himpunan titik V; V dan himpunan sisi E dan graf G dikatakan terhubung jika untuk setiap dua titik di G, terdapat path yang menghubungkan kedua titik tersebut. Jika tidak ada path yang menghubungkan maka G dikatakan tidak terhubung. Jika suatu graf hanya titik-titiknya diberi label maka pelabelan disebut pelabelan titik. Sisi paralel adalah dua sisi atau lebih yang memiliki dua titik yang sama. Jika diberikan n titik dan m sisi, terdapat banyak graf yang dapat dibentuk, baik terhubung atau tidak terhubung. Penelitian ini dilakukan dengan tujuan untuk menentukan banyak graf berlabel tanpa sisi paralel dan membangun sistem untuk perhitungannya jika diberikan 1 n 4 dan m 1 , dengan bentuk atau rumus umum untuk graf yang
ABSTRACT
REPRESENTATION AND COUNTING THE NUMBER OF LABELLED GRAPHS WITH MAXIMUM ORDER IS FOUR
WITHOUT PARALLEL EDGES
A graph G (V, E) is a structure that consists of the set of vertices V; V and the set of edges E and a graph G is said to be connected if for every pair of vertices in G, there is a path connecting them. If only every vertex is labeled then the graph is called as graph with vertex labelling, if only every edge is labeled then graph is called as edge labelling; and if both vertices and edges are labeled then the graph is called graph with total labelling. Parallel edges are two edges or more that have the same end points. The aim of this research is to determine the number of labeled graphs without parallel edges and establish a system for
REPRESENTASI DAN PENENTUAN BANYAKNYA
GRAF BERLABEL TANPA SISI PARALEL
BERORDE MAKSIMAL EMPAT
Oleh
Permata
Tesis
Sebagai Salah Satu Syarat Untuk Memperoleh Gelar
Magister Sains
Pada
Jurusan Matematika Program Studi Magister Matematika
Fakultas Matematika Dan Ilmu Pengetahuan Alam
MAGISTER MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
RIWAYAT HIDUP
Penulis dilahirkan di Lampung tepatnya di Kota Bumi pada 29 Maret 1982, dan berasal dari keluarga sederhana yang merupakan anak pertama dari dua bersaudara pasangan bapak Husin Thalib dan ibu Nurmaya. Pendidikan formal yang pernah ditempuh :
1. Sekolah Dasar Negeri 3 Labuhan Ratu pada tahun 1989-1994
2. Sekolah Menengah Pertama Negeri 20 Bandar Lampung pada tahun 1994-1997 3. Sekolah Menengah Atas Negeri 1 Bandar Lampung pada tahun 1997-2000 4. S1 Matematika di FMIPA Universitas Lampung pada tahun 2000-2005
PERSEMBAHAN
MOTTO
“Sesungguhnya orang-orang yang beriman dan mengerjakan kebajikan, niscaya diberi petunjuk oleh Allah karena keimanannya. Mereka di dalam surga yang
penuh kenikmatan, mengalir di bawahnya sungai-sungai”
SANWACANA
Alhamdulillah segala puji hanya bagi Allah SWT, dan sholawat serta salam senantiasa tercurah kepada nabi Muhammad SAW sehingga penulis dapat menyelesaikan pendidikan S2 dengan gelar Magister Sains di Universitas Lampung.
Penulis menyadari bahwa penulisan tesis ini tidak terlepas dari bantuan dan doa dari semua pihak. Terimakasih penulis ucapkan kepada :
1. Ibu Dra. Wamiliana, M.A, Ph.D selaku pembimbing pertama yang begitu sabar dalam membimbing dan memberikan semangat dalam menyelesaikan tesis ini.
2. Ibu Dr. Asmiati, S.Si., M.Si selaku pembimbing kedua yang memberikan semangat dan juga masukan dalam penulisan tesis ini.
3. Bapak Dr. Muslim Ansori, S.Si., M.Si selaku pembahas dan Pembimbing Akademik yang telah memberikan bimbingan dan motivasi.
4. Bapak Drs. Mustofa Usman, M.A., Ph.D, selaku Ketua Program Studi yang telah memberikan motivasi.
5. Bapak Drs. Tiryono Ruby, M.Sc, Ph.D selaku Ketua Jurusan Matematika yang baik hati.
7. Teman-teman Perguruan Tinggi Teknokrat atas dukungan dan bantuannya selama menyelesaikan studi ini.
8. Sahabat-sahabat terbaikku dan seperjuangan Zaenal dan Maskadi yang telah banyak membantu sejak awal melanjutkan studi S2 ini.
9. Teman-teman seperjuangan The First Generation Pak Anton, Pak Edy, Ibu Ike, Ibu Ayu, Mba Dwi, Mba Ade, Mba Herly, Mas Kris, Mas War, Mas Malik, Mas Rahman, Mba Ana, Agus, Cut, Fita, Nurman, Suly, Ayu, Viviana, Rini yang selalu menjalin kerjasama dan kebersamaan dalam sedih maupun senang, pengalaman yang takterlupakan.
Penulis menyadari tesis ini masih jauh dari kesempurnaan sehingga saran maupun kritik yang membangun sangat diharapkan. Semoga tulisan ini dapat memberikan manfaat dan semoga Allah SWT memberikan balasan yang lebih baik dan keberkahan kepada semua pihak yang telah membantu selesainya studi ini. Aamiin Yaa Robbal ‘Alamin.
Bandar Lampung, 25 Januari 2016
Penulis
DAFTAR ISI
Halaman
DAFTAR ISI
DAFTAR GAMBAR
DAFTAR TABEL
DAFTAR LAMPIRAN
I. PENDAHULUAN
1.1 Latar Belakang ... 1
1.2 Batasan Masalah ... 3
1.3 Tujuan Penelitian ... 3
1.4 Manfaat Penelitian ... 4
II. LANDASAN TEORI 2.1. Konsep Dasar Graf ... 5
2.2. Konsep Dasar Barisan ... 10
2.2. Konsep Dasar Pencacahan ... 11
III. METODE PENELITIAN 3.1. Waktu dan Tempat Penelitian ... 15
3.2. Penelitian yang telah dilakukan ... 15
IV. HASIL DAN PEMBAHASAN
4.1. Konstruksi Graf Berlabel Tanpa Sisi Paralel ... 19 4.2. Bentuk Umum Graf Berlabel Tanpa Sisi Paralel ... 28 4.3. Representasi Graf Berlabel Tanpa Sisi Paralel ... 57
V. PENUTUP
5.1. Kesimpulan ... 62 5.2. Saran ... 64
DAFTAR PUSTAKA
DAFTAR GAMBAR
Halaman
Gambar 1. Contoh graf dengan 4 titik dan 6 sisi ... 5
Gambar 2. Contoh graf dengan 1 titik pendant dan 1 titik terasing ... 6
Gambar 3. Contoh subgraf H dari graf G ... 6
Gambar 4. Contoh spanning subgraf H dari graf G ... 7
Gambar 5. Contoh isomorfis graf G1 dan G2 ... 7
Gambar 6. Contoh graf dengan salah satu walk ... 8
Gambar 7. Contoh graf dengan salah satu path ... 8
Gambar 8. Contoh graf dengan salah satu loop dan sisi paralel ... 8
Gambar 9. Contoh graf sederhana dan terhubung ... 9
Gambar 10. Contoh digraf dengan 4 titik ... 9
Gambar 11. Contoh tree dan spanning tree ... 9
Gambar 12. Flowchart Program ... 58
Gambar 13. Flowchart Fungsi Kombinasi ... 59
Gambar 14. Tampilan Perhitungan Graf Berlabel Tanpa Sisi Paralel ... 60
DAFTAR TABEL
Halaman
DAFTAR LAMPIRAN
Lampiran 1. Tabel Konstruksi Graf Berlabel Tanpa Sisi Paralel
I. PENDAHULUAN
1.1Latar Belakang
Perkembangan ilmu pengetahuan pada saat ini sangat pesat dalam bidang sains dan teknologi. Teori graf yang merupakan bidang ilmu matematika yang banyak digunakan dalam merepresentasikan permasalahan atau kondisi di kehidupan sehari-hari, khususnya dalam permasalahan desain jaringan dan terapan komputasi, misalnya : desain jaringan komputer, desain jaringan telekomunikasi, desain jaringan transportasi, desain jejaring sosial, dan lain-lain.
Secara sederhana, graf merupakan suatu diagram yang memuat informasi tertentu jika diinterpretasikan secara tepat. Dalam kehidupan sehari-hari, graf digunakan untuk menggambarkan berbagai macam struktur yang ada. Tujuannya adalah sebagai visualisasi objek-objek agar lebih mudah dimengerti. Teori graf dikemukan oleh seorang matematikawan Swiss, Leonhard Euler pada tahun 1736 sewaktu menyelesaikan masalah jembatan Konigsberg (Konigsberg Problem) yaitu bagaimana melewati tujuh jembatan yang menghubungkan daratan dan dibelah oleh sungai Pregel di Polandia masing-masing tepat satu kali dan kembali ketempat semula. Daratan yang dihubungkan oleh jembatan dinyatakan sebagai titikdan jembatan dinyatakan sebagai sisi.
2
jembatan yang menghubungkan daratan berjumlah ganjil, tetapi sebaliknya hal ini dapat terjadi jika banyaknya jembatan yang menghubungkan masing-masing daratan adalah berjumlah genap.
Suatu graf G(V,E) dengan V adalah suatu himpunan titik yang tidak boleh kosong dan E adalah himpunan sisi yang boleh kosong. Graf dikatakan terhubung jika terdapat path (lintasan) antara sebarang dua titik di graf G. Sisi paralel adalah dua atau lebih sisi yang menghubungkan dua titik yang sama dalam suatu graf dan loop adalah suatu sisi yang memiliki titik awal dan titik akhir yang sama.
Graf berlabel adalah suatu graf yang tiap titiknya dan atau sisinya memiliki label berupa bilangan asli. Jika suatu graf hanya titiknya diberi label maka pelabelan disebut pelabelan titik. Jika suatu graf hanya sisinya diberi label maka pelabelan disebut pelabelan sisi. Jika suatu graf titiknya dan sisinya diberi label maka pelabelan disebut pelabelan total.
Jika diberikan n titik dan m sisi; dengan n 1 dan m 1 , maka banyak graf yang dapat terbentuk, diantaranya adalah graf tak terhubung dan graf terhubung, dengan graf yang terbentuk memiliki loop dan atau sisi paralel didalamnya.
Adapun penelitian-penelitian yang telah dilakukan sebelumnya mengenai penentuan banyaknya suatu graf baik berupa graf tak terhubung berlabel dan graf terhubung berlabel, antara lain:
3
2. Arifah (2015), meneliti tentang penentuan banyaknya graf terhubung berlabel jika diberikan n titik, m sisi tanpa sisi paralel. Untuk n3 dan
Penelitian ini dimaksudkan untuk menentukan banyaknya graf berlabel (graf tidak terhubung dan graf terhubung) tanpa sisi paralel untuk n 1 dan m 1 serta membangun sistem untuk menghitung banyaknya graf tersebut.
1.2 Batasan Masalah
Pada penelitian ini akan dibatasi pada graf berlabel, khususnya pelabelan titik tanpa sisi paralel untuk 1 n 4dan m 1 .
1.3Tujuan Penelitian
Tujuan dari penelitian ini adalah:
4
2. Menentukan bentuk umum graf berlabel tanpa sisi paralel yang telah terbentuk.
1.4Manfaat Penelitian
Manfaat dari penelitian ini adalah:
1. Menambah pemahaman konsep teori graf dan aplikasinya khususnya tentang penentuan graf berlabel yang terbentuk.
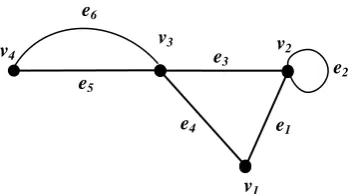
Gambar 1. Contoh graf dengan 4 titikdan 6sisi e1
e5
e3 e
2
e4
v3 v2
v1
v4
e6
II. LANDASAN TEORI
Pada bab ini akan diberikan beberapa istilah, definisi serta konsep-konsep yang mendukung dalam penelitian ini.
2.1 Konsep Dasar Teori Graf
Berikut ini akan diberikan konsep dasar teori graf yang bersumber dari Gross dkk (2014):
Suatu graf G = (V,E), beranggotakan dua himpunan V dan E, dengan anggota dari V disebut titik dari G dan anggota E disebut sisi dari G. Himpunan V adalah himpunan tak kosong yang berhingga dan himpunan E adalah himpunan dari satu atau dua titik dari V.
6
tersebut terhubung oleh sisi yang sama. Banyaknya n titik atau V n pada graf G disebut urutan atau orde dan banyak m sisi atau E m pada graf G disebut ukuran atau size. Untuk contoh dari Gambar 1 terlihat bahwa sisi e5, e6 menempel
pada titik v4 serta untuk titik v1 bertetangga dengan v2 dan v3.
Derajat (degree) dari suatu titik v pada graf G dinotasikan sebagai deg(v), adalah banyaknya sisi yang menempel pada titik v dengan loop terhitung dua. Untuk contoh dapat terlihat pada Gambar 1 bahwa deg(v1)= 2, deg(v2)= 4, deg(v3)= 4
dan deg(v4)= 2.
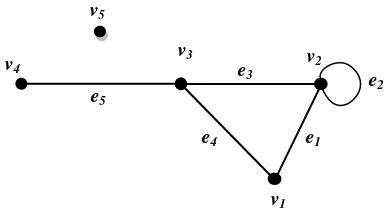
Titik terasing merupakan titik yang memiliki derajat nol, sedangkan titik pendant atau titik ujung adalah titik yang memiliki derajat satu. Untuk contoh pada Gambar 2 terlihat titik v4 merupakan titik pendant dan titik v5 merupakan titik
terasing.
Suatu subgraf dari graf G adalah graf H dengan V(H) V(G) dan E(H) E(G) maka H disebut sebagai subgraf dari G atau graf G adalah supergraf dari H.
7
Gambar 4. Contoh spanning subgraf H dari graf G v3 berkorespondensi satu-satu antara titik-titik di G1 dengan titi-titk di G2 serta antara sisi-sisi di G1 dengan sisi-sisi di G2.
Suatu walk pada graf G adalah barisan berhingga dari titik dan sisi,
8
Gambar 6. Contoh graf dengan salah satu walk
e3
Gambar 7.Contoh graf dengan salah satu path
e3 digunakan lebih dari satu kali atau berulang.
Salah satu path terlihat pada Gambar 7 yaitu v1 e1 v2 e2 v3 e4 v4.
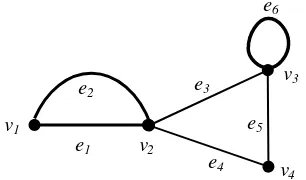
Suatu loop dari suatu graf adalah sisi yang menempel pada titik yang sama atau titik awal dan titik akhirnya sama, sedangkan sisi paralel adalah dua atau lebih sisi yang berada pada pasangan titik yang sama.
Salah satu loop terlihat pada Gambar 8 yaitu sisi e6 dan sisi paralelnya adalah
himpunan { e1, e2}.
Gambar 8. Contoh graf dengan salah satu loop dan sisi paralel
9
Gambar 9. Contoh graf sederhana dan terhubung
e1 sedangkan suatu graf G dikatakan terhubung jika diantara setiap pasang dari titik di G terdapat path yang menghubungkannya.
Suatu graf berarah (digraf) adalah suatu graf dengan setiap sisinya memiliki arah dengan sisi berarah memiliki satu titik ujung yang disebut ekor (tail) dan satu titik ujungnya disebut kepala (head) dengan arahnya dari ekor menuju kepal.
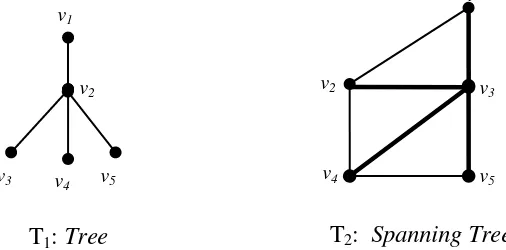
Suatu graf T disebut tree jika graf T merupakan graf terhubung yang tidak memiliki cycle atau sirkuit. Suatu graf T disebut spanning tree dari suatu graf G jika graf T adalah tree dan memuat semua titik dari graf G atau dengan kata lain graf T adalah spanning subgraf dari graf G yang tidak memuat cycle atau sirkuit dan kumpulan dari tree disebut dengan forest.
Gambar 10. Contoh digraf dengan 4 titik
e1
Gambar 11. Contoh tree dan spanning tree
10
2.2 Konsep Dasar Barisan
Barisan adalah suatu fungsi yang domainnya merupakan semua bilangan bulat dan dinotasikan dengan an (Rosen, 2012).
Secara umum barisan direpresentasikan dalam baris sebagai berikut:
1 2
, , ,...,
m m m n
a a a a
Contoh : Barisan bilangan 2, 4, 6, 8, 10, ...
Suatu barisan geometri adalah barisan yang memiliki bentuk a ar ar, , 2,...,arn,... dengan a dan r adalah bilangan riil serta r merupakan rasio (Rosen, 2012). Contoh: Barisan bilangan 1, 2, 4, 8, 16, ..., dengan a = 1 dan r = 2.
Suatu barisan geometri adalah barisan yang memiliki bentuk
, , 2 ,..., ,...
a a d a d a nd dengan a dan d adalah bilangan riil serta d adalah
merupakan beda (Rosen, 2012).
Contoh: Barisan bilangan 1, 4, 7, 10, 13, ..., dengan a = 1 dan d = 3. Diberikan barisan bilangan
an sebagai berikut:0, ,1 2,..., n
a a a a ... (1)
Beda pertama dari barisan (1) adalah:
1 1 1 1
0, 1, 2,..., n
D D D D , dengan D1n an1an
Secara rekurensi di definisikan beda orde ke k dari barisan (1) dengan orde k-1 sebagai beda sebelumnya adalah :
0, 1, 2,...,
k k k k
n
11
Proposisi 1: Diberikan barisan a a a0, ,1 2,...,an. Jika terdapat polinomial p(x) berderajat k dengan koefisien c sehingga an p n( ) untuk n = ,1,2,3,.…, maka barisan a a a0, ,1 2,...,an adalah barisan aritmatika orde k dengan beda adalah
k! c (Alonso,2000). Bukti :
Misalkan p x( )a x1 k a x2 k1a x3 k2... maka an a n1 k a n2 k1a n3 k2... sehingga an an1an a n1[( 1)kmk]a2[(n1)k1nk1] ...
cknk1 ▭
Oleh karena itu, untuk beda pertama dapat dibentuk p x( )kcxk1... yang berderajat k −1 dengan koefisien pertama kc sehingga D1n p n1( )
Dengan melakukan perulangan proses yang sama sebanyak k kali dapat disimpulkan bahwa : Dnk p nk( ) untuk suatu polinomial p nk( ) berderajat nol dengan koefisien pertama k!c sehingga Dnk k c! , untuk n = 0, 1, 2, 3, …
Berdasarkan Proposisi 1 dari barisan (1) terdapat polinomial p(x) dengan derajat k, ( ) 1 2 1 3 2 ...
k k k
p x a x a x a x , dengan an p n( ) untuk n = 0,1,2,3,.. maka barisan (1) yaituan a n1 ka n2 k1a n3 k2... adalah barisan aritmatika orde k
dengan beda pada orde k adalah sama. ▭
2.3 Konsep Dasar Pencacahan
12
terjadi dan percobaan 2 mempunyai m2 hasil percobaan yang mungkin maka jika
hanya salah satu dari dua percobaan itu saja yang dilakukan, maka terdapat m1 +
m2hasil jawaban (Rosen, 2012). pembatasan mengenai berapa kali dibolehkan ujian dalam setiap harinya, maka kemungkinan jadwal dapat dibuat sebanyak 5 x 5 = 25 pilihan.
Diberikan n. Nilai n! (dibaca “ n faktorial”) didefinisikan sebagai hasil kali semua bilangan bulat positif antara 1 sampai n:
! ( 1)( 2)( 3)....3.2.1
n n n n n
Dengan nol faktorial, didefinisikan 0!=1 (Rosen, 2012).
13
Contoh :
Berapa banyak cara untuk memilih 3 mahasiswa dari 5 mahasiwa yang akan menduduki posisi ketua, wakil dan sekretaris?
Penyelesaian:
Kombinasi r objek dari n objek dinotasikan dengan persamaan : !
Berapa banyak cara untuk memilih 5 pemain tenis dari 10 pemain tenis yang ada untuk mengikuti kejuaraan?
Misalkan permutasi yang berbeda dari n objek, dengan n1 banyaknya objek yang tidak dapat dibedakan untuk jenis 1, n2 banyaknya objek yang tidak dapat dibedakan untuk jenis 2, ..., dan nk banyaknya objek yang tidak dapat
dibedakan untuk jenis k maka
1 2
! ! !... !k
n
14
Contoh:
Berapa banyak cara untuk membagikan masing-masing 5 kartu kepada 4 pemain dari setumpuk kartu bridge?
Penyelesaian: 52! 5!5!5!5!32!
III. METODE PENELITIAN
3.1 Tempat dan Waktu Penelitian
Penelitian ini dilakukan di Program Studi Magister Matematika Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung. Waktu penelitian dilakukan pada semester ganjil tahun akademik 2015 - 2016.
3.2 Penelitian yang telah dilakukan
Adapun penelitian-penelitian yang telah dilakukan sebelumnya, antara lain:
1. Agreusson dan Raymon (2007)
16
Metode yang dilakukan pada penelitian ini adalah studi pustaka. Adapun tahap-tahap yang dilakukan dalam penelitian ini adalah sebagai berikut:
1. Menginventaris literatur baik berupa buku serta jurnal yang berkaitan dengan penelitian.
17
3. Melakukan observasi dan investigasi dengan cara menggambarkan graf berlabel baik berupa graf tak terhubung dan graf terhubung tanpa sisi paralel dengan 1 n 4 dan m 1 .
4. Mengelompokkan graf berlabel baik berupa graf tak terhubung berlabel dan graf terhubung berlabel untuk n titik dan m sisi yang sama.
5. Menghitung jumlah graf total berlabel baik berupa graf tak terhubung berlabel dan graf terhubung berlabel untuk n titik dan m sisi yang sama. 6. Menginvestigasi pola atau bentuk barisan yang terbentuk dari banyaknya graf
yang terbentuk dari n titik dan m sisi.
7. Menentukan bentuk umum untuk menentukan jumlah graf total berlabel tanpa sisi paralel dengan n titik dan m sisi.
18
Mulai
Tentukan banyaknya n titik dan m sisi dari graf yang akan diteliti
Observasi graf tak terhubung berlabel dan graf terhubung berlabel tanpa sisi paralel dengan 1 n 4 dan 1 m 10
Kelompokkan graf berdasarkan n titik dan m sisi yang sama dan menghitung jumlah graf yang terbentuk sehingga dapat terlihat pola yang terbentuk.
Gunakan rumus suku ke-m dengan menggunakan barisan aritmatika orde tinggi pada barisan bilangan yang diperoleh dari banyaknya graf tak terhubung berlabel, graf terhubung berlabel dan graf total berlabel tanpa sisi paralel dengan 1 n 4 dan 1 m 10
Membangun sistem perhitungan graf yang terbentuk dari bentuk umum ke dalam program
Tentukan bentuk umum atau rumus umum dari suku ke-m dalam bentuk kombinasi
V. PENUTUP
5.1.Kesimpulan
Berdasarkan hasil konstruksi dan observasi serta implementasi dari graf berlabel tanpa sisi paralel maka disimpulkan banyaknya graf berlabel tanpa sisi paralel adalah:
1. Untuk n 1 dan m 1 diperoleh bentuk atau rumus umum, yaitu:
- Banyaknya graf tak terhubung berlabel adalah G ' lt
1,m 0.- Banyaknya graf terhubung berlabel adalah G lt
1,m 1.- Banyaknya graf berlabel adalah
1,m G l 1.2. Untuk n2 dan m 1 diperoleh bentuk atau rumus umum, yaitu:
- Banyaknya graf tak terhubung berlabel adalah t
2,mm 1
63
- Banyaknya graf terhubung berlabel adalah t
3,m2m 1
- Banyaknya graf tak terhubung berlabel adalah
- Banyaknya graf terhubung berlabel adalah
- Banyaknya graf berlabel adalah
4,m 4m 4 m 1 5m 2 m 2 7m 164
5. Sistem yang telah dibangun dapat membantu dalam perhitungan banyaknya graf yang terbentuk secara cepat dan baik serta dapat memberikan output berupa gambar.
5.2 Saran
Berdasarkan kesimpulan dari hasil penelitian yang telah diuraikan, maka saran yang dapat diberikan untuk pengembangan lebih lanjut adalah :
1. Penelitian ini dapat dilanjutkan dalam penentuan bentuk umum untuk graf berlabel G l
n,m.2. Implementasi dalam bentuk komputasi atau program dapat lebih dinamis dalam menghasilkan output baik berupa hasil perhitungan maupun bentuk graf.
DAFTAR PUSTAKA
Agreusson,G and Raymon, D. G. 2007. Graph Theory Modeling, Apliccation, and Algorithms. Personal / Prentice Education Inc. New Jersey.
Alonso, J. 2000. Arithmetic Sequence Of Higher Order. Online. http://www.fq.math.ca/Scanned/14-2/alonso.pdf, diakses tanggal 2 September 2015.
Arifah, Umi, Nur. 2015.Penentuan Banyaknya Graf Terhubung Berlabel Tanpa Garis Paralel Dengan Banyaknya Titik Tiga atau Empat. Skripsi. Jurusan Matematika FMIPA Universitas Lampung, Bandar Lampung
Gross, L. Jonathan, Yellen, J., and Zhang, Ping. 2014. Handbook of Graph Theory. Taylor & Francis Group.New York.USA.
Rosen, H., Kenneth. 2012. Discrete Mathematics and Its Applications. McGraw-Hill. New York. USA.