ABSTRAK
PENENTUAN BANYAKNYA GRAF TAK TERHUBUNG TANPA LOOP
Oleh Rohandi
Graf G (V,E) dikatakan tak terhubung jika ada dua titik yang berbeda di G, tidak ada path yang menghubungkan dua titik tersebut. Suatu garis pada graf G yang memiliki titik awal dan titik akhir sama dinamakan loop. Pada graf tak terhubung berlabel tanpa loop dengan banyaknya titik n dan banyaknya garis m, serta garis maksimal yang membuat graf tak terhubung tanpa terbentuknya garis rangkap adalah , dapat terbentuk banyak graf. Sehingga, dalam penelitian ini dibahas terhubung yang terbentuk jika diberikan 4 titik dan m garis adalah
∑ ∑ ( ); untuk ,
dan ∑ ∑
( )
RIWAYAT HIDUP
Penulis dilahirkan di Lampung Tengah pada tanggal 27 Maret 1992. Penulis adalah anak pertama dari pasangan Bapak Rahim dan Ibu Sri Ambar Yani, kakak dari Ratna Sari dan Riski Apriansah.
Penulis menyelesaikan pendidikan Sekolah Dasar (SD) pada tahun 2004 di SD Negeri 1 Nunggalrejo Kecamatan Punggur , Lampung Tengah. Pendidikan Sekolah Menengah Pertama (SMP) di SMP Negeri 6 Metro pada tahun 2007, pendidikan Sekolah Menengah Atas (SMA) di SMA Negeri 1 Punggur pada tahun 2010.
FMIPA Unila. Lalu pada periode 2012/2013, penulis menjabat sebagai Kepala Bidang Eksternal HIMATIKA (Himpunan Mahasiswa Jurusan Matematika).
PERSEMBAHAN
Dengan penuh rasa syukur kepada Allah SWT. Atas
limpahan rahmat dan nikmat, sehingga saya dapat
menyelesaikan hasil karyaku ini
Kupersembahkan hasil karyaku ini untuk kedua orang tua
ku dirumah yang tak henti-hentinya mendo’akan ku supaya
diberi kelancaran dan kesuksesan hidup
Kedua adikku yang memberiku semangat dan memotifasi
diriku untuk menjadi contoh yang baik untuk mereka.
Seluruh keluarga besarku yang selalu memberi nasihat dan
semangat
Sahabat-sahabatku yang selalu membantu, menyemangati
dan mendukungku, serta orang yang selalu ada untuk
menemaniku
Dosen pembimbing dan penguji yang tak henti-hentinya
MOTO
“Doa ibu adalah kesuksesan di setiap jalanku”
“Hidup lah dengan bahagia bersama orang disekitar kita”
“Berusaha maksimal dan tersenyumlah ”
SANWACANA
Alhamdulillahi robbil ‘alamin, puji dan syukur penulis kepada Allah SWT atas
berkat rahmat dan karunia-Nya penulis dapat menyelesaikan skripsi ini. Shalawat serta salam selalu penulis haturkan kepada junjungan kita nabi besar Muhammad SAW yang menjadi sosok suri tauladan bagi kita semua.
Dalam proses penyelesaian skripsi ini, selalu mendapatkan bimbingan, bantuan dari berbagai pihak. Untuk itu penulis ingin mengucapkan terima kasih kepada : 1. Ibu Dra. Wamilliana, M .A., Ph.D., selaku pembimbing I yang senantiasa
sabar dalam memberikan bimbingan, pelajaran, arahan serta saran selama penyusunan skripsi ini.
2. Bapak Amanto, S.Si., M.Si., selaku dosen pembimbing II yang telah memberikan bimbingan dan pelajarannya selama ini.
3. Ibu Dr. Asmiati, S.Si., M.Si., selaku penguji yang telah memberikan saran dan kritik yang membangun bagi penulis.
4. Ibu Widiarti, S.Si., M.Si., selaku pembimbing akademik yang selalu memberikan saran dan dukungan bagi penulis.
4. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D., selaku Ketua Jurusan Matematika FMIPA Universitas Lampung.
Lampung.
7. Untuk kedua orang tuaku, kedua adikku dan seluruh keluarga besarku yang selalu memberikan do’a dan dukungannya bagi penulis.
8. Sahabat-sahabat penulis, Agustia Indriani, Agustina Ambar Wulan, Christy Engine Nita, Dian Ekawati, Dinda Ristanti, Tri Handayani, Hasby Alkarim, Miftah Farid Artama, Muhammad Ridho serta Sofyan Saputra yang selalu ada dan memberi semangat melalui keceriaan serta nasihatnya.
9. Untuk Suci Marita Damaiyanti yang selalu sabar menghadapiku, selalu memberikan semangat dan selalu menemaniku.
10. Sahabat seperjuangan Erwin Hendrianto, Herman, Suryadi, Rido, Angga dan semua teman-teman angkatan 2010 serta keluarga besar HIMATIKA.
11. Seluruh pihak yang telah membantu dalam penyusunan skripsi ini yang tidak dapat disebutkan satu persatu.
Akhir kata, penulis menyadari skripsi ini jauh dari kesempurnaan, akan tetapi semoga dapat berguna dan bermanfaat bagi kita semua.
Bandar Lampung, Oktober 2014 Penulis,
i
DAFTAR ISI
Halaman
DAFTAR ISI ... i
DAFTAR TABEL ... iii
DAFTAR GAMBAR ... iv
BAB I PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Batasan Masalah ... 4
1.3 Tujuan Penelitian... 4
1.4 Manfaat Penelitian... 4
BAB II TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf ... 7
2.2 Konsep Dasar Teknik Pencacahan... 9
BAB III METODE PENELITIAN 3.1 Teorema Penghitungan Graf ... 12
3.2 Waktu dan Tempat Penelitian ... 13
ii
IV. HASIL DAN PEMBAHASAN
4.1 Observasi ... 15 4.2 Menentukan Rumus Umum Graf Tak Terhubung
Tanpa Loop ... 20 V. KESIMPULAN
iii
DAFTAR TABEL
Halaman Tabel 1. Hasil kontruksi graf tak terhubung berlabel tanpa loop,
dan ... 15 Tabel 2. Hasil kontruksi graf tak terhubung berlabel tanpa loop,
iv
DAFTAR GAMBAR
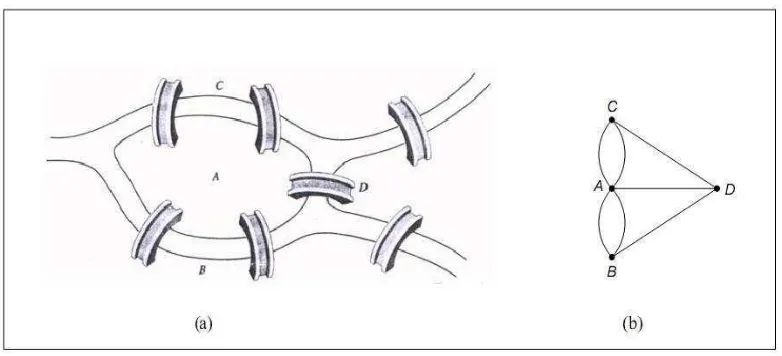
Halaman Gambar 1. (a) Jembatan Königsberg dan (b) graf yang merepresentasikan
jembatan Königsberg ... 2
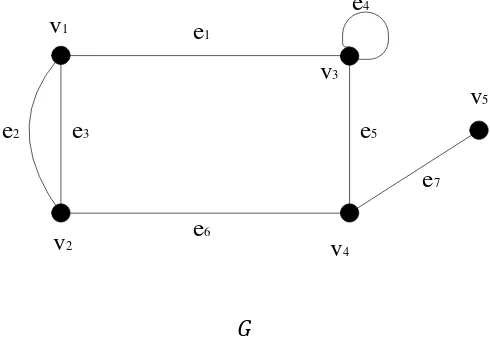
Gambar 2. Contoh graf dengan 5 titik dan 7 garis ... 6
Gambar 3. Contoh graf sederhana ... 7
Gambar 4. Contoh graf teratur (reguler graph) dengan empat titik dan berderajat 2 ... 8
Gambar 5. Contoh graf terhubung dan graf tidak terhubung ... 9
Gambar 6. Graf sederhana dengan n = 3 dan m = 2 ... 12
BAB I
PENDAHULUAN
1.1Latar Belakang
Teori graf merupakan salah satu kajian matematika yang memiliki banyak terapannya diberbagai bidang sampai saat ini. Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Representasi visual dari graf adalah dengan menyatakan objek sebagai noktah, bulatan, vertex atau titik, sedangkan hubungan antara objek dinyatakan dengan garis atau edge.
2
setiap jembatan itu hanya sekali dan kembali lagi ke tempat awal keberangkatan, tetapi mereka tidak dapat menjelaskan mengapa demikian.
Tahun 1736, seorang matematikawan Swiss, L.Euler, adalah orang pertama yang berhasil menemukan jawaban masalah itu dengan pembuktian yang sederhana. Ia memodelkan masalah ini ke dalam graf. Daratan dinyatakannya sebagai titik (vertex), dan jembatan dinyatakan sebagai garis yang disebut sisi (edge). Setiap titik diberi label huruf A, B, C, dan D. Jawaban yang dikemukakan oleh Euler adalah: orang tidak mungkin melalui ketujuh jembatan itu masing- masing satu kali dan kembali lagi ke tempat asal keberangkatan jika derajat setiap titik tidak seluruhnya genap. Derajat adalah banyaknya garis yang bersisian dengan titik. Sebagai contoh, simpul C memiliki derajat 3 karena ada tiga buah garis yang bersisian dengannya, simpul B dan D juga berderajat tiga, sedangkan simpul A berderajat 5. Karena semua titik berderajat ganjil, maka tidak mungkin dilakukan perjalananan seperti yang diinginkan tersebut.
3
Tahun-tahun berikutnya, banyak para ilmuan yang mengembangkan teori graf seperti G.R. Kirchoff, A. Coyley, Sir W.R. Hamilton sehingga teori graf mengalami perkembangan yang pesat.
Penerapan teori graf dalam kehidupan sehari-hari sangatlah luas, sehingga teori graf semakin berkembang. Banyak cabang ilmu pengetahuan yang menggunakan aplikasi teori graf diantaranya kimia, biologi, ilmu komputer, ekonomi dan lain-lain.
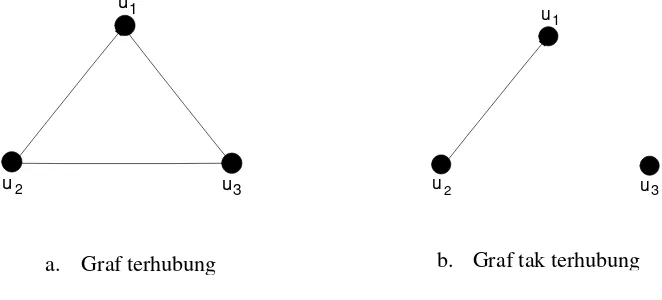
Graf G (V,E) dikatakan terhubung jika untuk setiap dua titik yang berbeda di G, ada suatu path yang menghubungkan titik tersebut. Sebaliknya jika tidak ada path yang menghubungkan maka G dikatakan graf tidak terhubung. Dalam suatu teori graf dikenal istilah loop, dimana loop adalah suatu garis dalam suatu graf yang memiliki titik awal dan titik akhir yang sama. Suatu graf dikatakan graf berlabel jika titik atau garisnya di kaitkan dengan suatu besaran tertentu.
4
loop untuk graf dengan kardinalitas yang sama.
Oleh karena itu, pada penelitian ini akan didiskusikan tentang banyaknya graf tak terhubung tanpa loop ( garis paralel diperbolehkan ) jika diberikan n titik dan m garis.
1.2Batasan Masalah
Dalam penelitian ini pembahasan dibatasi hanya untuk graf tak terhubung berlabel tanpa loop dengan dan , dengan n adalah banyaknya titik, | )| , dan m adalah banyaknya garis, | )| .
1.3Tujuan Penelitian
Adapun tujuan dari penelitian ini adalah menentukan banyaknya graf tak terhubung tanpa loop jika diberikan n titik dan m garis.
1.4Manfaat Penelitian
5
BAB II
TINJAUAN PUSTAKA
7
Pada graf terdapat istilah bertetangga ( adjacent ) dan menempel ( incident ) yang akan di jelaskan di bawah ini.
Dua titik dikatakan bertetangga ( adjacent ) jika ada garis yang menghubungkan keduanya. Suatu garis dikatakan menempel ( incident ) dengan suatu titik u, jika titik u merupakan salah satu ujung dari garis tersebut. ( Deo, 1989 )
Derajat atau degree dari titik v dinotasikan dengan d(v) dan menyatakan banyaknya sisi yang menempel pada titik v. ( Deo, 1989 ) Gambar 1 adalah contoh graf dimana titik adalah titik yang berderajat 3. Selanjutnya akan dijelaskan tentang definisi graf sederhana yang akan dijelaskan di bawah ini.
Graf sederhana adalah suatu graf tanpa loop dan tanpa garis paralel. ( Deo, 1989 )
u
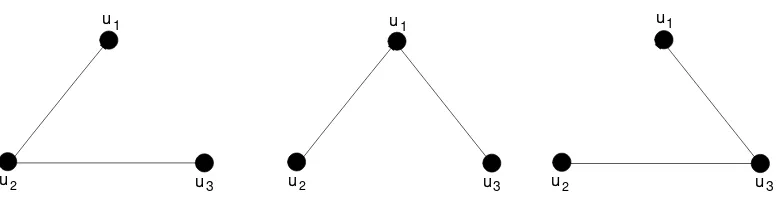
2 u3
u1
Gambar 3. Contoh graf sederhana
Penjelasan tentang definisi graf teratur ( reguler graph ) akan dijelaskan di bawah ini.
Graf yang setiap titiknya mempunyai derajat yang sama disebut graf teratur atau reguler. Apabila derajat setiap vertex adalah r, maka graf tersebut disebut sebagai
8
Gambar 4. Contoh graf teratur (reguler graph) dengan empat titik dan berderajat 2
Garis paralel adalah dua garis atau lebih yang memiliki dua titik ujung yang sama. Loop adalah garis yang titik awal dan ujungnya sama. ( Deo, 1989 )
Gambar 1 merupakan contoh graf yang memuat garis paralel dan loop.
Perjalanan ( walk ) adalah barisan berhingga dari titik dan garis dimulai dan diakhiri dengan titik, sedemikian sehingga setiap sisi menempel dengan titik sebelum dan sesudahnya. Jalan yang berawal dan berakhir pada titik yang sama disebut jalan tertutup. Pada Gambar 1, salah satu contoh jalan yaitu
, ( Deo,1989 )
Tidak hanya walk, tetapi dalam penelitian ini juga di perlukan pengertian tentang path ( lintasan ) yang diberikan sebagai berikut.
9
Gambar 5. Contoh graf terhubung dan graf tidak terhubung
2.2 Konsep Dasar Teknik Pencacahan
Kombinasi r elemen dari n elemen adalah jumlah pemilihan yang tidak terurut r elemen yang diambil dari n elemen . ( Munir, 2005 )
10
Urutan 1,2,3 sama dengan 1,3,2 atau 3,2,1 dan di hitung hanya sekali. Banyaknya kombinasi dari r objek yang diambil dari n objek yang tersedia dinotasikan .
Dalam kombinasi, tidak memperhatikan suatu urutan.
Teorema 1:
Banyaknya kombinasi n objek yang diambil sebanyak r objek adalah
)
III. METODE PENELITIAN
Pada bab ini akan diberikan teorema yang berhubungan dengan penelitian, tempat dan waktu penelitian serta metode penelitian yang digunakan.
3.1 Teorema Penghitungan Graf
Misalkan m,n dengan ( ), .
1. Graf merupakan graf sederhana dengan n titik. Banyaknya graf adalah
( )
2. Graf merupakan graf sederhana dengan n titik dan m garis. Banyaknya graf adalah :
( )
12
Penelitian ini dilakukan di Jurusan Matematika FMIPA Universitas Lampung pada tahun akademik 2013-2014.
3.3 Metode Penelitian
Langkah-langkah yang digunakan dalam penelitian ini adalah:
1. Mengumpulkan bahan literature serta studi kepustakaan yang berhubungan dengan graf.
2. Menentukan banyaknya titik dan garis yang akan dicari banyaknya graf tak terhubung yang terbentuk dari titik dan garis tersebut.
3. Menggambar graf tak terhubung tanpa loop untuk n=3 dan n=4 dengan , dengan n adalah titik dan m adalah garis.
13
7. Menentukan rumus untuk menghitung jumlah graf tak terhubung tanpa loop dengan n titik dan m garis.
Penyajian dalam bentuk diagram alir
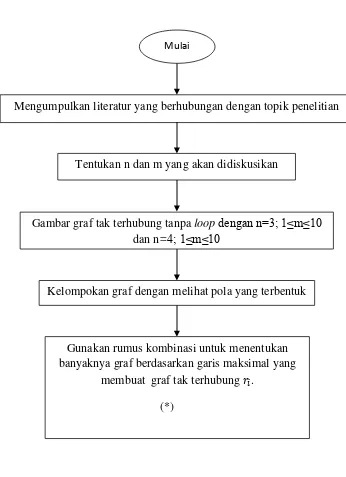
Mulai
Mengumpulkan literatur yang berhubungan dengan topik penelitian
Tentukan n dan m yang akan didiskusikan
Gambar graf tak terhubung tanpa loop dengan n=3; 1≤m≤10 dan n=4; 1≤m≤10
Kelompokan graf dengan melihat pola yang terbentuk
Gunakan rumus kombinasi untuk menentukan banyaknya graf berdasarkan garis maksimal yang
14
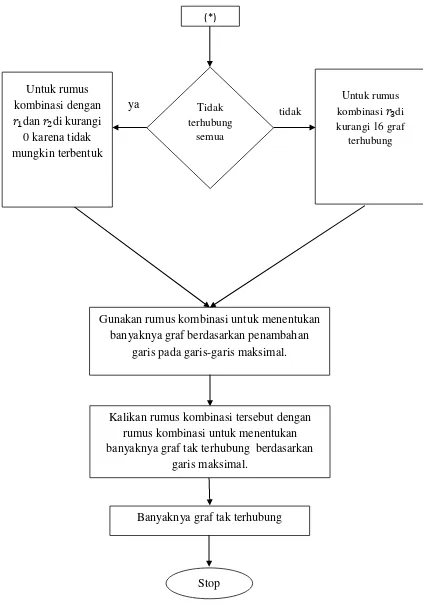
Gambar 7. Diagram alir metode penelitian Gunakan rumus kombinasi untuk menentukan
banyaknya graf berdasarkan penambahan garis pada garis-garis maksimal.
Kalikan rumus kombinasi tersebut dengan rumus kombinasi untuk menentukan banyaknya graf tak terhubung berdasarkan
V. KESIMPULAN
Berdasarkan observasi dan kontruksi graf tak terhubung berlabel tanpa loop, maka dapat diambil kesimpulan bahwa
34 dengan
n = banyaknya titik pada graf m = banyaknya garis pada graf
ri = garis maksimal yang membuat graf tidak terhubung tanpa adanya garis
rangkap yang terbentuk
n = banyaknya titik pada graf m = banyaknya garis pada graf
ri = garis maksimal yang membuat graf tidak terhubung tanpa adanya garis
rangkap yang terbentuk
DAFTAR PUSTAKA
Agreusson, G and Raymon, D. G. 2007. Graph Theory Modeling, Applications, and Algorithms. Pearson/Prentice education inc, New Jersey.
Deo, N. (1989). Graph Theory with Applications to Engineering and Computer Science. Prentice Hall Inc, New York.
Handayani, T. (2014). Penentuan Banyaknya Graf Terhubung Tanpa Loop. Skripsi.Bandar Lampung: Universitas Lampung.
Munir, Rinaldi. 2005. Matematika Diskrit Edisi Ketiga. Bandung : Informatika Bandung.