PENENTUAN BANYAKNYA GRAF BERLABEL TAK TERHUBUNG TANPA LOOP DENGAN LIMA TITIK

(1)

PENENTUAN BANYAKNYA GRAF BERLABEL TAK TERHUBUNG TANPA LOOP DENGAN LIMA TITIK

(Skripsi)

Oleh

Gusti Kadek Sandika

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

(2)

ABSTRAK

PENENTUAN BANYAKNYA GRAF BERLABEL TAK TERHUBUNG TANPA LOOP DENGAN LIMA TITIK

Oleh

Gusti Kadek Sandika

Graf G dikatakan tidak terhubung jika tidak ada path yang menghubungkan setiap pasangan titik di G. Suatu garis yang berawal dan berakhir pada titik yang sama disebut sebagai loop, sedangkan dua garis atau lebih yang menghubungkan dua titik yang sama disebut sebagai garis paralel. Jika diberikan titik, garis, dan garis, , dengan adalah banyaknya garis maksimal yang membuat graf tak terhubung dengan garis paralel dihitung satu, maka dapat dibentuk berbagai bentuk graf berlabel tak terhubung tanpa loop. Untuk dan banyaknya graf yang terbentuk dapat dinyatakan sebagai:

( )

(3)

PENENTUAN BANYAKNYA GRAF BERLABEL TAK TERHUBUNG TANPA LOOP DENGAN LIMA TITIK

Oleh

Gusti Kadek Sandika

Skripsi

Sebagai salah satu syarat untuk mencapai gelar Sarjana Sains

Pada

Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

(4)

(5)

(6)

(7)

DAFTAR RIWAYAT HIDUP

Penulis lahir di Darma Agung pada tanggal 21 Juni 1993 yang merupakan anak kedua dari tiga bersaudara pasangan Bapak Gusti Kade Winata dan Ibu Made Karini. Penulis memiliki satu orang kakak laki-laki bernama Gusti Putu Andita dan satu adik laki-laki bernama Gusti Komang Heryawan.

Riwayat pendidikan penulis menyelesaikan Taman Kanak-Kanak (TK) pada tahun 1999 di TK Pertiwi Jati Datar, Sekolah Dasar (SD) diselesaikan pada tahun 2005 di SDN I Darma Agung, Sekolah Menengah Pertama diselesaikan penulis pada tahun 2008 di SMPN I Seputih Mataram, dan pada tahun 2011 penulis menyelesaikan pendidikan Sekolah Menengah Atas di SMA Yayasan Pembina (YP) Unila Tanjung Karang.

(8)

(9)

“Biarlah dia mengangkat jiwanya dengan jiwanya sendiri,

janganlah jiwanya menjerumuskan dirinya; Sebab hanya jiwa lah teman jiwanya dan

hanya jiwalah musuh jiwanya”

(Bhagavad Gita VI-5)

“Hati yang gembira adalah obat yang manjur, tetapi semangat yang patah mengeringkan tulang”

(Amsal 17:22)

“Kesejahteraan dilimpahkan atasmu,

Berbahagialah kamu”

(Qs. 39:73)

“Bangun! Jangan lengah!

Tempuhlah kehidupan dengan benar”

(Dhamapada: 168)

“Santai dalam pembawaan, serius dalam pemikiran. Ya! Itu sangatlah baik”

(10)

“Dengan segala kekurangan dan kerendahan hati,

saya persembahkan skripsi ini kepada

Putera Puteri Bangsa Indonesia.

Semoga skripsi ini turut serta mewujudkan

salah satu cita-cita bangsa Indonesia

sesuai dengan amanat pembukaan UUD 1945

(11)

SANWACANA

Puji syukur kepada Tuhan Yang Maha Esa karena atas anugerah dan izin-Nya

skripsi dengan judul “Penentuan Banyaknya Graf Berlabel Tak Terhubung Tanpa

Loop dengan Lima Titik” dapat penulis selesaikan dengan baik.

Dapat diselesaikannya penelitian ini tidaklah terlepas dari bantuan, kerja sama, dan dukungan dari berbagai pihak. Pada kesempatan ini, penulis menyampaikan terimakasih kepada:

1. Ibu Dra. Wamiliana, M.A., Ph.D. selaku Pembimbing Utama yang telah banyak memberikan bimbingan, pelajaran, saran, dan dukungan dalam penyelesaian skripsi ini.

2. Bapak Ahmad Faisol, S.Si., M.Sc. selaku Pembimbing Pembantu yang memberikan pengarahan dan masukan untuk penulis.

3. Ibu Fitriani, S.Si., M.Sc. selaku Penguji yang telah memberikan kritik dan saran yang bermanfaat untuk penulis.

4. Bapak Drs. Tiyono Ruby, M.Sc., Ph.D. selaku Ketua Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA) Universitas Lampung.

5. Bapak Drs. Eri Setiawan, M.Si. selaku Pembimbing Akademik.

(12)

7. Dosen, staf, dan karyawan Jurusan Matematika FMIPA Unila yang telah memberikan ilmu pengetahuan dan bantuan kepada penulis.

8. Orang tua tercinta dan keluarga yang selalu mendoakan, memberikan dukungan dan motivasi kepada penulis.

9. Sahabat dan kawan-kawan penulis, Haidir Alam, Khairil Walid, Jordian Gevara, Erick Renaldi, Reno Saputra, Charissa Sudarisman, Umi Arifah, Dhia Fadhilah, Ni Putu Udya, Anissa Rizky, dan Pusya Paradhita yang selalu bersedia direpotkan dalam penyelesaian penelitian ini.

10.Nona Dela Dwi Antika yang menemani penulis melakukan penelitian hingga proses penyelesaian skripsi ini.

11.Kawan-kawan Mahasiswa Matematika, terkhusus Angkatan 2011 dan kawan-kawan HIMATIKA FMIPA Unila 2013-2014.

12.Seluruh pihak yang telah berperan dalam penyelesaian skripsi ini yang tidak dapat penulis sebutkan satu per satu.

Bandar Lampung, Agustus 2015 Penulis,

(13)

i DAFTAR ISI

Halaman

DAFTAR ISI ...i

DAFTAR TABEL ...iii

DAFTAR GAMBAR ...iv

BAB I PENDAHULUAN 1.1.Latar Belakang ...1

1.2.Batasan Masalah ...4

1.3.Tujuan Penelitian ...4

1.4.Manfaat Penelitian ...4

BAB II TINJAUAN PUSTAKA 2.1.Konsep Dasar Graf ...5

2.2.Teknik Dasar Pencacahan ...7

2.3.Penghitungan Graf (Graph Counting)...10

BAB III METODE PENELITIAN 3.1.Teorema Penghitungan Graf ...11

3.2.Waktu dan Tempat Penelitian ...12

(14)

ii BAB IV HASIL DAN PEMBAHASAN

4.1.Observasi ...14 4.2.Penentuan Rumus Umum untuk Graf dengan dan ...30

BAB V KESIMPULAN ...36

DAFTAR PUSTAKA

(15)

iii

DAFTAR TABEL

Halaman

Tabel 1. Hasil konstruksi graf dengan dan ...15

(16)

iv

DAFTAR GAMBAR

Halaman

Gambar 1.1. Jembatan Konigsberg (a) dan graf yang mempresentasikan

Jembatan Konigsberg (b) ...1

Gambar 2.1. Contoh graf G dengan 5 titik dan 7 garis ...5

Gambar 2.2. Contoh graf tak terhubung (a) dan contoh graf terhubung (b) ...6

Gambar 2.3. Contoh graf sederhana ...6

Gambar 3.1. Diagram alir prosedur penelitian ...13

Gambar 4.1. Pengelompokan graf dengan dan ...20

(17)

BAB I PENDAHULUAN

1.1.Latar Belakang

Suatu graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan objek-objek tersebut. Objek-objek tersebut disimbolkan dalam bentuk titik (vertex) sedangkan hubungan antar objek dinyatakan sebagai garis (edge).

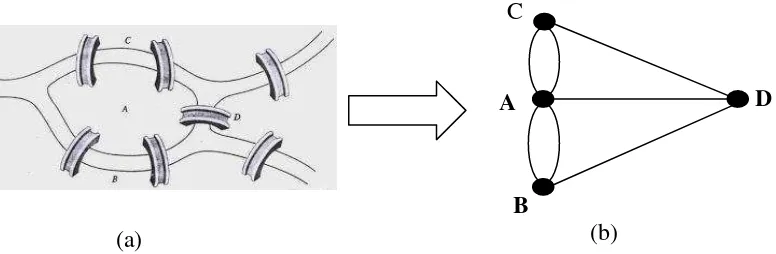
Perkembangan teori graf berawal ketika Leonhard Euler, seorang matematikawan berkebangsaan Swiss pada tahun 1736. Melalui tulisannya, Euler memberi solusi untuk menyelesaikan masalah jembatan Konigsberg yang sangat terkenal di Eropa. Masalah jembatan Konigsberg adalah mungkin atau tidaknya melewati tujuh jembatan yang ada di Kota Konigsberg masing-masing tepat satu kali dan kembali ketempat semula. Untuk memecahkan masalah tersebut, Euler memisalkan daratan dengan titik (vertex) dan jembatan dinyatakan dengan garis atau sisi (edge).

Gambar 1.1. Jembatan Konigsberg (a) dan graf yang mempresentasikan jembatan Konigsberg (b)

(a) (b)

A C

B

(18)

2 Euler berkesimpulan bahwa tidak mungkin seeorang dapat melalui tujuh jembatan masing-masing tepat satu kali dan kembali ketempat semula jika derajat tiap titik jumlahnya tidak genap. Derajat titik adalah banyaknya garis yang menempel pada satu titik. Kisah jembatan Konigsberg ini menjadi sejarah lahirnya teori graf.

Setelah masa Euler bermunculan peneliti-peneliti yang mengkaji tentang teori graf. Pada tahun 1847, G.R. Kirchoff berhasil mengembangkan teori pohon (Theory of trees) yang digunakan pada persoalan jaringan listrik. Sepuluh tahun kemudian, A. Cayley juga menggunakan konsep pohon untuk menjelaskan permasalahan kimia yaitu hidrokarbon. Pada masa ini juga lahir hal penting bagi teori graf yaitu konjektur empat warna, yang menyatakan bahwa untuk mewarnai sebuah atlas hanya dibutuhkan empat warna yang berbeda sedemikian sehingga setiap negara yang berbatasan memiliki warna yang berbeda. Para ahli teori graf berkeyakinan bahwa yang pertama kali mengemukakan masalah empat warna adalah A.F. Mobius pada tahun 1840. Pada tahun 1859 W.R. Hamilton berhasil menemukan suatu permainan yang diberi nama prominent cities yang menggunakan konsep-konsep teori graf.

(19)

3 Salah satu penelitian tentang teori graf selanjutnya adalah penelitian yang dilakukan oleh Harary dan Palmer yang dipublikasikan pada tahun 1973 tentang penghitungan banyaknya graf (graph enumeration). Dalam bukunya tentang penghitungan graf tersebut menjadi panduan bagi peneliti-peneliti selanjutnya dalam cara-cara penghitungan graf. Namun dalam tulisannya tersebut masih banyak hal-hal yang belum terpecahkan seperti banyaknya graf yang berlabel tak terhubung tanpa loop yang dapat dibentuk dari titik dan garis.

Selanjutnya, Rohandi pada tahun 2014 berhasil menentukan banyaknya graf tak terhubung tanpa loop untuk titik sebanyak 3 dan 4. Berdasarkan Rohandi (2014), banyaknya graf berlabel yang dapat dibentuk dengan 3 dan 4 titik adalah sebagai berikut:

1. Untuk n = 3; m ≥ 1; r = 1, 2. 

2. Untuk n = 4; m ≥ 1; r = 1, 2, 3.  m ≤ n

∑ ∑

 Untuk m ≥ n

∑ ∑ dengan:

(20)

4 garis maksimal yang membuat graf tidak terhubung tanpa adanya garis

rangkap yang terbentuk

Penelitian yang dilakukan oleh Rohandi hanya terbatas pada titik sebanyak 3 dan 4 dengan garis sebanyak , oleh sebab itu penulis tertarik untuk meneliti banyaknya graf berlabel tak terhubung tanpa loop yang dapat terbentuk dengan titik sebanyak dan garis sebanyak .

1.2.Batasan Masalah

Penelitian ini pembahasan dibatasi hanya untuk graf berlabel tak terhubung tanpa loop dengan titik sebanyak dan garis sebanyak .

1.3.Tujuan Penelitian

Adapun tujuan dari penelitian ini adalah untuk menentukan banyaknya graf berlabel tak terhubung tanpa loop dengan titik sebanyak dan garis sebanyak .

1.4.Manfaat Penelitian

1. Memperluas pengetahuan pengembangan keilmuan khususnya dalam bidang ilmu matematika mengenai perkembangan dari teori graf, yaitu tentang graf tak terhubung.

(21)

BAB II

TINJAUAN PUSTAKA

Pada bab ini akan diberikan definisi dan teorema yang berhubungan dengan penelitian yang dilakukan.

2.1.Konsep Dasar Graf

Graf G didefinisikan sebagai pasangan himpunan terurut (V(G),E(G)) dengan menyatakan himpunan titik dengan dan menyatakan himpunan garis yaitu pasangan tak terurut dari (Deo, 1989).

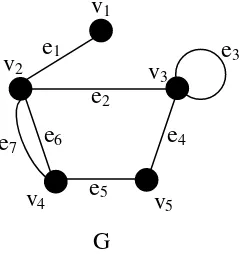
Gambar 2.1. Contoh graf G dengan 5 titik dan 7 garis

Walk adalah barisan berhingga dari titik dan garis, dimulai dan diakhiri dengan titik, sedemikian sehingga setiap garis menempel dengan titik sebelum dan sesudahnya. Tidak ada sisi yang muncul lebih dari sekali dalam satu walk.

v1

v2 _v

3

v4 v5

G e1 e2 e3 e4 e5

(22)

6 Lintasan (path) merupakan walk yang semua titiknya berbeda. Suatu graf G dikatakan terhubung jika terdapat lintasan (path) yang menghubungkan setiap pasangan titik di G. Jika tidak, maka G tidak terhubung (Deo, 1989).

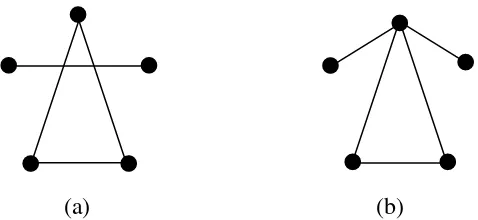
Gambar 2.2. Contoh graf tak terhubung (a) dan contoh graf terhubung (b)

Suatu garis yang berawal dan berakhir pada titik yang sama disebut sebagai loop, sedangkan dua garis atau lebih yang menghubungkan dua titik yang sama disebut sebagai garis paralel. Sebagai contoh pada Gambar 2.1, garis merupakan loop dan garis dan merupakan garis paralel. Graf sederhana adalah graf yang tidak mengandung loop atau garis paralel (Deo, 1989).

Gambar 2.3. Contoh graf sederhana

Jika suatu garis berujung di titik maka dan dikatakan saling incident satu sama lain. Sebagai contoh, pada Gambar 2.1, garis dan incident dengan titik . Dua atau lebih garis tidak paralel yang incident dengan titik yang sama disebut sebagai garis yang bertetangga (adjacent). Contohnya, pada Gambar 2.1, garis dan adalah garis-garis yang bertetangga. Dua titik dikatakan bertetangga jika titik tersebut menjadi titik-titik ujung dari suatu garis. Pada Gambar 2.1, salah satu contoh titik-titik yang bertetangga adalah titik dan .

(23)

7 Banyaknya garis yang menempel (incident) dalam satu titik dengan loop dihitung sebagai 2 garis disebut sebagai derajat (degree) dari suatu titik, dinotasikan sebagai . Sebagai contoh dalam Gambar 2.1, ,

, dan

Suatu graf G dikatakan graf berlabel jika titik atau garisnya di berikan suatu nilai atau data tertentu. Jika tidak maka graf G dikatakan graf tak berlabel. Pelabelan graf dapat berupa pelabelan titik, pelabelan garis, atau pelabelan titik dan garis. Jika pelabelan tersebut merupakan pelabelan titik dan garis, maka pelabelan tersebut disebut dengan pelabelan total (Deo, 1989).

2.2.Teknik Dasar Pencacahan

Jika suatu aktivitas dapat dibentuk dalam langkah berurutan dan langkah 1 dapat dilakukan dengan cara, langkah 2 dapat dilakukan dalam cara dan seterusnya sampai langkah ke dapat dilakukan dalam cara, maka banyaknya aktivitas berbeda yang mungkin adalah (Johnsonbaugh, 1997).

Suatu permutasi dari elemen yang berbeda adalah penyusunan elemen-elemen tersebut kedalam urutan yang dapat dibedakan. Suatu permutasi-r dari unsur yang berbeda merupakan sebuah pengurutan dari subhimpunan r-unsur dari . Banyaknya permutasi-r dari sebuah himpunan unsur yang berbeda dinyatakan dengan . Banyaknya permutasi-r dari sebuah himpunan unsur yang berbeda adalah

atau

(24)

8 ;

; (Johnsonbaugh, 1997)

Misalkan terdapat sebanyak unsur dan ada unsur yang masing-masing muncul kali, permutasi unsur tersebut adalah:

dengan Contoh:

Untuk menentukan banyaknya permutasi yang mungkin dari huruf-huruf yang menyusun kata “MATEMATIKA” dapat menggunakan permutasi dengan beberapa unsur yang sama. Banyaknya huruf dalam “MATEMATIKA” adalah sedangkan ada 2 huruf M, 3 huruf A, 2 huruf T, 1 huruf E, 1 huruf I dan 1 huruf K. Maka banyaknya cara menyusun huruf-huruf tersebut adalah:

Jadi banyaknya cara untuk menyusun huruf-huruf dalam kata “MATEMATIKA” adalah 15120 cara.

Diberikan suatu himpunan yang mengandung unsur yang berbeda:

a. Suatu r-kombinasi dari adalah seleksi tak terurut dari r-unsur (yakni subhimpunan r-unsur dari )

b. Banyaknya r-kombinasi dari suatu himpunan dengan n unsur yang berbeda

(25)

9 Banyaknya r-kombinasi dari sebuah himpunan dengan unsur yang berbeda adalah:

dengan

;

(Johnsonbaugh, 1997).

Misalkan terdapat objek yang akan dibagikan kedalam tempat yang berbeda. Maka banyaknya cara untuk menempatkan objek tersebut adalah

Contoh:

Empat bola akan dibagikan seluruhnya ke dalam 3 kotak. Banyaknya cara untuk menyusun bola-bola tersebut dapat ditentukan dengan menggunakan kombinasi dengan perulangan. Misalkan adalah banyak bola dan adalah banyak kotak maka banyaknya cara menyusun bola adalah:

(26)

10 2.3.Penghitungan Graf (Graph Counting)

Misal , dengan .

a. Banyaknya graf sederhana berlabel dengan titik dinyatakan sebagai

b. Banyaknya graf sederhana dengan titik dan garis dinyatakan

sebagai

(27)

BAB III

METODE PENELITIAN

Pada bab ini akan diberikan teorema yang berhubungan dengan penelitian, waktu dan tempat penelitian, dan metode yang digunakan dalam penelitian.

3.1.Teorema Penghitungan Graf Misal .

1. Banyaknya dari graf berlabel dengan titik, garis dan tidak mengandung loop dinyatakan sebagai:

2. Banyaknya dari graf berlabel dengan titik, dengan garis terbanyak dan tidak mengandung loop dinyatakan sebagai:

3. Banyaknya dari graf berlabel dengan titik, garis dinyatakan sebagai:

(28)

12

(Agreusson dan Raymon, 2007)

3.2.Waktu dan Tempat Penelitian

Penelitian ini dilakukan pada semester genap tahun ajaran 2014 – 2015 di Jurusan Matematika FMIPA Universitas Lampung.

3.3.Metode Penelitian

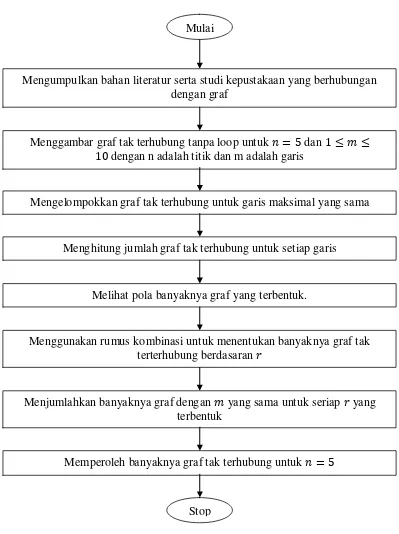
Langkah - langkah yang digunakan dalam penelitian ini adalah:

1. Mengumpulkan bahan literatur serta studi kepustakaan yang berhubungan dengan graf.

2. Menggambar graf tak terhubung tanpa loop untuk dan dengan n adalah titik dan m adalah garis.

3. Mengelompokkan graf tak terhubung untuk garis maksimal yang sama. 4. Menghitung jumlah graf tak terhubung untuk setiap garis.

(29)

13 Penyajian metode penelitian dalam bentuk diagram alir:

Gambar 3.1. Diagram alir prosedur penelitian Mulai

Mengumpulkan bahan literatur serta studi kepustakaan yang berhubungan dengan graf

Menggambar graf tak terhubung tanpa loop untuk dan dengan n adalah titik dan m adalah garis

Mengelompokkan graf tak terhubung untuk garis maksimal yang sama

Menghitung jumlah graf tak terhubung untuk setiap garis

Melihat pola banyaknya graf yang terbentuk.

Menggunakan rumus kombinasi untuk menentukan banyaknya graf tak terterhubung berdasaran

Menjumlahkan banyaknya graf dengan yang sama untuk seriap yang terbentuk

Memperoleh banyaknya graf tak terhubung untuk

(30)

BAB V KESIMPULAN

Berdasarkan observasi dan konstruksi graf berlabel tak terhubung tanpa loop dengan jumlah titik , maka dapat disimpulkan bahwa:

1. Banyaknya graf dengan dan dapat ditentukan dengan kaidah perkalian yaitu:

 Untuk diperoleh ( )

dengan:

: banyaknya titik : banyaknya garis

: banyaknya garis maksimal yang membuat graf tak terhubung dengan garis paralel dihitung satu

(31)

37 2. Banyaknya graf dengan dan adalah:

∑ ( )

( ) ( ) ( ) ( ) ( ) ( )

(32)

DAFTAR PUSTAKA

Agreusson, G. and Raymon, D. G. 2007. Graph Theory Modeling, Application, and Algorithms. Pearson/Prentice Education Inc, New Jersey.

Deo, N. 1998. Graph Teori with Applications to Engineering and Cooputer Science. Prentice Hall Inc, New York.

Harary, F. and Palmer, E.M. 1973. Graphical Enumeration. Academic Press, Inc. (London) Ltd., London.

Johnsonbaugh, R. 1998. Matematika Diskrit (Edisi Indonesia). Prenhallindo, Jakarta.

Liu, C.L. 1995. Dasar-Dasar Matematika Diskret. Gramedia Pustaka Utama, Jakarta.