SKRIPSI
EDWARD MP SIMAMORA 050803032
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PELABELAN SUPER EDGE MAGIC PADA KITE CYCLE GRAPH
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
EDWARD MP SIMAMORA 050803032
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2010
Judul : PELABELAN SUPER EDGE MAGIC PADA KITE CYCLE GRAPH
Kategori : SKRIPSI
Nama : EDWARD MP SIMAMORA
Nomor Induk Mahasiswa : 050803032
Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Medan, Juli 2010
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Ujian Sinulingga, M.Si Dra. Mardiningsih, M.Si NIP. 19560303 194803 1 004 NIP. 19630405 198811 2 001
Diketahui oleh
Departemen Matematika FMIPA USU Ketua,
ii
PERNYATAAN
PELABELAN SUPER EDGEMAGIC PADAKITE CYCLE GRAPH
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2010
EDWARD MP SIMAMORA 050803032
PENGHARGAAN
Puji dan syukur kehadirat Tuhan Yesus Kristus atas semua yang telah dibe-rikan sehingga penulis dapat menyelesaikan tulisan ini.Terpujilah Tuhan.
Penulis juga berterimakasih kepada semua pihak yang telah membantu pe-nulis dalam penyelesaian tulisan ini.Pertama-tama saya megucapkan terimakasih kepada ibu Dra.Mardiningsih,M.Si dan bapak Drs.Ujian Sinulingga,M.Si yang telah memberikan banyak masukan dan saran kepada penulis selama dalam pengerjaan tulisan ini.Penulis juga berterimakasih kepada bapak Drs.H Haluddin Panjaitan dan bapak Syahril Efendi,S.Si,M.IT sebagai dosen penguji penulis ,yang telah memberikan masukan kepada penulis.Penulis juga berterimakasih kepada bapak Dr.Saib Suwilo,M.Sc selaku Ketua Departemen Matematika FMIPA USU yang telah memberikan izin untuk mengerjakan tulisan ini.Penulis juga berterima kasih kepada seluruh dosen dan pegawai departemen matematika FMIPA USU yang telah membantu penulis selama menjalani pendidikan.
iv
ABSTRAK
GraphG= (V, E) disebut sebagai super edge magic jika terdapat pemetaan satu-satuλ dariV ∪E pada {1,2,3, . . . ,|V|+|E|}sehingga λ(V) ={1,2, . . . ,|V|}dan λ(x) +λ(xy) +λ(y) = k dimana k adalah suatu bilangan konstanta ajaib untuk setiap edge xy. Dalam tulisan ini, akan dikaji bahwa K2∪Cn adalah super edge
magic graf untukn= genap, serta untuk sebuah graf G= (n,2) kite adalah super edge magic juga untuk n = genap.
Super Edge Magic Labelling On Kite Cycle Graph
ABSTRACT
A Graph G(V, E) is called super eege-magic if there exists a one-to-one map λ from V ∪E onto {1,2,3, . . . ,|V|+|E|} such that λ(V) = {1,2,3, . . . ,|V|} and λ(x) +λ(xy) +λ(y) =k is constant for every edgexy. In this paper, we investigate K2∪Cnis a super edge magic graph ifn= even, anda also we investigateG= (n,2)
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK iv
ABSTRACT v
DAFTAR ISI vi
DAFTAR GAMBAR vii
1. PENDAHULUAN 1
1.1. Latar Belakang 1
1.2. Perumusan Masalah 2
1.3. Pembatasan Masalah 2
1.4. Tujuan Penelitian 3
1.5. Tinjauan Pustaka 3
1.6. Manfaat Penelitian 4
1.7. Metodologi Penelitian 4
2. LANDASAN TEORI 5
2.1. Konsep Dasar Graf 5
2.2. Jenis-jenis Graf 8
2.3. Terminologi Dasar 11
2.4. Pemetaan 14
2.5. Pelabelan Graf 15
3. PEMBAHASAN 19
3.1. PembuktianG= (n,2), kiteadalah super edge magic graf. 19 3.2. K2∪Cn adalah super edge magic graf 22
4. KESIMPULAN DAN SARAN 32
4.1. Kesimpulan 32
4.2. Saran 32
DAFTAR PUSTAKA 33
vi
Gambar Halaman
2.1 Graf 5
2.2 Simple Graf 6
2.3 Graf Kosong 7
2.4 Graf (7,8) 7
2.5 Graf Berarah dan Graf-Ganda Berarah 9
2.6 Graf Lengkap 10
2.7 Graf Teratur 10
2.8 Graf Bipartite 10
2.9 Graf 11
2.10 Graf Berbobot Dan Graf Berlabel 13
2.11 Gabungan Graf 13
2.12 Pemetaan Satu-satu 14
2.13 Pemetaan Korespondensi Satu-satu 15
2.14 edge magicvertex labeling 16
2.15 vertex magic total labeling 17
2.16 vertex magic edge labeling 17
2.17 edge magic total labeling 18
3.1 Graf untukn= 12 20
3.2 Graf untukn= 16 22
3.3 Graf untukn= 12 24
3.4 Graf untukn= 18 25
3.5 Graf untukn= 14 27
3.6 Graf untukn= 20 28
3.7 Graf untukn= 16 29
iv
ABSTRAK
GraphG= (V, E) disebut sebagai super edge magic jika terdapat pemetaan satu-satuλ dariV ∪E pada {1,2,3, . . . ,|V|+|E|}sehingga λ(V) ={1,2, . . . ,|V|}dan λ(x) +λ(xy) +λ(y) = k dimana k adalah suatu bilangan konstanta ajaib untuk setiap edge xy. Dalam tulisan ini, akan dikaji bahwa K2∪Cn adalah super edge
magic graf untukn= genap, serta untuk sebuah graf G= (n,2) kite adalah super edge magic juga untuk n = genap.
Super Edge Magic Labelling On Kite Cycle Graph
ABSTRACT
A Graph G(V, E) is called super eege-magic if there exists a one-to-one map λ from V ∪E onto {1,2,3, . . . ,|V|+|E|} such that λ(V) = {1,2,3, . . . ,|V|} and λ(x) +λ(xy) +λ(y) =k is constant for every edgexy. In this paper, we investigate K2∪Cnis a super edge magic graph ifn= even, anda also we investigateG= (n,2)
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Teori graf merupakan topik yang banyak mendapat perhatian saat ini, kare-na model - model yang ada pada teori graf bergukare-na untuk aplikasi yang luas. Walaupun teori graf berasal dari bidang ilmu matematika namun dalam penga-plikasiannya teori graf dapat dihubungkan dengan berbagai bidang ilmu dalam kehidupan sehari hari. Sedemikian banyaknya pengaplikasian graf dalam dunia ini, sehingga tidak ada habis-habisnya jika dibahas setiap aplikasi graf, karena se-tiap bidang ilmu dapat dikaitkan dengan graf seperti masalah jaringan komunikasi, transportasi, ilmu komputer, riset operasi, ilmu kimia, sosiologi, kartographi dan lain sebagainya.
Pelabelan graf merupakan suatu topik dalam teori graf. Objek kajiannya berupa graf yang secara umum direpresentasikan olehvertex atau edgeserta him-punan bagian bilangan cacah yang disebutlabel. Hingga saat ini pemanfaatan teori pelabelan graf sangat dirasakan peranannya, terutama pada sektor sistem komu-nikasi dan transportasi, navigasi geografis, radar, penyimpanan data komputer, dan pemancar frekuensi radio.
Dalam pelabelan juga telah banyak mengalami perkembangan baik dari ben-tuk pelabelannya maupun dari benben-tuk graf yang dilabeli. Dari benben-tuk pelabelan-nya, ada yang disebut pelabelan super edge magic ,edge magic, pelabelan total edge magic ataupun pelabelan super total edge magic
edge {x, y} di G, berlaku λ(x) +λ({x, y}) +λ(y) = k, untuk suatu konstanta tetap k. Sedangkan disebut pelabelan super edge magic jika λ(V) = {1,2, . . . , v} dan λ{E}={v+ 1, v+ 2, . . . , v+e}.
Pelabelan pertama kali diperkenalkan oleh Sadlack(1964),kemudian Stewart (1966). Sedangkan untuk pelabelan yang Berhubungan dengan Magic value per-tama kali diperkenalkan oleh Kotzig dan Rosa (1970) dalam jurnalnya Magic va-luation Of finite graph. Sejak saat itu hingga kini penelitian mengenaiedge magic masih hangat untuk diteliti.
Kite graph adalah Graf G∗Pm dimana G adalah graf terhubung dan Pm adalah lintasan dengan m vertex sehingga vertex akhir di Pm adalah vertex di G. Sedangkan jika graf G dengan v vertex dan e edge diberi label 1 hingga (v+e) demikian sehingga apabila setiap label edge dan dua buah vertex yang adjasen padaedge tersebut dijumlahkan menghasilkan jumlah yang sama, maka graf Graf Gdisebut edge magic graf.
W.D Wallis Telah menunjukkan bahwaG+(n,1),kiteadalah super edge ma-gic jikan adalah genap.dalam tulisan ini akan ditunjukkan bahwa G= (n,2), kite adalah super edge magic. W.D Wallis juga menunjukkan bahwa K2 ∪C3 bukan
super edge magic tetapiK2 ∪C4 adalah super edge magic.
1.2 Perumusan Masalah
Yang menjadi permasalahan dalam studi ini adalah apakah GrafG= (n,2), kitedan GrafK2∪Cn adalah super edge magic atau tidak jika n adalah genap.
1.3 Pembatasan Masalah
3
1.4 Tujuan Penelitian
Yang menjadi tujuan dalam penelitian ini adalah untuk mengkaji bahwa graf G= (n,2), kitedan graf K2∪Cn adalah pelabelan super edge magic.
1.5 Tinjauan Pustaka
Sebagai pendukung teori dalam penulisan studi ini, penulis menggunakan beberapa buku dan jurnal, antara lain :
Narsingh Deo,1980 pada bukunya menyatakan bahwa grafG= (V, E) terdiri dari himpunan V = {v1, v2, . . . ,} yang disebut vertex, dan himpunan lain E =
{e1, e2, . . .} dan disebut edge.
Tereza Kovarova, pada jurnalnya menyatakan pelabelan adalah sebuah pe-metaan dimana domainnya adalah himpunan beberapa elemen graf, himpunan dari vertex atau himpunan semua vertex dan edge, dimana himpunan tersebut adalah bilangan bulat positif.
Anton Kotzig dan Alexander Rosa, 1970. Sebuah graf G(m, n) dikatakan memiliki nilai ajaib (M-valuation), dengan konstanta c jika terdapat pemetaan satu-satuf :V(G)∪E(G)→ {1,2, . . . , m+n}sehingga f(a) +f(b) +f([a, b]) =C untuk semua [a, b]∈E(G).
Kristina Wijaya dan Edi Tri Baskoro, 2008 pada jurnalnya menyatakan bah-wa Pelabelan Total edge magic pada graf G dengan himpunan vertex V(G) dan himpunanedge E(G) adalah suatu pemetaan satu-satu pada λdari V(G)∪E(G) ke himpunan{1,2, . . . ,|V(G)∪E(G)|}yang mempunyai sifat bahwa untuk setiap edge{x, y}diG, berlakuλ(x) +λ({x, y})+λ(y) =k, untuk suatu konstanta tetap k.
1.6 Manfaat Penelitian
Adapun yang menjadi manfaat penelitian ini adalah kiranya dengan tulisan ini penelitian tentang pelabelan graf bertambah serta sebagai bahan literatur bagi
pembaca yang akan melakukan penelitian tentang pelabelan graf.terutama dalam pelabelan super edge magic kedepannya.
1.7 Metodologi Penelitian
Metode penelitian yang akan digunakan dalam studi ini adalah penelitian literature yaitu mengumpulkan informasi dari beberapa buku dan jurnal yang berhubungan dengan pengerjaan penelitian ini.Adapun sistematika penulisan yang akan dikerjakan adalah :
1. Menjelaskan Graf secara umum serta graf Kite danCycle serta graf komplit.
2. Menjelaskan Pelabelan secara umum.
3. Menjelaskan pengertian nilai magic,edge magic dan super edge magic
4. Mengkaji bahwa Graf G = (n,2), kite dan Graf K2∪Cn adalah super edge
magic jikan adalah genap.
BAB 2
LANDASAN TEORI
2.1 Konsep Dasar Graf
Definisi 2.1.1 Sebuah grafGadalah pasangan(V, E)dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang anggotanya adalah pasangan-pasangan tak berurut dan disebut dengan edge.
Gambaran umum mengenai graf diartikan sebagai diagram, dimana vertex disajikan berupa vertex dan dinotasikan dengan vi;i = 1,2,3, . . . , m dan edge disajikan berupa garis lurus atau garis lengkung yang menghubungkan dua buah vertex (vi, vj) dan dapat dinotasikan dengan ei;i= 1,2,3, . . . , n.
Definisi 2.1.1 menyatakan bahwa V tidak boleh kosong, sedangkan E boleh kosong. Jadi, sebuah graf dimungkinkan tidak mempunyai edge satu buah pun, tetapivertexnya harus minimal ada satu.
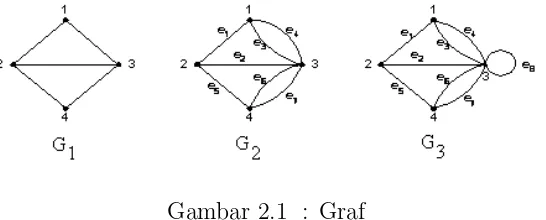
Sebagai ilustrasi dapat dilihat gambar 2.1 yaitu :
Gambar 2.1 : Graf
- G1 adalah graf dengan V ={1,2,3,4} dan E ={(1,2),(1,3),(2,3),(3,4)}.
- G2 adalah graf dengan V ={1,2,3,4} dan E ={(1,2),(2,3),(1,3),(2,4),
(3,4),(3,4)}={e1, e2, e3, e4, e5, e6, e7}
- G3 adalah graf dengan V ={1,2,3,4} dan E ={(1,2),(2,3),(1,3),(1,3),
(2,4),(3,4),(3,4),(3,3)}={e1, e2, e3, e4, e5, e6, e7, e8}
Definisi 2.1.2 Loop dan Edge Paralel
Sebuahedgeyang menghubungkan pasanganvertexyang sama yakni(vi, vj)disebut loop dan dua buah atau lebihedgeyang mempunyaivertex vertexujung yang sama disebutedge-edge yang paralel atau multiple edge. Pada gambar 2.1 dapat dilihat, gambar G1 tidak memiliki loop maupun edge pararel, sedangkan pada gambar G2
tidak memiliki loop tetapi memiliki edge paralel yaitu e3, e4 dan e1, e6. Dan pada
gambar G3 memiliki loop yaitu e8 dan edge pararel yaitu e3, e4 dan e1, e6.
Definisi 2.1.3 Graf Sederhana (Simple Graf)
Simple graf adalah graf yang tidak memuat loop dan edge-edge yang pararel.
Gambar 2.2 : Simple Graf
Definisi 2.1.4 Ketetanggaan (Adjacent)
Dua buah vertex pada graf dikatakan bertetangga bila kedua vertex tersebut ter-hubung langsung. Atau dapat kita sebutvj bertetangga dengan vk pada graf G jika
(vj, vk) adalah edge pada sebuah graf G.
Definisi 2.1.5 Bersisian (Incident)
7
Definisi 2.1.6 Vertex Terpencil (Isolated Vertex )
Vertexyang tidak memiliki edge yang bersisian dengannya atau tidak bertetangga dengan vertexlainnya disebut dengan vertex terpencil.
Definisi 2.1.7 Graf Kosong (Null Graf)
Graf yang himpunanedgenya merupakan himpunan kosong(Nn)disebut graf kosong, dimananadalah jumlah vertex.
Gambar 2.3 : Graf Kosong
Definisi 2.1.8 Derajat (Degree)
Derajat dari sebuah vertex vi dalam graf G adalah jumlah edge yang bersisian dengan vi, dengan loop dihitung dua kali. Bila jumlah edge yang bersisian dengan jumlah vertex vi adalah n maka degree dari vi adalah n sehingga d(vi) =n.
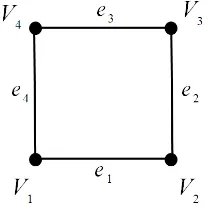
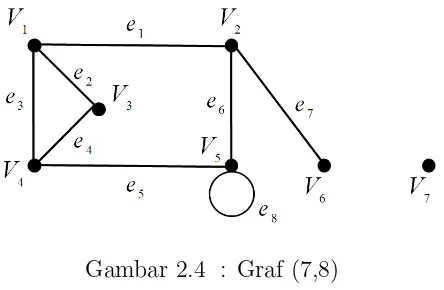
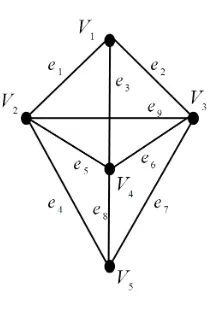
Gambar 2.4 : Graf (7,8)
Dari gambar 2.4 makaV ={v1, v2, v3, v4, v5, v6, v7}danE ={e1, e2, e3, e4, e5, e6, e7, e8}
- Vertex 1 bertetangga dengan vertex 2, 3 dan 4 tetapi tidak bertetangga dengan vertex 5 dan 6.
- Vertex5 bertetangga denganvertex 2 dan 4 tetapi tidak bertetangga dengan vertex 1, 3, 4 dan 6.
- Edge(1,2) bersisian dengan vertex 1 dan vertex 2.
- Edge(1,4) bersisian dengan vertex 1 dan vertex 4.
- Tetapi edge (3,4) tidak bersisian dengan vertex 1, 2, 5, 6 dan 7.
- Vertexterpencil adalah vertex 7.
- Derajat d(1) = d(2) =d(4) = 3, d(3) = d(5) = 2 dand(6) = 1 dan d(7) = 0.
2.2 Jenis-jenis Graf
Berdasarkan ada tidaknya gelang atau edge ganda pada suatu graf, maka graf digolongkan menjadi dua jenis:
1. Graf sederhana (Simple Graf)
Graf yang tidak mengandung gelang maupun edge-ganda dinamakan graf sederhana.
2. Graf tak-sederhana (Unsimple-Graf)
Graf yang mengandungedgeganda atau gelang dinamakan graf tak-sederhana (unsimple graf).
Berdasarkan jumlah vertex pada suatu graf, maka secara umum graf dapat digolongkan menjadi dua jenis:
9
2. Graf tak-berhingga (Unlimited Graf)
Graf yang jumlah vertexnya n tidak berhingga banyaknya disebut graf tak berhingga.
Berdasarkan orientasi arah pada edge, maka secara umum graf dibedakan atas 2 jenis:
1. Graf tak-berarah (Undirected Graf)
Graf yang edgenya tidak mempunyai orientasi arah disebut graf tak-berarah.
2. Graf berarah (Directed Graf atau Digraf )
Graf yang setiap edgenya diberikan orientasi arah disebut sebagai graf be-rarah.
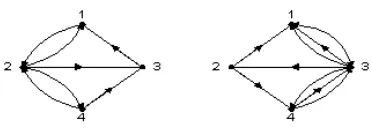
Gambar 2.5 : Graf Berarah dan Graf-Ganda Berarah
Ada juga graf sederhana khusus yang terdiri dari:
a. Graf lengkap (Complete Graf)
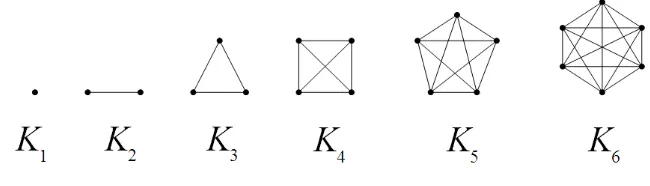
Graf lengkap ialah graf sederhana yang setiap vertexnya mempunyai edge ke semua vertex lainnya. Graf lengkap dengan n buah vertex dilambangkan dengan Kn. Jumlah edge pada graf lengkap yang terdiri darin buah vertex adalah n(n1)/2.
Gambar 2.6 : Graf Lengkap
b. Graf teratur (Regular Graf)
Graf yang setiap vertexnya mempunyai derajat yang sama disebut graf te-ratur. Apabila derajat setiap vertex adalah r, maka graf tersebut disebut sebagai graf teratur derajatr. Jumlah edge pada graf teratur adalah nr/2.
Gambar 2.7 : Graf Teratur
c. Graf bipartisi (Bipartite Graf)
Graf G yang himpunan vertexnya dapat dipisah menjadi dua himpunan bagian V1 dan V2, sedemikian sehingga setiap edge pada G menghubungkan
sebuah vertex di V1 ke sebuah vertex di V2 disebut graf bipartite dan
diny-atakan sebagai G(V1, V2).
11
2.3 Terminologi Dasar
Definisi 2.3.1 Walk
Suatu walk dalam graf G adalah suatu barisan berhingga dari vertex dan edge secara bergantian yang dimulai dan diakhiri dengan vertex sehingga setiap edge yang bersisian denganvertex sebelum dan sesudahnya, dimana sebuah edgehanya dilalui satu kali. Di dalam suatu walk pada sebuah graf dapat terjadi bahwa satu vertexdilalui lebih dari satu kali. Pada umumnya penulisan barisanwalk biasanya mengikutsertakan edgenya, tetapi boleh juga tidak.
Apabila vertexawal dan akhir dari suatu walk adalah sama, makawalk yang demikian disebut dengan closed walk (walk tertutup). Sedangkan bilavertex awal dan vertex akhir dari suatu walk berbeda, maka walk yang demikian disebut open walk (walk terbuka). Sebagai contoh diberikan pada gambar berikut :
Gambar 2.9 : Graf
Pada gambar tersebut dapat diambil beberapa walk diantaranya sebagai berikut :
- v1e1v2e4v6e7v5e6v3e2v1 (open walk)
- v1e2v3e6v5e7v6 (open walk)
Walk di atas boleh juga ditulis dengan cara sebagai berikut :
- v1v2v6v5v3v1 (closed walk)
- v1v3v5v6 (open walk)
Definisi 2.3.2 Trail
Walk yang semua edge di dalam setiap barisan harus berbeda disebut trail. Trail tertutup adalah suatu trail dengan vertexawal dan vertexakhir yang sama.
Dari gambar 2.11, salah satu contoh yang merupakantrailadalah : v1v2e3v3e6v5e7v6
e4v2e1v1
Definisi 2.3.3 Lintasan (Path)
Path dari suatu graf G adalah suatu walk yang keseluruhan vertex nya berbeda kecuali vertex awal dan vertex akhir yang boleh sama. Bila dalam suatu path di mana vertex awal dan akhir sama maka path yang demikian disebut closed path (path tertutup), sedangkan bila vertex awal dan akhir tidak sama maka disebut open path (path terbuka).
Sebagai contoh lihat gambar 2.11
- v1v3v5v3v2v6 (open path)
- v5v3v6v2v1v5 (closed path)
Definisi 2.3.4 Sirkuit (Cycle)
13
Definisi 2.3.5 Kite graf
Kite graf adalah suatu gabungan graf G dengan sebuah path yang mana vertex akhir dari path merupakan vertex dari G.
Definisi 2.3.6 Graf Berbobot Dan Graf Berlabel
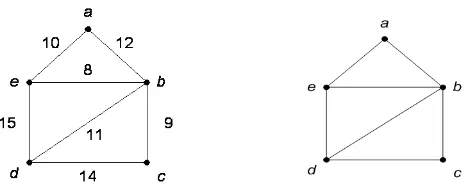
Graf berbobot graf yang setiap edgenya diberi sebuah bobot sedangkan graf berlabel adalah graf yang tidak memiliki bobot
Gambar 2.10 : Graf Berbobot Dan Graf Berlabel
Definisi 2.3.7 Graf gabungan
Misal ada dua buah graf G1 dan G2 dimana himpunan V(G1) dan V(G2) saling
asing begitu juga himpunan E(G1) dan E(G1) maka gabungan graf dinotasikan
G1∪G2 adalah graf yang mempunyai himpunanvertexV(G1∪G2) =V(G1)∪V(G2)
dan himpunan edge E(G1∪G2) =E(G1)∪E(G2).
Contoh:
Gambar 2.11 : Gabungan Graf
2.4 Pemetaan
Definisi 2.4.1 Misalkan AdanB adalah dua himpunan yang tidak kosong. Suatu cara atau aturan yang memasangkan setiap elemen dari himpunan Adengan tepat
satu elemen di himpunan B disebut pemetaan dari himpunan A ke himpunan B.
Pemetaan dari himpunan A ke himpunan B diberi notasi λ, yaitu λ:A→B.
Selanjutnya himpunan A disebut sebagai daerah asal (domain) dan himpunanB disebut daerah kawan (kodomain). Secara umum, pemetaan dapat digolongkan menjadi 3 golongan sebagai berikut :
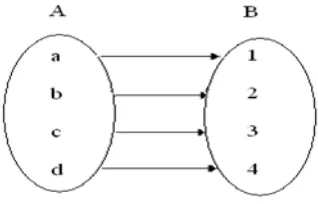
Definisi 2.4.2 Pemetaan satu-satu (injektif)adalah pemetaan dimana setiap elemen di daerah kodomain yang berpasangan mempunyai pasangan elemen tepat
satu di daerah domain, dapat dituliskan secara matematika berikut :
Pemetaan λ:A→B, injektif ↔ ∀x, y∈ A, λ(x) =λ(y)→x=y
Contoh :
Gambar 2.12 : Pemetaan Satu-satu
15
dituliskan secara matematika berikut : Pemetaan λ: A→ B, surjektif ↔ ∀x ∈ A,∃y∈B,∋λ(x) =y
Definisi 2.4.4 Pemetaan korespondensi satu-satu (bijektif) adalah peme-taan yang memenuhi pemepeme-taan injektif dan pemepeme-taan surjektif. Istilah ini berasal
dari kenyataan bahwa setiap elemen domain akan berkorespondensi secara unik ke
elemen kodomain dan sebaliknya.
Contoh:
Gambar 2.13 : Pemetaan Korespondensi Satu-satu
2.5 Pelabelan Graf
Definisi 2.5.1 Pelabelan pada suatu graf adalah sebarang pemetaan atau fungsi yang memasangkan unsur unsur graf (vertex atau edge) dengan bilangan (bi-asanya bilangan bulat positif ). Jika domain dari pemetaan adalah vertex, maka pelabelan disebut pelabelan vertex (vertex labeling). Jika domainnya adalah edge, maka disebut pelabelan edge (edge labeling), dan jika domainnya vertexdanedge, maka disebut pelabelan total (total labeling).
Pada graf terdapat banyak jenis pelabelan.
E ke himpunan bilangan integer positif yang berbeda, sehingga untuk setiap vertex v∈V, penjumlahan semua label edge e yang insiden terhadap vertexv sama.
Berikut ini beberapa jenis pelabelan ajaib pada suatu graf.
a. MisalkanG graf dengan himpunanvertex V dan himpunan edge E. Banyak vertexdiGadalahpdan banyakedgediGadalahq. Pelabelanvertex edge ajaib (edge-magic vertex labeling) pada graf G adalah pemetaan bijektif dari V pada himpunan {1,2,3, . . . , p} sehingga untuk sebarang edge(xy) di G berlaku (x) + (y) = k untuk suatu konstanta k. Selanjutnya k disebut konstanta ajaib padaG dan G disebut graf vertex edge ajaib.
Contoh:
Gambar 2.14 : edge magic vertex labeling
b. MisalkanG graf dengan himpunanvertex V dan himpunan edge E. Banyak vertex di G adalah p, banyakedge di G adalah q dan h merupakan banyak vertex dan edge pada graf G atau h = p+ q. Pelabelan total vertex ajaib (vertex-magic total labeling) pada graf G adalah pemetaan bijektif dariV E pada himpunan {1,2,3, . . . , h}sehingga untuk sebarangvertex xdi Gberlakuλ(x) +P
λ(xy) =k dengan y merupakan vertex yang berdekatan dengan vertexx. Selanjutnyak disebut konstanta ajaib pada Gdan G dise-but graf total vertex ajaib.
17
Gambar 2.15 : vertex magic total labeling
c. MisalkanG graf dengan himpunanvertex V dan himpunan edge E. Banyak vertexdiGadalahpdan banyakedgediGadalahq. Pelabelanedge vertex ajaib(vertex-magic edge labeling) pada grafGadalah pemetaan bijektif dari E pada himpunan {1,2,3, . . . , q} sehingga untuk sebarang vertex x di G berlaku:
X
λ(xy)
dengan ymerupakan vertex yang berdekatan dengan vertex x. Selanjutnyak disebut konstanta ajaib pada G dan Gdisebut graf edge vertex ajaib. Contoh:
Gambar 2.16 : vertex magicedge labeling
d. MisalkanG graf dengan himpunanvertex V dan himpunan edge E. Banyak vertex di G adalah p, banyakedge di G adalah q dan h merupakan banyak vertex dan edge pada graf G atau h =p+q. Pelabelan total edge ajaib (edge-magic total labeling) pada graf G adalah pemetaan bijektif dari V E pada himpunan{1,2,3, . . . , h}sehingga untuk sebarangedgexydiGberlaku (x) + (xy) + (y) = k.
Gdisebut graf total edge ajaib. Contoh:
BAB 3
PEMBAHASAN
Dalam tulisan ini akan ditunjukkan beberapa bentuk graf yang termasuk atau tidak termasuk dalam pelabelan super edge magic, dengan demikian dapat ditunjukkan bahwa graf tersebut adalah super edge magic graf. Sebuah kite(n, t) adalah sebuah cycle dengan panjang nserta dengan tadalah ekor yang menempel pada salah satu vertex cycle. Wallis et al. Telah menunjukkan kite(n,1) adalah super edge magicgraf. Dalam tulisan ini akan ditunjukkan bahwakite(n,2) adalah super edge magic graf jika n adalah genap. Preposisi berikut akan menunjukkan bahwa kite(n,2) adalah super edge magic graf dan juga akan ditunjukkan cara melabelinya.
3.1 Pembuktian G= (n,2), kite adalah super edge magic graf.
Proposisi 3.1.1 Andaikan G= (n,2), kite. GrafGadalah super edge magic jika n adalah genap.
Bukti. Andaikan v0, v1, . . . , vn−1, v0 adalah vertexdari Cn, Sebuahvertex v
berte-tangga dengan v0 dan vertex ω bertetangga dengan vertex v. Andaikan terdapat
pelabelansuper edge magicλdariGdengan bilangan magick. Sehinggaλ(v0) =α
dan λ(ω) =β. Maka
k(n+ 2) = X xy∈E(G)
{λ(x) +λ(xy) +λ(y)}
= 2 X x∈V(G)
λ(x) +λ(v0)−λ(ω) + X
xy∈E(G)
λ(xy)
= (n+ 2)(5n+ 13)
Hal ini mengakibatkan bahwa k −(α −β)/(n + 2) = (5n+ 13)/2 adalah bilangan rasional sehingga tidak intejer, karena 0<|(α−β)/(n+2)|<1. Sehingga n harus genap. Misalkan n = 2m+ 2 untuk bilangan bulat positif m. V(G) = {v0, v1, . . . , vn−1, v, w}danE(G) ={vivi+1|0≤i≤n−2}∪{vn−1v0}∪{v0v}∪{vw}
.
Diperoleh pelabelan λ:V ∪E → {1,2, . . . ,4m+ 8}
. Diambilm ganjil maka diperoleh label untuk setiap vertex sebagai berikut
λ(vi) =
(m−i+ 1)/2 untuk i= 0,2, ..., m−3, m−1
(3m−i+ 4)/2 untuk i= 1,3, ..., m−2, m
(3m−i+ 3)/2 untuk i=m+ 1, m+ 3, ...,2m
(5m−i+ 10)/2 untuk i=m+ 2, m+ 4, ...,2m+ 1
λ(v) = (3m+ 7)/2
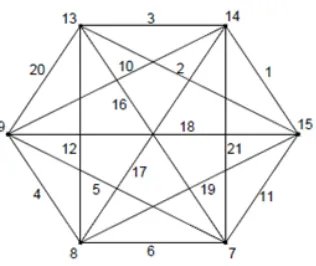
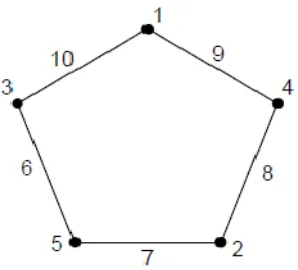
[image:31.612.149.476.251.608.2]λ(w) = (3m+ 5)/2
21
Gambar 3.1.Menunjukkan pelabelan pada bukti preposisi 2.1
λ(vivi+1) =
3m+i+ 9 jika 06i6m−i
3m+ 8 jika i=m
m+i+ 5 jika m+ 16i62m
λ(vn−1v0) = 3m+ 6
λ(v0v) = 3m+ 7
λ(vw) = 2m+ 5
Bila dilihat kembali gambar 3.1 maka akan dapat dilihat bahwaλadalah pelabelan
super edge magic dari G dengan bilangan edge magic sebagai berikut :
Dimana syarat suatu pelabelan edge magic dari graf G adalah: λ(v) +λ(vw) + λ(w) =k maka diperoleh 3m2+7 + (2m+ 5) + (3m+ 5)/2 = 5m+ 11 =k.
Ambilm genap maka akan diperoleh label sebagai berikut:
λ(vi) =
(m+i)/2 jika i= 0,2, ..., m−2
(3m+i+ 9)/2 jika i= 1,3, ..., m−1
(m+i+ 2)/2 jika i=m+ 1
(i−m−1)/2 jika i =m, m+ 2, ...,2m
(3m+ 6)/2 jika i=m+ 3, m+ 5, ...,2m−1
Sedangkan untuk pelabelan dari ekornya adalah :
λ(v) = (3m+ 8)/2
λ(w) = (3m+ 4)/2
Dan untuk pelabelanedgenya:
λ(vivi+1) =
3m−i+ 6 untuk i= 0,1, ..., m−2
2m+ 6 untuk i=m−1
4m−i+ 10 untuk i=m, m+ 1
5m−i+ 10 untuk i=m+ 2, m+ 3, ...,2m−1
λ(vn−1v0) = 3m+ 8
λ(v0v) = 3m+ 7
λ(vw) = 2m+ 5
Untuk mempermudah dapat dilihat gambar 3.2, sehingga ditunjukkan bahwa λ
[image:33.612.251.377.237.400.2]adalah pelabelan superedge magic dariGdengan nilai magic 5m+ 11 sehingga G adalah super edge magic.sehingga preposisi 3.1 terbukti.
Gambar 3.2 : Graf untuk n= 16
3.2 K2∪Cn adalah super edge magic graf
Komplit Graf adalah graf sederhana yang mana semua vertexnya dihubungkan oleh satuedge ,komplit graf biasanya dilambangkan dengan Kn yang berarti kom-plit graf dengan n vertex. Cycle adalah graf yang derajatnya selalu dua dimana jumlahvertexnya minimal 3 atau lebih, sebuah Cycle biasanya dilambangkan den-gan Cn yang berarti cycle graf dengan n vertex dimana n ≥ 3. Berikut ini akan ditunjukkan penggabungan dua buah graf yang saling disjoint merupakan super edge magic graf. Graf yang digabungkan adalah sebuah komplit graf dan sebuah cycle graf yang dinotasikan dengan K2 ∪Cn. W.D Wallis membuktikan bahwa
K2 ∪C3 bukan super edge magic tetapi K2∪C4 adalah super edge magic. Wallis
mengajukan untuk nilain yang bagaimana agarK2∪Cn adalah superedge magic.
23
Teorema 3.2.1 jika n adalah genap (n 6= 10) maka K2 ∪Cn adalah super edge
magic graf.
Bukti. Andaikan v0, v1, . . . , vn−1, v0 adalah vertex dari Cn serta u dan w adalah
vertex dari K2. Kemudian andaikan n = 2m untuk m bilangan bulat positif.
V(G) = {v0, v1, . . . , vn−1, u, w} dan E(G) = {vivi+1|0 ≤ i ≤ n −2} ∪ {vn−1v0} ∪
{uw}. Sehingga diperoleh pelabelan λ:V ∪E → {1,2, . . . , v+ 3} sebagai berikut : ambiln ≥6:
Case m≡0( mod 6).
λ(vi) =
m+ 2 +i/2 untuk i= 0,2, ..., m−2
(i+ 1)/2 untuk i= 1,3, ..., m−1
(3m+ 8)/2 untuk i=m
Untukm+ 1≤ i≤n−1, maka
λ(vi) =
(i+ 3)/2 untuk i≡1 (mod 6)
m+ 2 +i/2 untuk i≡2 (mod 6)
(i+ 5)/2 untuk i≡3 (mod 6)
m+ 3 +i/2 untuk i≡4 (mod 6)
(i+ 1)/2 untuk i≡5 (mod 6)
m+ 4 +i/2 untuk i≡0 (mod 6)
λ(u) = (m+ 2)/2
λ(w) = (3m+ 4)/2 Untuk labeledgenya dapat diperoleh dengan :
λ(vivi+1) =
4m−i+ 3 untuk06i6m−2
3m+ 2 untuk i=m−1
Gambar 3.3 : Graf untuk n= 12
Untukm≤i≤n−2, maka
λ(vivi+1) =
4m+ 2−i jika i≡1 (mod 3)
4m+ 1−i jika i≡ 2 (mod 3)
4m−i jika i≡ 2 (mod 3)
λ(v0vn−1) = 3m+ 4
λ(uw) = 3m+ 3
Gambar 3.3 sebagai ilustrasi. Dapat dilihat bahwaλ adalah superedgemagic dari Gdengan magic number 5m+ 6.
Case m≡3( mod 6)
λ(vi) =
m+ 2 +i/2 untuk i= 0,2, ..., m−1
(i+ 1)/2 untuk i= 1,3, ..., m−2
[image:35.612.184.444.292.448.2]25
Jikam+ 1≤i≤n−1, maka
λ(vi) =
(i+ 3)/2 untuk i≡1 (mod 6)
m+ 2 +i/2 untuk i≡ 2 (mod 6)
(i+ 5)/2 untuk i≡3 (mod 6)
m+ 3 +i/2 untuk i≡ 4 (mod 6)
(i+ 1)/2 untuk i≡5 (mod 6)
m+ 4 +i/2 untuk i≡0 (mod 6)
λ(u) = m+ 1 2 λ(w) = 3m+ 5
2
λ(vivi+1) =
4m−i+ 3 untuk06i6m−2
[image:36.612.178.450.99.615.2]3m+ 2 untuk i=m−1
Gambar 3.4 : Graf untuk n= 18
Jika m≤i≤n−2, maka
λ(vivi+1) =
4m+ 2−i jika i≡1 (mod 3)
4m+ 1−i jika i≡2 (mod 3)
4m−i jika i≡0 (mod 3)
λ(v0vn−1) = 3m+ 4
Dari gambar 3.4 dilihat bahwa λ adalah super edge magic dari G dengan magic number 5m+ 6.
Case m≡1( mod 6), maka
λ(vi) =
m+ 2 +i/2 jika i= 0,1, ..., m−1
(i+ 1)/2 jika i = 1,3, ..., m−2
(m+ 5)/2 jika i=m
Jikam+ 1≤i≤n−1, maka
λ(vi) =
(i+ 1)/2 jika i≡1 (mod 6)
m+ 4 +i/2 jika i≡2 (mod 6)
(i+ 3)/2 jika i≡3 (mod 6)
m+ 2 +i/2 jika i≡4 (mod 6)
(i+ 5)/2 jika i≡5 (mod 6)
m+ 3 +i/2 jika i≡0 (mod 6)
(m+ 3)/2 jika i≡m+ 2
λ(u) = (m+ 1) 2 λ(w) = (3m+ 5)
2
λ(vivi+1) =
4m−i+ 3 jika06i6m−2
3m+ 2 jika i=m−1
2m+i−1 jika m6 i6m+ 2 Jika m+ 3≤i≤n−2, maka
λ(vivi+1) =
4m+ 1−i jika i≡ 1 ( mod 3)
4m−i jika i≡ 2 ( mod 3)
4m+ 2−i jika i≡ 0 ( mod 3)
27
Gambar 3.5 : Graf untuk n= 14
Dari gambar 3.5 dapat dilihat bahwa λ adalah pelabelan super edge magic dari grafG dengan magic number 5m+ 6.
Case m≡4( mod 6), maka
λ(vi) =
m+ 2 +i/2 jika i= 0,2, ..., m−2
(i+ 2)/2 jika i= 1,3, ..., m−2
3m/2 + 4 jika i=m
Jikam+ 1≤i≤n−1, maka
λ(vi) =
(i+ 1)/2 jika i≡1 (mod 6)
m+ 4 +i/2 jika i≡2 (mod 6)
(i+ 3)/2 jika i≡3 (mod 6)
m+ 2 +i/2 jika i≡4 (mod 6)
(i+ 5)/2 jika i≡5 (mod 6)
m+ 3 +i/2 jika i≡0 (mod 6)
3m/2 + 3 jika i≡m+ 2
Jika m+ 3≤i≤n−2, maka
λ(vivi+1) =
4m+ 1−i jika i≡ 1 ( mod 3)
4m−i jika i≡ 2 ( mod 3)
Gambar 3.6 : Graf untuk n= 20
λ(v0vn−1) = 3m+ 4
λ(uw) = 3m+ 3
Dengan melihat gambar 3.6 maka dapat dilihat bahwa λ adalah pelabelan super edge magic dari graf G edge magic number 5m+ 6.
Case m≡2( mod 6)
λ(vi) =
m+ 2 +i/2 jika i= 0,2, ..., m−2
(i+ 1)/2 jika i = 1,3, ..., m−1
3m/2 + 4 jika i=m
(2m−i+ 7)/2 jika i=m+ 1, m+ 3
3m/2 + 3 jika i=m+ 2
2m−i/2 + 8 jika i=m+ 4, m+ 6
Jikai =m+ 5, m+ 7≤i≤n−1, maka
λ(vi) =
(i+ 5)/2 jika i≡1 (mod 6)
m+ 3 +i/2 jika i≡2 (mod 6)
(i+ 1)/2 jika i≡3 (mod 6)
m+ 4 +i/2 jika i≡4 (mod 6)
29
λ(u) = (m+ 2) 2 λ(w) = (3m+ 4)
[image:40.612.111.468.65.664.2]2
Gambar 3.7 : Graf untuk n= 16
λ(vivi+1) =
4m−i+ 3 jika06 i6m−2
3m+ 2 jika i =m−1
2m+i−1 jika m6i6m+ 2
3m−2 jika i=m+ 3
2m+i−9 jika m+ 4 6i6 m+ 6 Jikam+ 7≤i≤n−2, maka
λ(vivi+1) =
4m−i jika i≡ 1 ( mod 3)
4m+ 2−i jika i≡ 2 ( mod 3)
4m+ 1−i jika i≡ 0 ( mod 3)
Case m≡5( mod 6) λ(vi) =
m+ 2 +i/2 jika i= 0,2, ..., m−1
(i+ 1)/2 jika i= 1,3, ..., m−2
(m+ 5)/2 jika i=m
(4m−i+ 10)/2 jika i=m+ 1, m+ 3
(m+ 3)/2 jika i=m+ 2
(2m−i+ 13)/2 jika i=m+ 4, m+ 6
Jikai=m+ 5, m+ 7≤i≤n−1, maka
λ(vi) =
(i+ 5)/2 jika i≡1 (mod 6)
m+ 3 +i/2 jika i≡2 (mod 6)
(i+ 1)/2 jika i≡3 (mod 6)
m+ 4 +i/2 jika i≡4 (mod 6)
(i+ 3)/2 jika i≡5 (mod 6)
m+ 2 +i/2 jika i≡0 (mod 6)
λ(u) = m+ 1 2 λ(w) = 3m+ 5
[image:41.612.150.448.83.755.2]2
31
λ(vivi+1) =
4m−i+ 3 jika06 i6m−2
3m+ 2 jika i =m−1
2m+i−1 jika m6i6m+ 2
3m−2 jika i=m+ 3
2m+i−9 jika m+ 4 6i6 m+ 6 Jikam+ 7≤i≤n−2, maka
λ(vivi+1) =
4m−i jika i≡ 1 ( mod 3)
4m+ 2−i jika i≡ 2 ( mod 3)
4m+ 1−i jika i≡ 0 ( mod 3)
λ(v0vn−1) = 3m+ 4
λ(uw) = 3m+ 3
Dengan melihat gambar 3.8 dapat ditunjukkan bahwa λ adalah pelabelan super edge magic dengan magic number 5m+ 6. Dengan demikian graf Gadalah super edge magic.Dari case yang sudah dikerjakan maka dengan demikianteorema3.2
terbukti.
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Super edge magic graf dibentuk melalui pelabelan super edge magic. Dengan pembuktian yang sudah diperoleh maka graf G = (n,2) kite adalah super edge magic graph, begitu pula dengan gabungan graf antara c komplit graf K2 dan
cycle graf Cn(K2 ∪Cn) adalah super edge magic graf, karena berlaku pelabelan
super edge magic.
4.2 Saran
Dalam tulisan ini dibahas masalah pelabelan super edge magic untuk menge-tahui apakah graph tersebut adalah super edge magic graf . Bagi para pembaca
33
DAFTAR PUSTAKA
Adidarma Sepang, et al. 2008. Diakses tanggal 26 Februari 2010. pukul 19.34. Super Edge Magic Total Labeling on Unicyclic Graphs. Jour-nal.ui.ac.id/?hal=detailArtikel&q=366
Anton Kotzig dan Alexander Rosa. 1970. Diakses tanggal 1 Maret 2010. pukul 16.23. Magic Valuations of finite Graphs. www.cms.math.ca/cmb/v13/p451
Deo Narsingh.1980.Graph Theory with Applications to Engineering and Com-puter Science. New Delhi: Prentice Hall of India Privated Limited. Kristina Wijaya dan Edy Tri Baskoro. 2008. Diakses tanggal 25 Februari
2010, pukul 00.03.Pelabelan Total Sisi Ajaib pada Hasilkali Dua Graf.. personal.fmipa.itb.ac.id
Krishnappa, H.K, et al. 2000. Diakses tanggal 20 September 2009, pukul 07.51. Vertex Magic Total Labellings of Complete Graphs. Cstar.iiit.ac.in/ kkishore/vmt1-iwogl.pdf
H.Enomoto,et al.1998.Diakses tanggal 1 maret 2010.pukul 16.25. Induced graph theorem Magic valuation.www.cms.math.ca
Sin-Min Lee,et al.2007.diakses tanggal 1 maret 2010.pukul 16.30.on the edge-magic indices of (v, v+ 1).www.cms.math.ca
Gallian Joseph A.1997.Diakses tanggal 20 Februari 2010,pukul 10.30. A dy-namic survey of Graph labelling.jgallian@d.umn.edu
Nicholas cavenagh,et al.2006.Diakses tanggal 24 Februari 2010,pukul 21.37. Edge- magic group labelling of countable graphs.maths.unsw.edu.au