ASR
UNIV
TESIS
Oleh
SROI BENNY NOOR HARAHAP
117016011/TS
FAKULTAS TEKNIK
NIVERSITAS SUMATERA UTARA
MEDAN
KAJIAN INDEKS KERUSAKAN PADA STRUKTUR BANGUNAN
BAJA BERDASARKAN PENDEKATAN ENERGI AKIBAT
GEMPA KUAT
TESIS
Untuk Memperoleh Gelar Magister Teknik
Dalam Program Studi Teknik Sipil
Pada Fakultas Teknik Universitas Sumatera Utara
Oleh
ASROI BENNY NOOR HARAHAP
117016011/TS
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
MEDAN
AKIBAT GEMPA KUAT Nama Mahasiswa : Asroi Benny Noor Harahap Nomor Pokok : 117016011
Program : Teknik Sipil
Menyetujui:
Komisi Pembimbing
(Dr. Ing. Hotma Panggabean) (Ir. Daniel Rumbi Teruna, MT) Ketua Anggota
Ketua Program Studi Dekan
(Prof. Dr. Ir. Roesyanto, MSCE) (Prof. Dr. Ir. Bustami Syam, MSME)
Telah diuji pada Tanggal 3 Juli 2014
PANITIA PENGUJI TESIS
KETUA : Dr. Ing. Hotma Panggabean
ANGGOTA : Ir. Daniel Rumbi Teruna, MT Prof. Dr. Ing. Johannes Tarigan Ir. Sanci Barus, MT
Struktur Bangunan Baja Berdasarkan Pendekatan Energi Akibat Gempa Kuat” adalah karya saya dan belum pernah diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutif dari karya yang diterbitkan dari penulis lain telah disebutkan dalam tesis ini dan dicantumkan dalam daftar pustaka.
Medan, 3 Juli 2014
i ABSTRAK
Setiap struktur yang terbuat dari material apapun memiliki batas kekuatan mekanik. Hal ini dijelaskan oleh berbagai teori, dimana digambarkan dalam grafik stress-deformation bahwa material akan runtuh akibat pemberian beban yang melebihi kekuatan batasnya. Diketahui selama umur layan bangunan, struktur mengalami kerusakan, seperti yang diakibatkan oleh beban gempa. Kerusakan-kerusakan ini mengakibatkan perubahan dalam sifat-sifat dari sistem struktur. penggunaan indeks kerusakan memungkinkan kuantifikasi kerusakan. Drift atau Inter-story drift secara umum digunakan sebagai kriteria untuk melihat perilaku struktur akibat gempa. Namun, beberapa penelitian menyatakan bahwa kumulatif deformasi plastis lebih kuat pengaruhnya dibandingkan dengan drift dan inter-story drift dalam tingkat kerusakan struktur. Kumulatif deformasi plastis dapat dipertimbangkan melalui konsep energi, khususnya melalui plastis dissipasi histeresis energi demand.
Dalam tesis ini akan dibahas indeks kerusakan berdasarkan energi, dimana ada dua persamaan yang digunakan yaitu persamaan Boz rquez dan Cosenza. Model bangunan yang digunakan ada 3 jenis yaitu SMRF 4, SMRF 7, dan SMRF 10. Ketiga bangunan ini akan di analisa terhadap 4 gempa, dimana gempa-gempa tersebut diskalakan terhadap gempa rencana yang sesuai dengan peta gempa Indonesia 2010.
Dari penelitian yang dilakukan, dapat dilihat bahwa indeks kerusakan berhubungan langsung dengan enegi masuk terhadap struktur. Nilai indeks kerusakan terbesar untuk persamaan Boz rquez pada SMRF 4 sebesar 0.147 (rusak ringan), SMRF 7 sebesar 0.079 (rusak ringan), dan SMRF 10 sebesar 0.154 (rusak ringan), ketiga bangunan tersebut dipengaruhi oleh gempa Kobe. Untuk persamaan Cosenza, pada SMRF 4 sebesar 0.170 (rusak ringan), SMRF 7 sebesar 0.176 (rusak ringan), dan SMRF 10 sebesar 0.260 (rusak sedang), ketiganya diakibatkan oleh gempa Kobe.
limitation. This is explained by many theories as it is described in the graph of stress-deformation that material will fall down because its load has exceeded its strength limitation. It is known that during a structure serving age, the structure undergoes damage such as it is caused by earthquake. These damages bring about the change in the nature of the structural system, and the use of damage index enables the quantity of damage. Drift or inter-story drift is generally used as the criteria for finding out the structure behavior which has caused by earthquake. However, some researches have found that the cumulative plastic deformation has more significant influence than drift or inter-story drift in the level of structural damage. The cumulative plastic deformation can be considered through the concept of energy, especially through plastic dissipation hysteresis energy demand.
This thesis analyzed damage index, based on energy in which there were two equations were used: Bozórquez equation and Cosenza equation. There were three types of structure model: SMRF 4, SMRF 7, and SMRF 10. These three structures would be analyzed in four earthquakes in which the earthquakes were scaled against planned earthquakes, according to earthquake mapping in Indonesia in 2010.
The result of the research showed that damage index was directly correlated with incoming energy on structure. The biggest value of damage index for Bozórquez equation in SMRF 4 was 0.147 (lightly damaged), in SMRF 7 was 0.079 (lightly damaged), and in SMRF 10 was 0.154 (lightly damaged). The three structures were affected by Kobe earthquake. For Cosenza equation, in SMRF 4 was 0.170 (lightly damaged), in SMRF 7 was 0.176 (lightly damaged), and in SMRF10 was 0.260 (moderately damaged). The three structures were affected by Kobe earthquake.
iii
KATA PENGANTAR
Bismillahirrohmanirrohim, dengan mengucapkan Alhamdulillahi robbil alamin dan Puji Syukur kehadirat Allah SWT atas segala rahmat dan bimbingan-Nya sehingga penulis dapat menyelesaikan tesis ini dengan baik yang merupakan salah satu syarat untuk menyelesaikan program Magister pada bidang Rekayasa Struktur, Program Studi Teknik Sipil, Universitas Sumatera Utara.
Tesis ini yang berjudul “Kajian Indeks Kerusakan Pada Struktur Bangunan Baja Berdasarkan Pendekatan Energi Akibat Gempa Kuat” disusun penulis dengan harapan bukan hanya sebagai syarat untuk menyelesaikan program S2 tetapi dapat juga bermanfaat untuk meningkatkan pengetahuan para pembaca khususnya dalam dunia teknik sipil.
Penulis menyadari bahwa tesis ini bukanlah semata-mata karena kehebatan penulis. Banyak pihak yang telah banyak menyumbangkan tenaga dan pikiran dalam menyelesaikan tesisi ini, terutama kepada kedua orangtua saya.
Selain itu, saya juga mengucapkan terimakasih kepada Bapak Prof. Dr. dr. Syahril Pasaribu. DTM & H. M.Sc (CTM), Sp.A(k) selaku Rektor Universitas Sumatera Utara, Bapak Prof. Dr. Ir. Bustami Syam, MSME selaku Dekan Fakultas Teknik, dan Bapak Prof. Dr. Ir. Roesyanto, MSCE selaku Ketua program Studi Magister Teknik Sipil.
Nurmala Srg serta kedua mertua saya Imron Srg dan Rosmala Hrp yang telah memberikan doa serta dukungannya. Kepada istri tercinta Rinawaty Siregar, SKM terimakasih atas doa dan dukungannya. Untuk kedua kakak saya Nita Irmayani Hrp, SPd dan Neny Asnizar Hrp, SPd dan seluruh rekan-rekan seangkatan 2011. Kepada mereka semua, teman, rekan, kenalan dan saudara-saudara yang lain, yang tidak sempat disebutkan satu persatu, tidak ada yang dapat kami berikan sebagai balasan yang setimpal, kecuali hanya doa, semoga Allah SWT memberi berkat dan perlindungan-Nya, diberi-Nya umur panjang, kesejahteraan lahir dan batin, dan dipenuhi oleh rasa syukur di hatinya selama kehidupan di dunia.
Penulis menyadari bahwa tesis ini masih jauh dari sempurna, yang disebabkan keterbatasan pengetahuan dan kurangnya pemahaman penulis. untuk itu, penulis sangat mengharapkan kritik dan saran yang sifatnya membangun demi kesempurnaannya. Akhir kata saya mengucapkan terimakasih yang sebesar-besarnya dan semoga tesis ini dapat bermanfaat bagi para pembaca.
Medan, 3 Juli 2014 Penulis
v
RIWAYAT HIDUP
A. DATA PRIBADI
Nama : ASROI BENNY NOOR HARAHAP
Tempat/Tgl Lahir : Gunungtua Tonga, 22 Desember 1986
Alamat : Jl.Nagasati No.72 Gunungtua, Kec. Padang Bolak, Kab. Padang Lawas Utara
Email : [email protected]
Agama : Islam
Jenis Kelamin : Laki-laki
B. RIWAYAT PENDIDIKAN
1996 – 1999 : SDN 2 Padang Bolak 1999 – 2002 : SMPN 1 Padang Bolak 2002 – 2005 : SMAN 1 Padang Bolak
2005 – 2010 : Fakultas Teknik Jurusan Teknik Sipil USU
2011 – 2014 : Magister Teknik Sipil Program Pasca Sarjana USU
C. RIWAYAT PEKERJAAN
2010 – 2011 : PT.Diagram Consultant
: PT. Rekayasa Damper Pratama Consultant : Lembaga Pendidikan Keterampilan Paulin 2011 – 2012 : PT. Barata Indonesia
2012 – 2013 : PT. Bumi Torant Kencana
LEMBAR PENGESAHAN... PERNYATAAN...
ABSTRAK ... i
ABSTRACT ... ii
KATA PENGANTAR ... iii
RIWAYAT HIDUP... v
DAFTAR ISI ... vi
DAFTAR GAMBAR ... . x
DAFTAR TABEL ... xii
DAFTAR NOTASI ... xiv
BAB I PENDAHULUAN ... 1
1.1 Latar belakang ... 1
1.2 Permasalahan ... 2
1.3 Tujuan Penelitian ... 3
1.4 Pembatasan Masalah ... 4
1.5 Sistematika Penulisan ... 5
BAB II LANDASAN TEORI ... 7
2.1 Konsep Dasar Metode Energi ... 7
vii
2.1.2 Prosedur Menghitung Energi Masuk ... 12
2.1.3 Pengaruh Karakter Gerakan Tanah Pada Spektra Energi ... 14
2.1.4 Pengaruh Properties Struktur Pada Spektra Energi ... 15
2.2 Kerusakan Pada Struktur ... 15
2.3 Indeks Kerusakan ... 17
2.3.1 Indeks Kerusakan Roufaiel dan Meyer ... 18
2.3.2 Indeks Kerusakan Park - Ang ... 18
2.3.3 Indeks Kerusakan Zahrah dan Hall ... 20
2.3.4 Indeks Kerusakan Hwang dan Scribner ... 21
2.3.5 Indeks Kerusakan Cosenza ... 23
2.3.6 Indeks Kerusakan Boz rquez ... 24
2.4 Energi dan Distribusi Kerusakan pada Struktur Baja ... 29
2.5 Energi Histeresis ... 31
2.5.1 Energi Histeresis Demand ... 32
2.6 Karakteristik Gempa ... 33
2.6.1 Percepatan Puncak Tanah ... 33
2.6.2 Durasi Gempa ... 34
2.7 Getaran Gempa ... 35
2.8 Penskalaan Gempa ... 37
2.8.1 Skala PGA (Peak Ground Acceleration)... 37
2.8.2 Skala Ordinat ... 38
2.8.3 Least Square ... 38
2.8.7 Spectrum Matching ... 40
2.9 Accelerogram ... 40
BAB III PROSEDUR ANALISIS... 42
3.1 Modelisasi Struktur ... 42
3.2 Input Data ... 46
3.2.1 Dimensi Struktur ... 46
3.2.2 Beban Struktur ... 47
3.2.3 Properti Material ... 47
3.3 Prosedur Analisa ... 47
3.4 Persyaratan Perencanaan Struktur Baja ... 48
3.4.1 Waktu Getar Alami ... 49
3.4.2 Kinerja Batas Layan ... 50
3.4.3 Kinerja Batas Ultimit ... 50
3.5 Analisa Struktur dan Modeling ... 51
BAB IV ANALISA DAN PEMODELAN STRUKTUR ... 52
4.1 Perencanaan Struktur ... 52
4.2 Penskalaan Gempa dengan SeismoMatch ... 56
4.2.1 Loading dan spectral matching dari akselerogram ... 57
ix
4.2.3 Mendefinisikan Target Spektrum ... 59
4.2.4 Spectral Matching ... 61
4.3 Modelisasi Struktur dengan Abaqus ... 62
4.3.1 Preprocessing (Abaqus CAE)... 63
4.3.2 Simulasi... 67
4.3.3 Post Processing ... 68
BAB V HASIL DAN PEMBAHASAN ... 69
5.1 Perencanaan Struktur ... 69
5.2 Accelerogram dan Respon Spektrum Design ... 70
5.3 Inter-story Drift ... 71
5.4 Energi Masuk dan Energi Histeresis Demand ... 74
5.5 Karakteristik Struktur ... 79
5.6 Indeks Kerusakan Boz rquez ... 80
5.7 Indeks Kerusakan Cosenza ... 85
BAB VI KESIMPULAN DAN SARAN... 86
6.1 Kesimpulan ... 86
No Judul Halaman
2.1 Idealisasi model matematis SDOF (a) absolut dan (b) relatif... 10
2.2 Idealisasi model matematis MDOF (a) absolut dan (b) relatif ... 11
2.3 Pengertian parameter model Park-Ang, (a) histeresis lentur dan (b) hysteresis torsi ... 20
2.4 Pengertian parameter model Hwang dan Scribner (a) histeresis lentur dan (b) histeresis torsi ... 23
2.5 Pengertian Vy dan uy dari kurva kapasitas ... 24
2.6 Pengertian rotasi plastis komulatif ... 26
2.7 Evaluasi Cy dan Dy ... 28
2.8 Rotasi plastis komulatif struktur baja (Akbas 1997) ... 29
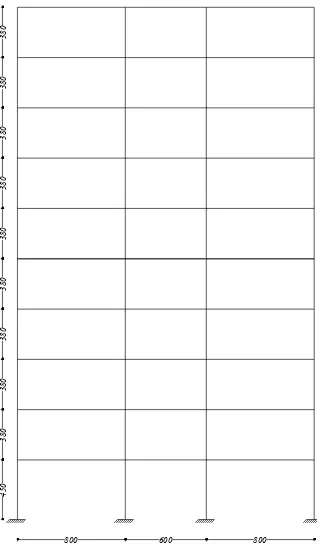
3.1 Steel Moment Resisting Frame (SMRF 10) ... 44
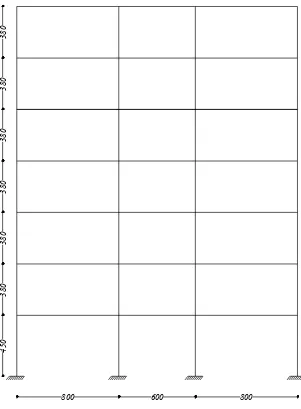
3.2 Steel Moment Resisting Frame (SMRF 7) ... 45
3.3 Steel Moment Resisting Frame (SMRF 4) ... 46
3.4 Diagram alir proses analisa ... 48
4.1 Input file SeimoMatch ... 59
4.2 Diagram alir proses running Abaqus ... 63
4.3 Viewport awal Abaqus CAE 6.10-1 ... 64
4.4 Viewport part Abaqus CAE 6.10-1 ... 64
xi
4.6 Hubungan kerja Preprocessor, Solver dan Postprocessor ... 68
5.1 Deskripsi Bangunan ... 69
5.2 Hasil Skala Respon Spektrum ... 71
5.3 Grafik Interstory drift – Lantai pada SMRF 4... 73
5.4 Grafik Interstory drift – Lantai pada SMRF 7... 73
5.5 Grafik Interstory drift – Lantai pada SMRF 10... 74
5.6 Time history Ei dan Eh total pada SMRF 4... 75
5.7 Time history Ei dan Eh total pada SMRF 7... 75
5.8 Time history Ei dan Eh total pada SMRF 10... 76
5.9 Distribusi energi histeresis tiap lantai SMRF 4 ... 78
5.10 Distribusi energi histeresis tiap lantai SMRF 7 ... 78
5.11 Distribusi energi histeresis tiap lantai SMRF 10 ... 79
No Judul Halaman
2.1 Ground Motion ... 41
3.1 Koefisien yang membatasi waktu getar alami fundamental struktur gedung ... 50
4.1 Perioda alami bangunan ... 53
4.2 Kinerja batas layan SMRF 4 ... 54
4.3 Kinerja batas layan SMRF 7 ... 54
4.4 Kinerja batas layan SMRF 10 ... 54
4.5 Kinerja batas ultimit SMRF 4 ... 55
4.6 Kinerja batas ultimit SMRF 7 ... 55
4.7 Kinerja batas ultimit SMRF 10 ... 55
5.1 Dimensi balok dan kolom SMRF 4 ... 69
5.2 Dimensi balok dan kolom SMRF 7 ... 70
5.3 Dimensi balok dan kolom SMRF 10 ... 70
5.4 Parameter struktur ... 80
5.5 Indeks kerusakan lokal gempa Kobe ... 81
5.6 Indeks kerusakan lokal gempa Lomaprieta ... 81
5.7 Indeks kerusakan lokal gempa Imperial Valley ... 81
5.8 Indeks kerusakan lokal gempa Northridge ... 81
5.9 Indeks kerusakan lokal gempa Kobe ... 82
5.10 Indeks kerusakan lokal gempa Lomaprieta ... 82
xiii
5.12 Indeks kerusakan lokal gempa Northridge ... 82
5.13 Indeks kerusakan lokal gempa Kobe ... 83
5.14 Indeks kerusakan lokal gempa Lomaprieta ... 83
5.15 Indeks kerusakan lokal gempa Imperial Valley ... 83
5.16 Indeks kerusakan lokal gempa Northridge ... 84
5.17 Indeks kerusakan global ... 84
5.18 Indeks kerusakan Cosenza ... 85
c = Damping ratio
Cy = Koefisien gempa
DHS = Indeks kerusakan oleh Hwang dan Scribner
DPA = Indeks kerusakan Park Ang
DRM = Indeks kerusakan Roufaiel dan Meyer
Dy = Perpindahan pada leleh pertama (mm)
Ed = Energi damping (Nm)
Eh = Energi histeresis (Nm)
EHC = Kapasitas energi histeresis plastis (Nm)
EHD = Energi histeresis demand (Nm)
Ehm = Energi histeresis demand maksimum (Nm)
Ei = Energi masuk (Nm)
Ek = Energi kenetik (Nm)
Es = Energi regangan elastis (Nm)
FEHi = Suatu faktor partisipasi energi yang menyumbang kontribusi yang
berbeda dari masing-masing lantai dengan kapasitas disipasi energi
sebuah frame
fm = Lenturan secant akibat pembebanan (mm)
fo = Lenturan sebelum leleh (mm)
fs = Gaya inersia (mm4)
fu = Lenturan akibat beban ultimit (mm)
xv
i = Jumlah siklus
k = Kekakuan struktur
Kmi = Kekakuan secant sesuai dengan umi
Ko = Kekakuan sebelum leleh
M = Jumlah total siklus leleh
m = Massa
NB = Jumlah blok di gedung
Neq = Jumlah leleh ekivalen
NS = Jumlah lantai
PSV = Kecepatan spektra
Qy = Kekuatan leleh struktur
T = Period of earthquake motion (sec)
To = Predominant period of alluvial deposit above base rock
uu = Perpindahan ultimit akibat beban statis
um = Perpindahan maksimum untuk beberapa siklus (mm)
umi = Perpindahan maksimum dalam siklus ke-i (mm)
uy = Perpindahan leleh (mm)
VE = Kecepatan ekivalen
W = Berat total struktur (kg)
Zf = Modulus section (mm4)
= Perpindahan daktilitas untuk beberapa siklus
u = Perpindahan daktilitas ultimit
= Percepatan
= Konstanta pengaruh dari beban siklus dan properties struktur
Ehi = Disipasi energi histeretik dalam siklus ke-i
pa = Kapasitas rotasi plastis komulatif
i ABSTRAK
Setiap struktur yang terbuat dari material apapun memiliki batas kekuatan mekanik. Hal ini dijelaskan oleh berbagai teori, dimana digambarkan dalam grafik stress-deformation bahwa material akan runtuh akibat pemberian beban yang melebihi kekuatan batasnya. Diketahui selama umur layan bangunan, struktur mengalami kerusakan, seperti yang diakibatkan oleh beban gempa. Kerusakan-kerusakan ini mengakibatkan perubahan dalam sifat-sifat dari sistem struktur. penggunaan indeks kerusakan memungkinkan kuantifikasi kerusakan. Drift atau Inter-story drift secara umum digunakan sebagai kriteria untuk melihat perilaku struktur akibat gempa. Namun, beberapa penelitian menyatakan bahwa kumulatif deformasi plastis lebih kuat pengaruhnya dibandingkan dengan drift dan inter-story drift dalam tingkat kerusakan struktur. Kumulatif deformasi plastis dapat dipertimbangkan melalui konsep energi, khususnya melalui plastis dissipasi histeresis energi demand.
Dalam tesis ini akan dibahas indeks kerusakan berdasarkan energi, dimana ada dua persamaan yang digunakan yaitu persamaan Boz rquez dan Cosenza. Model bangunan yang digunakan ada 3 jenis yaitu SMRF 4, SMRF 7, dan SMRF 10. Ketiga bangunan ini akan di analisa terhadap 4 gempa, dimana gempa-gempa tersebut diskalakan terhadap gempa rencana yang sesuai dengan peta gempa Indonesia 2010.
Dari penelitian yang dilakukan, dapat dilihat bahwa indeks kerusakan berhubungan langsung dengan enegi masuk terhadap struktur. Nilai indeks kerusakan terbesar untuk persamaan Boz rquez pada SMRF 4 sebesar 0.147 (rusak ringan), SMRF 7 sebesar 0.079 (rusak ringan), dan SMRF 10 sebesar 0.154 (rusak ringan), ketiga bangunan tersebut dipengaruhi oleh gempa Kobe. Untuk persamaan Cosenza, pada SMRF 4 sebesar 0.170 (rusak ringan), SMRF 7 sebesar 0.176 (rusak ringan), dan SMRF 10 sebesar 0.260 (rusak sedang), ketiganya diakibatkan oleh gempa Kobe.
limitation. This is explained by many theories as it is described in the graph of stress-deformation that material will fall down because its load has exceeded its strength limitation. It is known that during a structure serving age, the structure undergoes damage such as it is caused by earthquake. These damages bring about the change in the nature of the structural system, and the use of damage index enables the quantity of damage. Drift or inter-story drift is generally used as the criteria for finding out the structure behavior which has caused by earthquake. However, some researches have found that the cumulative plastic deformation has more significant influence than drift or inter-story drift in the level of structural damage. The cumulative plastic deformation can be considered through the concept of energy, especially through plastic dissipation hysteresis energy demand.
This thesis analyzed damage index, based on energy in which there were two equations were used: Bozórquez equation and Cosenza equation. There were three types of structure model: SMRF 4, SMRF 7, and SMRF 10. These three structures would be analyzed in four earthquakes in which the earthquakes were scaled against planned earthquakes, according to earthquake mapping in Indonesia in 2010.
The result of the research showed that damage index was directly correlated with incoming energy on structure. The biggest value of damage index for Bozórquez equation in SMRF 4 was 0.147 (lightly damaged), in SMRF 7 was 0.079 (lightly damaged), and in SMRF 10 was 0.154 (lightly damaged). The three structures were affected by Kobe earthquake. For Cosenza equation, in SMRF 4 was 0.170 (lightly damaged), in SMRF 7 was 0.176 (lightly damaged), and in SMRF10 was 0.260 (moderately damaged). The three structures were affected by Kobe earthquake.
1
BAB I
PENDAHULUAN
1.1 Latar Belakang
Setiap struktur yang terbuat dari material apapun memiliki batas kekuatan mekanik. Hal ini dijelaskan oleh berbagai teori, dimana digambarkan dalam grafik stress-deformation bahwa material akan runtuh akibat pemberian beban yang
melebihi kekuatan batasnya.
Diketahui selama umur layan bangunan, struktur mengalami kerusakan, seperti yang diakibatkan oleh beban gempa. Kerusakan-kerusakan ini mengakibatkan perubahan dalam sifat-sifat dari sistem struktur.
Penggunaan indeks kerusakan memungkinkan kuantifikasi kerusakan struktur yang disebabkan oleh gempa bumi untuk setiap elemen struktur. Indeks kerusakan yang ada didasarkan pada berbagai karakteristik, seperti jumlah siklik, daktilitas dan energi.
Sekarang ini, inter-story drift maksimum dan daktilitas demand ditargetkan sebagai parameter kinerja untuk mencapai pengendalian kerusakan struktur dalam struktur tahan gempa. Namun, ada banyak bukti bahwa dalam beberapa kasus, kinerja struktur terhadap lama durasi pergerakan tanah tidak dapat dijadikan karakter deformasi demand maksimum, dengan cara yang sedemikian rupa sehingga efek dari
deformasi plastis kumulatif demand harus diperhitungkan secara jelas selama
Pengaruh dari deformasi plastis kumulatif demand dapat dipertimbangkan melalui konsep energi, khususnya melalui plastis dissipasi histeresis energi demand. Penggunaan energi untuk tujuan ini awalnya dibahas oleh Housner (1956), dan telah digunakan oleh beberapa peneliti untuk mengusulkan metodologi berdasarkan energi yang bertujuan untuk menyediakan struktur tahan gempa dengan kapasitas dissipasi energi lebih besar atau sama dengan kebutuhan (Bojorquez dkk. 2008).
Karena batasan deformasi maksimum sebagai indikator utama dari kerusakan struktur, beberapa indeks kerusakan menjelaskan plastis dissipasi histeresis energi telah di rumuskan lebih baik dalam hal kerusakan struktur. Sebahagian besar penelitian telah dikhususkan untuk megkalibrasi indeks kerusakan untuk baja dan beton bertulang. Namun, ada tantangan untuk mempelajari dan mengkalibrasi penggunaan indeks tersebut untuk evaluasi struktur yang begitu kompleks. Dalam konteks ini, indeks kerusakan berdasarkan energi secara eksplisit menyumbang efek dari deformasi plastis kumulatif demand pada struktur baja.
1.2 Permasalahan
Dalam SNI 03-1726-2002 disebutkan bahwa perencanaan struktur itu di kontrol terhadap kinerja struktur, yaitu kinerja batas layan dan batas ultimit.
3
Kinerja batas ultimit gedung ditentukan oleh simpangan dan simpangan antar tingkat maksimum struktur gedung akibat gempa rencana dalam kondisi struktur gedung diambang keruntuhan, yaitu untuk membatasi kemungkinan terjadinya keruntuhan struktur gedung yang dapat menimbulkan korban jiwa manusia dan untuk mencegah benturan berbahaya antar gedung atau antar bagian struktur gedung yang dipisah dengan sela pemisah (dilatasi). Simpangan dan simpangan antar tingkat ini harus dihitung dari simpangan struktur gedung akibat pembebanan gempa nominal, dikalikan dengan suatu faktor pengali = 0,7 x R (untuk gedung beraturan).
Dalam pasal 8.2.2, disebutkan bahwa dalam segala hal simpangan antar tingkat yang dihitung dari simpangan struktur gedung untuk batas ultimit tidak boleh melampaui 0,02 x tinggi tingkat yang bersangkutan.
Artinya dengan pernyataan diatas bahwa kerusakan struktur itu didasarkan pada simpangan yang terjadi pada struktur. Menurut beberapa penelitian yang telah dilakukan menyebutkan bahwa karakter simpangan tersebut tidak dapat dijadikan sebagai karakter pada gempa dengan waktu yang lama (Hancock dan Boomer 2006). Karena itu, pengaruh deformasi plastis kumulatif demand harus dipertimbangkan. Pengaruh dari deformasi plastis kumulatif demand dapat dipertimbangkan melalui konsep energi, khususnya melalui plastis dissipasi histeresis energi demand.
1.3 Tujuan Penelitian
Adapun tujuan tulisan ini diantaranya:
2. Untuk memperkenalkan indeks kerusakan berdasarkan energi untuk MDOF.
3. Melihat pengaruh berbagai jenis dan karakteristik gempa terhadap respon struktur.
4. Untuk melihat kinerja struktur berdasarkan energi dan di bandingkan dengan peraturan gempa.
5. Untuk melihat hubungan indeks kerusakan antara displacement dan energi. 6. Untuk mengetahui berapa indeks kerusakan akibat beberapa catatan gempa
kuat. Dengan mengetahui berapa nilai indeks kerusakan, sehingga kita dapat menyimpulkan termasuk dalam kategori mana struktur baja tersebut.
1.4 Pembatasan Masalah
Penelitian ini membatasi masalah dalam hal: 1. Struktur yang dianalisa 2D
2. Untuk desain struktur: Wilayah gempa: 6
Fungsi bangunan: perkantoran Jenis tanah: sedang
3. Peraturan gempa yang digunakan menggunakan SNI 03-1729-2002.
4. Gempa yang menjadi analisa diantaranya ada 4 catatan gempa kuat di dunia:
5
3. Northridge. 4. Imperial Valley.
5. Indeks kerusakan berdasarkan persamaan Boz rquez dan Cosenza.
1.5 Sistematika Penulisan
Pembahasan mengenai latar belakang, metodologi, proses analisis hingga hasil analisis dalam tesisi ini akan disusun kedalam sejumlah bab dengan sistematika bab terurai berikut:
Bab I Pendahuluan
Berisi latar belakang, permasalahan, tujuan penelitian, pembatasan masalah, dan sistematika penulisan.
Bab II Landasan Teori
Dasar teori ini berisikan mengenai konsep energi, kerusakan struktur, histeresis energi, getaran gempa, penskalaan gempa dan indeks kerusakan. Bab III Prosedur Analisis
Berisikan langkah-langkah alur untuk penyelesaian permasalahan tersebut. Bab IV Analisa dan Pemodelan Struktur
Berisi perencanaan struktur, modelisasi struktur dalam program, dan prosedur analisa.
Bab V Hasil dan Pembahasan
Bab VI Kesimpulan dan Saran
7
BAB II
LANDASAN TEORI
2.1 Konsep Dasar Metode Energi
Perencanaan bangunan tahan gempa secara tradisional di rencanakan berdasarkan kekuatan, artinya sejumlah beban gempa statik, dikombinasikan dengan beban gravitasi, yang digunakan pada struktur sebagai kebutuhan kekuatan. Struktur dipilih berdasarkan prinsip kekuatan dimana struktur diambil harus lebih besar atau sama dengan kekuatan yang dibutuhkan. Namun demikian, struktur yang menerima gaya gempa dalam peraturan tidak ditetapkan bahwa struktur tidak boleh mengalami kerusakan. Struktur dirancang sehingga diharapkan harus melewati deformasi inelastis yang besar saat terjadi gempa.
(SDOF) berhubungan dengan spektra kecepatan struktur. Sejak saat itu, peneliti pada konsep energi semakin maju secara signifikan.
2.1.1 Persamaan Energi
Fungsi keseimbangan untuk SDOF elastis akibat beban gempa dapat ditunjukaan pada Persamaan 2.1:
9
seimbang untuk SDOF dapat ditulis sebagai:
Ek + Ed + Es + Eh = Ei (2.4)
Energi dalam persamaan diatas adalah energi relatif berdasarkan perpindahan relatif antara struktur. Energi absolut dapat diperkirakan dengan menggunakan perpindahan absolut yang dihubungkan dengan gerakan tanah dan perpindahan relatif. Uang dan Bertero (1988) menyatakan bahwa energi absolut lebih masuk akal dibandingkan dengan energi relatif, karena energi absolut bisa memperhitungkan pergerakan kekakuan struktur. Chopra (1995) menegaskan bahwa energi relatif lebih penting karena gaya pada struktur dihitung berdasarkan perpindahan relatif dan kecepatan relatif. Dengan membandingkan energi relatif dan absolut pada time history dari SDOF, Bruneau dan Wang (1996) menunjukkan bahwa konsepnya berlawanan, dia menyebutkan bahwa energi masuk absolut masih bisa berfluktuasi lama setelah berakhirnya eksitasi masuk. Mereka juga menyimpulkan bahwa energi relatif lebih berarti dari sudut pandang engineering.
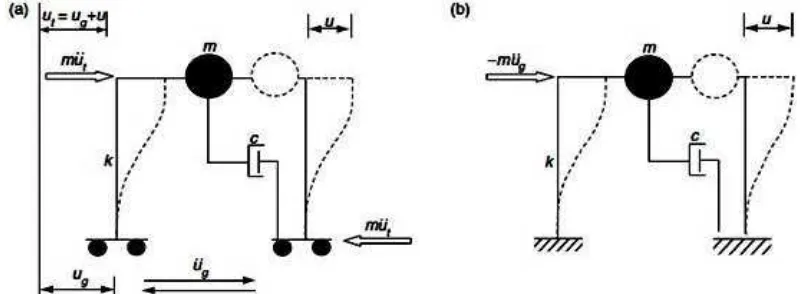
hampir sama ketika periode struktur berada dalam kisaran 0.3 – 5.0 detik. Dalam perencanaan berdasarkan energi, energi histeresis memberikan kontribusi dari deformasi plastik elemen struktur dihitung berdasarkan pada perpindahan relatif yang merupakan salah satu parameter desain yang paling penting. Untuk melihat perbedaan antara absolut dan relatif dapat kita lihat pada Gambar 2.1 untuk SDOF.
Gambar 2.1 Idealisasi model matematis SDOF (a) absolut dan (b) relatif Bentuk energi masuk absolut pada SDOF diperluas oleh Uang dan Bertero pada MDOF N-lantai sebagai berikut:
11
N = jumlah lantai.
Dengan cara yang sama, dimungkinkan untuk mengekspresikan energi relatif pada MDOF sebagai berikut:
Perbedaan antara formulasi energi absolut dan relatif untuk sistem MDOF dasarnya adalah perbedaan dalam energi kinetik, yang dapat dinyatakan sebagai berikut:
E’i = merupakan energi akibat gaya inersia.
Untuk modelisasi matematis energi relatif dan absolut pada MDOF dapat dilihat pada Gambar 2.2.
2.1.2 Prosedur Menghitung Energi Masuk
Housner (1956) memberikan persamaan untuk menghitung energi persatuan massa sebagi:
Dia menggunkan Persamaan 2.8 untuk perilaku elastis dan plastis. Zahran dan Hall (1984) memberikan persamaan untuk energi masuk persatuan massa sebagai:
dt
Akiyama (1985) memberikan persamaan energi masuk persatuan massa pada SDOF elastis sebagai:
Dimana VE merupakan kecepatan ekivalen. Dia merekomendasikan nilai VE
sebagai berikut:
VE = 2,5Tn untuk Tn TG
VE = 2,5TG untuk Tn TG
Dimana TG merupakan predominant period motion sebagai fungsi dari tipe
tanah. Nilai dari TG yaitu 0.4, 0.6, 0.8, dan 1 detik untuk tanah tipe I (tanah keras), II,
13
Kuwamura dan Galambos (1989) menggunakan persamaan Akiyama dan merekomendasikan nilai VE adalah:
= untuk untuk T TG
= untuk untuk T TG
Dimana IE adalah merupakan integral kuadrat dari percepatan tanah untuk
total durasi accelerogram tf.
dt
Menggunakan 40 akselerogram Fajfar dkk. (1989) menghitung energi masuk gempa untuk periode menengah (kecepatan wilayah - konstan) dengan rasio redaman 5% dan : 0.5 - 1.0 , dimana adalah rasio dari gaya leleh dengan mPGA, dimana PGA adalah percepatan tanah maksimum. Mereka merekomendasikan untuk
menghitung energi masuk persatuan massa sebagai:
2
tdi = durasi gerak kuat didefinisikan oleh Trifunac dan Brady (1975).
PGV = kecepatan tanah maksimum.
2.1.3 Pengaruh Karakter Gerakan Tanah Pada Spektra Energi
Dari hasil penelitian yang telah dilakukan oleh Payam Khashaee dkk. dalam laporan distribusi energi pada struktur, pengaruh intensitas gempa, durasi dan besar frekuensi pada energi input gempa dikaji dengan menggunakan 10 accelerogram dengan durasi pendek (tdi lebih pendek dari 8 s) dan 10 dengan durasi panjang (tdi
lebih dari 18 s). Durasi tdi dihitung menggunakan definisi yang diusulkan oleh
Trifunac dan Brady (1975), yang dikenal sebagai durasi berbasis intensitas. Mereka mendefinisikan durasi sebagai interval waktu antara lima dan sembilan puluh lima persen kontribusi dengan integral dari kuadrat percepatan tanah, lihat Persamaan 2.11.
Studi ini menunjukkan bahwa puncak accelerasi meningkat efektif, energi masuk juga meningkat, yang menunjukkan bahwa energi masuk berhubungan dengan intensitas gerakan tanah. Rasio energi seperti rasio energi histeretik maksimum dengan energi masuk maksimum Ehm / Eirm tidak terpengaruh oleh percepatan puncak
15
2.1.4 Pengaruh Properties Struktur pada Spektra Energi
Zahrah dan Hall (1984), dan Akiyama (1985) percaya bahwa daktilitas dan redaman tidak memiliki pengaruh yang signifikan pada energi masuk gempa. Perlu dicatat bahwa studi ini digunakan 4, 8, 1, dan 3 akselerogram. Housner (1956) percaya bahwa dalam merancang struktur untuk memenuhi energi demand, energi masuk elastis dihitung dari ½ m (PSV)2 dapat digunakan konservatif sebagai pengganti energi masuk inelastis. Akiyama menggunakan rekomendasi Housner itu, Persamaan 2.8, untuk mengembangkan sebuah metode desain berbasis energi untuk bangunan baja.
2.2 Kerusakan Pada Struktur
Setiap sistem struktur memiliki kerentanan terhadap kerusakan selama digunakan, dan dapat berbahaya bagi manusia yang menggunakan struktur tersebut apabila kerusakan yang terjadi dibiarkan tanpa dilakukan langkah perbaikan.
Secara umum pada bidang teknik sipil, material yang digunakan untuk struktur adalah beton bertulang, kayu dan baja. Kerusakan dapat disebabkan oleh faktor-faktor seperti korosi pada material, fatigue, beban hentak (impacts), dan beban yang berlebihan. Kerusakan struktur menyebabkan deviasi atau perubahan dari kondisi normal baik secara geometrik maupun properti material.
1. Karakteristik gempa yang terjadi a. Percepatan puncak muka tanah. b. Durasi gempa.
c. Frekwensi gempa. d. Panjang patahan.
2. Karakteristik lokasi dimana bangunan akan didirikan a. Jarak bangunan ke pusat gempa.
b. Struktur geologi antara bangunan ke pusat gempa. c. Jenis lapisan tanah dilokasi bangunan.
d. Waktur getar alami tanah dilokasi bangunan. 3. Karakteristik struktur
a. Waktu getar alami dari struktur bangunan. b. Redaman (damping) dari struktur bangunan.
c. Persyaratan dan konsep detailing yang direncanakan.
17
2.3 Indeks Kerusakan
Respon fisik struktur digunakan sebagai indikator tingkat kerusakan, yang disebut dengan parameter kerusakan. Respon struktur digunakan sebagai parameter kerusakan dapat dibagi menjadi:
1. Deformasi plastis struktur. 2. Disipasi energi.
3. Cyclic fatigue struktur. 4. Parameter dinamik struktur.
Kerusakan struktur dapat dibedakan pada tiga skala yaitu:
a. Skala lokal, dimana kerusakan terjadi pada tingkat cross-section. Sebagai contoh penjelasan adalah kerusakan bagian beton akibat tegangan tekan yang melebihi fc’ dari beton bertulang, ataupun sebaliknya tegangan pada baja yang melebihi tegangan plastisnya pada beton bertulang.
b. Skala menengah atau intermediate, dimana kerusakan dilihat pada skala suatu elemen atau member penyusun suatu sistem struktur.
c. Skala global, dimana kerusakan dilihat pada skala yang lebih besar, yaitu suatu sistem struktur secara utuh.
2.3.1 Indeks Kerusakan Roufaiel dan Meyer
Banon dkk. (1981) mengembangkan indeks kerusakan berdasarkan penyesuaian rasio dari kekakuan inisial dan kekakuan secant pada perpindahan maksimum akibat beban siklik. Mereka menyebutkan indeks kerusakan ini sebagai rasio kerusakan lentur. Kemudian, Roufaiel dan Meyer (1987) memodifikasi batas lentur, sebagaimana diberikan pada Persamaan 2.13:
0
Namun, persamaan ini tidak dapat dipercaya berindikasi pada saat lentur tidak dimasukkan pengaruh beban siklik.
2.3.2 Indeks Kerusakan Park-Ang
Park dan Ang (1985) mengusulkan kombinasi dari indeks kerusakan komulatif dan non komulatif. Model ini bisa didefenisikan pada Persamaan 2.14 berikut ini, dimana suku yang pertama berkaitan dengan daktilitas dan suku yang kedua merupakan energi komulatif normalisasi yang diserap oleh struktur.
19
Dimana:
uu = perpindahan ultimit akibat beban statis.
um = perpindahan maksimum untuk beberapa siklus.
uy = perpindahan leleh.
= perpindahan daktilitas untuk beberapa siklus.
u = perpindahan daktilitas ultimit.
= konstanta pengaruh dari beban siklus dan properties struktur. Ehm = energi histeresis demand maksimum.
Qy = kekuatan leleh struktur.
Park dan Ang menyatakan bahwa nilai indeks kerusakan terdiri dari beberapa tingkatan:
a. DPA< 0.1 Hanya retak-retak kecil. b. 0.1 DPA< 0.25 Rusak ringan.
c. 0.25 DPA< 0.4 Rusak sedang. d. 0.4 DPA< 1 Rusak berat. e. DPA 1 Runtuh.
dkk. (1997) menganalisa model ini dengan sejumlah data eksperimental dan menyimpulkan bahwa model Park dan Ang yang paling tepat untuk kegagalan yang dihasilkan dari perpindahan plastis demand.
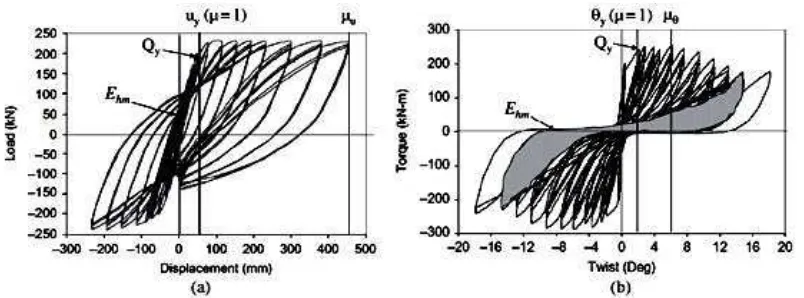
Gambar 2.3 Pengertian parameter model Park-Ang, (a) histeresis lentur dan (b) histeresis torsi
2.3.3 Indek Kerusakan Zahrah dan Hall
Indeks ini dikembangkan oleh Zahrah dan Hall (1984) tingkat kerusakan di struktur yaitu dengan jumlah leleh ekivalen. Indeks ini mencakup kebutuhan energi histeretik maksimum, perpindahan daktilitas, dan kekuatan leleh dari baja, seperti yang ditunjukkan dalam Persamaan 2.15:
) 1 ( y y
hm eq
u Q
E
N (2.15)
Dimana:
uy = perpindahan leleh.
= perpindahan daktilitas.
21
Qy = kekuatan leleh struktur.
Neq = jumlah leleh ekivalen.
Keuntungan dari indeks ini adalah bahwa hal itu mencerminkan potensi kerusakan yang terkait dengan jumlah total leleh dan deformasi inelastis kumulatif untuk seluruh durasi gerakan gempa. Ini adalah ukuran dari distribusi siklus amplitudo dan menunjukkan jumlah siklus pada perpindahan plastis maksimum dimana struktur harus mengembangkan untuk mendisipasi jumlah total permintaan energi histeresis (Ehm). Oleh karena itu, nilai-nilai Neq mendekati '1' menunjukkan
adanya satu siklus plastik besar dan khas dari gempa impulsif. Sedangkan nilai tinggi Neq mengacu pada sejumlah siklus plastik besar dan khas gempa durasi panjang.
Kerugian indeks ini adalah bahwa hal itu sangat tergantung pada karakteristik gerakan tanah dan menghasilkan nilai yang berbeda sesuai dengan gerakan tanah yang dipaksakan.
2.3.4 Indeks Kerusakan Hwang dan Scribner
Model ini mencakup kekakuan dan disipasi energi bersama dengan perpindahan dalam siklus tertentu. Definisi parameter untuk indeks ini ditunjukkan pada Gambar 2.4. Persamaan untuk perhitungan indeks kerusakan:
M = jumlah total siklus leleh. Ko = kekakuan sebelum leleh.
Ehi = disipasi energi histeretik dalam siklus ke-i.
umi = perpindahan maksimum dalam siklus ke-i.
Kmi = kekakuan secant sesuai dengan umi.
uy = perpindahan leleh.
Indeks kerusakan ini memberikan sama pentingnya dengan semua parameter (Hwang dan Scribner, 1984). Kerugian utama dari indeks ini adalah bahwa jangkauan tidak menyatu seperti indeks yang diusulkan oleh Park dan Ang. Selanjutnya, sangat tergantung pada properti penampang dan riwayat pembebanan. Ketergantungan ini membuat sulit untuk mengukur kerusakan.
23
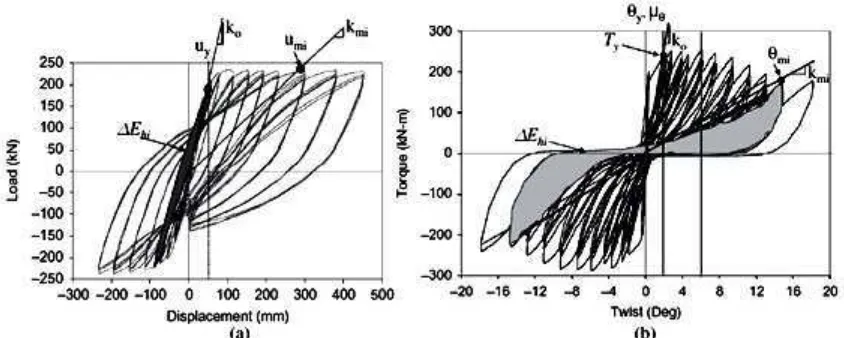
Gambar 2.4 Pengertian parameter model Hwang dan Scribner (a) histeresis lentur dan (b) histeresis torsi.
2.3.5 Indeks Kerusakan Cosenza
Cosenza dkk. (1993) mendeskripsikan indeks kerusakan sebagai berikut:
) 1 ( y y
H D
u V
E
I (2.17)
Dimana:
EH = energi histeresis demand.
= daktitilitas perpindahan.
Vy = gaya geser pada saat leleh pertama.
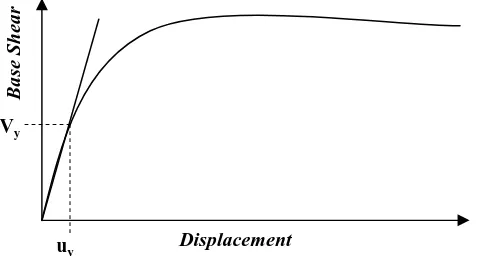
Untuk lebih jelasnya kita dapat melihat Gambar 2.5.
Gambar 2.5 Pengertian Vy dan uy dari kurva kapasitas
2.3.6 Indeks Kerusakan Boz rquez
Metodologi berdasarkan energi pada struktur adalah dimana energi yang tersedia pada struktur harus lebih besar atau sama dengan energi yang diterima struktur tersebut. Persyaratan struktur bangunan tahan gempa dapat dirumuskan sebagai berikut:
Energy Capacity Energy Demand (2.18) Energi akan diserap dan didissipasi oleh struktur, energi histeresis plastis Eh
dengan jelas berhubungan dengan kerusakan struktur. Eh dapat diartikan secara fisik
merupakan luas total area di bawah loop histeresis selama struktur menerima gempa. Oleh karena itu, akan lebih mudah menyatakan Persamaan 2.18 diatas dalam hal energi histeresis plastis:
EHC EHD (2.19)
Dimana:
EHC = kapasitas energi histeresis plastis.
EHD = energi histeresis demand.
Displacement
B
a
se
S
h
ea
r
uy
25
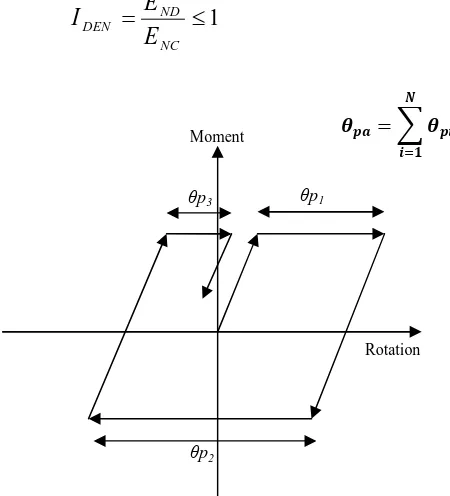
Persamaan 2.19 dapat dirumuskan sebagai indeks kerusakan berdasarkan energi:
1
dan EHC memiliki nilai yang sama maka dapat dianggap bahwa struktur runtuh. Oleh
karena itu ketika IDE = 1 sesuai dengan kegagalan struktur, nilai 0 berarti tidak ada
kerusakan struktur (berperilaku elastis). Dari sudut pandang fisik, persamaan ini merupakan keseimbangan antara kapasitas dan kebutuhan dalam hal energi. Dalam hal ini, formulasi ini mengikuti persamaan yang awalnya diberikan oleh Housner (1995) untuk konsep berdasarkan energi.
Menurut Persamaan 2.20, kerusakan struktur tergantung kepada keseimbangan antara kapasitas dan kebutuhan energi histeresis pada struktur. Sementara energi histeresis demand dapat diperoleh melalui analisa dinamis, suatu tantangan adalah bagaimana menentukan kapasitas energi histeresis pada struktur. Namun, perilaku lentur plastis biasanya berada pada ujung balok struktur, dalam kasus tertentu profil baja WF berada pada sayapnya. Kapasitas energi histeresis plastis pada balok struktur dapat diperkirakan sebagai berikut:
EHCm = 2 Zf fy pa (2.21)
Dimana:
Zf = modulus section.
fy = tegangan leleh baja.
Sambil melihat Persamaan 2.21 diatas menganggap bahwa energi plastis didisipasikan eksklusif melalui perilaku plastis di kedua ujung balok, definisi rotasi plastis kumulatif skematis diilustrasikan pada Gambar 2.6.
Persamaan 2.21 bisa digunakan bersamaan dengan Persamaan 2.20 untuk menghitung tingkat kerusakan pada struktur baja. Namun, untuk tujuan evaluasi kerusakan akan lebih mudah menormalkan energi histeresis EH sebagai berikut:
y
Persamaan 2.20 dapat dinyatakan dalam EN sebagai berikut:
1
27
Parameter yang digunakan pada Persamaan 2.23 sama dengan Persamaan 2.20. Keuntungan dari merumuskan masalah dalam hal EN adalah bahwa ini
merupakan parameter lebih stabil, dan secara kuantitatif dengan mudah dapat digunakan untuk tujuan praktis. Dengan kata lain, indeks kerusakan berdasarkan energi diusulkan di sini sesuai dengan rasio antara permintaan energi histeresis normal dan kapasitas energi histeresis normal, dan kondisi kegagalan diasumsikan IDEN sama dengan 1.
Dalam kasus struktur baja MDOF, tantangan utama untuk penggunaan praktis dari Persamaan 2.23 adalah definisi dari kapasitas energi dari struktur dalam hal frame struktur. Melalui pertimbangan bahwa dalam struktur baja biasa energi didisipasikan secara eksklusif oleh balok (yang merupakan hipotesis yang tepat untuk struktur kolom kuat – balok lemah), kapasitas energi sistem ini dapat diperkirakan
FEHi = faktor partisipasi energi yang menyumbang kontribusi yang berbeda
dari masing-masing lantai dengan kapasitas disipasi energi sebuah frame.
Cy = koefisien gempa.
Dy = perpindahan pada leleh pertama.
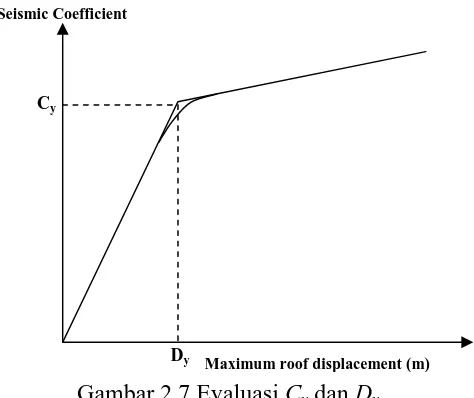
Cy dan Dy dapat diperoleh dari kurva kapasitas, seperti ditunjukkan pada
Gambar 2.7.
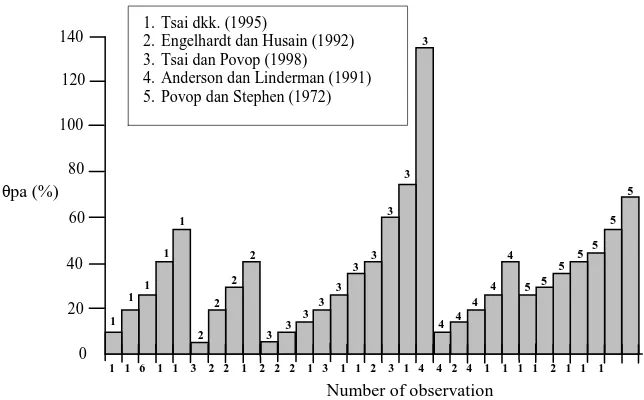
Persamaan 2.23 menunjukkan peran kapasitas rotasi plastis kumulatif dari elemen struktural dalam kapasitas disipasi energi total dari sebuah frame. Gambar 2.8 menunjukkan berbagai nilai pa dikumpulkan oleh Akbas (1997) dari pengujian
eksperimental dari frame baja dibebani oleh beban siklik. Berdasarkan hasil yang dikumpulkan oleh Akbas (1997), Boj rquez dkk. (2008) menemukan bahwa rotasi kapasitas plastik kumulatif frame baja merupakan fungsi kerapatan probabilitas lognormal dengan nilai median sebesar 0,23.
Gambar 2.7 Evaluasi Cy dan Dy
Meskipun pemilihan nilai pa untuk menghitung Persamaan 2.24, kapasitas
energi histeresis plastis struktur baja susah didapatkan, perlu ditekankan bahwa hasil eksperimental memberikan dasar yang cukup memadai untuk pemilihan tersebut.
Maximum roof displacement (m) Seismic Coefficient
29
Khususnya, nilai median dilaporkan oleh Boj rquez dkk. (2008) dan berdasarkan pada hasil eksperimen yang dikumpulkan oleh Akbas (1997) digunakan 0,23.
Gambar 2.8 Rotasi plastis komulatif struktur baja (Akbas 1997)
2.4 Energi dan Distribusi Kerusakan pada Struktur Baja
Untuk menghitung kontribusi dari struktur yang berbeda terhadap kapasitas total energi histeresis plastis pada MDOF, biasanya diperlukan untuk mengasumsikan distribusi disipasi energi plastis di sepanjang tinggi struktur. Sebagai contoh, Akbas dkk. (2001) mengusulkan distribusi linier, studi terbaru menunjukkan bahwa jika disipasi energi terkonsentrasi pada balok dari sebuah frame, distribusi lognormal merupakan pendekatan yang lebih baik (Boj rquez dkk. 2008). Sebuah faktor partisipasi energi histeresis plastis (FEH) perlu dibentuk untuk menjelaskan dengan
baik dalam Persamaan 2.24 untuk kontribusi yang berbeda setiap tingkat pada total kapasitas disipasi energi dari bangunan. Secara khusus, FEH dapat dirumuskan
1.Tsai dkk. (1995)
2.Engelhardt dan Husain (1992) 3.Tsai dan Povop (1998) 4.Anderson dan Linderman (1991) 5.Povop dan Stephen (1972)
sehingga dapat di evaluasi persentase dari kapasitas energi ultimit yang hilang selama gempa (lantai kritis memberikan kontribusi kapasitas disipasi energi penuhnya, kenyataannya yang dinyatakan melalui nilai kesatuan untuk FEH). Biasanya, ekspresi
untuk menggambarkan variasi FEH sepanjang tinggi bangunan berasal dari distribusi
energi plastis demand diperkirakan secara analitis pada prototype bangunan. Dari studi statistik 8 SMRF (Structure Moment Resisting Frame) baja pada beberapa durasi gerakan tanah yang lama, FEHi didapat dengan persamaan oleh Boj rquez dkk.
(2008) berikut ini:
Persamaan 2.26 dapat disederhanakan dari hasil analisa dinamik nonlinier dan analisa regresi menjadi persamaan berikut ini:
! 2
31
2.5 Energi Histeresis
Energi histeresis, diserap oleh struktur selama terjadi gempa kuat untuk mendorong sejumlah sistem struktur nonlinier, telah diakui oleh beberapa peneliti secara potensial berguna sebagai indikator kinerja gempa. Secara umum, loop histeresis stabil dengan besar kapasitas disipasi energi pada tingkat struktur diperkirakan menjamin kinerja deformasi yang lebih baik dari struktur, menyiratkan bahwa ada korelasi yang baik antara energi histeresis yang hilang dan deformasi inelastik demand. Gagasan ini sering didasarkan pada pengamatan yang dilakukan percobaan di kuasi-statis cyclic, di mana tampak jelas bahwa antara dua sistem dengan kekuatan yang sama, diuji di bawah beban siklik yang sama, satu dengan penyerapan energi yang lebih tinggi, yaitu penuh loop histeresis, harus menunjukkan kinerja yang superior. Dengan demikian, disipasi energi menjadi kunci bahan dari peraturan gempa modern. Oleh karena itu, dasar perencanaan gempa, definisi dari perilaku (reduksi) faktor q (atau R) memungkinkan bahwa kekuatan tinggi dari sistem elastis linear memiliki penyerapan energi nol dapat digantikan oleh perilaku disipasi efektif dari sistem elastoplastis dengan kekuatan geser dasar yang q kali lebih rendah (setidaknya perpindahan lebih berperan). Meskipun tidak ada pertanyaan tentang perlunya daktilitas, peran disipasi energi masih tidak sempurna untuk dipahami.
peningkatan redaman viscous. Peningkatan redaman disediakan sebagai fungsi langsung dari luas area di bawah kurva gaya-deformasi dari osilator nonlinier, kuantitas berhubungan baik dengan disipasi histeresis kuasi-statis. Hal ini tidak mengherankan bahwa disipasi energi yang lebih tinggi tampaknya menjadi setara dengan redaman tinggi, maka dari itu kinerja lebih baik.
2.5.1 Energi Histeresis Demand
Dalam perencanaan berdasarkan energi, kita harus membatasi kerusakan struktur dengan memberikan daktilitas dan kapasitas dissipasi energi yang cukup melalui histeresis dan redaman dalam struktur. Potensi kerusakan berhubungan dengan energi histeresis demand maksimum selama eksitasi dan selama perjalanan leleh terbesar. Kebutuhan energi histeresis dapat dihitung dari spektrum energi input jika rasio energi histeretik maksimum dengan energi input maksimum Ehm / Eirm
diketahui. Untuk menguji hubungan antara energi histeresis dan potensi kerusakan tiga rasio energi dianggap:
1. Rasio maksimum histeresis untuk energi input (Eh/Eir) m umumnya
terjadi selama perjalanan leleh terbesar.
2. Rasio energi histeresis maksimum energi input maksimum Ehm / Eirm
33
Dimana:
um = deformasi maksimum.
uy = deformasi leleh.
= um / uy adalah rasio daktilitas.
2.6 Karakteristik Gempa
Sebagaimana kita ketahui kerusakan yang diakibatkan gempa khususnya pada bangunan sangat tergantung terhadap karakteristik gempa. Akan dijelaskan beberapa karakteristik gempa dari beberapa sumber yang penulis ketahui.
2.6.1 Percepatan Puncak Tanah
Percepatan permukaan setempat adalah yang langsung mempengaruhi konstruksi. Karena itu, hal ini merupakan titik tolak dari perhitungan bangunan tahan gempa.
2.6.2 Durasi Gempa
Lamanya durasi gempa menentukan tingkat masukan energi ke dalam struktur, dan harus dipertimbangkan dalam semua analisis respon struktur linear dan non-linear. Ini memiliki peran penting dalam analisis likuifaksi (Trifunac, 1995) dan pemindahan permanen tanah, dan dalam prosedur dan algoritma untuk penilaian probabilistik respon struktur terhadap gempa bumi. Sebagai contoh, studi tentang distribusi statistik puncak pada respon struktur mengharuskan durasi gempa ditentukan. Studi ini menentukan probabilitas terlampaui tingkat perpindahan, gaya geser atau momen guling, untuk sejumlah waktu tertentu, pada setiap tingkat bangunan bertingkat. Durasi goncangan yang kuat juga diperlukan untuk generasi akselerogram buatan site-specific.
Pentingnya durasi gemetar untuk respon non-linear telah diakui, tetapi masih tidak digunakan dalam peraturan perencanaan bangunan. Pengaruh kelelahan dan leleh non-linear diabaikan, atau dianggap dengan cara yang disederhanakan. Definisi durasi yang jelas dan langsung, dan model skala menghubungkannya dengan parameter sumber gempa (Trifunac dkk.), karakteristik jalur propagasi, dan kondisi tanah daerah geologi dan lokasi di lapangan, diminta untuk memasukkan durasi dalam analisis dan desain struktur.
35
2.7 Getaran Gempa
Runtuhnya bagian antar muka pada sesar aktif, baik itu pada sesar mendatar (strike-slip fault), sesar normal (normal fault) maupun sesar terbalik (reverse fault), adalah merupakan sumber gempa. Luas dan volume bagian yang runtuh tersebut akan mempengaruhi besarnya energi yang dilepaskan ke segala arah dari dalam kerak bumi sampai ke permukaan bumi dalam bentuk gelombang getaran. Rekaman getaran gempa tidak mudah untuk diperoleh di Indonesia dan juga di banyak negara berkembang di berbagai belahan dunia yang terletak di kawasan rawan gempa. Sehingga model getaran gempa diperlukan untuk mewakili getaran gempa yang terjadi di lokasi. Getaran seperti ini disebut dengan gerakan tanah artifisial dan simulasi. Pada makalah ini semua getaran gempa yang tidak asli berasal dari patahan yang ditinjau disebut dengan model getaran gempa sedangkan proses membuatnya disebut dengan pemodelan getaran gempa.
Pemodelan getaran gempa terdiri dari:
1. Mengadopsi rekaman getaran gempa dari kawasan lain dan menskalakannya ke spektrum rencana gempa.
2. Mensimulasikan getaran gempa dan menskalakannya ke spektrum rencana gempa.
Pemodelan getaran gempa berdasarkan rekaman getaran gempa dari kawasan lain sangat lazim dipakai di dalam praktek karena lebih mudah dan praktis di dalam pelaksanaannya.
gempa, jarak lokasi ke sumber gempa, dan jenis sesar aktif) dengan lokasi tempat struktur bangunan gedung yang ditinjau berada (SNI 03-1726-2003). Untuk mengurangi ketidak-pastian mengenai kondisi lokasi ini, SNI 1726-2002 telah mengatur bahwa paling sedikit harus ditinjau 4 buah rekaman getaran gempa, dari 4 gempa yang berbeda untuk analisa repon riwayat waktu salah satunya harus diambil dari Gempa El Centro N-S yang telah direkam pada tanggal 15 Mei 1940 di California.
Metode pemilihan rekaman gempa lain adalah berdasarkan konsep probabilitas yang sudah mulai sering dipakai seperti yang diusulkan oleh Prof. Baker dari Universitas Stanford. Baker memperkenalkan cara memilih sekumpulan rekaman gempa yang dinamakan conditional mean spectrum (CMS). Dalam CMS, pertama-tama nilai spektrum percepatan disain pada perioda alami struktur ditentukan. Kemudian rekaman dipilih dari database berdasarkan skenario magnituda dan jarak terdekat. Setelah mengubah semua rekaman ke bentuk spektrum respon (Sa) dan ke bentuk log Sa, nilai rata-rata dan standar deviasinya kemudian dihitung. Lalu nilai epsilon (conditional mean) ditentukan untuk semua perioda dan dikalikan terhadap koefisien korelasi. Kemudian CMS dapat ditentukan dengan menjumlahkan nilai rata-rata log Sa kepada hasil kali epsilon dengan standar deviasi logaritma Sa.
37
ragam getar yang tinggi (higher mode effect). Ini berbeda bila struktur tersebut terkena getaran gempa dekat epek simpangan permanen dimana struktur akan cenderung memberikan respon yang besar pada kondisi ragam getar alami. Berdasarkan hal ini maka rekaman gempa harus dipilih secara hati-hati untuk analisa riwayat waktu.
2.8 Penskalaan Gempa
Untuk analisa riwayat waktu (time history analysis), rekaman gerakan tanah dipilih dan dijadikan sebagai respon spektrum disain. Ada beberapa metode dalam menskalakan gempa. Dibawah ini akan dijelaskan bebarapa metode menskalakan gempa.
2.8.1 Skala PGA (Peak Ground Acceleration)
Teknik skala ini yaitu memasukkan beberapa catatan gempa kemudian di match terhadap PGA target yaitu PGA peraturan gempa:
gmr ds
PGA PGA factor
Scala (2.29)
Dimana:
2.8.2 Skala Ordinat
Teknik skala ini yaitu penskalaan berdasarkan nilai respon spektrum pada perioda T yang sama dengan perioda alami struktur (T1) disingkat RSA (T1), mengacu kepada spektra desain yang ada pada peraturan gempa:
39 dan luas area pada percepatan respon spektrum yang ada diperaturan tetapi area yang diambil adalah area pada 1.2 T1 sampai dengan T2:
record spectrum sehingga sama pada peride 0 – 2 detik:
(2.33)
2.8.6 ASCE-7
Teknik skala ini memiliki metode yang sama dengan Partial Area perbedaan terletak pada periode yang ditinjau. Disini yaitu diantara 0.2T1 dan 1.5T1:
2.8.7 Spectrum Matching
Metode numerik untuk penyesuaian spektra telah diusulkan termasuk oleh Hancock dkk. (2006). Metode Hancock dkk. ini dipakai di dalam program SeismoMatch dan RSPMatch.
2.9 Accelelogram
Perbedaan gempa menghasilkan gerakan tanah dengan karakteristik gempa yang berbeda juga, gerakan tanah (ground motion) juga mengandung intensitas, frekuensi dominan dan durasi yang berbeda. Untuk melakukan analisa riwayat waktu (time history analysis) pada bangunan sangat di pertimbangkan, penskalaan berdasarkan nilai respon spektrum pada perioda T yang sama dengan perioda alami struktur (T1) disingkat RSA (T1), mengacu kepada spektra desain yang ada pada peraturan gempa. Ke empat accelerogram berbeda dipilih dari data PEER tahun 2011. Rekaman gerakan tanah pilihan (atau juga hasil simulasi) ini kemudian harus diskalakan berdasarkan spektrum respon percepatan disain setempat untuk rentang perioda alami 0,2T sampai dengan 1,5T. Hal ini dibuat agar seluruh ragam getar yang dimiliki struktur dapat terakomodir dalam analisa riwayat waktu. Metode penskalaan gerakan tanah ini disebut dengan metode penyesuaian spektra (spectral matching). Sejumlah metode numerik untuk penyesuaian spektra telah diusulkan termasuk oleh Hancock dkk. (2006). Metode Hancock dkk. ini dipakai di dalam program SeismoMatch.
Accelerogram ini disesuaikan (matching) terhadap respon spektrum desain
41
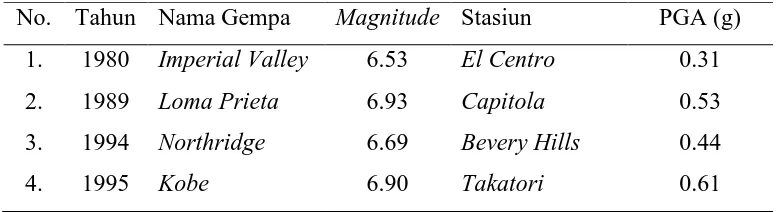
catatan accelerogram target spektrum menggunakan software seismomatch sampai dengan periode fundamental (T1). Rincian ground motion diberikan dalam Tabel 2.1.
Tabel 2.1.Ground Motion
No. Tahun Nama Gempa Magnitude Stasiun PGA (g) 1. 1980 Imperial Valley 6.53 El Centro 0.31
2. 1989 Loma Prieta 6.93 Capitola 0.53
3. 1994 Northridge 6.69 Bevery Hills 0.44
3.1 Modelisasi Struktur
Penelitian mengenai indeks kerusakan pada struktur berdasarkan energi harus dilakukan menggunakan proses pengukuran dan modelisasi struktur. Sehingga dapat dilakukan pencocokan antara besar tingkat kerusakan nyata pada suatu struktur dan seberapa besar tingkat kerusakan di dalam modelisasi struktur. Sebagai contoh adalah gedung Hotel Van Nuys yang rusak akibat gempa Northridge 1994, secara global lokasi kerusakan pada gedung ini telah di ketahui.
Namun, pada kesempatan ini penelitian hanya difokuskan untuk melakukan modelisasi struktur dalam kondisi tanpa kerusakan, tetapi peneliti akan memberikan gaya-gaya gempa kuat yang pernah terjadi di dunia. Sebagaiman telah disebutkan pada Bab I, langkah awal yang dilakukan yaitu merencanakan struktur baja sesuai dengan SNI 03-1726-2002 dengan data-data yang telah disesuaikan. Setelah struktur di desain dan memenuhi syarat terhadap SNI 03-1726-2002 dan SNI 03-1729-2002, dilanjutkan dengan melihat bagaimana perilaku struktur tersebut akibat pemberian ke-4 gaya gempa tersebut.
43
Untuk menghitung besarnya energi yang terdapat dalam struktur tersebut digunakan program komputer juga yaitu dengan menggunakan program Abaqus.
Sistem struktur akan dimodelkan dengan menggunakan metode elemen hingga. Dimana pada sebagian besar kasus system struktur akan dimodelkan dengan elemen portal 2 dimensi (space frame).
45
Gambar 3.3 Steel Moment Resisting Frame (SMRF 4)
3.2 Input Data
3.2.1 Dimensi Struktur
Sistem struktur pada penelitian ini, tinggi tingkat-1 yaitu = 450 cm dan untuk tingkat berikutnya 2 sampai lantai diatasnya yaitu sama 380 cm, untuk panjang bentang 800 cm, 600 cm, dan 800 cm.
47
3.2.2 Beban Struktur
Untuk tulisan ini diasumsikan beban yang bekerja hanya beban hidup (live), beban mati (dead) dan beban gempa (eq). Adapun besar masing-masing beban adalah:
a. Beban mati = 20 kN/m. b. Beban hidup = 10 kN/m. c. Beban gempa
Untuk desain struktur beban gempa yang digunakan sesuai dengan SNI 03-1726-2002. Sedangkan untuk analisa kerusakan digunakan ke-4 catatan gempa sebagaimana yang telah disebutkan pada Bab I sebelumnya.
3.2.3 Properti Material
Properties material struktur yang akan digunakan dalam pemodelan adalah: 1. Jenis material = Baja.
2. Massa jenis ( ) = 7,85 ton/m3. 3. Tegangan leleh (fy) = 270 Mpa.
4. Modulus elastisitas (E) = 200000 Mpa. 5. Poisson’s ratio ( ) = 0,3.
3.3 Prosedur Analisa
kaji terhadap ke-4 gempa kuat yang telah di skalakan terhadap lokasi gempa zona 6 (dalam hal ini diasumsikan bangunan di Aceh). Dengan bantuan program Abaqus kita bisa melihat berapa besar energi pada struktur tersebut.
Adapun diagram alir global prosedur untuk proses analisa pada tulisan ini dapat dilihat pada Gambar 3.4.
Gambar 3.4 Diagram alir proses analisa
3.4 Persyaratan Perencanaan Struktur Baja
49
3.4.1 Waktu Getar Alami (T)
Berdasarkan SNI 03-1726-2002 waktu getar struktur dapat didekati dengan rumus Reyleigh:
Wi = berat lantai ke-i, termasuk beban hidup yang sesuai (direduksi). zi = ketinggian lantai tingkat ke-i diukur dari taraf penjepitan lateral. Fi = beban gempa statik ekivalen pada lantai tingkat ke-i.
di = simpangan horizontal lantai tingkat ke-i (mm). g = percepatan gravitasi (9.81 m/det2).
n = nomor lantai tingkat paling atas.
Pada SAP 2000 waktu getar alami dapat diketahui secara otomatis dari ragam getar atau Modal Analysis dengan cara Run, kemudian Display – Show Mode Shape.
Tabel 3.1 Koefisien yang membatasi waktu getar alami fundamental struktur
Lokasi bangunan berada pada zona 6, maka = 0.15
3.4.2 Kinerja Batas Layan
Pada SNI 03-1726-2002 Pasal 8.1 disebutkan bahwa kinerja batas layan struktur gedung ditentukan oleh simpangan antar tingkat akibat pengaruh gempa rencana, yaitu untuk membatasi terjadinya pelelehan baja, peretakan beton yang berlebihan, mencegah kerusakan non struktur dan ketidaknyamanan penghuni.
Simpangan antar tingkat yang diizinkan tidak boleh melampaui 0,03/R x tinggi tingkat yang bersangkutan atau 30 mm, diambil yang terkecil.
3.4.3 Kinerja Batas Ultimit
51
benturan berbahaya antar gedung atau antar bagian struktur gedung yang dipisah dengan sela pemisah (sela dilatasi).
Simpangan dan simpangan antar tingkat ini harus dihitung dari simpangan struktur gedung akibat pembebanan gempa nominal, dikalikan dengan suatu faktor pengali = 0,7 x R (untuk gedung beraturan).
Dalam Pasal 8.2.2 disebutkan bahwa dalam segala hal simpangan antar tingkat yang dihitung dari simpangan struktur gedung untuk batas ultimit tidak boleh melampaui 0,02 x tinggi tingkat yang bersangkutan.
3.5 Analisa Struktur dan Modeling
4.1 Perencanaan Struktur
Sebelum melakukan perencanaan struktur, disini penulis memberikan berupa asumsi yang dijadikan sebagai dasar untuk perencanaan masing-masing struktur. Pertama, ketiga struktur tersebut dimodelkan menjadi 2D, hubungan (connection) antara kolom dan balok dianggap kaku (rigid connection) dan hubungan kolom ke pondasi dianggap jepit. Kemudian, untuk analisa beban gempa adalah respon spektrum. Untuk perencanaan struktur akan dilakukan dengan memakai program Sap 2000 dan dikontrol terhapa peraturan Indonesia. Ketiga bangunan tersebut dianalisa sesuai dengan peraturan Indonesia. Adapun tahapan-tahapan yang dilakukan secara garis besar di program Sap 2000 diantaranya:
1. Preprocesssor
a. Geometri struktur, pemilihan bentuk gometri struktur.
b. Define material, pemasukan data-data material yang digunakan.
c. Define section propeties, pembuatan dimensi dari masing-masing
balok dan kolom.
d. Drawing, pembuatan bentuk struktur.
e. Load case, pengaturan beban-beban yang dianalisa.
f. Load combination, pembuatan kombinasi beban.