APLIKASI PROGRAM INTEGER PADA PERUMAHAN BUMI SERGAI DI SEI RAMPAH
SKRIPSI
ERLINA
070803054
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
APLIKASI PROGRAM INTEGER PADA PERUMAHAN BUMI SERGAI DI SEI RAMPAH
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
ERLINA 070803054
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : APLIKASI PROGRAM INTEGER PADA
PERUMAHAN BUMI SERGAI DI SEI RAMPAH
Kategori : SKRIPSI
Nama : ERLINA
Nomor Induk Mahasiswa : 070803054
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, Juli 2013
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Henry Rani Sitepu, M.Si Dra. Elly Rosmaini, M.Si
NIP. 19530303 198303 1 002 NIP 19600520 19803 2 002
Diketahui/ Disetujui oleh:
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
ANALISIS KOMPONEN UTAMA SEBAGAI METODE UNTUK MENGATASI MASALAH MULTIKOLINEARITAS
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2012
PENGHARGAAN
Puji dan syukur penulis ucapkan kepada Allah SWT yang senantiasa memberikan
segala rahmat dan hidayah-Nya, dan yang telah memberi kekuatan akal dan fikiran
sehingga penulis dapat menyelesaikan skripsi ini dengan judul Aplikasi Program
Integer pada Perumahan Bumi Sergai di Sei Rampah.
Dalam kesempatan ini, penulis ingin mengucapkan terima kasih kepada Dra.
Elly Rosmaini, M.Si. selaku pembimbing I dan Drs. Henry Rani Sitepu, M.Si pembing
II yang telah menyediakan waktunya untuk membimbing dan memberikan pengarahan
kepada penulis sehingga penyusunan skripsi ini dapat diselesaikan. Dr. Esther S. M.
Nababan, M.Sc dan Drs. Gim Tarigan, M.Si selaku dosen penguji penulis yang telah
banyak memberi masukan yang sangat berarti sehingga selesainya skripsi ini. Prof.
Drs. Tulus, Vordipl.Math., Ph.D M.Sc dan Dra. Mardiningsih, M.Si selaku Ketua dan
Sekretaris Departemen Matematika Dekan dan Pembantu Dekan Fakultas Matematika
dan Ilmu Pengetahuan Alam beserta Civitas Akademi Universitas Sumatera Utara
Kedua orang tua saya Bapak H. Murti dan Ibu Hj. Saidah Siregar, kakak dan
abang penulis yang senantiasa memberikan dukungan doa dan materi kepada penulis.
Seluruh teman-teman kuliah dan junior matematika, khususnya kepada stambuk 2007
Aida, Pita, Minda, Erna, Nisa dan teman-teman yang tidak dapat penulis sebutkan satu
per satu yang telah memberikan dorongan semangat serta saran dalam pengerjaan
skripsi ini.
Dengan segala kerendahan hati Penulis menyadari banyak kekurangan dan
ketidaksempurnaan pada skripsi ini. Oleh karena itu, Penulis sangat mengharapkan
dan berterimakasih untuk semua bentuk saran dan kritikan yang membangun demi
menambah wawasan dan pengetahuan Penulis Akhir kata penulis mengucapkan
APLIKASI PROGRAM INTEGER PADA PERUMAHAN BUMI SERGAI DI SEI RAMPAH
ABSTRAK
Rumah tipe 65(X1) dan tipe 45(X2) akan dimodelkan ke dalam model matematika
berupa integer peogramming yang merupakan bagian dari masalah pemrograman linier, dimana variabel keputusan harus berupa bilangan bulat. Masalah integer
programming akan diselesaikan menggunakan metode branch and bound yang
terlebih dahulu merubah masalah integer programming ke bentuk pemrograman linier, kemudian digunakan metode simpleks untuk menyelesaikan masalah pemrograman linier tersebut. Fungsi tujuan memaksimalkan penjualan rumah Z = 180.000.000X1 +
140.000.000X2 dan fungsi kendala bahan-bahan bangunan. Jumlah rumah untuk tipe
65 adalah 36 unit dan tipe 45 sebanyak 62 unit.
APPLICATION OF INTEGER PROGRAMMING TO PERUMAHAN BUMI SERGAI IN SEI RAMPAH
ABSTRACT
A housing will be built in Sei Rampah the Earth Housing Sergai, with two types. Type 65 (X1) and type 45 (X2). This problem will be modeled in the form of mathematical
models peogramming integer that is part of a linear programming problem, where the decision variables must be integers. Integer programming problem will be solved using the branch and bound method to first change the integer programming problem into a linear programming form, then use the simplex method to solve the linear programming problem. With the objective function of the selling price of the house Z = 180.000.000X1 + 140.000.000X2 and constraint functions of building materials. The
number of homes for Type 65 are 36 units and type 45 as many as 62 units.
DAFTAR ISI
Daftar Gambar viii
Daftar Lampiran ix
Bab 1 Pendahuluan
1.1 Latar Belakang 1
1.2 Perumusan Masalah 4
1.3 Batasan Masalah 4
1.4 Tinjauan Pustaka 5
1.5 Tujuan Penelitian 7
1.6 Kontribusi Penelitian 7
1.7 Metode Penelitian 7
Bab 2 Landasan Teori
2.1 Linear Programming 8
2.1.1 Model Linier Programming 8
2.1.2 Asumsi-Asumsi Linear Programming 13
2.1.3 Terminologi Linier Programming 14
2.1.4 Unsur-unsur Linier Programming 15
2.2 Pemrograman Bilangan Bulat (Integer Programming) 19
2.3 Pencabangan dan Pembatasan (Branch and Bound) 27
Bab 3 Pembahasan
3.1 Pengumpulan Data 36
3.2 Hasil Pengumpulan Data 36
3.3 Perumusan Data ke dalam Model Matematika 38
3.4 Pengolahan Data 40
Bab 4 Kesimpulan dan Saran
4.1 Kesimpulan 49
4.2 Saran 49
DAFTAR TABEL
Nomor Judul Halaman
Tabel
2.1 Tabel Linear Programming 12
3.1 Data Perumahan Bumi Sergai 40
3.2 Tabel Simpleks 42
3.3 Tabel Simpleks I 42
3.4 Tabel Simpleks II 43
3.5 Tabel Simpleks III 43
3.6 Tabel Alternatif Pembulatan Jumlah Tipe Setiap Rumah
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
2.1 Flowchart Algoritma Branch and Bound untuk IP
Optimasi Maksimum 32
2.2 Flowchart Algoritma Branch and Bound untuk IP
Optimasi Minimum 33
2.3 Skema Pengolahan Data 35
3.1 Diagram Branch and Bound Perumahan Bumi Sergai
(Titik X1 yang dicabangkan) 46
3.2 Diagram Branch and Bound Perumahan Bumi Sergai
ix
DAFTAR LAMPIRAN
Nomor Judul Halaman
Lamp
1 Tabel QM 1 52
2 Tabel QM 2 53
3 Data Perumahan Bumi Sergai 55
4 Surat keputusan pengambilan data 56
5 Surat keputusan telah melakukan riset
Di Perumahan Bumi Sergai 57
6 Brosur Perumahan Bumi Sergai 58
APLIKASI PROGRAM INTEGER PADA PERUMAHAN BUMI SERGAI DI SEI RAMPAH
ABSTRAK
Rumah tipe 65(X1) dan tipe 45(X2) akan dimodelkan ke dalam model matematika
berupa integer peogramming yang merupakan bagian dari masalah pemrograman linier, dimana variabel keputusan harus berupa bilangan bulat. Masalah integer
programming akan diselesaikan menggunakan metode branch and bound yang
terlebih dahulu merubah masalah integer programming ke bentuk pemrograman linier, kemudian digunakan metode simpleks untuk menyelesaikan masalah pemrograman linier tersebut. Fungsi tujuan memaksimalkan penjualan rumah Z = 180.000.000X1 +
140.000.000X2 dan fungsi kendala bahan-bahan bangunan. Jumlah rumah untuk tipe
65 adalah 36 unit dan tipe 45 sebanyak 62 unit.
APPLICATION OF INTEGER PROGRAMMING TO PERUMAHAN BUMI SERGAI IN SEI RAMPAH
ABSTRACT
A housing will be built in Sei Rampah the Earth Housing Sergai, with two types. Type 65 (X1) and type 45 (X2). This problem will be modeled in the form of mathematical
models peogramming integer that is part of a linear programming problem, where the decision variables must be integers. Integer programming problem will be solved using the branch and bound method to first change the integer programming problem into a linear programming form, then use the simplex method to solve the linear programming problem. With the objective function of the selling price of the house Z = 180.000.000X1 + 140.000.000X2 and constraint functions of building materials. The
number of homes for Type 65 are 36 units and type 45 as many as 62 units.
BAB 1
PENDAHULUAN
1.1Latar Belakang
Optimasi adalah suatu proses pencarian hasil terbaik. Proses ini dalam analisis sistem
diterapkan terhadap alternatif yang dipertimbangkan, kemudian dari hasil tersebut
dipilih alternatif yang menghasilkan keadaan terbaik, yaitu dengan mencari solusi
optimum (maksimum atau minimum) sesuai dengan fungsi tujuan dan kendala yang
ada. Karena optimasi mencakup usaha untuk menemukan cara terbaik dalam
melakukan sesuatu pekerjaan dan cara terbaik dalam memecahkan suatu persoalan,
maka aplikasinya meluas pada hal-hal praktis dalam dunia industri, produksi,
perdagangan dan sebagainya.
Pertumbuhan jumlah penduduk yang terus meningkat berakibat kepada
kebutuhan akan rumah juga meningkat. Melihat keadaan ini banyak pengembang yang
bermunculan untuk menyediakan rumah tempat tinggal. Rumah yang dikembangkan
mulai dari rumah tipe sangat sederhana sampai tipe rumah mewah. Pengembang
biasanya lebih tertarik mengembangkan tipe rumah mewah karena keuntungan
marginalnya lebih bagus dibandingkan jika mengembangkan tipe rumah sederhana.
Namun disisi lain masyarakat lebih banyak membutuhkan tipe rumah sederhana sesuai
kemampuan mereka.
Menurut Lewis (1984 dalam Suparlan) masyarakat berpenghasilan rendah
adalah kelompok masyarakat yang mengalami tekanan ekonomi, sosial, budaya dan
politik yang cukup lama dan dapat menimbulkan budaya miskin. Sedangkan menurut
Asian Development Bank (ADB) masyarakat berpenghasilan rendah adalah
masyarakat yang tidak memiliki akses dalam menentukan keputusan yang
masyarakat; rendahnya kualitas hidup; buruknya etos kerja dan pola pikir mereka serta
lemahnya akses mereka terhadap aset lingkungan seperti air bersih dan listrik.
Kebutuhan akan rumah merupakan salah satu kebutuhan dasar (home needs)
bagi manusia setelah pangan dan sandang. Setiap individu manusia akan
mengutamakan pemenuhan kebutuhan dasar daripada kebutuhan sekundernya. Begitu
pula dengan kebutuhan akan rumah, setiap orang akan berusaha memenuhi kebutuhan
akan rumah dalam setiap tingkat kehidupan masyarakat dengan memperhatikan selera
dan kemampuan yang ada. Namun, tidak semua masyarakat bisa dengan mudah
membangun rumah, diperlukan berbagai hal sehingga rumah itu bisa didirikan dan
ditempati. Misalnya, tanah, kepemilikan tanah, struktur bangunan, tes kelayakan dan
perizinan pendirian bangunan. Banyak masyarakat yang tidak ingin direpotkan dengan
hal seperti itu, karena itu masyarakat yang ingin membangun atau membeli rumah
menempuh cara yang lebih efektif dan tidak menyita banyak waktu, yaitu dengan cara
membeli rumah sebuah agen rumah atau perumahan yang biasa disebut dengan
developer dan pembayarannya pun bisa dilakukan dengan cara tunai ataupun kredit
melalui sebuah lembaga perbankan yang sudah ditunjuk.
Rumah adalah bangunan yang berfungsi sebagai tempat tinggal atau hunian
dan sarana binaan keluarga. (Turner, 1972) menyatakan bahwa rumah mengandung
arti sebagai komoditi dan sebagai proses. Sebagai komoditi, rumah merupakan produk
yang bersifat ekonomis dan dapat diperjualbelikan berdasarkan permintaan dan
penawaran. Sebagai proses, rumah menggambarkan aktivitas manusia yang menjadi
proses penghuni rumah tersebut, yang dapat meningkat sesuai dengan kondisi sumber
daya yang ada serta pandangan atas kebutuhan sesuai persepsinya. Dalam hal ini
rumah tidak dapat dipandang sebagai bangunan fisik saja, namun lebih merupakan
bagaimana rumah tersebut digunakan penghuninya untuk saling berinteraksi dalam
suatu proses yang panjang.
Rumah merupakan salah satu bagian terpenting dalam kehidupan masyarakat.
Oleh sebab itu pemerintah akan selalu mengusahakan dalam tingkat kehidupan setiap
orang dengan memperhatikan selera dan kemampuan yang ada (Tito Soetalaksana,
prasarana. Bila telah dapat menunjang kehidupan dan perikehidupan manusia maka
disebut sebagai permukiman.
Sebuah perumahan akan dibangun di daerah Sei Rampah, Perumahan itu diberi
nama Bumi Sergai. Rumah-rumah yang akan dibangun mempunyai beberapa tipe,
yaitu tipe 45 dan tipe 65. Masalah yang akan dibahas adalah pengoptimalan
pemakaian bahan-bahan bangunan yang akan digunakan untuk membangun
rumah-rumah tersebut. Bahan-bahan tersebut terdiri dari semen, batu bata, pasir, seng, kayu,
gypsum, besi, paku, keramik dan batu koral. Agar pembangunan perumahan untuk
setiap tipe mencapai optimal maka digunakan sebuah metode branch and bound
dengan formulasi program integer ( program linier integer).
Program integer adalah program linear (Linear Programming) di mana
variabel-variabelnya bertipe integer. Program integer digunakan untuk memodelkan
permasalahan yang variabel-variabelnya berupa bilangan yang tidak bulat (bilangan
real). Program integer juga biasanya lebih dipilih untuk memodelkan suatu
permasalahan dengan variabel berupa bilangan real yang mana dalam memodelkan
permasalahan menuntut solusi berupa bilangan integer, misalnyakeuntungan produksi
3 pesawat dibandingkan dengankeuntungan produksi 3,5 pesawat akan menghasilkan
selisih keuntungan yang signifikan.
Model Program integer biasanya dipilih untuk permasalahan yang
variabel-variabelnya tidak dimungkinkan bertipe bilangan tidak bulat, misalnya: variabel
jumlah orang. Program integer dapat diselesaikan dengan banyak cara, antara lain :
menggunakan grafik, metode eliminasi dan substitusi dan sebagainya. Salah satu cara
yang cukup efektif untuk menyelesaikan program integer adalah dengan
mengaplikasikan algoritma Branch and Bound (Shieny, 2007).
Algoritma Branch and Bound adalah metode algoritma umum untuk mencari
solusi optimal dari berbagai permasalahan optimasi, terutama untuk optimasi diskrit
dan kombinatorial. Sebagaimana pada algoritma runut-balik (Backtracking), algoritma
Branch and Bound juga merupakan metode pencarian di dalam ruang solusi secara
membedakan keduanya adalah bila pada algoritma runut-balik (Backtracking), ruang
solusi dibangun secara dinamis berdasarkan skema DFS (Depth First Search), maka
pada algoritma Branch and Bound ruang solusi dibangun dengan skema BFS (Breadth
First Search) (Shieny, 2007).
Algoritma Branch and Bound banyak digunakan untuk memecahkan berbagai
macam permasalahan antara lain : persoalan Knapsack 0/1, Travelling Salesman
Problem (TSP), The N-Queens Problem (Persoalan N-Ratu), Graph Colouring
(Pewarnaan Graf), Sirkuit Hamilton, Integer Programming, Nonlinear Programming,
Quadratic Assignment Problem (QAP), Maximum Satisfiability Problem
(MAX-SAT), dan lain sebagainya. Berdasarkan kondisi-kondisi di atas maka penulis
mengambil judul tugas akhir ini sebagai : “APLIKASI PROGRAM INTEGER PADA PERUMAHAN BUMI SERGAI DI SEI RAMPAH”.
1.2Perumusan Masalah
Permasalahan dalam tulisan ini menentukan jumlah tipe rumah yang akan dibangun
sehingga memenuhi aspek pasar dalam penyediaan rumah sederhana, terjangkau dan
sesuai dengan kemampuan pembeli.
1.3Batasan Masalah
Banyak metode yang ada untuk menentukan penyelesaian integer programming.
Namun agar penyelesaian permasalahan tidak menyimpang dari pembahasan, penulis
merasa perlu membuat pembatasan permasalahan yaitu:
1. Hanya membahas metode branch and bound sebagai penyelesaian integer
programming.
2. Memaksimalkan penjualan rumah dengan fungsi kendala bahan bangunan.
3. Solusi optimum variabel keputusan harus bernilai integer
4. Model matematika diperoleh dari data yang diambil dari Perumahan Bumi
Sergai di Sei Rampah.
5. Asumsikan bahan bangunan yang dijadikan fungsi kendala yang parameternya
dalam model matematika. Bahan bangunan tersebut yaitu semen, pasir dan
keramik.
1.4Tinjauan Pustaka
Istilah integer programming atau integer linear programming berhubungan dengan
masalah program linier (linear programming) yang domain dari semua atau sebagian
variabel-variabel masalah dibatasi integer (Paul R. Thie, 1979).
Integer programming merupakan sebuah formulasi dalam operasi riset, yang
mempunyai potensi untuk diaplikasikan. Model-model integer programming muncul
di setiap aplikasi-aplikasi pemrograman matematis (mathematical programming),
seperti penganggaran modal, penempatan gudang dan penjadwalan ( Charles S.
Beighler dkk, 1979).
Program linier merupakan suatu model program linier yang khusus digunakan
untuk menyelesaikan suatu problem program linier di mana nilai variabel keputusan
yang penyelesain optimalnya harus merupakan bilangan bulat. Persyaratan bahwa
nilai variabel keputusan harus bilangan bulat (integer) seperti rumah, pabrik, tugas,
dan lain-lain (Parlin Sitorus, 1997).
Program integer atau dikenal dalam bahasa inggris dengan integer
programming merupakan bentuk khusus atau variasi dari program linear atau program
non linear, di mana satu atau lebih dari peubah-peubahnya dalam vektor
penyelesainnya memiliki nilai-nilai bukan pecahan atau angka bulat yang disebut
integer (Nasendi, B. D. dan Affendi Anwar, 1984).
Pemrograman linier integer adalah salah satu teknik analisis dari kelompok
teknik riset operasi yang memakai model matematika. Tujuannya adalah untuk
mencari, memilih, dan menentukan alternatif yang terbaik dari antara sekian alternatif
layak yang tersedia. Dikatakan linier karena peubah-peubah yang membentuk model
pemrograman dianggap linier. Pemrograman linier pada hakekatnya merupakan suatu
alternatif pemecahan masalah, kemudian dipilih mana yang terbaik diantaranya dalam
menyusun strategi dan langkah-langkah kebijakan lebih lanjut tentang alokasi sumber
daya dan dana yang terbatas guna mencapai tujuan atau sasaran yang diinginkan
optimal.
Maksimumkan
Kendala
Metode yang sangat berguna dalam memecahkan masalah pemrograman
matematis adalah branch and bound. Algoritma branch and bound, digunakan untuk
memecahkan masalah pemrograman integer. Algoritma ini berasal dari karya Land
dan Doig, diterbitkan pada tahun 1960 (Paul R. Thie, 1979).
Branch and bound pada dasarnya adalah strategi "membagi dan
menaklukkan". Idenya adalah untuk mempartisi daerah layak dalam subdivisi dan
kemudian dikelola lagi, jika diperlukan, untuk partisi lebih lanjut(Bradley dkk, 1977).
Awalnya algoritma branch and bound dipahami sebagai pemrograman
mundur(backtracking), namun telah ditemukan cara yang lebih umum dalam
pengaplikasian solusi integer dan mixed integer programming. Perhatikan bahwa
diperlukan batas atas dan bawah pada semua variabel. Kemudian dapat diasumsikan
bahwa semua batas bawah adalah nol karena transformasi sederhana akan selalu
mengubah semua variabel kembali ke asal. Jika N adalah nol, maka itu adalah integer
linear programming; jika semua variabel dibatasi dengan nol-satu, maka itu disebut
program bilangan bulat biner. Semua himpunan masalah dapat diselesaikan dengan
menggunakan prosedur branch and bound. Konsep yang mendasari strategi branch
berikut
[ ]
xj +1≥xj ≥[ ]
xj . Dimana [xj] adalah bilangan bulat (integer) yang lebihbesar, kurang dari atau sama dengan nilai xj (Charles S. Beighler dkk, 1979).
1.5Tujuan Penulisan
Tujuan penulisan ini adalah untuk memformulasikan jumlah berbagai tipe rumah yang
dibangun dalam pembangunan perumahan Bumi Sergai di Sei Rampah sehingga
mencapai solusi optimum dengan kendala berupa bahan bangunan yang variabel
keputusannya harus berupa bilangan bulat.
1.6Kontribusi Penelitian
Tulisan ini dapat menambah referensi yang berhubungan dengan masalah integer
programming dengan pendekatan algoritma branch and bound, dan menjadi bahan
pertimbangan untuk membangun perumahan Bumi Sergai tersebut.
1.7Metode Penelitian
Metode penelitian yang digunakan dalam masalah ini adalah :
1. Melakukan studi yang berhubungan dengan Integer Programming
menggunakan algoritma Branch and Bound berupa jurnal, artikel dan buku.
2. Observasi ke tempat penelitian dan memahami informasi dari teori yang
berkaitan dengan topik penelitian. Data yang diambil:
a. Bahan-bahan yang digunakan yaitu: batu bata, semen, pasir, seng, besi,
batu koral, gybsum, paku, kayu dan keramik.
b. Harga jual rumah per unit
c. Luas bangunan
3. Mengolah data yang diperoleh dari Perumahan Bumi Sergai di Sei Rampah,
memformulasikannya ke model matematika.
4. Kesimpulan dari hasil pengolahan data secara optimal dengan menggunakan
BAB 2
LANDASAN TEORI
2.1 Linear Programming
2.1.1 Model Linier Programming
Pemrograman linier adalah sebuah model matematik untuk menjelaskan suatu
persoalan optimasi. Istilah linier menunjukkan bahwa seluruh fungsi matematik di
dalam model harus berupa fungsi linier; sedang kata pemrograman dalam istilah ini
pada hakekatnya sinonim dengan perencanaan. Oleh karena itu, Pemrograman linier
mencakup perencanaan kegiatan-kegiatan untuk memperoleh hasil optimal, yaitu hasil
yang memberikan nilai tujuan terbaik ( Siswanto, 1990).
Pemrograman linier adalah suatu cara untuk menyelesaikan persoalan
pengalokasian sumber-sumber yang terbatas di antara beberapa aktivitas yang
bersaing, dengan cara yang terbaik yang mungkin dapat dilakukan (Dimyati dan A.
Dimyati, 1987).
Pokok pikiran yang utama dalam menggunakan program linier adalah
merumuskan masalah dengan jelas dengan menggunakan sejumlah informasi yang
tersedia. Sesudah masalah dirumuskan dengan baik, maka langkah berikutnya adalah
menerjemahkan masalah ini ke dalam bentuk model matematika, yang terang
mempunyai cara pemecahan yang lebih mudah dan rapi guna menemukan jawaban
terhadap masalah yang dihadapi ( Siagian, 1987).
Sebagai contoh dari pemecahan masalah dengan menggunakan program linier
adalah keadaan bagian produksi suatu perusahaan yang dihadapkan pada masalah
penentuan tingkat produksi masing-masing jenis produk dengan memperhatikan
untuk memperoleh tingkat keuntungan maksimal atau biaya yang minimal (Subagyo
et al., 1990).
Linier programming merupakan suatu model umum yang dapat digunakan
dalam pemecahan masalah pengalokasian sumber-sumber yang terbatas secara
optimal. Linier programming memakai suatu model matematis yang menggambarkan
masalah yang dihadapi. Linier memiliki arti bahwa semua fungsi matematis dalam
model harus merupakan fungsi-fungsi linier, sedangkan programming/pemrograman
dapat diartikan sebagai perencanaan. Dengan demikian linier programming dapat
didefinisikan sebagai membuat rencana kegiatan-kegiatan dengan menggunakan suatu
model umum dalam pemecahan masalah pengalokasian sumber daya-sumber daya
yang terbatas secara optimal.
Model pemrograman linier memiliki tiga unsur dasar, yaitu (1) variabel
keputusan merupakan variabel yang akan dicari dan memberi nilai yang paling baik
bagi tujuan yang hendak dicapai (2) fungsi tujuan menunjukkan fungsi matematik
yang harus dimaksimumkan atau diminimumkan dan mencerminkan tujuan yang
hendak dicapai, dan (3) fungsi kendala menunjukkan fungsi matematik yang menjadi
kendala bagi usaha untuk memaksimumkan atau meminimumkan fungsi tujuan dan
mewakili kendala-kendala yang harus dihadapi oleh organisasi (Siswanto, 1990).
Model dasar atau Persamaan linier dapat dirumuskan sebagai berikut :
Cari nilai-nilai yang dapat menghasilkan berbagai kombinasi
optimum (maksimum atau minimum) dari :
Dengan syarat bahwa fungsi tujuan tersebut memenuhi kendala sebagai
. . . .
. . . .
. . . .
atau dalam bentuk umumnya :
optimumkan (maksimumkan atau minimumkan) :
dengan syarat ikatan :
Untuk:
= Parameter yang dijadikan kriteria optimasi, atau koefisien peubah
pengambilan keputusan dalam fungsi tujuan.
= Peubah pengambilan keputusan atau kegiatan (yang ingin dicari; yang tidak
diketahui).
= Koefisien peubah pengambilan keputusan dalam kendala ke-i.
= Sumber daya yang terbatas, yang membatasi kegiatan atau usaha yang
bersangkutan; disebut pula konstanta atau “nilai sebelah kanan” dari kendala
ke-i.
= Nilai skalar kriteria pengambilan keputusan; suatu fungsi tujuan.
Konsep linier programming ditemukan dan diperkenalkan pertama kali oleh
George Dantzig yang berupa metode mencari solusi masalah linier programming
dengan banyak variabel keputusan. Kemudian banyak ahli yang bergabung dengan
Dantzig dalam konsep pengembangan linier programming. Paper pertamanya adalah
metode solusi yang bernama metode simplex. Dalam pengembangan linier
programming, Dantzig bekerjasama dengan Marshal Wood dan Alex O, dan masih
banyak para ahli yang lainnya ikut. Kemudian, setelah berhasil diterapkan pada sektor
pemerintah dan swasta, akhirnya disadari bahwa linier programming merupakan
masalah yang sangat membantu dalam analisis bidang bisnis.
Model Linier Programming ini merupakan bentuk dan susunan dalam
menyajikan masalah-masalah yang akan dipecahkan dengan teknik linier
programming. Dalam model linier programming dikenal 2 (dua) macam fungsi, yaitu :
1. Fungsi Tujuan (objective function) adalah fungsi yang menggambarkan
tujuan/sasaran di dalam permasalahan linier programming yang berkaitan dengan
pengaturan secara optimal, untuk memperoleh keuntungan maksimal atau biaya
minimal. Pada umumnya nilai yang akan dioptimalkan dinyatakan sebagai Z.
2. Fungsi Batasan (constraint function) adalah bentuk penyajian secara matematis
batasan-batasan kapasitas yang tersedia yang akan dialokasikan secara optimal ke
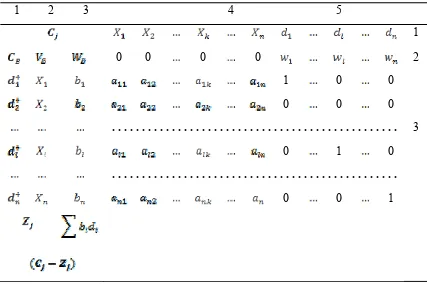
Tabel 2.1 Tabel Linier Programming
1 2 3 4 5
1
0 0 0 0 2
1 0 0
0 0 0
. . . 3
0 1 0
. . .
0 0 1
Kolom 1 : Faktor prioritas dan bobot untuk setiap variabel deviasi positif
(yakni variabel basis) dan memasukkan variabel deviasi artificial
seperti ditampilkan dalam kolom 2
Kolom 2 : Nilai total deviasi absolut, yang mewakili jumlah total deviasi dari
semua tujuan untuk tiap table sebagai iterasi proses pendapatan
Kolom 3 : Koefisien variabel keputusan
Kolom 4 : Matriks identitas menunjukkan pemasukan variabel deviasi negatif
Kolom 5 : Nilai sebelah kanan
Baris 1 : Variabel keputusan dan variabel deviasi
Baris 2 : Vektor baris dari penunjuk nol pada proses perhitungan
Baris 3 : Bobot untuk setiap variabel deviasi yang dimasukkan dalam
fungsi objektif
Bentuk standard dari pemrograman linier menurut Taha (1982) mempunyai
1. Seluruh fungsi pembatas nilai ruas kanannya tidak bernilai negatif
2. Seluruh variabel keputusan tidak bernilai negatif
3. Fungsi tujuan dapat berupa maksimasi atau minimasi
2.1.2 Asumsi-Asumsi Dasar Linier Programming
Dalam model linier programming terdapat asumsi-asumsi yang harus dipenuhi agar
permasalahan linier programming menjadi absah, adapun asumsi linier programming
adalah sebagai berikut :
1. Kesebandingan (Proportionality)
Asumsi ini menyatakan bahwa naik turunnya nilai Z dan penggunaan
sumber atau fasilitas yang tersedia akan berubah secara sebanding
(propotional) dengan perubahan tingkat kegiatan.
Contoh :
a.
Setiap pertamabahan 1 unit akan menaikkan Z sebesar
b.
Setiap pertama bahan 1 unit akan menaikkan penggunaan sumber
sebesar
2. Penambahan (Additivity)
Asumsi ini berarti bahwa nilai tujuan setiap kegiatan bersifat
independent (bebas/tidak saling bergantung) dan dalam linier programming
dianggap bahwa kenaikan nilai tujuan (Z) yang diakibatkan oleh suatu
kegiatan dapat langsung ditambahkan tanpa mempengaruhi bagian nilai
kegiatan lain.
misalnya :
dengan = 10 ; = 2
sehingga Z = 30 + 10 = 40
Andaikan bertambah 1 unit, maka sesuai dengan asumsi pertama,
nilai Z menjadi 40 + 3 = 43. Jadi nilai 3 karena kenaikan dapat langsung
ditambahkan pada nilai Z mula-mula tanpa mengurangi bagian Z yang
diperoleh dari kegiatan 2 ( ). Dengan kata lain, tidak ada korelasi antara
dan .
3. Pembagian (Divisibility)
Dalam linier programming diperbolehkan menggunakan angka
pecahan.
Misalnya :
Dari hasil perhitungan didapat nilai = 4,5 ; = 7,25 dan Z =
85.000,25.
Dalam hal tertentu nilai pecahan ini harus dibulatkan dengan
menggunakan integer, misalnya : jumlah mahasiswa diperguruan tinggi tidak
mungkin dalam bentuk pecahan.
4. Kepastian (Deteministic)
Asumsi ini menyatakan bahwa semua parameter yang terdapat dalam
model linier programming yang berupa , dan dapat diketahui secara
pasti.
2.1.3 Terminologi Linier Programming
Agar memahami dengan baik bidang yang dipelajari , pembaca selalu harus mengerti
istilah-istilah dan lambang-lambang khusus yang digunakan orang dalam bidang studi
itu. Berikut ini adalah definisi dari beberapa istilah dan lambang yang biasa digunakan
1. Variabel Keputusan (decision variable)adalah seperangkat variabel yang tidak
diketahui (dilambangkan , dengan j = 1, 2, . . . , n) yang akan dicari nilainya
(varibel keputusan)
2. Nilai Sebelah Kanan (Right hand side value) adalah nilai-nilai yang biasanya
menunjukkan ketersediaan sumber daya (dilambangkan dangan ) yang akan
ditentukan kekurangan atau kelebihan penggunaannya ( nilai sisi kanan ).
3. Variabel Dasar adalah variabel yang nilainya sama dengan sisi kanan dari
persamaan.
4. Kolom Kunci adalah kolom yang merupakan dasar untuk mengubah tabel.
Pilih kolom yang mempunyai nilai pada garis fungsi tujuan yang bernilai
negatif dengan angka terbesar.
5. Baris Kunci adalah baris yang merupakan dasar untuk mengubah tabel
tersebut. Untuk itu terlebih dahulu carilah indeks tiap-tiap baris dengan cara
membagi nilai-nilai pada kolom RHS dengan nilai yang sebaris pada kolom
kunci.
6. Angka kunci (pivot) merupakan perpotongan antara kolom kunci dengan baris
kunci.
2.1.4 Unsur-Unsur Linier Programming
Setiap model Linier Programming paling sedikit terdiri dari dua komponen yaitu :
fungsi tujuan, dan kendala.
Fungsi Tujuan
Adapun tujuan dalam linier programming, yaitu:
Minimumkan/Maksimumkan
Dalam hal ini peubah deviasi positif dan deviasi negatif adalah peubah-peubah
slek dan surplus.
Model Linier Programming, nilai yang tidak diketahui, tetapi akan
diselesaikan secara tidak langsung melalui minimisasi/maksimasi deviasi negatif dan
positif dari nilai RHS kendala tujuan. Linier programming mencari nilai solusi
Kendala Tujuan
Ada empat jenis kendala tujuan yang berlainan. Maksud setiap jenis kendala itu
ditentukan oleh hubungannya dengan fungsi tujuan. Pada Tabel 2.1 disajikan keempat
jenis kendala itu. Terlihat bahwa setiap jenis kendala tujuan harus punya satu atau dua
variabel deviasi yang ditempatkan pada fungsi tujuan. Dimungkinkan adanya
kendala-kendala yang tidak memiliki variabel deviasi. Kendala-kendala-kendala ini sama seperti
kendala-kendala persamaan linier. Persamaan pertama pada Tabel 2.1 maknanya
serupa dengan kendala pertidaksamaan ≤ dalam masalah program linier maksimasi.
Persamaan kedua maknanya serupa dengan kendala pertidaksamaan ≥ pada masalah
program linier minimisasi. Persamaan ketiga memperbolehkan deviasi dua arah yaitu
≤ dan ≥, tetapi persamaan ini mencari penggunaan sumber daya yang diinginkan sama dengan . Jika kendala persamaan dianggap perlu dalam perumusan model linier
programming, ia dapat dimasukkan dengan menempatkan sebuah artificial variabel
, seperti pada persamaan keempat.
Ada dua cara yang bisa digunakan untuk menyelesaikan persoalan-persoalan
pemrograman linier ini, yaitu cara grafis dan metode simpleks (Dimyati dan
A.Dimyati, 1992).
1. Metode Grafik
Metode grarik dapat digunakan pada pemrograman linier jika masalah yang
dihadapi mengandung tidak lebih dari dua variabel (Taha, 1982).
Menurut Dimyati dan A.Dimyati (1992), metode grafik telah
memberikan satu petunjuk penting bahwa untuk memecahkan
persoalan-persoalan pemrograman linier, hanya perlu memperhatikan titik ekstrem (titik
terjauh) pada ruang solusi atau daerah fisibel.
2. Metode Simpleks
Metode simpleks adalah prosedur pemecahan pemrograman linier yang lebih
efisien daripada metode grafik. Penerapan metode simpleks pada masalah
program linier dikembangkan untuk pertama kali oleh George Dantzig pada
Metode simpleks merupakan teknik yang paling berhasil
dikembangkan untuk memecahkan persoalan pemrograman linier yang
mempunyai jumlah variabel keputusan dan pembatas yang besar (Dimyati dan
A. Dimyati, 1992).
Perhitungan metode simpleks merupakan proses iterasi. Hal ini berarti
bahwa untuk mencapai solusi yang optimal, perhitungan dilakukan
berulang-ulang mengikuti pola standard secara sistematik. Karakteristik lain pada
metode simpleks adalah pada nilai fungsi tujuannya akan sama atau lebih besar
pada solusi terbaru dibandingkan dengan solusi terdahulu (Levin et el, 1982).
Di dalam menyelesaikan persoalan pemrograman linier dengan
menggunakan metode simpleks, bentuk dasar yang digunakan haruslah bentuk
standard (Dimyati dan A. Dimyati).
Menurut Gillet (1976), untuk mengubah suatu bentuk formulasi
pemrograman linier yang belum standard ke dalam bentuk standard dapat
dilakukan cara-cara sebagai berikut :
a. Peubah tambahan (slack variable)
Konversi fungsi ketidaksamaan lebih kecil sama dengan (≤) pada
fungsi pembatas memerlukan tambahan suatu peubah yang disebut
peubah tambahan, peubah ini menggambarkan tingkat
pengangguran dari sumber daya. Jika ada m fungsi ketidaksamaan
(≤) pada fungsi pembatas dan terdapat r peubah kebijaksanaan
dalam formulasi permasalahan maka dengan penambahan peubah
dimana adalah peubah tambahan (slack variable).
Penambahan peubah tambahan juga akan mengubah fungsi tujuan
menjadi :
maks / min
b. Peubah buatan
Apabila dalam fungsi pembatas terdapat ketidaksamaan lebih besar
sama dengan (≥) maka fungsi pembatas dapat diubah menjadi
bentuk persamaan dengan mengurangi pertidaksamaan oleh sebuah
peubah positif, sebagai berikut :
Peubah merupakan suatu peubah yang biasa disebut sebagai
peubah tambahan. Metode simpleks belum dapat diterapkan dengan
formulasi seperti di atas karena dalam metode simpleks dibutuhkan
kondisi-kondisi berikut:
1. Semua konstanta pada sisi kanan persamaan bernilai lebih besar
atau sama dengan nol.
2. Setiap persamaan harus mempunyai sebuah peubah
berkoefisien satu pada persamaan tersebut dan nol pada
persamaan yang lain.
Persamaan di atas, agar dapat diselesaikan dengan metode
simpleks, maka harus diubah menjadi :
Akibat penambahan peubah buatan maka perlu
penambahan suatu bilangan (-M) untuk masalah maksimasi pada
Pada fungsi pembatas yang berbentuk persamaan, peubah
buatan perlu ditambahkan untuk memenuhi kondisi (2) pada
metode simpleks. Perubahan fungsi pembatas yang berbentuk
persamaan dengan adanya penambahan peubah buatan adalah
sebagai berikut:
menjadi :
dan fungsi tujuannya menjadi :
2.2Pemrograman Integer (Integer Programming)
Persoalan Integer Programming (IP) adalah persoalan pemrograman
(programming) di mana pemecahan optimalnya harus menghasilkan bilangan
bulat (integer) jadi bukan pecahan. Dengan perkataan lain dari antara berbagai
bilangan bulat, harus dicari nilai-nilai variabel yang fisibel dan membuat fungsi
tujuan (Objective function) maksimum (Supranto, 1980).
Pemrograman integer (Integer Programming) adalah suatu model
pemrograman linier dengan variabel yang digunakan berupa bilangan bulat. jika
semua variabel harus berupa bilangan bulat, maka masalah tersebut dinamakan
pure integer programming. Jika hanya sebagian yang harus berupa integer, maka
disebut mixed integer programming. Integer programming dengan semua
variabelnya harus bernilai 0 atau 1 disebut 0-1 integer programming (Garfinkel
Program bilangan bulat adalah suatu bentuk dari program linier yang asumsi
divisibilitasnya melemah. Bentuk ini muncul karena kenyataannya tidak semua
variabel keputusan merupakan suatu angka pecahan (Dimyati dan A. Dimyati
1987).
Menurut Taha (1975), optimasi bilangan bulat bukan merupakan sebuah
persoalan matematika baru, dan dalam penelitian operasional dikenal sejak tahun
1940. Optimasi bilangan bulat penting digunakan pada pemecahan masalah yang
disusun sebagai sebuah hasil perkembangan pada bidang penelitian operasional,
terutama sekali pada persoalan program linier. Hal itu diperlukan untuk
pemecahan model penyusunan pada beberapa atau semua variabel keputusan agar
integer (bilangan bulat).
Pemrograman bilangan bulat (Integer programming)
dibutuhkan ketika keputusan harus dilakukan dalam bentuk bilangan bulat
(bukan pecahan yang sering terjadi bila kita gunakan metode simpleks).
Model matematis dari pemrograman bulat sebenarnya sama dengan model
linear programming, dengan tambahan batasan bahwa variabel keputusannya
harus bilangan bulat. Integer programming adalah suatu program linier dengan
tambahan persyaratan bahwa semua atau beberapa variabel bernilai bulat non
negatif, tetapi tidak perlu bahwa parameter model juga bernilai bulat.
Secara umum menurut Dimyati dan A. Dimyati (1992), model persoalan
pemrograman bilangan bulat (Integer Programming) dapat diformulasikan sebagai
berikut:
Maks/Min :
bilangan bulat (integer) untuk
Algoritma yang dianggap cukup baik untuk memberikan solusi optimum
dalam pemrograman bilangan bulat (Integer Programming) adalah pencabangan dan
pembatasan (branch and bound) dan pemotongan bidang datar (cutting plane)
(Dimyati dan A. Dimyati, 1992).
Ada berbagai pendekatan untuk masalah IP. Pendekatan yang akan dibahas di
bawah ini termasuk Pembulatan (Rounding), Cabang dan Batas (Branch and Bound),
Pemotongan Bidang Datar (Cutting Plane), Relaksasi Lagrangian (Lagrangian
Relaxation) dan Benders Dekomposisi (Benders Decomposition) (Bruce A. McCarl
dan T.H.Spreen, 1997).
a. Pemotongan Bidang Datar (Cutting Plane)
Ada berbagai algoritma yang tersedia untuk penyelesaian masalah IP. Alasan
banyaknya inilah bahwa tidak ada algoritma telah terbukti secara komputasi
yang efisien untuk semua masalah, dan dengan demikian pencarian kontinu
untuk algoritma-algoritma yang lebih efektif. Berdasarkan masalah pure
integer programming, yaitu, masalah LP standar dengan pembatasan integer
pada semua variabel. Ide fundamental yang mendasari algoritma gomory’s
cutting plane adalah untuk menambahkan kendala untuk masalah satu per satu
sehingga akhirnya memiliki masalah LP dengan solusi optimal dengan
koordinat integer (Paul R. Thie, 1979).
Pendekatan yang dilakukan dalam teknik pemotongan bidang datar
(Cutting plane) adalah dengan membuat pembatas tambahan yang memotong
ruang layak dari LP relaksasi sehingga dapat mengeliminasi solusi yang
tidak integer . Proses pemotongan akan terus berlangsung sehingga diperoleh
jawab dengan seluruh variabel (yang dikehendaki) berharga bilangan bulat
(integer) (Dimyati dan A. Dimyati, 1992).
Menurut Dimyati dan A. Dimyati (1992), keberhasilan teknik ini
hanya persoalan tertentu yang dapat diselesaikan dengan teknik ini. Karena itu,
sekarang teknik ini hampir tidak pernah lagi digunakan.
Algoritma IP pertama kali diselesaikan dengan konsep cutting plane.
Cutting plane menghapus bagian dari daerah fisibel tanpa menghapus poin
solusi bilangan bulat. Ide dasar di balik sebuah cutting plane adalah bahwa
titik bulat yang optimal dekat dengan solusi LP optimal, tetapi tidak jatuh di
persimpangan kendala sehingga kendala tambahan perlu dipaksakan.
Akibatnya, kendala yang ditambahkan untuk memaksa solusi LP integer
menjadi tidak layak tanpa menghilangkan solusi bilangan bulat. Hal ini
dilakukan dengan menambahkan kendala memaksa variabel nonbasis lebih
besar dari nilai nol kecil (Bruce A. McCarl dan T.H.Spreen, 1997).
Beberapa poin yang perlu diperhatikan untuk membuat pendekatan
Cutting plane. Pertama banyak pemotongan yang mungkin perlu diperbaiki
untuk memperoleh sebuah solusi integer. Kedua solusi integer pertama yang
ditemukan adalah solusi optimal. Solusi ini ditemukan setelah pemotongan
hanya ditambahkan ke daerah hasil solusi optimal. Akibatnya jika algoritma
solusi ditemukan, keluar tanpa sebuah solusi yang dapat diterima (Bruce A.
McCarl dan T.H.Spreen, 1997).
Algoritma bekerja sebagai berikut, pertama-tama menyelesaikan
masalah LP asli dengan mengabaikan pembatasan yang integer. Kemudian,
jika solusi ini memiliki semua koordinat integer, maka itu merupakan solusi
optimal untuk masalah IP, masalah selesai. jika tidak, buat kendala baru yang
akan menambah masalah. Kendala ini akan memiliki dua sifat dasar: pertama,
solusi optimal noninteger untuk masalah LP asli tidak akan memenuhi kendala
ini, dan kedua, semua solusi layak integer masalah asli akan memenuhi
kendala asli baru. Sehingga kendala ini pada dasarnya memotong subset dari
himpunan solusi layak untuk masalah LP, tapi subset yang tidak berisi integer
Langkah-langkah dari algoritma gomory’s cutting plane untuk masalah
IP murni:
1. Memecahkan masalah LP yang sesuai hanya mengabaikan pembatasan
integer pada X. Jika solusi ini memiliki semua koordinat integer, maka itu
adalah solusi optimal untuk masalah asli.
2. Jika tidak kendala baru ditambahkan ke masalah.
a) Untuk membangun kendala ini, memilih baris dari solusi akhir tabel
optimal dari masalah LP dengan non terpisahkan konstan istilah bi.
(menggunakan baris yang mengandung istilah konstan dengan nilai
pecahan terbesar dapat mengurangi jumlah iterasi yang diperlukan
untuk konvergensi.)
b) Seandainya baris ke-i dipilih dan persamaan yang sesuai adalah
Maka bentuk kendala
Dimana
fij = aij – [ aij ] = bagian pecahan dari aij
fi = bi – [ bi ] = bagian pecahan dari bi
x = sebuah variabel slack baru, terbatas menjadi nonnegatif dan
integral
c) Tambahkan kendala ini ke masalah dan kembali ke langkah 1.
(Paul R. Thie, 1979).
Kelemahan dari algoritma cutting plane adalah kesalahan-kesalahan
pada pembulatan yang dilakukan dalam perhitungan dapat menghasilkan
jawaban bilangan bulat yang salah. Selain itu jawaban dari persoalan masih
belum fisibel berarti tidak ada jawaban bilangan bulat yang diperoleh sampai
jawaban bilangan bulat yang optimal dicapai tadi, dan ini berarti bahwa tidak
ada jawaban bilangan bulat yang baik jika perhitungan dihentikan lebih awal
sebelum mencapai hasil jawaban yang optimal (Aswan, 1979).
Pembulatan adalah pendekatan yang paling naif untuk solusi masalah IP.
Pendekatan pembulatan melibatkan pemecahan masalah sebagai masalah LP
diikuti dengan upaya untuk membulatkan solusi ke solusi yang integer dengan:
a) menghilangkan semua bagian pecahan, atau b) mencari tahu solusi yang
memenuhi dimana nilai-nilai variabel yang disesuaikan dengan dekatnya lebih
besar atau lebih kecil nilai integer. Pembulatan mungkin adalah pendekatan
yang paling umum untuk memecahkan masalah IP. Masalah LP Sebagian
besar melibatkan variabel dengan nilai pecahan solusi yang pada kenyataannya
adalah integer (yaitu, kursi diproduksi, ayam dipotong). Istilah pecahan dalam
solusi tidak masuk akal, tetapi kadang-kadang dapat diterima jika pembulatan
memperkenalkan perubahan yang sangat kecil dalam nilai variabel
(pembulatan yaitu 1003421,1-1.003.421 atau bahkan 1.003.420 mungkin dapat
diterima) (Bruce A. McCarl dan T.H.Spreen, 1997).
Secara umum, pembulatan sering praktis, tetapi harus digunakan
dengan hati-hati. Salah satu harus membandingkan solusi yang dibulatkan dan
tidak dibulatkan untuk melihat apakah setelah pembulatan: a) kendala
memenuhi secara memadai, dan b) apakah perbedaan antara LP optimal dan
pembulatan nilai fungsi objektif cukup kecil. Jika demikian IP biasanya tidak
efektif dan solusi yang bulat dapat digunakan. Di sisi lain, jika ditemukan
fungsi tujuan bulat diubah secara bermakna atau kendala melanggar dari sudut
pandang pragmatis, maka latihan IP formal perlu dilakukan (Bruce A. McCarl
dan T.H.Spreen, 1997).
c. Relaksasi Lagrangian (Lagrangian Relaxation)
Relaksasi Lagrangian (Geoffrion (1974), Fisher (1981, 1985)) merupakan
salah satu bidang pengembangan algoritmik IP. Relaksasi Lagrangian
mengacu pada prosedur dimana beberapa kendala yang direlaksasikan ke
dalam fungsi tujuan menggunakan sebuah pendekatan yang dibentuk oleh
pengganda Lagrangian. Bentuk dasar Relaksasi Lagrangian untuk program
bilangan bulat campuran:
Maksimum CX + FY
Kendala AX + GY ≤ b
X ≥ 0, Y ≥ 0 dan integer
melibatkan penemuan suatu himpunan Lagrange Multiplier untuk beberapa
kendala dan merelaksasi himpunan kendala ke dalam fungsi tujuan. Mengingat
bahwa yang dipilih untuk direlaksasi himpunan kedua kendala menggunakan
lagrange multiplier masalah menjadi:
Maksimum CX + FY – λ( DH + HY – e )
AX + GY ≤ b
X ≥ 0, Y ≥ 0 dan integer
Ide utama adalah untuk menghilangkan kendala yang sulit dari masalah
sehingga program integer jauh lebih mudah untuk dipecahkan. Masalah IP
dengan struktur seperti itu dari masalah transportasi dapat langsung
diselesaikan dengan LP. Caranya kemudian adalah memilih kendala yang tepat
untuk direlaksasi dan untuk mengembangkan nilai-nilai untuk pengali lagrange
mengarah ke solusi yang tepat.
Relaksasi Lagrangian telah digunakan dalam dua pengaturan: 1) untuk
meningkatkan kinerja batas pada solusi, dan 2) untuk mengembangkan solusi
yang dapat disesuaikan secara langsung atau melalui heuristik sehingga
mereka layak dalam keseluruhan masalah (Fisher (1981, 1985)) . Sebuah hasil
penting Relaksasi Lagrangian adalah merelaksasi masalah yang memberikan
batas atas solusi untuk masalah yang tidak direlaksasi pada setiap tahap.
Relaksasi Lagrangian telah banyak digunakan dalam algoritma cabang dan
terikat untuk menurunkan batas atas untuk masalah untuk melihat apakah
traversal bawah yang dicabangkan layak (Bruce A. McCarl dan T.H.Spreen,
1997).
d. Dekomposisi Bender (Benders Decomposition)
Algoritma lain untuk IP disebut Dekomposisi Bender. Algoritma ini
memecahkan program bilangan bulat campuran melalui eksploitasi struktural.
Benders mengembangkan prosedur, selanjutnya disebut Dekomposisi Bender,
yang menguraikan masalah mixed integer menjadi dua masalah yang
diselesaikan secara iteratif - masalah utama bilangan bulat dan subproblem
Keberhasilan prosedur melibatkan struktur subproblem dan pilihan
subproblem tersebut. Prosedur dapat bekerja sangat buruk untuk struktur
tertentu.
Masalah dekomposisi mixed IP adalah:
Maksimum FX + CZ
Kendala GX ≤ b1
HX + AZ ≤ b2
DZ ≤ b3
X integer, Z ≥ 0
Pengembangan dekomposisi masalah ini berlangsung dengan iteratif
mengembangkan titik layak X* dan memecahkan subproblem yang:
Maksimum CZ
Kendala AZ ≤ b2 – HX* (α)
DZ ≤ b3 (γ)
Z ≥ 0
Solusi untuk subproblem ini menghasilkan variabel dual dalam tanda kurung.
Q merupakan penafsiran dari CZ. Dalam mengubah "master" Masalah
dibentuk sebagai berikut:
Penggunaan dekomposisi Benders melibatkan penguraian masalah
yang tepat dan / atau struktur masalah yang akan menuju kesatu titik dengan
cepat. Pernyataan umum yang dapat dibuat adalah:
a) Metode dekomposisi tidak bekerja dengan baik ketika variabel X yang
dipilih oleh masalah master tidak menghasilkan subproblem layak. Dengan
demikian, semakin akurat kendala dalam masalah master menggambarkan
kondisi subproblem, semakin cepat akan konvergensi. (Lihat Geoffrion dan
Graves, Danok, McCarl dan White (1978), Polito, Magnanti dan Wong,
b) Daerah feasible dari masalah master baik lebih dibatasi. (Lihat Magnanti
dan Wong,. Dan Sherali)
c) Bila mungkin, kendala harus dimasukkan dalam masalah master
menghalangi solusi layak yang belum realistis (suboptimal) untuk
keseluruhan masalah. (Lihat kendala mesin minimum di Danok, McCarl
dan White, 1978.)
(Bruce A. McCarl dan T.H.Spreen, 1997).
2.3Pencabangan dan Pembatasan (Branch and Bound)
Branch and bound bukan sebuah teknik solusi khusus terbatas untuk masalah integer
programming. Branch and bound adalah pendekatan solusi yang dapat diterapkan
pada beberapa jenis masalah. Pendekatan Branch and bound didasarkan pada prinsip
bahwa himpunan total solusi layak dapat dipartisi menjadi subset yang lebih kecil dari
solusi. Subset yang lebih kecil ini kemudian dapat dievaluasi secara sistematis sampai
solusi terbaik ditemukan. Ketika pendekatan Branch and bound diterapkan untuk
masalah integer programming, akan digunakan konjungsi dengan pendekatan solusi
noninteger yang normal (Paul R. Thie, 1979).
Menurut Taha (1975), untuk melaksanakan teknik pencabangan dan pembatasan
(branch and bound) ada dua operasi dasar, yaitu:
1. Pencabangan (Branching), merupakan pembagian persoalan jawab kontinu
menjadi subpersoalan di mana semuanya juga kontinu.
2. Pembatasan (Bounding), merupakan pembatasan setiap subpersoalan yang
dibuat dengan pencabangan. Batas ini penting untuk tingkatan jawab optimal
dari sub persoalan dan penemuan jawab optimal bilangan bulat.
Teknik pencabangan dan pembatasan (branch and bound) mencari solusi optimal
dari suatu persoalan pemrograman bilangan bulat (Integer Programming) dengan
mengenumerasi titik-titik dalam daerah fisibel dari suatu subpersoalan (Dimyati dan
Branch and Bound adalah algoritma umum untuk mencari solusi optimal dari
berbagai masalah optimasi. Metode ini pertama kali diperkenalkan oleh A.H. Land
dan A.G. Doig pada tahun 1960.
Gagasan penting dari cabang-dan-terikat adalah untuk membagi daerah layak dan
mengembangkan batas pada z*. Untuk masalah maksimisasi, batas bawah
adalah nilai tertinggi dari setiap titik bulat layak yang diperoleh. Batas atas diberikan
oleh nilai optimal dari program linier yang asli atau dengan nilai terbesar untuk fungsi
tujuan pada setiap kotak yang "menggantung". Langkah selanjutnya, harus
mencabangkan ke (pindah ke) subdivisi lain dan menganalisanya. Begitu selanjutnya,
jika solusi belum diperoleh
i) Program linier atas Lj tidak layak
ii) Solusi optimal program linier atas Lj adalah integer; atau
iii) Nilai dari solusi program linier zj atas Lj memenuhi zj≤ (jika maksimasi),
maka Lj tidak perlu dibagi. Dalam kasus ini, IP terminologi mengatakan bahwa Lj
telah terukur (fathomed). kasus (i) disebut fathoming oleh ketidaklayakan, (ii)
fathoming oleh kebulatan dan (iii) fathoming oleh batas (Bradley dkk, 1977).
Prinsip dasar metode ini adalah memecah daerah fisibel suatu masalah program
linier dengan membuat subproblem-subproblem. Ada dua konsep dasar dalam
algoritma branch and bound :
1. Branching adalah proses membagi-bagi permasalahan menjadi
subproblem-subproblem yang mungkin mengarah ke solusi.
2. Bounding adalah suatu proses untuk mencari/menghitung batas atas (dalam
masalah minimisasi) dan batas bawah (dalam masalah maksimisasi) untuk
solusi optimal pada subproblem yang mengarah ke solusi.
Metode branch and bound diawali dengan menyelesaikan program linier dari
suatu masalah program integer. Jika semua nilai variabel keputusan solusi optimal
sudah berupa integer, maka solusi tersebut merupakan solusi optimal program linier
integer. Jika tidak, dilakukan pencabangan dan penambahan batasan pada program
Winston (2004) menyebutkan bahwa nilai fungsi objektif optimal untuk program
linier integer lebih kecil sama dengan nilai fungsi objektif optimal untuk program
linier (masalah maksimisasi), sehingga nilai fungsi objektif optimal program linier
merupakan batas atas bagi nilai fungsi objektif optimal untuk masalah program linier
integer.
Diungkapkan pula oleh Winston (2004) bahwa nilai fungsi objektif optimal untuk
suatu kandidat solusi merupakan batas bawah nilai fungsi objektif optimal untuk
masalah program linier integer asalnya. Suatu kandidat solusi diperoleh jika solusi
dari suatu subproblem sudah memenuhi kendala integer pada masalah program linier
integer, artinya semua variabelnya sudah bernilai integer.
Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi
dengan metode branch and bound :
1) Langkah 0
Didefinisikan z sebagai batas bawah dari nilai fungsi objektif (solusi) program
linier integer yang optimal. Pada awalnya ditetapkan z = -∞ dan i = 0.
2) Langkah 1
Subproblem program linier (PL)(i) dipilih sebagai bagian masalah berikutnya
untuk dipecahkan. Subproblem PL(i) diselesaikan.
a) Jika PL(i) terukur dan solusi program linier yang ditemukan lebih baik
maka batas bawah z diperbarui. Jika tidak bagian masalah (subproblem)
baru i dipilih dan langkah 1 diulangi. Jika semua subproblem telah
dipecahkan, maka proses dihentikan.
b) Jika PL(i) tidak terukur, proses dilanjutkan ke langkah 2 untuk melakukan
pencabangan PL(i)
Suatu subproblem dikatakan terukur (fathomed) jika terdapat kondisi sebagai
berikut :
1. Subproblem tersebut tak fisibel, sehingga tidak dapat menghasilkan solusi
optimal untuk program linier integer.
2. Subproblem tersebut menghasilkan suatu solusi optimal dengan semua
objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya,
maka solusi ini menjadi kandidat solusi optimal dan nilai fungsi
objektifnya menjadi batas bawah nilai fungsi objektif optimal bagi masalah
program linier integer pada saat itu. Bias jadi subproblem ini menghasilkan
solusi optimal untuk masalah program linier integer.
3. Nilai fungsi objektif optimal untuk subproblem tersebut tidak melebihi
batas bawah saat itu, maka subproblem ini dapat dieliminasi.
3) Langkah 2
Dipilih salah satu variabel xj yang nilai optimalnya adalah yang tidak
memenuhi batasan integer dalam solusi PL(i). Bidang
disingkirkan dengan membuat dua subproblem program linier, yaitu
dan , sehingga diperoleh kendala subproblem baru sebagai
berikut :
a. Subproblem baru 1 : kendala subproblem lama + kendala
b. Subproblem baru 2 : kendala subproblem lama + kendala
dengan didefinisikan sebagai integer terbesar yang kurang dari atau sama
dengan . Selanjutnya kembali ke langkah 1 (Winston, 1975).
Ringkasan langkah-langkah metode branch and bound dalam menentukan solusi
integer optimal untuk model maksimisasi adalah sebagai berikut:
a) Dapatkan solusi simpleks optimal dari model program linear dengan batasan
integer yang dilepaskan
b) Tentukan solusi simpleks relaxed sebagai batas atas sedangkan solusi hasil
pembulatan ke bawah sebagai batas bawah pada node 1.
c) Pilih peubah dengan bagian pecahan yang terbesar untuk percabangan.
Ciptakan dua batasan baru untuk peubah ini yang mencerminkan pembagian
nilai integer. Hasilnya adalah sebuah batasan ≤ dan sebuah batasan ≥.
d) Ciptakan dengan node baru, satu dengan batasan ≤ dan satu dengan batasan ≥
e) Selesaikan model program linear relaxed dengan batasan baru yang
f) Solusi simpleks relaxed adalah merupakan batas atas pada tiap node, dan
solusi maksimum integer merupakan batas bawah dari node.
g) Jika proses ini menghasilkan solusi integer feasible dengan nilai batas atas
terbesar pada akhir node mana saja, maka solusi integer optimal tercapai. Jika
tidak muncul suatu solusi integer fisibel, lakukan percabangan dari node
dengan batas atas terbesar.
h) Ulangi langkah c.
(Winston, 2004)
Suatu bentuk khusus dari algoritma cabang dan terikat untuk nol-satu program
yang dikembangkan oleh Balas. Algoritma ini disebut enumerasi implisit. Metode ini
juga telah diperluas untuk kasus bilangan bulat campuran seperti yang diterapkan di
Inisialisasi pohon ruang
solusi Branch and bound
Mulai
Inisialisasi pohon ruang
solusi Branch and bound
Mulai
Keuntungan dari cara pencabangan dan pembatasan adalah cara yang efisien
untuk mendapatkan seluruh jawaban layak (fisibel), sedangkan kerugian cara ini
adalah ia akan rnencari seluruh jawaban program linier pada setiap titik. Pada
persoalan yang besar akan memerlukan waktu yang cukup lama, terutama bila yang
Mulai
Data harga perumahan dan
ketersediaan bahan baku
Formulasi permasalahan penentuan peubah keputusan
Sesuai dengan permasalahan
Formulasi fungsi tujuan
Maksimasi keuntungan
Pemrograman linier
Solusi optimal dan
non integer
Solusi integer
Ya
Pemograman Bilangan Bulat
(Integer Programming)
Metode Branch
and Bound
Tidak
Selesai
BAB 3
PEMBAHASAN
3.1Pengumpulan Data
Data yang ada adalah data yang diperoleh dari hasil pencatatan, dan wawancara
dengan pihak Perumahan Bumi Sergai tentang hal-hal yang berhubungan dengan
masalah data yang diperlukan dalam studi kasus skripsi ini.
Adapun data yang diperlukan sebagai berikut :
a. Tipe rumah yang dibangun
b. Harga penjualan untuk setiap tipe perumahan
c. Luas bangunan untuk setiap tipe rumah
d. Luas tanah bangunan untuk setiap tipe rumah
e. Bahan-bahan yang digunakan
f. Banyaknya bahan yang diperlukan untuk masing-masing tipe perumahan
g. Perkiraan banyaknya rumah yang akan dibangun
3.2 Hasil Pengumpulan Data
Data yang diperoleh dari hasil pencatatan, dan wawancara dengan pihak Perumahan
Bumi Sergai adalah sebagai berikut:
1. Tipe rumah yang dibangun di Perumahan Bumi Sergai ada dua yaitu tipe 65
dan tipe 45
2. Data harga penjualan dari masing-masing tipe rumah. Adapun rincian harga
dari kedua tipe rumah yang akan menjadi fungsi objektif penelitian adalah
sebagai berikut:
a. Tipe rumah 65 dengan harga penjualan Rp 180.000.000
3. Luas bangunan unuk kedua tipe rumah masing-masing yaitu tipe 65 dengan
luas 65 m2 dan tipe 45 dengan luas 45 m2
4. Luas tanah banguan untuk masing-masing tipe rumah yaitu 98 m2
5. Bahan-bahan yang digunakan batu bata, semen, pasir, besi, batu koral, seng,
gypsum, paku, kayu, dan keramik
6. Banyaknya bahan yang diperlukan berdasarkan luas bangunan masing-masing
tipe rumah, yaitu:
a. Tipe rumah 65/98, adalah:
Batu bata : 11.000 satuan per buah
Semen : 120 satuan per sak
Pasir : 19 satuan per m3
Besi : 75 satuan per batang
Batu koral : 6 satuan per m3
Seng : 45 satuan per lembar
Gypsum : 20 satuan per lembar
Paku : 20 satuan per kg
Kayu : 75 satuan per batang
Keramik : 65 satuan per kotak
b. Tipe rumah 45/98, adalah:
Batu bata : 9.000 satuan per buah
Semen : 100 satuan per sak
Pasir : 16 satuan per m3
Besi : 60 satuan per batang
Batu koral : 5 satuan per m3
Seng : 35 satuan per lembar
Gypsum : 18 satuan per lembar
Paku : 17 satuan per kg
Kayu : 60 satuan per batang
Keramik : 45 satuan per kotak
7. Banyaknya rumah yang diperkirakan akan dibangun adalah 100 rumah,
sehingga perkiraan banyaknya bahan yang tersedia, yaitu :
Batu bata : 1.002.000 satuan per buah
Pasir : 1680 satuan per m3
Besi : 6750 satuan per batang
Batu koral : 560 satuan per m3
Seng : 4000 satuan per lembar
Gypsum : 2000 satuan per lembar
Paku : 1880 satuan per kg
Kayu : 6750 satuan per batang
Keramik : 5150 satuan per kotak
3.3Perumusan Data ke dalam Model Matematika
Data tentang harga penjualan rumah, luas bangunan, luas tanah bangunan, banyaknya
bahan yang diperlukan berdasarkan luas bangunan dan perkiraan banyaknya rumah
yang akan dibangun diformulasikan ke dalam model matematika, sehingga dapat
diketahui berapa banyak rumah yang dibangun untuk setiap tipe rumah. Salah satu
metode penyelesaian permasalahan integer programming adalah dengan
menggunakan metode branch and bound yang khusus dibahas dalam skripsi ini.
Penulis membentuk permasalahan tersebut ke dalam model matematika.
Tujuannya memaksimumkan banyaknya rumah yang harus dibangun untuk setiap tipe
rumah pada Perumahan Bumi Sergai di Sei Rampah.
Karena penulis mengasumsikan yang menjadi parameter untuk fungsi kendala
adalah tidak integer dan hanya sebagian dari bahan bangunan yang akan dijadikan
fungsi kendala. Maka penulis hanya menggunakan sebagian dari bahan tersebut, yaitu:
pasir, semen dan keramik. Dengan syarat hasil optimal yang diperoleh menggunakan
seluruh bahan menjadi kendala dengan metode simpleks sama dengan hanya
Tabel 3.1 Data Perumahan Bumi Sergai
Sumber: Brosur Perumahan Bumi Sergai di Sei Rampah (2011)
Untuk fungsi tujuan yang dimaksimalkan adalah harga penjualan rumah. Dengan
masing-masing harga jual rumah seperti tabel 4.1 . Formulasi fungsi tujuan (Z) dengan
memaksimalkan harga penjualan rumah adalah:
Maksimumkan : Z = 180.000.000 X1 + 140.000.000 X2
Keterangan: X1 = Tipe rumah 65
X2 = Tipe rumah 45
180.000.000 = Harga jual tipe 65 per unit
140.000.000 = Harga jual tipe 45 per unit
Untuk fungsi kendala batasan yang digunakan adalah bahan bangunan. Bahan
bangunan yang digunakan adalah semen, pasir, batu bata, seng, keramik dan
sebagainya. Tapi penulis hanya mengambil semen, pasir dan keramik sebagai batasan,
karena penggunaan seluruh atau sebagian bahan sebagai batasan tidak mempengaruhi
nilai Z yang diperoleh setelah diselesaikan dengan QM. Berdasarkan luas lahan yang
tersedia untuk mendirikan bangunan, maka maksimal bahan yang tersedia untuk pasir
sebanyak 1680 m3. Sedangkan, menurut luas bangunan masing-masing tipe rumah,
pasir yang diperlukan sebanyak 19 m3 untuk tipe 65 dan 16 m3 untuk tipe 45.
Formulasi fungsi kendala dengan batasan bahan pasir adalah:
19 X1 + 16 X2 ≤ 1680
dengan: 19 = jumlah pasir yang digunakan untuk tipe 65
16 = jumlah pasir yang digunakan untuk tipe 45
1680 = jumlah pasir yang tersedia untuk kedua tipe rumah
Untuk semen sebanyak 13000 sak, dengan 120 sak untuk tipe 65 dan 100
sak untuk tipe 45. Formulasi fungsi kendala dengan batasan bahan semen yaitu:
120 X1 + 100 X2 ≤ 13000
100 = jumlah semen yang digunakan untuk tipe 45
13000 = jumlah semen yang tersedia untuk kedua tipe rumah
Untuk keramik sebanyak 5150 kotak, dengan 65 kotak untuk tipe 65 dan
45 kotak untuk tipe 45. Formulasi fungsi kendala dengan batasan bahan keramik
yaitu:
65 X1 + 45 X2 ≤ 5150
dengan: 65 = jumlah keramik yang digunakan untuk tipe 65
45 = jumlah keramik yang digunakan untuk tipe 45
5150 = jumlah keramik yang tersedia untuk kedua tipe rumah
Berdasarkan uraian data diatas, dapat di modelkan menjadi sebagai berikut:
Maksimumkan : Z = 180.000.000 X1 + 140.000.000 X2
3.4Pengolahan Data
Langkah awal: Merubah model matematika menjadi bentuk baku simpleks dengan cara menambahkan batasan dengan variabel slack pada peridaksamaan lebih kecil
sama dengan atau mengurangi dengan variabel surplus.
Pada pertidaksamaan lebih besar sama dengan :
(+) Variabel slack pada batasan ≤
(-) Variabel surplus pada batasan ≥
Bentuk baku simpleks :
Tabel 3.2 Tabel Simpleks
Variabel
Basis
X1 X2 X3 X4 X5 Nilai
kanan
X3 19 16 1 0 0 1680
X4 120 100 0 1 0 13000
X5 65 45 0 0 1 5150
Zj - Cj -180.000.000 -140.000.000 0 0 0
Setelah diselesaikan dengan program QM maka diperoleh :
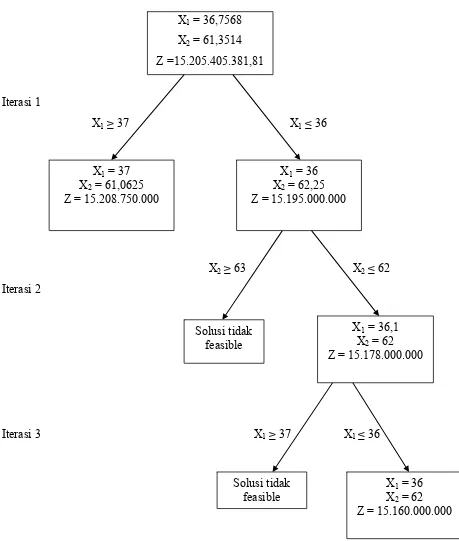
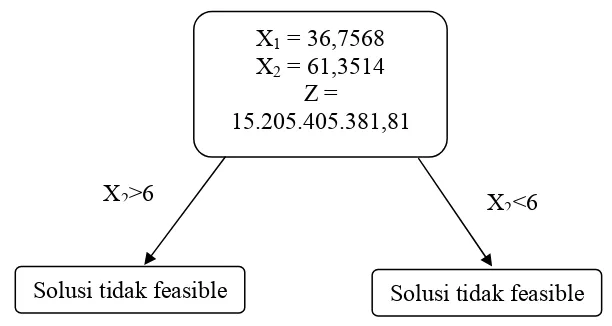
X1 = 36,7568
X2 = 61,3514
Z = 15.205.405.381,81
Sedangkan jika diselesaikan dengan metode simpleks:
Tabel 3.3 Tabel Simpleks I
Variabel
Basis
X1 X2 X3 X4 X5 Nilai Kanan
X3 19 16 1 0 0 1680
X4 120 100 0 1 0 13000
X5 65 45 0 0 1 5150
Zj - Cj -180.000.000 -140.000.000 0 0 0
Kolom Pivot (Peubah yang masuk) dan baris pivot (Peubah yang keluar). Pada tabel
Simpleks I adalah kolom X1 yang memiliki nilai terkecil dan baris X5 yang memiliki
Tabel 3.4 Tabel Simpleks II
Kolom Pivot (Peubah yang masuk) dan baris pivot (Peubah yang keluar) pada tabel
simpleks II adalah X2 yang memiliki nilai terkecil dan X3 yang memiliki hasil bagi
terkecil.
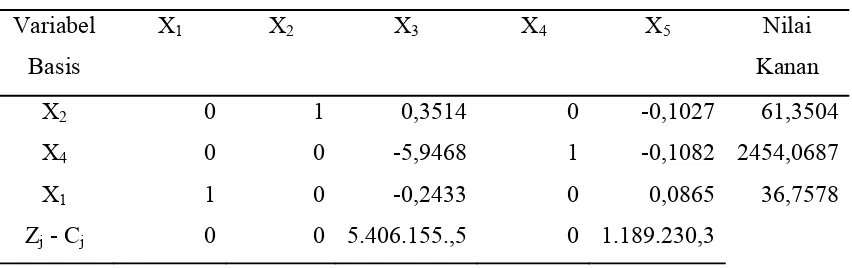
Tabel 3.5 Tabel Simpleks III
Variabel
Tabel Simpleks III menjelaskan bahwa semua nilai tidak mengandung harga negatif
lagi, sehingga hasil yang diperoleh sudah merupakan penyelesaian optimal. Dan
diperoleh:
X1 = 36,7578
X2 = 61,3504
Z = 15.205.405.381,81
Tapi karena yang diinginkan solusi optimal yang berupa integer maka masalah ini
belum selesai. Ini adalah pembulatan jumlah tipe rumah dengan cara coba-coba (trial