Prosiding
Seminar Nasional
Mahasiswa S3 Matematika
Forum Komunikasi Mahasiswa S-3 Matematika se-Indonesia
Bekerja Sama Dengan Jurusan Matematika FMIPA UGM
s
ha i
a sw
M
i
s aS
a
k
i -3 n
u M
a
m t
o e
K m
a
muroF atik
Indonesia
s
ha i
a sw
M
i
s aS
a
k
i -3 n
u M
a
m t
o e
K m
a
muroF atik
Indonesia
REVITALISASI D A N SOSIALISASI DIRI
U N T U K B E R P E R A N A K T I F D A L A M
PENINGKATAN KUALITAS PENELITIAN &
PENDIDIKAN MATEMATIKA DI INDONESIA
Editor :
Muslim Ansori
Ismail Djakaria
Dhoriva Urwatul Wutsqa
Agus Maman Abadi
M. Andy Rudhito
Umu Sa’adah
Karyati
Hasih Pratiwi
Generator Frame Wavelet Ketat dari Kelas Box Spline Multivariate (Mahmud Yunus,
JannyLindiarni,Hendra Gunawan) ……….
334
Generalized Regression dalam Pendugaan Area Kecil (Anang Kurnia,Khairil A.
Notodiputro,Asep Saefuddin, danI Wayan Mangku) ………
346
Chain Ladder Method as a Gold Standard to Estimate Loss Reserves (Aceng K.
Mutaqin,Dumaria R. Tampubolon,Sutawanir Darwis) ……….
356
Optimalisasi Respon Ganda pada Metode Respon Permukaan (Response Surface) dengan Pendekatan FungsiDesirability(Hari Sakti Wibowo,I Made Sumertajaya,
Hari Wijayanto) ……….
365
Sifat Penaksir Simulated MLE pada Respon Multinomial (Jaka Nugraha) …………..
376
Estimasi Model Probit pada Respons Biner Multivariat Menggunakan MLE dan
GEE (Jaka Nugraha) ……….
386
Analisis Komponen Utama Temporar (Ismail Djakaria) ……….
399
PendekatanDynamic Linear ModelatauState Space Modelpada Pendugaan Area
Kecil (Small Area Estimation) (Kusman Sadik dan Khairil Anwar Notodiputro) …….
411
Pengembangan Algoritma EM untuk Data Tidak Lengkap (Incomplete Data) pada
Model Log-Linear (Kusman Sadik) ………...
422
CRUISE sebagai Metode Berstruktur Pohon (Tree-Structured) pada Data
Non-Biner (Kusman Sadik) ………...
433
ModelProportional Hazards CoxdenganMissing Covariates(Nurkaromah
Dwidayati,Sri Haryatmi,Subanar) ……….
447
Aplikasi Mixture Distribution dalam Pemodelan Resiko Aktuaria (Adhitya Ronnie
Effendie) ………
459
Analisis Komponen Utama Probabilistik pada DataMissing(Ismail Djakaria) ……..
464
Malakah Bidang Terapan
Bilangan Ramsey untuk Graf BintangS6dan Graf Bipartit LengkapK2,N,N=2,3,4
(Isnaini Rosyida) ……….
476
H-supermagic labelings ofccopies of some graphs (Tita Khalis Maryati,A.N.M.
Pengembangan Algoritma EM untuk
Data Tidak Lengkap
(Incomplete Data) pada Model Log-Linear
Kusman Sadik
Departemen Statistika, FMIPA IPB Jl. Raya Dramaga, Kampus IPB Dramaga, Bogor
e-mail : [email protected]
Abstrak
Pada data kategori terkadang terdapat beberapa data yang tidak lengkap pada salah satu kategorinya, sehingga ringkasan dari data kategori dalam bentuk tabel kontingensinya terbagi menjadi dua bagian yaitu tabel kontingensi data lengkap dan data tidak lengkap. Analisa yang dapat digunakan untuk kasus tersebut adalah dengan memodelkan data lengkap mengunakan model log-linear. Kemudian dilakukan pendugaan data tidak lengkap menggunakan algoritma EM. Algoritma EM terdiri dari dari dua tahapan yaitu
tahapan M (Maximization) diperoleh dari pendugaanmaksimum likelihoodberupa nilai
proporsi setiap sel pengamatan, tahapan E (Expectation) merupakan proses
pendistribusian data tidak lengkap berdasarkan proporsi yang telah ditentukan sehingga setiap nilai sel pengamatan mengalami penyesuaian nilai. Algoritma EM ini merupakan proses iterasi yang terus berlangsung hingga diperoleh nilai yang konvergen. Data yang digunakan dalam penelitian ini adalah status kesehetan bayi setelah dilahirkan di dua
klinik yang berbeda. Data yang diamati adalahclinic(C),prenatal care(P) dansurvival
(S). Terdapat data tidak lengkap pada kategori clinic. Model Log-linear terbaik untuk
data lengkap adalah model (SC,PC) karena memiliki nilai uji kebaikan suai dan model ini cukup sederhana untuk mendistribusikan data tidak lengkap ke data lengkap dibandingkan model lainnya. Model ini memberi gambaran hubungan antara peubah
clinic(C) dengan peubah lainnya.
Kata kunci : incomplete data, EM algorithm, prenatal care, survival, maximum
likelihood
1. Pendahuluan
1.1. Latar Belakang
Data kategori terkadang dapat berupa gabungan dari data-data yang tidak lengkap pada
satu atau beberapa kategori. Tidak lengkapnya data dapat diakibatkan oleh nonresponsedari
subjek yang terobservasi, sehingga dianggap sebagai data missing atau data hilang. Kondisi
dan di analisis menggunakan model loglinear (Fuchs Camil,1992). Namun pemodelan yang
sempurna untuk seluruh data dapat dilakukan apabila data tidak lengkap diduga terlebih
dahulu, karena kondisi tersebut tidak dapat diabaikan (nonignorable) terkait dengan nilai
peluang di setiap sel kategori dan akan mempengaruhi pendugaan parameter di dalam model
(Park Taesung dan Morton B.Brown,1994).
Algoritma EM dapat dijadikan solusi di dalam pendugaan data tidak lengkap. Iterasi
dari algoritma tersebut dilakukan sehingga diperoleh nilai dugaan pada setiap sel pengamatan
yang konvergen ke satu nilai,
Penentuan model terbaik yang dilakukan pada data tidak lengkap dapat di lihat dari
nilai uji nisbah kemungkinan dari masing-masing model, nilai yang terbesar menunjukkan
bahwa model tersebut lebih baik dibandingkan model lainnya.
Sebagai ilustrasi untuk memudahkan pemahaman algoritma EM, maka dalam
penelitian ini digunakan data kategori cross sectional berupa status keadaan bayi setelah
dilahirkan pada dua klinik yang berbeda.
1.2. Tujuan
Penelitian ini bertujuan mempelajari pendugaan data tidak lengkap dengan algoritma
EM pada model loglinear, dan menentukan pemodelan terbaik untuk data studi kasus status
keadaan bayi setelah dilahirkan pada dua klinik yang berbeda.
2. Tinjauan Pustaka
2.1. Model Loglinear pada Tabel Kontingensi
Data kategori merupakan jenis data dengan skala pengukuran nominal dan ordinal.
Ringkasan dari data kategori ini dapat ditampilkan menggunakan tabel kontingensi, yang
berupa total dari seluruh obervasi setiap kategori atau persentasi dari total di setiap kategori
(Morgan dan Andrew F Siegel, 1996).
Analisis tabel kontingensi berdimensi besar dilakukan pada setiap pasangan peubah
dalam tabel dua arah. Menurut Fienberg (1978) memiliki banyak kelemahan antara lain :
1. Mengaburkan hubungan marginal antara pasangan-pasangan peubah ketegori
Kusman Sadik
Seminar Nasional Matematika-FKMS3MI 2008
424
2. Tidak dapat mengamati hubungan pasangan-pasangan peubah secara simultan.
3. Mengabaikan kemungkinan adanya interaksi tiga peubah dan interaksi yang lebih
tinggi lainnya.
Oleh karena itu diperlukan analisis lain untuk tabel kontingensi berdimensi besar, diantaranya
menggunakan model loglinear.
Model loglinear menggambarkan hubungan beberapa kategori, dengan pendekatan
loglinear ini dari model dapat dihitung nilai harapan(mijk) setiap sel dalam tabel kontingensi,
bentuk dari model loglinear dan interpretasi parameter-parameter dalam model sama dengan
ANOVA(Agresti,1990).
2.2. Model Loglinear pada Tabel Kontingensi
Tiga Arah
Tabel kontingensi tiga arah dengan ukuran i x j x k dapat dibentuk dari N observasi
yang terdiri dari tiga peubah X, Y, dan R. Peubah X terdiri dari i kategori, Y terdiri dari j
kategori dan R terdiri dari k kategori. Bentuk model lengkap XYR (saturated model), di
gambarkan dalam bentuk :
XYR ijk XR ik YR jk XY ij R k Y j X i ijk
m
log (1)
dimana : 0 k R k j Y j i X
i
dan 0 ...
k XYR ijk j YR jk j XY ij i XYij
untuk : i = 1, 2, ..., I j = 1, 2, ...,J dan
k = 1, 2,...K
Keterangan :
: Rataan seluruh observasi
X i
: Pengaruh utama ke i pada kategori X
Y j
: Pengaruh utama ke j pada kategori Y
R k
: Pengaruh utama ke k pada kategori R
XY ij
YR jk
: Interaksi kategori Y ke j dengan kategori R ke k
XR ik
: Interaksi kategori X ke i dengan kategoriR ke k
XYR ijk
: Interaksi kategori X ke i dengan kategoriY ke j dan kategori R ke k
Pendugaan parameter dalam model diatas dapat diperoleh dengan cara sebagai berikut :
...
ijk logmijk
...
..
X i
i kR .k....
... .
.
Y j
j ijXY ij.i...j....
... .. . . .
YR jk j k
jk ... .. .. .
ik i k XR ik ... .. . . .. . . .
ijk
ij
ik
jk
i
j
k
XYR ijk
Pada dasarnya model yang terbentuk dari tabel kontingensi dapat diuraikan menjadi
beberapa model loglinear (model hirarki), tersusun dari model sederhana tanpa adanya
interaksi antara kategori, hingga model lengkap yang seluruh interaksi ada didalam model
tersebut (Little dan Donald, 1997).
Uji Kebaikan Suai
Model yang dicobakan dapat dilihat kesesuaiannya dengan menggunakan uji kebaikan
suai khi-kuadrat Pearson
2 dan statitstik uji nisbah kemungkinan (likelihood rasio testKusman Sadik
Seminar Nasional Matematika-FKMS3MI 2008
426
Uji Khi-kuadrat Pearson
2Statistik kebaikan suai khi-kuadrat untuk tiga peubah dapat dihitung dengan rumus:
k ijk
ijk ijk
j
i
m
m
n
22
(2)nijkadalah nilai pengamatan, sedangkan mijkadalah nilai harapan dari kolom-ijk.
Uji Nisbah Kemungkinan (G2)
Statistik nisbah kemungkinan dapat di hitung dengan rumus:
ijk ijk k
ijk j
i n
m n
G 2 2
log (3)Logaritma ditentukan dengan bilangan dasar e atau lebih dikenal dengan logaritma natural.
Hipotesis yang di uji adalah :
H0: Model memiliki kebaikan suai
H1: Model tidak memiliki kebaikan suai
Statistik uji 2 Pearson dan G2 menyebar asimtotik menurut sebaran khi-kuadrat (2)
dengan derajat bebas berupa pengurangan jumlah sel terhadap banyaknya parameter bebas
(Little dan Donald, 1997).
Jika terdapat lebih satu model yang sesuai maka dilakukan pemilihan model yang
memiliki kebaikan suai paling baik. Pemilihan dapat dilakukan dengan menguji hipotesis
berikut :
H0: Pilih Model pertama
H1: Pilih model kedua
Statistik ujinya :
2 ) 2 ( 2
) 1 ( 2
G
G
G
Kaidah pengujian yang digunakan adalah jika lebih kecil dari 2 maka H0 diterima
pada taraf nyata dengan derajat bebas adalah selisih dari derajat bebas kedua model yang
dibandingkan.
2.3. Algoritma EM
Algoritma EM adalah salah satu metode yang digunakan secara luas untuk menghitung
penduga kemungkinan maksimum dari data yang tidak lengkap (Little dan Donald, 1997).
Ada dua tahapan dasar dalam algoritma ini, yaitu :
1. Tahapan E (Expectation) yaitu tahapan mencari nilai harapan bersyarat dari data tidak
lengakap dengan syarat data lengkap dan pendugaan parameter dari suatu fungsi
kemungkinanl(
|Y), yang kemudian nilai harapan yang diperoleh di subsitusikan kedalam data hilang. Tahapan E dalam EM dapat ditentukan sebagai berikut :
mist obs mis t
dY Y
Y f Y l
Q () ()
, | |
|
(5)
2. Tahapan M dalam algoritma EM menentukan iterasi penentuan nilai penduga terbaru
(t+1)
dengan memaksimumkan :
( 1) ( )
( )
|
|
t tt
Q
Q
(6)Untuk semua nilai
Dalam kasus data tidak lengkap pada data kategori, kedua tahapan penting algoritma
EM didefinisikan bahwa setiap tahapan E dari algoritma EM menentukan besarnya frekuensi
pada sel pengamatan semu dengan mengalokasikan totalmarginal dari data tidak lengkap ke
dalam sel yang tidak terobservasi. Sedangkan tahapan M menghasilkan pendugaan
maksimum likelihood dari sel frekuensi pengamatan semu tersebut dengan cara
memaksimumkan pendugaan posterior dari parameter model. Kedua tahapan tersebut
dilakukan terus menerus hingga pada akhirnya diperoleh nilai dugaan pada tahap M yang
konvergen terhadap satu nilai (Park dan Morton, 1994).
Tahapan pendugaan data hilang dengan algoritma EM, (Little dan Donald, 1997)
Kusman Sadik
Seminar Nasional Matematika-FKMS3MI 2008
428
1.Menghitung nilai peluang di setiap sel pengamatan dengan menggunakan statistik
cukup yang di peroleh dengan pendugaan maksimumlikelihood.
2.Menduga nilai harapan di setiap dengan mendistribukan data tidak lengkap ke dalam
tiap sel pengamatan berdasarkan proporsi peluangnya.
3.Ulangi langkah 1-2 sampai memperoleh nilai dugaan parameter yang konvergen ke
satu nilai tertentu.
Setelah diperoleh hasil pendugaan yang konvergen ke satu nilai. Kekonvergenan dapat
diartikan bahwa nilai disetiap pengamatan utnuk beberapa iterasi akhir tidak mengalami
perubahan.
3. Bahan dan Metode
Ilustrasi yang digunakan untuk memahami pendugaan data tidak lengkap dengan
metode EM adalah data mengenai status keadaan bayi setelah dilahirkan pada dua klinik
berbeda. Peubah yang digunakan dalam penelitian ini yaitu:
Peubah Kategori Kode
Survival died, survived S
Prenatal Care less, more P
Clinic A,B C
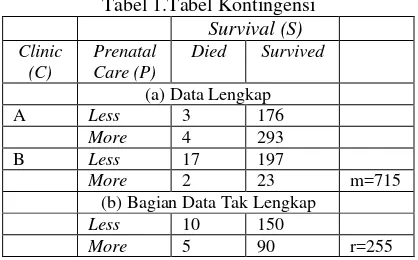
Ringkasan data di tampilkan ke dalam tabel kontingensi tiga arah pada Tabel 1. Ukuran tabel
[image:9.612.216.425.552.682.2]tersebut 2 x 2 x 2.
Tabel 1.Tabel Kontingensi
Survival (S)
Clinic (C)
Prenatal Care (P)
Died Survived
(a) Data Lengkap
A Less 3 176
More 4 293
B Less 17 197
More 2 23 m=715
(b) Bagian Data Tak Lengkap Less 10 150
More 5 90 r=255
Total seluruh responden yang berpartisipasi adalah 970 orang (m + r = 970), namun
hanya 715 terisi lengkap (m = 715), sedangkan 255 tidak lengkap (r= 225) terhadap peubah
clinic(C), sehingga 255 data ini yang akan di distribusikan ke dalam sel-sel pengamatan.
Metode yang digunakan :
1. Menentukan model terbaik dari data lengkap yang tersedia.
2. Menentukan nilai peluang setiap sel pengamatan.
3. Menentukan nilai harapan setiap sel dengan mendistribusikan data tak lengkap
berdasarkan nilai peluangnya, hingga konvergen.
4. Menentukan model terbaik setelah data di perbaiki.
4. Hasil dan Pembahan
4.1. Model Loglinear pada Tabel Kontingensi
Model hirarki yang dapat di uraikan dari tabel kontingensi berdimensi tiga ada 19
model loglinear. Sembilan dari model tersebut di tampilkan pada lampiran 1, sedangkan
sepuluh model lainnya di peroleh dari permutasi interaksi peubah-peubah pada model (3),
(4), (5), (7), dan (8). Analisa dalam penelitian ini hanya menggunakan empat model, karena
model-model tersebut dapat menggambarkan hubungan antara peubah clinic (C) dengan
peubah-peubah lainnya. Empat model tersebut yaitu : model lengkap (SPC), model (SP, SC,
PC), model (SC, PC), model (SP, SC).
Hasil dari nilai uji kebaikan suai (G2dan2) yang ditampilkan pada lampiran 2 untuk
setiap model, menunjukan bahwa model yang memiliki kebaikan suai terbaik hanya tiga
model saja yaitu model (SPC), model (SP, SC, PC), model (SC, PC)., hal ini diperoleh dari
pembandingan nilai uji kebaikan suai dengan nilai pada tabel khi-kuadrat dengan derajat
bebas masing-masing model.Jika nilai kebaikan suai lebih besar dari pada nilai tabel
khi-kuadrat pada taraf nyata 5 % maka kesimpulan yang diambil adalah menerima H0 atau
diintrepretasikan bahwa model memiliki kebaikan suai. Oleh karena ada lebih dari satu model
yang memiliki kebaikan suai maka untuk menentukan model terbaik perlu dilakukan analisa
Kusman Sadik
[image:11.612.216.426.133.233.2]Seminar Nasional Matematika-FKMS3MI 2008
430
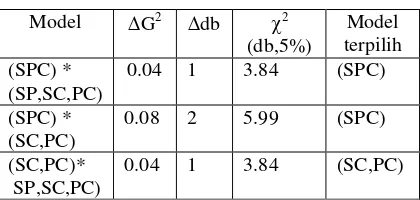
Tabel 2.hasil pemilihan model terbaik.
Model G2 db 2
(db,5%)
Model terpilih (SPC) *
(SP,SC,PC)
0.04 1 3.84 (SPC)
(SPC) * (SC,PC)
0.08 2 5.99 (SPC)
(SC,PC)* SP,SC,PC)
0.04 1 3.84 (SC,PC)
Model (SPC) ini merupakan model yang mengambarkan seluruh interaksi antar
peubah secara lengkap.Penentuan nilai peluang setiap sel pengamatan pada model lengkap
(SPC) dapat diproporsikan secara sempurna, dari model ini diperoleh nilai kebaikan suai (G2
dan2) nol dan derajat bebasnya juga nol.
Pada model (SP, SC, PC) dan model (SC, PC) memiliki nilai kebaikan suai yang
terkecil dibandingkan dengan model lainnya, hal ini menunjukkan kedua model ini yang
terbaik dan mengindikasikan bahwa antara peubah survival (S), prenatal (P) berhubungan
dengan peubah clinic (C). Namun pada model (SC, PC) tidak dapat menjelaskan hubungan
antara peubahsurvival(S) dengan peubahprenatal(P) berbeda dengan model (SP, SC, PC).
Oleh karena itu untuk pendugaan EM model yang digunakan adalah model (SC, PC) karena
di nilai lebih sederhana dan akan lebih mudah dalam mendistribusikan data tak lengkap.
4.2. Analisa Algoritma EM
Analisa algoritma EM meliputi pendistribusian dari data tidak lengkap ke dalam data
lengkap menggunakan nilai peluang bersyarat, kemudian menduga nilai di setiap sel
pengamatan dari data lengkap. Setiap nilai peluang yang diperoleh di tentukan oleh model
loglinear. Hasil dari algoritma EM pada model (SC, PC) berhenti pada iterasi ke 4, hal ini di
sebabkan pada iterasi ke 4 telah menunjukan nilai yang konvergen pada satu nilai di dalam
tahapan E. Jika iterasi itu di lanjutkan, maka pada iterasi selanjutnya akan diperoleh penduga
nilai sel pengamatan yang sama dengan iterasi ke 4.
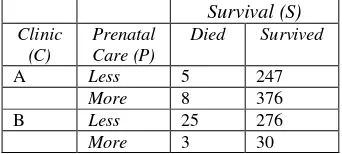
Nilai akhir dari iterasi yang diperoleh merupakan gabungan dari data lengkap dengan
Tabel 3. Nilai Akhir Pendugaan Data Tak Lengkap dengan Metode EM
Survival (S)
Clinic (C)
Prenatal Care (P)
Died Survived
A Less 5 247
More 8 376
B Less 25 276
More 3 30
Total dari seluruh data tidak berubah yaitu 970 namun nilai sel pengamatan di dalam
tiap kategori berubah. Sel pengamatan yang mendapatkan pendistribusian data terbesar
adalah sel padaclinic(C) A, prenatal care(P) untuk kategori moredan survival(S) untuk
kategorisurvived., sel tersebut mendapat tambahan sebesar 83, hal ini terjadi karena proporsi
awal pada sel tersebut terbesar pula.
5. Kesimpulan
Algoritma EM untuk data tidak lengkap pada model loglinear merupakan metode yang
cukup baik digunakan, karena dalam algoritma EM terjadi proses pendistribusian data tidak
lengkap ke data lengkap berdasarkan nilai peluang bersyaratnya, dan penentuan nilai peluang
ditentukan oleh model loglinear yang digunakan.
Model loglinear terbaik dalam ilustrasi yang dapat digunakan untuk algoritma EM
adalah model (SC, PC) karena model ini memiliki nilai kebaikan suai yang terkecil dan
model cukup sederhana dibanding dengan model (SP, SC, PC). Sedangkan proses dari
pendistribusian data tidak lengkap dengan algoritma EM tidak membutuhkan iterasi yang
besar. Pada iterasi ke 4 sudah menunjukkan nilai yang konvergen,
Daftar Pustaka
Agresti, Alan. 1990.Categorical Data Analysis. NewYork: Jhon Wiley & Sons.
Fienberg, Stephen E. 1998. The Analysis of Cross-Classified Categorical Data. The Massachusetts Institute of Technology.
Kusman Sadik
Seminar Nasional Matematika-FKMS3MI 2008
432
Little, R J A., and Donald B. Rubbin. 1987. Statistical Analysis with Missing Data. New York: John Wiley & Sons.
Morgan, Charles J., and Andrew F Siegel. 1996.Statistic and Data Analysi.New York: John Wiley & Sons.