Downscaling Methodology Development Using Arftificial Neyral Network (Case Study of Indramayu’s Rainfall).

(1)

(STUDI KASUS CURAH HUJAN INDRAMAYU)

MUHAMMAD RAFI MUTTAQIN

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

(2)

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini Saya menyatakan bahwa tesis Pengembangan Metodologi Downscaling Menggunakan Jaringan Saraf Tiruan (Studi Kasus Curah Hujan Indramayu) adalah karya Saya sendiri dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Januari 2012

Muhammad Rafi Muttaqin

(3)

ABSTRACT

MUHAMMAD RAFI MUTTAQIN. Downscaling Methodology Development

Using Arftificial Neyral Network (Case Study of Indramayu’s Rainfall). Under direction of AGUS BUONO as chairman and AZIZ KUSTIYO as member of advisory commitee.

The unexpected climate change results a long period wet and dry so it makes many agricultural areas damage. This is cause the farmers failed to harvest so the production of food will be decreased. To solve this problem, we need a model that can estimate the climate and rainfall so it can determine the suitable cropping pattern with the climate. Statistical downscaling modeling commonly used to model the changes of the weather. This study develops a statistical downscaling model that use artificial neural network with some of GCM data as an input in training. In this study, the GCM data is input for training. Before training this data is grouped into 5 groups. The results obtained indicate that some of the GCM can approach the average of monthly rainfall. However, in some extreme point, the result have not managed to reach and close to results of observation. The best results obtained with the correlation Bondan station at 0.4976 and the worst results obtained Krangkeng station with a correlation of 0.3704. In this study also can be seen that the estimators can be influenced by the location of the observation. The location is adjacent to the sea tend to have the results of a relatively lower correlation compared with the location that far from the sea.

(4)

RINGKASAN

MUHAMMAD RAFI MUTTAQIN. Pengembangan Metodologi Downscaling Menggunakan Jaringan Saraf Tiruan (Studi Kasus Curah Hujan Indramayu). Dibimbing oleh AGUS BUONO dan AZIZ KUSTIYO.

Peristiwa iklim ekstrim terkait El Niño-Southern Oscillation (ENSO) telah menimbulkan dampak yang signifikan pada sektor pertanian di Indonesia. Pada peristiwa ENSO hangat atau biasa dikenal dengan istilah El Niño, biasanya terjadi penundaan awal musim hujan dan bertambah panjangnya musim kemarau. Peristiwa El Niño seringkali dikaitkan dengan meluasnya kekeringan di berbagai daerah yang menyebabkan turunnya produksi pertanian karena kurangnya persediaan air. Sebaliknya, pada periode ENSO dingin, atau dikenal dengan istilah La Niña, kejadian hujan meningkat melebihi kondisi rata-rata sehingga meningkatkan peluang terjadinya banjir di berbagai daerah di Indonesia. Implikasinya pada sektor pertanian ialah semakin meningkatnya wilayah persawahan yang tergenang banjir dan merusak tanaman, sehingga menyebabkan meningkatnya kemungkinan gagal panen.Perubahan iklim regional/lokal ini bisa bersifat spesifik antar daerah sehingga membutuhkan data dengan resolusi cukup tinggi yang tidak bisa didapat dari data luaran general circulation model (GCM) yang memiliki resolusi horizontal yang sangat rendah. Oleh karena itu untuk mendapatkan informasi dengan resolusi yang cukup tinggi, diperlukan pemanfaatan teknik downscaling. Metode downscaling dengan pendekatan dinamik dapat dilakukan dengan menggunakan simulasi model iklim regional (regional climate model, RCM) yang disimulasi berdasarkan informasi data GCM.

(5)

mencapainya. Oleh karena itu, dalam studi ini akan dikembangkan metodologi downscaling menggunakan JST dengan pengelompokan data terlebih dahulu sebelum dilakukan pelatihan. Hal ini diharapkan dapat memperbaiki pola yang dihasilkan oleh penelitian sebelumnya.

Tujuan utama dari penelitian ini adalah mengembangkan JST untuk melakukan downscaling dari data GCM curah hujan bulanan (studi kasus Indramayu). Oleh karena itu, penelitian ini diharapkan dapat memperbaiki model yang telah dihasilkan oleh penelitian sebelumnya. Manfaat yang diharapkan dari hasil penelitian ini adalah para pihak terkait dapat mengantisipasi perubahan curah hujan sejak dini. Dengan demikian model ini dapat menjadi bahan pertimbangan petani atau pengelola perkebunan dalam menentukan tanaman apa yang cocok untuk kondisi iklim pada masa yang akan datang. Ruang lingkup dari penelitian ini adalah data curah hujan yang digunakan berasal dari stasiun hujan yang berada di daerah Indramayu (13 stasiun) dari tahun 1979 – 2002 serta data General Circulation Model (GCM) yang digunakan adalah sebanyak 6 model (1901 – 2000).

Secara keseluruhan model yang dihasilkan oleh pelatihan menggunakan JST lebih baik dari penelitian sebelumnya yang dihasilkan oleh Buono (2010). Hal ini ditunjukkan dengan tercapainya beberapa titik yang pada penelitian sebelumnya tidak dapat dicapai oleh hasil penduga. Pola hasil prediksi yang dihasilkan oleh model JST mengikuti pola dari hasil pengamatan langsung di lapangan. Akan tetapi dalam keadaan ekstrim, penduga yang dihasilkan belum dapat menduga secara baik nilai yang dihasilkan oleh pengamatan langsung.

(6)

© Hak Cipta Milik IPB, Tahun 2012 Hak Cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah

b. Pengutipan tersebut tidak merugikan kepentingan wajar IPB

(7)

PENGEMBANGAN METODOLOGI DOWNSCALING

MENGGUNAKAN JARINGAN SARAF TIRUAN

(STUDI KASUS CURAH HUJAN INDRAMAYU)

MUHAMMAD RAFI MUTTAQIN

Tesis

Sebagai salah satu syarat untuk memperoleh gelar

Magister Ilmu Komputer pada

Program Studi Magister Ilmu Komputer

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

(8)

(9)

Nama : Muhammad Rafi Muttaqin

NIM : G 651090151

Disetujui, Komisi Pembimbing

Dr. Ir. Agus Buono, M.Si, M.Kom Aziz Kustiyo, S.Si, M.Kom

Ketua Anggota

Diketahui,

Ketua Program Studi Dekan Sekolah Pascasarjana

Ilmu Komputer

Dr. Ir. Agus Buono, M.Si, M.Kom Dr. Ir. Dahrul Syah, M.Sc.Agr

(10)

Puji syukur kehadirat Allah SWT, atas berkat rahmat dan hidayah-Nya penulis dapat menyelesaikan penulisan usulan penelitian sebagai syarat dalam menyelesaikan perkuliahan di Magister Komputer, Ilmu Komputer, Institut Pertanian Bogor. Tidak lupa shalawat serta salam semoga senantiasa di berikan kepada Nabi Muhammad, SAW, keluarganya, dan umatnya sampai akhir zaman.

Penulis melakukan penelitian tentang pengembangan metodologi downscaling menggunakan jaringan saraf tiruan untuk studi kasus curah hujan Kabupaten Indramayu. Untuk data GCM yang digunakan dalam penelitin ini terdiri atas 6 model dan untuk data observasi digunakan 13 titik koordinat stasiun curah hujan di Indramayu. Dengan menerapkan metode jaringan saraf tiruan diharapkan dapat berguna untuk memodelkan curah hujan antara luaran GCM dengan data observasi sehingga dapat memprediksi dan menduga curah hujan dengan lebih baik.

Penulis mengucapkan terima kasih atas bantuan dan dukungan dari semua pihak yang mendukung baik secara langsung maupun tidak langsung dalam pelaksanaan kuliah maupun penelitian yang akan dilaksanakan. Cinta dan rasa syukur yang sedalam-dalamnya penulis sampaikan untuk :

1. Abi KH. Muhammad Husni Thamrin, atas nasihat, doa, dan dukungannya selama penulis melaksanakan tesis ini,

2. Mamah Heni Yuliati dan Papap Busrol Karim, atas dukungan materil dan non materil selama penulis kuliah di Pasca Sarjana Institut Pertanian Bogor. 3. Ibu Nurul Aini dan Bapa Harry Juandi, atas doa dan dukungannya selama ini. 4. Istriku tercinta Laras Nurharini S,Pd, atas doa, cinta, dan kasih sayangnya

selama penulis menempuh pendidikan di Institut Pertanian Bogor.

5. Bapak Dr. Ir. Agus Buono, M.Si, M.Kom dan Bapak Aziz Kustiyo, S.Si, M.Kom atas kesabarannya dalam memibimbing penulis dan masukan selama bimbingan di pascasarjana Ilmu Komputer IPB untuk segera menyelesaikan pendidikan.

(11)

7. Teteh-tetehku tercinta, Teh Lina, Teh Wulan, dan Teh Rani, atas dukungan dan doanya selama penulis menempuh pendidikan di IPB.

8. Adik iparku, Tiara dan Tiwi, atas doa dan dukungan kepada penulis dalam penulisan tesis ini.

9. Rekan-rekan seperjuangan angkatan XI S2 Ilmu Komputer IPB (Alm Pak Oke Hendrady, Pak Mukhlis, Pak Tahir, Mas Mawan, Pak Rico, Pak Iyan, Mas Kamal, Mas Supriyanto, Asyar, Aries M, Pak Yusuf, Bu Zuriati, Bu Dewi, Bu Sinta, Bu Retno, Pak Boy, Pak Azhari) atas kebersamaan dan bantuannya selama kuliah dan penelitian di MKOM IPB, khususnya Asyhar yang selalu membantu penulis dalam menyelesaikan tesis ini.

Penulis menyadari bahwa dalam penulisan tesis ini masih banyak kekurangan. Kritik, saran dan masukan dalam penelitian ini sangat penulis harapkan, demi sempurnanya tesis ini di kemudian hari.

Bogor, Januari 2012

(12)

RIWAYAT HIDUP

Penulis dilahirkan di kota Purwakarta pada tanggal 20 Agustus 1987 dari pasangan Busrol Karim dan Euis Heni Yuliati. Penulis merupakan anak keempat dari empat bersaudara.

Saat masih kecil, penulis mengenyam pendidikan anak-anak di SDN A. Yani X Purwakarta (1993-1999). Kemudian, penulis melanjutkan pendidikan menengahnya ke SMP Insan Kamil Bogor (1999 – 2002), lalu SMA Insan Kamil Bogor (2002-2004) setelah mengikuti kelas akselerasi pada SMA Insan Kamil. Setelah lulus SMA pada tahun 2004, penulis berkesempatan melanjutkan studi di IPB melalui jalur Seleksi Penerimaan Mahasiswa Baru (SPMB) di Departemen Ilmu Komputer, Fakultas Matematika dan Ilmu Pengetahuan Alam dan lulus pada tahun 2008. Penulis pernah bekerja sebagai asisten dosen pada program diploma 3 Teknik Komputer, Institut Pertanian Bogor pada tahun 2009.

Pada tahun 2009, penulis diterima sebagai mahasiswa Sekolah Pascasarjana program studi Ilmu Komputer Institut Pertanian Bogor sampai sekarang. Penulis

(13)

DAFTAR TABEL ... ii

2.1 Model Sirkulasi Umum ... 4

2.2 Downscaling ... 6

2.3 Jaringan Saraf Tiruan (Neural Network) ... 8

2.3.1 Backpropagation... 10

2.3.2 Fungsi Aktivasi ... 11

2.3.3 Algoritme Pelatihan Backpropagation ... 13

2.3.4 Algoritme Pelatihan Lavenberg-Marquardt ... 15

2.4 K-fold Cross Validation ... 17

2.5 Jarak Euclid ... 17

BAB III DATA DAN METODOLOGI ... 18

3.1 Data Penelitian ... 18

3.2 Metode Penelitian ... 18

3.3 Lingkup Pengembangan Sistem ... 23

BAB IV HASIL DAN PEMBAHASAN ... 24

4.1 Pemodelan Downscaling Menggunakan Jaringan Saraf Tiruan (JST) ... 24

(14)

BAB V SIMPULAN DAN SARAN ... 32

5.1 Simpulan ... 32

5.2 Saran ... 32

DAFTAR PUSTAKA ... 33

LAMPIRAN ... 35

DAFTAR TABEL Halaman 1 Skala grid model-model GCM dan negara yang mengembangkannya ... 5

2 Model GCM dan negara pembuatnya ... 18

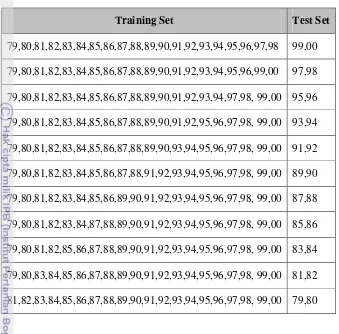
3 Pembagian data latih dan data uji. ... 20

4 Rataan nilai NRMSE dan korelasi pada hidden layer 50 dan 100 ... 24

(15)

DAFTAR GAMBAR

Halaman

1 Visualisasi Layering pada GCM ... 6

2 Ilustrasi proses downscaling, (Sumber : Sutikno 2008) ... 7

3 Sel neuron pada manusia ... 8

4 Arsitektur Jaringan Saraf Tiruan ... 10

5 Fungsi sigmoid biner dengan range (0,1) ... 11

6 Fungsi sigmoid bipolar dengan range (-1,1) ... 12

7 Fungsi Identitas ... 12

8 Diagram alur penelitian ... 19

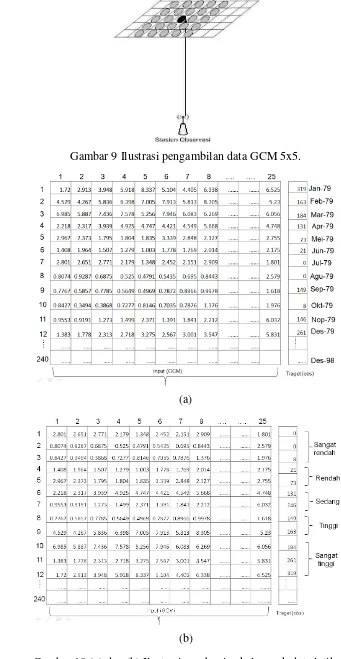
9 Ilustrasi pengambilan data GCM 5x5. ... 21

10 (a) dan (b) Ilustrasi pembagian kelompok data latih. ... 21

11 Struktur JST yang akan digunakan. ... 22

12 Grafik hasil perbandingan rataan observasi bulanan dengan hasil prediksi luaran seluruh model GCM untuk JST-1. ... 25

13 Grafik hasil perbandingan rataan observasi bulanan dengan hasil prediksi luaran seluruh model GCM untuk JST-2. ... 25

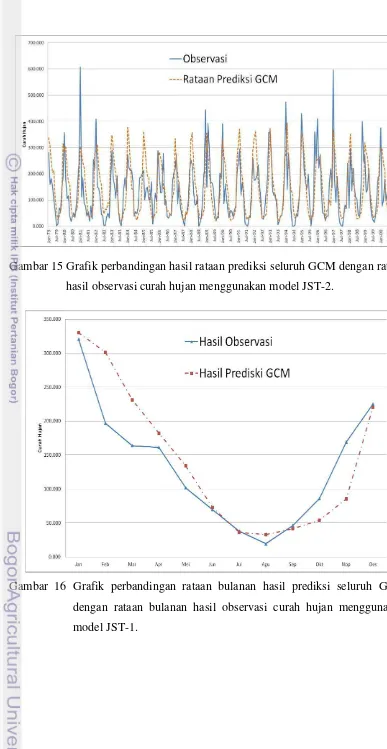
14 Grafik perbandingan hasil rataan prediksi seluruh GCM dengan rataan hasil observasi curah hujan menggunakan model JST-1. ... 26

15 Grafik perbandingan hasil rataan prediksi seluruh GCM dengan rataan hasil observasi curah hujan menggunakan model JST-2. ... 27

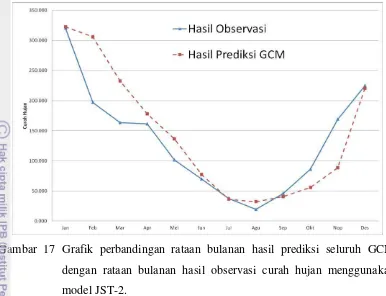
16 Grafik perbandingan rataan bulanan hasil prediksi seluruh GCM dengan rataan bulanan hasil observasi curah hujan menggunakan model JST-1. ... 27

17 Grafik perbandingan rataan bulanan hasil prediksi seluruh GCM dengan rataan bulanan hasil observasi curah hujan menggunakan model JST-2. ... 28

18 Grafik perbandingan hasil observasi pada stasiun Bondan dengan hasil prediksi. ... 30

19 Grafik perbandingan hasil observasi pada stasiun Krangkeng dengan hasil prediksi. ... 30

20 Sebaran lokasi stasiun serta besaran nilai korelasi. ... 31

(16)

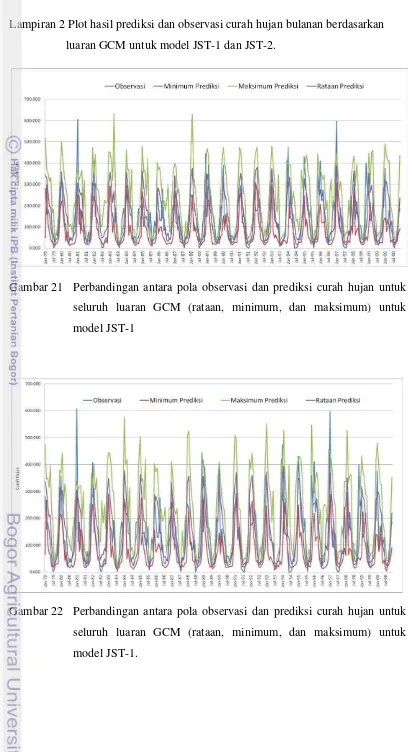
22 Perbandingan antara pola observasi dan prediksi curah hujan untuk seluruh luaran GCM (rataan, minimum, dan maksimum) untuk model JST-1. ... 37

DAFTAR LAMPIRAN

Halaman 1 Contoh struktur jaringan saraf tiruan. ... 36 2 Plot hasil prediksi dan observasi curah hujan bulanan berdasarkan luaran GCM

(17)

Peristiwa iklim ekstrim terkait El Niño-Southern Oscillation (ENSO) telah menimbulkan dampak yang signifikan pada sektor pertanian di Indonesia. Pada peristiwa ENSO hangat atau biasa dikenal dengan istilah El Niño, biasanya terjadi penundaan awal musim hujan dan bertambah panjangnya musim kemarau (Kirono et al. 1999; Moron et al. 2009). Peristiwa El Niño seringkali dikaitkan dengan meluasnya kekeringan di berbagai daerah yang menyebabkan turunnya produksi pertanian karena kurangnya persediaan air. Sebaliknya, pada periode ENSO dingin, atau dikenal dengan istilah La Niña, kejadian hujan meningkat melebihi kondisi rata-rata sehingga meningkatkan peluang terjadinya banjir di berbagai daerah di Indonesia. Implikasinya pada sektor pertanian ialah semakin meningkatnya wilayah persawahan yang tergenang banjir dan merusak tanaman, sehingga menyebabkan meningkatnya kemungkinan gagal panen.

Akibat perubahan iklim ekstrim di bidang pertanian, maka harus dihadapi dengan penuh perencanaan dan melibatkan berbagai pihak terkait, baik pemerintah setempat sampai masyarakatnya. Sayangnya, hingga saat ini penggunaan informasi iklim dalam mengelola resiko iklim masih belum umum. Dalam hal ini, penyediaan informasi iklim yang efektif dan tepat guna sangat perlu untuk terus dievaluasi dan dikembangkan, sebab peruabahan iklim dapat memberikan dampak yang lebih besar dalam bidang pertanian. Oleh karena itu, perencanaan yang menyeluruh baik jangka pendek maupun jangka panjang sangat diperlukan. Hal ini merupakan tantangan yang cukup besar terutama dalam konteks aplikasi pengelolaan resiko iklim (climate risk management, CRM).

(18)

tersebut, masing-masing memiliki kelebihan dan kekurangan dan juga memiliki tingkat kemampuan prediksi yang mungkin berbeda pada suatu wilayah tertentu.

Perubahan iklim di masa yang akan datang akibat peningkatan suhu global diproyeksikan dapat menciptakan pergeseran pola iklim sehingga memungkinkan terjadinya peningkatan peluang resiko khususnya di sektor pertanian. Untuk mengatasi hal ini diperlukan perencanaan jangka panjang melibatkan analisis iklim berdasarkan pilihan-pilihan skenario yang mungkin terjadi di masa depan. Perubahan iklim juga diantisipasi dapat mengubah rentang iklim, meningkatkan frekuensi dan amplitudo kejadian iklim ekstrim, dan pergeseran kondisi iklim regional hingga lokal. Perubahan iklim regional/lokal ini bisa bersifat spesifik antar daerah sehingga membutuhkan data dengan resolusi cukup tinggi yang tidak bisa didapat dari data luaran general circulation model (GCM) yang memiliki resolusi horizontal yang sangat rendah. Oleh karena itu untuk mendapatkan informasi dengan resolusi yang cukup tinggi, diperlukan pemanfaatan teknik downscaling. Metode downscaling dengan pendekatan dinamik dapat dilakukan dengan menggunakan simulasi model iklim regional (regional climate model, RCM) yang disimulasi berdasarkan informasi data GCM.

(19)

1.2 Perumusan Masalah

Berdasarkan latar belakang tersebut model GCM mempunyai banyak sekali informasi yang dapat dimanfaatkan untuk peramalan iklim. Akan tetapi model GCM ini memiliki resolusi horisontal yang sangat rendah sehingga diperlukan teknik downscaling untuk mendapatkan resolusi yang cukup tinggi. Dengan resolusi yang cukup tinggi, maka informasi dalam GCM yang ada dapat diperoleh.

Berdasarkan penelitian sebelumnya (Buono, 2010), pemodelan curah hujan dengan data GCM dengan teknik downscaling menggunakan JST kurang dapat mewakili data observasi. Oleh karena itu, dalam studi ini akan dikembangkan metodologi downscaling menggunakan JST dengan pengelompokan data terlebih dahulu sebelum dilakukan pelatihan. Hal ini diharapkan dapat memperbaiki pola yang dihasilkan oleh penelitian sebelumnya.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah mengembangkan JST untuk melakukan downscaling dari data GCM curah hujan bulanan (studi kasus Indramayu). Oleh karena itu, penelitian ini diharapkan dapat memperbaiko model yang telah dihasilkan oleh penelitian sebelumnya.

1.4 Manfaat Penelitian

Manfaat yang diharapkan dari hasil penelitian ini adalah para pihak terkait dapat mengantisipasi perubahan curah hujan sejak dini. Dengan demikian model ini dapat menjadi bahan pertimbangan petani atau pengelola perkebunan dalam menentukan tanaman apa yang cocok untuk kondisi iklim pada masa yang akan datang.

1.5 Ruang Lingkup Penelitian

Ruang lingkup dari penelitian ini adalah sebagai berikut:

 data curah hujan yang digunakan adalah data yang berasal dari stasiun hujan yang berada di daerah Indramayu (13 stasiun) dari tahun 1979 - 2002.

(20)

Model sirkulasi umum atau general circulation model (GCM) merupakan suatu penggambaran matematis dari sejumlah besar interaksi fisika, kimia, dan dinamika atmosfer bumi (Von Stroch et al. 1993 dalam Sutikno 2008). GCM ini menduga perubahan iklim dan disajikan tiga layer, yaitu layer horisontal dengan ukuran 100 hingga 600 km, 10 hingga 20 layer vertikal di atmosfer dan kadangkala 30 layer di samudra, seperti disajikan pada Gambar 1.

Dengan resolusi yang begitu kasar, maka GCM tidak bisa menangkap fitur penting pada suatu area (region) tertentu yang menjadi fokus kajian dampak perubahan iklim. Namun demikian, GCM ini bisa dijalankan (di-run) untuk mengestimasi kepekaan iklim terhadap kondisi yang berbeda seperti perubahan gas rumah kaca (GRK). Oleh karena itu, model GCM memberikan beberapa keuntungan seperti tertera pada Sutikno (2008), yaitu : (1) dapat digunakan untuk mengestimasi perubahan iklim global dalam merespon terhadap peningkatan konsentrasi GRK, (2) estimasi peubah iklim (curah hujan, suhu, kelembaban) secara fisik sesuai dengan model-model fisika, (3) estimasi peubah cuaca (angin, radiasi, penutupan awan, kelembaban tanah) yang berikutnya menjadi masukan bagi analisis mengenai dampak, (4) mampu menyimulasi keragaman iklim siklus harian. Disamping kelebihan seperti disebutkan di atas, beberapa kelemahannya adalah : (1) resolusi terlalu kasar, sehingga terjadi gap antara hasil simulasi global, regional dan lokal, (2) model tersebut sulit mengkopel dengan model-model sirkulasi lautan, dan (3) proses-proses umpan balik atmosfer-biosfer tidak terpenuhi. Untuk menjembatani gap antara hasil global dengan regional dan lokal, maka diperlukan satu model yang dikenal dengan nama downscaling.

(21)

Indonesia adalah model dengan resolusi horisontal yang tinggi dan skema konveksi yang komprehensif (Sutikno 2008).

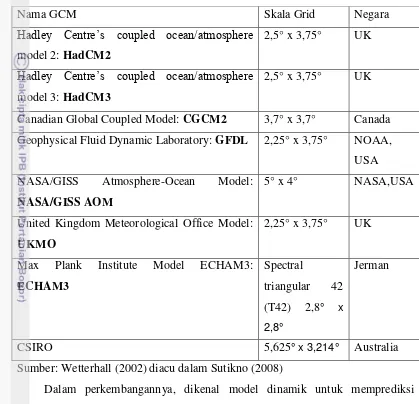
Tabel 1 Skala grid model-model GCM dan negara yang mengembangkannya

Nama GCM Skala Grid Negara

Hadley Centre’s coupled ocean/atmosphere

model 2: HadCM2

2,5° x 3,75° UK

model 3: HadCM3

2,5° x 3,75° UK

Canadian Global Coupled Model: CGCM2 3,7° x 3,7° Canada Geophysical Fluid Dynamic Laboratory: GFDL 2,25° x 3,75° NOAA,

USA NASA/GISS Atmosphere-Ocean Model:

NASA/GISS AOM

5° x 4° NASA,USA

United Kingdom Meteorological Office Model: UKMO

Sumber: Wetterhall (2002) diacu dalam Sutikno (2008)

(22)

input awal yang sedikit berbeda. Gambar 1 menunjukkan visualisasi layering pada GCM.

2.2 Downscaling

Downscaling didefinisikan sebagai upaya menghubungkan antara sirkulasi peubah skala global (peubah penjelas) dan peubah skala lokal (peubah respon, Sutikno 2008). Istilah downscaling sering salah jika diartikan secara tekstual yaitu suatu cara untuk meningkatkan resolusi. Downscaling lebih menunjukkan proses perpindahan dari peubah penjelas ke peubah respon, yaitu perpindahan dari skala besar ke skala kecil (regional/titik). Gambar 2 memberikan ilustrasi proses downscaling.

Pendekatan statistical downscaling (SD) menggunakan data regional (statistic dynamical downscaling) atau global (statistical downscaling) untuk

(23)

memperoleh hubungan fungsional antara skala lokal dengan skala global GCM, seperti model regresi. Pendekatan SD disusun berdasarkan adanya hubungan antara grid skala besar (prediktor) dengan grid skala lokal (respon) yang dinyatakan dengan model statistik yang dapat digunaan untuk menterjemahkan anomali-anomali skala global yang menjadi anomali dari beberapa peubah iklim lokal (Zorita dan Storch 1999, dalam Wigena 2006). Dalam hal ini SD merupakan suatu fungsi transfer yang menggambarkan hubungan fungsional sirkulasi atmosfer global dengan unsur-unsur iklim lokal, yang bentuk umumnya adalah :

(24)

2.3 Jaringan Saraf Tiruan (Neural Network)

Jaringan saraf tiruan (JST) merupakan salah satu sistem pemrosesan informasi yang didesain dengan menirukan cara kerja otak manusia dalam menyelesaikan suatu masalah dengan melakukan proses belajar melalui perubahan bobot sinapsisnya. Jaringan saraf tiruan mampu mengenali kegiatan dengan berbasis data pada masa lalu. Data masa lalu akan dipelajari oelh jaringan saraf tiruan sehingga mempunyai kemampuan untuk memberi keputusan terhadap data yang belum pernah dipelajari (Hermawan 2006).

Jaringan saraf tiruan didefinisikan sebagai suatu system pemerosesan informasi yang mempunyai karakteristik menyerupai jaringan saraf manusia. JST tercipta sebagai suatu generalisasi model matematis dari pemahaman manusia (human cognition) yang didasarkan atas asumsi sebagai berikut:

1 Pemrosesan informasi terjadi pada elemen sederhana yang disebut neuron (Gambar 3).

2 Isyarat mengalir di antara sel saraf/neuron melalui suatu sambungan penghubung,

3 Setiap sambungan penghubung memiliki bobot yang bersesuaian. Bobot ini akan digunakan untuk menggandakan/mengalikan isyarat yang akan dikirim melaluinya.

4 Setiap sel saraf akan menerapkan fungsi aktivasi terhadap isyarat hasil penjumlahan berbobot yang masuk kepadanya untuk menentukan isyarat keluarannya.

Gambar 3 Sel neuron pada manusia

(25)

Berbeda dengan metode lain, algoritma untuk JST beroperasi secara langsung dengan angka sehingga data yang tidak numerik harus diubah menjadi data numerik. Dibandingkan dengan cara perhitungan konvensional, JST tidak memerlukan atau menggunakan suatu model matematis atas permasalahan yang dihadapi. Oleh karena itu, JST juga dikenal sebagai model free-estimator.

JST memiliki sejumlah besar kelebihan dibandingkan dengan metode perhitungan lainnya (Hermawan 2006), yaitu:

1 Kemampuan mengakuisisi pengetahuan walaupun dalam kondisi ada gangguan dan ketidakpastian. Hal ini karena JST mampu melakukan generalisasi, abstraksi, dan ekstraksi terhadap properti statistik dari data..

2 Kemampuan mereprentasikan pengetahuan secara fleksibel. JST dapat menciptakan sendiri representasi melalui pengaturan sendiri atau kemampuan belajar (self organizing).

3 Kemampuan untuk memberikan toleransi atas suatu distorsi (error/fault), di mana gangguan kecil pada data dapat dianggap hanya sebagai noise (guncangan) belaka.

4 Kemampuan memproses pengetahuan secara efisien karena memakai sistem paralel, sehingga waktu yang diperlukan untuk mengoperasikannya menjadi lebih singkat.

Walaupun memiliki beberapa kelebihan, JST juga mempunyai sejumlah keterbatasan, antara lain kekurangmampuannya dalam melakukan operasi-operasi numerik dengan presisi tinggi, operasi algoritma aritmatik, operasi logika, dan operasi simbolis serta lamanya proses pelatihan yang terkadang membutuhkan waktu berhari-hari untuk jumlah data yang besar.

JST memiliki kemampuan yang sangat baik untuk beberapa aplikasi, antara lain klasifikasi, asosiasi, self organizing, dan optimasi. Karakteristik JST ditentukan oleh:

1 Pola hubungan antar-neuron (disebut dengan arsitektur jaringan),

2 Metode penentuan bobot-bobot sambungan (disebut dengan pelatihan atau proses belajar jaringan),

(26)

Pembagian aristektur JST bisa dilihat dari kerangka kerja dan skema interkoneksi. Kerangka kerja JST bisa dilihat dari jumlah lapisan (layer) dan jumlah node pada setiap lapisan. Lapisan-lapisan penyusun JST dapay dibagi menjadi tiga (Gambar 4), yaitu:

1 Lapisan input (input layer)

Node-node di dalam lapisan input disebut unit-unit input. Unit-unit input menerima input dari dunia luar. Input yang dimasukkan merupakan penggambaran dari suatu masalah.

2 Lapisan tersembunyi (hidden layer)

Node-node di dalam lapisan tersembunyi disebut unit-unit tersembunyi. Output dari lapisan ini tidak secara langsung dapat diamati.

3 Lapisan output (output layer)

Node-node pada lapisan output disebut unit-unit output. Keluaran dari lapisan ini merupakan output JST terhadap suatu permasalahan.

Gambar 4 Arsitektur Jaringan Saraf Tiruan (Sumber: http://yeni.herdiyeni.staff.ipb.ad.id)

2.3.1 Backpropagation

(27)

manfaat untuk beberapa kasus, akan tetapi pelatihannya membutuhkan waktu yang lebih lama. Maka pada umumnya orang mulai mencoba mengguanakan sebuah lapisan tersembunyi terlebih dahulu (Siang 2005).

Backpropagation melatih jaringan untuk mendapatkan keseimbangan antara kemampuan jaringan untuk mengenali pola yang digunakan selama pelatihan serta kemampuan jaringan untuk memberikan respon yang benar terhadap pola masukan yang serupa dengan pola yang dipakai selama pelatihan.

2.3.2 Fungsi Aktivasi

Fungsi aktivasi merupakan fungsi yang menentukan level aktivasi, yakni keadaan internal sebuah neuron dalam jaringan syaraf tiruan. Dalam backpropagation, fungsi aktivasi yang dipakai harus memenuhi beberapa syarat, yaitu kontinu, terdiferensial dengan mudah dan meruapakan fungsi yang tidak turun.

Fungsi aktivasi yang sering digunakan antara lain:

 Fungsi Sigmoid Biner

Fungsi ini merupakan fungsi yang umum digunakan (Siang 2005). Range-nya adalah (0,1) dan didefinisikan sebagai:

(2)

dengan turunan pertama:

(3)

Fungsi sigmoid biner ini diilustrasikan pada Gambar 5.

Gambar 5 Fungsi sigmoid biner dengan range (0,1) 1

(28)

 Fungsi Sigmoid Bipolar

Fungsi sigmoid bipolar merupakan fungsi yang memiliki range (-1,1) dan didefinisikan sebagai:

(4)

dengan turunan:

(5)

Fungsi sigmoid bipolar digambarkan pada Gambar 6.

Gambar 6 Fungsi sigmoid bipolar dengan range (-1,1)

 Fungsi Identitas

Fungsi aktivasi identitas akan menghitung nilai output dari neuron dan mengembalikan nilai tersebut menggunakan fungsi linier. Fungsi identitas didefinisikan sebagai: dimana . Fungsi identitas dapat dilihat pada Gambar 7.

Gambar 7 Fungsi Identitas f(x)

(29)

2.3.3 Algoritme Pelatihan Backpropagation

Pelatihan backpropagation meliputi 3 fase. Fase pertama adalah fase maju. Pola masukan dihitung maju mulai dari lapisan masukan hingga lapisan keluaran menggunakan fungsi aktivasi yang ditentukan. Fase kedua adalah fase mundur. Selisih antara keluaran jaringan dengan target yang diinginkan merupakan kesalahan yang terjadi. Kesalahan tersebut dipropagasikan mundur, dimulai dari garis yang berhubungan langsung dengan unit-unit di lapisan keluaran. Fase ketiga adalah modifikasi bobot untuk menurunkan kesalahan yang terjadi. Contoh struktur jaringan saraf tiruan yang akan digunakan pada algoritme ini dapat dilihat pada Lampiran 1.

Algoritme pelatihan backpropagation adalah sebagai berikut:

Langkah 0. Inisialisasi bobot (biasanya digunakan nilai acak yang kecil) Langkah 1. Selama syarat henti salah, lakukan langkah 2-9

Langkah 2. Untuk setiap pasangan pelatihan (masukan dan target), lakukan 3-8 Fase 1 : Propagasi maju.

(30)

)

Langkah 6. Setiap unit output (Yk,k=1,...,m) menerima sebuah pola target yang

sesuai dengan pola masukan pelatihannya. Unit tersebut menghitung informasi kesalahan  (t_k y_k)f'(y_in_k)

Kemudian menghitung koreksi bobot (digunakan untuk mengubah wjk nanti), wjk kzj

dan menghitung koreksi bias w₀_k _k

serta mengirimkan nilai _k ke unit lapisan di bawahnya

Langkah 7. Setiap unit tersembunyi (Zj,j=1,...,p) menghitung selisih input (dari

unit-unit pada layer diatasnya) lalu mengalikannya dengan turunan fungsi aktivasi untuk menghitung informasi error. selanjutnya menghitung koreksi bobot untuk mengubah vij sebesar

i

(31)

mencapai epoh maksimum, maka selesai; jika tidak maka kembali ke langkah 1.

Nilai toleransi () yang digunakan adalah 0 1

2.3.4 Algoritme Pelatihan Lavenberg-Marquardt

Algoritme pelatihan Lavenberg-Marquardt (LM) merupakan algoritme pelatihan yang memiliki kemampuan memperoleh nilai konvergen yang cepat dibandingkan dengan algoritme pelatihan lain dalam kasus fungsi aproksimasi (Beale et al 2011). Langkah dasar dari algoritme Lavenberg-Marquardt (LM) adalah penentuan matriks Hessian untuk mencari bobot-bobot dan bias koneksi yang digunakan dalam pelatihan JST (Warsito 2007). Matriks Hessian adalah turunan kedua dari fungsi kinerja terhadap setiap komponen bobot dan bias. Untuk memudahkan komputasi, matriks Hessian diubah dengan pendekatan iterative pada setiap epoch selama algoritme pelatihan berjalan. Proses perubahannya dilakukan dengan menggunakan fungsi gradien. Apabila fungsi kinerja yang digunakan berbentuk jumlah kuadrat error (SSE), maka matriks Hessian dapat diestimasi dengan persamaan berikut:

(15)

Dimana:

: parameter Marquardt I : matriks identitas

J : matriks Jakobian yang terdiri dari turunan pertama error jaringan terhadap masing-masing komponen bobot dan bias.

(32)

Algoritme pelatihan dengan metode Levenberg-Marquardt dapat dijabarkan sebagai berikut:

Langkah 0 :

 Inisialisasi bobot awal dengan bilangan acak kecil

 Inisialisasi epoch 0, MSE 0

 Tetapkan maksimum epoch parameter LM ( ), faktor dan target error.

Langkah 1 :

Jika kondisi penghentian belum terpenuhi (epoch < epoch maksimum atau MSE > target error), lakukan langkah berikutnya.

Langkah 2 :

 Epoch = epoch + 1

 Untuk setiap data pelatihan, lakukan langkah 3 – 4. Langkah 3 :

Unit/neuron output Y menerima target pola yang berhubungan dengan pola input pelatihan. Jika diberikan N pasangan input data pelatihan (Xr, tr), r = 1,2,…,N, dengan Xr adalah input dan tr adalah target yang akan dicapai. Kesalahan pada suatu data pelatihan ke-r didefinisikan sebagai:

er = tr - yr (16)

dengan :

(33)

Vektor kesalahan oleh vektor bobot dan bias koneksi w menjadi e(w) berukuran Nx1 yang tersusun dari er(w), dengan r = 1,2,…,N.

Hitung fungsi jumlah kuadrat error dengan persamaan:

(18) Hitung matriks Jacobian untuk vektor bobot dan bias koneksi:

(19)

untuk r = 1,2,…N

a. Hitung matriks Hessian untuk vektor bobot dan bias koneksi.

(20)

b. Hitung perubahan vektor bobot dan bias dengan persamaan berikut:

(21)

c. Hitung vektor bobot dan bias baru.

(22)

d. Hitung kesalahan yang terjadi oleh bobot dan bias koneksi yang baru.

(23)

e. Bandingkan E(w) dengan E(w(baru)).

 Jika E(w) <= E(w(baru)) maka didapatkan dan kembali ke langkah a.

 Jika E(w) > E(w(baru)) maka didapatkan

(24)

(25)

Kembali ke langkah 2.

2.4 K-fold Cross Validation

K-fold cross validation dilakukan untuk membagi training set dan test set. K-fold cross validation mengulang k-kali untuk membagi sebuah himpunan contoh secara acak menjadi k subset yang saling bebas, setiap ulangan disisakan satu subset untuk pengujian dan subset lainnya untuk pelatihan (Tang et al 2008).

2.5 Jarak Euclid

Jarak Euclid adalah jarak antara dua titik dalam runag Euclid. Jarak Euclid didefinisikan sebagai berikut:

(26)

(34)

Data yang digunakan dalam penelitian ini adalah data curah hujan untuk Kabupaten Indramayu yang terdiri dari dua (2) data, yaitu (1) data lauaran GCM yang diperoleh dari hasil kerjasama antara BMKG, Institut Pertanian Bogor (IPB) dan International Research Institute (IRI) terdiri dari tahun 1901 – 2000. , dan (2) data observasi yang diambil dari stasiun hujan yang berada di wilayah Indramayu sebanyak 13 stasiun yang terdiri dari 22 tahun yaitu tahun 1979 sampai dengan tahun 2000. Data Mode GCM yang digunakan beserta negara asal pembuatnya dapat dilihat pada Tabel 2.

Tabel 2 Model GCM dan negara pembuatnya

Nama Model GCM Negara Pembuat

Pacific_20c3m_cgcm3.1_t47, Canada

Stasiun observasi curah hujan yang digunakan dalam penelitian ini adalah sebagai berikut, stasiun Bangkir, Bondan, Cidempet, Cikedung, Jatibarang, Jatinyuat, Kedokan Bunder, Krangkeng, Lohbener, Sudikampiran, Sudimampir, Sukadana, dan Sumurwatu.

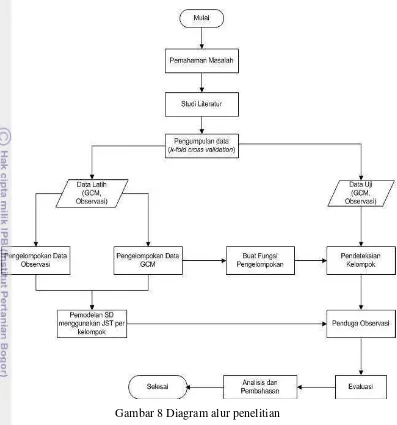
3.2 Metode Penelitian

(35)

Gambar 8 Diagram alur penelitian

(36)

Tabel 3 Pembagian data latih dan data uji.

(37)

Gambar 9 Ilustrasi pengambilan data GCM 5x5.

(a)

(b)

(38)

Setelah semuanya terbagi menjadi lima kelompok, maka dilakukan proses JST berdasarkan kelompok sehingga hasil yang didapat adalah lima model JST yaitu JST untuk kelompok sangat rendah, rendah, sedang, tinggi, dan sangat tinggi. Data GCM berperan sebagai masukan untuk JST, dan data observasi berperan sebagai targetnya dan jumlah hidden layer yang diujicobakan adalah 50 dan 100. Struktur JST yang digunakan dapat dilihat pada Gambar 11.

Gambar 11 Struktur JST yang akan digunakan.

Setelah data untuk pelatihan proses JST telah selesai dilakukan, maka akan dilakukan proses untuk pengujian JST. Data uji yang akan digunakan adalah data GCM dan data observasi selama 2 periode (tahun) yaitu sebanyak 24 buah baris data. Penentuan kelompok ini menggunakan metode jarak Euclid. Data yang digunakan untuk menghitung jarak Euclid adalah data GCM untuk pengujian. Data GCM ini akan dihitung dengan masing-masing data GCM yang terdapat pada setiap kelompok pada data latih. Tujuan dari pengelompokkan ini adalah untuk menentukan model JST yang akan dipakai dalam tahap pengujian. Apabila data GCM untuk pengujian ini lebih dekat jaraknya dengan data GCM kelompok rendah, maka satu baris data GCM untuk pengujian ini dan data observasinya akan masuk ke kelompok rendah dan akan diuji menggunakan JST untuk kelompok rendah.

(39)

Setelah melakukan evaluasi, tahap dokumentasi akan dilakukan sampai penelitian ini selesai.

3.3 Lingkup Pengembangan Sistem

Perangkat keras yang digunakan berupa Personal Computer (PC) dengan spesifikasi:

 processor: Intel Core i5 3.20 GHz,

 memori: 2 GB, dan

 harddisk: 500 GB.

Perangkat lunak yang digunakan yaitu:

 sistem operasi: Windows 7 Ultimate,

 Matlab 7.7.0, dan

(40)

Percobaan pada penelitian ini dilakukan dengan menggunakan metode pelatihan jaringan saraf tiruan (JST) backpropagation dengan jumlah neuron pada hidden layer sebanyak 50 dan 100 buah neuron. Terdapat dua buah model JST yang digunakan dalam penelitian ini, pertama model JST menggunakan jumlah neuron pada hidden layer sebanyak 50 dan 100 dengan parameter menggunakan algoritma pelatihan Levenberg-Marquardt dan nilai gradien minimum sebesar

_{untuk selanjutnya disebut JST-1, sedangkan yang kedua, model JST}

menggunakan jumlah neuron pada hidden layer sebnayak 50 dan 100 dengan menggunakan parameter algoritma pelatihan Levenberg-Marquardt dan nilai gradien minimum sebesar , untuk selanjutnya disebut JST-2.

Jumlah neuron hidden layer pada percobaan ini pertama kali dilakukan dengan jumlah 50 dan 100 buah. Jumlah ini digunakan hanya untuk melihat terlebih dahulu jumlah neuron hidden layer mana yang terbaik pada penelitian ini. Setelah dilakukan percobaan, maka dihasilkan jumlah dengan neuron hidden layer sebanyak 100 buah lebih baik dari 50 buah. Hasil ini dapat dilihat dari rataan nilai NRMSE dan korelasi pada setiap model JST (JST-1 dan JST-2) untuk jumlah neuron hidden layer 50 dan 100 (Tabel 4). Dengan demikian percobaan selanjutnya untuk setiap model luaran GCM hanya menggunakan jumlah neuron hidden layer sebanyak 100 buah.

Tabel 4 Rataan nilai NRMSE dan korelasi pada hidden layer 50 dan 100

(41)

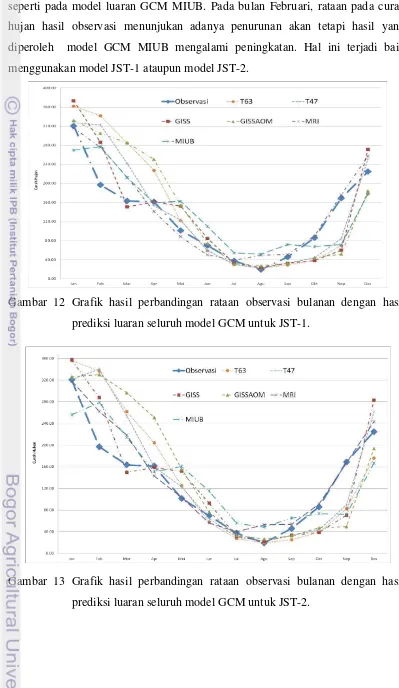
langsung meskipun ada beberapa model GCM yang menunjukan hal sebaliknya, seperti pada model luaran GCM MIUB. Pada bulan Februari, rataan pada curah hujan hasil observasi menunjukan adanya penurunan akan tetapi hasil yang diperoleh model GCM MIUB mengalami peningkatan. Hal ini terjadi baik menggunakan model JST-1 ataupun model JST-2.

Gambar 12 Grafik hasil perbandingan rataan observasi bulanan dengan hasil prediksi luaran seluruh model GCM untuk JST-1.

(42)

Untuk bulan Januari, model yang dihasilkan JST dengan menggunakan model luaran yang dapat mendekati hasil observasi adalah MRI untuk JST-1 dan CGCM_T47 untuk JST-2. Pada bulan Februari, hasil prediksi yang mendekati haasil observasi adalah model luaran GCM MRI untuk kedua model JST. Pada bulan Maret, model luaran GCM GISS untuk kedua model JST mendekati dengan hasil observasi. Untuk bulan April, model luaran GCM yang mendekati hasil observasi adalah GISS untuk JST-1 dan CGCM_T47 untuk JST-2. Pada bulan Mei, model luaran MRI untuk JST-1dan JST-2 berhasil mendekati hasil observasi. Pada bulan Juni, model luaran GCM GISSAOM untuk JST-1 dan CGCM_T47 untuk JST-2 berhasil mendekati dengan hasil observasi. Pada bulan Juli, September, Oktober, dan Nopember hasil luaran GCM MRI dengan kedua model JST berhasil mendekati hasil observasi. Sedangkan pada bulan Agustus, nilai hasil prediksi JST dengan luaran GCM CGCM_T63 berhasil mendekati nilai hasil observasi. Pada bulan Desember, nilai hasil observasi berhasil didekat oleh model luaran GCM CGCM_T47 untuk JST-1 dan GCM MRI untuk model JST-2. Hasil tersebut menunjukkan bahwa prediksi curah hujan setiap bulan dapat didekati dengan menggunakan model luaran GCM yang berbeda.

Hasil grafik jika seluruh nilai prediksi yang dihasilkan JST-1 dan JST-2 dengan rataan hasil enam model GCM Gambar 14 dan Gambar 15 untuk seluruh periode (22 tahun) serta Gambar 16 dan Gambar 17 untuk rataan bulanan dalam periode tersebut.

(43)

Gambar 15 Grafik perbandingan hasil rataan prediksi seluruh GCM dengan rataan hasil observasi curah hujan menggunakan model JST-2.

(44)

Gambar 17 Grafik perbandingan rataan bulanan hasil prediksi seluruh GCM dengan rataan bulanan hasil observasi curah hujan menggunakan model JST-2.

Rataan nilai korelasi dan nilai NRMSE untuk hasil prediksi menggunakan JST-1 dan JST-2 hampir sama. Rataan nilai korelasi untuk JST-1 adalah 0.427 dan untuk JST-2 adalah 0.423. Sedangkan untuk rataan nilai NRMSE pada JST-1 adalah 12.167 dan pada JST-2 adalah 12.191. Karena rataan nilai korelasi dan NRMSE pada JST-1 sedikit lebih baik dari JST-2 maka akan dibahas hasil dari setiap stasiun dengan menggunakan JST-1. Perbedaan antara JST-1 dan JST-2 adalah JST-2 memerlukan lebih banyak waktu pelatihan dibandingkan dengan JST-1. Hal ini dikarenakan parameter yang diubah adalah parameter gradien minimum. Parameter gradien minimum merupakan salah satu parameter untuk memberhentikan pelatihan pada JST. Jika parameter ini diperkecil, maka pelatihan tidak akan berhenti sampai mencapai nilai gradien minimum yang telah ditentukan.

4.2 Hasil Prediksi Untuk Setiap Stasiun Hujan

(45)

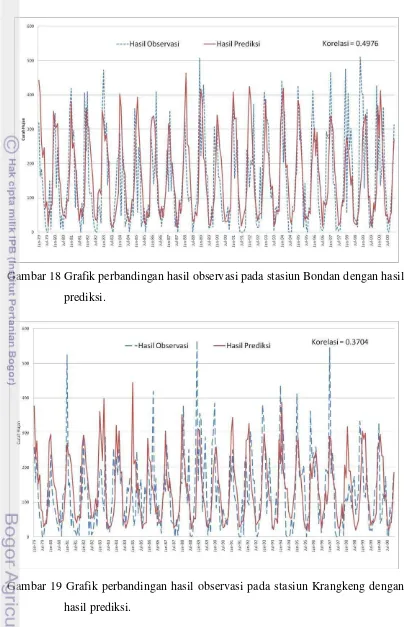
sebesar 0.4976 dan hasil yang terendah diperoleh stasiun Krangkeng dengan nilai korelasi sebesar 0.3704.

Tabel 5 Rataan korelasi setiap stasiun

Stasiun Rataan Korelasi

(46)

Gambar 18 Grafik perbandingan hasil observasi pada stasiun Bondan dengan hasil prediksi.

Gambar 19 Grafik perbandingan hasil observasi pada stasiun Krangkeng dengan hasil prediksi.

(47)

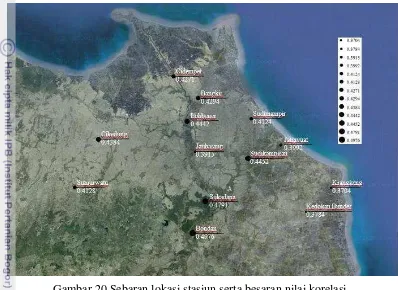
korelasi yang rendah. Sebaliknya, lokasi pengamatan yang jauh dari laut (Bangkir, Cidempet, Lohbener, Sukadana, Bondan, Sudikmapiran, Cikedung) cenderung memiliki nilai korelasi yang lebih tinggi. Peta sebaran lokasi beserta besar kecilnya nilai korelasi dapat dilihat pada Gambar 20.

(48)

Kesimpulan dari penelitian ini adalah hasil yang didapatkan dapat menunjukkan bahwa beberapa model GCM dapat mendekati nilai rataan curah hujan bulanan. Hasil prediksi yang paling bagus diperoleh stasiun Bondan dengan nilai korelasi sebesar 0.4976 dan nilai korelasi terendah diperoleh stasiun Krangkeng dengan nilai korelasi sebesar 0.3704. Lokasi pengamatan cenderung berpengaruh dengan hasil prediksi. Jika lokasi pengamatan berada dekat dengan laut, maka nilai korelasi cenderung rendah sedangkan jika lokasi pengamatan berada jauh dari laut, maka nilai korelasi yang dihasilkan cenderung lebih besar.

Hasil yang didapatkan cenderung mengikuti pola yang dihasilkan oleh data observasi. Akan tetapi masih terdapat kelemahan, yaitu pada beberapa titik ekstrim, hasil prediksi tidak dapat mencapai nilai ekstrim tersebut.

5.2 Saran

(49)

Abdi H. 2007. Distance. Neil Salkind (Ed.) (2007). Encyclopedia of Measurement and Statistics, The University of Texas: Dallas.

Aldrian E, Gates, Lydia D, Widodo FH. 2003. Variability of Indonesian Rainfall and the Influence of ENSO and Resolution in ECHAM4 Simulations and in the Reanalyses. Max Planck Institute for Meteorology.

Beale Mark Hudson, Hagan Martin T, Demuth Howard B. 2011. Neural Network

ToolBox User’s Guide. The MathWorks, Inc: United States.

Buono, A. et al. 2010. A Neural Network Architecture for Statistical Downscaling Technique : A Case Study in Indramayu District. Dipublikasi dalam International Conference, The Quality Information for Competitive

Agricultural Based Production System and Commerce (AFITA). http://repository.ipb.ac.id/handle/123456789/41728 [23 Mei 2011].

Cawley GC, Haylock M, Dorling SR, Goodess C, Jones PD. 2003. Statistical Downscaling with Artificial Neural Networks. U.K: University of East Anglia, Norwich. ESANN'2003 proceedings - European Symposium on Artificial Neural Networks Bruges (Belgium), 23-25 April 2003, d-side publi., ISBN 2-930307-03-X, pp. 167-172.

Hagan Martin T, Mohammad B Menhaj. 1994. Training Feedforward with the Marquardt Algorithm. IEEE Transactions On Neural Networks, Vol. 5, No. 6, November.

Hermawan A. 2006. Jaringan Saraf Tiruan Teori dan Aplikasi. Penerbit Andi: Yogyakarta.

Puspitaningrum D. 2006. Pengantar Jaringan Saraf Tiruan. Penerbit Andi: Yogyakarta.

Tang Lei, Payam Rafaelizadeh, Huan Liu. 2008. Cross-Validation. Arizona State University: USA.

(50)

Sutikno. 2008. Statistical Downscaling Luaran GCM dan Pemanfaatannya untuk Peramalan Produksi Padi.. Disertasi. Institut Pertanian Bogor, Bogor.

Warsito Budi, Sri Sumiyati. 2007. Prediksi Curah Hujan Kota Semarang Dengan Feedforward Neural Network Menggunakan Algoritma Quasi Newton BFGS Dan Levenberg-Marquardt. Jurnal Presipitasi Vol. 3 No. 2 September 2007, ISSN 1907-187X.

(51)

(52)

(53)

Lampiran 2 Plot hasil prediksi dan observasi curah hujan bulanan berdasarkan luaran GCM untuk model JST-1 dan JST-2.

Gambar 21 Perbandingan antara pola observasi dan prediksi curah hujan untuk seluruh luaran GCM (rataan, minimum, dan maksimum) untuk model JST-1

(54)

ABSTRACT

MUHAMMAD RAFI MUTTAQIN. Downscaling Methodology Development

Using Arftificial Neyral Network (Case Study of Indramayu’s Rainfall). Under direction of AGUS BUONO as chairman and AZIZ KUSTIYO as member of advisory commitee.

The unexpected climate change results a long period wet and dry so it makes many agricultural areas damage. This is cause the farmers failed to harvest so the production of food will be decreased. To solve this problem, we need a model that can estimate the climate and rainfall so it can determine the suitable cropping pattern with the climate. Statistical downscaling modeling commonly used to model the changes of the weather. This study develops a statistical downscaling model that use artificial neural network with some of GCM data as an input in training. In this study, the GCM data is input for training. Before training this data is grouped into 5 groups. The results obtained indicate that some of the GCM can approach the average of monthly rainfall. However, in some extreme point, the result have not managed to reach and close to results of observation. The best results obtained with the correlation Bondan station at 0.4976 and the worst results obtained Krangkeng station with a correlation of 0.3704. In this study also can be seen that the estimators can be influenced by the location of the observation. The location is adjacent to the sea tend to have the results of a relatively lower correlation compared with the location that far from the sea.

(55)

Peristiwa iklim ekstrim terkait El Niño-Southern Oscillation (ENSO) telah menimbulkan dampak yang signifikan pada sektor pertanian di Indonesia. Pada peristiwa ENSO hangat atau biasa dikenal dengan istilah El Niño, biasanya terjadi penundaan awal musim hujan dan bertambah panjangnya musim kemarau (Kirono et al. 1999; Moron et al. 2009). Peristiwa El Niño seringkali dikaitkan dengan meluasnya kekeringan di berbagai daerah yang menyebabkan turunnya produksi pertanian karena kurangnya persediaan air. Sebaliknya, pada periode ENSO dingin, atau dikenal dengan istilah La Niña, kejadian hujan meningkat melebihi kondisi rata-rata sehingga meningkatkan peluang terjadinya banjir di berbagai daerah di Indonesia. Implikasinya pada sektor pertanian ialah semakin meningkatnya wilayah persawahan yang tergenang banjir dan merusak tanaman, sehingga menyebabkan meningkatnya kemungkinan gagal panen.

Akibat perubahan iklim ekstrim di bidang pertanian, maka harus dihadapi dengan penuh perencanaan dan melibatkan berbagai pihak terkait, baik pemerintah setempat sampai masyarakatnya. Sayangnya, hingga saat ini penggunaan informasi iklim dalam mengelola resiko iklim masih belum umum. Dalam hal ini, penyediaan informasi iklim yang efektif dan tepat guna sangat perlu untuk terus dievaluasi dan dikembangkan, sebab peruabahan iklim dapat memberikan dampak yang lebih besar dalam bidang pertanian. Oleh karena itu, perencanaan yang menyeluruh baik jangka pendek maupun jangka panjang sangat diperlukan. Hal ini merupakan tantangan yang cukup besar terutama dalam konteks aplikasi pengelolaan resiko iklim (climate risk management, CRM).

(56)

tersebut, masing-masing memiliki kelebihan dan kekurangan dan juga memiliki tingkat kemampuan prediksi yang mungkin berbeda pada suatu wilayah tertentu.

Perubahan iklim di masa yang akan datang akibat peningkatan suhu global diproyeksikan dapat menciptakan pergeseran pola iklim sehingga memungkinkan terjadinya peningkatan peluang resiko khususnya di sektor pertanian. Untuk mengatasi hal ini diperlukan perencanaan jangka panjang melibatkan analisis iklim berdasarkan pilihan-pilihan skenario yang mungkin terjadi di masa depan. Perubahan iklim juga diantisipasi dapat mengubah rentang iklim, meningkatkan frekuensi dan amplitudo kejadian iklim ekstrim, dan pergeseran kondisi iklim regional hingga lokal. Perubahan iklim regional/lokal ini bisa bersifat spesifik antar daerah sehingga membutuhkan data dengan resolusi cukup tinggi yang tidak bisa didapat dari data luaran general circulation model (GCM) yang memiliki resolusi horizontal yang sangat rendah. Oleh karena itu untuk mendapatkan informasi dengan resolusi yang cukup tinggi, diperlukan pemanfaatan teknik downscaling. Metode downscaling dengan pendekatan dinamik dapat dilakukan dengan menggunakan simulasi model iklim regional (regional climate model, RCM) yang disimulasi berdasarkan informasi data GCM.

(57)

1.2 Perumusan Masalah

Berdasarkan latar belakang tersebut model GCM mempunyai banyak sekali informasi yang dapat dimanfaatkan untuk peramalan iklim. Akan tetapi model GCM ini memiliki resolusi horisontal yang sangat rendah sehingga diperlukan teknik downscaling untuk mendapatkan resolusi yang cukup tinggi. Dengan resolusi yang cukup tinggi, maka informasi dalam GCM yang ada dapat diperoleh.

Berdasarkan penelitian sebelumnya (Buono, 2010), pemodelan curah hujan dengan data GCM dengan teknik downscaling menggunakan JST kurang dapat mewakili data observasi. Oleh karena itu, dalam studi ini akan dikembangkan metodologi downscaling menggunakan JST dengan pengelompokan data terlebih dahulu sebelum dilakukan pelatihan. Hal ini diharapkan dapat memperbaiki pola yang dihasilkan oleh penelitian sebelumnya.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah mengembangkan JST untuk melakukan downscaling dari data GCM curah hujan bulanan (studi kasus Indramayu). Oleh karena itu, penelitian ini diharapkan dapat memperbaiko model yang telah dihasilkan oleh penelitian sebelumnya.

1.4 Manfaat Penelitian

Manfaat yang diharapkan dari hasil penelitian ini adalah para pihak terkait dapat mengantisipasi perubahan curah hujan sejak dini. Dengan demikian model ini dapat menjadi bahan pertimbangan petani atau pengelola perkebunan dalam menentukan tanaman apa yang cocok untuk kondisi iklim pada masa yang akan datang.

1.5 Ruang Lingkup Penelitian

Ruang lingkup dari penelitian ini adalah sebagai berikut:

 data curah hujan yang digunakan adalah data yang berasal dari stasiun hujan yang berada di daerah Indramayu (13 stasiun) dari tahun 1979 - 2002.

(58)

Model sirkulasi umum atau general circulation model (GCM) merupakan suatu penggambaran matematis dari sejumlah besar interaksi fisika, kimia, dan dinamika atmosfer bumi (Von Stroch et al. 1993 dalam Sutikno 2008). GCM ini menduga perubahan iklim dan disajikan tiga layer, yaitu layer horisontal dengan ukuran 100 hingga 600 km, 10 hingga 20 layer vertikal di atmosfer dan kadangkala 30 layer di samudra, seperti disajikan pada Gambar 1.

Dengan resolusi yang begitu kasar, maka GCM tidak bisa menangkap fitur penting pada suatu area (region) tertentu yang menjadi fokus kajian dampak perubahan iklim. Namun demikian, GCM ini bisa dijalankan (di-run) untuk mengestimasi kepekaan iklim terhadap kondisi yang berbeda seperti perubahan gas rumah kaca (GRK). Oleh karena itu, model GCM memberikan beberapa keuntungan seperti tertera pada Sutikno (2008), yaitu : (1) dapat digunakan untuk mengestimasi perubahan iklim global dalam merespon terhadap peningkatan konsentrasi GRK, (2) estimasi peubah iklim (curah hujan, suhu, kelembaban) secara fisik sesuai dengan model-model fisika, (3) estimasi peubah cuaca (angin, radiasi, penutupan awan, kelembaban tanah) yang berikutnya menjadi masukan bagi analisis mengenai dampak, (4) mampu menyimulasi keragaman iklim siklus harian. Disamping kelebihan seperti disebutkan di atas, beberapa kelemahannya adalah : (1) resolusi terlalu kasar, sehingga terjadi gap antara hasil simulasi global, regional dan lokal, (2) model tersebut sulit mengkopel dengan model-model sirkulasi lautan, dan (3) proses-proses umpan balik atmosfer-biosfer tidak terpenuhi. Untuk menjembatani gap antara hasil global dengan regional dan lokal, maka diperlukan satu model yang dikenal dengan nama downscaling.

(59)

Indonesia adalah model dengan resolusi horisontal yang tinggi dan skema konveksi yang komprehensif (Sutikno 2008).

Tabel 1 Skala grid model-model GCM dan negara yang mengembangkannya

Nama GCM Skala Grid Negara

model 2: HadCM2

2,5° x 3,75° UK

model 3: HadCM3

2,5° x 3,75° UK

Canadian Global Coupled Model: CGCM2 3,7° x 3,7° Canada Geophysical Fluid Dynamic Laboratory: GFDL 2,25° x 3,75° NOAA,

USA NASA/GISS Atmosphere-Ocean Model:

NASA/GISS AOM

5° x 4° NASA,USA

United Kingdom Meteorological Office Model: UKMO

Sumber: Wetterhall (2002) diacu dalam Sutikno (2008)

(60)

input awal yang sedikit berbeda. Gambar 1 menunjukkan visualisasi layering pada GCM.

2.2 Downscaling

Downscaling didefinisikan sebagai upaya menghubungkan antara sirkulasi peubah skala global (peubah penjelas) dan peubah skala lokal (peubah respon, Sutikno 2008). Istilah downscaling sering salah jika diartikan secara tekstual yaitu suatu cara untuk meningkatkan resolusi. Downscaling lebih menunjukkan proses perpindahan dari peubah penjelas ke peubah respon, yaitu perpindahan dari skala besar ke skala kecil (regional/titik). Gambar 2 memberikan ilustrasi proses downscaling.

Pendekatan statistical downscaling (SD) menggunakan data regional (statistic dynamical downscaling) atau global (statistical downscaling) untuk

(61)

memperoleh hubungan fungsional antara skala lokal dengan skala global GCM, seperti model regresi. Pendekatan SD disusun berdasarkan adanya hubungan antara grid skala besar (prediktor) dengan grid skala lokal (respon) yang dinyatakan dengan model statistik yang dapat digunaan untuk menterjemahkan anomali-anomali skala global yang menjadi anomali dari beberapa peubah iklim lokal (Zorita dan Storch 1999, dalam Wigena 2006). Dalam hal ini SD merupakan suatu fungsi transfer yang menggambarkan hubungan fungsional sirkulasi atmosfer global dengan unsur-unsur iklim lokal, yang bentuk umumnya adalah :

(62)

2.3 Jaringan Saraf Tiruan (Neural Network)

Jaringan saraf tiruan (JST) merupakan salah satu sistem pemrosesan informasi yang didesain dengan menirukan cara kerja otak manusia dalam menyelesaikan suatu masalah dengan melakukan proses belajar melalui perubahan bobot sinapsisnya. Jaringan saraf tiruan mampu mengenali kegiatan dengan berbasis data pada masa lalu. Data masa lalu akan dipelajari oelh jaringan saraf tiruan sehingga mempunyai kemampuan untuk memberi keputusan terhadap data yang belum pernah dipelajari (Hermawan 2006).

Jaringan saraf tiruan didefinisikan sebagai suatu system pemerosesan informasi yang mempunyai karakteristik menyerupai jaringan saraf manusia. JST tercipta sebagai suatu generalisasi model matematis dari pemahaman manusia (human cognition) yang didasarkan atas asumsi sebagai berikut:

1 Pemrosesan informasi terjadi pada elemen sederhana yang disebut neuron (Gambar 3).

2 Isyarat mengalir di antara sel saraf/neuron melalui suatu sambungan penghubung,

3 Setiap sambungan penghubung memiliki bobot yang bersesuaian. Bobot ini akan digunakan untuk menggandakan/mengalikan isyarat yang akan dikirim melaluinya.

4 Setiap sel saraf akan menerapkan fungsi aktivasi terhadap isyarat hasil penjumlahan berbobot yang masuk kepadanya untuk menentukan isyarat keluarannya.

Gambar 3 Sel neuron pada manusia

(63)