Lampiran A-1
Listing Tampilan Menu Utama
using System;
public partial class FormUtama : Form {
public FormUtama() {
InitializeComponent(); }
private void enkripsiToolStripMenuItem_Click(object sender, EventArgs e) {
Enkripsi frm = new Enkripsi(); //frm.MdiParent = this;
frm.Show(); }
private void dekripsiToolStripMenuItem_Click(object sender, EventArgs e) {
Dekripsi frm = new Dekripsi(); //frm.MdiParent = this;
frm.Show(); }
private void FormUtama_Load(object sender, EventArgs e) {
//byte[] asli = new byte[16] { 0x32, 0x88, 0x31, 0xe0, 0x43, 0x5a, 0x31, 0x37, 0xf6, 0x30, 0x98, 0x07, 0xa8, 0x8d, 0xa2, 0x34 };
//byte[] key = new byte[16] { 0x2b, 0x28, 0xab, 0x09, 0x7e, 0xae, 0xf7, 0xcf, 0x15, 0xd2, 0x15, 0x4f, 0x16, 0xa6, 0x88, 0x3c };
Lampiran A-2
//}
//Console.WriteLine("cipher teks = " + s); //s = "";
//for (int i = 0; i < 16; i++) //{
// s += decipher[i].ToString("x2") + " "; //}
//Console.WriteLine("decipher teks = " + s); }
private void exitToolStripMenuItem_Click(object sender, EventArgs e) {
this.Close(); }
private void label1_Click(object sender, EventArgs e) {
}
private void aboutToolStripMenuItem_Click(object sender, EventArgs e) {
About frm = new About(); //frm.MdiParent = this; frm.Show();
Lampiran A-3
public partial class Enkripsi : Form {
private BigInteger E, n, d; private Rijndael rij; private RSA rsa;
private String lokasiFileBuka = ""; private String statusSimpan = ""; public Enkripsi()
{
InitializeComponent(); }
private void Form1_Load(object sender, EventArgs e) {
}
private void button1_Click(object sender, EventArgs e) {
if (txtTeks.Text != "" || txtKey.Text != "") {
int panjangEnkripsi = 0; int penanda = 0;
panjangEnkripsi = (int)Math.Ceiling(((double)txtTeks.Text.Length / 16)); byte[] asli = new byte[16];
byte[] key = Encoding.ASCII.GetBytes(txtKey.Text.PadRight(16, ' '));
rij = new Rijndael(key);
for (int i = 0; i < panjangEnkripsi; i++) {
string teksTemp = "";
if (i == panjangEnkripsi - 1) {
int berapaBykPotong = txtTeks.Text.Length - penanda; teksTemp = txtTeks.Text.Substring(penanda,
berapaBykPotong);
teksTemp = teksTemp.PadRight(16, ' '); }
else
{
teksTemp = txtTeks.Text.Substring(penanda, 16); }
Lampiran A-4
private void btnEnkripKey_Click(object sender, EventArgs e) {
if (txtKey.Text != "") {
private void button1_Click_1(object sender, EventArgs e) {
private void openFileDialog1_FileOk(object sender, CancelEventArgs e) {
System.IO.Stream strm; strm = openFileDialog1.OpenFile();
lokasiFileBuka = openFileDialog1.FileName.ToString();
System.IO.FileStream inp = System.IO.File.OpenRead(lokasiFileBuka); System.IO.StreamReader input = new System.IO.StreamReader(inp); try
{
while (input.Peek() > -1) {
string teks = input.ReadToEnd();
Lampiran A-5
}
private void btnSimpan_Click(object sender, EventArgs e) {
private void saveFileDialog1_FileOk(object sender, CancelEventArgs e) {
if (statusSimpan == "rijndael") {
StringBuilder sb = new StringBuilder(); sb.Append(txtTeksEnk.Text);
using (StreamWriter outfile = new StreamWriter(saveFileDialog1.FileName, false))
else if (statusSimpan == "rsa") {
String teksYangInginDisimpan = "";
teksYangInginDisimpan += txtKeyEnk.Text + Environment.NewLine; teksYangInginDisimpan += d.ToString() + Environment.NewLine; teksYangInginDisimpan += n.ToString();
StringBuilder sb = new StringBuilder(); sb.Append(teksYangInginDisimpan);
using (StreamWriter outfile = new StreamWriter(saveFileDialog1.FileName, false))
private void button2_Click(object sender, EventArgs e) {
Lampiran A-6
private void button3_Click(object sender, EventArgs e) {
private void button4_Click(object sender, EventArgs e) {
public partial class Dekripsi : Form {
private RSA rsa; private Rijndael rij;
private String statusBukaFile = ""; public Dekripsi()
{
InitializeComponent(); }
private void button2_Click(object sender, EventArgs e) {
}
private void Dekripsi_Load(object sender, EventArgs e) {
Lampiran A-7
private void btnEnkripKey_Click(object sender, EventArgs e) {
if (txtKeyEnk.Text != "" || txtD.Text != "" || txtN2.Text != "") {
private void btnEnkripTeks_Click(object sender, EventArgs e) {
if (txtKey.Text != "" || txtTeksEnk.Text != "") {
int panjangEnkripsi = 0; int penanda = 0;
panjangEnkripsi = (int)Math.Ceiling(((double)txtTeksEnk.Text.Length / 16)); byte[] cipher = new byte[16];
byte[] key = Encoding.ASCII.GetBytes(txtKey.Text.PadRight(16, ' '));
rij = new Rijndael(key);
for (int i = 0; i < panjangEnkripsi; i++) {
int len = txtTeksEnk.Text.Length;
string teksTemp = txtTeksEnk.Text.Substring(penanda, 16); int z = 0;
foreach (char c in teksTemp) {
cipher[z] = (byte)System.Convert.ToInt32(c); z++;
}
byte[] decipher = rij.dekripsi(cipher); for (int j = 0; j < decipher.Length; j++)
//byte[] cipher = new byte[txtTeksEnk.Text.Length];
//byte[] key = Encoding.ASCII.GetBytes(txtKey.Text.PadRight(16, ' '));
//rij = new Rijndael(key); //int z = 0;
//foreach (char c in txtTeksEnk.Text) //{
// cipher[z] = (byte)System.Convert.ToInt32(c); // z++;
//}
//byte[] decipher = rij.dekripsi(cipher);
//for (int i = 0; i < decipher.Length; i++)
Lampiran A-8
private void button2_Click_1(object sender, EventArgs e) {
private void openFileDialog1_FileOk(object sender, CancelEventArgs e) {
if (statusBukaFile == "rijndael") {
while (input.Peek() > -1) {
string teks = input.ReadToEnd();
txtTeksEnk.Text = teks;
else if (statusBukaFile == "rsa") {
System.IO.Stream strm; strm = openFileDialog1.OpenFile();
System.IO.FileStream inp =
System.IO.File.OpenRead(openFileDialog1.FileName.ToString()); System.IO.StreamReader input = new System.IO.StreamReader(inp); int indeks = 0;
try
{
while (input.Peek() > -1) {
string teks = input.ReadLine(); if (indeks == 0)
Lampiran A-9
private void groupBox2_Enter(object sender, EventArgs e) {
}
Lampiran A-10
public byte[] enkripsi(byte[] teks) {
byte[] hasil = new byte[16];
this.State = new byte[4, 4];
for (int putaran = 1; putaran < 10; putaran++) {
Lampiran A-11
{
byte[] hasil = new byte[16];
this.State = new byte[4, 4];
for (int putaran = 9; putaran >= 1; putaran--) {
public void addRoundKey(int putaran) {
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
this.State[i, j] = (byte)((int)this.State[i, j] ^ (int)this.w[putaran, i, j]);
this.State[i, j] = this.Sbox[(this.State[i, j] >> 4), (this.State[i, j] & 0x0f)];
}
this.State[i, j] = this.iSbox[(this.State[i, j] >> 4), (this.State[i, j] & 0x0f)];
Lampiran A-12 (int)gfmultby01(temp[2, i]) ^ (int)gfmultby01(temp[3, i]));
this.State[1, i] = (byte)
((int)gfmultby01(temp[0, i]) ^ (int)gfmultby02(temp[1, i]) ^ (int)gfmultby03(temp[2, i]) ^ (int)gfmultby01(temp[3, i]));
Lampiran A-13
((int)gfmultby01(temp[0, i]) ^ (int)gfmultby01(temp[1, i]) ^ (int)gfmultby02(temp[2, i]) ^ (int)gfmultby03(temp[3, i]));
this.State[3, i] = (byte)
((int)gfmultby03(temp[0, i]) ^ (int)gfmultby01(temp[1, i]) ^ (int)gfmultby01(temp[2, i]) ^ (int)gfmultby02(temp[3, i]));
}
this.State[0, i] = (byte)
((int)gfmultby0e(temp[0, i]) ^ (int)gfmultby0b(temp[1, i]) ^ (int)gfmultby0d(temp[2, i]) ^ (int)gfmultby09(temp[3, i]));
this.State[1, i] = (byte)
((int)gfmultby09(temp[0, i]) ^ (int)gfmultby0e(temp[1, i]) ^ (int)gfmultby0b(temp[2, i]) ^ (int)gfmultby0d(temp[3, i]));
this.State[2, i] = (byte)
((int)gfmultby0d(temp[0, i]) ^ (int)gfmultby09(temp[1, i]) ^ (int)gfmultby0e(temp[2, i]) ^ (int)gfmultby0b(temp[3, i]));
this.State[3, i] = (byte)
((int)gfmultby0b(temp[0, i]) ^ (int)gfmultby0d(temp[1, i]) ^ (int)gfmultby09(temp[2, i]) ^ (int)gfmultby0e(temp[3, i]));
} }
private static byte gfmultby01(byte b) {
return b; }
private static byte gfmultby02(byte b) {
if (b < 0x80)
return (byte)(int)(b << 1); else
return (byte)((int)(b << 1) ^ (int)(0x1b)); }
private static byte gfmultby03(byte b) {
return (byte)((int)gfmultby02(b) ^ (int)b); }
private static byte gfmultby09(byte b) {
return (byte)((int)gfmultby02(gfmultby02(gfmultby02(b))) ^ (int)b);
}
Lampiran A-14
private static byte gfmultby0d(byte b) {
return (byte)((int)gfmultby02(gfmultby02(gfmultby02(b))) ^ (int)gfmultby02(gfmultby02(b)) ^ (int)(b));
}
private static byte gfmultby0e(byte b) { 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76},
/*1*/ {0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0},
/*2*/ {0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15},
/*3*/ {0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75},
/*4*/ {0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84},
/*5*/ {0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf},
/*6*/ {0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8},
/*7*/ {0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2},
/*8*/ {0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73},
/*9*/ {0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb},
/*a*/ {0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79},
/*b*/ {0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08},
/*c*/ {0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a},
/*d*/ {0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e},
/*e*/ {0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf},
/*f*/ {0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16} };
}
Lampiran A-15 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb},
/*1*/ {0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb},
/*2*/ {0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e},
/*3*/ {0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25},
/*4*/ {0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92},
/*5*/ {0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84},
/*6*/ {0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06},
/*7*/ {0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b},
/*8*/ {0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73},
/*9*/ {0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e},
/*a*/ {0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b},
/*b*/ {0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4},
/*c*/ {0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f},
/*d*/ {0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef},
/*e*/ {0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61},
/*f*/ {0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d} };
}
Lampiran A-16
{
byte[] result = new byte[4];
result[0] = this.Sbox[word[0] >> 4, word[0] & 0x0f]; result[1] = this.Sbox[word[1] >> 4, word[1] & 0x0f];
result[2] = this.Sbox[word[2] >> 4, word[2] & 0x0f]; result[3] = this.Sbox[word[3] >> 4, word[3] & 0x0f]; return result;
}
private byte[] rotWord(byte[] word) {
byte[] result = new byte[4]; result[0] = word[1];
for (int putaran = 1; putaran < 11; putaran++) { (int)temp[i] ^ (int)Rcon[putaran-1, i]);
Lampiran A-17
public BigInteger e, n, d; public string cipher, decipher;
static Random random = new Random(DateTime.Now.Millisecond); public double waktuEnkripsi;
static BigInteger GenerateLargePrime(int length) {
Primality primality = new Primality(); string numbers = "";
for (int i = 0; i < length; i++) {
numbers += random.Next(0, 10); }
Lampiran A-18
public static BigInteger nilaiD(BigInteger ex, BigInteger totien) {
public void enkripsi(string teks) {
if (p.ToString().Length == q.ToString().Length && p < q) {
foreach (char c in teks) {
BigInteger a = BigInteger.ModPow(c, e, n); cipher += a.ToString() + " ";
}
Lampiran A-19
public void dekripsi(string teks) {
int i = 0; string s = ""; decipher = "";
while (i < teks.Length) {
if (teks.Substring(i, 1) != " ") {
s += teks.Substring(i, 1); }
else
{
BigInteger eS = BigInteger.Parse(s); BigInteger eD = (BigInteger)d; BigInteger eN = (BigInteger)n;
BigInteger a = BigInteger.ModPow(eS, eD, eN); if (a > 256)
a = a % 256; decipher += (char)a;
s = ""; }
i++;
71
DAFTAR PUSTAKA
[1] Ariyus, Doni. 2008. Pengantar Ilmu Kriptografi. penerbit Andi: Jogjakarta, Indonesia.
[2] Ariyus, Doni. 2006. Computer Security. Penerbit Andi: Yogyakarta.
[3] Arsendi. 2011. Penerapan Algoritma AES Rijndael Untuk Keamanan File
Audio. Skripsi. Universitas Sriwijaya.
[4] Joux, Antoni. 2009. Algorithmic Cryptonaysis. Taylor and Francis group: Boca Raton.
[5] Konheim, Alan G. 2007. Computer Security And Cryptography. John Wiley Publication.
[6] Smart, Nigel. 2004. Cryptography-An Introduction. 3rd edition.
[7] Munir, Rinaldi. 2006. Kriptografi. Bandung,Indonesia : penerbit informatika [8] Mollin, Richard A. 2007. An Introduction to Cryptography. second edition.
Taylor & Francis group: Boca Raton.
[9] Mollin, Richard A. 2005. Codes The Guide to Secrecy from Ancient to Modern
Times. Taylor & Francis Group, Llc.
[10] Rijmen,Daemen. 2002. The Design Of Rijndael: Springer.
[11] Sadikin, Rifki. 2012. Kriptografi untuk keamanan jaringan. Yogyakarta: Andi. [12] Schneier, Bruce. Applied Crytography. 2nd edition.
BAB 3
ANALISIS DAN PERANCANGAN SISTEM
3.1. Analisis Masalah
Jika A dan B mengirim sebuah pesan rahasia menggunakan algoritma kriptografi simetris, maka harus disepakati kunci yang akan digunakan, kunci tersebut nantinya dipakai untuk enkripsi dan dekripsi. Oleh sebab itu proses pertukaran kunci harus sangat dijaga keamanan nya. Jika ada pihak C yang mengetahui proses percakapan pada saat A dan B menyepakati kunci yang digunakan, maka C akan dengan mudah untuk mendekripsikan cipherteks dengan kuci tersebut.
Aplikasi yang akan dirancang terdiri dari dua buah algoritma yaitu Rijndael dan RSA. Utuk melakukan pengamanan data dilakukan dengan dua tahapan yaitu tahapan enkripsi plainteks dengan menggunakan algoritma simetris dan kemudian tahap enkripsi kunci simentris (session key) dengan menggunakan kunci publik, hal ini bertujuan untuk menjaga kerahasiaan kunci.
3.2. Analisis Sistem
3.2.1. Analisis kebutuhan perangkat lunak
Fitur-fitur utama yang disediakan perangkat lunak antara lain:
1. Fitur Encrypt
Perangkat lunak yang dibangun memiliki fitur enkripsi untuk memulai tahapan enkripsi terhadap plainteks dan cipherteks. Didalam fitur enkripsi ini terdapat
buttonopen, button enkripsi plainteks, button enkripsi sessionkey, button
savefile. Button open berfungsi untuk membuka file di dalam folder yang akan
diamankan atau bisa langsung melakukan penginputan plainteks pada form input plainteks. Button enkripsi plainteks berfungsi untuk menjalankan enkripsi setelah memasukkan key yang diinginkan. Button enkripsi sessionkey berfungsi untuk mengekripsiskan sessionkey menggunakan kunci publik yang telah disimpan atau dibangkitkan. Button SaveFile berfungsi untuk menyimpan
file cipherteks dan cipherkey ke dalam folder yang diinginkan.
2. Fitur dekripsi
Perangkat lunak yang dibangun memiliki fitur dekripsi untuk memulai tahapan dekripsi cipherteks dan cipherkey. Di dalam fitur dekripsi ini terdapat button
open, button dekripsi cipherteks, button dekripsi cipherkey, button SaveFile.
Button Open berfungsi untuk membuka file yang telah terenkripsi sebelumnya
di dalam folder. Button dekripsi cipherkey berfungsi untuk menjalankan dekripsi dengan menggunakan privetkey. Button dekripsin cipherteks berfungsi untuk mendekripsikan cipherteks dengan menggunakan sessionkey hasil dekripsi. Button SaveFile berfungsi untuk menyimpan file kedalam folder yang diinginkan.
3. Fitur pembangkitan kunci RSA
Pada perangkat lunak yang dibangun terdapat fitur pembangkitan kunci RSA secara acak, untuk menghasilkan kunci privat dan kunci publik. Pada saat
button enkripsi digunakan, maka sistem akan secara otomatis membangkitkan
3.2.2. Analisis kebutuhan fungsional dan non-fungsional sistem
Kebutuhan fungsional yang harus dipenuhi agar sistem berjalan dengan lancar:
1. Sistem dapat membuka file apabila file yang diambil dari dalam folder adalah file berupa *.txt.
2. Sistem dapat melakukan enkripsi plainteks dengan menggunakan algoritma Rinjdael dan melakukan enkripsi terhadap sessionkey dengan menggunakan kunci publik RSA.
3. Sistem dapat melakukan dekripsi cipherteks dengan menggunakan algoritma Rinjdael dan melakukan dekripsi cipherkey dengan menggunakan kunci publik RSA.
4. Sistem mampu melakukan pembangkitan kunci yang kemudian menyimpan kunci yang telah dibangkitkan
5. Sistem dapat menyimpan file yang dienkripsi dan didekripsi dalam bentuk
file *.txt.
6. Sistem dapat melakukan reset terhadap file dan key yang telah diinputkan untuk menggantikan file dan key yang baru.
Kebutuhan non-fungsional terhadap sistem adalah:
1. Sistem yang dibangun memiliki interface yang menarik dan mudah dimengerti oleh user.
2. Sistem yang dibangun tidak membutuhkan banyak biaya karena tidak menggunakan perangkat keras sebagai pendukung.
3.3.Perancangan Sistem
Perancangan sistem merupakan tahapan untuk membangun kerangka sistem yang akan dibuat. Tahapan ini nantinya akan menghasilkan gambaran dasar dari sistem yang akan dibangun. Perancangan dilakukan berdasarkan hasil analisis yang telah dilakukan pada bab sebelumnya.
3.3.1. Skema kosep dasar perancangan sistem
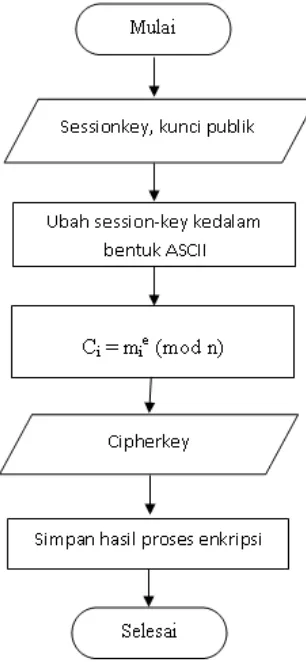
Berikut ini adalah diagram konsep yang akan dilakukan pada tugas akhir ini, diagram konsep ini akan mempermudah dalam perancang sistem yang akan dibuat. Pada tahap awal plainteks terlebih dahulu diproses dengan menggunakan algoritma Rijndael untuk melakukan enkripsi terhadap plainteks kemudian dilanjutkan dengan enkripsi terhadap sessionkey menggunakan algoritma RSA. Hasil akhir dari proses ini akan menghasilkan cipherteks dan cipherkey.
Gambar 3.1 Konsep Perancangan Proses Pengamanan
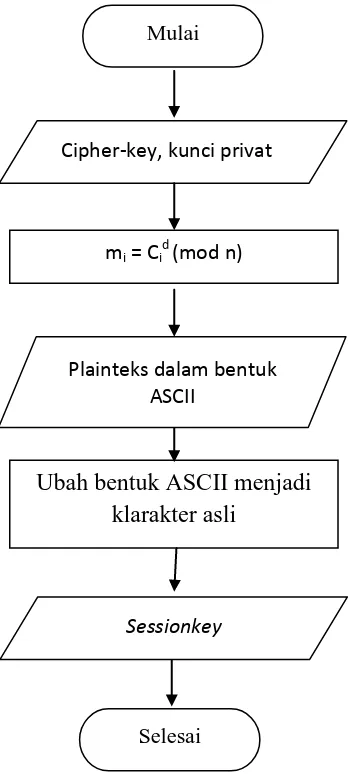
Untuk proses dekripsi, langkah pertama adalah mendekripsi cipherkey terlebih dahulu dengan menggunakan kunci privat pada algoritma RSA untuk mendapatkan kembali sessionkey dan kemudian mendekripsikan cipherteks untuk memperoleh pesan asli. Langkah proses dekripsi dapat dilihat pada Gambar 3.2 berikut.
Gambar 3.2 Konsep Perancangan Proses Pendekripsian
Plainteks dan Session key [Sadikin, 2012]
3.3.2. Dekripsi umum parangkat lunak
Perangkat lunak yang dibangun mampu melakukan enkripsi dan dekripsi terhadap file teks dan sessionkey yang dihasilkan oleh algoritma kunci simetris.
Data yang bekerja dalam sistem perangkat lunak yang dibangun yaitu: 1. Plainteks
yaitu file sesungguhnya yang masih dalam bentuk tulisan seperti pada umumnya.
2. Sessionkey
yaitu kunci simetri yang akan dipertukarkan dan digunakan untuk enkripsi
plainteks dan dekripsi cipherteks. Sessionkey selanjutnya akan dienkripsi
3. Cipherteks
yaitufile yang telah disandikan menjadi bentuk yang tidak terbaca. 4. Cipherkey
yaitu kunci simetri (sessionkey) yang telah disandikan kedalam bentuk yang sulit dimengerti.
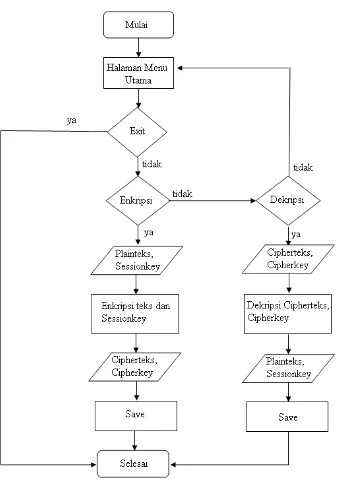
3.3.3. Rancangan proses kerja sistem secara umum
Dalam penerapannya pengirim akan melakukan enkripsi terhadap plainteks dengan menggunakan sessionkey kemudian mengenkripsikan kembali sessionkey tersebut agar tetap terjaga kerahasiaannya dengan menggunakan kunci publik penerima. Untuk proses dekripsi penerima pesan terlebih dahulu mendekripsikan pesan cipherkey yang diterima dengan menggunkan kunci privat yang dimilikinya untuk mendapatkan kembali sessionkey. Setelah sessionkey diperoleh kemudian akan dilakukan dekripsi
cipherteks untuk mendapatkan plainteks. Rancangan proses kerja sistem secara umum
dapat dilihat pada Gambar 3.3.
3.4. Diagram Alir (Flowchart)
Flowchart adalah rangkain bagan yang menggambarkan urutan suatu proses kegiatan
dalam mencapai tujuan yang diinginkan. Untuk Flowchart proses enkripsi Rijndael dapat dilihat pada gambar 3.4.
Flowchart proses dekripsi ciphertek pada algoritma Rijndael seperti Gambar 3.5.
Flowchart pembangkitan kunci privat dan kunci publik pada algoritma RSA dapat
dilihat pada Gambar 3.7.
Flowchart proses enkripsi sessionkey dengan algoritma RSA dapat dilihat pada
Gambar 3.8.
Flowchart proses dekripsi cipherkey dengan menggunakan kunci privat pada
algoritma RSA dapat dilihat pada Gambar 3.9.
Gambar 3.8 Flowchart Proses Dekripsi Cipherkey pada Algoritma RSA Selesai
Ubah bentuk ASCII menjadi klarakter asli
Mulai
Cipher-key, kunci privat
mi = Ci d
(mod n)
Sessionkey
Flowchart gambaran umum sistem ini menggambarkan proses yang terjadi pada
sistem secara umum.
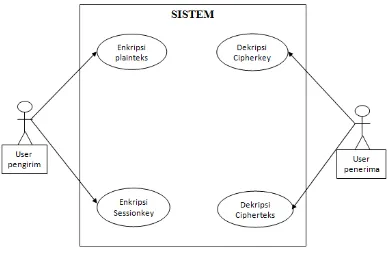
3.5.Use Case Diagram
Use Case Diagram adalah diagram pemodelan setiap aspek dan kegiatan didalam
sebuah sistem. Selain itu use case diagram juga menggambarkan semua aktor yang melakukan aktifitas didalam sistem.
Gambar 3.10 Use Case Diagram pada Sistem Enkripsi Rijndael dan RSA
Use case diagram yang ditunjukan pada Gambar 3.10 memiliki dua aktor yang
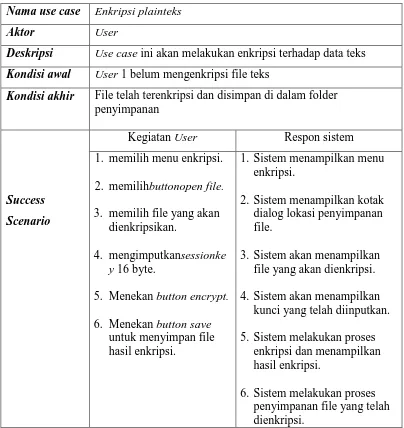
Untuk tabel kegiatan Use Case enkripsi plainteks dijabarkan pada tabel 3.1. Tabel tersebut menjelaskan setiap kegiatan user pada saat melakukan proses enkripsi serta respon sistem terhadap perintah user.
Table 3.1 Kegiatan Use Case Enkripsi Plainteks
Nama use case Enkripsi plainteks
Aktor User
Deskripsi Use case ini akan melakukan enkripsi terhadap data teks
Kondisi awal User 1 belum mengenkripsi file teks
Kondisi akhir File telah terenkripsi dan disimpan di dalam folder penyimpanan
Kegiatan User Respon sistem
Success
Scenario
1. memilih menu enkripsi. 2. memilihbuttonopen file. 3. memilih file yang akan
dienkripsikan.
4. mengimputkansessionke
y 16 byte.
5. Menekan button encrypt. 6. Menekan button save
untuk menyimpan file hasil enkripsi.
1. Sistem menampilkan menu enkripsi.
2. Sistem menampilkan kotak dialog lokasi penyimpanan file.
3. Sistem akan menampilkan file yang akan dienkripsi. 4. Sistem akan menampilkan
kunci yang telah diinputkan. 5. Sistem melakukan proses
enkripsi dan menampilkan hasil enkripsi.
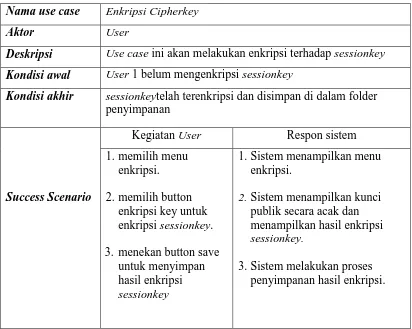
Untuk tabel kegiatan Use Case enkripsi Sessionkey dijabarkan pada tabel 3.2. Tabel tersebut menjelaskan setiap kegiatan user pada saat melakukan proses enkripsi
sessionkey serta respon sistem terhadap perintah user. Pada tahapan enkripsi
sessionkey terdapat button enkripsi key, button tersebut secara otomatis melakukan
proses pembangkitan kunci publik RSA dan melakukan enkripsi terhadap sessionkey.
Tabel 3.2 Kegiatan Use Case Enkripsi Sessionkey
Nama use case Enkripsi Cipherkey
Aktor User
Deskripsi Use case ini akan melakukan enkripsi terhadap sessionkey
Kondisi awal User 1 belum mengenkripsi sessionkey
Kondisi akhir sessionkeytelah terenkripsi dan disimpan di dalam folder
penyimpanan
Kegiatan User Respon sistem
Success Scenario
1.memilih menu enkripsi. 2.memilih button
enkripsi key untuk enkripsi sessionkey. 3. menekan button save
untuk menyimpan hasil enkripsi
sessionkey
1.Sistem menampilkan menu enkripsi.
2.Sistem menampilkan kunci publik secara acak dan menampilkan hasil enkripsi
sessionkey.
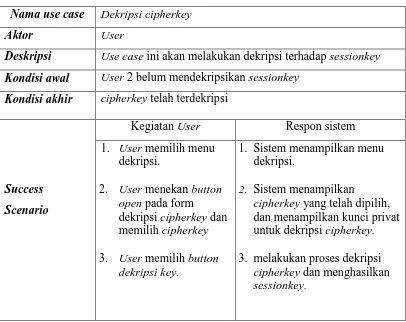
Untuk tabel kegiatan Use Case dekripsi cipherkey dijabarkan pada tabel 3.3. Tabel tersebut menjelaskan setiap kegiatan user pada saat melakukan proses dekripsi
cipherkey serta respon sistem terhadap perintah user. Tahapan ini user
mendekripsikan cipherkey untuk mendapatkan kembali sessionkey yang digunakan kembali untuk proses dekripsi cipherteks. Proses dekripsi cipherkey ini menggunakan kunci privat dari algoritma RSA yang telah dibangkitkan sebelumnya.
Tabel 3.3 Kegiatan Use Case Dekripsi Cipherkey
Nama use case Dekripsi cipherkey
Aktor User
Deskripsi Use case ini akan melakukan dekripsi terhadap sessionkey
Kondisi awal User 2 belum mendekripsikan sessionkey
Kondisi akhir cipherkey telah terdekripsi
Kegiatan User Respon sistem
Success
Scenario
1. User memilih menu
dekripsi.
2. User menekan button open pada form
dekripsi cipherkey dan memilih cipherkey 3. User memilih button
dekripsi key.
1. Sistem menampilkan menu dekripsi.
2. Sistem menampilkan
cipherkey yang telah dipilih,
dan menampilkan kunci privat untuk dekripsi cipherkey. 3. melakukan proses dekripsi
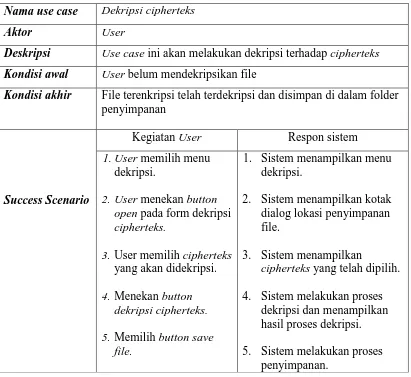
Untuk tabel kegiatan Use Case dekripsi ciherteks dijabarkan pada tabel 3.4. Tabel tersebut menjelaskan setiap kegiatan user pada saat melakukan proses dekripsi
cipherteks serta respon sistem terhadap perintah user. Tahap ini user mendekripsikan
cipherteks dengan menggunkan sessionkey untuk mendapatkan kembali plainteks
dengan proses algoritma Rijndael.
Tabel 3.4 Kegiatan Use case Dekripsi Cipherteks.
Nama use case Dekripsi cipherteks
Aktor User
Deskripsi Use case ini akan melakukan dekripsi terhadap cipherteks
Kondisi awal User belum mendekripsikan file
Kondisi akhir File terenkripsi telah terdekripsi dan disimpan di dalam folder penyimpanan
Kegiatan User Respon sistem
Success Scenario
1.User memilih menu
dekripsi.
2.User menekan button open pada form dekripsi cipherteks.
3.User memilih cipherteks yang akan didekripsi.
4.Menekan button
dekripsi cipherteks.
5.Memilih button save
file.
1. Sistem menampilkan menu dekripsi.
2. Sistem menampilkan kotak dialog lokasi penyimpanan file.
3. Sistem menampilkan
cipherteks yang telah dipilih.
4. Sistem melakukan proses dekripsi dan menampilkan hasil proses dekripsi. 5. Sistem melakukan proses
3.6. Perancangan Interface
Perancangan interface bertujuan untuk memahami fungsi-fungsi dari bagian yang terdapat pada sistem serta memudahkan dalam pengelolaan agar sistem berjalan sebagaimana mestinya.
3.6.1. Rancangan menu utama
Rancangan menu utama merupakan tampilan saat sistem pertama kali dijalankan. Pada halaman ini terdapat fungsi button enkripsi, dekripsi, button about dan button exit.
Button enkripsi akan mengarahkan user ke dalam halaman enkripsi, Button dekripsi
akan mengarahkan user ke halaman dekripsi, dan Button about berisikan tentang biodata penulis dan keterangan aplikasi.
3.6.2. Rancangan halaman enkripsi
Pada halaman proses enkripsi terdapat dua buah bagian yaitu bagian proses Rijndael dan RSA. Pada rancangan tampilan Proses Rijndael terdapat kolom utuk pengimputan
sessionkey dan kolom plainteks. Button buka file berfungsi untuk membuka direktori
penyimpanan file *.txt yang akan dienkripsikan. Button enkripsi plainteks berfungsi untuk melakukan proses enkripsi terhadap plainteks.
Untuk form proses RSA terdiri dari kolom teks terenkripsi untuk menampilkan hasil enkripsi, kolom key terenkripsi untuk menampilkan hasil enkripsi (cipherkey). Pada bagian bawah terdapat kolom untuk kunci publik e dan kunci privat d. Button
enkripsikey berfungsi untuk enkripsi sessionkey. Button save berfungsi untuk
menyimpan hasil proses enkripsi kunci. Untuk rancangan proses enkripsi seperti Gambar 3.13 berikut.
3.6.3. Rancangan halaman dekripsi
Halaman dekripsi merupakan proses mengembalikan cipeherteks dan cipherkey kebentuk plainteks dan sessionkey. Pada rancangan halaman dekripsi terdapat kolom teks terenkripsi untuk menampilkan cipherteks, kolom key terenkripsi untuk menampilkan cipherkey, dan kolom kunci privat yang akan digunakan pada proses dekripsi cipherkey. Button dekripsi key berfungsi untuk melakukan proses dekripsi untuk mendapatkan sessionkey dan Button dekripsi teks berfungsi untuk mengembalikan cipherteks kebentuk plainteks. Untuk rancangan proses dekripsi dapat dilihat pada Gambar 3.14.
BAB 4
IMPLEMENTASI DAN PENGUJIAN
4.1. Proses Algoritma Rijndael
Pada bab sebelumnya telah dibahas teori tentang proses algoritma Rijdael dalam melakukan enkripsi dan dekripsi terhadap suatu plainteks.
4.1.1 Ekspansi kunci
Proses ekspansi kunci terdiri dari beberapa operasi yaitu: 1. Rot Word
Operasi pemindahan byte. Byte terujung dari sessionkey dipindahkan ke ujung lainnya tanpa mengubah keterurutan komponen lain. Rot word berarti menukarkan posisi baris ke-1 dengan baris ke-4, baris ke-2 dengan ke-1, baris ke-3 dengan ke-2 dan baris ke-4 dengan ke-3.
2. S-box
Fungsi tabel ini sama seperti pada pembahasan sebelumnya. Substitution box merupakan tabel yang mensubtitusikan nilai byte dengan nilai yang telah ditentukan. Hasil dari rot word pada gambar diatas akan disubtitusikan dengan sebuah s-box Rijndael (AES).
Gambar 4.2 Proses Subtitusi Byte S-Box dengan
Hasil Rot Word (Munir, 2006)
3. R-con
Operasi ini merupakan eksponensiasi dari bilangan bulat 2 dalam semesta Rijndael finite field. R-con menghasilkan putaran yang tetap dari larik kata dan berisi nilai yang diberikan oleh [xi-1, {00},{00},{00}] dengan xi-1 dari I ke 1.
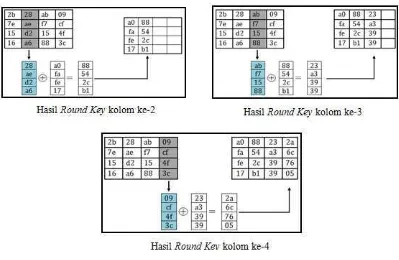
Langkah selanjutnya menentukan kolom ke-1 pada round key pertama.Lakukan XOR antara chipper key, hasil SubBytes dan R-con.
Gambar 4.4 Proses Pengisian Kolom Ke-1 pada
Round Key Pertama (Arsendi, 2011)
Untuk proses pengisian kolom Roundkey selanjutnya dapat dilihat pada langkah berikut.
Kemudian langkah-langkah di atas diulang 9 kali lagi untuk mendapatkan 9 buah roundkey berikutnya. Maka didapatkan hasil 10 roundkey.
Gambar 4.6 Hasil Seluruh Roundkey (Munir, 2006)
4.1.2 Enkripsi plainteks
Enkripsi plainteks terdiri dari teks asli 16 byte dan kunci 16 byte: Plaintek (HEX) : 32 88 31 e0 43 51 31 37 f6 30 98 07 a8 8d a2 34 Session key ( HEX) : 2b 28 ab 09 7e ae f7 cf 15 d2 15 4f 16 a6 88 3c
Tiap elemen dari array state diisi dengan 8-bit teks (1 byte) dalam notasi HEX. Urutan pengisian dimulai dari kolom awal (c=0) sampai kolom terakhir c=3 dan dari barisawal (r=0) sampai baris akhir (r=3). Untuk proses selanjutnya dilakukan
addrounkey yang pertama dengan menggunakan fungsi XOR antara plainteks dan
sessionkkey
Gambar 4.7 Proses Pengisian Array State
Pada awal enkripsi, input plainteks 128-bit yang akan disalin ke suatu array yang diberi nama array state. Proses enkripsi dimulai dengan suatu proses yang disebut AddRoundKey. Proses selanjutnya adalah 9 putaran yang masing-masing putaran terdiri dari empat macam proses yaitu:
1. Transformasi SubByte
Untuk proses SubByte menggunakan S-box seperti yang telah dijelaskan pada bab sebelumnya. Dua digit bilangan HEX akan direpresentasikan kedalam koordinat x dan y. hasilnya dapat dilihat seperti berikut.
Gambar 4.8 Hasil Represenatasi Bilangan HEX
dengan Menggunakan S-Box
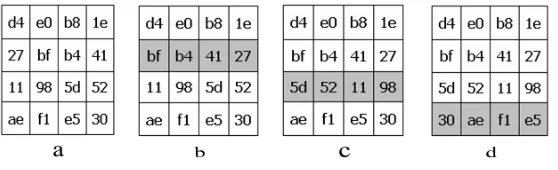
2. Transformasi ShiftRows
Baris ke-1 bergeser 1 byte ke kiri, baris ke-2 bergeser 2 byte ke kiri, sampai didapatkan hasil terakhir setelah menggeser baris ke-3 sebanyak 3 byte ke kiri .
3. Transformasi MixColumn
Transformasi MixColumn merupakan proses perkalian matrik
Gambar 4.10 Hasil Proses MixColumn (ariyus, 2008)
4. Transformasi AddRoundkey
Untuk proses AddRoundkey kali ini sama seperti proses sebelumnya namun
subkey dibangkitkan dari kunci utama (sessionkey) dengan menggunakan proses
ekspansi kunci. Setiap subkey hasil ekpansi berbeda setiap putarannya.Tiap kolom dari array state dikenakan XOR dengan kolom round key. Proses ini dilakukan terhadap seluruh kolom array state.
.
Gambar 4.11 Operasi Transformasi Addroundkey
Dengan Fungsi XOR (ariyus 2008)
5. Final round
Pada putaran terakhir yaitu putaran ke 10 proses transformasi MixColumn tidak dilakukan namun hanya terdiri dari 3 proses yaitu SubByte, ShiftRows,
Setelah semua proses dilakukan maka akan didapat nilai cipherteks pada putaran terakhir. Untuk hasil keseluruhan tiap putarannya dapat dilihat pada tabel hasil proses enkripsi algoritma Rijndael berikut ini.
Table 4.1 Hasil Proses Enkripsi
Table 4.1 Hasil Proses Enkripsi (lanjutan)
4.1.3 Dekripsi plainteks
Tahapan dekripsi merupakan Invers dari keempat proses pada saat enkripsi dan kemudian urutan prosesnya dipertukarkan. Untuk urutan proses dekripsi yaitu
InversShiftRows, Invers SubBytes, Addroundkeys, dan Invers MixColumns. Table 4.2
menunjukan hasil dari setiap tahapan dekripsi Rijndael.
Tabel 4.2 Proses Dekripsi Cipherteks Menjadi Plainteks
Roun d
Start Round Invers Shift rows
Tabel 4.2 Proses Dekripsi Cipherteks Menjadi Plainteks (lanjutan)
Roun d
Start Round Invers Shift rows
4.2.Algoritma Kriptografi RSA
Prinsip kerja algoritma RSA ini terletak pada sulitnya memfaktorkan bilangan yang besar menjadi faktor prima. Pemfaktoran bertujuan untuk mendapatkan kunci privat. Jika bilangan tersebut tidak dapat difaktorkan, maka keamanan algoritma RSA tetap terjamin. Proses algoritma RSA terdiri dari beberapa tahapan yaitu:
1. Misalkan diperoleh nilah p=71 dan q= 107. maka proses pembangkitan kunci dapat dilakukan sebagai berikut:
a. Dapatkan nilai n, dimana n= p*q, dan n bersifat tidak rahasia. n= p *q
n= 71 * 107 n= 7595
b. Dapatkannilai Ф(n), dimana Ф(n)=( p-1)*(q-1),
Ф(n)= (p-1)*(q-1) Ф(n)= 70 * 106 Ф(n)=7420
c. Pilih sebuah bilangan bulat kecil e. dimana GCD(e, Ф(n)) = 1 e= 391
d. Hitung nilai d sebagai kunci privat. d = (1+k*Ф(n))/e . nilai k dibangkitkan
secara acak sehingga didapat sebuah nilai yang integer.
� = 1 +� ∗Ф(n)
�
� = 1 + 87∗7420
391 = 1651
Jadi nilai d adalah = 1651.
Dari proses pembangkitan kunci diatas maka diperoleh: Kunci publik (e,n) = 391,7595
4.2.1. Proses Enkripsi RSA
Untuk melakukan enkripsi dengan metode RSA, setelah didapatkan kunci publik dan kunci privat, maka plainteks harus diubah ke dalam kode ASCII desimal.
Plainteks (HEX) : 2b 28 ab 09 7e ae f7cf 15 d2 15 4f 16 a6 88 3c
Table 4.3 Konversi Karakter Plainteks ke Kode ASCII Desimal
Plainteks Kode ASCII
2b 43
28 40
ab 171
09 09
7e 126
ae 174
f7 247
cf 207
15 21
d2 210
15 21
4f 79
16 22
a6 166
88 136
Setelah semua plainteks dikonversikan kedalam kode ASCII maka akan dilakukan proses enkripsi setiap karakter.
Tabel 4.4 Proses Enkripsi Algoritma RSA
I mi E n ci = mie mod n
1 43 391 7595 3732
2 40 391 7595 1125
3 171 391 7595 234
4 09 391 7595 6519
5 126 391 7595 3381
6 174 391 7595 6684
7 247 391 7595 7408
8 207 391 7595 858
9 21 391 7595 4361
10 210 391 7595 5635
11 21 391 7595 4361
12 79 391 7595 79
13 22 391 7595 7183
14 166 391 7595 166
15 136 391 7595 5561
4.2.2. Proses dekripsi RSA
Untuk melakukan dekripsi terhadap cipherteks setiap blok cipherteks didekripsi kembali menjadi blok plainteks.
Tabel 4.5 Proses Dekripsi Algoritma RSA
i ci D n mi = cid mod n
1 3732 1651 7595 43
2 1125 1651 7595 40
3 234 1651 7595 171
4 6519 1651 7595 09
5 3381 1651 7595 126
6 6684 1651 7595 174
7 7408 1651 7595 247
8 858 1651 7595 207
9 4361 1651 7595 21
10 5635 1651 7595 210
11 4361 1651 7595 21
12 79 1651 7595 79
13 7183 1651 7595 22
14 166 1651 7595 166
15 5561 1651 7595 136
Setelah blok cipherteks didekripsi menjadi blok plainteks dalam bentuk kode ASCII desimal kemudian konversikan kembali kedalam bentuk kode Hex sehingga diperoleh nilai plainteks seperti semula.
Table 4.6 Konversi Karakter Kode ASCII Desimal ke Plainteks (HEX)
Kode ASCII desimal Plainteks (HEX)
43 2b
40 28
171 ab
09 09
126 7e
174 ae
247 f7
207 cf
21 15
210 d2
21 15
79 4f
22 16
166 a6
136 88
4.3. Impelementasi pada Sistem
Pada sub bab ini akan membahas tentang sistem yang telah dibangun serta cara kerja dari sistem tersebut.
4.3.1. Tampilan awal sistem
Halaman pertama yang tampil ketika sistem dijalankan adalah halaman main menu yang terdiri dari menu Enkripsi, menu dekripsi, dan menu about. Gambar 4.12 merupakan tampilan pada saat sistem pertama kali dijalankan.
4.3.2. Tampilan Menu Enkripsi
Menu Enkripsi digunakan oleh user, ketika menu ini dipilih oleh user, maka akan muncul halaman proses enkripsi yang digunakan untuk melakukan enkripsi file text dan sessionkey. Gambar 4.13 merupakan halaman menu Enkripsi.
Setelah masuk ke dalam menu Enkripsi, User dapat melakukan proses openfile dengan menekan tombol buka file teks. Hasil proses openfile enkripsi dapat dilihat pada Gambar 3.14.
Untuk melakukan proses enkripsi plainteks, user diminta memasukkan kunci 16 byte terlebih dahulu dan menekan tombol Enkripsi plainteks.
Setelah proses enkripsi plainteks berhasil dilakukan maka akan di tampilkan hasil enkripsi pada kolom Teks Terenkripsi seperti Gambar 3.15.
Untuk proses enkripsi sessionkey dilakukan dengan menggunakan kunci publik. Ketika user menekan tombol Enkripsi Key maka sistem akan menampilkan pasangan kunci (e,n dan d,n) yang akan digunakan secara acak serta sessionkey yang telah terenkripsi. Hasil enkripsi sessionkey ditampilkan pada kolom Key Terenkripsi. Dengan demikian proses enkripsi secara keseluruhan berhasil dilakukan. Gambar 3.16 merupakan hasil enkripsi secara keseluruhan.
Gambar 4.17 Tampilan Hasil Proses Enkripsi
4.3.3. Tampilan Menu Dekripsi
Menu Dekripsi digunakan oleh user, ketika menu ini dipilih oleh user, maka akan muncul halaman untuk dekripsi cipherkey dan cipherteks. Tampilan halaman proses dekripsi seperti Gambar 4.17.
Setelah masuk ke dalam menu dekripsi, Pengguna dapat melakukan proses
openfile dengan menekan tombol Buka File untuk membuka file cipherteks dan
cipherkey. Gambar 4.18 menunjukan cipeherteks dan cipherkey yang ingin didekripsi.
Gambar 4.19 Tampilan Hasil Inputan Cipherteks dan Cipherkey
Proses dekripsi ini dilakukan dengan mendekripsikan cipherkey terlebih dahulu, user memilih tombol Dekripsi Key untuk mendapat sessionkey. Sessionkey hasil dekripsi ditampilkan pada kolom key paling bawah.
Proses selanjutnya yaitu dekripsi cipherteks menggunakan sessionkey. Hasil dekripsi ini ditampilakan pada kolom plainteks. Gambar 4.20 berikut menunjukan hasil proses dekripsi secara keseluruhan.
Gambar 4.20 Tampilan Hasil Proses Dekripsi
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Berdasarkan hasil proses yang telah dilakukan baik secara teori dan pengujian terhadap sistem yang telah dibuat maka dapat ditarik kesimpulan:
1. Sistem yang dibangun mampu mengenkripsi dan dekripsi file teks *.txt saja. 2. Panjang kunci algoritma Rijndael pada sistem ini hanya 128-bit.
3. Hasil penelitian ini diperoleh sistem enkripsi dan dekripsi terhadap plainteks dan kunci simetris (sessionkey) dengan kombinasi algoritma Rijndael dan RSA.
4. Hasil enkripsi plainteks pada sistem yang dibangun berupa kode karakter, sedangkan untuk enkripsi sessionkey berupa kode number.
5.2Saran
Sebagai bahan pertimbangan untuk pengembangan sistem kedepan agar menjadi lebih baik, berikut ada beberapa saran yang dapat dijadikan pertimbangan:
1. Untuk pengembangan selanjutnya aplikasi ini diharapkan mampu mengenkripsi dan dekripsi file teks *.doc, dan jenis file teks lainnya yang sering digunakan.
2. Untuk hasil enkripsi sessionkey sebaiknya dalam bentuk kode karakter bukan dalam bentuk ciphernumber agar kelihatan lebih rapi.
6
BAB 2
TINJAUAN PUSTAKA
2.1. Kriptografi
Kriptografi berasal dari bahasa Yunani, cryptosdan graphein. Cryptosberarti rahasia dan graphein berarti tulisan. Menurut terminologinya kriptografi adalah ilmu dan seni untuk menjaga keamanan pesan ketika dikirim dari suatu tempat ke tempat yang lain. Kriptografi telah dikenal sejak ribuan tahun lalu, bahkan beberapa ahli mengatakan ilmu penyembunyian pesan ini telah dikenal sejak zaman mesir kuno, masyarakat mesir menulisnya dalam bentuk hieroglyphy yang bentuk tulisannya tidak standard dalam aturan penulisan pesan. (Konheim, 2007).
Kriptografi dapat pula diartikan sebagai ilmu atau teknik-teknik matematika yang berhubungan dengan aspek keamanan informasi seperti kerahasian, integritas data, serta otentikasi. Prinsip dasar kriptografi adalah menyembunyikan informasi dalam bentuk sedemikian rupa sehingga hanya orang-orang yang berhak saja yang dapat mengetahui isi informasi yang disembunyikan itu. (Smart, 2004).
Dalam algoritma kriptografi dikenal beberapa komponen yaitu: 1. Enkripsi
merupakan suatu proses pengubahan pesan asli yang disebut plainteks menjadi suatu kode yang tidak bisa dimengerti atau disebut juga
7
2. Dekripsi
merupakan proses pengubahan cipherteks menjadi plainteks. Algoritma yang digunakan untuk dekripsi tentu berbeda dengan algoritma yang digunakan untuk enkripsi.
3. Kunci
Berfungsi untuk melakukan enkripsi dan dekripsi. Berdasarkan jenis kunci yang digunakan kriptografi terbagi dua yaitu algoritma kriptografi simetris dan algoritma kriptografi asimetris.
4. Plainteks
merupakan pesan asli (clearteks). Agar pesan tidak dapat dimengerti maknanya oleh pihak lain, maka pesan akan diproses menggunakan algoritma kriptografi untuk menjadi kode-kode yang tidak bisa dipahami. 5. Cipherteks
merupakan bentuk pesan yang telah disandikan sehingga tidak bisa dibaca karena berupa karakter yang tidak mempunyai makna.
Dari lima komponen dalam kriptografi tersebut saling berhubungan. Plainteks dan cipherteks merupakan hasil pemetaan dari fungsi enkripsi dan dekripsi dengan menggunakan sebuah kunci. Misalkan P menyatakan plainteks, C menyatakan
cipherteks, dan k menyatakan kunci, maka fungsi enkripsi dan dekripsi dapat ditulis
Ek (P) = C maka Dk (C) = P sehingga Dk (Ek(P)) = P. (Munir, 2006).
2.1.1. Algoritma kriptografi kunci simetris
8
Contoh algoritma kunci simetris yang terkenal salah satunya adalah DES (Data Encryption Standard), AES Rijndael, dan IDE, kelemahan pada algoritma kunci simetris, kunci harus didistribusi dengan aman, jika ada n pengguna maka dibutuhkan jumlah kunci sebanyak n(n-1)/2 kunci. Jika kunci berhasil ditemukan oleh pihak yang tidak berhak, maka sistem kriptografi tidak lagi aman. Dibalik kelemahan di atas, terdapat juga keuntungan dari penggunaan algoritma ini yaitu prosesnya lebih cepat jika dibandingkan dengan kriptografi asimetri. Keuntungan inilah yang menjadi dasar mengapa algoritma ini masih banyak digunakan dan terus dikembangkan.
Gambar 2.1 Skema Kriptografi Simetri (Munir, 2006)
2.1.2. Algoritma kriptografi kunci asimetri
Whitfield Diffie dan Martin Hellman memperkenalkan konsep kriptografi kunci publik (kunci asimetris) pada tahun 1976. Pada algoritma asimetris kunci terbagi menjadi dua bagian yaitu:
1. Kunci umum (public key): kunci yang boleh diketahui semua orang (dipublikasikan).
2. Kunci rahasia (private key): kunci yang dirahasiakan (hanya boleh diketahui oleh satu orang saja).
Kunci privat,K
Plainteks
User A Enkripsi
Ek(P)=C
Ciphertext Dekripsi
Dk(C)=P
User B Kunci privat,K
9
Seseorang dapat mengirim sebuah pesan rahasia dengan menggunakan kunci publik tetapi pesan cipherteks hanya dapat didekripsi dengan kunci rahasia yang dimiliki penerima pesan.
Gambar 2.2 Skema Kriptografi Asimetri (Munir, 2006)
Aplikasi kunci publik dapat diimplementasi menjadi tiga kategori: 1. Kerahasian data
Kriptografi kunci-publik dapat digunakan untuk menjaga kerahasiaan data melalui mekanisme enkripsi dan dekripsi. Contoh algoritma untuk aplikasi ini adalah RSA, Knapsack, dan Elgamal.
2. Tanda-tangan digital
Kriptografi kunci publik dapat digunakan untuk membuktikan otentikasi pesan maupun otentikasi pengirim. Contoh algoritma untuk aplikasi ini adalah RSA, DSA, dan Elgamal.
3. Pertukaran kunci (key exchange)
Algoritma kriptografi kunci publik dapat digunakan untuk pengiriman kunci simetri (sessionkey). Contoh algoritmanya adalah RSA dan Diffie-hellman.
Dalam implementasinya, sistem kriptografi kunci publik bukan pengganti sistem kriptografi simetris. Sistem kriptografi kunci publik tidak digunakan untuk mengengkripsi pesan, melainkan untuk mengenkripsi kunci pada sistem kriptografi simetris. Dengan sistem kriptografi kunci publik maka pertukaran kunci pada sistem kriptigrafi simetris dapat dilakukan dengan aman.
Enkripsi Ek1(P)=C
Kunci publik K1
Plainteks P
User A
Ciphertext C Dekripsi Dk2(C)=P
User B
Kunci privat K2
10
2.2. Jenis-Jenis Serangan Terhadap Kriptografi
Serangan terhadap sistem kriptografi dapat dikelompokkan dengan beberapa cara:
1. Berdasarkan keterlibatan penyerang dalam komunikasi: a. Serangan aktif
Pada jenis serangan ini, penyerang mengintervensi komunikasi secara langsung dan ikut mempengaruhi sistem untuk keuntungan dirinya. Misalnya penyerang mengubah aliran pesan seperti menghapus sebagian
ciphertext, mengubah ciphertext, menyisipkan potongan ciphertext palsu,
me-replay pesan lama, mengubah informasi yang tersimpan, dan sebagainya. Serangan yang termasuk jenis serangan aktif adalah
man-in-the-middle attack.
b. Serangan pasif
Pada jenis serangan ini, penyerang tidak terlibat dalam komunikasi antara pengirim dan penerima, namun penyerang menyadap semua pertukaran pesan antara kedua entitas tersebut. Tujuannya adalah untuk mendapatkan sebanyak mungkin informasi yang digunakan untuk kriptanalisis. Beberapa metode penyadapan data antara lain:
1) Wiretapping: penyadap mencegat data yang ditransmisikan pada
saluran komunikasi dengan menggunakan sambungan perangkat keras. 2) Electromagnetic eavesdropping: penyadap mencegat data yang
ditransmisikan melalui saluran wireless, misalnya radio dan
microwave.
2. Berdasarkan banyaknya informasi yang diketahui oleh kriptanalis: a. Ciphertext-only attack
11
b. Known-plaintext attack
Ini adalah jenis serangan dimana kriptanalis memiliki pasangan plainteks dan cipherteks yang berkoresponden. Beberapa pesan yang formatnya terstruktur membuka peluang kepada kriptanalis untuk menerka plainteks dari cipherteks yang bersesuaian.
c. Chosen-plaintext attack
Serangan jenis ini lebih hebat dari pada known-plaintext attack, karena kriptanalis dapat memilih plainteks yang dimilikinya untuk dienkripsikan, yaitu plainteks yang lebih mengarahkan penemuan kunci.
d. Chosen-ciphertext attack
Ini adalah jenis serangan dimana kriptanalis memilih cipherteks untuk didekripsikan dan memiliki akses ke plainteks hasil dekripsi (misalnya terhadap mesin elektronik yang melakukan dekripsi secara otomatis). Jenis serangan ini biasanya dipakai pada sistem kriptografi.
e. Chosen-text attack
Ini adalah jenis serangan yang merupakan kombinasi chosen-plaintext dan
chosen-ciphertext attack.
3. Berdasarkan teknik yang digunakan dalam menemukan kunci: a. Exhaustive attack atau brute force attack
Ini adalah serangan untuk mengungkap plainteks atau kunci dengan mencoba semua kemungkinan kunci.
b. Analytical attack
12
2.3. Algoritma AES Rijndael
Pada tahun 1997 NIST (National Institute of Standards and Technology) berniat ingin mencari pengganti algoritma DES, hal ini dikarenakan dalam tempo 96 hari 70 ribu PC berhasil membobol kunci DES, kemudian pada tahun 1998 hanya dalam tempo 22 hari, sehingga dibuat suatu mesin khusus untuk memecahkan algoritma DES. Mesin tersebut terbukti dapat memecahkan 25% kunci DES dalam waktu 2,3 hari dan dapat memecahkan seluruh kunci DES dalam waktu rata-rata 4,3 hari. Karena alasan tersebut NIST ingin mengadakan kompetisi yang diikuti para kriptografer seluruh dunia agar segara mendapatkan pengganti dari algoritma DES.(Arriyus, 2008).
Pada tanggal 9 Agustus 1999, NIST melalui seleksi yang sangat ketat mengumumkan 5 finalis yang akan memasuki seleksi akhir yaitu MARS, RC6, Rijndael, Serpent, dan Twofish. Pada seleksi akhir tanggal 2 Oktober 2000 maka terpilihlah Rijndael sebagai pemenang. Algoritma Rijndael dibuat oleh Dr. Vincent Rijmen dan Dr. Joan Daemen. Evaluasi terhadap algoritma Rijndael tersebut dapat dilihat dari beberapa sudut pandang berikut ini:
1. Dari segi general security
a. Belum ada serangan yang serius dalam memecahkan skema dari Rijndael
b. Rijndael menggunakan komponen S-Box non linear.
c. Rijndael memiliki struktur matematika yang bisa terus mengalami perkembangan.
2. Dari segi enkripsi dekripsi
a. Memiliki kode yang sangat rumit.
b. Enkripsi dekripsi Rijndael berbeda satu dengan yang lainnya.
c. Rijndael mendukung penuh ukuran blok dan ukuran kunci 128 bit, 192bit, dan 256 bit.
13
Algoritma Rijndael mampu menangani panjang kunci dan ukuran blok yang berbeda, panjang kunci dan ukuran blok yang telah ditentukan adalah 128, 192, dan 256. Ukuran blok dapat dihitung dengan (Nb= block length / 32) dan panjang kunci (Nk= key length / 32). Nilai Nb dan Nk yang akan dipakai mempengaruhi jumlah putaran (Nr) yang terjadi pada saat proses enkripsi dan dekripsi. Tabel 2.1 akan menunjukan perbedaan jumlah putaran (Nr) berdasarkan panjang kunci dan ukuran blok yang digunakan. (Mollin, 2007).
Tabel 2.1 Perbandingan Jumlah Putaran pada Rijndael (Rijman & daemen, 2002)
Nr Nb= 4 Nb= 6 Nb= 8
Nk= 4 10 12 14
Nk= 6 12 12 14
Nk= 8 14 14 14
Algoritma Rijndael memiliki tiga para meter yaitu:
1. Plainteks : array yang berukuran 16 byte, yang berisi data masukan. 2. Cipherteks : array yang berukuran 16 byte, yang berisi hasil enkripsi. 3. Key : array yang berukuran 16 byte, yang berisi kunci ciphering.
14
2.3.1. Proses enkripsi algoritma Rijndael
Proses enkripsi untuk algoritma Rijndael yang beroperasi pada panjang blok 128-bit dengan kunci 128-bit, total putaran (Nr) yang dilakukan hingga diperoleh cipherteks adalah 10 kali putaran. Secara garis besar proses enkripsi algoritma Rijndael diperlihatkan pada Gambar 3.3.
Gambar 2.3 Diagram Proses Enkripsi Rijndael
Urutan proses enkripsi Rijndael dalam mengamankan plainteks yaitu: 1. Key Expantion
15
2. Addroundkey
Untuk proses Addroundkey yang pertama dilakukan XOR antara state awal (plaintext) dengan kunci utama, sedangkan Addroundkey yang selanjutnya pada tiap putaran, merupakan hasil key ekspantion dari kunci utama (sessionkey).
3. Putaran (Nr) sebanyak Nr-1
Pada proses ini akan dilakukan beberapa putaran, jumlah putaran telah ditentukan seperti yang telah dijelaskan sebelumnya. Pada tahap ini dilakukan 9 kali putaran, yaitu:
a. Sub Bytes
Pada proses ini dilakukan subtitusi menggunkan table S-box. Dua digit bilangan HEX yang merupakan representasi 1 byte dari tiap teks menjadi koordinat untuk substitusi pada S-box. Digit pertama sebagai koordinat x dan digit kedua sebagai koordinat y, perpotongan baris x dengan kolom y merupakan nilai yang akan diambil. (Rijmen & Daemen, 2002).
Tabel 2.2 S-Box yang Digunakan dalam Transformasi
16
b. ShiftRows
Proses pergeseran baris array state dengan menggeser baris ke-r dalam
array state ke kiri sebanyak r byte. Baris ke-0 dari blok tidak mengalami
pergeseran. Baris ke-1 bergeser 1 byte ke kiri, baris ke-2 bergeser 2 byte ke kiri, sampai akhirnya didapatkan hasil terakhir setelah menggeser baris ke-3 sebanyak ke-3 byte ke kiri. Berikut adalah table jumlah pergeseran berdasarkan blok Nb. (Rijmen & Daemen,2002).
Tabel 2.3 Jumlah Pergeseran Pada Tahap Shift Rows
(Rijmen & Daemen,2002)
Nb C0 C1 C2 C3
4 0 1 2 3
6 0 1 2 3
8 0 1 4 4
c. MixColoumns
17
Transformasi ini dinyatakan sebagai perkalian matriks:
s’(x) = a(x)⊗s(x)
s’0,c = ({02} •s0,c) ⊕ ({03}•s1,c ) ⊕s2,c⊕s3,c
s’1,c = s0,c⊕ ({02} •s1,c) ⊕ ({03}•s2,c ) ⊕s3,c
s’2,c = s0,c⊕s1,c⊕ ({02} •s1,c) ⊕ ({03}•s3,c )
s’3,c = ({03}•s0,c ) ⊕s0,c⊕s1,c⊕ ({02} •s3,c)
Gambar 2.4Perkalian Matriks MixColumn() Rijndael
d. Addround key
Dilakukan dengan fungsi XOR antara array state sebelumnya dengan round key. Proses ini akan terus berulang sebanyak Nr-1 sesuai besarnya blok data dan panjang kunci.
Setelah semua proses dilakukan sebanyak Nr-1, proses terakhir adalah final round. Pada tahap ini proses MixColumns tidak dilakukan.
4. Final round
Proses untuk putaran terakhir hanya dilakukan tiga tahap saja, proses dari ketiga tahap tersebut sama seperti proses pada tahap sebelumnya yaitu:
a. SubBytes.
b. ShiftRows.
c. AddRoundKey.
S’0,c 02 03 01 01 S’0,c
S’1,c
=
01 02 03 01 S’1,c
S’2,c 01 01 02 03 S’2,c
18
2.3.2. Proses dekripsi algoritma Rijndael (AES)
Proses dekripsi algoritma Rijndael tidak jauh berbeda dengan proses enkripsi namun berbeda pada urutan prosesnya saja. Untuk urutan proses dekripsi yaitu:
1. Key Expantion
Pada proses dekripsi juga dilakukan ekspansi kunci. Kunci pada proses enkripsi kemudian diekspansi terlebih dahulu untuk menghasilkan
RoundKey yang akan digunakan pada setiap putaran.
2. AddRoundKey
Dilakukan proses XOR antara state awal (cipherteks) dengan key terakhir hasil ekspansi. Tahap ini disebut juga initial round.
19
3. Putaran sebanyak Nr-1 kali Proses yang dilakukan pada setiap putaran adalah:
a. InvShiftRow
Pergeseran baris-baris array state ke kanan dengan aturan pergesaran sama seperti pada tahap enkripsi.
b. InvByteSub
Dilakukan substitusi byte dengan menggunakan tabel substitusi kebalikan (inverse S-box). Tabel substitusi dapat dilihat pada Tabel 2.4.
Tabel 2.4 S-Box yang Digunakan dalam Transformasi
20
c. AddRoundKey
Pada proses ini dilakukan XOR antara state sekarang dengan round key. d. InvMixColumn
Seperti pada proses MixColumn, InvMixColumn juga dilakukan pengacakan di masing-masing data pada kolom array state.
4. Final round
Proses untuk putaran terakhir hanya dilakukan tiga tahap saja, proses dari ketiga tahap tersebut sama seperti proses pada tahap sebelumnya, yaitu: a. InvShiftRow
b. InvSubByte
c. AddRoundKey
2.3.3. Key expantion
Algoritma Rijndael (AES) membuat suatu ekspansi kunci untuk menghasilkan suatu
key schedule. Jika ekspansi kunci yang diperlukan Rijndael (AES) Nb(Nr+1) word,
sehingga bisa digunakan AES 128 bit, maka 4(10+1)=40 word=44x32 bit=1408 bit
subkey. Ekspansi dari 128 menjadi 1408 bit subkey, proses ini disebut dengan key
schedule. Subkey ini diperlukan karena setiap round merupakan suatu inisial dari Nb
word untuk Nr=0 dan 2 Nb untuk Nr=1, 3 untuk Nr=2,…,11 Nb untuk Nr=10, dari
21
2.4.Algoritrma Kriptografi RSA
Sistem kriptografi asimetris pertama kali dipublikasikan pada tahun 1997 oleh Whitfield Diffie dan Martin Hellman dari Stanford University. Penelitian mereka membahas tentang pendistribusian kunci rahasia pada saluran komunikasi umum, metode ini kemudian dikenal dengan nama algoritma Diffie Hellman. Algoritma ini beranjak dari hasil penelitian sistem kriptografi asimetris yang pertama kali dilakukan oleh James H. Ellis, Clifford Cocks, dan Malcom Williamson pada tahun1970. Namun sayangnya algoritma tersebut dirahasiakan dan tidak dipublikasikan.
Berkat penemuan tersebut pada tahun 1976 tiga orang ilmuan dari MIT (Massachusset Institute Of Technology) yaitu Ron Rivest, Adi Shamir, dan Leonard Adleman, mencoba mengembangkan teknik algoritma kriptografi kunci publik, algoritma tersebut kemudian dikenal dengan naman RSA. (Munir, 2006).
RSA merupakan salah satu algoritma kriptografi yang bersifat asimetris, artinya setiap pengguna memiliki sepasang kunci, satu kunci untuk enkripsi dan satu kunci lagi untuk dekripsi. Kunci enkripsi (public-key) bersifat tidak rahasia sedangkan untuk kunci dekripsi dirahasiakan (private-key). Untuk kunci publik disimbulkan dengan e dan untuk kunci privat disimbulkan dengan d. karena kunci enkripsi tidak sama dengan kunci dekripsi itulah kriptografi RSA disebut kunci asimetris. Kekuatan algoritma RSA terletak pada tingkat kesulitan dalam memfaktorkan bilangan menjadi faktor primanya.
Pada algoritma RSA terdapat 3 langkah utama yaitu key generation (pembangkitan kunci), enkripsi, dan dekripsi. Kunci pada RSA mencakup dua buah kunci, yaitu public key dan private key. Public key digunakan untuk melakukan enkripsi, dan dapat diketahui oleh orang lain. Sedangkan private key tetap dirahasiakan dan digunakan untuk melakukan dekripsi. Besaran besaran yang digunakan pada RSA adalah sebagai berikut :
1. p dan q bilangan prima (dirahasiakan)
22
4. e (kunci enkripsi) (tidak rahasia) 5. d( kunci dekripsi ) (dirahasiakan) 6. m (Plainteks) (dirahasiakan) 7. c ( Cipherteks ) (tidak rahasia)
Proses pembangkitan kunci atau RSA adalah sebagai berikut:
1. Pilih dua buah bilangan prima sembarang p dan q. Jaga kerahasiaan p dan
q ini.
2. Hitung n = p * q. Besaran n ini tidak dirahasiakan.
3. Hitung φ(n)= (p-1) * (q-1). Sekali φ(n) telah dihitung, p dan q dapat
dihapus untuk mencegah diketahuinya oleh pihak lain.
4. Pilih sebuah bilangan bulat untuk kunci publik e, yang relatif prima terhadap n (GCD(e, φ(n)) = 1) dengan syarat e ≠ (p-1), e ≠ (q-1), dan e < n.
5. Kunci publik (Public Key) = (n,e)
6. Hitung kunci privat (d). Kunci privat dapat dihitung dengan persamaan:
dengan syarat k dan d adalah anggota bilangan bulat. Nilai k = 1, 2, 3, ...,n diperoleh nilai d yang bulat. Nilai itu yang akan dipakai sebagai kunci pribadi untuk dekripsi pesan.
Proses enkripsi dapat dilakukan dengan:
Sedangkan proses dekripsi dilakukan dengan:
Dalam implementasi sebenarnya, nilai p dan q diharapkan sangat besar sekali (misalnya 100 digit) agar pekerjaan memfaktorkan n menjadi faktor primanya menjadi sangat sukar, sehingga lebih susah untuk ditembus.
Ci = Pi e
mod n
Pi = Ci d
mod n
�=1 +�φ(n)