PEMODELAN NILAI TUKAR RUPIAH TERHADAP DOLAR
AMERIKA MENGGUNAKAN
HIDDEN
MARKOV SATU
WAKTU SEBELUMNYA
SRI RAMADANIATY
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Pemodelan Nilai Tukar Rupiah terhadap Dolar Amerika Menggunakan Hidden Markov Satu Waktu Sebelumnya adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Mei 2015
Sri Ramadaniaty
ABSTRAK
SRI RAMADANIATY. Pemodelan Nilai Tukar Rupiah terhadap Dolar Amerika Menggunakan Hidden Markov Satu Waktu Sebelumnya. Dibimbing oleh BERLIAN SETIAWATY dan RUHIYAT.
Nilai tukar Rupiah terhadap Dolar Amerika telah menjadi salah satu acuan penting dalam pergerakan perekonomian Indonesia. Perubahan nilai tukar Rupiah merupakan suatu kejadian yang bisa terjadi kapan saja dalam jangka waktu yang panjang dan perubahan yang terjadi mungkin terjadi kembali di masa mendatang. Jika penyebab kejadian diasumsikan tidak diamati secara langsung dan membentuk rantai Markov, maka pasangan penyebab kejadian dan data nilai tukar Rupiah dapat dimodelkan oleh model hidden Markov. Dalam tugas akhir ini digunakan model
hidden Markov satu waktu sebelumnya, di mana nilai Rupiah saat ini bergantung pada nilai Rupiah satu waktu sebelumnya dan penyebabnya di waktu sekarang dan satu waktu sebelumnya. Parameter model diduga dengan menggunakan Maximum Likelihood dan perhitungannya menggunakan algoritme iteratif Expectation Maximization (EM). Proses komputasi numerik dilakukan dengan menggunakan
softwareMathematica 10. Setelah penduga parameter didapatkan maka nilai tukar Rupiah terhadap Dolar Amerika dapat diduga. Akurasi model diukur menggunakan
mean absolute percentage error (MAPE). Diperoleh MAPE 4.48% dengan satu kali iterasi.
Kata kunci: algoritme EM, MAPE, model hidden Markov, nilai tukar Rupiah
ABSTRACT
SRI RAMADANIATY. Modeling the Exchange Rate of Rupiah to American Dollar using Previous Time Hidden Markov. Supervised by BERLIAN SETIAWATY and RUHIYAT.
An exchange rate of Rupiah to American Dollar has become one of important reference for Indonesian economic movement. The movement of the exchange rate of Rupiah is an event that can occur anytime in a long period and possible to reoccur in the future. If the cause of event is not observed directly and forms a Markov chain, so the pair of the cause and an exchange rate of Rupiah can be modeled by hidden Markov. In this thesis the previous time hidden Markov model is used. This model assumes that the present exchange rate of Rupiah depends on the previous exchange rate of Rupiah and the present and previous cause. Model parameter is estimated by using maximum likelihood method and the calculation uses iterative algorithm expectation maximization (EM). Numerical computation is done by using Mathematica 10. After the parameter model is obtained, then the exchange rate of Rupiah to American Dollar can be estimated. Model accuracy is measured by using mean absolute percentage error (MAPE). Resulted MAPE is 4.48% with one iteration.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
PEMODELAN NILAI TUKAR RUPIAH TERHADAP DOLAR
AMERIKA MENGGUNAKAN
HIDDEN
MARKOV SATU
WAKTU SEBELUMNYA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PRAKATA
Puji dan syukur ke Hadirat Allah SWT yang telah memberikan rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul Pemodelan Nilai Tukar Rupiah terhadap Dolar Amerika Menggunakan Hidden
Markov Satu Waktu Sebelumnya.
Penulis mengucapkan terimakasih kepada:
1. Dr Berlian Setiawaty, MS dan Ruhiyat, MSi selaku dosen pembimbing yang telah memberikan ilmu, bimbingan, saran, arahan dan motivasi bagi penulis selama skripsi, dan kepada Ir Ngakan Komang Kutha Ardana, MSc selaku dosen penguji.
2. Papa (Prof Dr Ahmad Husein Ritonga, MAg), Mama (Dra Mariatul Hasanah Harahap), kak Fatimah Raihani (Ayu) & kak Soleh, kak Lainatussifa (Dede), Naila Hidayati dan M. Farhan Akhwan atas segala doa, nasehat, dukungan, dan kasih sayangnya.
3. Staf Departemen Matematika: Ibu Susi, Bapak Yono, Ibu Ade, dan Bapak Deni atas kesabaran dan bantuannya selama ini.
4. Kak Tyas, kak Juni, kak Hendra, Nisa, Putri Putu, Eka, Betry, mbak Peni, Ando, Murzani, Agung, Marin, Okta, Susi, Shovi, Pupu, serta teman-teman Matematika 47 lainnya, Wisma Pelangi, Lordu dan teman seperjuangan atas doa dan semangatnya selama ini.
Penulis berharap skripsi ini dapat bermanfaat bagi berbagai pihak.
Bogor, Mei 2015
DAFTAR ISI
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
LANDASAN TEORI 2
Ruang Contoh, Kejadian, dan Peluang 2
Peubah Acak dan Sebarannya 3
Nilai Harapan 4
Rantai Markov 5
Algoritme Expectation Maximization (EM) 8
Mean Absolute Percentage Error (MAPE) 9
MODEL HIDDEN MARKOV SATU WAKTU SEBELUMNYA 9
Model Hidden Markov 9
Model Hidden Markov Satu Waktu Sebelumnya 10
PEMODELAN NILAI TUKAR RUPIAH TERHADAP DOLAR AMERIKA 18
Data Input Nilai Tukar Rupiah 18
Model Hidden Markov Satu Waktu Sebelumnya 19
Penentuan Nilai Awal Parameter 19
Hasil Program 20
SIMPULAN 21
DAFTAR PUSTAKA 21
LAMPIRAN 22
DAFTAR GAMBAR
1 Perubahan nilai tukar Rupiah terhadap Dolar Amerika per bulan 18 2 Plot persamaan baru dari data yang akan dikurangi rataannya 19 3 Perubahan nilai tukar Rupiah terhadap Dolar Amerika per bulan dan
nilai dugaan yang didapatkan 20
DAFTAR LAMPIRAN
1 Bukti Lema 1 22
2 Bukti persamaan (28) sampai dengan (32) 23
3 Program untuk mencari nilai dugaan menggunakan software
Mathematica 10 35
1
PENDAHULUAN
Latar Belakang
Rupiah termasuk soft currency, yaitu mata uang yang mudah berfluktuasi ataupun terdepresiasi, karena perekonomian negara asalnya relatif kurang mapan, sedangkan mata uang negara Amerika Serikat disebut hard currency, karena kemampuannya untuk memengaruhi nilai mata uang yang lebih rendah.
Nilai tukar Rupiah menjadi acuan penting dalam pergerakan naik-turunnya grafik perekonomian Indonesia. Indikasi dari pergerakan ekonomi bisa dilihat dari pergerakan nilai tukar Rupiah itu sendiri. Nilai tukar Rupiah sejatinya terus bergerak setiap hari seperti mata uang lainnya di dunia.
Modal yang beredar di Indonesia, terutama di pasar finansial, sebagian besar adalah modal asing. Ini membuat nilai Rupiah sedikit banyak bergantung pada kepercayaan investor asing terhadap prospek bisnis di Indonesia. Semakin baik iklim bisnis di Indonesia, maka akan semakin banyak investor asing di Indonesia, dan dengan demikian nilai Rupiah akan semakin kuat. Sebaliknya, semakin negatif pandangan investor terhadap Indonesia, Rupiah akan kian melemah.
Faktor yang memengaruhi Rupiah salah satunya adalah kondisi politik-ekonomi. Melemahnya nilai tukar Rupiah berdampak pada harga komoditi impor, baik yang menjadi objek konsumsi maupun alat produksi, serta kenaikan nilai Rupiah dari hutang luar negeri.
Perubahan nilai tukar mata uang merupakan suatu kejadian yang bisa terjadi kapan saja dalam periode waktu yang panjang. Ramalan nilai tukar Rupiah terhadap Dolar Amerika merupakan informasi penting yang dapat digunakan pemerintah untuk menentukan kebijakan di bidang ekonomi, perdagangan, dan pariwisata.
Model hidden Markov (Hidden Markov Model, HMM) adalah sebuah model stokastik yang tersusun dari dua buah proses stokastik, yaitu rantai Markov untuk menampung penyebab proses yang diamati serta proses yang diamati itu sendiri.
Perubahan nilai tukar Rupiah merupakan suatu kejadian yang bisa terjadi kapan saja dan dalam jangka waktu yang panjang. Dengan asumsi perubahan yang terjadi pada waktu yang lalu mungkin terjadi kembali di masa mendatang, sehingga hal ini merupakan suatu proses stokastik. Faktor penyebab kejadian (state) tersebut dapat berkembang menurut model rantai Markov di mana state yang akan datang hanya dipengaruhi oleh state sekarang dan bebas terhadap state yang lalu. Jika penyebab kejadian diasumsikan tidak diamati secara langsung (hidden) dan membentuk rantai Markov, maka pasangan kejadian dan penyebabnya dapat dimodelkan dengan model hidden Markov.
Permasalahan yang dibahas dalam karya ilmiah ini adalah penggunaan model deret waktu hidden Markov dalam menggambarkan perilaku nilai tukar Rupiah terhadap Dolar Amerika. Dalam deret waktu hidden Markov, kejadian yang diamati selain diamati oleh faktor penyebab kejadian, juga dipengaruhi oleh kejadian sebelumnya.
2
Dalam model ini akan dicari penduga parameter yang memaksimumkan peluang terjadinya suatu kejadian. Metode Maximum Likelihood dan algoritme
Expectation Maximum (EM algorithm) Baum dan Petrie (1966) adalah metode yang digunakan untuk pendugaan parameter tersebut.
Setelah pendugaan parameter yang memaksimumkan peluang terjadinya suatu kejadian didapatkan, maka diharapkan dapat dilakukan suatu penarikan kesimpulan yang optimal dan peramalan state.
Tujuan Penelitian
Tujuan dari karya ilmiah ini adalah:1. Mengkaji deret waktu hidden Markov satu waktu sebelumnya beserta pendugaan parameternya.
2. Memodelkan nilai tukar Rupiah terhadap Dolar Amerika menggunakan deret waktu hidden Markov satu waktu sebelumnya.
LANDASAN TEORI
Ruang Contoh, Kejadian, dan Peluang
Definisi 1 (Percobaan Acak)
Suatu percobaan yang dapat diulang dalam keadaan yang sama di mana hasil dari percobaan ini tidak dapat ditebak dengan tepat namun dapat diketahui semua kemungkinan hasilnya disebut percobaan acak (Ross 1996).
Definisi 2 (Ruang Contoh dan Kejadian)
Himpunan dari semua kemungkinan hasil yang muncul dari suatu percobaan acak disebut ruang contoh, dinotasikan Ω. Suatu kejadian adalah himpunan bagian dari Ω (Grimmet dan Stirzaker 1992).
Definisi 3 (Medan-�)
Medan-� adalah suatu himpunan ℱ yang anggotanya adalah himpunan bagian dari ruang contoh Ω serta memenuhi syarat-syarat sebagai berikut:
a. � ℱ.
b. Jika , , … ℱ maka ∞= ℱ. c. Jika ℱ maka ℱ
(Ross 1996).
Definisi 4 (Ukuran Peluang)
Ukuran peluang � pada Ω , ℱ adalah fungsi �: ℱ → [ , ] yang memenuhi:
3 b. Jika , , … ℱ adalah himpunan yang saling lepas, yaitu ∩ = ∅
untuk setiap pasangan , di mana ≠ , maka � ∞= = ∑∞= � . Pasangan Ω , ℱ, � disebut ruang peluang (Grimmet dan Stirzaker 1992).
Definisi 5 (Kontinu Absolut)
Jika dan merupakan dua peluang pada Ω , ℱ . Ukuran peluang dikatakan kontinu absolut terhadap ukuran peluang jika = berimplikasi = , untuk setiap ℱ. Dinotasikan ≪ (Royden 1963).
Definisi 6 (Peluang Bersyarat)
Jika � > maka peluang bersyarat dari kejadian setelah diketahui kejadian ialah
� | =� ∩
� (Grimmet dan Stirzaker 1992).
Definisi 7 (Kejadian Saling Bebas)
Kejadian A dan B dikatakan saling bebas jika � ∩ = � ⋅ � . Misal adalah himpunan indeks. Himpunan kejadian { : } disebut saling bebas jika
�( � ) = ∏ �� untuk setiap himpunan bagian berhingga dari
(Grimmet dan Stirzaker 1992).
Peubah Acak dan Sebarannya
Definisi 8 (Peubah Acak)
Misalkan ℱ adalah medan-� dari Ω. Peubah acak merupakan fungsi : Ω → ℝ di mana {� � Ω: � } ℱ untuk setiap ℝ (Grimmet dan Stizaker 1992).
Peubah acak dinotasikan dengan huruf besar, sedangkan nilai dari peubah acak tersebut dinotasikan dengan huruf kecil.
Definisi 9 (Fungsi Sebaran)
Fungsi sebaran dari peubah acak adalah suatu fungsi : ℝ → [ , ] di mana = � (Grimmet dan Stirzaker 1992).
Definisi 10 (Peubah Acak Diskret)
Peubah acak dikatakan peubah acak diskret jika nilainya hanya pada himpunan bagian yang berhingga atau himpunan terhitung dari ℝ (Ross 1996).
Definisi 11 (Fungsi Massa Peluang)
Fungsi massa peluang dari peubah acak diskret adalah fungsi : ℝ → [ , ] di mana = � = , ∀ ℝ (Grimmet dan Stirzaker 1992).
Definisi 12 (Peubah Acak Kontinu)
4
terintegralkan. Selanjutnya fungsi disebut fungsi kepekatan peluang (probability density function) bagi (Ross 1996).
Definisi 13 (Fungsi Sebaran Bersama Dua Peubah Acak)
Fungsi sebaran bersama dua peubah acak dan merupakan suatu fungsi
: ℝ → [ , ] yang didefinisikan oleh , = � , (Grimmet
dan Stirzaker 1992).
Definisi 14 (Fungsi Sebaran dan Kepekatan Peluang Bersama Dua Peubah Acak Kontinu)
Peubah acak dan disebut peubah acak kontinu yang menyebar bersama jika
, ℝ fungsi sebaran bersamanya dapat diekspresikan sebagai berikut
, = ∫ ∫−∞ −∞ , untuk suatu fungsi : ℝ → [ , ] yang
terintegralkan. Fungsi di atas disebut fungsi kerapatan peluang bersama peubah acak kontinu dan , , = , (Ross 1996).
Definisi 15 (Fungsi Kepekatan Peluang Marjinal)
Misalkan dan adalah peubah acak kontinu yang menyebar bersama dengan fungsi sebaran , dan fungsi kepekatan bersama , . Fungsi kepekatan peluang marjinal dari peubah acak dan adalah berturut-turut
= ∫∞ ,
−∞ dan = ∫ ,
∞
−∞
(Ross 1996).
Definisi 16 (Fungsi Kepekatan Peluang Bersyarat)
Misalkan dan adalah peubah acak kontinu dengan fungsi kepekatan peluang marjinal > , maka fungsi kepekatan peluang bersama dari dengan syarat
= adalah | | =� ,
� (Grimmet dan Stirzaker 1992).
Nilai Harapan
Definisi 17 (Nilai Harapan Peubah Acak Diskret)
Misalkan adalah peubah acak diskret dengan fungsi massa peluang = � = maka nilai harapan dari adalah [ ] = ∑ , asalkan jumlah tersebut konvergen mutlak (Hogg dan Craig 1995).
Definisi 18 (Nilai Harapan Peubah Acak Kontinu)
Misalkan adalah peubah acak kontinu dengan fungsi kepekatan peluang maka nilai harapan adalah [ ] = ∫−∞∞ , asalkan integralnya ada (Hogg dan Craig 1995).
Definisi 19 (Nilai Harapan Bersyarat)
5 dengan syarat = adalah [ | = ] = ∫−∞∞ | | (Hogg dan Craig 1995).
Teorema 1 (Teorema Dasar Kalkulus Bagian 1)
Jika kontinu pada [ , ], maka fungsi yang didefinisikan oleh = ∫
�
adalah kontinu pada [ , ] dan terdiferensialkan pada , dan ′ = . Bukti dapat dilihat pada Stewart (1998).
Definisi 20 (Himpunan dan Fungsi Konveks)
Misalkan S ⊂ ℝ� adalah himpunan vektor. Maka S disebut sebagai himpunan konveks jika untuk semua �, �′ S dan [ , ] maka − � + �′ S. Misalkan merupakan fungsi dengan peubah � yang terdefinisi pada himpunan konveks S, maka disebut sebagai fungsi konveks jika memenuhi persamaan
( − � + �′) − � + �′ (Osborne 1997).
Teorema 2 (Fungsi Konveks)
Misalkan fungsi yang memiliki turunan kedua. adalah fungsi konveks jika dan hanya jika � , ∀� S dan merupakan fungsi strictly convex jika
� > , ∀� S. Bukti dapat dilihat pada Osborne (1997).
Teorema 3 (Ketaksamaan Jensen)
Misalkan adalah peubah acak dengan [ ] berhingga dan adalah fungsi konveks, maka [ ] [ ] . Bukti dapat dilihat pada Krantz (1999).
Rantai Markov
Definisi 21 (Ruang State)
Misalkan ⊂ ℝ merupakan nilai dari barisan peubah acak, maka disebut ruang
state (Grimmet dan Stirzaker 1992).
Definisi 22 (Proses Stokastik)
Proses stokastik = { �, } adalah suatu koleksi dari peubah acak yang memetakan suatu ruang contoh Ω ke suatu ruang state (Ross 1996).
Dalam hal ini dianggap sebagai waktu dan nilai dari peubah acak � sebagai
state (keadaan) dari proses pada waktu .
Definisi 23 (Rantai Markov dengan Waktu Diskret)
Proses stokastik { �, = , , , … }, dengan ruang state{ , , , … , }, disebut rantai Markov dengan waktu diskret jika untuk setiap = , , , … berlaku
� � = | �− = , �− = �− , … , = = � � = | �− = =
6
Jadi untuk suatu rantai Markov, sebaran bersyarat dari sebarang state saat ini
� dengan syarat state yang lalu , , , … , �− dan state satu waktu sebelumnya �− adalah bebas terhadap semua state yang lalu, dan hanya bergantung pada state
satu waktu sebelumnya. Hal ini disebut sebagai sifat Markov (Markovian Property). Proses di atas dapat digambarkan sebagai -state rantai Markov dengan peluang transisi { } dengan , = , , , … , . Nilai dari menyatakan peluang bahwa jika proses tersebut berada pada state , maka berikutnya akan beralih ke state . Karena adalah nilai peluang dan proses tersebut harus bertransisi, maka
i. , untuk , { , , , … , }.
ii. ∑�= = , untuk { , , , … , }.
Peluang transisi ini dapat ditulis dalam matriks � yang disebut sebagai matriks transisi. � = ( )
��= [
… �
… �
⋮ ⋮
� �
⋮ ⋮
… ��
] dengan menyatakan baris dan
menyatakan kolom dari matriks �. Definisi 24 (Matriks Transisi)
Misalkan { �, = , , , … } adalah rantai Markov dengan ruang state
{ , , , … , }. Matriks transisi � = ( )
�� adalah matriks dari peluang transisi
= � � = | �− = untuk , { , , … , } (Grimmet dan Stirzaker 1992).
Definisi 25 (Terakses)
Peluang bahwa pada waktu ke- proses berada pada state dengan syarat state awal adalah dinotasikan . Suatu state disebut terakses dari state (notasi: → , jika ada sebuah bilangan bulat sehingga > di mana adalah peluang bahwa pada waktu ke- proses berada pada state dengan syarat state awal adalah (Ross 1996).
Definisi 26 (Berkomunikasi)
Dua state dan dikatakan berkomunikasi (notasi: ↔ ), jika state dapat diakses dari state dan state dapat diakses dari state (Ross 1996).
Definisi 27 (Kelas State)
Suatu kelas dari state adalah suatu himpunan takkosong sehingga semua pasangan state yang merupakan anggota dari berkomunikasi satu dengan yang lainnya, serta tak ada state yang merupakan anggota yang berkomunikasi dengan suatu state yang bukan anggota dari (Ross 1996).
Definisi 28 (Rantai Markov Tak Tereduksi)
7
Definisi 29 (First-Passage Time Probability)
menyatakan peluang bahwa mulai dari state , proses bertransisi untuk pertama kali ke state , terjadi pada waktu . Peluang ini disebut first-passage time probability. Jadi untuk setiap = , , , …
= � = , ≠ , untuk setiap − | =
, { , , , … }, dan = untuk semua , { , , , … }. Selanjutnya, untuk
setiap , { , , , … }, definisikan = ∑∞= (Ross 1996).
Definisi 30 (Recurrent dan Transient)
State disebut recurrent jika = dan disebut transient jika < (Ross 1996).
Teorema 4 (Recurrent dan Transient)
State adalah recurrent jika ∑∞= = ∞ dan transient jika ∑∞= < ∞. Bukti dapat dilihat pada Ross (1996).
Definisi 31 (Periode, Periodik, dan Aperiodik)
1. Suatu state disebut memiliki periode jika = untuk semua yang tidak habis dibagi , dan adalah bilangan bulat terbesar yang memenuhi sifat ini. Dengan kata lain, suatu state disebut memiliki periode jika adalah persekutuan pembagi terbesar (the greatest common divisor) bagi sehingga
> .
2. Suatu state dengan periode sama dengan satu disebut aperiodik, sedangkan
state dengan periode disebut periodik
(Ross 1996).
Definisi 32 (PositiveRecurrent dan Null Recurrent)
Suatu state disebut berulang positif (positive recurrent) jika state tersebut adalah berulang (recurrent) serta berlaku: jika proses dimulai dari state maka nilai harapan dari waktu sampai proses tersebut kembali ke state adalah bilangan terhingga (finite). State recurrent yang tidak positive recurrent disebut null recurrent (Ross 1996).
Definisi 33 (Ergodic)
Rantai Markov dengan positive recurrent dan aperiodik disebut ergodic (Ross 1996).
Teorema 5 (Rantai Markov Ergodic Tak Tereduksi)
Untuk rantai Markov ergodic tak tereduksi lim
→∞ ada dan nilainya tak tergantung
dari . � = lim
→∞ , adalah solusi unik tak negatif dari
� = ∑ �
�
=
, = , , … ,
8
∑ � =
�
=
.
Bukti dapat dilihat pada Ross (1996).
Definisi 34 (Vektor Peluang Steady State)
Vektor peluang � = � , � , � , … , �� , yang setiap komponennya menyatakan bahwa proses akan berturut-turut berada pada state , , , … , , untuk → ∞ di mana
� �= = ∑ � �= | �− = � �− =
�
=
= ∑ � �− = = �
�
=
disebut vektor peluang steady state atau sebaran steady state. Karena � adalah vektor peluang, maka harus memenuhi syarat bahwa semua unsurnya adalah bilangan taknegatif serta jumlahnya adalah sama dengan satu. Sebaran steady state
sering juga disebut sebaran stasioner atau sebaran setimbang (equilibrium distribution) dari rantai Markov yang bersangkutan (Ross 1996).
Algoritme
Expectation Maximization
(EM)
Misalkan {��, Θ} adalah himpunan ukuran peluang yang terdefinisi pada Ω, ℱ dan kontinu absolut terhadap � . Misalkan � ⊂ ℱ. Fungsi Likelihood yang digunakan untuk menghitung penduga parameter berdasarkan informasi � yaitu medan-� yang dibangun oleh adalah
= [ �� | �].�
Maximum Likelihood Estimator (MLE) didefinisikan oleh ̂ arg max
� Θ .
Umumnya MLE sulit dihitung secara langsung oleh karena itu algoritme
Expectation Maximization (EM) memberikan suatu metode aproksimasi berulang (iteratif). Langkah-langkah dalam metode tersebut adalah:
1. Atur nilai awal parameter ̂ dengan = .
2. Atur ∗ = ̂ dan hitung Φ , ∗ dengan Φ , ∗ = �∗[ ��
��∗| �].
3. Cari ̂ + arg max
� Θ Φ , ∗ .
4. Ganti dengan + dan ulangi langkah 2 sampai 4 hingga kriteria hentinya tercapai, yaitu ketika selisih ̂ + dan ̂ kurang dari suatu bilangan yang sangat kecil. Bilangan tersebut dapat ditentukan sesuai dengan seberapa besar ketelitian yang diinginkan.
Misalkan = log , karena turunan kedua dari selalu positif
9 maka merupakan fungsi konveks. Karena log merupakan fungsi konveks, maka berdasarkan ketaksamaan Jensen dapat dihasilkan barisan { ̂ , > } yang merupakan fungsi likelihood yang takturun, yaitu
log ( ̂ + ) − log ( ̂ ) Φ( ̂ + , ̂ ) .
Bentuk Φ , ∗ disebut Pseudo Likelihood bersyarat (Elliot 1995).
Mean Absolute Percentage Error
(MAPE)
Mean Absolute Percentage Error (MAPE) adalah rataan persentase kesalahan absolut pada tiap periode dibagi dengan nilai observasi yang nyata untuk periode tersebut. Rumus MAPE adalah sebagai berikut
� = %∑ | �− �
� | �=
dengan n menyatakan banyaknya data yang digunakan, � menyatakan nilai yang sebenarnya, dan � menyatakan nilai dugaan. (Mynsbrugge 2010)
MODEL
HIDDEN
MARKOV SATU WAKTU
SEBELUMNYA
Model
Hidden
Markov
Model hidden Markov terdiri atas sepasang proses stokastik { �, �}. { �} dengan state { , , … , } adalah proses penyebab kejadian yang tidak diamati secara langsung dan membentuk rantai Markov, sedangkan { �} adalah proses observasinya.
Pada saat � berada pada state � = , maka proses yang diamati � menyebar normal dengan nilai harapan dan ragam � . Fungsi kepekatan peluang bersyarat dari � dengan syarat � = adalah
�| �= =
√ �� exp (
−( �− )
� )
dengan = , , … , . Peluang tak bersyarat proses yang tidak diamati � berada pada state adalah
� �= = �
dengan { , , … , }. Karena { �} rantai Markov maka matriks peluang transisinya � = ( )
��
= � � = | �− =
dengan { , , … , }. Dari persamaan (1) dan (2) serta definisi fungsi kerapatan peluang bersyarat, maka didapatkan fungsi kerapatan peluang bersama � dan � =
, yaitu
(2) (1)
10
�, �= = �| �= ∙ � �=
= �
� √ �exp (
−( �− )
� )
sehingga
� � �; � = = ∫ �
� √ �exp (
−( �− )
� ) �
�
−∞ .
Berdasarkan Teorema Dasar Kalkulus bagian pertama didapatkan
�, � = = �∫
�
� √ �exp (
−( �− )
� ) �
�
−∞
= �
� √ �exp (
−( �− )
� ).
Fungsi kepekatan peluang marjinal tak bersyarat dari � diperoleh dengan menjumlahkan �, �= untuk semua kemungkinan nilai dari , yaitu:
� = ∑�= �, �= .
Dari persamaan (1), (2), (3), (4), dan (5) diperoleh
, … , � = ∑�= …∑��= � … �− � , = … �, � = .
Jadi karakteristik model hidden Markov dicirikan oleh parameter-parameternya yaitu: = { , �, �, �}, dengan = , , … , � , � = � , � , … , �� , � =
� , � , … , �� dan � = ( )�×�.
Model
Hidden
Markov Satu Waktu Sebelumnya
Karakteristik Model
Pada subbab ini akan dibahas model deret waktu hidden Markov satu waktu sebelumnya yang didefinisikan pada ruang state (Ω, ℱ, �) berupa persamaan berikut:
� = �∗ + � �−∗ �− + ��
dengan:
��~ , � bebas stokastik identik.
{ �} proses yang diamati dan bernilai skalar dengan ruang state . { �∗} rantai Markov dengan ruang state ∗ = { , } dan matriks transisi.
�∗= [ ∗ ∗
∗ ∗ ] dengan ∗ = � �∗ = | �−∗ = dan ∑ = = , ∀ =
, , , ∀ , = , .
c = , dan � = � , � ℝ , dengan , , dan � , � merupakan konstanta real.
�∗) =
�∗ dan � �−∗ =� �−∗ . = { , �∗, �, � }.
Karena � tidak hanya bergantung pada �∗ tetapi juga pada �−∗ , maka agar tetap memenuhi sifat Markov perlu didefinisikan peubah baru � di mana:
(7) (4)
11
� = , jika �∗ = dan �−∗ = � = , jika �∗ = dan �−∗ = � = , jika �∗ = dan �−∗ = � = , jika �∗ = dan �−∗ =
Lema 1
{ �} adalah rantai Markov dengan ruang state { , , , } dan matriks transisi:
� = [ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ].
Bukti dapat dilihat pada Lampiran 1.
Selanjutnya, karena ��~ , � bebas stokastik identik maka dapat diperoleh fungsi sebaran bagi ��:
�� � = � �� � = ∫ √ ��exp
− ��−
� ��
�
= ∫ √ ��exp − ��
� ��
� .
Berdasarkan persamaan (7) dan (9) diperoleh fungsi sebaran bagi �:
� � = � � � = � �∗ + � �−∗ �− + �� �
= � �� �− �∗ − � �−∗ �−
= ∫ √ ��exp − ��
� ��
�− �∗−� �−∗ �− .
Misalkan
= �− �∗ − � �−∗ �−
maka
� � = ∫ √ ��exp
− �� � �� � dan � � = � � � = � � � � �
= √ ��exp − �� �
�.
= √ ��exp − �− �∗−� �−∗ �−
� ×
= √ ��exp − �− �∗−� �−∗ �−
� .
Misalkan �� adalah medan-� yang dibangun oleh , , , … , �. Karena
� merupakan rantai Markov 4 state maka terdapat 4 fungsi kepekatan peluang bagi � . Kumpulan fungsi kerapatan peluang tersebut dalam vektor ×
dilambangkan dengan �, sehingga diperoleh:
12 = [ √ �� − �− −� �− � √ �� − �− −� �− � √ �� − �− −� �− � √ �� − �− −� �− � ] .
Misalkan ��|�− = ��|�− ��|�− ��|�− ��|�− � melambangkan vektor × di mana ��|�− pada vektor mempresentasikan � � = |��− ; dan ⊗ melambangkan perkalian dalam elemen per elemen, maka
��|�− ⊗ � = [ �� �= |��− ; �= |��− ; � �= |��− ; � �= |��− ; ] ⊗ [ �| �= , ��− ; �| �= , ��− ; �| �= , ��− ; �| �= , ��− ; ] = [ �� � = |��− ; ⋅ �| � = , ��− ; � = |��− ; ⋅ �| � = , ��− ; � � = |��− ; ⋅ �| � = , ��− ; � � = |��− ; ⋅ �| � = , ��− ; ] .
Berdasarkan persamaan (12) maka dapat ditulis:
� �, �= |��− ; = � � = |��− ; ∙ �| �= , ��− ; sehingga diperoleh: �|��− ; = ∑ = � �, � = |��− ; = ∑ = � � = |��− ; ∙ �| �= , ��− ; = � � = |��− ; ∙ �| � = , ��− ; +� � = |��− ; ∙ �| �= , ��− ; +� � = |��− ; ∙ �| �= , ��− ; +� � = |��− ; ∙ �| �= , ��− ; . �|��− ; = ∑ = � �, � = |��− ; = �′(�̂�|�− ⊗ �)
di mana �′ = [ ].
Berdasarkan persamaan (13) dan (14) maka dapat diperoleh
13 sehingga berdasarkan persamaan (13), (14), dan (15) diperoleh
� � = |��; = � �, �= |��− ; �|��− ; . �̂�|� = �̂�|�− ⊗ � �′(�̂�|�− ⊗ �). �̂�+ |� = � �+ = |��; = ∑ � �+ = | �= , ��; � � = |��; = = ∑ � �+ = | �= , ��; � = �̂�|� = ∑ = �̂�|�. = , , , . �̂�+ |� = [ ∗ �̂ �|� + ∗ �̂�|� ∗ �̂ �|� + ∗ �̂�|� ∗ �̂ �|� + ∗ �̂�|� ∗ �̂ �|� + ∗ �̂�|�] = [ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ] [ �̂�|� �̂�|� �̂�|� �̂�|�] = � ∙ �̂�|�. �̂�+ |� = ��∙ �̂�|�.
Salah satu pendekatan yang dapat digunakan untuk memilih nilai awal bagi �̂�|�− adalah dengan membuat �̂ | sama dengan vektor dari peluang tak bersyarat
� = [� � � � ] yang memenuhi sifat ergodic, yaitu:
�� = �
� + � + � + � = .
Pendugaan Parameter
Fungsi kepekatan peluang marjinal tak bersyarat dari � diperoleh dengan menjumlahkan �, � = ; untuk semua kemungkinan nilai dari , yaitu:
�; = ∑�= �, �= ; ��− .
, , , … , �; = ∏��= �|��−
sehingga fungsi log likehood untuk menduga parameter populasi adalah
= ∑ log �|��−
�
�=
Penduga kemungkinan maksimum likelihood ̂ diperoleh dengan memaksimumkan persamaan (22) dengan kendala � + � + � + � = dan � untuk = , , , . Untuk menyelesaikan masalah tersebut maka digunakan metode Lagrange, yaitu
= + − � − � − � − �
lalu persamaan (23) diturunkan masing-masing terhadap � , , dan � .
14
Berdasarkan persamaan (20), (22), dan (23) diperoleh
� � = − � − � − � − � = � + � + � + � = . � � � = � � � =
� ∑��= log �; = ∑ � �;� ∙
�
�= �| �= ; = .
� � = � � =
∑��= log �; = ∑��= � �;� ∙( ��− )∙� �, � = ; = .
� �
� =
� �
� =
� ∑��= log �; = ∑
� �, �= ;� � �;� ∙ − � + ( �− ) � � �= = .
Penduga kemungkinan maksimum bagi diperoleh dengan memaksimumkan: = ∑��= log �|��− ; dengan membuat turunan pertama dari log likehood terhadap parameter sama dengan nol, maka diperoleh
15 =
( �|��− ; ̂)� �= |��− ; ∙ ( �| � = , ��− ; ̂)
=
( �|��− ; ̂)� � = |��− ; ∙ ( �| �= , ��− ; ̂)
Bukti dapat dilihat pada Lampiran 2.
Karena persamaan (28) sampai (32) taklinear, maka untuk mencapai penduga kemungkinan maksimum bagi digunakan algoritme iteratif yang merupakan kasus khusus dari prinsip EM.
Langkah-langkah yang harus dilakukan adalah:
1. Tentukan banyaknya data (T) yang akan diamati serta tentukan juga nilai , , , … , � dan matriks transisi
� = [ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ].
2. Beri nilai awal bagi ̂ yang dilambangkan dengan ̂ = ( ̂ , ̂ , �̂ , �̂ , �̂ ). 3. Cari fungsi kepekatan bersyarat bagi � untuk setiap = , , … , dengan
cara � = [ ( �| �= , ��− ; ̂) ( �| �= , ��− ; ̂) ( �| �= , ��− ; ̂) ( �| �= , ��− ; ̂)] = [
√ ��̂exp (
−( �− ̂ − �̂ �− )
�̂ )
√ ��̂exp (
−( �− ̂ − �̂ �− )
�̂ )
√ ��̂exp (
−( �− ̂ − �̂ �− )
�̂ )
√ ��̂exp (
−( �− ̂ − �̂ �− )
�̂ )]
.
4. Penarikan kesimpulan optimal dan peramalan untuk setiap waktu pada contoh dapat diperoleh melalui iterasi:
4.1 Tentukan nilai awal bagi �̂�|�− yang dilambangkan dengan �̂ | 4.2 Beri nilai awal =
4.3 Untuk = , cari nilai dari
16
= �( � = |��− ; ̂) ∙√ ��̂exp (−( �− ̂ −�̂�̂ �− ) ) +
�( � = |��− ; ̂) ∙√ ��̂exp (−( �− ̂ −�̂�̂ �− ) ) +
�( � = |��− ; ̂) ∙√ ��̂exp (−( �− ̂ −�̂�̂ �− ) ) +
�( � = |��− ; ̂) ∙√ ��̂exp (−( �− ̂ −�̂�̂ �− ) ) .
�̂�|� =
[
�( � = |��; ̂)
�( � = |��; ̂)
�( � = |��; ̂)
�( � = |��; ̂)]
= �̂�|�− ⊗ �
�′(�̂�|�− ⊗ �)
�̂�+ |� =
[
�( �+ = |��; ̂)
�( �+ = |��; ̂)
�( �+ = |��; ̂)
�( �+ = |��; ̂)]
= � ∙ �̂�|�
= + .
4.4 Ulangi mulai dari langkah 4.3. Hentikan jika = . Lanjutkan ke langkah 5.
5. Misalkan =
( �|��− ; ̂ )�( � = |��− ; ̂ ) ∙ ( �| �= , ��− ; ̂ )
=
( �|��− ; ̂ )�( �= |��− ; ̂ ) ∙ ( �| � = , ��− ; ̂ )
=
( �|��− ; ̂ )�( � = |��− ; ̂ ) ∙ ( �| � = , ��− ; ̂ )
=
( �|��− ; ̂ )�( �= |��− ; ̂ ) ∙ ( �| �= , ��− ; ̂ )
cari nilai dari:
=∑ [ (= −�̂ − )+ ( −�̂ − )]
∑= + .
= ∑ [ (��= �− �̂∑ [ + ]��− ) + ( �− �̂ �− )]
�= .
� = ∑��= �−∑ [ �− ̂ + �− ̂ ]
�− [ + ]
�
�= .
� =∑��= �−∑ [ �− ̂ + �− ]
�− [ + ]
�
17
� = ∑ [ + + + ]�
�=
∙ ∑��= [ � − −� �− + �− −� �− +
�− −� �− + �− −� �− ].
6. Beri nama parameter yang dihasilkan pada langkah 4 dengan ̂ + = ( ̂ , ̂ , �̂ , �̂ , �̂ ) dan = , , , … , − .
7. Cari P yang baru, yaitu:
�̂�|� = �̂�|�⨀ {�′⋅ [�̂
�+ |� ÷ �̂�+ |�]}
̂ =∑��=∑� �� = , �+ = |��;
�+ = |��; �
�=
� �− = | � = , ��; = � � = |��; � �− = | � = , ��;
≈ � � = |��; � �− = | �= , ��;
=� � = |��; �� �− = | �= , ��;
�= |��;
=� � = |��; � ��− = |��; � �= | �− = ;
�= |��;
=�̂�|� × �̂�− |�− × �̂�|�
� �− = |��; = ∑ � �− = , � = |��;
�
=
(Kim 1994)
̂ =
∑ �̂�|�×�̂�− |�− ×�
�̂�|� �
�=
∑ ∑ �̂�|�×�̂�− |�− ×�
�̂�|� �
= � �=
Bukti dapat dilihat pada Hamilton (1990).
8. Ulangi mulai dari langkah 2. Hentikan jika = . Gunakan parameter yang sudah dihasilkan untuk mencari nilai harapan bagi nilai tukar Rupiah yang akan datang.
[ �| �= , ��− ; ] = [ �∗ + � �−∗ �− + ��| �= , ��− ; ]
= �∗ + � �−∗ ∫ �− �− | �= , ��− ; �
̂�= E[ �|��− ; ̂ � ] = ∫
18
= ∫ �∑ �(X� = |��− ; ̂ � ) ( �|X� = , ��− ; ̂� ) �
�
=
= ∑ ��|�− ⋅ E[ �|X� = , ��− ; ̂ � ] �
=
.
PEMODELAN NILAI TUKAR RUPIAH TERHADAP
DOLAR AMERIKA
Pada bab ini akan dibahas pemodelan nilai tukar Rupiah terhadap Dolar Amerika. Namun terlebih dahulu akan dibahas mengenai data input yang digunakan sebagai data observasi pada model. Kemudian dilanjutkan dengan pemodelan masalah nilai tukar Rupiah terhadap Dolar Amerika.
Data Input Nilai Tukar Rupiah
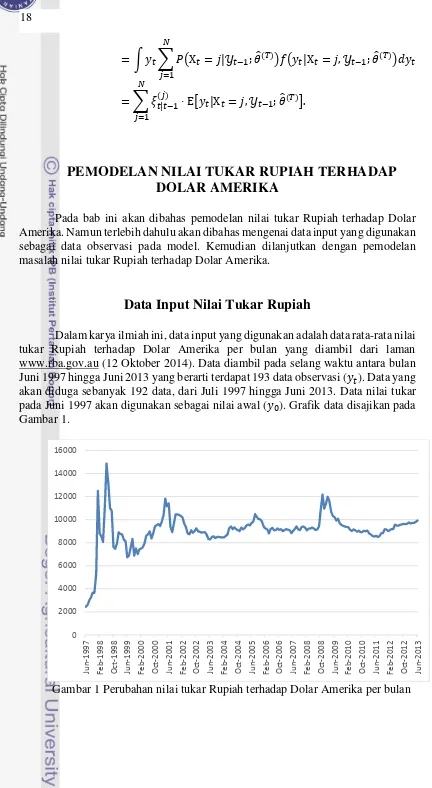
[image:28.595.66.498.47.835.2]Dalam karya ilmiah ini, data input yang digunakan adalah data rata-rata nilai tukar Rupiah terhadap Dolar Amerika per bulan yang diambil dari laman www.rba.gov.au (12 Oktober 2014). Data diambil pada selang waktu antara bulan Juni 1997 hingga Juni 2013 yang berarti terdapat 193 data observasi ( �). Data yang akan diduga sebanyak 192 data, dari Juli 1997 hingga Juni 2013. Data nilai tukar pada Juni 1997 akan digunakan sebagai nilai awal ( ). Grafik data disajikan pada Gambar 1.
Gambar 1 Perubahan nilai tukar Rupiah terhadap Dolar Amerika per bulan
[image:28.595.104.496.486.759.2]19
Model
Hidden
Markov Satu Waktu Sebelumnya
Perilaku nilai tukar Rupiah terhadap Dolar Amerika sudah pernah dimodelkan menggunakan model hidden Markov satu waktu sebelumnya oleh Setiawaty dan Ardana (2013), Santoso (2008), dan Retnoningtyas (2014).
Setiawaty dan Ardana (2013) menggunakan persamaan: �= �∗ + � �∗ �− + ��, sedangkan Santoso (2008) dan Retnoningtyas (2014)
menggunakan persamaan: �−
�∗ = �( �− − �∗) + ��, di mana { �∗} adalah rantai Markov, { � } adalah penyebab nilai tukar Rupiah dan �� menyebar normal. Pada Setiawaty dan Ardana (2013) diperoleh MAPE 4.31%, pada Retnoningtyas (2014) digunakan nilai awal = [ .
. ] , � = . , � = [ .. ], dan � = , dengan MAPE 4.14%.
Model hidden Markov yang akan digunakan pada tugas akhir ini adalah:
� = �∗ + � �−∗ �− + ��
seperti pada bab sebelumnya. Berdasarkan model di atas nilai tukar Rupiah saat ini diasumsikan tidak hanya bergantung pada faktor penyebab saat ini dan satu waktu sebelumnya, tetapi juga bergantung pada nilai tukar Rupiah satu waktu sebelumnya. Pada model hidden Markov di atas akan di cari nilai duga parameternya agar hasil yang didapat mendekati nilai yang sebenarnya. Pada tugas akhir ini akan dibangkitkan nilai awal yang tepat agar keakuratan model meningkat. Keakuratan dianggap baik bila MAPE < 5%.
Penentuan Nilai Awal Parameter
Data dibagi menjadi dua bagian, bagian pertama data dari Juni 1997 hingga Mei 2013 dan bagian kedua data dari Juli 1997 hingga Juni 2013 ( �), kedua data kemudian diplot. Nilai yang akan diplot adalah = � terhadap = �− . Persamaan baru yang didapatkan yaitu
= . + .
20
dengan nilai awal . , . . Hasil dari satu kali iterasi nilai pendugaan yang digunakan adalah . , . . Nilai awal � yang digunakan dibangkitkan dari interval [ . , ], dengan nilai awal . , . . Hasil dari satu kali iterasi nilai pendugaan � yang digunakan adalah . , . .
Penentuan Nilai Awal P
Sedangkan nilai awal P dibangkitkan secara acak dari interval peluang [0,1], karena . Hasil dari satu kali iterasi nilai pendugaan yang digunakan untuk � adalah [
.
. ..
.
. ..
].
Penentuan Nilai Awal �
Nilai awal untuk parameter � yang digunakan dibangkitkan dari interval nilai [100,2000] yang merupakan selang dari standar deviasanya. Nilai awal yang � dibangkitkan sebesar . . Hasil dari satu kali iterasi nilai pendugaan � yang digunakan adalah . × 7.
Hasil Program
Dari bagian sebelumnya nilai dugaan parameter yang digunakan untuk membangkitkan dugaan nilai tukar Rupiah adalah = . , =
. , � = . , � = . , � = . × 7. Galat nilai dugaan
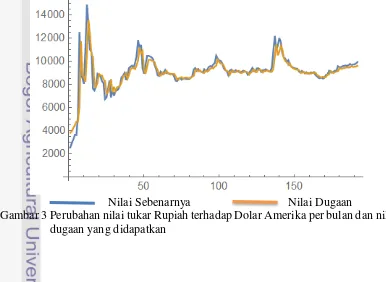
[image:30.595.85.471.519.801.2]yang ditunjukkan oleh MAPE sebesar 4.48037 % diperoleh melalui satu kali iterasi seperti yang tertera pada Lampiran 3. Hal ini terjadi karena pada karya ilmiah ini model dianggap baik apabila nilai dari MAPE < 5%. Nilai tukar Rupiah dan nilai dugannya tertera pada Lampiran 4. Hasil pendugaan model dapat dilihat pada Gambar 3.
Nilai Sebenarnya Nilai Dugaan
21
SIMPULAN
Model deret waktu hidden Markov satu waktu sebelumnya pada tugas akhir ini dapat memodelkan dengan cukup baik perubahan nilai tukar Rupiah terhadap Dolar Amerika. Hal ini terlihat dari nilai dugaan yang mendekati nilai sebenarnya, dengan MAPE yang dihasilkan sebesar 4.48%.
DAFTAR PUSTAKA
Baum LE, Petrie T. 1966. Statistical inference for probabilistic functions of finite Markov chain. Annal of Mathematical Statistics. 37(6):1554-1563.doi:10.1214/aoms/1177699147.
Elliot RJ, Anggoun L, Moore JB. 1995. Hidden Markov Models Estimation and Control. New York (US): Springer Verlag.
Grimmet GR, Stirzaker DR. 1992. Probability and Random Processes. Ed ke-2. Oxford (GB): Clarendon Press.
Hamilton JD. 1990. Analysis of time series subject to changes in regime. Journal of Econometrics. 45(2):39-70.doi:10.1016/0304-4076(90)90093-9.
Hogg RV, Craig AT. 1995. Introduction to Mathematical Statistics. Ed. ke-5. New Jersey (US): Prentice Hall, Englewood Cliffs.
Kim CJ. 1994. Dynamic linear models with Markov-switching. Journal of Econometrics. 60(2):1-22.doi:10.1016/0304-4076(94)90036-1.
Krantz SG. 1999. Handbook of Complex Variables. Boston (US): Birkhauser. Mynsbrugge JV. 2010. Bidding strategies using price based unit commitment in a
deregulated power market [tesis]. Leuven (BE): Katholieke Universiteit Leuven.
Osborne MJ. 1997. Concave and Convex Function of Many Variable. Canada (CA): University of Toronto.
Ross SM. 1996. Stochastic Process. Ed ke-2. New York (US): John Wiley & Sons. Royden HL. 1963. Real Analysis. New York (US): The Macmilan Company. Retnoningtyas A. 2014. Kajian Numerik Model Hidden Markov Satu Waktu
Sebelumnya Untuk Nilai Tukar Rupiah Terhadap Dolar Amerika [skripsi]. Bogor (ID): Institut Pertanian Bogor.
Santoso DH. 2008. Pemodelan Nilai Tukar Rupiah Terhadap US Dollar
Menggunakan Deret Waktu Hidden Markov Satu Waktu Sebelumnya [skripsi]. Bogor (ID): Institut Pertanian Bogor.
Setiawaty B, Ardana NKK. 2013. Modeling the exchange of Rupiah to American Dollar using hidden Markov. Presentation paper of IICMA 2013; 2013 Nov 6-8; Yogyakarta, Indonesia.
22
Lampiran 1 Bukti Lema 1
Karena { �∗} rantai Markov, maka { �} rantai Markov dengan matriks transisi
� = [ ].
Misalkan ∗ melambangkan � �∗ = | �−∗ = maka
= � �= | �− = = � �∗ = , �−∗ = | �−∗ = , �−∗ =
=� ��∗= , �−∗ = , �−∗ =
�−∗ = , �−∗ =
= � �∗= | �−∗ = , �−∗ = = � �∗ = | �−∗ = = ∗ .
= � � = | �− = = � �∗ = , �−∗ = | �−∗ = , �−∗ =
=� �∗= ,� �−∗ = , �−∗ = , �−∗ =
�−∗ = , �−∗ =
= .
Dengan cara perhitungan yang sama akan didapatkan
= ∗
=
= ∗
=
= ∗
=
=
= ∗
=
= ∗
=
= ∗
=
= ∗
maka diperoleh matriks transisi � = [
∗ ∗
∗ ∗ ∗ ∗
∗ ∗
23
Lampiran 2 Bukti persamaan (28) sampai dengan (32)
�|��− ; = ∑ = � �, �= |��− ;
= ∑ = � � = |��− ; ∙ �| �= , ��− ;
= � � = |��− ; ∙√ �� − �− −�� �− + � �= |��− ; ∙√ �� − �− −�� �−
+� �= |��− ; ∙√ �� − �− −�� �− + � � = |��− ; ∙√ �� − �− −�� �− .
Berdasarkan persamaan (14), diperoleh
� �|��− ;� = �
�= |��− ; ∙√ �� {− �− −�� �− } − ( �− −�� �− ) −
+� �= |��− ; ∙√ �� {− �− −�� �− } − ( �− �−� �− ) − .
= � �= |��− ; ∙ �| � = , ��− ; ( �− �−� �− )+� �= |��− ; ∙ �| � = , ��− ; ( �− �−� �− ).
Jika diketahui fungsi log-likelihood sebagai berikut
ℒ = ∑ log �|��− ;
�
�=
,
Untuk memperoleh nilai , , � , � , � yang memaksimumkan fungsi log-likehood, maka turunan pertama dari ℒ harus sama dengan nol.
ℒ � = ∑
� �|��− ;� ∙
� �|��− ;�
�
�=
⇔ ∑ [�
�|��− ;� � � = |��− ; ∙ �| � = , ��− ;
( �− −� �− )
� +
� �=
� �|��− ;� � � = |��− ; ∙ �| �= , ��− ;
( �− −� �− )
� ]
=
(14)
24
� ∑ [� �|��− ;� � � = |��− ; ∙ �| �= , ��− ; ( �− − � �− ) +
� �=
� �|��− ;� � � = |��− ; ∙ �| �= , ��− ; ( �− − � �− )]
=
∑ [�
�|��− ;� � � = |��− ; ∙ �| �= , ��− ; �− − � �− +
� �=
� �|��− ;� � �= |��− ; ∙ �| � = , ��− ; �− − � �− ]
=
∑ [�
�|��− ;� � � = |��− ; ∙ �| �= , ��− ; �− � �− +
� �=
� �|��− ;� � �= |��− ; ∙ �| � = , ��− ; �− � �− ]
= ∑ [�
�|��− ;� � � = |��− ; ∙ �| � = , ��− ; +� �|��− ;� � � = |��− ; ∙ �| �= , ��− ; ]
�
�=
= ∑ [�
�|��− ;� � �= |��− ; ∙ �| �= , ��− ; +� �|��− ;� � � = |��− ; ∙ �| �= , ��− ; ]
�
�= .
Misalkan
=
�|��− ; � � = |��− ; ∙ �| �= , ��− ;
=
�|��− ; � �= |��− ; ∙ �| � = , ��− ; .
maka dapat dituliskan
∑[ �− � �− + �− � �− ] = ∑ +
�
�= �
�=
25
⇔
=
∑ = [ (−
� − )+
(−
� − )]∑=
+
seperti yang telah diklaim pada persamaan (28). Berdasarkan persamaan (14) diperoleh
�( �|��− ;�̂)= �
�= |��− ; ∙√ �� − �− −�� �− − ( �− �−� �− ) − +
� � = |��− ; ∙√ �� − �− −�� �− − ( �− �−� �− ) −
= � � = |��− ; ∙ ( �| � = , ��− ; ̂)( �− �−� �− )+ � � = |��− ; ∙ ( �| � = , ��− ; ̂)( �− �−� �− )
ℒ �
= ∑ �(
�|��− ;�̂)∙
�( �|��− ;�̂)=
�
�=
⇔ ∑ [�(
�|��− ;�̂)� �= |��− ; ∙ ( �| �= , ��− ; ̂)
( �− −� �− )
� +
� �=
�( �|��− ;�̂)� � = |��− ; ∙ ( �| � = , ��− ; ̂)
( �− −� �− )
� ]
=
⇔� ∑ [�(
�|��− ;�̂)� � = |��− ; ∙ ( �| � = , ��− ; ̂) �− − � �− +
� �=
�( �|��− ;�̂)� �= |��− ; ∙ ( �| � = , ��− ; ̂) �− − � �− ]
=
26
∑ [�(
�|��− ;�̂)� � = |��− ; ∙ ( �| � = , ��− ; ̂) �− − � �− +
� �=
�( �|��− ;�̂)� �= |��− ; ∙ ( �| � = , ��− ; ̂) �− − � �− ]
=
⇔ ∑ [�(
�|��− ;�̂)� �= |��− ; ∙ ( �| �= , ��− ; ̂) �− � �− +
� �=
�( �|��− ;�̂)� � = |��− ; ∙ ( �| � = , ��− ; ̂) �− � �− ]
= ∑ [�(
�|��− ;�̂)� � = |��− ; ∙ ( �| �= , ��− ; ̂) +�( �|��− ;�̂)� �= |��− ; ∙ ( �| � = , ��− ; ̂) ]
�
�=
= ∑ [�(
�|��− ;�̂)� �= |��− ; ∙ ( �| �= , ��− ; ̂) +�( �|��− ;�̂)� �= |��− ; ∙ ( �| �= , ��− ; ̂)]
�
�= .
Misalkan
=
( �|��− ; ̂)� �= |��− ; ∙ ( �| � = , ��− ; ̂)
=
( �|��− ; ̂)� � = |��− ; ∙ ( �| � = , ��− ; ̂)
maka dapat dituliskan
∑[ �− � �− + �− � �− ]
�
�=
= ∑[ + ]
�
�=
= −∑ [��= �− �∑ [ + ]��− + �− � �− ]
�=
seperti yang diklaim pada persamaan (29).
27 Berdasarkan persamaan (14) diperoleh
� �|��− ,�
� = � � = |��− ; ∙√ �� {
− �− −� �−
� }
− ( �− −� �− ) − �−
�
+� �= |��− ; ∙√ �� {− �− −�� �− } − ( �− −�� �− ) − �−
= � � = |��− ; ∙√ �� {− �− −�� �− }( �− −�� �− ) �−
+� �= |��− ; ∙√ �� {− �− −�� �− }( �− −�� �− ) �− .
ℒ �
� = ∑ � �|��− ,� ∙
�
�= �( �|���− ,�̂)=
∑ [�
�|��− ,� � � = |��− ; ∙ �| � = , ��− ,
( �− −� �− ) �−
� +
� �=
� �|��− ,� � �= |��− ; ∙ �| � = , ��− ,
( �− −� �− ) �−
� ]
=
� ∑ [� �|��− ,� � �= |��− ; ∙ �| � = , ��− , ( �− − � �− ) �− +
� �=
� �|��− ,� � � = |��− ; ∙ �| �= , ��− , ( �− − � �− ) �− ]
=
∑ [�
�|��− ,� � � = |��− ; ∙ �| � = , ��− , ( �− − � �− ) �− +
� �=
� �|��− ,� � � = |��− ; ∙ �| �= , ��− , ( �− − � �− ) �− ]
=
28
∑ [�
�|��− ,� � � = |��− ; ∙ �| � = , ��− , �− − � �− �− +
� �=
� �|��− ,� � �= |��− ; ∙ �| � = , ��− , �− − � �− �− ]
=
∑ [�
�|��− ,� � � = |��− ; ∙ �| � = , ��− , �− �− +
� �=
� �|��− ,� � �= |��− ; ∙ �| � = , ��− , �− �− ]
= ∑ [�
�|��− ,� � �= |��− ; ∙ �| � = , ��− , � �− �− +
� �=
� �|��− ,� � �= |��− ; ∙ �| � = , ��− , � �− �− ]
= � ∑ [�
�|��− ,� � �= |��− ; ∙ �| � = , ��− , �− +
� �=
� �|��− ,� � �= |��− ; ∙ �| � = , ��− , �− ].
Misalkan
=
( �|��− ; ̂)� � = |��− ; ∙ ( �| �= , ��− ; ̂)
=
( �|��− ; ̂)� �= |��− ; ∙ ( �| � = , ��− ; ̂)
sehingga diperoleh
∑ [�=� �− �− + �− �− ]= � ∑ [��= �− + �− ]
� = ∑ [��= ∑ [�− �− + �− �− ]
�− + �− ]
� �=
29
� = ∑��= �−∑ [ �− + �− ]
�− [ + ]
� �=
seperti yang diklaim pada persamaan (30). Berdasarkan persamaan (14) diperoleh
� �|��− ,�
� = � � = |��− ; ∙√ �� {
− �− −� �−
� }
− ( �− −� �− ) − �−
�
+� � = |��− ; ∙√ �� {− �− −�� �− } − ( �− −�� �− ) − �−
= � � = |��− ; ∙√ �� {− �− −�� �− }( �− −�� �− ) �−
+� � = |��− ; ∙√ �� {− �− −�� �− }( �− −�� �− ) �− .
ℒ �
� = ∑ � �|��− ,� ∙
�
�= � �|���− ,� =
∑ [�
�|��− ,� � � = |��− ; ∙ �| � = , ��− ,
( �− −� �− ) �−
� +
� �=
� �|��− ,� � �= |��− ; ∙ �| � = , ��− ,
( �− −� �− ) �−
� ]
=
∑ [�
�|��− ,� � � = |��− ; ∙ �| � = , ��− ,
�− �− − � �− �−
� +
� �=
� �|��− ,� � �= |��− ; ∙ �| � = , ��− ,
�− �− − � �− �−
� ]
=
30
� ∑ [� �|��− ,� � �= |��− ; ∙ �| � = , ��− , �− �− − � �− �− +
� �=
� �|��− ,� � � = |��− ; ∙ �| �= , ��− , �− �− − � �− �− ]
=
∑ [�
�|��− ,� � � = |��− ; ∙ �| � = , ��− , �− �− − � �− �− +
� �=
� �|��− ,� � � = |��− ; ∙ �| �= , ��− , �− �− − � �− �− ]
=
∑ [�
�|��− ,� � � = |��− ; ∙ �| � = , ��− , �− �− − � �− +
� �=
� �|��− ,� � �= |��− ; ∙ �| � = , ��− , �− �− − � �− ]
=
∑ �− [�
�|��− ,� � � = |��− ; ∙ �| �= , ��− , �− +
� �=
� �|��− ,� � � = |��− ; ∙ �| �= , ��− , �− ]
= ∑ [�
�|��− ,� � �= |��− ; ∙ �| � = , ��− , � �− +
� �=
� �|��− ,� � �= |��− ; ∙ �| � = , ��− , � �− ]
= � ∑ [�
�|��− ,� � � = |��− ; ∙ �| �= , ��− , �− +
� �=
� �|��− ,� � � = |��− ; ∙ �| �= , ��− , �− ].
31 Misalkan
=
( �|��− ; ̂)� �= |��− ; ∙ ( �| �= , ��− ; ̂)
=
( �|��− ; ̂)� � = |��− ; ∙ ( �| � = , ��− ; ̂)
maka dapat dituliskan
∑�=� �− [ �− + �− ]= � ∑ [��= �− + �− ]
� =∑��= ∑ [�− [ �− + �− ]
�− + �− ]
� �=
� =∑��= �−∑[ �− + �− ]
�− [ + ]
� �=
Seperti yang telah diklaim pada persamaan (31).
� �| �− ;�
� = � �= |��− ; −
�
�� − (−( �− −� �− )
� ) + � �= |��− ; √ �� (
−( �− −� �− )
� )
( �− −� �− )
�
+� �= |��− ; − � �� − (−( �− �−� �− ) ) + � �= |��− ; √ �� (−( �− �−� �− ) )( �− −�� �− )
+� �= |��− ; − � �� − (−( �− �−� �− ) ) + � �= |��− ; √ �� (−( �− �−� �− ) )( �− −�� �− )
+� �= |��− ; − � �� − (−( �− �−� �− ) ) + � �= |��− ; √ �� (−( �− �−� �− ) )( �− −�� �− ) .
� �| �− ;�
� = −� � = |��− ;
�
�� √ �� (
−( �− −� �− )
� ) + � � = |��− ; √ �� (
−( �− −� �− )
� )
( �− −� �− )
�
32
−� �= |��− ; �� √ ��� (−( �− �−� �− ) ) + � �= |��− ; √ �� (−( �− �−� �− ) )( �− −�� �− )
−� �= |��− ; �� √ ��� (−( �− �−� �− ) ) + � �= |��− ; √ �� (−( �− �−� �− ) )( �− −�� �− )
−� � = |��− ; �� √ ��� (−( �− �−� �− ) ) + � � = |��− ; √ �� (−( �− �−� �− ) )( �− −�� �− )
= � �= |��− ; √ �� (−( �− �−� �− ) ) (−� +( �− −�� �− ) ) +
� �= |��− ; √ �� (−( �− �−� �− ) ) (−� +( �− −�� �− ) ) +
� �= |��− ; √ �� (−( �− �−� �− ) ) (−� +( �− −�� �− ) ) +
� �= |��− ; √ �� (−( �− �−� �− ) ) (−� +( �− −�� �− ) )
= � �= |��− ; √ �� (−( �− �−� �− ) ) (−� +( �−� −� �− ) ) +
� �= |��− ; √ �� (−( �− �−� �− ) ) (−� +( �−� −� �− ) ) +
� �= |��− ; √ �� (−( �− �−� �− ) ) (−� +( �−� −� �− ) ) +
� �= |��− ; √ �� (−( �− �−� �− ) ) (−� +( �−� −� �− ) ) +.
33
ℒ �
� = ∑ � �|��− ,� ∙
�
�= � �|���− ;� =
∑ [�
�|��− ,� � �= |��− ; �| �= , ��− ; (
−� +( �− −� �− )
� ) +
� �=
� �|��− ,� � �= |��− ; �| �= , ��− ; (
−� +( �− −� �− )
� ) +
� �|��− ,� � �= |��− ; �| �= , ��− ; (
−� +( �− −� �− )
� ) +
� �|��− ,� � �= |��− ; �| �= , ��− ; (
−� +( �− −� �− )
� )]
=
∑ [�
�|��− ,� � � = |��− ; �| � = , ��− ; ( �− − � �− ) +
� �=
� �|��− ,� � �= |��− ; �| �= , ��− ; ( �− − � �− ) +
� �|��− ,� � �= |��− ; �| �= , ��− ; ( �− − � �− ) +
� �|��− ,� � �= |��− ; �| �= , ��− ; ( �− − � �− ) ]
= � ∑ [�
�|��− ,� � � = |��− ; �| � = , ��− ; +� �|��− ,� � � = |��− ; �| �= , ��− ; +
� �=
� �|��− ,� � � = |��− ; �| �= , ��− ; +� �|��− ,� � � = |��− ; �| � = , ��− ; ] .
Misalkan
=
�|��− ; � � = |��− ; ∙ �| �= , ��− ;
34
=
�|��− ; � �= |��− ; ∙ �| � = , ��− ;
=
�|��− ; � �= |��− ; ∙ �| � = , ��− ;
=
�|��− ; � � = |��− ; ∙ �| �= , ��− ;
maka dapat dituliskan
∑��= [ ( �− − � �− ) + ( �− − � �− ) + ( �− − � �− ) + ( �− − � �− ) ]= � ∑ [ + + + ]��=
� =∑ [ ( �− − � �− ) + ( �− − � �− ) + ( �− − � �− ) + ( �− − � �− ) ]
� �=
∑ [ + + + ]�
�= .
Seperti yang diklaim pada persamaan (32).
35
Lampiran 3 Program untuk mencari nilai dugaan parameter menggunakan
39
41
Lampiran 4 Nilai tukar Rupiah terhadap Dolar Amerika dan nilai dugaannya
t Nilai Rupiah Nilai Dugaan t Nilai Rupiah Nilai Dugaan
1 2604.67 3834.63 45 10415.10 9630.26
2 2990.20 3970.84 46 11820.00 10081.70
3 3278.69 4272.48 47 11154.90 11180.90
4 3665.43 4498.19 48 11410.80 10660.50
5 3649.86 4800.78 49 9365.21 10860.80
6 5350.08 4788.59 50 8921.75 9260.27
7 12499.60 6118.84 51 9685.15 8913.31
8 8800.59 11712.6 52 10455.20 9510.59
9 8549.89 8818.51 53 10459.60 10133.10
10 8050.47 8622.36 54 10399.50 10116.50
11 11175.40 8231,62 55 10328.90 10069.50
12 14875.30 10676.60 56 10189.80 10014.20
13 13199.70 13571.40 57 9655.76 9905.41
14 10999.80 12260.40 58 9319.99 9487.59
15 10788.90 10539.20 59 8789.21 9224.89
16 7625.74 10374.20 60 8730.52 8809.61
17 7474.30 7899.31 61 9079.96 8763.69
18 7929.63 7780.83 62 8866.59 9037.09
19 8900.73 8137.07 63 9011.96 8870.15
20 8763.05 8896.86 64 9237.44 8983.89
21 8725.57 8789.14 65 8976.46 9160.30
22 8275.23 8759.82 66 8949.13 8956.11
23 8129.72 8407.47 67 8874.92 8934.73
24 6729.84 8293.62 68 8901.55 8876.67
25 6875.77 7198.36 69 8903.25 8897.50
26 7609.34 7312.54 70 8675.76 8898.83
27 8324.66 7886.48 71 8319.53 8720.84
28 6875.58 8446.14 72 8279.89 8442.13
29 7500.00 7312.39 73 8505.13 8411.12
30 7012.85 7800.93 74 8559.38 8587.34
31 7433.41 7419.79 75 8400.24 8629.79
32 7483.31 7748.83 76 8495.60 8505.28
33 7615.19 7787.87 77 8505.41 8579.89
34 7950.58 7891.06 78 8470.67 8587.56
35 8620.75 8153.47 79 8452.38 8560.38
36 8735.38 8677.80 80 8462.64 8546.07
37 8979.73 8767.49 81 8583.48 8554.10
38 8364.65 8958.67 82 8689.75 8648.64
39 8790.72 8477.43 83 9263.61 8731.79
40 9415.31 8810.79 84 9412.11 9180.78
41 9527.45 9299.47 85 9182.65 9296.96
42 9615.52 9387.20 86 9333.90 9117.43
43 9445.66 9456.11 87 9175.88 9235.77
42
t Nilai Rupiah Nilai Dugaan t Nilai Rupiah Nilai Dugaan
89 9017.36 9043.84 134 9152.68 9060.28
90 9309.37 8988.11 135 9429.71 9093.99
91 9160.64 9216.58 136 10875.80 9310.73
92 9265.02 9100.21 137 12174.40 10442.10
93 9489.57 9181.88 138 10949.80 11458.20
94 9574.96 9357.57 139 11354.50 10500.00
95 9506.42 9424.38 140 11989.50 10826.70
96 9718.48 9370.75 141 11615.00 11313.50
97 9819.62 9536.67 142 10682.70 11020.50
98 10475.20 9615.80 143 10314.70 10291.10
100 10215.40 1-128.70 144 10223.10 10003.20
101 10049.40 9925.42 145 9915.47 9931.46
102 10024.40 9795.59 146 10079.80 9690.79
103 9825.54 9775.99 147 9670.49 9819.38
104 9387.48 962