A Comparation Between SVD and SSVD Method on Image Compression

PERBANDINGAN METODE SVD DAN SSVD

PADA KOMPRESI CITRA

KHAERONI

SEKOLAH PASCA SARJANA

INSTITUT PERTANIAN BOGOR

PERYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis dengan judul Perbandingan Metode SVD dan SSVD pada Kompresi Citra adalah karya saya sendiri dengan arahan dari komisi pembimbing, dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Februari 2012

ABSTRACT

KHAERONI. A Comparation Between SVD and SSVD Method on Image Compression. Supervised by SRI NURDIATI and SISWADI.

Data compression is the process of converting an input data into other data which has a smaller size. The data can be a file on a computer or a buffer in the computer’s memory. Compression is useful because it helps reduce the consumption of resources such as data space or transmission capacity. The use of singular value decomposition (SVD) in image compression has been widely studied. If the image, when considered as a matrix, has low rank, or can be approximated sufficiently well by a matrix of low rank, then SVD can be used to find this approximation. That is, by not include some elements of the image, the approximation has been able to represents the original image. This thesis presents a variation for SVD image compression technique proposed by Ranade et al. called SSVD. This variation can be viewed as a preprocessing step in which the input image is permuted by independent data permutation after it is fed to the standard SVD algorithm. Likewise, this decompression algorithm can be viewed as the standard SVD algorithm followed by a postprocessing step which applies the inverse permutation. On experimenting with some standard images, SSVD performs substantially better than SVD. This thesis also presents experiment evidence with other simulated images, which appears that SSVD isn’t better than SVD.

RINGKASAN

KHAERONI. Perbandingan Metode SVD dan SSVD pada Kompresi Citra. Dibimbing oleh SRI NURDIATI dan SISWADI.

Kompresi data adalah proses mengubah sebuah data masukan menjadi data yang lain yang memiliki ukuran yang lebih kecil. Data tersebut bisa berupa file di komputer atau sebuah buffer di dalam memori komputer. Tujuan kompresi pada citra adalah untuk mengurangi ketidakrelevanan dan redundansi data citra dengan maksud agar disimpan atau dikirimkan dalam bentuk yang lebih efisien.

Pemanfaatan singular value decomposition (SVD) atau dekomposisi nilai singular untuk mengompres citra telah cukup lama dipelajari. Jika suatu matriks citra berpangkat rendah atau dapat diaproksimasi cukup baik oleh suatu matriks yang juga berpangkat rendah, maka SVD dapat digunakan untuk menentukan aproksimasi tersebut (Ranade et al. 2006). Artinya, dengan tidak menyertakan beberapa elemen dari citra aproksimasi tersebut sudah dapat merepresentasikan citra aslinya.

Ranade et al. (2006) menjelaskan salah satu modifikasi dari proses atau metode kompresi menggunakan SVD dan dari beberapa percobaan memberikan hasil kompresi yang lebih baik dibandingkan dengan metode kompresi SVD. Metode modifikasi ini dikenal dengan nama shuffle-SVD (SSVD). Dinamakan demikian karena sebelum dilakukan dekomposisi, matriks A terlebih dahulu dipermutasi dengan sebuah data permutasi independen.

Ranade et al. (2006) mengklaim bahwa teknik shuffle yang diterapkan terhadap metode SVD untuk mengompres citra selalu memberikan hasil yang lebih baik daripada tanpa menerapkan shuffle. Demikian juga dengan Hafsah et al. (2007) menyatakan bahwa metode SSVD selalu lebih baik daripada metode SVD dalam mengompres citra.

Tujuan dari penelitian ini adalah untuk menyusun algoritme kompresi citra menggunakan SVD dan SSVD kemudian mengetahui efektivitas penerapan teknik shuffle terhadap metode SVD dan mengetahui benar atau tidaknya klaim bahwa teknik shuffle yang diterapkan pada metode SVD selalu memberikan hasil yang lebih baik daripada tanpa di-shuffle sebelumnya.

Penelitian ini menggunakan metode studi literatur dan kemudian mengimplementasikan metode kompresi citra ke dalam program komputer menggunakan software MATLAB. Pada bagian awal, diberikan contoh implementasi metode SVD dan SSVD pada beberapa matriks. Langkah ini dilakukan untuk melihat apakah SSVD selalu bekerja lebih baik daripada metode SVD. Selain itu pada penelitian ini kedua metode juga diterapkan pada beberapa citra yang direpresentasikan oleh sebuah matriks. Tujuan dari langkah ini adalah untuk mengetahui apakah metode SSVD selalu memberikan hasil yang lebih baik dibandingkan dengan metode SVD.

menggunakan bahasa pemrograman MATLAB. Tahap kedua adalah membandingkan efektivitas teknik shuffle yang diajukan oleh Ranade et al. (2006) dengan cara menerapkan teknik tersebut terhadap metode SVD untuk beberapa citra dan kemudian menghitung MSE yang dihasilkan oleh setiap metode. Tahap ketiga adalah memberikan contoh kontra ketidakefektifan teknik shuffle tersebut.

Untuk membandingkan perbedaan metode SVD dan SSVD dilakukan dengan cara mengukur kualitas citra hasil kompresi dari masing-masing metode. Untuk menentukan kualitas citra yang telah dikompres digunakan pengukuran baku yaitu MSE. Semakin kecil nilai MSE antara citra asli dan citra hasil kompresi, semakin baik kompresi citra tersebut (Hafsah 2007).

Kompresi citra menggunakan SVD pertama kali dilakukan dengan mengambil nilai piksel citra melalui MATLAB. Kemudian ditentukan SVD matriks A dengan menggunakan built in function MATLAB yaitu svd() untuk menentukan matriks U,  dan V. Langkah berikutnya adalah memotong nilai U,  dan V sesuai dengan rank yang diinginkan, misalnya p, sehingga diperoleh nilai Up, p dan Vp. Terakhir matriks Ap diperoleh dengan cara merekonstruksi Up, p dan Vp.

Langkah kompresi citra menggunakan SSVD didahului dengan melakukan permutasi terhadap matriks citra A dengan suatu permutasi independen P yang disebut dengan shuffle (Ranade et al. 2006). Matriks yang dihasilkan, misalkan X = P(A) kemudian didekomposisi menggunakan SVD. Misalkan





1 T

p p p p

X P U  V merupakan aproksimasi untuk A.

Proses shuffle ini dilakukan dengan harapan bahwa rank matriks citra akan berkurang dari rank sebelumnya. Pada beberapa citra, proses shuffle yang diterapkan tidak mengurangi nilai rank atau justru menjadi lebih besar dari rank sebelumnya walau dengan tingkat ketelitian atau toleransi yang cukup besar.

Dari hasil pengujian terhadap citra lena484.jpg, dapat disimpulkan bahwa teknik shuffle yang diterapkan pada metode SVD bekerja cukup efektif. Terbukti bahwa, selain mengurangi MSE teknik shuffle yang diterapkan juga mampu mengurangi ukuran file citra menjadi lebih kecil daripada metode SVD sendiri. Akan tetapi, untuk citra sample_101.jpg, pada beberapa kasus, teknik shuffle yang diterapkan baik pada metode SVD maupun SSVD memperlihatkan perilaku yang berbeda dengan sebelumnya. Penerapan teknik shuffle justru memperbesar MSE dan ukuran file citra walaupun dengan perbedaan yang sangat kecil. Demikian juga untuk citra sample_900.jpg.

Secara umum dapat disimpulkan bahwa teknik shuffle yang diterapkan pada metode SVD tidak selalu bekerja lebih baik daripada metode SVD sendiri. Pada beberapa citra, metode SSVD bekerja lebih baik. Akan tetapi pada citra yang lain metode SSVD tidak bekerja lebih baik. Jadi efektivitas metode SSVD juga ditentukan oleh pemilihan sampel citra yang digunakan. Selain itu, metode SSVD juga bergantung pada pemilihan rank (parameter kompresi). Dengan demikian justifikasi bahwa metode SSVD bekerja selalu lebih baik daripada metode SVD tidak dapat dibenarkan.

© Hak Cipta milik IPB, tahun 2012 Hak Cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah.

b. Pengutipan tersebut tidak merugikan kepentingan yang wajar IPB. 2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya

PERBANDINGAN METODE SVD DAN SSVD

PADA KOMPRESI CITRA

KHAERONI

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

SEKOLAH PASCA SARJANA

INSTITUT PERTANIAN BOGOR

Judul Tesis : Perbandingan Metode SVD dan SSVD pada Kompresi Citra Nama : Khaeroni

NRP : G551090341

Disetujui Komisi Pembimbing :

Dr. Ir. Sri Nurdiati, M.Sc Dr. Ir. Siswadi, M.Sc

Ketua Anggota

Diketahui :

Ketua Program Studi Dekan Sekolah Pascasarjana

Matematika Terapan

Dr. Ir. Endar H. Nugrahani, M.S. Dr. Ir. Dahrul Syah, M.Sc.Agr.

PRAKATA

Segala puja dan puji syukur hanya pantas bermuara pada Allah SWT. Dia– lah yang memberikan kita sebanyak–banyak kenikmatan. Sebesar apapun kesyukuran kita, tidak akan pernah bisa menyamai kenikmatan yang telah Dia berikan. Maha Suci Engkau dengan segala Kuasa-Mu. Atas Kuasa-Nya pula, tesis yang berjudul Perbandingan Metode SVD dan SSVD pada Kompresi Citra ini dapat penulis selesaikan.

Penulis mengakui dan menyadari bahwa selama proses penulisan tugas akhir ini tidak luput dari bantuan banyak pihak. Mulai dari material, moral, spiritual, dan juga psikologis. Karena itu, dalam kesempatan kali ini penulis hendak menyampaikan sebanyak-banyak terima kasih kepada:

1. Allah SWT yang telah menganugerahi kita hikmah. Sehingga kita diberi pemahaman melebihi malaikat. Kasih Sayang-Nya yang tiada batas, menghindarkan kita dari kejahiliahan.

2. Istri tercinta, Sri Apriatni, S.Pd atas do’a, dukungan, dan kesabarannya.

3. Bapak Rektor dan Dekan Fakultas Tarbiyah dan Adab serta Bapak EkoWahyu Wibowo, M.Si selaku atasan penulis di Pusat Komputer IAIN “SMH” Banten yang telah memberikan izin untuk melanjutkan studi di SPs IPB.

4. Ibu Dr. Ir. Sri Nurdiati, M.Sc dan Bapak Dr. Ir. Siswadi, M.Sc, selaku komisi pembimbing yang telah memberikan pengarahan, masukan, dan bimbingan, serta bersedia untuk direpotkan.

5. Bapak Dr. Sugi Guritman sebagai penguji luar komisi yang telah memberikan masukan dan koreksi yang sangat berharga saat ujian tesis.

6. Segenap dosen Program Studi Matematika Terapan SPs IPB.

7. Bapak, ibu, kakak, dan adik-adikku tercinta atas doanya untuk penulis.

8. Teman-teman mahasiswa Program Studi Matematika Terapan SPs IPB, khususnya angkatan 2009.

9. Serta semua pihak yang tidak bisa penulis sebutkan satu-per-satu. Semoga setiap yang penulis libatkan dalam penyusunan tesis ini dibalas setiap kebaikannya dengan kebaikan yang lain secara berlipat.

Sebuah kenyataan bahwa tesis ini masih terdapat banyak kekurangan. Oleh karena itu, saran dan kritik demi perbaikan dan kemajuan penulis dalam penyusunan karya ilmiah dikesempatan yang akan datang sangat penulis nantikan melalui e-mail khaeroni@iainbanten.ac.id atau web site www.khaeroni.net. Semoga karya yang sederhana ini dapat bermanfaat bagi ummat. Khoirunnas an fa ahum linnas. In tansurullaha yan surkum wa yu tsabbit aqdaa ma kum. Sebaik-baik manusia adalah yang paling bermanfaat bagi manusia. Barang siapa yang menolong agama Allah, niscaya Allah akan menolongnya dan meneguhkan pijakannya.

Bogor, Februari 2012

RIWAYAT HIDUP

Penulis dilahirkan di Serang pada tanggal 18 Maret 1983 dari Bapak Abdul Adim dan Ibu Yumnah. Penulis merupakan anak kelima dari tujuh bersaudara.

Tahun 2001 penulis lulus dari SMA Negeri 1 Serang dan lulus seleksi masuk Universitas Gadjah Mada melalui jalur Ujian Masuk Perguruan Tinggi Negeri (UMPTN) pada Program Studi Matematika Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam dan selesai pada tahun 2005.

DAFTAR ISI

Halaman

DAFTAR TABEL ... ... xi

DAFTAR GAMBAR ... ... xii

DAFTAR LAMPIRAN ... ...xiv

I. PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Rumusan Penelitian ... 3

1.3 Tujuan Penelitian ... 3

II. TINJAUAN PUSTAKA ... 5

2.1 Nilai Singular ... 5

2.2 Norm Vektor ... 5

2.3 Norm Matriks ... 5

2.3.1 Norm Frobenius ... 6

2.3.2 p-norm Matrix ... 6

2.4 Mean Square Error ... 6

2.5 Dekomposisi Nilai Singular ... 7

2.6 Ruang Null dan Ruang Kolom ... 8

2.7 Rayleigh Quotient ... 9

2.8 Diagonalisasi ... 10

2.9 Karhunen–Loève Transform ... 10

2.10 Konsep Dasar Kompresi Data ... 11

2.10.1 Principal Component Basis ... 13

2.11 Konsep Teori Informasi ... 14

2.12 Aproksimasi Matriks Rank Rendah ... 15

2.13 Citra Digital ... 15

2.13.1 Representasi Citra Digital ... 15

2.13.2 Menyimpan dan Menampilkan Citra Digital ... 18

2.13.3 Tipe Citra Digital pada MATLAB ... 20

2.14 Kompresi Citra Digital ... 21

2.14.1 Teknik Kompresi Citra Digital ... 23

2.14.2 Kompresi Citra dengan SVD ... 26

2.14.3 Kompresi Citra dengan SSVD ... 27

2.14.4 Atribut Kompresi Citra Digital ... 29

2.15 Citra dan Pengolahan Citra di MATLAB ... 30

2.15.1 Membaca dan Menulis File Citra ... 30

2.15.2 Menampilkan Citra di MATLAB ... 32

III. METODE PENELITIAN ... 35

3.3.2 Membandingkan Efektivitas Teknik Shuffle ... 37 IV. HASIL DAN PEMBAHASAN ... 43

DAFTAR TABEL

Halaman 2.1 Fungsi untuk membaca dan menulis file citra pada MATLAB ... 30 2.2 Fungsi untuk menampilkan citra ... 33 4.1 Nilai-nilai MSE dan rank dari matriks A, A1, X1, dan X1–1 ... 49

4.2 Nilai-nilai MSE dan rank dari matriks B, B1, Y1, dan Y1–1 ... 49

DAFTAR GAMBAR

Halaman 2.1 Vektor data didekati dalam terminologi arahnya. ... 11 2.2 The Pixel Coordinate System. ... 16 2.3 Contoh Vector Image. ... 16 2.4 Contoh bentuk rasterized dari huruf ‘a’ diperbesar 16 kali dan

menggunakan piksel dengan ketelitian ganda. ... 17 2.5 Bidang warna RGB Image dengan class double. ... 21

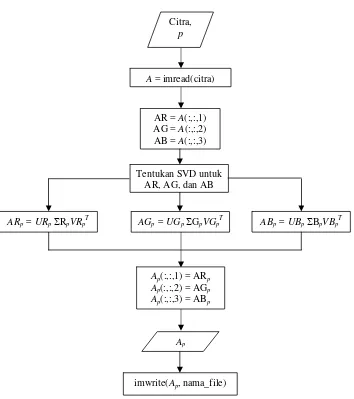
2.6 Citra format bitmap yang ditampilkan dengan penampil citra IrfanView. ... 22 2.7 Informasi detail file citra lena.bmp melalui IrfanView. ... 22 2.8 Contoh Run-length Encoding. ... 23 2.9 Contoh hasil Run-length Encoding. ... 24 2.10 Contoh informasi file citra dengan format JPEG. ... 25 2.11 Menampilkan file citra dalam MATLAB. ... 33 2.12 Menggunakan subplot. ... 34 3.1 Skema pemrosesan metode SVD untuk citra berwarna. ... 38 3.2 Skema pemrosesan metode SSVD. ... 39 3.3 Diagram penghitungan MSE antara citra asli dengan citra hasil

4.7 Citra SVD_r20_lena484.jpg. ... 57 4.8 Citra SSVD_r20_lena484.jpg. ... 58 4.9 Citra SVD_r65_lena484.jpg. ... 59 4.10 Citra SSVD_r65_lena484.jpg. ... 59 4.11 Grafik respon perubahan rank terhadap MSE dari kedua metode untuk

citra lena484.jpg. Rank/term yang digunakan adalah 1, 2, 3, 4, 5, 10, 20, 40, 65, 80, 100, 120, 140, 180, dan 200. ... 62 4.12 Citra simulasi. ... 64 4.13 Hasil kompresi citra sample_101.jpg dengan parameter kompresi

65 . ... 65 4.14 Hasil kompresi citra sample_900.jpg dengan parameter kompresi

DAFTAR LAMPIRAN

1 BAB I

PENDAHULUAN

1.1 Latar Belakang

Internet kini menjadi media yang efektif dan efisien untuk memperoleh

informasi. Baik itu berupa teks biasa (plain text) seperti artikel maupun berupa gambar. Salah satu jenis gambar yang sering disertakan dalam suatu laman web

(web page) adalah citra (image). Besar kecilnya ukuran citra akan memengaruhi cepat lambatnya laman tersebut terbuka. Oleh karena itu, dilakukan beberapa cara

untuk mempercepat terbukanya sebuah laman yang memuat citra. Salah satu cara

mempercepatnya adalah dengan mengompres citra tersebut. Tujuannya adalah

agar citra yang disertakan ukurannya menjadi lebih kecil sehingga beban yang

diberikan kepada browser dalam membuka laman tersebut menjadi lebih kecil dengan tanpa kehilangan kelayakan citra untuk dilihat secara kasat mata. Selain

itu, juga dapat mengurangi ruang penyimpanan di dalam media penyimpanan.

Kompresi data adalah proses mengubah sebuah data masukan menjadi data yang

lain yang memiliki ukuran yang lebih kecil. Data tersebut bisa berupa file di komputer atau sebuah buffer di dalam memori komputer. Tujuan kompresi pada citra adalah untuk mengurangi ketidakrelevanan dan redundansi data citra dengan

maksud agar disimpan atau dikirimkan dalam bentuk yang lebih efisien.

Pemanfaatan singular value decomposition (SVD) atau dekomposisi nilai singular untuk mengompres citra telah cukup lama dipelajari. Beberapa di

antaranya seperti yang dituliskan oleh Scheick (1997) dalam Linear Algebra with Applications dan Khaeroni (2005) dalam Pemampatan Citra Menggunakan Dekomposisi Nilai Singular.

Jika suatu citra (yang juga merupakan matriks) berpangkat rendah (low rank) atau dapat diaproksimasi cukup baik oleh suatu matriks yang juga berpangkat rendah, maka SVD dapat digunakan untuk menentukan aproksimasi

tersebut (Ranade et al. 2006). Artinya, dengan tidak menyertakan beberapa elemen dari citra aproksimasi tersebut sudah dapat merepresentasikan citra

Ranade et al. (2006) menjelaskan salah satu modifikasi dari proses atau metode kompresi menggunakan SVD dan dari beberapa percobaan memberikan

hasil kompresi yang lebih baik dibandingkan dengan metode kompresi SVD.

Metode modifikasi ini dikenal dengan nama shuffle-SVD (SSVD). Dinamakan demikian karena sebelum dilakukan dekomposisi, matriks A terlebih dahulu dipermutasi dengan sebuah data permutasi independen P.

Misalkan X adalah matriks hasil permutasi sedemikian sehingga X = P(A).

Matriks X kemudian didekomposisi menggunakan SVD. Misalkan rank dari A

adalah r dan aproksimasi rank p dari X adalah Xp dengan p ≤ r. Secara empiris diperoleh bahwa untuk nilai p yang sama, P–1(Xp) akan menghasilkan aproksimasi yang lebih baik untuk A dibandingkan Ap, di mana P–1 menyatakan permutasi balikan (re-shuffle) dari P. Dengan melakukan shuffle (SSVD) diharapkan akan diperoleh hasil kompresi yang lebih baik dibandingkan bila tidak di-shuffle

sebelumnya (SVD).

Sementara Hafsah et al. (2007) membandingkan hasil penerapan metode SSVD pada pemrosesan secara global dengan pemrosesan secara blocking dimana

block yang digunakan adalah square-block pada pemrosesan citra dan dengan teknik blocking dan ukuran block-nya seragam (uniform). Dari penelitian yang dilakukan dapat disimpulkan bahwa melalui pemrosesan secara global SSVD

lebih unggul dibandingkan SVD, tetapi melalui pemrosesan terhadap block yang dipilah-pilah (blocking) SSVD tidak terbukti lebih unggul dibandingkan SVD.

Ranade et al. (2006) dan Hafsah et al. (2007) menerapkan metode SVD dan SSVD terhadap citra keabuan (grayscale image), baik dengan teknik global maupun teknik blocking. Penelitian ini menerapkan metode SVD dan SSVD terhadap citra berwarna (color image) dengan teknik global kemudian membandingkan hasil kompresi dari kedua metode tersebut secara empiris.

Ranade et al. (2006) mengklaim bahwa teknik shuffle yang diterapkan terhadap metode SVD untuk mengompres citra selalu memberikan hasil yang lebih baik

daripada tanpa menerapkan shuffle. Demikian juga dengan Hafsah et al. (2007)

menyatakan bahwa metode SSVD selalu lebih baik daripada metode SVD dalam

3

1.2 Rumusan Penelitian

Untuk memudahkan langkah-langkah dan metode penelitian, maka dibuat

rumusan dari penelitian ini, yaitu sebagai berikut:

1. Bagaimana algoritme kompresi citra menggunakan SVD dan SSVD.

2. Bagaimana efektivitas penerapan teknik shuffle terhadap metode SVD. 3. Bagaimana kebenaran klaim bahwa teknik shuffle yang diterapkan pada

metode SVD selalu memberikan hasil yang lebih baik daripada tanpa

di-shuffle sebelumnya.

1.3 Tujuan Penelitian

Berdasarkan latar belakang masalah di atas, maka tujuan dari penelitian ini

adalah untuk menyusun algoritme kompresi citra menggunakan SVD dan SSVD

kemudian mengetahui efektivitas penerapan teknik shuffle terhadap metode SVD dan mengetahui benar atau tidaknya klaim bahwa teknik shuffle yang diterapkan pada metode SVD selalu memberikan hasil yang lebih baik daripada tanpa

5 BAB II

TINJAUAN PUSTAKA

2.1 Nilai Singular

Diberikan A matriks m x n dengan rank(A) = r. Akar nilai ciri positif dari

ATA disebut dengan nilai singular dari A (Goldberg 1991).

2.2 Norm Vektor

Norm vektor (vector norm) pada n didefinisikan sebagai fungsi

: n

f   sedemikian sehingga untuk setiap ,x yn dan  memenuhi ketiga aksioma berikut.

(1) f x

 

0 dan f x

 

  0 x 0 (2) f x



y



 f x

 

 f y

 

(3) f

 

x   f x

 

Untuk selanjutnya norm vektor x ditulis  x  (Golub dan Loan 1996). Salah satu jenis dari norm vektor adalah p-norm vektor dan didefinisikan sebagai





1

1 , 1

p p _p

n p

x  x   x p .

Dengan menggunakan definisi di atas, diperoleh norm 1, 2, dan ∞ untuk

sebarang n

x sebagai berikut

 





 

1 1

1 ₁

2 2 ₂

2 1 2 1 max n T n i i n

x x x

x x x x x

x _ x

             

Untuk selanjutnya, jika tidak disebutkan secara jelas, simbol x digunakan untuk

menyatakan 2

x .

 

2.3 Norm Matriks

setiap ,A Bmxn dan  memenuhi ketiga aksioma berikut: (1) f A

 

0 dan f A

 

  0 A 0

(2) f A B







 f A

 

 f B

 

(3) f

 

A  f A

 

Untuk memudahkan penulisan, norm matriks A ditulis A sehingga A  f A

 

(Golub dan Loan 1996).

2.3.1 Norm Frobenius

Untuk sebarang matriks A berukuran m x n, norm Frobenius (Frobenius

Norm) dari matriks A didefinisikan sebagai (Meyer 2000)





2 2 , T ij F i j

A 



a trace A A

2.3.2 p-normMatrix

Untuk sebarang matriks A berukuran m x n, p-norm dari matriks A

didefinisikan sebagai (Golub dan Loan 1996)

1 max

p

p _x p

A Ax

 

Untuk selanjutnya, jika tidak disebutkan secara jelas, simbol A digunakan untuk

menyatakan 2

A .

2.4 Mean Square Error

Mean Square Error (MSE) merupakan salah satu ukuran yang dapat

digunakan untuk menentukan kualitas suatu aproksimasi. Misalkan matriks A

berukuran m x n dan B merupakan aproksimasi untuk A. Jika aij menyatakan

elemen baris ke-i dan kolom ke-j dari A, maka MSE antara matriks A dengan B

didefinisikan sebagai





2

1 1 1 MSE m n ij ij i j a b mn  

7

Dari sini MSE dapat dinyatakan dalam norm Frobenius, yaitu



 







2

1 1

MSE A B _F trace A B T A B

mn mn

    

 

2.5 Dekomposisi Nilai Singular

Misalkan A sebarang matriks berukuran m x n dengan rank(A) = r.

Singular Value Decomposition (SVD) atau dekomposisi nilai singular dari A

adalah faktorisasi dalam bentuk

T

A U V  (2.1)

dengan U = [U1 U2 . . . Um] dan V = [V1 V2 . . . Vn] merupakan matriks ortogonal.

Matriks U berukuran m x m dan V berukuran n x n, dan 0

0 0



 

   

  adalah

matriks berukuran m x n dengan  diag( ₁, ₂,,_r) dan

1 2 r 0

  _  (Nicholson 2001).Dari sini, _{, , ,}

, 0

0 0

T

m n m m n n

m n

A U _ _ V

  .

Misalkan A sebarang matriks berukuran m x n dan ₁,,_n menyatakan

nilai ciri dari matriks ATA. Selanjutnya digunakan notasi sedemikian sehingga

1 2 3 n.

   

Misalkan x y, menyatakan hasil kali dalam baku antara vektor x dan

vektor y. Diambil sebarang {V1, . . ., Vn} basis ortonormal untuk n dan Vi

merupakan vektor ciri yang bersesuaian dengan nilai ciri dari ATA, yaitu _i untuk

setiap i. Dengan kata lain {V1, . . ., Vn} merupakan basis ciri ortonormal untuk

ATA. Karena {V1, V2, . . ., Vn} ortonormal maka Vi,Vj 0 untuk i j dan ,

i i

V V 2 2

1 1.

i

V

   Sehingga untuk setiap Vi dapat ditulis

,

i j ij

V V  (2.2)

Perhatikan bahwa untuk setiap i dan j

, ( )T T( T ) T( ) , .

i j i j i j i j j j i j j ij

AV AV  AV AV V A AV V V  V V   (2.3)

2

i AVi

  untuk setiap i = 1, 2, . . ., n. Terlihat bahwa i 0 untuk setiap i. Sehingga bilangan

i i

   untuk i = 1, 2, . . ., r

tidak lain merupakan nilai singular dari A dengan ₁₂ _r 0 dan

2 ₂

i i

AV  (2.4)

untuk setiap i.

2.6 Ruang Null dan Ruang Kolom

Misalkan A sebarang matriks berukuran m x n dengan A = [A1 A2 . . . An]

Himpunan N(A) = {x n: Ax = 0}  n disebut ruang null (null space) dari A

dan CS(A) = {x m: x = ₁A₁+₂A₂+. . .+nAn, i } 

m

disebut ruang

kolom (column space) dari A (Anton 2000).

Lemma 2.1 (Nicholson 2001)

Misalkan A sebarang matriks berukuran m x n dan rank(A) = r dan {V1, . . ., Vn}

merupakan basis ciri ortonormal untuk ATA.

1) Matriks A memiliki tepat r nilai singular.

2) {AV1, AV2, . . ., AVr} merupakan basis ortogonal untuk CS(A).

Bukti pada Lampiran 1, sub 1.1.

Dari Lemma di atas, diperoleh AV_i _i 0, i = 1, 2, . . ., r. Jika didefinisikan vektor unit

1

i i

i

U AV



 (2.5)

untuk i = 1, 2, . . ., r dalam m, maka {U1, U2, . . ., Ur} merupakan himpunan

yang ortonormal. Kemudian ditentukan sebanyak m – r vektor yang saling

ortogonal dengan {U1, U2, . . ., Ur} dan Uj 1, j = r + 1, . . ., m. Sehingga {U1,

9

dibentuk U = [U1U2 . . . Um] dan V = [V1V2 . . . Vn].

Perhatikan pula bahwa

2

, / , / 1/ ( ) ,

1/ ( ) , ( / ) .

T

i j i i j j i j i j

i j i j j j i ij ij

U U AV AV V A AV

V V

   

      

 

  

Jika Ui menyatakan kolom ke-i dari U maka UiT adalah baris ke-i dari U

T

.

Diperoleh (U UT )_ij U U_iT _j dan

, [ ] [ ]

T T

i j j i ji ij

U U _U U _{ } U U _    I,

, [ ] [ ]

T T

i j j i ji ij

V V _V V _{ } V V _    I. Jadi U dan V ortogonal.

Teorema 2.1 (Goldberg 1991)

Diberikan A sebarang matriks berukuran m x n dengan rank(A) = r dan nilai

singular ₁_r. Jika didefinisikan U, , dan V seperti uraian di atas, maka U

dan V matriks ortogonal dan A dapat didekomposisikan sebagai

T

A U V (2.6)

Bukti pada Lampiran 1, sub 1.2.

2.7 Rayleigh Quotient

Diberikan A matriks simetri berukuran n x n dengan nilai ciri ₁_n. Misalkan x, y sebarang vektor tak nol di n. Karena A simetri maka

, ,

Ax y  x Ay x y,  n. Rayleigh Quotient R(x) dari matriks simetri A

terhadap x dengan x0 didefinisikan sebagai R x( ) Ax x,₂

x

 (Scheick 1997).

Teorema 2.2 (Scheick 1997)

1) Jika x adalah vektor ciri dari A yang bersesuaian dengan i maka R(x) =i,

untuk suatu i.

2) ₁R x( )_n.

3) λ1 = max{R(x) dan λn = min{R(x) .

Bukti pada Lampiran 1, sub 1.3.

Teorema 2.3 Extended Maximal Principle (Scheick 1997)

Diberikan A matriks simetri berukuran n x n dengan nilai ciri  ₁ ₂ _n dan

 

1 n k _k

e _ merupakan basis ciri ortogonal untuk A, maka:

1) ₁max{ ( ) :R x x0} (2.7)

2) _i max{ ( ) :R x x0,xe e₁, ₂,,e_i1} untuk i2,,n. (2.8) Bukti pada Lampiran 1, sub 1.4.

2.8 Diagonalisasi

Diberikan matriks A berukuran n x n. Matriks A dikatakan dapat

didiagonalkan (diagonalizable) jika terdapat matriks invertibel  sedemikian sehingga 1A  merupakan matriks diagonal atau A 1. Dalam hal ini dikatakan  mendiagonalkan matriksA (Nicholson 2001).

Untuk setiap matriks simetri R, terdapat matriks ortogonal  sedemikian sehingga    TR atau R   dimana  merupakan matriks diagonal yang entrinya merupakan nilai ciri dari matriks R (Jain 1989). Dengan demikian

dapat ditulis

k k k

R   , 1 ≤ k≤n

dimana _k merupakan vektor ciri dari R yang bersesuaian dengan nilai ciri _k.

2.9 Karhunen–Loève Transform

Definisi lebih lengkap mengenai Karhunen–Loève Transform dapat dilihat

pada Jain (1989). Misalkan x adalah vektor acak berukuran n x 1, dengan x[k]

11

E[xxT] adalah matriks autokorelasi dari x, jelas bahwa R = RT atau R merupakan

matriks simetri. Misalkan vk adalah vektor ciri matriks R yang bersesuaian

dengan nilai ciri _k. Himpunan {_k} dibentuk dari {vk} dengan terlebih dahulu

melakukan proses ortogonalisasi dan normalisasi sehingga tetap berlaku (Jain

1989)

k k k

R   , untuk 1 ≤ k≤n

Jika   



₁ ₂  _n



maka  merupakan matriks ortogonal (uniter) sehingga   T 1

.

Karhunen–Loève Transform (KLT) dari x didefinisikan sebagai (Jain

1989)

T

y  x

2.10 Konsep Dasar Kompresi Data

Diberikan n vektor data X1, X2, . . ., Xn  m. Kemudian dicari

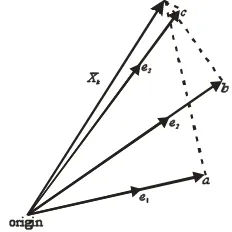
[image:39.595.271.387.466.582.2]

vektor-vektor e1, e2, . . . dengan arah yang terbaik untuk vektor data tersebut.

Gambar 2.1 Vektor data didekati dalam terminologi arahnya.

Untuk suatu vektor unit e maka f e e, merupakan proyeksi vektor dari f

pada span{e}. Pada Gambar 2.1, misalkan proyeksi vektor Xk pada ruang yang

dibangun oleh e1 adalah a, begitu juga untuk proyeksi vektor Xk pada ruang yang

dibangun oleh e2 dan e3 adalah b dan c. Terlihat pada gambar di atas,

dibandingkan dengan vektor a dan b, vektor c merupakan vektor yang arahnya

aproksimasi, jarak antara Xk dengan vektor proyeksi ini adalah yang paling dekat.

Sehingga masalah yang timbul adalah meminimumkan X_kc atau sama dengan meminimumkan X_k c 2, maka

2 2 2

k k

X c  X  c

dan nilai dari X_k 2 adalah tetap maka meminimumkan X_kc 2 sama dengan

meminimumkan  c 2 atau memaksimumkan c 2.

Perhatikan bahwa,

2 2 2

2 2

3 3 3 3 3

, , ,

k k k

c  X e e  X e e  X e

Misalkan 2

1

( ) ,

n

k k

D e X e







maka D(e) merupakan ukuran seberapa baik e

menunjuk pada arah Xk, k = 1, . . ., n sebagai sebuah himpunan. Misalkan pertama

kali dipilih vektor unit e = e1, maka vektor arah ini akan memaksimumkan

jumlahan tersebut. Untuk mendapatkan arah terbaik berikutnya, dicari suatu

vektor e  e1 dengan D(e) maksimum, katakan vektor ini e2. Secara umum,

setelah ditemukan e1, . . ., ep-1, dicari e = ep yang ortogonal dengan vektor-vektor

tersebut dan memaksimumkan D(e).

Perhatikan bahwa 2

1 1

( ) ,

n n

T T

k k k

k k

D e X e e X X e

 









, sehingga

( )_{D e} _{e XX e}T T _{e Qe}T _{, (2.9)}

dengan

1

[ _n]

X  X  X dan Q = XXT. (2.10)

Permasalahan di atas dapat disajikan sebagai berikut:

Memaksimumkan eTQe dengan e 1. Jika diberikan e1, . . ., ep-1, permasalahan di atas menjadi

Memaksimumkan eTQe dengan e 1, dan e  e1, . . ., ep-1.

Permasalahan tersebut tidak lain merupakan extended maximal principle

13

Menurut Teorema 2.3 vektor pemaksimal R(e) merupakan vektor ciri dari Q yang

ortogonal, sebut e1, e2, . . .em. Menurut Teorema 2.2, diperoleh barisan nilai

maksimumnya adalah D e( )₁ ₁, D e( )₂ ₂, . . . , D e( _m)_m, dengan

1 2 m

  _ tak lain merupakan akar ciri dari Q. Di lain pihak, perhatikan bahwa akar ciri tak nol dari Q=XXT tak lain adalah  _i  _i2 dan vektor ciri–nya adalah ei = Ui dengan X = UVT merupakan SVD dari X dengan nilai singular

dari X adalah _i.

2.10.1 Principal Component Basis

Basis

 

e_k m_k1 untuk m yang ditemukan melalui proses di atas adalah ortonormal karena U ortogonal. Dengan demikian, setiap x m dapat ditulis

2

1

, , / , .

m

i i i i i i

i

x e  x e e x e







  (2.11)

Koordinat dari x di dalam basis ini, yaitu _i, disebut principal components dari x.

Basis

 

ek m_k1 disebut principal component basis.

Permasalahan yang muncul dalam kompresi data adalah berapa banyak _i

yang diperlukan untuk merepresentasikan x? Misalkan

1 p

p i i

i

s e







merupakan

proyeksi dari x pada span

 

1 p k _k

e _ . Dari sini,

2 2 2 2 2 2 2 2 2 2

1 1 1 1 1

p p

m m m

p p i i i i i i i

i i i i i p

x s x s  e  e   

     

   



















.

Jika residu ini diabaikan maka sp bisa diterima sebagai aproksimasi untuk

x. Kemudian ditentukan berapa banyak term yang dibutuhkan jika x adalah salah

satu dari Xk. Perhatikan bahwa

2 2

1 1

m m

T T

p i i i

i p i p

x s  e xx e

   

 







Jika diambil x = Xk dan dijumlahkan semua atas k serta dari kenyataan bahwa

i i i

2

1 1 1 1 1 1 1

( ) .

n n m m n m m

T T T T T

k p k i k k i i k k i i i i

k k i p i p k i p i p

X s X e X X e e X X e e Qe 

          

 

   _{ }  

 



 









Sehingga untuk merepresentasikan x dalam himpunan

 

X_k n_k1, cukup dengan memilih p sedemikian sehingga

1 1 m i i p m i i     





(2.12)

kecil.

Selanjutnya, proyeksi suatu vektor x dapat dihitung dengan memotong

ekspansi principal components-nya

1 1 1 1 , p p T T

p i i i i p p

i i

s x e e e e x e e e e x

 

   









_{ }  _{ }  _ (2.13)

Jika dengan mengambil nilai p seperti di atas dapat diterima, berarti sub-ruang

span

 

1 p k _k

e _ memuat sebagian besar informasi sebenarnya.

2.11 Konsep Teori Informasi

Teori informasi pertama kali diperkenalkan oleh Shannon (1948). Teori

tersebut dianggap sebagai dasar teori penelitian kompresi data (Zadeh 1965;

Acharya dan Ray 2005). Shannon membuktikan bahwa terdapat batas pada

kompresi data lossless. Batas itu disebut entropy rate yang disimbolkan dengan H.

Nilai H bergantung pada sumber informasi, sehingga memungkinkan untuk

melakukan kompresi sumber informasi secara lossless dengan nilai kompresi

mendekati H (Hafsah 2007).

Shannon juga menemukan teori kompresi data lossy yang dikenal dengan

teori rate-distortion. Pada kompresi data lossy, data yang telah diekstrak tidak

harus sama dengan data asli (original). Meskipun demikian, sejumlah distorsi

15

2.12 Aproksimasi Matriks Rank Rendah

Misalkan A matriks berukuran m x n dengan rank(A) = r dan SVD dari A

dinyatakan sebagai

1 r

T i i i i

A U V







(2.14)

Jika nilai singular p₁,,r lebih kecil dibandingkan dengan 1,,p maka dengan ‘membuang’ sebanyak r – p term pada (2.14) akan memberikan

aproksimasi untuk A dan memiliki rank yang lebih kecil daripada r (Greenacre

1984). Teorema aproksimasi dengan rank rendah (low rank approximation)

pertama kali dinyatakan dan dibuktikan oleh Eckart dan Young (1936) dan pada

beberapa jurnal disebut dengan Eckart-Young Theorem. Teorema tersebut

menyebutkan bahwa jika matriks A berukuran m x n dengan rank(A) = r dan SVD dari A adalah 

1 r

T i i i i

A U V







  maka

1 p

T

p i i i

i

A U V







merupakan aproksimasi

terbaik dengan rankp untuk A, yaitu Ap meminimumkan 



 







2 1 1 ( ) m n T ij ij i j

a x trace A X A X

 

   



(2.15)

untuk setiap matriks X dengan rankp atau kurang (Greenacre 1984).

2.13 Citra Digital

2.13.1 Representasi Citra Digital

Komputer menampilkan citra sebagai koleksi titik-titik (dot) yang disebut

dengan pixel (picture element) atau piksel. Informasi visual disimpan dalam

struktur data array atas bit-bit bilangan. Setiap titik dari gambar dipetakan ke satu

atau lebih bit dalam memori komputer.

Citra digital dibangun oleh piksel-piksel yang dapat dianggap sebagai

sebuah titik kecil pada layar. Citra dengan ukuran m x n adalah citra yang

dibangun oleh m piksel pada arah vertikal dan n piksel pada arah horisontal. Citra

digital direpesentasikan dengan suatu matriks atas bilangan-bilangan di mana

setiap bilangan tersebut merepresentasikan nilai intensitas di suatu titik. Titik pada

levels.

Jika C adalah matriks citra berukuran m x n maka Crc adalah nilai

intensitas pada posisi yang bersesuaian dengan entri pada baris r dan kolom c citra

[image:44.595.210.361.196.331.2]

yang direpresentasikan oleh matriks tersebut.

Gambar 2.2 The Pixel Coordinate System.

Salah satu cara untuk merepresentasikan sebuah citra menggunakan

komputer adalah dengan menyatakan sebuah citra menggunakan angka-angka

untuk merepresentasikan entri-nya berdasarkan posisi dan ukuran bentuk

geometris dan bentuk seperti garis, kurva, persegi, atau lingkaran. Citra seperti ini

disebut dengan citra vektor (vector image).

draw circle

center 0.5, 0.5 radius 0.4 fill-color yellow stroke-color black stroke-width 0.05 draw circle

center 0.35, 0.4 radius 0.05 fill-color black draw circle

center 0.65, 0.4 radius 0.05 fill-color black draw line

start 0.3, 0.6 end 0.7, 0.6 stroke-color black stroke-width 0.1

[image:44.595.87.481.493.736.2]

17

Citra yang disimpan dan ditampilkan dengan cara yang sama disebut

bitmapped image atau bitmap (Sutopo 2002). Citra bitmap (atau raster images)

adalah “foto digital”, bentuk yang paling sering digunakan untuk

merepresentasikan citra alami dan juga merupakan bentuk grafis dengan detail

yang sangat banyak. Citra bitmap bisa juga menyatakan bagaimana suatu grafis

disimpan ke dalam memori video komputer. Terminologi bitmap merujuk pada

bagaimana memberikan pola bit-bit di dalam peta piksel ke suatu warna yang

spesifik.

Gambar 2.4 Contoh bentuk rasterized dari huruf ‘a’ diperbesar 16 kali dan

menggunakan piksel dengan ketelitian ganda.

Citra bitmap berbentuk sebuah larik (array) di mana nilai pada setiap

elemen disebut dengan piksel (pixel – picture element) yang bersesuaian dengan

warna yang diberikan oleh citra tersebut. Setiap garis horisontal di dalam citra

disebut dengan garis pindai (scan line). Huruf ‘a’ direpresentasian dengan sebuah

matriks berukuran 12 x 14 sebagaimana yang diperlihatkan pada Gambar 2.3,

bilangan-bilangan di dalam matriks menggambarkan tingkat kecerahan

(brightness) dari pikselnya. Bilangan yang lebih besar bersesuaian dengan area

2.13.2 Menyimpan dan Menampilkan Citra Digital

Citra digital memerlukan ruang penyimpanan yang besar. Untuk

merepresentasikan citra berukuran 640 x 480 piksel, di mana setiap piksel

direpresentasikan dengan 1 byte memori (merepresentasikan bilangan 0–255),

memerlukan 640 x 480 x 1 byte = 307.200 byte = 300 KB = 0.29 MB memori.

Komputer menyimpan sebuah file citra ke dalam disk atau media

penyimpanan lainnya dalam bentuk biner (binary). Komputer menyimpan

informasi data piksel dan metadata yang berisi informasi pendukung tambahan,

seperti dimensi dan tag. Menyimpan sebuah file citra erat kaitannya dengan

format penyimpanan yang digunakan. Biasanya file citra disimpan oleh software

tertentu yang akan menerapkan algoritme sesuai dengan format digunakan. Salah

satu format penyimpanan yang sering digunakan adalah JPEG (Joint

Photographic Experts Group).

Format JPEG merupakan skema kompresi file bitmap. Awalnya, file yang

menyimpan hasil foto digital memiliki ukuran yang besar sehingga tidak praktis.

Dengan format baru ini, hasil foto yang semula berukuran besar berhasil

dikompresi sehingga ukurannya kecil.

Format ini dikembangkan pada awal tahun 1980 oleh Joint Photographic

Experts Group (JPEG). JPEG merupakan format yang paling sering digunakan di

internet. Implementasi format JPEG terbaru dimulai sejak tahun 1996 dan

semakin berkembang dengan inovasi format baru yang menyertai perkembangan

teknologi yang memanfaatkan format JPEG lebih luas. Walaupun format JPEG

merupakan metode kompresi gambar yang gratis, sebuah perusahaan bernama

Forgent pada tahun 2002 mempatenkan format ini dan akan menarik biaya lisensi.

Segera grup JPEG mengumumkan sebuah format JPEG 2000 sebagai sebuah

format pengganti. Namun dua hal di atas terlambat, karena JPEG sudah digunakan

secara luas dan hak paten belum ditetapkan oleh pengadilan.

Standar kompresi file gambar yang dibuat oleh kelompok JPEG ini

menghasilkan kompresi yang sangat besar tetapi dengan akibat berupa adanya

distorsi pada gambar yang hampir selalu tidak terlihat. JPEG adalah sebuah

19

berkualitas tinggi dalam ukuran file yang sangat kecil. Format file grafis ini telah

diterima oleh Telecommunication Standardization Sector atau ITU-T dan

Organisasi Internasional untuk Standardisasi atau ISO. JPEG kebanyakan

digunakan untuk melakukan kompresi gambar menggunakan analisis Discrete

Cosine Transform (DCT). Meskipun kompresi gambar JPEG sangatlah efisien dan

selalu menyimpan gambar dalam kategori warna true color (24 bit), format ini

bersifat lossy yang berarti bahwa kualitas gambar dikorbankan bila tingkat

kompresi yang dipilih semakin tinggi.

Ketika ada file citra berukuran 100 x 100 piksel dan disimpan dengan

format JPEG maka file tersebut akan dimanipulasi dengan suatu algoritme yang

membuang nilai di posisi-posisi tertentu karena memang tidak dilihat manusia.

Format penyimpanan JPEG bisa lebih kecil daripada ukuran file sebenarnya

karena ia membuang beberapa data warna yang tidak terlalu tampak secara visual

oleh indera mata manusia. Intinya, jika mata manusia sulit melihatnya maka

komputer tidak perlu menyimpannya. Dengan tingkat kompresi moderat dan jika

dilihat sepintas, secara visual, citra berformat JPEG sulit dibedakan dengan citra

asli. Bagaimana JPEG melakukan hal tersebut dapat dilihat pada

referensi-referensi terkait.

Terdapat perbedaan terminologi antara ‘menyimpan’ dan ‘menampilkan’.

Format JPEG, BMP, PNG, DWF, GIF, dan adalah format penyimpanan. Supaya

bisa dilihat, format penyimpanan itu harus dibuka, dibaca, dan direkonstruksi ke

dalam format penampilan. Lazimnya format penampilan adalah bitmap. Oleh

karena itu, semua format penyimpanan itu akan selalu menampilkan citra dalam

format bitmap yang berarti bahwa ukuran citra di memori akan selalu tetap sesuai

dengan resolusinya. Dalam hal ini harus ada mekanisme rekonstruksi dari

menyimpan ke menampilkan, kemudian dari menampilkan ke menyimpan.

Mekanisme ini disebut algoritme. Algoritme ini biasanya yang membedakan

2.13.3 Tipe Citra Digital pada MATLAB

MATLAB menyimpan citra sebagai larikan (array) dua dimensi, yaitu

matriks. Setiap elemen dari matriks ini bersesuaian dengan satu piksel dalam citra

yang ditampilkan. Sebagai contoh, suatu citra yang terdiri atas 200 baris dan 300

kolom atas titik-titik warna yang berbeda, disimpan oleh MATLAB sebagai

matriks berukuran 200 x 300. Oleh karena itu, bekerja dengan citra di MATLAB

serupa dengan bekerja terhadap sebarang matriks data yang lain. Sebagai contoh,

untuk mengambil piksel tunggal dari suatu matriks citra digunakan operasi

pengacuan matriks biasa, misal I(2,15). Perintah ini mengembalikan nilai piksel

pada baris ke-2 dan kolom ke-15 citra I.

MATLAB mampu mengolah banyak tipe citra digital, salah satunya adalah

RGB image. RGB (Red, Green, Blue) image atau dikenal dengan nama truecolor

image, di dalam MATLAB disimpan sebagai larikan data berukuran m x n x 3

yang menggambarkan komponen-komponen warna merah, hijau, dan biru untuk

setiap piksel. Warna pada tiap piksel ditentukan dengan kombinasi intensitas

warna merah, hijau, dan biru yang disimpan dalam tiap bidang warna pada lokasi

piksel tersebut. Format file RGB, menyimpan RGB images sebagai citra 24-bit

dengan masing-masing komponen warna merah, hijau, dan biru adalah 8-bits.

Dari sini diperoleh kemungkinan 16 juta kombinasi warna untuk satu piksel.

Suatu larikan RGB MATLAB bisa dari class double, uint8, atau uint16.

Larikan RGB dari class double setiap komponennya warna merupakan

suatu nilai di antara 0 and 1. Piksel yang komponen warnanya (0,0,0) ditampilkan

sebagai hitam, dan piksel yang komponen warnanya (1,1,1) ditampilkan sebagai

putih. Ketiga komponen warna dari tiap piksel disimpan sepanjang dimensi ketiga

dari larikan data. Sebagai contoh komponen warna merah, hijau, dan biru dari

piksel (10,5) disimpan dalam RGB(10,5,1), RGB(10,5,2), dan RGB(10,5,3).

21

Gambar 2.5 Bidang warna RGB Image dengan class double.

2.14 Kompresi Citra Digital

Kompresi citra merupakan salah satu bentuk kompresi data. Kompresi

citra digital adalah proses digital dimana jumlah data (dalam ukuran bit) pada citra

direduksi sesuai dengan yang diinginkan (Thyagarajan 2006). Pada kompresi

citra, pengodean entropy biasanya didahului oleh dekorelasi untuk mengurangi

redundansi pada data citra dan kompresi lossy didahului oleh kuantisasi.

Keefektifan kompresi citra dapat diikur melalui kuantitas kompresi yang dicapai

dan melalui kualitas citra yang direkonstruksi (Hafsah 2007).

Citra bitmap mengambil banyak memori, kompresi citra mengurangi

jumlah memori yang dibutuhkan untuk menyimpan sebuah citra di dalam disk.

Secara sederhana, citra RGB 8 bit berukuran 1600 x 1200 membutuhkan 1600 x

1200 x 3 bytes = 5760000 bytes = 5.5 MB di memori. Ini adalah ukuran citra

tanpa kompresi. Citra bitmap merepresentasikan setiap piksel dengan setiap

bilangan satu per satu. Hal ini membuat citra yang disimpan dalam format bitmap

sangat bergantung dengan ukuran (resolusi). Gambar 2.6 menampilkan citra

dengan format bitmap yang ditampilkan dengan penampil citra IrfanView.

Rasio kompresi (compression ratio) adalah perbandingan antara citra hasil

kompresi dengan citra sebelum dilakukan kompres, sebagai contoh untuk citra

yang disebutkan di atas, disimpan sebagai file JPEG dengan ukuran 512 KB dan

[image:49.595.218.411.112.300.2]

[image:50.595.89.427.110.372.2]

Gambar 2.6 Citra format bitmap yang ditampilkan dengan penampil citra IrfanView.

Citra di atas berukuran 512 pada arah vertikal dan 512 piksel pada arah

horisontal, merupakan citra RGB dengan kedalaman warna 8 bit setiap bidang

warna, sehingga kedalaman warna untuk setiap piksel adalah 24 bit. Oleh karena

itu, ukuran file citra di memori adalah 512 x 512 x 24 = 6291456 bit = 786432

byte = 768 KB. Informasi detail citra ini ditampilkan dalam Gambar 2.7.

[image:50.595.196.373.520.741.2]

23

Dari gambar di atas, terlihat bahwa citra tersebut membutuhkan ruang

penyimpanan yang sama besar dengan memori yang dibutuhkan oleh citra

tersebut untuk ditampilkan, yaitu 768 KB karena citra disimpan dalam format

bitmap.

2.14.1 Teknik Kompresi Citra Digital

Ada dua macam teknik untuk mengompres citra, yaitu lossless dan lossy

(Castleman 1996). Teknik lossless memberikan jaminan bahwa citra yang telah

di-decompress benar-benar identik dengan citra sebelum dikompres, misalnya Run

Length encoding, Huffman encoding, Entropy coding (Lempel/Ziv), dan area

coding (Hafsah 2007). Ketika sebuah citra dikompres secara lossless maka

pengulangan dan kemungkinan-kemungkinan digunakan untuk merepresentasikan

semua informasi menggunakan memori yang lebih sedikit. Citra asli juga

kemudian dapat dikembalikan (decompress). Salah satu metode kompresi lossless

yang paling sederhana adalah Run-Length Ecoding (RLE). RLE meng-encode

nilai yang sama yang berulang sebagai satu bagian pada data secara keseluruhan.

70, 5, 25, 5, 27, 4, 26, 4, 25, 6, 24, 6, 23,

3, 2, 3, 22, 3, 2, 3, 21, 3, 5, 2, 20, 3, 5, 2, 19, 3, 7, 2, 18, 3, 7, 2, 17, 14, 16, 14, 15,

[image:51.595.136.488.454.740.2]

3, 11, 2, 14, 3, 11, 2, 13, 3, 13, 2, 12, 3, 13, 2, 11, 3, 15, 2, 10, 3, 15, 2, 8, 6, 12, 6, 6, 6, 12, 6, 64

Pada Gambar 2.8, gambar rumah hitam putih telah dikompres dengan

menggunakan RLE. Gambar bitmap tersebut terlihat sebagai satu string panjang

dari piksel hitam atau putih, encoding-nya adalah berapa banyak byte warna yang

sama muncul setelah warna yang lain.

70, 15, 0, 15, 0, 15, 0, 10, 5, 25, 5, 15, 0, 10,

5, 27, 6, 15, 0, 12, 4, 26, 4, 15, 0, 11, 4, 25, 4, 15, 0, 10, 6, 24, 6, 15, 0, 9, 6, 23, 6, 15, 0, 8,

3, 2, 3, 22, 3, 2, 3, 15, 0, 7, 3, 2, 3, 21, 3, 2, 3, 15, 0, 6, 3, 5, 2, 20, 3, 5, 2, 15, 0, 5, 3, 5, 2, 19, 3, 5, 2, 15, 0, 4, 3, 7, 2, 18, 3, 7, 2, 15, 0, 3, 3, 7, 2, 17, 3, 7, 2, 15, 0, 2 14, 16, 14, 15, 0, 1

14, 15, 14, 15,

3, 11, 2, 14, 3, 11, 2, 14, 3, 11, 2, 13, 3, 11, 2, 13, 3, 13, 2, 12, 3, 13, 2, 12, 3, 13, 2, 11, 3, 13, 2, 11, 3, 15, 2, 10, 3, 15, 2, 10, 3, 15, 2, 8, 3, 15, 2, 8, 6, 12, 6, 6, 6, 12, 6, 6,

[image:52.595.83.490.208.488.2]

6, 12, 6, 64 6, 12, 6, 15, 0, 15, 0, 15, 0, 15, 0, 4

Gambar 2.9 Contoh hasil Run-length Encoding.

Pada gambar di atas, hasil encoding yang baru adalah 113 nibbles, satu

nibble adalah 4 bit dan dapat merepresentasikan nilai di antara 0 dan 4, sehingga

hanya dibutuhkan 113 x 4 : 8 = 56.5 byte untuk menyimpan semua nilai-nilai

tersebut. Kapasitas penyimpanan ini lebih kecil dari 93 byte jika citra disimpan

dengan citra 1 bit dan jauh lebih kecil dari 750 byte jika digunakan satu byte untuk

setiap piksel.

Beberapa aplikasi tidak membutuhkan pengembalian data keseluruhan dari

citra aslinya, oleh karena itu digunakan teknik lossy. Contoh teknik ini adalah

transformcoding (SVD/KLT/DCT/Wavelets/ Gabor), vectorquantisation, metode

segmentasi dan aproksimasi, metode spline aproksimasi (Interpolasi

Bilinear/Regulariasi), dan Fractal Coding (texture synthesis, iterated function

25

Teknik kompresi citra lossy mengambil keuntungan dari ketidakmampuan

mata manusia untuk melihat hal-hal yang sangat kecil dan dari fakta bahwa

beberapa jenis informasi jauh lebih penting daripada informasi yang lainnya.

Kompresi lossy ditentukan oleh nilai akurasi citra terekonstruksi yang dapat

diterima sejalan dengan peningkatan kompresi. Jika distorsi yang terjadi dapat

ditolerir maka peningkatan pada kompresi menjadi signifikan (Gonzales dan

Woods 2002). Keuntungan kompresi citra lossy adalah kecacatannya tidak dapat

terdeteksi melalui penglihatan manusia. Contoh kompresi lossy adalah JPEG.

Pada JPEG implementasi format file kompresinya berdasarkan DCT bersama

dengan algoritme lossless akan memberikan rasio kompresi yang sangat bagus.

Cara JPEG bekerja sangat cocok untuk citra dengan rentang tonal yang kontinu

seperti foto, logo, teks hasil pemindaian, dan citra-citra yang lain dengan banyak

kontur ketajaman/garis. Gambar berikut menampilkan informasi detail file citra

[image:53.595.221.404.415.641.2]

dalam format JPEG.

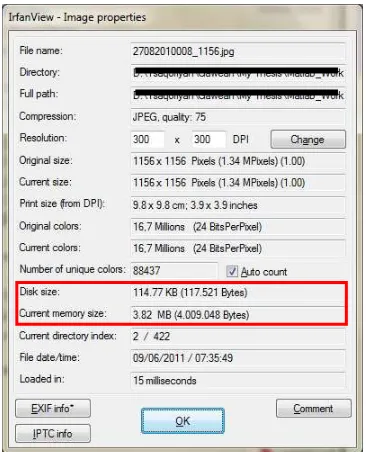
Gambar 2.10 Contoh informasi file citra dengan format JPEG.

Informasi yang tertera pada gambar di atas menyebutkan bahwa citra

berukuran 1156 x 1156 piksel. Ukuran memori yang dibutuhkan untuk

3915.05 KB = 3.82 MB. Tetapi, dengan menggunakan format JPEG citra tersebut

hanya membutuhkan 114.77 KB untuk disimpan di dalam disk. Penampil

IrfanView melakukan decoding (decompress) terhadap file citra yang disimpan di

dalam disk sebelum ditampilkan sehingga ukurannya di dalam disk yang semula

114.7 KB menjadi 3.82 MB setelah di-load ke dalam memori (RAM) komputer.

2.14.2 Kompresi Citra dengan SVD

Diberikan citra A matriks real dengan ukuran m x n dan rank(A) = r.

Matriks ini tidak dipandang sebagai transformasi linear atau sebuah objek aljabar.

Matriks ini secara sederhana merupakan tabel dengan mn bilangan dan akan

ditentukan aproksimasi yang menangkap tampilan data yang paling signifikan.

Rank matriks menunjukkan banyaknya kolom atau baris yang saling bebas

linear, maka rank juga merupakan ukuran redundansi (Kalman 1996). Matriks

dengan rank rendah memiliki banyak redundansi sehingga dapat diekspresikan

dengan lebih efisien. Sebagai contoh, misalkan B merupakan matriks berukuran m

x n dengan rank 1, maka semua kolom-kolom dari B merupakan kelipatan antara

satu dan lainnya (ruang kolom berdimensi 1). Jika u merupakan basis dari ruang

kolom B, maka setiap kolom merupakan kelipatan dari u. Misalkan kolom ke-j

dari B adalah vju maka



1 2



T n

B v u v u  v u uv . Sebanyak mn entri matriks

B ditentukan oleh m entri pada kolom dan n entri pada baris. Dengan analogi yang

sama dapat diperoleh kompresi yang sangat besar untuk A jika A dapat

diaproksimasi oleh matriks dengan rank 1. Akan lebih sedikit menyimpan m + n

entri untuk merepresentasikan aproksimasi dengan rank 1 untuk A daripada

sebanyak mn entri matriks A (Kalman 1996).

Pertama kali ditentukan SVD dari matriks A, yaitu A = UVT dimana 0

,

0 0



 

   

   diag(σ1, σ2, ..., σr) dan σ1 ≥ σ2 ≥ ... ≥ σr > 0. Matriks U dan V

ortogonal dan σi merupakan nilai singular dari A. Aproksimasi dengan rankp dari

A dengan p ≤ r adalah Ap = UppVpT di mana p adalah matriks  tetapi hanya

27

kolom pertama U dan Vp berisi p kolom pertama V. Dekomposisi seperti ini cukup

menarik karena Up, p, dan VpT menghasilkan aproksimasi terbaik dengan rankp

untuk A (Ranade et al. 2006) dalam terminologi bahwa rekonstruksi ketiga

matriks tersebut menghasilkan aproksimasi dengan rank p yang paling baik untuk

A. Ukuran baik atau tidaknya aproksimasi tersebut bisa menggunakan ukuran

secara matematis seperti MSE atau penilaian secara kualitatif, yaitu menurut

pengamatan secara kasat mata.

Jika SVD dari A adalah A = UVT, diperoleh A = σ1U1V1T+ σ2U2V2T+ ... +

σrUrVrT+ 0Ur+1Vr+1T+ 0 + ... Karena nilai singular pada  disusun dengan urutan dari yang terbesar ke yang terkecil (decreasing order) maka suku-suku yang nilai

singularnya sangat kecil tidak banyak berpengaruh pada citra A. Dari sini dapat

ditentukan aproksimasi untuk A dengan rank yang lebih kecil dari r, misalkan Ap

= σ1U1V1T + σ2U2V2T + ... + σpUpVpT, dan p < r. Dengan melakukan seperti ini

matriks citra akan disimpan dengan sejumlah bilangan yang berulang (vektor yang

tidak bebas linear), sehingga ketika disimpan file citra akan mengambil ruang

penyimpanan yang lebih kecil.

Langkah kompresi citra dengan metode SVD seperti yang diuraikan di atas

adalah dengan mengambil sebanyak p (atau kurang) kolom dari U, p kolom dari

V, dan p x p sub-matriks dari . Representasi ini cukup baik jika A memiliki rank

rendah.

2.14.3 Kompresi Citra dengan SSVD

Diberikan A matriks berukuran N x N dengan N = n2 untuk suatu bilangan

bulat n. Kemudian dipilih operator shuffle P untuk A. Ranade et al. (2006)

membentuk X = P(A) dengan langkah sebagai berikut:

(i) Memecah A menjadi blok berukuran n x n

(ii) Mengambil blok ke-i pada urutan mayor baris dan menyusun kembali nilai

pixel citra pada mayor baris menjadi baris ke-i dari X. Untuk lebih jelasnya,

diberikan rumus sebagai berikut:

, ( mod ) ( mod ) [ , ]

i j

X n i n n j n A i j

n n

  _  _ _

 _{ }  _{ } 

Sebagai contoh, diberikan matriks sebagai berikut

1 2 3 4

5 6 7 8

9 10 11 12

13 14 15 16

A             

Matriks di atas berukuran 4 x 4 dan 4 = 22, sehingga n = 2. Pertama kali

matriks A dipecah menjadi blok n x n, yaitu blok berukuran 2 x 2 sebagai berikut

1 2 3 4

5 6 7 8

9 10 11 12

13 14 15 16

A             

Diperoleh empat blok berukuran n x n dengan urutan blok ke-1 adalah 1 2 5 6

 

 

 ,

blok ke-2 adalah 3 4

7 8

 

 

 , blok ke-3 adalah

9 10

13 14

 

 

 , dan blok ke-4 adalah

11 12

15 16

 

 

 .

Kemudian baris-baris pada blok ke-i disusun kembali menjadi baris ke-i.

Baris-baris blok ke-1 disusun menjadi baris ke-1 dari X. Baris-baris blok ke-2

disusun menjadi baris ke-2 dari X. Baris-baris blok 3 disusun menjadi baris

ke-3 dari X. Terakhir, baris-baris blok ke-4 disusun menjadi baris ke-4 dari X.

Dengan demikian, diperoleh matriks hasil shuffle sebagai berikut:

1 2 5 6

3 4 7 8

9 10 13 14

11 12 15 16

X             

Setiap citra dalam penyusunan ini, yaitu setiap kolom dari X dibangun

dengan mengambil satu elemen dari setiap blok A. Dalam kasus SSVD, citra-citra

penyusunnya merupakan sub-sample dari citra asli yang memiliki resolusi rendah.

Titik ke-j dari setiap sample diambil dari n x n blok tunggal citra asli.

29

kompresi dilakukan mengambil p kolom dari U, p kolom dari V dan p x p

submatriks dari . Representasi ini akan baik jika X memiliki rank rendah. Dengan melakukan shuffle, Ranade et al.<