MODEL REGRESI LATEN PADA EFEK PLASEBO
DIANA PURWANDARI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
DIANA PURWANDARI. Model Regresi Laten pada Efek Plasebo. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan NGAKAN KOMANG KUTHA ARDANA.
Analisis regresi mempelajari bentuk hubungan antara peubah respons dengan satu atau lebih peubah prediktor. Analisis akan bertambah kompleks ketika melibatkan prediktor laten, yaitu peubah yang tidak teramati. Model regresi dengan prediktor laten disebut model regresi laten. Model regresi laten memainkan peran penting dalam pemodelan data dengan peubah laten, misalnya efek plasebo pada penyembuhan depresi. Pada model regresi laten ini, prediktor laten diasumsikan kontinu dan diduga menggunakan distribusi beta. Parameter model diduga dengan algoritma EM (Expectation-Maximization). Implementasi model dilakukan dengan menggunakan
software R 2.13.1. Hasil analisis data suatu penelitian efek plasebo pada penyembuhan depresi menunjukkan tingkat kesesuaian yang tinggi.
ABSTRACT
DIANA PURWANDARI. Latent Regression Model on Placebo Effect. Under supervision of ENDAR HASAFAH NUGRAHANI and NGAKAN KOMANG KUTHA ARDANA.
Regression analysis models the relationship between response variables with one or more predictor variables. The complexity of the analysis will increase, when it involves latent predictors, which are unobserved. Regression model with latent predictor is called latent regression model. Latent regression model has an important role in data modelling with latent variables, such as placebo effect in healing of depression. In this latent regression model, the latent predictor is assumed to be continue and is estimated by using beta distribution. The parameters of the model are estimated by EM (Expectation-Maximization) algorithm. This algorithm is implemented using R 2.13.1 software. The result of data analysis of a placebo effect research on the healing of depression shows a high level of concordance.
MODEL REGRESI LATEN PADA EFEK PLASEBO
DIANA PURWANDARI
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul : Model Regresi Laten Pada Efek Plasebo
Nama : Diana Purwandari
NIM : G54070011
Disetujui
Pembimbing I
Dr. Ir. Endar H. Nugrahani, MS.
NIP. 19631228 198903 2 001
Pembimbing II
Ir. Ngakan Komang Kutha Ardana, M.Sc.
NIP. 19640823 198903 1 001
Diketahui
Ketua Departemen Matematika
Dr. Dra. Berlian Setiawaty, MS.
NIP. 19650505 198903 2 004
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya serta shalawat dan salam kepada Nabi Muhammad SAW sehingga karya ilmiah ini berhasil
diselesaikan. Penyusunan karya ilmiah ini juga tidak lepas dari peranan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Orang tua tercinta: Ateng Rachmat dan Ida Nurdiana yang telah mencurahkan kasih sayangnya, doa, dukungan, kesabaran, kepercayaan, adik Riandi Angga Permana dan Ghina Shoda Nabilah, Om Risdiana serta keluarga besar baik dari papah maupun dari mamah. 2. Dr. Ir. Endar Hasafah Nugrahani, M.S selaku dosen pembimbing I yang telah membimbing,
memberikan ilmu, kesabaran, motivasi, dan bantuannya selama penulisan skripsi ini.
3. Ir. Ngakan Komang Kutha Ardana, M.Sc selaku dosen pembimbing II yang telah membimbing, memberikan ilmu, saran, motivasi, dan bantuannya selama penulisan skripsi ini. 4. Dr. Ir. Budi Suharjo, MS selaku dosen penguji yang telah memberikan saran yang terkait
dengan skripsi.
5. Staf Departemen Matematika: Pak Yono, Bu Susi, Mas Heri, Pak Bono, Bu Ade, Mas Deni, dan lainnya yang telah memberikan banyak bantuan dan dukungan.
6. Teman-Teman Matematika 44 yang mendukung proses penyusunan karya ilmiah ini: Lukmanul Hakim, Dwi Tanty, Herlan, Wahyu Sudrajat, Yanti AA.
7. Kakak kelas angkatan 41, 42, dan 43 yang selalu menjadi panutan baik.
8. Teman-teman Matematika angkatan 44: Wahyu, Ayum, Iam, Fikri, Wenti, Ririh, Sri, Fajar, Mutia, Rachma, Ayung, Iful, Cita, Tanty, Arina, Deva, Yuyun, Lingga, Masayu, Ruhiyat, Yogie, Lugina, Yanti, Selvie, Nurul, Pepi, Devi, Istiti, Iresa, Sari, Anis, Aqil, Lilis, Imam,
Aswin, Eka, Aze, Ali, Vianey, Nadiroh, Nurus, Na’im, Dhika, Ima, Dora, Atik, Nunuy, Yuli,
Fani, Phunny, Dian, Rofi, Della, Tyas, Denda, Pandi, Rizqy, Indin, Sholih, Siska, Lili, Tita, Lina, Endro, Lukman, Puying, Tendhy, Ikhsan, Chopa, dan Zae.
9. Adik-adik Matematika angkatan 45 dan 46 yang selalu memberikan dukungan.
10.Sahabatku: Yanti Anjarwati Abbas, Masayu Nur Dzikriyana, Indin Fabrina F, Maryam, Chichi Ryzki, Noe dan Norita yang memberikan semangat, motivasi dan saran-saran.
11.Teman-teman HIMALAYA: Dita, Dwi, Dede Hermanudin, kakak Aris, kakak Arif dan lainnya 12.Teman-teman kosan ceriwis: Ari dan Fahri atas motivasi dan kebersamaannya.
13.Semua pihak yang telah membantu sehingga bisa terselesaikan karya ilmiah ini.
Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.
Bogor, November 2011
RIWAYAT HIDUP
Penulis dilahirkan di Tasikmalaya pada tanggal 10 Maret 1990 dari pasangan Ateng Rachmat dan Ida Nurdiana. Penulis merupakan anak pertama dari tiga bersaudara.
Pendidikan yang telah ditempuh oleh penulis antara lain SDN Kawalu 2 tahun 1995-2001, SMPN 2 Tasikmalaya tahun 2001-2004, SMAN 1 Tasikmalaya tahun 2004-2007. Penulis diterima di Institut Pertanian Bogor melalui jalur USMI (Undangan Seleksi Mahasiswa IPB) pada tahun 2007. Penulis memilih mayor Matematika dengan minor Statistika Terapan, Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis menjadi asisten mata kuliah Kalkulus II (S1) pada semester ganjil tahun akademik 2009-2010, dan asisten praktikum mata kuliah fisika dasar I (S1) pada semester ganjil dan genap tahun akademik 2009-2010. Pada tahun 2007, penulis memperoleh juara 1 lomba baca puisi tingkat asrama TPB IPB dan juara 2 lomba baca puisi islami IPB. Pada tahun 2010, penulis memperoleh juara 2 lomba baca puisi IPB Art Contest dan juara 3 musikalisasi drama FMIPA IPB. Pada tahun 2011, penulis memperoleh juara 1 lomba baca puisi IPB Art Contest dan juara 1 lomba baca puisi IPB NEO EKSMUS.
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN ... viii
I PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Tujuan ... 1
1.3 Ruang Lingkup ... 1
II TINJAUAN PUSTAKA ... 2
2.1 Analisis Regresi ... 2
2.2 Peubah Acak dan Distribusi ... 3
2.3 Distribusi Bernoulli ... 3
2.4 Family Beta dan Distribusi Beta ... 3
2.5 Matriks ... 3
2.6 Metode Maximum Likelihood ... 4
2.7 Algoritma K-Means ... 4
III METODE PENELITIAN ... 4
3.1 Studi Literatur ... 4
3.2 Sumber Data ... 5
3.3 Analisis dan Pemrograman ... 5
IV PEMBAHASAN ... 5
4.1 Efek Plasebo ... 5
4.2 Model Regresi Laten ... 5
4.3 Metode Pendugaan Parameter ... 6
4.4 Aplikasi pada Efek Plasebo ... 7
V SIMPULAN DAN SARAN ... 9
5.1 Simpulan ... 9
5.2 Saran ... 9
DAFTAR PUSTAKA ... 9
LAMPIRAN ... 10
DAFTAR GAMBAR
Halaman
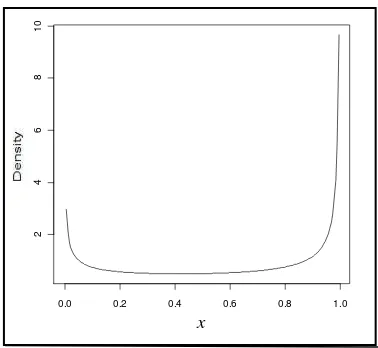
1 Plot kepadatan beta dengan a = 0.5 dan b = 0.3 untuk variabel laten x ... 7
2 Histogram data pasien depresi rawat jalan ... 7
3 Histogram penurunan depresi ... 8
4 Grafik estimasi model regresi laten ... 8
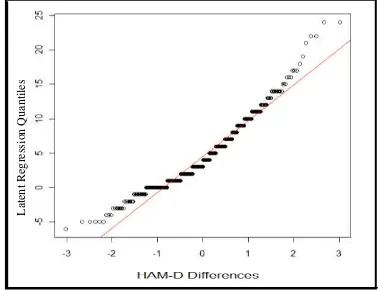
5 Plot kuantil-kuantil model regresi laten untuk data depresi ... 8
DAFTAR LAMPIRAN
Halaman 1 Pembuktian Teorema Estimasi � ... 112 Penjelasan Model Regresi Linear Multivariat ... 13
3 Pembuktian Persamaan (24) ... 14
4 Pembuktian Persamaan (26) ... 15
5 Pembuktian Teorema Trace ... 16
6 Pembuktian Pendugaan Parameter � dengan Algoritma EM (Expectation-Maximization) 18
7 Kode R untuk Gambar 1 ... 22
8 Kode R sebagai Pendefinisian Awal (Tarpey & Petkova) ... 23
9 Kode R untuk Algoritma K-Means, Maximum Likelihood dan Algoritma EM (Tarpey & Petkova) ... 25
10 Kode R untuk Plot Kuantil-Kuantil Data Depresi ... 28
I PENDAHULUAN
1.1Latar Belakang Penelitian
Analisis regresi mempelajari bentuk hubungan antara peubah respons (y) dengan satu atau lebih peubah prediktor (x) terutama untuk menelusuri pola hubungan yang modelnya belum diketahui. Dalam analisis regresi dipelajari bagaimana peubah tersebut berhubungan dan dinyatakan dalam persamaan matematika. Untuk melihat hubungan antara peubah respons dan peubah prediktor secara simultan dapat menggunakan analisis regresi linear.
Analisis regresi linear dibedakan menjadi dua, yaitu analisis regresi linear sederhana dan analisis regresi linear berganda. Perbedaan kedua analisis tersebut terletak pada banyaknya peubah prediktor. Analisis regresi linear sederhana terdapat satu peubah prediktor, sedangkan analisis regresi linear berganda terdapat lebih dari satu peubah prediktor (Draper & Smith 1992).
Analisis akan bertambah kompleks ketika melibatkan peubah laten, yaitu peubah yang tidak teramati (unobserved variable). Misalkan nilai kuantitas pada peubah laten diperoleh melalui prosedur estimasi (perkiraan). Sebuah model regresi dengan prediktor laten (tidak teramati) disebut regresi laten (Tarpey & Petkova 2010).
Salah satu kasus yang dapat diselesaikan dengan model regresi laten yaitu efek plasebo. Efek plasebo adalah efek sugesti yang membuat orang percaya untuk sembuh dengan sejenis obat tertentu. Keunggulan efek plasebo dapat digunakan dalam berbagai hal, terutama dalam pengobatan dan penyembuhan.
Salah satu penyakit yang bisa disembuhkan dengan efek plasebo adalah depresi. Depresi merupakan salah satu contoh penyakit yang dapat berubah secara kontinu dan tidak diketahui untuk waktu yang lama. Penelitian yang dilakukan oleh Beecher tentang the powerfull placebo menunjukkan bahwa 32% pasien sembuh karena efek plasebo. Namun, penelitian tersebut tidak memberikan model yang cocok untuk efek plasebo itu sendiri. Oleh karena itu, model regresi laten diusulkan untuk dikaji pada efek plasebo.
Pada penelitian ini, akan dilakukan analisis mengenai model regresi laten pada efek plasebo dengan prediktor laten kontinu menggunakan distribusi beta. Penelitian ini diharapkan dapat memberikan model yang cocok untuk efek plasebo. Metode yang digunakan untuk model regresi laten yaitu algoritma EM (Expectation Maximization).
Algoritma EM tergantung pada peubah yang tidak teramati. Algoritma EM dinilai layak digunakan karena terdapat dua tahapan pada setiap iterasi yaitu tahap maximization
(M-step) dan tahap expectation (E-step). Algoritma ini mengulang tahapan expectation
(E-Step) yang menghitung dugaan kemungkinan dengan memasukkan peubah tersembunyi seolah-olah peubah itu diamati. Tahapan maximization (M-Step) merupakan tahapan yang menghitung dugaan maximum likelihood parameter dengan memaksimalkan dugaan kemungkinan yang diperoleh dari E-Step. Nilai parameter yang diperoleh dari M-Step digunakan kembali untuk memulai E-Step yang selanjutnya. Proses ini akan berulang sehingga dicapai konvergensi nilai
likelihood (Dempster et al. 1997).
1.2Tujuan
Tujuan dari karya ilmiah ini adalah untuk menganalisis model regresi laten, menduga parameter dengan metode maximum likelihood dan algoritma EM (Expectation Maximization) serta mengaplikasi model pada efek plasebo dalam pengobatan depresi.
1.3Sistematika Penulisan
2
II LANDASAN TEORI
2.1 Analisis Regresi
Analisis regresi adalah analisis yang digunakan untuk menganalisis data dan mengambil kesimpulan yang bermakna tentang hubungan kebergantungan yang mungkin ada. Tujuan analisis regresi yaitu untuk mengevaluasi hubungan antara satu peubah dengan satu peubah lainnya atau satu peubah dengan beberapa peubah lainnya.
Peubah dapat dibedakan menjadi dua jenis, yaitu peubah prediktor atau peubah bebas, dan peubah respons atau peubah takbebas. Peubah prediktor adalah peubah yang dapat ditentukan atau diatur (misalnya suhu input) atau yang nilainya dapat diamati. Namun, tidak dapat dikendalikan (misalnya kelembaban udara luar). Akibat perubahan yang disengaja atau yang terjadi pada peubah prediktor, suatu pengaruh atau efek dipancarkan ke peubah lain disebut peubah respons.
(Draper & Smith 1992)
Regresi Linear Sederhana
Regresi linear sederhana adalah persamaan regresi yang menggambarkan hubungan antara satu peubah prediktor (x) dan peubah respons (y), hubungan keduanya dinyatakan dalam fungsi linear, sehingga hubungan kedua peubah tersebut dapat dituliskan dalam bentuk persamaan:
= 0+ 1 + (1)
dengan
0 : parameter regresi, 1 : parameter regresi,
: peubah respons, : peubah prediktor, : galat.
(Draper & Smith 1992)
Regresi Linear Berganda
Regresi linear berganda adalah persamaan regresi yang menggambarkan hubungan antara peubah respons (y) dan banyak peubah prediktor (x). Model regresi linear berganda yang melibatkan p peubah prediktor adalah
= 0+ 1 1 + 2 2 + + + i.(2)
Bentuk umum regresi berganda adalah
0 1
p
i j ij i
j
y x
(3)dengan
: peubah respons, : peubah prediktor,
0 : perpotongan (intercept),
: koefisien parameter dengan j= 1, 2,…, p, : galat.
(Draper & Smith 1992)
Pendugaan Koefisien Regresi Linear Berganda
Metode kuadrat terkecil adalah suatu metode untuk menghitung koefisien regresi sampel sebagai penduga koefisien regresi populasi (�), sedemikian sehingga jumlah galat kuadrat memiliki nilai terkecil. Secara matematis, model regresi dapat dinyatakan sebagai berikut:
= �+� (4)
dengan
Y : vektor peubah respons berukuran n × m
dengan n adalah banyaknya peubah respons yang diamati,
X : vektor peubah prediktor berukuran n×p, dengan p adalah banyaknya peubah prediktor,
�: vektor koefisien berukuran p×m,
�: vektor galat berukuran n × m yang berdistribusi ℕ(0,�).
(Draper & Smith 1992)
Asumsi dasar untuk atau , yaitu: 1. � = atau � = �, 2. �(�) = �2�atau �(�) = �2�.
Analisis regresi linear berganda menganalisis pengaruh 1, 2,…, terhadap y dengan menduga koefisien-koefisien
�0,�1,�2,…,� . Analisis ini menggunakan
metode jumlah kuadrat terkecil (least sum
square), yaitu dengan meminimumkan 2 1
n
i i
diperoleh nilai dugaan bagi �.
3
Teorema Estimasi �
Jika = �+�, dengan �×( + ) rank
+ 1 < , maka nilai � yang
meminimumkan 2 1
n
i i
adalah�= ( ′ )− ( ′ ). (5)
Bukti dapat dilihat pada Lampiran 1.
(Rencher & Schaalje 2008)
2.2 Peubah Acak dan Distribusi
Definisi Peubah Acak
Misalkan Ω adalah ruang contoh dari suatu percobaan acak. Fungsi � yang terdefinisi pada Ω yang memetakan setiap unsur ∈ Ω ke satu dan hanya satu bilangan real � = disebut peubah acak.
Ruang dari � adalah himpunan bagian bilangan real = { ∶ =� , ∈ Ω }.
(Hogg et al. 2005)
Definisi Peubah Acak Diskret
Peubah acak � dikatakan diskret jika himpunan semua nilai { 1, 2,...} merupakan himpunan tercacah.
(Grimmett & Stizaker1992)
Definisi Peubah Acak Kontinu
Peubah acak � dikatakan kontinu jika fungsi distribusi komulatifnya adalah fungsi kontinu untuk setiap ∈�.
(Hogg et al. 2005)
Definisi Fungsi Distribusi
Jika suatu peubah acak, fungsi distribusinya didefinisikan sebagai
= �[ ≤ ] (6)
untuk setiap ∈(−∞, +∞).
(Ghahramani 2000)
2.3 Distribusi Bernoulli
Suatu percobaan acak yang menghasilkan dua kemungkinan (sukses dan gagal) disebut percobaan Bernoulli. Peubah acak X disebut mempunyai sebaran Bernoulli, jika X
merupakan peubah acak pada percobaan
Bernoulli dengan 1, jika sukses, 0, jika gagal.
X
Jika p menyatakan peluang sukses, maka X
merupakan fungsi kerapatan peluang
� = (1− )1− , untuk = 0, 1.
(Hogg & Craig 1995)
2.4 Family Beta dan Distribusi Beta
Definisi Family Beta
Misalkan Y suatu peubah acak dengan
( ; , ) merupakan fungsi kepekatan
peluang dari peubah acak dengan parameter
a dan b, maka ( ; , ) dapat dikatakan sebagai family beta jika dapat dibentuk sebagai berikut:
= 1
( , )
( − ) − ( − ) −1
( − ) + −
(7) dengan ≤ ≤ dan > 0, > 0
merupakan fungsi parameter ( , ).
(Johnson et al. 1995)
Definisi Distribusi Beta
Suatu peubah acak dikatakan mempunyai distribusi beta dengan parameter
> 0 dan > 0 jika fungsi kepekatannya
diberikan oleh
1 1
1
( ) (1 )
( , )
X
f x x x
B
(8)
dengan
1
1 1
0
( , ) (1 )
B
x x dx dan0 < < 1. Rataan dan ragam :
,
(9)
2
2 .
( ) ( 1)
(Hogg & Craig 1995)
2.5 Matriks
Definisi Matriks Identitas
Matriks identitas adalah matriks �=
yang berorde × , dengan
= 1, = ,
0, ≠ .
(Leon 1998) (10)
4
Definisi Matriks Simetris
Suatu matriks A berorde × disebut simetris jika ′= .
(Leon 1998)
Definisi Invers
Suatu matriks yang berorde ×
dikatakan taksingular jika terdapat matriks sehingga = =�. Matriks dikatakan invers multiplikatif dari matriks . Invers multiplikatif dari matriks taksingular secara sederhana disebut juga sebagai invers dari matriks dan dinotasikan dengan −1.
(Leon 1998)
Definisi Transpos
Transpos dari suatu matriks =
berorde × adalah matriks =
berorde × yang didefinisikan oleh
=
untuk setiap dan . Transpos dari dinotasikan oleh ′.
(Leon 1998)
Definisi Trace
Trace adalah fungsi yang didefinisikan hanya pada matriks persegi. Misalkan A
adalah matriks × , trace dari matriks A
adalah jumlah dari elemen-elemen diagonal dari matriks A,
� =
=1
.
(Magnus & Neudecker 1999)
Teorema Trace
Misalkan adalah skalar dan A dan B
adalah matriks yang masing-masing memiliki orde × , maka:
1. tr( + ) = tr + tr , 2. tr( ) = tr( ), 3. tr( ′) = tr( ), 4. tr( ) = tr( ).
Bukti dapat dilihat pada Lampiran 4. (Magnus & Neudecker 1999)
2.6 Metode Maximum Likelihood
Misalkan 1, 2,…, adalah peubah acak i.i.d dengan fungsi kepekatan peluang
( ; �), dengan � diasumsikan skalar dan
tidak diketahui, maka prosedur fungsi
likelihood dapat dituliskan sebagai berikut:
� ,� = ( ,�)
=1
,� ∈Ω
dengan = ( 1, 2,…, ).
Fungsi loglikelihood dari � ,� , dapat dinotasikan dengan:
,� = log� ,�
= log ,� ,� ∈Ω.
=1
(14) Pendugaan parameter dengan metode
maximum likelihood estimation dapat diperoleh dari ,�
� = 0.
(Hogg & Craig 1995)
2.7 Algoritma K-Means
Algoritma K-Means merupakan salah satu metode pengelompokan data tidak berhirarki yang berusaha mempartisi data yang ada ke dalam satu atau lebih gerombol.
(Hair et al. 1995)
III METODE PENELITIAN
Karya ilmiah ini disusun melalui studi literatur mengenai regresi laten, sumber data pasien depresi, analisis dan pemrograman dari data sekunder menggunakan software R
2.13.1.
3.1 Studi Literatur
Studi literatur meliputi pencarian berbagai informasi yang berhubungan dengan topik yang dibahas yaitu regresi laten.
Langkah-langkah penelitian:
1. Menelusuri model regresi laten yang sesuai,
2. Mengestimasi parameter model regresi ketika x berupa laten menggunakan K-means, maximum likelihood dan algoritma
EM,
3. Melakukan aplikasi pada efek plasebo. (13)
5
3.2 Sumber Data
Data yang digunakan untuk penelitian ini adalah data sekunder mengenai pasien depresi rawat jalan yang bersumber dari Tarpey dan Petkova (2010) dengan komunikasi via e-mail. Objek penelitian adalah pasien laki-laki dan perempuan berusia 18 - 65 tahun. Jumlah responden depresi dalam penelitian adalah 393 orang. Tarpey dan Petkova melihat perubahan tingkat gejala depresi menggunakan skala Hamilton Depression Rating (HAM-D).
3.3 Analisis dan Pemrograman
Tahapan analisis dan pemrograman yang dilakukan dalam penelitian ini sebagai berikut:
1. Membangun model regresi laten
Tahap pertama ini akan dibangun model regresi dengan inisialisasi setiap parameter, kemudian disimpan dalam bentuk file emnorm.r.
2. Melakukan pengelompokan data dengan algoritma K-means, yaitu dengan menentukan inisialisasi nilai awal k, komponen means dan perkiraan matriks kovarian.
3. Melakukan pendugaan algoritma EM, yaitu dengan menentukan inisialisasi nilai sigma, perkiraan nilai parameter beta, mengerjakan tahap E-step dan M-step.
IV PEMBAHASAN
4.1 Efek Plasebo
Plasebo adalah istilah medis untuk sejenis obat tanpa bahan kimia yang kadang hanya berisi gula atau cairan garam. Efek plasebo adalah efek sugesti yang membuat orang percaya untuk sembuh dengan sejenis obat tertentu. Efek plasebo digunakan dalam pengobatan dan penyembuhan. Efek ini lebih menekankan pada faktor psikologis dan keyakinan untuk sembuh.
4.2 Model Regresi Laten
Analisis multivariat merupakan salah satu jenis analisis statistik yang digunakan untuk menganalisis data dengan data yang digunakan berupa banyak peubah prediktor dan banyak peubah respons. Bentuk hubungan analisis regresi linear ganda yaitu beberapa peubah prediktor terhadap satu peubah respons. Model regresi laten pada efek plasebo:
= �+� (15)
dengan
: peubah respons p-variat, : prediktor laten (tidak teramati)
berdimensi r,
� : parameter,
� : galat(� ~ℕ(0,�)).
Penjelasan model regresi linear multivariat dapat dilihat pada Lampiran 2. Jika populasi terdiri dari dua sub populasi laten (orang yang mengalami efek plasebo dan orang yang tidak
mengalami efek plasebo), maka prediktor laten pada persamaan (15) memiliki distribusi Bernoulli. Misalkan p = P(x = 1) dan asumsikan bahwa menyebar distribusi
ℕ( ,�) dengan � adalah matriks kovarian definit positif. Kepadatan marjinal (�) pada
y dinamakan model campuran terbatas:
=� = 0 � = 0 +� = 1
(�| = 1)
= 1− ℕ �;�1,� + ℕ(�;�2,�) (16)
dengan �1 = 0, �2 = 0 + 1 dan ℕ(�;�,�) merupakan hasil fungsi kepadatan normal berganda dengan rataan vektor � dan matriks kovarians �.
Distribusi Bernoulli memiliki probabilitas 0 dan 1. Cara alami untuk menggeneralisasi model campuran terbatas yaitu dengan mengganti prediktor Bernoulli 0−1 oleh distribusi kontinu pada interval (0, 1) yang kepadatannya berbentuk U. Pilihan alami untuk distribusi pada x adalah distribusi beta dengan kepadatan ( ; , ) yang didefinisikan dalam parameter a dan b.
; , = ΓΓ +Γ −1 1− −1
dengan 0 < < 1.
Family beta menghasilkan berbagai bentuk kepadatan salah satunya kepadatan berbentuk U. Kepadatan ini menyediakan generalisasi kontinu dari distribusi Bernoulli diskret.
� = ( ,�)
6
Kepadatan bersama untuk x dan y dalam persamaan (15) adalah
,� = � ; 0, 1,� ; ,
= ℕ(�; 0+ 1 ,�) ; ,
dengan ; , merupakan distribusi beta yang diberikan dalam persamaan (17). Kepadatan marjinal hasilnya adalah
� = 1
2��exp{−(� − 0− 1 )′�
−1 1
0
� − 0− 1 /2} ( ; , )� .
4.3 Metode Pendugaan Parameter
Ada beberapa metode yang digunakan untuk menduga parameter, antara lain metode momen, metode Bayes, metode maximum likelihood, dan algoritma EM ( Expectation-Maximization). Pendugaan parameter yang digunakan pada penelitian ini adalah metode
maximum likelihood dan algoritma EM
(Expectation-Maximization).
Metode Maximum Likelihood
Metode maximum likelihood adalah suatu metode yang baik untuk memperoleh sebuah parameter tunggal. Misalkan 1, 2,… ,
masing-masing peubah acak saling bebas dengan sebaran yang memiliki fungsi kepekatan peluang ; � , dengan 0≤ � ≤ 1,� Ω dan Ω adalah ruang contoh. Fungsi kepekatan peluang bersama dari
1, 2,… , adalah � � 1, 2, …, =
1 � 2 � … � yang disebut
juga sebagai fungsi likelihood.
Fungsi sederhana dari x1, x2, … ,xn yaitu
(x1, x2, … , xn), sehingga �=u(x1, x2, … , xn)
membuat fungsi kemungkinan L maksimum untuk semua � Ω. Statistik u(x1, x2, … , xn)
disebut penduga maximum likelihood dari � yang dinotasikan dengan � = u(X1, X2, … ,
Xn). Untuk menduga parameter dengan
menggunakan metode maximum likelihood
tidak bisa secara langsung karena datanya tidak teramati, untuk itu dapat digunakan algoritma EM.
Algoritma Expectation-Maximization
Algoritma Expectation-Maximization adalah suatu algoritma yang sangat handal untuk pendugaan parameter dengan menggunakan metode maximum likelihood
dari fungsi likelihood pada data yang tidak teramati (McLachlan & Krishnan 2008). Proses algoritma EM dilakukan dengan dua tahap, yaitu:
E-Step (Tahapan Expectation)
Merupakan tahapan untuk menghitung ekspektasi bersyarat dari fungsi loglikelihood
dengan prediktor laten. Misalkan � adalah suatu nilai awal, maka E-Step didefinisikan
( �(�;�)| ) (20)
dalam aplikasi pada efek placebo, � didefinisikan sebagai matriks koefisien:
�= �0′
�1′
(21)
dengan � berdimensi 2 × p, masing-masing kolom p dari � merupakan intercept dan slope
koefisien regresi untuk setiap peubah respons
p. X merupakan matriks yang kolom pertama terdiri dari 1 dan kolom kedua terdiri dari prediktor laten �, = 1, 2, …, n, Y merupakan matriks berdimensi n×p, dan �merupakan matriks kovarian definit positif. Model regresi laten dapat ditulis sebagai
= �+�. (22)
Likelihood untuk model regresi laten dinyatakan sebagai berikut :
� �,� = 2� −2 � −2
exp{−� [�−1 − � ′( − �)]/2}. (23)
Misalkan = [ | ] dan ′ = [ ′ | ], maka nilai harapan dari
� [�−1 − � ′( − �) bersyarat
adalah
� �−1 − � ′ − � =
� [�−1{ ′ − ′ � − �′ ′ +�′( ′ )�}].
(24)
Pembuktian persamaan (24) dapat dilihat pada Lampiran 3. ′ dan � definit positif, sehingga pada E-Step diperoleh
( �(�;�)| ) =−
2 ln 2� −2ln �
−0.5� [�−1{ ′ − ′ � − �′ ′
+�′( ′ )�}]. (25)
Misalkan � = ( ′ )−1 ′ maka persamaan
(24) dapat dinyatakan kembali sebagai:
� [�−1{( ′ − � ′ � ′ ) + � − � ′
′
(� − �)}]. (26)
(18)
7
Pembuktian persamaan (26) dapat dilihat pada Lampiran 4. Bagian dari trace pada persamaan (26) yang melibatkan parameter � dapat dinyatakan sebagai berikut:
� �−1 � − � ′ � − � ′
=� � − � �′ −1 � − � ′
=� [( ′ )1/2(� − �)�−1 � − � ′( ′ )1/2].
(27) Hasil E-Step dapat dinyatakan kembali sebagai:
( �(�;�)| ) =−
2 ln 2� −2ln �
−0.5� [�−1{ ′ − � ′ � − �′ ′ � ′
+�′( ′ )�}].
(28)
M-Step (Tahapan Maximization)
Merupakan tahapan untuk mendapatkan parameter baru � dengan memaksimumkan
( �(�;�)| ), yang dinyatakan sebagai berikut:
( ( �(�;�)| ))
�
sehingga diperoleh � =�= ′ −1 ′ .
Proses E-Step dan M-Step ini dilakukan terus secara iteratif sampai diperoleh suatu nilai dugaan parameter � yang konvergen. Langkah-langkah mencari nilai dugaan parameter � menggunakan algoritma EM
dapat dilihat pada Lampiran 5.
4.4 Aplikasi pada Efek Plasebo
[image:16.595.322.511.82.256.2]Algoritma EM yang dijelaskan terdahulu akan diuji menggunakan berbagai pengaturan parameter untuk model regresi laten. Untuk setiap pengaturan parameter, 50 himpunan data diberikan dengan masing-masing ukuran sampel n = 100. Sebagai ilustrasi, peubah laten x menyebar distribusi beta dengan parameter a = 0.5 dan b = 0.3 menghasilkan kerapatan berbentuk U. Galat menyebar distribusi normal dengan rataan = 0 dan standar deviasi � = 0.5.
Gambar 1 Plot kepadatan beta dengan a = 0.5 dan b = 0.3 untuk peubah laten x.
Kurva pada Gambar 1 merupakan kurva distribusi beta dengan x peubah laten. Kurva tersebut menghasilkan kerapatan berbentuk U. Hasilnya mendukung bahwa tidak ada dua kelas berbeda dari subjek (orang-orang yang mengalami efek plasebo dan orang-orang yang tidak mengalaminya). Kode R untuk Gambar 1 dapat dilihat pada lampiran 7. Jumlah responden depresi dalam Tarpey dan Petkova sebanyak 393 orang dalam satu minngu. Salah satu cara yang digunakan dalam menduga sebaran pasien depresi selama satu minggu adalah dengan melihat kesesuaian histogram data. Histogram data pasien depresi rawat jalan selama satu minggu dapat dilihat pada Gambar 2.
Gambar 2 Histogram data pasien depresi rawat jalan.
0.0 0.2 0.4 0.6 0.8 1.0
2
4
6
8
10
Latent Beta Distribution for Simulation
[image:16.595.323.514.497.652.2]8
Histogram pada Gambar 2 menunjukkan bahwa data pasien depresi berdistribusi beta. Pasien depresi yang mendapatkan efek plasebo ternyata mengalami perubahan positif. Efek plasebo telah diketahui ada di penelitian depresi dan efek ini cenderung untuk meningkatkan suasana hati. Tampaknya masuk akal atribut peubah laten untuk efek plasebo dalam penelitian ini. Karena efek plasebo adalah laten, model dari gejala depresi pada minggu pertama merupakan fungsi kekuatan efek plasebo x.
Jika x dalam persamaan (15) adalah Bernoulli, maka model menjelaskan bahwa terdapat dua jenis subjek. Dua jenis subjek tersebut, yaitu orang-orang yang mengalami efek plasebo dan orang-orang yang tidak mengalaminya. Jika x kontinu, maka model menjelaskan bahwa masing-masing subjek mengalami efek plasebo berderajat variasi. Perubahan tingkat gejala depresi dari awal sampai minggu pertama diukur pada skala
[image:17.595.120.510.236.377.2]Hamilton Depression Rating (HAM-D).
Gambar 3 Histogram penurunan depresi.
Perubahan positif dari awal sampai minggu pertama menunjukkan penurunan depresi seperti terlihat pada Gambar 3. Kurva pada Gambar 3 merupakan suatu perhitungan kerapatan non-parametik dari y yang menunjukkan distribusi miring (condong) kanan. Perubahan positif menunjukkan berbagai derajat peningkatan antara subjek yang relatif baik. Kurva solid merupakan perkiraan kepadatan non-parametrik, kurva putus-putus merah merupakan perkiraan kepadatan regresi laten, dan kurva hijau putus-putus merupakan perkiraan kepadatan campuran dua komponen terbatas.
Gambar 4 Grafik estimasi model regresi laten.
Estimasi model regresi laten adalah
= −0.279 + 26.604 yang ditunjukkan pada Gambar 4. Interpretasinya adalah semakin besar nilai efektivitas plasebo maka akan memberikan perubahan suasana hati yang semakin tinggi.
Pada awalnya (minggu pertama) efek plasebo berubah secara kontinu, mulai dari yang sangat lemah sampai cukup kuat sehingga distribusi efek plasebo condong ke arah lebih baik. Efek plasebo masih bervariasi tetapi kita mulai melihat segmentasi ke dalam dua kelompok.
Gambar 5 Plot kuantil-kuantil model regresi laten untuk data depresi.
0.0 0.2 0.4 0.6 0.8 1.0 0 5 10 15 20 25 x y P er u b ah an S u as an a Ha ti Non-parametrik
--- Laten
--- Campuran
= −0.279 + 26.604
x (Tingkat Efektivitas Plasebo)
[image:17.595.321.511.572.717.2]9
Plot kuantil dari histogram pada minggu pertama dapat dilihat pada Gambar 5. Berdasarkan Gambar 5, pola pancaran titik-titik untuk model regresi laten hampir membentuk garis lurus tetapi pada ekor kanan menyimpang dari rentang data. Hal ini dikarenakan terdapat dua kelompok, yaitu kelompok yang tidak ada pengaruh efek plasebo dan kelompok yang kuat pengaruh plasebo. Berdasarkan ide dasar uji Sharpio-Wilks untuk normalitas, �2 yang diperoleh
sebesar 0.95. Koefisien �2 ini menunjukkan
bahwa pendekatan model regresi laten cocok untuk gugus data pengamatan efek placebo pada studi depresi.
Pendugaan parameter model dilakukan dengan menggunakan Software-R. Kode R sebagai pendefinisian awal dapat dilihat pada Lampiran 8 dan kode R untuk algoritma K-means, maximum likelihood danalgoritma EM
dapat dilihat pada Lampiran 9. Kode R untuk plot kuantil-kuantil model regresi laten untuk data depresi dapat dilihat pada Lampiran 10.
V SIMPULAN DAN SARAN
5.1 Simpulan
Simpulan yang dapat diambil setelah melakukan penelitian dan pengumpulan data tentang model matematika, yaitu semakin besar nilai efektivitas plasebo maka akan memberikan perubahan suasana hati yang semakin tinggi. Persamaan regresi laten yang menggambarkan efek plasebo pada studi depresi adalah
= -0.279 + 26.604 x.
Parameter model regresi laten tersebut diduga dengan menggunakan metode maximum
likelihood dan algoritma EM ( Expectation-Maximization).
5.2 Saran
1. Penelitian lebih lanjut diharapkan mengkaji dengan distribusi lain yang memungkinkan untuk prediktor laten dengan faktor-faktor lain yang memengaruhi gejala depresi pada efek plasebo.
2. Perlu diketahui substansi dari fenomena masalah yang dikaji untuk memilih model yang dianggap cocok, sehingga pemilihan model akan sesuai dengan fakta yang dijumpai.
DAFTAR PUSTAKA
Dempster AP, Laird NM, Rubin D. 1997. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. B 39, 1-38.
Draper N, Smith H. 1992. Analisis Regresi Terapan. Ed ke-2. Jakarta: PT Gramedia Pustaka Utama.
Ghahramani S. 2005. Fundamental of Probability and Random Processes. Ed ke-2. New Jersey: Prentice Hall.
Grimmett GR, Stirzaker DR. 1992.
Probability and Random Processes. Ed ke-2. Oxford: Clarendon Press.
Hair JF et al. 1995. Multivariate Data Analysis. Ed ke-4. New Jersey: Prentice Hall.
Hogg RV, Craig AT. 1995. Introduction to Mathematical Statistics. Ed ke-5. New Jersey: Prentice Hall.
Hogg RV, Craig AT, McKean JW. 2005.
Introduction to Mathematical Statistics.
Ed ke-6. New Jersey: Prentice Hall.
Johnson NL, Kotz S, Balakrishnan N. 1995.
Continuous Univariate Distributions. New York: J Wiley.
Leon SJ. 1998. Linear Algebra with Applications. Ed ke-5. New Jersey: Prentice Hall.
Magnus JR, Neudecker. 1999. Matrix Differential Calculus with applications in statistics and Econometrics. Ed revisi. New York: J Wiley.
McLachlan GJ, Krishnan T. 2008. The EM Algorithm and Extension. Ed ke-2. New Jersey: J Wiley.
Rencher AC, Schaalje GB. 2008. Linear Models in Statistics. Ed ke-2. New Jersey: J Wiley.
10
11
Lampiran 1 Pembuktian Teorema Estimasi �
Bentuk umum regresi linear berganda:
= 0+ +
=1
Persamaan diobservasi sebanyak n pengamatan sehingga:
0 1 11 2 12 1 1
1
0 1 21 2 22 2 2
2
0 1 1 2 2
11 12 1 0 1
21 22 2 1 2
1 2 ... ... ... 1 ... 1 ... 1 ... p p p p
n n n p np n
p
p
p
n n np
x x x
y
x x x
y
y x x x
x x x
x x x
x x x
n
Metode Kuadrat Terkecil (Least Square)
Meminimumkan 2 2 1 1 ( ) n n
i i i
i i
y y
dengan kendala parameternya, yaitu:dengan 1, 2,...,
j j p
, ideal 2
1 0 0 n i i
^ 2 2 1 1 ( ) n ni i i
i i y y
2 0 1 1 ˆ [ ( )] p ni j ij
i j
y x
2 2
0 0
1 1 1
ˆ ˆ
[ 2 ( ) ( ) ]
p p
n
i i j ij j ij
i j j
y y x x
2 2 2 2
0 0 0
1 1 1 1
ˆ ˆ ˆ
[ 2 2 2 ]
p p p
n
i i i j ij j ij j ij
i j j j
y y y x x x
2 2 1 0 1 1 ( ) ˆ0 ( 2 2 2 ) 0
n
i n p
i
ij i ij j ij
i j
j
x y x x
0 2 1 1 ˆ2 ( ) 0
p n
ij i ij j ij
i j
x y x x
2 0 1 1 ˆ( ) 0
p n
ij i ij j ij
i j
x y x x
Dalam bentuk matriks:
�′�= ( − �)′( − �)
=�′� − �′ ′ − ′ �+�′ ′ �
12
Lampiran 1 (Lanjutan)
�(�′�)
�� =
↔�( ′ − �′ ′�� +�′ ′ �)=
↔ − ′ + ′ �=
↔ − ′( × �) (� × )+ ′( × �) � × �( × ) =
↔ ′ = ′ �
↔ ′ − ′ �= ′ − ′
↔ ��= ′ − ′
↔ �= ′ − ′
Sehingga diperoleh �= ′ − ′ .
13
Lampiran 2 Penjelasan Model Regresi Linear Multivariat
Misalkan untuk peubah respons sebanyak 2 atau terdapat Y1dan Y2serta 3 peubah prediktor, maka 11 12
21 22
1 2
=
1 11
1 21
12 13
22 23
1 1 2 3
01 02 11 12 21 22
1 2
+
11 12 21 22
1 2
.
Jika terdapat p peubah respons Y dan r peubah prediktor x, terdapat sejumlah persamaan model regresi:
11 1
⋱
1
=
1 11
1 21
12 1 22 23
1 1 2
01 02 11 12
… 0
… 1
1 2
⋱ …
+
11 1 21 2
1
dengan �= [ 1, 2,…, ], � = 0, Var(�) = �.
Model regresi linear multivariat adalah
( × )= ( ×( +1))�(( +1)× )+� × .
14
Lampiran 3 Pembuktian Persamaan (24)
Diketahui
[� [�−1 − � ′( − �)]| ]
Akan dibuktikan Persamaan (22), yaitu
� [�−1{ ′ − ′ � − �′ ′ +�′( ′ )�}]
dengan
=
′ = ′
Bukti:
[� [�−1 − � ′( − �)]| ]
↔ [� [�−1( ′ − �′ ′)( − �)]| ]
↔ [� �−1 ′ − ′ � − �′ ′ +�′ ′ � ]
↔ [� �−1 ′ − ′ � − �′ ′ +�′ ′ � ]
↔ � [�−1{ ′ − ′ � − �′ ′ +�′( ′ )�}]
15
Lampiran 4 Pembuktian Persamaan (26)
Diketahui Persamaan (22), yaitu
� [�−1{ ′ − ′ � − �′ ′ +�′( ′ )�}]
Akan dibuktikan bahwa Persamaan (24) ekivalen dengan Persamaan (22), yaitu
� [�−1{ ′ − � ′ � ′ + (� − �)′ ′ (� − �)}]
merupakan matriks yang kolom pertama terdiri dari 1 dan kolom kedua terdiri dari prediktor laten �, i = 1, 2, … , n sehingga ′ merupakan matriks ukuran 2 × 2 yang simetri, maka:
′
′= ′
dengan
� = ( ′ )−1 ′
↔ � ′ = ′ ( ′ )−1 ′
↔ � ′ = ′
↔( � ′ )′= ( ′ )′
↔ � ′ ′′ = ′
↔ � ′ ′ = ′
Bukti:
� [�−1{ ′ − ′ � − �′ ′ +�′( ′ )�}]
↔ � [�−1{ ′ − � ′ � − �′′ ′ +�′( ′ )�}]
↔ � [�−1{ ′ − � ′ � −′ �′ � ′ +�′( ′ )�}]
↔ � [�−1{ ′ − � ′ � −′ �′ � ′ +�′( ′ )� − � ′ ′ +� ′ ′ }]
↔ � [�−1{ ′ − � ′ � −′ �′ � ′ +�′( ′ )� − � ′ � ′ +� ′ � ′ }]
↔ � [�−1{ ′ − � ′ � ′ +� ′ � − � ′ ′ � −′ �′ � ′ +�′ �′ }]
↔ � [�−1{ ′ − � ′ � ′ + (� ′ − �′ ′ ′ )(� − �)}]
↔ � [�−1{ ′ − � ′ � ′ + (� − �)′ ′ (� − �)}]
16
Lampiran 5 Pembuktian Teorema Trace
Diketahui trace:
� =
=1
Misalkan adalah skalar dan A dan B adalah matriks yang masing-masing memiliki orde × .
Bukti:
1. Diketahui tr + tr
Akan dibuktikan bahwa tr( + )
Bukti:
tr + tr =
=1
+
=1
= ( + )
=1
= tr( + ).
2. Diketahui tr( )
Akan dibuktikan bahwa tr( )
Bukti:
tr =
=1
=
=1
= tr( ).
3. Diketahui tr( )
Akan dibuktikan bahwa tr( ′)
Bukti:
tr =
=1
= 11+ 22+ 33+ +
= tr( ′).
4. Diketahui tr( )
Akan dibuktikan bahwa tr( ) Bukti:
tr = ( )
=1
= ( ) + ( )
=1
=
=1 =1
17
Lampiran 5 (Lanjutan)
=
=1 =1
=
=1
= ( )
=1
= tr( ).
18
Lampiran 6 Pembuktian Pendugaan Parameter � dengan Algoritma EM ( Expectation-Maximization)
E-Step (Tahapan Expectation) Diketahui persamaan model regresi laten:
= �+�
Fungsi likelihood untuk persamaan model regresi:
� �,� = 2� −2 � −2exp{−� [�−1 − � ′( − �)]/2}
Fungsi loglikelihood persamaan di atas menjadi:
ln� �,� = ln [ 2� −2 � −2exp{−� [�−1 − � ′( − �)]/2}]
=−
2 ln 2� −2ln � −0.5� [�
−1 − � ′( − �)]
�−1merupakan matriks kovarian simetri yang berorde × , sehingga (�−1)′= (�−1).
Ekspektasi dari fungsi loglikelihood bersyarat Y :
(ln�(�;�)| ) = {−
2 ln 2� −2ln � −0.5� [�−
1 − � ′( − �)]| }
=−
2 ln 2� −2ln � −0.5 {� [�
−1 − � ′( − �)]| }
berdasarkan Lampiran 1, diperoleh:
=−
2 ln 2� −2ln � −0.5 � �
−1{ ′ − ′ � − �′ ′ +�′( ′ )�}
=−
2 ln 2� −2ln � −0.5 � �−
1 ′ − �−1 ′ � − �−1�′ ′ +�−1�′( ′ )� …(i)
berdasarkan Lampiran 2, diperoleh:
=−
2 ln 2� −2ln � −0.5 � [�
−1 ′ − �−1� ′ � − �′ −1�′ ′ +�−1�′( ′ )�]
=−
2 ln 2� −2ln � −0.5� [�
−1 ′ − �−1� ′ � −′ �−1�′ � ′ +�−1�′( ′ )�]
…(ii) dari persamaan …(i)
(ln�(�;�)| )
=−
2 ln 2� −2ln � −0.5 � �
−1 ′ − �−1 ′ � − �−1�′ ′ +�−1�′( ′ )�
berdasarkan Teorema trace, diperoleh:
=−
2 ln 2� −2ln � −0.5 � [�−
1 ′ ] + 0.5 � [�−1 ′ �] + 0.5 � [�−1�′ ′ ]
−0.5 � [�−1�′ �′ ]
=−
2 ln 2� −2ln � −0.5 � [�
−1 ′ ] + 0.5 � [�−1 ′ �] + 0.5 � [(�−1�′ ′ )′]
−0.5 � [�−1�′ �′ ]
=−
2 ln 2� −2ln � −0.5 � [�
−1 ′ ] + 0.5 � [�−1 ′ �] + 0.5 � [ ′ �(�−1)′]
19
Lampiran 6 (Lanjutan)
=−
2 ln 2� −2ln � −0.5 � [�
−1 ′ ] + 0.5 � [�−1 ′ �] + 0.5 � [ ′ ��−1]
−0.5 � [�−1�′ �′ ]
=−
2 ln 2� −2ln � −0.5 � [�
−1 ′ ] + 0.5 � [�−1 ′ �] + 0.5 � [�−1 ′ �]
−0.5 � [�−1�′ �′ ]
=−
2 ln 2� −2ln � −0.5 � �−
1 ′ +� �−1 ′ � −0.5 � [�−1�′ �′ ]
M-Step (Tahapan Maximization)
Pendugaan parameter � diperoleh dengan memaksimumkan harapan dari fungsi loglikelihood
bersyarat Y :
( (ln�(�;�)| ))
� = 0
↔ (− 2 ln 2� −2ln � −0.5 � �
−1 ′ +� �−1 ′ � −0.5 � [�−1�′ �′ ])
� = 0
↔0−0−0 + (� �
−1 ′ � −0.5 � [�−1�′ �′ ]
� = 0
↔ �−1 ′ ′− (0.5 � [�−
1�′ �′ ])
� = 0
↔ ′ (�−1)′− (0.5 � [�−
1�′ �′ ])
� = 0
↔ ′ �−1− (0.5 � [�−
1�′ �′ ])
� = 0
Penjelasan:
�[0.5 � [�−1�′ �′ ]] = 0.5 � [�−1(��)′ �′ + [�−1�′ ′ (��)]]
= 0.5 � [�−1(��)′ �′ + 0.5tr[�−1�′ ′ (��)]
= 0.5 � [� ′ (��)′(�−1)′) + 0.5tr[�−1�′ ′ (��)]
= 0.5 � [�−1 �′′ (��)] + 0.5 tr[�−1�′ ′ (��)]
= 0.5 tr[�−1�′ ′ (��)] + 0.5 tr[�−1�′ ′ (��)]
= tr[�−1�′ ′ ]��
[tr[�−1�′ ′ �]]
� =[�−
1
�′ ′ ]′
= ′ ′�(�−1)′
= �′ (�−1)
diperoleh
↔ ′ �−1− �′ (�−1) = 0
↔ ′ �−1= ��′ −1
20
Lampiran 6 (Lanjutan)
dari persamaan …(ii)
(ln�(�;�)| )
=−
2 ln 2� −2ln � −0.5� [�
−1 ′ − �−1� ′ � −′ �−1�′ � ′ +�−1�′( ′ )�]
berdasarkan Teorema trace, diperoleh:
=−
2 ln 2� −2ln � −0.5� (�
−1 ′ ) + 0.5� (�−1� ′ �′ ) + 0.5� (�−1�′ � ′ )
−0.5� (�−1�′( ′ )�)
=−
2 ln 2� −2ln � −0.5� (�
−1 ′ ) + 0.5� (�−1� ′ �′ ) + 0.5� ([�−1�′ � ′ ]′)
−0.5� (�−1�′( ′ )�)
=−
2 ln 2� −2ln � −0.5� (�
−1 ′ ) + 0.5� (�−1� ′ �′ ) + 0.5� (�−1� ′ �′ )
−0.5� (�−1�′( ′ )�)
=−
2 ln 2� −2ln � −0.5� (�
−1 ′ ) +� (�−1� ′ �′ )−0.5� (�−1�′( ′ )�)
Pendugaan parameter � diperoleh dengan memaksimumkan harapan dari fungsi loglikelihood
bersyarat Y :
( (ln�(�;�)| ))
� = 0
↔ (− 2 �ln 2� )− (2ln � )
� −
(0.5� (�−1 ′ ))
� +
(� (�−1�′ ′ �))
�
− (0.5� (�
−1�′( ′ )�))
� = 0
↔ (� (�
−1�′ ′ �))
� −
(0.5� (�−1�′( ′ )�))
� = 0
Penjelasan:
�(� (�−1�′ ′ �)) =� (�−1�′ ′ )��
(� (�−1�′ ′ �))
� =(�−
1�′ ′
)′
= ′ ′�(�−1)′
= ′ ��−1
�[0.5 � [�−1�′ �′ ]] = 0.5 � [�−1(��)′ �′ + [�−1�′ ′ (��)]]
= 0.5 � [�−1(��)′ �′ + 0.5tr[�−1�′ ′ (��)]
= 0.5 � [� ′ (��)′(�−1)′) + 0.5tr[�−1�′ ′ (��)]
= 0.5 � [�−1 �′′ (��)] + 0.5 tr[�−1�′ ′ (��)]
= 0.5 tr[�−1�′ ′ (��)] + 0.5 tr[�−1�′ ′ (��)]
= tr[�−1�′ ′ ]��
21
[tr[�−1�′ ′ �]]
� =[�−
1�′ ′ ]′
= ′ ′�(�−1)′
= �′ (�−1)
diperoleh
↔ ′ ��−1− �′ (�−1) = 0
↔ ′ ��−1= ��′ −1
↔ ′ −1 ′ ��−1�= ′ −1 ��′ −1�
↔�=�.
Jadi pendugaan parameter, yaitu:
� =�= ′ −1 ′ .
22
Lampiran 7 Kode R untuk Gambar 1
23
Lampiran 8 Kode R sebagai Pendefinisian Awal (Tarpey & Petkova)
> # procedure EMNORM > # procedure EMNORM >
> # input: k Number of Mixture components > # y N-vector of observed data
> # prior k-vector of initial prior probabilities > # mu k by p matrix of initial means
> # var k array of initial p by p covariance matrices > # pool indicator for equality of variances:
> # pool<-0: unequal variances; pool<-1: equal variances >
> # output prior final initial probabilities > # mu final means
> # var final variances
> # loglik value of (complete data) log-likelihood > # nit number of iterations of EM-algorithm > # post posterior probability estimates >
> emnorm <- function(k,y, prior, mu, var, pool) + {
+ N <- dim(y)[1] # number of observations + p <- dim(y)[2] # dimension of data + eps <- .000000001 # convergence criterion + change <- 1 # initial test value for convergence + maxiter <- 2000 # maximum number of iterations + nit <- 0 # initialize iteration counter
+ #param <- c(prior, mu, var) # arrange all parameters in a vector + post <- matrix(0, N, k) # open matrix for posterior probabilities + while (change > eps && nit <= maxiter) # start iterations
+ {
+ options(digits = 6) # format for the display of numerical results + muold <- mu # store old parameter values
+ varold <- var + priorold <- prior +
+ # Evaluate component densities and the log-likelihood + f <- matrix(0,N,k)
+ i <- 0 + for(i in 1:k-1) + {
+ i <- i+1 + expo <
-0.5*diag(as.matrix(sweep(y,2,mu[i,]))%*%solve(var[,,i])%*%as.matrix(t(sweep(y,2,mu[i,])))) + w <- eigen(var[,,i])
+ f[,i] <- prior[i,1]*(2*pi)^(-p*.5)/sqrt(exp(sum(log(w$values))))*exp(expo) + }
+ loglik <- sum(log(as.matrix(apply(f,1,sum)))) # evaluate log-likelihood function +
+ # Compute posterier probabilities for each component + i <- 0
+ for(i in 1:k-1) + {
+ i <- i+1
24
Lampiran 8 (Lanjutan)
+ post <- as.matrix(post) +
+
+ # comment next line out if you don't want a protocol of the algorithm + #cat(format(c(nit,loglik), justify = "right"), fill = T)
+
+ prior <- as.matrix(apply(post, 2, mean)) # M-step: prior probabilities +
+ mu <- as.matrix(t(post)) %*%as.matrix(y)/N # M-step: means + i <- 0
+ for(i in 1:k-1) + {
+ i <- i+1
+ mu[i,] <- mu[i,]/prior[i,1] + }
+ +
+ varcommon <- matrix(0,p,p) + i <- 0
+ for(i in 1:k-1) + {
+ i <- i+1
+ var[,,i] <- 1/(N*prior[i,])*t(y)%*%as.matrix(diag(post[,i]))%*%as.matrix(y)- as.matrix(mu[i,])%*%mu[i,] # m-step: variances
+ varcommon <- varcommon+var[,,i]*prior[i,1] + }
+ if (pool ==1) + {
+ var <- array(varcommon, c(p,p,k)) # M-step: common variance + }
+ change1 <- max(abs(prior - priorold)) # test value for convergence + change2 <- max(abs(mu-muold))
+ change3 <- max(abs(var-varold))
+ change <- max(change1,change2, change3) +
+
+ nit <- nit + 1 # increase interation counter + }
+ if (nit >= maxiter)
+ cat("algorithm did not converge in ") # warning message if convergence + maxiter # is not reached
+ " iterations"
+ results <- list("prior" = prior, "mu" = mu, "var " = var, + "loglik" = loglik, "nit" = nit, "post" = post)
25
Lampiran 9 Kode R untuk Algoritma K-Means, Maximum Likelihood dan Algoritma EM (Tarpey & Petkova)
> source("emnorm.r")
> y <- read.table("improvement.dat",header=F) > y <- as.matrix(y)
> hist(y,20, freq=FALSE, xlab="Difference", main="Prozac Difference Data",ylab="Relative Frequency")
> n<- dim(y)[1] > plot(density(y)) > t <- seq(0,1, by = .005) > shapiro.test(y)
> k <- 2
> prior <- matrix(1,k)/k > pool <- 0
> S <- cov(y) > p <- dim(y)[2]
> kmean <- kmeans(y, k, iter.max = 100) > mu <- as.matrix(sort(kmean$centers)) > var <- array(S, c(p,p, k))
> results <- emnorm(k,y, prior, mu, var, pool)
> muvar<- t(matrix(cbind(results$prior,results$mu,results$var),6,1)) > s <- sqrt(sum(kmean$withinss)/n) # initial value of sigma > bhat <- matrix(1,2,1)
> bhat[1,1] <- results$mu[1] # Initial values for beta0 and beta1 estimates > bhat[2,1] <- -results$mu[1]+results$mu[2]
> ab <- matrix(1,2,1) > nit <- 1
> maxiter <- 200 > while ( nit <= maxiter) + {
+ nit <- nit+1 + xx <- matrix(0,n,4) + for(i in 1:n) + {
+ yi = y[i,1]
+ fd<- function(x) {dnorm(yi, mean=(bhat[1,1] +bhat[2,1]*x), sd=s, log = FALSE)*x^(ab[1,1]-1)*(1-x)^(ab[2,1]-1)}
+ fx<- function(x) {dnorm(yi, mean=(bhat[1,1]+bhat[2,1]*x), sd=s, log = FALSE)*x^ab[1,1]*(1-x)^(ab[2,1]-1)}
+ fx2<- function(x) {dnorm(yi, mean=(bhat[1,1]+bhat[2,1]*x), sd=s, log = FALSE)*x^(ab[1,1]+1)*(1-x)^(ab[2,1]-1)}
+ flx<- function(x) {dnorm(yi, mean=(bhat[1,1]+bhat[2,1]*x), sd=s, log = FALSE)*log(x)*x^(ab[1,1]-1)*(1-x)^(ab[2,1]-1)}
+ flx2<- function(x){dnorm(yi, mean=(bhat[1,1]+bhat[2,1]*x), sd=s, log = FALSE)*log(1-x)*x^(ab[1,1]-1)*(1-x)^(ab[2,1]-1)}
+ denom <- integrate(fd, 0, 1) + numx <- integrate(fx, 0,1) + numx2 <- integrate(fx2,0,1) + numlx <- integrate(flx, 0,1) + numlx2<- integrate(flx2,0,1)
+ xx[i,1] <- numx$value/denom$value + xx[i,2] <- numx2$value/denom$value + xx[i,3] <- numlx$value/denom$value + xx[i,4] <- numlx2$value/denom$value + }
26
Lampiran 9 (Lanjutan)
+ xprimex[1,2] <- sum(xx[,1]) + xprimex[2,1] <- xprimex[1,2] + xprimex[2,2] <- sum(xx[,2]) + x0 <- matrix(1,n,2)
+ x0[,2] <- xx[,1]
+ bhat <- solve(xprimex)%*%t(x0)%*%y
+ s<-sqrt((t(y)%*%y - t(bhat)%*%xprimex%*%bhat)/n) + xbar <- as.matrix(apply(xx,2,mean))
+ m1 <- xbar[1,1] + m2 <- xbar[2,1]
+ ab[2,1] <- m1*(1-m1)^2/(m2-m1^2) + m1 -1 + ab[1,1] <- ab[2,1]*m1/(1-m1)
+ S <- matrix(0,2,1) + Info <- matrix(0,2,2) + eps <- 0.0000001 + change <- 100 + while (change > eps) + {
+ abold <- ab
+ S[1,1] <- n*(digamma(ab[1,1]+ab[2,1])-digamma(ab[1,1]))+sum(xx[,3]) + S[2,1] <- n*(digamma(ab[1,1]+ab[2,1])-digamma(ab[2,1]))+sum(xx[,4]) + Info[1,1] <- n*(trigamma(ab[1,1]+ab[2,1])-trigamma(ab[1,1]))
+ Info[2,2] <- n*(trigamma(ab[1,1]+ab[2,1])-trigamma(ab[2,1])) + Info[2,1] <- n*(trigamma(ab[1,1]+ab[2,1]))
+ Info[1,2] <- Info[2,1] + Info<- -Info
+ ab <- ab + solve(Info)%*%S
+ change <- t(ab-abold)%*%(ab-abold) + }
+ kb <- gamma(ab[1,1]+ab[2,1])/(gamma(ab[1,1])*gamma(ab[2,1])) + loglike <- -n/2*log(2*pi)-.5*n*log(s^2) -.5/s^2*(t(y)%*%y -
2*t(bhat)%*%t(x0)%*%y+t(bhat)%*%xprimex%*%bhat)+n*log(kb) +(ab[1,1]-1)*sum(xx[,3]) +(ab[2,1]-1)*sum(xx[,4])
+ yhatlatent <- bhat[1,1] + bhat[2,1]*x0[,2]
+ yhatmix <- results$mu[1,1]*results$post[,1] + results$mu[2,1]*results$post[,2] + mseLatent <- t(y-yhatlatent)%*%(y-yhatlatent)/(n-5)
+ mseMix <- t(y - yhatmix)%*%(y-yhatmix)/(n-5) + abline(0,1)
+ cat("iteration ", nit, "\n") + cat("loglike =", loglike, "\n") + cat("Parameter Estimate", "\n") + cat("beta0: ", bhat[1,1], "\n") + cat("beta1: ", bhat[2,1], "\n") + cat("alpha0: ", ab[1,1], "\n") + cat("alpha1: ", ab[2,1], "\n") + cat("sigma: ", s, "\n") + cat("\n")
+ cat("\n")
+ bpfit<-gamma(ab[1,1]+ab[2,1])/(gamma(ab[1,1])*gamma(ab[2,1]))*t^(ab[1,1]-