OPTIMASI MODEL
RANTAI PASOKAN AGROINDUSTRI
COCODIESEL
DENGAN MENGGUNAKAN ALGORITMA GENETIKA
Oleh:
YUVI ANDRIA
F34103021
2007
FAKULTAS TEKNOLOGI PERTANIAN
INSTITUT PERTANIAN BOGOR
FAKULTAS TEKNOLOGI PERTANIAN
INSTITUT PERTANIAN BOGOR
OPTIMASI MODEL
RANTAI PASOKAN AGROINDUSTRI
COCODIESEL
DENGAN MENGGUNAKAN ALGORITMA GENETIKA
SKRIPSI
Sebagai salah satu syarat untuk memperoleh gelar
SARJANA TEKNOLOGI PERTANIAN
Pada Fakultas Teknologi Pertanian
Institut Pertanian Bogor
Oleh:
YUVI ANDRIA
F34103021
Disetujui,
Bogor, Juli 2007
Dr. Ir. Yandra Arkeman, M.Eng Hendra Gunawan, S.TP
Yuvi Andria. F34103021. Optimasi Model Rantai Pasokan AgroindustriCocodiesel
Dengan Menggunakan Algoritma Genetika. Dibawah bimbingan Yandra Arkeman dan Hendra Gunawan. 2007.
RINGKASAN
Manajemen rantai pasokan adalah suatu pendekatan untuk mengintegrasikan secara efisien antara pemasok, perusahaan manufaktur, penggudangan, dan penjualan sehingga produk diproduksi dan didistribusikan pada jumlah, tempat, dan waktu yang tepat, dengan tujuan untuk memenuhi kebutuhan permintaan dan meminimisasi biaya total keseluruhan (cost efficient). Model rantai pasokan agroindustri yang optimal adalah rantai yang memiliki kombinasi paling baik dan
efisien sehingga dapat diperoleh TSCC (Total Supply Chain Cost) yang paling
minimum. Kombinasi tersebut merupakan masalah pencarian (searching) untuk
mengoptimalkan TSCC dari parameter-parameter rantai pasokan dalam suatu ruang
pencarian tertentu (search space). Teknik optimasi terbaru yang berasal dari bidang
Artificial Inteligence adalah algoritma genetika (Genetic Algorithms) merupakan
salah satu alternatif teknik pencarian (searching technique) heuristik yang bersifat
tangguh, adaptif, dan efisien.
Algoritma genetika dapat mencari solusi optimal berdasarkan pada mekanisme sistem natural yaitu genetika dan seleksi alam. Solusi minimum TSCC dari model rantai pasokan agroindustri tersebut dapat dipecahkan dengan menggunakan algoritma genetika dengan lebih efektif dan efisien. Penelitian ini bertujuan untuk : Merancang model rantai pasokan agroindustri dengan berdasarkan model transportasi, inventori, dan distribusi; Merancang bangun program algoritma genetika untuk optimasi model rantai pasokan agroindustri dan melihat efisiensi pencarian solusi optimum yang dilakukan algoritma genetika; Melakukan kajian penerapan program algoritma genetika yeng telah dibuat untuk rantai pasokan agroindustricocodiesel.
Implementasi pada penelitian ini adalah rancang bangun program algoritma
genetika untuk optimasi model rantai pasokan agroindustri yaitu program GASCM
(Genetic Algorithms for Supply Chain Management) Ver. 1.0 yang dibuat
menggunakan bahasa pemrograman Borland Delphi 7.0 dengan acuan program
Simple Genetic Algoritms(SGA). Telah dilakukan pengembangan dari fungsi-fungsi
maupun prosedur-prosedur dalam program antara lain Fungsi FitFunc untuk
menghitung fungsi TSCC; Prosedur InitPop yaitu inisialisasi populasi dengan
representasi integer dan memenuhi suatu kendala-kendala/constrained; FungsiSelect
adalah fungsi untuk menseleksi kromosom dengan teknik seleksi turnamen (tournament selection); dan Prosedur Statistic dikembangkan menjadi dalam bentuk grafik.
Hasil penelitian ini menunjukkan bahwa program GASCM Ver. 1.0 sangat
efisien dalam menemukan solusi TSCC minimum dari model rantai pasokan
agroindustri. Pada kasus 1 (numerical example) untuk rantai pasokan agroindustri
2x2x2, solusi minimum dapat tercapai pada generasi ke-270 dengan nilai TSCC 1525.
Algoritma genetika hanya mengeksplorasi 3,5 % total ruang pencarian (total search
ditunjukan oleh kasus 2 (numerical example) untuk rantai pasokan agroindustri 4x3x4
dan kasus 3 untuk studi kasus skenario rantai pasokan agroindustricocodiesel.
Rantai pasokan agroindustri cocodiesel merupakan skenario rantai pasokan
agroindustri 2x2x2 yang berada pada Propinsi Kalimantan Barat dan Tengah. Skenario berdasarkan data-data sekunder dan informasi-informasi riil tentang
agroindustri cocodiesel Pemasok kelapa pertama (Supplier-1) berada di daerah
kabupaten Sambas (Kalimantan Barat) sedangkan untuk pemasok kelapa kedua (Supplier-2) berada di daerah kabupaten Pontianak (Kalimantan Barat). Untuk
agroindustricocodiesel ke-1 berada pada wilayah Sintang (Kalimantan Barat) dan
agroindustricocodiesel ke-2 berada di wilayah Rantaupulut (Kalimantan Tengah).
Permintaan untuk cocodiesel ke-1 bagi para nelayan berada di daerah pesisir
pantai selat Karimata (Kalimantan Barat) dan kebutuhan permintaan cocodiesel
ke-2 untuk industri-industri maupun SPBU berada di kawasan Kalimantan Tengah.
Hasil optimasi algoritma genetika terhadap skenario rantai pasokan
agroindustricocodiesel tersebut adalah sebagai berikut : Jumlah pasokan kelapa
dari pemasok-1 ke agroindustri-1 sebanyak 408.875 butir; jumlah pasokan kelapa dari pemasok-1 ke agroindustri-2 sebanyak 0 butir; jumlah pasokan kelapa dari pemasok-2 ke agroindustri-1 sebanyak 341.125 butir; jumlah pasokan kelapa dari
pemasok-2 ke agroindustri-2 sebanyak 1.000.000 butir; jumlah cocodiesel dari
agroindustri-1 ke permintaan-1 sebanyak 100.000 liter; jumlah cocodiesel dari
agroindustri-1 ke permintaan-2 sebanyak 0 liter; jumlah cocodiesel dari
agroindustri-2 ke permintaan-1 sebanyak 0 liter; jumlah cocodiesel dari
agroindustri-2 ke permintaan-2 sebanyak 200.000 liter; jumlah persediaan
cocodiesel pada agroindustri-1 sebanyak 50.000 liter; dan jumlah persediaan
Yuvi Andria. F34103021. Agroindustrial of Cocodiesel Supply Chain Model Optimization with Genetic Algorithms. Supervised by Yandra Arkeman and Hendra Gunawan. 2007.
SUMMARY
Supply chain management is a set of approaches utilized to efficiently integrate supplier, manufacturers, warehouses, and stores, so that merchandise is produced and distributed at the right quantities, to the right locations, at the right time, in order to minimize systemwide costs while satisfying service level requirement. Agroindustrial supply chain model can optimize if the model have a best and efficient network combinations in order to minimize Total Supply Chain Cost (TSCC). The combination of supply chain parameters is a search problem within certain search space to optimize the TSCC. The newest optimization method is Genetic Algorithms, as one of the Artificial Inteligence tool for heuristic searching technique, which is very robust, adaptive, and efficient.
Genetic Algorithms search the best solutions based on the natural system like natural genetic and the process of evolution. The best solution of TSCC in agroindustrial supply chain model can solve with genetic algorithms very efficient and effective. The aim of this research is to : Build the agroindustrial supply chain model based on transportation, inventory, and distribution model; Build a genetic algorithms program for optimize an agroindustrial supply chain model and see the efficiency of the best solution searching with genetic algorithms; Studying and applying genetic algorithms program that have been made for the cocodiesel agroindustrial supply chain.
The implementation of this research is build a genetic algorithms program, GASCM (Genetic Algorithms for Supply Chain Management) Ver. 1.0 created with
Borland Delphi 7.0 language compiler based on Simple Genetic Algoritms (SGA) program. There are some development of the functions and procedures in the
program: FitFunc function, to calculate TSCC function; InitPop procedure, for
initialization of population with integer representation and constrained; Select
function, to select the chromosome withtournament selection; andStatistic procedure
have been developed into chart visualization.
The result of this research showGASCM Ver. 1.0 program is very efficient to
find the best or minimum solutions of TSCC from agroindustrial supply chain model. Case-1 is a numerical example for 2x2x2 agroindustrial supply chain, the minimum solution can reach at generation-270 with TSCC value is 1525. Genetic algorithms only explore 3,5 % of total search space to get the best solution at case-1. Efficiency of genetic algorithms increase if the search space is more bigger. It show by case-2 (numerical example) for 4x3x4 agroindustrial supply chain and case-3 for case study agroindustrial of cocodiesel supply chain scenario.
(Kalimantan Barat), and the second demand is for an industrials and SPBU that locate in area of Middle Kalimantan.
KATA PENGANTAR
Alhamdulillahi rabbil ’alamin, puji dan syukur penulis panjatkan kepada
Allah SWT, karena dengan rahmat dan karunia-Nya penulis dapat menyelesaikan
skripsi yang berjudul ” Optimasi Model Rantai Pasokan Agroindustri Cocodiesel
Dengan Menggunakan Algoritma Genetika” dengan baik. Skripsi ini disusun
berdasarkan kegiatan penelitian yang dilakukan oleh penulis pada bulan Maret
2007 hingga bulan Juli 2007. Pada kesempatan ini penulis menyampaikan terima
kasih kepada berbagai pihak yang telah membantu dalam penyelesaian skripsi ini :
1. Dr. Ir. Yandra Arkeman, M.Eng., sebagai pembimbing I yang telah
memberikan pengarahan, bimbingan, dan saran dalam penyelesaian skripsi.
2. Hendra Gunawan, S.TP, sebagai pembimbing II yang telah memberikan
pengarahan, informasi, dan bimbingan.
3. Dr. Ir. Dwi Setyaningsih M.Si, sebagai dosen penguji pada ujian skripsi, dan
atas bantuan infomasi serta masukan data sekunder agroindustri cocodiesel.
4. Papa, Mama, serta adikku yang telah memberikan dukungan, semangat, kasih
sayang, dan doa yang tercurah.
5. Anggy, Ayip, Desminda, Devi, Vie-vie, Mona, Imam, Sylvilia, Adam, Renata,
Syahrian, Detri, dan teman-teman TIN 40 atas dukungannya sehingga penulis
tetap semangat dalam penulisan skripsi ini.
6. Semua pihak yang telah memberikan bantuan selama penulis melakukan
kegiatan penelitian, hingga skripsi ini selesai dengan baik.
Semoga skripsi ini dapat bermanfaat bagi semua pihak.
Bogor, Juli 2007
RIWAYAT HIDUP
Penulis dilahirkan di kota Bogor pada tanggal 14
Desember 1985 dari pasangan Ahmad Badjuri dan Suyanti.
Penulis adalah anak pertama dari dua bersaudara. Pada tahun
1990 penulis masuk Taman Kanak-Kanak Al Khairiyah Bogor
dan lulus tahun 1991. Penulis melanjutkan sekolah di SDN Pabrik
Gas 2 Bogor dan lulus pada tahun 1997. Tahun 1997, penulis melanjutkan sekolah
ke SLTPN 5 Bogor dan lulus tahun 2000. Pada tahun yang sama penulis
melanjutkan pendidikan ke SMUN 5 Bogor dan lulus pada tahun 2003.
Pada tahun 2003, penulis lulus seleksi masuk IPB melalui jalur Undangan
Seleksi Masuk IPB (USMI) dan diterima di departemen Teknologi Industri
Pertanian, Fakultas Teknologi Pertanian. Selama perkuliahan penulis sempat
menjadi asisten mata kuliah Penerapan Komputer tahun ajaran 2006/2007 dan
asisten Sistem Informasi Manajemen pada tahun ajaran yang sama. Penulis
melaksanakan Praktek Lapang selama dua bulan (3 Juli – 25 Agustus 2006) di
BPPT-Sapi Perah Cikole, Lembang, Bandung. Penulis mendapatkan beasiswa
DAFTAR ISI
halaman
KATA PENGANTAR... i
RIWAYAT HIDUP ... ii
DAFTAR ISI ... iii
DAFTAR TABEL ... vi
DAFTAR GAMBAR... vii
DAFTAR LAMPIRAN ... ix
I. PENDAHULUAN ... 1
A. LATAR BELAKANG ... 1
B. TUJUAN ... 3
C. RUANG LINGKUP ... 3
II. TINJAUAN PUSTAKA ... 4
A.SUPPLY CHAIN MANAGEMENT... 4
B. TEKNIK OPTIMASI ... 10
C.LINEAR PROGRAMMING DAN INTEGER LINEAR PROGRAMMING .... 10
D. MODEL TRANSPORTASI ... 13
E. ALGORITMA GENETIKA ... 15
1. Prosedur Umum Algoritma Genetika ... 16
2. Representasi Kromosom ... 17
3. FungsiFitness ... 18
4. Operator-Operator Algoritma Genetik ... 18
5. Perbandingan Algoritma Genetik dengan Teknik Optimasi Konvensional ... 24
F. KELAPA DANCOCODIESEL ... 25
G. PENELITIAN TERDAHULU ... 29
III. METODOLOGI PENELITIAN ... 31
A. KERANGKA PEMIKIRAN ... 31
IV. PEMBAHASAN ... 38
A. MODEL RANTAI PASOKAN AGROINDUSTRI ... 38
1. Asumsi ... 38
2. Identifikasi Variabel Keputusan ... 39
3. Identifikasi Kendala-Kendala ... 40
4. Perumusan Fungsi Tujuan ... 41
5. Penyusunan Model ... 42
B. REPRESENTASI KROMOSOM ... 43
C. FUNGSI FITNESS ... 44
D. SELEKSI (SELECTION) ... 44
E. PENYILANGAN (CROSSOVER) ... 45
F. MUTASI (MUTATION) ... 45
G. IMPLEMENTASI PROGRAM (GASCM VER. 1.0) ... 45
H. STUDI KASUS ... 51
1. Kasus 1 :Agroindustrial SCM 2x2x2 ... 51
a. Parameter-parameter Algoritma Genetika ... 53
b. Inisialisasi Populasi Awal ... 53
c. Evaluasi dan Seleksi Kromosom ... 54
d. Penyilangan dan Mutasi ... 55
e. Hasil Running ProgamGASCM Ver. 1.0 ... 59
f. Efisiensi Algoritma Genetika ... 61
2. Kasus 2 :Agroindustrial SCM 4x3x4 ... 63
a. Parameter-parameter Algoritma Genetika ... 66
b. Inisialisasi Populasi Awal ... 66
c. Evaluasi dan Seleksi Kromosom ... 67
d. Penyilangan dan Mutasi ... 69
e. Hasil Running ProgamGASCM Ver. 1.0 ... 70
f. Efisiensi Algoritma Genetika ... 72
3. Kasus 3 : Skenario kasus rantai pasokan agroindustricocodiesel... 73
a. Parameter-parameter Algoritma Genetika ... 76
b. Inisialisasi Populasi Awal ... 76
OPTIMASI MODEL
RANTAI PASOKAN AGROINDUSTRI
COCODIESEL
DENGAN MENGGUNAKAN ALGORITMA GENETIKA
Oleh:
YUVI ANDRIA
F34103021
2007
FAKULTAS TEKNOLOGI PERTANIAN
INSTITUT PERTANIAN BOGOR
FAKULTAS TEKNOLOGI PERTANIAN
INSTITUT PERTANIAN BOGOR
OPTIMASI MODEL
RANTAI PASOKAN AGROINDUSTRI
COCODIESEL
DENGAN MENGGUNAKAN ALGORITMA GENETIKA
SKRIPSI
Sebagai salah satu syarat untuk memperoleh gelar
SARJANA TEKNOLOGI PERTANIAN
Pada Fakultas Teknologi Pertanian
Institut Pertanian Bogor
Oleh:
YUVI ANDRIA
F34103021
Disetujui,
Bogor, Juli 2007
Dr. Ir. Yandra Arkeman, M.Eng Hendra Gunawan, S.TP
Yuvi Andria. F34103021. Optimasi Model Rantai Pasokan AgroindustriCocodiesel
Dengan Menggunakan Algoritma Genetika. Dibawah bimbingan Yandra Arkeman dan Hendra Gunawan. 2007.
RINGKASAN
Manajemen rantai pasokan adalah suatu pendekatan untuk mengintegrasikan secara efisien antara pemasok, perusahaan manufaktur, penggudangan, dan penjualan sehingga produk diproduksi dan didistribusikan pada jumlah, tempat, dan waktu yang tepat, dengan tujuan untuk memenuhi kebutuhan permintaan dan meminimisasi biaya total keseluruhan (cost efficient). Model rantai pasokan agroindustri yang optimal adalah rantai yang memiliki kombinasi paling baik dan
efisien sehingga dapat diperoleh TSCC (Total Supply Chain Cost) yang paling
minimum. Kombinasi tersebut merupakan masalah pencarian (searching) untuk
mengoptimalkan TSCC dari parameter-parameter rantai pasokan dalam suatu ruang
pencarian tertentu (search space). Teknik optimasi terbaru yang berasal dari bidang
Artificial Inteligence adalah algoritma genetika (Genetic Algorithms) merupakan
salah satu alternatif teknik pencarian (searching technique) heuristik yang bersifat
tangguh, adaptif, dan efisien.
Algoritma genetika dapat mencari solusi optimal berdasarkan pada mekanisme sistem natural yaitu genetika dan seleksi alam. Solusi minimum TSCC dari model rantai pasokan agroindustri tersebut dapat dipecahkan dengan menggunakan algoritma genetika dengan lebih efektif dan efisien. Penelitian ini bertujuan untuk : Merancang model rantai pasokan agroindustri dengan berdasarkan model transportasi, inventori, dan distribusi; Merancang bangun program algoritma genetika untuk optimasi model rantai pasokan agroindustri dan melihat efisiensi pencarian solusi optimum yang dilakukan algoritma genetika; Melakukan kajian penerapan program algoritma genetika yeng telah dibuat untuk rantai pasokan agroindustricocodiesel.
Implementasi pada penelitian ini adalah rancang bangun program algoritma
genetika untuk optimasi model rantai pasokan agroindustri yaitu program GASCM
(Genetic Algorithms for Supply Chain Management) Ver. 1.0 yang dibuat
menggunakan bahasa pemrograman Borland Delphi 7.0 dengan acuan program
Simple Genetic Algoritms(SGA). Telah dilakukan pengembangan dari fungsi-fungsi
maupun prosedur-prosedur dalam program antara lain Fungsi FitFunc untuk
menghitung fungsi TSCC; Prosedur InitPop yaitu inisialisasi populasi dengan
representasi integer dan memenuhi suatu kendala-kendala/constrained; FungsiSelect
adalah fungsi untuk menseleksi kromosom dengan teknik seleksi turnamen (tournament selection); dan Prosedur Statistic dikembangkan menjadi dalam bentuk grafik.
Hasil penelitian ini menunjukkan bahwa program GASCM Ver. 1.0 sangat
efisien dalam menemukan solusi TSCC minimum dari model rantai pasokan
agroindustri. Pada kasus 1 (numerical example) untuk rantai pasokan agroindustri
2x2x2, solusi minimum dapat tercapai pada generasi ke-270 dengan nilai TSCC 1525.
Algoritma genetika hanya mengeksplorasi 3,5 % total ruang pencarian (total search
ditunjukan oleh kasus 2 (numerical example) untuk rantai pasokan agroindustri 4x3x4
dan kasus 3 untuk studi kasus skenario rantai pasokan agroindustricocodiesel.
Rantai pasokan agroindustri cocodiesel merupakan skenario rantai pasokan
agroindustri 2x2x2 yang berada pada Propinsi Kalimantan Barat dan Tengah. Skenario berdasarkan data-data sekunder dan informasi-informasi riil tentang
agroindustri cocodiesel Pemasok kelapa pertama (Supplier-1) berada di daerah
kabupaten Sambas (Kalimantan Barat) sedangkan untuk pemasok kelapa kedua (Supplier-2) berada di daerah kabupaten Pontianak (Kalimantan Barat). Untuk
agroindustricocodiesel ke-1 berada pada wilayah Sintang (Kalimantan Barat) dan
agroindustricocodiesel ke-2 berada di wilayah Rantaupulut (Kalimantan Tengah).
Permintaan untuk cocodiesel ke-1 bagi para nelayan berada di daerah pesisir
pantai selat Karimata (Kalimantan Barat) dan kebutuhan permintaan cocodiesel
ke-2 untuk industri-industri maupun SPBU berada di kawasan Kalimantan Tengah.
Hasil optimasi algoritma genetika terhadap skenario rantai pasokan
agroindustricocodiesel tersebut adalah sebagai berikut : Jumlah pasokan kelapa
dari pemasok-1 ke agroindustri-1 sebanyak 408.875 butir; jumlah pasokan kelapa dari pemasok-1 ke agroindustri-2 sebanyak 0 butir; jumlah pasokan kelapa dari pemasok-2 ke agroindustri-1 sebanyak 341.125 butir; jumlah pasokan kelapa dari
pemasok-2 ke agroindustri-2 sebanyak 1.000.000 butir; jumlah cocodiesel dari
agroindustri-1 ke permintaan-1 sebanyak 100.000 liter; jumlah cocodiesel dari
agroindustri-1 ke permintaan-2 sebanyak 0 liter; jumlah cocodiesel dari
agroindustri-2 ke permintaan-1 sebanyak 0 liter; jumlah cocodiesel dari
agroindustri-2 ke permintaan-2 sebanyak 200.000 liter; jumlah persediaan
cocodiesel pada agroindustri-1 sebanyak 50.000 liter; dan jumlah persediaan
Yuvi Andria. F34103021. Agroindustrial of Cocodiesel Supply Chain Model Optimization with Genetic Algorithms. Supervised by Yandra Arkeman and Hendra Gunawan. 2007.
SUMMARY
Supply chain management is a set of approaches utilized to efficiently integrate supplier, manufacturers, warehouses, and stores, so that merchandise is produced and distributed at the right quantities, to the right locations, at the right time, in order to minimize systemwide costs while satisfying service level requirement. Agroindustrial supply chain model can optimize if the model have a best and efficient network combinations in order to minimize Total Supply Chain Cost (TSCC). The combination of supply chain parameters is a search problem within certain search space to optimize the TSCC. The newest optimization method is Genetic Algorithms, as one of the Artificial Inteligence tool for heuristic searching technique, which is very robust, adaptive, and efficient.
Genetic Algorithms search the best solutions based on the natural system like natural genetic and the process of evolution. The best solution of TSCC in agroindustrial supply chain model can solve with genetic algorithms very efficient and effective. The aim of this research is to : Build the agroindustrial supply chain model based on transportation, inventory, and distribution model; Build a genetic algorithms program for optimize an agroindustrial supply chain model and see the efficiency of the best solution searching with genetic algorithms; Studying and applying genetic algorithms program that have been made for the cocodiesel agroindustrial supply chain.
The implementation of this research is build a genetic algorithms program, GASCM (Genetic Algorithms for Supply Chain Management) Ver. 1.0 created with
Borland Delphi 7.0 language compiler based on Simple Genetic Algoritms (SGA) program. There are some development of the functions and procedures in the
program: FitFunc function, to calculate TSCC function; InitPop procedure, for
initialization of population with integer representation and constrained; Select
function, to select the chromosome withtournament selection; andStatistic procedure
have been developed into chart visualization.
The result of this research showGASCM Ver. 1.0 program is very efficient to
find the best or minimum solutions of TSCC from agroindustrial supply chain model. Case-1 is a numerical example for 2x2x2 agroindustrial supply chain, the minimum solution can reach at generation-270 with TSCC value is 1525. Genetic algorithms only explore 3,5 % of total search space to get the best solution at case-1. Efficiency of genetic algorithms increase if the search space is more bigger. It show by case-2 (numerical example) for 4x3x4 agroindustrial supply chain and case-3 for case study agroindustrial of cocodiesel supply chain scenario.
(Kalimantan Barat), and the second demand is for an industrials and SPBU that locate in area of Middle Kalimantan.
KATA PENGANTAR
Alhamdulillahi rabbil ’alamin, puji dan syukur penulis panjatkan kepada
Allah SWT, karena dengan rahmat dan karunia-Nya penulis dapat menyelesaikan
skripsi yang berjudul ” Optimasi Model Rantai Pasokan Agroindustri Cocodiesel
Dengan Menggunakan Algoritma Genetika” dengan baik. Skripsi ini disusun
berdasarkan kegiatan penelitian yang dilakukan oleh penulis pada bulan Maret
2007 hingga bulan Juli 2007. Pada kesempatan ini penulis menyampaikan terima
kasih kepada berbagai pihak yang telah membantu dalam penyelesaian skripsi ini :
1. Dr. Ir. Yandra Arkeman, M.Eng., sebagai pembimbing I yang telah
memberikan pengarahan, bimbingan, dan saran dalam penyelesaian skripsi.
2. Hendra Gunawan, S.TP, sebagai pembimbing II yang telah memberikan
pengarahan, informasi, dan bimbingan.
3. Dr. Ir. Dwi Setyaningsih M.Si, sebagai dosen penguji pada ujian skripsi, dan
atas bantuan infomasi serta masukan data sekunder agroindustri cocodiesel.
4. Papa, Mama, serta adikku yang telah memberikan dukungan, semangat, kasih
sayang, dan doa yang tercurah.
5. Anggy, Ayip, Desminda, Devi, Vie-vie, Mona, Imam, Sylvilia, Adam, Renata,
Syahrian, Detri, dan teman-teman TIN 40 atas dukungannya sehingga penulis
tetap semangat dalam penulisan skripsi ini.
6. Semua pihak yang telah memberikan bantuan selama penulis melakukan
kegiatan penelitian, hingga skripsi ini selesai dengan baik.
Semoga skripsi ini dapat bermanfaat bagi semua pihak.
Bogor, Juli 2007
RIWAYAT HIDUP
Penulis dilahirkan di kota Bogor pada tanggal 14
Desember 1985 dari pasangan Ahmad Badjuri dan Suyanti.
Penulis adalah anak pertama dari dua bersaudara. Pada tahun
1990 penulis masuk Taman Kanak-Kanak Al Khairiyah Bogor
dan lulus tahun 1991. Penulis melanjutkan sekolah di SDN Pabrik
Gas 2 Bogor dan lulus pada tahun 1997. Tahun 1997, penulis melanjutkan sekolah
ke SLTPN 5 Bogor dan lulus tahun 2000. Pada tahun yang sama penulis
melanjutkan pendidikan ke SMUN 5 Bogor dan lulus pada tahun 2003.
Pada tahun 2003, penulis lulus seleksi masuk IPB melalui jalur Undangan
Seleksi Masuk IPB (USMI) dan diterima di departemen Teknologi Industri
Pertanian, Fakultas Teknologi Pertanian. Selama perkuliahan penulis sempat
menjadi asisten mata kuliah Penerapan Komputer tahun ajaran 2006/2007 dan
asisten Sistem Informasi Manajemen pada tahun ajaran yang sama. Penulis
melaksanakan Praktek Lapang selama dua bulan (3 Juli – 25 Agustus 2006) di
BPPT-Sapi Perah Cikole, Lembang, Bandung. Penulis mendapatkan beasiswa
DAFTAR ISI
halaman
KATA PENGANTAR... i
RIWAYAT HIDUP ... ii
DAFTAR ISI ... iii
DAFTAR TABEL ... vi
DAFTAR GAMBAR... vii
DAFTAR LAMPIRAN ... ix
I. PENDAHULUAN ... 1
A. LATAR BELAKANG ... 1
B. TUJUAN ... 3
C. RUANG LINGKUP ... 3
II. TINJAUAN PUSTAKA ... 4
A.SUPPLY CHAIN MANAGEMENT... 4
B. TEKNIK OPTIMASI ... 10
C.LINEAR PROGRAMMING DAN INTEGER LINEAR PROGRAMMING .... 10
D. MODEL TRANSPORTASI ... 13
E. ALGORITMA GENETIKA ... 15
1. Prosedur Umum Algoritma Genetika ... 16
2. Representasi Kromosom ... 17
3. FungsiFitness ... 18
4. Operator-Operator Algoritma Genetik ... 18
5. Perbandingan Algoritma Genetik dengan Teknik Optimasi Konvensional ... 24
F. KELAPA DANCOCODIESEL ... 25
G. PENELITIAN TERDAHULU ... 29
III. METODOLOGI PENELITIAN ... 31
A. KERANGKA PEMIKIRAN ... 31
IV. PEMBAHASAN ... 38
A. MODEL RANTAI PASOKAN AGROINDUSTRI ... 38
1. Asumsi ... 38
2. Identifikasi Variabel Keputusan ... 39
3. Identifikasi Kendala-Kendala ... 40
4. Perumusan Fungsi Tujuan ... 41
5. Penyusunan Model ... 42
B. REPRESENTASI KROMOSOM ... 43
C. FUNGSI FITNESS ... 44
D. SELEKSI (SELECTION) ... 44
E. PENYILANGAN (CROSSOVER) ... 45
F. MUTASI (MUTATION) ... 45
G. IMPLEMENTASI PROGRAM (GASCM VER. 1.0) ... 45
H. STUDI KASUS ... 51
1. Kasus 1 :Agroindustrial SCM 2x2x2 ... 51
a. Parameter-parameter Algoritma Genetika ... 53
b. Inisialisasi Populasi Awal ... 53
c. Evaluasi dan Seleksi Kromosom ... 54
d. Penyilangan dan Mutasi ... 55
e. Hasil Running ProgamGASCM Ver. 1.0 ... 59
f. Efisiensi Algoritma Genetika ... 61
2. Kasus 2 :Agroindustrial SCM 4x3x4 ... 63
a. Parameter-parameter Algoritma Genetika ... 66
b. Inisialisasi Populasi Awal ... 66
c. Evaluasi dan Seleksi Kromosom ... 67
d. Penyilangan dan Mutasi ... 69
e. Hasil Running ProgamGASCM Ver. 1.0 ... 70
f. Efisiensi Algoritma Genetika ... 72
3. Kasus 3 : Skenario kasus rantai pasokan agroindustricocodiesel... 73
a. Parameter-parameter Algoritma Genetika ... 76
b. Inisialisasi Populasi Awal ... 76
d. Penyilangan dan Mutasi ... 78
e. Hasil Running ProgamGASCM Ver. 1.0 ... 79
f. Efisiensi Algoritma Genetika ... 84
V. KESIMPULAN DAN SARAN ... 85
A. KESIMPULAN ... 85
B. SARAN ... 86
DAFTAR PUSTAKA ... 87
DAFTAR TABEL
halaman
Tabel 1. Standar mutu minyak kelapa ... 25
Tabel 2. Daftar variabel keputusan dalam rantai pasokan agroindustri ... 40
Tabel 3. Daftar variabel-variabel biaya dan kendala pada kasus 1 ... 51
Tabel 4. Daftar variabel-variabel biaya dan kendala pada kasus 2 ... 63
DAFTAR GAMBAR
halaman
Gambar 1. ModelSupply Chain Management ... 6 Gambar 2. Struktursupply chain yang disederhanakan ... 7
Gambar 3. Representasi kromosom string biner (Syarif dan Mitsuo, 2003) .. 17
Gambar 4. Representasi kromosom string integer ... 17
Gambar 5.Permutation RepresentationuntukTravelling Salesman ... 18
Gambar 6. Representasi kromosom bentuk matrik untuk masalah transportasi
(David, 1996) ... 18
Gambar 7. Diagram alir algoritma genetika (Wang, 1999) ... 19
Gambar 8. Penyilangan satu titik (one point crossover) ... 21
Gambar 9. Ilustrasi Metode PMX (Gen dan Cheng, 1997) ... 22
Gambar 10. Ilustrasi Operator Mutasi ... 23
Gambar 11. Pohon kelapa ... 25
Gambar 12. Penampang melintang kelapa ... 25
Gambar 13. Reaksi transesterifikasicocodiesel (Hamilton, 2004) ... 27
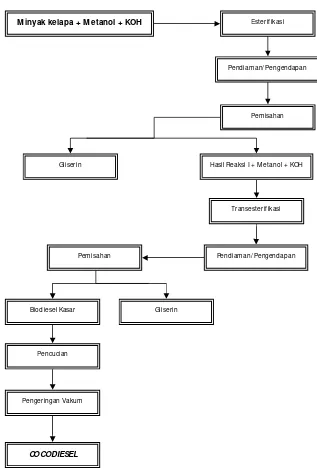
Gambar 14. Diagram alir pengolahan biodiesel dari minyak kelapa ... 28
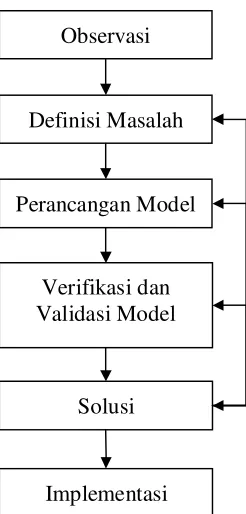
Gambar 15. Diagram alir metode ilmiah (Taylor, 2002) ... 33
Gambar 16. Diagram alir penelitian ... 34
Gambar 17. Perancangan Design ModelSupply Chain Strategis/Taktis ... 35
Gambar 18. Model jaringan rantai pasokan agroindustri ... 39
Gambar 19. Representasi kromosom integer dari variabel-variabel keputusan 43
Gambar 20. TampilanUser InterfaceGASCM Ver. 1.0 ... 47
Gambar 21. Struktur program utama GASCM Ver. 1.0 ... 47
Gambar 22. Jaringan rantai pasokan agroindustri 2x2x2 ... 51
Gambar 23. Representasi kromosom rantai pasokan agroindustri 2x2x2 ... 53
Gambar 24. Populasi awal kasus 1 ... 54
Gambar 25. Penyilangan kromosom(3) dan kromsom(11) generasi ke-0 untuk
kasus 1 ... 56
Gambar 26. Populasi baru Pop(1) pada kasus 1 ... 57
Gambar 28. Variabel ilegal akibat mutasi pada kasus 1 ... 58
Gambar 29. Grafik nilai fitness rata-rata dan fitness minimum tiap
generasi pada kasus 1 ... 59
Gambar 30. Grafik frekuensi penyilangan dan mutasi tiap generasi
pada kasus 1 ... 60
Gambar 31. Solusi optimal rantai pasokan agroindustri 2x2x2 ... 61
Gambar 32. Jaringan rantai pasokan agroindustri 4x3x4 ... 63
Gambar 33. Representasi kromosom rantai pasokan agroindustri 4x3x4 ... 66
Gambar 34. Populasi awal kasus 2 ... 67
Gambar 35. Populasi Pop(1) pada kasus 2 ... 69
Gambar 36. Grafik nilai fitness rata-rata dan fitness minimum tiap
generasi pada kasus 2 ... 70
Gambar 37. Grafik frekuensi penyilangan dan mutasi tiap generasi
pada kasus 2 ... 70
Gambar 38. Solusi optimal rantai pasokan agroindustri 4x3x4 ... 71
Gambar 39. Skenario jaringan rantai pasokan agroindustricocodiesel... 73
Gambar 40. Skenario jaringan rantai pasokan agroindustricocodiesel
(perbesaran gambar) ... 74
Gambar 41. Representasi kromosom rantai pasokan agroindustricocodiesel. 76
Gambar 42. Populasi awal Pop(0) kasus 3 ... 77
Gambar 43. Hasil penyilangan induk populasi awal Pop(0)
pada kasus 3 ... 79
Gambar 44. Hasil mutasi generasi ke-2 pada kasus 3 ... 79
Gambar 45. Grafik nilai fitness rata-rata dan fitness minimum tiap
generasi pada kasus 3 ... 81
Gambar 46. Grafik nilai fitness minimum generasi ke-7249
hingga generasi ke-7429 pada kasus 3 ... 82
Gambar 47. Grafik frekuensi penyilangan dan mutasi tiap generasi
DAFTAR LAMPIRAN
halaman
Lampiran 1. Skenario Rantai Pasokan AgroindustriCocodiesel... 90
Lampiran 2. Laporan awal hasil running GASCM Ver. 1.0 untuk kasus 1 .... 96
Lampiran 3. Laporan detail hasil running GASCM Ver. 1.0 untuk kasus 1.... 97
Lampiran 4. Laporan awal hasil running GASCM Ver. 1.0 untuk kasus 2 .... 104
Lampiran 5. Laporan detail hasil running GASCM Ver. 1.0 untuk kasus 2.... 105
Lampiran 6. Laporan awal hasil running GASCM Ver. 1.0 untuk kasus 3 .... 113
I. PENDAHULUAN
A. LATAR BELAKANG
Istilah manajemen rantai pasokan berasal dari istilah manajemen
logistik. Manajemen logistik sudah dikenal sejak tahun 1781. Adapun definisi
logistik ini adalah proses yang secara strategis mengatur pengadaan,
pergerakan, penyimpanan material, komponen, persediaan barang jadi (dan
aliran informasi yang berhubungan) dalam organisasi serta saluran
pemasarannya sedemikian rupa sehingga keuntungan sekarang dan masa yang
akan datang dapat dimaksimalkan dengan memenuhi permintaan yang
memiliki biaya operasional terendah (cost effective).
Dengan berkembangnya ilmu pengetahuan dan teknologi, supply chain
management (SCM) atau manajemen rantai pasokan telah menjadi bagian yang sangat penting bagi perusahaan untuk menghadapi pasar global yang
semakin kompetitif. Istilah rantai pasokan (supply chain) menunjukkan suatu
jaringan yang kompleks dari pilihan suatu fasilitas dan distribusi yang
menjalankan fungsi-fungsi dari pengadaan material, tranformasi material
menjadi barang setengah jadi dan barang jadi, dan distribusi barang jadi
kepada pelanggan. Dibutuhkan suatu model rantai pasokan untuk
mengoptimalkan rantai pasokan tersebut. Model rantai pasokan digunakan
untuk meminimisasi total biaya rantai pasokan keseluruhan atauTotal Supply
Chain Cost (TSCC).
Model rantai pasokan yang dibuat dalam penelitian ini adalah model
rantai pasokan pada agroindustri. Keputusan bagi permasalahan rantai pasokan
yang ada di agroindustri adalah dengan merencanakan, membuat, dan
mengatur rantai pasokan dari hulu ke hilir secara efektif dan efisien, yaitu dari
mulai pengadaan bahan baku (supplier) hasil pertanian, proses produksi,
pengendalian persediaan (inventori), hingga pemasaran (demand).
Pada penelitian ini, model rantai pasokan agroindustri hanya berkaitan
dengan masalah transportasi, inventori, dan distribusi aliran bahan baku dan
biaya TSCC. Dari model tersebut akan dapat diperoleh suatu pengaturan
distribusi dari sumber-sumber yang menyediakan bahan baku ataupun produk
ke tempat-tempat yang membutuhkan, serta penanganan jumlah inventori
yang harus disimpan pada agroindustri. Alokasi harus diatur sedemikian rupa,
karena terdapat perbedaan biaya-biaya alokasi dari satu sumber ke
tempat-tempat tujuan berbeda-beda, dan juga dari beberapa sumber ke suatu tempat-tempat
tujuan juga berbeda-beda, serta pertimbangan biaya penyimpanan inventori di
agroindustri.
Model dari rantai pasokan agroindustri tersebut sangat rumit dan
kompleks karena merupakan suatu kombinasi dari parameter-parameter rantai
pasokan. Untuk itu dibutuhkan suatu teknik optimasi yang baik untuk
mengefisienkan model dan salah satu teknik optimasi terbaru adalah algoritma
genetika (Genetic Algorithms). Algoritma genetika merupakan salah satu
teknik pencarian (searching technique) yang bersifat tangguh, adaptif, dan
efisien yang berasal dari bidang ilmu Artificial Inteligence. Algoritma
genetika dapat mencari solusi optimal berdasarkan pada mekanisme sistem
natural yaitu perubahan struktur genetika dan seleksi alam. Algoritma genetik
sangat cocok untuk memecahkan masalah optimasi yang kompleks. Solusi
optimal TSCC dari model rantai pasokan agroindustri tersebut dapat
dipecahkan menggunakan algoritma genetika dengan lebih efektif dan efisien.
Studi kasus model rantai pasokan agroindustri yang akan dianalisis
dalam penelitian ini adalah model rantai pasokan agroindustri cocodiesel.
Cocodiesel merupakan bahan bakar alternatif pengganti solar yang dibuat dari
bahan baku kelapa (minyak kelapa). Cocodiesel memiliki emisi rendah, titik
nyala yang tinggi, dan merupakan senyawa mono alkil ester dari trigliserida
ester yang cukup baik. Bahan baku cocodiesel tersedia melimpah karena
kelapa tersebar luas di seluruh pulau di Indonesia, terutama di daerah dekat
pantai. Model rantai pasokan cocodiesel ini akan dikaji, dianalisis, dan
dirancang untuk mendapatkan solusi TSCC yang optimal dengan
B. TUJUAN PENELITIAN
Penelitian ini dilakukan dengan tujuan sebagai berikut :
1. Merancang model rantai pasokan agroindustri dengan berdasarkan model
transportasi, inventori, dan distribusi.
2. Merancang bangun program algoritma genetika untuk optimasi model
rantai pasokan agroindustri dan melihat efisiensi pencarian solusi optimum
yang dilakukan algoritma genetika.
3. Melakukan kajian penerapan program algoritma genetika yeng telah dibuat
untuk rantai pasokan agroindustricocodiesel.
C. RUANG LINGKUP
Ruang lingkup penelitian ini dibatasi pada pemodelan rantai pasokan
agroindustri yang merupakan integrasi model jaringan transportasi, inventori
dan distribusi yang dimulai dari hulu ke hilir (supplier, agroindustri, dan
konsumen), serta merancang program algoritma genetika untuk optimasi
II. TINJAUAN PUSTAKA
A. SUPPLY CHAIN MANAGEMENT
Dalam lingkungan manufaktur, perbaikan terhadap produktivitas
mengalami pembenahan terus-menerus dan hal itu telah menjadi isu besar bagi
setiap orang. Sejak komputer ditemukan dan digunakan secara luas dalam
industri perdagangan, Teknologi Informasi telah menyodorkan berbagai
macam solusi dalam rangka perbaikan tingkat produktivitas. Sekitar 30 tahun
lampau MRP (Material Requirement Planning/Perencanaan Permintaan
Barang) hadir di dunia. Inilah awal mulanya komputer menambah sistem
perencanaan guna mendukung bidang manufaktur. MRP telah berkembang
begitu pesat di seluruh dunia dan pada setiap industri manufaktur sebagaimana
komputer berkembang menjadi populer. Penagihan atas barang - yang
sebelumnya dilakukan dengan menggunakan kertas, kini semuanya dilakukan
secara digital dan ditayangkan dalam komputer sehingga bisa diperhitungkan
berapa jumlah barang untuk memenuhi perencanaan produksi atas produk
akhir. Setelah penggunaan MRP menjadi populer, metode tersebut mengalami
pembenahan secara bertahap dengan perubahan nama seperti MRP II
(Manufactur Resource Planning), CIM (Computer Integrated Manufacturing), dan ERP (Enterprise Resource Planning).Ini semua dilakukan dalam rangka
memperbaikicomputing powerdarihardwaredanIT Technology.
Dalam MRP II kapasitas manufaktur dipertimbangkan dalam
perencanaan produksi oleh karena itu berbagai ekses yang berkaitan dengan
masalah penyediaan produk yang terjadi dibawah MRP dengan suatu
perencanaan yang besar dapat dihindari. CIM (Computer Integrated
Manufacturing)adalah gagasan yang menggabungkan sistem produksi dengan sistem penjualan. Dengan memadukan sistem penjualan dan operasi melalui
pertukaran data harian atau dalam komputer yang tersentralisasi, berbagai
perubahan yang terjadi dalam jumlah penjualan dapat terefleksi dalam
perencanaan produksi. Hal ini sangat esensial dalam mengatasi fluktuasi pasar.
Selanjutnya, ERP(Enterprise Resource Planning)muncul belakangan.
dalam perusahaan manufactur dalam suatu lingkungan yang sama. Area bisnis
yang dilingkup oleh ERP adalah: akuntansi keuangan, akuntansi pengendalian,
penjualan, manajemen material, pembelian, perencanaan produksi, manajemen
sumberdaya manusia, dan sebagainya. Semua aplikasi bisnis dapat dinyatakan
dalam sebuah komputer kecil (Unix machine, atau Windows NT Machine)
sama dengan komputer mainframe IBM pada tahun 1980-an. Data antara
setiap bagian dalam perusahaan dapat menjadi transparan.
Kegiatan-kegiatan tersebut merupakan kegiatan yang memfokuskan
pada satu perusahaan. Namun demikian dapat terjadi masalah apabila
perusahaan tersebut berhubungan dengan perusahaan ataupun pemasok bahan
baku dalam rangka untuk memenuhi permintaan konsumen. Masalah yang
muncul karena adanya penyekatan ketika diterapkan konsep Supply Chain
Management. Kegiatan perencanaan produksi, distribusi, transportasi dilihat sebagai aktivitas yang terpisah satu sama lain. Ketika konsumen menjadi
semakin kritis, mereka menuntut penyediaan produk secara tepat tempat, tepat
waktu. Perusahaan manufaktur yang antisipatif akan hal tersebut akan
mendapatkan pelanggan sedangkan yang tidak antisipatif akan kehilangan
pelanggan. Supply chain management menjadi satu solusi terbaik untuk
memperbaiki tingkat produktivitas antara perusahaan-perusahaan yang
berbeda. (Anonim, 2001)
Konsep supply chain merupakan konsep baru dalam melihat persoalan
logistik. Konsep lama melihat logistik lebih sebagai persoalan intern
masing-masing perusahaan, dan pemecahannya dititikberatkan pada pemecahan secara
intern di perusahaan masing-masing. Dalam konsep baru ini, masalah logistik
dilihat sebagai masalah yang lebih luas yang terbentang sangat panjang sejak
dari bahan dasar sampai barang jadi yang dipakai konsumen akhir, yang
merupakan mata rantai penyediaan barang.Supply Chain Management (SCM)
atau rantai pengadaan adalah suatu sistem tempat organisasi menyalurkan
barang produksi dan jasanya kepada para pelanggan. Rantai ini juga
merupakan jaringan dari berbagai organisasi yang saling berhubungan yang
mempunyai tujuan yang sama, yang sebaik mungkin menyelenggarakan
Supply chain management is a set of approaches utilized to efficiently integrate supplier, manufacturers, warehouses, and stores, so that merchandise is produced and distributed at the right quantities, to the right locations, at the right time, in order to minimize systemwide costs while satisfying service level requirement (David Simchi Levi et al., 2000).
Berdasarkan definisi tersebut, supply chain dapat dikatakan sebagai logistic
network. Ada beberapa pemain utama yang memiliki kepentingan dalam
manajemensupply chain, yaitu :
1. Suppliers
2. Manufacturers
3. Distribution
4. Retail Outlets
5. Customer
Hubungan mata rantai dari pelaku-pelaku tersebut dapat berbentuk
mata rantai yang terhubung satu dengan yang lain. Model supply chain
dikembangkan oleh A.T. Kerney sejak tahun 1994, seperti pada Gambar 1
[image:31.612.163.496.416.544.2](Christopher, 1998).
Gambar 1. ModelSupply Chain Management
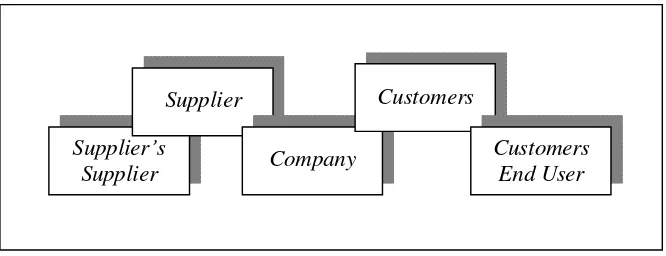
Supply chain terfokus pada sisi hulu dan hilir, setelah menelaah adanya perubahan dan perkembangan dalam sifat, intensitas, ketergantungan, dan
tuntutan para pelanggan. Sisi hulu meliputi hubungan antar sub suppliers
suppliers manufacturer, sedangkan sisi hilir meliputi manufacturer wholesalers retailers customers. Hal ini merupakan manifestasi dari
customer oriented dalam supply chain management pada Gambar 2. (Zabidi, 2001)
Supplier s Supplier
Supplier
Company
Customers
Gambar 2. Struktursupply chainyang disederhanakan
Prinsip utama dalam Supply Chain Management ialah menciptakan
sinkronisasi aktifitas-aktifitas yang beragam dan membutuhkan pendekatan
holistik. Prinsip mengintegrasikan aktifitas-aktifitas dalam supply chain ialah
untuk menciptakan sebuah resultan yang besar bukan hanya bagi tiap anggota
rantai, tetapi bagi keseluruhan sistem (Zabidi, 2001).
Supply chain menunjukkan hubungan yang lengkap dari sejumlah perusahaan atau organisasi yang bersama-sama mengumpulkan atau mencari,
mengubah, dan mendistribusikan barang dan jasa kepada pelanggan akhir
(Djokopranoto, 2002). Perkembangan sistem yang semakin maju
mempengaruhi cara mengoptimalkansupply chainsehingga mencapai manfaat
yang sesungguhnya. Terdapat beberapa hal yang berkaitan dengan
optimalisasisupply chain, yaitu :
1. Tuntutan pelanggan yang terus berkembang
2. Kekuasanretailer yang semakin besar
3. Kendala dalam pencapaian optimalisasi
4. Kendala dalam membangun kepercayaan
5. Kemitraan sebagai solusi
6. Teknologi informasi sebagai katalisator (Handoko, 2003)
Keunggulan kompetitif dari SCM adalah bagaimana ia mampu
me-manage aliran barang atau produk dalam suatu rantai supply. Dengan kata lain, model SCM mengaplikasikan bagaimana suatu jaringan kegiatan
produksi dan distribusi dari suatu perusahaan dapat bekerja bersama-sama
untuk memenuhi tuntutan konsumen. Tujuan utama dari SCM adalah:
pernyerahan/pengiriman produk secara tepat waktu demi memuaskan
konsumen, mengurangi biaya, meningkatkan segala hasil dari seluruh supply
Manufaktur r
Distribution Center
Wholesaler Retailer
Supplier End
Customer
Hulu/upstream Hilir/downstream
Aliran produk
Aliran biaya
chain (bukan hanya satu perusahaan), mengurangi waktu, memusatkan kegiatan perencanaan dan distribusi. (Anonim, 2001)
Ada banyak paket software dari SCM yang sesuai dengan kondisi
pasar. Perusahaan yang telah menerapkan SCM sangat sukses dalam
memperbaiki tingkat produktivitasnya, penjualan, distribusi, minimisasi biaya
dan tentunya meningkatkan keuntungan secara dramatis. Sistem SCM
memiliki kemampuan sebagai berikut :
1. Aliran informasi bergerak sangat cepat dan akurat antara elemen jaringan
supply chain seperti: Pabrik, Suppliers, Pusat distribusi, Konsumen, dan sebagainya).
2. Informasi bergerak sangat cepat untuk menanggapi perpindahan produk.
3. Setiap elemen dapat mengatur dirinya
4. Terjadi integrasi dalam proses permintaan dan penyelesaian produk
Peralatan fungsional yang dimiliki sistem SCM adalah :
1. Demand management/forecasting
Perangkat peralatan dengan menggunakan teknik-teknik peramalan
secara statistik. Perangkat ini dimaksudkan untuk mendapatkan hasil
peramalan yang lebih akurat.
2. Advanced planning and scheduling
Suatu peralatan dalam rangka menciptakan taktik perencanaan,
jangka menengah dan panjang berikut keputusan-keputusan menyangkut
sumber yang harus diambil dalam rangka melengkapi jaringansupply.
3. Transportation management
Suatu fungsi yang berkaitan dengan proses pendisitribusian produk
dalamsupply chain.
4. Distribution and deployment
Suatu alat perencanaan yang menyeimbangkan dan mengoptimalkan
jaringan distribusi pada waktu yang diperlukan. Dalam hal ini, Vendor
Managed Invetory dijadikan pertimbangan dalam rangka optimasi.
5. Production planning
Perencanaan produksi dan jadwal penjualan menggunakan taraf
6. Available to-promise
Tanggapan yang cepat dengan mempertimbangkan alokasi,
produksi dan kapasitas transportasi serta biaya dalam keseluruhan rantai
supply.
7. Supply chain modeler
Perangkat dalam bentuk model yang dapat digunakan secara mudah
guna mengarahkan serta mengontrol rantai supply. Melalui model ini,
mekanisme kerja dari konsepsupply chaindapat diamati.
8. Optimizer
The optimizeribarat jantung dari sistem supply chain management.
Dalamnya terkandung: linear & integer programming, non-linear
programming, heuristics and genetic algorithms. Genetic algorithms atau
algoritma genetika adalah suatu computing technology yang mampu
mencari serta menghasilkan solusi terbaik atas jutaan kemungkinan
B. TEKNIK OPTIMASI
Optimasi adalah suatu pendekatan normatif untuk mengidentifikasikan
penyelesaian terbaik dalam pengambilan keputusan dari suatu permasalahan.
Penyelesaian permasalahan dalam teknik optimasi diarahkan untuk
mendapatkan titik maksimum atau titik minimimum dari fungsi yang
dioptimumkan. Tujuan dari optimasi adalah untuk meminimumkan usaha
yang diperlukan atau biaya operasional dan memaksimumkan hasil yang
diinginkan. Jika usaha yang diperlukan atau hasil yang diharapkan dapat
dinyatakan sebagai fungsi dari peubah keputusan, maka optimasi dapat
didefinisikan sebagai proses pencapaian kondisi maksimum dan minimum dari
fungsi tersebut (Maarif, 1989).
Teknik optimasi dapat digunakan untuk fungsi yang berkendala dan
fungsi tidak berkendala. Penyelesaian permasalahan dapat berbentuk
persamaan maupun pertidaksamaan. Unsur penting dalam masalah optimasi
adalah fungsi tujuan, yang sangat bergantung pada sejumlah peubah masukan.
Peubah-peubah ini dapat tidak saling bergantung atau saling bergantung
melalui satu atau lebih kendala (Bronson, 1982).
Fungsi tujuan secara umum merupakan langkah minimisasi biaya atau
penggunaan bahan baku, maksimisasi hasil atau pemanfaatan bahan-bahan
produksi atau proses, dan sebagainya. Penentuan fungsi tujuan dikaitkan
dengan permasalahan yang dihadapi (Maarif, 1989).
Cleland dan Kacaogln (1980), menjelaskan bahwa penyelesaian
masalah optimasi dengan program matematika dapat dilakukan melalui
program linier, program tak linier, program integer, dan program dinamik.
C. LINEAR PROGRAMMING DAN INTEGER LINEAR PROGRAMMING
Linear programming atau program linier adalah suatu metode pemecahan masalah dalam suatu riset operasi yang digunakan untuk
memecahkan suatu masalah penentuan alokasi yang sedemikian rupa dari
sumber yang terbatas yang sama-sama dibutuhkan oleh beberapa macam
kepentingan yang saling berhubungan untuk suatu tujuan, sehingga tujuan
adalah maksimasi atau minimasi fungsi tujuan sesuai dengan persyaratan yang
dikehendaki fungsi kendala. Contoh persoalan maksimasi antara lain
maksimasi keuntungan, hasil produksi, jam kerja dan lain sebagainya.
Persoalan minimasi misalnya minimasi biaya, jarak, biaya penyimpanan,
biaya distribusi , dan sebagainya.
Progran linier berkaitan dengan penjelasan suatu dunia nyata sebagai
suatu model matematik yang terdiri dari sebuah fungsi linier dan beberapa
kendala linier (Mulyono,1991). Persoalan yang harus diselesaikan dengan
program linier harus memenuhi lima persyaratan, yaitu :
1. Fungsi tujuan yang diselesaikan harus jelas dan tegas
2. Harus ada sesuatu yang akan diperbandingkan, misalnya kombinasi antara
tenaga kerja dengan mesin otomatis
3. Sumber daya harus terbatas misalnya anggaran biaya yang akan
dikeluarkan terbatas
4. Fungsi tujuan dan kendala harus bisa diekspresikan secara matematis
5. Peubah-peubah yang membutuhkan fungsi tujuan harus memiliki
hubungan fungsional atau keterkaitan. Hubungan keterkaitan dapat
diartikan saling mempengaruhi, interaksi, interdependensi, dan
sebagainya.
Dalam model matematis program linier mempunyai dua macam fungsi,
yaitu fungsi tujuan dan fungsi kendala. Fungsi tujuan adalah fungsi yang
menggambarkan sasaran dari persoalan program linier yang berkaitan dengan
pengaturan sumber daya secara optimal. Fungsi kendala adalah fungsi yang
menggambarkan secara matematis kapasitas yang tersedia yang akan
dialokasikan secara optimal ke berbagai kegiatan (Subagyo et.al., 1989).
Maks/Min. ………..…….. (1.1)
Fungsi kendala :
i n
j
j ij m
i
b
X
a
(
,
,
)
11
=
≥
≤
∑
∑
=
= ………..…….. (1.2)
0
≥
j
X
………..…….. (1.3)Notasi aij, bi, Cj merupakan konstanta
i = 1, 2 , 3, ..., m
j = 1, 2, 3, ..., n
Dimana :
Cj = Parameter yang dijadikan kriteria optimasi atau merupakan kontribusi
setiap satuan keluaran kegiatan j terhadap nilai Z.
Xj = Peubah/parameter keputusan.
aij = Banyaknya sumber i yang diperlukan untuk menghasilkan setiap unit
keluaran kegiatan j.
bi = Banyaknya sumber i yang tersedia untuk dialokasikan ke setiap unit
kegiatan.
m = Jumlah kendala.
n = Jumlah kegiatan yang menggunakan sumberdaya yang terbatas tersebut.
∑
=
=
nj
j j
X
C
Z
Ada beberapa asumsi dasar yang melandasi program linier. Asumsi tersebut
adalah :
1. Linearitas, yaitu perbandingan antara input dengan input lainnya atau suatu
input dengan output biasanya tepat dan tidak tergantung pada tingkat
produksi.
2. Proporsionalitas, yaitu naik turunnya nilai fungsi tujuan (Z) dan
penggunaan sumberdaya atau fasilitas yang tersedia akan berubah secara
sebanding proporsional dengan perubahan tingkat kegiatan.
3. Additivitas, yaitu nilai tujuan tiap kegiatan tidak saling mempengaruhi,
atau kenaikan dari nilai tujuan (Z) yang diakibatkan oleh kenaikan suatu
kegiatan dapat ditambahkan tanpa mempengaruhi bagian nilai Z yang
diperoleh dari kegiatan lain.
4. Divisibilitas, yaitu peubah-peubah keputusan Xj jika diperlukan dapat
berupa bilangan pecahan.
5. Deterministik, yaitu semua parameter yang terdapat dalam model program
linier (aij, bi, cj) dapat diperkirakan dengan pasti meskipun jarang dengan
tepat (Subagyo et al., 1989)
Integer linear programming berhubungan dengan penyelesaian
masalah-masalah program matematis yang mengasumsikan beberapa atau semua
variabelnya bernilai integer non negatif. Suatu program linier disebut
campuran atau murni tergantung pada apakah beberapa atau semua
variabelnya terbatas untuk nilai-nilai integer. Metode integer programming
dapat dikelompokkan ke dalam metode pemotongan (cutting method) dan
metode penelusuran (search method) (Taha, 1992).
D. MODEL TRANSPORTASI
Metoda transportasi merupakan metode yang digunakan untuk
mengatur distribusi dari sumber-sumber yang menyediakan produk yang
sama, ke tempat-tempat yang membutuhkan secara optimal. Alokasi produk
alokasi dari satu sumber ke tempat-tempat tujuan berbeda-beda, dan dari
beberapa sumber ke suatu tempat tujuan juga berbed-beda. (Yolanda, 2005).
Menurut Russel dan Taylor (2003), model transportasi adalah suatu
teknik kuantitatif yang digunakan untuk menentukan cara menyelenggarakan
transportasi dengan biaya seminimal mungkin. Model transportasi merupakan
salahsatu bentuk khusus atau variasi dari program linier yang dikembangkan
khusus untuk memecahkan masalah-masalah yang berhubungan dengan
transportasi dan distribusi produk dari berbagai sumber ke berbagai tujuan.
Ciri khusus dari suatu model transportasi ini adalah :
1. Terdapat sejumlah sumber dan sejumlah tujuan tertentu
2. Kuantitas barang yang didistribusikan dari setiap sumber dan kuantitas
yang dibutuhkan oleh setiap tujuan
3. Kesesuaian jumlah barang terhadap permintaan maupun kapasitas suatu
sumber
4. Biaya pengangkutan tertentu dari suatu sumber ke suatu tujuan
Model umum untuk permasalahan transportasi adalah :
Minimukan
∑∑
= =
=
mi n
j
ij ij
X
C
Z
1 1
Kendala
∑
==
n
j
i ij a
X 1
, i = 1, 2, 3, ….m
∑
==
n
i
j ij b
X 1
, j = 1, 2, 3, …. n
Dan Xij ≥0untuk seluruh i dan j
E. ALGORITMA GENETIKA
Pada buku berjudulAdaptation in Natural and Artificial Systems tahun
1975 oleh John Holland, seorang professor di Universitas Michigan,
ditemukan sebuah konsep baru pencarian secara tersusun untuk optimasi
solusi masalah yang rumit dan komplek menggunakan persamaan matematika
berdasarkan evolusi tiruan (artificial evolution) yang dikenal dengan nama
algoritma genetika (Strafaci, 2002).
Pada tahun 1989, David Goldberg, meluncurkan buku berjudulGenetic
Algorithm in Search, Optimization, and Machine Learning setelah berhasil mengaplikasikan algoritma genetika untuk perancangan sistem perpipaan
distribusi gas alam. Berdasarkan hasil risetnya, ia berhasil membuktikan
bahwa algoritma genetika menghasilkan solusi untuk menyelesaikan
permasalahan perancangan sistem perpipaan distribusi gas alam berdasarkan
parameter-parameter kesuksesan sistem perancangan pipa. Saat ini algorima
genetika diaplikasikan pada berbagai bidang antara lain, seperti pada desain
mesin jet pesawat terbang, prediksi tingkat suku bunga, pengendalian
persediaan (inventori), perencanaan dan penjadwalan produksi, dan
otomatisasi sistem produksi.
Algoritma genetika dapat mencari solusi minimum dan maksimum dari
fungsi satu variabel bebas dengan representasi dasar atau biner. Untuk fungsi
yang lebih kompleks atau lebih dari satu variabel bebas dapat menggunakan
representasi float atau integer. Hal tersebut dilakukan untuk penyederhanaan
sistem, karena gen biner akan menyebabkan besarnya ukuran kromosom.
(Basuki, 2003).
Algoritma genetika telah terbukti dapat digunakan untuk
menyelesaikan permasalahan searching dan optimasi yang mempunyai
kompleksitas yang tinggi seperti TSP (Travelling Salesman Problem),
penjadwalanflow shop, danjob shop. TSP adalah suatu permasalahan dimana
seorang sales harus mengunjungi sejumlah-n kota dengan jarak yang paling
pendek, dengan syarat satu kota hanya dikunjungi satu kali. Solusi TSP adalah
jalur yang melewati semua kota dan jaraknya paling pendek (Basuki, 2003).
sejumlah-m mesin tanpa urutan proses. Sedangkan penjadwalan job shop
masalah penempatan sejumlah-n job pada sejumlah-m mesin dengan urutan
proses. Solusi terbaik dari kedua permasalahan tersebut adalah
meminimumkan waktu penyelesaian semua job (makespan) (Mattfeld, 2003).
Michaelewicz, Vignaux, dan Hobbs telah mengembangkan algoritma
genetika untuk menyelesaikan masalah transportasi nonliner yang disebut
dengan program GENETIC-2. Program tersebut mampu menyelesaikan
masalah transportasi Tailor dan menangani beberapa tipe dari fungsi biaya
(Gen dan Cheng, 1997).
Algoritma genetika telah berhasil diaplikasikan oleh Tate dan Smith
dalam masalah perancangan tata letak pabrik. Tata letak pabrik berkaitan
dengan pengaturan fasilitas fisik dan tata letak mesin-mesin. Masalah tersebut
merupakan masalah kombinatorial sehingga teknik heuristik seperti algoritma
genetik dapat diterapkan dengan baik (Gen dan Cheng, 1997).
Algoritma genetika mampu menyelesaikan masalah time series
forecasting yaitu teknik peramalan data berdasarkan data-data pada periode
sebelumnya.Time series forecasting dirumuskan sebagai berikut :
∑
=+ = +
n
i i i n ax a
x
1
0 1
Keberhasilan peramalan di dalam time series forecasting sangat ditentukan
oleh nilai ai dan jumlah periode data yang digunakan(n). Algoritma genetika
dapat digunakan untuk mengoptimasi ai (Basuki, 2006).
1. Prosedur Umum Algoritma Genetika
Prosedur umum algoritma genetika adalah sebagai berikut :
Langkah 1 : Pengkodean (encoding) calon solusi danset-up beberapa
parameter awal : jumlah individu, probabilitas,
penyilangan dan mutasi, dan jumlah generasi maksimum
Langkah 2 : t 0 {inisialisasi awal}
Pembangkitan acak sejumlah n kromosom pada generasi
ke-0
Langkah 3 : Evaluasi masing-masing kromosom dengan menghitung
nilaifitness-nya
xi : data pada periode ke-i
Langkah 4 : Seleksi beberapa kromosom dari sejumlah n individu
yang memiliki nilaifitness terbaik
Langkah 5 : Rekombinasikan kromosom terpilih dengan cara
melakukan penyilangan (crossover) dan mutasi
(mutation)
Langkah 6 : t t + 1
Update jumlah generasi dan kembali ke Langkah 2 sampai jumlah generasi maksimum tercapai
Algoritma genetika melakukan pencarian pada sejumlah solusi
fisibel yang direpresentasikan sebagai jumlah kromosom yang disebut
populasi. Kromosom-kromosom pada populasi dibangun secara acak dan
berevolusi melalui beberapa generasi (iterasi) berurutan. Kromosom yang
dihasilkan pada suatu generasi diharapkan lebih baik dari generasi
sebelumnya.
Kriteria penghentian (stopping criteria) dalam pencarian solusi
optimal pada algoritma genetik dapat dilakukan dengan cara menetukan
jumlah generasi maksimum, menentukan selisih nilai fitness rata-rata
tertentu antara suatu generasi dengan generasi sebelumnya, dan
menentukan tingkat keragaman (homogenitas) struktur kromosom.
2. Representasi Kromosom
Dalam memulai penerapan suatu algoritma genetika untuk
memecahkan masalah optimasi, perlu adanya pengkodean sebagai variabel
keputusan. Representasi kromosom yang pertama kali diperkenalkan oleh
Holland (1975) adalah representasi string biner. Dalam representasi ini,
sebuah kromosom terdiri dari beberapa elemen yang disimbolkan dengan
angka nol (0) dan satu (1).
Gen dan Chen (1997), memperkenalkan bentuk representasi baru
yang disebut permutation representation, path representation atau
order-based representation. Dalam perkembangannya, David (1996) menggunakan representasi kromosom berbentuk matrik untuk
Gambar 3. Representasi kromosom string biner
(Syarif dan Mitsuo, 2003)
Gambar 4. Representasi kromosom string integer
Gambar 5.Permutation RepresentationuntukTravelling Salesman
(Gen dan Cheng, 1997)
Gambar 6. Representasi kromosom bentuk matrik untuk masalah transportasi
(David, 1996)
3. Fungsi Fitness
Kromosom-kromosom pada setiap generasi dievaluasi dengan
menggunakan alat ukur yang disebut dengan fungsi fitness. Nilai fitness
suatu kromosom menunjukkan kualitas kromosom tersebut dalam suatu
populasi. Bentuk fungsi fitness didefinisikan sesuai masalah yang akan
diselesaikan.
Suatu fungsi fitness digunakan untuk memberikan ciri dan
mengukur seberapa baik sebuah solusi (Chen, Ian dan Cao, 2003). Fungsi
fitness adalah fungsi yang akan mengukur tingkat kebugaran suatu
kromosom dalam populasi. Semakin besar nilai fitness, semakin bugar
1 1 0 0 1 1 0 1 1
1 2 3 4 5 . . . n
3 2 5 4 7 1 6 9 8
1 2 3 4 5 . . . n
0 0 5 0 3
0 4 0 0
1 2
1
2
i
.
. .
j
0
0 0 5 7 0
3 1 0 0 2
8 7 3 5 7 9 6 3 1
pula kromosom dalam populasi sehingga semakin besar kemungkinan
kromosom tersebut dapat tetap bertahan pada generasi berikutnya.
4. Operator-Operator Algoritma Genetik
Pencarian kromosom (solusi) baru pada populasi dilakukan dengan
menggunakan operator-operator genetik yang terdiri atas operator seleksi
[image:44.612.149.495.227.665.2](selection), penyilangan (crossover), dan mutasi (mutation). Diagram alir algoritma genetik dapat dilihat pada Gambar 7 :
Gambar 7. Diagram alir algoritma genetika (Wang, 1999) Representasi
solusi ke dalam kromosom
Inisialisasi (Initialization)
Evaluasi (Evaluation)
Selesai (Terminate) ?
Seleksi (Selection)
Selesai
Penyilangan (Crossover)
Mutasi (Mutation)
Evaluasi (Evaluation)
Perbaikan (Repair)
a. Seleksi (Selection) kromosom
Setelah populasi awal terbentuk, setiap kromosom dalam
populasi dievaluasi dengan menghitung nilai fungsifitnessnya. Setelah
itu proses pembentukan generasi baru diawali dengan seleksi
kromosom. Seleksi adalah proses pemilihan beberapa kromosom untuk
dijadikan sebagai kromosom induk bagi generasi berikutnya. Menurut
Syarif dan Mitsuo (2003), kromosom terpilih untuk masing-masing
populasi di dalam generasi yang berikutnya berdasarkan nilaifitness.
Populasi kromosom untuk generasi berikutnya dihasilkan
menggunakan salah satu teknik seleksi kromosom yaitu seleksi cakram
rolet (roulette wheel selection). Teknik ini disebut seleksi rolet sebab
dapat dipandang sebagai pemutaran suatu cakram rolet. Setiap
kromosom menempati suatu daerah (slot) pada cakram rolet dengan
proporsi luasnya sebanding dengan proporsi nilai fitness
masing-masing kromosom dalam populasi. Proporsi dalam cakram rolet juga
menunjukkan peluang masing-masing kromosom untuk terpilih
menjadi induk (parent) pada generasi berikutnya. Teknik seleksi
lainnya adalah seleksi turnamen (tournament selection). Seleksi ini
akan membandingkan antara dua buah kromosom dalam populasi yang
dipilih secara acak. Salah satu dari kromosom akan terpilih apabila
memenuhi atau mendekati nilaifitness. (Hopgood, 2001)
b. Penyilangan (Crossover) kromosom
Setelah proses penyeleksian kromosom, langkah berikutnya
adalah melakukan penyilangan terhadap pasangan-pasangan
kromosom. Penyilangan (crossover) dikenal sebagai operator
penggabungan ulang (recombination) yang paling utama dalam
algoritma genetik. (Syarif dan Mitsuo, 2003). Menurut Chen, Ian dan
Cao (2003), penyilangan akan menukar informasi genetik antara dua
kromosom induk yang terpilih dari proses seleksi untuk membentuk
dua anak. Operator penyilangan bekerja pada sepasang kromosom
induk untuk menghasilkan dua kromosom anak dengan menukarkan
Operator penyilangan biasanya dihubungkan dengan peluang
penyilangan. Peluang penyilangan (Pc) adalah rasio antara jumlah
kromosom yang diharapkan mengalami penyilangan dalam setiap
generasi dengan jumlah kromosom total dalam populasi. Nilai Pc
biasanya cukup tinggi (berkisar antara 0,6 – 1). Proses penyilangan
akan terjadi pada sepasang kromosom jika suatu bilangan yang
dibangkitkan secara acak (r), 0 r 1, nilainya kurang dari atau sama
dengan Pc. Bilangan acak tersebut dibangkitkan setiap kali akan
menyilangkan sepasang kromosom. Tingkat penyilangan yang tinggi
menyebabkan semakin besar kemungkinan algoritma genetik
mengeksplorasi ruang pencarian sekaligus mempercepat ditemukannya
solusi optimum. Peluang penyilangan yang tepat dan efektif hanya
dapat diketahui melalui pengujian (experiment) khusus terhadap
masalah yang bersangkutan. Misalnya ditentukan nilaiPc = 0.9.
Operator penyilangan yang sering digunakan dalam algoritma
genetic sederhana (simple genetic algorithm) adalah penyilangan satu
titik (one point crossover) (Holland, 1975). Penyilangan satu titik ini
cocok digunakan untuk kromosom dengan representasi biner (1 dan 0).
Berikut Gambar 8 adalah ilustrasi proses penyilangan satu titik :
Gambar 8. Penyilangan satu titik (one point crossover)
0 1 1 0 1 1 0 1 1 Parent 1
1 1 0 1 1 0 1 1 0 Parent 2
0 1 1 0 1 0 1 1 0 Offspring 1
Pada beberapa kasus, penyilangan satu titik tidak cocok digunakan
karena dapat menghasilkan kromosom yang ilegal. Untuk itu Goldberg
dan Lingle (1985) memperkenalkan teknik PMX (Partially Mapped
Crossover) untuk mencegah timbulnya kromosom ilegal dengan
[image:47.612.195.499.195.663.2]adanya metode perbaikan (repairing procedure).
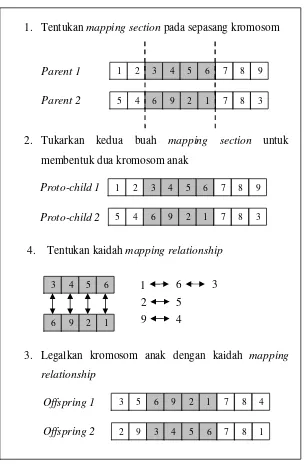
Gambar 9. Ilustrasi Metode PMX (Gen dan Cheng, 1997)
1 2 3 4 5 6 7 8 9 Parent 1
5 4 6 9 2 1 7 8 3 Parent 2
1 2 3 4 5 6 7 8 9 Proto-child 1
5 4 6 9 2 1 7 8 3 Proto-child 2
1. Tentukanmapping sectionpada sepasang kromosom
2. Tukarkan kedua buah mapping section untuk
membentuk dua kromosom anak
3 4 5 6
6 9 2 1
1 6 3
2 5
9 4
3. Legalkan kromosom anak dengan kaidah mapping
relationship
3 5 6 9 2 1 7 8 4 Offspring 1
2 9 3 4 5 6 7 8 1 Offspring 2
c. Mutasi (Mutation) kromosom
Operator mutasi bekerja pada sebuah gen dalam suatu
kromosom. Operator mutasi hanya operator tambahan atau operator
sekunder tetapi dapat berperan sangat besar dalam menemukan solusi
yang optimum. Operasi ini akan menjadi sangat penting apabila nilai
fitness kromosom dalam populasi cenderung sama atau sudah
mencapai konvergen bias (premature konvergen). Akibatnya, operator
seleksi akan mengalami kesukaran memilih kromosom terbaik untuk
dilakukan penyilangan. Dengan adanya operator mutasi, struktur suatu
kromosom dapat dimodifikasi agar dihasilkan kromosom dengan
struktur baru yang memiliki nilaifitness lebih baik.
Menurut Syarif dan Mitsuo (2003), mutasi pada umumnya
digunakan untuk mencegah tidak adanya kehilangan informasi
sehingga dilaksanakan dengan pertukaran informasi di dalam
kromosom. Operator mutasi dapat bersifat konstruktif maupun
destruktif terhadap suatu kromosom, tetapi karena probabilitasnya
yang