Modifikasi Model Kermack

(1)

–

MC.KENDRICK

UNTUK PENYEBARAN PENYAKIT CACAR

DWI BUDI ROHYATI

G54104035

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

ABSTRAK

DWI BUDI ROHYATI. Modifikasi Model Kermack – Mc.Kendrick untuk Penyebaran Penyakit Cacar. Dibimbing oleh HADI SUMARNO dan N. K. KUTHA ARDANA.

Dalam model penyebaran penyakit, asumsi yang dipertimbangkan antara lain besarnya laju penularan, besarnya laju penyembuhan, dan dapat atau tidaknya penyebaran terjadi ketika periode prodromoral (waktu diantara saat munculnya gejala awal dengan munculnya bintik merah). Kermack – Mc.Kendrick (1927) memodelkan penyebaran penyakit melalui dua tipe yaitu persamaan diferensial (model SIR) dan persamaan integral. Model SIR mengasumsikan penyebaran suatu penyakit dapat terjadi tepat setelah seseorang terinfeksi dengan laju penularan dan penyembuhan konstan. Asumsi tersebut terkadang tidak masuk akal, karena dalam periode suatu infeksi terdapat masa inkubasi. Sedangkan, persamaan integral yang digunakan oleh Kermack – Mc.Kendrick berguna dalam memodelkan timbulnya penyebaran penyakit menular dengan laju penularan dan penyembuhan yang tidak konstan.

Karya ilmiah ini bertujuan untuk mempelajari penyebaran penyakit cacar dengan menggunakan modifikasi model Kermack – Mc.Kendrick tipe persamaan integral yang dilakukan oleh Aldis dan Robert. Pada model ini, jumlah penderita baru per unit waktu (incidence of infection) melibatkan empat lokasi, yaitu rumah, tempat kerja (termasuk sekolah), tempat umum, dan rumah sakit. Linearisasi dilakukan pada model tersebut. Selanjutnya transformasi Laplace digunakan. Linearisasi model Kermack – Mc.Kendrick tipe persamaan integral dapat diaplikasikan untuk mengevaluasi berbagai intervensi. Solusi numerik dapat diperoleh dengan menggunakan program komputasi Mathematica6.0.

(3)

ABSTRACT

DWI BUDI ROHYATI. Modification of Kermack – Mc.Kendrick model for the spread of Smallpox disease. Supervised by HADI SUMARNO and N.K KUTHA ARDANA.

In the modeling of the spread of disease, several assumptions were considered, i.e. the transmission rate, the recovery rate, and could or not the transmission occur in the prodomoral period (the time between the first symptoms and the appearance of body rash). Kermack – Mc. Kendrick (1927) modelled the spread of disease into two types: Differential Equations (SIR model) and Integral Equations. In the SIR model relies on the assumptions that the spread of disease could be occurred right after someone infected with the transmission rate and the removed rate are constant. Sometimes these assumptions are unrealistic, because there are incubation lifetime in the infectious period. On the other hand, the Integral Equation used by Kermack – Mc.Kendrick is particularly useful for modeling the spread of infectious diseases with non-constant transmission and removed rate.

In this study, modeling the spread of smallpox disease was studied, i.e. using the modification of integral equation type of Kermack – Mc.Kendrick model by Aldis and Robert. In this model, the incidence of infection involves four locations: houses, workplaces (includes school) and hospitals. Linearization was applied in this model. Futher the Laplace transform was applied. Linearization of Kermack – Mc.Kendrick model was applied for evaluate several interventions. The numerical solution was obtained using the Mathematica 6.0 computer software.

(4)

MODIFIKASI MODEL KERMACK

–

MC.KENDRICK

UNTUK PENYEBARAN PENYAKIT CACAR

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh:

DWI BUDI ROHYATI

G54104035

DEPARTEMEN MATEMATIKA

FAKULTAS METEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(5)

Judul

: Modifikasi Model Kermack

–

Mc.Kendrick untuk Penyebaran

Penyakit Cacar

Nama

:

Dwi Budi Rohyati

NRP

:

G54104035

Menyetujui:

Pembimbing I,

Dr. Ir Hadi Sumarno, MS

NIP. 131 430 804

Pembimbing II,

Ir. N. K. Kutha Ardana, M.Sc

NIP. 131 842 412

Mengetahui:

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. drh. Hasim, DEA

NIP. 131 578 806

(6)

PRAKATA

Puji dan syukur penulis panjatkan kehadirat Allah SWT atas rahmat, berkah serta nikmat sehat sehingga penulis mampu menyelesaikan karya ilmiah ini. Shalawat serta salam tercurah kepada junjungan kita nabi besar Muhammad SAW yang telah memberikan suri tauladan tak henti-hentinya kepada umatnya hingga akhir jaman. Karya ilmiah ini merupakan masalah baru yang dianggap menarik oleh penulis. Di samping itu, karya ilmiah ini merupakan syarat untuk memperoleh gelar Sarjana Sains pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Penulis mengucapkan terimakasih yang sebesar-besarnya kepada semua pihak yang telah membantu penyelesaian karya ilmiah ini, terutama kepada Bapak Hadi Sumarno selaku Pembimbing I dan Bapak N.K Kutha Ardana selaku Pembimbing II yang telah meluangkan waktu, tenaga dan pikirannya untuk membimbing, memberikan dorongan dan pengarahan kepada penulis hingga penulisan karya ilmiah ini selesai. Ucapan terima kasih juga ditunjukkan kepada Bapak Paian Sianturi selaku dosen penguji atas saran dan masukan yang telah Bapak berikan. Terimakasih kepada Penny, Aji dan Fredrick yang telah bersedia menjadi pembahas dalam seminar tugas akhir penulis. Terimakasih kepada Michael G.Robert atas bantuan yang diberikannya.

Penulis mengucapkan terimakasih yang paling dalam kepada orang tua penulis, yaitu Soedarno (Papa) dan Suwati (Mama) atas segala doa, restu, usaha, pengorbanan, serta curahan kasih sayang yang telah diberikan hingga saat ini. Untuk adik-adik penulis; Dede, Wendah, Dati dan Mia, serta keluarga besar penulis. Kasih sayang dan dukungan mereka sangat berarti.

Terimakasih untuk Dian, Beirut, Alip, Mas Angga, Jonggrang, Enyon, Eeph, Abank dan Yeni atas saran, dukungan, doa serta persahabatan yang terjalin. Untuk Mami inyonk, LiaY, Ilie, Eyyi, Niken, Moko, Taufik, Situl, Kurenz, Mba Umi, Ela, Akbar, Miera, Akoh, Kak Lilie, Jaja, Moko, Abi, Puji, Mba Uli, T Yuda, T Marlin terima kasih atas bantuan, dukungan dan doanya. Untuk seluruh mantan penghuni wisma Lukita, penghuni ponytail bawah, teman-teman Matematika 41, kakak-kakak kelas dan adik-adik kelas lainnya yang tidak dapat penulis sebutkan satu persatu, terima kasih atas kebersamaannya. Terimakasih kepada keluarga besar SMA P.B Jendral Soedirman. Penulis juga mengucapkan terimakasih kepada Dosen-dosen di Departemen Matematika, terima kasih atas ilmu yang telah Bapak dan Ibu berikan, serta staf Departemen Matematika: Bu Susi, Bu Ade, Mas Deny, Mas Yono, Mas Bono, Bu Marisi, dan Mba Yanti terima kasih atas bantuan selama di Departemen Matematika. Akhirnya penulis mengucapkan terimakasih kepada semua pihak yang ikut membantu dan tidak dapat penulis sebutkan satu persatu.

Penulisan karya ilmiah ini tidak mungkin luput dari kekurangan, oleh karena itu kritik dan saran dari semua pihak akan sangat membantu demi kesempurnaan penulisan ini. Harapan penulis adalah semoga penulisan karya ilmiah ini akan memberikan manfaat bagi para pembacanya.

Bogor, September 2008

(7)

RIWAYAT HIDUP

Dwi Budi Rohyati dilahirkan di Jakarta pada tanggal 28 February 1986. Penulis merupakan anak pertama dari pasangan Soedarno dan Suwati yang bertempat tinggal di Jln. Al Bashor No.19 Rt 012/003 Kelurahan Dukuh Kecamatan Kramat Jati, Jakarta Timur. Jenjang pendidikan penulis dilalui tanpa hambatan berarti. Pada tahun 1992 penulis mulai bersekolah di SDN Dukuh 09 Pagi di Jakarta. Tahun 1998 penulis melanjutkan sekolah ke SLTPN 20 BR Jakarta. Pada tahun 2004 penulis lulus dari SMUN 62 Jakarta dan berhasil menjadi mahasiswi Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur USMI (Undangan Seleksi Masuk IPB) pada tahun yang sama.

Selama mengikuti kegiatan perkuliahan penulis aktif dalam keanggotaan himpunan profesi Departemen Matematika yang dikenal dengan nama GUMATIKA. Periode 2005/2006 penulis aktif sebagai staf Departemen Sosinkom GUMATIKA. Pada periode 2006/2007 penulis aktif sebagai staf Kestari GUMATIKA. Selama masa kepengurusan di himpunan profesi GUMATIKA, penulis sering mengikuti kepanitiaan berbagai kegiatan seperti Matematika Ria 2006, Welcome Ceremony Mathematics 2006, “MIPA sport tournament” pada tahun 2006, Try Out SPMB

(8)

DAFTAR ISI

Halaman

DAFTAR ISI…. ... vi

DAFTAR TABEL ... vii

DAFTAR GAMBAR ... vii

DAFTAR LAMPIRAN ... vii

I. PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

II. LANDASAN TEORI ... 2

Teorema Dasar Kalkulus ... 2

Nilai Reproduksi Dasar ... 2

Persamaan Diferensial Biasa Linear dan taklinear ... 2

Nilai Eigen dan Vektor Eigen ... 2

Matriks Taknegatif ... 2

Matriks Tak Tereduksi ... 2

Vektor Eigen Dominan... 2

Transformasi Laplace ... 3

Teorema Konvolusi ... 3

Fungsi Dirac Delta ... 3

Transformasi Laplace pada Fungsi Dirac Delta ... 3

Notasi ... 4

III. PEMODELAAN ... 4

3.1 Perumusan Model ... 4

3.1.1 Model Kermack – Mc.Kendrick Tipe Persamaan Integral ... 4

3.1.2 Model SIR ... 4

3.2 Hubungan antara Model Kermack – Mc.Kendrick dengan Model SIR... 5

3.3 Modifikasi Model Kermack – Mc.Kendrick Tipe Persamaan Integral... 6

3.3.1 Epidemik Ringan ... 7

3.3.2 Epidemik Berat ... 7

IV. CONTOH KASUS ... 8

4.1 Parameter Input ... 8

4.2 Intervensi ... 10

4.3 Hasil dan Pembahasan ... 11

4.3.1 Nilai Reproduksi Dasar (R0) ... 11

4.3.2 Laju Pertumbuhan epidemik (r) ... 12

4.3.3 Incidence of infection ... 12

4.3.4 Distribusi Penderita ... 14

V. KESIMPULAN ... 14

DAFTAR PUSTAKA ... 15

(9)

DAFTAR TABEL

Halaman

Tabel 1. Waktu Infeksi dan Parameter yang digunakan Dalam Komputasi ...8

Tabel 2. Nilai Reproduksi Dasar ... 11

Tabel 3. Nilai Laju Pertumbuhan Epidemik ... 12

Tabel 4. Incidence of infection ... 12

DAFTAR GAMBAR

Halaman Gambar 1. Fungsi Delta Dirac ... 3

Gambar 2. Model SIR ... 4

Gambar 3. Laju Kontak ... 6

Gambar 4. Grafik infectifity kernel untuk Penyebaran Cacar di Rumah ... 9

Gambar 5. Grafik infectifity kernel untuk Penyebaran Cacar di Tempat Kerja dan Tempat Umum 9 Gambar 6. Grafik infectifity kernel untuk Penyebaran Cacar di Rumah Sakit ... 9

Gambar 7. Grafik Nilai Reproduksi Dasar untuk Berbagai Perlakuan ... 11

Gambar 8. Grafik Laju Pertumbuhan Epidemik untuk Berbagai Perlakuan ... 12

Gambar 9. Grafik incidence of infenction untuk Tanpa Intervensi, SV, VH, VW, dan VH-VW .... 13

Gambar 10. Grafik incidence of infenction untuk Tanpa Intervensi, QH, QW, CC dan SH ... 13

Gambar 11. Grafik incidence of infenction untuk Tanpa Intervensi, VH, QW, QH, SH-QH-VH, dan SH-CC ... 13

Gambar 12. Grafik Distribusi Penderita ... 14

DAFTAR LAMPIRAN

Halaman Lampiran 1. Pembuktian Persamaan (3.17) ... 17

Lampiran 2. Pembuktian determinan sama dengan 0 ... 18

Lampiran 3. Pembuktian Persamaan (3.25) ... 19

Lampiran 4. Hasil Simulasi dari Berbagai Perlakuan yang Berbeda ... 20

Lampiran 5. Program Mathematica 6.0 yang digunakan dalam Perhitungan... 21

(10)

I.

PENDAHULUAN

I.1 Latar Belakang

Penyakit cacar (smallpox) merupakan salah satu penyakit mematikan yang pernah ada di dunia. Kata smallpox sendiri berasal

dari bahasa latin yang berarti “berbintik”.

Penyakit ini dicirikan dengan demam tinggi dan bintik-bintik merah pada kulit.

Cacar merupakan penyakit yang mudah menyebar dan hanya dapat ditularkan oleh manusia. Penyakit ini diperkirakan sudah ada sejak beratus-ratus tahun yang lalu. Sejak abad 15-18, penyakit cacar membuat rekor di Eropa sebagai penyakit yang menyebabkan bencana besar terhadap kehidupan manusia. Pada tahun 1967 World Health Organization

(WHO) melakukan program vaksinasi untuk membasmi penyakit cacar. Usaha tersebut dinilai sangat efektif. Kasus terakhir terjadi di Somalia pada tahun 1977. Setelah sukses melakukan program vaksinasi, pada bulan Mei 1980 WHO menyatakan bahwa penyakit cacartelah menghilang.

Penyakit cacar disebabkan oleh virus variola. Virus variola dapat bertahan hidup selama beberapa jam di luar tubuh manusia dengan syarat tidak terkena sinar matahari. Saat ini virus variola hanya terdapat di dua tempat, yaitu State Research Center of Virology and Biotechnology (Rusia) dan

Center for Diseases Control and Prevention

(CDC, Amerika Serikat). Di kedua tempat tersebut, virus variola digunakan untuk penelitian. Sejak WHO menyatakan bahwa penyakit cacar telah menghilang, vaksinasi cacar tidak dilakukan lagi. Akibatnya saat ini diperkirakan lebih dari 90% populasi penduduk di dunia tidak memiliki kekebalan sama sekali terhadap penyakit cacar.

Penyakit cacar diduga akan muncul kembali sebagai senjata potensial untuk bioterorisme. Jika virus variola dengan sengaja disebarkan pada suatu wilayah yang populasinya tidak memiliki kekebalan terhadap penyakit cacar, maka penyakit tersebut dapat muncul kembali. Selain itu, penyakit cacar akan mengancam wilayah lain, sehingga diperlukan intervensi untuk mencegah penyebarannya.

Untuk menganalisis dinamika penyebaran penyakit, terdapat banyak model yang dapat digunakan. Dalam memodelkan penyebaran penyakit, terdapat beberapa asumsi yang harus dipertimbangkan, antara lain besarnya laju penularan, besarnya laju penyembuhan, dan dapat atau tidaknya penyebaran terjadi ketika periode prodromal (waktu diantara munculnya gejala awal dengan munculnya bintik merah).

Kermack - Mc.Kendrick (1927) memodelkan penyebaran penyakit melalui dua tipe yaitu persamaan diferensial (model SIR) dan persamaan integral. Model SIR mengasumsikan penyebaran suatu penyakit dapat terjadi tepat setelah seseorang terinfeksi dengan laju penularan dan laju penyembuhan yang konstan. Ketiga asumsi tersebut terkadang tidak masuk akal, karena dalam periode suatu infeksi terdapat masa inkubasi. Sedangkan, persamaan integral yang digunakan oleh Kermack – Mc.Kendrick sangat berguna dalam memodelkan timbulnya penyebaran penyakit menular dan mudah untuk dibuat parameternya.

Dalam tulisan ini akan dibahas modifikasi model Kermack – Mc.Kendrick tipe persamaan integral yang dilakukan oleh Aldis dan Robert. Pada model ini, jumlah penderita baru per unit waktu (incidence of infection) melibatkan empat lokasi, yaitu rumah, tempat kerja (termasuk sekolah), tempat umum dan rumah sakit. Linearisasi dapat dilakukan pada model persamaan integral, karena perhatian tertuju pada waktu awal penyebaran dan pengaruh dari berbagai intervensi. Setelah melakukan linearisasi, teori transformasi Laplace dapat digunakan. Linearisasi model persamaan integral Kermack - Mc.Kendrick dapat diaplikasikan untuk mengevaluasi berbagai intervensi untuk mencegah penyebaran penyakit cacar.

I.2 Tujuan

(11)

II.

LANDASAN TEORI

Teorema Dasar Kalkulus Andaikan kontinu pada [a,b].

1. Jika , maka

.

2. , dengan F

antiturunan sebarang dari f, yakni . (Stewart 2001) Persamaan Diferensial Biasa Linear dan Taklinear

Sebuah persamaan diferensial biasa orde ke-n dikatakan linear jika dapat ditulis dalam bentuk umum:

(1.1) Persamaan diferensial biasa yang tidak dapat ditulis seperti bentuk umum di atas disebut persamaan diferensial biasa taklinear.

(Farlow 1994) Nilai Reproduksi Dasar ( )

Nilai reproduksi dasar ( ) menggambarkan rata-rata jumlah infeksi sekunder yang disebabkan oleh datangnya seorang individu yang terinfeksi ke dalam N

populasi yang rentan terinfeksi. Dengan mengetahui angka nilai reproduksi dasar ( ) maka dapat diprediksi kepesatan dari penyebaran infeksi penyakit pada populasi.

Jika >1 maka infeksi penyakit akan menyebar di dalam suatu populasi, sedangkan jika maka infeksi penyakit tidak akan menyebar di dalam populasi karena banyaknya individu yang terinfeksi kemudian akan berkurang atau lebih sedikit dari jumlah individu yang terinfeksi untuk pertama kali.

(Mulyanah 2008) Nilai Eigen dan Vektor Eigen

Misalkan A adalah matriks , suatu vektor taknol x di dalam disebut vektor eigen dari A jika untuk suatu skalar yang disebut nilai eigen dari A, berlaku:

(1.2) Vektor x disebut vektor eigen yang bersesuaian dengan nilai eigen . Untuk mencari nilai eigen dari matriks A yang berukuran , maka persamaan (1.3) dapat dituliskan sebagai berikut:

(1.3) dengan I matriks identitas. Persamaan (1.3) mempunyai solusi tak nol jika dan hanya jika

(1.4) Persamaan (1.4) disebut persamaan karakteristik.

(Leon 2001) Matriks Taknegatif

Suatu matriks A disebut matriks taknegatif jika dan disebut matriks positif jika

untuk setiap i dan j.

(Leon 2001) Matriks Taktereduksi

Matriks taknegatif A dikatakan sebagai matriks yang tereduksi jika terdapat suatu partisi dari himpunan indeks {1,2,...,n} ke dalam himpunan-himpunan takkosong yang saling lepas I1 dan I2 sehingga apabila

dan . Jika tidak demikian, A disebut matriks yang taktereduksi.

(Leon 2001)

Spectral Radius

Jika A adalah matriks berukuran dengan nilai eigen , maka

spectral radius dari A adalah

(www.wolfram.com) Nilai Eigen dan Vektor Eigen Dominan

Jika A adalah matriks taknegatif dan tak tereduksi yang memiliki sebuah nilai eigen real positif terbesar r sehingga

, (1.6)

untuk sembarang nilai eigen dari A. Nilai

eigen r disebut nilai eigen dominan dan vektor eigen dominan dari matriks A adalah vektor eigen yang bersesuaian dengan r.

(Minc 1988) Transformasi Laplace

Misalkan adalah fungsi yang

terdefinisi pada (0,∞). Transformasi Laplace

dari didefinisikan sebagai fungsi yang diberikan oleh integral

Daerah asal dari adalah semua nilai s

yang integralnya terdefinisi. Transformasi Laplace dari dinotasikan oleh atau

).

(12)

Teorema Konvolusi

Misalkan dan adalah fungsi kontinu yang terdefinisi pada . Konvolusi dari dan dinotasikan dengan , didefinisikan sebagai

Jika dan adalah fungsi kontinu dari order eksponensial maka

(1.9)

Dimana dan ,

sehingga dalam bentuk inverse

(1.10) Bukti:

Berdasarkan definisi transformasi Laplace,

Misalkan , maka

dan mengganti dengan , sehingga diperoleh

Jika integral pada t (dari hingga ) diubah ke dalam bentuk integral pada (dari 0 hingga

t), maka

.

Terbukti (Farlow,1994)

Fungsi Dirac Delta

Fungsi dirac delta (fungsi impuls satuan) yang dinotasikan dengan didefinisikan

sebagai “fungsi” yang memenuhi dua sifat matematika, yakni:

(Farlow 1994) Transformasi Laplace pada Fungsi Dirac Delta

Transformasi Laplace dari fungsi unit impulse atau fungsi dirac delta

didefinisikan sebagai

. (1.13) Bukti:

Untuk mendapatkan Transformasi Laplace dari , pertama cari transformasi dari

rata-rata fungsi impulse ,

kemudian mencari limit dari ketika

Karena pembilang dan penyebut pada persamaan di atas mendekati 0 ketika ,

maka gunakan aturan L’Hopital untuk

mendapatkan limit

sehingga diperoleh .

Terbukti (Farlow 1994)

Gambar 1 Fungsi Delta Dirac

(13)

Notasi

Notasi yang digunakan dalam karya ilmiah ini antara lain:

peluang terjadinya penyebaran dari individu yang telah terinfeksi (infected) selama hari ke individu yang rentan terinfeksi (suspectible); penderita dari wilayah lain ( index

case, orang); laju penularan; laju penyembuhan;

peluang masih terinfeksi pada waktu hari setelah terinfeksi;

= total populasi (orang);

laju kontak per individu yang dapat terinfeksi;

laju kontak dari individu yang sebelumnya telah terinfeksi pada lokasi l ke individu yang terinfeksi pada lokasi k;

perbandingan antara jumlah individu yang dapat berinteraksi dengan seorang penderita pada lokasi k dengan besarnya populasi; nilai reproduksi dasar.

III.

PEMODELAN

3.1 Perumusan Model

Kermack – Mc.Kendrick memodelkan penyebaran penyakit melalui dua tipe, yaitu persamaan diferensial (model SIR) dan persamaan integral.

3.1.1 Model Kermack – Mc.Kendrick tipe persamaan integral

Kermarck-Mc Kendrick (Diekmann dkk, 2000) memodelkan jumlah penderita baru per unit waktu (incidence of infection) sebagai berikut:

Jumlah individu yang rentan terkena infeksi di suatu populasi pada waktu t adalah

Asumsi - asumsi yang digunakan pada model Kermack – Mc.Kendrick tipe persamaan integral antara lain:

1. populasi tertutup, sehingga tidak ada individu yang keluar masuk populasi; 2. tidak ada kelahiran atau kematian dalam

populasi;

3. seluruh individu pada awalnya rentan terinfeksi;

4. semua parameter dan variabel yang digunakan tak negatif;

5. individu yang sembuh dari infeksi memiliki imunitas untuk infeksi selanjutnya.

3.1.2 Model SIR

Pada model SIR, total populasi N dibagi ke dalam tiga buah kelompok sebagai berikut.

1. Kelompok individu sehat yang rentan terinfeksi (the susceptible, S).

2. Kelompok individu yang terinfeksi dan dapat menularkan infeksi (the invecticves, I ).

3. Kelompok individu yang telah sembuh dan kemudian kebal dari penyakit (the recovered, R).

Total populasi adalah

. (3.3)

Gambar 2 menjelaskan laju perpindahan antara ketiga kelompok dengan parameter , yaitu laju penularan penyakit dan laju penyembuhan ( ) yang konstan. Laju penularan suatu penyakit proporsional dengan laju pertemuan individu yang rentan terinfeksi dengan individu yang terinfeksi, sehingga dijelaskan dengan bentuk perkalian . Model SIR terdiri dari tiga sistem persamaan diferensial biasa taklinear.

Terdapat beberapa asumsi yang digunakan pada model SIR antara lain:

1. Populasi N (t) tertutup, sehingga tidak ada individu yang keluar masuk populasi.

S

I

R

(14)

2. Tidak ada kelahiran atau kematian dalam populasi.

3. Adanya kepastian proporsi populasi, yaitu

S dan sisanya I. Per satuan waktu, proporsi individu I membuat secara potensial merupakan interaksi penularan.

4. Setiap individu pada populasi memiliki kesempatan yang sama untuk berinteraksi dengan individu yang terinfeksi.

5. Individu yang sembuh dari infeksi memiliki imunitas untuk infeksi selanjutnya.

6. Diasumsikan bahwa setiap pembagian kelompok terdiri dari individu yang sama sehatnya atau sama sakitnya.

7. Persamaan dideskripsikan mengikuti model deterministik yang memasukkan nilai konstan untuk setiap parameternya. 8. Semua parameter dan variabel yang

digunakan tak negatif.

3.2 Hubungan antara Model Kermack-Mc.Kendrick dengan Model SIR Pada bagian ini akan dibahas hubungan antara model Kermack-Mc.Kendrick dengan model SIR. Model SIR merupakan kasus khusus dari model Kermack – Mc.Kendrick karena diformulasikan dalam persamaan diferensial biasa taklinear. Pada model SIR, terdapat asumsi laju penularan ( dan laju penyembuhan yang konstan. Asumsi tersebut

mengakibatkan dan

. [bukti lihat Diekmann & Heesterbeek 2000].

Pada model SIR, jumlah individu yang terkena infeksi adalah

Dengan menggunakan asumsi

, maka persamaan di atas menjadi

sehingga persamaan (3.7) dapat dituliskan sebagai

Jumlah individu yang sembuh dari penyakit adalah

Persamaan (3.4) diperoleh dengan menurunkan persamaan (3.2) terhadap t

sebagai berikut:

Berdasarkan Teorema Dasar Kalkulus

Dari persamaan (3.1) diperoleh

Dengan menggunakan asumsi bahwa , maka

,

sehingga diperoleh persamaan (3.4)

Terbukti Persamaan (3.5) diperoleh dengan menurunkan persamaan (3.8) terhadap t

sebagai berikut:

(15)

Rumah

k = 1

Rumah Sakit

k = 4

Tempat umum

k = 3 Tempat kerja

k = 2

Subtitusikan persamaan (3.1) ke dalam persamaan di atas, sehingga

Dengan menggunakan asumsi bahwa , maka

Berdasarkan persamaan (3.7) , persamaan (3.10) menjadi

,

Terbukti

Diketahui bahwa , sehingga

. Persamaan (3.6) diperoleh dengan menurunkan terhadap t

Berdasarkan persamaan (3.4) dan (3.5), maka

Terbukti 3.3 Modifikasi Model Kermack–Mc.

Kendrick tipe persamaan integral Dalam bagian ini akan dipelajari modifikasi model Kermack - Mc.Kendrick tipe persamaan integral yang dilakukan oleh Aldis dan Robert. Pada model ini, jumlah penderita baru per unit waktu (incidence of infection) melibatkan empat lokasi, yaitu rumah, tempat kerja (termasuk sekolah), tempat umum dan rumah sakit.

Incidence of infection di lokasi k yang terinfeksi pada waktu t disebabkan adanya kontak dengan individu yang teinfeksi pada waktu . Jika incidence of infection

melibatkan n lokasi, maka incidence of infection menjadi

(3.11)

Entri dari matriks laju kontak adalah laju kontak dari individu yang telah terinfeksi pada lokasi l ke individu yang terinfeksi pada lokasi

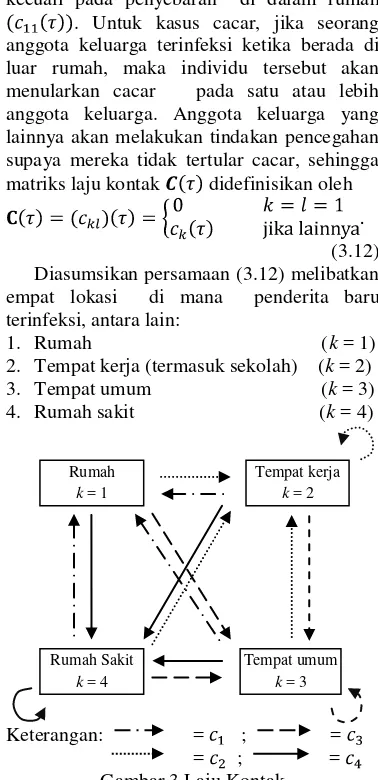
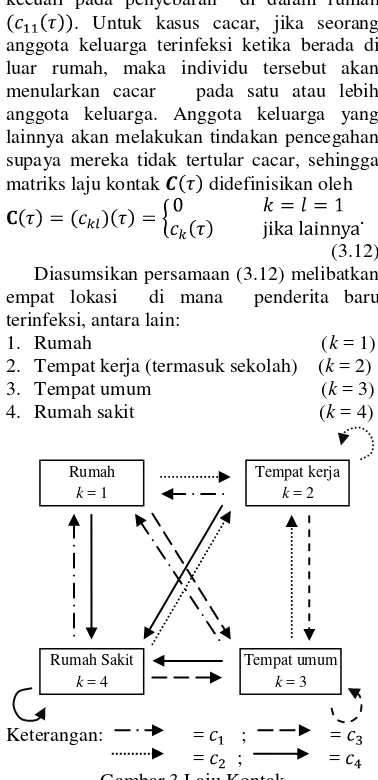
k. Diasumsikan bahwa laju kontak bergantung pada lokasi dimana individu terinfeksi, kecuali pada penyebaran di dalam rumah . Untuk kasus cacar, jika seorang anggota keluarga terinfeksi ketika berada di luar rumah, maka individu tersebut akan menularkan cacar pada satu atau lebih anggota keluarga. Anggota keluarga yang lainnya akan melakukan tindakan pencegahan supaya mereka tidak tertular cacar, sehingga matriks laju kontak didefinisikan oleh

(3.12) Diasumsikan persamaan (3.12) melibatkan empat lokasi di mana penderita baru terinfeksi, antara lain:

1. Rumah (k = 1) 2. Tempat kerja (termasuk sekolah) (k = 2) 3. Tempat umum (k = 3) 4. Rumah sakit (k = 4)

Keterangan: = ; = = ; =

Gambar 3 Laju Kontak

Dengan n = 4, incidence of infection menjadi

(3.13) Untuk mempermudah perhitungan, model di atas dapat dilinearisasi dengan mengambil asumsi jumlah individu yang rentan terinfeksi sama dengan total populasi ( ) , sehingga

(16)

Penderita dari luar ( ) digambarkan dengan fungsi dirac delta. Diasumsikan wabah terjadi karena adanya seorang individu yang terinfeksi di tempat umum, sehingga

. (3.15) Dengan melakukan transfomasi Laplace pada kedua ruas, maka

Pada persamaan di atas, transformasi Laplace dilambangkan dengan overbars

Berdasarkan definisi transformasi Laplace pada fungsi dirac delta akan diperoleh

,

sehingga transformasi Laplacenya merupakan sebuah unit vektor

.

Bentuk matriks dari fungsi transformasi variabel s adalah

(3.16) Transformasi Laplace pada model linear (3.14) akan menghasilkan

(3.17) [bukti lihat Lampiran 1].

Jumlah penderita baru yang diharapkan terinfeksi pada lokasi k oleh seseorang yang sebelumnya telah terinfeksi pada lokasi l

adalah

sehingga matriks generasi berikutnya didefinisikan sebagai

(3.19) Nilai reproduksi dasar merupakan spectral radius dari matriks generasi berikutnya

. (3.20) Dengan menggunakan program Mathematica 6.0 maka nilai reproduksi dasar

(3.21)

Berdasarkan nilai reproduksi dasar suatu wabah akan menjadi epidemik ringan jika dan akan menjadi epidemik berat

jika .

3.3.1 Epidemik ringan

Epidemik ringan terjadi jika . Pada epidemik ringan, perubahan banyaknya individu yang rentan terjangkit (S) dinilai cukup kecil bila dibandingkan dengan total populasi N, sehingga jika diasumsikan bahwa , maka asumsi tersebut dinilai cukup akurat. Total individu yang terinfeksi (ukuran epidemik) pada sebuah epidemik ringan adalah

(3.22) Dengan menggunakan program Mathematica 6.0, solusi untuk epidemik ringan adalah vektor

(3.23) 3.3.2 Epidemik berat

Epidemik berat terjadi ketika . Jika maka infeksi penyakit dapat menyebar dalam populasi. Model linear (3.14) dapat digunakan untuk menduga laju pertumbuhan dari sebuah epidemik (r) . Incidence of infection akan meningkat secara eksponensial

, (3.24)

dengan . Untuk mendapatkan

solusi taktrivial dari persamaan (3.17) maka matriks haruslah singular, sehingga nilai r dapat diperoleh dari nilai s yang membuat determinan sama dengan 0 (Aldis & Robert 2005).

Proporsi incidence of infection pada masing-masing lokasi infeksi adalah

(17)

VI. CONTOH KASUS

4.1 Parameter Input

Untuk cacar , peluang terjadinya penyebaran dari individu yang telah terinfeksi selama hari ke individu yang rentan terinfeksi dimodelkan dengan fungsi:

dengan asumsi:

Semua individu yang terinfeksi dapat menularkan cacar antara dan setelah mereka terinfeksi.

Tidak ada yang dapat menularkan cacar sebelum infeksi mulai aktif ( ) atau sesudah berakhirnya infeksi ( ).

Nilai dan keterangan dari parameter lain yang digunakan dalam komputasi terdapat pada tabel 1.

Tabel 1 Waktu infeksi dan parameter lain yang digunakan dalam komputasi Parameter Nilai Deskripsi

12 Waktu ketika timbulnya gejala awal (hari) 14 Waktu ketika infeksi mulai aktif (hari)

16 Waktu ketika bintik-bintik merah muncul (hari)

16 Waktu ketika individu yang terinfeksi tidak dapat beraktivitas (hari) 19 Waktu ketika individu yang terinfeksi perlu dirawat di rumah sakit

(hari)

25 Waktu ketika infeksi penyakit mulai berkurang (hari) 27 Waktu berakhirnya infeksi penyakit (hari)

3.2 Nilai reproduksi dasar 50.000 Total populasi (orang)

1 Banyaknya penderita dari wilayah lain (orang) 0.1 Proporsi anggota keluarga yang divaksinasi 0.1 Proporsi petugas kesehatan yang divaksinasi 0.9 Proporsi anggota keluarga yang dikarantina 0.9 Proporsi petugas kesehatan yang dikarantina 0.05 Faktor skala rumah sakit yang terkontrol dari infeksi 0.5 Faktor skala keadaan waspada

Penyakit cacar dapat menyebar jika terjadi kontak antara individu yang telah terinfeksi dengan individu yang rentan terinfeksi. Untuk penyebaran infeksi di dalam rumah, diasumsikan bahwa seseorang mengurangi kontak dengan anggota keluarga lainnya pada waktu akhir masa inkubasi. Laju kontak berakhir ketika individu yang terinfeksi masuk rumah sakit, sehingga fungsi laju kontak untuk individu yang terinfeksi di rumah adalah

Laju kontak untuk individu yang terinfeksi di tempat kerja dan tempat umum menggunakan asumsi-asumsi sebagai berikut.

Fungsi laju kontak pada lokasi tempat kerja dan tempat umum memiliki bentuk yang sama.

Lokasi tempat kerja dan tempat umum memiliki penurunan laju kontak yang lebih cepat bila dibandingkan dengan laju kontak untuk lokasi rumah.

Fungsi laju kontak untuk individu yang terinfeksi di tempat kerja dan tempat umum adalah

(18)

Infectifity kernel menggambarkan peluang penyebaran pada suatu lokasi. Infectifity kernel di rumah dapat dimodelkan dengan

(4.5) Infectifity kernel di tempat kerja dan tempat umum adalah

(4.6)

sedangkan infectifity kernel di rumah sakit

(4.7)

Dengan menggunakan software Mathematica 6.0, didapatkan grafik infectifity kernel pada lokasi rumah, tempat kerja, tempat umum dan rumah sakit.

Keterangan: = ; = =

Gambar 4 Grafik infectifity kernel untuk penyebaran cacar di rumah.

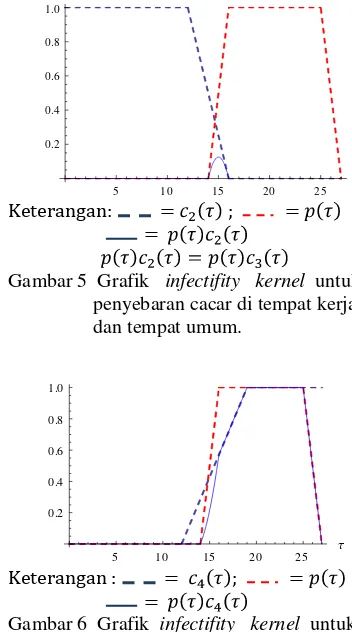
Keterangan: = ; = =

Gambar 5 Grafik infectifity kernel untuk penyebaran cacar di tempat kerja dan tempat umum.

Keterangan : = ; = =

Gambar 6 Grafik infectifity kernel untuk penyebaran cacar di rumah sakit.

Infectifity kernel untuk keempat lokasi dimulai pada waktu infeksi mulai aktif ( 14 hari). Gambar 4 menunjukkan grafik infectifity kernel untuk penyebaran cacar di rumah. Pada lokasi rumah, infectifity kernel meningkat hingga munculnya bintik-bintik merah, lalu menurun hingga individu yang terinfeksi di lokasi rumah dirawat di rumah sakit.

Berdasarkan asumsi yang digunakan, grafik infectifity kernel di lokasi tempat umum dan tempat kerja memiliki bentuk yang sama.

Infectifity kernel akan meningkat, kemudian menurun hingga individu yang terinfeksi tidak dapat melakukan aktivitas di tempat umum maupun tempat kerja (Gambar 5).

Gambar 6 menjelaskan tentang infectifity kernel untuk penyebaran cacar di rumah sakit. Pada lokasi rumah sakit, infectifity kernel akan terus meningkat hingga individu yang terinfeksi masuk rumah sakit. Infectifity kernel

akan konstan hingga pada saat mulai berkurangnya infeksi (sakit) , kemudian

infectifity kernel mulai berkurang dan menurun hingga individu yang terinfeksi sembuh dari penyakit cacar.

Dari ketiga grafik di atas, terlihat jelas bahwa peluang untuk terjadinya penyebaran

5 10 15 20 25

 0.2 0.4 0.6 0.8 1.0

5 10 15 20 25

0.2 0.4 0.6 0.8 1.0

5 10 15 20 25

(19)

terbesar terdapat pada lokasi rumah sakit. Peluang untuk terjadinya penyebaran pada lokasi tempat umum dan tempat kerja relatif kecil.

4.2 Intervensi

Berbagai intervensi dapat dilakukan untuk mencegah terjadinya penyebaran penyakit cacar . Diasumsikan intervensi tidak dimulai sebelum penderita dari wilayah lain teridentifikasi ketika waktu bintik-bintik merah mulai muncul ( . Untuk penyakit cacar, beberapa intervensi yang dapat dilakukan antara lain:

a.Penanganan dini (Strict vigilance, SV) Pada intervensi penanganan dini (SV), individu yang terinfeksi akan dirawat di rumah sakit sehari setelah munculnya bintik-bintik merah. Intervensi ini dapat dimodelkan dengan membuat waktu untuk merawat individu yang terinfeksi menjadi sehari setelah munculnya bintik-bintik

merah ( . Intervensi

penanganan dini akan dikombinasikan dengan berbagai intervensi lainnya. b.Karantina anggota keluarga (Household

vaccination, QH)

Intervensi ini dilakukan dengan cara mengkarantina anggota keluarga di dalam rumah. Intervensi karantina anggota keluarga dapat mencegah penyebaran infeksi ke luar rumah. Anggota keluarga yang terinfeksi tidak dapat berinteraksi dengan individu yang berada di tempat kerja maupun tempat umum. Intervensi ini dapat dimodelkan dengan mengalikan laju kontak dari rumah ke tempat kerja ( ) dan laju kontak dari rumah ke tempat umum ( ) dengan proporsi anggota keluarga yang tidak dikarantina (

c.Karantina petugas kesehatan (Workplace Quarantine,QW)

Karantina petugas kesehatan merupakan intervensi yang dapat dilakukan dengan cara mengkarantina petugas kesehatan di dalam rumah. Intervensi ini dapat mengurangi laju kontak dari tempat kerja ke tempat kerja dan tempat umum. Intervensi karantina petugas kesehatan dapat dimodelkan dengan mengalikan laju kontak dari tempat kerja ke tempat kerja ( ) dan laju kontak dari tempat kerja ke tempat umum ( ) dengan proporsi

petugas kesehatan yang tidak dikarantina (1- ).

d.Vaksinasi anggota keluarga (Household vaccination, VH)

Intervensi ini dapat dilakukan dengan cara memvaksinasi anggota keluarga. Jika proporsi anggota keluarga yang divaksinasi adalah , maka vaksinasi anggota keluarga dimodelkan dengan mengalikan jumlah penderita baru yang diharapkan terinfeksi pada lokasi rumah ( ) dengan besarnya proporsi anggota keluarga yang tidak divaksinasi (1- .

e.Vaksinasi petugas kesehatan (Workplace vaccination, VW)

Vaksinasi petugas kesehatan merupakan suatu intervensi yang dilakukan dengan cara memvaksinasi petugas kesehatan. Jika merupakan proporsi anggota proporsi petugas kesehatan yang divaksinasi, maka intervensi ini dapat dimodelkan dengan mengalikan jumlah penderita baru yang diharapkan terinfeksi pada lokasi tempat kerja ( ) dengan proporsi petugas kesehatan yang tidak divaksinasi (1- .

f. Keadaan waspada (Cautious Contact, CC)

Kegelisahan masyarakat terhadap penyakit cacar dapat merubah perilaku masyarakat. Masyarakat menjadi lebih peduli terhadap kebersihan diri sendiri maupun lingkungan. Untuk menggambarkan perubahan ini (keadaan waspada), faktor skala pencegahan terjadinya kontak ( ) dikalikan dengan perbandingan antara jumlah individu yang dapat berinteraksi dengan seorang penderita pada lokasi rumah, tempat kerja dan tempat umum dengan besarnya populasi ( .

(20)

4.3 Hasil dan Pembahasan

Nilai untuk waktu infeksi dan parameter lainnya diberikan pada tabel 1. Hasil simulasi dari intervensi dan kombinasi beberapa intervensi yang berbeda terdapat pada lampiran. Diasumsikan seorang individu yang terinfeksi datang ke suatu populasi yang berjumlah 50.000 orang ( N = 50.000). Pada keadaan awal model diasumsikan memiliki

distribusi awal penderita (

dan semua penderita akan diisolasi di rumah sakit pada waktu . Diasumsikan intervensi tidak dimulai sebelum penderita dari wilayah lain teridentifikasi ketika waktu bintik-bintik merah mulai

muncul ( .

4.3.1 Nilai Reproduksi Dasar ( )

Tabel 2 Nilai Reproduksi Dasar ( )

Perlakuan Nilai Reproduksi Dasar ( )

Tanpa Intervensi 3.2

SV; VH; VW; VW-VH; QH; QW 2.49 – 2.68

CC; SH; SH-VH; SH-QH; SH-VH-QH;SH-QW 1.08 – 1.96

SH-CC 0.77

Dengan mengetahui angka nilai reproduksi dasar maka dapat diprediksi kepesatan dari penyebaran infeksi penyakit pada populasi. Tanpa adanya intervensi, nilai reproduksi dasar ( ) untuk penyakit cacar adalah 3.2. Hal ini berarti nilai , sehingga wabah cacar akan menjadi epidemik berat. Penanganan dini (SV) membuat nilai reproduksi dasar turun menjadi 2.68 . Intervensi SV, VH, VW, VW-VH, QH dan

QW hanya memiliki selisih nilai reproduksi dasar yang kecil.

Kombinasi antara intervensi perawatan intensif dan karantina petugas kesehatan (SH-QW) membuat nilai reproduksi dasar mendekati satu (1.08), namun tidak membuat wabah cacar menjadi epidemik ringan. Epidemik ringan ( ) akan terjadi jika dilakukan kombinasi antara intervensi perawatan intensif dan keadaan waspada

(SH-CC). .

Gambar 7 Grafik Nilai Reproduksi Dasar ( ) untuk berbagai perlakuan. Gambar di atas menunjukkan nilai

reproduksi dasar ( ) untuk berbagai perlakuan. Dari grafik dapat dilihat bahwa tanpa intervensi maka akan diperoleh nilai reproduksi dasar terbesar. Intervensi SV, VH,

VW, VW-VH, QH dan QW memiliki selisih nilai reproduksi dasar yang kecil. Intervensi SH-CC menghasilkan nilai reproduksi dasar dibawah satu.

3.2

2.68 2.64 2.61 2.57 _2.5 _2.49

1.96

1.47 1.43

1.11 1.1 1.08 0.77 0 0.5 1 1.5 2 2.5 3 3.5 Tanpa Intervensi

SV VH VW VH-VW QH QW CC SH SH-VH SH-QH SH-QH-VH

SH-QW SH-CC

R0

(21)

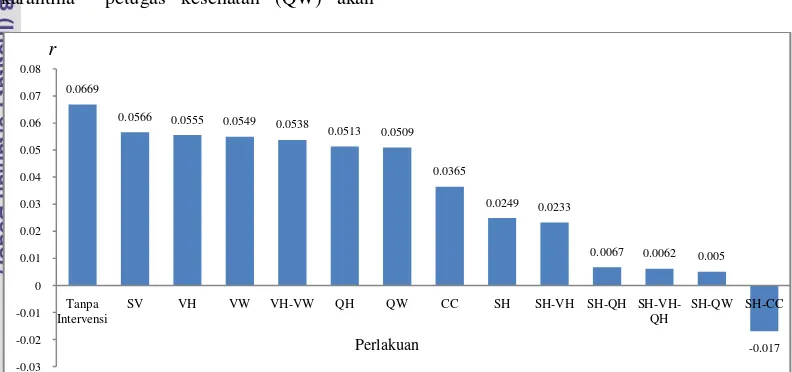
4.3.2 Laju pertumbuhan epidemik ( r )

Tabel 3 Nilai laju pertumbuhan epidemik (r)

Perlakuan Laju Pertumbuhan Epidemik (r)

Tanpa Intervensi 0.0669

SV; VW; VH; VW-VH 0.053 – 0.056

QH; QW; CC; SH; SH-VH 0.023 – 0.051

SH-QH; SH-VH-QH; SH-QW 0.005 – 0.0067

SH-CC -0.017

Tanpa intervensi, wabah cacar akan meningkat secara eksponensial dengan nilai laju pertumbuhan epidemik sebesar 0.0669. Penanganan dini (SV) akan menurunkan nilai

r menjadi 0.056. Intervensi vaksinasi anggota keluarga (VH), karantina petugas kesehatan (VW), maupun kombinasi antata keduanya (VH-VW) memiliki selisih nilai r yang kecil.

Karantina anggota keluarga (QH) dan karantina petugas kesehatan (QW) akan

memberikan nilai laju pertumbuhan epidemik yang hampir sama. Keadaan waspada (CC) akan membuat nilai laju pertumbuhan menjadi setengah dari nilai laju pertumbuhan cacar. Nilai laju pertumbuhan epidemik terkecil diperoleh dengan cara mengkombinasi intervensi perawatan intensif dengan karantina petugas kesehatan (SH-QW).

Gambar 8 Grafik Laju Pertumbuhan epidemik (r) untuk berbagai perlakuan. Dari Gambar 8 dapat dilihat laju

pertumbuhan epidemik (r) untuk berbagai perlakuan. Tanpa adanya intervensi untuk penyakit cacar maka akan diperoleh laju pertumbuhan epidemik terbesar. Intervensi SV, VH, VW, VW-VH, QH, QW memiliki

selisih laju pertumbuhan epidemik yang kecil. SH-CC memiliki laju pertumbuhan epidemik yang bernilai negatif, sehingga seiring bertambahnya waktu, incidence of infection

akan berkurang.

4.3.3 Incidence of infection

Tabel 4 Incidence of infection dan persentasenya

Perlakuan Incidence of infection

t = 130 (hari)

Persentase (%)

Tanpa intervensi 6033.97 100

SV; VH; VW; VH-VW 1099.53-1571.19 18.22-26.04

QH; QW; CC; SH; SH-VH 20.82-793.74 0.34-13.15

SH-QH; SH-VH-QH; SH-QW 1.91-2.40 0.031-0.039

SH-CC 0.11 0.002

0.0669

0.0566 0.0555 0.0549 0.0538

0.0513 0.0509

0.0365

0.0249 _0.0233

0.0067 0.0062 0.005

-0.017 -0.03 -0.02 -0.01 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 Tanpa Intervensi

SV VH VW VH-VW QH QW CC SH SH-VH SH-QH SH-VH-QH

SH-QW SH-CC

r

(22)

Tanpa intervensi, besarnya incidence of infection untuk penyakit cacar adalah 6033,97 orang. Dengan adanya intervensi penanganan dini, incidence of infection dapat berkurang menjadi 26,04%. Dapat dilihat bahwa intervensi perawatan intensif memiliki pengaruh yang cukup besar dalam pengendalian wabah cacar. Intervensi SH-QW, SH-QH, SH-VH-QH dapat mengurangi

incidence of infection hingga 99,94%. Intervensi SH-CC dapat mengendalikan wabah cacar hingga menjadi epidemik ringan.

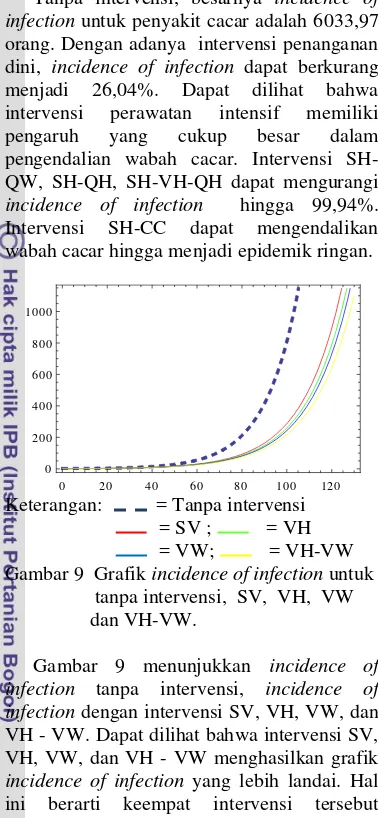
Keterangan: = Tanpa intervensi = SV ; = VH = VW; = VH-VW Gambar 9 Grafik incidence of infection untuk tanpa intervensi, SV, VH, VW dan VH-VW.

Gambar 9 menunjukkan incidence of infection tanpa intervensi, incidence of infection dengan intervensi SV, VH, VW, dan VH - VW. Dapat dilihat bahwa intervensi SV, VH, VW, dan VH - VW menghasilkan grafik

incidence of infection yang lebih landai. Hal ini berarti keempat intervensi tersebut memiliki pengaruh yang berarti dalam pengendalian wabah cacar.

Keterangan: = Tanpa intervensi = QH ; = QW = CC ; = SH Gambar 10 Grafik incidence of infection untuk tanpa intervensi, QH, QW, CC dan SH.

Dari Gambar 10 dapat dilihat bahwa intervensi SH memiliki grafik yang lebih

landai bila dibandingkan dengan intervensi lainnya. Gambar 10 menunjukkan bahwa intervensi SH memiliki pengaruh pengendalian wabah cacar yang lebih besar daripada intervensi QH, QW, dan CC.

Keterangan: = Tanpa intervensi

= SH-VH; = SH-QW = SH-QH; = SH-CC = SH-QH-VH

Gambar 11 Grafik incidence of infection untuk tanpa intervensi, SH-VH, SH-QW, SH-QH, SH-QH-VH dan SH-CC.

Dari Gambar 11 dapat dilihat bahwa intervensi SH-QW, SH-QH, dan SH-QH-VH menghasilkan grafik incidence of infection

yang lebih landai daripada intervensi SH-VH . Hal ini berarti intervensi SH-QW, SH-QH, dan SH-QH-VH memiliki pengaruh pengendalian wabah cacar yang lebih besar daripada intervensi SH-VH. Seiring bertambahnya waktu, intervensi SH-CC akan membuat incidence of infection semakin berkurang.

0 20 40 60 80 100 120 0 200 400 600 800 1000

0 20 40 60 80 100 120

0 100 200 300 400

0 20 40 60 80 100 120

(23)

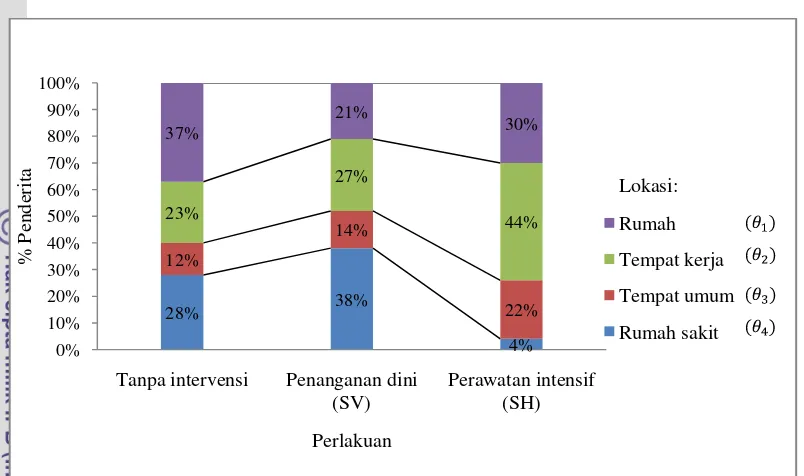
4.3.4 Distribusi Penderita

Gambar 12 Grafik Distribusi Penderita . Gambar 12 menunjukkan bahwa tanpa

intervensi, proporsi incidence of infection

paling besar terdapat pada rumah. Penanganan dini (SV) membuat individu yang terinfeksi lebih cepat dirawat di rumah sakit sehingga dapat meningkatkan peluang untuk terjadinya penyebaran infeksi di rumah sakit. Hal ini mengakibatkan jumlah individu baru yang terinfeksi paling besar terdapat pada rumah sakit.

Perawatan intensif (SH) dapat mengurangi jumlah individu yang dapat berinteraksi dengan seorang penderita pada rumah sakit, sehingga proporsi incidence of infection

paling kecil terdapat pada rumah sakit. Kombinasi antara perawatan intensif dengan intervensi lainnya dapat membuat distribusi penderita paling kecil terdapat pada rumah sakit. Distribusi penderita paling besar terdapat di tempat kerja.

KESIMPULAN

Modifikasi model Kermack-Mc.Kendrick tipe persamaan integral yang melibatkan empat lokasi dapat diaplikasinya pada penyakit cacar. Nilai reproduksi dasar akan banyak berkurang bila dilakukan intervensi perawatan intensif (SH) atau keadaan waspada (CC) untuk mengurangi kontak. Intervensi vaksinasi anggota keluarga atau karantina petugas kesehatan tidak terlalu memengaruhi nilai reproduksi dasar. Intervensi vaksinasi anggota keluarga maupun petugas kesehatan

membutuhkan intervensi lain untuk mengurangi incidence of infection hingga jumlah yang dapat diterima. Karantina anggota keluarga dinilai cukup efektif dalam pengendalian penyakit cacar.

Intervensi perawatan intensif (SH) memberikan pengaruh besar pada pengendalian penyakit cacar. Kombinasi antara perawatan intensif (SH) dengan keadaan waspada (CC) dapat membuat penyebaran cacar menjadi epidemik ringan.

28% 38% 4% 12% 14% 22% 23% 27% 44% 37% 21% 30% 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%

(24)

DAFTAR PUSTAKA

Aldis GK, Roberts MG. 2005. An integral equation model for the control of a smallpox outbreak. Mathematical Biosiences 195: 1-22.

Anderson RM, May RM. 1991. Infectious diseases of humans: dynamics and control. Oxford University Press.

Diekmann O, Heesterbeek JAP. 2000.

Mathematical epidemiology of infectious diseases: model building, analysis and interpretation. Chichester: Wiley.

Farlow SJ. 1994. An Introduction to Differential Equation and Their Application. New York: Mc Graw-Hill. Gunawan AW, Achmadi SS, Arianti L.

2004. Pedoman Penyajian Karya Ilmiah. Bogor: IPB Press.

Leon SJ. 2001. Aljabar Linear dan Aplikasinya. Alit Bondan, penerjemah; Hilarius Wibi, editor. Jakarta: Erlangga. Terjemahan dari: Linear Aljebra with Aplication.

Minc. 1988. Nonnegative Matrices. New York: Wiley.

Mulyanah L. 2008. Model SIR pada Penularan Penyakit Influenza dengan Populasi yang Terinfeksi Virus [skripsi]. Bogor : Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Roberts MG. 2004. Modelling strategies for minimizing the impact of an imported exotic infection. Proc. R. Soc. (Lond.) Ser.

B. 271, 2411-2415.

Roberts MG. 2006. Modelling strategies for containing an invading infection.

Mathematical Population Studies, 13:205-214.

Stewart J. 2001. Kalkulus Jilid 1. Edisi Ke-4. Susila IN, Gunawan H, penerjemah; Mahanani N, Hardani W, editor. A Division of International Thomson Publishing Inc. Terjemahan dari: Calculus, Fourth Edition.

WHO.http://www.who.int/factsheets/mediacen tre/smallpox[17 Juli 2008].

(25)

(26)

Lampiran 1 Pembuktian persamaan (3.17)

Dari persamaan (3.17) jumlah penderita baru per unit waktu didefinisikan sebagai

Dengan menggunakan transformasi Laplace pada kedua ruas, maka diperoleh

sehingga

Misalkan maka persamaan di atas menjadi

Pada persamaan di atas, transformasi Laplace dilambangkan dengan overbars (misalkan :

). Didefinisikan ,sehingga

Pindahkan persamaan ke ruas kiri

=

sehingga diperoleh

(27)

Lampiran 2 Pembuktian determinan sama dengan 0

Dari persamaan (3.17) jumlah penderita baru per unit waktu didefinisikan sebagai

Diketahui bahwa dan , sehingga

Dengan menggunakan transformasi Laplace pada kedua ruas, maka diperoleh

sehingga

Didefinisikan ,sehingga

Pindahkan persamaan ke ruas kiri

Misal s - r =0 maka s = r, sehingga

Untuk mendapatkan solusi taktrivial maka matriks haruslah singular, sehingga nilai r

(28)

Lampiran 3 Pembuktian persamaan (3.25) Persamaan (3.17) dapat dituliskan dalam bentuk

Sehingga akan diperoleh .

Proporsi incidence of infection pada lokasi rumah

Proporsi incidence of infection pada lokasi tempat kerja

Proporsi incidence of infection pada lokasi tempat umum

Diketahui bahwa , sehingga

(29)

Lampiran 4 Hasil simulasi dari beberapa perlakuan yang berbeda

No. Perlakuan Nilai reproduksi dasar (Ro)

Incidence of infection

(pada t =130)

Persentase (%)

Laju pertumbuhan epidemik (r)

Distribusi Penderita Rumah

( )

Tempat kerja ( )

Tempat umum Rumah sakit ( ) 1. Tanpa

Intervensi 3.2 6033.97 100 0.0669 0.3682 0.2345 0.1172 0.2800

2 SV 2.68 1571.19 26.04 0.0566 0.2106 0.2738 0.1369 0.3785

3 VH 2.64 1372.59 22.75 0.0556 0.1961 0.2782 0.1391 0.3865

4 VW 2.61 1260.74 20.89 0.0549 0.2150 0.2528 0.1404 0.3917

5 VH-VW 2.57 1099.53 18.22 0.0538 0.2004 0.2568 0.1426 0.4001

6 QH 2.50 793.74 13.15 0.0513 0.2244 0.2962 0.1481 0.4208

7 QW 2.49 750.195 12.43 0.0509 0.2256 0.2982 0.1491 0.4245

8 CC 1.96 115.494 1.914 0.0365 0.1539 0.1850 0.0925 0.5685

9 SH 1.47 25.5226 0.422 0.0249 0.3033 0.4404 0.2202 0.0360

10 SH-VH 1.43 20.8209 0.35 0.0234 0.2864 0.4508 0.2254 0.0372

1 SH-QH 1.11 2.40676 0.039 0.0067 0.3656 0.5783 0.2892 0.0523

12 SH-VH-QH 1.10 2.2595 0.0374 0.0062 0.3433 0.5825 0.2913 0.0542

13 SH-QW 1.08 1.9176 0.0317 0.005 0.3719 0.5936 0.2968 0.0569

(30)

Lampiran 5 Program Mathematica 6.0 yang digunakan dalam perhitungan

Parameter yang digunakan dalam komputasi

e  12; a 14; b  16; w 16; h1  19; h2 w 1; c 25; d  27; R0 3.2; n  50 000; vh 0.1; vw  0.1; fh 0.05; fc  0.5; qh  0.9; qw 0.9; expectedinitialcasedistr  0.35, 0.2, 0.1, 0.35;

t  130;

Matriks Generasi Berikutnya Next Generation Matriks nextgenerations,a,b,c,x:

0,1s,b,x,1s,b,x,1s,b,x,2s,c,2s,c,2s,c,2s,c,3s,3s,3s, 3s,4s,x,4s,x,4s,x,4s,x a0 0,1s,b,x,1s,b,x,1s,b,x,21s,2s,c, 2s,c,2s,c,31s,3s,3s,3s,4s,x,4s,x,4s,x,4s,x a1 0,1s,b,x,1s,b,x,1s,b,x,2s,c,22s, 2s,c,2s,c,3s,32s,3s,3s,4s,x,4s,x,4s,x,4s,x a2

nilaieigen, vektoreigen Eigensystemnextgeneration0, 0, 0, 0, h1;

Nilai Reproduksi Dasar Ro

nilaieigen4 .10, 0,h1K1,20, 0K2,30K3,40,h1K4

1

2K2K3K4 K2K3K4 4 K1K2K3K4 

Solusi untuk epidemik kecil

InverseIdentityMatrix4nextgeneration0, 0, 0, 0,h1 .10, 0,h1K1,20, 0K2,30K3,40,h1K4.0,0,1,0  MatrixForm

K1

1K2K1 K2K3K1 K3K4K1 K4 K2K1 K2 1K2K1 K2K3K1 K3K4K1 K4

1K2K1 K2K4K1 K4

1K2K1 K2K3K1 K3K4K1 K4

K4K1 K4 1K2K1 K2K3K1 K3K4K1 K4

Peluang penyebaran penyakit

p: a

ba ab 1 bc

d

(31)

Peluang penyebaran penyakit

p: a

ba ab 1 bc

d

dc cd 0 True

Laju kontak di rumah

c1,x:

1 0e

x

xe ex 0 True

Laju kontak di tempat kerja

c2:

1 0e

w

we ew 0 True

Laju kontak di tempat umum

c3:

1 0e

w

we ew 0 True

Laju kontak di rumah sakit

c4,x:

0 e e

xe ex 1 x

Program Mathematica 6.0 untuk mencari grafik infectifity kernel di lokasi rumah

Plotc1, h1, p, pc1, h1, , 0, d, AxesLabel  Automatic, PlotStyle Dashed, Dashed, Red, Blue

5 10 15 20 25



(32)

Program Mathematica 6.0 untuk mencari grafik infectifity kernel di lokasi tempat kerja

ShowPlotc2, , 0, d, PlotStyle  Dashed, Plotp, , 0, d, PlotStyle Dashed, Red, Plotpc2, , 0, w, PlotStyle  Blue

5 10 15 20 25

0.2 0.4 0.6 0.8 1.0

Program Mathematica 6.0 untuk mencari grafik infectifity kernel di lokasi tempat umum

ShowPlotc3, , 0, d, PlotStyle  Dashed, Plotp, , 0, d, PlotStyle Dashed, Red, Plotpc3, , 0, w, PlotStyle  Blue

5 10 15 20 25

0.2 0.4 0.6 0.8 1.0

Program Mathematica 6.0 untuk mencari grafik infectifity kernel di lokasi rumah sakit

Plotc4, h1, p, pc4, h1, , 0, d, PlotStyle  Dashed, Dashed, Red, Blue, AxesLabel  Automatic

5 10 15 20 25 

(33)

Fungsi transformasi variabel s

1s,b,x:

n w1_₀__s_p____c1___,_x___ _b_₀

1vhn w10 __s

pc1,x b1

21s:n w2 0



s

p 1qhc2

22s:n w1 0



s

p 1qwc2

2s,c:

n w20 __s

pc2 c0

1vwn w2₀spc2 c1

31s:n w3 0



s

p 1qhc3

32s:n w3 0



s

p 1qwc3

3s:n w3 0



s

pc3

4s,x:n w4 0



s

pc4,x

Pendefinisian Nilai Reproduksi Dasar dan Vektor Eigen terbesar nilaireproduksidasar  nilaieigen4;

vektoreigenterbesar  vektoreigen4;

Perhitungan Nilai w

vektoreigenterbesarnormalized  vektoreigenterbesarTotalvektoreigenterbesar;

Nilai w

nilaiw  NSolvevektoreigenterbesarnormalized  expectedinitialcasedistr, nilaireproduksidasar  R0, w1, w2, w3, w4

w10.0000295385, w20.0000768, w30.0000384, w42.27797106

Nilai w untuk Keadaan Waspada Cautious contact,CC

nilaiwcc  ReplacePartnilaiw, 1, 1, 2 nilaiw1, 1, 2fc, 1, 2, 2  nilaiw1, 2, 2fc, 1, 3, 2  nilaiw1, 3, 2fc

(34)

Nilai w untuk intervensi Perawatan IntensifStrict Hospital, SH nilaiwsh  ReplacePartnilaiw, 1, 4, 2  nilaiw1, 4, 2fh

w10.0000295385, w20.0000768, w30.0000384, w41.13898107

Nilai w untuk kombinasi intervensi Keadaan waspada dan Perawatan Intensif CCSH

nilaiwccsh  ReplacePartnilaiw, 1, 1, 2  nilaiw1, 1, 2fc, 1, 2, 2  nilaiw1, 2, 2fc, 1, 3, 2  nilaiw1, 3, 2fc,

1, 4, 2  nilaiw1, 4, 2fh

w10.0000147692, w20.0000384, w30.0000192, w41.13898107

Matriks Generasi Berikutnya Next Generation Matrix

nextgenerationmatrixe,a,b,c,x:

nextgeneration0,a,b,c,x .nilaiw e0 nextgeneration0, a,b,c,x .nilaiwcc e1 nextgeneration0, a,b,c,x .nilaiwsh e2 nextgeneration0,a,b,c,x .nilaiwccsh e3

Nilai Reproduksi Dasar

R0e,a,b,c,x:MaxEigenvaluesnextgenerationmatrixe,a,b,c, x

Persamaan Karakteristik

characteristiceqss,e,a,b,c,x:

DetIdentityMatrix4nextgenerations,a,b,c,x .nilaiw e0 DetIdentityMatrix4nextgenerations,a,b,c,x .nilaiwcc e1 DetIdentityMatrix4nextgenerations,a,b,c,x .nilaiwsh e2 DetIdentityMatrix4nextgenerations,a, b,c,x .nilaiwccsh e3