ABSTRAK
BENTUK-BENTUK ISOMORFISME
GRAF WRAPPED BUTTERFLY NETWORK DAN GRAF CYCLIC-CUBES
Oleh
RIRIN SEPTIANA
Isomorfis merupakan konsep kekongruenan yang dapat diterapkan diberbagai bidang ilmu, termasuk graf. Graf Wrapped Butterfly Networks dan Cyclic-Cubes merupakan dua graf yang memiliki definisi yang berbeda. Kesamaan dari kedua graf ini adalah memiliki jumlah vertex yang sama dengan rumus jumlah vertexnya . Dari teorema Has dan Lin [2009], kedua graf Wrapped Buterfly Networks dan Cyclic-Cubes merupakan dua graf yang saling isomorfis. Dalam tulisan ini akan didiskusikan bentuk-bentuk graf Wrapped Buterfly Networks yang isomorfis dengan graf Cyclic-Cubes dan penggambaran kedua graf tersebut.
I. PENDAHULUAN
1.1 Latar Belakang
Perkembangan teknologi dan ilmu pengetahuan alam saat ini terjadi begitu pesat di berbagai kalangan, khususnya di dunia pendidikan dan keilmuan. Sehingga, sangat diharapkan ada penemuan-penemuan baru yang dapat menyokong keberlanjutan keilmuan di Indonesia khususnya dan di dunia pada umumnya. Penemuan-penemuan baru dalam keilmuan ini yang kemudian akan menambah khasanah yang dapat dijadikan sebagai referensi bagi seluruh kalangan yang berkepentingan terhadap suatu bidang ilmu tertentu.
Graf merupakan salah satu ilmu yang menarik untuk digali dan dikembangkan, salah satunya tentang isomorfisme graf. Dalam mempelajari graf sering ditemukan dua bentuk graf yang berbeda yang cukup rumit dengan banyaknya vertex dan edge. Namun, ternyata setelah direpresentasikan ternyata graf tersebut isomorfis. Tidak jarang juga ditemukan dua graf yang sederhana dan memiliki kemiripan secara visual. Namun, setelah dilakukan representasi terhadap graf tersebut ternyata kedua graf tersebut tidak isomorfis. Cyclic-Cubes dan Wrapped Butterfly
di telinga banyak orang termasuk bentuk dari kedua graf tersebut. Hal ini yang menjadi motivasi bagi penulis untuk mendiskusikan bentuk-bentuk isomorfisme dua jenis graf yang berbeda tersebut yaitu, Cyclic-Cubes dan Wrapped Butterfly Networks (WB).
1.2 Batasan Masalah
Dalam penelitian ini, agar pembahasan tidak meluas maka masalah dibatasi pada diskusi tentang bentuk-bentuk Wrapped Butterfly Networks (WB) (n,k) dan Cyclic-Cubes dengan nilai dan serta memperlihatkan bentuk dari Wrapped Butterfly Networks (WB) (n,k) yang isomorfis dengan graf Cyclic-Cubes.
1.3 Tujuan Penelitian
Tujuan penelitian ini adalah untuk mengetahui bentuk-bentuk Wrapped Butterfly Networks (WB) (n,k) yang isomorfis dengan graf Cyclic-Cubes.
1.4 Manfaat Penelitian
Manfaat penelitian ini adalah :
1. Menambah pengetahuan tentang Wrapped Butterfly Networks (WB) (n,k) yang isomorfis dengan graf Cyclic-Cubes.
III. METODE PENELITIAN
3.1 Waktu dan Tempat Penelitian
Penelitian ini dilakukan pada semester genap tahun ajaran 2011-2012 bertempat di jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.
3.2Metode Penelitian
Berikut ini adalah langkah atau tahapan dalam melakukan penelitian ini yang dilakukan oleh penulis sehingga penelitian yang dilakukan dapat berjalan dengan terstruktur dan terarah.
1. Langkah pertama dalam melakukan penelitian ini adalah mengumpulkan referensi (buku-buku) yang berhubungan dengan penelitian.
2. Menjelaskan definisi-definisi, teorema, serta memberikan contoh-contoh beberapa istilah yang digunakan dalam penelitian ini.
3. Merepresentasikan beberapa bentuk graf Wrapped Butterfly Networks (WB) (n,k) untuk dan .
5. Mendiskusikan bentuk graf Wrapped Butterfly Networks (WB) (n,k) yang isomorfis dengan graf Cyclic-Cubes dengan menggunakan teorema berikut:
Teorema 3.3 isomorfis dengan WB (n,k) Bukti:
Untuk setiap vertex pada graf WB (n,k), didefinisikan fungsi pemetaan V(WB(n,k)) pada V( ) mengikuti sebagai berikut:
Sehingga, jelas bahwa adalah fungsi bijektif.
Misalkan dan adalah vertex yang berbeda pada WB (n,k). Kemudian dan adalah dua vertex yang berbeda pada mengikuti sebagai berikut:
. Sehingga . Sama
halnya dengan juga berimplikasi dengan (Hsing dan Kuan Lin, 2009).
6. Menyimpulkan hasil penelitian sesuai dengan tujuan penelitian yang dilakukan.
Langkah-langkah penelitian ini dapat digambarkan dalam diagram alir sebagai berikut:
Studi Literatur
Menjabarkan definisi, teorema dan contoh
Menentukan Jenis Graf
Menjelaskan dan mendefinisikan isomorfis graf
Menjelaskan tentang Cyclic-Cubes Mulai
Menjelaskan tentang Wrapped Butterfly Networks (WB) (n,k)
Selesai
II. TINJAUAN PUSTAKA
Dalam bab ini akan dijelaskan beberapa pengertian tentang graf, isomorfis graf, Cyclic-Cubes, Wrapped Butterfly Networks (WB) (n,k) dan beberapa istilah yang
berkaitan dengan bahasan dalam penelitian ini. Hal mendasar yang harus diketahui dan difahami untuk menunjang penelitian ini adalah pengertian graf. Dalam suatu referensi dijelaskan bahwa graf didefinisikan sebagai berikut:
Definisi 2.1 Graf G = (V,E) terdiri dari objek V = yang disebut vertex (titik) yang tidak kosong, dan objek E = yang unsur-unsurnya disebut edge (garis) yang boleh kosong, sehingga setiap edge diidentifikasi dengan pasangan ( , ) dari vertex. Vertex , berhubungan dengan edge disebut vertex akhir dari . Representasi paling umum dari graf adalah dengan cara diagram, dimana vertex direpresentasikan sebagai titik dan setiap edge sebagai garis yang menghubungkan vertex (Deo,1989).
Gambar 1. Graf Lengkap
Gambar 2. Graf Bipartite
Gambar 3. Graf Kubus
Gambar 4. Graf Euler a1
a4 a3 a2
Dari semua graf tersebut ada yang memiliki bentuk yang kongruen atau isomorfis antara satu dengan yang lainya. Dalam geometri, dua bangun atau bidang dikatakan ekuivalen (dan disebut dengan kongruen) jika keduanya memiliki ciri-ciri atau sifat yang sama. Begitupun, dua graf dikatakan ekuivalen (dan disebut isomorfis) jika keduanya memiliki ciri-ciri yang sama pada istilah dalam teori graf. Dua graf G dan G* dikatakan isomorfis jika ada korespondensi 1-1 antara vertex dari kedua graf tersebut dan antara edge dari kedua graf tersebut sehingga terjadi hubungan.
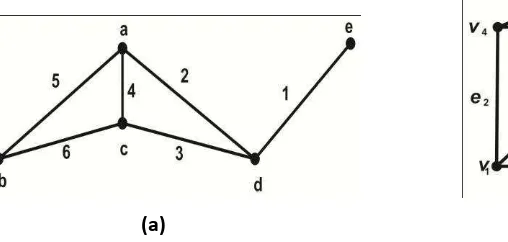
Gambar 5. Contoh dua graf yang isomorfis
Sebagai contoh, dua graf pada Gambar 1 adalah isomorfis. Korespondensi antara dua graf adalah: vertexs a,b,c,d, dan e berkoresponden dengan , , , , dan
. Edges 1,2,3,4,5, dan 6 berkoresponden dengan , , , , , dan . Hal tersebut di atas dapat dibuktikan dengan definisi dari isomorfis dari dua graf harus memiliki:
1. Jumlah vertex yang sama. 2. Jumlah edge yang sama.
3. Mempertahankan adjacency dari setiap vertex. (Deo,1989).
Dalam buku yang lain disebutkan bahwa isomorfisme dari G ke H adalah fungsi memiliki jumlah edge yang berbeda untuk graf yang berbeda pula. Misal G adalah graf tanpa loop dan v adalah vertex dari graf G. Degree dari v adalah jumlah edge yang bertemu (menempel) pada v dan dinotasikan dengan deg v (Wilson dan Watkins,1990).
Dalam teori graf ada istilah graf tertutup atau yang biasa disebut dengan circuit. Untuk memahami tentang circuit ada istilah walk dan path yang harus dipahami. Walk didefinisikan sebagai urutan berhingga dari vertex dan edge, dimulai dan
diakhiri dengan vertex, sehingga setiap edge adalah terjadi dengan vertex sebelumnya dan mengikutinya. Tidak ada edge muncul lebih dari satu kali dalam walk. Hal yang mungkin terjadi dalam walk adalah dimulai dan diakhiri dengan
vertex yang sama, walk yang demikian disebut dengan walk tertutup. Suatu walk
yang tidak tertutup disebut dengan walk terbuka.
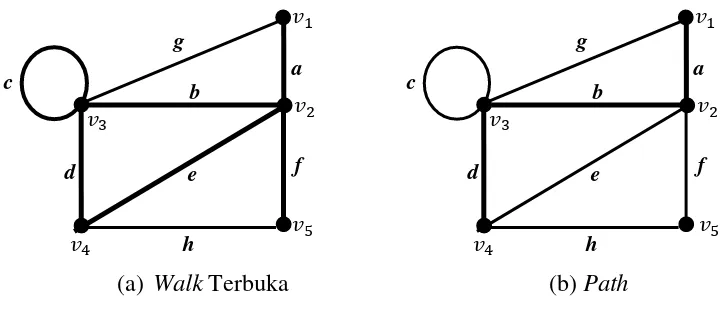
Path adalah walk terbuka yang tidak ada vertex yang dilalui lebih dari satu kali.
Circuit adalah suatu walk tertutup yang tidak mempunyai pengulangan vertex
(a) Walk Terbuka (b) Path Gambar 6. Contoh Walk dan Path
Berikut ini akan diberikan contoh graf yang merupakan circuit.
Gambar 7. Tiga circuit yang berbeda
Dua vertex yang saling berhubungan disebut bertetangga atau adjacent.
Jika e = {u,v} adalah suatu garis yang menghubungkan titik u dan v pada graf G, maka titik u disebut bertetangga (adjacent) dengan titik v dan garis e menempel (incidence) pada u dan v (Lipschutz and Lipson,2002).
Graf memiliki keunikan dan keragaman bentuk dan jenisnya. Contohnya, dalam penjabaran sebelumnya telah dijelaskan graf circuit. Namun, ada juga graf yang tidak mengandung circuit yaitu pohon atau tree. Pohon (tree) adalah graf terhubung yang tidak mengandung circuit. Dilihat dari definisi pohon (tree) maka pohon (tree) tidak memiliki loop atau garis paralel (karena keduanya element circuit). Tree dengan satu vertex disebut null tree (tree tanpa simpul) (Deo, 1989).
Gambar 9. Contoh tree dengan vertex 1,2,3, dan 4
Suatu tree T disebut sebagai spanning tree dari graf terhubung G jika T adalah subgraf dari G dan T mengandung semua vertex dari graf G.
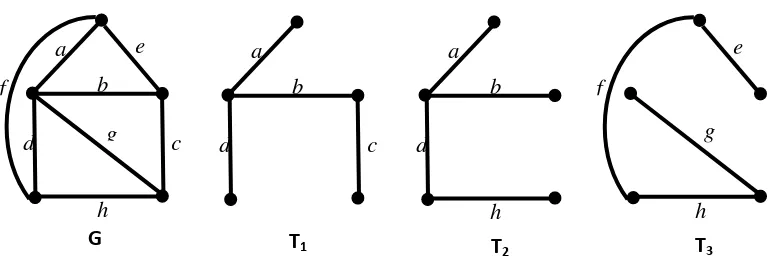
Gambar 10. Graf dan 3 Spanning Tree.
Setiap graf terhubung memiliki paling sedikit satu spanning tree. Edge pada suatu spanning tree T disebut dengan branch. Edge dari graf G yang tidak terdapat pada
spanning tree disebut chord. Pada gambar 10, untuk graf G dan spanning tree T1
maka edge a,b,c dan d adalah branch dan edge e,f,g dan h adalah chord. Untuk graf G dan spanning tree T2, edge a,b,d dan h adalah branch dan edge c,e,f, dan g
adalah chord. Untuk graf G dengan spanning tree T3, e,f,g dan h adalah branch
dan edge a,b,c dan d adalah chord. Jumlah branch adalah rank dan jumlah chord adalah nullity (Deo, 1989).
Selain dari istilah-istilah yang telah diuraikan sebelumnya, ada jenis graf yang unik dalam segi bentuk dan nama yang dimiliki seperti graf Cyclic-Cubes, Wrapped Butterfly Networks (WB) (n,k) seperti yang telah disebutkan di
sebelumnya.
Definisi 2.2 Graf Cyclic-Cubes didefinisikan sebagai graf yang memiliki vertex dan setiap vertex direpresentasikan dengan n-bit vektor, yang merupakan
permutasi siklik dari untuk . Dengan kata lain, vertex di dapat dituliskan sebagai berikut:
Untuk mendefinisikan edge pada graf , pertama akan didefinisikan fungsi untuk setiap , pemetaan onto kepada dirinya sendiri, sesuai dengan definisi berikut ini:
Setiap adalah fungsi bijektif karena dipetakan pada dirinya sendiri. Setiap vertex mempunyai pasangan vertex dan untuk semua
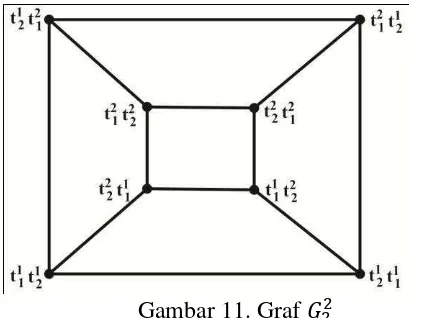
. Contohnya pada graf , vertex akan memiliki pasangan vertex , , , dan (Hsing dan Kuan Lin, 2009).
Definisi 2.2 yang telah dijabarkan sebelumnya dapat digunakan untuk menggambar graf Cyclic-cubes.
Berikut ini adalah salah satu contoh bentuk graf Cyclic-cubes,
Definisi 2.3 Graf Wrapped Butterfly Networks (WB) (n,k) didefinisikan sebagai graf yang mempunyai vertex dan setiap vertexnya direpresentasikan dengan (n-1)-bit vektor dimana dan untuk semua .
V. KESIMPULAN DAN SARAN
5.1 Kesimpulan
Dari pembahasan yang telah dilakukan dapat disimpulkan sebagai berikut: 1. Diperoleh bentuk-bentuk graf Wrapped Butterfly Networks (WB) (n,k)
dan graf cyclic-cubes dengan nilai k = 2 dan .
2. Pasangan graf Wrapped Butterfly Networks (WB) (n,k) dan graf cyclic-cubes yang isomorfis adalah , , , dan .
5.2 Saran
BENTUK-BENTUK ISOMORFISME
GRAF WRAPPED BUTTERFLY NETWORK DAN GRAF CYCLIC-CUBES
Oleh
RIRIN SEPTIANA
Skripsi
Sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana Sains
Pada
Jurusan Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
MENGESAHKAN
1. Tim Penguji
Ketua : Dra. Wamiliana, M.A., Ph.D. ………
Sekretaris : Fitriani, S.Si., M.Sc. ………
Penguji
Bukan Pembimbing : Ahmad Faisol, S.Si., M.Sc. ………
2. Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Prof. Suharso, Ph.D.
NIP. 19690530 199512 1 001
PERSEMBAHAN
Satu persembahan kecil untuk kedua orang tua, Bapak Waimin dan Ibu Ranem, kakang
Sugino beserta keluarga, mbak Suprihatin beserta keluarga, mbak Sulis beserta keluarga,
dan kepada seluruh pelaku dakwah di Universitas Lampung yang telah memberikan
segalanya untuk terselesaikan karya ini atas izin Allah SWT, semoga memberi manfaat
Judul Skripsi : BENTUK-BENTUK ISOMORFISME GRAF WRAPPED BUTTERFLY NETWORKS DAN CYCLIC-CUBES
Nama Mahasiswa : Ririn Septiana Nomor Pokok Mahasiswa : 0817031050
Jurusan : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam
MENYETUJUI
1. Komisi Pembimbing
Dra. Wamiliana, M.A., Ph.D. Fitriani, S.Si., M.Sc.
NIP. 19631108 198902 2 001 NIP. 198406272006042001
2. Mengetahui
Ketua Jurusan Matematika
MOTTO
“Wahai Orang
-orang yang beriman! Jika kamu menolong
agama Allah, niscaya Dia akan menolongmu dan meneguhkan
kedudukanmu”
(Qs. Muhammad:7)
“Maka sesungguhnya bersama kesulitan ada kemudahan,
sesungguhnya bersama kesulitan ada kemudahan”
(Qs. Asy-Syarh:5-6)
“Barangsiapa merintis jalan mencari ilmu maka Allah akan
memudahkan baginya
jalan ke syurga”
BENTUK-BENTUK ISOMORFISME
GRAF WRAPPED BUTTERFLY NETWORK DAN GRAF CYCLIC-CUBES
(Skripsi)
Oleh
RIRIN SEPTIANA 0817031050
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
RIWAYAT HIDUP
Penulis adalah bungsu dari empat bersaudara dari pasangan Bapak Waimin dan Ibu Ranem yang dilahirkan pada tanggal 07 September 1989 di Simpang Agung, Kecamatan Seputih Agung, Lampung Tengah.
Penulis memulai pendidikan formal di TK Pancabakti Simpang Agung pada tahun 1996. Kemudian pendidikan tingkat dasar dilalui dan diselesaikan di SD Negeri 2 Simpang Agung pada tahun 2002, kemudian penulis melanjutkan pendidikan tingkat menengah di SMP Negeri 1 Seputih Agung dan diselesaikan pada tahun 2005 dan menyalesaikan pendidikan sekolah tingkat atas pada tahun 2008 di SMA Negeri 1 Terbanggi Besar.
SANWACANA
Puji syukur kepada Allah SWT atas izin dan ridho-Nya penulis dapat menyelesaikan skripsi ini. Shalawat serta salam atas Nabi Muhammad SAW, tauladan terbaik sepanjang masa.
Pada proses penyusunan skripsi ini, penulis memperoleh banyak dukungan, kritik, dan saran yang membangun sehingga skripsi ini mampu penulis selesaikan. Untuk itu penulis ingin mengucapkan terima kasih kepada :
1. Ibu Dra. Wamiliana, M.A., Ph.D., selaku dosen pembimbing utama yang telah meluangkan waktu dari padatnya kesibukan beliau untuk membimbing dan mengoreksi, hingga skripsi ini selesai.
2. Bapak Fitriani, S.Si., M.Sc., selaku dosen pembimbing pembantu yang telah banyak membantu dan memberikan pengarahan dalam proses penyusunan skripsi ini.
3. Bapak Ahmad Faisol, S.Si., M.Sc., selaku dosen penguji bukan pembimbing yang memberi penulis masukan dan saran.
4. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D., selaku Ketua Jurusan Matematika FMIPA Universitas Lampung.
5. Bapak Amanto, M.Si., selaku pembimbing akademik.
x 8. Bapak, Ibu, Kakang beserta keluarga, Mbak Suprihatin beserta keluarga, Mbak Sulis beserta keluarga, yang telah memberikan dukungan secara finansial dan moril, doa yang tiada putus, nasihat dan semangat yang sangat membantu selama penyusunan skripsi.
9. Anike, Tiyul temen seperjuangan di kosan, Lisa, Mila, Mira, Marlina, Isna,
Ichi, Ma’rufah, Nuy, Ivip, Tika, Diah, Darwis dan temen-temen seangkatan
lainya yang tidak bisa disebutkan semua, trimakasih atas do’a, dukungan,
kritik dan saran serta kebersamaan yang telah diberikan.
10. Keluarga Besar ROIS FMIPA periode 2010-2011, Bu Wak, Wo Lisa, Teteh Tanti, Devi, Ningrum, Umi Okta, Dewi, Tiwi, Anike, Wahyu, Alan, Darwis, Endrik, Agus, Harjono, Edi, Imam, Bang Febri, dan seluruh Anggota bidang dan biro yang telah memberikan ukhuwah dan pelajaran hidup.
11. Keluarga Besar BEM FMIPA Kabinet “Bersatu dan Bangkit”, Alan, Usman,
Annalia, Edi, Irke, Eka Sulpin, Ani, Zahra, Firda, Sule, Ilfa, Udin, Pipin, Rifky, Ruri, ST, Ariyanti, dan seluruh pengurus yang telah memberikan semangat dan kekeluargaan dari hati.
12. Semua pihak yang telah membantu selama ini, yang tidak dapat disebutkan satu persatu.
Bandar Lampung, Januari 2013 Penulis