ANALISA THREE DIMENSIONAL BANGUNAN SINGLE STORY
YANG MENGGUNAKAN MULTY FRICTION PENDULUM
SYSTEM PADA STRUKTUR
TESIS
Oleh
ANDREAS MULIANTA SARAGIH
057016004/TS
SEKOLAH PASCASARJANA
UNIVERSITAS SUMATERA UTARA
MEDAN
ANALISA THREE DIMENSIONAL BANGUNAN SINGLE STORY
YANG MENGGUNAKAN MULTY FRICTION PENDULUM
SYSTEM PADA STRUKTUR
TESIS
Untuk Memperoleh Gelar Magister Teknik dalam Program Studi Teknik Sipil
pada Sekolah Pascasarjana Universitas Sumatera Utara
Oleh
ANDREAS MULIANTA SARAGIH
057016004/TS
SEKOLAH PASCASARJANA
UNIVERSITAS SUMATERA UTARA
MEDAN
Telah diuji pada
Tanggal 9 Agustus 2008
PANITIA PENGUJI TESIS
Ketua : Dr. Ing. Hotma Panggabean
Anggota : 1. Ir. Daniel R. Teruna, MT
2. Prof. Dr. Ing. Johannes Tarigan
3. Prof. Dr. Ir. Bachrian Lubis, M.Sc
Analisa Three- Dimensional Bangunan Single Story yang Menggunakan Multy Friction Pendulum System pada Struktur adalah analisa 3 dimensi dengan 2 arah gerakan horijontal dan 1 arah rotasi bangunan lantai 1, dimana MFPS bergerak dengan gesekan bila terjadi gempa.
ABSTRAK
Analisa 3 dimensi dimodelkan dengan metode numerik pada struktur yang menggunakan MFPS dari perhitungan bearing sampai struktur lantai 1.
Analisa 3 dimensi menggunakan teknik solusi Metode New Mark’s , karena metode ini digunakan untuk analisa non linear dan struktur mempunyai damping yang tidak proposional.
Pada contoh kasus struktur dimodelkan 3 dimensi dengan 12 elemen batang yang dibebani beban tetap dan beban Gempa Elcentro diselesaikan dengan SAP 2000 versi 10 diperoleh perbedaan analisa sumbu x pada waktu (t) = 0.16888 detik, beban hidup pada lantai 1 = 3 000 kgf/m dan pada base = 1 500 kgf/m adalah:
Tanpa base isolator yaitu:
Perpindahan antar lantai/ inter story (u1 – ub) = - 3.24 – 0 = - 3.24 cm (arah ke kiri) Kecepatan bangunan (ú1 – úb) = -5.2488 cm/det (arah ke kiri) Percepatan bangunan ( 1 – b) = -11.2488 cm/det² (arah ke kiri)
Dengan Multi Fricyion Pendulum System yaitu:
Perpindahan antar lantai (u1 – ub) = - 0. 0233 – 0. 0234 = - 0. 0467 cm (arah ke kiri) Kecepatan bangunan (ú1 – úb) = -0.00109 cm/det (arah ke kiri)
Percepatan bangunan ( 1 – b) = -3.4 E-05 cm/det² (arah ke kiri)
Jadi diambil kesimpulan bahwa Gaya Gempa Elcentro di reduksi oleh Multi Friction Pendulum System pada perpindahan = 98%, kecepatan = 99% , dan percepatan = 99,9%.
ABSTRACT
Analysis of Three- Dimensional one story Multy Friction Pendulum system considering three degrees of freedom at each floor; two perpendicular horizontal motions and in plane rotation, if earthquake come.
Analysis of Three- Dimensional with Numeric Methode formulas Model of Multy Friction Pendulum System structure will be calculate from bearing to first floor structure.
Analysis of Three- Dimensional used New Mark’s Methode for solution, because this methode used non linear analysis and structure has damping unproporsional.
In example cases of model three dimensional strucuture with 12 elemen and constant load and Elcentro Earthquake load will be finish with SAP 2000 version 10 can get of different analysis -x – axis of time (t) = 0.16888 second, live load fisrt floor = 3000 kgf/m and base 1500 kgf/m :
Displacement inter story (u1 – ub) = - 3.24 – 0 = - 3.24 cm (left)
Unbase isolator :
Building velocity (ú1 – úb) = -5.2488 cm/sec (left) Building acceleration ( 1 – b) = -11.2488 cm/sec² (left)
Multi Friction Pendulum System :
Displacement inter story (u1 – ub) = - 0. 0233 – 0. 0234 = - 0. 0467 cm (left) Building velocity (ú1 – úb) = -0.00109 cm/sec(left)
Building acceleration ( 1 – b) = -3.4 E-05 cm/sec² (left)
Solution of Multy Friction Pendulum System can reduce Elcentro earthquake from displacement = 98%, velocity = 99% , and acceleration = 99,9%.
K A T A P E N G A N T A R
Dengan memanjatkan Puji dan syukur kehadirat Tuhan yang Maha Esa atas
segala berkat dan rahmat-Nya maka dapatlah saya menyelesaikan laporan Thesis ini.
Adapun Thesis ini dengan judul “ Analisa Three- Dimensional Bangunan
Single Story yang Menggunakan Multy Friction Pendulum System pada
Struktur (Literatur)”.
Multy Friction Pendulum System telah hadir dengan metode pekerjaan yang baik
sebagai desain resistan akan gempa dari struktur- struktur. Dan dengan Multy Friction
Pendulum System bangunan mampu mereduksi gempa sampai 80%, sehingga
bangunan tidak mempunyai kerusakan yang berarti pada waktu gempa terjadi. Struktur
three dimensional tidak dapat dimodelkan dengan aplikasi analisa satu dimensional,
kemudian secara kompleks analisa tiga dimensional haruslah dikerjakan yang akan
ditunjukan dalam tesis ini.
Dalam proses penulisan dan pelaksanaan tesis ini banyak pihak yang telah
turut menyumbang pikiran, saran, motivasi, material dan spiritual, untuk itu penulis
tidak lupa menyampaikan terima kasih yang sebesar- besarnya kepada:
1. Bapak DR. Ing. Hotma Panggabean, sebagai dosen pembimbing I saya, yang
telah banyak meluangkan waktu membimbing dan menyelesaikan tesis ini.
2. Bapak Ir. Daniel Rumbi Teruna, MT sebagai Dosen Pembimbing II saya, yang
3. Bapak Dr. Ir. Roesyanto, MSCE, selaku Ketua Program Studi Magister Teknik
Sipil PPs. Universitas Sumatera Utara.
4. Bapak Ir. Rudi Iskandar, MT, selaku Sekretaris Program Studi Magister
Teknik Sipil PPs. Universitas Sumatera Utara
5. Ibu Prof. Dr. Ir. T. Chairun Nisa B, M. Sc selaku Direktur Pascasarjana
Universitas Sumatera Utara
6. Bapak Prof. Chairuddin P. Lubis, DTM & H. Sp. AK selaku Rektor
Universitas Sumatera Utara
7. Seluruh dosen dan staf pengajar Magistrer Teknik Sipil Universitas Sumatera
Utara
8. Drs. Johannes Djamurah Saragih (+) dan ibu saya Rosalina Dolan Br. Purba
yang selalu mendorong dan memberikan motivasi
9. Sahabat- sahabat satu kelas dan sahabat yang lain di Jurusan Struktur
Bangunan dan Program Pasca Sarjana Universitas Sumatera Utara
Penulis sadar bahwa tesis ini masih jauh dari sempurna, sehingga kritik dan
saran diharapkan. Penulis juga berharap semoga laporan tesis ini dapat bermanfaat
bagi perkembangan ilmu pengetahuan.
Medan, Agustus 2008
Penulis
Andreas Mulianta Saragih
RIWAYAT HIDUP
A. DATA PRIBADI
Nama : Andreas Mulianta Saragih
Tempat/Tgl. Lahir : Lubuk Pakam/ 11 September 1970
Alamat : Jl. Pantai Labu no. 47 Dsn. Kediri Kec. Beringin
Deli Serdang, 20552, Sumatera Utara
Agama : Katholik
Anak ke - : 4
Jenis Kelamin : Laki- laki
B. RIWAYAT PENDIDIKAN
- SD RK Serdang Murni Lubuk Pakam 1977 – 1983
- SMPN 1 Lubuk Pakam 1983 – 1986
- SMA RK St. Thomas 1 Medan 1986 – 1989
- Fakultas Teknik Jurusan Teknik Sipil
Universitas Darma Agung Medan 1997 – 1999
- Magister Teknik Sipil Program Pasca Sarjana USU 2005 – 2008
C. RIWAYAT PEKERJAAN
- Perencana dan Pelaksana Gudang di Lubuk Pakam 1999
- Perencanaan Guest House di Cikini Jakarta Pusat 2001
- Perencana dan Pelaksana Jembatan Kecil di Lubuk Pakam 2002
- Perencana dan Pelaksana Gruoting Bak Penyimpanan Air
di Lubuk Pakam 2003
- Perencana dan Pelaksana Rumah Tinggal di Tanjung Sari Medan 2004
- Perencana danPelaksana Renovasi Rumah Tinggal
di Simalingkar Medan 2005
- Perencana dan Pelaksana Dinding Penahan Tanah
di Lubuk Pakam 2006
- Perencana dan Pelaksana Gudang Penyimpanan di Lubuk Pakam 2007
- Dosen Politeknik Mandiri Bina Prestasi (MBP) Medan 2005-2008
DAFTAR ISI
ABSTRAK ……….……….... i
ABSTRACT ………..……….…. ii
K A T A P E N G A N T A R ... iii
RIWAYAT HIDUP ... v
DAFTAR ISI ... vii
DAFTAR TABEL ... x
DAFTAR GAMBAR ……….………. xii
DAFTAR NOTASI ………. xv
1. PENDAHULUAN ... 1
1. 1. Latar Belakang Masalah ... 1
1.2. Tinjauan Literatur... ... 2
1.3. Studi Banding ... 7
2. LANDASAN TEORI... 9
2. 1. Rumus Single Degree Of Freedom………..……….… 9
2. 2. Struktur SDOF Tanpa Redaman……….………. 11
2. 3. Struktur SDOF Dengan Redaman ……….…………..… 12
2.4. Analisa Sistem - Sistem Linear Single Degree Of Freedom 16
2.5. Analisa Getaran Bebas ……….………….. 16
2. 7. Multi Degree Of Freedom.……….… 28
2. 8. Analisa Single Story Linear... 31
3. ANALISA SINGLE STORY NON- LINEAR ... 58
3.1. Metode Hilber’s ... 59
3.2. Metode Newmark’s ß ... 61
3.3. Prakiraan Solusi ... 73
4. ANALISA DASAR MATRIKS MASSA DAN KEKAKUAN ... 77
4.1. Determinan Matriks Massa ... ... 77
4.2. Determinan Matriks Kekakuan ... 86
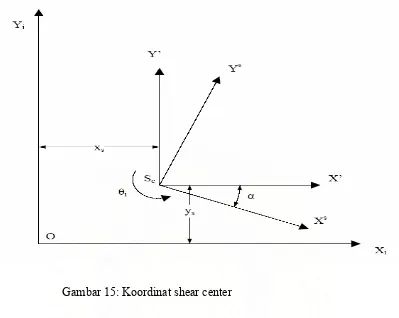
4.3. Determinan Pada Lokasi Shear Center ... .. 93
4.4. Friction (Gesekan)... 102
4. 4. 1. Data – data Bahan Sebagai Selimut Bearing ... 103
4.5. Aplikasi Pada Struktur Single Story ... 106
4.6. Kriteria Perkerasan ... 114
4.7. Prosedur Solusi ... 123
4. 8. Analisa Three Dimensional Bangunan Single Story
Dengan Menggunakan Program SAP 2000 Versi 10…………. 126
4. 9. Analisa Three Dimensional Bangunan Single Story Dengan Base Isolator Multi Friction Pendulum Sistem Dengan Beban Gempa Elcentro Dengan Menggunakan Program SAP 2000 Versi 10 ……… 144
4.10. Grafik ... 165
5. KESIMPULAN DAN SARAN... 174
DAFTAR TABEL
Nomor Judul Hal
1 Assembled Joint Masses ……… 135
2 Base Reactions………. 135
3 Case - Static 1 - Load Assignments………... 135
4 Combination Definitions………... 136
5 Connectivity – Frame……….. 136
6 Element Forces – Frames………... 136
7 Element Joint Forces – Frames……….. 139
8 Frame Loads – Distributed………. 140
9 Frame Section Assignments……… 140
10 Function - Time History ………. 141
11 Joint Coordinates………. 142
12 Joint Displacements………. 143
13 Joint Reactions………. 143
14 Material List 2 - By Section Property……….. 143
15 Assembled Joint Masses……….. 154
16 Base Reactions……… 154
17 Case - Static 1 - Load Assignments………. 154
18 Combination Definitions………. 155
19 Connectivity – Frame……….. 155
21 Element Deformations – Links……… 156
22 Element Forces – Frames……… 156
23 Element Forces – Links……… 159
24 Element Joint Forces – Frames………. 159
25 Element Joint Forces – Links……… 160
26 Frame Loads – Distributed……… 160
27 Function – Time History – User………. 160
28 Joint Coordinates……… 162
29 Joint Displacements……… 163
30 Joint Reactions……… 163
31 Link Property Definitions 08 - Sliding Isolator…………. 163
32 Material List 2 - By Section Property……… 163
33 Material Properties 04 - Design Concrete……….. 163
DAFTAR GAMBAR
Nomor Judul Hal
1 Sistem SDOF ideal……… 10
2 Dampak damping pada getaran bebas……… 14
3 Respon Getaran Bebas Tanpa Redaman……… 18
4 Gambaran Vektor Rotasi dari Getaran Bebas……… 19
5 Respon Getaran Bebas dengan Damping Kritis……… 20
6 Respon beban harmonik dari inisial kondisi pada situasi steady state………. 24
7 Respon beban harmonik dari inisial kondisi pada situasi transient……….. 24
8 Respon beban harmonik dari inisial kondisi pada situasi total R(t)………. 24
9 Derivative dari Integral Duhamel (tanpa redaman)………… 26
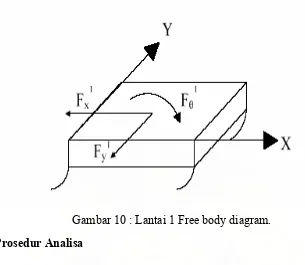
10 Lantai 1 Free body diagram... 32
11 Superstructure Free Body Diagram... 33
12 Metode Percepatan Linear... 42
13 Sistem Koordinat... 79
14 Sistem Koordinat Matriks Kekakuan... 86
15 Koordinat shear center... 94
17 Skema Perkerasan Kinetik... 116
18 Frame Section Assignment……….. 126
19 Frame Loads – Distributed……….. 127
20 Axial Force Diagram (Modal) – Mode 1- Periode 0, 21163. 128
21 Joint Reactions (Modal) – Mode 1- Periode 0,2163………. 129
22 Longitudinal Reinforcing Area………. 130
23 Displacement Tampak 2 Dimensi Sumbu X……… 131
24 Displacement Tampak 2 Dimensi Sumbu Y……… 132
25 Frame Section Assignment……… 144
26 Local Axes……… 145
27 Conectivity Multy Friction Pendulum System………. 146
28 Frame Loads – Distributed………..…………. 147
29 Axial Force Diagram - mode 1- Periode 3,38840…………. 148
30 Longitudinal Reinforcing Area………. 149
31 Displacement Tampak 2 Dimensi pada Sumbu -X………. 150
32 Displacement Tampak 2 Dimensi Pada Sumbu –Y……….. 151
33 Grafik Perpindahan pada Sumbu – X... 165
34 Grafik Perpindahan pada Sumbu – Y... 166
35 Grafik Perpindahan pada Sumbu Rotasi... 167
36 Grafik Kecepatan Bangunan pada Sumbu – X... 168
37 Grafik Kecepatan Bangunan pada Sumbu – Y... 169
39 Grafik Percepatan Bangunan pada Sumbu – X... 171
40 Grafik Percepatan Bangunan pada Sumbu –Y... 172
DAFTAR NOTASI
: Solusi Parameter Pertama di dalam parameter (2-31)
: Solusi Parameter Pertama di dalam persamaan (2-32)
: Matriks damping pada bearing
: Matriks damping pada lantai ke- i
:Karakteristik Konstan pada saat transisi dari kelakuan elastis kePlastis.
: Vektor percepatan pada bearing
: Vektor kecepatan pada bearing
: Vektor displacement pada bearing
: Vektor percepatan selama gempa
: Daerah percepatan vertical selama gempa
: Vektor percepatan relative lantai ke –i pada bearing
: Vektor kecepatan dari lantai ke- i relative pada bearing
:Vektor Displacement untuk lantai ke -i relative pada bearing
: Kenaikan elastis displacement
: Kenaikan plastic displacement
: Kenaikan total Gaya
: Kenaikan translasi pada permukaan hasil
: Parameter plastis ke persamaan (C-18)
: Parameter perkerasan pada persamaan (C-25)
: Eccentricity (jarak perhitungan ) diantara dan
: Eccentricity (jarak perhitungan) diantara dan
: Gaya inersia di –n pada lantai i
: Gaya perlawanan elastis di- n pada lantai i
: Gaya damping di- n pada lantai ke- i
F
Fin : Gaya gesek di dalam -n- pada lantai ke- i
: Eccentricity(jarak perhitungan)pada lantai ke-i, diantara dan
: Eccentricity(jarak perhitungan)pada bearing, diantara dan
: Masa pada titik tengah dari lantai i (b untuk lantai bearing, 1
untuk lantai pertama)
: Percepatan vertical selama gempa
: Matriks kekakuan untuk level bearing.
: Bearing Kekakuan elastis
: Matriks kekakuan untuk lantai i
: Matrix massa untuk lantai ke- i
: Matriks massa total, pertama diberikan di dalam persamaan (2-7)
: Massa dari lantai ke- i
: Vektor normal pada permukaan hasil
: Sumbu perubahan pada koordinat asal
: Penggunaan matriks sebagai solusi untuk model percepatan tambahan.
: Penggunaan vector sebagai solusi untuk model percepatan tambahan.
: Vektor tanda dari nilai absolute pada kecepatan bearing
: Waktu awal
: Displacement dari massa ke-i, di titik tengah sepanjang
: Gaya potong instant pada bearing di dalam urutan ke- i
: Gaya pada urutan ke- i
: Displacement dari massa ke-i dititik tengah sepanjang
: Displacement untuk lantai ke- i sepanjang
: Displacement untuk lantai ke- i sepanjang
: Model vector percepatan lantai ke-i
: Model vector kecepatan lantai ke- i
: Model vector displacement lantai ke- i
: Model vector percepatan superstructure
: Vektor translasi pada permukaan hasil
: Penggunaan parameter Hilber’s metode analisa non-linear
(Hilber, 1977)
: Orientasi kekakuan dari element j pada lantai ke- i
: Parameter solusi superstructure
: Penggunaan parameter Newmark’s untuk metode analisa non-linear
: Penggunaan parameter Newmark’s untuk metode analisa non-linear
(Hilber, 1977)
: Gaya residual solusi non-linear
: Interval waktu
: Rotasi (torsi) displacement dari pusat massa diteruskan
: Koefficient gesekan
: Damping ratio pada lantai ke- i mode ke- n
: Waktu, dari awal sampai akhir dari single time step
: Model matriks lantai ke-i
: Model shape j untuk lantai ke- i
: Frekuensi damped dari lantai ke- i di model n
1. PENDAHULUAN
1. 1. Latar Belakang Masalah
Base Isolator adalah salah satu jenis anti gempa yang banyak digunakan untuk
proteksi struktur bangunan dari gempa bumi. Secara umum pada penelitian diperoleh
gambaran gerakan satu- dimensi. Respon struktur tidaklah terbatas pada gerakan satu
dimensi, dan dampak Torsional dari gerakan banyak dimensi mendukung gerakan-
gerakan perpindahan secara horijontal. Suatu struktur tiga dimensi tidak dapat
dimodelkan/ divariasikan dengan analisa satu dimensi; kemudian struktur tiga dimensi
yang kompleks akan di bahas pada penulisan thesis ini.
Multy Friction Pendulum System adalah konsep penting pada teknik gempa.
Khususnya pembahasan Multy Friction Pendulum System adalah proses lebih lanjut untuk
mendesain suatu struktur bangunan yang resistan terhadap gempa bumi. Secara desain
haruslah sangat teliti begitu juga di dalam aplikasi penggunaannya di lapangan; dimana
konsep ini telah dianalisa semenjak base isolator telah ditemukan. Yang penting di dalam
Multy Friction Pendulum System adalah suatu alat yang dapat mereduksi energi gempa
dari bearing yang terletak pada pondasi pada kekakuan yang sangat rendah. Fungsi dari
bearing adalah memperpanjang periode dari struktur, dimana gaya bergerak dan
displacement dari struktur adalah yang direduksi oleh Multy Friction Pendulum System ,
dan struktur bangunan jauh dari kerusakan yang berat.
Salah satu dari struktur bangunan yang menggunakan Multy Friction Pendulum
System di desain secara teliti dan lebih fleksibel dari elemen- elemen struktur, cukup kaku
dan tahan terhadap beban angin yang kencang dan resiatan terhadap amplitudo gaya
gempa horijontal. Bearing- bearing pada Multy Friction Pendulum System memiliki initial
kekakuan yang cukup tinggi dan akan cepat merespon atau mereduksi percepatan gempa
pada struktur.
1.2. Tinjauan Literatur
Ada beberapa literatur dan paper – paper serta buku- buku yang membahas Multy
Friction Pendulum System di dalam struktur. Di mana analisa secara tiga dimensi dari
struktur sekarang ini secara umum di bahas di dalam literatur thesis ini.
James. M. Kelly adalah seorang peneliti yang terkenal penulisannya tentang Base
Isolatore. Bukunya, Earthquake Resistant Design With Rubber (1966), adalah
dari penelitiannya adalah pentingnya efek- efek rotasi dari gaya yang bekerja pada
struktur yang menggunakan base isolator. Bagian ini menganalisa tiga derajat kebebasan
(three degrees of freedom) – x dan - y sebagai gaya horijontal dan derajat kebebasan torsi
(torsional degree of freedom) di dalam permodelan dari struktur. System three degree of
freedom adalah bagian penelitian dari Pan dan Kelly di dalam jurnal Earthquake
Engineering and Structural Dinamics tahun 1983. Metode ini menggunakan sistem three
degree of freedom oleh Kelly dan berbeda di dalam pemaparan pada pembahasan Kelly
yang terfokus pada reaksi tiga model gaya di dalamnya. Formulasi- formulasi ini
dipaparkan dengan reaksi gaya yang divariasikan.
Abe, tahun 2004 dengan beberapa percobaan dan penelitiannya yaitu perilaku
bearing dapat menentukan perilaku bangunan antara lain kekakuan dan berbagai kelakuan/
prilaku langsung dari struktur. Test- test yang dilakukan adalah percobaan beban pada
struktur seperti biasanya pada percobaan waktu perkuliahan, yaitu dengan beban konstan
vertikal dan variabel beban horijontal dilakukan; atau penentuan resistant kelakuan dari
bearing- bearing di bawah pembelokan atau pergerakan yang kecil. Penelitian terus
berkembang yaitu dengan menggunakan permodelan matematik yang sangat menentukan
Dengan memperhatikan Respon struktur pada tahap penelitian, menurut Abe
(2004), dengan menggunakan model pada base dan meneruskan penelitian Ozdemir
(1973) yaitu perilaku bearing dengan permodelannya. Model ini menunjukan suatu
penelitian yang akurat dari kelakuan bearing- bearing dengan pembebanan. Dimana,
model ini sangat spesifik terhadap kondisi beban vertikal yang dilakukan pada bearing
selama percobaan di laboratorium. Penelitian ini dibagi dua bagian beban vertikal , dan
pembebanan lainya dengan penelusuran yang berbeda pula.
Penelitian ini dilanjutkan oleh Abe (2004), yaitu dorongan gaya vertikal yang
memberikan suatu efek reaksi pada bearing yaitu kekakuan dan kerusakan bangunan.
Dampak ini menunjukan bahwa ada respon pada lapisan timah di rubber bearing, yaitu
diantara celah lapisan dari rubber. Dampak itu akan memberikan adanya perubahan
bentuk pada gaya kerusakan dan nilai kekakuan datang lebih stabil, dan tidak banyak gaya
dorongan selama beban vertikal. Seterusnya penelitian memberikan keyakinan adanya
sebuah reaksi diantara pertukaran beban vertikal dan respon dari bearing- bearing. Untuk
kelanjutan penelitian ini, yaitu adanya asumsi percepatan vertikal pada struktur selama
sangat dirahasiakan nilai kecepatan gravitasi, dimana gaya reaksi vertikal mempengaruhi
bearing- bearing dan tidak akan mempunyai dampak yang penting pada bangunan.
Penelitian paper Abe (2004) yaitu penggunaan model base dan meneruskan
penelitian Ozdemir (1973). Penelitian ini akan berguna sekali, yaitu suatu perbedaan
penggunaan formulasi. Ziegler (1959) memodifikasi pekerjaan Prager’s dengan peraturan
perkerasan, dan terus berkembang dengan teori- teorinya yaitu perkerasan kinetik. Teori
ini memperoleh pengembangan dengan modifikasi dan pada penelitian semakin sempurna
pada reaksi gaya perubahan (deformasi) bentuk pada beton prategang. Konsep Ziegler
akan memudahkan penelitian pada waktu pemaparan.
Mostaghel dan Khodaverdian (1988) menuliskan sebuah paper tentang Respon
Dynamic dari Base Isolator Struktur dimana suatu formulasi struktur rangka dari beberapa
sumber formulasi penelitian dituliskan pada paper mereka. Penulisan mereka terfokus
pada sistem Friction Pendulum Base Isolator, dan keterangan mengenai komponen friction
pada perkembangan penulisannya. Penelitian ini mereka tulis dalam suatu makalah yaitu
derajat kebebasan horijontal serta gaya vertikal, dan memperhitungkan efek dari friction
Penelitian seorang Doctor (Ph D) Ahmad El- Hajj (1933), dipublikasikan di
Universitas Pittsburgh (USA), yaitu dasar untuk mengetahui penulisan Multy Friction
Pendulum System. Penulisan rumusan ini diteliti dan sudah mendekati kesamaam dengan
penelitian El- Hajj’s, kemudian jumlah dan koreksi diteliti dan dimodivikasikan dan
selesailah penelitian tersebut. Penelitian ini memberikan banyak pandangan dimensi pada
base isolator, kemudian berkembang dengan adanya gaya horijontal dan gaya rotasi,
kemudian penelitian ini dilanjutkan oleh Pan dan Kelly dengan sebuah paper dengan topik
dimensi base isolator di tahun 1983. Modivikasi Ziegler (1959) tentang teori- teori yang
meneliti persamaan- persamaan, yaitu modifikasi dari formula beton prategang yang
diteliti secara lebih akurat pada gaya reaksi perubahan bentuk pada strutur bangunan.
Penelitian- penelitian respon bearing- bearing yang lain secara akurat yaitu dengan
menggunakan Metode Hilber - yang diperoleh dari Metode NewMark’s -ß . Metode
Hillber’s (1977) dengan modifikasi mempunyai nilai kekakuan dan waktu secara detail
sebagai perkembangan yang aktual dari Respon Struktur.
Penelitian dari Universitas Taichung Taiwan yang dilakukan C. S. Tsai yaitu
membuat suatu base isolator struktur dengan tipe sliding. Penelitiannya dengan membuat
ton. Pada keempat kolomnya dipasang Multi Friction Pendulum System dengan suatu jari-
jari tertentu, kemudian struktur tersebut diberi Gempa Elcentro (USA, 1940), Kobe, Chi-
Chi, dll. Penelitian ini memberi hasil pada bidang base isolator yaitu kegunaan base
isolator yang dapat mereduksi energi gempa pada struktur sampai di atas 70%.
1.3. Studi Banding
Penelitian ini adalah mengambil hasil penelitian dan penulisan dari ahli
sebelumnya dengan kurun waktu yang cukup lama tentang Multy Friction Pendulum
System. Tidak hanya kembali kepada rumus- rumus dan mengembangkan penelitian ini
serta memperhatikan dampak dari gerakan derajat kebebasan Torsional, dan ini terlihat
pada penulisan Kelly, dimana dalam rumusannya diperoleh hasil yaitu komponen-
komponen friction (gesekan) serta analisa- analisa lainnya. Konsep Respon Dinamika
pada Multy Friction Base Isolator Struktur juga diteliti pada penulisan mereka .
Prosedur ini diperlihatkan dalam analisa penelitian Single Story dari Multy
Friction Base Isolator Structure. Dan analisa ini bertambah kompleks dan sulit jika terus
dilanjutkan dan dikembangkan. Begitu juga pada bagian bearing dan bagian lantai
pertama diperoleh hasil analisa yang menarik pada kasus ini, walupun pada kondisi yang
Ada dua prosedur analisa pada Single Story Nonlinear Multy Friction Pendulum
Base Isolator Structure. Analisa pada lantai pertama diasumsikan pada perhitungan
Linear, dengan konsep penulisan Multy Friction Pendulum Base Isolator. Kemudian
analisa pada bagian bearing- bearing adalah analisa Non linear.
Analisa yang lain yaitu dengan mengembangkan dan membentuk multi story
struktur bangunan. Prosedur yang lain yaitu asumsi linear dengan perhitungan waktu pada
superstruktur. Analisa Penggunaan Multy Friction Pendulum System base isolator adalah
suatu prioritas utama dalam topik thesis ini.
Multy Friction Pendulum System base isolator secara komplit tidaklah efektif
untuk menentukan karakteristik dari jenis- jenis gempa bumi, kenyataannya pada
penelitian dengan percobaan- percobaan, yaitu hal yang terpenting di dalam penelitian
adalah mengetahui areal atau wilayah bangunan, serta mengetahui sejarah gempa bumi
dan karakteristik- karakteristik tanah, dan semuanya ini dilakukan sebelum kita
mengerjakan penelitian Multy Friction Pendulum System base isolator pada suatu struktur
2. LANDASAN TEORI
2. 1. Rumus Single Degree Of Freedom
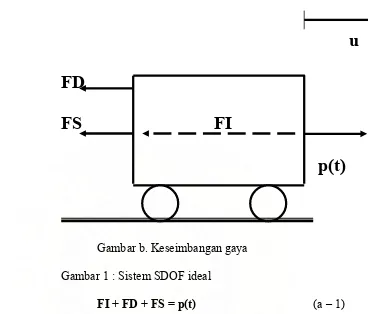
Persamaan gerakan pada gambar (a) adalah memberikan 3 prosedur dan dapat
disimpulkan. Suatu kasus yang simple akan lebih mudah cara penggunaan rumusnya
sebagai ekspresi persamaan dari semua gaya yang bekerja dengan massa. Pada gambar
(b), gaya bekerja dari displacement degree of freedom diaplikasikan kepada beban p(t)
dan kemudian 3 gaya datang dari arah gerakan getaran, gaya inersia (FI), gaya
damping (FD) dan gaya elastis (FS). Persamaan getaran ini adalah ekspresi dari
persamaan gaya- gaya tersebut, yaitu:
u
c
m
p(t)
k
[image:32.619.131.538.347.615.2]
u
FD
FS
FI
p(t)
Gambar b. Keseimbangan gaya
Gambar 1 : Sistem SDOF ideal
FI + FD + FS = p(t) (a – 1)
Kembali pada gaya yang bekerja dari sisi sebelah kiri, persamaan ini yaitu
suatu fungsi dari displacement u atau derivative ; Gaya – gaya bekerja yang positif
akan memberikan pilihan respon dengan displacement negative, tentunya dengan
beban yang positif pula.
Gaya elastis pertama. Ini memberikan hasil dari kekakuan dan displacement.
FS = k u (a – 2)
Sama dengan prinsip Alembert, yaitu Gaya Inersia adalah hasil dari massa dan
percepatan:
[image:33.619.162.530.127.441.2]Jika mekanisme viscous damping adalah suatu asumsi, maka Gaya damping adalah
hasil dari damping konstan c dengan kecepatan.
FD = c ú (a – 4)
Persamaan (a – 2) adalah substitusi ke persamaan (a – 1), maka persamaan gerakan
dari SDOF ini di peroleh yaitu:
m ü + c ú + k u = p (t) (a – 5)
2. 2. Struktur SDOF Tanpa Redaman
Gerakan dari sistem SDF, adalah gambaran dari idealnya single story dengan
batasan pada sistem saat redaman, maka bagian utama dari gaya luar p(t) adalah suatu
gambaran persamaan (a- 5). Dan gaya luar p(t) = 0 memberikan perbedaan persamaan
dari getaran bebas, dimana sistem- sistem dengan damping (c = 0) adalah khusus
untuk :
m ü + k u = 0 (a)
Getaran bebas adalah sistem yang tidak terganggu dari posisi keseimbangan statis
seperti massa pada beberapa displacement u (0) dan velocity ú (0) dengan waktu nol,
kemudian persamaan gerakan itu menjadi:
u = u(0) ú = ú(0) (b)
Ini adalah suatu inisial kondisi, yaitu solusi dari homogeneus, berbeda dengan
persamaan yang menggunakan metode standard (coba dilihat persamaan sebelumnya):
u(t) =
u (0) cos n t + ú (0)n sin n t (c)
n = k/m (d)
Waktu untuk sistem tanpa redaman menjadi komplit dalam satu putaran pada
gerakan bebas yaitu periode alami dari getaran pada sistem, ini kita sebut dengan Tn,
dalam satuan detik. Dan ini adalah suatu relasi dari sirkulasi frekuensi alami pada
getaran, n, dengan satuan radian per detik:
Tn = 2
/
n (e)Pada sistem yang lain menggunakan 1/ Tn yaitu putaran dalam 1 detik. Ini adalah
gerakan frekuensi natural pada getaran yaitu sebagai berikut:
fn
=
1Tn (f)
Satuan dari fn adalah Hertz (Hz) [putaran per detik(cps)];
fn adalah suatu relasi gerakan ke n.
2. 3. Struktur SDOF Dengan Redaman
Gaya luar p(t) = 0 pada persamaan (a – 5) diperoleh persamaan diferensial
dengan getaran bebas pada sistem SDF dengan damping yaitu:
m ü + c ú + k u = 0 (g)
Dengan dibagi massa maka diperoleh hasil yaitu:
ü + 2 n ú + n² u = 0 (h)
= c = c / ccr
(2m n) (i)
Kemudian diperoleh suatu persamaan lagi yaitu:
ccr = 2 m n = 2
√
k m = 2 k/
n (j)Solusi persamaan (g) dari sistem- sistem dengan c < ccr atau < 1 yaitu:
- n t
u (t) = e u (0) cos Dt + ú(0) + n u (0) sin Dt (k)
D
D = n
√
1 - ² (l)Pada persamaan (k) spesial dengan sistem tanpa redaman ( = 0) mulai dari persamaan
(c).
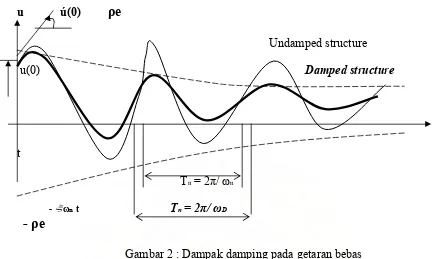
Persamaan (k) pada grafik, akan diperlihatkan suatu respon getaran bebas pada
sistem SDF dengan damping rasio ( = 0. 05 atau 5% ). Pada perbandingan suatu
respon getaran bebas dengan sistem yang sama di luar dampingnya.
u ú(0)
e
Undamped structure
u(0) Damped structure
t
Tn = 2 / n
- n t Tn = 2 / D
- e
Gambar 2 : Dampak damping pada getaran bebas
Periode alami dari getaran kerusakan, TD = 2 / D, adalah suatu reaksi pada periode
natural Tn di luar damping yaitu:
TD = Tn
√ 1 - ² (m)
Amplitudo dari displacement pada sistem tanpa redaman adalah sama pada semua
proses getaran, tetapi sistemnya adalah redaman amplitudo, dan penambahan pada
setiap gerakan dari getaran yaitu :
= [u(0)]² + ú (0) + n u (0) ² (n)
D
Solusi persamaan differensial (h) mendapatkan persamaan yaitu:
st
[image:37.619.98.530.112.371.2]Dengan substitusi diperoleh:
st
( s² + 2 n s + n² ) e = 0 (p)
Dengan pengembangan pada semua nilai t apabila :
s² + 2 n s + n² = 0 (q)
Persamaan (q), yang mana telah diketahui pada persamaan karakteristik, di dapat dua
arah:
s1, 2 = n (- ± i
√
1- ² )Secara umum diperoleh solusi: ( r )
s1t s2t
u (t) = A1 e + A2 e
Dimana dengan substitusi persamaan ( r ) ,maka diperoleh persamaan yaitu :
- i D t i D t -i D t
u (t) = e (A1 e + A2 e ) (s)
Dimana A1 dan A2 menjadi konstan yaitu:
D = n
√
1 - ² (t)Diteruskan dengan fungsi trigonometri yaitu: - i n t
u (t) = e (A cos D t + B sin D t ) (u)
Dimana A dan B adalah konstan sebelum dideterminan. Persamaan ini tampak pada
kesatuan inisial kondisi dengan proses sepanjang garis- garis yaitu :
A = u (0)
B = ú (0) + n u (0) (w)
2.4. Analisa Sistem – Sistem Linear Single Degree Of Freedom
Jika suatu proses penggabungan adalah asumsi gaya pada percepatan üg(t),
kemudian respon dari system SDOF Linear memberikan dukungan pada percepatan
maka diperoleh persamaan:
ü + 2 ú + ² u = - üg (t) (b - 1)
Dimana u adalah displacement massa relatif dengan dukungan untuk bergerak.
2.5. Analisa Getaran Bebas
Pada pembahasan sebelumnya persamaan gerakan dari sistem SDOF diperoleh
suatu kesatuan persamaan yaitu:
m ü (t) + c ú (t) + k u (t) = p (t) (b – 2)
Dengan mempelajari persamaan ini dapat digunakan suatu cara yaitu gambaran respon
dari sistem yang simple. Dimana ini selalu diingat dan diperlihatkan sama dengan
respon koordinat secara umum dari sistem yang kompleks yang telah diulangi pada
sistem SDOF.
Solusi persaman (b – 2) memberi jawaban pertama dari persamaan
homogeneus dengan sisi sebelah kanan adalah nol yaitu:
m ü (t) + c ú (t) + k u (t) = 0 (b – 3)
Menempatkan gerakan- gerakan dengan gambaran gaya terkumpul menjadi nol
dinamakan adalah Free vibration (getaran bebas), yaitu respon getaran bebas ini
diperoleh dari sistem dimana diperoleh suatu hasil saat ini.
u (t) = G e (b – 4) Substitusi pada persamaan (b – 3) adalah:
st
(m s² + c s + k) G e = 0 (b – 5)
st
Setelah dibagi m G e dan dapat mengubah notasi menjadi:
² = k/m (b – 6)
Persamaan (b – 5) menjadi:
s² + (c/m) s + ² = 0 (b – 7)
Nilai s akan memberikan nilai c dari ekspresi ; jadi tipe dari getaran kembali ke
persamaan (b – 4) akan ditunjukan di dalam sistem damping.
2.5.1. Getaran Bebas Tanpa Redaman
Jika sistem diredam, maka c = 0, nilai ini pada s akan memberikan suatu
persamaan pada (b – 7) adalah:
s = ± i
(b – 8)
Respon ini berpengaruh pada persamaan (b – 4) yaitu:
i t - i t
u (t) = G1 e + G2 e (b – 9)
Ada 2 tambahan jawaban dari 2 nilai yaitu s dan konstanta- konstanta G1
dan G2 dengan kembali pada getaran amplitudo. Persamaan (b – 9) dapat diletakan
pada kumpulan gaya yang lain sebagai koreksi pada persamaan – persamaan Euler.
± i t
e = cos t ± i sin t (b – 10)
u (t) = A sin t + B cos t (b – 11)
Pada konstanta A dan B diperoleh dengan penambahan inisial kondisi, sebagai contoh
displacement u (0) dan kecepatan ú (0) pada waktu t = 0, dimana sistem getaran
bebas memiliki nilai inisial. Dengan mudah dapat diperoleh u (0) = B dan ú (0)
= A ; kemudian persamaan (b – 11) kembali:
u (t) = [ú(0) / ] sin t + u (0) cos t (b – 12)
T = 2 /
u(t) ú(0)
u(0) t
/
Gambar 3 : Respon Getaran Bebas Tanpa Redaman
Frekuensi yang kembali ke - f , yaitu selalu kembali diperlihatkan pada
getaran frekuensi yang memberikan :
f = / 2 (b – 13)
Dan perulangan kembali adalah Perioda T,
T = 2 / = 1/f (b – 14)
Dapat diekspresikan pada :
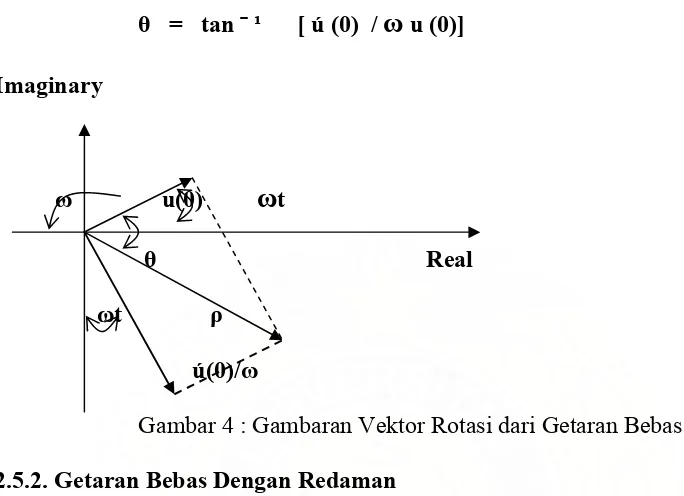
u (t) = cos ( t - ) (b – 15)
Getaran amplitudo adalah:
Pada phase penambahan adalah:
= tan ¯ ¹ [ ú (0) / u (0)] (b – 17)
Imaginary
u(0) t
Real
t
[image:42.619.118.460.140.388.2]ú(0)/
Gambar 4 : Gambaran Vektor Rotasi dari Getaran Bebas
2.5.2. Getaran Bebas Dengan Redaman
Jika damping dipergunakan di dalam suatu sistem, didapat sebuah solusi dari
persamaan (3 – 7) yaitu menjadikan suatu respon sebagai berikut:
s = - c / 2m ± (c / 2m)² - ² (b - 18)
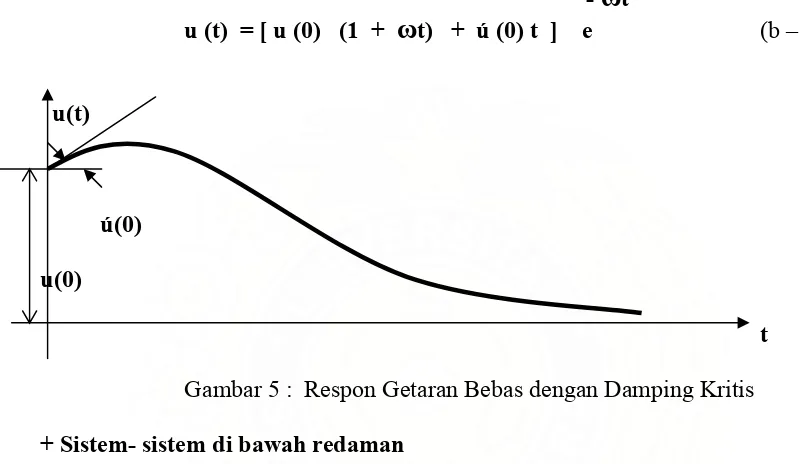
+ Damping Kritis
Jika persamaan (b – 18) adalah kesatuan hasil yang diperoleh menuju nol,
maka c/2m = , kemudian damping kritis dengan nilai Cc adalah:
Cc = 2 m (b – 19)
Kemudian nilai persamaan (b – 18) adalah :
s = - c = - (b – 20)
2m
- t
u (t) = (G1 + G2 t) e (b – 21)
Pada waktu inisial kondisi diperoleh hasil dari persamaan respon damping kritis yaitu:
- t
u (t) = [ u (0) (1 + t) + ú (0) t ] e (b – 22)
u(t)
ú(0)
u(0)
t
Gambar 5 : Respon Getaran Bebas dengan Damping Kritis
+ Sistem- sistem di bawah redaman
Jika redaman dapat melewati batas kritis, maka kembali ke persamaan (b – 19)
yaitu c < 2m dan dapat dilihat pada persamaan (b – 18) dan ini haruslah negatif.
Evaluasi dari respon getaran bebas pada kasus ini, akan diekspresikan ke damping
rasio yaitu dan damping kritis dengan nilai yaitu:
= C = C (b – 23)
Cc 2 m
Kemudian ditelusuri dari Persamaan (b – 22) ke persamaan (b – 18) diperoleh:
[image:43.619.95.497.213.445.2]
Atau perubahan tanda arah yaitu dengan kembali menjadi suatu simbol baru D
yaitu:
s = - ± i D (b – 24)
Dimana: D = 1 - ² (b – 25)
D = Frekuensi damping vibrasi
2.5.3. Respon pada Beban Harmonik
Respon pada beban harmonik ini akan memberikan suatu asumsi yang utama
pada beban luar harmonik p (t) dari amplitudo po dan frekuensi sirkulasinya .
Pada kasus ini persamaan differensial pada getaran menjadi:
m (t) + c ú (t) + k u (t) = po sin t (b – 26)
2.5.3.1. Sistem Tanpa Redaman
Sistem beban harmonic tanpa redaman, diperoleh persamaan getaran adalah:
m (t) + k u (t) = po sin t (b – 27)
Solusi yang sempurna dari persamaan ini adalah respon getaran bebas yaitu:
uc (t) = A sin t + B cos t (b – 28)
Respon pada beban harmonik dapat diasumsikan menjadi harmonik dan pase beban
sebagai berikut:
u p(t) = G sin t (b – 28)
Dimana amplitudo G adalah sebagai suatu evaluasi. Substitusi Persamaan (b – 28)
ke dalam pesamaan ( b – 27) adalah:
Dengan mengambil sin t (secara umum tidak sama dengan nol) dan k dan
bukan k/m = ² diperoleh hasil yaitu:
G [1 - ( ² / ²) ] = po / k (b – 30)
Respon amplitudo adalah:
G = po 1 (b – 31)
k (1 - ²)
Dimana adalah perbandingan rasio dari frekuensi beban alami dengan frekuensi
getaran bebas yaitu:
= / (b – 32)
Secara umum diperoleh solusi hasil getaran hamonik dengan sistem tanpa
redaman akan memberikan kombinasi sebagai solusi koplementari dan solusi
partikuler, dimana diperoleh nilai dari G dengan persamaan (b – 31) yaitu:
u (t) = uc (t) + up (t) = A sin t + B cos t + (po/ k) [1 /(1- ²)]
sin t (b – 33)
Untuk sistem ini mulai dari masa tenggang pada inisial kondisi u(0) = ú(0) = 0, maka
akan memudahkan untuk mengarahkan konstanta- konstanta dengan membagi suatu
nilai yaitu:
A = - po 1 B = 0 (b – 34)
k (1- ²)
Dan kemudian memberikan respon kepada persamaan (b – 33) yaitu:
Dimana :
po/k = u st = displacement statis, contoh dimana displacement akan dihasilkan dari
beban po aplikasi statis.
1/(1- ²) = faktor manifikasi (MF), kembali ke efek amplitudo dinamik dari
aplikasi beban Harmonik.
Sin t = komponen respon pada frekuensi dari aplikasi beban = respon steady
state, dan Kemudian relasi kepada beban.
sin t = komponen respon dari frekuensi getaran alami = efek getaran bebas
yang dimasukan ke inisial kondisi.
2.5.3.2. Sistem Redaman
Kembali kepada persamaan dengan redaman persamaan (b – 27) dengan
memasukan m, dan bukan c/m = 2 yaitu:
(t) + 2 ú (t) + ² u (t) = (po/m) sin t (b – 33)
up
MF
t
Tp = 2 /
uc
x MF
t
T = 2 /
Gambar 7 : Respon beban harmonik dari inisial kondisi pada situasi transient
u
t
Frekuensi rasio = 2/3
Gambar 8: Respon beban harmonik dari inisial kondisi pada situasi total R(t)
Asumsi dari struktur menuju damping kritis, adalah kasus dari semua struktur
partikuler:
- t
uc (t) = e (A sin D t + B cos D t) (b – 34)
Solusi partikuler pada beban harmonik adalah:
Dengan substitusi persamaan (b – 35) ke (b – 34) dengan menggunakan sin t ke
cos t diperoleh hasil yaitu:
[- G1 ² - G2 (2 ) + G1 ²] sin t = (po/m) sin t (b – 36a)
[- G2 ² + G1 (2 ) + G2 ²] cos t = 0 (b – 36b)
2.6. Respon Beban Dinamik Secara Umum Integral Duhamel Untuk Sistem
Tanpa Redaman
Secara umum respon struktur pada durasi pendek dapat digunakan sebagai
dasar dalam rumus evaluasi respon pada beban dinamik umum. Ini akan dituliskan
secara hati- hati karena prosedur ini adalah masukan dari finite durasi, dan ini akan
datang pada durasi beban menuju nol. Secara differensial interval waktu d , prosedur
respon dari beban p( ) adalah cara yang tepat (untuk t > ):
du(t) = [p( ) d / m ] sin (t – ) (b – 37)
Di dalam ekspresi ini, du(t) kembali secara respon differensial pada kelebihan impuls
differensial dan memberikan respon history untuk t > ; maka hasil ini tidak akan
merubah nilai u selama interval waktu dt.
p(t)
p( )
t
(t – )
Response du(t)
Gambar 9: Derivative Integral Duhamel (tanpa redaman)
Untuk sistem linear elastis, total respon dapat diambil dengan cara pilihan dari
semua respon differensial selama beban history, dengan integral persamaan (b – 37)
adalah:
t
u(t) = 1/ m ∫o p( ) sin (t – ) d (b – 38)
Persamaan (b – 38) secara umum disebut Integral Duhamel dari sistem tanpa
redaman. Ini boleh digunakan sebagai respon evaluasi dari SDOF tanpa redaman
dengan kesatuan beban dinamik p(t), walaupun kasus ini adalah beban- beban secara
evaluasi menjadi kesatuan secara numerik.
Persamaan (b – 38) akan diekspresikan pada kesatuan:
t
u(t) = ∫o p( ) h (t – ) d (b – 39)
Dimana dengan menggunakan simbol baru dapat didefinisikan yaitu:
h(t – ) (1/m ) sin (t – ) (b – 40)
Respon getaran bebas haruslah memberikan solusi, secara umum yaitu:
t
u(t) = ú(0)/ sin t + u(0) cos t + 1/m ∫o p( ) sin (t – )d (b – 41)
Persamaan Integral Duhamel diekspresikan pada respon dari sistem redaman
pada beban dinamik umum adalah ekivalen dengan analisa tanpa redaman dengan
respon getaran bebas dengan beban differensial p( ) d adalah subjektif pada
eksponennya. Susunannya adalah u(0) = 0 dan kemudian ú (0) = [p( ) d ] /m
pada persamaan sebelumnya yaitu:
- (t- )
du (t) = e [ p( ) d / m D sin D(t – ) ] t > (b – 42)
Respon differensial dikembangkan lebih lagi pada interval beban dengan nilai yaitu:
t - (t – )
u (t) = (1/m D) ∫ 0 p( ) e sin D (t – ) d (b – 43)
Perpaduan tersebut menunjukan persamaan (b – 43) dengan integral persamaan (b –
39) sebagai respon impuls dengan unit dan sistem redaman yaitu:
- (t – )
h(t – ) = (1/m D) e sin D (t – ) (b – 44)
Dari evaluasi numerik pada respon sistem redaman diperoleh:
u (t) = A(t) sin Dt - B(t) cos D t (b – 45)
Dimana, pada kasus ini yaitu:
t
A(t) = (1/m D) ∫ p(t) e cos D d 0 t
e
(b – 46)
t
B(t) = (1/m D) ∫ p(t) e sin D d
0 t e Integral pertama diperoleh:
A(t) = ( / m D) [ 1/ (t) ] (b – 47)
Rumus ini dapat diekpresikan dengan proses yang berbeda- beda yaitu:
Dengan menggunakan ( = 1):
A A
(t) = [ (t – ) + p(t - ) cos D (t – ) exp (- ) (b – 48)
1 1
Dengan peraturan trapezoidal ( = 2) : A A
(t) = [ (t – )+ p(t - ) cos D(t – )]exp (- )+ p(t) cos Dt (b–49) 2 2
Dengan peraturan Simpson ( = 3) : A A
(t) = [ (t – ) + p(t - ) cos D (t – )]exp (- )
2 2 4p(t - ) cos D(t – )exp (- ) + p(t) cos Dt
(b – 50)
Tambahan B(t) memberikan ekspresi yang sama kepada fungsi- fungsi sinus.
2. 7. Multy Degree Of Freedom
Persamaan gerakan dapat diekspresikan pada keseimbangan gaya- gaya yang
efektif dengan banyak derajat kebebasan. Secara umum ada 4 tipe dari gaya akan
digabungkan yaitu beban sebagai aplikasi dari luar pi(t) dan dengan banyak gaya
solusi dari gerakan yaitu, Inersia FIi, damping FDi, dan elastis FSi. Dari semua
banyak derajat kebebasan keseimbangan dinamik dapat diekspresikan yaitu:
FI1 + FD1 + FS1 = p1(t)
FI2 + FD2 + FS2 = p2(t)
FI3 + FD3 + FS3 = p3(t) (c – 1)
Atau vektor gaya- gaya disatukan di dalam kumpulan matriks yaitu,
FI + FD + FS = p(t) (c – 2)
Dimana MDOF ekivalen dengan SDOF pada persamaan (a – 1)
Secara umum gaya elastis adalah kumpulan dari displacement dari semua
struktur yaitu:
FS1 = k11 u1 + k12 u2 + k13 u3 + …+ k1n un (c – 3a)
Hal yang sama, gaya elastis masuk ke dalam degree of freedom u2 adalah:
FS2 = k21 u1 + k22 u2 + k23 u3 + … + k2n un (c – 3b)
Dan secara umum:
FSi = ki1 u1 + ki2 u2+ ki3 u3 + … + kin un (c – 3c)
Di dalam matriks, secara komplit dari gaya elastis dapat dituliskan:
FS1 k11 k12 k13 … k1i … k1N u1
FS2 k21 k22 k23 … k2i … k2N u2
. = ……… .. (c – 4)
FSi ki1 ki2 ki3 … kii … kiN ui
. ……… .
Atau secara simbolis, FS = k u (c – 5)
Jika asumsi dari damping berhubungan dengan kecepatan, tipe redaman, gaya-
gaya damping berhubungan dengan derajat kebebasan mungkin sebagai ekspresi dari
damping untuk dituliskan. Sebagai penelusuran persamaan (c – 5), komplit dari gaya-
gaya damping adalah:
FD2 c21 c22 c23 … c2i … c2N ú2
. = ……… . (c – 6)
FDi ci1 ci2 ci3 … cii … ciN úi
. ……….. .
Atau secara simbolis dapat dituliskan, FD = c ú (c – 7)
Gaya- gaya inersia mungkin dapat juga diekspresikan secara menyeluruh dari
koefisien- koefisien massa. Hubungan ini berelasi kepada percepatan dari derajat
kebebasan sehingga menghasilkan gaya- gaya inersia, secara penelusuran dari
persamaan (c – 5), gaya- gaya inersia diekspresikan menjadi:
FI1 m11 m12 m13 … m1N ü1
FI2 m21 m22 m23 … m2N ü2
. = ………. . (c – 8)
FIi mi1 mi2 mi3 … miN üi
. ……… .
Secara simbolis dapat dituliskan, FI = c ü (c – 9)
Substitusi persamaan (c – 5 ), (c – 7), dan (c – 9) ke dalam persamaan (c – 2)
memberikan secara komplit dengan keseimbangan dinamis pada struktur, yaitu pada
semua derajat kebebasan :
Persamaan ini adalah MDOF ekivalen dengan persamaan (a – 5); yang lain dari
persamaan SDOF dikembangkan dengan matriks dalam persamaan (c – 10), matriks
lain dihubungkan kepada bagian derajat kebebasan yang digunakan di dalam
displacement- displacement dari struktur. Persamaan (c – 10) diekpresikan kepada
persamaan- persamaan dari getaran untuk memperbaiki respon dari sistem MDOF.
2. 8. Analisa Single Story Linear
Perhitungan pada Respon Dinamik struktur bangunan pada daerah spesifik
yang ruang geraknya adalah suatu proses yang sangat kompleks. Pada penjabaran
persamaan- persamaan dari struktur bangunan serta dengan analisa time history pada
waktu yang sedikit menuju suatu nilai yang akurat. Analisa ini adalah yang pertama
kalinya ditemukan yaitu secara three dimensional struktur bangunan one- story (satu
lantai) dengan tiga derajat kebebasan yaitu: dua pendekatan arah gerakan horijontal
dan daerah rotasi (torsi). Perhitungan 3 derajat kebebasan ini mendekati level redaman
(isolasi) pada lantai pertama yaitu total mendekati 6 derajat kebebasan. Untuk langkah
Gambar 10 : Lantai 1 Free body diagram.
2.8.1. Prosedur Analisa
Analisa ini adalah penjabaran persamaan gerakan lantai satu dengan lantai
berikutnya. Gambar 1 menunjukan gambaran kembali ke free body diagram dengan
potongan struktur secara cermat dan akurat menuju ke lantai dua, dan yang jelas tetap
pada lantai 1. Gaya- gaya elastis dan gaya- gaya damping selama terjadi guncangan
dapat terlihat pada gambar, tetapi kenyataannya pada bagian
perpindahan(displacement) dan kecepatan(velocity) dari struktur, secara teliti,
berlangsung pada setiap lantai. Dengan mempelajari secara teliti pada gambar 10
[image:55.619.151.456.114.379.2](2 -1)
Gambar 11: Superstructure Free Body Diagram
Gambar 11: menyatakan free body diagram dari gambar struktur dan yang dipotong
diantara bearing dan pada lantai, kemudian didapat hitungan yang akurat pada
struktur. Pada kenyataannya dari gambar 10, gerakan gaya elastis dan gaya damping
tidak tampakan. Ada juga gaya gesekan bearing pada lantai base, tetapi juga tidak
diperlihatkan. Gambaran gaya gesekan bergantung pada kecepatannya. Dengan
memperhatikan gambar 11 persamaan dalam kurung dapat dituliskan dalam sebagai
[image:56.619.119.485.116.458.2](2-2)
Dimana :
Gaya inertia lantai ke- i
Gaya Damping lantai ke- i
Gaya Elastis lantai ke- i
Gaya gesekan pada level bearing
lantai ke - i; b untuk base, 1 untuk lantai 1 (atap)
Rumusan ini terjadi selama gesekan pada bearing yang dianalisa secara teliti ;
dan gesekan pada lantai akan diabaikan. Untuk memperjelas kasus gesekan pada level
bearing, sangat simpel menyusun koefisien gesekan yaitu , dan menjadi nol serta
proses yang diperoleh dari suatu solusi.
Dari persamaan (1) dan (2) diaplikasikan kepada 3 bagian; 2 arah horijontal
dan arah torsional dengan kembali pada momen- momennya. Pada penulisan
persamaan ini adalah dengan 3 derajat kebebasan, dan persamaan matriks dituliskan
(2-3)
(2-4)
Persamaan (2- 2) dan (2-3) dapat dikembangkan menjadi:
(2-5)
2.8.2. Persamaan- Persamaan Pada Gerakan Level Bearing.
Persamaan (4) dapat dikembangkan sesuai dengan persamaan semula. Dimana
gaya gesekan tidaklah setimbang di dalamnya. Dengan definisinya, gaya gesekan
adalah persamaan yang normal dan gesekannya biasa dengan constanta . Gaya- gaya
normal di dalam rumusan ini akan mengambil massa matriks secara berulang kali dan
percepatan vertikal total dari struktur bangunan, adalah gaya gravitasi yang
dijabarkan langsung pada percepatan vertikal gempa pada bearing- bearing, seperti
(2-6)
Yang mana:
(2-7)
(2-8)
(2-9)
(2-11)
percepatan gempa vertikal
Catatan matriks kekakuan adalah bagian kekakuan dari proses penjabaran.
Vektor perpindahan (displacement) dapat diperoleh selama posisi tepat pada
metode dasar, dimana pada kombinasi linear dari mode shapes akan digunakan
prakiraan displacement (perpindahan). Displacement (perpindahan) akan memberikan
catatan fungsi dari mode shapes pada struktur yaitu:
(2-12)
(2-13)
Vektor- vektor disatukan dalam banyak model, yaitu normal dan koordinat.
lainnya yaitu deformasi (perubahan) dari struktur, dari persamaan (12) dan persamaan
(13).
Model Shapes akan dijabarkan sebagai solusi umum pada masalah Nilai
Eigen.
(2-14)
(2-15)
Mode Shapes secara aktual menggunakan Vektor Eigen dari persamaan (2-14) dan
persamaan (2-15) dan frekuensi- frekuensi alami pada perhitungan penggunaan nilai
Eigen. Matriks dasar akan memberikan perhitungan hasil yaitu :
(2-16)
Dasar matriks lantai 1, , adalah bagian persamaan (2-14) dan mariks pada base
pada bearing- bearing, , adalah penjabaran pada persamaan (2-15).
Kolom- kolom matriks dasar diteruskan ke model shapes, dengan kolom
banyak model dari displacement (perpindahan), dan suatu kombinasi pada bagian 3
komponen yang aktual dari Respon struktur yaitu pada persamaan (2-12) dan (2-13).
Dimana, kontribusi dasar displacement (perpindahan) yang lain pada 3 derajat
kebebasan dari setiap lantai.
Mode Shapes adalah massa dengan sifat normal yang memberikan relasi
sebagai berikut:
(2-17)
Persamaan (2-6) akan dipermudah, dengan menggunakan persamaan (2-17), dengan
subtitusi pertama persamaan (2-12) yaitu :
(2-18)
Kemudian, dengan analisa perhitungan cara yang lain pada persamaan deformasi dari
model matriks untuk level bearing, diteruskan menjadi persamaan:
Kemudian, massa dengan sifat normal memberikan persamaan (2-17), adalah
menggunakan cara yang sederhana dengan ekspresi yaitu:
(2-20)
Persamaan matriks ini tetap pada 3 persamaan gerakan, yaitu 1 dari beberapa model
displacement (perpindahan). Yang lain dari 3 persamaan ditunjukan pada persamaan
(2-21), dengan n=1,2, atau 3, dengan kembali ke model displacement (perpindahan)
yang diteruskan pada persamaan:
(2-21)
Dengan substitusi menjadi:
(2-22)
(2-24)
(2-25)
Persamaan (2-22) adalah suatu ortogonal dari banyak model. Catatan, persamaan
(2-23) adalah matriks damping yang klasik. Untuk perhitungan yang simple digunakan
damping klasik akan pada thesis ini. diberikan dengan cara kembali kepada
damping ratio dari tiap lantai dengan model j. Persamaan- persamaan (2-24) dan
persamaan (2-25) adalah hasil dari matriks dengan banyak aplikasi dengan
Gambar 12 : Metode Percepatan Linear.
Persamaan (2-21) adalah tidak memberikan banyak solusi. Penyelesaian displacement
(perpindahan) dari struktur adalah dengan menggunakan fungsi waktu, dan dengan
penjabaran linear interpolasi akan memberikan nilai perubahan pada percepatan
(acceleration). Gambar 3 menunjukan Metode Percepatan Linear, di dalam percepatan
prakiran garis lurus yang tidak diketahui percepatannya selama interval waktu
berlangsung.
Situasi ini akan akurat dengan penggunaan waktu yang sedikit dan lebih efisien
disebut ∆t. Sebagai contoh, daerah percepatan gempa diredam pada Lembah bagian
irigasi dari Utara- Selatan tahun 1940 Elcentro, dan gempa bumi California adalah
meredam suatu interval waktu ∆t = 0,02 detik (sumber, Copra 2001).
Metode percepatan linear, diekpresikan pada model percepatan dari lantai
pertama dan gaya percepatan yang kemudian dituliskan sebagai berikut.
(2-26)
(2-27)
(2-28)
(2-29)
Sekarang, dengan substitusi persamaan (2-26) ke persamaan (2-29) ke dalam
persamaan (2-21) , maka persamaan menjadi:
(2-30)
Di dalam n = 1,2, dan 3
(2-31)
(2-32)
Persamaan (2-30) adalah sama dengan second- order non- homogeneous dengan
perbedaan persamaan dari solusi komplit dan solusi partikulir. Solusi homogeneous,
adalah solusi persamaan (2-30) jika sisi sebelah kanan di kalkulasikan menjadi nol,
yaitu:
(2-33)
Frekuensi damping alami dituliskan dalam bentuk:
Bilangan- bilangan konstan dan pada persamaan (2-33) dan batas
pengambilan initial condition akan di determinan.
Solusi mendekati ke persamaan (2-30) adalah:
(2-35)
Dengan substitusi ke persamaan (2-35) dan diderivasi ke persamaan (2-30), constan
pada serta diperoleh hasil yaitu:
(2-36)
(2-37)
Kombinasi dari solusi kompleks persamaan (2-33) dan solusi istimewa dari persamaan
(2-35) diekspresi kepada yaitu:
Dapat dilihat dari gambar 3, , menjadi dan mendekati suatu nilai
:
(2-39)
(2-40)
Nilai dapat digunakan langsung untuk merubah menjadi konstan dan , dan
pada pelaksanaan persamaan- persamaan (2-39) dan (2-40) kepada persamaan (2-38)
akan menjadi:
(2-41)
(2-42)
Sekarang persamaan disusun menjadi dengan substitusi persamaan (2-41) dan
(2-42) kembali memberikan solusi ke persamaan (2-38), dan memberikan ekpresi dari
adalah :
(2-43)
(2-44)
(2-45)
(2-46)
(2-47)
Hampir mendekati suatu persamaan baru yaitu dengan model kecepatan (velocity)
akan memberikan persamaan (2-38) dengan membuat suatu bagian yang teliti pada
waktu dan evaluasi yaitu . Model kecepatan (velocity) dapat dituliskan sebagai
berikut:
(2-48)
Dimana :
(2-49)
Model percepatan dapat juga diberikan pada persamaan (2-38) mendapatkan 2 bagian
dengan teliti dari waktu. Model percepatan dapat dituliskan sebagai berikut:
(2-51)
Dimana:
(2-52)
(2-53)
Dengan menggunakan persamaan (2-32), persamaan (2-51) dapat dituliskan sebagai
berikut:
(2-54)
Persamaan (2-54) di dalam kesatuannya dapat digunakan sebagai solusi dengan
menggunakan waktu sebagai metode, dan determinan dari respon bearing, serta
diperoleh redaman percepatan gempa dengan respon gaya- gaya yang bekerja pada
lantai pertama. Dimana, respon gaya pada lantai pertama belum diketahui. Kemudian
formulasi dibagi dan dideterminan dengan persamaan- persamaannya pada level
2.8.3. Gerakan Dari Persamaan- persamaan Lantai Pertama
Dari gerakan persamaan- persamaan pada lantai pertama, model- model shape
akan mendekati massa orthonormal dan dilanjutkan ke massa matriks .
Prakiraan ini membawa matriks massa untuk digunakan ke persamaan (2-5):
(2-55)
(2-56)
(2-57)
Kemudian, gaya damping adalah suatu asumsi yang klasik , dan dapat dipergunakan
dengan matriks diagonal. Prosedur ini diteruskan seperti mengerjakan persamaan
deformasi (2-6) ke persamaan (2-21), persamaan (2-5) dapat dituliskan sebagai
(2-58) Kemudian:
(2-59)
(2-60) Sekarang persamaan (2-58) dapat dituliskan dengan menggunakan metode persamaan percepatan linear yaitu :
(2-61)
Persamaan ini dapat dituliskan dengan menggunakan fungsi waktu . Pada waktu
integrasi, dan permodelan fungsi percepatan bersama model- model fungsi kecepatan
diteruskan menjadi :
(2-62)
Dengan fungsi integrasi didapat secara teliti yaitu model fungsi displacement dengan
(2-63) Evaluasi persamaan (2-58) dengan menggunakan waktu dan disubstitusi ke dalam
persamaan (2-61), (2-62), dan (2-63), dengan penambahan ke persamaan (2-58),
dapat ditulis yaitu :
(2-64)
Kemudian :
(2-65)
(2-66)
(2-67)
Dengan persamaan 64) diperoleh suatu fenomena. Dengan substitusi persamaan
(2-54) ke persamaan (2-64), maka apablia tidak mengetahui kecepatan pada bearing yang
(2-68)
Disamping persamaan (2-68) menjadi bagian dari dan formula (rumus) tambahan
dengan penjabaran sec