Pendugaan parameter model dinamik dengan menggunakan metode kuadrat terkecil dan implementasinya dengan mathematica

PENDUGAAN PARAMETER MODEL DINAMIK HIV

DENGAN MENGGUNAKAN METODE KUADRAT

TERKECIL DAN IMPLEMENTASINYA DENGAN

MATHEMATICA

EMTA HARIATI SURBAKTI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRAK

EMTA HARIATI SURBAKTI. Pendugaan Parameter Model Dinamik HIV dengan Menggunakan Metode Kuadrat Terkecil dan Implementasinya dengan Mathematica. Dibimbing oleh N. K. KUTHA ARDANA dan RETNO BUDIARTI.

ABSTRACT

EMTA HARIATI SURBAKTI. Parameter Estimation of HIV Dynamic Model Using Least Squares Method and its Implementation with Mathematica. Supervised by NGAKAN KOMANG KUTHA ARDANA and RETNO BUDIARTI.

PENDUGAAN PARAMETER MODEL DINAMIK HIV

DENGAN MENGGUNAKAN METODE KUADRAT

TERKECIL DAN IMPLEMENTASINYA DENGAN

MATHEMATICA

EMTA HARIATI SURBAKTI

G54060114

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Judul : Pendugaan Parameter Model Dinamik HIV dengan Menggunakan

Metode Kuadrat Terkecil dan Implementasinya dengan

Mathematica

Nama : Emta Hariati Surbakti

NRP : G54060114

Menyetujui

Pembimbing I

Pembimbing II

Ir. N. K. Kutha Ardana, M.Sc. Ir. Retno Budiarti, MS.

NIP. 19640823 198903 1 001 NIP. 19610729 198903 2 001

Mengetahui

Ketua Departemen Matematika

Dr. Berlian Setiawaty, M.S.

NIP 19650505 198903 2 004

KATA PENGANTAR

Puji Tuhan, terima kasih kepada Tuhan Yesus Kristus buat setiap kasih dan anugrah-Nya sehingga karya ilmiah ini dapat diselesaikan. Penyusunan karya ilmiah ini juga tidak terlepas dari dukungan dan bantuan berbagai pihak. Penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Keluarga: Ayah, Ibu, Bang Alex, Kak Margaret dan Kak Dewi terima kasih buat dukungan dan motivasinya.

2. Ir. N. K. Kutha Ardana, M.Sc. selaku dosen pembimbing I, Ir. Retno Budiarti, MS. selaku pembimbing II. Terima kasih atas waktu, ilmu yang diberikan dan kesabarannya dalam membimbing penulis.

3. Dr. Ir. Endar H. Nugrahani, MS. selaku dosen penguji. Terima kasih atas waktu dan ilmu yang sangat bermanfaat bagi penulis.

4. Semua pihak-pihak yang tidak bisa disebutkan satu persatu yang turut membantu dalam penyelesaian karya ilmiah ini.

Penulis menyadari tulisan ini masih memiliki kekurangan dan jauh dari kesempurnaan. Oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca.

Semoga karya ilmiah ini bermanfaat bagi kita semua, bagi dunia ilmu pengetahuan khususnya Matematika.

Bogor, Maret 2011

RIWAYAT HIDUP

Penulis lahir di Kabanjahe (Medan-Sumatra Utara) pada tanggal 03 April 1988 sebagai anak bungsu dari empat bersaudara, anak dari Salam Surbakti dan Saripah Ginting.

Tahun 2000 penulis lulus dari SDN 02 Munte. Tahun 2003 penulis lulus dari SLTPN 1 Munte. Tahun 2006 penulis lulus dari SMAN 17 Medan dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur Seleksi Penerimaan Mahasiswa Baru (SPMB). Pada tahun 2007, penulis masuk jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

DAFTAR ISI

Halaman

DAFTAR ISI ... vii

DAFTAR GAMBAR... viii

DAFTAR TABEL ... viii

DAFTAR LAMPIRAN ... viii

PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

LANDASAN TEORI 2.1 Persamaan Diferensial Biasa ... 1

2.2 Persamaan Diferensial Mandiri ... 1

2.3 Sistem Persamaan Diferensial Mandiri ... 1

2.4 Metode Kuadrat Terkecil ... 2

2.5 Pendugaan Parameter Model Dinamik ... 2

2.6 Analisis Galat ... 3

2.6.1 Galat ... 3

2.6.2 Persentase Rataan Galat Mutlak ... 3

2.6.3 Box-Plot ... 3

MODEL DAN DATA 3.1 Pemodelan ... 4

3.2 Model ... 4

3.3 Data ... 5

HASIL DAN PEMBAHASAN 4.1 Pembangkitan Data Hipotetik ... 5

4.2 Pendugaan Parameter ... 6

4.3 Analisis Akurasi Pendugaan ... 9

SIMPULAN DAN SARAN 5.1 Simpulan ... 10

5.2 Saran ... 10 DAFTAR PUSTAKA ... 10

LAMPIRAN ... 11

11

DAFTAR GAMBAR

Halaman

1 Digram alur pendugaan parameter ... 2

2 Diagram kotak (box-and-whisker plot) ... 3

3 Diagram model nonlinear ... 4

4 Tebaran data untuk populasi N,X,Y dan Z ... 5

5 Grafik dengan parameter dugaan untuk populasi N(t) ... 7

6 Grafik dengan parameter dugaan untuk populasi X(t) ... 7

7 Grafik dengan parameter dugaan untuk populasi Y(t) ... 7

8 Grafik dengan parameter dugaan untuk populasi Z(t) ... 7

9 Gabungan grafik dengan parameter dugaan N(t), X(t), Y(t) dan Z(t) ... 8

10 Tebaran data dan grafik dengan parameter dugaan untuk populasi N(t) ... 8

11 Tebaran data dan grafik dengan parameter dugaan untuk populasi X(t) ... 8

12 Tebaran data dan grafik dengan parameter dugaan untuk populasi Y(t) ... 8

13 Tebaran data dan grafik dengan parameter dugaan untuk populasi Z(t) ... 8

14 Gabungan antara tebaran data dan grafik dengan parameter dugaan untuk populasi N(t), X(t), Y(t), dan Z(t) ... 8

15 Diagram kotak untuk setiap state variableN, X, Y dan Z ... 9

DAFTAR TABEL

Halaman 1 Perbandingan nilai parameter awal dan parameter akhir ... 6

2 Nilai MAPE untuk setiap state variable ... 9

3 Q1, Q2, Q3, nilai max, nilai min dan rataan dari galat untuk setiap state variable ... 9

DAFTAR LAMPIRAN

Halaman 1 Pembangkitan data hipotetik ... 12

2 Pendugaan parameter ... 15

3 Gambar grafik model dengan parameter hasil dugaan ... 16

4 Gambar gabungan tebaran data dan model dengan parameter hasil dugaan ... 17

5 Pencarian galat ... 19

I PENDAHULUAN

1.1 Latar Belakang

Dalam model dinamik, pembahasan seringkali hanya berkisar pada masalah titik tetap, kestabilan dan analisanya dengan menggunakan parameter-parameter yang sudah diberikan atau diketahui. (Gao 1995, Ackerman 1986). Pada kenyataanya, nilai-nilai parameter tersebut sulit diperoleh pada dunia nyata. Di sisi lain apabila terdapat sejumlah data pengamatan, belum tentu model yang dipunyai cocok dengan data tersebut.

Tulisan ini membahas tentang teknik pendugaan parameter model dinamik berdasarkan segugus data pengamatan untuk suatu model yang sudah diketahui. Pendugaan parameter dapat dilakukan secara langsung ataupun tidak langsung jika segugus data diberikan beserta representasi model dinamiknya. Pendugaan parameter model dinamik secara tidak langsung dimulai dengan mencari solusi analitik dari model dinamik kemudian dilanjutkan dengan melakukan regresi. Namun tidak semua model dinamik dapat ditentukan solusi analitiknya. Oleh karena itu, diperkenalkan pendugaan secara langsung yakni dengan menggunakan metode

pendugaan parameter model dinamik. Metode yang sering digunakan adalah metode kuadrat terkecil. Pendugaan parameter model dinamik dengan menggunakan metode kuadrat terkecil telah diaplikasikan pada beberapa model dinamik.

Model yang digunakan dalam tulisan ini adalah model dinamik epidemik HIV/AIDS (De Arazoza 1999). Model dinamik epidemik HIV tersebut berupa model nonlinear, selanjutnya model dinamik HIV/AIDS akan diduga parameternya berdasarkan segugus data pengamatan dengan metode kuadrat terkecil.

1.2 Tujuan

Tujuan dari penulisan ini adalah:

1. Mengkaji metode pendugaan parameter suatu model dinamik.

2. Mengimplementasikan metode pendugaan parameter kuadrat terkecil pada model dinamik epidemik HIV ke dalam program

Mathematica.

II LANDASAN TEORI

2.1 Persamaan Diferensial Biasa

Persamaan diferensial biasa diartikan sebagai suatu persamaan yang melibatkan turunan pertama atau lebih dari fungsi sebarang y, terhadap peubah x, yang dinyatakan sebagai :

( ) ( , , ', '', ..., n ) 0

F x y y y y = (1)

(Rice 1993)

2.2 Persaman Diferensial Mandiri

Persamaan diferensial mandiri didefinisikan sebagai persamaan diferensial yang secara eksplisit tidak menyertakan variabel waktu t. Misalkan diberikan persaman diferensial orde 1.

( ) dx

F x

dt = (2) Persamaan diferensial (2) adalah mandiri karena tidak menyertakan

t

pada ruas sebelah kanan.

(Lomen 1988)

2.3 Sistem Persaman Diferensial Mandiri Bila persamaan diferensial F x( ) pada persamaan (2) adalah suatu matriks berukuran m x m, maka diperoleh sistem persamaan diferensial mandiri berikut:

1 2 )

( , , ...,

i

i m

dx

F x x x

dt

= untuk i=1,2,...,m

atau

1

1 1 2

2

2 1 2

) ) ( , , ..., ( , , ..., m m dx

F x x x

dt

dx

F x x x

dt

=

=

(3)

#

#

#

#

#

1 2 )

( , , ...,

m

i m

dx

F x x x

dt =

Jika pada persamaan (3) x x₁, ₂, ...,x_m

2 ( ) d F dt = x

x , dengan x(0) = x0

(Lomen 1988)

2.4 Metode Kuadrat Terkecil (Least Square, LS)

Misalkan ˆ ( , )x t p adalah solusi dari sistem persamaan diferensial. Salah satu metode yang lazim digunakan untuk menduga parameter p adalah metode kuadrat terkecil yaitu dengan meminimumkan jumlah kuadrat galatnya. Adapun persamaannya adalah sebagai berikut:

{

_ˆ 2

}

min S( )p =∑ =_in₁(x_i−x t_i( , ))p

Besaran_xidiperoleh melalui

pengamatan yang dilakukan secara diskrit pada waktu_ti, i=1, 2, ...,n

2.5 Pendugaan Parameter Model Dinamik Diketahui model dinamik yang melibatkan

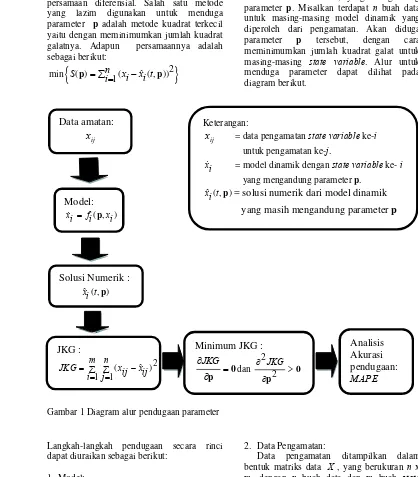
m buah state variable, yang mengandung parameter p. Misalkan terdapat n buah data untuk masing-masing model dinamik yang diperoleh dari pengamatan. Akan diduga parameter p tersebut, dengan cara meminimumkan jumlah kuadrat galat untuk masing-masing state variable. Alur untuk menduga parameter dapat dilihat pada diagram berikut.

Gambar 1 Diagram alur pendugaan parameter

Langkah-langkah pendugaan secara rinci dapat diuraikan sebagai berikut:

1. Model:

Model dinamik dengan state variable ke-i, ( , )

x= f_i p x_i dengan i=1, 2, ..,m

2. Data Pengamatan:

Data pengamatan ditampilkan dalam bentuk matriks data X, yang berukuran n x

m, dengan n buah data dan m buah state variable. Data amatan: ij

x

Model: ( , )

x_i= f_i p x_i

Solusi Numerik : ˆ ( , )

x t_i p

JKG : 2 ˆ ( ) 1 1 m n

JKG x_ij x_ij

i j

= ∑ ∑ −

= =

Minimum JKG :

JKG

∂ = ∂p 0dan

2

2

JKG

∂ > ∂p 0 Keterangan:

ij

x

= data pengamatan state variable ke-i

untuk pengamatan ke-j.

xi = model dinamik dengan state variable ke- i

yang mengandung parameter p. ˆ ( , )

x t_i p = solusi numerik dari model dinamik yang masih mengandung parameter p

3

11 21 31 1

12 22 32 2

13 23 33 3

1 2 3

x x x x_m

x x x x_m

X x x x x

n m m

x_n x _n x _{n xmn}

=

⎛

⎞

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎝

⎠

" " " # # # % # "

xijadalah data pengamatan state variable ke-i

untuk pengamatan ke- j.

3. Jumlah Kuadrat Galat 2 ˆ

( )

1 1

m n

JKG x_ij x_ij

i j

= ∑ ∑ −

= =

dengan _xij adalah data pengamatan dan ˆ_xij

adalah hasil dari evaluasi model dinamik yaitu ( , )

x= f_i p x_i untuk state variable ke-i untuk pengamatan ke-j.

4. Minimum Jumlah Kuadrat Galat:

JKG

∂ = ∂p 0dan

2

2

JKG

∂ > ∂p 0

Sehingga diperoleh parameter yang diduga ˆ

( )p . Parameter model dinamik yang diduga akan semakin baik jika memiliki jumlah kuadrat galat yang kecil.

(Thornley dan Johnson 1990)

2.6 Analisis Akurasi Pendugaan

Misalkan n buah data pengamatan untuk masing-masing state variable ke-i

dengan pengamatan ke-j {_xij, i=1, 2, ...,m

dan j=1, 2, ...,m}, dan ˆ_xij adalah solusi

numerik dari model dinamik untuk masing-masing data pengamatan state variable ke-i,

untuk pengamatan ke- j.

2.6.1 Galat

Galat untuk masing-masing state variable ke-i pada setiap pengamatan ke-j

didefinisikan:

ˆ (x x )

ij ij ij

e

= − ;i=1, 2, ...,mdan

1, 2, ...,

j= n

(Mathews 1992)

2.6.2 Persentase Rataan Galat Mutlak (Mean Absolute Percentage Error) Persentase rataan galat mutlak (MAPE) untuk masing-masing state variable ke-i

didefinisikan: ˆ ( ) 1 100% 1 x x

n ij ij

MAPEi _j

n _xij

−

= ∑ ×

=

Keakuratan suatu penduga parameter dapat dilihat dari nilai MAPE, semakin kecil nilai yang diperoleh maka pendugaan parameter akan memiliki nilai yang semakin akurat atau semakin baik.

2.6.3 Box-Plot

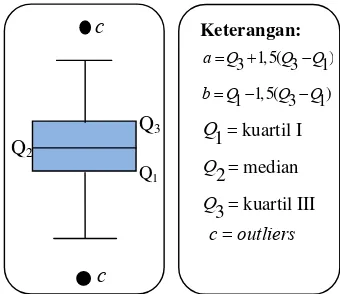
Cara lain untuk melihat hasil galat untuk setiap state variable adalah menggunakan diagram kotak (boxplot). Diagram kotak pada Gambar (2) menampilkan lima titik yaitu :

tiga kuartil (Q Q Q₁, ₂, ₃) dan dua batas yaitu

batas atas dan batas bawah (a,b).

Selisih Q_{3 dan 1}Q menggambarkan

tingkat keragaman suatu data. Semakin besar nilainya maka data semakin beragam. Nilai-nilai yang berada di atas a atau di bawah b

diidentifikasi sebagai pencilan (outliers).

Gambar 2 Diagram kotak (box-and-whisker plot).

Keterangan:

1,5( )

3 3 1

1,5( )

1 3 1

a Q Q Q

b Q Q Q

= + −

= − −

1

Q = kuartil I

2

Q = median

3

Q = kuartil III

c = outliers

c

c Q3

Q1

4

III MODEL DAN DATA

3.1 Pemodelan

Model yang digunakan dalam tulisan ini adalah model dinamik HIV dengan diagram komparteman sebagai berikut:

Gambar 3 Diagram model tak linear

Dengan keterangan :

N : populasi orang aktif secara seksual atau rentan,

X : jumlah populasi positif HIV yang tidak tahu bahwa mereka terinfeksi,

Y : jumlah populasi positif HIV yang tahu bahwa mereka terinfeksi,

Z : jumlah kasus AIDS,

α : tingkat dimana HIV positif yang rentan tidak diketahui sebagai hasil infeksi mereka secara individual pada kelas X.

k : tingkat di mana HIV positif terdeteksi,

β : tingkat di mana HIV positif berkembang jadi AIDS .

μ : tingkat kematian populasi yang aktif secara seksual,

u : tingkat kematian akibat AIDS δ : perekrutan ke dalam kelas rentan,

v : imigrasi yang tidak diketahui sebagai pengidap HIV positif.

ρ : imigrasi kasus AIDS.

Dari diagram di atas dapat dilihat bahwa model dinamik HIV teridiri dari empat kelas state variable yaitu state variableN, X,

Y dan Z. Seiring dengan berjalannya waktu, laju perubahan populasi yang aktif secara seksual atau rentan (N) akan bertambah sebesar δ dan akan berkurang dengan laju kematian sebesar μN. Populasi yang rentan jika terjangkit HIV tapi tidak tahu bahwa dia terkena HIV dimasukkan kedalam kelas X.

Laju perubahan populasi yang tidak tahu bahwa mereka terinfeksi HIV (X) akan bertambah sebesar v dan berkurang dengan laju kematian sebesar μX. Dari kelas X tedapat dua kemungkinan:

• Jika populasi yang tidak tahu bahwa mereka terinfeksi HIV (X) kemudian akhirnya tahu bahwa mereka terinfeksi HIV maka dimasukkan ke dalam kelas Y dengan laju kejadian sebesar kX. Populasi Y akan berkurang dengan laju kematian sebesar μY.

•Jika populasi yang tidak tahu bahwa mereka terinfeksi HIV (X) ternyata terkena AIDS dimasukkan ke dalam kelas Z. Laju perubahan populasi Z akan bertambah sebesar ρ dan akan bertambah juga apabila populasi Y ternyata terjangkit AIDS dengan laju sebesar βY. Populasi Z akan berkurang dengan laju kematian sebesar u.

3.2 Model

Dari penjelasan di atas maka diperoleh model dinamik tak linear sebagai berikut:

dN NX N dt α μ δ = − − + ( ) dX

NX k X v

dt =α − + +μ β + ₍₄₎

( )

dY

kX Y

dt = − μ β+

dZ

X Y uZ

dt =β +β − +ρ

dengan

dN

dt : laju populasi yang aktif secara

seksual atau rentan.

dX

dt : laju populasi yang tidak tahu bahwa

mereka terinfeksi HIV.

dY

dt : laju populasi yang tahu bahwa

mereka terinfeksi HIV.

dZ

dt : laju popolasi yang terkena AIDS.

3.3 Data

Karena tidak adanya data pengamatan langsung, data pengamatan diperoleh secara hipotetik berdasarkan solusi numerik model dinamik dengan nilai parameter diketahui, kemudian diberi galat bilangan acak.

N X Y

Z δ μN αNX μX v

kX μY

βX

βY

ρ

5

IV HASIL DAN PEMBAHASAN

4.1 Pembangkitan Data Hipotetik

Data dibangkitkan dengan bantuan

software Mathematica yaitu dengan cara

mencari solusi numerik dari model dinamik dengan memberikan nilai parameter awal sebagai berikut:

α = 0.01

k = 0.4554 μ= 0.0053 β= 0.1087

v = 20

u = 0.3027 ρ = 1 δ = 27

dan nilai awal sebagai berikut:

N0 = 50 X0 = 230

Y0 = 94 Z0 = 3

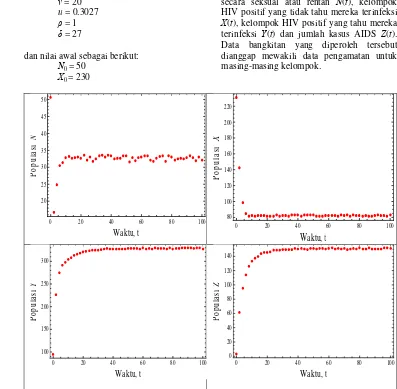
Kemudian dari solusi yang diperoleh ditambahkan bilangan antara -1 sampai 1 secara acak sehingga diperoleh tebaran data seperti pada Gambar (4). Langkah-langkah membangun data hipotetik untuk model ini dapat dilihat secara rinci di Lampiran 1.

Gambar (4) memperlihatkan tebaran data bangkitan model HIV epidemik. Masing-masing untuk kelompok populasi yang aktif secara seksual atau rentan N(t), kelompok HIV positif yang tidak tahu mereka terinfeksi

X(t), kelompok HIV positif yang tahu mereka terinfeksi Y(t) dan jumlah kasus AIDS Z(t). Data bangkitan yang diperoleh tersebut dianggap mewakili data pengamatan untuk masing-masing kelompok.

Gambar 4 Tebaran data untuk populasi N, X, Y dan Z.

Pada Gambar (4) terlihat bahwa tebaran data untuk populasi yang aktif secara seksual atau rentan N(t), menyebar secara acak berada di antara N = 30 sampai N = 33 dalam selang waktu dari t = 0 sampai t = 100. Tebaran data untuk populasi yang tidak tahu

bahwa mereka terinfeksi HIV X(t) mula-mula mengalami penurunan dari X = 230 sampai X

= 98, kemudian tebaran data tersebut menyebar secara acak di antara X = 84 sampai

X = 81 dalam selang waktu t = 6 sampai

t = 100. Tebaran data untuk kelompok

0 20 40 60 80 100

20 25 30 35 40 45 50 Waktu, t P opu las i N

0 20 40 60 80 100

80 100 120 140 160 180 200 220

Waktu, t

P

opu

las

i

X

0 20 40 60 80 100

100 150 200 250 300 Waktu, t P opu las i Y

0 20 40 60 80 100

6

populasi yang tahu bahwa mereka terinfeksi HIV positif mengalami kenaikan secara pesat dari Y = 94 sampai Y = 325 dalam selang waktu t = 0 sampai t = 32, kemudian tebaran data perlahan menaik dari Y = 327 sampai Y = 329 dalam selang waktu t = 34 sampai

t = 100. Tebaran data jumlah kasus AIDS menaik secara pesat dari Z = 2sampai Z = 146 dalam selang waktu t = 0 sampai t = 22.

Kemudian data mengalami kenaikan secara perlahan dari Z = 148 sampai Z = 151 dalam selang waktu t = 24 sampai t = 100.

4.2 Pendugaan Parameter

Parameter model dinamik ini akan diduga dari segugus data yang sebelumnya telah dibangkitkan. Pada kasus ini jumlah data yang digunakan adalah sebanyak 51 buah data untuk masing-masing kelompok.

Parameter yang terdapat pada masing-masing kelompok dapat dirinci sebagai berikut:

1. Kelompok populasi yang aktif secara seksual atau rentan (N) mengandung parameter α, μ,dan .δ

2. Kelompok populasi yang tidak tahu bahwa mereka terinfeksi (X) mengandung parameter α,k, μ,β,dan .v

3. Kelompok populasi yang tahu bahwa mereka terinfeksi (Y) mengandung parameterk, μ, dan β.

4. Kelompok populasi jumlah kasus AIDS (Z) mengandung parameter ,β u,dan .ρ

Langkah-langkah untuk menduga parameter di atas dapat dilihat pada Lampiran 2. Pendugaan parameter dilakukan dengan meminimumkan jumlah kuadrat galat, yang diimplementasikan dengan bantuan software

Mathematica. Fungsi utama yang digunakan

yaitu NDSolve yang digunakan untuk menentukan solusi numerik dari sistem persamaan diferiensial pada model epidemik HIV yaitu x= f_i( ,p x_i) dan FindMinimum

untuk mencari nilai jumlah kuadrat galat yang paling minimum atau paling kecil. Adapun

hasil yang diperoleh dari rangkaian proses di atas adalah: ˆ 0.0100546 ˆ _0.452706 ˆ 0.0152954 ˆ _0.0980932 ˆ 19.4691 k v α μ β = = = = = ˆ 0.294526 ˆ 4.11255 ˆ=27.6102 u ρ δ = =

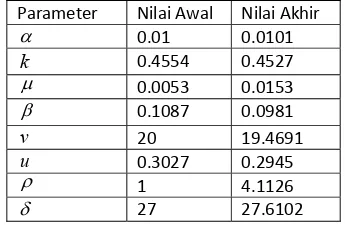
Untuk lebih memperjelas perbedaan antara nilai parameter awal dan parameter yang telah berhasil diduga, maka diberikan tabel perbandingan parameter awal dan parameter akhir di bawah ini:

Tabel 1 Perbandingan nilai parameter awal dan parameter akhir.

Parameter Nilai Awal  Nilai Akhir 

α 0.01 0.0101 

k  0.4554 0.4527  μ 0.0053 0.0153  β 0.1087 0.0981 

v 20 19.4691 

u 0.3027 0.2945 

ρ 1 4.1126 

δ 27 27.6102 

Dari tabel di atas dapat dilihat bahwa nilai parameter awal dan parameter hasil dugaan memiliki nilai yang hampir sama kecuali untuk parameter ρ. Selanjutnya, dari hasil pendugaan parameter di atas maka persamaan (4) dapat dibuat menjadi:

0.0101 0.0153 27.6102

dN

NX N

dt = − − +

0.0101 (0.4527 0.0153 0.0981) 19.4691 dX

NX X

dt = − + + + ₍₅₎

0.4527 (0.0153 0.0981) dY

X Y

dt= − +

0.0981 0.0981 0.2945 4.1126 4.1126

dZ

X Y Z

7

Berikut adalah gambar grafik model dinamik epidemk HIV dengan parameter yang sudah diduga.

.

Gambar 5 Grafik dengan parameter dugaan untuk kelompok populasi yang aktif secara seksual atau rentan

N(t).

Pada Gambar (5) terlihat bahwa jumlah populasi yang aktif secara seksual atau rentan menurun dengan cepat dari N = 50 sampai

N = 17 dalam selang waktu t = 0 sampai t = 2, kemudian menaik dari N = 24 sampai N = 29 dalam selang t = 4 sampai t = 6 dan kemudian konstan di antara N = 32 dalam selang t = 8 sampai t = 100.

Gambar 6 Grafik dengan parameter dugaan untuk kelompok populasi yang tidak tahu bahwa mereka terinfeksi

X(t).

Pada Gambar (6) terlihat bahwa jumlah populasi yang tidak tahu bahwa mereka terinfeksi HIV menurun dengan cepat dari X = 230 sampai X = 81 dalam selang waktu t = 0 sampai t = 10. Kemudian jumlah

populasi X(t) konstan disekitar X = 82 dari selang t = 12 sampai t = 100.

Gambar 7 Grafik dengan parameter dugaan untuk kelompok poulasi yang tahu bahwa mereka terinfeksi HIV positif Y(t).

Pada Gambar (7) terlihat bahwa jumlah populasi yang tahu bahwa mereka terinfeksi HIV positif menaik secara linear logaritmik dari Y = 94 sampai Y = 327 dalam selang t = 0 sampai t = 42. Kemudian konstan diantara N = 328 dari dalam selang waktu

t = 44 sampai t = 100.

Gambar 8 Grafik dengan parameter dugaan untuk jumlah kasus AIDS Z(t).

Pada Gambar (8) terlihat bahwa jumlah kasus AIDS menaik secara linear logaritmik dari Z = 3 sampai Z = 149 dalam selang t = 0 sampai t = 34. Kemudian konstan di sekitar Z

= 150 dalam selang t = 36 sampai t = 100.

0 20 40 60 80 100

20 25 30 35 40 45 50 Waktu, t P op u las i N

0 20 40 60 80 100

80 100 120 140 160 180 200 220 Waktu, t P op u las i X

0 20 40 60 80 100

100 150 200 250 300 Waktu, t P op u las i Y

0 20 40 60 80 100

8

Gambar 9 Gabungan grafik dengan parameter dugaan N(t),X(t), Y(t) dan Z(t).

Pada Gambar (9) terlihat bahwa jumlah populasi yang tahu bahwa mereka terinfeksi HIV positif Y(t) memiliki jumlah yang paling besar, diikuti oleh jumlah kasus AIDS Z(t),

kemudian diikuti jumlah populasi yang tidak tahu bahwa mereka terinfeksi HIV positif X(t) dan yang paling kecil adalah jumlah populasi yang aktif secara seksual atau rentan N(t).

Untuk lebih memperjelas hasil yang diperoleh, berikut perbandingan antara data bangkitan dengan model pada persamaan (5) yang telah menggunakan parameter dugaan. Perbandingan tersebut dapat dilihat pada Gambar (10)-(14)

Gambar 10 Tebaran data dan grafik dengan parameter dugaan untuk populasi N(t).

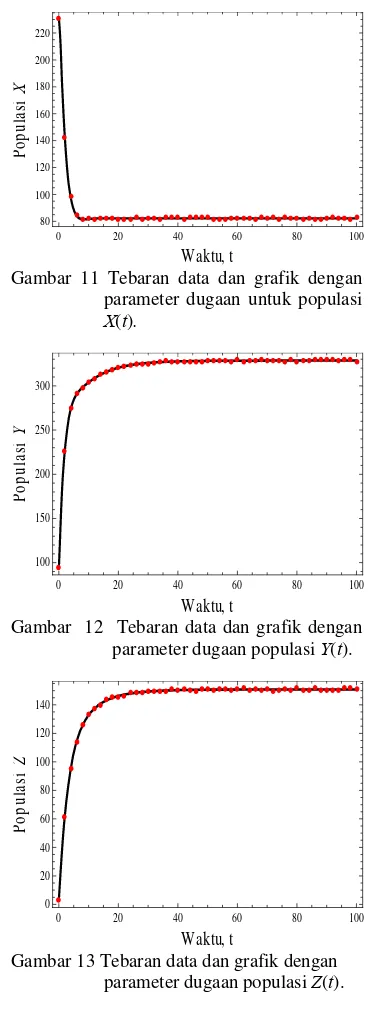
Gambar 11 Tebaran data dan grafik dengan parameter dugaan untuk populasi

X(t).

Gambar 12 Tebaran data dan grafik dengan parameter dugaan populasi Y(t).

Gambar 13 Tebaran data dan grafik dengan parameter dugaan populasi Z(t).

Y (t)

Z (t)

X (t)

N (t)

0 20 40 60 80 100

0 100 200 300 400 Waktu, t P op u las i

0 20 40 60 80 100

20 25 30 35 40 45 50 Waktu, t P op u las i N

0 20 40 60 80 100

80 100 120 140 160 180 200 220 Waktu, t P opu las i X

0 20 40 60 80 100

100 150 200 250 300 Waktu, t P op u las i Y

0 20 40 60 80 100

9

Gambar 14 Gabungan antara gafik tebaran data dan grafik dengan parameter dugaan untuk N(t), X(t), Y(t), dan

Z(t).

Terlihat dari Gambar (10), (11), (12) dan (13), pada kolompok populasi yang aktif secara seksual atau rentan (N), kelompok populasi yang tidak tahu bahwa mereka terinfeksi (X), kelompok populasi yang tahu bahwa mereka terinfeksi (Y), dan kelompok jumlah kasus AIDS (Z), gafik masing-masing kelompok berada di sekitar tebaran data. Juga terdapat sebagian data yang tepat dilalui oleh grafik dengan parameter dugaan tersebut.

4.3 Analisis Akurasi Pendugaan

Untuk melihat seberapa besar galat yang diperoleh, dapat ditentukan dari persentase rataan galat mutlak (MAPE), implementasi secara lengkap dapat dilihat di Lampiran 5.

Berikut akan ditampilkan tabel analisis persentase rataan galat mutlak untuk setiap

state variable.

Tabel 2 Nilai MAPE untuk setiap state variable.

State Variable  MAPE

Populasi yang aktif secara seksual atau rentan (N)

1.6150 %

Populasi yang tidak tahu mereka terinfeksi HIV (X)

0.5653 %

Jumlah kasus AIDS (Z) 0.3553 %

Populasi yang tahu mereka terinfeksi HIV (Y)

0.2002%

Nilai MAPE untuk setiap state variable

secara berturut-turut dapat dilihat pada Tabel 2. Nilai MAPE yang diperoleh berkisar 0.20-1.62%. Nilai MAPE ini menyatakan seberapa besar persentase penyimpangan data pengamatan terhadap model. Kelompok populasi yang aktif secara seksual atau rentan (N) memiliki persentase MAPE yang paling besar yaitu 1.62%. Ini berarti penyimpangan data pengamtan terhadap model untuk kelompok jumlah kasus AIDS memiliki persentase yang paling besar. Populasi yang tahu bahwa mereka terinfeksi HIV positif (Y) memiliki MAPE paling kecil yaitu 0.20% yang berarti untuk data populasi yang tahu bahwa mereka terinfeksi HIV positif memiliki rataan penyimpangan mutlak sebesar 0.20% dari model dugaan. Semakin kecil nilai MAPE maka semakin kecil tingkat penyimpangan data terhadap model.

Cara lain untuk melihat hasil galat untuk setiap state variable adalah menggunakan diagram kotak (box-plot). Pada Gambar (18) diberikan diagram kotak untuk keempat state variable untuk model epidemik HIV.

Selisih Q_{3 dan 1}Q menggambarkan

tingkat keragaman suatu data, semakin besar nilainya maka data semakin beragam. Data yang digunakan dalam diagram kotak ini adalah persentase galat mutlak dari masing-masing state variable.

Gambar 15 Diagram kotak untuk setiap state variableN, X, Y, dan Z.

Untuk lebih memperjelas box-plot di atas, berikut akan diberikan tabel tentang Q1, Q2,

Q3, nilai maksimum, nilai minimum dan

rataan dari galat untuk setiap state variable.

Y

(

t

)

Z

(

t

)

X

(

t

)

N

(

t

)

0 20 40 60 80 100

0 100 200 300 400

Waktu, t

P

op

u

las

i

ææ

N X Z Y

10

Tabel 3 Q1, Q2, Q3, nilai max, nilai min dan rataan dari galat untuk setiap state variable.

State variable  Q1  Q2 Q3 Max Min Rataan 

N  0.5837%  1.6150% 2.1889% 3.8718% 0.0586%  1.4875%  X  0.3268%  0.5653% 0.8195% 1.2107% 0.0181%  0.5945%  Y  0.1187%  0.2002% 0.2407% 0.3093% 0.0122%  0.1835%  Z  0.2401%  0.3553% 0.4981% 0.4981% 0.0010%  0.4840% 

Dari diagram kotak dan tabel di atas dapat dilihat bahwa kesalahan relatif hasil parameter dugaan untuk metode kuadrat terkecil secara umum mempunyai tingkat keragaman yang relatif kecil yaitu berkisar antara 0.58-2.19% untuk populasi yang aktif secara seksual atau rentan (N), 0.33-0.82% untuk populasi yang

tidak tahu bahwa mereka terinfeksi HIV (X), 0.12-0.24% untuk populasi yang tahu bahwa mereka terinfeksi HIV (Y), dan 0.24-0.50% untuk jumlah kasus AIDS (Z). Dari diagram kotak juga teridentifikasi adanya sebuah data pencilan (outlier) untuk state variable Z.

V SIMPULAN DAN SARAN

5.1 Simpulan

Pendugaan parameter model dinamik dengan metode kuadrat terkecil telah dikaji melalui peminimuman jumlah kuadrat galat. Pendugaan parameter model dinamik ini diimplementasikan pada model epidemik HIV/AIDS dengan bantuan software Mathematica.

Dilihat dari nilai parameter awal dan parameter parameter yang sudah berhasil diduga, didapat bahwa tidak ada perbedaan yang terlalu jauh antara kedua parameter tersebut. Dengan kata lain parameter awal dan

parameter penduga memiliki nilai yang hampir sama.

Nilai MAPE terbesar yang diperoleh yaitu pada kelompok populasi yang aktif secara seksual atau rentan N(t) yaitu 1.62% dan yang terkecil yaitu pada kelompok populasi yang tahu bahwa mereka terinfeksi HIV Y(t) yaitu sebesar 0.20%.

5.2 Saran

Tema karya ilmiah ini masih terbuka untuk dikembangkan. Salah satunya adalah pengembangan metode untuk pembandingan dengan menggunakan metode robust.

DAFTAR PUSTAKA

De Arazoza H et al. 1999. Modeling HIV epidemic under concact tracing-the Cuban case. Journal of Theoretical Medicine 2:267-274.

Huber P. 1981. Robust Statistics. Jhon Willey & Sons, New York, 153-199.

Gao LQ, Hethcote WH, Lorca M. 1995. Four SEI Endemic Models with Periodicity and Separatrices. Math Biosci. 128:157-184.

Lomen D, Mark J. 1988. Differential

Equations. New Jersey: Prentice-Hall,

Inc.

Mathews JH. 1992. Numerical Methods for Mathematics, Science, and Enginering.

London: Prentice-Hall.

Rice BJ, Mark J. 1994. Ordinary Differential

Equations: with Aplications. Ed ke-3.

California Pacific Grove.

Thornly JHM, Johnson IR. 1990. Comparison of Model with Experiment : Model Fitting in Plant and Crop Modelling.

11

12

Lampiran 1

Membangkitkan Data Hipotetik

Clear[modelhipotetik,stateVar,sol,data,n,x,y,z,datan,datax,datay,d ataz,gbrn,gbrx,gbry,gbrz,α,δ,k,μ,β,v,u,ρ,

model,penduga,modelpenduga,solpenduga,gbrpendugan, gbrpendugax,gbrpendugay,gbrpendugaz]

modelhipotetik={n'[t]==-0.01 n[t] x[t]-0.0053 n[t]+30, x'[t]==0.01 n[t] x[t]-(0.4554+0.0053+0.1087) x[t]+20, y'[t]==0.4554 x[t]-(0.0053+0.1087) y[t],

z'[t]==0.1087 x[t]+0.1087 y[t]-0.3027 z[t]+0.0001, n[0] 50,x[0]==230,y[0] 94,z[0]==3};

stateVar={n,x,y,z};

sol=Flatten[NDSolve[modelhipotetik,stateVar,{t,0,100}]]

{n→InterpolatingFunction[{{0.,100.}},<>], x→InterpolatingFunction[{{0.,100.}},<>], y→InterpolatingFunction[{{0.,100.}},<>], z→InterpolatingFunction[{{0.,100.}},<>]}

Berarti menyelesaikan sistem persamaan diferensial untuk n[t], x[t], y[t], dan z[t] dengan nilai awal n[0]=50, x[0] = 230, y[0] = 94, dan z[0] = 3. Untuk jangka waktu t = 0 sampai t = 100 yang disimpan dalam variabel sol.

SeedRandom[5];

data=Table[{t,(n[t]/.sol)+Random[Real,{-1,1}], (x[t]/.sol)+Random[Real,{-1,1}],

(y[t]/.sol)+Random[Real,{-1,1}],

(z[t]/.sol)+Random[Real,{-1,1}]},{t,0,100,2}]; datan=data/.{t_,n_,x_,y_,z_}->{t,n}

datax=data/.{t_,n_,x_,y_,z_}->{t,x} datay=data/.{t_,n_,x_,y_,z_}->{t,y} dataz=data/.{t_,n_,x_,y_,z_}->{t,z}

Berarti: Membangun data hipotetik dengan cara menambahkan bilangan acak antara -1 sampai 1 pada n[t], menambahkan bilangan acak antara -1sampai 1 pada data x[t], menambahkan bilangan acak antara -1 sampai 1 pada y[t],dan menambahkan bilangan acak antara -1 sampai 1 pada z[t], dengan selisih dua satuan waktu. Data hipotetik inilah yang akan mewakili data pengamatan.

Berikut adalah data hipotetik yang diperoleh:

Data hipotetik untuk n[t].

13

Data hipotetik untuk x[t].

{{0,230.697},{2,142.145},{4,98.2487},{6,84.6397},{8,81.407},{10,82 .4275},{12,81.136},{14,82.2556},{16,82.3137},{18,82.6121},{20,81.6 294},{22,81.8753},{24,81.8196},{26,82.7986},{28,81.7409},{30,82.37 62},{32,81.9878},{34,81.3518},{36,82.7713},{38,83.212},{40,82.7105 },{42,81.5737},{44,82.8252},{46,82.7129},{48,83.1809},{50,83.2084} ,{52,81.7373},{54,81.403},{56,81.8171},{58,82.3437},{60,82.4021},{ 62,82.4332},{64,81.9353},{66,81.7717},{68,83.1939},{70,82.0897},{7 2,82.9269},{74,81.7332},{76,83.0373},{78,82.505},{80,82.5504},{82, 81.7001},{84,82.0126},{86,81.5188},{88,81.7209},{90,82.4554},{92,8 3.1443},{94,82.6836},{96,81.9104},{98,81.631},{100,83.1494}}

Data hipotetik untuk y[t].

{{0,94.2257},{2,226.22},{4,274.365},{6,291.406},{8,297.937},{10,30 4.126},{12,307.667},{14,313.205},{16,315.113},{18,317.843},{20,321 .215},{22,321.537},{24,322.751},{26,324.177},{28,324.741},{30,325. },{32,325.812},{34,327.831},{36,327.853},{38,327.418},{40,327.189} ,{42,327.316},{44,327.119},{46,327.293},{48,327.755},{50,328.899}, {52,328.467},{54,328.066},{56,327.985},{58,327.83},{60,329.292},{6 2,327.673},{64,328.535},{66,327.839},{68,329.254},{70,328.85},{72, 329.005},{74,328.794},{76,327.734},{78,329.38},{80,327.619},{82,32 8.269},{84,328.769},{86,329.483},{88,329.262},{90,329.396},{92,329 .293},{94,328.543},{96,329.294},{98,329.331},{100,327.591}}

Data hipotetik untuk z[t].

{{0,2.79608},{2,61.2914},{4,95.3988},{6,113.695},{8,125.908},{10,1 33.274},{12,137.16},{14,140.081},{16,143.776},{18,145.405},{20,145 .385},{22,146.613},{24,148.406},{26,148.412},{28,148.995},{30,149. 627},{32,149.544},{34,149.198},{36,149.808},{38,150.996},{40,150.0 58},{42,150.85},{44,150.011},{46,149.744},{48,151.047},{50,151.305 },{52,150.614},{54,151.222},{56,150.74},{58,150.583},{60,151.168}, {62,151.532},{64,150.615},{66,151.113},{68,150.112},{70,151.282},{ 72,149.878},{74,150.12},{76,151.286},{78,149.96},{80,151.639},{82, 150.153},{84,150.073},{86,151.754},{88,150.27},{90,150.114},{92,15 0.279},{94,149.932},{96,151.666},{98,151.72},{100,151.258}}

Berikut adalah grafik data n[t], x[t], y[t], dan z[t].

gbrn ListPlot datan, PlotStyle , , , PointSize . ,

PlotRange , , waktu t ,populasi rentan n ,

0 20 40 60 80 100

20 25 30 35 40 45 50

Waktu, t

P

opu

las

i

14

gbrx ListPlot datax, PlotStyle , , , PointSize . ,

PlotRange , , waktu t ,populasi x ,

gbry ListPlot datay, PlotStyle , , , PointSize . ,

PlotRange , , waktu t ,populasi y ,

gbrz ListPlot dataz, PlotStyle , , , PointSize . ,

PlotRange , , waktu t ,populasi z ,

0 20 40 60 80 100

80 100 120 140 160 180 200 220

Waktu, t

Po

p

u

la

si

X

0 20 40 60 80 100

100 150 200 250 300

Waktu, t

Po

p

u

la

si

Y

0 20 40 60 80 100

0 20 40 60 80 100 120 140

Waktu, t

P

opu

las

i

15

Lampiran 2

Pendugaan Parameter

leastSquare model_List, data_List, stateVar_List, par_List

Module dataModel, prm, peta, sumSq, hsl, sol, bnr, selang, nilaiPar, penduga, dataSolusiPenduga, koefDet , dataModel Drop #, &/@ ;

#, &/@ // ;

__ #, # nilaiPar ;

hsl NDSolve model, stateVar, , data , , data , //Flatten; sol # , &/@ ;

, , data , , data , , data , data , ; Plus@@Plus@@ bnr dataModel ^ & ;

#, &/@ ;

, ;

model:={n'[t]==-α n[t] x[t]-μ n[t]+δ, x'[t]==α n[t] x[t]-(k+μ+β) x[t]+v, y'[t]==k x[t]-(μ+β) y[t],

z'[t]==β x[t]+β y[t]-u z[t]+ρ, n[0]==50,x[0]==230,y[0]==94,z[0]==3 };

stateVar={n,x,y,z}; par={

{α,0,0.5}, {k,0,0.5}, {μ,0,0.1}, {β,0,0.3}, {v,18,22}, {u,0,1}, {ρ,0,3}, {δ,0,1} };

penduga=leastSquare[model,data,stateVar,par]

{0.0100546,0.452706,0.0152954,0.0980932,19.4691,0.294526, 4.11255,27.6102}

Berarti : menduga nilai parameter model dengan menggunakan metode kuadrat terkecil, sehingga diperoleh nilai dugaan parameter sebagai berikut: α = 0.0100546, k = _0.452706, μ = 0.0152954, β = 0.0980932, v = _19.4691, u = _0.294526, ρ = 4.11255,dan δ=27.6102.

dataSolusiPenduga Block #, # penduga;

hsl NDSolve model, stateVar, , data , , data , //Flatten; sol # , &/@ ;

bnr Table sol, , data , , data , , data , data , & ;

16

Lampiran 3

Gambar Grafik Model dengan Parameter Hasil Dugaan

gbrPenduga Block #, # penduga;

hsl NDSolve model, stateVar, , data , , data , //Flatten; sol # , &/@ ; #, , data , , data ,

, PlotStyle . 7 , , , ,

DisplayFunction , &/@ & ; Show gbrPenduga , Frame , ,

" ", " "

Show gbrPenduga , Frame , , " ", " "

Show gbrPenduga , Frame , , " ", " "

0 20 40 60 80 100

20 25 30 35 40 45 50

Waktu, t

P

op

u

las

i

N

0 20 40 60 80 100

80 100 120 140 160 180 200 220

Waktu, t

P

opu

las

i

X

0 20 40 60 80 100

100 150 200 250 300

Waktu, t

P

opu

las

i

17

Show gbrPenduga , Frame , , " ", " "

Gabungan antara grafik model dengan parameter dugaan n[t],x[t],y[t], dan z[t]

Show gbrPenduga , gbrPenduga , gbrPenduga , gbrPenduga ,

Frame , , " ", " , , , "

0 20 40 60 80 100

0 20 40 60 80 100 120 140

Waktu, t

P

opu

las

i

Z

Y

(

t

)

Z

(

t

)

X

(

t

)

N

(

t

)

0 20 40 60 80 100

0 100 200 300 400

Waktu, t

P

opu

las

18

Lampiran 4.

Gambar Grafik Gabungan Tebaran Data dan Model dengan Parameter

Hasil Dugaan

Berikut adalah grafik perbandingan data hipotetik dengan model dugaan untuk n[t], x[t], y[t], dan z[t].

dataModel=Drop[#,1]&/@data;

selangWaktu=Flatten[Take[#,1]&/@data];

dataGbr=Table[{selangWaktu[[t]],#[[t]]},{t,Length [dataModel]}]&/@Transpose[dataModel];

gbrData=ListPlot[#,PlotStyle

->{Hue[.7],PointSize[0.015]},DisplayFunction ->Identity,PlotRange->All]&/@dataGbr;

Show gbrPenduga , gbrData , Frame True, Axes False, FrameLabel Waktu t ,Populasi n

Show gbrPenduga , gbrData , Frame , , " ", " "

0 20 40 60 80 100

20 25 30 35 40 45 50

Waktu, t

P

opu

las

i

N

0 20 40 60 80 100

80 100 120 140 160 180 200 220

Waktu, t

P

opu

la

si

19

Show gbrPenduga , gbrData , Frame , , " ", " "

Show gbrPenduga , gbrData , Frame True, Axes False, FrameLabel "Waktu t ", "Populasi z "

Gambar gabungan grafik tebaran data dan grafik dugaan parameter untuk x t , y t dan z t . Show gbrPenduga , gbrData , gbrPenduga , gbrData ,

gbrPenduga , gbrData , gbrPenduga , gbrData , Frame , , " ", " , , , "

0 20 40 60 80 100

100 150 200 250 300

Waktu, t

Po

p

u

las

i

Y

0 20 40 60 80 100

0 20 40 60 80 100 120 140

Waktu, t

P

opu

las

i

Z

Y

(

t

)

Z

(

t

)

X

(

t

)

N

(

t

)

0 20 40 60 80 100

0 100 200 300 400

Waktu, t

P

op

u

las

20

Lampiran 5.

Pencarian Nilai Galat

Mencari nilai Persentase Galat Absolute untuk setiap state variable N, X, Y, dan Z

galat Abs dataModel dataSolusiPenduga /dataModel

{{1.1334,0.301989,0.239483,7.29325},{3.87183,0.309832,0.0363674,0. 0103362},{2.57529,0.549198,0.216394,0.258228},{2.55895,0.513362,0. 309268,0.552588},{2.6783,0.185556,0.120894,0.241644},{0.190531,0.8 40387,0.088578,0.435666},{1.06536,1.21069,0.300542,0.201067},{0.38 7279,0.0181178,0.200183,0.475298},{0.261651,0.0236484,0.223327,0.4 5316},{0.541315,0.39324,0.175102,0.368766},{0.31231,0.798681,0.237 309,0.542739},{2.46503,0.493765,0.170976,0.377496},{2.08279,0.5620 02,0.19769,0.319326},{0.939269,0.626891,0.0770461,0.0773656},{2.89 998,0.659079,0.157814,0.000950005},{0.768247,0.117205,0.280748,0.1 78071},{2.1046,0.355917,0.192261,0.0718208},{2.17541,1.14058,0.296 924,0.45768},{0.756161,0.593998,0.201756,0.170501},{2.35806,1.1204 5,0.0122035,0.52092},{1.70161,0.520891,0.146867,0.177373},{1.01903 ,0.865437,0.159911,0.287478},{0.560473,0.658722,0.261283,0.318969} ,{0.180216,0.523758,0.240824,0.536823},{1.63234,1.08354,0.125713,0 .299462},{1.81221,1.11612,0.201717,0.445205},{3.50639,0.663563,0.0 540591,0.031065},{0.221887,1.07694,0.081435,0.35534},{2.79867,0.56 5288,0.116506,0.0245822},{0.0586248,0.077759,0.172325,0.089789},{0 .990563,0.148631,0.265697,0.29002},{1.72575,0.186232,0.23246,0.522 905},{1.61495,0.42028,0.0263843,0.0876582},{2.12744,0.621179,0.189 404,0.238505},{2.94723,1.099,0.238653,0.430413},{0.321302,0.231431 ,0.113965,0.343884},{1.26431,0.780557,0.159107,0.591554},{2.08144, 0.668611,0.093803,0.431023},{3.1119,0.912395,0.230472,0.341848},{1 .63907,0.273103,0.269679,0.540707},{1.01659,0.328005,0.267097,0.57 229},{2.20236,0.709304,0.0693252,0.412734},{0.84117,0.325617,0.082 4486,0.466671},{0.359885,0.933309,0.29884,0.645488},{0.849979,0.68 3672,0.231378,0.335871},{0.0919587,0.21311,0.271819,0.440283},{1.6 3894,1.04,0.240558,0.329896},{0.317932,0.488548,0.0125928,0.562274 },{2.40562,0.450806,0.24049,0.587037},{0.607023,0.794657,0.25168,0 .622081},{2.09151,1.04603,0.278225,0.318383}}

Berarti mencari nilai galat mutlak untuk setiap state variable.

Needs "StatisticalPlots`"

BoxWhiskerPlot galat, BoxLabels " ", " ", " ", " "

Berarti menampilkan gambar box-whisker galat untuk setiap state variable. ææ

N X Z Y

21

Untuk mencari nilai Q1, Q2, Q3, nilai max, nilai min dan rataan dari galat untuk setiap state variable , data galat mutlak yang diperoleh dari Mathematica dimasukkan ke Excel. sehingga diperoleh hasil sebagai berikut:

State variable  Q1  Q2 Q3 Max Min  Rataan