ANALISIS MODEL NEURO-GARCHDAN MODEL
BACKPROPAGATIONUNTUK PERAMALAN
INDEKS HARGA SAHAM GABUNGAN
SKRIPSI
ADE IRMA APRILIA 100803010
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
ANALISIS MODEL NEURO-GARCHDAN MODEL
BACKPROPAGATIONUNTUK PERAMALAN
INDEKS HARGA SAHAM GABUNGAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
ADE IRMA APRILIA 100803010
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
i
PERSETUJUAN
Judul : Analisis Model Neuro-GARCH dan Model
Backpropagation untuk Peramalan Indeks Harga Saham Gabungan
Kategori : Skripsi
Nama : Ade Irma Aprilia Nomor Induk Mahasiswa : 100803010 Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alama (FMIPA) Universitas Sumatera Utara
Diluluskan di Medan, April 2014
Komisi Pembimbing :
Pembimbing 2, Pembimbing 1,
Drs. Partano Siagian, M.Sc. Dr. Suwarno Ariswoyo, M.Si. NIP. 19511227 198003 1 001 NIP. 19500321 198003 1 001
Diketahui/Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
ii
PERNYATAAN
ANALISIS MODEL NEURO-GARCH DAN MODEL BACKPROPAGATIONUNTUK PERAMALAN
INDEKS HARGA SAHAM GABUNGAN
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, April 2014
iii
PENGHARGAAN
Bismillaahirrahmaanirrahiim
Puji dan syukur penulis ucapkan kepada Allah SWT Yang Maha Esa dan Kuasa
atas limpahan rahmat dan karunia-Nya sehingga skripsi ini dapat diselesaikan.
Pada skripsi ini penulis mengambil judul tentang Analisis Model Neuro-GARCH dan Model Backpropagation untuk Peramalan Indeks Harga Saham Gabungan.
Dalam penyusunan skripsi ini banyak pihak yang membantu, sehingga
dengan segala rasa hormat penulis mengucapkan terima kasih kepada:
1. Bapak Dr. Suwarno Ariswoyo, M.Si. selaku dosen dan pembimbing 1 yang
berkenan dan rela mengorbankan waktu, tenaga, dan pikiran guna memberikan
petunjuk dan bimbingannya dalam penulisan skripsi ini.
2. Bapak Drs. Partano Siagian, M.Sc. selaku dosen dan pembimbing 2 yang juga
berkenan dan rela mengorbankan waktu, tenaga, dan pikiran guna memberikan
petunjuk dan bimbingannya dalam penulisan skripsi ini.
3. Bapak Dr. Pasukat Sembiring, M.Si. dan Bapak Drs. Gim Tarigan, M.Si.
selaku komisi penguji atas masukan dan saran yang telah diberikan demi
perbaikan skripsi ini.
4. Bapak Dr. Sutarman, M.Sc. selaku dekan FMIPA USU.
5. Bapak Prof. Dr. Tulus, M.Si. dan Ibu Dr. Mardiningsih, M.Si. selaku ketua
dan sekretaris Departemen Matematika FMIPA USU.
6. Ibunda tercinta Mari, S.Pd., Ayahanda tercinta Rustam Efendi dan adik-adikku
Nurul Mustaqima dan M. Chandra Mufti tersayang atas segala pengertian,
kesabaran, dukungan, dan kasih sayang yang telah diberikan kepada penulis
selama di bangku perkuliahan hingga akhirnya menyelesaikan skripsi ini.
7. Teman-teman angkatan 2010 tersayang terkhusus untuk Kesebelasan, Aan,
Dodo, dan masih banyak lagi yang tak tersebutkan namanya yang telah
membantu penulis dengan memberikan semangat dan doa dalam
iv
8. Senior dan Junior di IM3, Kak Evi, Kak Ningrum, Kak Putri, Bang Gilang, Awang, Budi, dan masih banyak lagi yang tak tersebutkan namanya yang telah
membantu penulis dengan memberikan semangat dan doa dalam
menyelesaikan tulisan ini.
Penulis juga menyadari masih banyak kekurangan dalam skripsi ini, baik
dalam teori maupun penulisannya. Oleh karena itu, penulis mengharapkan saran
dari pembaca demi perbaikan bagi penulis. Semoga segala kebaikan dalam bentuk
bantuan yang telah diberikan mendapat balasan dari Allah SWT. Akhirnya penulis
berharap semoga tulisan ini bermanfaat bagi para pembaca.
Medan, April 2014
Penulis
v
ANALISIS MODEL NEURO-GARCHDAN MODEL BACKPROPAGATIONUNTUK PERAMALAN
INDEKS HARGA SAHAM GABUNGAN
ABSTRAK
Salah satu masalah yang dihadapi dalam proses peramalan adalah masalah heteroskedastisitas. Heteroskedastisitas banyak terjadi terutama pada data keuangan. Model General Auto Regressive Conditional Heteroskedasticity
(GARCH) dan jaringan saraf tiruan model Backpropagation merupakan metode yang dapat digunakan pada data yang mengalami heteroskedastisitas. Dalam penelitian ini kedua model tersebut dikombinasikan menjadi sebuah model yang disebut Neuro-GARCH. Peramalan dilakukan pada data Indeks Harga Saham Gabungan bulan Februari 2014 dengan menggunakan data bulan Januari-Desember 2013. Selain menggunakan model Neuro-GARCH juga dilakukan peramalan dengan model Backpropagation. Hasil dari peramalan kedua metode ini dibandingkan berdasarkan nilai Mean Absolute Percentage Error (MAPE). Dari hasil yang diperoleh diketahui bahwa model Neuro-GARCHlebih baik dalam meramalkan Indeks Harga Saham Gabungan jika dibandingkan dengan model
Backpropagation dilihat dari MAPEmasing-masing model yaitu 0,46615% untuk model Neuro-GARCHdan 1,845% untuk model Backpropagation.
vi
ANALYSIS OF NEURO-GARCH AND BACKPROPAGATION MODELS FOR FORCASTING COMPOSITE STOCK PRICE INDEX
ABSTRACT
One of the problems encountered in the process of forecasting is the problem of heteroscedasticity. Heteroscedasticity occurred primarily in financial data. General Auto Regressive Conditional Heteroskedasticity (GARCH) Model and Backpropagation neural network model are methods that can be used on the data that is experiencing heteroscedasticity. In this paper, both models are combined into a model called Neuro-GARCH. Forecasting is done on the data Composite Stock Price Index in January and February 2014 using data from January to December 2013. Not only using Neuro-GARCH models, this paper also performed Backpropagation forecasting model. The results of the two forecasting methods are compared based on the value of the Mean Absolute Percentage Error (MAPE). From the results obtained it is known that the Neuro-GARCH model in forecasting Composite Stock Price Index better when compared with the model of Backpropagation seen MAPE of each model is 0,46615% for Neuro-GARCH model and 1.845 % for backpropagation model.
vii
Daftar Lampiran xi
Bab 1. Pendahuluan 1
Bab 2. Tinjuan Pustaka 7
2.1. Stasioneritas 7
2.1.1. Uji Kestasioneran Data 7
2.2. Heteroskedastisitas 10
2.2.1. Uji Heteroskedastisitas 11
2.3. Uji Pemilihan Model Terbaik 12
2.3.1. Uji Akaike Information Criterion (AIC) 12 2.3.2..Uji Schwarz Information Criterion (SIC) 13
2.3.3. Uji Kelayakan Model 13
2.4. Maximum Likelihood Method (Metode Kemungkinan Maksimum) 14 2.5.General Autoregressive Conditional Heteroscedasticity (GARCH) 16 2.5.1. Langkah-Langkah Pemodelan GARCH 20
2.6. Jaringan Saraf Tiruan 21
2.6.1. Arsitektur Jaringan 23
2.6.2. Fungsi Aktivasi 25
2.6.3. Algoritma Belajar dan Pelatihan 26
2.6.4. Backpropagation 27
2.6.5. Momentum 31
2.6.6. Aplikasi Backpropagationdalam Peramalan 32
2.7. Neuro-GARCH 34
Bab 3. Metode Penelitian 36
3.1 Merumuskan Masalah 36
viii
3.3. Pengamatan dan Pengumpulan Data 36
3.3.1. Indeks Harga Saham Gabungan 37
3.3.2. Indeks Harga Saham Gabungan di Bursa Efek
Indonesia (BEI) 37
3.4. Membuat Landasan Teori 38
3.5. Analisis Data IHSG dengan Model Neuro-GARCH 38 3.6. Analisis Data IHSG dengan Model Backpropagation 39
3.7. Membandingkan Hasil Peramalan 40
3.8. Membuat Kesimpulan 40
Bab 4. Hasil dan Pembahasan 41
4.1 Analisis Data dengan Menggunakan Model Neuro-GARCH 41 4.1.1. Peramalan dengan Menggunakan Model GARCH 41 4.1.1.1. Identifikasi Kestasioneran Data 41 4.1.1.2..Membentuk Persamaan Autoregresi Sebagai
Model Awal 47
4.1.1.3..Pengujian Heteroskedastisitas atau Efek ARCH
pada Residual 47
4.1.1.4. Estimasi Parameter Model GARCH 47
4.1.1.5. Uji Kelayakan Model 48
4.1.1.6. Peramalan 49
4.1.2..Peramalan Data dengan Menggunakan
Model Backpropagation 49
4.2. Analisis Data dengan Menggunakan Model Backpropagation 59 4.3. Perbandingan Hasil Peramalan Model Neuro-GARCHdengan
Model Backpropagation 68
Bab 5. Kesimpulan dan Saran 70
5.1. Kesimpulan 70
5.2. Saran 71
Daftar Pustaka 72
ix
DAFTAR TABEL
Nomor Judul Halaman
Tabel
x
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
2.1 Sebuah Sel Saraf Tiruan 23
2.2. Jaringan Layar Tunggal 24
2.3. Jaringan Layar Jamak 25
4.1. Korelogram Data IHSG 43
4.2. Korelogram Data IHSG Setelah Pembedaan 45
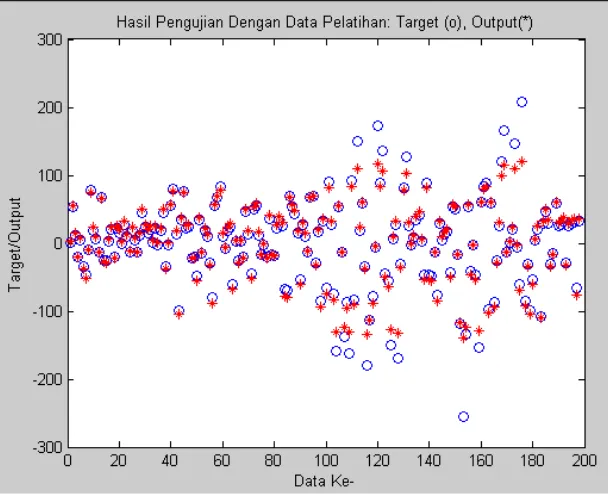
4.3 Hasil Pelatihan Sampai 5000 Epoch 53
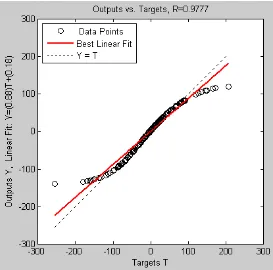
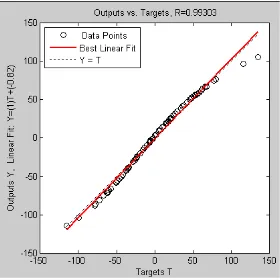
4.4. Hubungan Target dengan OutputJaringan untuk Data Pelatihan 55 4.5. Perbandingan antara Target dengan OutputJaringan untuk Data
Pelatihan 56
4.6. Hubungan Target dengan OutputJaringan untuk Data Pengujian 58 4.7. Perbandingan antara Target dengan OutputJaringan untuk Data
Pengujian 59
4.8. Hasil Pelatihan Sampai 5000 Epoch 63
4.9. Hubungan Target dengan OutputJaringan untuk Data Pelatihan 65 4.10. Perbandingan antara Target dengan OutputJaringan untuk Data
Pelatihan 66
4.11. Hubungan Target dengan OutputJaringan untuk Data Pengujian 67 4.12. Perbandingan antara Target dengan OutputJaringan untuk Data
xi
DAFTAR LAMPIRAN
Nomor Judul Halaman
Lamp
1. Data IHSG (Januari-Desember 2013) 73
2. Hasil Pembedaan (Differencing) 80
3. Analisis Data Menggunakan Program Eviews8 87 4. Data yang Akan Dilatih pada Model Neuro-GARCH 90 5. Data yang Akan Diuji pada Model Neuro-GARCH 95
6. Hasil Peramalan Model Neuro-GARCH 97
7. Data yang Akan Dilatih pada Model Backpropagation 98 8. Data yang Akan Diuji pada Model Backpropagation 102 9. Perhitungan Tingkat Keakuratan Antara Data Aktual dan Ramalan
dengan Menggunakan Model Neuro-GARCH 104
10. Perhitungan Tingkat Keakuratan Antara Data Aktual dan Ramalan
v
ANALISIS MODEL NEURO-GARCHDAN MODEL BACKPROPAGATIONUNTUK PERAMALAN
INDEKS HARGA SAHAM GABUNGAN
ABSTRAK
Salah satu masalah yang dihadapi dalam proses peramalan adalah masalah heteroskedastisitas. Heteroskedastisitas banyak terjadi terutama pada data keuangan. Model General Auto Regressive Conditional Heteroskedasticity
(GARCH) dan jaringan saraf tiruan model Backpropagation merupakan metode yang dapat digunakan pada data yang mengalami heteroskedastisitas. Dalam penelitian ini kedua model tersebut dikombinasikan menjadi sebuah model yang disebut Neuro-GARCH. Peramalan dilakukan pada data Indeks Harga Saham Gabungan bulan Februari 2014 dengan menggunakan data bulan Januari-Desember 2013. Selain menggunakan model Neuro-GARCH juga dilakukan peramalan dengan model Backpropagation. Hasil dari peramalan kedua metode ini dibandingkan berdasarkan nilai Mean Absolute Percentage Error (MAPE). Dari hasil yang diperoleh diketahui bahwa model Neuro-GARCHlebih baik dalam meramalkan Indeks Harga Saham Gabungan jika dibandingkan dengan model
Backpropagation dilihat dari MAPEmasing-masing model yaitu 0,46615% untuk model Neuro-GARCHdan 1,845% untuk model Backpropagation.
vi
ANALYSIS OF NEURO-GARCH AND BACKPROPAGATION MODELS FOR FORCASTING COMPOSITE STOCK PRICE INDEX
ABSTRACT
One of the problems encountered in the process of forecasting is the problem of heteroscedasticity. Heteroscedasticity occurred primarily in financial data. General Auto Regressive Conditional Heteroskedasticity (GARCH) Model and Backpropagation neural network model are methods that can be used on the data that is experiencing heteroscedasticity. In this paper, both models are combined into a model called Neuro-GARCH. Forecasting is done on the data Composite Stock Price Index in January and February 2014 using data from January to December 2013. Not only using Neuro-GARCH models, this paper also performed Backpropagation forecasting model. The results of the two forecasting methods are compared based on the value of the Mean Absolute Percentage Error (MAPE). From the results obtained it is known that the Neuro-GARCH model in forecasting Composite Stock Price Index better when compared with the model of Backpropagation seen MAPE of each model is 0,46615% for Neuro-GARCH model and 1.845 % for backpropagation model.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Peramalan merupakan suatu kegiatan memperkirakan apa yang terjadi pada masa
mendatang berdasarkan nilai masa lalu (Makridakis, 1999). Kegiatan peramalan
ini sedang banyak dibicarakan. Hal ini disebabkan semakin meningkatnya
kesadaran untuk mempersiapkan dan mengantisipasi segala kejadian di masa
mendatang. Peramalan dibutuhkan di berbagai bidang seperti bidang ekonomi dan
sosial politik.
Dalam melakukan peramalan tidak selalu berjalan dengan lancar. Terdapat
banyak kendala yang dihadapi sehingga hasil peramalan yang diperoleh tidak
akurat. Salah satu kendala yang sering dihadapi dalam kegiatan peramalan adalah
data yang memiliki ragam yang cukup besar atau varians datanya tidak konstan.
Dalam statistik, kejadian ini disebut dengan heteroskedastisitas. Masalah
heteroskedastisitas biasanya terjadi pada data ekonomi.
Salah satu model peramalan yang dapat digunakan untuk data yang
bersifat heteroskedastik adalah Autoregressive Conditional Heteroskedasticity
(ARCH). Model ARCH pertama kali diperkenalkan oleh Robert F. Engle (Juli, 1982). Model ini dikembangkan terutama untuk menjawab persoalan tentang
adanya volatilitas (varians tak konstan) pada data ekonomi dan bisnis, khususnya
dalam bidang keuangan. Menurut Engle, varians residual yang berubah-ubah ini
terjadi karena varians residual tidak hanya fungsi dari variabel independen tetapi
tergantung seberapa besar residual di masa lalu sehingga varians residual yang
terjadi saat ini akan sangat bergantung pada residual periode sebelumnya. Oleh
regresinya dilakukan pula peramalan pada varians residualnya sehingga varians
residual data akan berubah setiap waktu.
Model ini kemudian dikembangkan oleh Bollerslev pada tahun 1986
menjadi General Autoregressive Conditional Heteroskedasticity (GARCH) yaitu varians residual tidak hanya bergantung dari residual periode lalu tetapi juga
bergantung varians residual periode lalu.
Selain model tersebut, model yang sering digunakan dalam peramalan
adalah jaringan saraf tiruan model Backpropagation. Model ini dikenal sebagai model yang sangat baik dalam peramalan karena hasil peramalan yang diperoleh
akurat dan memiliki kesalahan yang relatif kecil. Model dengan jaringan saraf
tiruan ini dilatih dengan seperangkat data untuk bisa mengenal dan
mengidentifikasi pola data. Proses pelatihan ini disebut tahap belajar (learning process). Tahap belajar adalah bagaimana sebuah konfigurasi jaringan dapat dilatih untuk mempelajari data historis yang ada. Dengan pelatihan ini,
pengetahuan yang terdapat pada data dapat diserap dan direpresentasikan oleh
nilai-nilai bobot koneksinya. Backpropagation adalah salah satu metode dari jaringan saraf tiruan yang dapat diaplikasikan dengan baik dalam bidang
peramalan (forecasting). Backpropagation melatih jaringan untuk mendapatkan keseimbangan antara kemampuan jaringan mengenali pola yang digunakan
selama trainingserta kemampuan jaringan untuk memberikan respon yang benar terhadap pola masukan yang serupa namun tidak sama dengan pola yang dipakai
selama pelatihan (Siang, 2005).
Dalam peramalan, hal terpenting yang akan dicapai adalah hasil peramalan
dengan nilai erroryang minimum. Semakin kecil nilai errormaka semakin akurat
hasil peramalan yang diperoleh. Dalam sebuah penelitian Hakim (2012)
menggunakan model ARIMA sebagai input pada jaringan saraf model
Backpropagation (Neuro-ARIMA). Hasilnya menunjukkan bahwa model Neuro
Neuro-ARCH (kombinasi antara model ARCH dengan jaringan saraf tiruan
Backpropagation) untuk meramalkan data saham beberapa perusahaan dan membandingkannya dengan jaringan saraf tiruan Backpropagation. Dengan membandingkan nilai MSE dan MAD diperoleh bahwa peramalan data saham menggunakan model Neuro-ARCH lebih baik daripada jaringan saraf tiruan
Backpropagation karena model Neuro-ARCH memiliki nilai MSEdan MADyang
lebih kecil daripada jaringan saraf tiruan Backpropagation.
Dalam penelitian lain Theta R. Ramadhani meramalkan return saham tiga perusahaan go public dengan mengkombinasikan model GARCH sebagai pengembangan model ARCH dengan model Backpropagation atau disebut juga model Neuro-GARCH. Dengan menggunakan algoritma pelatihan Quasi Newton
pada pelatihan jaringannya penelitian ini memberi kesimpulan bahwa model
kombinasi Neuro-GARCH menghasilkan peramalan yang lebih baik daripada model Backpropagationkarena memilikiMSEdan MADyang lebih kecil.
Dari penelitian-penelitian tersebut penulis tertarik untuk menerapkan
teknik gabungan antara jaringan saraf tiruan dengan model GARCH yang selanjutnya disebut dengan Neuro-GARCHdalam meramalkan nilai Indeks Harga Saham Gabungan (IHSG) kemudian membandingkannya dengan peramalan
dengan menggunakan jaringan saraf tiruan model Backpropagation.
Berdasarkan uraian tersebut, penulis mengambil judul penelitian “Analisis Model Neuro-GARCH dan Model Backpropagation untuk Peramalan Indeks Harga Saham Gabungan”.
1.2 Perumusan Masalah
Berdasarkan pendahuluan dirumuskan masalah apakah dengan membuat model
GARCH pada data kemudian hasilnya dijadikan input pada model
langsung menjadikan data aktual sebagai input pada model Backpropagation
dilihat dari MAPEpada masing-masing model.
1.3 Pembatasan Masalah
Masalah yang diteliti dibatasi pada penghitungan nilai MAPE pada hasil peramalan dengan model Neuro-GARCH dan model Backpropagation. Dalam penelitian ini peramalan hanya dilakukan pada Indeks Harga Saham Gabungan
untuk dua bulan kedepan (Januari dan Februari 2014) tanpa menghitung besarnya
resiko yang terkandung pada saham sehingga tidak dilakukan peramalan terhadap
model volatilitasnya. Data yang digunakan diperoleh dari Web resmi Bursa Efek
Indonesia (www.idx.co.id) yaitu data harian saham pada IHSG periode Januari
2013-Februari 2014 Dalam hal ini data hanya sebagai bahan untuk
perhitungannya dan tidak memperhatikan bagaimana pengaruh dan fenomena
yang terjadi pada data yang digunakan.
1.4 Tujuan Penelitian
Tujuan dari penelitian ini adalah mengkaji model Neuro-GARCH sebagai model kombinasi antara model GARCHdan model Backpropagationdalam meramalkan data Indeks Harga Saham Gabungan.
1.5 Manfaat Penelitian
Penelitian ini diharapkan dapat bermanfaat sebagai informasi bahwa dapat
diperoleh model baru untuk melakukan peramalan dengan menggabungkan
1.6 Metodologi Penelitian
Metodologi penelitian yang digunakan untuk menyelesaikan permasalahan dalam
tugas akhir ini adalah sebagai berikut:
1. Studi literatur
Tahap ini dilakukan dengan mengidentifikasi permasalahan, mengkaji dan
menganalisis model peramalan data volatilitas General Autoregressive Conditonal Heteroscedasticity, jaringan saraf tiruan model
Backpropagation, dan kombinasi kedua model tersebut yakni model
Neuro-GARCH. Penelusuran referensi ini bersumber dari buku, jurnal
maupun penelitian yang telah ada sebelumnya mengenai hal-hal yang
berhubungan dengan Neuro-GARCH dan model Backpropagation dalam penggunaannya untuk peramalan.
2. Pengumpulan data
Pada tahap ini dilakukan pengambilan data Indeks Harga Saham
Gabungan (IHSG). Data yang digunakan diperoleh dari Web resmi Bursa Efek Indonesia (www.idx.co.id) yaitu data harian saham pada IHSG
periode Januari 2013-Februari 2014.
3. Membuat landasan teori
Setelah mendapatkan data yang dimaksud, selanjutnya dilakukan
pembahasan secara teoritis mengenai metode yang digunakan dalam
penelitian berdasarkan hasil studi literatur. Hal ini dilakukan untuk
mengetahui bagaimana metode yang digunakan dalam kajian teorinya
sebelum digunakan dalam penelitian. Pembahasan ini di tuangkan dalam
4. Peramalan data IHSG dengan Neuro-GARCHdan model Backpropagation
Pada tahap ini dilakukan peramalan data IHSG dengan model Neuro-GARCH dan model Backpropagation kemudian dihitung MAPE (Mean Absolute Percentage Error) dari masing-masing model.
5. Membandingkan hasil peramalan
Pada tahap ini dilakukan peramalan dengan Neuro-GARCH kemudian hasil peramalan yang diperoleh dibandingkan dengan hasil peramalan
dengan model Backpropagationdilihat dari MAPE. Keakuratan peramalan dapat dilihat berdasarkan MAPE yang diperoleh dari masing-masing
metode. Jika MAPElebih kecil berarti metode tersebut lebih akurat.
6. Membuat kesimpulan
Pada tahap ini dibuat kesimpulan hasil analisis data sekaligus memberikan
BAB 2
TINJAUAN PUSTAKA
2.1Stasioneritas
Stasioneritas berarti bahwa tidak terdapat perubahan yang drastis pada data. Fluktuasi data berada di sekitar suatu nilai rata-rata yang konstan, tidak tergantung pada waktu dan variansi dari fluktuasi tersebut. (Makridakis, 1995)
Sekumpulan data dinyatakan stasioner jika nilai rata-rata dan varians dari data time series tersebut tidak mengalami perubahan secara sistematik sepanjang waktu atau dengan kata lain rata-rata dan variansnya konstan. Kestasioneran data ini berkaitan dengan metode estimasi yang digunakan. Tidak stasionernya data akan mengakibatkan kurang baiknya model yang diestimasi. Selain itu apabila
data yang digunakan dalam model ada yang tidak stasioner, maka data tersebut dipertimbangkan kembali validitas dan kestabilannya. Salah satu penyebab tidak stasionernya sebuah data adalah adanya autokorelasi. Bila data distasionerkan maka autokorelasi akan hilang dengan sendirinya, karena itu transformasi data untuk membuat data yang tidak stasioner menjadi stasioner sama dengan transformasi data untuk menghilangkan autokorelasi.
2.1.1 Uji Kestasioneran Data
pengamatan dengan lag kurang dari . Adapun nilai autokorelasi untuk lag 1, 2, 3, …, k dapat dicari dengan persamaan berikut:
(2.1)
di mana:
autokorelasi pada lag ke-
= data pengamatan ke-
= rata-rata data
= data pengamatan
ke-Suatu nilai koefisien autokorelasi dikatakan tidak berbeda secara signifikan apabila nilainya berada pada suatu rentang nilai yang diperoleh dari nilai kesalahan standar dan sebuah nilai kepercayaan. Nilai kesalahan standar dari autokorelasi lag ke- adalah:
(2.2)
di mana:
standar error atau kesalahan standar
= banyaknya data,
Nilai autokorelasi parsial lag ke- digunakan persamaan berikut:
(2.3)
di mana:
= autokorelasi populasi
= autokorelasi populasi
kestasioneran data. Ada beberapa macam pengujian yang dapat dilakukan yaitu Uji Bartlett, Uji Box-Pierce, Uji Ljung-Box(LB) dan Unit Root Test.
Uji stasioner data dilakukan dengan menguji stasioneritas pada data asli. Dalam penelitian ini kestasioneran data akan diuji dengan menggunakan Unit Root Test. Apabila hasil pengujian menunjukkan bahwa data tidak stasioner maka dilakukan modifikasi untuk memperoleh data yang stasioner. Salah satu cara yang umum dipakai adalah metode pembedaan (differencing), yaitu mengurangi nilai pada suatu periode dengan nilai data periode sebelumnya. Apabila tetap tidak stasioner maka dilakukan pembedaan lagi.
Uji akar unit (Unit Root Test) merupakan pengujian yang sangat populer dan dikenalkan oleh David Dickey dan Whyne Fuller. Dalam uji ini dibentuk persamaan regresi dari data aktual pada periode ke- dan ke- -1. Dalam uji akar
unit digunakan model berikut:
(2.4)
Jika koefisien regresi dari ( , maka disimpulkan bahwa terdapat masalah bahwa tidak stasioner. Dengan demikian dapat disebut mempunyai
“unit root” atau berarti data tidak stasioner.
Bila persamaan (2.4) dikurangi sisi kanan dan kiri maka
persamaannya menjadi:
(2.5)
(2.6)
atau dapat ditulis dengan:
(2.7)
di mana:
= hasil difference data pada periode ke- = data aktual periode ke-
= data aktual periode ke-
= koefisien regresi
= error yang white noise dengan mean=0 dan varians=
Pada tahap ini sudah dilakukan pembedaan sebagai metode untuk menanggulangi masalah ketidakstasioneran data. Kemudian data akan diuji kembali. Dari persamaan (2.7) dapat dibuat hipotesis:
Jika hipotesis ditolak dengan derajat kepercayaan maka
artinya terdapat unit root, sehingga data time series tidak stasioner. Dengan
membentuk persamaan regresi antara dan akan diperoleh koefisien
regresinya, yaitu .
Hipotesis yang digunakan dalam uji akar unit (Unit Root) menjelaskan bahwa apabila hasil uji menyatakan nilai Augmented Dickey-Fuller test statistic lebih kecil nilai kritis pada derajat kepercayaan tertentu atau nilai tingkat signifikansinya lebih kecil dari derajat kepercayaan , maka hipotesis nol
yang menyatakan bahwa data tersebut tidak stasioner ditolak dan demikian sebaliknya.
2.2 Heteroskedastisitas
Heteroskedastisitas merupakan suatu kondisi apabila suatu data memiliki varians residual yang tidak konstan atau dengan kata lain situasi saat varians dari
faktor pengganggu adalah tidak sama untuk semua observasi. Jika kesalahan
estimator yang dihasilkan tetap konsisten, tetapi tidak lagi efisien karena ada estimator lain yang memilki varians yang lebih kecil daripada estimator yang memiliki residual yang bersifat heteroskedastisitas. Adanya masalah heteroskedastisitas juga menjadi indikasi adanya efek ARCH pada data.
2.2.1 Uji Heteroskedastisitas
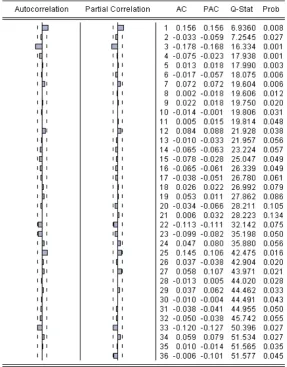
Untuk mendeteksi heteroskedastisitas dapat diketahui dengan mengamati beberapa ringkasan statistik dari data. Pengujian efek ARCH pada suatu data dapat dilakukan dengan mengamati koefisien autokorelasi dari data tersebut. Keberadaan efek ARCH ditunjukkan dengan nilai autokorelasi yang signifikan pada 15 beda kala pertama yang diperiksa dari perilaku AC (Autocorrelation) dan PAC (Partial Autocorrelation). Pada tahap ini juga dilakukan pengujian terhadap eksistensi efek ARCH pada suatu data dengan mengamati AC dan PAC. Keberadaan efek ARCH ditunjukkan dengan nilai koefisien autokorelasi dari data yang signifikan pada 15 beda kala pertama (Firdaus, 2006).
Selain itu dibutuhkan pula uji formal untuk memutuskannya. Uji formal untuk mendeteksi adanya heteroskedastisitas antara lain uji korelasi Rank Spearman, uji Park, Goldfeld−Quandt, uji Breusch-Pagan Godfrey (uji BPG), uji white, dan uji Lagrange Multiplier.
Uji Lagrange Multiplier sering disebut sebagai ARCH-LM test. Hal ini disebabkan selain mendeteksi adanya heteroskedastisitas pada data, uji ini juga menunjukkan adanya efek ARCH yang menjadi pembahasan pada penelitian ini. Oleh karen itu, uji Lagrange Multiplier (ARCH-LM test) akan digunakan pada penelitian ini untuk menguji heteroskedastisitas dan efek ARCH.
adalah bahwa varians residual bukan hanya fungsi dari variabel independen tetapi tergantung pada residual kuadrat pada periode sebelumnya (Enders, 1995).
Berikut merupakan langkah pengujian efek ARCH: Hipotesis:
(tidak terdapat efek ARCH)
(terdapat efek ARCH)
Statistik Uji:
(2.8)
di mana:
taraf signifikansi
jumlah variabel independen
residual kuadrat terkecil rata-rata sampel dari T
nilai probabilitas Kriteria keputusan:
ditolak jika atau .
2.3 Uji Pemilihan Model Terbaik
2.3.1 Uji Akaike Information Criterion (AIC)
AIC digunakan untuk memilih model terbaik. Jika dua model
dibandingkan, maka model dengan nilai AIC terkecil merupakan model yang lebih
AIC = = (2.9)
di mana:
SSE = Sum Square Error = = 2
k = jumlah parameter dalam model n = jumlah observasi (sampel)
2.3.2 Uji Schwarz Information Criterion (SIC)
Kegunaan SIC pada prinsipnya tidak berbeda dengan AIC. Semakin kecil nilai AIC dan SIC maka semakin baik sebuah model. SIC digunakan untuk menentukan panjang lag atau lag yang optimum. Rumusan SIC adalah sebagai
berikut:
SIC = = (2.10)
di mana:
SSE = Sum Square Error = = 2
k = jumlah parameter dalam model n = jumlah observasi (sampel)
3.3.3 Uji Kelayakan Model
Setelah mendapatkan model yang terbaik dilakukan uji kelayakan terhadap model yang telah diperoleh. Uji yang dilakukan adalah uji terhadap residual yang mencakup histogram-normality test dan uji efek ARCH.
variabel didistribusikan secara normal atau tidak. Untuk melihat kenormalan residual dapat dilihat pada probabilitas statistik Jarque Bera yang yang ditunjukkan histogram. Formula uji statistik JarqueBera adalah:
(2.11)
di mana:
= kurtosis
= skewness statistik
Adapun hipotesis yang digunakan dalam uji normalitas ini adalah:
(residual tidak berdistribusi normal)
(residual berdistribusi normal)
Sebagai pengujian terakhir dilakukan pengujian signifikansi parameter. Suatu parameter dikatakan signifikan jika memiliki pengaruh nyata terhadap model.
Signifikansi dapat dilihat dari nilai probabilitas yang lebih kecil dari derajat kepercayaan.
2.4. Maximum Likelihood Method (Metode Kemungkinan Maksimum)
Maximum Likelihood Method atau metode kemungkinan maksimum adalah teknik yang sangat luas dipakai dalam penaksiran suatu parameter distribusi data dan tetap dominan dipakai dalam pengembangan uji -uji yang baru (Lehmann, 1986). Berikut penjelasan tentang maximum likelihood method pada persamaan regresi.
Jika terdapat sebuah model:
(2.12)
(2.13)
Maka fungsi densitas probabilitas residual yang berdistribusi normal untuk setiap eksperimen adalah:
(2.15)
(2.16)
(2.17)
karena dan maka fungsi densitas
(2.17) menjadi:
(2.18)
dan densitas keseluruhan untuk observasi adalah:
(2.19)
Fungsi Likelihood-nya adalah:
(2.21)
Dengan mensubstitusikan nilai dan
maka persamaan (2.21) menjadi:
(2.22)
Untuk mendapatkan nilai parameter-parameter dan , maka persamaan (2.22) diturunkan terhadap parameter-parameter tersebut satu per satu seperti berikut:
(2.23)
(2.24)
dan seterusnya sampai semua nilai parameter diperoleh.
2.5General Autoregressive Conditional Heteroscedasticity (GARCH)
Model General Autoregressive Conditional Heteroscedasticity (GARCH) adalah model yang digunakan dalam peramalan data yang memiliki permasalahan heteroskestisitas tanpa menghilangkan heteroskedastisitas tersebut. Model ini dikembangkan oleh Bollerslev (1986) dari model ARCH yang ditemukan oleh Robert F. Engle (1982). Engle menemukan bahwa varians residual data akan berubah setiap waktu bergantung pada residual periode sebelumnya. Untuk persamaan autoregresi:
(2.25)
(2.26) residual pada periode ke-
varians dari residual periode ke-
komponen konstanta
parameter ARCH
kuadrat residual periode ke-
Persamaan (2.27) adalah model ARCH berorde p atau biasa dinotasikan dengan ARCH (p). Sementara itu, Bollerslev mengembangkan model ARCH dengan menemukan bahwa varians residual tidak hanya bergantung dari residual periode lalu tetapi juga bergantung varians residual periode lalu. Untuk persamaan autoregresi:
(2.28)
memiliki varians residual berikut:
varians dari residual periode ke-
komponen konstanta parameter ARCH
= kuadrat residual periode ke-
= parameter GARCH
= varians residual periode
ke-Persamaan (2.30) adalah model GARCH berorde (p,q) atau biasa dinotasikan dengan GARCH (p,q). Diketahui bahwa pada model GARCH varians
residual ( ) tidak hanya bergantung dari residual periode lalu ( ) tetapi juga
bergantung varians residual periode lalu ( ). Model ini dibangun untuk
menghindari orde yang terlalu tinggi pada model ARCH berdasarkan prinsip parsimoni atau memilih model yang paling sederhana.
Menurut Tsay (2005) nilai residual dengan (persamaan 2.14) dikatakan mengikuti model GARCH (p,q) jika:
(2.31)
(2.32)
dengan
Persamaan varians yang memenuhi persamaan GARCH (p,q)
menghubungkan antara varians residual pada waktu ke- dengan varians residual pada waktu sebelumnya.
Jika persamaan GARCH ditulis ke dalam operator B (Backshift), di mana B dikalikan terhadap dan sebagai koefisien residual dan varian residual sehingga diperoleh:
atau (2.33)
maka persamaan (2.31) menjadi:
(2.35)
atau
(2.36)
koefisien-koefisien dalam model GARCH (p,q) harus bernilai positif.
Model ARCH ( ) didefinisikan sebagai berikut:
(2.37)
akan diperlihatkan bahwa model GARCH (p,q) dapat menggantikan model ARCH berorde tak hingga atau ARCH ( ) dengan mengurangkan persamaan (2.36)
dengan pada sisi kanan dan kiri maka diperoleh sebagai berikut:
(2.38)
(2.39)
(2.40)
(2.41)
dengan dan , sehingga terbukti bahwa model GARCH
(p,q) dapat menggantikan model ARCH( ).
Model GARCH yang paling sederhana dan paling sering digunakan adalah model GARCH (1,1). Model ini secara umum dinyatakan sebagai berikut (Bollerslev,1986):
(2.42)
Model ARCH dan GARCH tidak dapat diestimasi dengan menggunakan Ordinary Least Square (OLS) tetapi dengan menggunakan maximum likelihood
estimation method atau metode kemungkinan maksimum dalam analisis parameternya.
2.5.1 Langkah-Langkah Pemodelan GARCH
Dalam memodelkan data dengan model GARCH untuk tujuan peramalan langkah-langkah yang dilakukan adalah sebagai berikut:
1. Identifikasi
Identifikasi dengan memeriksa data hasil pengamatan apakah sudah stasioner atau belum dengan membuat grafik AC dan PAC. Selain itu kestasioneran data juga akan diuji menggunakan Unit Root Test. Hal ini perlu dilakukan karena untuk membentuk model GARCH diperlukan data yang stasioner.
2. Uji Heteroskedastisitas
Pada tahap ini, data sudah dibentuk dalam model autoregresi sehingga uji heteroskedastisitas menggunakan uji Lagrange Multiplier dilakukan terhadap residual dari model autoregresi terbaik yang didapat. Secara
spesifik model autoregresi yang digunakan adalah model ARIMA. 3. Estimasi dan Pengujian Parameter
Langkah selanjutnya setelah menguji keberadaan efek ARCH atau heteroskedastisitas residual model ARIMA adalah membentuk model GARCH dan mengestimasi parameter model dengan menggunakan metode kemungkinan maksimum atau maximum likelihood method.
4. Uji Pemilihan Model Terbaik
kelayakan model akan dilihat kenormalan residual model, sedangkan pada uji signifikansi akan dilihat apakah parameter hasil estimasi sudah baik atau mempunyai pengaruh yang nyata terhadap model.
5. Penggunaan Model untuk Peramalan
Apabila model sudah memenuhi uji-uji yang dilakukan pada uji pemilihan model terbaik, maka model siap digunakan untuk peramalan.
2.6Jaringan Saraf Tiruan
Jaringan saraf tiruan (JST) atau disebut juga dengan neural network (NN), adalah jaringan dari sekelompok unit pemroses kecil yang dimodelkan berdasarkan jaringan saraf manusia. Jaringan saraf tiruan merupakan sistem adaptif yang dapat merubah strukturnya untuk memecahkan masalah berdasarkan informasi eksternal maupun internal yang mengalir melalui jaringan tersebut. Secara sederhana, JST adalah sebuah alat pemodelan data statistik non-linier. JST dapat digunakan untuk memodelkan hubungan yang kompleks antara input dan output untuk menemukan pola-pola pada data.
Jaringan saraf merupakan salah satu sistem pemrosesan informasi yang didesain dengan menirukan cara kerja otak manusia dalam menyelesaikan suatu
masalah dengan melakukan proses belajar melalui perubahan bobot sinapsisnya. Jaringan saraf tiruan mampu mengenali kegiatan dengan berbasis pada data masa lalu. Data masa lalu akan dipelajari oleh jaringan sehingga mempunyai kemampuan untuk memberi keputusan terhadap data yang belum pernah dipelajari (Hermawan, 2006).
Siang (2005) mengemukakan bahwa jaringan saraf tiruan adalah sistem informasi yang memiliki karakteristik mirip dengan jaringan saraf tiruan biologi. Jaringan saraf tiruan dibentuk sebagai generalisasi model matematika dari jaringan saraf biologi, dengan asumsi bahwa:
b. Sinyal dikirimkan di antara neuron-neuron melalui penghubung-penghubung.
c. Penghubung antar neuron memiliki bobot yang akan memperkuat atau memperlemah sinyal.
d. Untuk menemukan output, setiap neuron menggunakan fungsi aktivasi (biasanya bukan fungsi linier) yang dikenakan pada jumlah input yang diterima. Besarnya output ini selanjutnya dibandingkan dengan suatu batas ambang.
Jaringan saraf tiruan ditentukan oleh 3 hal:
a. Pola hubungan antar neuron (disebut arsitektur jaringan).
b. Metode untuk menentukan bobot penghubung (disebut metode training/ learning/ algoritma).
c. Fungsi aktivasi (fungsi transfer).
Setiap neuron tersebut berfungsi untuk menerima atau mengirim sinyal dari atau ke neuron-neuron lainnya. Pengiriman sinyal disampaikan melalui penghubung. Kekuatan hubungan yang terjadi antara setiap neuron yang saling terhubung dikenal dengan nama bobot.
Arsitektur jaringan dan algoritma pelatihan sangat menentukan model-model jaringan saraf tiruan. Arsitektur tersebut gunanya untuk menjelaskan arah
x
1x
2x
3Y
W1
W2
W3
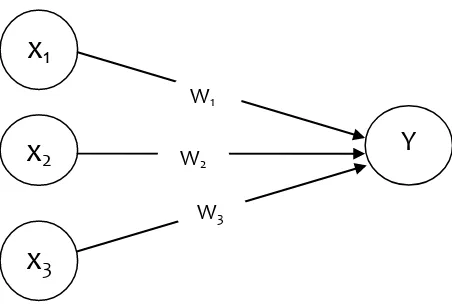
Gambar 2.1. Sebuah Sel Saraf Tiruan
Y menerima input dari neuron x1, x2, dan x3 dengan bobot hubungan masing-masing adalah w1, w2 dan w3. Ketiga impuls neuron yang ada dijumlahkan net = x1w1+ x2w2+x3w3. Besarnya impuls yang diterima oleh Y mengikuti fungsi aktivasi y = f(net). Apabila nilai fungsi akivasi cukup kuat, maka sinyal akan diteruskan. Nilai fungsi aktivasi (keluaran model jaringan) juga dapat dipakai sebagai dasar untuk merubah bobot.
2.6.1 Arsitektur Jaringan
Arsitektur jaringan saraf tiruan digolongkan menjadi 3 model:
1. Jaringan Layar Tunggal
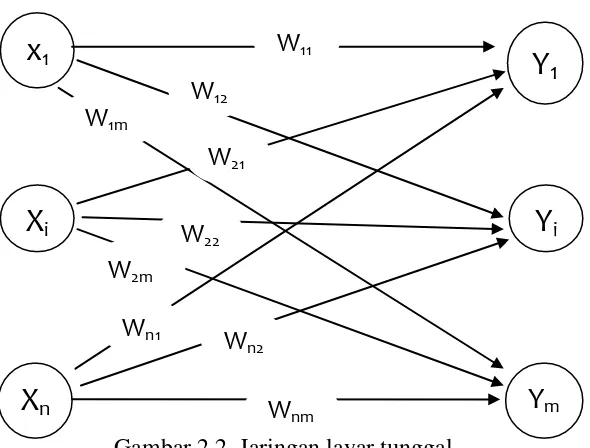
Gambar 2.2. Jaringan layar tunggal
Pada Gambar 2.2. diperlihatkan bahwa arsitektur jaringan layar tunggal dengan n buah masukan (x1, xi,..., xn) dan m buah keluaran (Y1,
Yi,..., Ym). Dalam jaringan ini semua unit input dihubungkan dengan semua
unit output. Tidak ada unit input yang dihubungkan dengan unit input lainnya dan unit output pun demikian.
2. Jaringan Layar Jamak
Jaringan ini merupakan perluasan dari layar tunggal. Dalam jaringan ini, selain unit input dan output, ada unit-unit lain yang sering disebut layar tersembunyi. Layar tersembunyi ini tersebut bisa saja lebih dari satu, sebagai contoh perhatikan Gambar 2.3 dibawah ini:
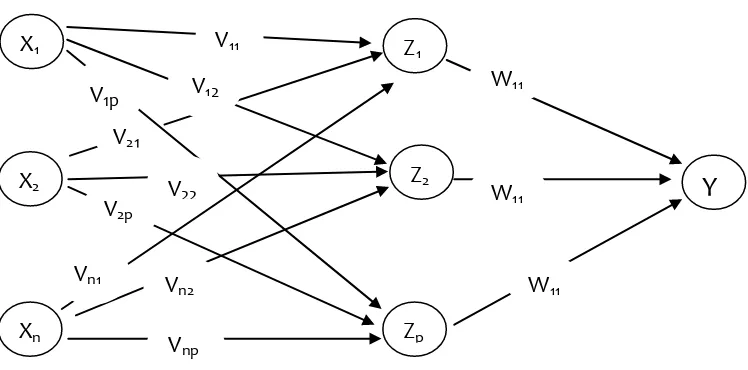
Gambar 2.3. Jaringan layar jamak
Pada Gambar 2.3. diperlihatkan jaringan dengan n buah unit masukan (x1, x2,..., xn), sebuah layar tersembunyi yang terdiri dari p buah
unit (z1, z2...,zp) dan 1 buah unit keluaran. Jaringan layar jamak dapat
menyelesaikan masalah yang lebih kompleks dibandingkan dengan layar tunggal, meskipun kadangkala proses pelatihan lebih kompleks dan lama.
3. Jaringan Reccurent
Model jaringan recurrent mirip dengan jaringan layar tunggal ataupun ganda. Hanya saja, ada neuron output yang memberikan sinyal pada unit input (sering disebut feedback loop). Dengan kata lain sinyal mengalir dua
arah, yaitu maju dan mundur.
2.6.2 Fungsi Aktivasi
Siang (2004) menyebutkan bahwa fungsi aktivasi digunakan untuk menentukan keluaran suatu neuron. Dalam jaringan saraf tiruan, argumen fungsi aktivasi adalah net masukan (kombinasi linier masukan dan bobotnya). Jika net
maka fungsi aktivasinya adalah .
Beberapa fungsi aktivasi yang sering dipakai adalah sebagai berikut: a. Fungsi Treshold (batas ambang)
(2.43)
Dalam beberapa kasus, fungsi threshold yang dibuat tidak berharga 0 atau 1, tapi berharga -1 atau 1 (sering dibuat threshold bipolar).
(2.44)
b. Fungsi Sigmoid
(2.45)
Fungsi sigmoid sering dipakai karena nilai fungsinya yang terletak antara 0 dan 1 dan dapat digunakan dengan mudah.
(2.46)
c. Fungsi Identitas
(2.47)
Fungsi ini sering dipakai apabila diharapkan keluaran jaringan berupa sembarang bilangan riil (bukan hanya pada range [0,1] atau [1,-1]).
2.6.3 Algoritma Belajar dan Pelatihan
Dalam jaringan saraf tiruan terdapat konsep belajar atau pelatihan sehingga jaringan-jaringan yang dibentuk akan belajar melakukan generalisasi karakteristik
rangka melakukan pengaturan bobot, sehingga pada akhir pelatihan akan diperoleh bobot-bobot yang baik.
Dalam menyelesaikan suatu permasalahan, jaringan saraf tiruan memerlukan algoritma belajar atau pelatihan yaitu bagaimana sebuah konfigurasi jaringan dapat dilatih untuk mempelajari data historis yang ada. Dengan pelatihan ini, pengetahuan yang terdapat pada data dapat diserap dan direpresentasikan oleh nilai-nilai bobot koneksinya.
Berdasarkan cara modifikasi bobotnya, ada dua macam pelatihan yang dikenal, (Siang 2005) yaitu sebagai berikut:
1. Pelatihan Dengan Supervisi (Supervised Training)
Dalam pelatihan dengan supervisi, terdapat sejumlah pasangan data (masukan, target, dan keluaran) yang dipakai untuk melatih jaringan hingga diperoleh bobot yang diinginkan. Pada setiap pelatihan, suatu masukan diberikan ke jaringan. Jaringan akan memproses dan mengeluarkan keluaran. Selisih antara keluaran jaringan dengan target (keluaran yang diinginkan) merupakan kesalahan yang terjadi. Jaringan akan memodifikasi bobot sesuai dengan kesalahan tersebut.
2. Pelatihan Tanpa Supervisi (unsupervised Training)
Dalam pelatihannya, perubahan bobot jaringan dilakukan berdasarkan parameter tertentu dan jaringan dimodifikasi menurut ukuran parameter tersebut. Model yang menggunakan pelatihan ini adalah model jaringan kompetitif.
2.6.4 Backpropagation
Backpropagation melatih jaringan untuk mendapatkan keseimbangan antara kemampuan jaringan mengenali pola yang digunakan selama training serta kemampuan jaringan untuk memberikan respon yang benar terhadap pola masukan yang serupa namun tidak sama dengan pola yang dipakai selama pelatihan (Siang, 2005).
Menurut Siang (2005)terdapat tiga fase dalam pelatihan Backpropagation yaitu :
1. Fase 1, yaitu propagasi maju
Dalam propagasi maju, setiap sinyal masukan dipropagasi (dihitung maju) ke layar tersembunyi hingga layar keluaran dengan menggunakan fungsi aktivasi yang ditentukan.
2. Fase 2, yaitu propagasi mundur
Kesalahan (selisih antara keluaran jaringan dengan target yang diinginkan) yang terjadi dipropagasi mundur mulai dari garis yang berhubungan langsung dengan unit-unit di layar keluaran.
3. Fase 3, yaitu perubahan bobot
Pada fase ini dilakukan modifikasi bobot untuk menurunkan kesalahan
yang terjadi. Ketiga fase tersebut diulang-ulang terus hingga kondisi penghentian dipenuhi.
Algoritma pelatihan untuk jaringan dengan satu layar tersembunyi (dengan fungsi aktivasi sigmoid biner) adalah sebagai berikut :
Langkah 1 : Inisialisasi semua bobot dengan bilangan acak kecil.
Langkah 2 : Jika kondisi penghentian belum terpenuhi, lakukan langkah 2 sampai langkah 9.
Fase I : Propagasi maju
Langkah 4: Tiap unit masukan menerima sinyal dan meneruskannya ke unit tersembunyi di atasnya.
Langkah 5 : Hitung semua keluaran di unit tersembunyi .
(2.48)
(2.49)
Langkah 6 : Hitung semua keluaran jaringan di unit
(2.50)
(2.51)
Fase II : Propagasi mundur
Langkah 7: Hitung faktor unit keluaran berdasarkan kesalahan disetiap unit keluaran
(2.52)
merupakan unit kesalahan yang akan diperbaiki dalam
perubahan bobot layar di bawahnya (langkah 7).
Hitung suku perubahan bobot (yang akan dipakai nanti
untuk merubah bobot dengan laju percepatan
Langkah 8 : Hitung faktor unit tersembunyi berdasarkan kesalahan di setiap unit tersembunyi
(2.53)
Faktor unit tersembunyi :
(2.54)
Hitung suku perubahan bobot (yang akan dipakai nanti
untuk merubah bobot )
Fase III : Perubahan bobot
Langkah 9 : Hitung semua perubahan
Perubahan bobot garis yang menuju unit tersembunyi :
Langkah 10 : Setelah diperoleh bobot yang baru dari hasil perubahan bobot, fase pertama dilakukan kembali kemudian dibandingkan hasil keluaran dengan target apabila hasil keluaran telah sama dengan target dan toleransi error maka proses dihentikan.
Setelah pelatihan selesai dilakukan, jaringan dapat dipakai untuk pengenalan pola. Dalam hal ini, hanya propagasi maju (langkah 4 dan 5) saja yang dipakai untuk menentukan keluaran jaringan.
Dalam beberapa kasus pelatihan yang dilakukan memerlukan iterasi yang banyak sehingga membuat proses pelatihan menjadi lama. Untuk mempercepat iterasi dapat dilakukan dengan parameter α atau laju pemahaman. Nilai α terletak
antara 0 dan 1 (0 ≤ α ≤ 1). Jika harga α semakin besar, maka iterasi yang dipakai semakin sedikit. Akan tetapi jika harga α terlalu besar, maka akan merusak pola yang sudah benar sehingga pemahaman menjadi lambat.
2.6.5 Momentum
Dalam backpropagation, standar perubahan bobot didasarkan atas gradien yang terjadi untuk pola yang dimasukkan saat itu. Modifikasi dilakukan dengan merubah bobot yang didasarkan atas arah gradien pola terakhir dan pola sebelumnya (momentum) yang dimasukkan. Jadi perhitungannya tidak hanya pola masukan terakhir saja. Momentum ditambahkan untuk menghindari perubahan bobot yang mencolok akibat adanya data yang sangat berbeda dengan data yang lain. Jika beberapa data terakhir yang diberikan ke jaringan memiliki pola serupa (berarti arah gradien sudah benar), maka perubahan bobot dilakukan secara cepat. Namun jika data terakhir yang dimasukkan memiliki pola yang berbeda dengan pola sebelumnya, maka perubahan bobot dilakukan secara lambat. Dengan penambahan momentum, bobot baru pada waktu ke (t+1) didasarkan atas bobot pada waktu t dan (t-1). Disini harus ditambahkan dua variabel yang mencatat besarnya momentum untuk dua iterasi terakhir.
Jika μ adalah konstanta (0 ≤ μ ≤ 1) yang menyatakan parameter momentum maka bobot baru dihitung berdasarkan persamaan berikut ini:
(2.55)
dengan,
bobot awal pola kedua (hasil itersai pola pertama)
bobot awal pada iterasi pertama
dan
(2.56)
dengan,
bobot awal pola kedua (hasil iterasi pola pertama)
2.6.6 Aplikasi Backpropagation dalam Peramalan
Peramalan adalah salah satu bidang yang paling baik dalam mengaplikasikan metode Backpropagation. Secara umum, masalah peramalan dapat dinyatakan dengan sejumlah data runtun waktu (time series) x1, x2,..., xn. Masalahnya adalah
memperkirakan berapa harga xn+1 berdasarkan x1, x2,..., xn. Jumlah data dalam satu
periode (misalnya satu tahun) pada suatu kasus dipakai sebagai jumlah masukan dalam Backpropagation. Sebagai targetnya diambil data bulanan pertama setelah periode berakhir.
Langkah-langkah membangun struktur jaringan untuk peramalan sebagai berikut:
1. Transformasi Data
Dilakukan transformasi data agar kestabilan taburan data dicapai dan juga untuk menyesuaikan nilai data dengan range fungsi aktivasi yang digunakan dalam jaringan. Jika ingin menggunakan fungsi aktivasi sigmoid (biner), data harus ditransformasikan dulu karena interval keluaran fungsi aktivasi sigmoid adalah [0.1]. Data bisa ditransformasikan ke interval [0.1]. Tapi akan lebih baik jika
ditransformasikan ke interval yang lebih kecil, misalnya pada interval [0,1.0,9], karena mengingat fungsi sigmoid nilainya tidak pernah mencapai 0 ataupun 1. Untuk mentransformasikan data ke interval [0,1.0,9] dilakukan dengan transformasi linier sebagai berikut :
Transformasi Linier selang [a.b]
(2.57)
dengan,
nilai minimum data aktual keseluruhan nilai maksimum data aktual keseluruhan
Dengan transformasi ini, maka data terkecil akan menjadi 0,1 dan data terbesar akan menjadi 0,9 (Siang, 2005).
2. Pembagian Data
Pembagian data dilakukan dengan membagi data penelitian menjadi data pelatihan dan pengujian. Komposisi data pelatihan dan pengujian bisa dilakukan dengan trial and error, namun komposisi data yang sering digunakan adalah sebagai berikut:
a. 90% untuk data pelatihan dan 10% untuk data pengujian. b. 80% untuk data pelatihan dan 20% untuk data pengujian. c. 70% untuk data pelatihan dan 30% untuk data pengujian. d. Dan seterusnya
Proses pembagian data ini sangat penting, agar jaringan
mendapat data pelatihan yang secukupnya. Jika data yang dibagi kurang dalam proses pelatihan maka akan menyebabkan jaringan mungkin tidak dapat mempelajari taburan data dengan baik. Sebaliknya, jika data yang dibagi terlalu banyak untuk proses pelatihan maka akan melambatkan proses pemusatan (konvergensi). Masalah overtraining (data pelatihan yang berlebihan) akan memyebabkan jaringan cenderung untuk menghafal data yang dimasukan daripada mengeneralisasi.
3. Perancang Arsitektur Jaringan Yang Optimum
4. Pemilihan Koefisien Pemahaman dan Momentum
Dalam hal ini pemilihan koefisien pemahaman dan momentum mempunyai peranan yang penting untuk struktur jaringan yang akan dibangun. Dalam membangun jaringan yang akan digunakan dalam peramalan, hasil keputusan yang kurang memuaskan dapat diperbaiki dengan penggunaan koefisien pemahaman dan momentum secara trial and error untuk mendapatkan nilai bobot yang paling optimum agar MSE dan MAD jaringan dapat diperbaiki.
5. Memilih dan Menggunakan Arsitektur Jaringan yang Optimum
Tingkat keakuratan ramalannya akan dinilai setelah jaringan dibangun. Jaringan yang optimum dinilai dengan melihat nilai MSE (Mean Square Error) terkecil.
(2.58)
di mana:
bilangan ramalan
nilai aktual pada waktu
nilai ramalan pada waktu
6. Pemilihan jaringan optimum dan penggunaannya untuk peramalan
Jaringan dengan nilai MSE terkecil dipilih sebagai jaringan yang optimum untuk digunakan dalam peramalan.
2.7 Neuro-GARCH
bebas pada model GARCH menjadi input pada jaringan saraf tiruan model Backpropagation dan variabel terikatnya menjadi target.
Dengan demikian untuk persamaan autoregresi ,
dan menjadi input dan menjadi target. Begitu pula untuk persamaan variansi
dan menjadi input dan
Indonesia (www.idx.co.id) yaitu data harian IHSG periode Januari 2013-Februari 2014 (Lampiran 1).
3.3.1 Indeks Harga Saham Gabungan
Indeks harga saham merupakan ringkasan pengaruh simultan dan kompleks dari berbagai macam variabel yang berpengaruh, terutama kejadian-kejadian ekonomi. Bahkan saat ini, indeks harga saham tidak banyak menampung kejadian-kejadian ekonomi saja, tetapi juga kejadian-kejadian sosial, politik dan keamanan. Dengan demikian indeks harga saham dapat dijadikan sebagai parameter kesehatan ekonomi suatu negara dan sebagai dasar melakukan analisis statistik atas kondisi pasar terakhir (current market). Pengukuran indeks harga saham memerlukan dua macam waktu, yaitu waktu dasar dan waktu berlaku. Waktu dasar akan dipakai sebagai perbandingan, sedangkan waktu berlaku merupakan waktu di mana kegiatan akan diperbandingkan dengan waktu dasar.
3.3.2 Indeks Harga Sahan Gabungan di Bursa Efek Indonesia (BEI)
Indeks harga saham gabungan (Composite Stock Price Indeksi) merupakan suatu
nilai yang digunakan untuk mengukur kinerja saham yang tercatat di suatu bursa efek. Indeks harga saham gabungan ini ada yang dikeluarkan oleh bursa efek yang bersangkutan secara resmi dan ada yang dikeluarkan oleh instansi swasta tertentu seperti media massa keuangan dan institusi saham.
Untuk mengetahui besarnya indeks harga saham gabungan, dipergunakan rumus beikut:
dengan : Total harga semua saham pada saat berlaku
: Total harga semua saham pada waktu dasar.
3.4Membuat Landasan Teori
Setelah mendapatkan data yang dimaksud, selanjutnya dilakukan pembahasan secara teoritis mengenai metode yang digunakan dalam penelitian berdasarkan hasil studi literatur. Hal ini dilakukan untuk mengetahui bagaimana metode yang digunakan dalam kajian teorinya sebelum digunakan dalam penelitian. Pembahasan ini terdapat dalam tinjauan pustaka.
3.5 Analisis Data IHSG dengan Model Neuro-GARCH
Pada tahap ini dilakukan peramalan data IHSG dengan model Neuro-GARCH
yakni dengan menganalisis data menggunakan metode GARCH terlebih dahulu kemudian menggunakan hasil analisisnya sebagai input pada model Backpropagation. Setelah itu dihitung MAPE dari hasil peramalan model. Sebagai alat bantu perhitungan dalam melakukan analisis data dengan model Neuro-GARCH peneliti menggunakan software Eviews 8 pada analisis GARCH dan Matlab 7.0 pada analisis Backpropagation. Adapun langkah-langkah yang dilakukan dalam peramalan data IHSG dengan model Neuro-GARCH adalah sebagai berikut:
1. Peramalan dengan menggunakan model GARCH a. Identifikasi kestasioneran data.
d. Estimasi parameter model GARCH. e. Uji kelayakan model.
f. Peramalan.
2. Peramalan kembali data hasil peramalan model GARCH dengan menggunakan model Backpropagation
a. Menetapkan tujuan sistem. b. Menentukan fungsi aktivasi. c. Transformasi data.
d. Pembagian data.
e. Perancangan arsitektur jaringan yang optimum. f. Penentuan koefisien laju pemahaman dan momentum.
g. Pemilihan arsitektur jaringan yang optimum sehingga siap digunakan dalam peramalan.
3.6 Analisis Data IHSG dengan Model Backpropagation
Pada tahap ini dilakukan peramalan data IHSG dengan model Backpropagation kemudian dihitung MAPE dari hasil peramalan model. Dalam melakukan analisis data dengan model Backpropagation peneliti
menggunakan software Matlab 7.0 sebagai alat bantu perhitungan. Adapun langkah-langkah yang dilakukan dalam peramalan data IHSG dengan model Backpropagation adalah sebagai berikut:
1. Menetapkan tujuan sistem. 2. Menentukan fungsi aktivasi. 3. Transformasi data.
4. Pembagian data.
7. Pemilihan arsitektur jaringan yang optimum sehingga siap digunakan dalam peramalan.
3.7 Membandingkan Hasil Peramalan
Pada tahap ini setelah dilakukan peramalan dengan Neuro-GARCH kemudian hasil peramalan yang diperoleh dibandingkan dengan hasil peramalan dengan jaringan saraf tiruan model Backpropagation dilihat dari nilai MAPE. Keakuratan peramalan dapat dilihat berdasarkan MAPE yang diperoleh dari masing-masing metode. Jika MAPE lebih kecil berarti metode tersebut lebih akurat.
3.8Membuat Kesimpulan.
BAB 4
HASIL DAN PEMBAHASAN
4.1 Analisis Data dengan Menggunakan Model Neuro-GARCH
Analisis data dengan menggunakan model Neuro-GARCH dilakukan dengan membentuk model GARCH dan melakukan peramalan dengan model yang dihasilkan. Setelah mendapatkan hasil dari peramalan dengan model GARCH, maka akan diterapkan model Backpropagation terhadap hasil tersebut.
4.1.1 Peramalan dengan Menggunakan Model GARCH 4.1.1.1 Identifikasi Kestasioneran Data
dengan kesalahan standar:
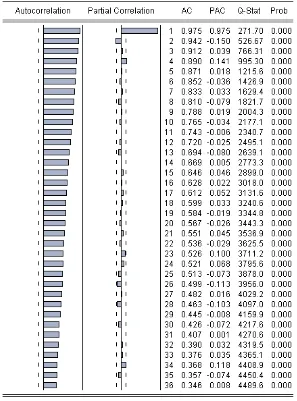
Gambar 4.1. Korelogram data IHSG
Terlihat pada Gambar 4.1. bahwa grafik dari AC turun secara terus menerus namun tidak mendekati 0, sedangkan pada PAC pada lag pertama masih melewati batas interval. Terlihat bahwa nilai AC masih jauh dari nilai kesalahan standar, sehingga diindikasikan bahwa data tidak stasioner. Hal ini diperkuat dengan hasil pengujian Unit Root Test yang menunjukkan bahwa nilai
lebih besar daripada pada semua derajat kepercayaan (Lampiran 3).
data belum stasioner maka dilakukan pembedaan atau differencing untuk mendapatkan data yang stasioner. Proses pembedaan data asli adalah:
Selengkapnya hasil pembedaan data IHSG dapat dilihat pada lampiran 2.
Setelah dilakukan pembedaan, data diuji kembali dengan uji unit akar dan
Gambar 4.2. Korelogram data IHSG setelah pembedaan
dengan kesalahan standar
4.1.1.2Membentuk PersamaanAutoregresi Sebagai Model Awal
Persamaan autoregresi yang diperoleh untuk data Indeks Harga Saham Gabungan adalah model yang paling baik secara statistik. Diperoleh bahwa model terbaik adalah model ARIMA (0,1,1) berbentuk .
4.1.1.3Pengujian Heteroskedastisitas atau Efek ARCH pada Residual
Setelah memperoleh model terbaik maka langkah selanjutnya adalah melihat apakah terdapat efek ARCH atau heteroskedastisitas pada residual model tersebut. Dengan menggunakan uji ARCH-LM yang terdapat pada program Eviews 8
(Lampiran 3.c) diketahui bahwa nilai F sebesar 9,284775 > sebesar 5,991 sehingga mengindikasikan adanya heteroskedastisitas pada residual. Hal ini sejalan dengan probabilitasnya yang berada jauh di bawah derajat kepercayaan 0,05. Hipotesis nol bahwa pada residual terdapat efek ARCH diterima. Dengan demikian model GARCH dapat langsung digunakan tanpa menghilangkan heteroskedastisitas pada model.
4.1.1.4Estimasi Parameter Model GARCH
Setelah diketahui bahwa model GARCH dapat diterapkan, maka langkah selanjutnya adalah mengestimasi parameter model dengan menggunakan Maximum Likelihood Method yang terdapat pada Eviews 8. Dari beberapa orde model GARCH akan diseleksi untuk dilihat model mana yang paling baik dilihat dari nilai AIC dan SIC terkecil yang terdapat pada tabel berikut:
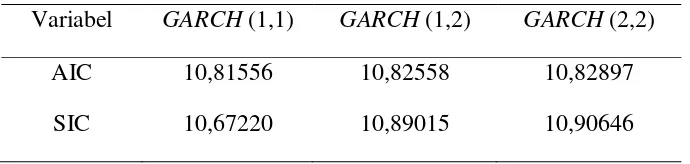
Tabel 4.1 Tabel Nilai AIC dan SIC
Variabel GARCH (1,1) GARCH (1,2) GARCH (2,2)
AIC 10,81556 10,82558 10,82897
Hasil pada tabel menunjukkan bahwa nilai AIC dan SIC dari model GARCH untuk beberapa orde tidak terlalu berbeda. Tetapi di antara ketiga model
tersebut model GARCH (1,1) memiliki nilai AIC dan SIC yang paling kecil. Disimpulkan bahwa GARCH (1,1) adalah model terbaik sehingga akan digunakan dalam peramalan IHSG pada penelitian ini. Dengan menggunakan Maximum Likelihood Method yang telah tersedia pada program Eviews 8 (Lampiran 3.d) estimasi parameter model GARCH (1,1) dari model pendahuluan ARIMA (0,1,1) sebagai berikut:
4.1.1.5Uji Kelayakan Model
Setelah memperoleh parameter persamaan GARCH (1,1) akan dilakukan pengujian kelayakan model tersebut untuk melihat efek ARCH, normalitas pada residual, dan signifikasi parameter yang sudah diestimasi. Untuk melihat apakah residual berdistribusi normal atau tidak digunakan histogram-normality test (Lampiran 3.e). Kenormalan residual diketahui dengan menghitung nilai statistik Jarque Bera. Perhitungan nilai Jarque Bera diperlihatkan di bawah ini:
Hasil pengujian memperlihatkan bahwa nilai Jarque Bera
sebesar 5,991 dan probabilitas Jarque Bera adalah 0,145217 (Lampiran 3.f)
berdistribusi normal. Uji efek ARCH memberikan hasil yang menerima H0 yaitu tidak terdapat efek ARCH pada residual model. Hal ini terlihat dari nilai F sebesar
2,0333282 < sebesar 5,991 nilai probabilitasnya yang lebih besar derajat kepercayaan 0,05 (Lampran 3.f). Begitu pula pada probabilitas parameter model semua probabilitasnya sudah menunjukkan bahwa koefisien signifikan. Dari hasil pengujian sudah memenuhi kelayakan model sehingga model sudah dapat digunakan dalam peramalan.
4.1.1.6Peramalan
Model GARCH (1,1) yang diperoleh akan digunakan untuk meramalkan nilai Sebagaimana telah disebutkan, pada penelitian ini dilakukan peramalan pada Indeks Harga Saham Gabungan saja tanpa meramalkan nilai varians. Hal ini disebabkan peneliti hanya ingin melihat nilai IHSG beberapa periode ke depan tanpa menghitung value at risk yang dihitung menggunakan nilai varians. Dengan persamaan ARIMA (0,1,1):
diperoleh nilai dan sebanyak 283 data. Nilai dan akan menjadi
input dan nilai akan menjadi target pada model Backpropagation. Nilai yang dihasilkan masih berupa nilai karena pada analisis data awal dilakukan
pembedaan untuk mendapatkan hasil yang stasioner. Pada tahap akhir akan dilakukan transformasi untuk mendapatkan nilai IHSG yang asli.
4.1.2 Peramalan Data dengan Menggunakan Model Backpropagation
Perancangan model peramalan IHSG dengan metode jaringan saraf tiruan model Backpropagation terdiri dari langkah-langkah sebagai berikut:
Model jaringan yang dibangun menggunakan hasil peramalan yang telah diperoleh dari model GARCH dengan software Matlab 7.0.
2. Menentukan fungsi aktivasi
Fungsi tansig, sigmoid biner (log sigmoid), dan purelin masing-masing digunakan sebagai fungsi aktivasi pada lapisan tersembunyi pertama, lapisan tersembunyi pertama dan keluaran.
3. Transformasi Data
Data ditransformasi linear pada selang [0,1.0,9]. Oleh karena itu keluaran yang dihasilkan jaringan akan berada pada nilai 0 sampai 1. Untuk mendapatkan nilai sebenarnya dari keluaran perlu dilakukan proses detransformasi linear.
4. Pembagian Data
Data hasil peramalan dengan model GARCH dibagi menjadi 70% data pelatihan dan 30% data pengujian. Terdapat 283 data harian dari Januari 2103-Februari 2014, sehingga data pelatihan 70% dari 283 = 198,1 hari, digenapkan menjadi 198 hari (198 data) dan 30% sisanya = 84,9 hari digenapkan menjadi 85 hari (85 data) adalah data pengujian (Lampiran 4 dan Lampiran 5).
5. Perancangan arsitektur jaringan yang optimum
Peramalan IHSG ditentukan oleh nilai dan hasil peramalan model GARCH dengan dan menjadi input dan menjadi target.
Arsitektur jaringan dibentuk dari 2 input, lapisan tersembunyi pertama dengan 10 neuron, lapisan tersembunyi kedua dengan 5 neuron dan 1 keluaran.
6. Penentuan koefisien laju pemahaman dan momentum
7. Pemilihan arsitektur jaringan yang optimum siap digunakan pada peramalan
Pengolahan data Indeks Harga Saham Gabungan dengan metode backpropagation jaringan saraf tiruan dengan software Matlab 7.0 dapat diperlihatkan sebagai berikut:
Kemudian dibangun jaringan saraf dengan metode pembelajaran gradient descent dengan momentum (traingdm):
>> net=newff(minmax(pn),[10 5 1],{'tansig','logsig','purelin'},'traingdm');
4. Set bobot awal secara acak
Inisialisasi bobot awal dilakukan dengan bilangan acak dan dilakukan
sampai menghasilkan MSE paling kecil (MSE ≥ 0). Dalam penelitian ini bobot yang sudah didapatkan sehingga menghasilkan MSE terkecil mendekati 0 adalah sebagai berikut:
Bobot awal lapisan input ke lapisan tersembunyi pertama: >> net.IW{1,1}=[…];
Bobot bias awal lapisan input ke lapisan tersembunyi pertama: >> net.b{1,1}=[…];
Bobot bias awal lapisan tersembunyi pertama ke lapisan tersembunyi kedua:
>> net.b{2,1}=[…];
Bobot awal tersembunyi kedua lapisan output: >> net.LW{3,2}=[…];
Bobot bias awal tersembunyi kedua ke lapisan output: >> net.b{3,1}=[…];
5. Sebelum dilakukan pelatihan, ditetapkan terlebih dahulu parameter parameter yang digunakan sebagai berikut:
>> net.trainParam.epochs = 5000; >> net.trainParam.goal = 0.05; >> net.trainParam.lr =0.1; >> net.trainParam.show = 200; >> net.trainParam.mc = 0.2;
6. Kemudian dilakukan proses: >> net=train(net,pn,tn);pause
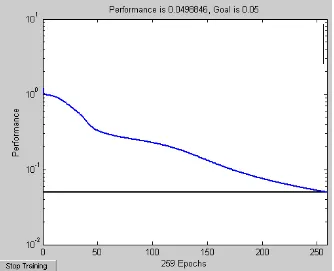
Gambar 4.3. Hasil pelatihan sampai 5000 epoch (iterasi)
Pada Gambar 4.3. terlihat bahwa performance jaringan telah goal (berhenti saat nilai MSE terkecil jaringan lebih kecil dari batas nilai goalnya) dimana 0,00498846 < 0,05dan berhenti pada epoh ke-259.
8. Untuk melihat bobot akhir: >> BobotAkhir_Input = net.IW{1,1} >> BobotAkhir_Bias_Input=net.b{1,1} >> BobotAkhir_Lapisan1=net.LW{2,1} >> BoobotAkhir_Bias_Lapisan1=net.b{2,1}
>> BobotAkhir_Lapisan2=net.LW{3,2} >> BobotAkhir_Bias_Lapisan2=net.b{3,1}
9. Melakukan simulasi dan pengujian dilakukan terhadap data-data yang ikut dilatih: