ANALISIS PENGARUH MONOTONIK PADA GRAF
ASIKLIK BERARAH
TESIS
Oleh
ERIEK MANIUR LUMBAN TOBING
097021004/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
ANALISIS PENGARUH MONOTONIK PADA GRAF
ASIKLIK BERARAH
T E S I S
Diajukan Sebagai Salah Satu Syarat
untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
ERIEK MANIUR LUMBAN TOBING 097021004/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
Judul Tesis : ANALISIS PENGARUH MONOTONIK PADA GRAF ASIKLIK BERARAH
Nama Mahasiswa : Eriek Maniur Lumban Tobing Nomor Pokok : 097021004
Program Studi : Matematika
Menyetujui, Komisi Pembimbing
(Dr. Saib Suwilo, M.Sc) (Prof. Dr. Tulus, M.Si)
Ketua Anggota
Ketua Program Studi Dekan
(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)
Telah diuji pada Tanggal 16 Juni 2011
PANITIA PENGUJI TESIS
Ketua : Dr. Saib Suwilo, M.Sc Anggota : 1. Prof. Dr. Tulus, M.Si
ABSTRAK
Ada beberapa hubungan yang terdapat diantara efek monotonik dan efek lemah monotonik dan kemonotonan pada kondisi harapan pasti. Ada beberapa contoh yang disediakan untuk menunjukkan bahwa hubungan-hubungan tersebut memi-liki batasan yang tidak sedikit. Selanjutnya, efek monotonik dapat digunakan sebagai tanda-tanda edge pada graf asiklik berarah kausal bahkan digunakan pa-da modifikasi efek kualitatif. Teori tersebut diaplikasikan papa-da sebuah contoh. Konsep kemonotonan dapat digunakan sebagai asumsi uji ada tidaknya variabel meragukan pada masing-masing contoh.
ABSTRACT
Various relationships are shown hold between monotonic effects and weak mono-tonic effects and the monomono-tonicity of certain conditional expectations. Countere-xamples are provided to show that the results do not hold under less restrictive conditions. Monotonic effects are furthermore used to relate signed edges on a causal directed acyclic graph to qualitative effect modification. The theory is app-lied to an example. Monotonicity assumptions are used to construct a test for whether there is a variable that counfounds in each counterexamples.
KATA PENGANTAR
Dengan segala kerendahan hati dan penuh sukacita, penulis mengucapkan puji syukur ke hadirat Tuhan Yang Maha Kuasa atas segala anugerah dan berkat-Nya yang telah diberikan, sehingga penulis dapat menyelesaikan tesis dengan judul : ANALISIS PENGARUH MONOTONIK PADA GRAF ASI-KLIK BERARAH. Tesis ini merupakan salah satu syarat universitas menyele-saikan studi pada Program Studi Magister Matematika FMIPA Universitas Su-matera Utara. Pada kesempatan ini, penulis menyampaikan terima kasih sebesar-besarnya kepada: Prof.Dr.dr.Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara
Dr.Sutarman, M.Scselaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam yang telah memberikan kesempatan kepada penulis untuk mengikuti Pro-gram Studi Magister Matematika di FMIPA Universitas Sumatera Utara.
Prof.Dr.Herman Mawengkang selaku Ketua Program Studi Magister Mate-matika FMIPA Universitas Sumatera Utara yang telah banyak memberikan ban-tuan dalam penulisan tesis ini.
Dr.Saib Suwilo, M.Scselaku Pembimbing Utama penulisan tesis ini dan Sekre-taris Program Studi Magister Matematika FMIPA Universitas Sumatera Utara.
Prof.Dr Tulus, M.Siselaku Pembimbing Kedua yang juga telah banyak mem-berikan bimbingan kepada penulis dalam penulisan tesis ini.
Seluruh Staf Pengajarpada Program Studi Magister Matematika FMIPA Uni-versitas Sumatera Utara yang telah banyak memberikan ilmu pengetahuan selama masa perkuliahan.
Saudari Misiani, S.Si selaku Staf Administrasi Program Studi Magister Ma-tematika FMIPA Universitas Sumatera Utara yang telah memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.
sebesar-besarnya dan penghargaan setinggi-tingginya kepada orang tuaRustam Effendi Lumban Tobing dan Siti Delima Sitanggang yang telah mencurahkan kasih sayang dan dukungan kepada penulis, terlebih pada adik-adikSiska Jane Lum-ban Tobing, Ryan Tommi Lumban Tobing dan Agatha Serena Lumban Tobing yang telah memberikan semangat dan dorongan kepada penulis. Penulis menyadari bahwa tesis ini masih jauh dari sempurna. Untuk itu penulis meng-harapkan kritik dan saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak-pihak lain yang memerlukannya. Terima Kasih.
Medan, Juni 2011
Penulis,
RIWAYAT HIDUP
Eriek Maniur Lumban Tobing dilahirkan di Medan pada tanggal 19 April 1985 dari pasangan bapak Rustam Effendi Lumban Tobing dan Ibu Siti Delima Sitanggang dan merupakan anak pertama dari empat bersaudara. Penulis meru-pakan lulusan SD Swasta Methodist-6 Medan, SMP Methodist-6 Medan, SMA Negeri 12 Medan. Pada tahun 2003 penulis melanjutkan perkuliahan jenjang Strata Satu(S1) di Universitas Negeri Medan dan lulus tahun 2008.
DAFTAR ISI
Halaman
ABSTRAK i
ABSTRACT ii
KATA PENGANTAR iii
RIWAYAT HIDUP v
DAFTAR ISI vi
DAFTAR GAMBAR viii
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 1
1.3 Tujuan Penelitian 2
1.4 Kontribusi Penelitian 2
1.5 Metode Penelitian 2
BAB 2 TINJAUAN PUSTAKA 3
BAB 3 LANDASAN TEORI 6
3.1 Definisi Efek Monotonik 6
3.2 Efek Monotonik dan Kondisi Ekspektasi 8 3.3 Efek Modifikasi dan Efek Monotonik 16
BAB 4 PEMBAHASAN 20
BAB 5 KESIMPULAN DAN SARAN 26
5.2 Saran 26
DAFTAR GAMBAR
Nomor Judul Halaman
4.1 Graf berarah dengan 4 verteks dan 5 arcs 22
4.2 Graf berarah dengan 4 verteks dan 5 arcs 23
ABSTRAK
Ada beberapa hubungan yang terdapat diantara efek monotonik dan efek lemah monotonik dan kemonotonan pada kondisi harapan pasti. Ada beberapa contoh yang disediakan untuk menunjukkan bahwa hubungan-hubungan tersebut memi-liki batasan yang tidak sedikit. Selanjutnya, efek monotonik dapat digunakan sebagai tanda-tanda edge pada graf asiklik berarah kausal bahkan digunakan pa-da modifikasi efek kualitatif. Teori tersebut diaplikasikan papa-da sebuah contoh. Konsep kemonotonan dapat digunakan sebagai asumsi uji ada tidaknya variabel meragukan pada masing-masing contoh.
ABSTRACT
Various relationships are shown hold between monotonic effects and weak mono-tonic effects and the monomono-tonicity of certain conditional expectations. Countere-xamples are provided to show that the results do not hold under less restrictive conditions. Monotonic effects are furthermore used to relate signed edges on a causal directed acyclic graph to qualitative effect modification. The theory is app-lied to an example. Monotonicity assumptions are used to construct a test for whether there is a variable that counfounds in each counterexamples.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Graf adalah himpunan pasang berurut himpunan verteksV dan himpunan edge E, dimanaV 6=∅. Graf berarah D adalah graf yang masing-masing edgenya memiliki arah, yang selanjutnya disebut arc. Graf asiklik berarah adalah graf berarah dimana tidak terdapat siklik berarah.
Graf asiklik berarah merupakan model yang sangat populer yang digunakan untuk mempelajari hubungan-hubungan antara verteks-verteks, juga dapat di-gunakan untuk mempelajari hubungan-hubungan antara variabel-variabel dalam suatu data.
Pada graf asiklik berarah, verteks merepresentasikan variabel-variabel da-ta, sedangkan arc merepresentasikan informasi atau pengaruh yang terjadi antara variabel-variabel tersebut. Contohnya, arc A → B merepresentasikan nilai pro-babilitas Aterhadap nilai probabilitas B.
Nilai-nilai probabilitas yang terjadi pada graf asiklik berarah tidak menutup kemungkinan menunjukkan suatu kecenderungan naik, tidak turun atau turun, tidak naik. Kecenderungan tersebut selanjutnya disebut monotonik.
Pada graf asiklik berarah, monontonik yang terjadi tentunya memiliki arti, khususnya dalam mempelajari hubungan-hubungan antara verteks-verteks. Oleh karena itu, tesis ini menganalisa apa pengaruh terjadinya monotonik dalam graf asiklik berarah terhadap suatu penarikan kesimpulan
1.2 Perumusan Masalah
2
1.3 Tujuan Penelitian
Tujuan penelitian ini adalah menganalisis sifat-sifat probabilistik mengenai efek monotonik dan efek lemah monotonik pada graf asiklik berarah.
1.4 Kontribusi Penelitian
Salah satu kontribusi penelitian adalah memperkaya khasanah ilmu penge-tahuan khususnya pada graf asiklik berarah.
1.5 Metode Penelitian
Penelitian ini dilakukan dengan menggunakan metode tinjauan pustaka. Adapun langkah-langkah yang akan dilakukan adalah sebagai berikut:
1. Menjelaskan notasi yang digunakan dan mendefinisikan graf asiklik berarah.
2. Menganalisis hubungan-hubungan verteks pada graf asiklik berdasarkan con-toh-contoh yang akan ditampilkan.
3. Mendefinisikan konsep efek monotonik dan efek lemah monotonik pada graf asiklik berarah.
4. Menampilkan sejumlah hasil yang berhubungan dengan efek lemah mono-tonik pada kondisi pasti.
5. Menampilkan sejumlah hasil yang berhubungan dengan efek lemah mono-tonik setelah dimodifikasi.
BAB 2
TINJAUAN PUSTAKA
Ada beberapa peneliti yang telah mempertimbangkan variasi kemonotonan pada graf, graf asiklik berarah ataupun di Bayesian Network. Sifat monoton pada graf memiliki ruang lingkup yang besar untuk dipelajari. Sifat monoton bisa diuji dengan uji one-sided error. Sifat graf P dikatakan monoton jika graf tersebut tertutup terhadap pertukaran tempat edge dan verteks. Dengan kata lain, jika graf G tidak memenuhi P maka sebarang graf yang memuat G sebagai subgraf tidak memenuhiP, (Alon dan Shapira, 2005).
Himpunan pasang berurut (G, f), dengan GrafGdan fungsif, grafG memi-liki path monoton jika dan hanya jika G memuat subgraf dan sikelnya memiliki panjang minimal 5, (Bialostochi dan roditty, 1986).
Pada konteks graf asiklik, ada 5 kemungkinan hubungan antara verteks yaitu: (XY) tidak memiliki edge yang berarti tidak memiliki hubungan kausal, (X − Y) memiliki edge yang tidak berarah berarti tidak memiliki intepretasi kausal, (Y →X) memiliki arc berarti memiliki variasi diY dengan variabel lain-nya konstan dan mengakibatkan variasi yang linear di X, (X →Y) memiliki arc berarti memiliki variasi diX dengan variabel lainnya konstan dan mengakibatkan variasi yang linear di Y, (X → Y) memiliki edge dua arah berarti intepretasi hubungan kausal 2 arah antara X dan Y, (Yang et al, 2005).
4
Pearl (1995) mengatakan, suatu graf asiklik berarah kausal merupakan him-punan verteks-verteks (x1, ..., xn) dan edge berarah diantara verteks-verteks
se-hingga graf tidak mempunyai siklik setiap verteks xi pada graf asiklik berarah
memiliki persamaan struktural non-parametrikxi =fi(pai, εi) dimanapai
orang-tua xi pada graf,εi bebas satu sama lain. Selanjutnya,O digunakan untuk
meno-tasikan ruang sampel εi dan ωi yang digunakan untuk menotasikan sebuah titik
partikular dalam ruang sampel. Persamaan struktural non-parametrik ini dilihat sebagai bentuk umum dari path analisis dan model persamaan linier struktural (Pearl, 1995; 2000) yang dikembangkan oleh Wright (1921) dalam literatur genetik dan Haavelmo (1943) dalam literatur ekonometrik.
Graf asiklik berarah dapat ditafsirkan sebagai perwakilan hubungan kausal. Persamaan struktural non-parametrik disimbolkan sebagai counterfactual hubu-ngan-hubungan antara variabel-variabel yang ada dalam graf. Persamaan-persa-maan tersebut mereprensentasikan counterfactual yang lebih tepat dari counter-factual sebelumnya yang diperoleh dengan menggunakan substitusi rekursif. Ke-butuhanεibebas satu sama lain merupakan kebutuhan yang penting dimana tidak
ada variabel yang tidak ada di graf, dimana jika termasuk dalam graf tersebut akan menjadi orangtua dari satu atau lebih variabel (Pearl,1995; 2000). Selan-jutnya, Penafsiran kausal dari graf asiklik berarah dapat ditemukan dari peneliti-peneliti lainnya (Pearl,1995; 2000; Spirtes et.al, 2000; David, 2002; Robins, 2003).
Suatu verteks C dikatakan sebagai commoncause dari A dan Y jika ada sebuah path berarah dari C keY tanpa melaluiA dan sebuah path berarah dari
C ke A tanpa melaluiY. v1, , vn : i < j dengan kata lain vi bukan datang dari
vj. Suatu Collider merupakan verteks partikular pada suatu path dimana kedua
verteks sebelum dan verteks berikutnya pada path memiliki edge ke dan edge dari, dimana edgenya memiliki tanda panah. Suatu path antara A dan B dikatakan blok yang diberikan oleh beberapa himpunan variabelZ jika salah satunya adalah variabel dalam Z pada path yang bukan Collider terhadap diri sendiri maupun datangnya dalam Z. Jika semua path antara A dan B terblok yang diberikan
Z maka A dan B dikatakan d-separated Z, itu telah ditunjukkan bahwa jika A
5
Selanjutnya, notasi (A ∪B|Z) menotasikan bahwa A bebas dari B yang diberikan Z; (A∪B|Z)Gmenotasikan bahwa A danB merupakan d-separated Z
pada graf G. Kerangka graf asiklik berarah kausal telah dijamin berguna untuk menentukan apakah himpunan variabel-variabel yang diberikan atau tak satupun merupakan syarat cukup untuk mengontrol keraguan. Hasil yang paling penting untuk melihat ini adalah kriteria backdoor path (Pearl,1995). Suatu backdoor path adalah path dimana dimulai dengan sebuah edge berarah ke dalamA. Pearl (1995) menunjukkan bahwa pengaruh variabel A dan outcome Y, Jika sebuah himpunan variabel-variabelZ dimana tidak ada variabel variabel Z yang datang dari A dan Z memblok semua path backdoor dari A ke Y kemudian, keadaan Z
BAB 3
LANDASAN TEORI
Ada beberapa definisi, proposisi, dan lemma dari efek monoton yang akan dikenalkan dalam bentuk persamaan struktural nonparametrik graf asiklik be-rarah.
3.1 Definisi Efek Monotonik
Definisi 3.1 Persamaan struktural non-parametrik untuk beberapa verteks Y di graf asiklik berarah kausal dengan keluarga A dapat dituliskan: Y =f fpay, A, εy
dimana(gpa)
Y merupakan keluarga-keluarga dariY selainA; Adikatakan memiliki
efek monotonik positif di Y jika untuk setiap (gpa)Y dan εY, f(fpaY, A1, εY) >
f(fpaY, A2, εY); A1 ≥ A2. A dikatakan memiliki efek monotonik negatif di Y jika untuk setiap (gpa)Y danεY, f(fpaY, A1, εY)6f(fpaY, A2, εY); A1 ≥A2.
Proposisi 3.2 Variabel A memiliki efek monotonik positif di Y jika dan hanya jika untuk setiap ω dan nilai-nilai (gpa)Y, Ya1,payf (ω)>Ya0,fpay(ω);a1 >a0.
Bukti. Dengan menggunakan Definisi 3.1, karena A memiliki efek monotonik positif berarti untuk setiappay dan εy berlaku
f(pay, a1, εy)≥f(pay, a0, εy) ; a1 ≥a0
f(pay, a1, εy(w))≥f(pay, a0, εy(w)) ; a1 ≥a0
Yai,pay(w)≥Ya0,pay(w) ; a1 ≥a0.
Jika untuk setiap wdan pay, berlaku
Yai,pay(w)≥Ya0,pay(w) ; a1 ≥a0,
maka pertidaksamaan di atas dapat ditulis
7
Definisi 3.3 Andai variabel A merupakan keluarga dari beberapa variabel Y dan
f
paY menotasikan keluarga Y selain A. A dikatakan memiliki efek lemah
mono-tonik positif diY jika fungsi survivor S(y|a,fpaY) =P(Y > y|A=a,fpaY);a1 ≥a0 maka S(y|a0,fpaY) ≥ S(y|a0,fpaY) untuk setiap y dan fpaY; A dikatakan
memili-ki efek lemah monotonik negatif di Y jika fungsi survivor S(y|a,fpaY) = P(Y > y|A=a,fpaY);a1 ≥a0 maka S(y|a0,fpaY)≤S(y|a1,fpaY) untuk setiap y dan fpaY.
Proposisi 3.4 JikaAmemiliki efek monotonik positif diY makaAjuga memiliki efek lemah monotonik positif di Y.
Bukti. Karena A memiliki efek monotonik positif di Y, untuk a1 ≥ a0
diper-olehlah S(y|a1,fpaY) =P(Y > y|a1,fpaY =P{f(fpaY, a1, εY) > y} ≥P{f(fpaY, a0, εY)> y}=P(Y > y|a0,pafY =S(y|a1,fpaY).
Definisi 3.5 Sebuah edge pada graf asiklik berarah kausal dari X ke Y bertan-da positif jika X memiliki efek monotonik positif di Y. Sebuah edge dari X ke Y bertanda negatif jika X memiliki efek monotonik negatif di Y. Jika X tidak
memiliki efek monotonik positif maupun efek monotonik negatif di Y, maka edge dari X ke Y dikatakan tanpa tanda.
Definisi 3.6 Tanda sebuah path pada graf asiklik berarah kausal merupakan pro-duct dari masing-masing edge yang membentuk path tersebut. Jika salah satu edge pada path tidak memiliki tanda maka tanda dari path dikatakan tak terdefinisikan.
Definisi 3.7 Dua variabel X dan Y dikatakan berasosiasi monotonik positif jika setiap path berarah dari X ke Y atau dari Y ke X bertanda positif dan setiap common causeCi dariX danY sehingga setiap path berarah dariCi keX memiliki
tanda yang sama dengan setiap path berarah dariCi ke Y. Dua variabelX dan Y
dikatakan berasosiasi monotonik negatif jika setiap path berarah dariX ke Y atau dariY keX bertanda negatif dan setiap common cause Ci dariX danY sehingga
setiap path berarah dari Ci ke X memiliki tanda yang berlawanan dengan setiap
8
3.2 Efek Monotonik dan Kondisi Ekspektasi
Lemma 3.8 Jika h(y, a, r) tak turun di y dan a dan S(y|a, r) = P(Y > y|A =
a, R=r)tak turun di a untuk setiapy maka E(h(Y, A, R)|A=a, R=r) juga tak turun di a.
Bukti. Untuka≥a′diperoleh
E(h(Y, A, R)|A=a, R=r)−E(h(Y, A, R)|A=a′, R=r) Hasil yang diperoleh bernilai non-negatif karena kedua integral tersebut bernilai non-negatif untuka=≥a′.
Proposisi 3.9 Andai edge A−Y ada dan positif. MisalX menotasikan beberapa himpunan yang tidak berasal dari Y untuk setiap y termasuk fpaY, Keluarga Y selain A, maka E(Y|X =x, A=a) tak turun untuk setiap nilai x.
Bukti. DiberikanE(Y|X =x, A=a) =E(Y|fpaY, A=a) dan karenaAmemiliki efek monotonik positif(lemah), diperolehlah bahwaS(y|a,fpaY) yang tak turun di
a dan menurut Lemma 3.8 bahwa E(Y|X = x, A = a) = E(Y|fpaY, A = a) tak turun dia.
Lemma 3.10 Andai A tak berasal dari Y dan misal Q menotasikan himpunan ancestorAatauY dimana tak berasal dariA. MisalR = (R1, ..., Rm)menotasikan
daftar berurut dari beberapa himpunan verteks-verteks path berarah dari A ke Y sehingga untuk setiap I backdoor path dari Ri keY terblok oleh Ri, ..., R(i−1), A dan Q. Misal V0 = A dan Vn = Y dan misal V1, ..., V(n −1) daftar berurut setiap verteks dimana bukan anggota R tetapi ada dalam path berarah dari A ke
9
Bukti. Untuk membuktikan lemma ini, selanjutnya path dari A keB dikatakan frontdoor path dari A ke B jika path tersebut dimulai edge berarah yang tanda panahnya keluar dari A. Misal Qk dan Rk subhimpunan dari Q dan R secara
berturut-turut dimana Vk ancestornya. Akan ditunjukkan bahwa
S(Vk|a, v1, ..., vk−1, q, r) = S(vk|a, v1, ..., vk−1, q, rk) = S(vk|a, v1, ..., vk−1, qk, rk) = S(vk|pavk).
JikaRk =R, maka persamaan pertama terpenuhi. Andai Rk 6=R sehingga
Rm bukan ancestorV
k. Semua path frontdoor dariRm keVk harus collider karena
Rm bukan ancestor Vk. Collider ini tidak ada di dalam A, V1, ..., Vk−1, Q, R1, ..., Rm−1 karena semua variabel tak berasal dari Rm. Karena itu, semua path-path
frontdoor dari Rm ke Vk akan terblok oleh A, V1, ..., Vk−1, Q, R1, ..., Rm−1.
Se-mua path backdoor dariRm keVk dengan satu edge pergi keVk akan terblok oleh
A, V1, ..., Vk−1, Q, R1, ..., Rm−1 (pavk akan terdiri dari variabelA, V1, ..., Vk−1, Q, R
k
karena ada satu path berarah dari Vk ke Y dan Q termasuk semua ancestor Y
yang tidak berada di path berarah dariAkeY). Semua path backdoor dariRm ke
Vk dengan satu edge yang keluar dariVk akan terblok olehA, Q, R1, ..., Rm−1.
Se-lain itu, ada satu path backdoor dari Rm ke Y melalui Vk tidak terblok oleh
A, Q, R1, ..., Rm−1. Tetapi, semua path backdoor dari Rm ke Vk dengan satu
edge keluar dari Vk dimana terblok oleh A, Q, R1, ..., Rm−1 juga akan terblok oleh A, V1, ..., Vk−1, Q, R1, ..., Rm−1. Ini dikarenakan satu path yang satu edgenya
ke-luar dariVk yang terblok olehA, Q, R1, ..., Rm−1tetapi tidak terblok olehA, V1, ..., Vk−1, Q, R1, ..., Rm−1 dimana memerlukan salah satu dari V1, ..., Vk−1, katakan Vp
collider di path atau asal collider. Jika salah satu V1, ..., Vk−1 adalah collider
ke-mudian path tersebut akan terblok oleh keluarga collider karena semua keluarga dari V1, ..., Vk−1 ada di dalam A, V1, ..., Vk−1, Q, R1, ..., Rm−1. Jika salah satu dari V1, ..., Vk−1, katakanVp yang merupakan asal dari collider kemudian tidak satupun
path berarah dari collider ke Vp berisi verteks-verteks di R1, ..., Rm−1 selain itu,
path tersebut tidak akan terblok olehA, Q, R1, ..., Rm−1; untuk alasan yang sama,
collider itu sendiri tidak berada diR1, ..., Rm−1. Demikian pula, collider itu sendiri
satu-satunya di pathV1, ..., Vp−1 karena merupakan ancestor dariVp dimana path
berarah sampai Vp tidak terblok oleh R. Meskipun begitu, jika collider adalah
salah satu diantara V1, ..., Vp−1 maka path tersebut terblok oleh keluarga collider
10
Hal ini mengatakan bahwa semua path backdoor dari Rm ke Vk dengan edge
ke-luar dariVk terblok olehA, V1, ..., Vk−1, Q, R1, ..., Rm−1. Telah ditunjukkan bahwa
Semua path backdoor dari Vk ke
Q
Qk akan terblok oleh pavk jika diberikan
A, V1, ..., Vk−1, Qk, Rk. Karena Vk tidak berasal dari
Q
Qk semua frontdoor dari
Vk ke
Q
Qk memiliki paling sedikit satu collider yang berasal dari Vk. Collider
tersebut tidak berada didalam A, V1, ..., Vk−1, Qk, Rk karena seluruh himpunan
yang tidak berasal dari Vk dan juga collider tersebut akan mem-blok path
front-door dari Vk ke
Q
Qk. Oleh karena Vk dan
Q
Qk adalah d-separated jika diberikan
A, V1, ..., Vk−1, Qk, Rk diperolehlah
11
Bukti. Misal V0 = A; Vn = Y dan V1, ..., Vn−1 daftar semua verteks yang tidak
ada didalamRtetapi ada di path-path berarah dariAkeY sehingga paling sedikit satu path berarah dari masing-masing verteks ke Y yang tidak terblok oleh R. MisalVk =V1, ..., Vk. Ini dapat ditunjukkan secara induksi, dimulai dengann=k
dan untuk setiap iterasi k iterasi dengan menggantikan negasi keluarga dari Vk
dengan edge-edge negatif ke Vk, itu cukup untuk memperoleh satu graf sehingga
semua edge pada semua path berarah dari A ke Y tidak ter-blok oleh R yang memiliki tanda positif.
Dapat dituliskan dengan :
E(E(...E(E(1(Vn> v)|A, Vn−1Vn−1, Q, R)|A, Vn−2, Q, R)|...|A, V1, Q, R)|A, Q, R).
Jika dinyatakan dalamA, Vn−1\Vi, Q diperoleh,
E(1(Vn > v)|A, Vn−1, Q, R
tidak turun di Vi untuki = 1, ..., n−1 karenaVi memiliki efek lemah monotonik
positif atau tidak ada efek padaVn. Jika dinyatakan dalamA, Vn−1\{Vi, Vn−1}, Q, R diperoleh :
E(1(Vn > v)|A, Vn−1, Q, R)
Bukan merupakan fungsi tak turun dari vi dan vn−1. Selanjutnya, menurut
Lemma 3.10 diperoleh bahwa S(vn−1|a, v1, ..., vn−2, q, r) = S(vn−1|pavn−1) dan juga S(vn−1|a, v1, ..., vn−2, q, r) = S(vn−1|pavn−1) tidak turun di vi untuk setiap
a, v1, vi−1, vi+1, ..., vn−2, q, r karena Vi memiliki efek lemah monotonik positif atau
tidak memiliki efek atas Vn−1. Menurut Lemma 3.8, dapat dinyatakan dalam, A, Vn−1\Vi, Q, R,
E(E(1(Vn> v)|A, Vn−1Vn−1, Q, R)|A, Vn−2, Q, R)
Tidak turun di dalam vi untuk i = 1, ..., n−2. Dapat juga dinyatakan dalam
A, Q, Rdiperoleh,
E(...E(E(1(Vn> v)|A, Vn−1Vn−1, Q, R)|A, Vn−2, Q, R)|...|A, V1, Q, R)
Bukan merupakan fungsi turun v1 dan v0= a dan karenaA memiliki efek lemah
12
E(E(...E(E(1(Vn> v)|A, Vn−1Vn−1, Q, R)|A, Vn−2, Q, R)|...|A, V1, Q, R)|A, Q, R).
tidak akan turun di a.
Proposisi 3.12 Andai A tak berasal dari Y dan misal X menotasikan beberapa himpunan yang yang tak berasal dari A yang mem-blok setiap backdoor path dari
A ke Y. Misal R = (R1, ..., Rm) menotasikan daftar berurut beberapa himpunan
verteks-verteks pada path berarah dari A ke Y sehingga untuk setiap I backdoor path dari Ri ke Y ter-blok oleh Ri, ..., Ri−1, A dan X. Jika setiap path berarah dari A ke Y bertanda positif kecuali kemungkinan melalui R maka S(y|a, x, r)
dan hE(y|a, x, r) tak turun di a.
Bukti. Misal Q himpunan ancestor dari A atau Y yang tidak berasal dari
A. Perlu diingat, jika untuk setiap i path backdoor dari Ri ke Y tidak terblok
oleh R1, ..., Ri−1, A dan X kemudian path-path backdoor juga akan ter-blok oleh R1, ..., Ri−1, A dan Q karena untuk setiap path backdoor dari Ri ke X, ada
be-berapa anggota dari {A} ∪Q yang melalui path tersebut. Menurut Lemma 3.8, karena Q memblok semua path backdoor dari A ke Y diperoleh, S(y|a, x, r) =
E(E(Y > y)|a, Q, x, r|a, x, r) = E(E(1(Y > y)|a, Q, r)|a, x, r) = E(E(1(Y > y)|a, W, r)|a, x, r).
Dimana W subset Q yang salah satu keluarga Y atau keluarga verteks path berarah dari A ke Y. Misal W′ subset W dimana ada satu path ke Y
tidak terblok oleh A, X, R maka E(E(1(Y > y)|a, W, r)|a, x, r) = E(E(1(Y > y)|a, W′, r)|a, x, r).
Semua path backdoor dariA ke W′ terblok jika diberikanR dan X oleh X karena X memblok semua path backdoor dari A ke Y. Sebarang path frontdoor dari A keW′ termasuk ke dalam satu collider karena verteks-verteks diW′ tidak berasal dari A. Collider tersebut tidak berada di X karena X tidak berasal dari
A. Andai collider memuat beberapa verteks Ri; menurut hipotesis semua path
backdoor dari Ri ke Y ter-blok oleh R1, ..., Ri−1, A dan X. Oleh karena path
frontdoor dariAkeW′akan ter-blok olehR1, ..., Ri−1, AdanX yang lainnya, ada
path backdoor dariRi keY melaluiW′ tidak ter-blok olehR1, ..., Ri−1, A dan X.
13
R dan X salah satunya oleh collider atau oleh satu verteks di R atau X. Telah ditunjukkan bahwa semua path dariAkeW′ter-blok jika diberikanR danX dan juga W′ saling bebas dengan A jika diberikan R dan X diperoleh, E(E(1(Y > y)|a, W′, r)|a, x, r) =E(E(1(Y > y)|a, W′, r)|x, r) =E(E(1(Y > y)|a, Q, r)|x, r).
Telah ditunjukkan bahwa S(y|a, x, r) = E(E(1(Y > y)|a, Q, r)|x, r). Karena
E(1(Y > y)|a, Q, r) tidak turun di a untuk setiap q diperoleh. Dengan kata lain, karena S(y|a, x, r) tidak turun di a, menurut Lemma 3.8, E(y|a, x, r) juga tidak turun dia.
Akibat 3.13 MisalX menotasikan beberapa himpunan tak berasal dariAdimana memblok setiap backdoor path dari Ake Y. Jika setiap path berarah antaraAdan
Y bertanda positif maka S(y|a, x)dan E(y|a, x)tak turun di a.
Proposisi 3.14 Andai A tidak berasal dari Y, dimana A biner, A dan Y positif monotonik berasosiasi maka E(Y|A)tak turun di A.
Proposisi 3.14 merupakan keadaan khusus dari Proposisi 3.15 denganR =∅ dan Q=∅.
Proposisi 3.15 Andai A tidak berasal dari Y, dimana Y biner, A dan Y positif monotonik berasosiasi maka E(A|Y)tak turun di Y.
Akibat 3.16 Andai A biner dan A dan Y positif monotonik berasosiasi maka
E(Y|A)tak turun di A.
14 Misal (C1, ..., Cn) menotasikan daftar berurut dari variabel-variabel di C. Misal
Qc variabel-variabel di Qyang merupakan commoncause dari C dan misalQn =
Q\Qc. Misal Qdi merupakan variabel-variabel Qc yang berasal dari Ci. Misal
Cd
i menotasikan variabel-variabel di C yang berasal dari Ci dan Misal Cin =
C{Ci, Cid}. Menurut Proposisi 3.12, E(Y|A, Q, C) tidak turun di masing-masing
Ci dariCuntuk setiapi,A, di Proposisi 3.12 menjadi himpunan{Qn, Qc\Qdi, Cin}
dan R di Proposisi 3.12 menjadi himpunan{Qd
i, Cid, a}. Selanjutnya,
Tidak turun di masing-masing dimensickarena pembilang dan penyebutnya tidak turun di masing-masing dimensic(Proposisi 3.12) untuk setiap pemilihani, A di dalam Proposisi 3.12 menjadi Ci, X di dalam Proposisi 3.12 menjadi himpunan
15
Pertidaksamaan kedua terpenuhi karena pernyataan tersebut sama dengan per-nyataan sebelumnya = E(Y|A = 0, Q = q, C = c) yang tidak turun di masing-masing dimensi daric dan P(C =c|A= 1, Q=q) =vq(c)P(C =c|A= 0, Q=q)
bernilai lebih besar daripada P(C =c|A= 0, Q=q) karena vq(c) tidak turun di
masing-masing c. Oleh karena itu, E(Y|A=a, Q=q) tidak turun di a.
Proposisi 3.18 Andai A tak berasal dari Y dan Y biner. Misal Q himpunan variabel-variabel yang tak berasal dari Y maupun A dan misal C commoncause dari A dan Y yang tak ada di Q. Jika setiap path berarah dari A ke Y bertanda positif dan setiap path berarah dari C ke A tak melalui Q bertanda sama seperti setiap path berarah dariC keY tak melalui {Q, A} maka E(A|Y, Q) tak turun di Y.
Bukti. Dengan menggunakan iterasi diperoleh :
E(A|Y =y, Q=q) =X
Seperti pembuktian Proposisi 3.17, menurut Proposisi 3.12 dimana Q =q,
P(Y=1|A,c,Q=q)
P(Y=1|Q=q bukan merupakan fungsi turun di A dan masing-masing dimensi
C. Sama halnya dengan, P(PY(=0Y=0|A,c,Q|Q==qq) bukan merupakan fungsi turun di A dan masing-masing dimensiC. JikaC =c, A=adanQ=q, P(YP=(yY|A,C=y|=Qc,Q=q=q) memili-ki jumlah nilai fungsi sama dengan 1EC,A
P(Y=y|A=a,C=c,Q=q)
P(Y=y|Q=q)
= PP((YY==yy||QQ==qq)) = 1.
16
Akibat 3.19 Andai A biner. Misal Q himpunan-himpunan variabel yang tak berasal dari Y maupun A dan misal C commoncause dari A dan Y yang tak berada diQ. Jika setiap path berarah dari A keY bertanda positif dan setiap path berarah dariC keA tak melalui {Q, Y} bertanda sama dengan setiap path berarah dari C ke Y tak melalui {Q, A} maka E(Y|A, Q) tak turun di Y.
3.3 Efek Modifikasi dan Efek Monotonik
Jika keadaan pada variabel yang bersangkutan, tanda efek dari satu variabel yang lainnya berbeda-beda diantara keadaan variabel, maka kondisi variabel tersebut dikatakan efek modifikasi kualitatif. Definisi berikut menjelaskan kondisi efek modifikasi kualitatif secara utuh.
Definisi 3.20 Suatu variabelQdikatakan efek modifikasi pada efek kausal AAtas Y jika Q tidak berasal dari A dan jika ada dua level di A, katakan a0 dan a1,
sehingga E(YA=a1|Q = q)−E(YA=a0|Q = q) tidak konstan di q. Selanjutnya,
Q dikatakan efek modifikasi kualitatif jika ada dua level di A, katakan a0 dan
a1, dan dua level di Q, katakan q0 dan q1 sehingga tanda (E(YA=a1|Q = q)−
E(YA=a0|Q=q1))6=tanda(E(YA=a1|Q=q0)−E(YA=a0|Q=q1)).
Efek-efek monotonik dan efek lemah monotonik sangat erat hubungannya dengan konsep efek modifikasi kualitatif. Tepatnya dapat dilihat dalam Proposisi 3.9 dan 3.23.
Proposisi 3.21 Andai bahwa beberapa keluarga A1 di Y sehingga edge A1− Y bertanda positif kemudian tidak ada keluarga A2 di Y dimana efek modifikasi kualitatif untuk efek kausal A1 pada Y, salah satunya tidak terpenuhi atau tak lebih dari beberapa stratum C =c dari Y selain A1 dan A2.
17
negatif atas Y. Jika A2 merupakan efek modifikasi kualitatif dari efek kausal
A1 maka ada dua nilai A1, katakan a∗
Keadaan kasus pertama dan kedua itu analogi. Oleh karena itu,
X
18
dan A1 juga tidak memiliki efek lemah monotonik negatif.
Hasil yang sama juga diperoleh jika edge A1 −Y bertanda negatif. Akan
ditunjukkan kontrapositif dari Proposisi 3.9 sebagai Akibat.
Akibat 3.22 Andai bahwa beberapa keluarga A2 di Y merupakan efek modifikasi kualitatif untuk efek kausal dari keluarga A1 di Y, salah satunya tidak terpenuhi atau tak lebih dari beberapa stratum C =c di keluarga Y selain A1 dan A2 maka A1 memiliki efek lemah monotonik positif maupum efek lemah monotonik negatif
di Y.
Jika ada variabel meragukan antara A dan Y maka Proposisi 3.9 dapat dituliskan secara umum seperti Proposisi 3.23.
Proposisi 3.23 Andai bahwa semua path berarah dari A ke Y bertanda posi-tif(atau negatif) maka tidak ada efek modifikasi kualitatif Q pada graf asiklik be-rarah untuk efek kausal A di Y.
Bukti. Misal C menotasikan semua verteks yang tidak berasal dari A dimana salah satu keluarga Y atau keluarga verteks di path berarah antara A dan Y. Dengan menggunakan iterasi diperoleh, E(YA=a1|Q = q)−E(YA=a0|Q = q) =
Q=q). Sama halnya, jika dituliskan dengan
X
E(YA=a1|C=c)P(C =c|Q=q)−
X
19
Menurut Pearl (1995), hal itu diperlukan untuk menunjukkan bahwa (Y∪Q|C, A)GA˜, dimana GA˜ menotasikan graf yang diperoleh dengan menghapus semua tanda
panah yang mengarah ke A pada graf asiklik berarah. Sebarang path frontdoor dari Y ke Q di GA˜ akan ter-blok oleh sebuah collider. Sebarang path
back-door dari Y ke Q di GA˜ akan ter-blok oleh C . Oleh karena itu, diperoleh
bah-wa E(YA=a1|Q = q)− E(YA=a0|Q = q) =
P
c
E(YA=a1|C =c)P(C =c|Q=q)−
P
c
E(YA=a0|C =c)P(C=c|Q=q). Karena C akan memblok semua path back-door dari A keY maka diperoleh
P
c
E(Y|C =c, A=a1)P(C =c|Q=q)−P
c
E(Y|C =c, A=a0)P(C =c|Q=q) =P
c
E(Y|C=c, A=a1)−E(Y|C =c, A=a0)P(C=c|Q=q).
Jika ada Q efek modifikasi kualitatif untuk efek kausal A atas Y kemudian ada sebuah nilai q0 sehingga E(YA=a1|Q = q0)−E(YA=a0|Q = q0) < 0. Tetapi, karena semua path anataraA danY bertanda positif dan karenaC memblok dari
A ke Y, dengan menggunakan Proposisi 3.12 yang tidak turun dia dan juga
E(YA=a1|Q=q0)−E(YA=a0|Q=q0) =
P
c
BAB 4
PEMBAHASAN
Menurut definisi efek monotonik, graf asiklik berarah kausal berkorespon-densi dengan sebuah himpunan persamaaan struktural non-parametrik. Efek monotonik sangat berhubungan dengan kemonotonan variabel-variabel kendala yang ditunjukkan dalam proposisi-proposisi.
Beberapa persamaan struktural non-parametrik dapat diperoleh dari iden-tical distribusi X = (X1, ..., Xn) dan {XV=v}V⊂X,v∈supp(V) (Pearl, 2000). Pada
konteks ini, karakteristik graf asiklik berarah kausal merupakan petunjuk ba-gi counterfactual-counterfactualnya bukan persamaan struktural non-parametrik (Robins, 2003), efek monotonik positif juga dapat diketahui jika untuk setiapfpaY, nilai probabilitas P(Ya1,fpaY ≥Ya0,paYf ) = 1; a1 =a0.
Jika kondisi seperti ini terpenuhi pada sebuah himpunan persamaan struk-tural non-parametrik, maka kondisi seperti ini juga akan terpenuhi untuk sem-barang persamaan struktural non-parametrik yang diperoleh dari distribusi yang sama untuk X dan {XV=v}V⊂X,v∈supp(V). Jika untuk a1 = a0 himpunan {ω : Ya1,paYf (ω)< Ya0,paYf (ω)}sama dengan nol maka Ya1,fpaY dan Ya0,paYf dapat
didefini-sikan kembali pada himpunan ini sehinggaYa1,paYf (ω)≥Ya0,paYf (ω) untuk setiap ω
dan distribusi X dan {XV=v}V⊂X,v∈supp(V) yang lainnya tidak diganti.
Karena untuk sembarang nilaiω yang diamati, hasil yang diperoleh bernilai kurang dari satu, keberadaan efek monotonik tidak teridentifikasi. Hasil yang teridentifikasi sebenarnya memiliki kondisi yang lemah ketika data semua vari-abel graf asiklik berarah diamati. Karenanya, diperkenalkan konsep efek lemah monotonik yang didefinisikan seperti pada Definisi 3.3.
21
tanda pada sebuah edge dapat diberikan sebagai tanda efek monotonik dan efek lemah monotonik, seperti definisi tanda path pada umumnya.
Selanjutnya graf asiklik berarah kausal yang memiliki tanda pada edge-edgenya disebut dengan graf asiklik berarah kausal bertanda. Teorema yang akan diberikan dalam path yang sudah bertanda sehingga mudah diaplikasikan pada efek monotonik dan efek lemah monotonik.
Pada Definisi 3.7, Telah ditunjukkan Vander Weele dan Robins (2009) bahwa jika X dan Y berasosiasi monotonik positif makaCov(X, Y)≥0 dan jikaX dan
Y berasosiasi monotonik negatif maka Cov(X, Y)≤0. Selanjutnya, akan dikem-bangkan beberapa hasil berkaitan dengan kemonotonan pada kondisi ekspektasi pasti seperti pada lemma.
Seperti Lemma 3.8 yang dibuktikan dengan diintegralkan berpartisi dan akan digunakan untuk membuktian serangkaian proposisi-proposisi. Diasumsikan bahwa variabel random yang dipertimbangkan telah memenuhi kondisi regular. Jika kondisi fungsi distibutif kumulatif terdifrensiabel secara kontinu maka kon-disi regular juga akan terpenuhi. Lemma 3.8 digunakan pada salah satu fungsi
h(y, a, r) =y atau untuk fungsi survivor dimana relevan memenuhi kondisi regu-lar. Oleh karena itu kondisi regular pada distribusi variabel random merupakan keperluan agar integral secara partisi dapat dilakukan.
Proposisi 3.12, 3.14 dan 3.15 merupakan dasar hasil untuk kemonotonan dari kondisional ekspektasi. Untuk kondisional ekspektasi beberapa variabel Y agar menjadikan A monotonik, diperlukan himpunan semua variabel-variabel yang memblok semua backdoor path dariAkeY. Untuk membuktikan Proposisi terse-but, digunakanlah Lemma 3.10 dan Lemma 3.11 berikutnya.
Lemma 3.11 dan Proposisi 3.12 merupakan hasil yang diperoleh Wellman (1990) dan Druzdel (1993). Khususnya, Lemma 3.11 jika R = ∅, maka hasilnya merupakan pengulangan hasil dari Wellman (1990). Lemma 3.11 merupakan ben-tuk umum dari hasil Wellman (1990) dan Druzdzel (1993) dengan mengkondisikan verteksR = (R1, ..., Rm) berada di path berarah dariA ke Y. Proposisi 3.12
se-lanjutnya merupakan generalisasi Lemma 3.11 dengan menempatkan himpunanQ
22
beberapa himpunanX yang tak berasal dari Adimana memblok setiap backdoor path dariA keY. Proposisi 3.15 merupakan keadaan khusus dari Proposisi 3.18 dengan R =∅ dan Q=∅.
Proposisi 3.14 dan 3.15 memerlukan kondisi variabel yang biner. Beberapa contoh yang akan dikonstruksikan menunjukkan bahwa jika variabelnya tidak bi-ner maka kondisional ekspektasi tak turun walaupun A dan Y positif monotonik berasosiasi.
Contoh 1 : Gambar graf asiklik berarah berikut bertanda positif seperti dibawah ini. Menurut Proposisi 3.12, diperoleh bahwa E(Y|A = a, C = c, R = r) dan
Gambar 4.1 Graf berarah dengan 4 verteks dan 5 arcs
Contoh 2 : Gambar graf asiklik berarah berikut bertanda seperti dibawah ini. Jika A biner, maka menurut Proposisi 3.17, E(Y|A = a, C = c, Q = q),
E(Y|A = a, Q = q), E(Y|A = a, C = c) dan E(Y|A = a) tak turun di
a. Jika Y biner maka menurut Proposisi 3.18 E(A|Y = y, C = c, Q = q),
E(A|Y =y, Q=q),E(A|Y =y, C =c), dan E(A|Y =y) tak turun diy.
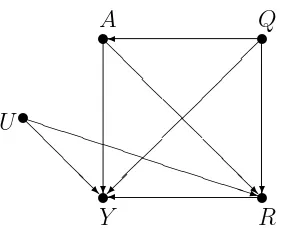
Contoh 3 : Andai diberikan sebuah graf asiklik seperti pada Gambar 4.3 berikut. Misal A menotasikan kegiatan merokok, R menotasikan kolesterol tinggi, dan
23
Gambar 4.2 Graf berarah dengan 4 verteks dan 5 arcs
Merokok dapat mengakibatkan penggumpalan darah sampai penyakit kardio-vaskuler. MisalQmenotasikan beberapa variabel yang meragukan yang menghu-bungkan antara merokok dan Penyakit variabel tak terukur yang kemungkinan mengaburkan hubungan antara kolesterol tinggi dan penyakit kardiovaskuler. Pa-da gambar ini terPa-dapat keraguan apakah variabel U merupakan penyebab dari
R dan oleh karena itu edge dari U ke R disimbolkan edge tak berarah. Menu-rut Pearl (2001) ada kemungkinan memperkirakan efek langsung dengan cara
YA=a1,R=r−YA=a0,R=r yaitu efek langsung merokok pada penyakit kardiovaskuler dengan mempertimbangkan kolesterol tinggi, pada gambar graf dibawah ini jika
U bukan penyebabR. Anggap meskipun U diragukan, keberadaan edge U keR, telah diketahui bahwa hubungan antara A dan Y dikatakan monotonik dimana
P(Y > y|A=a, R=r, Q=q, U =u) tak turun diauntuk setiapy, r, q, u. Selan-jutnya, akan di uji secara statistik dengan membuat variabelU sebagai hipotesis nol yang meragukan hubungan antara R dan Y.
t
Gambar 4.3 Graf berarah dengan 5 verteks dan 8 arcs
24
rut Proposisi 3.12,E(Y|A=a, R=r, Q=q) tak turun dia untuk setiapr danq. Jika hipotesis alternatifnya bahwaU merupakan penyebabR, Proposisi 3.12 tidak dapat dipakai karena adanya path backdoornyaR-U-Y tidak ter-blok diantara R
dan Y, dengan kata lain kemonotonan hubungan tidak terjadi. Konsekuensi, jika
E(Y|A = a, R = r, Q = q) tidak monotonik di a maka hipotesis nolnya ditolak yang mengatakan U bukan merupakan penyebabR.
Dikonstruksikan sebuah uji statistik sederhana pada kasus A, R dan Y
dimana semuanya biner (cf Robins dan Greenland) dengan hipotesis nol tidak ada U pada Gambar 4.3. Misal ni,j,q menotasikan banyak stratum Q = q
de-ngan A = i, R = j dan Misal di,j,q menotasikan banyak stratum Q = q dengan
A =i, R = j, Y = 1. Misal pi,j,q menotasikan probabilitas P(Y = 1|A = i, R =
j, Q=q).
Jika hipotesis nol yang mengatakan tak ada U di graf diatas, maka menu-rut Proposisi 3.12 bahwa p1,j,q −p0,j,q ≥ 0 untuk setiap j dan q. Diperolehlah
Untuk menguji hipotesis nol yang menyatakan tidak ada edge dari U ke R
25
z =
d1,j,q
n1,j,q −
d0,j,q
n0,j,q
qd
1,j,q(n1,j,q−d1,j,q)
n3
1,j,q +
d0,j,q(n0,j,q−d0,j,q)
n3 0,j,q
dengan daerah kritis z > z1−j sampai pada uji satu titik.
Jika uji gagal untuk menolak hipotesis nolnya, maka tidak dapat disimpulkan bahwa tanda panah dari U ke R itu tidak ada. Jika pertidaksamaan E(Y|A =
a1, R = r, Q=q) ≤E(Y|A =a0, R =r, Q= q) terpenuhi untuk setiap a1 ≤a2, maka keadaan ini potensial konsisten dengan ada dan tidaknya edge dariU keR. Jika, uji menolak hipotesis nolnya maka dapat disimpulkan bahwa edge dariU ke
BAB 5
KESIMPULAN DAN SARAN
Pada bab ini diberikan kesimpulan yang diperoleh dari hasil penelitian pada bab sebelumnya. Selanjutnya akan diberikan saran untuk penelitian lebih lanjut.
5.1 Kesimpulan
Analisis hubungan-hubungan yang terjadi diantara verteks dihubungkan oleh arc memiliki bermacam-macam variasi mulai dari efek monotonik, efek lemah monotonik sampai pada kemonotonan yang memerlukan modifikasi secara kuali-tatif. Ketika variabel-variabel pada graf asiklik berarah kausal menunjukkan efek lemah monotonik, hubungan-hubungan tersebut mencerminkan adanya variabel lain yang meragukan.oleh karena itu diperlukan suatu uji keberadaan variabel meragukan untuk memetukan jenis efeknya.
5.2 Saran
Untuk penulisan di masa yang akan datang, penulis menyarankan agar:
1. Mempertimbangkan apakah ada kemungkinan meminimalkan batasan diR, Jika setiap path berarah dariA keY bertanda positif kecuali kemungkinan melaluiR maka S(y|a, x, r) dan hE(y|a, x, r) tak turun dia.
2. Mengembangkan suatu algoritma sebagai uji terhadap keberadaan variabel yang meragukan.
DAFTAR PUSTAKA
Alon Noga and Shapira Asaf.(2005). Every Monotone Graph Property is Testable. Maryland,USA.
Bialostocki A and Roditty.Y.(1987).A Monotone Path in an Edge-Ordered Graph. Internat J. Math and Math. Sci, 10:315-320.
Druzdzell J.M. and Henrion M.(1993). Efficient Reasoning in Qualitative Proba-bilistic Networks. InProceedings of the 11th Annual Conference on Artificial Inteligence pages 548-553.
Geiger D. et.all (1990). Identifying Independence in Bayesian Networks.Networks. 20:507-534.
Haavelmo T.(1943). The Statistical Implications of a System of simultaneous Equa-tions. Econometrica 11:1-12.
Lauritzen L.S, et.al.(1990). Independence Properties of Directed Markov Fields.
Networks.20:491-505
Pearl.J. (1993) Causal Diagrams for empirical research.Biometrika, 82:669-688. Tian Jin and Pearl Judea.(2002). On the testable implications of causal models
with hidden variables. In Proceedings of the Conference on Uncertainty in Artificial Intelligence, pages 519-527. Morgan Kaufmann, San Fransisco. Van der Gaag L. C., Bodlaender H. L., and Ad Feelders.(2004). Monotonicity
in Bayesian networks. In Proceedings of the Conference on Uncertainty in Artificial Intelligence, pages 519-527, Banff Canada. AUAI Press.
VanderWeele Tyler J. and Robins James M..(2007). Four types of effect modifica-tion, a classification based on directed acyclic graphs. Epidemiol, 18:561-568 VanderWeele Tyler J. and Robins James M.(2008). Empirical and counterfactual
conditions for sufficient cause interactions. Biometrika, 95:49-61.
VanderWeele Tyler J. and Robins James M.(2009). Signed directed acyclic graphs for causal inference.Journal of the Royal Statistical Society B.
Verma Thomas S. and Pearl Judea.(1988). Causal networks: Semantics and ex-pressiveness. In Proceedings of the conference on Uncerainty in Artificial In-telligence, 4:352-359.
Wellman Michael P.(1990). Fundamental concepts of qualitative probabilistic net-works. Artificial Intelligence, 20:557-585.