Bifurkasi Hopf Pada Model Mangsa Pemangsa Tipe Leslie Dengan Fungsi Respons Holling Tipe Iii

(1)

BIFURKASI HOPF PADA MODEL MANGSA-PEMANGSA

TIPE LESLIE DENGAN FUNGSI RESPONS

HOLLING TIPE III

VIVIE SUNDARI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Bifurkasi Hopf pada Model Mangsa-pemangsa Tipe Leslie dengan Fungsi Respons Holling Tipe III adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

(4)

ABSTRAK

VIVIE SUNDARI. Bifurkasi Hopf pada Model Mangsa-Pemangsa Tipe Leslie dengan Fungsi Respons Holling Tipe III. Dibimbing oleh ALI KUSNANTO dan JAHARUDDIN.

Mangsa-pemangsa merupakan salah satu fenomena alam yang dipelajari untuk studi dampak keseimbangan alam yang diakibatkan oleh dua spesies yang berinteraksi. Terdapat beberapa model matematis untuk memodelkan peristiwa mangsa-pemangsa. Dalam karya ilmiah ini direkonstruksi model mangsa-pemangsa Tipe Leslie dengan fungsi respons Holling tipe III. Simulasi dilakukan untuk melihat pengaruh parameter terhadap kestabilan sistem. Dengan memilih nilai parameter yang tepat, diperoleh satu sampai dengan empat titik tetap. Dinamika populasi mangsa-pemangsa pada model ini dibagi menjadi empat kasus. Pada kasus kedua, terjadi perubahan kestabilan titik tetap dari spiral stabil menjadi spiral takstabil, disertai adanya kemunculan limit cycle. Kemunculan limit cycle tersebut menandakan terjadi bifurkasi Hopf.

Kata kunci: bifurkasi Hopf , Holling tipe III, limit cycle, mangsa-pemangsa.

ABSTRACT

VIVIE SUNDARI. Hopf Bifurcations in Predator-Prey System of Leslie Type with Holling Type III of Response Functional. Supervised by ALI KUSNANTO and JAHARUDDIN.

The occurance of predator-prey is a natural phenomenon which is intended to study the impact of the natural balance caused by two interacting species. There are several mathematical models to describe prey predator events. In this paper we analyzed predator-prey model of Leslie type with Holling type III of response functional. The simulations are conducted to reveal the parameters influence on the stability of the system. By choosing appropriate parameter values, we may obtaine one to four equilibrium points. The prey predator population dynamics was simulated based on four cases. In the second case, the stable spiral changed into an unstable spiral with existence of a limit cycle. The presence of limit cycle shows the occurence of the Hopf bifurcation.

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

BIFURKASI HOPF PADA MODEL MANGSA-PEMANGSA

TIPE LESLIE DENGAN FUNGSI RESPONS

HOLLING TIPE III

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(6)

(7)

(8)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala nikmat, rahmat, dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Judul karya ilmiah ini adalah Bifurkasi Hopf pada Model Mangsa-pemangsa Tipe Leslie dengan Fungsi Respons Holling Tipe III. Penyusunan karya ilmiah ini tidak lepas dari bantuan beberapa pihak. Oleh karena itu, penulis mengucapkan terimakasih kepada:

1 Keluarga tercinta: Ayah Aden Djalaludin dan Ibu Erlin Herlina serta adik Ramadihasan Fadillah yang selalu memberikan doa, motivasi dan kasih sayang tiada henti,

2 Bapak Drs Ali Kusnanto, MSi dan Bapak Dr Jaharuddin, MS selaku dosen pembimbing atas segala kesabaran, ilmu, saran dan motivasinya, serta Bapak Dr. Paian Sianturi selaku dosen penguji.

3 Staf tata usaha Departemen Matematika IPB.

4 Nurlita Fikadhilla selaku sahabat yang telah memberikan motivasi, mengingatkan, dan menyemangati selama ini,

5 Teman-teman “Ameroet” (Aca, Nenden, Fika, Laras, Aisyah, Syifa, Novitadayanti, dan Yuli) yang senantiasa memberikan warna yang lebih indah selama di Departemen Matematika IPB,

6 Teman-teman mahasiswa Matematika 49 yang senantiasa berjuang bersama-sama dan saling memotivasi,

7 Kakak- kakak mahasiswa Matematika 48, teman-teman mahasiswa Matematika 50 dan 51 terima kasih atas doa dan semangatnya selama ini,

8 Semua pihak yang telah membantu dalam penyusunan karya ilmiah ini. Semoga karya ilmiah ini bermanfaat.

(9)

DAFTAR ISI

DAFTAR TABEL vi

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

DAFTAR TABEL x

PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 2

LANDASAN TEORI 2

HASIL DAN PEMBAHASAN 8

Pemodelan 8

Pembahasan 9

Analisis Kestabilan Titik Tetap � = , 11

Analisis Kestabilan Titik Tetap �∗ = ∗, ∗ 11

Bifurkasi Hopf 18

SIMULASI NUMERIK 21

Dinamika Populasi Mangsa-Pemangsa Kasus (a) 22

Dinamika Populasi Mangsa-Pemangsa Subkasus (b1) 23

Dinamika Populasi Mangsa-Pemangsa kasus (c) 25

Dinamika Populasi Mangsa-Pemangsa Subkasus (b2) 26

SIMPULAN DAN SARAN 31

Simpulan 31

Saran 31

DAFTAR PUSTAKA 32

LAMPIRAN 33

(10)

DAFTAR TABEL

1 Pemilihan nilai parameter model 22

2 Titik tetap, nilai eigen dan kestabilan pada kasus (a) 22 3 Titik tetap, nilai eigen dan kestabilan pada subkasus (b1) 23 4 Titik tetap, nilai eigen dan kestabilan pada kasus (c) 25

5 Nilai parameter subkasus (b2) 26

6 Titik tetap, nilai eigen dan kestabilan pada subkasus (b2) 26 7 Titik tetap, nilai eigen dan kestabilan pada subkasus (b2), β=0.9 27 8 Titik tetap, nilai eigen dan kestabilan pada subkasus (b2), β=0.27 28 9 Titik tetap, nilai eigen dan kestabilan pada subkasus (b2), β=0.5 29

DAFTAR GAMBAR

10 Bidang solusi mangsa 26

11 Bidang solusi pemangsa kasus (c) 26

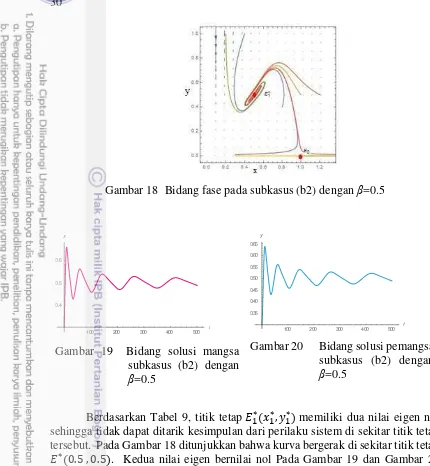
12 Bidang fase pada subkasus (b2) dengan β=0.9 27 13 Bidang solusi mangsa subkasus (b2) dengan β=0.9 27 14 Bidang solusi pemangsa subkasus (b2) dengan β=0.9 27 15 Bidang fase pada subkasus (b2) dengan β=0.27 28 16 Bidang solusi mangsa subkasus (b2) dengan β=0.27 29 17 Bidang solusi pemangsa subkasus (b2) dengan β=0.27 29 18 Bidang fase pada subkasus (b2) dengan β=0.5 30 19 Bidang solusi mangsa subkasus (b2) dengan β=0.5 30 20 Bidang solusi pemangsa subkasus (b2) dengan β=0.5 30

DAFTAR LAMPIRAN

1 Penondimensionalan model 33

2 Penentuan titik tetap 35

3 Penentuan matriks Jacobi 36

4 Titik tetap pada kasus (a) 37

5 Titik tetap pada kasus (c) 38

(11)

(12)

(13)

PENDAHULUAN

Latar Belakang

Dalam ekosistem, terjadi hubungan antara makhluk hidup dengan lingkungannya yang cukup kompleks dan saling memengaruhi. Dalam pola interaksi hubungan tersebut ikut dilibatkan terjadinya siklus biogekimia, yaitu sejumlah aliran energi dan juga rantai makanan. Aliran energi merupakan hubungan saling ketergantungan antar spesies, aliran energi tersebut dapat berdampak positif bagi keduanya (simbiosis mutualisme), berdampak negatif bagi keduanya (persaingan), maupun dapat berdampak positif bagi salah satu spesies dan berdampak negatif bagi spesies yang lain (mangsa-pemangsa). Rantai makanan merupakan lintasan konsumsi makanan yang melibatkan beberapa spesies. Bagian paling sederhana dari rantai makanan berupa interaksi antara spesies mangsa (prey) dan spesies pemangsa (predator).

Populasi mangsa memunyai persediaan cukup di dalam lingkungannya, sedangkan populasi pemangsa memiliki makanan yang bergantung pada jumlah mangsa. Apabila populasi mangsa terbatas, maka populasi pemangsa akan mengalami penurunan sesuai dengan jumlah proporsi mangsanya. Oleh karena itu, hubungan antara mangsa-pemangsa sangat erat. Tanpa adanya mangsa, pemangsa kemungkinan besar tidak dapat hidup. Dalam hal ini pemangsa berfungsi sebagai pengendali populasi mangsa. Berdasarkan fungsi predator itulah terbentuk keseimbangan jumlah populasi dari mangsa-pemangsa.

Interaksi antara mangsa-pemangsa dapat diilustrasikan dalam suatu model matematika yang terdiri atas satu atau lebih persamaan maupun pertaksamaan. Persamaan ini dapat melibatkan variabel dengan turunan-turunannya yang selanjutnya disebut persamaan diferensial.

(1959) memperkenalkan fungsi respons. Fungsi respons dalam ekologi adalah jumlah makanan yang dimakan oleh pemangsa sebagai fungsi kepadatan makanan. Secara umum fungsi respons bergantung pada banyak faktor, misalnya kepadatan mangsa, efisiensi pemangsa dalam mencari dan membunuh mangsanya, waktu penanganan, dan lain-lain. Dalam hal ini fungsi respons dibagi atas tiga macam, yaitu fungsi respons tipe I, tipe II, dan tipe III (Garrot et al. 2009).

Fungsi respons tipe I terjadi pada pemangsa yang memiliki karakteristik pasif, artinya pemangsa tersebut lebih suka menunggu mangsanya. Fungsi respons tipe II terjadi pada pemangsa yang memiliki karakteristik aktif dalam mencari mangsanya. Fungsi respons tipe III terjadi pada pemangsa yang akan mencari populasi mangsa lain ketika populasi mangsa yang dimakannya mulai berkurang.

(14)

2

Tujuan Penelitian Penelitian ini bertujuan untuk :

1 Merekonstruksi model mangsa-pemangsa tipe Leslie dengan perumuman fungsi respons Holling tipe III yang dituliskan oleh Huang et al. (2013), 2 Menganalisis kestabilan model mangsa-pemangsa tipe Leslie dengan

perumuman fungsi respons Holling tipe III yang sudah dinondimensionalkan,

3 Menunjukkan adanya bifurkasi Hopf pada model tersebut.

LANDASAN TEORI

Sistem Persamaan Diferensial

Sistem persamaan diferensial ordo satu dengan persamaan dan buah fungsi yang tak diketahui , , … , dapat ditulis sebagai berikut:

̇ = , ,

Jika linear, maka sistem persamaan diferensial di atas disebut linear, sebaliknya jika tidak linear maka sistem persamaan diferensial di atas disebut taklinear. Jika tidak bergantung secara eksplisit pada t, yaitu , = , maka disebut sistem persamaan diferensial mandiri (Braun 1983).

Misalkan diberikan sistem persamaan diferensial sebagai berikut: ̇ = , ℝ .

Titik ∗ disebut titik tetap jika memenuhi ∗ = . Titik tetap disebut juga titik kritis atau titik kesetimbangan (Tu 1994).

Misalkan titik ∗ adalah titik tetap sebuah sistem persamaan diferensial mandiri dan adalah solusi yang memenuhi kondisi awal = dengan ≠ ∗_._Titik ∗_{dikatakan titik tetap stabil jika}_{∀ > , ∃ >} _dengan_{| −} ∗_{| <} _{, maka}_| ₋ ∗_{| < , ∀ >}_{. Titik} ∗_{dikatakan titik tetap}_takstabil

jika ∃ > , ∀ > dengan | − ∗| < , maka | − ∗| , ∀ > (Verhulst 1990).

(15)

3 ̇ = , ,

(1) ̇ = , .

Misalkan ∗, ∗ adalah titik tetap dari persamaan (1), maka ∗, ∗ = dan

∗_, ∗ ₌ _{. Misalkan} _{= −} ∗_dan _{= −} ∗_{, maka didapatkan:}

̇ = ̇ = ∗_{+ ,} ∗₊ _,

̇ = ̇ = ∗_{+ ,} ∗_{+ .}

Dengan melakukan pendekatan ekspansi Taylor dua peubah, maka didapatkan sistem sebagai berikut:

̇ = ∗_, ∗ ₊ ₊ _{+ �} _{, ,}

= + + � , , ,

(2) ̇ = ∗_, ∗ ₊ ₊ _{+ �} _{, ,}

= + + � , , .

Persamaan (2) dapat dituliskan dalam bentuk matriks sebagai berikut:

[ ̇̇] =

[ ]

[ ] + � , , .

Karena � , , → artinya nilai dari � , , mendekati nol, maka nilainya dapat diabaikan. Oleh karena itu, didapatkan persamaan linear:

[ ̇̇] = �[ ], (3)

dengan matriks A yaitu:

� =

[ ]

.

(16)

4

Misal A adalah sebuah matriks berukuran n x n, maka sebuah vektor tak nol di ℝ dinamakan vektor eigen dari A, jika � adalah kelipatan skalar dari , yaitu:

� = � ,

untuk suatu skalar �. Skalar � ini dinamakan nilai eigen dari A, sedangkan dinamakan vektor eigen yang bersesuaian dengan �.

Untuk mencari nilai eigen dari matriks A yang berukuran n x n, maka dituliskan kembali � = � sebagai:

� = � , atau

� − � = , (4)

dengan merupakan matriks identitas. Persamaan (4) akan memunyai penyelesaian tak nol jika dan hanya jika:

det � − � = . (5)

Persamaan (5) dinamakan persamaan karakteristik � (Anton 1987). Analisis Kestabilan

Misalkan diberikan system persamaan diferensial yang memiliki bentuk seperti berikut:

̇ = + ,

̇ = + , (6)

Matriks koefisien dari system persamaan diferensial (6) ialah: � = [ ].

Berdasarkan persamaan (5), maka persamaan karakteristiknya menjadi: det − � _{− � = ,}

sehingga diperoleh persamaan:

� − trace � � + det � = ,

dengan

(17)

5 Dengan demikian diperoleh nilai eigen dari A adalah:

� , = trace � ± √trace � − det � .

Berdasarkan nilai determinan dan trace matriks A, nilai eigen � dan � akan memenuhi tiga kasus berikut:

I. Kasus I

Jika det � < , maka nilai eigen adalah bilangan real dan berbeda tanda sehingga titik tetap merupakan titik sadel.

II. Kasus II

Jika det � > , maka nilai eigen dapat berupa bilangan real dengan tanda yang sama (titik tetap berupa simpul) atau bilangan kompleks conjugate (titik tetap berupa spiral atau center).

a. trace � − det � > .

 Jika trace � > dan kedua nilai eigen real bernilai positif, maka titik tetap bersifat simpul takstabil.

 Jika trace � < dan kedua nilai eigen real bernilai negatif, maka titik tetap bersifat simpul stabil.

b. trace � − det � < .

 Jika trace � > dan kedua nilai eigen imajiner ± � , maka titik tetap bersifat spiral takstabil.

 Jika trace � < dan kedua nilai eigen imajiner ± � , maka titik tetap bersifat spiral stabil.

 Jika trace � = dan kedua nilai eigen imajiner ± � , maka titik tetap bersifat center.

c. trace � − det � = .

Parabola trace � − det � = adalah garis batas antara simpul dan spiral. Star nodes atau degenerate terletak pada parabola ini. Jika kedua nilai eigen bernilai sama maka titik tetap bersifat simpul sejati.

III. Kasus III

Jika det � = , setidaknya ada satu nilai eigen yang sama dengan nol. Maka titik tetap merupakan titik tak terisolasi.

(Strogatz 1994). Akar persamaan orde tiga

Misalkan persamaan orde tiga memiliki bentuk umum sebagai berikut :

+ + + = . (7)

Berdasarkan Spiegel dan Liu (2002), akar-akar dari persamaan (7) adalah: = + − ,

(18)

6 maka akar-akar dari persamaan (7) dapat ditentukan berdasarkan nilai diskriminannya.

(i) Jika ∆ > , maka persamaan orde tiga tersebut memiliki satu akar real dan dua akar kompleks.

(ii) Jika ∆= , maka semua akar dari persamaan orde tiga tersebut merupakan akar real dengan setidaknya ada dua akar kembar.

(iii) Jika∆ < , maka persamaan orde tiga tersebut akan memiliki akar real

(Spiegel dan Liu 2002).

Penondimensionalan

Penondimensionalan adalah suatu metode untuk menjadikan peubah dan parameter model yang sebelumnya memiliki dimensi (populasi/orang/binatang, waktu, populasi/waktu) menjadi peubah yang tanpa dimensi. Dengan menjadikan semua peubah dan parameter tanpa dimensi maka perbandingan antar parameter dapat dilakukan. Dengan penondimensionalan ini akan mengakibatkan suatu persamaan dengan banyak parameter akan menjadi persamaan dengan lebih sedikit parameter. Biasanya penondimensionalan mengelompokkan beberapa parameter dengan sebuah parameter tunggal (Strogatz 1994). Sebagai contoh, diberikan model mangsa-pemangsa berikut:

(19)

7 maka diperoleh model dengan satu parameter yaitu:

̇ = − , ̇ = − + .

Fungsi Respons

Misalkan dan menyatakan banyaknya mangsa dan pemangsa pada waktu . Menurut Freedman (1980) sistem mangsa-pemangsa tipe Gauss dinyatakan sebagai persamaan diferensial berikut:

̇ = , −

(9) ̇ = − + ,

dengan , merupakan fungsi kontinu dan terturunkan yang menyatakan spesifikasi laju pertumbuhan mangsa tanpa adanya kehadiran pemangsa dan

memenuhi , = > , , = , , < , , < , dan

� , > untuk setiap > . Pertumbuhan logistik , = − ⁄

dianggap sebagai prototipe dan memenuhi semua asumsi.

Pada persamaan (9), merupakan fungsi respons yang menggambarkan jumlah mangsa yang akan dimakan pemangsa. Jumlah mangsa yang akan dimakan pemangsa tersebut akan meningkat seiring dengan meningkatnya kerapatan pemangsa. Fungsi yang menjelaskan bagaimana pemangsa mengkonversi mangsa dalam pertumbuhan pemangsa adalah dan parameter menunjukkan efisiensi pemangsa dalam mengkonversi mangsa ke dalam pertumbuhan mereka, sedangkan parameter adalah angka kematian pemangsa.

Bifurkasi

Strogatz (1994) menjelaskan bahwa struktur kualitatif dari suatu sistem dinamika dapat berubah karena adanya perubahan dari parameter sistem tersebut. Hal inilah yang disebut bifurkasi. Bifurkasi adalah perubahan jumlah titik tetap atau kestabilan titik tetap dalam suatu sistem dinamik. Nilai parameter ketika terjadinya bifurkasi dinamakan titik bifurkasi. Salah satu jenis bifurkasi yaitu Bifurkasi Hopf.

(20)

8

HASIL DAN PEMBAHASAN

Pemodelan

Model mangsa-pemangsa tipe Leslie merupakan salah satu modifikasi dari model mangsa-pemangsa Lotka Volterra. Dalam model Lotka Volterra, laju pertumbuhan pemangsa dipengaruhi oleh keberadaan mangsa secara langsung dan akan terjadi kepunahan pemangsa jika tidak ada populasi mangsa. Pada model mangsa-pemangsa tipe Leslie laju pertumbuhan pemangsa tidak hanya dipengaruhi oleh ketersediaan populasi mangsa tetapi juga sistem pertahanan hidup populasi pemangsa. Selanjutnya, Huang et al. (2013) mengembangkan model mangsa-pemangsa tipe Leslie dengan penambahan fungsi respons Holling tipe III. Fungsi respons Holling tipe III menggambarkan tingkat pertumbuhan populasi pemangsa yang cenderung mencari populasi mangsa lain ketika populasi mangsa yang dimakannya mulai berkurang. Model mangsa-pemangsa tipe Leslie dengan fungsi respons Holling tipe III yang dituliskan oleh Huang et al.(2013) dinyatakan sebagai berikut:

̇ = − − ₊ _{+ ,}

(10) ̇ = _{− ℎ ,}

di mana , > dan konstanta , �, , , , ℎ > dengan: : banyaknya populasi mangsa pada waktu (populasi) : banyaknya populasi pemangsa pada waktu (populasi) : daya dukung lingkungan (populasi)

: laju pertumbuhan intrinsik mangsa tanpa adanya pemangsa (1/waktu) : laju pertumbuhan intrinsik pemangsa (1/waktu)

ℎ : jumlah mangsa yang diperlukan untuk mendukung populasi pemangsa pada kesetimbangan ketika = ℎ

: tingkat kejenuhan pemangsa

Persamaan (10) dengan banyak parameter ditransformasikan ke bentuk yang lebih sederhana dengan cara penondimensionalan model. Skala parameter yang digunakan, yaitu:

̂ → , ̂ → , � → ,

(21)

9 ̇ = − − ₊ _{+ ,}

(11) ̇ = ( − ),

di mana , > 0, setelah tanda topi dibuang.

(Bukti lampiran 1) Pembahasan

Titik tetap persamaan (11) diperoleh dengan menyelesaikan persamaan:

�

� = dan �

� = , yaitu:

− − ₊ _{+ = ,} ₍₁₂₎

( − ) = . (13)

Dengan menyederhanakan persamaan (12) diperoleh persamaan sebagai berikut:

+ − + − + − = . (14)

(Bukti lampiran 2) Penyelesaian persamaan (13) adalah

= , (15)

atau

= . (16)

Substitusi = ke persamaan (12), diperoleh = atau = . Karena nilai = tidak memenuhi persamaan (14), diperoleh titik tetap � = , .

Substitusi persamaan (16) ke persamaan (14) akan diperoleh:

+ ( + − ) + − − = . (17)

(22)

10

Kemudian ditentukan pula , , dan pada persamaan (18) sebagai berikut:

=

(23)

11 Analisis Kestabilan Titik Tetap � = ,

Dengan melakukan pelinearan pada persamaan (11) diperoleh matriks Jacobi sebagai berikut :

� = sehingga dihasilkan matriks Jacobi sebagai berikut:

� , = (− − + + ).

Dengan menyelesaikan persamaan karakteristik det _� _, − � = diperoleh nilai eigen untuk matriks _� _, , yaitu:

� = − dan � = .

Parameter diasumsikan bilangan real yang bernilai positif sehingga � < dan � > . Akibatnya, titik tetap � , memiliki kestabilan yang bersifat sadel.

Analisis Titik Tetap �∗ ∗, ∗

Menurut Strogatz (1994), analisis kestabilan pada titik tetap �∗ ∗, ∗ dapat dilakukan dengan memerhatikan nilai-nilai eigen untuk matriks _{� ,} .

Dari matriks Jacobi (20) diperoleh det ( �∗ dan trace ( �∗ sebagai Dengan menyelesaikan persamaan karakteristik det _� ∗_, ∗ − � = diperoleh nilai eigen untuk matriks _�∗ ∗_, ∗ , yaitu:

� , =

trace( �∗ ∗, ∗ ± √ trace( �∗ ∗_, ∗ − det( _�∗ ∗_, ∗

(24)

12

Untuk menyederhanakan persamaan (19), dapat dimisalkan:

= _��+ − + − , (23)

sehingga, persamaan (19) dapat dituliskan sebagai berikut:

∆=− + ( +

(c) Jika ∆< , maka sistem memiliki tiga titik tetap positif yang berbeda, yaitu: �∗ ∗_, ∗ _,_�∗ ∗_, ∗ _{, dan}_�∗ ∗_, ∗ _.

Bukti Teorema 1 (a) Bukti kasus (a)

Pada kasus (a) Teorema 1, berdasarkan sifat akar persamaaan pangkat tiga, jika ∆> maka persamaan (15) memiliki 1 akar real dan 2 akar kompleks. Berdasarkan sifat fisis dari sistem, ∈ ℝ dan > maka sistem hanya memiliki 1 akar real positif yaitu ∗. Dengan demikian sistem hanya memiliki titik tetap positif yang tunggal yaitu �∗= ∗, ∗ .

(Bukti lampiran 4) Kestabilan titik tetap �∗ = ∗, ∗ pada kasus (a) ditunjukkan melalui simulasi numerik.

(b) Bukti kasus (b)

(25)

13 Karena ∆= , maka persamaan (25) memberikan:

= + ( + − ) − − ( + − ) , Bukti subkasus (b1)

Pada subkasus (b1) Teorema 1 perhatikan kondisi ketika ∆= dan > , persamaan (19) dapat dituliskan sebagai berikut:

(

Dengan menyelesaikan persamaan (27) diperoleh:

= − ₋+ dan = − ₋− . (28)

(26)

14

− − − ₊+ ₊ + ₊ ₊ = . (31)

Substitusikan persamaan (30) ke persamaan (31) maka diperoleh:

− + ₊ ₊ = ,

atau

− − − = . (32)

Kemudian, substitusikan persamaan (31) ke persamaan (32), diperoleh:

− − ₋+ − − ₋− − = . (33)

Dengan menyelesaikan persamaan kuadratik (33), diperoleh dua akar real berbeda yaitu:

Kestabilan titik tetap �∗ ∗, ∗ pada subkasus (b1) Teorema 1 akan ditunjukkan melalui simulasi numerik. Sedangkan, kestabilan titik tetap �∗ ∗, ∗ yang akan ditunjukkan pada pembahasan mengenai bifurkasi Hopf.

Bukti subkasus (b2)

(27)

15 Persamaan ∆= dapat dituliskan sebagai berikut:

∆= − + ( + − �_�+ − − �_�+ − ) = ,

atau

+ − ( + − ) − ( + − ) = . (35)

Selanjutnya, substitusikan persamaan (34) ke persamaan (35), sehingga diperoleh persamaan berikut:

+ − − − / _{− −} _{− = .} (36) Penyelesaian persamaan (36) adalah

= − .

Substitusikan = − ke persamaan (34) sehingga diperoleh persamaan berikut:

+ − − = − − − , (37)

Penyelesaian persamaan (37) adalah:

= − + .

Jika det( � = , maka diperoleh persamaan sebagai berikut:

− − − ₊+ ₊ + ₊ ₊ = . (38)

Kemudian, jika parameter = − dan = −� + disubstitusikan ke persamaan (38), maka diperoleh:

(28)

16

melalui simulasi numerik. (c) Bukti kasus (c)

Pada kasus (c) Teorema 2.1, yaitu kondisi ketika ∆< , menurut Spiegel dan Liu (2002) akan diperoleh tiga akar real yaitu ∗, ∗, dan ∗.

(Bukti lampiran 4) Kestabilan dari ketiga titik tetap tersebut akan ditunjukkan melalui simulasi numerik.

Teorema 2

Dengan memerhatikan subkasus (b1) pada Teorema 1, jika parameter , , = +�_−� , −� +�+_−� ,_� −�_+� dan < < , maka sistem (11) memiliki dua titik tetap positif yaitu:

(i) �∗ −�

Berdasarkan bukti subkasus (b1) Teorema 1, diperoleh:

∗₌

(29)

17

= −_{+ .} (43)

Jika persamaan (43) disubstitusikan ke persamaan (40) dan persamaan (41), maka parameter dan parameter dapat dituliskan menjadi:

= +

pembahasan mengenai bifurkasi Hopf, sedangkan kestabilan titik tetap �∗ −�

+� ,

� +�

−� +� ditunjukkan melalui simulasi numerik.

Teorema 3

Dengan memerhatikan subkasus (b2) pada Teorema 1, diperoleh dua kondisi sebagai berikut:

(i) Jika , = − , −� + dan ≠

− + .

(ii) Jika , , = − , +

− , − + .

Bukti Teorema 3

(30)

18

+ + − +

− = , (47)

dengan menyelesaikan persamaan (47) diperoleh nilai =

− + . Ketika

trace( � ≠ , maka ≠

− + . Parameter dapat bernilai lebih besar

maupun lebih kecil dari

− + . Kestabilan titik tetap �∗ ∗, ∗ pada

subkasus (b2) Teorema 2 akibat adanya perubahan nilai parameter akan ditunjukkan melalui simulasi numerik.

Bifurkasi Hopf

Diketahui bahwa nilai eigen titik tetap �∗ ∗, ∗ pada subkasus (b1) Teorema 1 dapat diperoleh sebagai:

� , = trace( � ± √ trace( � − det( � .

Bifurkasi Hopf terjadi ketika kesetimbangan mengalami perubahan kestabilan dan adanya limit cycle (Strogatz 1994). Perubahan kestabilan tersebut yakni perubahan titik tetap yang mulanya memiliki kestabilan spiral stabil menjadi spiral takstabil ataupun sebaliknya.

Syarat perlu agar bifurkasi Hopf tercapai adalah jika kondisi berikut terpenuhi:

trace( � = dan

trace( � − det( � < .

Ketika trace( � = diperoleh persamaan (38) sebagai berikut :

= − ₋+ dan = − ₋− . (48)

Selain itu, diperoleh titik tetap �∗ ∗, ∗ di mana ∗ = − . Berdasarkan asumsi, ∗ > sehingga − > . Akibatnya, bifurkasi Hopf akan dipenuhi jika

< < . (49)

Kemudian, substitusikan ∗ = ��

��+ −� pada trace( � = . Sehingga

(31)

19

= −_{+ .} (50)

Parameter yang diperoleh pada persamaan (48), (49), dan (50) merupakan parameter batas yang harus terpenuhi agar bifurkasi Hopf dapat tercapai. Kemudian, substitusikan persamaan (48) dan (50) ke sistem persamaan (11), sehingga persamaan (11) dapat dituliskan sebagai berikut:

̇ = − − _+�

−� −

� +�+

−� +

,

(51) ̇ = − −₊ .

Untuk mengetahui kestabilan dari titik tetap �∗ ∗, ∗ dari subkasus (b1) Teorema 1, dimisalkan = − −�

� + dan = −

� +�

+� −� . Selanjutnya,

dengan menggunakan ekspansi deret Taylor, sistem persamaan (51) dapat dituliskan menjadi:

̇ = − −₊ + + + + −

+ + + _{− +}+ − + − +

+ − − + − + + � | , | ,

̇ = ₋+ − − + ₋ + + ₋+

− − ₊ + + + ₋ +

− ₋+ + − ₊+ + � | , | .

(52) Berdasarkan persamaan (52) variabel-variabel dapat di transformasi menjadi matriks sebagai berikut:

= √ ₊ − ₊ −_{+ )} .

(32)

20

̇ = −√ ₊− + , ,

(53) ̇ = √ ₊− + , ,

dengan fungsi , dan , sebagai berikut: ,

= √ − √ + _{− − +}+ − − +₊ − +

+ − + ₊− +

+ √ + + − + − +

√ − +

+ − − − + ₊− + − +

+ √ + + − − − +₊ − − + − +

− − + − + ₊− + − +

−√ − − + + − + − +

√ + +

+ � | , | ,

dan

, = − −₊ + − + √ − √₊ + +

+ − ₊ + + � | , | .

Bilangan Liapunov (Perko 1996) dapat dinyatakan sebagai berikut:

= | { + + +

+ [ ( + − ( + −

+ ]}|

= =

= − + − + −₊ + − + > .

(33)

21

SIMULASI NUMERIK

Dinamika populasi mangsa-pemangsa dapat digambarkan melalui kurva dalam bidang fase dan bidang solusi untuk menentukan kestabilan populasi mangsa dan pemangsa pada kurun waktu tertentu. Simulasi numerik dilakukan dengan cara mensubstitusikan nilai-nilai parameter yang ditentukan berdasarkan analisis kondisi persamaan pada model populasi mangsa-pemangsa. Proses komputasi pada simulasi ini menggunakan software Wolfram Mathematica 10.0.

Diasumsikan bahwa laju pertumbuhan intrinsik dari mangsa tanpa adanya pemangsa lebih besar dibandingkan laju pertumbuhan intrinsik pemangsa adalah tetap dengan daya lingkungan adalah . Saat melakukan penondimensionalan model, diperoleh bahwa = yang mereprentasikan tingkat interaksi antara mangsa dan pemangsa dan =

ℎ � yang sebanding

dengan tingkat kesetimbangan pemangsa tanpa adanya mangsa .

Dalam simulasi ini, terdapat empat parameter, yaitu : , , , dan . Nilai-nilai parameter yang digunakan tersebut harus terlebih dahulu memenuhi parameter batas keberadaan titik tetap pada sistem mangsa-pemangsa tipe Leslie dengan fungsi respons Holling tipe III, yaitu : < < yang menyatakan bahwa tingkat interaksi antara mangsa dan pemangsa, < < yang menyatakan tingkat kesetimbangan pemangsa tanpa adanya mangsa, dan > yang menyatakan bahwa semakin besar nilai dari maka menunjukkan bahwa fungsi respon dari Holling tipe III tersebut memberikan pengaruh yang semakin kecil bagi interaksi antar mangsa.

Parameter diasumsikan bernilai . yang menunjukkan bahwa laju pertumbuhan intrinsik dari mangsa tanpa adanya pemangsa dua kali lipat lebih besar dibandingkan laju pertumbuhan intrinsik pemangsa . Parameter diasumsikan bernilai . dan parameter diasumsikan bernilai . Pemilihan parameter-parameter ini bertujuan untuk memperlihatkan perubahan dari struktur titik tetap pada kasus (a), subkasus (b1), dan kasus (c) pada Teorema 1 serta kestabilan dari titik tetapnya sekaligus menunjukkan keberadaan bifurkasi Hopf pada subkasus (b1) Teorema 1.

Pada subkasus (b2) Teorema 1, parameter diasumsikan bernilai − , sedangkan parameter diasumsikan bernilai . saat >

− + ,

diasumsikan bernilai . saat <

− + , dan diasumsikan bernilai .

saat =

− + . Pemilihan parameter-parameter tersebut bertujuan untuk

(34)

22

Tabel 1 Pemilihan nilai parameter model

Kasus Parameter

a . . −

b

b1 . . − .

b2

(i) . . −

(ii) . . −

(iii) . . −

c . . −

Dinamika Populasi Mangsa-Pemangsa Kasus (a)

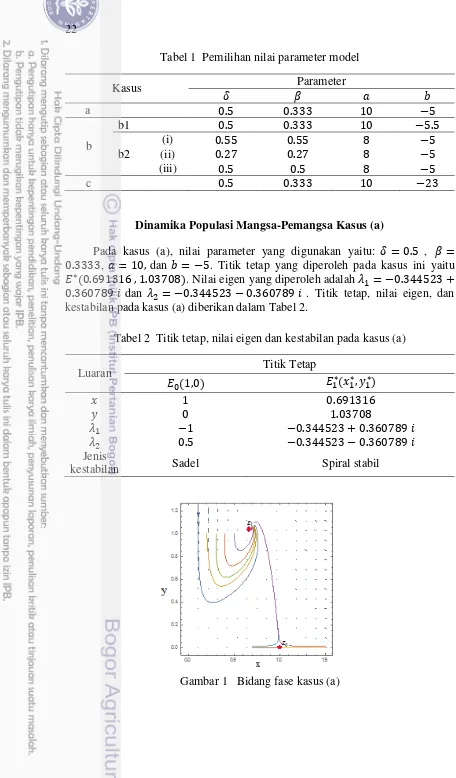
Pada kasus (a), nilai parameter yang digunakan yaitu: = . , = . , = , dan = − . Titik tetap yang diperoleh pada kasus ini yaitu �∗ _. _{, .} _{. Nilai eigen yang diperoleh adalah}_{� = − .} ₊

. � dan � = − . − . � . Titik tetap, nilai eigen, dan kestabilan pada kasus (a) diberikan dalam Tabel 2.

Tabel 2 Titik tetap, nilai eigen dan kestabilan pada kasus (a)

Luaran Titik Tetap

� , �∗ ∗, ∗

. .

� − − . + . �

� . − . − . �

Jenis

kestabilan Sadel Spiral stabil

(35)

23

Gambar 2 Bidang solusi mangsa kasus (a)

Gambar 3 Bidang solusi pemangsa kasus (a)

Pada Gambar 1 ditunjukkan ilustrasi bidang fase dari beberapa nilai awal di sekitar titik tetap. Terdapat dua buah titik tetap, di mana kedua populasi menuju titik tetap �∗ . , . serta memperlihatkan bahwa jenis kestabilan titik tetapnya adalah spiral stabil. Selain itu, pada Gambar 1 ditunjukkan adanya titik tetap � , dengan kestabilannya yang bersifat sadel. Pada Gambar 2 ditunjukkan bahwa dengan nilai awal tertentu, di awal periode populasi mangsa mengalami kenaikan yang drastis kemudian populasi mangsa mengalami penurunan hingga menyebabkan kestabilan mangsa menuju pada = . . Pada Gambar 3 diperlihatkan bahwa dengan nilai awal tertentu, terjadi peningkatan populasi pemangsa secara terus menerus, kemudian populasi pemangsa mengalami penurunan hingga menyebabkan kestabilan pemangsa menuju pada = . .

Dinamika Populasi Mangsa-Pemangsa Subkasus (b1)

Pada subkasus (b1), diambil beberapa parameter yang memenuhi kondisi persamaan model mangsa-pemangsa yaitu: = . , = . , = , dan = − . , dengan menggunakan parameter-parameter yang diberikan, diperoleh dua titik tetap, nilai eigen dan kestabilan pada subkasus (b1) dan diberikan dalam Tabel 3.

Tabel 3 Titik tetap, nilai eigen dan kestabilan pada subkasus (b1)

Luaran

kestabilan Sadel Sadel Spiral takstabil

(36)

24

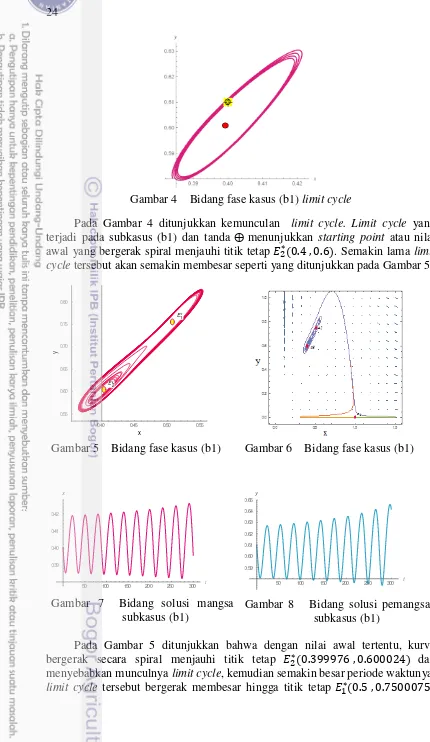
Gambar 4 Bidang fase kasus (b1) limit cycle

Pada Gambar 4 ditunjukkan kemunculan limit cycle. Limit cycle yang terjadi pada subkasus (b1) dan tanda ⨁ menunjukkan starting point atau nilai awal yang bergerak spiral menjauhi titik tetap �∗ . , . . Semakin lama limit cycle tersebut akan semakin membesar seperti yang ditunjukkan pada Gambar 5.

Gambar 5 Bidang fase kasus (b1) Gambar 6 Bidang fase kasus (b1) menyebabkan munculnya limit cycle, kemudian semakin besar periode waktunya, limit cycle tersebut bergerak membesar hingga titik tetap �∗ . , .

(37)

25 berada di dalam limit cycle yang lebih besar . Pada Gambar 6 ditunjukkan bahwa limit cycle yang terus membesar dan semakin lama limit cycle tersebut akan hilang pada waktu tertentu. Selain itu, pada Gambar 6 ditunjukkan adanya titik tetap � , yang bersifat sadel. Pada Gambar 7 dan Gambar 8 ditunjukkan bahwa dengan nilai awal yang diberikan, di awal periode populasi mangsa dan pemangsa pada kasus (b1) mengalami kenaikan setelah itu mengalami penurunan yang drastis. Kemudian, pertumbuhan kedua populasi mengalami osilasi secara terus menerus, sehingga kedua populasi tersebut tidak stabil menuju ke suatu nilai.

Dinamika Populasi Mangsa-Pemangsa kasus (c)

Pada kasus (c) diambil beberapa parameter sebarang yang memenuhi kondisi persamaan model mangsa-pemangsa yaitu: = . , = . , dan = . Kemudian dipilih nilai parameter = − . Titik tetap, nilai eigen, dan kestabilan pada kasus (c) diberikan dalam Tabel 4.

Tabel 4 Titik tetap, nilai eigen dan kestabilan pada kasus (c) Luaran

Titik tetap

� , �∗ ∗_, ∗ _�∗ ∗_, ∗ _�∗ ∗_, ∗

. . .

� − . . − .

� . − . . − .

Jenis

kestabilan Sadel Sadel

Simpul

takstabil Simpul stabil

(38)

26

Gambar 10 Bidang solusi mangsa kasus (c)

Gambar 11 Bidang solusi pemangsa kasus (c)

Bidang fase pada kasus (c) ditunjukkan oleh Gambar 9. Terdapat empat titik tetap berbeda, yaitu � , , �∗ ∗, ∗ , �∗ ∗, ∗ , dan �∗ ∗, ∗ . Dengan �∗ ∗_, ∗ _{merupakan titik tetap}_{takstabil dan titik tetap}_�∗ ∗_, ∗ _merupakan

titik tetap stabil. Sedangkan titik tetap � , dan titik tetap �∗ ∗, ∗ merupakan titik tetap yang bersifat sadel. Pada Gambar 10 ditunjukkan bahwa dengan nilai awal yang diberikan, populasi mangsa bergerak stabil menuju =

. sedangkan pada Gambar 11 ditunjukkan bahwa dengan nilai awal yang diberikan, populasi pemangsa bergerak stabil menuju = . .

Dinamika Populasi Mangsa-Pemangsa Subkasus (b2)

Pada subkasus (b2), diasumsikan nilai parameter , yaitu: = − . Dengan menetapkan nilai parameter , dapat diperoleh nilai parameter-parameter lain dan diberikan dalam Tabel 5. Selain itu dapat diperoleh titik tetap tunggal dari masing masing kondisi , nilai eigen dan kestabilan pada subkasus (b2) dan diberikan dalam Tabel 6.

Tabel 5 Nilai parameter subkasus (b2) Nilai

Tabel 6 Titik tetap, nilai eigen dan kestabilan pada subkasus (b2)

Luaran

(39)

27 Pada subkasus (b2) kondisi pertama, diambil beberapa parameter sebarang yang memenuhi kondisi persamaan model mangsa-pemangsa yaitu: = − , =

. , = . , dan = . Titik tetap, nilai eigen, dan kestabilan pada kasus (b2) kondisi pertama diberikan dalam Tabel 7.

Tabel 7 Titik tetap, nilai eigen dan kestabilan pada subkasus (b2), β=0.9

Luaran Titik tetap

� , �∗ ∗_, ∗

. .

� − − .

� .

Jenis kestabilan Sadel Simpul stabil

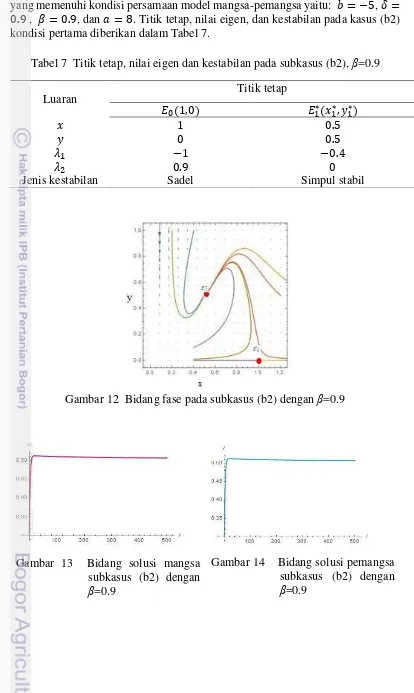
Gambar 12 Bidang fase pada subkasus (b2) dengan β=0.9

Gambar 13 Bidang solusi mangsa subkasus (b2) dengan

β=0.9

Gambar 14 Bidang solusi pemangsa subkasus (b2) dengan

(40)

28

Pada Gambar 12 ditunjukkan bidang fase dari kasus (b2) dengan β=0.9. Pada Gambar 12 ditunjukkan bahwa terdapat dua titik tetap dengan beberapa nilai awal yang bergerak mendekati titik tetap �∗ . , . , sehingga pada subkasus (b2) dengan β=0.9 kestabilannya bersifat simpul stabil. Selain itu, pada Gambar 12 ditunjukkan adanya titik tetap � , yang bersifat sadel. Pada Gambar 13 dan Gambar 14 ditunjukkan bahwa dengan nilai awal yang diberikan, populasi mangsa dan pemangsa pada kasus (b2) dengan β=0.9 di awal periode mengalami kenaikan yang drastis, kemudian populasi mangsa dan pemangsa tersebut akan stabil menuju ke suatu nilai, yaitu = . dan = . .

Pada subkasus (b2) kondisi kedua, diambil nilai parameter sembarang yang memenuhi kondisi persamaan model mangsa-pemangsa yaitu: = − , = . , = . , dan = . Titik tetap, nilai eigen, dan kestabilan pada kasus (b2) kondisi pertama diberikan dalam Tabel 8.

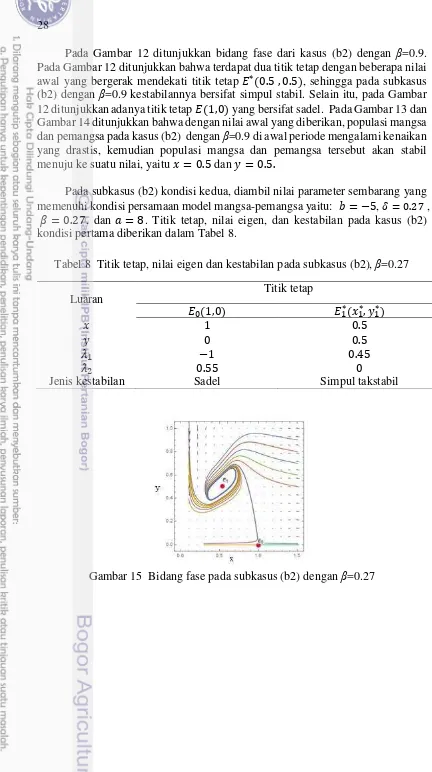
Tabel 8 Titik tetap, nilai eigen dan kestabilan pada subkasus (b2), β=0.27 Luaran

Titik tetap

� , �∗ ∗_, ∗

. .

� − .

� .

Jenis kestabilan Sadel Simpul takstabil

(41)

29 menjauhi titik tetap tersebut, sehingga kestabilannya bersifat tak terisolasi yang takstabil. Selain itu, pada Gambar 15 ditunjukkan adanya titik tetap � , yang bersifat sadel. Pada Gambar 16 ditunjukkan bahwa dengan nilai awal yang diberikan, populasi mangsa berosilasi secara terus menerus dengan simpangan yang sama di sekitar titik = . . Selanjutnya, pada Gambar 17 menunjukkan bahwa populasi pemangsa juga berosilasi secara terus menerus dengan simpangan yang sama di sekitar titik = . .

Pada subkasus (b2) kondisi ketiga, diambil beberapa parameter sebarang yang memenuhi kondisi persamaan model mangsa-pemangsa yaitu: = − , =

. , = . , dan = . Titik tetap, nilai eigen, dan kestabilan pada kasus (b2) kondisi pertama diberikan dalam Tabel 9.

Tabel 9 Titik tetap, nilai eigen dan kestabilan pada subkasus (b2), β=0.5

Luaran Titik tetap

(42)

30

Gambar 18 Bidang fase pada subkasus (b2) dengan β=0.5

Gambar 19 Bidang solusi mangsa subkasus (b2) dengan

β=0.5

Gambar 20 Bidang solusi pemangsa subkasus (b2) dengan

β=0.5

Berdasarkan Tabel 9, titik tetap �∗ ∗, ∗ memiliki dua nilai eigen nol sehingga tidak dapat ditarik kesimpulan dari perilaku sistem di sekitar titik tetap tersebut. Pada Gambar 18 ditunjukkan bahwa kurva bergerak di sekitar titik tetap �∗ _{. , .} _{. Kedua nilai eigen bernilai nol Pada Gambar 19 dan Gambar 20}

ditunjukkan bahwa populasi mangsa dan pemangsa mengalami osilasi secara terus menerus dengan simpangan yang tak beraturan.

100 200 300 400 500 t 0.4

0.5 0.6 x

100 200 300 400 500 t 0.35

(43)

31

SIMPULAN DAN SARAN

Simpulan

Dari analisis model mangsa-pemangsa tipe Leslie dengan fungsi respons Holling tipe III diperoleh satu, dua, tiga, atau empat titik tetap dari setiap kasus yang berbeda. Kestabilan titik tetap � bersifat sadel. Sedangkan titik tetap yang lain bergantung pada nilai parameter-parameter lainnya. Dalam analisis ini, konstanta dari fungsi respons Holling tipe III merupakan parameter yang paling berpengaruh terhadap perubahan jumlah titik tetap serta kestabilannya. Dalam mengamati dinamika populasi mangsa-pemangsa pada model ini, terlebih dahulu dibagi menjadi empat kasus yang berbeda.

Pada kasus pertama, diperoleh dua titik tetap. Titik tetap yang pertama bersifat sadel, sedangkan titik tetap yang lain bersifat spiral stabil. Kemudian ketika nilai konstanta dari fungsi respons Holling tipe III tersebut diperkecil (yaitu pada kasus kedua), terjadi perubahan pada banyaknya titik tetap dan kestabilan dari masing masing titik tetap. Pada titik tetap pertama dan kedua, kestabilannya bersifat sadel. Sedangkan, pada titik tetap yang lain kestabilannya bersifat spiral takstabil. Adanya perubahan kestabilan dari spiral stabil menjadi spiral takstabil inilah yang mengindikasikan terjadinya fenomena bifurkasi Hopf yang disertai dengan kemunculan limit cycle.

Pada kasus ketiga, terdapat dua buah titik tetap. Titik tetap pertama bersifat sadel titik tetap kedua bersifat tak terisolasi. Ketika nilai parameter yang merepresentasikan tingkat kesetimbangan pemangsa tanpa adanya mangsa diperbesar, titik tetap kedua mengalami perubahan kestabilan menjadi simpul stabil. Sedangkan ketika nilai dari parameter yang merepresentasikan tingkat kesetimbangan pemangsa tanpa adanya mangsa diperkecil, maka titik tetap tersebut bersifat simpul takstabil.

Pada kasus keempat diperoleh empat titik tetap. Titik tetap pertama dan kedua bersifat sadel, titik tetap ketiga bersifat simpul stabil, dan titik tetap keempat bersifat simpul takstabil.

Saran

(44)

32

DAFTAR PUSTAKA

Anton H. 1987. Aljabar Linear Elementer. Jakarta (ID): Erlangga.

Braun M. 1983. Differential Equations and Their Applications. New York: Springer-Verlag.

Freedman HI.1980. Deterministic Mathematical Models in Population Ecology. New York: Marcel Dekker.

Garrott RA, White PJ, Watson FGR. 2009. The Ecology of Large Mammals in Central Yellowstone Sixteen Years of Integrated Field Studies. San Diego (US): Elsevier.

Huang J, Song J, Ruan S. 2013. Bifurcations in a predator-prey system of Leslie type with generalized Holling tipe III functional response. J. Differential Equations, 257:1721-1752. doi: 10.1016/j.de.2014.04.024

Spiegel MR, Liu J. 2002. Mathematical Handbook of Formulas and Tables

(Schaum’s Outlines). United States of America: McGraw-Hill

Strogatz SH. 1994. Nonlinear Dynamics and Chaos, with Application to Physics, Biology, Chemistry, and Engineering. Massachusetts (US): Addison-Wesley Publishing Company.

Tu PNV. 1994. Dynamical System An Introduction with Application in Economics and Biology. Second Revised and Enlarged Edition. Germany: Springer Verlag. Verhulst F. 1990. Nonlinear Differential Equation and Dynamical System.

(45)

33

LAMPIRAN

Lampiran 1 Penondimensionalan model Tinjau kembali model persamaan (10):

̇ = − −

+ + ,

̇ = _{− ℎ .}

Dilakukan penondimensionalan sistem untuk mendapatkan parameter yang lebih sederhana. Skala parameter yang digunakan yaitu :

̂ → , ̂ → , � → ,

̂ → , ̂ → , → , → ℎ .

= − − �

� + � +

,

= − − ₊ _{+ ,}

= − −

+ + ,

= − − ₊ _{+ .} (54)

� ₌

� − ℎ � ,

= _� _{− ℎ} ,

= _{− ℎ} ,

(46)

34

= _{− ℎ} . (55)

Misalkan

= , = _ℎ.

Substitusikan dan kedalam persamaan (54) dan (55) sehingga diperoleh model persamaan (12) berikut :

= − − ₊ _{+ ,}

(47)

35 Lampiran 2 Penentuan titik tetap

Titik tetap persamaan (11) diperoleh dengan menyelesaikan persamaan dari

�

� = dan �

� = , sehingga dapat diuraikan sebagai berikut :

Ketika �

� = diperoleh :

⟺ − − ₊ _{+ = ,}

⟺ − ₊+ ₊+ − = ,

⟺ − + + − = ,

⟺ ( − + + − = ,

⟺ − + + − = ,

(48)

36

Lampiran 3 Penentuan matriks Jacobi

Misalkan model persamaan (11) dapat dituliskan sebagai berikut: , = ̇ = − − ₊ _{+ ,}

, = ̇ = − .

Dengan melakukan pelinearan didapatkan matriks Jacobi sebagai berikut:

� =

( )

 = − − ₊ ₊

= − − + +₊ −₊ +

= − − ₊ +₊

 = − − ₊ ₊

= − ₊ ₊

 = −  = −

 =  = −

� =

(

− ₊+ ₊ − ₊ ₊

−

(49)

37 Lampiran 4 Titik tetap pada kasus (a)

Pada kasus (a) Teorema 1, jika ∆> , makaka berdasarkan rumusan menurut Spiegel dan Liu (2002) persamaan (17) akan memiliki satu akar real dan dua akar kompleks. Namun, karena ∈ ℝ maka pada kasus (a) akan dihasilkan 1 titik tetap yaitu �∗ ∗, ∗ . Dengan ∗= + − dan ∗ = �

� ∗. Titik ∗

dan ∗ dapat diuraikan sebagai berikut:

(50)

38

Lampiran 5 Titik tetap pada kasus (c)

Pada kasus (c) Teorema 1, jika ∆> , maka berdasarkan rumusan menurut menurut Speiegel dan Liu (2002) persamaan (17) akan memiliki tiga akar real berbeda, yaitu:

∗ _{= √− cos ( �) −} _,

∗ _{= √− cos � +} ° ₋ _,_dan ∗ _{= √− cos ( � +} °_{) −} _,

dengan cos � =

√− .

Tiga akar real yang diperoleh dari persamaan (17) pada kasus (c) dapat diuraikan sebagai berikut:

∗ _{= −} + +��₊

√− − ₊ − + +�� _cos

[

arccos

[

( + − − + +_�� − − + +_�� )

√ − +(− + +�_�)

6 _]

] ,

∗ _{= −} + +��_{+ √−} − ₊ − + +�� _sin

[ +

arccos

[

( + − − + +_�� − − + +_�� )

√ − +(− + +�_�)

6 ]

(51)

39

∗ _{= −} + +��_{+ √−} − ₊ − + +�� _sin

[ −

arccos

[

( + − − + +_�� − − + +_�� )

√ − +(− + +�_�)

6 _]

(52)

40

Lampiran 6 Program plot bidang fase kasus (a) (Gambar 1) ≔ . ; ≔ . ; ≔ ; ≔ − ;

P1=VectorPlot[{x*(1-x)-((x^2*y)/(a*x^2 + b*x +1)), y*( – *y/x)},{x,0,1.5},{y,0,1.5}];

Ode1[x0_,y0_]:=NDSolve[{x’[t]==x[t]*(1

-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

y’[t]==y[t]*( − *y[t]/x[t]), x[0]==x0, y[0]==y0},

{x[t],y[t]},{t,0,100}]; Sol[1]=ode1[.1,1];

Sol[2]=ode1[.2,1]; Sol[3]=ode1[.3,1]; Sol[4]=ode1[.4,1]; Sol[5]=ode1[.5,1]; Sol[6]=ode1[0.3,0]; Sol[7]=ode1[0.3,0.01]; Sol[8]=ode1[1.5,0]; Sol[9]=ode1[1.5,0.01];

P2=ParametricPlot[Evaluate[Table[{x[t],y[t]}./Sol[i], {i,9}]],{t,0,100},PlotRange->{{0,1.5},{0,1}}, PlotPoints->100, AxesLabel->{”x”,”y”}];

(53)

41 Lampiran 7 Program plot bidang solusi mangsa kasus (a) (Gambar 2)

≔ . ; ≔ . ;

Manipulate[Module[{plt1,plt2,sol,x0=xx0,y0=yy0},

sol=NDSolve[{x’[t]==x[t]*(1

-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

y’[t]==y[t]*(( − *y[t]/x[t]),x[t/;t 0]==x0,

y[t/;t 0==y0} ,{x[t],y[t]},{t,0,50}]; plt1=ParametricPlot[{t,x[t]}/.sol,{t,0,50},

PlotRange->All,AspectRatio->0.6,PlotStyle-> {RGBColor[0.89,0.09,0.5],Thick},AxesLabel-> {t,x}];

plt2=StreamPlot[[{x*(1-x)-((x^2*y)/(a*x^2+b*x +1)), y*( – *y/x)},{x,0,1},{y,0,1}, FrameLabel->

{{Style[Row[{Style[”y”,

Italic],”(”,Style[”t”, Italic,”)”}],14],None},

{{Style[Row[{Style[”x”,

Italic],”(”,Style[”t”,Italic,”)”}],14],Style [Row[{Style[”The phase portrait of system”,

Bold]}],14]}}, StreamPoints->50]; Show[plt1, ImageSize-> {300,300}]], Delimiter,

{{xx0,.50,”x0”},0,50,.01,ImageSize->Small,

Appearance-> ”Labeled”},

{{yy00,.50,”y0”},0,50,.01,ImageSize->Small, Appearance-> ”Labeled”},

(54)

42

Lampiran 8 Program plot bidang solusi pemangsa kasus (a) (Gambar 3) ≔ . ; ≔ . ;

-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

y’[t]==y[t]*(( − *y[t]/x[t]),x[t/;t 0]==x0,

y[t/;t 0==y0} ,{x[t],y[t]},{t,0,50}]; plt1=ParametricPlot[{t,y[t]}/.sol,{t,0,50},

PlotRange->All,AspectRatio->0.6,PlotStyle-> {RGBColor[0.21,0.65,0.79],Thick},AxesLabel-> {t,y}];

{{yy00,.50,”y0”},0,50,.01,ImageSize->Small,

(55)

43

Lampiran 9 Program plot bidang fase subkasus (b1) limit cycle (Gambar 4)

Manipulate[Module[ ≔ . , ≔ . , eqns, solns, plot1, plot2},

Eqns={Derivative[1][x][t]==x[t]*(1-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

Derivative[1][y][t]== y[t]*(( − *y[t]/x[t]), x[0]=-.4, y[0]=0.61};

Solns=Quiet@NDSolve[eqns,{x,y},{t,0,time}, AccuracyGoal -> 3];

plot1=Plot[{x[t]/.solns, y[t]/.solns},{0,t,time}, PlotStyle->{RGBColor[0.,0.67,0.76],

RGBColor[1.,0.2,0.45]},PlotRange->{0,All}, Frame->True,FrameLabel->{”time”,

Row[{Style[”y”,RGBColor[1.,0.2,0.45],Medium], Style[”x”,RGBColor[0.,0.67,0.76],Medium]}]},

AspectRatio -> 1, ImageSize ->{300,300}];

plot2=ParametricPlot[{x[t],y[t]}/.solns,{t,0,time}, AspectRatio -> 1, PlotRange -> All, PlotStyle ->{RGBColor[1.,0.28,0.73]},ImagePadding->

{{Automatic, Automatic}, {Automatic,10}}, Frame -> True,FrameLabel-> {Style [”x”, Black,

Medium], Style[”y”,Black,Medium]}, ImageSize

-> {300,300},

PlotStyle->RGBColor[0.,0.67,0.76]}];

GraphicsRow[{plot2}]],{{time,125},100,10000, Appearance -> ”Labeled”, ImageSize -> Tiny},

{{a,10,”a”},10.,50, Appearance-> ”Labeled”,ImageSize

-> Tiny},

{{b,-5.50006,”b”},

-10.,50,Appearance-> ”Labeled”,ImageSize -> Tiny},

(56)

44

Lampiran 10 Program plot bidang fase subkasus (b1) (Gambar 5) ≔ . ; ≔ . ; ≔ ; ≔ − . ;

-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

y’[t]==y[t]*( − *y[t]/x[t]), x[0]==x0, y[0]==y0},

{x[t],y[t]},{t,0,100}]; Sol[1]=ode1[.4,.61];

Sol[2]=ode1[0.3,0]; Sol[3]=ode1[0.3,0.01]; Sol[4]=ode1[1.5,0]; Sol[5]=ode1[1.5,0.01];

P2=ParametricPlot[Evaluate[Table[{x[t],y[t]}./Sol[i], {i,5}]],{t,0,100},PlotRange->{{0,1.5},{0,1}}, PlotPoints->100, AxesLabel->{”x”,”y”}];

(57)

45 Lampiran 11 Program plot bidang fase subkasus (b1) (Gambar 6)

Manipulate[Module[ ≔ . , ≔ . , eqns, solns, plot1, plot2},

Eqns={Derivative[1][x][t]==x[t]*(1-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

Derivative[1][y][t]== y[t]*(( − *y[t]/x[t]), x[0]=-.4, y[0]=0.61};

Solns=Quiet@NDSolve[eqns,{x,y},{t,0,time}, AccuracyGoal -> 3];

plot1=Plot[{x[t]/.solns, y[t]/.solns},{0,t,time}, PlotStyle->{RGBColor[0.,0.67,0.76],

RGBColor[1.,0.2,0.45]},PlotRange->{0,All}, Frame->True,FrameLabel->{”time”,

Row[{Style[”y”,RGBColor[1.,0.2,0.45],Medium], Style[”x”,RGBColor[0.,0.67,0.76],Medium]}]},

AspectRatio -> 1, ImageSize ->{300,300}];

plot2=ParametricPlot[{x[t],y[t]}/.solns,{t,0,time}, AspectRatio -> 1, PlotRange -> All, PlotStyle ->{RGBColor[1.,0.28,0.73]},ImagePadding->

{{Automatic, Automatic}, {Automatic,10}}, Frame -> True,FrameLabel-> {Style [”x”, Black,

Medium], Style[”y”,Black,Medium]}, ImageSize

-> {300,300},

PlotStyle->RGBColor[0.,0.67,0.76]}];

GraphicsRow[{plot2}]],{{time,1125},100,10000, Appearance -> ”Labeled”, ImageSize -> Tiny},

{{a,10,”a”},10.,50, Appearance-> ”Labeled”,ImageSize

-> Tiny},

{{b,-5.50006,”b”},

-10.,50,Appearance-> ”Labeled”,ImageSize -> Tiny},

(58)

46

Lampiran 12 Program plot bidang solusi mangsa subkasus (b1) (Gambar 7)

≔ . ; ≔ . ;

-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

y’[t]==y[t]*(( − *y[t]/x[t]),x[t/;t 0]==x0,

Italic],”(”,Style[”t”, Italic,”)”}],14],None}, {{Style[Row[{Style[”x”,

Style[”parameters,Bold,10],

{{a,10,”a”},0,50,.01,ImageSize->Small,

{{b,-5.50006,”b”},-50,50,.01,ImageSize->Small, Appearance-> ”Labeled”},

Delimiter,

Style[”initial conditions”,Bold,10],

{{xx0,.4,”x0”},0,50,.01,ImageSize->Small, Appearance-> ”Labeled”},

(59)

47 Lampiran 13 Program plot bidang solusi pemangsa subkasus (b1)

(Gambar 8)

{{b,-5.50006,”b”},-50,50,.01,ImageSize->Small, Appearance-> ”Labeled”},

Delimiter,

(60)

48

Lampiran 14 Program plot bidang fase kasus (c) (Gambar 9) restart: with(plots): with(Detools):

iniset:={seq(seq([0,i,j],i=0.4..7),j=0.5..9)} ≔ . ; ≔ . ; ≔ ; ≔ − ;

Kasusc:=diff(x(t),t)=(x(t)*(1-x(t))-(x(t)^2*y(t))/(a*x(t)^2+b*x(t)+1), diff(y(t),t)=y(t)*( - *y(t)/x(t)):

Deplot([kasusc],[x(t),y(t)],t=- 10..10,iniset,stepsize=0.1,x=-0.1..2.2,y=-0.1..3.5,arows=SLIM,color=black,

(61)

49 Lampiran 15 Program plot bidang solusi mangsa kasus (c) (Gambar 10)

≔ . ; ≔ . ;

-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

y’[t]==y[t]*(( − *y[t]/x[t]),x[t/;t 0]==x0,

plt2=StreamPlot[[{x*(1-x)-((x^2*y)/(a*x^2+b*x +1)), y*( – *y/x)},{x,0,1},{y,0,1}, FrameLabel-> {{Style[Row[{Style[”y”,

{{b,-23,”b”},-50,50,.01,ImageSize->Small, Appearance-> ”Labeled”},

Delimiter,

(62)

50

Lampiran 16 Program plot bidang solusi pemangsa kasus (c) (Gambar 11) ≔ . ; ≔ . ;

-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

y’[t]==y[t]*(( − *y[t]/x[t]),x[t/;t 0]==x0,

{{b,-23,”b”},-50,50,.01,ImageSize->Small, Appearance-> ”Labeled”},

Delimiter,

(63)

51 Lampiran 17 Program plot bidang fase subkasus (b2) dengan β=0.9

(Gambar 12)

≔ . ; ≔ . ; ≔ ; ≔ − ;

-x[t])-((x[t])^2*y[t]/(a*(x[t])^2+b*x[t]+1)),

y’[t]==y[t]*( − *y[t]/x[t]), x[0]==x0, y[0]==y0},

{x[t],y[t]},{t,0,100}]; Sol[1]=ode1[.4,1];

Sol[2]=ode1[1,.5]; Sol[3]=ode1[.2,1]; Sol[4]=ode1[1.2,.5]; Sol[5]=ode1[.8,.4]; Sol[6]=ode1[.5,.5]; Sol[7]=ode1[1,0]; Sol[8]=ode1[0.3,0]; Sol[9]=ode1[0.3,0.01]; Sol[10]=ode1[1.5,0]; Sol[11]=ode1[1.5,0.01];

P2=ParametricPlot[Evaluate[Table[{x[t],y[t]}./Sol[i], {i,11}]],{t,0,100},PlotRange->{{0,1.2},{0,1.5}}, PlotPoints->100, AxesLabel->{”x”,”y”}];

(64)

52

Lampiran 18 Program plot bidang solusi mangsa subkasus (b2) dengan β=0.9 (Gambar 13)