Bifurkasi hopf model mangsa-pemangsa dengan waktu tunda

(1)

BIFURKASI HOPF MODEL MANGSA-PEMANGSA DENGAN

WAKTU TUNDA

NI NYOMAN SURYANI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*

Dengan ini saya menyatakan bahwa skripsi berjudul Bifurkasi Hopf Model Mangsa-Pemangsa dengan Waktu Tunda adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Juli 2014

Ni Nyoman Suryani

(4)

Waktu Tunda. Dibimbing oleh ALI KUSNANTO dan NGAKAN KOMANG KUTHA ARDANA.

Dalam karya ilmiah ini dipelajari akibat dari waktu tunda dan tingkat pemanenan konstan pada dinamika model mangsa-pemangsa Lotka-Volterra. Dalam model ini, waktu tunda diberikan pada interaksi antar mangsa dari persamaan mangsa. Selanjutnya mangsa dan pemangsa akan dipanen dengan tingkat pemanenan yang konstan. Dalam model ini terdapat satu, dua, atau tiga titik tetap. Ketika terdapat dua titik tetap positif, satu diantaranya stabil. Perubahan parameter waktu tunda dari kecil menjadi besar dari batas waktu tunda kritis menyebabkan perubahan kestabilan titik tetap stabil menjadi tidak stabil, disertai adanya kemunculan limit cycle. Kemunculan limit cycle tersebut menandakan bahwa model mangsa pemangsa dengan tingkat pemanenan dan waktu tunda terjadi Bifurkasi Hopf.

Kata kunci: mangsa-pemangsa, limit cycle, waktu tunda, tingkat pemanenan konstan, bifurkasi Hopf.

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

BIFURKASI HOPF MODEL MANGSA-PEMANGSA DENGAN

WAKTU TUNDA

NI NYOMAN SURYANI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(6)

(7)

Judul Skripsi : Bifurkasi Hopf Model Mangsa-Pemangsa dengan Waktu Tunda Nama : Ni Nyoman Suryani

NIM : G54100076

Disetujui oleh

Drs Ali Kusnanto, MSi Pembimbing I

Ir Ngakan Komang Kutha Ardana, MSc Pembimbing II

Diketahui oleh

Dr Toni Bakhtiar, MSc Ketua Departemen

(8)

Puji dan syukur penulis panjatkan kepada Ida Sang Hyang Widhi Wasa atas segala karunia-Nya sehingga karya ilmiah yang berjudul Bifurkasi Hopf Model Mangsa-Pemangsa dengan Waktu Tunda berhasil diselesaikan.

Terima kasih penulis ucapkan kepada ayah, ibu, kakak, serta keluarga besar atas doa, dukungan, dan kasih sayangnya. Ungkapan terima kasih juga penulis sampaikan kepada Bapak Drs Ali Kusnanto, MSi dan Bapak Ir Ngakan Komang Kutha Ardana, MSc selaku pembimbing, serta Dr Ir Endar H Nugrahani, MS yang telah banyak memberi saran. Tak lupa juga ucapan terima kasih kepada seluruh dosen dan staf Departemen Matematika IPB atas segala ilmu yang diberikan dan bantuannya selama perkuliahan, serta teman-teman KMHD IPB 47, Brahmacarya Bogor, Matematika 46 dan 47 yang telah banyak membantu dalam proses penyusunan tugas akhir ini.

Semoga karya ilmiah ini bermanfaat.

Bogor, Juli 2014

(9)

DAFTAR ISI

DAFTAR TABEL viii

DAFTAR GAMBAR viii

DAFTAR LAMPIRAN viii

PENDAHULUAN 1

Latar Belakang 1

Tujuan 2

TINJAUAN PUSTAKA 2

HASIL DAN PEMBAHASAN 6

Model Matematika 6

Analisis Model Tanpa Waktu Tunda 8

Simulasi Numerik Model Tanpa Waktu Tunda 9

Dinamika Populasi Mangsa Pemangsa Kasus 1 9

Analisis Model dengan Waktu Tunda 11

Simulasi Numerik Model dengan Waktu Tunda 15

SIMPULAN 19

DAFTAR PUSTAKA 20

(10)

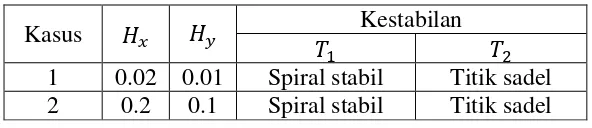
1 Pemilihan nilai tingkat pemanenan konstan 9

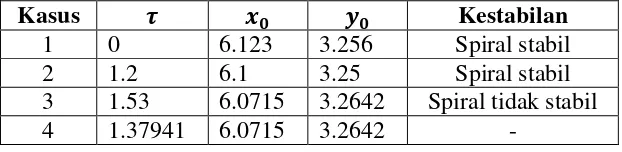
2 Pemilihan nilai awal dan waktu tunda model 15

DAFTAR GAMBAR

6 Bidang solusi mangsa kasus 1 (a) dan pemangsa kasus 1 (b) 16

7 Bidang fase kasus 2 16

8 Bidang solusi mangsa kasus 2 (a) dan pemangsa kasus 2 (b) 16

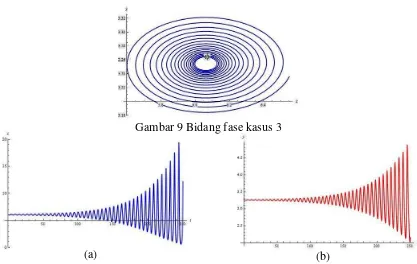
9 Bidang fase kasus 3 17

10Bidang solusi mangsa kasus 3 (a) dan pemangsa kasus 3 (b) 17

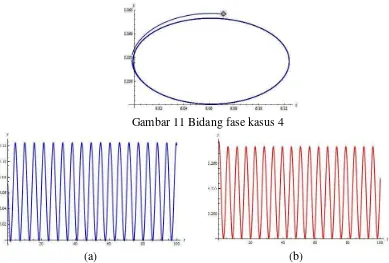
11Bidang fase kasus 4 18

12Bidang solusi mangsa kasus 4 (a) dan pemangsa kasus 4 (b) 18

DAFTAR LAMPIRAN

1 Penentuan kondisi keberadaan titik tetap model (12) 21

2 Penentuan kestabilan titik tetap model (12) 22

3 Kode program simulasi numerik kasus 1 model (12) 23 4 Kode program simulasi numerik kasus 2 model (12) 24

5 Linearisasi model (11) 25

6 Penentuan persamaan karakteristik (14) 26

7 Penentuan akar persamaan karakteristik (18) 28

8 Penentuan waktu tunda kritis (21) 29

9 Penentuan turunan implisit persamaan karakteristik (14) 31

10 Penjabaran fungsi sign 32

11 Penjabaran kondisi transversalbilitas 34

(11)

PENDAHULUAN

Latar Belakang

Peningkatan atau penurunan jumlah populasi makhluk hidup merupakan fenomena yang sering terjadi di alam. Proses tersebut dapat dilihat dari proses rantai makanan yang merupakan lintasan konsumsi makanan dan terdiri atas beberapa spesies organisme. Bagian paling sederhana dari suatu rantai makanan berupa interaksi dua spesies, yaitu interaksi antara spesies mangsa (prey) dan pemangsa (predator). Kehadiran pemangsa tentunya akan memberikan pengaruh terhadap jumlah mangsa, sehingga secara alami proses rantai makanan tersebut mempengaruhi proses keseimbangan jumlah populasi di muka bumi.

Sistem interaksi mangsa-pemangsa dapat dimodelkan dalam suatu model matematika. Dengan model mangsa-pemangsa, sebuah fenomena akan lebih mudah dipahami dan dapat digunakan untuk memprediksikan populasi atau spesies pada tahun tertentu. Pada tahun 1926, seorang ilmuan matematika Itali bernama Vito Volterra untuk pertama kalinya menyusun sebuah persamaan diferensial sederhana untuk menjelaskan dinamika populasi dua spesies yang berinteraksi yaitu mangsa dan pemangsa. Model Lotka-Volterra merupakan salah satu dari awal model mangsa-pemangsa dan dengan bentuk model yang cukup sederhana menyebabkan model ini banyak digunakan sebagai dasar pengembangan model yang lebih realistis. Dari waktu ke waktu bentuk model mangsa-pemangsa dimodifikasi sehingga dapat menggambarkan dengan teliti keadaan yang sebenarnya (Edelstein-Keshet 1988).

Dalam konteks interaksi mangsa-pemangsa, beberapa studi mengatakan bahwa perlakuan kepada populasi lebih lanjut dapat mempertimbangkan proses tingkat pemanenan dan waktu tunda. Model mangsa pemangsa dengan pemanenan sering kali mengaitkan populasi dengan masalah ekonomi. Pengaruh dari tingkat pemanenan konstan telah dipelajari oleh Holmberg dan hasilnya menunjukkan bahwa kuota tangkapan dapat menyebabkan osilasi serta kekacauan dan meningkatkan risiko eksploitasi (Toaha dan Hassan 2008).

(12)

pada keadaan sebelumnya. Hal ini penting untuk dipertimbangkan dalam memodelkan pertumbuhan populasi karena laju pertumbuhan populasi tidak hanya bergantung pada jumlah populasi pada waktu t tetapi juga bergantung pada waktu sebelumnya atau pada waktu .

Berdasarkan permasalahan tersebut, dalam karya ilmiah ini akan dibahas atau dikaji lebih jauh tentang model mangsa-pemangsa dengan tingkat pemanenan konstan dan waktu tunda. Dari model ini akan dianalisis kestabilan serta dinamika populasi mangsa pemangsa terhadap waktu.

Tujuan

Penulisan karya ilmiah ini bertujuan untuk :

1. Merekonstruksi model mangsa-pemangsa dengan waktu tunda dan tingkat pemanenan konstan.

2. Mempelajari pengaruh waktu tunda pada model mangsa-pemangsa dengan tingkat pemanenan konstan.

3. Menganalisis perubahan kestabilan titik tetap dari model mangsa-pemangsa dengan tingkat pemanenan dan waktu tunda.

4. Menunjukkan terjadinya bifurkasi Hopf pada model mangsa-pemangsa dengan tingkat pemanenan dan waktu tunda.

TINJAUAN PUSTAKA

Suatu sistem persamaan diferensial (SPD) dinyatakan sebagai berikut: ̇ , (1) eksplisit maka disebut persamaan diferensial mandiri yang dapat ditulis:

̇ . (2)

Titik disebut titik tetap jika . Titik tetap disebut juga titik keseimbangan atau titik kritis. Menurut Verhulst (1990), jika merupakan titik tetap sebuah SPD dan x(t) adalah solusi SPD dengan nilai awal dengan

x0 ≠ , titik dikatakan titik tetap stabil jika untuk sebarang radius ρ > 0 terdapat r > 0 sedemikian sehingga jika posisi awal x0 memenuhi | | maka solusi x(t) memenuhi | | , untuk setiap t > 0.

(13)

sebelumnya. Bentuk umum persamaan diferensial tundaan untuk ,

Dengan adanya persamaan tundaan yang berbentuk taklinear, perlu dilakukan sebuah pelinearan agar dapat diselesaikan secara eksplisit. Misalkan diberikan sistem persamaan diferensial dengan dua persamaan dan dua peubah seperti berikut:

Dengan melakukan pendekatan ekspansi Taylor dua peubah maka didapatkan sistem sebagai berikut:

̇

,

dengan merupakan galat yang cukup kecil. Selanjutnya diperoleh: ̇ ̇ .

(14)

Bentuk (4) disebut model terlinearkan dari model taklinear (Strogatz 1994). Misalkan matriks A berukuran , maka suatu vektor taknol x di

dengan I adalah matriks identitas. Persamaan (6) mempunyai solusi tak nol jika dan hanya jika

. (7)

Persamaan (7) disebut persamaan karakteristik dari matriks A (Tu 1994).

Analisis kestabilan titik tetap dilakukan melalui matriks Jacobi, yaitu matriks A. Penentuan kestabilan titik tetap didapat dengan melihat nilai-nilai eigennya, yaitu dengan yang diperoleh dari .

(15)

Sedangkan menurut Strogatz (1994) titik tetap dengan nilai eigen kompleks yang dinotasikan sebagai berikut:

,

dengan asumsi , bersifat spiral stabil jika dan bersifat spiral tak stabil jika .

Selanjutnya, Strogatz (1994) menjelaskan bahwa struktur kualitatif dari suatu sistem dinamika dapat berubah karena adanya perubahan dari parameter sistem dinamika tersebut. Hal inilah yang disebut bifurkasi. Bifurkasi adalah perubahan jumlah atau kestabilan titik tetap (titik kestabilan) dalam suatu sistem dinamik. Nilai parameter ketika terjadinya bifurkasi dinamakan titik bifurkasi. Salah satu jenis bifurkasi, yaitu bifurkasi Hopf.

Bifurkasi Hopf adalah kemunculan siklus batas (limit cycle) dari kesetimbangan dalam sistem dinamis yang dihasilkan oleh persamaan diferensial biasa, saat kesetimbangan mengalami perubahan stabilitas yang melalui sepasang nilai eigen imajiner murni. Bifurkasi dapat bersifat superkritis atau subkritis yang mengakibatkan limit cycle menjadi stabil atau tidak stabil. Limit cycle sendiri merupakan orbit tertutup yang terisolasi. Terisolasi artinya bahwa orbit di sekelilingnya menuju atau menjauhi siklus limit. Bifurkasi dapat bersifat superkritis atau subkritis yang mengakibatkan limit cycle menjadi stabil atau tidak stabil.

Berdasarkan persamaan karakteristik untuk menentukan kestabilan suatu titik tetap dapat menggunakan Routh-Hurwitz Criterion 1. Misalkan adalah bilangan asli dan jika dengan persamaan polinomial karakteristik:

. (8)

Nilai eigen dari persamaan (8) akan mempunyai bagian real negatif jika dan hanya jika determinan matriks untuk dengan:

adalah positif. Menurut kriteria Routh-Hourwitz pada teorema di atas untuk suatu nilai i (untuk i=2,3,4), titik tetap akan stabil jika dan hanya jika:

(16)

Cara yang digunakan untuk mengetahui kemungkinan adanya akar real positif dari sebuah persamaan polinom berderajat n adalah dengan menggunakan aturan tanda Descartes yang dinyatakan sebagai berikut, misalkan

teorema dalam menentukan jenis kestabilan titik keseimbangan sebagai berikut  Teorema 1 (Kar 2003)

Jika nilai eigen dari sebuah persamaan karakteristik bernilai positif dan teorema 1 terpenuhi dan persamaan karakteristik dalam bentuk polinom berderajat

n mempunyai akar real positif, maka titik keseimbangan adalah stabil asimtotik untuk .

Setelah menemukan nilai waktu tunda kritis dan akar karakteristik yang terdapat pada garis imajiner , kemudian akan diselidiki kondisi transversalbilitas. Menurut Kar (2003), kondisi transversalbilitas adalah kondisi yang dapat menyebabkan perubahan sifat kestabilan dari titik tetap ketika waktu tunda berubah. Untuk itu perlu diketahui bahwa akar karakterisik akan bergerak menuju bidang imajiner yang positif ketika waktu tunda membesar melebihi waktu tunda kritis . Kriteria untuk kondisi transversalbilitas adalah

(17)

daya dukung lingkungan dapat berubah, akibatnya pertumbuhan populasi akan mengalami penundaan. Penundaan tersebut menyebabkan penurunan populasi tetapi kemudian terjadi peningkatan sehingga terjadi osilasi pada pertumbuhan populasi. Persamaan Logistik tidak dapat mendeskripsikan pertumbuhan populasi pada kasus keterlambatan (waktu tunda). Oleh karena itu dikembangkan suatu model pertumbuhan logistik dengan waktu tunda. Model logistik dengan perlambatan dikenal sebagai persamaan perlambatan Hutchinson. Berikut adalah model populasi predator prey dengan perlambatan yang diperkenalkan oleh May

(1974),

Dalam model (10), jika dimisalkan adalah populasi mangsa pada waktu dan adalah populasi pemangsa pada waktu , maka dapat dilihat laju pertumbuhan mangsa tumbuh secara logistik. laju pertumbuhan populasi mangsa dipengaruhi oleh kematian alami yang berkurang sebesar karena adanya interaksi atau persaingan dengan individu sebelumnya ( ) serta berkurang sebesar karena pemangsaan oleh populasi pemangsa. Laju pertumbuhan populasi pemangsa akan terus berkurang secara eksponensial sebesar apabila tidak ada kehadiran populasi mangsa dan akan bertambah sebesar ketika pemangsa menyerang mangsa. Selanjutnya model (10) dikembangkan dengan mempertimbangkan asumsi tingkat pemanenan konstan.

r : laju pertumbuhan intrinsik mangsa,

K : daya dukung lingkungan

b : faktor logistik,

c : laju kematian pemangsa,

α : koefisien yang menunjukkan penurunan mangsa karena kehadiran satu individu pemangsa,

β : koefisien yang menunjukkan penambahan pemangsa karena kehadiran satu individu mangsa,

τ : waktu tunda,

Hx : tingkat pemanenan terhadap populasi mangsa,

Hy : tingkat pemanenan terhadap populasi pemangsa.

(18)

merupakan pemanenan dengan hasil atau jumlah yang tetap pada populasi mangsa dan pemangsa setiap periode waktu panen.

Analisis Model Tanpa Waktu Tunda

Berikut ini adalah sistem persamaan model (11) yang akan dianalisis tanpa menggunakan waktu tunda yaitu .

Model (12) menyatakan bahwa laju pertumbuhan mangsa terjadi secara normal dan tidak adanya masa penundaan. Laju pertumbuhan mangsa berkurang karena interaksi atau persaingan yang terjadi antara individu mangsa pada masa yang sama. Hal pertama yang harus dilakukan dalam menganalisis persamaan (12) adalah mencari titik tetap dengan membuat kuadran positif. Oleh karena itu, harus diasumsikan bahwa

. Jika bernilai positif, maka dari persamaan perlu diasumsikan bahwa

Model (12) akan memiliki dua buah titik tetap pada saat

,

atau ekuivalen dengan

( , untuk .

Titik tetap yang akan diperoleh adalah dan Titik tetap bersifat stabil asimtotik, sedangkan kestabilan titik tetap adalah tidak stabil, bersifat titik sadel.

(19)

( .

Persamaan karakteristik yang diperoleh dari matriks Jacobi adalah

,

Dinamika populasi mangsa-pemangsa dapat digambarkan melalui kurva dalam bidang fase dan bidang solusi yang menggambarkan populasi mangsa dan pemangsa pada kurun waktu tertentu. Simulasi numerik dilakukan dengan cara mensubtitusikan nilai yang ditentukan berdasarkan analisis kondisi persamaan model populasi mangsa-pemangsa dengan tingkat pemanenan konstan dan tanpa waktu tunda. Simulasi numerik dilakukan untuk menunjukkan hasil analisis model (12) dan hanya akan ditunjukkan dengan dua kasus.

Dalam simulasi ini, nilai-nilai parameter yang digunakan harus terlebih dahulu memenuhi batas keberadaan titik tetap. Nilai parameter yang bernilai tetap untuk setiap simulasi yang digunakan, yaitu . Nilai parameter yang akan berubah pada kedua kasus tersebut adalah nilai parameter tingkat pemanenan konstan. Pemilihan nilai parameter tingkat pemanenan konstan ditujukkan untuk memperlihatkan bahwa titik tetap akan bersifat stabil.

(20)

kasus ini ada dua, yaitu dan . Nilai eigen titik tetap pertama adalah , sehingga kestabilan titik tetap bersifat spiral stabil. Sedangkan nilai eigen yang diperoleh pada titik tetap kedua adalah dan , sehingga kestabilan titik tetap bersifat titik sadel.

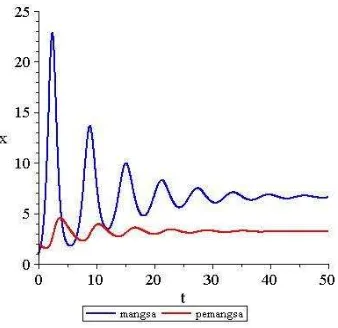
Pada Gambar 1, diberikan ilustrasi bidang fase di sekitar titik tetap dimana kedua populasi secara spiral menuju titik tetap serta diperlihatkan bahwa jenis kestabilan titik tetapnya spiral stabil. Gambar 2 memperlihatkan bahwa interaksi antara mangsa dan pemangsa mengalami osilasi di awal periode waktu kemudian keduanya menuju nilai yang stabil.

Dinamika Populasi Mangsa Pemangsa Kasus 2

Pada kasus kedua, nilai parameter tingkat pemanenan konstan yang digunakan telah diberikan pada Tabel 1. Titik tetap positif yang diperoleh pada kasus ini ada dua, yaitu dan . Nilai eigen titik tetap pertama adalah sehingga kestabilan titik tetap bersifat spiral stabil. Sedangkan nilai eigen yang diperoleh pada titik tetap kedua adalah dan , sehingga kestabilan titik tetap bersifat titik sadel.

Gambar 1 Bidang fase kasus 1 Gambar 2 Bidang solusi kasus 1

(21)

Pada Gambar 3, diberikan ilustrasi bidang fase di sekitar titik tetap yang menunjukkan kedua populasi secara spiral menuju titik tetap serta diperlihatkan bahwa jenis kestabilan adalah spiral stabil. Penurunan nilai parameter dan ini ternyata tidak menyebabkan perubahan kestabilan kedua titik tetap. Titik tetap akan selalu bersifat spiral stabil sedangkan titik tetap akan selalu bersifat titik sadel apabila kedua nilai parameter pemanenan diubah dan menuju nilai nol. Sama halnya dengan Gambar 2, Gambar 4 memperlihatkan bahwa interaksi antara mangsa dan pemangsa mengalami osilasi di awal periode waktu dengan simpangan yang semakin kecil kemudian keduanya menuju nilai yang stabil.

Analisis Model dengan Waktu Tunda

Hasil analisis dan simulasi model (12) menunjukkan bahwa titik tetap bersifat stabil. Pemberian waktu tunda akan menyebabkan perubahan kestabilan titik tetap dari stabil menjadi tidak stabil. Dalam menganalisa kestabilan titik tetap dengan waktu tunda perlu terlebih dahulu dilakukan linearisasi sistem persamaan (11) dengan transformasi dan Persamaan karakteristik dari persamaan (13) adalah sebagai berikut

, (14)

Menurut kriteria Routh-Hurwitz, nilai eigen dari persamaan karakteristik akan bernilai real dan negatif atau kompleks dengan bagian real negatif jika dan hanya jika

(22)

Oleh sebab itu, dengan tanpa adanya waktu tunda maka titik tetap akan bersifat stabil asimtotik jika dan hanya jika memenuhi kondisi (15).

Selanjutnya untuk menentukan sifat kestabilan ketika adanya waktu tunda atau adalah dengan memisalkan akar karakteristik. Kestabilan titik tetap ditentukan oleh bagian real solusi persamaan karakteristik (14). Misalkan adalah akar persamaan karakteristik (14), titik keseimbangan akan stabil jika . Jika terdapat suatu nilai tundaan kritis yang dapat menyebabkan sehingga merupakan akar imajiner murni persamaan (14), maka titik tetap mengalami perubahan sifat kestabilan. Dengan mensubtitusi , ke persamaan (14) maka diperoleh

_.

Dengan mengganti suku eksponensial ke bentuk trigonometri, bentuk persamaan tersebut berubah menjadi

.

Persamaan tersebut akan bernilai nol jika bagian imajiner dan realnya sama dengan nol, sehingga didapatkan

Eliminasi terhadap dilakukan dengan mengkuadratkan masing-masing ruas persamaan (16) menjadi

,

.

Kemudian kedua persamaan dijumlahkan serta dikelompokkan sesuai pangkat , maka diperoleh polinomial derajat empat

. (17)

(23)

persamaan (17) merupakan polinomial berderajat genap, bila didefinisikan sebagai akar dari persamaan (17) maka akan diperoleh

{ √ } (18)

Menurut aturan tanda Descrates, persamaan (17) akan memiliki paling tidak satu akar real positif jika variasi perubahan tanda koefisien polinomnya lebih dari satu atau sama dengan satu. Dari persamaan (18) dapat diketahui jika

dan , (19)

menyebabkan persamaan polinom (17) tidak memiliki variasi perubahan tanda koefisien sehingga persamaan (18) tidak memiliki akar real positif. Dalam hal ini akan ditinjau jika

, , dan , (20)

akan ada dua solusi positif dari persamaan (18). Dengan demikian persamaan (17) memiliki akar imajiner murni . Sehingga dengan mensubtitusi ke persamaan (16) maka akan diperoleh nilai tunda kritis

{

( ( }

(21) Setelah menemukan nilai kritis tundaan yang memuat akar karakteristik yang terdapat pada garis imajiner maka dimungkinkan terjadi bifurkasi pada titik tersebut, kemudian akan diselidiki kondisi transversalbilitas dengan membuktikan bahwa akar karakteristik akan bergerak menuju bidang imajiner yang positif ketika waktu tunda membesar melebihi waktu tunda Bifurkasi terjadi apabila persamaan (14) memenuhi kondisi transversalbilitas (9).

Jika merupakan fungsi dalam , ,

dapat dicari dengan menggunakan turunan implisit dari persamaan karakteristik (14) sebagai berikut

(24)

{ }

Oleh karena itu, kondisi transversalbilitas terpenuhi dan karenanya terjadi bifurkasi di , .

 Teorema 3 (Kar 2003)

(25)

[ , dan tidak stabil ketika

[ ,

untuk beberapa bilangan bulat positif m. Oleh karena itu terdapat bifurkasi di titik tetap ketika

Simulasi Numerik Model dengan Waktu Tunda

Simulasi numerik model mangsa pemangsa dengan tingkat pemanenan konstan dan waktu tunda dilakukan untuk menunjukkan bahwa terdapat pengaruh waktu tunda pada kestabilan titik tetap model. Proses komputasi ini menggunakan sistem aljabar komputer Mathematica 9.

Nilai-nilai parameter yang akan digunakan harus terlebih dahulu memenuhi batas keberadaan titik tetap dan sama seperti yang digunakan pada simulasi model mangsa-pemangsa dengan tingkat pemanenan dan tanpa waktu tunda. Nilai parameter yang bernilai tetap untuk setiap simulasi yaitu . Nilai parameter tingkat pemanenan konstan yang akan digunakan juga akan bernilai tetap yaitu dan . Selain parameter yang telah disebutkan, perlu dilakukan pemilihan nilai awal dan parameter waktu tunda yang ditujukkan untuk memperlihatkan perubahan kestabilan titik tetap. Pada simulasi ini akan disediakan empat kasus untuk menunjukkan keberadaan bifurkasi Hopf.

Tabel 2 Pemilihan nilai awal dan waktu tunda model

Kasus Kestabilan

Kasus pertama menggunakan nilai parameter , serta nilai awal yang telah diberikan pada Tabel 2. Titik tetap yang diperoleh pada kasus ini, yaitu . Nilai eigen yang diperoleh adalah , sehingga kestabilan titik tetap bersifat spiral stabil.

(26)

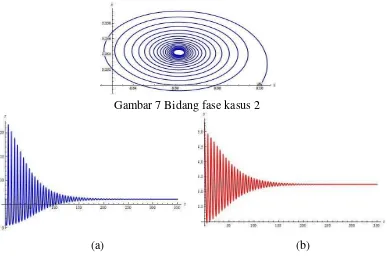
Gambar 8 Bidang solusi mangsa kasus 2 (a) dan pemangsa kasus 2 (b)

(a) (b)

Gambar 5 merupakan ilustrasi bidang fase di sekitar titik tetap yang menunjukkan kedua populasi stabil menuju titik tetap dan diperlihatkan bahwa jenis kestabilan titik tetapnya adalah spiral stabil.

Gambar 6 (a) dan 6 (b) memperlihatkan bahwa di awal waktu populasi mangsa dan pemangsa memiliki dinamika pertumbuhan yang tidak stabil. Setelah itu, populasi mangsa dan pemangsa mengalami kestabilan pada titik(56.84,6.046) dan (59.48,3.252). Hal ini menunjukkan bahwa jumlah populasi mangsa terlebih dahulu mengalami kestabilan lalu diikuti dengan kestabilan jumlah populasi pemangsa.

Kasus kedua menggunakan nilai parameter , serta nilai awal yang telah diberikan pada Tabel 2. Titik tetap yang diperoleh pada kasus ini, yaitu .

(a) (b)

Gambar 6 Bidang solusi mangsa kasus 1 (a) dan pemangsa kasus 1 (b)

(27)

Gambar 7 menunjukkan kurva bergerak secara spiral menuju titik tetap

. Kestabilan dinamika populasi mangsa pemangsa dapat

dilihat dalam bidang solusi Gambar 8 (a) dan 8 (b). Di awal pertumbuhan populasi mangsa-pemangsa terjadi ketidakstabilan jumlah, lalu semakin lama akan menuju kestabilan pada titik (371, 6.063) dan (388.9, 3.25). Hal ini menunjukkan bahwa jumlah populasi mangsa terlebih dahulu mengalami kestabilan lalu diikuti dengan kestabilan jumlah populasi pemangsa. Perbedaan bidang solusi kasus pertama dan kedua terlihat jelas pada Gambar 6 dan Gambar 8, yaitu dengan memberikan menyebabkan perubahan jenis kestabilan menjadi tidak stabil. Kestabilan dinamika populasi mangsa pemangsa dapat dilihat dalam bidang solusi gambar 10 (a) dan 10 (b). Di awal pertumbuhan populasi mangsa-pemangsa terjadi osilasi dengan simpangan yang kecil, namun semakin lama nilai simpangannya semakin besar sehingga menyebabkan kedua populasi tidak stabil.

(a)

Gambar 10 Bidang solusi mangsa kasus 3 (a) dan pemangsa kasus 3 (b) Gambar 9 Bidang fase kasus 3

(28)

Kasus keempat menggunakan nilai parameter , serta nilai awal yang telah diberikan pada Tabel 1. Titik tetap yang diperoleh pada kasus ini, yaitu penaikan nilai .

Kemunculan limit cycle pada Gambar 11 menunjukkan bahwa pada saat

terjadi bifurkasi Hopf. Gambar 11 juga menunjukkan bahwa sistem

kehilangan kestabilannya, yang berarti kedua populasi tidak menuju ataupun menjauhi titik tetap . Gambar 12 menunjukkan bahwa kedua populasi akan terus berosilasi dengan nilai simpangan yang sangat besar selama peroide waktu t. Oleh karena itu, merupakan titik kritis dari waktu tunda. Pada saat kestabilan akan selalu bersifat stabil tetapi apabila maka titik tetap akan kehilangan sifat kestabilannya dan menyebabkan munculnya

limit cycle. Pada saat tetapi kurang dari titik kritis yang kedua, kestabilan menjadi tidak stabil dan terdapat periode bifurkasi. Dengan mengikuti Teorema 3, akan didapatkan titik kritis waktu tunda sebagai berikut,

, ,

,

, .

(a) (b)

(29)

SIMPULAN

(30)

DAFTAR PUSTAKA

Edelstein-Keshet L. 1988. Mathematica Models in Biology. New York (US): Random House.

Kar TK. 2003. Selective Harvesting in a Prey-Predator Fishery with Time Delay.

Mathematical and Computer Modelling. 38:449-458.

Kuang Y. 1993. Delay Differential Equation with Application in Population Dynamics. Boston: Academic Press.

May RM. 1974. Stability and Complexity of Model Ecosystems. New Jersey (US): Princeton University Press.

Strogatz SH. 1994. Nonlinear Dynamic and Chaos with Application to Physics, Biology, Chemistry, and Engineering. New York (US): Addison-Wesley Publishing Company.

Toaha S, Hassan MA. 2008. Stability Analysis of Predator-Prey Population Model with Time Delay and Constant Rate of Harvesting. Punjab University of Mathematics. 40:37-48.

Tu PNV. 1994. Dynamical System. An Introduction with Application in Economics and Biology. Heidelberg (DE): Springer-Verlag.

Verhulst F. 1990. Nonlinear Differential Equations and Dynamical System. New York (US): Springer-Verlag.

(31)

Lampiran 1 Penentuan kondisi keberadaan titik tetap model (12)

Titik tetap persamaan (12) ditentukan dengan membuat persamaan menjadi

(32)

Lampiran 2 Penentuan kestabilan titik tetap model (12) Misalkan

Dengan melakukan pelinearan model (12) didapat matriks Jacobi seperti berikut

(33)

Lampiran 3 Kode program simulasi numerik kasus 1 model (12)

 Kode untuk mengevaluasi titik tetap pada matriks Jacobi [ ] [ ]

[ ]

 Kode untuk mendapatkan nilai eigen titik tetap

[ ]

 Kode untuk gambar bidang fase kasus 1 (Gambar 1) { [ ] }

[ ] [ ]

[ ]

 Kode untuk gambar bidang solusi kasus 1 (Gambar 2)

(34)

Lampiran 4 Kode program simulasi numerik kasus 2 model (12)  Kode untuk mencari titik tetap

[ ] [ ]

 Kode untuk matriks Jacobi

[ ] [ ]

[ ]

 Kode untuk gambar bidang fase kasus 2 (Gambar3) { [ ] }

[ ] [ ]

[ ]

 Kode untuk gambar bidang solusi kasus 2 (Gambar 4)

(35)

Lampiran 5 Linearisasi model (11)

Sistem persamaan (11) akan dilinearisasi dengan transformasi dan . Subtitusi dan ke persamaan (11)

Dengan mengabaikan perkalian antar variabel dan antar konstanta, maka didapatkan persamaan berikut:

̇

Atau ekuivalen dengan

(36)

(37)

Dengan

,

(38)

Lampiran 7 Penentuan akar persamaan karakteristik (18)

Dengan mengganti suku eksponensial menjadi trigonometri maka persamaannya menjadi

.

Persamaan tersebut akan bernilai nol jika bagian imajiner dan realnya sama dengan nol, sehingga didapatkan

Eliminasi terhadap dilakukan dengan mengkuadratkan masing-masing ruas persamaan menjadi

,

.

Kemudian kedua persamaan dijumlahkan serta dikelompokkan sesuai pangkat ,

(39)

Lampiran 8 Penentuan waktu tunda kritis (21) Dari persamaan (16) didapatkan

Subtitusi ke persamaan (16) untuk mendapatkan nilai τ Misalkan

(40)

Untuk mendapatkan nilai , maka dilakukan cara manipulasi aljabar seperti berikut

{ _}

(41)

(42)

Lampiran 10 Penjabaran fungsi sign Pada masing-masing suku akan dilakukan manipulasi aljabar agar mendapatkan bagian real saja untuk digunakan pada fungsi sign

(43)

Sehingga

{

}

Dari persamaan (17), telah diketahui bahwa

maka diperoleh { }

{

} { } .

Selanjutnya pada pecahan tersebut hanya akan dikaji pembilangnya saja karena penyebutnya dalam bentuk kuadratik berderajat genap yang akan selalu bernilai positif

(44)

Lampiran 11 Penjabaran kondisi transversalbilitas

{ }

{ ( √

}

{√ } ,

sehingga

| . Lalu

{ }

{ ( √

}

{ √ },

akibatnya

(45)

(46)

(47)

Lampiran 14 Program plot bidang solusi pemangsa kasus 1 (Gambar 6 (b))

(48)

(49)

Lampiran 16 Program plot bidang solusi mangsa kasus 2 (Gambar 8 (a))

(50)

(51)

(52)

(53)

(54)

(55)

(56)

(57)

RIWAYAT HIDUP

Penulis dilahirkan di Tangerang pada tanggal 29 Oktober 1992. Penulis merupakan anak ketiga dari tiga bersaudara pasangan Putu Seneng dan Ni Made Warsika. Penulis menyelesaikan pendidikan Sekolah Dasar di SDN Danau Batur pada tahun 2004, Sekolah Menengah Pertama di SMP Nusantara 1 Tangerang pada tahun 2007, Sekolah Menengah Atas di SMAN 5 Tangerang pada tahun 2010, dan pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB dan diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Selama perkuliahan penulis aktif di beberapa organisasi kampus maupun luar kampus, yaitu Kesatuan Mahasiswa Hindu Dharma (KMHD) IPB, Gugus Mahasiswa Matematika (Gumatika), dan Brahmacarya Bogor. Pada tahun 2010-2011, penulis aktif sebagai anggota KMHD IPB dan Brahmacarya Bogor. Pada tahun 2011-2012, penulis aktif sebagai Bendahara II KMHD IPB. Pada tahun 2012-2013, penulis aktif sebagai Bendahara Umum KMHD IPB dan Staf Divisi

Math Event Gumatika. Selain itu penulis juga aktif dalam kepanitiaan acara nasional sebagai Bendahara Umum dalam IPB Mathematics Challenge pada tahun 2013.