BIFURKASI HOPF PADA MODEL MANGSA-PEMANGSA
HOLLING-TANNER TIPE II
MUHAMMAD BUCHARI GAIB
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Bifurkasi Hopf pada Model Mangsa-Pemangsa Holling-Tanner Tipe II adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
MUHAMMAD BUCHARI GAIB. Bifurkasi Hopf pada Model Mangsa-Pemangsa Holling-Tanner Tipe II. Dibimbing oleh ALI KUSNANTO dan PAIAN SIANTURI.
Dalam karya ilmiah ini dipelajari model mangsa-pemangsa Holling-Tanner tipe II dan keberadaan dari bifurkasi Hopf. Dari model ini, diperoleh tiga titik tetap, dengan salah satu titik bersifat sadel. Dinamika populasi mangsa-pemangsa model ini dibagi menjadi empat kasus, dimana setiap kasusnya dilakukan penaikkan nilai parameter tingkat interaksi antara mangsa dan pemangsa. Pada kasus ketiga, terjadi perubahan kestabilan titik dari spiral stabil menjadi spiral tak stabil dan kemunculan limit cycle. Ini merupakan sifat bifurkasi Hopf. Selanjutnya, pada kasus keempat hampir terjadi kepunahan kedua populasi, karena tingkat interaksi kedua populasi ini semakin tinggi. Secara umum, dapat disimpulkan bahwa penaikkan nilai parameter interaksi antara mangsa dan pemangsa memengaruhi kestabilan populasi. Populasi mangsa dan pemangsa akan stabil ketika tingkat interaksi kedua populasi rendah, sedangkan tingkat interaksi yang tinggi menyebabkan kepunahan terhadap kedua populasi.
Kata kunci: bifurkasi Hopf, Holling-Tanner tipe II, limit cycle, mangsa-pemangsa.
ABSTRACT
MUHAMMAD BUCHARI GAIB. Hopf Bifurcation in Prey-Predator Model of Holling-Tanner Type II. Supervised by ALI KUSNANTO and PAIAN SIANTURI.
In this paper a mathematical prey-predator model of Holling-Tanner type II and the existence of Hopf bifurcation were studied. In this model, three fixed points are obtained, in which one of them is a saddle point. The prey-predator population dynamics was simulated based on four cases, by increasing the interaction value of prey and predator. In the third case, the stable spiral changed into an unstable spiral and also observed the presence of limit cycles. This is known as Hopf bifurcation. Furthermore, for the fourth case both populations were almost extincted due to the increase of the interaction rate. Generally, it can be concluded that increasing the value of prey and predator interaction rate would change the stability of population. The prey-predator population will be stable when the prey and predator interaction rate is low, whereas the higher interaction rate would cause the extinction of both prey and predator populations.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
BIFURKASI HOPF PADA MODEL MANGSA-PEMANGSA
HOLLING-TANNER TIPE II
MUHAMMAD BUCHARI GAIB
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul Skripsi : Bifurkasi Hopf pada Model Mangsa-Pemangsa Holling-Tanner Tipe II
Nama : Muhammad Buchari Gaib NIM : G54090055
Disetujui oleh
Drs Ali Kusnanto, MSi Dr Paian Sianturi
Pembimbing I Pembimbing II
Diketahui oleh
Dr Toni Bakhtiar, MSc Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah yang berjudul Bifurkasi Hopf pada Model Mangsa-Pemangsa Holling-Tanner Tipe II berhasil diselesaikan.
Terima kasih penulis ucapkan kepada ayah, ibu, adik, serta seluruh keluarga besar atas dukungan, motivasi, kasih sayang dan doa yang tiada henti-hentinya. Ungkapan terima kasih juga disampaikan kepada Bapak Drs Ali Kusnanto, MSi dan Bapak Dr Paian Sianturi selaku pembimbing atas arahan, bimbingan, dan motivasi dalam menyelesaikan tugas akhir ini, kepada Ibu Dr Ir Endar Hasafah Nugrahani, MS yang telah banyak memberi saran dan perbaikan, serta kepada seluruh dosen dan staf Departemen Matematika IPB atas segala ilmu yang diberikan dan bantuannya selama perkuliahan. Tak lupa juga ucapan terima kasih kepada teman-teman UKM MAX!! dan Solfegio band, serta sahabat Matematika 45, 46, 47, dan 48 yang telah banyak membantu dalam proses penyusunan tugas akhir ini.
Semoga karya ilmiah ini bermanfaat.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Tujuan 2
LANDASAN TEORI 2
PEMODELAN 4
PEMBAHASAN 5
Penentuan Titik Tetap Model 5
Analisis Kestabilan Titik Tetap Model 6
Bifurkasi Hopf 8
SIMULASI 10
Dinamika Populasi Mangsa Pemangsa Kasus 1 11
Dinamika Populasi Mangsa Pemangsa Kasus 2 11
Dinamika Populasi Mangsa Pemangsa Kasus 3 12
Dinamika Populasi Mangsa Pemangsa Kasus 4 13
SIMPULAN 14
DAFTAR PUSTAKA 15
LAMPIRAN 16
DAFTAR TABEL
1 Kondisi kestabilan titik tetap �3 8
2 Pemilihan nilai parameter model 10
DAFTAR GAMBAR
1 Hubungan antar parameter 9
2 Bidang fase kasus 1 11
3 Bidang solusi kasus 1 11
4 Bidang fase kasus 2 12
5 Bidang solusi kasus 2 12
6 Bidang fase kasus 3 13
7 Bidang solusi kasus 3 13
8 Bidang fase kasus 4 14
9 Bidang solusi kasus 4 14
DAFTAR LAMPIRAN
1 Penondimensialan Model 16
2 Penentuan titik tetap model 18
3 Penentuan nilai eigen model 21
4 Program plot bidang fase kasus 1 (gambar 2) 24
5 Program plot bidang solusi kasus 1 (gambar 3) 24
6 Program plot bidang fase kasus 2 (gambar 4) 24
7 Program plot bidang solusi kasus 2 (gambar 5) 24
8 Program plot bidang fase kasus 3 (gambar 6) 24
9 Program plot bidang solusi kasus 3 (gambar 7) 25
10Program plot bidang fase kasus 4 (gambar 8) 25
PENDAHULUAN
Latar Belakang
Makhluk hidup terdiri atas bermacam-macam spesies yang membentuk komunitas dan hidup bersama. Makhluk hidup selalu bergantung kepada makhluk hidup lain. Ada beberapa jenis hubungan yang dapat terjadi antarspesies, salah satunya adalah predasi. Predasi adalah hubungan antara mangsa (prey) dan pemangsa (predator), dimana tiap pemangsa akan bersaing dengan individu lain yang sejenis untuk memperoleh mangsanya guna mempertahankan hidup. Di dalam hubungan tersebut pemangsa juga berperan sebagai pengontrol populasi mangsa.
Pemangsa (predator) merupakan suatu organisme yang mencari, memburu, dan memakan organisme lain. Sedangkan mangsa (prey) adalah organisme yang diburu dan dimakan oleh pemangsa. Interaksi antara mangsa dan pemangsa merupakan kejadian berulang yang terjadi secara terus-menerus dan kehadiran keduanya dapat saling memengaruhi populasi satu sama lain.
Dalam memelajari interaksi antara mangsa dan pemangsa, sangat penting untuk menentukan bentuk spesifik dari respon fungsional yang menggambarkan jumlah mangsa yang dikonsumsi setiap pemangsa. Respon fungsional itu sendiri bergantung pada beberapa faktor, di antaranya jumlah dari masing-masing mangsa dan pemangsa, daya dukung lingkungan, tingkat kejenuhan pemangsa, dan tingkat persaingan antarpemangsa. Kehadiran pemangsa merupakan faktor yang secara langsung memengaruhi populasi mangsa. Andaikan setiap pemangsa hanya memiliki satu jenis mangsa, maka konsumsi yang berlebih berakibat jumlah mangsa dapat berkurang dengan cepat yang keduanya kepada kepunahan. Oleh karena itu, tingkat pertumbuhan mangsa diharapkan lebih besar daripada tingkat pertumbuhan pemangsa.
Fenomena mangsa-pemangsa menjadi salah satu fenomena alam yang patut dipelajari, bukan hanya untuk upaya pelestarian organisme tersebut tetapi juga dampak keseimbangan alam yang diakibatkan oleh populasi keduanya di masa yang datang. Alfred Lotka dan Vito Volterra dalam Gotelli (1998) mengembangkan sepasang persamaan diferensial yang menggambarkan fenomena mangsa-pemangsa untuk pertama kali yang dikenal sebagai model Lotka-Volterra. Salah satu kekurangan dari model Lotka-Volterra adalah ketergantungan pada asumsi yang tidak realistis, yaitu populasi mangsa dapat tumbuh tanpa batas saat ketidakhadiran pemangsa. Setelah itu, mulai berkembang beberapa model yang merupakan modifikasi dari model Lotka-Volterra, salah satunya adalah model Holling-Tanner yang mampu memberikan gambaran adanya kompetisi yang terjadi di antara para mangsa saat kepadatan yang tinggi. Pada saat kepadatan yang tinggi, para mangsa akan bersaing untuk mempertahankan sumber daya mereka.
2
Tujuan
Penulisan karya ilmiah ini bertujuan untuk:
1 Memelajari model mangsa-pemangsa Kuang dan Li (2007) dan menunjukkan terjadinya bifurkasi Hopf,
2 Membandingkan karakteristik kestabilan titik tetap dari model mangsa-pemangsa Holling-Tanner tipe II.
LANDASAN TEORI
Misalkan diberi sistem persamaan diferensial taklinear sebagai berikut:
= . (1)
Persamaan (1) disebut sistem dimensi satu atau sistem orde satu dengan (�)
adalah nilai real fungsi dari waktu dan ( ) adalah nilai real fungsi dari . Persamaan (1) mempunyai titik tetap = ∗ jika memenuhi ∗ = 0. Titik tetap disebut juga titik kritis atau titik kesetimbangan (Tu 1994).
Untuk suatu sistem persamaan diferensial taklinear, analisis kestabilannya dilakukan melalui pelinearan. Misalkan dilakukan pelinearan terhadap persamaan (1). Dengan menggunakan ekspansi Taylor di sekitar titik tetapnya diperoleh:
= +�( ). (2)
Persamaan (2) merupakan sistem persamaan diferensial taklinear dengan matriks Jacobi, mencari nilai eigen dari matriks yang berukuran × maka persamaan (3) dapat dituliskan kembali sebagai berikut:
− Ι = 0, (4)
3
det − Ι = − Ι = 0. (5)
Persamaan (5) disebut persamaan karakteristik dari matriks (Anton dan Rorres 2004).
Misalkan
= .
Dari persamaan (5), maka persamaan karakteristiknya menjadi
− − = 0,
Dengan demikian diperoleh nilai eigen dari matriks sebagai berikut:
1,2 =
�± �2−4Δ
2 .
Menurut Strogatz (1994), untuk menentukan kestabilan dari suatu sistem dapat dilihat dari nilai Δ . Ada 3 kasus untuk nilai Δ, yaitu:
Δ< 0.
Jika kedua nilai eigen berbeda tanda maka titik tetap bersifat sadel. Δ> 0.
�2−4Δ> 0.
Jika �> 0 dan kedua nilai eigen real bernilai positif, maka titik tetap bersifat simpul tak stabil. nilai eigen bernilai sama mama titik tetap bersifat simpul sejati.
Δ= 0.
4
Selanjutnya, Strogatz (1994) menjelaskan bahwa struktur kualitatif dari suatu sistem dinamika dapat berubah karena adanya perubahan dari parameter sistem dinamika tersebut. Hal inilah yang disebut bifurkasi. Bifurkasi adalah perubahan jumlah atau kestabilan titik tetap (titik kestabilan) dalam suatu sistem dinamik. Nilai parameter ketika terjadinya bifurkasi dinamakan titik bifurkasi. Salah satu jenis bifurkasi, yaitu bifurkasi Hopf.
Bifurkasi Hopf adalah kemunculan siklus batas (limit cycle) dari kesetimbangan dalam sistem dinamis yang dihasilkan oleh persamaan diferensial biasa, saat kesetimbangan mengalami perubahan stabilitas yang melalui sepasang nilai eigen imajiner murni. Bifurkasi dapat bersifat superkritis atau subkritis yang mengakibatkan limit cycle menjadi stabil atau tidak stabil. Limit Cycle sendiri merupakan orbit tertutup yang terisolasi. Terisolasi artinya bahwa orbit di sekelilingnya menuju atau menjauhi siklus limit.
Misalkan:
= , , ∈ � , (6)
adalah sistem persamaan diferensial mandiri orde dua yang bergantung pada parameter � . Diasumsikan bahwa matriks Jacobi = ( 0 , ) memiliki sepasang nilai eigen kompleks
1,2 = ±� , (7)
yang menjadi imajiner murni saat = 0, yaitu 0 = 0 dan 0 = 0 > 0. Kemudian, ketika melewati 0 stabilitas kesetimbangan berubah.
PEMODELAN
Dalam karya ilmiah ini dibahas model mangsa-pemangsa Holling-Tanner tipe II yang menggambarkan suatu rantai makanan antara satu spesies pemangsa dan satu spesies mangsa. Berikut ini adalah sistem persamaan modelnya:
(�) =� 1− − r : laju pertumbuhan intrinsik mangsa, K : daya dukung lingkungan,
c : koefisien interaksi antara mangsa dan pemangsa yang berpengaruh terhadap laju pertumbuhan mangsa,
f : koefisien interaksi antara mangsa dan pemangsa yang berpengaruh terhadap laju pertumbuhan pemangsa,
5 Respon fungsional pada model di atas dinyatakan dengan
� =
+ yang menggambarkan laju pemangsaan dan ketersediaan makanan (mangsa). Laju pertumbuhan intrinsik mangsa (r) dipengaruhi oleh laju pertumbuhan pemangsa y, dimana x tumbuh secara logistik. Laju pertumbuhan populasi pemangsa dipengaruhi oleh kemampuan maksimum pemangsa dalam mencari mangsa (f) dan tingkat kejenuhan pemangsaan (m) dikurangi laju kematian pemangsa (d).
Persamaan (8) dengan banyak parameter ditransformasikan ke bentuk yang lebih sederhana dengan cara penondimensialan model. Skala parameter yang digunakan, yaitu:
(Bukti persamaan (9) dapat dilihat pada Lampiran 1) dengan
=� , = , �= . (10)
Dalam persamaan (9), parameter merepresentasikan tingkat pertumbuhan mangsa, parameter merepresentasikan tingkat kematian pemangsa, dan parameter � merepresentasikan tingkat interaksi antara mangsa dan pemangsa.
6
(Bukti penentuan titik tetap model dapat dilihat pada Lampiran 2) Titik tetap �3 ∗, ∗ akan berada di kuadran pertama jika memenuhi:
∗ > 0 atau �+ − �
� > 0, (13)
∗ > 0 atau − �+ − � ( − �)
� > 0. (14)
Agar persamaan (13) dan (14) terpenuhi, maka:
> 1− � dan <�. (15)
Pada saat =�, titik tetap �3 akan menyatu dengan titik tetap �2. Pada saat
= 1−
�, titik tetap �3 akan menyatu dengan titik tetap �1.
Analisis Kestabilan Titik Tetap Model
Dengan melakukan pelinearan pada persamaan (9), diperoleh matriks Jacobi sebagai berikut: Jacobi persamaan (9) yang dievaluasi pada titik tetap tersebut. Selanjutnya, kestabilan di sekitar titik tetap diperiksa.
Titik tetap �1 0,0 disubstitusikan ke dalam persamaan matriks Jacobi persamaan (9), sehingga dihasilkan matriks Jacobi
(0,0)=
0 0 − .
Dengan menyelesaikan persamaan karakteristik � 0,0 − = 0, diperoleh nilai eigen untuk matriks 0,0 , yaitu:
7 Karena parameter diasumsikan tidak negatif, maka 1 > 0 dan 2 < 0. Karena kedua nilai eigen real berbeda tanda, maka kestabilan titik tetap �1 0,0 bersifat sadel (Strogatz 1994).
(Bukti pelinearan di titik tetap �1 dapat dilihat pada Lampiran 3) Titik tetap �2 1,0 disubstitusikan ke dalam persamaan matriks Jacobi persamaan (9), sehingga dihasilkan matriks Jacobi
(1,0) = − −
1 0 − +� .
Dengan menyelesaikan persamaan karakteristik � 1,0 − = 0, diperoleh nilai eigen untuk matriks 1,0 yaitu:
1 =− , 2 = − +�.
Karena parameter diasumsikan bernilai positif, maka 1 < 0 dan 2 bergantung pada nilai parameter dan � yang digunakan. Jika <�, maka kestabilan titik tetap �2 bersifat sadel, dan bersifat simpul stabil jika > � (Strogatz 1994).
(Bukti pelinearan di titik tetap �2 dapat dilihat pada Lampiran 3) Titik tetap �3 ∗, ∗ disubstitusikan ke dalam persamaan matriks Jacobi persamaan (9), sehingga dihasilkan matriks Jacobi
8
Berikut adalah tabel kondisi kestabilan titik tetap �3 ∗, ∗ yang diperoleh. Tabel 1 Kondisi kestabilan titik tetap �3
Diketahui bahwa nilai eigen titik tetap �3 ∗, ∗ adalah sebagai berikut: 1,2 =
1 2
1
�2 ± ,
dengan � didefinisikan pada persamaan (10).
Jika = 0 dan < 0, maka dihasilkan nilai eigen yang bernilai imajiner murni. Nilai eigen yang bernilai imajiner murni mengakibatkan kestabilan bersifat center. Ketika < 0 dan < 0, kestabilan titik tetap bersifat spiral stabil. Sedangkan ketika > 0 dan < 0, kestabilan titik tetap berubah menjadi spiral tak stabil. Dalam kasus ini, fenomena perubahan kestabilan tersebut dikenal sebagai bifurkasi Hopf.
9 Syarat perlu agar bifurkasi Hopf tercapai adalah jika:
= 0 (18)
dan
< 0 (19)
Dari persamaan (16), (18) dan (17), (19) diperoleh:
= 1− −
2 1− �
�2 , (20)
dan
4� 2 � −1 ( − �)2 < 0. (21)
Karena semua parameter pada persamaan (8) bernilai positif, maka
4� 2 > 0 dan ( − �)2 > 0. Persamaan (21) akan dipenuhi jika
�< 1. (22)
Dari persamaan (20) dan (22) diperoleh suatu parameter batas yang mengakibatkan terjadinya bifurkasi Hopf pada �3.
Misalkan parameter batas keberadaan �3pada persamaan (15) digambarkan sebagai kurva 1: � = dan 2: �=
1− , serta parameter batas terjadinya bifurkasi Hopf pada �3 pada persamaan (20) digambarkan sebagai kurva
3: = 1− −
2 1−�
�2 dan 4: �= 1. Hubungan antara parameter-parameter
yang terlibat dapat dilihat pada Gambar 1, yang menunjukkan daerah kemunculan limit cycle.
Gambar 1 Hubungan antar parameter
10 dikenal sebagai bifurkasi Hopf. Bifurkasi Hopf terjadi pada daerah yang dibatasi oleh kurva 2 dan 3. Pada saat melewati kurva 2, titik tetap �3 akan menghilang karena menyatu dengan titik tetap �1 sehingga limit cycle akan ikut menghilang.
SIMULASI
Dinamika populasi mangsa-pemangsa dapat ditunjukkan melalui kurva bidang solusi yang menggambarkan populasi mangsa dan pemangsa pada kurun waktu tertentu. Dengan ini, masing-masing variabel dan parameter membutuhkan suatu nilai awal untuk proses komputasi. Proses komputasi pada simulasi ini menggunakan software Maple 13.
Diasumsikan bahwa laju pertumbuhan intrinsik dari mangsa (r) dan kemampuan maksimum pemangsa dalam mencari mangsa (f) adalah tetap dengan daya dukung lingkungan adalah K. Saat penondimensionalan model, diketahui bahwa = � sebanding dengan tingkat pertumbuhan mangsa tanpa kehadiran pemangsa, = sebanding dengan tingkat kematian pemangsa yang secara tidak langsung menyatakan tingkat kepunahan pemangsa, dan �= sebanding dengan tingkat interaksi antara mangsa dan pemangsa.
Dalam simulasi ini, nilai-nilai parameter yang digunakan harus terlebih dahulu memenuhi parameter batas keberadaan titik tetap �3, yaitu < � yang mengartikan tingkat kematian pemangsa lebih kecil daripada tingkat interaksi antara mangsa dan pemangsa, dan > �−
� yang mengartikan laju pertumbuhan mangsa lebih besar daripada pemangsa. Parameter diasumsikan bernilai 0.4, parameter diasumsikan bernilai 0.5, dan parameter � dipilih bernilai antara 0.55 sampai dengan 0.9. Pemilihan nilai-nilai parameter ini ditujukan untuk memperihatkan perubahan struktur titik tetap dan kestabilannya sekaligus menunjukkan keberadaan bifurkasi Hopf.
Tabel 2 Pemilihan nilai parameter model
Kasus � ��
1 0.4 0.5 0.55 Simpul stabil
2 0.4 0.5 0.7 Spiral stabil
11 Dinamika Populasi Mangsa Pemangsa Kasus 1
Pada kasus ini, nilai parameter yang digunakan adalah � = 0.55, serta nilai awal 0 = 1 dan 0 = 1. Titik tetap �3 yang diperoleh pada kasus ini, yaitu
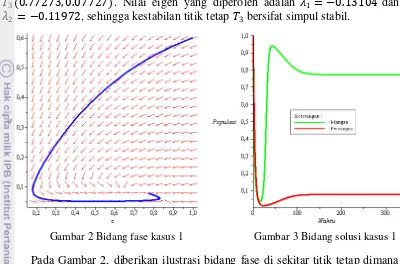
�3(0.77273, 0.07727). Nilai eigen yang diperoleh adalah 1 = −0.13104 dan 2 = −0.11972, sehingga kestabilan titik tetap �3 bersifat simpul stabil.
Gambar 2 Bidang fase kasus 1 Gambar 3 Bidang solusi kasus 1
Pada Gambar 2, diberikan ilustrasi bidang fase di sekitar titik tetap dimana kedua populasi stabil menuju titik tetap �3. Diperlihatkan bahwa jenis kestabilan titik tetapnya adalah stabil.
Gambar 3 memperlihatkan bahwa di awal waktu kedua populasi mengalami penurunan jumlah, dimana populasi pemangsa hampir mengalami kepunahan. Setelah itu, populasi mangsa mengalami pertumbuhan sehingga suplai makanan bagi pemangsa terpenuhi yang mengakibatkan populasi pemangsa ikut mengalami pertumbuhan. Saat populasi pemangsa mulai berkembang, populasi mangsa mengalami penurunan jumlah dan pada akhirnya kedua populasi tersebut stabil menuju ke suatu nilai.
Dinamika Populasi Mangsa Pemangsa Kasus 2
12
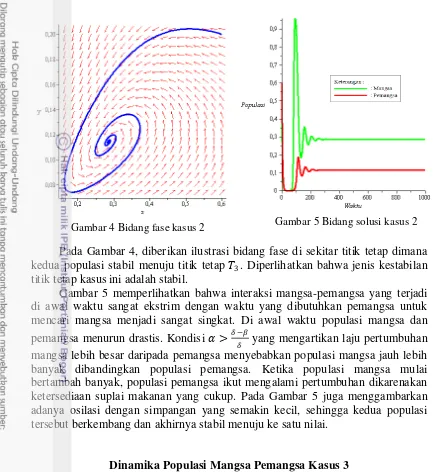
Gambar 4 Bidang fase kasus 2 Gambar 5 Bidang solusi kasus 2
Pada Gambar 4, diberikan ilustrasi bidang fase di sekitar titik tetap dimana kedua populasi stabil menuju titik tetap �3. Diperlihatkan bahwa jenis kestabilan titik tetap kasus ini adalah stabil.
Gambar 5 memperlihatkan bahwa interaksi mangsa-pemangsa yang terjadi di awal waktu sangat ekstrim dengan waktu yang dibutuhkan pemangsa untuk mencari mangsa menjadi sangat singkat. Di awal waktu populasi mangsa dan pemangsa menurun drastis. Kondisi > �−� yang mengartikan laju pertumbuhan mangsa lebih besar daripada pemangsa menyebabkan populasi mangsa jauh lebih banyak dibandingkan populasi pemangsa. Ketika populasi mangsa mulai bertambah banyak, populasi pemangsa ikut mengalami pertumbuhan dikarenakan ketersediaan suplai makanan yang cukup. Pada Gambar 5 juga menggambarkan adanya osilasi dengan simpangan yang semakin kecil, sehingga kedua populasi tersebut berkembang dan akhirnya stabil menuju ke satu nilai.
Dinamika Populasi Mangsa Pemangsa Kasus 3
13
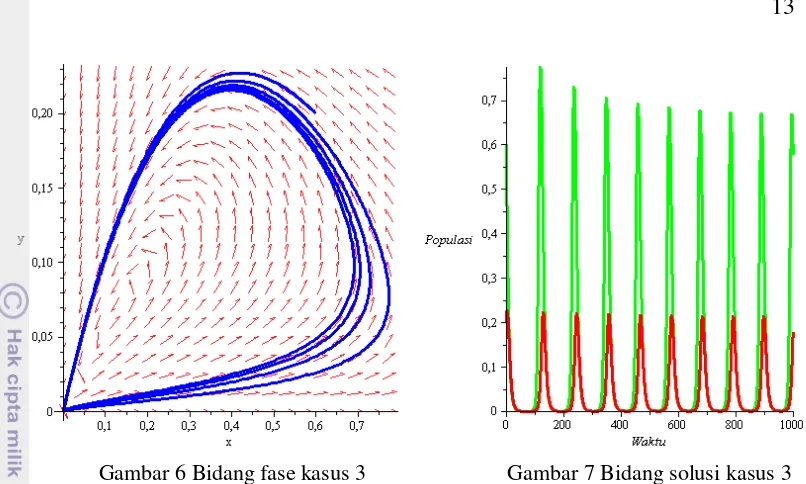
Gambar 6 Bidang fase kasus 3 Gambar 7 Bidang solusi kasus 3
Pada Gambar 6, penaikan nilai parameter � ini menyebabkan munculnya limit cycle. Fenomena keberadaan limit cycle dengan berubahnya nilai suatu parameter sistem merupakan sifat bifurkasi Hopf. Jika nilai � terus dinaikkan maka bentuk limit cycle akan semakin membesar sampai suatu kondisi yang mengakibatkan bentuk limit cycle mengecil kembali dan selanjutnya menghilang.
Sama halnya dengan Gambar 5, pada Gambar 7 ini diberikan gambaran bahwa interaksi mangsa-pemangsa yang terjadi di awal waktu sangat ekstrim dengan waktu yang dibutuhkan pemangsa untuk mencari mangsa menjadi sangat singkat. Namun pada subkasus ini osilasi yang terjadi memiliki nilai simpangan yang tetap, sehingga kedua populasi tidak stabil menuju ke suatu nilai.
Dinamika Populasi Mangsa Pemangsa Kasus 4
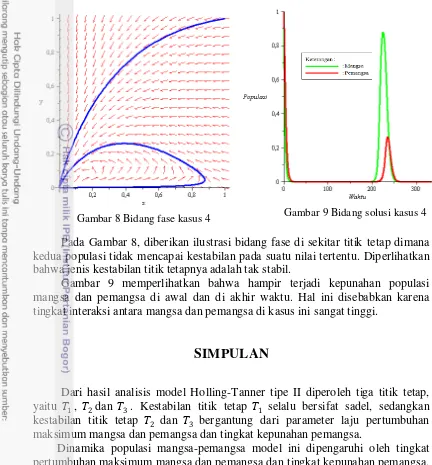
Pada kasus ini, nilai parameter yang digunakan adalah �= 0.832, serta nilai awal 0 = 1 dan 0 = 1. Titik tetap �3 yang diperoleh pada kasus ini, yaitu
14
Gambar 8 Bidang fase kasus 4 Gambar 9 Bidang solusi kasus 4
Pada Gambar 8, diberikan ilustrasi bidang fase di sekitar titik tetap dimana kedua populasi tidak mencapai kestabilan pada suatu nilai tertentu. Diperlihatkan bahwa jenis kestabilan titik tetapnya adalah tak stabil.
Gambar 9 memperlihatkan bahwa hampir terjadi kepunahan populasi mangsa dan pemangsa di awal dan di akhir waktu. Hal ini disebabkan karena tingkat interaksi antara mangsa dan pemangsa di kasus ini sangat tinggi.
SIMPULAN
Dari hasil analisis model Holling-Tanner tipe II diperoleh tiga titik tetap, yaitu �1, �2dan �3. Kestabilan titik tetap �1 selalu bersifat sadel, sedangkan kestabilan titik tetap �2 dan �3 bergantung dari parameter laju pertumbuhan maksimum mangsa dan pemangsa dan tingkat kepunahan pemangsa.
Dinamika populasi mangsa-pemangsa model ini dipengaruhi oleh tingkat pertumbuhan maksimum mangsa dan pemangsa dan tingkat kepunahan pemangsa. Dalam mengamati dinamika populasi mangsa pemangsa ini, terlebih dahulu dibagi dalam 4 kasus yang memiliki jenis kestabilan yang berbeda-beda.
Dengan memilih nilai parameter yang tepat, dapat ditunjukkan keberadaan dari bifurkasi Hopf. Pada kasus ketiga terjadi perubahan kestabilan titik tetap
15
DAFTAR PUSTAKA
Anton H, Rorres C. 2004. Aljabar Linear Elementer. Ed ke-8. Indriasari R, Harmein I, Penerjemah. Jakarta (ID): Erlangga.
Gotelli NJ. 1998. A Primer of Ecology. Ed ke-2. Sunderland (BG): Sinauer Associates Inc.
Kuang Y, Li B. 2007. Heteroclinic bifurcation in the Michaelis-Menten-type-ratio-dependent predator-prey system. Society for Industrial and Applied Mathematics. 67(5):1453-1464.doi:10.1137/060662460.
Strogatz SH. 1994. Nonlinear Dynamics and Chaos with Application to Physics, Biology, Chemistry, and Engineering. Massachusets (US): Addison-Wesley Publishing Company.
16
Dilakukan penondimensionalan untuk mendapatkan sistem persamaan dengan parameter yang lebih sederhana. Skala parameter yang digunakan, yaitu
17 Misalkan
= � , = , �=
Substitusikan , ,� ke dalam persamaan (23) dan (24). Sistem persamaan baru menjadi:
(�) = 1− − +
18
Lampiran 2 Penentuan titik tetap model
Titik tetap persamaan (9) ditentukan dengan membuat persamaan menjadi
Substitusikan persamaan (27) ke persamaan (26), sehingga diperoleh:
19
1− = 1− +
+ = 1− 1− 29
Substitusikan persamaan (29) ke persamaan (28)
=� 1− 1−
Substitusikan persamaan (30) ke persamaan (31), sehingga diperoleh:
= � �+ − �
Substitusikan = 0 ke persamaan (12), sehingga diperoleh:
20
Substitusikan = 0 ke persamaan (11), sehingga diperoleh:
lim
→0 1− − + = 0
(1− ) = 0
= 0 ∨ = 1 (33)
21 Lampiran 3 Penentuan nilai eigen model
Misalkan model 1 dituliskan sebagai berikut:
, = (�) = 1− −
+ ,
, = (�) =− + � + .
Dengan melakukan pelinearan didapat matriks Jacobi sebagai berikut:
22
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik � 1,0 − = 0, sehingga diperoleh: sadel karena kedua nilai eigen berbeda tanda (Strogatz 1994).
Pelinearan titik tetap �2 1,0
Substitusikan titik tetap 1 ke dalam matrik Jacobi model 1 (1,0) = − −
1 0 − +� .
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik � 1,0 − = 0 sehingga diperoleh:
Substitusikan titik tetap 2 ke dalam matrik Jacobi model 1
( ∗, ∗) =
24
Lampiran 4 Program plot bidang fase kasus 1 (Gambar 2)
restart : with(linalg) : with(Detools) : with(plots) :
Lampiran 5 Program plot bidang solusi kasus 1 (Gambar 3)
restart : with(linalg) : with(Detools) : with(plots) :
Lampiran 6 Program plot bidang fase kasus 2 (Gambar 4)
restart : with(linalg) : with(Detools) : with(plots) :
Lampiran 7 Program plot bidang solusi kasus 2 (Gambar 5)
restart : with(linalg) : with(Detools) : with(plots) :
Lampiran 8 Program plot bidang fase kasus 3 (Gambar 6)
25
Lampiran 9 Program plot bidang solusi kasus 3 (Gambar 7)
restart : with(linalg) : with(Detools) : with(plots) : L := [D(x)(t) = . � . 1− � − � . �
� + � , D(y)(t) =− . � +
�. � . �
� + � ]
∶= 0.4∶ ∶= 0.5∶ � ≔0.77∶
display (phaseportrait (L, [x(t), y(t)]), t = 0..1000, [[x(0) = 0.6, y(0) = 0.2]], stepsize = .1 scene = [t, x(t)], labels = [‘Waktu’, ‘Populasi’], , linecolour = [green]),
phaseportrait (L, [x(t), y(t)]), t = 0..1000, [[x(0) = 0.6, y(0) = 0.2]], style = POINT, stepsize = .1 scene = [t, y(t)], labels = [‘Waktu’, ‘Populasi’], , linecolour = [red])).
Lampiran 10 Program plot bidang fase kasus 4 (Gambar 8)
restart : with(linalg) : with(Detools) : with(plots) : L := [D(x)(t) = . � . 1− � − � . �
� + � , D(y)(t) =− . � +
�. � . �
� + � ]
∶= 0.4∶ ∶= 0.5∶ � ≔0.832 ∶
phaseportrait (L, [x(t), y(t)]), t = 0..300, [[x(0) = 1, y(0) = 1]], stepsize = .1, linecolour = [blue]).
Lampiran 11 Program plot bidang solusi kasus 4 (Gambar 9)
restart : with(linalg) : with(Detools) : with(plots) : L := [D(x)(t) = . � . 1− � − � . �
� + � , D(y)(t) =− . � +
�. � . �
� + � ]
∶= 0.4∶ ∶= 0.5∶ � ≔0.832∶
display (phaseportrait (L, [x(t), y(t)]), t = 0..325, [[x(0) = 1, y(0) = 1]], stepsize = .1 scene = [t, x(t)], labels = [‘Waktu’, ‘Populasi’], , linecolour = [green]),
26
RIWAYAT HIDUP
Penulis dilahirkan di Gorontalo pada tanggal 12 April 1991. Penulis merupakan anak pertama dari lima bersaudara pasangan Darwin Gaib dan Fatra Nurlaela Kamaru. Penulis menyelesaikan pendidikan Sekolah Dasar di SDN 61 Gorontalo pada tahun 2003, Sekolah Menengah Pertama di SMPN 1 Gorontalo pada tahun 2006, Sekolah Menengah Atas di MAN Insan Cendekia Gorontalo pada tahun 2009, dan pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB dan diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama perkuliahan, penulis menjadi asisten praktikum Sistem Dinamika Dasar tahun ajaran 2013/2014. Penulis juga aktif di beberapa organisasi kampus, yaitu Gugus Mahasiswa Matematika (GUMATIKA) dan Unit Kegiatan Mahasiswa (UKM) Music Agriculture X-pression!! (MAX!!). Pada tahun 2009-2010, aktif sebagai anggota UKM MAX!!. Pada tahun 2011, penulis aktif sebagai Staf Divisi Pengembangan Sumber Daya Manusia (PSDM) GUMATIKA dan Manajer Divisi Musik UKM MAX!!. Pada tahun 2012 penulis aktif sebagai Staf Divisi Math Event GUMATIKA dan Bendahara Umum UKM MAX!!, dan pada tahun 2013 penulis aktif sebagai Dewan Penasihat UKM MAX!!.