Masalah Optimisasi Superstruktur Sintesis Jaringan Air Dengan Ketidakpastian

MASALAH OPTIMISASI SUPERSTRUKTUR SINTESIS JARINGAN AIR DENGAN KETIDAKPASTIAN

TESIS

Oleh

M. NATSIR

107021023/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI MAGISTER MATEMATIKA

UNIVERSITAS SUMATERA UTARA MEDAN

MASALAH OPTIMISASI SUPERSTRUKTUR SINTESIS

JARINGAN AIR DENGAN KETIDAKPASTIAN

T E S I S

Diajukan Sebagai Salah Satu Syarat untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika Pada Fakultas

Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara

Oleh M. NATSIR 107021023/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI MAGISTER MATEMATIKA

UNIVERSITAS SUMATERA UTARA MEDAN

Judul : MASALAH OPTIMISASI SUPERSTRUKTUR SINTESIS JARINGAN AIR DENGAN KETIDAKPASTIAN

Nama : M. Natsir Nomor Pokok : 107021023/MT Program Studi : Matematika

Menyetujui, Komisi Pembimbing

Prof. Dr. Tulus, M.Si Prof. Dr. Opim Salim S, M.Sc

Ketua Anggota

Ketua Program Studi Dekan

Prof. Dr. Herman Mawengkang Dr. Sutarman, M.Sc

Telah diuji pada:

Tanggal: 11 Agustus 2012

PANITIA PENGUJI TESIS

Ketua : Prof. Dr. Tulus, M.Si

Anggota : 1. Prof. Dr. Opim Salim S, M.Sc 2. Dr. Saib Susilo, M.Sc

ABSTRAK

Pada tesis ini dibahas masalah optimisasi superstruktur sintesis jaringan air dengan ketidakpastian suatu sistem jaringan air terpadu dengan menggunakan proses dan operasi pengolahan air yang tergabung pada jaringan tunggal sede-mikian hingga total biaya konstruksi jaringan dan operasionalnya optimal dan meminimalkan secara global.

Disain jaringan harus layak dan optimal atas himpunan skenario yang diten-tukan dan memenuhi syarat optimal yang berbeda. Parameter operasional tidak pasti dalam sistem ini merupakan jumlah kontaminasi yang dihasilkan dalam unit proses dan penetrasi kontaminasi di dalam unit pemurnian.

Pengoptimalan superstruktur dengan menggabungkan semua alternatif de-sain yang layak untuk pengolahan air limbah atau mendaur ulang dengan model pemograman non linier integer campuran multi skenario non konvek yang meru-pakan suatu model pemograman stokastik multi stage deterministik.

Model MINLP dapat digunakan untuk menemukan desain jaringan yang op-timal dengan nomor yang berbeda dari aliran dalam jaringan pipa. Strategi yang dikemukakan dengan mengandalkan batas pada variabel yang diturunkan seba-gai persamaan umum yang diperoleh dengan pemeriksaan fisik dan menggunakan logika spesifikasi yang dibutuhkan untuk menyelesaikan model.

ABSTRACT

The problem of optimal sintesis of an integrated water system is discussed

in this tesis, where water using processes and water treatment operations are

com-bined into a single network such that the total cost of building the network and

operating it optimally is globally minimized.

The network has to be designed to be feasible and optimal over a given set of

scenarios in which different operational conditions hold. The uncertain operational

parameters in the system are the amount of contaminants generated in the process

units and the extent of removal of the contaminants inside the treatment units.

We optimize a superstructure that incorporates all feasible design

alternati-ves for waste water treatment, reuse and recycle, with a multiscenario nonconvex

mixed integer nonlinear programming model, which is a deterministic equivalent

of a multi stage stochastic programming model with recourse.

The MINLP model can be used to find optimal network designs with different

number of streams in the piping network. In this work, we propose to represent

the bounds on the variables as general equations obtained by physical inspection of

the superstructure and using logic specifications needed for solving the model.

Keyword: Global optimization, Integrated water networks, Nonconvex MINLP,

KATA PENGANTAR

Puji syukur penulis panjatkan kehadirat Allah SWT yang telah memberik-an kesempatmemberik-an dmemberik-an kekuatmemberik-an kepada penulis untuk menyelesaikmemberik-an tugas akhir yang berjudul Masalah Optimisasi Superstruktur Sintesis Jaringan Air Dengan Ketidakpastian sebagai salah satu syarat untuk memperoleh gelar Magister pa-da Program Pasca Sarjana Jurusan Matematika Fakultas Matematika pa-dan ilmu Pengetahuan Alam Universitas Sumatera Utara.

Penghargaan dan ucapan terima kasih penulis sampaikan kepada pihak-pihak yang telah membantu dan memberikan kontribusi sehingga selesainya tesis ini yaitu :

Bapak Prof.Dr.dr.Syahril Pasaribu, DTM&H, M.Sc,(CTM) Sp,A(K) selaku Rektor Universitas Sumatera Utara yang telah memberikan kesempatan kepada penulis untuk menempuh pendidikan di universitas Sumatera Utara.

Bapak Prof. Dr. Herman Mawengkang, Ketua Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah memberikan motivasi dan pengarahan sehingga selesainya tesis ini.

Bapak Prof. Dr. Tulus, MSi, sebagai Pembimbing I dan Ketua Jurusan Matematika FMIPA Universitas Sumatera Utara yang telah banyak membantu untuk keberhasilan penulis.

Bapak Prof. Dr. Opim Salim S, M.Sc, Pembimbing II yang telah membim-bing dan memberikan arahan untuk kesempurnaan tesis ini.

Bapak Dr. Sutarman, M.Sc , sebagai Penguji dan Dekan Fakultas Mate-matika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, yang telah mem-berikan kesempatan kepada penulis untuk mengikuti Program Magister Mate-matika di FMIPA Universitas Sumatera Utara.

Bapak dan Ibu Dosen Program Studi Magister Matematika FMIPA Univer-sitas Sumatera Utara yang telah memberikan materi perkuliahan dan pembekalan selama perkuliahan sehingga selesainya tesis ini.

Ibu Misiani, S.Si, staf administrasi Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang banyak membantu bidang administrasi.

Rekan-rekan Dosen Jurusan Matematika FMIPA Universitas Riau yang te-lah bahu membahu, senasib sepenaggungan dalam mengapai cita-cita untuk mening-katkan mutu dan layanan kepada mahasiswa.

Bapak Rektor Universitas Riau dan Dekan FMIPA Universitas Riau yang telah memberikan bantuan dan rekomendasi, izin belajar serta motivasi kepada penulis dalam menyelesaikan perkuliahan ini.

Isteri tercinta Nurlina, S.Pd, Ananda Mickey Elsen SE, Ferry Hendersen dan Meilly Olivia yang telah memberikan dorongan dan semangat kepada penulis dalam menyelesaikan perkuliahan ini.

Semoga Yang Maha Kuasa berkenan membalasnya dan pahala setimpal dan semoga Tesis ini dapat memberikan kontribusi optimal kepada pihak yang me-merlukannya.

FMIPA UNIVERSITAS SUMATERA UTARA Penulis

RIWAYAT HIDUP

M. Natsir dilahirkan di Bukittinggi tanggal 21 Dersember 1955, anak kedua dari empat bersaudara. Menamatkan SD tahun 1969 di SD Negeri 2 Pekanbaru, SMP Negeri 3 Pekanbaru tahun 1972 dan SMA Negeri I Pekanbaru tahun 1975.

Melanjutkan pendidikan ke Jurusan Matematika FIPIA Universitas Riau dan menyelesaikan Program Sarjana Muda [Gelar BSc] tahun 1979 serta melan-jutkan program Sarjana lengkap Jurusan Matemtika FMIPA Universitas Riau tahun 1981 dan menyelesaikannya tahun 1984.

Tahun 1981 Penulis diterima sebagai tenaga administrasi dan Mutasi men-jadi tenaga pengajar / Dosen tahun 1984 serta mendapatkan Sertifikasi sebagai Dosen Profesional mulai Januari 2011 dalam bidang Matematika.

DAFTAR ISI

Halaman

ABSTRAK . . . i

ABSTRACT . . . ii

KATA PENGANTAR . . . iii

RIWAYAT HIDUP . . . v

DAFTAR ISI . . . vi

DAFTAR TATA NAMA . . . viii

BAB 1 PENDAHULUAN . . . 1

1.1 Latar Belakang . . . 1

1.2 Perumusan Masalah . . . 4

1.3 Tujuan Penelitian . . . 4

1.4 Manfaat Hasil Penelitian . . . 4

1.5 Metodologi Penelitian . . . 5

BAB 2 SUPERSTRUKTUR UMUM DAN OPTIMISASI GLOBAL DESAIN PROSES JARINGAN AIR TERPADU . . . 7

BAB 3 PEMROGRAMAN STOKASTIK . . . 11

3.1 Pengertian Pemrograman Stokastik . . . 11

3.2 Program Stokastik Dua Tahap . . . 14

3.3 Pengertian Dasar Program Stokastik Tahap Ganda . . . 18

3.4 Ilustrasi Pemrograman Stokastik . . . 28

BAB 4 MASALAH OPTIMISASI SUPERSTRUKTUR SINTESIS JARINGAN AIR DENGAN KETIDAKPASTIAN . . . 36

4.1 Model Multiscenario MINLP . . . 38

4.1.1 Fungsi Tujuan . . . 39

4.2.1 Satuan Mixer . . . 41

4.2.2 Satuan Splitter . . . 41

4.2.3 Satuan Proses . . . 42

4.2.4 Satuan Pemurnian . . . 42

4.2.5 Pemotongan Keterikatan Batas . . . 43

4.2.6 Desain Kendala . . . 43

4.2.7 Hubungkan Batasan . . . 44

BAB 5 KESIMPULAN DAN RISET LANJUTAN . . . 45

5.1 Kesimpulan . . . 45

5.2 Riset Lanjutan . . . 45

DAFTAR TATA NAMA

• Himpunan & Indeks

i, k Indeks aliran j Kontaminasi

m Mixer

min Aliran masuk kedalam mixer m

mout Aliran keluar dari mixer m

M U Himpunan dari mixer-mixer n Skenario

N Himpunan skenario-skenario P Unit Proses

Pin Aliran masuk kedalam Unit Proses P

Pout Aliran keluar dari Unit Proses P

P U Himpunan dari Unit-unit Proses s Splitter

sin Aliran masuk kedalam splitter s

sout Aliran keluar dari splitter s

SU Himpunan dari splitter-splitter t Unit Treatment

tin Aliran masuk kedalam Unit Treatment t

tout Aliran keluar dari Unit Treatment t

T U Himpunan dari Unit Treatment

• Parameter

AR Faktor tahunan untuk investment pada unit treatment dan pipa

CF W Biaya air bersih

CiL

dalam skenario n CiU

J n Batas atas konsentrasi dari kontaminan j dalam alirani

dalam skenario n Ci

p Koefisien biaya yang terkait dengan eksistensi pipa i

FiL

n Batas bawah flow pada aliran idalam skenario n

FiU

n Batas atas flow pada aliran i dalam skenario n

FiL _{Batas bawah pada variabel disain F}i

FiU _{Batas atas pada variabel disain F}i

H Jam Operasi pabrik per annum

ICt _{Koefisien biaya investasi untuk Unit Treatment t}

IPi _{Koefisien biaya investasi untuk pipa i}

Lp_jn Proses kontaminan j dalam unit proses p pada skenario n

Lp_jw Proses kontaminan j dalam unit proses p pada kasus skenario worst OCt _{Koefisien biaya operasi untuk Unit Treatment t}

Pn Probability assigned pada occurence scenario n

Pp _{Kebutuhan air dalam unit proses p}

P Mi _{Koefisien biaya operasi pompa air melalui pipa i}

α Eksponen fungsi biaya, 0< α≤1 βr

jn 1 - (Rasio penghapusan untuk kontaminan j dalam unitr(dalam %)

dalam skenario n)/100

βr

jw 1 - (Rasio penghapusan untuk kontaminan j dalam unitr(dalam %)

dalam skenario worst w)/100

∂ Eksponen fungsi biaya, 0< ∂ ≤1 τ_inf, τ_iny Pengali Lagrange

• Variabel Kontinu

Ci

jn Konsentrasi kontaminan j dalam alirani dalam skenario n

Cin

jn Konsentrasi kontaminan j dalam aliran discharge pada lingkungan

dalam skenario n fi

fout

jn Alur kontaminan j dalam aliran keluar pada lingkungan i dalam

skenario n Fi

n Flowrate aliran i dalam skenario n

Fout

n Flowrate aliran keluar pada lingkungan dalam skenario n

Fi _{Alur dari aliran maksimum air dalam pipa i}

F Wn Pengaliran air bersih pada sistem dalam skenario n

ABSTRAK

Pada tesis ini dibahas masalah optimisasi superstruktur sintesis jaringan air dengan ketidakpastian suatu sistem jaringan air terpadu dengan menggunakan proses dan operasi pengolahan air yang tergabung pada jaringan tunggal sede-mikian hingga total biaya konstruksi jaringan dan operasionalnya optimal dan meminimalkan secara global.

Disain jaringan harus layak dan optimal atas himpunan skenario yang diten-tukan dan memenuhi syarat optimal yang berbeda. Parameter operasional tidak pasti dalam sistem ini merupakan jumlah kontaminasi yang dihasilkan dalam unit proses dan penetrasi kontaminasi di dalam unit pemurnian.

Pengoptimalan superstruktur dengan menggabungkan semua alternatif de-sain yang layak untuk pengolahan air limbah atau mendaur ulang dengan model pemograman non linier integer campuran multi skenario non konvek yang meru-pakan suatu model pemograman stokastik multi stage deterministik.

Model MINLP dapat digunakan untuk menemukan desain jaringan yang op-timal dengan nomor yang berbeda dari aliran dalam jaringan pipa. Strategi yang dikemukakan dengan mengandalkan batas pada variabel yang diturunkan seba-gai persamaan umum yang diperoleh dengan pemeriksaan fisik dan menggunakan logika spesifikasi yang dibutuhkan untuk menyelesaikan model.

ABSTRACT

The problem of optimal sintesis of an integrated water system is discussed

in this tesis, where water using processes and water treatment operations are

com-bined into a single network such that the total cost of building the network and

operating it optimally is globally minimized.

The network has to be designed to be feasible and optimal over a given set of

scenarios in which different operational conditions hold. The uncertain operational

parameters in the system are the amount of contaminants generated in the process

units and the extent of removal of the contaminants inside the treatment units.

We optimize a superstructure that incorporates all feasible design

alternati-ves for waste water treatment, reuse and recycle, with a multiscenario nonconvex

mixed integer nonlinear programming model, which is a deterministic equivalent

of a multi stage stochastic programming model with recourse.

The MINLP model can be used to find optimal network designs with different

number of streams in the piping network. In this work, we propose to represent

the bounds on the variables as general equations obtained by physical inspection of

the superstructure and using logic specifications needed for solving the model.

Keyword: Global optimization, Integrated water networks, Nonconvex MINLP,

BAB 1 PENDAHULUAN

1.1 Latar Belakang

Proses Industrialisasi mengkonsumsi sejumlah besar air yang digunakan

un-tuk operasi pembersihan, proses pemisahan, uap dan pembangkit listrik,

pendi-ngin, dan lain lain. Proses ini pada gilirannya menghasilkan sejumlah air limbah,

yang biasanya diproses di unit pengolahan sebelum dikirim ke lingkungan

pembu-angan. Kekurangan air bersih, peningkatan pembiayaan dalam proses pemurnian

air serta peraturan lingkungan yang ketat pada limbah industri, memberikan

mo-tivasi yang kuat untuk mengembangkan teknik dan pendekatan untuk mendesain

proses jaringan air yang lebih efisien.

Dua pendekatan utama untuk disain optimisasi dari sistem jaringan air

ada-lah teknologi pemurnian air dan pemrograman matematika. Sebuah kajian

komp-rehensif dari pendekatan serta metode yang sistematis dari disain diteliti oleh

El-Halwagi (1997), Mann dan Liu (1999), Bagajewicz M (2000), dan Foo (2009).

Gagasan sintesis jaringan air dianalisis oleh El-Halwagi (1997). Setelah

itu pendekatan pencapaian untuk meminimumkan penggunaan air bersih

dikem-bangkan oleh Wang dan Smith (1994a; 1994b, 1995) dan kemudian diperluas dan

diperbarui oleh sejumlah peneliti (Biegler, L. T., Grossmann, I. E. & Westerberg,

A. W. (1997), Doyle & Smith, (1997), Kuo & Smith, (1997), dan Foo, (2009)).

Superstruktur jaringan air terpadu dianalisis oleh Ahmetovic dan

dan operasi pengolahan air limbah dengan asumsi semua koneksi dianggapa layak

termasuk regenarasi air / penggunaan kembali air pada seluruh unit proses dan

unit treatment / pemurnian.

Superstruktur sintesis jaringan air dengan ketidakpastian secara umum

me-rupakan proses dari sejumlah parameter yang dapat berubah sepanjang operasi

suatu proses jaringan pada suatu data yang belum ada kepastiannya. Oleh karena

itu untuk manyatukan suatu jaringan yang beroperasi dengan ketidakpastian

ada-lah dengan mengkonstruksi suatu desain yang layak dan pengoptimalan terhadap

nilai-nilai parameter yang tidak pasti tersebut. Ada dua pendekatan utama untuk

menuju tujuan yaitu didasarkan pada fleksibilitas, dan yang lainnya didasarkan

pada pemograman stokastik dan memastikan kelayakan desain dengan

menyesu-aikan variabel kendala dalam sistem ketika parameter yang tidak pasti tersebut

berubah (Karuppiah dan Grossmann ,2008).

Kedua pendekatan dapat dianggap sebagai model untuk tujuan optimisasi

dan kelayakan secara simultan dicapai. Pada pendekatan pemrograman stokastik

dua tahap langkah pertama yang diperoleh adalah tentang biaya yang diharapkan

dan langkah kedua adalah meminimumkan biaya operasional. Beberapa metode

untuk penyelesaian pemograman stokastik telah diteliti oleh Ahmed S.,

Bersih-malani & Sahinidis, (2004), Norkin, Pflug,& Ruszczynski, (1998), Takriti, Birge &

Louveaux (1996). Suatu tinjauan ulang terbaru tentang teknik untuk optimisasi

dengan ketidakpastian dianalisis oleh Sahinidis (2004).

di-rumuskan sebagai suatu model pemograman multi skenario deterministik untuk

suatu masalah proses sintesis jika parameter yang tidak-pasti merupakan suatu

sa-tuan nilai-nilai terbatas dalam bentuk berikut:

minZd,xn =f

0

(d) +X

n

Pnfn(xn, θn)

dengan kendala

hn(d, xn, θn) = 0

gn(d, xn, θn) ≤ 0

∀n∈N, d∈D, xn∈X, θn ∈θ

dimana

• d berkoresponden dengan variabel disain stage pertama,

• xn adalah vektor dari variabel state pada stage kedua dalam skenario n,

• θn merupakan vektor parameter tidak pasti di dalam skenario,

• pn adalah peluang operasional kejadian skenario n.

Beberapa variabel state merupakan variabel kendali, yang dapat

meng-operasikan jaringan yang beroperasi secara optimisasi ketika parameter yang tidak

pasti berubah. Variabel disain d harus dipilih pada langkah yang pertama dan

tidak bisa diubah pada langkah yang kedua ketika jaringan dioperasikan.

Ba-nyaknya skenario di dalam model diberi oleh |N|. Batasan Persamaan hn secara

normal berkaitan dengan keseimbangan energi dan massa pada setiap skenario.

Ketidaksamaan gn yang diperoleh berkaitan dengan spesifikasi disain dan

P

nPnfn(xn, θn) merupakan ekspektasi total biaya operasi dari sistem untuk

se-mua skenario yang sangat tergantung kepada pemilihan variabel disain stage

per-tama.

1.2 Perumusan Masalah

Model yang telah dikembangkan pada riset terdahulu oleh para peneliti

de-ngan adanya kondisi ketidakpastian hanya mencakup tentang kelayakan desain

jaringan sintesis, Perumusan masalah dalam penelitian ini adalah

mengembangk-an model tidak hmengembangk-anya terhadap desain jaringmengembangk-an tetapi juga mencakup parameter

tidak pasti dalam sistem yang dapat berubah selama operasi proses sintesis.

1.3 Tujuan Penelitian

Tujuan penelitian ini membahas model masalah optimisasi superstruktur

sintesis jaringan air dengan ketidakpastian yang mencakup Model Multiscenario

MINLP untuk fungsi tujuan dan Model MINLP untuk unit mixer, unit splitter

,unit proses dan unit treatment yang memformulasikan keseimbangan material

ke-seluruhan / aliran dan keseimbangan kontaminan yang beroperasi dengan kondisi

operasional tidak pasti.

1.4 Manfaat Hasil Penelitian

Manfaat yang diperoleh dari hasil penelitian ini diharapkan dapat

membe-rikan kontribusi dan manfaat optrimal bagi pihak yang membutuhkannya,

keti-dakpastian dan meminimumkan biaya pada masalah optimisasi global terutama

pada disain dengan ketidakpastian pada superstruktur dari jaringan air terpadu

dengan optimisasi superstruktur sebagai formulasi masalah pemograman nonlinier

integer campuran.

1.5 Metodologi Penelitian

Penelitian ini bersifat studi kepustakaan, mengkaji dan mendalami dari dua

sumber utama yaitu melalui artikel Global optimization of multi skenario mixed

integer nonlinear programming models arising in the synthesis of integrated

wa-ter networks under uncertainty. Compuwa-ters & Chemical Engineering, 32(1-2),

145-160 (Karuppiah dan Grossmann, 2008) dan melalui artikel General

Supers-tructure and Global Optiimization for the Design of Integrated Process Water

Networks , Computers & Chemical Engineering, 14(12) 126-140. (E.Ahmetovic

and Grossmann, 2006), dan juga dengan menelusuri dan menganalisis

bebera-pa buku teks dan journal terkait dengan model pemograman stokastik nonliner

integer campuran dalam menyelesaikan masalah optimisasi suatu superstruktur

sintesis jaringan air dengan ketidakpastian dan melakukan kajian terhadap materi

utama dan pendukung tesis ini dengan pendekatan :

• Telaah riset terdahulu tentang beberapa kajian yang telah dihasilkan dan

dirumuskan oleh para peneliti.

• Formulasikan model pemograman stokastik, pemograman stokastik dua

pemograman stokastik dan rumuskan beberapa definisi dan teorema

terka-it.

• Analisis kajian tentang model Multiscenario MILP untuk Fungsi Tujuan

serta model MINLP untuk Satuan Mixer, Satuan Splitter, Satuan proses,

Satuan Pemurnian / Treatment, Pemotongan Keterikatan Batas, Desain

BAB 2

SUPERSTRUKTUR UMUM DAN OPTIMISASI GLOBAL DESAIN PROSES JARINGAN AIR TERPADU

Pendekatan pemrograman matematika yang didasarkan pada optimisasi

su-perstruktur dari jaringan air diberikan oleh Takama, Kuriyama, Shiroko & Umeda

(1980) dan merupakan sebagai sistem yang terdiri dari air dan air limbah dengan

menggunakan unit treatment/pemurnian. Selain itu superstruktur yang

diha-silkan dari semua kemungkinan serta penggunaan kembali/regenerasi air de-ngan

merumuskan masalah alokasi air yang optimal dalam bidang industri sebagai

ma-salah pemrograman nonlinier. Solusi dari formulasi pemrograman matematika

untuk masalah ini telah diteliti oleh Bagajewicz (2000).

Dalam banyak penelitian, total jaringan air didekomposisi menjadi dua

ba-gian (jaringan dengan menggunakan air dan air limbah pada jaringan operasi

pemurnian) yang diselesaikan secara terpisah. Kuo dan Smith (1997) menyajikan

perluasan metodologi untuk disain sistem terdistribusi pengolahan limbah cair

yang sebelumnya diberikan oleh Wang dan Smith (1994b).

Mereka mempresentasikan suatu peningkatan metode untuk

memformulasi-kan laju aliran dalam proses treatment/pemurnian air dan distribusi beban antara

beberapa proses pengolahan. Selain itu, Galan dan Grossmann (1998) membahas

disain yang optimal dari jaringan air limbah terdistribusi dengan

mempertim-bangkan beberapa kontaminan. Mereka meneliti sebuah prosedur pencarian

heu-ristik yang didasarkan pada penyelesaian terurut model relaksi linier dan mo-del

pendekatan penyelesaian optimisasi global. Selain itu, model ini telah diperluas

untuk memilih teknologi treatment/pemurnian yang berbeda untuk mena-ngani

modul pemisahan membran. Savelski dan Bagajewicz (2003) mengembangkan

kondisi optimisasi yang diperlukan (konsentrasi outlet maksimum dari air-dengan

menggunakan unit dan monotonicy konsentrasi) untuk sistem jaringan air tunggal

dan ganda pada suatu lokasi industri. Mereka menggunakan kondisi ini untuk

me-reduksi bentuk nonlinier dalam model jaringan air yang timbul dalam persamaan

keseimbangan massa dalam bentuk bilinear (konsentrasi kali laju aliran) dengan

menunjukkan bahwa model nonlinier jaringan air untuk komponen tunggal dapat

dilinierisasi.

Quesada dan Grossmann (1995) meneliti suatu prosedur untuk optimisasi

global jaringan proses bilinear dengan aliran multi komponen. Prosedur tersebut

didasarkan pada teknik reformulasi-linearisasi yang diterapkan ke model nonlinier

untuk mendapatkan formulasi pemrograman linier relaksi pada optimisasi global.

Castro, Teles dan Novais (2009) meneliti penyelesaian strategi dua tahap untuk

disain yang optimal dari jaringan air limbah yang didistribusikan dengan beberapa

kontaminan. Pada tahap pertama, metode dekomposisi yang digunakan untuk

menggantikan program nonlinier dengan penurunan program linier untuk setiap

unit pengolahan. Pada tahap kedua, jaringan yang dihasilkan digunakan sebagai

titik awal untuk solusi dari model nonlinier dengan penyelesaian optimal lokal.

Masalah mengkonstruksi total jaringan air telah dibahas oleh Doyle dan

Smith (1997) dengan meneliti suatu metode yang didasarkan pada

Untuk mengatasi kesulitan yang berhubungan dengan model optimasi

nonlini-er, mereka menggunakan model linier untuk memberikan inisialisasi untuk model

nonlinier. Alva-Argez, Kokossis dan Smith (1998) meneliti metodologi terpadu

untuk disain sistem air industri. Strategi dekomposisi mereka didasarkan pada

prosedur rekursif dimana Masalah Integer Campuran Nonlinier (MINLP)

diper-luas menjadi Mixed Integer Linear Programming (MILPs). Huang, Chang, Ling,

dan Chang (1999) meneliti sebuah model matematika untuk memastikan

penggu-naan air yang optimal. Mereka mempresentasikan modifikasi dari superstruktur

yang diteliti oleh Takama, Kuriyama, Shiroko, dan Umeda (1980) dalam

persa-maan model disain semua fasilitas pengolahan air limbah dan semua unit yang

memanfaatkan proses atau utilitas air sehingga diperoleh perbaikan dari disain

pa-da skala besar. Feng pa-dan Seider (2001) meneliti suatu struktur jaringan dengan

sumber air internal yang digunakan yaitu menyederhanakan struktur jaringan

perpipaan serta operasi dan kontrol pada industri besar yang melibatkan proses

penggunaan air. Gunaratnam, Alva-Argaez, Kokossis, Kim, dan Smith (2005)

mempresentasikan disain otomatis sistem distribusi air optimal untuk memenuhi

tuntutan proses dan treatment yang optimal dari aliran limbah cair secara

bersa-maan. Mereka menggunakan pendekatan optimasi dua-tahap untuk memecahkan

model MINLP dengan penggunaan MILP dalam tahap pertama untuk

mengini-sialisasi masalah dan pada tahap kedua dengan menggunakan MINLP. Selain itu,

kompleksitas jaringan dikendalikan dengan memastikan flowrates yang dapat

di-tolerir dalam batas minimum dalam jaringan. Metodologi tersebut menghasilkan

Karuppiah dan Grossmann (2006) membahas masalah sintesis yang

optimi-sasi dari sistem air terpadu yang terdiri dari air yang menggunakan proses dan

operasi pengolahan air. Li dan Chang (2007) mengembangkan suatu strategi

ini-sialisasi efisien untuk memecahkan model NLP dan MINLP untuk jaringan air

dengan beberapa kontaminan. Dalam model MINLP mereka merumuskan

ham-batan struktural untuk memanipulasi kompleksitas structural yang menghasilkan

suatu penyelesaian optimal dengan strategi inisialisasi yang setidaknya sama

ba-iknya dengan hasil yang telah diteliti sebelumnya dengan perhitungan waktu lebih

sedikit untuk mencapai konvergensi. Pada tahun yang sama, Alva-Argaez,

Kokos-sis, dan Smith (2007) meneliti pendekatan sistematis untuk mena-ngani kembali

air di kilang minyak.

Karuppiah dan Grossmann (2008) menyajikan formulasi untuk

mengopti-malkan jaringan air terpadu operasi di bawah kondisi tidak pasti dari beban

kontaminan dalam unit proses dan kepindahan kontaminan dari unit treatment.

Mereka merumuskan multi-skenario nonconvex Model MINLP untuk

mengopti-misasikan sebuah operasi global jaringan air terpadu dengan ketidakpastian.

Se-lanjutnya, mereka meneliti suatu algoritma yang menggabungkan konsep relaksasi

Lagrangian dan relaksasi non konvek untuk menghasilkan batas-batas kuat untuk

optimisasi global.

Sebagian besar analisis didasarkan pada linierisasi model nonlinier, atau

menggunakan model linier untuk memberikan inisialisasi untuk model nonlinier,

BAB 3

PEMROGRAMAN STOKASTIK

3.1 Pengertian Pemrograman Stokastik

Persoalan keputusan dapat dimodelkan dengan menggunakan program

ma-tematik, tujuannya adalah untuk pastikan nilai maksimum atau minimum.

Ke-putusan yang dihasilkan bergantung kepada kendala yang dibatasi oleh sumber

dana, persyaratan minimum dan lain-lain. Keputusan dinyatakan oleh variabel

berupa bilangan cacah atau nonnegatif. Sebagai contoh dari persoalan data

ter-masuk biaya perunit, rata-rata produksi, penjualan atau kapasitas.

Andaikan keputusan dinyatakan dengan variabel (x1, x2, . . . , xn). Sebagai

contoh xi menyatakan produksi ke-i dari n produk. Bentuk umum program

ma-tematikanya adalah :

minZ =f(x)

kendala fi(x)≥bi, i= 1,2, . . . , n (3.1.1)

x≥0, x∈X

dimana X adalah himpunan bilangan real non negatif.

Program stokastik adalah sebuah nama yang menyatakan program

mate-matika yang dapat berupa linear, cacah, cacah campuran, non linear dengan

me-nampilkan elemen stokastik pada data. Sehingga program stokastik dapat dinyata

bahwa :

a. Pada program matematika deterministik, data adalah bilangan-bilangan

b. Pada program stokastik, data merupakan bilangan tidak pasti yang disajikan

sebagai distribusi peluang.

Program stokastik adalah merupakan program matematika, dimana

bebe-rapa data yang termuat pada tujuan atau kendala mengandung ketidakpastian,

ketidakpastian biasanya dicirikan oleh distribusi peluang pada parameter.

Walau-pun ketidakpastian didefinisikan dengan tepat, tetapi pada prakteknya diberikan

beberapa skenario yang spesifik dan distribusi peluang gabungan yang cepat.

Ada dua model dalam permasalahan program stokastik, yaitu :

1. Recourse Models (Model Rekursif)

2. Probabilistically Constrained Models (Model Kendala Berpeluang)

Dalam persoalan program stokastik adalah membuat sebuah keputusan sekarang

dan meminimumkan biaya rata-rata harapan sebagai konsekuensi dari keputusan,

paradigma ini dikenal sebagai modelrecourse. Andaikanxadalah vektor

keputus-an ykeputus-ang diambil, dkeputus-any(w) adalah sebuah vektor keputusan yang menyatakan aksi

terbaru atau konsekuensi dari x. Himpunan berbeda yang berisi y akan dipilih

dari tiap-tiap hasil yang mungkin dari w. Formulasi dua tahapnya adalah

minh1(x) +E[h2 y(w), w

]

kendala

f1(x, y(w)) ≤ 0, ∀w∈W

M M (3.1.2)

fk(x, y(w)) ≤ 0, ∀w∈W

x∈X, y(w)∈Y

dimana himpunan kendalaf1, f2, . . . , fk, menggambarkan hubungan antara

kepu-tusan tahap pertama x dan keputusan tahap kedua y(w). Dicatat bahwa

diper-syaratkan tiap-tiap kendala dipenuhi dengan peluang 1, atau untuk setiapw∈W

yang mungkin. Fungsih2 merupakan penyelesaian yang sering muncul dari

perso-alan matematika. Tidak dibutuhkan untuk membuat korelasi yang berubah-ubah

(recourse) untuk keputusan tahap pertama, perlu untuk dibuat korelasi yang

ter-baik.

Untuk persoalan tahap ganda, pengaruh keputusan sekarang akan ditunggu

untuk beberapa ketidakpastian yang diselesaikan kembali (direalisasikan),

sehing-ga pembuatan keputusan yang lain didasarkan pada apa yang terjadi. Tujuannya

adalah untuk meminimumkan biaya yang diharapkan dari semua keputusan yang

diambil.

Pada beberapa kasus, dapat digunakan suatu model yang lebih tepat

un-tuk mencoba pastikan sebuah keputusan, yang mana keputusan tersebut dijamin

oleh himpunan kendala yang akan dipenuhi oleh sebuah peluang tertentu.

yang dirumuskan sebagai berikut :

minZ =f(x)

kendala P[g1(x)≤0, . . . , gm(x)≤0]≥α

h1(x)≤0 (3.1.3)

h2(x)≤0

x∈X

3.2 Program Stokastik Dua Tahap

Banyak persoalan perencanaan dan manajemen yang mengandung resiko

dan ketidakpastian dibahas dan diselesaikan dengan program stokastik dua

ta-hap. Persoalan stokastik dengan kompensasi dari divergensi pada sistem dengan

kendala mempunyai aplikasi yang lebih banyak dari pada model program yang

lain. Penyelesaian persoalan program stokastik dua tahap berisi vektor acak dan

vektor deterministik. Pada tahap pertama, penyelesaian persoalan rencana awal

deterministik akan dibuat. Pembentukan rencana awal deterministik

dilakuk-an sebelum kondisi acak dari persoaldilakuk-an ditentukdilakuk-an. Sebuah vektor acak pada

penyelesaian persoalan yang sesuai digunakan untuk merencanakan kompensasi

divergensi, spesifikasi parameter dari persoalan akan muncul pada tahap kedua.

Tujuan dari manager pada persoalan di atas adalah meminimum nilai rata-rata

biaya, yang mana tidak hanya termasuk pengeluaran pada tahap perencanaan

pendahuluan tetapi juga pada tahap kedua yang diperlukan untuk

mengkompen-sasi pada divergensi di dalam sistem kendala persoalan. Jika persoalan program

ren-cana awal deterministik akan menjamin keberadaan (eksistensi) vektor acak di

dalam kompensasi untuk sistem yang divergen.

Andaikan terdapat persoalan berikut :

min(C, X) (3.2.1)

A0_{X =B}0 _(3.2.2)

AX =B (3.2.3)

X ≥0 (3.2.4)

dimana

C = {cj}, j = 1,2, . . . , m

B = {bi}, i= 1,2, . . . , m

B0 =

b0_k , k = 1,2, . . . , m

A0 = a0_kj

, k= 1,2, . . . , m; j = 1,2, . . . , n

A = kaijk, i= 1,2, . . . , m; j = 1,2, . . . , n

Andaikan elemen dari matriksA=A(ω), vektorB =B(ω) danC =C(ω) bernilai

acak. Maka untuk proses penyelesaian dari persoalan (3.2.1 - 3.2.4) akan dibagi

menjadi dua tahapan, sebelum pengamatan dari parameter acak pada kondisi

dari tahap pertama dipilih rencana non-negatif deterministik X0 _{yang memenuhi}

kondisi (3.2.2) pada tahap kedua ditentukan spesifikasi ω0

dari setiap kejadian

acak yang bersamaan (sesuai) dengan nilai A(ω0

) dan B(ω0

). Hitung divergensi

B(ω0_{)− A(ω}0_)X0 _{yang muncul pada kondisi (3.2.3) setelah realisasi ω}0 _{∈ Ω.}

berikut

pensasi yang berisi elemen acak. Sehingga diasumsikan bahwa realisasi acak ω

yang diamati pada tahap kedua tidak bergantung pada pemilihan rencana

pen-dahuluan X0_.

Perhatikan persoalan program matematika berikut :

Tentukan vektor X berdimensi n dan vektor Y(ω) berdimensi n1, ω ∈ Ω. Yang

menghasilkan

H adalah vektor penalty yang bergantung pada nilai kompoinen dari vektorY(ω)

yang mana merupakan kompensasi divergensi. E adalah notasi ekspekstasi

mate-matika setelah ditentukan rencana awalX0_{, dipilih komponen vektorY(ω) dengan}

cara menjamin penalty minimum untuk kompensasi divergensi pada kondisi dari

persoalan. Dengan kata lain, setelah ditentukan vektor X0_{, perlu menyelesaikan}

Persoalan (3.2.10) akan menpunyai banyak rencana, vektorY(ω) tidak dapat

ditentukan pada tiap ω ∈Ω yang menjamin penemuan kondisi (3.2.8). Persoalan

(3.2.6-3.2.9) dikenal sebagai persoalan program stokastik dua tahap dan persoalan

(3.2.10) adalah persoalan tahap kedua.

Model dan pendekatan dari penyelesaian persoalan program stokastik dua

tahap dapat digunakan untuk perspektif perencanaan dan operasional

manaje-men, karena selalu terdapat keacakan yang mempengaruhi yang sudah

direnca-nakan pada sistem manajemen (pelaksanaan). Model dua tahap juga kurang

sensentif terhadap perubahan pada parameter dari kondisi persoalan, yang

me-nyebabkan lebih stabil. Akibatnya vektor dapat diterima untuk rencana tahap

pertama yang diperlukan untuk setiap ω ∈Ω, terdapat vektor Y ≥0 sedemikian

hingga

D(ω)Y(ω) =B(ω)−A(ω)X (3.2.11)

Andaikan kendala tambahan yang disebutkan secara implisit pada (3.2.11)

muncul pada tahap kedua dari persoalan yang dihasilkan; dan andaikan kondisi

yang ditentukan pada vektor non-negatif X dari persamaan (3.2.7) sudah

diten-tukan.

Andaikan himpunanK1 ={X :A0 =B0, X ≥0}didefinisikan oleh kendala

yang sudah ditentukan tetapi K2 = {X : ∀ω ∈ Ω,∃Y ≥ 0, A(ω)X = B(ω)−

D(ω)Y(ω)} didefinisikan oleh kendala yang dihasilkan. Maka himpunan K =

K1 ∩K2 adalah himpunan vektor X yang layak memenuhi persoalan

A0_X

= B, X ≥ 0 dan sampai itu, persoalan tahap kedua (3.2.3) akan memiliki

banyak rencana.

Untuk perhitungan lanjutan diperlukan hasil berikut :

Teorema 3.2.1 HimpunanK dengan vektor X pada persoalan program stokastik dua tahap adalah konveks.

Bukti : K = K1∩K2 tetapi K1 = {X : A0 = B0, X ≥ 0} adalah konveks.

Definisikan untukω ∈Ω yang ditentukan pada himpunanK2ω ={X|∃Y(ω)≥0}

sedemikian hingga A(ω)X = B(ω)−D(ω)Y(ω) adalah konveks. Hal ini

menya-takan bahwa K2 =∩ω∈ΩK2ω dan K =K1∩K2 adalah himpunan konveks sebagi

pertolongan himpunan konveks.

3.3 Pengertian Dasar Program Stokastik Tahap Ganda

Persoalan program stokastik dinamik digeneralisasi oleh kasus dua tahap.

Banyak persoalan praktis yang berupa perencanaan, perancangan dan manajemen

tidak dapat digambarkan dengan bantuan model statis. Untuk model bertujuan,

metode program stokastik tahap ganda seringkali digunakan. Model program

stokastik tahap ganda dan metode untuk realisasi secukupnya bergantung pada

informasi mengenai nilai parameter di dalam kondisi persoalan, dimana memiliki

waktu untuk membuat keputusan selanjutnya. Persoalan dinamik dari tiap-tiap

tahap berurutan disyaratkan untuk melengkapi kompensasi divergensi yang

dikon-disikan oleh kondisi realisasi persoalan dan oleh pembuatan keputusan tercepat

tahap peluang yang memenuhi kendala tidak melebih nilai tertentu yang

diberik-an sebelumnya atas ekspektasi matematika pada fungsi dari divergensi di dalam

kondisi yang dibatasi oleh bilangan yang diberikan atau nilai dari fungsi pada

parameter acak yang direalisasikan pada tahap sebelumnya.

Persoalan dinamik akan memiliki salah satu bentuk yaitu : tidak dapat

di-kondisikan, kondisi probabilistik atau kendala statistik. Untuk persoalan dinamik

dengan kendala tidak dapat dikondisikan, karakteristik keputusan adalah

membu-at pada basis informasi mengenai distribusi yang dikombinasikan oleh parameter

acak dari kondisi pada semua tahapan. Pada persoalan dinamik dengan kondisi

dua kasus kendala dapat dibedakan menjadi : (a) momen pembuatan keputusan

hanya realisasi dari parameter acak pada tahap sebelumnya yang diperkirakan

diketahui dan (b) momen pembuatan keputusan melengkapi informasi yang

ter-sedia mengenai realisasi parameter acak yang dinyatakan dengan tahapan, tetapi

nilai dari parameter acak pada tahapan berurutan tidak diketahui.

Penyelesaian optimisasi untuk persoalan program stokastik dinamik dapat

diperoleh dengan strategi murni atau campuran. Pada komponen kasus akhir dari

penyelesaian atau karakteristik statistik dari distribusi yang memberikan

penye-lesaian akan bergantung pada nilai parameter acak di dalam kondisi persoalan,

yang direalisasikan oleh momen pembuatan keputusan.

Untuk perhitungan selanjutnya dalam analisis persoalan program stokastik

tahap ganda, didefinisikan konsep yang diberikan berikut ini. Andaikan terdapat

ωi, dimana Ω0 berisi satu elemen ω0. Andaikan Ωk adalah descartian product

Ωi, i = 1,2, . . . , k; ωk = (ω1, . . . , ωk), Ωn = Ω dan andaikan pada Ω diberikan

ukuran probabilistikpyang didefinisikan dengan cara : jikaA⊂Ωk_makapk_{(A) =}

p(A×Ωk+1

×. . .×Ωn_{). Diperkenalkan ruang probabilistik (Ω,Σ, P) dengan} P

berkaitan dengan σ-algebra, definisikan Pk sebagai kondisi ukuran probabilistik

pada Ωk

Pk A|ωk−

1

∈B

= Pk(A×B) Pk(Ωk×B)

untuk sembarang A⊂Ωk, B ⊂Ωk−1.

Xk_{dinyatakan sebagaidescartian productX}

i, i= 1,2, . . . , k; Xk= (x1, . . . , xk)

∈ Xk_{, X}n _{≡ X dimana X}

0,X1, . . . ,Xn adalah barisan himpunan dari struktur

sembarangXk _∈Xk_{, k}

= 0,1, . . . , ndan himpunan X termasuk satu titik X0.

Andaikan mk diberikan sebagai fungsi vektor pada ϕk(ωk,Xk) berdimensi

untuk setiap ωk _{∈ Ω}k_{, X}k _{∈ X}k_{, k = 1, . . . , n dan juga untuk setiap ω ∈ Ω}

pada himpunan X fungsi ϕ0(ωn,Xn). Masukkan himpunan acak G0_k = G0_k(ωk)

danbk(ωk−1)mkfungsi vektorBkdinyatakan sebagai ruang Banach yang termasuk

pada fungsi vektor berdimensibk(ωk−1)Pk_i=1mi. Akhirnya,Eωk U(ω

k₎ ωk−1

me-nyatakan kondisi ekspektasi matematika U(ωk_{) dibawah perkiraan realisasi ω}k−1

yang diketahui.

Andaikan dibahas model berbeda pada persoalan program stokastik tahap

Andaikan terdapat persoalan program stokastik tahap ganda :

Eϕ0 = ω

n_{, X}n_{)→inf, (3.3.1)}

Eϕk = ω

k_{, X}k_)≥b

k (3.3.2)

Xk _∈G

k, k= 1,2, . . . , n (3.3.3)

Untuk memformulasi persoalan secara lengkap, diperlukan titik luar apakah

ken-dala yang tidak dapat dikondisikan atau kondisional, apakah penyelesaian

perso-alan ditentukan dengan strategi murni atau strategi campuran, dan di dalam kelas

fungsi yang terukur atau distribusi yang akan mendapatkan penyelesaian.

Per-soalan praktisnya akan bergantung pada makna isi, penyelesaian pada tiap-tiap

tahap dapat dihitung sebagai vektor deterministik atau sebagai rule-function

pa-da penyelesaian pa-dari realisasi pa-dan parameter acak yang diobservasi pa-dari kondisi,

atau sebagai distribusi pastikan distribusi kontinu Xk dengan perkiraan

infor-masi yang diperlukan mengenai nilai yang direalisasikan data initial acak yang

diperoleh model konkrit untuk persoalan dan struktur informasinya ditentukan

oleh keputusan selanjutnya. Di dalam syarat-syarat yang diajukan oleh Ermolyev

(1970), hasil-hasil persoalan stokastik tahap ganda dari rangkaian tipe

Pengamatan - Keputusan - Pengamatan - . . .- Keputusan

Keputusan - Pengamatan - Keputusan - . . .- Keputusan

dikondi-sikan adalah

Pemilihan beberapa kelas yang paling menarik untuk aplikasi dari sejumlah

struktur informasi yang merupakan persyaratan persoalan program tahap ganda

dengan kendala kondisional. Model kongkrit dari (3.3.1)-(3.3.3) pada kasus

perso-alan dengan kendala kondisional, diselesaikan dengan strategi campuran adalah:

R

Penyelesaian persoalan akan menjadi himpunan fungsi distribusi FXk

|ωk.

Biasa-nya untuk mengatakan persoalan diselesaikan dengan distribusi yang ditentukan

kemudian jika FXk

|ωk didefinisikan setelah realisasi dan pengamatan parameter

acak ωk_{, distribusi yang ditentukan kemudian bergantung pada X}k−1 _{dan ω}k_.

Dikatakan bahwa persoalan yang diselesaikan dengan distribusi yang ditentukan

sebelumnya, jika FXk

|ωk didefinisikan setelah realisasi dan pengamatan ωk−1

te-tapi sebelum pengamatan ωk_{, distribusi yang ditentukan sebelumnya bergantung}

pada Xk−1 _{dan ω}k−1_.

strategi murni, model konkrit (3.3.1)-(3.3.3) akan menjadi :

Fungsi Xk dari parameter acak yang direalisasikan dan diamati pada kondisi dari

persoalan merupakan penyelesaian. Persoalan diselesaikan dengan aturan yang

ditentukan kemudian jika keputusan dibuat setelah realisasi dan pengamatanωk_;

aturan-aturan yang ditentukan kemudian untuk penyelesaian sedemikian

hing-ga Xk _{= X}k_(ωk_{). Dikatakan bahwa persoalan diselesaikan dengan aturan yang}

ditentukan sebelumnya jika keputusan dibuat setelah realisasi dan pengamatan

ωk−1_{, tetapi sebelum pengamatan ω}k_{. Pada kasus aturan sebelumnya :}

Xk _=Xk_(ωk−1₎

Biasanya, persoalan (3.3.7) - (3.3.9) atau (3.3.10) - (3.3.12) dikenal

seba-gai persoalan stokastik tahap ganda dengan rigid model, jika kondisi (3.3.8) atau

(3.3.11) tidak dihadirkan, keputusan tiap-tiap tahap dibuat setelah observasi

kon-disi dan keputusan pada tahap sebelumnya.

Relasi tertentu yang dimiliki antara determinasi domain untuk persoalan

dengan kendala yang tidak dapat dikondisikan dan kendala yang dapat

dikondi-sikan. Pernyataan berikut akan menggeneralisasi hasil yang diperoleh, yang telah

dikerjakan oleh Eismer (1971) untuk persoalan stokastik tahap ganda parsial

AndaikanU adalah himpunan penyelesaian yang layak untuk persoalan

sto-kastik tahap ganda dengan kendala yang tidak dapat dikondisikan

U ={Xk∈Gi×. . .×Gn

adalah himpunan penyelesaian (aturan penyelesaian, distribusi

sebelum atau sesudah penyelesaian) pada persoalan dengan kendala kondisional.

Teorema 3.3.1 Himpunan U dan V adalah terhubung oleh relasi

U =

domain penyelesaian layak dari persoalan (3.3.4) - (3.3.6) dan (3.3.7) - (3.3.9)

strategi campuran atau strategi murni) bersamaan bentunya jika dan hanya jika

Ebk(ωk−1) =bk.

Pernyataan di atas menyebabkan kemungkinan untuk memformulasi ulang

hasil kualitatif dan seringkali juga menghitung metode yang dikerjakan untuk

persoalan dengan kelas tertentu dan untuk investigasi konstruktif pada persoalan

kelas lain.

Relasi antara distribusi penyelesaian dan aturan penyelesaian sangat

mena-rik. Jika fungsiϕ0 adalah konveks dan komponen fungsi vektor ϕk adalah konkaf

pada X dengan tiap-tiap ω, maka nilai optimisasi dari fungsi objektif yang

dica-pai pada distribusi penyelesaian dapat dicadica-pai juga dengan aturan penyelesaian.

Konveksitas dari ϕ0 dan −ϕk tidak menghabiskan kondisi dengan strategi

opti-misasi murni dan strategi campuran yang didefinisikan menyatu dan nilai sama

dari fungsi tujuan.

Nilai fungsi tujuan untuk aturan optimisasi sebelumnya pada persoalan

sto-kastik tahap ganda di dalam rigid model dengan nilai fungsi tujuan didistribusi

penyelesaian optimisasi sebelumnya.

Pernyataan lebih tegas untuk aturan penyelesaian sesudahnya dan distribusi

penyelesaian diberikan berikut.

Teorema 3.3.2 (a) Andaikan ukuran probabilistik Fω di dalam Ω ≡ Ωn

ada-lah kontinu (b) andaikan terdapat fungsi positif g0(ω) dan gk(ωk) berkendala atas

aturan optimisasi sesudahnya untuk persoalan stokastik tahap ganda didefinisikan

oleh nilai yang sama pada fungsi tujuan sebagai distribusi penyelesaian optimisasi

sesudahnya.

Teorema 3.3.2 untuk persoalan stokastik satu tahap telah dibuktikan oleh Judin

(1972).

Persoalan program stokastik tahap ganda dengan kendala kondisional dapat

disubstitusikan untuk sistem persamaan yang memenuhi pemisahan tahapan.

An-daikan akan dibahas persoalan (3.3.10)-(3.3.12) yang diselesaikan dengan strategi

murni (dengan penyelesaian sebelum aturan penyelesaian sesudahnya).

Untuk definisi domain pada persoalan tahap ke-iberkaitan dengan

himpun-an :

Ki = {Xi ∈G0|∃{yi+1 ∈G0_i+1, . . . , yn ∈G0n};

Eωi[ϕ_i(ωi, Xi)|ωi−1]≥b_i(ωi−1),

Eωi+s[ϕ_i(ωi+s, xi, y_i+1, . . . , y_i+s)|ωi+s−1]

≥ bi+s(ωi+s−1), (3.3.13)

jika

∀ωi+s−1, . . . , ωn−1, s = 1,2, . . . , n−1}

G0

i menyatakan proyeksiGi terhadap hyper-plane dari kordinat yang

didefi-nisikan oleh komponen vektorXi. Persyaratan keberadaan dari vektoryi+s, s =

1,2, . . . , n−iyang memenuhi kondisi (3.3.13) adalah ekivalen terhadap

menye-lesaikan persoalan (3.3.10)-(3.3.12) adalah kondisiK1 6= Φ (fungsi objektif (3.3.10)

dengan asumsi berkendala). Jika disamping K1 6= Φ, Ki 6= Φ, i= 2,3, . . . , n.

Fungsi tujuan dari persoalan Qi(Xi) pada tahap ke-i mengatakan

kondi-sional ekspektasi matematika ϕ0(ωn, Xn) pada asumsi semua tahapan sebelum

tahap ke-i, himpunanωi−1 _{merupakan parameter yang direalisasikan dengan}

kon-disi persoalan dan komponen keputusan himpunan Xi−1_{, dan sesudah tahapan}

ke-ikeputusan optimisasi berikutnya : X∗

i+1, . . . , Xn∗ :

Qi(Xi) =Eωn

|ωi−1(ωn, Xi−1, X_i, X_i+1, . . . , X_n∗). (3.3.14)

Sejauh ini, definisi penyelesaian aturan optimisasi pada tahap ke-i dari persoalan

stokastik tahap ganda direduksi untuk menyelesaikan persoalan program

mate-matika berikut

inf

Xi∈Xi

Qi(Xi) (3.3.15)

Aturan sesudahnya untuk penyelesaian adalah : Xi =Xi(ωi), yi+s=yi+s(ωi+s); s=

1,2, . . . , n−i, dan aturan sebelumnya untuk penyelesaian adalah :

Xi =Xi(ωi−1); yi+s =yi+s(ωi+s−1); s= 1,2, . . . , n−i.

Jika fungsi tujuan dapat dipisahkan, yaitu ϕ0(ωn, Xn) = P_jn=1ϕ0j(ωj, Xj) kita

mempunyai

Qi(Xi) =Eωi

|ωi−1{ϕ₀(ωi, Xi) +Q∗_i+1(ωi, Xi)}.

dimana

Q∗_i(ωi−1

, Xi−1) = inf

Xi∈Ki

Eωi

|ωi−1{ϕ₀(ωi, Xi) +Q∗

i+1(ω

dengan i=n

Analog dengan persoalan pemisahan tahapan untuk persoalan stokastik tahap

ganda dengan strategi campuran yang dikonstruksikan.

3.4 Ilustrasi Pemrograman Stokastik

Banyak persoalan keputusan praktis dapat dimodelkan sebagai program

li-near berikut :

dengan menggunakan notasi matriks-vektor, formulasi dari persoalan (3.4.1)

da-pat dituliskan sebagai :

aplikasi dari persoalan di atas dapat ditemukan pada produksi industri,

trans-portasi, agriculture, energi, ekologi, keteknikan dan banyak lagi. Pada persoalan

(3.4.1), koefisien cj (misalnya faktor harga), aij (misalnya produktivitas) dan bi

(misalnya kapasitas) diasumsikan bernilai real yang sudah ditetapkan dan akan

pastikan nilai optimisasi dengan variabel keputusan xj, yang memenuhi kendala

Model (3.4.1) hanya dapat menghasilkan representasi layak dari persoalan

real ketika fungsi disyaratkan (misalnya fungsi biaya atau fungsi produksi) linear

pada variabel keputusan. Jika kondisi secara substansial dilanggar, sebagai

con-toh karena biaya marginal meningkat atau penurunan keuntungan marginal dari

produksi, dapat digunakan bentuk model yang lebih umum dari persoalan yaitu : min g0(x)

kendala gi(x)≤0, i= 1, . . . , m

x∈X ⊂ R

  

 

(3.4.3)

bentuk persoalan (3.4.3) sering dikenal sebagai persoalan program matematika.

Dapat dipahami bahwa himpunan X adalah sebuah fungsi gi : in → i, i =

0,1,2, . . . , m yang diberikan oleh proses pemodelan.

Kebergantungan pada sifat-sifat pada persoalan yang mendefinisikan fungsi

gi dan himpuman X, program (3.4.3) dikenal sebagai :

(a) Linear, jika himpunanXadalahpolyhedral konveksdan fungsigi, i= 0,1, . . . , m

adalah linear.

(b) Nonlinear, jika paling sedikit satu fungsigi, i= 0,1, . . . , madalah nonlinear

atauX tidak himpunanpolyhedral konveks; program nonlinear dapat dibagi

lagi menjadi program :

(b1) Konveks, jika X ∩ {x|gi(x) ≤ 0, i = 0,1, . . . , m} adalah himpunan

konveks dang0 adalah fungsi konveks (secara khusus jika fungsigi, i=

0,1, . . . , m adalah konveks dan X adalah himpunan konveks)

(b2) Nonkonveks, jika salah satuX∩ {x|gi(x)≤0, i= 0,1, . . . , m} adalah

Kasus (b2) di atas dibicarakan juga pada optimisasi global. Kelas spesial lain

dari persoalan dikenal sebagai program bilangan cacah (campuran), yang muncul

akibat disyaratkannya himpunan X (paling sedikit beberapa) variabel xj, j =

1, . . . , n hanya mengambil nilai cacah. Selama empat dekade terakhir,

perkem-bangan metode komputasi untuk menyelesaikan program matematika sangat

meng-gembirakan, dan persoalan berskala besar dapat diselesaikan dengan efisien dan

realibilitas yang tinggi.

Banyaknya situasi pemodel yang sering muncul karena ketidakpastian

(ti-dak pantas) pada asumsi bahwa koefisiencj, aij, bi atau fungsigi (dan himpunan

X) pada persamaan (3.4.1) dan (3.4.3) ditetapkan sebagai deterministik. Sebagai

gantinya produktivitas yang akan datang dalam suatu persoalan produksi, aliran

kedalam yang menuju resorvoir yang terhubung ke stasiun Hydropower,

kebu-tuhan pada bermacam-macam titik (node) dalam jaringan transportasi dan

se-terusnya, seringkali lebih tepat dimodelkan sebagai parameter yang mengandung

ketidakpastian, dimana lebih baik dikarakteristik dengan distribusi peluang.

Ketidakpastian dari nilai realisasi tidak selalu dapat digantikan oleh nilai

rata-rata atau beberapa estimasi lain (yang ditetapkan) selama proses pemodelan.

Karena itu, kebergantungan pada situasi praktis pada persoalan (3.4.1) dan (3.4.3)

tidak selalu mendapatkan model yang tepat untuk menggambarkan persoalan

yang akan diselesaikan. Sebelum masuk ke model yang lebih umum dari program

stokastik, akan digunakan persoalan produksi melalui ilustrasi berikut.

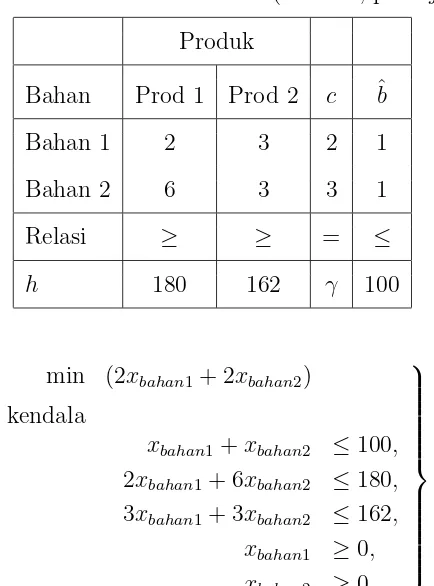
Dari dua bahan mentah yaitu bahan 1 dan bahan 2, dapat dihasilkan dua

produk-si berbeda yaitu prod 1 dan prod 2. Biaya produkproduk-si perunit dari bahan mentah

dinyatakan sebagai unit biaya pada bahan mentah c = (cbahan1, cbahan2)T,

kebu-tuhan untuk produksi h= (hprod1, hprod2)T dan kapasitas produksi adalah ˆb yaitu

jumlah total maksimum dari bahan mentah yang dapat diproses, diberikan dalam

Tabel 3.1 .

Tabel 3.1 : Produktivitasπ (bahani, prod j) Produk

Dengan menggunakan metode grafik, diperoleh penyelesaian

ˆ

xbahan1 = 36, xˆbahan2 = 18, γ(ˆx) = 126 (3.4.5)

yang merupakan penyelesaian optimisasi tunggal untuk persoalan diatas.

Persoalan di atas telah digambarkan oleh (3.4.4) dan diselesaikan oleh (3.4.5)

dengan persyaratan produktivitas, biaya perunit, kebutuhan dan kapasitas (tabel

perenca-naan produksi. Seringkali terjadi, beberapa data-produktivitas dan kebutuhan

berubah-ubah (acak). Akibatnya keputusan perencanaan produksi belum dapat

dibuat karena nilai data tidak eksak.

Asumsikan karena disebabkan statistik, diketahui bahwa :

hprod1 = 180 + ˜ζ1,

dimana ˜ζj adalah variabel acak dimodelkan dengan menggunakan distribusi

nor-mal, ˜η1 dan ˜η2 adalah distribusi seragam dan distribusi eksponensial. Dengan

parameter :

untuk sederhananya, diasumsikan bahwa keempat variabel acak adalah saling

in-dependen, karena variabel acak ˜ζ1,ζ˜2, dan ˜η2 adalah tidak terbatas, dibatasi

in-terval kepercayaan 99% (kecuali µ). Sehingga diperoleh variabel acak realisasi ˜

Sebagai ganti dari program linear (3.3.9), diberikan program linear stokastik

Persoalan keputusan di atas, tidak terdefinisi karena semuanya tidak jelas apakah

”min” dapat diperoleh sebelum realisasi (ζ1, ζ2, η1, η2) dari (˜ζ1, ζ˜2, η˜1, η˜2)

diketahui. Sebagai perbandingan, persoalan deterministik dari persoalan di atas

adalah

ˆ

x= (ˆxbahan1,xˆbahan2) = (36, 18), γ= 126

Perencanaan produksinya adalah

ˆ

y= (ˆybahan1, yˆbahan2) = (20, 30), γ = 130,

ˆ

z = (ˆzbahan1, zˆbahan2) = (50, 22), γ = 166,

ˆ

v = (ˆvbahan1, vˆbahan2) = (58, 6), γ = 134,   

 

(3.4.10)

yang merupakan penyelesaian tunggu dan lihat.

Penyelesaian tunggu dan lihat tidak diperlukan karena rencana produksi

mengandung ketidak pastian yang hanya memberikan informasi mengenai

kebu-tuhan dan produktivitas acak. Lebih praktisnya, kita dapat pastikan rencana

produksi untuk meminimumkan jumlah biaya tahap pertama mula-mula (yaitu

produksi) dan biaya recourse rata-rata sebagai ganti dari variabel acak ˜ζ1, ζ˜2, η˜1,

dan ˜η2) digunakan notasi vektor acak ˜ξ = (˜ζ1, ζ˜2, η˜1, η˜2)T . Selanjutnya

diper-kenalkan untuk tiap-tiap kendala stokastik pada (3.4.9) sebuah variabel recourse

yi( ˜ξ), i= 1,2.

Program stokastik pada (3.4.9) akan diubah menjadi program stokastik

h1( ˜ξ) := hprod1 = 180 + ˜ζ1,

0,∀i) maka persoalan (3.4.11) menjadi program linear yang dikenal sebagai

struk-tur dekomposisi dual

Penyelesaian persoalan (3.4.12) adalah sebuah program linear biasa, diperoleh

penyelesaian ¯x

¯

dimana penyelesaian dari PL (3.4.4) akan menghasilkan total biaya rata-rata

γ(¯x) = 204.561 dengan realibilitas yang diperoleh adalah ρ(¯x) = 0.9497 dengan

BAB 4

MASALAH OPTIMISASI SUPERSTRUKTUR SINTESIS JARINGAN AIR DENGAN KETIDAKPASTIAN

Dalam penelitin ini ini analisis sintesis optimisasi jaringan air terpadu

(Ka-ruppiah dan Grossmann, 2006a), dengan menggunakan unit proses (misalnya

reak-tor, unit pembersih), unit pengolahan/pemurnian /treatment air (misalnya

mem-bran, sentrifus), mixer dan splitter yang beroperasi dengan kondisi operasional

ti-dak pasti secara sistematis menganalisis semua disain alternatif dan superstruktur

sistem air terpadu yang dikonstruksi dengan berbagai interkoneksi antara semua

unit dan optimisasi global untuk memperoleh jaringan dengan biaya minimum.

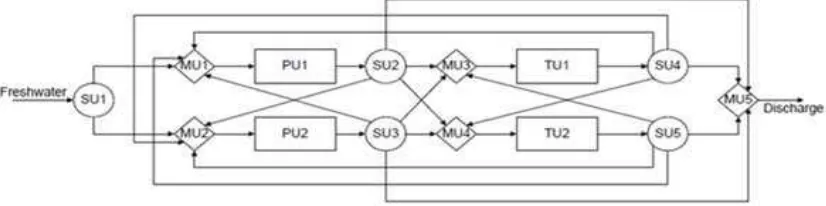
Ilustratif superstruktur jaringan air dengan dua unit proses dan dua unit

pemurnian ditunjukkan pada Gambar. 1 .

Gambar 1 : Superstruktur jaringan terpadu dengan 2 unit Proses dan 2 unit Pemurnian air

Sebuah penjelasan rinci untuk menurunkan superstruktur jaringan air

ter-padu dianalisis oleh Karuppiah dan Grossmann (2006a). Ide dasarnya adalah

bahwa ada satu bahagian air menggunakan unit proses dengan aliran air tetap

yang dipenuhi oleh sumber air bersih atau air limbah yang berasal dari suatu

pro-ses yang memenuhi batasan yang ditolerir tentang jumlah konsentrasi kontaminan

Air limbah yang dihasilkan oleh suatu proses diperlakukan dalam satu set

unit pengolahan air untuk dibuang ke tempat pembuangan limbah atau kembali

diproses / dimurniklan / daur ulang untuk digunakan kembali dengan

menggu-nakan suatu operasi.

Tingkat kontaminan dalam debit aliran berada pada ambang batas yang

ditentukan. Proses jaringan air terpadu mempunyai parameter tidak pasti dalam

kadar kontaminan yang dihasilkan di dalam unit proses dan rasio penghapusan

kontaminan dalam unit pemurnian.

Parameter tidak pasti terdapat pada nilai-nilai yang berbeda pada titik

wak-tu yang berbeda selama operasi jaringan. Karena jaringan terpadu saling

ber-hubungan, maka perubahan dalam parameter tidak pasti dapat mempengaruhi

semua bagian dari jaringan dan tidak mungkin untuk mengoperasikan jaringan

tanpa melanggar pembatasan debit atau tingkat kontaminan dalam saluiran ke

unit proses. Untuk menghindari situasi ini, efek dari ketidakpastian dalam beban

kontaminan dan perubahan kontaminan aliran diperhitungkan pada saat

meran-cang jaringan. Oleh karena itu perumusan masalah disain merupakan masalah

pemrograman stokastik two - stage / dua tahap dengan stage pertama adalah

pe-milihan jaringan dan stage kedua pengoperasian jaringan yang bertujuan untuk

mengkonstruksi suatu jaringan dengan biaya minimal.

Stage pertama biaya modal termasuk biaya investasi untuk pipa yang

ter-gantung pada laju aliran maksimum yang dapat dialiri dalam pipa, dan biaya

limbah aliran ditangani oleh unit pengolahan. Biaya operasi jaringan muncul pada

stage kedua, yang meliputi biaya memperoleh air bersih untuk digunakan dalam

unit proses, biaya memompa aliran tertentu air melalui pipa-pipa (volume aliran

ini kurang dari volume aliran maksimum yang dapat dilalui dalam pipa-pipa) dan

biaya operasi pengolahan limbah cair di unit pemurnian.

Keputusan yang berkaitan dengan stage pertama diambil sebelum

muncul-nya ketidakpastian dalam sistem,

(i) Apakah sambungan pipa aliran ada antara dua potong peralatan,

(ii) Laju aliran air maksimum yang dapat dilalui dalam pipa masing-masing

dan,

(iii) Volume maksimum air limbah untuk dibersihkan di setiap unit pemurnian.

Keputusan ini sesuai dengan variabel desain dalam masalah dan sekali

di-pilih, variabel desain tersebut tetap sepanjang durasi operasi jaringan dan tidak

dapat diubah selama operasi. Keputusan stage kedua adalah aliran air yang akan

dipompa melalui pipa masing-masing dalam jaringan air bersih untuk

dipenggu-naan pada berbagai waktu selama operasi. Perubahan selama operasi jaringan

tergantung pada nilai-nilai yang diambil oleh parameter tidak pasti.

4.1 Model Multiscenario MINLP

Model matematika jaringan yang beroperasi dengan ketidakpastian dalam

sistem melalui penggunaan skenario. Operasi jaringan dibagi atas skenario yang

nilai-nilai yang berbeda yang dikenal [N]. Persamaan model aliran memastikan bahwa

aliran residu / sisa di setiap unit aliran memegang dalam skenario setiap dan juga

konsentrasi kontaminan dalam aliran debit dan di aliran aliran masuk ke aliran

unit proses aliran mengalir dengan batas yang ditentukan dalam masing-masing

skenario. Beberapa asumsi yang terlibat dalam pemodelan sistem tersebut adalah:

A. Total laju aliran sungai dianggap sama dengan air murni dalam aliran

de-ngan aliran kontaminan individu diabaikan (level ppm).

B. Tidak ada kehilangan air di dalam unit proses atau unit pengolahan

C. Jaringan ini dioperasikan dengan kondisi isotermal dan isobar.

4.1.1 Fungsi Tujuan

Perluasan formulasi nonkonvek NLP untuk sintesis jaringan air terpadu

me-rumuskan model multi skenario MINLP. Fungsi: tujuannya adalah untuk

memi-nimalkan jumlah biaya modal (dikeluarkan hanya sekali pada saat membangun

jaringan) dan biaya operasi dari jaringan yang dikeluarkan selama setiap skenario

n ∈N. Fungsi Tujuan diberikan sebagai berikut :

minZp = AR

CF W = Biaya air bersih ($ /ton)

AR = Annualized faktor untuk investasi pada unit pemurnian dan pipa(/tahun)

Ci

p = koefisien Biaya sesuai dengan keberadaan pipa i($)

F Wn = Air Bersih asupan ke dalam sistem dalam skenario n (ton / jam)

IPi_(Fi_{) = Biaya investasi pipa i ($)}

ICt_(Fi₎α_{= InvestasiiF biaya t unit pengolahan dengan aliran keluar i ($)}

P Mi_Fi

n = Biaya memompa air di dalam pipa idi n skenario ($ /jam) nF

OCt_Fi

n = Biaya operasi darit unit pengolahan dengan aliran keluar i($ jam)

Pn = Probabilitas terjadinya skenarion

$ = Satuan Biaya.

Variabel biner disain yiberkaitan dengan keberadaan aliran / pipa i

perta-ma, variabel kontinu stage pertama merupakan aliran maksimum yang ditolerir

dalam sebuah pipai sementara vektorFi

n adalah variabel state stage kedua, yang

sesuai dengan aliran air dalam pipa i selama skenario n. Variabel state stage

ke-dua secara implisit tergantung pada variabel disain stage pertama, dan karenanya

biaya operasi stage kedua juga secara implisit tergantung pada keputusan stage

pertama.

merupakan biaya modal stage pertama :

merupakan ekspektasi biaya operasi stage kedua.

4.2 Model MINLP

4.2.1 Satuan Mixer

Keseluruhan aliran menyeimbangkan dengan keseimbangan kontaminasi

in-dividu untuk suatu satuan mixerm∈M Udengan himpunan aliran masuki∈min

, dan suatu aliran keluar k∈mout disajikan dalam persamaan (4.2.1) dan (4.2.2).

Persamaan (4.2.2) memuat suku-suku bilinier yang merupakan suatu sumber

non-konvekas sdari model optimisasi. Aliran keseimbangan diperoleh pada setiap

ske-nario n ∈ N dan Ci

jn merupakan konsentarsi kontaminasi j (dalam ppm) dalam

aliran I pada skenario n

F_nλ = X

i∈min

F_ni ∀m∈M U, k∈mout, ∀n ∈N (4.2.1)

F_nλC_jnλ = X

i∈min

F_niC_jni ∀j, ∀m∈M U, k∈mout, n ∈N (4.2.2)

Semua aliran{Fni}dan konsentrasi kontaminasi {Cjmi }dalam sistem adalah

non-negative dengan batas tertentu.

4.2.2 Satuan Splitter

Splitter satuans∈SU konsisten dari suatu aliran masukk ∈sin dan suatu

himpunan aliran keluar i yang dinotasikan dengan himpuan sout. Keseluruhan

ske-nario diberikan dalam persamaan (4.2.3) dan (4.2.4), yaitu

F_RK = X

i∈sout

F_RI ∀s ∈SU, k ∈Sin, ∀n ∈N (4.2.3)

C_jnj = Ck

jn ∀j, ∀s∈SU, ∀i∈sout, k ∈sin, ∀n∈N (4.2.4)

4.2.3 Satuan Proses

Persamaan keseimbangan aliran untuk setiap skenario satuan prosesp∈P U

dengan suatu aliran masuk i ∈ pin dan aliran keluar k ∈ pout yang ditunjukkan

persamaan (4.2.5) dan (4.2.6), dimana persamaan (4.2.5) berkaitan dengan

ke-seluruhan keseimbangan aliran tersebut dan persamaan (4.2.6) berkaitan pada

keseimbangan komponen individual. Proses setiap kontaminasi j dalam satuan

proses diberikan oleh Lp_j(dalam kg/jam) merupakan suatu sumber ketidak

pas-tian dalam jaringan dan mempunyai nilai berbeda dalam setiap scenario n yang

dinyatakan dalam bentuk persamaan :

Fnk =Fni =Pp ∀p∈P U, i ∈Pin, k∈Pout, ∀n ∈N (4.2.5)

PpC_jni +Lp_jn×103 =PpC_jnk ∀j, ∀p∈P U, i ∈Pin, k∈Pout, ∀n ∈N (4.2.6)

4.2.4 Satuan Pemurnian

Persamaan (4.2.7) dan (4.2.8) menguraikan keseimbangan aliran dan

ke-seimbangan konsentrasi kontaminasi, untuk semua skenario untuk suatu satuan

keluar i∈tout

F_nk = F_ni ∀t∈T U, i ∈tout, k∈tin, ∀n ∈N (4.2.7)

C_jnj = β_jnk C_jnk ∀j, ∀t ∈T U, i ∈tout, k ∈tin, ∀n ∈N (4.2.8)

Perbandingan penghapusan kontaminasi di dalam satuan pemurnian adalah

berbeda pada setiap skenarion. Parameterβi

j = 1−{(perbandingan penghapusan

untuk contaminant j di dalam satuan t (dalam %/100)) dan ini diperoleh pada

perbedaan nilai dalam setiap skenarion(βi

jn)}. Semua parameter yang tidak pasti

di dalam sistem diasumsikan bebas antara satu dengan lainnya.

4.2.5 Pemotongan Keterikatan Batas

Dengan menambahkan batasan persamaan (4.2.9) terhadap model yang asal

berdasarkan pada keseimbangan kontaminasi untuk keseluruhan sistem dalam

rangka memperkuat relaksasi yang konvek dari model multi skenario MINLP

(Ka-ruppiah & Grossmann, 2006a)

n dan Cjnout merupakan flow dan konsentrasi contaminant j di dalam

aliran keluar pada lingkungannya di dalam skenario n.

4.2.6 Desain Kendala

Batasan ini menghubungkan variabel disain yi _{dan ˆF}i _{yang ditunjukkan}

persamaan berikut

Yang mengimplementasikan bahwa jika suatu pipa ada, aliran maksimum di

da-lamnya merupakan suatu nilai antar batas tertentu dan jika tidak demikian

flo-wrate maksimum di dalam pipa mendekati kosong.

4.2.7 Hubungkan Batasan

Batasan keras [hard] yang menghubungkan variabel dari tiap skenario

de-ngan variabel disain diberikan dalam persamaan (4.2.11). Secara phisik, batasan

variabel disain ˆFi _{yang merupakan aliran maksimum bisa dilalui suatu pipa i,}

harus lebih besar dari aliran di dalam aliran yang melewati pipa idi dalam setiap

skenario n ∈N (yang dinotasikan denganFi n)

ˆ

Fi ≥F_ni ∀i, ∀n ∈N (4.2.11)

Model Multi skenario MINLP meliputi persamaan (4.1.1)-(4.2.11)

merupak-an bentuk optimisasi global dmerupak-an penyelesaimerupak-an model ini merupakmerupak-an nilai dari

vari-abel disain yang menggambarkan Jaringan topologi dan juga merupakan varivari-abel

control (Fi

n ∀i, ∀n∈N) yang merupakan aliran air untuk dipompa pada setiap

pipa i, di dalam setiap skenario n. Nilai-Nilai variabel state yang merupakan

konsentrasi kontaminasi dalam semua aliran dalam jaringan etiap scenario juga

BAB 5

KESIMPULAN DAN RISET LANJUTAN

5.1 Kesimpulan

Model Multiscenario MINLP merupakan model yang tepat untuk dapat

di-aplikasikan dalam fungsi tujuan dalam masalah optimisasi superstruktur jaringan

air tepadu dengan ketidakpastian sedemikian dapat meminimalkan total

pembia-yaan dan model MINLP untuk keseimbangan aliran / material keselutuhan serta

keseimbangan kontaminan dalam Unit Mixer, Splitter, Proses dan Treatment /

Pemurnian. Pemilihan desain superstruktur jaringan air terpadu dapat

memini-malkan total pembiayaan yang diproses dalam unit pemurnian / treatment untuk

operasi penggunaan air.

5.2 Riset Lanjutan

a. Untuk menindak lanjuti hasil penelitian ini disarankan untuk

mengkonstruk-si model sebuah jaringan yang berfungmengkonstruk-si ganda dengan regeneramengkonstruk-si industri

penggunaan air dan pengolahan air limbah dan air dalam penyimpanan

(reservoir) dalam integrasi langsung. Selain itu, beberapa utilitas jaringan

mungkin berfungsi sebagai regenerasi air dalam induistri yang dapat

difor-mulasikan dalam model tersebut.

b. Pengembangan model desain jaringan untuk fleksibilitas dengan

ketidakpas-tian yang terdapat dalam skenario dapat dimasukkan ke dalam model

de-ngan menggunakan fuzzy atau stokastik parameter dimana Interplant