Bahan ajar Kalkulus Integral 2009 Writingby

 

APLIKASI INTEGRAL

1. LUAS DAERAH BIDANG

Misalkan f(x) kontinu pada a ≤ x ≤ b, dan daerah tersebut dibagi menjadi n sub interval h1,

h2, …, hn yang panjangnya ∆1x, ∆2x, …, ∆nx (anggap ∆1x = ∆2x = … = ∆nx), ambil sebarang

titik x = xi pada masing-masing hi dan bentuk persegi panjang yang alasnya hi (jadi

panjangnya ∆ix) dan tingginya f(xi).

Persegi panjang tersebut disebut sebagai persegi panjang pendekatan dengan luas = f(x.i) ∆ix.

Sehingga jumlah luas n persegi panjang adalah :

∆

Luasan tersebut merupakan pendekatan dari luas daerah yang dibatasi oleh f(x), sumbu X,

dan garis-garis x = a dan x = b. Jika ∆kx Æ0, maka banyaknya subinterval n Æ∞, sehingga

luas daerah tersebut adalah :

lim_∞ ∆

      |    

Ada beberapa hal yang harus diketahui adalah :

A. Jika f(x) kontinu pada a ≤ x ≤ b dan f(x) ≥ 0 pada interval tersebut maka luas daerah yang

dibatasi oleh f(x), x = a, x = b, dan sumbu X adalah

 

B. Jika f(x) kontinu pada a ≤ x ≤ b dan f(x) ≤ 0 pada interval tersebut maka luas daerah yang

dibatasi oleh f(x), x = a, x = b, dan sumbu X adalah

 

C. Jika f(x) kontinu pada a ≤ x ≤ b dan bertukar tanda, maka luas daerah yang dibatasi oleh

f(x) ≤ 0, x = a, x = b, dan sumbu X sama dengan penjumlahan luas masing-masing

daerah. Misal pada gambar :

Maka Æ Luas = Luas I + Luas II + Luas III

Jadi

     

Atau secara umum luas daerah yang dibatasi oleh f(x), x = a, x = b, dan sumbu X adalah

  | |

D. Luas daerah yang dibatasi oleh grafik x = f(y), garis-garis y = a, y = b, dan sumbu Y

adalah :

  | |

E. Kalau fungsi f(x) dan g(x) kontinu pada a ≤ x ≤ b, secara umum berlaku bahwa luas

seperti tampak pada gambar berikut :

atau bila f(y) dan g(y) kontinu pada a ≤ y ≤ b, maka luas daerah yang dibatasi oleh f(y),

g(y), garis y = a, dan y = b, adalah :

seperti tampak pada gambar berikut :

∫

−

=

=

b

a

dx

x

g

x

f

L

Luas

(

)

(

)

 

∫

−

=

=

b

a

dy

y

g

y

f

L

 

Catatan Penting :

Untuk menghitung luas suatu daerah bidang dengan integral, secara umum bisa dilakukan

langkah-langkah sebagai berikut :

1. Buat gambar daerah yang dimaksud, juga persegi panjang pendekatannya dengan tebal ∆x (bila persegi panjang tegak / vertikal) atau ∆y (bila persegi panjang mendatar / horizontal).

2. Tentukan luas persegi panjang pendekatan, tentukan batas kiri / kanan (untuk yang tegak)

atau batas bawah / atas (untuk yang mendatar). Kemudian gunakan integral untuk

menghitung jumlah luas persegi panjang tersebut yang banyaknya dibuat menjadi ∞.

Contoh pemakaian integral untuk menghitung luas daerah :

1. Luas daerah yang dibatasi oleh parabola y = x2 – 4, garis x = 0, x = 3, dan sumbu X adalah :

Jadi luas daerah tersebut adalah :

(

)

(

)

∫

−

−

+

∫

−

=

2

0

3

2 2 2

4

4

dx

x

dx

3 2 3 2 0 3 4 3 1 4 3 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ −

= x x x x

⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ −

= .8 4.2

3 1 3 . 4 27 . 3 1 0 2 . 4 8 . 3 1 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − = 8 3 8 12 3 27 8 3 8 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − = 3 16 3 9 3 16 3 7 3 16 + = 3 23 =

Jika dilakukan penghitungan nilai integral secara langsung, maka akan terjadi kesalahan

yaitu

(

)

∫

− =3 0 2 4 dx x

Luas 3 4 3₀ 3 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋

= x x .27 4.3 0

3 1 − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋

= =9−12=−3

Æ (salah !!! tidak ada besar luasan yang bernilai negatif).

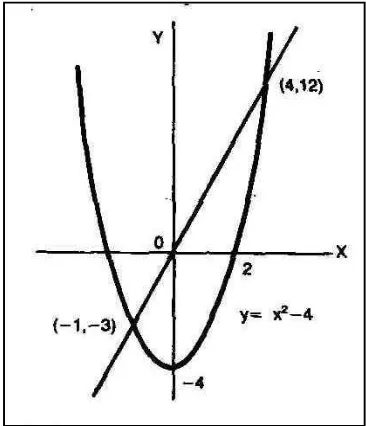
2. Hitung luas daerah yang dibatasi oleh parabola y = x2 – 4 dan garis y = 3x.

Titik potong parabola f(x) = y = x2 – 4 dan garis lurus g(x) = y = 3x adalah (4, 12) dan (1,

-3)*

*) y = x2 – 4 dipotongkan dengan garis y = 3x maka x2 – 4 = 3x atau x2 - 4 - 3x = 0.

Dengan menggunakan pencarian akar kuadrat dari persamaan kuadrat x2 – 4 - 3x = 0,

diperoleh (x– 4)(x + 1) = 0, berarti x = 4 atau x = -1. Untuk x = 4, maka y = 12, dan

untuk x = -1, maka y = -3. Sehingga diperoleh pasangan titik potong kedua kurva yaitu

[image:7.612.143.326.143.356.2]

 

Grafik dari kurva seperti berikut :

Sesuai dengan kondisi (E), maka dapat dihitung luas daerah sbb :

( ) ( )

∫

−

− =4

1

dx x g x f

Luas

∫

−

− − =4

1 2

3 4 xdx

x

∫

−

− − =4

1 2

4 3x dx x

selanjutnya perlu diselidiki tanda-tanda dari persamaan kuadrat tersebut yaitu :

x2 - 3x - 4 = (x – 4)(x + 1).

+ + + - - - + + + -1 4

Jadi pada interval -1 ≤ x ≤ 4, x2 - 3x – 4 ≤ 0 sehingga penghitungan luas dilakukan dengan

(

)

∫

− − − − =4 1 2 4 3x dx x Luas

∫

− + + − =4 1 2 4 3x dx

x 3 2 4 4₁

2 3 3 1 − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− + +}

= x x x

( )

( )

( )

⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− − + − + −} − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− + +}

= . 1 4. 1

2 3 1 . 3 1 4 . 4 4 . 2 3 4 . 3

1 3 2 3 2

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{+ −} − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− + +} = 4 2 3 3 1 16 2 48 3 64 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ = 6 13 6 112 6 125 =

Sebagai catatan bahwa jika dilihat dari gambar, maka pada interval -1 ≤ x ≤ 4, kurva garis

terletak di atas kurva parabola yang berarti bahwa g(x) – f(x) bernilai positif atau 3x – (x2 –

4) positif, sehingga luas daerah yang dibatasi kedua kurva tersebut bisa langsung dihitung

menggunakan :

(

)

∫

− − = 4 1 ) ( )

(x f x dx g

Luas

∫

{

(

)

}

− − − = 4 1 2 4

3x x dx

∫

(

)

− + − =4 1 2 4

3x x dx

∫

(

)

− + + − =4 1 2 4 3x dx x

6 125

=

3. Luas daerah satu ruas sikloida x = t – sin t, y = 1 – cos t seperti ditunjukkan pada gambar

berikut adalah :

Luas satu ruas dapat diambil misalnya untuk t = 0 sampai 2π. Karena x = t – sin t, maka

 

Sehingga

∫

=

=2π 0 t dx y Luas

∫

= − −

= 2π 0 ) cos 1 ( ) cos 1 ( t dt t t

∫

= − = 2π

0 2 ) cos 1 ( t dt t

∫

= + −

= 2π 0 2 ₎ cos cos 2 1 ( t dt t t

∫

∫

∫

= = =

+

−

=

π 2π π

0 2 0 2 2 0

cos

cos

2

1

t t t

dt

t

dt

t

dt

∫

= + −

= π π 2π 0

2 2

0 2

0 2sin | cos

| t dt t t t

untuk menghitung nilai integral

∫

= π 2 0 2 cos t dt

t gunakan kesamaan fungsi trigonometri cos2t = 1 -

sin2t, sehingga

∫

= π 2 0 2 cos t dt t

∫

= − = 2π

0 2 ) sin 1 ( t dt t

∫

∫

= = − = π 2π

0 2 2 0 sin 1 ( t t dt t dt

∫

= − = π 2π

∫

= π 2 0 2 sin t dt

t dihitung menggunakan kesamaan trigonometri ₍₁−_cosx₎=_2sin2 1₂x_{, dengan}

demikian sin2t = ½(1 - cos2t) sehingga

∫

= π 2 0 2 sin t dt t

∫

= − = 2π

0 ) 2 cos 1 ( 2 1 t dt t

∫

= − = 2π

0 ) 2 cos 1 ( 2 1 t dt t

∫

∫

= = − = 2π π

0 2 0 2 cos 2 1 1 2 1 t t dt t dt

∫

= − = π 2π

0 2

0 cos2

2 1 | 2 1 t dt t t .

Dengan substitusi u = 2t, maka du = 2 dt, sehingga

∫

= π 2 0 2 cos t tdt

∫

=

= 2π

0 2 1 cos t du u

∫

=

= 2π 0 cos 2 1 t du u π π 2 0 2

0 sin2 |

2 1 | sin 2 1 t u = = .

Jadi

∫

= − π 2 0 2 ) cos 1 ( t dt

t ₀2π ₀2π ₀2π ₀2π sin2 |₀2π 2 1 . 2 1 | 2 1 | | sin 2

| t t t t

t − + − +

= π π π π π 2 0 2 0 2 0 2 0 2

0 sin2 |

2 1 . 2 1 | sin 2 | 2 1 |

| t t t t

t + − − +

= π π π π 2 0 2 0 2 0 2

0 sin2 |

4 1 | sin 2 | 2 1 |

2t − t − t + t

 

π π

π 2

0 2

0 2

0 sin2 |

4 1 | sin 2 | 2 3

t t

t − +

=

) 0 sin 4 1 4 sin 4 1 ( ) 0 sin 2 2 sin 2 ( 2 . 2 3

− +

− −

= π π π

0 0 3 − +

= π =3π

Latihan :

1. Hitung luas daerah yang dibatasi oleh parabola y = 4x – x2 dan sumbu X.

Sebagai bantuan, grafik kurvanya adalah :

2. Tentukan luas daerah yang dibatasi oleh parabola y2 = 4x dan garis y = 2x – 4 dengan garfik

3. Hitung luas daerah antara y = 6x – x2 dan y = x2 – 2x. Grafik digambarkan seperti berikut :

4. Tentukan luas daerah yang di dalam y2 = x2 – x4 dengan grafik simetri terhadap sumbu X

 

Luas daerah bisa dihitung dengan menghitung 4 kali luas pada kuadran pertama. Luas

daerah di kuadran pertama adalah :

∫

−

=1 0

4 2

1 x x dx

Luas sehingga luas daerah keseluruhan adalah =

∫

−

1

0

4 2

4 x x dx