APLIKASI METODE CUTTING PLANE DALAM OPTIMISASI
JUMLAH PRODUKSI TAHUNAN PADA PT. BUDI RAYA
PERKASA
SKRIPSI
NICO
100803050
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
APLIKASI METODE CUTTING PLANE DALAM OPTIMISASI
JUMLAH PRODUKSI TAHUNAN PADA PT. BUDI RAYA
PERKASA
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar sarjana sains
NICO
100803050
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Aplikasi Metode Cutting Plane dalam
Optimisasi Jumlah Produksi Tahunan pada PT. Budi Raya Perkasa
Kategori : Skripsi
Nama : Nico
Nomor Induk Mahasiswa : 100803050
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam
(FMIPA) Universitas Sumatera Utara
Disetujui di Medan, Januari 2014
Komisi Pembimbing :
Pembimbing 2, Pembimbing 1,
Drs. Gim Tarigan, M.Si Prof. Dr. Drs. Iryanto, M.Si NIP. 195502021986011001 NIP. 194604041971071001
Disetujui Oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
APLIKASI METODE CUTTING PLANE DALAM OPTIMISASI
JUMLAH PRODUKSI TAHUNAN PADA PT. BUDI RAYA
PERKASA
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya sendiri, kecuali
beberapa kutipan dan ringkasan yang masing-masing disebutkan
sumbernya.
Medan, Januari 2014
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Pemurah dan Maha Penyayang, atas limpahan karunia-Nya penulis dapat menyelesaikan penyusunan skripsi ini dengan judul “Aplikasi Metode Cutting Plane dalam Optimisasi Jumlah Produksi Tahunan pada PT. Budi Raya Perkasa” dalam waktu yang ditetapkan.
Ucapan terima kasih penulis sampaikan kepada Bapak Prof. Dr. Drs. Iryanto, M.Si dan Bapak Drs. Gim Tarigan, M.Si selaku pembimbing, Bapak Dr. Parapat Gultom, M.SIE dan Ibu Dr. Esther Sorta M. Nababan, M.Sc selaku pembanding yang telah meluangkan waktunya dan memberikan saran-saran yang berharga selama penyusunan skripsi ini. Panduan ringkas, padat dan profesional telah diberikan kepada penulis dalam menyelesaikan skripsi ini. Ucapan terima kasih juga penulis tujukan kepada Ketua dan sekertaris Departemen Matematika FMIPA USU, Bapak Prof. Dr. Tulus, M.Si. Ph.D dan Ibu Dra. Mardiningsih, M.Sc, Dekan FMIPA USU, Dr. Sutarman, M.Sc dan Pembantu dekan FMIPA USU, semua dosen dan pegawai Matematika FMIPA USU, rekan-rekan kuliah khususnya mahasiswa Matematika stambuk 2010, kakak-kakak senior Matematika, terutama Meliani dan Christian Hermawan, dan sepupu saya David Linus yang banyak membantu dalam pengumpulan data. Akhirnya tidak terlupakan kepada Papa, Mama, Adik penulis, dan semua ahli keluarga yang selama ini memberikan bantuan dan dorongan yang penulis perlukan. Tanpa dukungan dari semua pihak yang penulis sebutkan sebelumnya, penulis tidak akan pernah berhasil menyelesaikan skripsi ini.
Medan, Januari 2014 Penulis
APLIKASI METODE CUTTING PLANE DALAM OPTIMISASI JUMLAH PRODUKSI TAHUNAN PADA PT. BUDI RAYA PERKASA
ABSTRAK
PT. Budi Raya Perkasa merupakan perusahaan yang bergerak di bidang manufaktur yang memproduksi berbagai jenis ukuran matras spring bed dengan tipe Maxi Coil, seperti 80 x 200 cm, 140 x 200 cm, dan 200 x 200 cm. Perusahaan ini melakukan produksinya berdasarkan ketersediaan bahan baku, jumlah permintaan, kapasitas mesin, dan tenaga kerja. Untuk itu, PT. Budi Raya Perkasa perlu mengoptimalkan jumlah produksi matras spring bed sehingga tujuan utama PT. Budi Raya Perkasa dapat tercapai. Metode yang akan digunakan untuk menyelesaikan permasalahan tersebut adalah metode cutting plane. Metode
cutting plane merupakan metode yang digunakan untuk menyelesaikan program linier bilangan bulat, baik bilangan bulat murni maupun campuran dengan penambahan batasan baru yang disebut gomory. Batasan gomory diberikan jika nilai dari variabel keputusan belum bulat (bernilai pecahan). Hasil pembahasan dengan menggunakan metode cutting plane dari permasalahan jumlah produksi yang optimal bagi PT. Budi Raya Perkasa, yaitu matras ukuran 80 x 200 cm, 140 x 200 cm, dan 200 x 200 cm berturut-turut adalah 155 unit, 160 unit, dan 170 unit.
APPLICATION OF CUTTING PLANE METHOD IN OPTIMIZATION OF TOTAL PRODUCTION ANNUAL IN PT. BUDI RAYA PERKASA
ABSTRACT
PT . Budi Raya Perkasa is a company move in manufacturing which produces various kinds of spring bed mattress size with Maxi Coil type, such as 80 x 200 cm, 140 x 200 cm, and 200 x 200 cm. This company is based on the availability of raw material production, the number of requests, machine capacity, and labor. For that, PT. Budi Raya Perkasa needs to optimize the amount of mattress spring bed production so the main goal of PT. Budi Raya Perkasa can be achieved. Method that will be used to solve these problems is the cutting plane method. Cutting plane method is the method used to solve integer linear programming, either pure or mixed integer with the addition of new constraints called gomory. gomory constraints will be given if the value of the variable has not been integer (fractional value). Result of the problem with cutting plane method from the optimal production quantities for PT. Budi Raya Perkasa, that is mattress size 80 x 200 cm, 140 x 200 cm, and 200 x 200 cm consecutive are 155 units, 160 units, and 170 units.
DAFTAR ISI
Halaman
Persetujuan ii
Pernyataan iii
Penghargaan iv
Abstrak v
Abstract vi
Daftar Isi vii
Daftar Tabel viii
Daftar Lampiran ix
Bab 1. Pendahuluan
1.1. Latar belakang 1
1.2. Perumusan Masalah 2
1.3. Batasan Masalah 2
1.4. Tujuan Penelitian 3
1.5. Manfaat Penelitian 3
1.6. Lokasi Penelitian 3
1.7. Metodologi Penelitian 4
Bab 2. Tinjauan Pustaka
2.1. Produksi 5
2.2. Persediaan Bahan Baku 6
2.3. Permintaan 6
2.4. Tenaga Kerja 7
2.5. Mesin 7
Bab 3. Metode Penelitian
3.1. Program Integer 8
3.2. Metode Simpleks 9
3.3. Metode Cutting Plane 12
3.4. Metode Dual Simpleks 16
Bab 4. Pembahasan
4.1. Pengolahan Data 18
4.2. Perumusan Fungsi Tujuan 20
4.3. Perumusan Fungsi Kendala 21
4.4. Analisis Metode Cutting Plane 23
Bab 5. Kesimpulan dan Saran
5.1. Kesimpulan 27
5.2. Saran 27
DAFTAR TABEL
Nomor Judul Halaman
Tabel
3.1. Optimum Masalah Program Linier 13 3.2. Setelah Penambahan Pemotongan Fraksional 15 4.1. Biaya Produksi Matras Spring Bed 18
4.2. Bahan Baku yang Dibutuhkan 19
4.3. Persediaan Bahan Baku Matras Spring Bed Tahun 2012 19 4.4. Jumlah Permintaan Matras Spring Bed Tahun 2012 19 4.5. Waktu Produksi dengan Ketersediaan Tenaga Kerja
Tahun 2012 20
DAFTAR LAMPIRAN
Nomor Judul Halaman
Lamp
APLIKASI METODE CUTTING PLANE DALAM OPTIMISASI JUMLAH PRODUKSI TAHUNAN PADA PT. BUDI RAYA PERKASA
ABSTRAK
PT. Budi Raya Perkasa merupakan perusahaan yang bergerak di bidang manufaktur yang memproduksi berbagai jenis ukuran matras spring bed dengan tipe Maxi Coil, seperti 80 x 200 cm, 140 x 200 cm, dan 200 x 200 cm. Perusahaan ini melakukan produksinya berdasarkan ketersediaan bahan baku, jumlah permintaan, kapasitas mesin, dan tenaga kerja. Untuk itu, PT. Budi Raya Perkasa perlu mengoptimalkan jumlah produksi matras spring bed sehingga tujuan utama PT. Budi Raya Perkasa dapat tercapai. Metode yang akan digunakan untuk menyelesaikan permasalahan tersebut adalah metode cutting plane. Metode
cutting plane merupakan metode yang digunakan untuk menyelesaikan program linier bilangan bulat, baik bilangan bulat murni maupun campuran dengan penambahan batasan baru yang disebut gomory. Batasan gomory diberikan jika nilai dari variabel keputusan belum bulat (bernilai pecahan). Hasil pembahasan dengan menggunakan metode cutting plane dari permasalahan jumlah produksi yang optimal bagi PT. Budi Raya Perkasa, yaitu matras ukuran 80 x 200 cm, 140 x 200 cm, dan 200 x 200 cm berturut-turut adalah 155 unit, 160 unit, dan 170 unit.
APPLICATION OF CUTTING PLANE METHOD IN OPTIMIZATION OF TOTAL PRODUCTION ANNUAL IN PT. BUDI RAYA PERKASA
ABSTRACT
PT . Budi Raya Perkasa is a company move in manufacturing which produces various kinds of spring bed mattress size with Maxi Coil type, such as 80 x 200 cm, 140 x 200 cm, and 200 x 200 cm. This company is based on the availability of raw material production, the number of requests, machine capacity, and labor. For that, PT. Budi Raya Perkasa needs to optimize the amount of mattress spring bed production so the main goal of PT. Budi Raya Perkasa can be achieved. Method that will be used to solve these problems is the cutting plane method. Cutting plane method is the method used to solve integer linear programming, either pure or mixed integer with the addition of new constraints called gomory. gomory constraints will be given if the value of the variable has not been integer (fractional value). Result of the problem with cutting plane method from the optimal production quantities for PT. Budi Raya Perkasa, that is mattress size 80 x 200 cm, 140 x 200 cm, and 200 x 200 cm consecutive are 155 units, 160 units, and 170 units.
BAB 1
PENDAHULUAN
1.1. Latar Belakang
Permasalahan yang sering dihadapi industri ataupun perusahaan adalah bagaimana mengoptimalkan jumlah produksi dengan ketersediaan bahan baku yang terbatas, jumlah permintaan, kapasitas mesin, dan tenaga kerja sehingga dapat memenuhi tujuan utama dari perusahaan, yaitu memperoleh keuntungan. Optimasi produksi diperlukan perusahaan agar suatu produksi dapat menghasilkan produk dalam kuantitas yang diharapkan sehingga perusahaan dapat mencapai tujuannya.
Tujuan dari perusahaan akan tercapai apabila faktor-faktor produksi yang terbatas digunakan seefisien mungkin. Faktor-faktor produksi tersebut dapat berupa modal, mesin produksi, bahan baku, bahan pembantu, dan tenaga kerja.
Masalah pengoptimalan jumlah produksi merupakan hal yang sangat menarik untuk dianalisis, karena dengan mengetahui secara pasti tingkat produksi yang tepat, dapat pula meningkatkan keuntungan yang maksimal bagi perusahaan. Terdapat banyak metode untuk mengoptimalkan jumlah produksi. Salah satunya adalah metode cutting plane. Aplikasi metode cutting plane sangat tepat dan dapat digunakan karena dalam produksi, hasil yang didapat harus integer.
ini melakukan produksinya berdasarkan ketersediaan bahan baku, jumlah permintaan, kapasitas mesin, dan tenaga kerja.
PT. Budi Raya Perkasa belum mampu menentukan jumlah produksi optimal untuk masing-masing produk yang dihasilkan. Ini dikarenakan perusahaan belum mampu menentukan komposisi produk yang optimum. Untuk itu, PT. Budi Raya Perkasa perlu mengoptimalkan jumlah produksi matras spring bed dengan ketersediaan bahan baku yang dimiliki, jumlah permintaan, kapasitas mesin, dan tenaga kerja pada setiap periodenya sehingga tujuan utama PT. Budi Raya Perkasa dapat tercapai.
Dari semua permasalahan di atas, penulis tertarik untuk mengaplikasikan metode cutting plane dalam optimisasi jumlah produksi tahunan pada PT. Budi Raya Perkasa.
1.2. Perumusan Masalah
Permasalahan yang akan dibahas dalam penelitian ini adalah :
1. Perusahaan belum mampu menentukan jumlah produksi yang optimal untuk masing-masing produk.
2. Perusahaan belum mampu menentukan komposisi produk yang optimum.
1.3. Batasan Masalah
Agar penelitian yang dilakukan dapat menghasilkan penelitian yang fokus dan akurat, maka diberikan batasan masalah sebagai berikut :
1. Penelitian ini hanya fokus dalam optimisasi jumlah produksi matras spring bed
pada PT. Budi Raya Perkasa.
3. Kendala produksi yang dibahas adalah jumlah bahan baku yang tersedia, jumlah permintaan, kapasitas mesin, dan tenaga kerja.
4. Data yang digunakan adalah data produksi tahun 2012.
5. Pengolahan data optimisasi menggunakan program integer dengan metode
cutting plane.
1.4. Tujuan Penelitian
Tujuan dari penelitian ini adalah menerapkan metode cutting plane untuk mengoptimalkan jumlah produksi tahunan matras spring bed pada PT. Budi Raya Perkasa sehingga dapat menghasilkan kuantitas yang optimal.
1.5. Manfaat Penelitian
Manfaat dari penelitian ini adalah sebagai berikut :
1. Sebagai masukan atau informasi yang bermanfaat bagi PT. Budi Raya Perkasa. 2. Dapat digunakan sebagai tambahan informasi dan referensi bacaan bagi yang
hendak melakukan penelitian serupa.
1.6.Lokasi Penelitian
1.7.Metodologi Penelitian
Langkah-langkah yang digunakan dalam penelitian ini adalah sebagai berikut : 1. Studi pustaka
Tahap ini dimulai dengan studi kepustakaan yaitu mengumpulkan bahan referensi, mempelajari serta menggali informasi baik dari buku, skripsi, jurnal, maupun situs internet mengenai produksi dan metode cutting plane.
2. Melakukan peninjauan dan pengambilan data pada PT. Budi Raya Perkasa secara langsung.
3. Analisa dan pengolahan data
a. Data yang diperoleh diformulasikan ke dalam bentuk program integer. b. Model yang telah diubah diselesaikan dengan menggunakan metode
BAB 2
TINJAUAN PUSTAKA
2.1. Produksi
Produksi adalah transformasi atau pengubahan faktor produksi menjadi barang produksi, atau suatu proses di mana inputs diubah menjadi outputs. Perusahaan berusaha mencapai efisiensi produksi, yaitu menghasilkan barang dan jasa dengan biaya paling rendah untuk suatu jangka waktu tertentu (Suparmoko, 1992).
Manajemen produksi adalah kegiatan untuk mengatur agar dapat menciptakan dan menambahkan kegunaan (utility) sesuatu barang atau jasa. Fungsi produksi adalah bertanggung jawab atas pengolahan bahan baku dan penolong/pembantu menjadi barang jadi atau jasa yang akan memberikan hasil pendapatan bagi perusahaan. Dalam setiap proses produksi, suatu perusahaan harus mempunyai kemampuan untuk dapat menggunakan sumber-sumber di dalam perusahaan (internal resources) sebanding dengan bahan-bahan dan jasa-jasa yang diolah menjadi produk. Dengan demikian, terlihat bahwa banyaknya bahan-bahan yang dapat disediakan akan menentukan besarnya penggunaan sumber-sumber di dalam perusahaan pabrik tersebut, dan demikian pula dengan kelancarannya (Assauri, 1999).
Sebuah perusahaan harus bisa menghasilkan produk yang bisa bersaing di pasaran. Dengan desain yang menarik dan bahan yang berkualitas diharapkan produk spring bed dapat memenuhi selera konsumen (Yulianto, 2003).
barang atau jasa. Integrasi tersebut menggabungkan dua atau lebih sumber daya dalam berbagai kombinasi yang terbaik (Herjanto, 1997).
2.2. Persediaan Bahan Baku
Persediaan adalah suatu aktiva yang meliputi barang-barang milik perusahaan dengan maksud untuk dijual dalam suatu periode usaha normal, atau persediaan barang-barang yang masih dalam pengerjaan atau proses produksi, ataupun persediaan bahan baku dasar yang menunggu penggunaannya dalam suatu proses produksi (Assauri, 1999).
Bahan baku merupakan bahan yang membentuk bagian integral produk jadi. Untuk itu, pengelolaan bahan baku dengan baik sangat diharapkan agar tidak menghambat kegiatan-kegiatan lain dalam suatu industri. Persediaan bahan baku di dalam perusahaan adalah merupakan hal yang sangat wajar untuk dikendalikan dengan baik. Setiap perusahaan yang menghasilkan produk (perusahaan-perusahaan yang menyelenggarakan proses produksi) akan memerlukan persediaan bahan baku ini. Baik disengaja maupun tidak disengaja, perusahaan yang bersangkutan ini akan menyelenggarakan persediaan bahan baku yang menunjang jalannya proses produksi dalam perusahaan yang bersangkutan (Lusia, 1993).
2.3. Permintaan
Permintaan adalah jumlah barang yang rela dan mampu dibeli oleh para pelanggan selama periode tertentu dan kondisi tertentu. Permintaan merupakan hubungan antara harga dan jumlah barang yang diminta (Idahnaita, 2013).
barang maka semakin sedikit jumlah barang yang diminta konsumen. Sebaliknya, semakin rendah atau murah harga suatu barang maka semakin banyak jumlah barang yang diminta konsumen (Idahnaita, 2013).
2.4. Tenaga Kerja
Tenaga kerja dibutuhkan untuk melakukan proses transformasi dari bahan menjadi barang jadi yang dikehendaki oleh perusahaan. Dalam hal ini, tenaga kerja sebagai suatu faktor produksi yang berbeda dengan bahan baku dan mesin-mesin (Gitosudarmo, 2002).
2.5. Mesin
BAB 3
METODE PENELITIAN
3.1. Program Integer
Optimasi integer bukan merupakan sebuah persoalan matematika baru, dan dalam penelitian operasional dikenal sejak tahun 1940. Optimisasi integer penting digunakan pada pemecahan masalah yang disusun sebagai sebuah hasil perkembangan pada bidang penelitian operasional, terutama sekali pada persoalan program linier. Hal itu diperlukan untuk penentuan model penyusunan pada beberapa atau semua variabel keputusan agar integer (Taha, 1996).
Anggaplah model persoalan program integer :
Fungsi tujuan :
Maksimumkan :
Maka diperoleh,
z = j
n
j j
x
c
1
dimana adalah konstanta.
dengan kendala :
. . . . . . . . dan Maka diperoleh, j n j ij
x
a
1( ) bi ;
0
j
x semua bilangan cacah, dimana adalah konstanta.
Disimpulkan, model persoalan program integer dapat diformulasikan sebagai berikut :
Maksimumkan : z = j n j j
x
c
1dengan kendala :
j n j ij
x
a
1( ) bi ;
0
j
x semua bilangan cacah,
dimana adalah konstanta (Siagian, 2006).
3.2. Metode Simpleks
Program linier yang melibatkan lebih dari dua atau banyak variabel sulit diselesaikan dengan metode grafik. Dalam keadaan ini kebutuhan metode yang lebih umum menjadi nyata. Metode umum itu dikenal dengan nama metode simpleks yang dirancang untuk menyelesaikan masalah program linier, baik yang melibatkan dua atau lebih dari dua variabel (Dimyati dan Dimyati, 1992).
Untuk dapat memahami uraian selanjutnya, berikut ini diberikan pengertian dari beberapa terminologi dasar yang banyak digunakan dalam membicarakan metode simpleks. Untuk itu, perhatikan model program linier berikut ini :
Fungsi tujuan : Maksimumkan atau minimumkan
Fungsi pembatas : . . . . . . . . dan Jika didefinisikan: n n mn m m n n b b b B x x x X a a a a a a a a a A . . ; . . ; ... . . . . . . . . ... ... 2 1 2 1 2 1 2 22 21 1 12 11
Maka pembatas dari model tersebut dapat dituliskan ke dalam bentuk sistem persamaan AX = B.
Definisi : 1. Solusi basis
Solusi basis untuk AX = B adalah solusi di mana terdapat sebanyak-banyaknya
m variabel berharga bukan nol. Untuk mendapatkan solusi basis dari AX = B
maka sebanyak (n – m) variabel harus dinolkan. Variabel-variabel yang dinolkan ini disebut variabel nonbasis. Selanjutnya, dapatkan harga dari n – (n
–m) = m variabel lainnya yang memenuhi AX = B, yang disebut variabel basis. 2. Solusi basis fisibel
Jika solusi variabel pada suatu solusi basis berharga nonnegatif, maka solusi itu disebut solusi basis fisibel.
3. Solusi fisibel titik ekstrim
Yang dimaksud dengan solusi fisibel titik ekstrem atau titik sudut ialah solusi fisibel yang tidak terletak pada suatu segmen garis yang menghubungkan dua solusi fisibel lainnya (Dimyati dan Dimyati, 1992).
Untuk menyelesaikan persoalan program linier maksimasi dengan menggunakan metode simpleks, lakukanlah langkah-langkah berikut :
1. Konversikan formulasi persoalan ke dalam bentuk standar. 2. Cari solusi basis fisibel.
3. Jika seluruh variabel nonbasis mempunyai koefisien nonnegatif (artinya berharga positif atau nol) pada baris fungsi tujuan [baris persamaan z yang biasa disebut baris nol atau baris (zj – cj)], maka solusi basis fisibel sudah optimal. Jika pada baris nol masih ada variabel dengan koefisien negatif, pilihlah salah satu variabel yang paling negatif pada baris nol itu. Variabel ini akan memasuki status variabel basis, karena itu variabel ini disebut sebagai variabel yang masuk basis atau entering variable.
3.3. Metode Cutting Plane
Metode cutting plane merupakan metode yang digunakan untuk menyelesaikan program linier bilangan bulat, baik bilangan bulat murni maupun campuran dengan penambahan batasan baru yang disebut gomory. Batasan gomory
diberikan jika nilai dari variabel keputusan belum bulat (bernilai pecahan). Batasan-batasan tersebut secara efektif akan menyingkirkan beberapa ruang penyelesaian yang tidak berisi titik bilangan bulat yang layak, tetapi tidak pernah menyingkirkan satupun titik bilangan bulat yang layak (Taha, 1996).
Metode cutting plane dikembangkan untuk menemukan jawaban optimal bagi program integer. Metode ini dilakukan dengan menambahkan suatu batasan yang dinamakan batasan gomory. Penambahan batasan gomory dilakukan pada tabel optimal sehingga dapat mempersingkat perhitungan (Siagian, 2006).
Metode cutting plane digunakan untuk permasalahan yang variabel keputusannya harus bulat. Program linier tidak efektif untuk menyelesaikan permasalahan tersebut sehingga dikembangkan metode cutting plane yang lebih efektif dan memberikan hasil yang lebih baik (Dimyati dan Dimyati, 1992).
Langkah-langkah prosedur gomory diringkas seperti berikut :
1. Selesaikan masalah program integer dengan menggunakan metode simpleks. Jika masalah sederhana, ia dapat diselesaikan dengan pendekatan grafik, sehingga pendekatan gomory kurang efisien.
2. Periksa solusi optimum. Jika semua variabel basis memiliki nilai integer, solusi optimum integer telah diperoleh dan proses solusi telah berakhir. Jika satu atau lebih variabel basis masih memiliki nilai pecah, teruskan ke tahap 3. 3. Buatlah suatu batasan gomory dan cari solusi optimum melalui prosedur dual
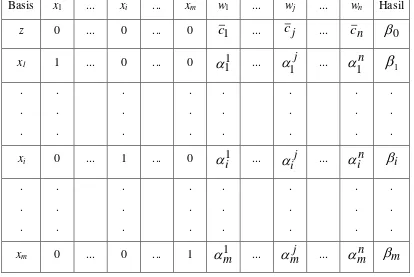
Tabel 3.1. Optimum Masalah Program Linier
Basis x1 ... xi ... xm w1 ... wj ... wn Hasil
z 0 ... 0 ... 0
c
1 ...c
j ...c
n
0x1 1 ... 0 ... 0
11 ... j1
... n1
1. . . . . . . . . . . . . . . . . . . . . . . .
xi 0 ... 1 ... 0
1i ... ji
... ni
i. . . . . . . . . . . . . . . . . . . . . . . .
xm 0 ... 0 ... 1
1m ...
mj ...
mn
mdimana :
Variabel xi (i = 1, …, m) adalah variabel basis. Variabel wj (j = 1, ..., n) adalah variabel nonbasis.
Tentukan baris sumber dengan menentukan baris variabel keputusan yang akan dibulatkan. Jika lebih dari satu, dipilih nilai pecahan terbesar.
j n j j i i i
w
x
1
,
i tidak integer (baris sumber)Anggaplah :
i i
i
[
]
f
ij j
i j
i
[
]
f
dimana : ]
[i adalah integer terbesar sehingga [i] i ]
[ij adalah integer terbesar sehingga [ ] j i
j
i
Disimpulkan bahwa 0 fi 1 dan 0 fij 1, yaitu fi dan fij adalah pecahan positif sehingga
j n j j i i i
w
x
1
j n j ij j i i ii
f
f
w
x
1)
]
([
]
[
j n j ij j n j j i i ii
f
w
f
w
x
1 1]
[
]
[
j n j j i i i j n j iji
f
w
x
w
f
1 1]
[
]
[
Agar semua variabel xi dan wj adalah integer, maka sisi kanan dari persamaan di atas haruslah integer yang berakibat sisi kiri juga harus integer. Dengan diketahui fij 0 dan wj 0 untuk semua i dan j dapat disimpulkan bahwa
0
1
j n j ijw
f
Akibatnya,1
1
j i
n
j ij
i
f
w
f
f
Karena
j n
j ij
i
f
w
f
1
haruslah integer berdasarkan pengembangannya, satu kondisi untuk memenuhi sifat integer ini menjadi :
0
1
j n j iji
f
w
f
0
1
j i
n
j ij
i
f
w
S
f
Batasannya dapat ditulis dalam bentuk :
n j i j iji
f
w
f
S
1
atau
nj ij j i
i
f
w
f
S
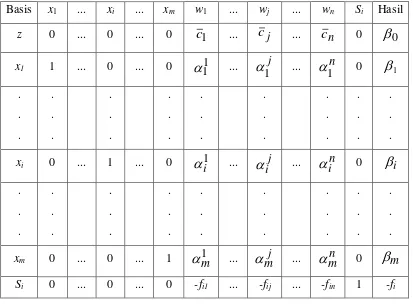
Tabel 3.2. Setelah Penambahan Pemotongan Fraksional
Basis x1 ... xi ... xm w1 ... wj ... wn Si Hasil
z 0 ... 0 ... 0
c
1 ...c
j ...c
n 0
0x1 1 ... 0 ... 0
11 ... j 1
... n1
0
1. . . . . . . . . . . . . . . . . . . . . . . . . . .
xi 0 ... 1 ... 0
1i ... ji
... ni
0
i. . . . . . . . . . . . . . . . . . . . . . . . . . .
xm 0 ... 0 ... 1
1m ...
mj ...
mn 0
mSi 0 ... 0 ... 0 -fi1 ... -fij ... -fin 1 -fi
Dimana Si adalah variabel slack nonnegatif yang berdasarkan definisinya haruslah integer. Persamaan batasan ini mendefinisikan pemotong fraksional. Dari tabel 3.2., wj = 0 dan Si= -fi tidak layak. Ini berarti bahwa batasan baru tersebut tidak dipenuhi oleh solusi yang diberikan. Metode dual simpleks dapat dipergunakan untuk mengatasi ketidaklayakan ini yang setara dengan memotong bidang solusi ke arah solusi integer optimal.
Metode cutting plane ini mempunyai dua kelemahan :
1. Kesalahan pembulatan yang muncul dalam perhitungan otomatis akan mendistorsi data semula terutama dengan bertambahnya ukuran masalah. 2. Solusi masalah tetap tidak layak, artinya tidak ada solusi integer yang dapat
diperoleh sampai solusi integer optimal dicapai. Ini berarti bahwa tidak ada solusi integer yang baik jika perhitungan dihentikan sebelum mencapai solusi integer yang optimal (Taha, 1996, Dimyati dan Dimyati, 1992).
Kelemahan pertama dapat diatasi dengan penggunaan integer murni. Metode ini dimulai dengan tabel awal yang semuanya terdiri dari integer yang sesuai dengan metode dual simpleks. Kemudian dilakukan penambahan gomory
sehingga penambahannya ke tabel akan mempertahankan sifat integer dari semua koefisien (Taha, 1996, Dimyati dan Dimyati, 1992).
Kelemahan kedua dapat menggunakan metode cutting plane yang dimulai dengan integer dan layak, tetapi tidak optimal. Iterasi yang berlanjut tetap layak dan integer sampai solusi optimum dicapai (Taha, 1996, Dimyati dan Dimyati, 1992).
3.4. Metode Dual Simpleks
Apabila pada suatu iterasi kita mendapat persoalan program linear yang sudah optimum (berdasarkan kondisi optimalitas), tetapi belum fisibel (ada pembatas nonnegatif yang tidak terpenuhi), maka persoalan tersebut harus diselesaikan dengan menggunakan metode dual simpleks. Syarat digunakannya metode ini adalah bahwa seluruh pembatas harus merupakan ketidaksamaan yang bertanda ( ), sedangkan fungsi tujuan bisa berupa maksimasi atau minimasi (Dimyati dan Dimyati, 1992).
1. Leaving variable (kondisi fisibilitas)
Yang menjadi leaving variable pada dual simpleks adalah variabel basis yang memiliki harga negatif terbesar. Jika semua variabel basis telah berharga positif atau nol, berarti keadaan fisibel telah tercapai.
2. Entering variable (kondisi optimalitas)
a. Tentukan rasio antara koefisien persamaan z dengan koefisien persamaan
leaving variable. Abaikan penyebut yang positif atau nol. Jika semua penyebut berharga positif atau nol, berarti persoalan yang bersangkutan tidak memiliki solusi fisibel.
BAB 4
PEMBAHASAN
4.1. Pengolahan Data
Pengolahan data dalam penelitian ini meliputi data biaya produksi, bahan baku yang tersedia, jumlah permintaan, ketersediaan tenaga kerja, dan kapasitas mesin untuk tahun 2012 pada PT. Budi Raya Perkasa. Harga 1 unit matras ukuran 80 x 200 cm (tipe A), 140 x 200 cm (tipe B), dan 200 x 200 cm (tipe C) berturut-turut adalah Rp. 809.000, Rp. 1.227.000, dan Rp. 1.656.000.
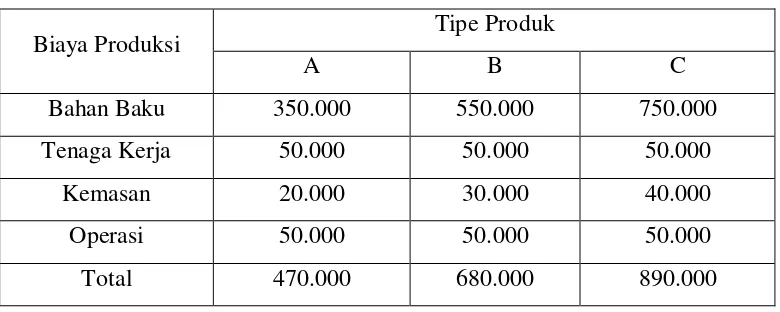
[image:30.595.118.508.474.630.2]Biaya produksi untuk menghasilkan 1 unit produk tipe A, B, dan C dalam satuan rupiah ditampilkan pada tabel 4.1.
Tabel 4.1.Biaya Produksi Matras Spring Bed
Biaya Produksi Tipe Produk
A B C
Bahan Baku 350.000 550.000 750.000
Tenaga Kerja 50.000 50.000 50.000
Kemasan 20.000 30.000 40.000
Operasi 50.000 50.000 50.000
Total 470.000 680.000 890.000
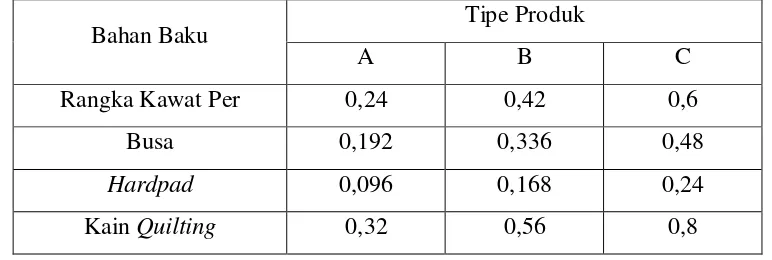
Tabel 4.2.Bahan Baku yang Dibutuhkan
Bahan Baku Tipe Produk
A B C
Rangka Kawat Per 0,24 0,42 0,6
Busa 0,192 0,336 0,48
Hardpad 0,096 0,168 0,24
Kain Quilting 0,32 0,56 0,8
dimana :
Tebal busa = 3 cm
Tinggi rangka kawat per = 15 cm
[image:31.595.202.425.417.530.2]Bahan baku matras spring bed tahun 2012 yang disediakan untuk menghasilkan 1 unit produk tipe A, B, dan C ditampilkan pada tabel 4.3.
Tabel 4.3.Persediaan Bahan Baku Matras Spring Bed Tahun 2012
Bahan Baku Persediaan
Rangka Kawat Per 206,4
Busa 170,5
Hardpad 100,5
Kain Quilting 300,25
Jumlah permintaan matras spring bed tahun 2012 untuk produk tipe A, B, dan C dalam satuan unit ditampilkan pada tabel 4.4.
Tabel 4.4.Jumlah Permintaan Matras Spring Bed Tahun 2012 Tipe Produk Permintaan
A 155
B 167
[image:31.595.202.421.629.717.2]Waktu produksi untuk menghasilkan 1 unit produk tipe A, B, dan C dalam satuan jam dengan ketersediaan tenaga kerja ditampilkan pada tabel 4.5. Waktu tenaga kerja adalah 40 jam seminggu dengan waktu kerja 50 minggu setahun dan jumlah tenaga kerja adalah 15 orang, maka waktu tenaga kerja adalah 50 x 40 x 15 = 30.000 jam.
Tabel 4.5.Waktu Produksi dengan Ketersediaan Tenaga Kerja Tahun 2012 Tipe Produk Waktu Produksi Waktu Tenaga Kerja
A 20
30.000
B 35
C 50
Waktu produksi untuk menghasilkan 1 unit produk tipe A, B, dan C dalam satuan jam dengan ketersediaan kapasitas mesin ditampilkan pada tabel 4.6. Waktu mesin adalah 40 jam seminggu dengan waktu kerja 50 minggu setahun dan jumlah mesin adalah 6 unit, maka waktu mesin adalah 50 x 40 x 6 = 12.000 jam.
Tabel 4.6.Waktu Produksi dengan Kapasitas Mesin Tahun 2012
Tipe Produk Waktu Produksi Waktu Mesin
A 10
12.000
B 17
C 25
Pada tahun 2012, PT. Budi Raya Perkasa menjual produk matras spring bed tipe A, B, dan C berturut-turut sebanyak 140, 152, dan 155.
4.2. Perumusan Fungsi Tujuan
Asumsikan :
[image:32.595.147.475.461.548.2]= Banyaknya tipe C yang diproduksi
Total biaya produksi 1 unit tipe A adalah Rp. 470.000. Total biaya produksi 1 unit tipe B adalah Rp. 680.000. Total biaya produksi 1 unit tipe C adalah Rp. 890.000.
Keuntungan yang diperoleh dari 1 unit produk adalah sebagai berikut : Tipe A adalah Rp. 809.000 – Rp. 470.000 = Rp. 339.000.
Tipe B adalah Rp. 1.227.000 – Rp. 680.000 = Rp. 547.000. Tipe C adalah Rp. 1.656.000 – Rp. 890.000 = Rp. 766.000.
Maka fungsi tujuan dapat dirumuskan sebagai berikut :
Maksimum :
atau x 1.000
4.3. Perumusan Fungsi Kendala
Fungsi kendala terdiri dari persediaan bahan baku, jumlah permintaan, ketersediaan tenaga kerja, dan kapasitas mesin.
1. Model fungsi kendala dari persediaan bahan baku.
Untuk memodelkan fungsi kendala, data yang digunakan adalah data dari tabel bahan baku yang dibutuhkan dan persediaan bahan baku matras spring bed tahun 2012 di atas sehingga dapat dirumuskan sebagai berikut :
Rangka kawat per :
Busa :
Kain quilting :
2. Model fungsi kendala dari jumlah permintaan.
Pada model ini, data yang digunakan adalah data diantara penjualan perusahaan dan data dari tabel jumlah permintaan matras spring bed tahun 2012 di atas sehingga dapat dirumuskan sebagai berikut :
Tipe A :
Tipe B :
Tipe C :
atau
Tipe A :
Tipe B :
Tipe C :
3. Model fungsi kendala dari ketersediaan tenaga kerja.
Untuk memodelkan fungsi kendala, data yang digunakan adalah data dari tabel waktu produksi dengan ketersediaan tenaga kerja tahun 2012 di atas dapat dirumuskan sebagai berikut :
4. Model fungsi kendala dari kapasitas mesin.
Pada model ini, data yang digunakan adalah data dari tabel waktu produksi dengan kapasitas mesin tahun 2012 di atas dapat dirumuskan sebagai berikut :
4.4. Analisis Metode Cutting Plane
Permasalahan di atas dapat diformulasikan ke dalam program integer dan dapat diselesaikan dengan metode cutting plane.
Dari permasalahan diperoleh :
Fungsi tujuan : Maksimum :
atau x 1.000
Fungsi kendala :
1. Kendala dari persediaan bahan baku.
2. Kendala dari jumlah permintaan.
3. Kendala dari ketersediaan tenaga kerja.
4. Kendala dari kapasitas mesin.
Bentuk standarnya menjadi :
Fungsi tujuan : Maksimum :
atau x 1.000
Fungsi kendala :
Proses pengerjaan dengan menggunakan metode cutting plane dari pembahasan permasalahan di atas dapat dilihat di lampiran 1 - lampiran 5 (halaman 30 - halaman 52).
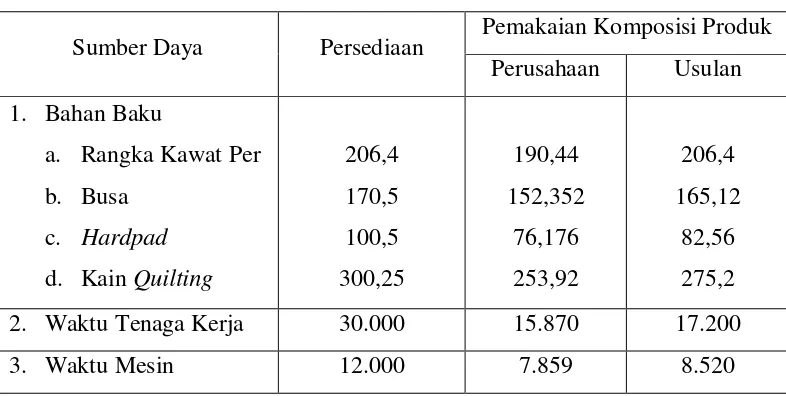
Tabel 4.7. Usulan Pemakaian Komposisi Produk Optimal
Sumber Daya Persediaan Pemakaian Komposisi Produk Perusahaan Usulan 1. Bahan Baku
a. Rangka Kawat Per b. Busa
c. Hardpad
d. Kain Quilting
206,4 170,5 100,5 300,25
190,44 152,352
76,176 253,92
206,4 165,12
82,56 275,2
2. Waktu Tenaga Kerja 30.000 15.870 17.200
3. Waktu Mesin 12.000 7.859 8.520
[image:37.595.112.512.104.297.2]Usulan jumlah produksi optimal dari penulis ditampilkan pada tabel 4.8.
Tabel 4.8. Usulan Jumlah Produksi Optimal
Produksi Permintaan
Pasar
Tipe Produk Perusahaan Usulan
A 140 155 155
B 152 160 167
C 155 170 170
Dari tabel di atas, dapat dilihat bahwa perusahaan belum dapat menentukan pemakaian komposisi produk secara optimal sehingga produk yang dihasilkan untuk masing-masing tipe belum optimal. Untuk itu, dibutuhkan usulan pemakaian komposisi produk yang optimal sehingga produk yang dihasilkan diharapkan optimal. Di samping itu, keuntungan yang akan diperoleh perusahaan diharapkan maksimal. Dengan demikian, tujuan utama perusahaan diharapkan tercapai.
menggunakan metode cutting plane dari permasalahan jumlah produksi yang optimal bagi PT. Budi Raya Perkasa dengan kendala bahan baku yang tersedia, jumlah permintaan, ketersediaan tenaga kerja, dan kapasitas mesin, yaitu tipe A, B, dan C berturut-turut adalah 155 unit, 160 unit, dan 170 unit dengan keuntungan Rp. 270.285 x 1.000 = Rp. 270.285.000. Jadi, selisih keuntungannya adalah Rp. 20.951.000.
Pembahasan masalah di atas tidak mempertimbangkan faktor ketidakpastian. Di samping itu, asumsi data setiap tahun sama sehingga tidak dapat digunakan sebagai acuan peramalan (forecasting).
Metode cutting plane diharapkan mampu mengoptimalkan jumlah produksi pada perusahaan tersebut. Selain itu, dalam pengerjaannya metode
cutting plane cukup efektif karena dapat mempersingkat perhitungan. Penambahan batasan gomory pada metode cutting plane secara efektif akan menyingkirkan beberapa ruang penyelesaian yang tidak berisi titik bilangan bulat yang layak, tetapi tidak pernah menyingkirkan satupun titik bilangan bulat yang layak. Dalam mencari solusi optimal integer secara manual, metode cutting plane
memerlukan waktu yang lebih efisien karena metode ini hanya fokus pada solusi yang masih bernilai pecahan.
BAB 5
KESIMPULAN DAN SARAN
5.1. Kesimpulan
Berdasarkan hasil olahan di atas dapat diambil beberapa kesimpulan sebagai berikut :
1. Penambahan batasan gomory pada metode cutting plane secara efektif akan menyingkirkan beberapa ruang penyelesaian yang tidak berisi titik bilangan bulat yang layak, tetapi tidak pernah menyingkirkan satupun titik bilangan bulat yang layak sehingga dapat mempersingkat perhitungan.
2. Pembahasan masalah tidak mempertimbangkan faktor ketidakpastian. Di samping itu, asumsi data setiap tahun sama sehingga tidak dapat digunakan sebagai acuan peramalan (forecasting).
3. Dari hasil analisis diperoleh jumlah produksi yang optimal bagi PT. Budi Raya Perkasa, yaitu matras ukuran 80 x 200 cm, 140 x 200 cm, dan 200 x 200 cm berturut-turut adalah 155 unit, 160 unit, dan 170 unit.
5.2. Saran
2. Pada penelitian ini, penulis menggunakan metode cutting plane. Metode
DAFTAR PUSTAKA
Assauri, S. 1999. Manajemen Produksi dan Operasi. FE UI. Jakarta.
Dimyati, T.T. dan Dimyati, A. 1992. Operations Research Model-Model Pengambilan Keputusan. Sinar Baru Algesindo. Bandung.
Gitosudarmo, I. 2002. Manajemen Operasi. BPFE. Yogyakarta.
Herjanto, E. 1997. Manajemen Produksi dan Operasi. Grasindo. Jakarta. Idahnaita, R.S. 2013. Ekonomi Mikro. IBBI. Medan.
Lusia, V. 1993. Penggunaan Program Bilangan Bulat (Integer Programming) dalam Perencanaan Produksi di PT. Djaya Beverages Bottling Company Jakarta. [Skripsi]. Bogor: Institut Pertanian Bogor, Program Sarjana. Siagian, P. 2006. Penelitian Operasional: Teori dan Praktek. Universitas Indonesia
(UI-Press). Jakarta.
Suparmoko, M. 1992. Ekonomika untuk Manajer. Ed ke-1. BPFE. Yogyakarta. Taha, H.A. 1996. Riset Operasi, Jilid I. Ed ke-5. Editor: Dr. Lyndon Saputra.
Binarupa Aksara. Jakarta.
Lampiran 1. Pembahasan Menggunakan Metode Dual Simpleks
Iterasi Awal Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12
w1 0 0,24 0,42 0,6 1 0 0 0 0 0 0 0 0 0 0 0 206,4
w2 0 0,192 0,336 0,48 0 1 0 0 0 0 0 0 0 0 0 0 170,5
w3 0 0,096 0,168 0,24 0 0 1 0 0 0 0 0 0 0 0 0 100,5
w4 0 0,32 0,56 0,8 0 0 0 1 0 0 0 0 0 0 0 0 300,25
w5 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 155
w6 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 167
w7 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 170
w8 0 -1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 -140
w9 0 0 -1 0 0 0 0 0 0 0 0 0 1 0 0 0 -152
w10 0 0 0 -1 0 0 0 0 0 0 0 0 0 1 0 0 -155
w11 0 20 35 50 0 0 0 0 0 0 0 0 0 0 1 0 30000
w12 0 10 17 25 0 0 0 0 0 0 0 0 0 0 0 1 12000
Zj – Cj -339 -547 -766 0 0 0 0 0 0 0 0 0 0 0 0 0
Keterangan :
1. Pada iterasi di atas, = -155 terpilih sebagai leaving variable
2.
3. Baris pivot adalah baris dikalikan -1
9. Baris yang baru : baris 10.Baris yang baru : baris Iterasi 1 Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12
w1 0 0,24 0,42 0 1 0 0 0 0 0 0 0 0 0,6 0 0 113,4
w2 0 0,192 0,336 0 0 1 0 0 0 0 0 0 0 0,48 0 0 96,1
w3 0 0,096 0,168 0 0 0 1 0 0 0 0 0 0 0,24 0 0 63,3
w4 0 0,32 0,56 0 0 0 0 1 0 0 0 0 0 0,8 0 0 176,25
w5 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 155
w6 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 167
w7 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 15
w8 0 -1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 -140
w9 0 0 -1 0 0 0 0 0 0 0 0 0 1 0 0 0 -152
x3 766 0 0 1 0 0 0 0 0 0 0 0 0 -1 0 0 155
w11 0 20 35 0 0 0 0 0 0 0 0 0 0 50 1 0 22250
w12 0 10 17 0 0 0 0 0 0 0 0 0 0 25 0 1 8125
Zj - Cj -339 -547 0 0 0 0 0 0 0 0 0 0 -766 0 0 118730
Keterangan :
1. Pada iterasi di atas, = -152 terpilih sebagai leaving variable
2.
3. Baris pivot adalah baris dikalikan -1
9. Baris yang baru : baris 10.Baris yang baru : baris Iterasi 2 Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12
w1 0 0,24 0 0 1 0 0 0 0 0 0 0 0,42 0,6 0 0 49,56
w2 0 0,192 0 0 0 1 0 0 0 0 0 0 0,336 0,48 0 0 45,028
w3 0 0,096 0 0 0 0 1 0 0 0 0 0 0,168 0,24 0 0 37,764
w4 0 0,32 0 0 0 0 0 1 0 0 0 0 0,56 0,8 0 0 91,13
w5 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 155
w6 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 15
w7 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 15
w8 0 -1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 -140
x2 547 0 1 0 0 0 0 0 0 0 0 0 -1 0 0 0 152
x3 766 0 0 1 0 0 0 0 0 0 0 0 0 -1 0 0 155
w11 0 20 0 0 0 0 0 0 0 0 0 0 35 50 1 0 16930
w12 0 10 0 0 0 0 0 0 0 0 0 0 17 25 0 1 5541
Zj - Cj -339 0 0 0 0 0 0 0 0 0 0 -547 -766 0 0 201874
Keterangan :
1. Pada iterasi di atas, = -140 terpilih sebagai leaving variable
2.
3. Baris pivot adalah baris dikalikan -1
9. Baris yang baru : baris 10.Baris yang baru : baris Iterasi 3 Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12
w1 0 0 0 0 1 0 0 0 0 0 0 0,24 0,42 0,6 0 0 15,96
w2 0 0 0 0 0 1 0 0 0 0 0 0,192 0,336 0,48 0 0 18,148
w3 0 0 0 0 0 0 1 0 0 0 0 0,096 0,168 0,24 0 0 24,324
w4 0 0 0 0 0 0 0 1 0 0 0 0,32 0,56 0,8 0 0 46,33
w5 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 15
w6 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 15
w7 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 15
x1 339 1 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 140
x2 547 0 1 0 0 0 0 0 0 0 0 0 -1 0 0 0 152
x3 766 0 0 1 0 0 0 0 0 0 0 0 0 -1 0 0 155
w11 0 0 0 0 0 0 0 0 0 0 0 20 35 50 1 0 14130
w12 0 0 0 0 0 0 0 0 0 0 0 10 17 25 0 1 4141
Zj - Cj 0 0 0 0 0 0 0 0 0 0 -339 -547 -766 0 0 249334
Keterangan :
1. Pada baris Zj– Cj : -766 paling minimum, maka masuk dalam basis
2.
3. Baris pivot adalah baris tetap
8. Baris yang baru : baris
9. Baris yang baru : baris 10.Baris yang baru : baris Iterasi 4 Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12
w1 0 0 0 0 1 0 0 0 0 0 -0,6 0,24 0,42 0 0 0 6,96
w2 0 0 0 0 0 1 0 0 0 0 -0,48 0,192 0,336 0 0 0 10,948
w3 0 0 0 0 0 0 1 0 0 0 -0,24 0,096 0,168 0 0 0 20,724
w4 0 0 0 0 0 0 0 1 0 0 -0,8 0,32 0,56 0 0 0 34,33
w5 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 15
w6 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 15
w10 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 15
x1 339 1 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 140
x2 547 0 1 0 0 0 0 0 0 0 0 0 -1 0 0 0 152
x3 766 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 170
w11 0 0 0 0 0 0 0 0 0 0 -50 20 35 0 1 0 13380
w12 0 0 0 0 0 0 0 0 0 0 -25 10 17 0 0 1 3766
Zj - Cj 0 0 0 0 0 0 0 0 0 766 -339 -547 0 0 0 260824
Keterangan :
1. Pada baris Zj– Cj : -547 paling minimum, maka masuk dalam basis
2.
3. Baris pivot adalah baris tetap
4. Baris yang baru : baris 5. Baris yang baru : baris
8. Baris yang baru : baris
9. Baris yang baru : baris 10.Baris yang baru : baris Iterasi 5 Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12
w1 0 0 0 0 1 0 0 0 0 -0,42 -0,6 0,24 0 0 0 0 0,66
w2 0 0 0 0 0 1 0 0 0 -0,336 -0,48 0,192 0 0 0 0 5,908
w3 0 0 0 0 0 0 1 0 0 -0,168 -0,24 0,096 0 0 0 0 18,204
w4 0 0 0 0 0 0 0 1 0 -0,56 -0,8 0,32 0 0 0 0 25,93
w5 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 15
w9 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 15
w10 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 15
x1 339 1 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 140
x2 547 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 167
x3 766 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 170
w11 0 0 0 0 0 0 0 0 0 -35 -50 20 0 0 1 0 12855
w12 0 0 0 0 0 0 0 0 0 -17 -25 10 0 0 0 1 3511
Zj - Cj 0 0 0 0 0 0 0 0 547 766 -339 0 0 0 0 269029
Keterangan :
1. Pada baris Zj– Cj : -339 paling minimum, maka masuk dalam basis
2.
3. Baris pivot adalah baris dikalikan
7. Baris yang baru : baris 8. Baris yang baru : baris
9. Baris yang baru : baris 10.Baris yang baru : baris Iterasi 6 Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12
w8 0 0 0 0 4,16667 0 0 0 0 -1,75 -2,5 1 0 0 0 0 2,75
w2 0 0 0 0 -0,8 1 0 0 0 0 0 0 0 0 0 0 5,38
w3 0 0 0 0 -0,4 0 1 0 0 0 0 0 0 0 0 0 17,94
w4 0 0 0 0 -1,3333 0 0 1 0 0 0 0 0 0 0 0 25,05
w5 0 0 0 0 -4,1667 0 0 0 1 1,75 2,5 0 0 0 0 0 12,25
w9 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 15
w10 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 15
x1 339 1 0 0 4,16667 0 0 0 0 -1,75 -2,5 0 0 0 0 0 142,75
x2 547 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 167
x3 766 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 170
w11 0 0 0 0 -83,333 0 0 0 0 0 0 0 0 0 1 0 12800
w12 0 0 0 0 -41,667 0 0 0 0 0,5 0 0 0 0 0 1 3483,5
Zj - Cj 0 0 0 1412,5 0 0 0 0 -46,25 -81,5 0 0 0 0 0 269961
Keterangan :
1. Pada baris Zj– Cj : -81,5 paling minimum, maka masuk dalam basis
2.
3. Baris pivot adalah baris dikalikan
6. Baris yang baru : baris 7. Baris yang baru : baris
Iterasi 7 Metode Dual Simpleks Solusi Optimal
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12
w8 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 15
w2 0 0 0 0 -0,8 1 0 0 0 0 0 0 0 0 0 0 5,38
w3 0 0 0 0 -0,4 0 1 0 0 0 0 0 0 0 0 0 17,94
w4 0 0 0 0 -1,3333 0 0 1 0 0 0 0 0 0 0 0 25,05
w7 0 0 0 0 -1,6667 0 0 0 0,4 0,7 1 0 0 0 0 0 4,9
w9 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 15
w10 0 0 0 0 1,66667 0 0 0 -0,4 -0,7 0 0 0 1 0 0 10,1
x1 339 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 155
x2 547 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 167
x3 766 0 0 1 1,66667 0 0 0 -0,4 -0,7 0 0 0 0 0 0 165,1
w11 0 0 0 0 -83,333 0 0 0 0 0 0 0 0 0 1 0 12800
w12 0 0 0 0 -41,667 0 0 0 0 0,5 0 0 0 0 0 1 3483,5
Zj - Cj 0 0 0 1276,67 0 0 0 32,6 10,8 0 0 0 0 0 0 270361
Karena baris dan kolom B 0, maka permasalahan telah optimal. Diperoleh .
Lampiran 2. Pembahasan Menggunakan Metode Cutting Plane
Pemilihan Gomory 1 Metode Cutting Plane
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12
w8 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 15
w2 0 0 0 0 -0,8 1 0 0 0 0 0 0 0 0 0 0 5,38
w3 0 0 0 0 -0,4 0 1 0 0 0 0 0 0 0 0 0 17,94
w4 0 0 0 0 -1,3333 0 0 1 0 0 0 0 0 0 0 0 25,05
w7 0 0 0 0 -1,6667 0 0 0 0,4 0,7 1 0 0 0 0 0 4,9
w9 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 15
w10 0 0 0 0 1,66667 0 0 0 -0,4 -0,7 0 0 0 1 0 0 10,1
x1 339 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 155
x2 547 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 167
x3 766 0 0 1 1,66667 0 0 0 -0,4 -0,7 0 0 0 0 0 0 165,1
w11 0 0 0 0 -83,333 0 0 0 0 0 0 0 0 0 1 0 12800
w12 0 0 0 0 -41,667 0 0 0 0 0,5 0 0 0 0 0 1 3483,5
Zj - Cj 0 0 0 1276,67 0 0 0 32,6 10,8 0 0 0 0 0 0 270361
Pada tabel optimal di atas dipilih sebagai batasan gomory, maka
n
j
i j ij
i f w f
S
1
Jadi, persamaan batasan gomory dari persamaan di atas adalah :
Penambahan Gomory 1 Metode Cutting Plane
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12 S1
w8 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 15
w2 0 0 0 0 -0,8 1 0 0 0 0 0 0 0 0 0 0 0 5,38
w3 0 0 0 0 -0,4 0 1 0 0 0 0 0 0 0 0 0 0 17,94
w4 0 0 0 0 -1,3333 0 0 1 0 0 0 0 0 0 0 0 0 25,05
w7 0 0 0 0 -1,6667 0 0 0 0,4 0,7 1 0 0 0 0 0 0 4,9
w9 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 15
w10 0 0 0 0 1,66667 0 0 0 -0,4 -0,7 0 0 0 1 0 0 0 10,1
x1 339 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 155
x2 547 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 167
x3 766 0 0 1 1,66667 0 0 0 -0,4 -0,7 0 0 0 0 0 0 0 165,1
w11 0 0 0 0 -83,333 0 0 0 0 0 0 0 0 0 1 0 0 12800
w12 0 0 0 0 -41,667 0 0 0 0 0,5 0 0 0 0 0 1 0 3483,5
S1 0 0 0 0 -0,66667 0 0 0 -0,6 -0,3 0 0 0 0 0 0 1 -0,1
Zj - Cj 0 0 0 1276,67 0 0 0 32,6 10,8 0 0 0 0 0 0 0 270361
Lampiran 3. Pembahasan Menggunakan Metode Dual Simpleks
Gomory 1 Iterasi Awal Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12 S1
w8 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 15
w2 0 0 0 0 -0,8 1 0 0 0 0 0 0 0 0 0 0 0 5,38
w3 0 0 0 0 -0,4 0 1 0 0 0 0 0 0 0 0 0 0 17,94
w4 0 0 0 0 -1,33333 0 0 1 0 0 0 0 0 0 0 0 0 25,05
w7 0 0 0 0 -1,66667 0 0 0 0,4 0,7 1 0 0 0 0 0 0 4,9
w9 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 15
w10 0 0 0 0 1,66667 0 0 0 -0,4 -0,7 0 0 0 1 0 0 0 10,1
x1 339 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 155
x2 547 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 167
x3 766 0 0 1 1,66667 0 0 0 -0,4 -0,7 0 0 0 0 0 0 0 165,1
w11 0 0 0 0 -83,3333 0 0 0 0 0 0 0 0 0 1 0 0 12800
w12 0 0 0 0 -41,6667 0 0 0 0 0,5 0 0 0 0 0 1 0 3483,5
S1 0 0 0 0 -0,66667 0 0 0 -0,6 -0,3 0 0 0 0 0 0 1 -0,1
Zj - Cj 0 0 0 1276,67 0 0 0 32,6 10,8 0 0 0 0 0 0 0 270361
Keterangan :
1. Pada iterasi di atas, = -0,1 terpilih sebagai leaving variable
2.
3. Baris pivot adalah baris dikalikan
7. Baris yang baru : baris 8. Baris yang baru : baris 9. Baris yang baru : baris 10.Baris yang baru : baris 11.Baris yang baru : baris
Gomory 1 Iterasi 1 Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12 S1
w8 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 15
w2 0 0 0 0 0 1 0 0 0,72 0,36 0 0 0 0 0 0 -1,2 5,5
w3 0 0 0 0 0 0 1 0 0,36 0,18 0 0 0 0 0 0 -0,6 18
w4 0 0 0 0 0 0 0 1 1,19999 0,6 0 0 0 0 0 0 -2 25,25
w7 0 0 0 0 0 0 0 0 1,9 1,45 1 0 0 0 0 0 -2,5 5,15
w9 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 15
w10 0 0 0 0 0 0 0 0 -1,9 -1,45 0 0 0 1 0 0 2,49999 9,85
x1 339 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 155
x2 547 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 167
x3 766 0 0 1 0 0 0 0 -1,9 -1,45 0 0 0 0 0 0 2,49999 164,85
w11 0 0 0 0 0 0 0 0 74,9996 37,4998 0 0 0 0 1 0 -125 12812,5
w12 0 0 0 0 0 0 0 0 37,4998 19,2499 0 0 0 0 0 1 -62,5 3489,75
w1 0 0 0 0 1 0 0 0 0,9 0,45 0 0 0 0 0 0 -1,5 0,15
Zj - Cj 0 0 0 0 0 0 0 -1116,4 -563,7 0 0 0 0 0 0 1914,99 270169
Keterangan :
1. Pada baris Zj– Cj : -1116,4 paling minimum, maka masuk dalam basis
2.
4. Baris yang baru : baris
5. Baris yang baru : baris 6. Baris yang baru : baris
7. Baris yang baru : baris 8. Baris yang baru : baris 9. Baris yang baru : baris 10.Baris yang baru : baris
11.Baris yang baru : baris
12.Baris yang baru : baris 13.Baris yang baru : baris
Gomory 1 Iterasi 2 Metode Dual Simpleks
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12 S1
w8 0 0 0 0 -1,11112 0 0 0 0 -0,5 0 1 0 0 0 0 1,66667 14,8333
w2 0 0 0 0 -0,8 1 0 0 0 0 0 0 0 0 0 0 0 5,38
w3 0 0 0 0 -0,4 0 1 0 0 0 0 0 0 0 0 0 0 17,94
w4 0 0 0 0 -1,33333 0 0 1 0 0 0 0 0 0 0 0 0 25,05
w7 0 0 0 0 -2,11112 0 0 0 0 0,5 1 0 0 0 0 0 0,66667 4,83333
w9 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 15
w10 0 0 0 0 2,11112 0 0 0 0 -0,5 0 0 0 1 0 0 -0,66667 10,1667
x1 339 1 0 0 -1,11112 0 0 0 0 -0,5 0 0 0 0 0 0 1,66667 154,833
x2 547 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 167
x3 766 0 0 1 2,11112 0 0 0 0 -0,5 0 0 0 0 0 0 -0,66667 165,167
w11 0 0 0 0 -83,3333 0 0 0 0 0 0 0 0 0 1 0 0 12800
w12 0 0 0 0 -41,6667 0 0 0 0 0,50002 0 0 0 0 0 1 0 3483,5
w5 0 0 0 0 1,11112 0 0 0 1 0,5 0 0 0 0 0 0 -1,66667 0,16667
Keterangan :
1. Pada baris Zj– Cj : -5,49828 paling minimum, maka masuk dalam basis
2.
3. Baris pivot adalah baris dikalikan
4. Baris yang baru : baris 5. Baris yang baru : baris 6. Baris yang baru : baris
7. Baris yang baru : baris 8. Baris yang baru : baris 9. Baris yang baru : baris
10.Baris yang baru : baris
Gomory 1 Iterasi 3 Metode Dual Simpleks Solusi Optimal
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12 S1
w8 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 15
w2 0 0 0 0 -0,8 1 0 0 0 0 0 0 0 0 0 0 0 5,3799994
w3 0 0 0 0 -0,4 0 1 0 0 0 0 0 0 0 0 0 0 17,94
w4 0 0 0 0 -1,33333 0 0 1 0 0 0 0 0 0 0 0 0 25,05
w7 0 0 0 0 -3,22224 0 0 0 -1 0 1 0 0 0 0 0 2,33334 4,6666659
w9 0 0 0 0 -2,22223 0 0 0 -2 0 0 0 1 0 0 0 3,33333 14,666667
w10 0 0 0 0 3,22224 0 0 0 1 0 0 0 0 1 0 0 -2,33334 10,333334
x1 339 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 155
x2 547 0 1 0 -2,22223 0 0 0 -2 0 0 0 0 0 0 0 3,33333 166,66667
x3 766 0 0 1 3,22224 0 0 0 1 0 0 0 0 0 0 0 -2,33334 165,33333
w11 0 0 0 0 -83,3333 0 0 0 0 0 0 0 0 0 1 0 0 12800
w12 0 0 0 0 -42,7778 0 0 0 -1 0 0 0 0 0 0 1 1,66674 3483,3333
w6 0 0 0 0 2,22223 0 0 0 2 1 0 0 0 0 0 0 -3,33333 0,3333333
Zj - Cj 0 0 0 1252,67 0 0 0 11 0 0 0 0 0 0 0 35,9943 270357
Lampiran 4. Pembahasan Menggunakan Metode Cutting Plane
Pemilihan Gomory 2 Metode Cutting Plane
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12 S1
w8 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 15
w2 0 0 0 0 -0,8 1 0 0 0 0 0 0 0 0 0 0 0 5,3799994
w3 0 0 0 0 -0,4 0 1 0 0 0 0 0 0 0 0 0 0 17,94
w4 0 0 0 0 -1,33333 0 0 1 0 0 0 0 0 0 0 0 0 25,05
w7 0 0 0 0 -3,22224 0 0 0 -1 0 1 0 0 0 0 0 2,33334 4,6666659
w9 0 0 0 0 -2,22223 0 0 0 -2 0 0 0 1 0 0 0 3,33333 14,666667
w10 0 0 0 0 3,22224 0 0 0 1 0 0 0 0 1 0 0 -2,33334 10,333334
x1 339 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 155
x2 547 0 1 0 -2,22223 0 0 0 -2 0 0 0 0 0 0 0 3,33333 166,66667
x3 766 0 0 1 3,22224 0 0 0 1 0 0 0 0 0 0 0 -2,33334 165,33333
w11 0 0 0 0 -83,3333 0 0 0 0 0 0 0 0 0 1 0 0 12800
w12 0 0 0 0 -42,7778 0 0 0 -1 0 0 0 0 0 0 1 1,66674 3483,3333
w6 0 0 0 0 2,22223 0 0 0 2 1 0 0 0 0 0 0 -3,33333 0,3333333
Zj - Cj 0 0 0 1252,67 0 0 0 11 0 0 0 0 0 0 0 35,9943 270357
Pada tabel optimal di atas dipilih sebagai batasan gomory, maka
n
j
i j ij
i f w f
S
1
Jadi, persamaan batasan gomory dari persamaan di atas adalah :
Penambahan Gomory 2 Metode Cutting Plane
Basis / C 339 547 766 0 0 0 0 0 0 0 0 0 0 0 0 0 0 B
x1 x2 x3 w1 w2 w3 w4 w5 w6 w7 w8 w9 w10 w11 w12 S1 S2
w8 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 15
w2 0 0 0 0 -0,8 1 0 0 0 0 0 0 0 0 0 0 0 0 5,3799994
w3 0 0 0 0 -0,4 0 1 0 0 0 0 0 0 0 0 0 0 0 17,94
w4 0 0 0 0 -1,33333 0 0 1 0 0 0 0 0 0 0 0 0 0 25,05
w7 0 0 0 0 -3,22224 0 0 0 -1 0 1 0 0 0 0 0 2,33334 0 4,6666659
w9 0 0 0 0 -2,22223 0 0 0 -2 0 0 0 1 0 0 0 3,33333 0 14,666667
w10 0 0 0 0 3,22224 0 0 0 1 0 0 0 0 1 0 0 -2,33334 0 10,333334
x1 339 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 155
x2 547 0 1 0 -2,22223 0 0 0 -2 0 0 0 0 0 0 0 3,33333 0 166,66667
x3 766 0 0 1 3,22224 0 0 0 1 0 0 0 0 0 0 0 -2,33334 0 165,33333
w11 0 0 0 0 -83,3333 0 0 0 0 0 0 0 0 0 1 0 0 0 12800