Elastoviscoplasticity with plastic strain memory
R. El Abdi, H. Samrout, G. Gambart
Laboratoire de Structures et de Mécanique Appliquée, I.U.T. de Rennes, Département G.M.P., 3, rue du Clos Courtel - B.P. 1144, 35014 Rennes Cedex, France
(Received 23 November 1998; revised and accepted 18 December 1998)
Abstract – An elastoviscoplastic three-dimensional model is proposed in order to predict the response of brake discs for a High Speed Train (T.G.V.),
which are subjected simultaneously to mechanical and thermal loadings. This elastoviscoplastic law is based on the internal thermodynamic variables and takes into account the non-linear kinematic and isotropic hardening with plastic strain memory effect. A metallurgical analysis shows no structural transformation in the material up to 600◦C.Elsevier, Paris
1. Introduction
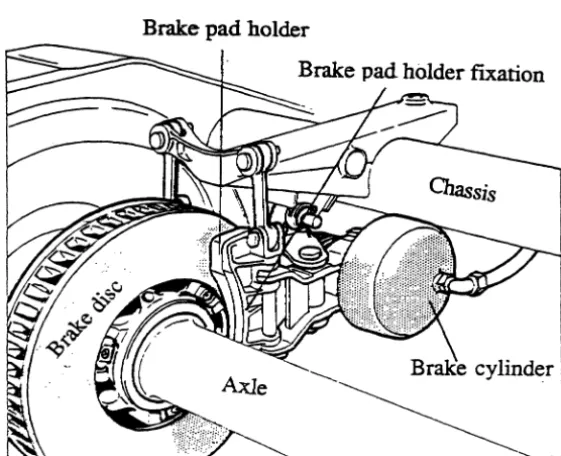
The brake discs of the High Speed Train (T.G.V.) used under cyclic loading due to the application of brake pads, are machined from cast or wrought steel. The brake pads are of an organic material which ensures the train speed reduction. The application of the brake pads lead to an heat flux which is assumed uniform on the friction area of the disc (figure 1).
Experimental studies of the steel used in the brake disc reveal a very complex behaviour under cyclic and monotonic loading. In addition to the classical Bauschinger effect and cyclic softening, a memory effect of the plastic strain is observed.
The present work uses a set of constitutive equations developed to describe as correctly as possible the main experimental results obtained under cyclic loading conditions at varying temperatures (Samrout et al., 1996a,b). The constitutive equations, developed at O.N.E.R.A. (Chaboche, 1989), assumes a decomposition of hardening into kinematic and isotropic parts, each obeying respective differential equations. The kinematic hardening is introduced in a non-linear form.
For the determination of the set of constitutive equation parameters, an optimization software developed by O.N.E.R.A. (Chaboche et al., 1991) was used.
2. Constitutive equations
The constitutive equations governing the elastoviscoplastic behaviour of complex structures under thermo-mechanical loading, must take into account complex phenomena such as viscoplasticity, cyclic softening or hardening, relaxation and strain memory effect. These phenomena have been studied by many scientists es-pecially in the recent years (Chaboche, 1978; Nouailhas, 1989; Kawai, 1987; Krempl, 1984; Marquis, 1987; Nouailhas, 1987a,b; Tanaka, 1987).
Figure 1. Brake disc with a brake pad assembly.
The general expression of this model is the following:
(every underlined mathematical variable(ξ )denotes a tensor) (a) Partition of strain
ε=εe+εp, (1)
whereεis the total strain tensor,εeis the elastic strain tensor andεpis the viscoplastic strain tensor. (b) Anisothermal elastic law
εe= 1+ν E(T )σ −
ν
E(T )Tr(σ )I+α(T )(T −T0)I , (2)
whereE(T )is the elastic modulus,νis the Poisson ratio, α(T )is the thermal expansion coefficient, T0is the reference temperature in◦C, σ is the stress tensor,I denotes the unit tensor and Tr(σ )=σ
kk in the Cartesian
component notation.
(c) Viscoplastic strain rate
˙
εp=
∂ ∂σ =
3 2p˙
σ′−X′
J (σ−X) where p˙=
J (σ−X)−R−k∗
K∗
n∗
. (3)
The brackets are defined byhwi =wH (w).H (w)is the Heaviside function(H (w)=0 ifw <0, H (w)=1 ifw>0)andis the viscoplastic potential.
J (σ−X)is defined by Von-Mises criterion:
J (σ−X)= 3
2 σ
′−
X′: σ′−X′
1/2
whereσ′andX′are respectively the deviatoric part of the stress tensorσ and of the kinematic hardening tensor
X, k∗is a material parameter (temperature dependent) corresponding to the initial size of the elastic domain.
K∗is the viscoplastic resistance,n∗is the rate sensitivity coefficient andRis the isotropic internal stress or the
drag stress.
Assuming viscoplastic incompressibility, we suppose the presence of an elastic domain in the stress space. Its evolution is described by:
f =J (σ−X)−R−k∗60. (5)
(d) The non-linear kinematic hardening
Widely used in France (Chaboche, 1977; Marquis, 1979;. . .), these kinematic equations were initially introduced by Armstrong and Frederick (1966). Non-linearities are given as a back stress term in the Prager’s rule:
X is the kinematic internal stress tensor or back stress tensor,c∗ is the kinematic parameter of the hardening anda∗is the stress saturation of the non-linear kinematic model. In practice, we use many kinematical variables (Chaboche et al., 1983). For our study we have chosen two variables:
X=X
(e) Plastic strain range memorization and isotropic hardening
That internal variables keep a memory of the prior maximum plastic strain range was proposed by Chaboche et al. (1979). The general formulation consists of introducing a non-hardening surface in the plastic strain space. The evolution of this surface is described by:
F =2
3J εp−ξ
−q60, (8)
whereqandξare respectively the radius and the center of this surface. Note that evolution of the non-hardening domain is allowed only whenF =0.
The selected evolution rule forq andξ is defined by:
˙
In Eq. (9)nandn1 are respectively the unit normals to the yield surface (f =0) and to the memory surface
(F =0)andη∗is a memory plastic strain parameter, introduced by Ohno (1982) in order to allow a progressive
memorization.
The isotropic hardening corresponds to slow changes during plastic flow. Its main role is to describe the cyclic softening. The simple isotropic rule can be written as:
dR=b∗(Q∗−R)dp withR(0)=0, (10)
experimental tests, two isotropic variables are introduced; one annotedR2for the fast decrease of stress in the first cycles, another variable annotedR1describing the slow evolution of stress during cycling until steady state is reached. The variablesR1andR2are defined by:
˙
R1=b∗(Q−R1)p˙; R˙2=bst∗(Qst∗−R2)p˙; R=R1+R2. (11)
In Eq. (11),Qst∗ represents the value ofR2 in the stabilized state andbst∗ represents the stabilization curve steepness for the isotropic hardeningR2.
The strain memory effect has been introduced by means of an additional internal variable which keeps a memory of the largest plastic strain range. The asymptotic isotropic stateQin Eq. (11) will therefore be:
˙
Q=2m∗ Q∗M−Q ˙
q, (12)
qis the internal variable corresponding to the radius of the memory surfaceF (see Eq. (8)).
Under tensile-compressive cycling,q=1εpmax/2, being the maximum plastic strain range.Q∗M andm
∗are
material and temperature dependent parameters.
Relation (12) is integrated and the saturation value of the hardening variableR1becomes:
Q=Q∗M.(1−exp(−m∗.1εp)). (13)
The use of this model (Eq. (1)–(13)) needs the determination of the parameters n∗, k∗, K∗, a∗
1, c∗1, a∗2, c∗2, b∗,
Qst∗, bst∗, η∗, m∗, and Q∗
M which depend on material and temperature. These parameters must minimize the
error between experimental curves and numerical curves deduced from the model.
3. On the parameters identification procedure
The material used in the brake disc is the 28CrMo V5-8 steel. On the basis of experimental results obtained at Ecole des Mines d’Albi Carmaux (Samrout et al., 1996a), cylindrical samples were submitted to uniaxial cyclic loadings (under tensile-compressive loadings) for several strain range 1%61ε61.8% at different temperatures 20◦C6T 6600◦C and a cyclic softening effect was observed.
In opposite to the three-axial loadings which are difficult to control, the uniaxial cyclic loadings allow determining all the model parameters and are easy to achieve and to explain.
The model deduced from the uniaxial test is sufficient for a good reproduction of the real three-dimensional behavior of the material (Chaboche, 1986; Ben Cheikh, 1987).
In order to identify the set of parameters at each temperature, we had to perform: − Monotonic relaxation test,
− Cyclic test run at several imposed strain ranges without holding time until rupture.
Table I gives the different experimental conditions.
The identification software Agice has a least squares method for the optimization of different parameters using the experimental results. Tables II and III give the different parameters at 300 and 500◦C. The unit of
material parametersk∗, a∗
Table I. Different experimental conditions used in the test sequence.
Table II. Material parameters for 28CrMo V5-8 steel at 300◦C.
k∗ a1∗ c∗1 a2∗ c∗2 b∗ bst∗ Qst∗ η∗ m∗ Q∗M n∗ K∗
201 272 2378 276 221 1.8 20 −40 0.2 338 −131 17 528
Table III. Material parameters for 28CrMo V5-8 steel at 500◦C.
k∗ a1∗ c∗1 a2∗ c∗2 b∗ bst∗ Qst∗ η∗ m∗ Q∗M n∗ K∗
162 162 2457 207 300 1.8 20 −40 0.2 399 −135 14 600
4. Introduction of the obtained constitutive equations into a Finite Element model
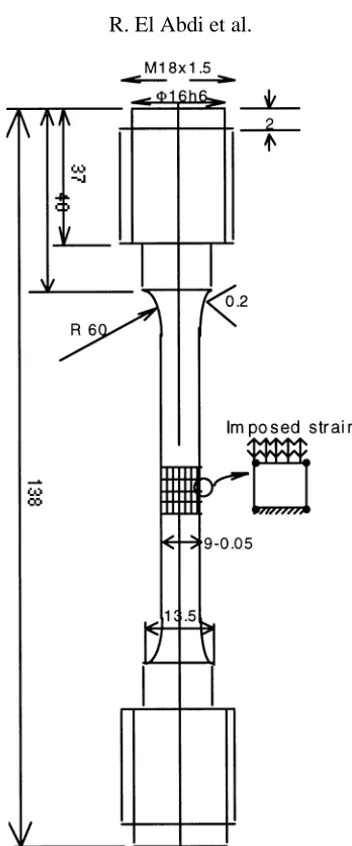
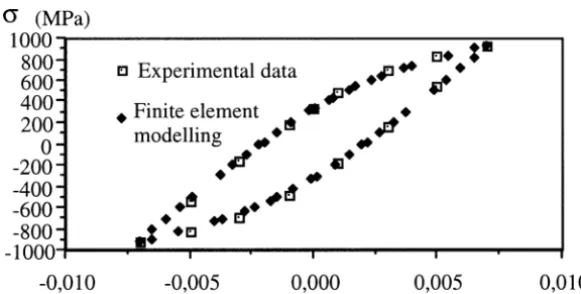
This section presents simulations of cyclic behaviour of 28CrMo V5-8 steel in different strain ranges. These parameters were introduced into a finite elements program Castem 2000. Figure 2 shows an axisymmetric version of this sample. Only one finite element was used for the simulation. This element in the middle of the sample was submitted to an imposed strain (figure 2). If1σ =σmaxi−σmini, figures 3 and 4 give a comparison
between experimental data and the finite element modelling for the strain range1ε=1.4% and1ε=1.8% when the temperature is at 20◦C.
Figure 5 gives the simulation curve for the relaxation test at the same temperature. Figure 6 shows the stabilized curve(σ−ε)for1ε=1.4% at 20◦C. In all cases, we have good agreement between the experimental data and the finite element modelling deduced from the proposed constitutive model.
5. Metallurgical analysis
(a) About the hypothesis of microstructural stability
The material in the railway brake discs is a resistant steel which has been submitted to thermal processing before its use. The austenising temperature of 975◦C was imposed over 5 hours. After this stage, the discs were submitted to a water quench. After quenched, the structure consists of martensite and residual austenite. Because of the high level of hardness of this structure, the brake discs were tempered in a furnace at 635◦C
for 9 hours before being air cooled. The final structure obtained is a tempered martensite which offers a better resistance to shattering. Table IV gives the chemical composition of 28CrMo V5-8 steel.
Figure 2. Axisymmetric view of the sample.
Figure 4. Comparison between experimental curve and finite element simulation for strain range1ε=1.8% at 20◦C.
Figure 5. Comparison between experimental data and numerical curve of the relaxation test at 20◦C (ε=4%).
– Preparation of the specimens
Etching polished metal surfaces with a chemical reagent is a means of differentiating the metal’s structural constituents when as is most often the case, they are not readily distinguishable. The usual practice for etching a polished surface is to immerse it in a cold etchant (Nital) for a required period time. The etching is then stopped by washing the specimen with water and drying it rapidly with hot air. This method gives clean metal surfaces which are generally free from all etching debris.
– Measuring the hardness
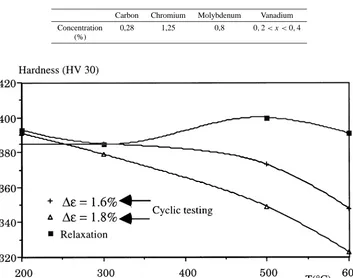
The Vickers hardness of the specimens was determined with a load of 30 daN. Various points of the measure taken on every specimen were distributed over the surface in order to obtain representative results. We note a hardness stability for the relaxation tests in the temperature field (figure 7). For the cyclic tests, the hardness stays stable until 300◦C whatever the imposed strain (figure 7). Above 500◦C we have declining hardness
which grows in speed when the strain increases. The reduction of this mechanical characteristic becomes more pronounced as we approach the tempering temperature.
(b) Analysis under an optical microscope
The object of the micrography is to reveal the internal structure of the alloy, which depends on its crystallography and its constitution. This is why an analysis under a light microscope is necessary for a polished and etched surface. We have observed inclusions in the material. Their locations are visible in the
Table IV. Chemical composition of 28CrMo V5-8 steel.
Carbon Chromium Molybdenum Vanadium
Concentration 0,28 1,25 0,8 0,2< x <0,4
(%)
Photo 1. Microstructure after relaxation test under 20◦C.
Photo 2. Microstructure after cyclical test at1ε=1.8% under 600◦C.
adjoining photos where a phenomenon has turned the surrounding structure black. The microstructure shows no appreciable change, even the one which was submitted to1ε=1.8% (see photos 1 and 2).
The observation of the microstructure shows the presence of martensite needles called acicular martensite. Although the martensite needles directions seem to be aleatory, we can observe a particular orientation inside every initial grain of the austenite (see (De Ferry, 1966)).
The decreasing hardness can be explained by a new coalescence of the precipitations in the matrix. As opposed to the microstructure, the decreasing hardness is the result of the influence of the temperature and the imposed strain during the cyclic tests as shown in figure 7. Therefore, during the cyclic loading, the hardness slowly decreases as the test temperature increases up to 500◦C (as does the mechanical toughness). This decreasing tendency becomes considerably more pronounced above 500◦C.
However, the hypothesis of microstructural stability of the material stays valid as far as 600◦C.
6. Conclusion
This paper presents an elastoviscoplastic three-dimensional model for the steel 28CrMo V5-8. The emphasis is put on the incorporation of strain memory terms and the use of two isotropic hardening variables in order to better simulate the behaviour of materials such 28CrMo V5-8 steel used in the brake discs of the High Speed Train (T.G.V.).
Mention is not made of the difficulties in chosing the initial values for every parameter. The numerical method introduced in the software Agice is based on an integration complex scheme for the resolution of the implicit differential equations.
The determination of the various parameters is based on the experimental results which include some measurement errors. There is no uniqueness of the values of material parameters. However, the obtained parameters approach as well as can be expected, those in the experimental curves. These parameters have a stationary aspect; a small perturbation do not alter the final results.
A metallurgical analysis shows no structural transformation in the material below 600◦C. Beyond 635◦C
which is the steel’s tempering temperature, structural transformations must be included in the model.
Under a complex and repeated loading from the pressure of the brake pads on the friction surface, the brake disc suffer damage. In addition, we must determine the friction effects and the exchange coefficients between the brake disc and the brake pads. Before a good numerical modelization of the brake disc is achieved, we must therefore couple the proposed anisothermal model with a damage law and also introduce the suitable exchange coefficients. This is what we shall do in our subsequent work.
Acknowledgments
This work uses an optimization software Agice developed by the “Office National d’Etudes et de Recherche Aérospatiales (Chatillon, France)” and the co-operation of this office is gratefully acknowledged.
References
Armstrong, P.J., Frederick, C.O., 1966. A mathematical representation of the multiaxial Bauschinger effect. G.E.G.B. Report RD/B/N 731. Ben Cheikh, A., 1987. Elastoviscoplasticité à température variable. Thèse de Doctorat, Université de Paris-VI.
Chaboche, J.L., 1989. Lois de comportement en plasticité cyclique et en viscoplasticité cyclique. Int. J. of Plasticity 5 (3), 247–302.
Chaboche, J.L., Nouailhas, D., Savalle, S., 1991. Agice: Logiciel pour 1’identification interactive graphique des lois de comportement. La Recherche Aérospatiale 3, Mai–Juin, 59–76.
Chaboche, J.L., 1978. Description thermodynamique et phénoménologique de la viscoplasticité cyclique avec endommagement. Thèse de Doctorat d’Etat, Université Paris 6.
Chaboche, J.L., 1977. Viscoplastic constitutive equations for the description of cyclic and anisotropic behaviour of metals. In: 17th Polish Conf. on Mechanics of Solids, Szczyrk. Bull. de 1’Acad. Polonaise des Sciences, Séries Sc. et Techn. 25, p. 33.
Chaboche, J.L., Dang, V., Cordier, G., 1979. Proc. of SMIRT 5. Division L., Berlin.
Chaboche, J.L., 1986. EVPCYCL: Un code d’éléments finis en viscoplasticité cyclique. La Recherche Aérospatiale 2, Mars-Avril, 91–112. De Ferry, 1966. Metallographia – Tome II and V. Presses Académiques Européennes S.C., Bruxelles.
Kawai, M., Ohashi, Y., 1987. Coupled effect between creep and plasticity of type 316 stainless steel at elevated temperature. In: Desai et al. (Eds), 2nd Int. Conf. on Constitutive laws for Engineering Materials: Theory and Applications, Tucson, Arizona, Elsevier.
Krempl, E., Yao, D., 1984. The viscoplasticity theory based on overstress applied to ratchetting and cyclic hardening. In: 2nd Int. Conf. on Low-Cycle Fatigue and Elasto-Plastic Behaviour of Materials, Munich.
Marquis, D., Lemaitre, J., 1987. Modelling elasto-plasticity, damage and aging as coupled behaviour in engineering materials. In: Int. Colloquium on Mechanisms and Mechanics of Plasticity, Aussois, France.
Marquis, D., 1979. Sur un modèle de plasticité rendant compte du comportement cyclique. In: 3èmeCongrès Français de Mécanique, Nancy. Nouailhas, D., 1989. Unified modelling of cyclic viscoplasticity. Application to austenitic stainless steels. Int. J. of Plasticity. 5, 501–520. Nouailhas, D., 1987a. A viscoplastic modelling applied to stainless steel behaviour. In: Desai et al. (Eds), 2nd Int. Conf. on Constitutive Laws for Engineering Materials: Theory and Applications, Tucson, Arizona, Elsevier.
Nouailhas, D., 1987b. Modélisation de 1’écrouissage et de la restauration en viscoplasticité cyclique. In: Int. Colloquium on Mechanisms and Mechanics of Plasticity, Aussois, France.
Ohno, N., 1982. A constitutive model of cyclic plasticity with a non-hardening strain region. J. Appl. Mech. 49, 721.
Samrout, H., El Abdi, R., Levaillant, C., Delagnes, D., 1996a. Optimisation des paramètres de la loi de comportement d’un acier de disque de freins pour matériel ferroviaire. In: First International Conference on Integrated Design and Manufacturing in Mechanical Engineering, Nantes, Avril, pp. 937–946.
Samrout, H., El Abdi, R., Levaillant, C., Delagnes, D., Tico, B., 1996b. Un modèle viscoplastique anisotherme d’un acier de disques de frein pour matériel ferroviaire. Centre International de 1’Automobile, STRUCOME96, October, Pantin.