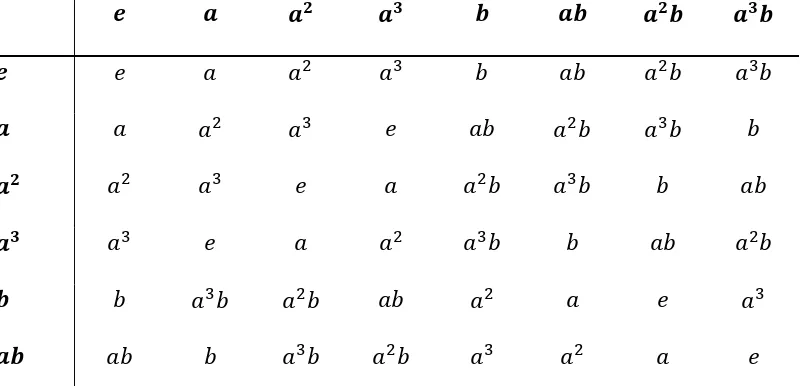DIGRAFF CAYLEYY DARI GRRUP
Skripssi
PRO
Di
OGRAM ST FA
iajukan untu Mempe
Prog
Rosa
TUDI MAT AKULTAS
UNIVERS Y
uk Memenuuhi Salah Saatu Syarat roleh Gelarr Sarjana Saains gram Studi MMatematikaa
Oleh:
alia Gustari Eksi Utamii NIM: 053114007
TEMATIKKA JURUSAAN MATEEMATIKA S SAINS DAAN TEKNOLOGI
SITAS SANNATA DHAARMA YOGYAKAARTA
MATHE
Presen
EMATICS S SCI
nted as Parti To Obtai Rosa Stude STUDY PR ENCE AN SANATA Y ii ial Fulfillm n the Sarjan
In Mathem By: alia Gustari ent Number: ROGRAM D TECHN DHARMA YOGYAKA 2009
ent of the RRequirementts na Sains Deegree
matics
Eksi Utamii : 0531140077
MATHEMMATICS DEEPARTMEENT NOLOGY FFACULTY
A UNIVERRSITY ARTA
HALAMAN PERSEMBAHAN
Skripsi ini penulis persembahkan kepada: Yesus Kristus & Bunda Maria (Pegangan hidup penulis dalam setiap langkah),
Yohanes Chrisostomus Pramonco Hardioto & Elisabet Sri Rahayu (Orang tua penulis),
Keluarga Besar Program Studi Matematika Universitas Sanata Dharma (Khususnya mahasiswa angkatan 2005),
Albertus Aditya Budi Nugroho (Gembulz),
Semua Pihak yang telah membantu terbentuknya skripsi ini.
vii
ABSTRAK
Digraf Cayley dari grup adalah gambaran grafis dari suatu grup yang diberikan oleh himpunan pembangkitnya. Digraf ini menyediakan metode untuk menggambarkan suatu grup, dan menghubungkan dua cabang penting dari matematika modern yaitu grup dan graf. Digraf Cayley dari grup digunakan untuk melihat orde dari beberapa elemen grup dan untuk menentukan nilai dari sebarang hasil kali dari pembangkit atau inversnya.
viii
given by a set of generators. These digraphs provide a method of visualizing a group, and connect two important branches of modern mathematics, i. e. groups and graphs. The Cayley digraphs of groups are used to see the order of some elements of a group and to determine the value of any product of the generators or their inverses.
x
penulis dapat menyelesaikan skripsi ini. Skripsi ini ditulis untuk memenuhi salah satu syarat memperoleh gelar sarjana sains Program Studi Matematika.
Selama penulisan skripsi ini penulis menyadari bahwa banyak pihak yang telah berperan besar dalam memberikan dukungan, bimbingan, maupun kerjasa-manya. Oleh karena itu, penulis mengucapkan banyak terima kasih kepada:
1. Ibu M. V. Any Herawati, S.Si., M.Si., selaku dosen pembimbing skripsi yang telah membimbing dan mendampingi penulis selama penulisan skripsi ini.
2. Bapak Yosef Agung Cahyanta, S.T., M.T., selaku Dekan Fakultas Sains dan Teknologi.
3. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku Ketua Program Studi Matematika dan dosen penguji yang telah memberikan koreksi dan saran kepada penulis.
4. Romo Prof. Dr. Frans Susilo, SJ, selaku Dosen Pembimbing Akademik dan dosen penguji yang telah memberikan koreksi dan saran kepada penulis. 5. Bapak Z. Tukija dan Ibu Erma Linda S. R. yang telah banyak membantu
dalam proses administrasi.
6. Perpustakaan Paingan Universitas Sanata Dharma dan seluruh karyawannya yang telah banyak membantu dalam penyediaan bahan dan fasilitas selama penulisan skripsi ini.
7. Bapak Y. C. Pramonco H. dan Ibu E. Sri Rahayu, selaku orang tua penulis yang selalu mendukung penulis.
8. Teman-teman mahasiswa angkatan 2005 Program Studi Matematika.
xi
Penulis berharap semoga skripsi ini dapat memberikan manfaat bagi se-mua orang yang membacanya. Apabila terdapat kesalahan penulisan dan ucapan, penulis mohon maaf yang sebesar-besarnya.
DAFTAR ISI
Halaman
HALAMAN JUDUL ……….. i
HALAMAN JUDUL DALAM BAHASA INGGRIS …...……….…… ii
HALAMAN PERSETUJUAN PEMBIMBING ………. iii
HALAMAN PENGESAHAN ………...………. iv
HALAMAN PERSEMBAHAN ………. v
PERNYATAAN KEASLIAN KARYA ………. vi
ABSTRAK ……….………… vii
ABSTRACT ………...…… viii
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ……….….. ix
KATA PENGANTAR ……… x
DAFTAR ISI ……….. xii
DAFTAR TABEL ……….. xiv
DAFTAR GAMBAR ……….………..……….…. xv
BAB I PENDAHULUAN ……….………...……..… 1
A. 1 B. Rumusan Masalah ……….………...………... 3
Latar Belakang Masalah ……….………. Batasan Masalah ……….…………...……...….. Manfaat Penulisan ………...… Sistematika Penulisan ……….……...……. Teori Grup ……….………...…. 2. Grup Berhingga dan Subgrup ……….……….…….… 4. Grup Siklik dan Pembangkit ……….…….……….…. 12
C. 3 D. Tujuan Penulisan ……….……...…………. 4
E. 4 F. Metode Penulisan ……….... 4
G. 5 BAB II TEORI GRUP DAN TEORI GRAF ………...….. 7
A. 7 1. Grup ………..………...……. 7
10 3. Darab Langsung ………...….…………...…. 12
xiii
5. Grup Permutasi …………..……….………...….
8. Homomorfisma dan Isomorfisma ……….
Graf Berarah Atau Digraf ……….………...….…
RAF CAYLEY DARI GRUP ………...………
tasan dan Sirkuit Hamilton Dalam Digraf Cayley dari Grup ….... BAB VI AP
AFIK KOMPUTER DARI POLA PERULANGAN TIPE
tode Escher ………
UTUP ……….……….……...…
an ………..………
DAFTAR PUSTAKA ………...…………. 19 6. Grup Dihedral ……...……….……….…….. 26 7. Koset, Teorema Lagrange, Subgrup Normal, dan Grup Faktor ... 30 35 B. Teori Graf ……….……...…….... 37
1. 37
2. Lintasan dan Sirkuit Hamilton ……….…...…...…….. 39
BAB III DIG 43
A. Digraf Cayley dari Grup ……….……. 43
B. Lin 52
LIKASI DIGRAF CAYLEY DARI GRUP UNTUK MEMBUAT GR
ESCHER PADA BIDANG HIPERBOLIK …….………. 63
A. Me ……. 63
B. Metode Douglas Dunham ……….………... 67
BAB V PEN …… 74
A. Kesimpulan ……….…...….……. 74
B. Sar .……. 75
DAFTAR TABEL
Halaman
Tabel 2. 1 Beberapa Contoh Grup ………... 9
Tabel 2. 2 Tabel Operasi untuk ……….…………...… 18
Tabel 2. 3 Tabel Operasi untuk ……….……….………....… 24
Tabel 2. 4 Grup Selang-seling untuk Permutasi Genap dari {1, 2, 3, 4} ... 26
Tabel 2. 5 Tabel Operasi untuk ……….……… 29
DAFTAR GAMBAR
Halaman
Gambar 2. 1 Graf G ………... 38
Gambar 2. 2 Graf Berarah G ……….……… 39
Gambar 2. 3 Graf Sederhana yang Memuat Lintasan dan Sirkuit ……..….…. 40
Gambar 2. 4 Salah Satu Penyelesaian Teka-Teki “Perjalanan Keliling Dunia” ………...……… 42
Gambar 2. 5 Graf Sederhana G1, G2, dan G3 ………. 42
Gambar 3. 1 Digraf Cay({1}: ) ……….…… 45
, Gambar 3. 6 Digraf Cay({(12)(34), (123)}: ) ………..………...… 49
Da 53 Gambar 3. 10 ), dan (a, 0), ( 1)}: …… , 1)}: Gambar 3. 15 Digraf Cay({(r, 0), (f, 0), (e, 1)}: ) ………….…….…. 62
Poincare pada Bida 65 Gambar 4. 3 Gambar 3. 2 Digraf Cay({(1, 0), (0, 1)}: ) ………..………….. 46
Gambar 3. 3 Digraf Cay( : ) ………...……… 47
Gambar 3. 4 Digraf Cay({(12), (123)}: ) ……… 48
Gambar 3. 5 Digraf Cay({(12), (13)}: ) ……….………. 48
Gambar 3. 7 Digraf Cay({a, b}: ) ………...…….……… 50
Gambar 3. 8 Digraf Cay({a, b}: ) ………...……… 51
Gambar 3. 9 Lintasan Hamilton lam Digraf Cay({(1, 0), (0, 1)}: ) dari (0, 0) ke (2, 1) ………...………..….. Sirkuit Hamilton Dalam Digraf Cay({a, b}: ) ………...…..…. 53
Gambar 3. 11 Digraf Cay({(1, 0), (0, 1)}: ) …………...………. 55
Gambar 3. 12 Simpul (a, b), ( 1, 1 1) ……….. 55
Gambar 3. 13 Digraf Cay({(1, 0, ) ……...………. 57
Gambar 3. 14 Digraf Cay({(r, 0), (f, 0), (e ) ……...………. 61
Gambar 4. 1 Teselasi Segitiga Dalam Model Cakram ng Hiperbolik ……….……… 64
Gambar 4. 2 Cetakan Asli Circle Limit I Milik Escher ……… Terjemahan Komputer dari Desain Dalam Cetakan Circle Limit I Milik Escher ………. 66
Gambar 4. 4 Graf Cayley dari Grup [6, 4] dengan Lintasan Hamilton ….…… 69
xvi
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Dunia matematika memiliki berbagai macam cabang di dalamnya. Dari berbagai macam cabang tersebut, di antaranya adalah aljabar abstrak dan matematika diskret. Aljabar abstrak dan matematika diskret mempelajari topik-topik yang berbeda. Dalam aljabar abstrak dibahas mengenai grup, ring, lapangan, beserta sifat-sifatnya. Sedangkan dalam matematika diskret dibahas mengenai relasi, graf, aljabar Boole, dan kombinatorik. Di antara topik-topik tersebut terdapat dua topik yang cukup menarik, yaitu grup dan graf.
Ketika membicarakan tentang aljabar abstrak atau struktur aljabar, hal pertama yang muncul adalah grup. Grup menjadi topik yang sangat penting dalam aljabar abstrak karena topik ini dibahas pertama kali dalam banyak buku aljabar abstrak. Grup dan sifat-sifatnya juga mendasari topik-topik yang dibahas selanjutnya dalam aljabar abstrak, seperti ring dan lapangan. Begitu juga dalam digraf Cayley dari grup, grup menjadi topik yang sangat penting karena akan dibentuk penggambaran dari suatu grup dengan menggunakan himpunan pembangkitnya.
Salah satu topik yang dibahas dalam teori graf dan digunakan dalam digraf Cayley dari grup yaitu graf berarah atau digraf. Graf berarah atau digraf merupakan himpunan berhingga dari titik-titik, yang disebut vertex atau simpul,
dan himpunan busur berpanah, yang disebut arc atau busur, yang menghubungkan beberapa vertex atau simpul. Digraf dapat digunakan untuk menyatakan relasi antara unsur-unsurnya (simpul dan busur). Digraf memiliki peranan yang sangat penting dalam digraf Cayley dari grup karena menjadi bentuk penggambaran dari suatu grup.
Grup dan graf adalah dua cabang penting dalam matematika modern. Antara grup dan graf dihubungkan dalam satu topik yaitu digraf Cayley dari grup. Gagasan ini mula-mula didapatkan oleh seorang matematikawan bernama Arthur Cayley pada tahun 1878. Digraf Cayley dari grup merupakan gambaran grafis dari suatu grup yang diberikan oleh himpunan pembangkitnya. Sebenarnya digraf Cayley dari grup merupakan topik yang sangat menarik tetapi tidak semua buku aljabar memuat topik ini. Digraf Cayley dari grup menyediakan metode untuk menggambarkan suatu grup sehingga grup dapat lebih mudah dipahami karena adanya gambaran nyata berupa digraf.
Misalkan G adalah grup berhingga dan S adalah himpunan pembangkit untuk G. Digraf Cayley dari grup G dengan himpunan pembangkit S, yang dinotasikan dengan Cay(S:G), dapat didefinisikan sebagai berikut.
1. Setiap elemen dari G adalah simpul dari Cay(S:G).
2. Untuk x dan y di G, terdapat sebuah busur dari x ke y jika dan hanya jika xs = y untuk suatu s S.
Digraf Cayley dari grup melibatkan dua teori penting, yaitu teori grup dan teori graf. Beberapa pokok bahasan dalam teori grup yang berhubungan dengan topik ini antara lain grup siklik dan pembangkit, grup permutasi, grup
3
dihedral, darab langsung. Sedangkan beberapa pokok bahasan dalam teori graf yang berhubungan dengan topik ini antara lain graf berarah atau digraf, lintasan dan sirkuit Hamilton. Pembahasan mengenai lintasan dan sirkuit Hamilton berhubungan dengan syarat perlu dan syarat cukup sangat penting dalam membahas digraf Cayley dari grup. Lintasan dan sirkuit Hamilton akan digunakan dalam pengaplikasian digraf Cayley dari grup.
B. Rumusan Masalah
Pokok permasalahan yang akan dibahas dalam skripsi ini antara lain: 1. Apakah yang dimaksud dengan digraf Cayley dari grup?
2. Apa saja landasan teori yang dibutuhkan untuk membentuk digraf Cayley dari suatu grup?
3. Bagaimana membentuk digraf Cayley dari suatu grup? 4. Bagaimana aplikasi digraf Cayley dari grup?
C. Batasan Masalah
Batasan masalah dalam skripsi ini antara lain:
1. Membahas mengenai digraf Cayley yang terbentuk dari suatu grup. 2. Membahas aplikasinya, yaitu untuk membuat grafik komputer dari
pola perulangan tipe Escher pada bidang hiperbolik, tetapi tidak menyertakan algoritmanya.
D. Tujuan Penulisan
Skripsi ini bertujuan untuk memenuhi salah satu persyaratan untuk memperoleh gelar Sarjana Sains dalam bidang matematika. Selain itu, tujuan dari penulisan skripsi ini adalah:
1. Mempelajari tentang pembentukan digraf Cayley dari suatu grup. 2. Mengetahui aplikasi digraf Cayley dari grup.
E. Manfaat Penulisan
Manfaat yang diharapkan dari penulisan skripsi ini adalah:
1. Dapat memahami mengenai pembentukan digraf Cayley dari suatu grup.
2. Dapat mengetahui tentang aplikasi digraf Cayley dari grup.
F. Metode Penulisan
Penulisan skripsi ini menggunakan metode studi pustaka, yaitu dengan menggunakan buku-buku, jurnal-jurnal, dan makalah-makalah yang telah dipublikasikan dalam media cetak maupun internet sehingga dalam skripsi ini tidak ditemukan hal baru.
5
G. Sistematika Penulisan
BAB I PENDAHULUAN
A. Latar Belakang Masalah B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan
BAB II TEORI GRUP DAN TEORI GRAF A. Teori Grup
1. Grup
2. Grup Berhingga dan Subgrup 3. Darab Langsung
4. Grup Siklik dan Pembangkit 5. Grup Permutasi
6. Grup Dihedral
7. Koset, Teorema Lagrange, Subgrup Normal, dan Grup Faktor
8. Homomorfisma dan Isomorfisma B. Teori Graf
1. Graf Berarah Atau Digraf 2. Lintasan dan Sirkuit Hamilton
BAB III DIGRAF CAYLEY DARI GRUP A. Digraf Cayley dari Grup
B. Lintasan dan Sirkuit Hamilton Dalam Digraf Cayley dari Grup
BAB IV APLIKASI DIGRAF CAYLEY DARI GRUP UNTUK MEMBUAT GRAFIK KOMPUTER DARI POLA PERULANGAN TIPE ESCHER PADA BIDANG HIPERBOLIK
A. Metode Escher
B. Metode Douglas Dunham
BAB II
TEORI GRUP DAN TEORI GRAF
A. Teori Grup
1. Grup
Definisi 2. 1
Misalkan G adalah himpunan. Operasi biner pada G adalah fungsi yang
mengawankan setiap pasangan terurut elemen-elemen di G dengan suatu elemen
di G.
Dengan kata lain, operasi biner pada himpunan S adalah suatu
pemetaan dari ke S. Untuk setiap di , elemen dari S
dinotasikan dengan . Operasi biner memasangkan sebarang a dan b
elemen-elemen dari S dengan elemen dari S. Dengan demikian, dapat
dikatakan bahwa operasi adalah operasi biner pada S jika operasi tersebut
, ,
tertutup dalam S, yaitu adalah elemen dari S.
Contoh 2. 1
Misalkan dan · adalah operasi biner biasa dari penjumlahan dan perkalian
dalam , dan misalkan | . Tentukan apakah H tertutup terhadap
(a) penjumlahan dan (b) perkalian.
Untuk bagian (a), hanya dibutuhkan pengamatan bahwa 1 dan
di H, tetapi bahwa 1 4 dan 5 . Sehingga H tidak tertutup
terhadap penjumlahan.
1
2 4 5
bahwa , sehingga H tertutup terhadap perkalian.
Definisi 2. 2
Misalkan G adalah himpunan tak kosong bersama dengan operasi biner (biasa
disebut perkalian) yang mengawankan ke setiap pasangan terurut ,
elemen-elemen di G dengan suatu elemen di G dinotasikan dengan . G adalah grup
terhadap operasi ini jika tiga sifat berikut dipenuhi.
untuk semua a, b, c di
titas. Terdapat sebuah elemen e (disebut identitas) di G sedemikian
pat b di G (disebut invers dari a)
Jika suatu grup mempunyai sifat komutatif sedemikian hingga
untuk setiap pasangan elemen-elemen a dan b di grup G, maka dapat dikatakan
grup tersebut adalah grup komutatif atau grup Abel.
Untuk bagian (b), andaikan dan . Menggunakan pengertian
bahwa r dan s di H, dapat dilihat bahwa harus terdapat bilangan bulat n dan m di
sedemikian hingga dan . Akibatnya, .
Dengan karakteristik elemen di H dan kenyataan bahwa , ini berarti
1) Asosiatif. Operasi bersifat asosiatif jika
G.
2) Iden
hingga untuk semua a di G.
3) Invers. Untuk setiap elemen a di G terda
9 Beberap Elemen s Grup Abel a contoh grup diberikan dalam Tabel 2. 1 di bawah ini.
Tabel 2. 1
Beberapa Contoh Grup
Grup Operasi Identitas Bentuk Inver
penjumlahan 0 k –k ya
perkalian 1 m/n,
m, n>0
n/m ya
penjumlahan
mod n
0 k n–k ya
perkalian 1 x 1/x ya
GL(2, F) perkalian
matriks
1 0
1 ,
ad–bc≠0
0 tidak
U( dengan
fpb(k, n
elesaian untuk
kx=1 mod n
han
antar
(0, ..., 0) (a1, ..., an) (–a1, –a2, ..., –an) ya
SL(2, F) perkalian 1 0 ,
ad–bc=1
tidak
n) perkalian
mod n
penjumla
1 k,
)=1 peny ya komponen matriks 0 1 Keterangan
adalah bilangan rasional positi
adalah himpunan bilangan bulat modulo n;
adalah himpunan bilangan real tak nol;
GL(2, F) adalah himpunan matriks 2 2 dengan entri-entrinya bilangan real dan determinannya tak nol;
U(n) adalah himpunan bilangan bulat k yang kurang dari n dan , 1
untuk 1
| , , . . . , ; 2
real), (bilangan kompleks), atau (bilangan bulat
t seba ng dari , , , atau .
Definisi 2. 3
Banyaknya elemen dari suatu grup G (berhingga atau tak hingga), dinotasikan
dengan | |, disebut orde dari G. Jika | | berhingga, maka G disebut grup erhingga dan jika | | tak hingga, maka G disebut grup tak hingga.
0, 1, 2, … , 1 untuk 1 adalah n atau | | dan
adalah grup berhingga karena | | berhingga sehingga adalah grup Abel
berhingga karena juga adalah grup Abel.
himpunan f;
;
adalah himpunan , , . . . ,
SL(2, F) adalah himpunan matriks 2 dengan entri-entrinya dari (bilangan
rasional), (bilangan
modulo p dengan p bilangan prima) dan determinannya 1;
F dapa ra
2. Grup Berhingga dan Subgrup
b
11
Definisi 2. 4
Orde dari suatu elemen a dalam sutu grup adalah bilangan bulat positif terkecil
n sedemikian hingg . Dalam notasi penjumlahan menjadi
G
a . Jika
tidak terdapat bilangan bulat seperti itu, maka a dikatakan mempunyai orde tak
hingga. Orde dari suatu elemen a dinotasikan dengan | |.
, 9 terhadap operasi penjumlahan
modulo 10, karena 1 · 2 2, 2 · 2 4, 3 · 2 6, 4 · 2 8, 5 · 2 0, dapat wa |2| 5. Dengan cara yang sama, dapat ditunjukkan bahwa
Definisi 2. 5
Jika H adalah himpunan bagian dari grup G dan H adalah grup terhadap operasi
dari G, maka H disebut subgrup dari G, dinotasikan dengan H ≤ G atau G ≥ H.
atau G > H berarti H ≤G tetapi H ≠G, subgrup ini disebut subgrup
bgrup dari G yang
ejati dar . Jika { adalah elemen identitas dari G
t subg
disebut dari G.
Contoh 2. 4
Satu-satunya subgrup sejati tak trivial dari 0, 1, 2, 3 adalah {0, 2}.
Contoh 2.3
Dengan mengingat grup 0, 1, 2, …
diketahui bah
|0| 1, |7| 10, |5| 2, |6| 5.
Notasi H < G
sejati dari G. Sedangkan, su terdiri dari G atau dirinya sendiri
disebut subgrup tak s i G e} , maka
subgrup {e} disebu rup trivial dari G, sedangkan subgrup yang bukan {e}
subgrup tak trivial
Perhatikan bahwa {0, 3} bukan subgrup dari , karena {0, 3} tidak tertutup
3. Darab Langsung
Definisi 2. 6
Misalkan {G1, G2, ..., Gn} adalah himpunan berhingga dari grup. Darab langsung
1 2 Gn, ditulis sebagai … , adalah himpunan semua
i adalah elem i
, … , dengan dilakukan
engan operasi pada Gi.
5, 7 , 10 1, 3, 7, 9 ,
9 , 7, 1 , 7, 3 , 7,
sedangkan dua komponen kedua dikerjakan den
modulo 10.
4. Grup Siklik dan Pembangkit
Invers dari suatu elemen a dari suatu grup dinotasikan dengan .
Notasi ini digunakan untuk suatu grup terhadap operasi perkalian. dari G , G , ...,
pasangan terurut n komponen dengan komponen ke- en dari G.
Dengan simbol, … , , … , | , di mana
, , … , , , … , ,
d
Contoh 2. 5 8 1, 3,
8 10 1, 1 , 1, 3 , 1, 7 , 1, 9 , 3, 1 , 3, 3 , 3, 7 , 3, 9 , 5, 1 ,
5, 3 , 5, 7 , 5, 7 , 7, 9 .
Hasil kali (3, 7)(7, 9) = (5, 3), karena dua komponen pertama dikerjakan dengan
13
Definisi 2. 7
Jika n adalah bilangan bulat positif, maka digunakan untuk menunjukkan hasil
kali dari a dan dirinya sendiri untuk n faktor, yaitu · · … · .
Jika 0, maka , dengan e adalah elemen identitas di grup tersebut. Jika
a .
Jika
Teorema 2. 1
ika a adalah suatu elemen dari suatu grup dan m, n adalah bilangan bulat, maka
eksponen berikut.
Bukti:
Akan dibuktikan menggunakan prinsip induksi matematis.
Untuk n positif.
Persamaan tersebut benar untuk n = 1, karena
. Andaikan persamaan tersebut benar untuk n = k, berarti
. Kemudian akan dibuktikan persamaan tersebut benar
untuk n = k + 1. Perhatikan bahwa
.
n adalah bilangan bulat negatif, mak
· · , maka .
J
berlaku hukum
1) .
2) .
1) Misalkan m tetap dan n variabel.
b) Untuk n negatif.
Akan dibuktikan persamaan tersebut benar untuk n = −k dengan
kan bahwa . Perhati
· · … · · · … ·
.
Dengan cara yang sama, dapat dibuktikan untuk n tetap dan m variabel.
2) Misalkan m tetap dan n variabel.
a) Untuk n positif.
Persamaan tersebut benar untuk n = 1, karena
. Andaikan persamaan tersebut benar untuk n =
k, berarti . Kemudian akan dibuktikan persamaan tersebut
benar untuk
.
b) Untuk n negatif.
engan
Dengan cara yang sama, dapat dibukti
n = k + 1. Perhatikan bahwa
Akan dibuktikan persamaan tersebut benar untuk n = −k d
. Perhatikan bahwa
.
kan untuk n tetap dan m variabel.
15
Contoh 2. 6
, , , .
Jika G adalah sua
Bukti:
(ab)(b-1a-1) = ((ab)b-1)a-1 (hukum asosiatif)
= (a(bb-1))a-1 (hukum asosiatif)
Sama halnya dengan (b-1a-1)(ab) = e. Karena itu, dengan definisi (aa-1 = a-1a = e
)-1 = b-1a-1.
■
Definisi 2. 8
grup siklik jika terdapat elemen a di G sedemikian hingga
} disebut
himpunan pembangkit dari G. Notasi menyatakan bahwa G adalah grup
bangkit a.
adalah grup siklik dengan pembangkit 1 dan –1.
odulo n adalah grup siklik dengan pembangkit 1 dan 1 1.
Tidak seperti yang hanya mempunyai dua pembangkit, dapat mempuny
lebih dari satu pembangkit bergantung pada n yang diberikan. Teorema 2. 2
tu grup, maka (ab)-1 = b-1a-1 untuk semua a dan b di G.
= (ae)a-1 = aa-1 = e.
),
(ab
Grup G disebut
| . Elemen a tersebut disebut pembangkit dari G dan {a
siklik dengan pem
Contoh 2. 7
Grup terhadap penjumlahan
Demikian juga untuk , grup 0, 1, 2, … , 1 untuk 1 terhadap
penjumlahan m
Misalkan 1 3 5 7 . Untuk memeriksanya, sebagai
3 8, … a
8, … 2, 4, 6, 0 .
a
bgrup il dari G yang mem
h G, mak
terdapat himpunan berhingga | yang membangkitkan G, maka G
dikatakan dibangkitkan secara berhingga dan ditulis | . Jika
1, 2, … , , maka , , … , .
Teorema 2. 3
Jika G adalah grup dan en subgrup
G yang dibangkitkan oleh | tepatnya adalah elemen-elemen dari G yang
berupa hasil kali berhingga dari pangkat bulat dari ai, di mana suatu pangkat ai
tertentu dapat terjadi beberapa kali dalam hasil kali tersebut.
Menurut Definisi 2. 8, H adalah subgrup terkecil dari G yang memuat | .
H dan
contoh, 3 , perhatikan bahwa 3 3, 3 3 8, 3 3
dalah himpunan 3, 6, 1, 4, 7, 2, 5, 0 . Sehingga 3 adalah
pembangkit dari . Tetapi 2 bukan pembangkit dari karena 2
2, 2 2 8, 2 2 2
Definisi 2. 9
Misalk n G adalah grup dan untuk dengan I adalah sebarang
himpunan indeks. Su terkec uat | disebut
subgrup yang dibangkitkan oleh | . Jika subgrup ini adala a
| dikatakan membangkitkan G dan ai disebut pembangkit dari G. Jika
untuk , maka elemen-elem H dari
Bukti:
17
Andaikan K menyatakan himpunan dari semua hasil kali berhingga dari pangkat
bulat dari ai. Misalkan … . Maka dan
· · … · , karena sifat-sifat subgrup. Sehingga
.
… . Maka K H
tkan bahwa K adalah subgrup dari H yang memuat | , maka
ali elem
osiatif. Misalkan
… . Sehingga
… …
.
Untuk , dengan Teorem
… … .
Sebagai contoh, (a1)3(a2)2(a1)-7 berada di K dan [(a1)3(a2)2(a1)-7]-1 = (a1)7(a2)-2(a1)-3
berada di K lagi.
H dan K memuat | karena
| , maka H K.
Akan diperliha
H K.
Perhatikan bahwa hasil k en di K adalah di K lagi. Misalkan,
… . Sehingga … .
Perhatikan juga bahwa hasil kali elemen di K memenuhi sifat as
…
…
… … .
Karena (ai)0 = e, diperoleh
a 2. 2 dapat diperoleh
Jadi, K adalah subgrup dari
Jadi, terbukti bahwa K = H.
■
Contoh 2. 8
1, 0 , 0, 1 artinya grup dibangkitkan oleh (1, 0) dan
Dengan menggunakan Teorema 2. 3, elemen-elemen dari grup
n(1, 0) + m(0, 1)| n, m } = {(0(1, 0) + 0(0, 1)), (0(1, 0) + 1(0, 1))
1(0 )), (0(1, 0) + 2(0, 1)), (2(1, 0) + 0(0, 1)),
)), …} = {(0, 0), (0, 1),
(1, 0), (1, 1), (2, 0), (2, 1)}.
dinyatakan dengan , , , , , , , . Tabel
Tabel Operasi untuk (0, 1).
adalah { ,
(1(1, 0) + 0(0, 1)), (1(1, 0) + , 1
(1(1, 0) + 2(0, 1)), (2(1, 0) + 1(0, 1)), (2(1, 0) + 2(0, 1
Contoh 2. 9 Grup kuarternion
operasi atau tabel Cayley untuk adalah sebagai berikut.
Tabel 2. 2
19
Grup kuarternion juga dapat din ,
, . Dengan kata lain, dibangkitkan oleh a
yatakan dengan , |
dan b yang memenuhi
persamaan , , dan . Berikut ini akan diperlihatkan
ibangkitkan oleh a dan b tersebut.
5. rup Per utasi
Definisi 2. 10
ungsi : disebut satu-satu atau injektif jika dan hanya jika bila m
setiap , terdapat sedemikian
ika adalah satu-satu dan pada.
bahwa d
G m
F
aka . Fungsi : disebut pada atau surjektif jika untuk
sehingga . Fungsi :
Contoh 2. 10
Fungsi : dengan bukan satu-satu karena 2 2 4
tetapi 2 2 dan tidak pada karena daerah hasilnya adalah himpunan bagian
jati dari semua bilangan tak negatif di . Akan tetapi : dengan
satu-satu dan pada .
Definisi 2. 11
Misalkan : dan : . Komposisi dan , dinotasikan dengan
, adalah pemetaan dari A ke C, dinotasikan dengan : ,
didefinisikan dengan untuk semua a di A.
Definisi 2. 12
Permutasi dari suatu himpunan A adalah fungsi bijektif dari A ke A.
Contoh 2. 11
utasi himp kan deng
2, α(2) = 3,
t dapat dinyatakan dengan cara lain, yaitu 1
2 23 31 44 dan
1
2 21 34 43 . Komposisi permutasi dikerjakan dari kanan ke kiri. Misalkan 1 2 3
1 44 12 21 34 34 13 22 34 41 . Sebagai contoh, 3 berada = α(β(1))
a 2. 4
Jika A adalah suatu himpunan tak kosong dan SA adalah himpunan semua
permutasi dari A, maka SA merupakan suatu grup terhadap komposisi permutasi. se
Misalkan perm α dan β dari unan {1, 2, 3, 4} dinyata an α(1) =
α(3) = 1, α(4) = 4 dan β(1) = 2, β(2) = 1, β(3) = 4, β(4) = 3. Permutasi
tersebu
2 3
di bawah 1, karena (αβ)(1) = α(2) = 3.
21
Bukti:
ktikan bahwa (SA, ◦) me
Akan dibu menuhi tiga syarat di dalam Definisi 2. 2, yaitu
asosiatif, mempunyai elemen identitas, dan mempunyai elemen invers. Tetapi
sebelumnya akan dibuktikan bahwa (SA, ◦) tertutup terhadap komposisi permutasi.
Andaikan π1 dan π2 adalah permutasi dari A. Menurut teorema tentang komposisi
fungsi, m 1 2 a1, a2 A
π1 ◦ π2 bersifat satu-satu, j (a1) = (π1 ◦
a2. Akan dibuktikan bahwa π1◦ π2 bersifat satu-satu. Karena (π1◦
π1
bersifat satu-satu, berlaku π2(a1) = π2(a2), dan karena π2 bersifat satu-satu juga,
1 2. Terbukti bahwa (π1◦π2)(a1) = (π1◦π2)(a2) →a1 = a2. Oleh karena
1 2
1 2
setiap b A, terda
untuk setiap a’ A, terdapat a’’ A sehingga π2(a’’) = a’. Oleh karena itu, (π1◦
π2)(a’’) = π1(π2(a’’)) = π1(a’) = b, sehingga π1 ◦ π2 bersifat pada. Maka m
dari A. Terbukti bahwa π1◦ π2
A, (π1◦ (π2◦π3))(a) = ((π1◦π2) ◦π3)(a). Misalkan a A. Berlaku (π1◦ (π2◦π3))(a)
= π1((π2 ◦ π3)(a)) = π1(π2(π3(a)) = (π1 ◦ π2)(π3(a)) = ((π1 ◦ π2) ◦ π3)(a), sehingga
aka π ◦ π juga adalah fungsi dari A ke A. Misalkan .
Komposisi permutasi ika dipenuhi (π1 ◦ π2)
π2)(a2) → a1 =
π2)(a1) = (π1 ◦ π2)(a2), sehingga diperoleh π1(π2(a1)) = π1(π2(a2)). Karena
berlaku a = a
itu, π ◦π bersifat satu-satu.
Akan dibuktikan bahwa π ◦ π bersifat pada, yaitu untuk setiap b A, terdapat a
A sehingga (π1 ◦ π2)(a) = b. Misalkan b A. π1 bersifat pada, berarti untuk
pat a’ A sehingga π1(a’) = b, dan π2 bersifat pada, berarti
enurut
Definisi 2.13, π1 ◦π2 merupakan suatu permutasi
SA.
Akan dibuktikan bahwa (SA, ◦) memenuhi sifat asosiatif. Andaikan π1, π2, π3 SA.
diperoleh (π1 ◦ (π2 ◦π3))(a) = ((π1◦ π2) ◦ π3)(a), untuk setiap a A. Jadi, menurut
Definisi 2. 11 diperoleh π1◦ (π2◦ π3) = (π1◦π2) ◦π3. Terbukti bahwa sifat asosiatif
dipenuhi.
Akan dibuktikan bahwa (SA, ◦) mempunyai elemen identitas. Permutasi i, di mana
i(a) = a, untuk setiap a A, merupakan elemen identitas di SA. Misalkan π SA
dan i permutasi identitas di SA. Akan dibuktikan bahwa π ◦ i = i ◦ π = π. Akan
ditunjukkan bahwa (π ◦ i)(a) = (i ◦ π)(a) = π(a), untuk setiap a A. Karena
berlaku i(a) = a, untuk setiap a A, diperoleh (π◦i)(a) = π(i(a)) = π(a) = i(π(a)) =
(i◦π)(a) sehingga (π◦ i)(a) = (i◦π)(a) = π(a), akibatnya π◦i = i◦ π = π. Terbukti
bahwa terdapat elemen identitas i SA, sehingga π◦i = i◦π = π.
Akan dibuktikan bahwa setiap elemen di (SA, ◦) mempunyai invers. Untuk setiap π
π
-1 -1 -1 -1 -1
Jadi, π◦ π-1 dan π-1◦ π merupakan permutasi identitas dari himpunan A, sehingga
berlaku π◦ π-1 = π-1 ◦ π = i. Terbukti bahwa untuk setiap π S , terdapat elemen
invers π-1 SA, sehingga π◦π-1 = π-1◦π = i.
Jadi, terbukti bahwa S membentuk grup terhadap komposisi permutasi.
■
Grup permutasi dari suatu himpunan A adalah himpunan permutasi dari A yang
membentuk grup terhadap komposisi fungsi.
SA, terdapat elemen invers π-1 SA, yaitu permutasi yang membalik arah fungsi
, di mana untuk setiap a, a’ A, π(a’) = a ↔ π-1(a) = a’. Misalkan a, a’ A.
Karena berlaku i(a) = a, dan jika π(a’) = a maka π-1(a) = a’, akibatnya i(a) = a =
π(a’) = π(π (a)) = (π ◦ π )(a) dan i(a’) = a’ = π (a) = π (π(a’)) = (π ◦ π)(a).
A
A
23
Definisi 2. 14
Misalkan A = {1, 2, …, n}. Himpunan semua permutasi dari A disebut grup
simetri berderajat n dan dinotasikan dengan Sn. Elemen dari Sn mempunyai bentuk
1 2
S m mpunyai 1 · … · 3 · 2 · 1 ! elemen.
1 3 2 2 1 3 3 2 1
Terdapat notasi lain yang biasa digunakan untuk menyatakan permutasi
1 2 3 4 5 6
. Siklis yang hanya mempunyai satu
tas dapat
ditulis α= (12)(346).
1 2 …
… .
n e
Contoh 2. 12
Misalkan S3 menyatakan himpunan semua fungsi satu-satu dari {1, 2, 3} ke
dirinya sendiri. S3 terhadap komposisi fungsi adalah grup dengan enam elemen,
yaitu
1 2 3
1 2 3 , 1 2 32 3 1 , 1 2 33 1 2 ,
1 2 3 , 1 2 3 , 1 2 3 .
yang disebut notasi siklis. Misalkan permutasi
2 1 4 6 5 3 dalam
notasi siklis dinyatakan dengan α = (12)(346)(5) karena 1→2→2→1,
3→4→4→6→6→3, dan 5→5. Suatu pernyataan dari bentuk (α1, α2, …, αm)
disebut siklis dengan panjang m atau siklis-m
Contoh 2. 13
Enam elemen dari S3 dalam notasi siklis dinyatakan dengan ε= (1)(2)(3) = (1), α
2 β
= (1)(23)=(23), αβ = (12)(3) = (12), α2β = (13)(2) = (13).
S
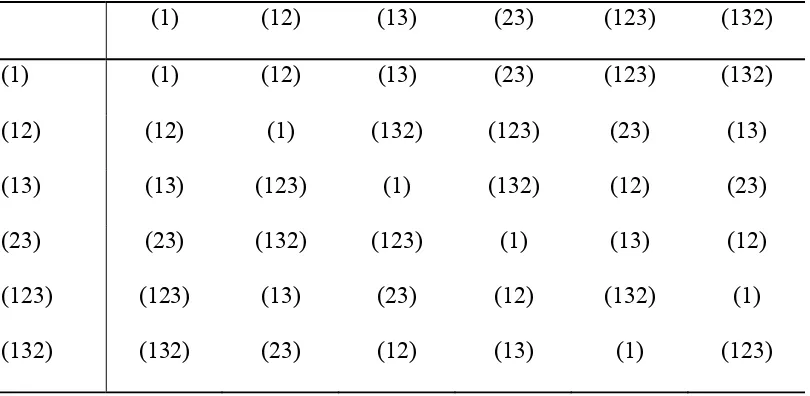
Tabel 2. 3
Tabel Operasi untuk
(1) (12) (13) 3) (123) (132)
= (123), α = (132),
Jadi, 3 = {(1), (12), (13), (23), (123), (132)}. Tabel operasi atau tabel Cayley
untuk adalah sebagai berikut.
(2
(1) (1) (12) (13) (23) (123) (132)
(12) (12) (1) (132) (123) (23) (13)
(13) (13) (123) (1) (132) (12) (23)
(23) (23) (132) (123) (1) (13) (12)
(123) (123) (13) (23) (12) (132) (1)
(132) (132) (23) (12) (13) (1) (123)
Teorem
suatu hasil kali dari siklis
banyaknya genap, maka setiap dekomposisi α ke dalam suatu hasil kali dari
siklis-2 harus mempunyai siklis-siklis-2 yang jumlahnya genap.
Dengan simbol, jika α = β1β2 … βr dan α = γ1γ2 … γs, di mana β dan γ adalah
siklis-2, maka r dan s adalah keduanya genap atau keduanya ganjil. a 2. 5
25
Bukti:
ahwa β1β2 … βr = γ1γ2 … γs menyatakan ε = (γ1γ2 … γs)(β1β2 … βr)-1 =
γ1γ2 … γs βr-1 … β2-1β1-1 = γ1γ2 … γsβr … β2β1, karena invers dari siklis-2 adalah
. Sehingga dengan lemma yang menyatakan bahwa jika ε= β1β2 …
r
■
uatu permuta ang da inyata ebagai l kali iklis g
aknya gen ang d permutasi genap tu pe yan t
takan sebagai hasil kali dari si ang banyaknya ganjil yang disebut
utasi gan
utasi genap dari bol dinotasikan dengan An
berderajat n.
An mempunyai ! Perhatikan b
dirinya sendiri
β, di mana β adalah siklis-2, maka r adalah genap (lemma dan buktinya dapat
dilihat dalam buku Contemporary Abstract Algebra, halaman 98-99), menjamin
bahwa s + r adalah genap. Ini menghasilkan bahwa r dan s adalah keduanya genap
atau keduanya ganjil.
Definisi 2. 15
S si y pat d kan s hasi dari s -2 yan
bany ap y isebut . Sua rmutasi g dapa
dinya klis-2 y
perm jil.
Definisi 2. 16
Grup perm n sim dan disebut grup
selang-seling
elemen.
Contoh 2. 14
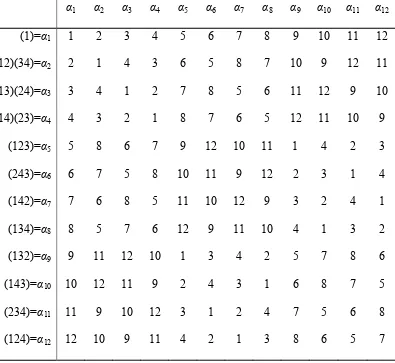
Grup permutasi genap dari {1, 2, 3, 4} atau grup selang-seling diberikan dalam
Tabel 2. 4
Grup Selang-seling untuk Permutasi Genap dari {1, 2, 3, 4}
α1 α2 α3 α4 α5 α6 α7 α8 α9 α10 α11 α12
(1)=α1 1 2 3 4 5 6 7 8 9 10 11 12
(12)(34)=α2 2 1 4 3 6 5 8 7 10 9 12 11
(13)(24)=α3 3 4 1 2 7 8 5 6 11 12 9 10
(14)(23)=α4 4 3 2 1 8 7 6 5 12 11 10 9
(123)=α5 5 8 6 7 9 12 10 11 1 4 2 3
(243)=α6 6 7 5 8 10 11 9 12 2 3 1 4
(142)=α7 7 6 8 5 11 10 12 9 3 2 4 1
(134)=α8 8 5 7 6 12 9 11 10 4 1 3 2
(132)=α9 9 11 12 10 1 3 4 2 5 7 8 6
(143)=α10 10 12 11 9 2 4 3 1 6 8 7 5
(234)=α11 11 9 10 12 3 1 2 4 7 5 6 8
(124)=α12 12 10 9 11 4 2 1 3 8 6 5 7
6. Grup Dihedral
Definisi 2. 17
Simetri bidang dari bangun F pada bidang adalah fungsi bijektif dari bidang
tersebut ke dirinya sendiri yang memetakan F pada F dan mempertahankan jarak
(untuk sebarang titik p dan q pada bidang, jarak dari bayangan p ke bayangan q
27
Teorema 2. 6
Himpunan semua simetri bidang dari bangun F dengan operasi komposisi
membentuk grup.
Bukti:
Akan dibuktikan bahwa komposisi simetri bidang dari bangun F bersifat tertutup.
isalkan π1 d 2 adalah sime id d ba n M ru r 2
π1 ◦ p n gsi ijek . S nju a n uk n w ◦
k jar . M lk a, dan (a, ar
, ( ◦π )) (π2 (a) 2(π ))
(π ), π )) ren 2 a lah et
(a ren 1 a lah et
Te w ko osi sim F erupakan fungsi
bij e ertahankan jarak.
Ak ka ba k o im ri b ng ri b gu bersifat asosiatif.
M π n d si tri ang ari gu . Menurut Teorema
2. π ◦ = 1 ◦ ◦ e kti hw om e bid g d
ba s as tif
kan dibuktikan bahwa komposisi simetri bidang dari bangun F mempunyai
elemen identitas. Simetri bidang i dari bangun F, di mana i(a) = a, untuk setiap a
en identitas dalam himpunan semua simetri bidang dari
alkan π adalah simetri bidang dari bangun F dan i simetri bidang
identitas. Akan dibuktikan bahwa π ◦ i = i◦ π = π. Akan ditunjukkan bahwa (π ◦
M an π tri b ang ari ngu F. enu t Teo ema . 4,
π2 meru aka fun b tif ela tny aka dib tika bah a π1 π2
mempertahan an ak isa an b F d b) adalah jarak ant a a
dengan b.
d((π2◦π1)(a) π2 1)(b = d (π1 ), π 1(b
= d 1(a 1(b (ka a π da sim ri)
= d , b) (ka a π da sim ri)
rbukti bah a mp si etri bidang dari bangun m
ektif dan m mp
an dibukti n hwa omp sisi s et ida da an n F
isalkan π1, 2, da π3 a alah me bid d ban n F
4, π1◦ ( 2 π3) (π π2) π3. T rbu ba a k posisi sim tri an ari
ngun F ber ifat osia .
A
F, merupakan elem
i)(a) = (i◦π)(a) = π(a), untuk setiap a F. Karena berlaku i(a) = a, untuk setiap a
F, diperoleh (π◦ i)(a) = π(i(a)) = π(a) = i(π(a)) = (i◦ π)(a) sehingga (π◦i)(a) =
(i ◦ π)(a) = π(a), akibatnya π ◦ i = i ◦ π = π. Terbukti bahwa terdapat elemen
identitas i dalam himpunan semua simetri bidang dari bangun F, sehingga π◦ i = i
π adalah simetri bidang dari bangun F,
terdapat elemen invers π-1 adalah simetri bidang dari bangun F, yaitu simetri
embalik arah simetri bidang π, di mana untuk setiap a, a’ F, π(a’)
uk setiap π dalam himpunan semua simetri bidang dari bangun F,
= i.
Definisi 2. 18
Grup yang terdiri dari semua simetri dari segi-n beraturan dengan operasi
komposisi disebut grup dihedral.
otasikan dengan Dn.
◦π = π.
Akan dibuktikan bahwa setiap elemen dalam himpunan semua simetri bidang dari
bangun F mempunyai invers. Untuk setiap
bidang yang m
= a ↔π-1(a) = a’. Misalkan a, a’ F. Karena berlaku i(a) = a, dan jika π(a’) = a
maka π-1(a) = a’, akibatnya i(a) = a = π(a’) = π(π-1(a)) = (π◦ π-1)(a) dan i(a’) = a’
= π-1(a) = π-1(π(a’)) = (π-1 ◦ π)(a). Jadi, π ◦ π-1 dan π-1 ◦ π merupakan simetri
bidang identitas dari bangun F, sehingga berlaku π ◦ π-1 = π-1 ◦ π = i. Terbukti
bahwa unt
terdapat elemen invers π-1, sehingga π◦π-1 = π-1◦π
Jadi, terbukti bahwa himpunan semua simetri bidang dari bangun F dengan
operasi komposisi membentuk grup.
■
29
Contoh 2. 15
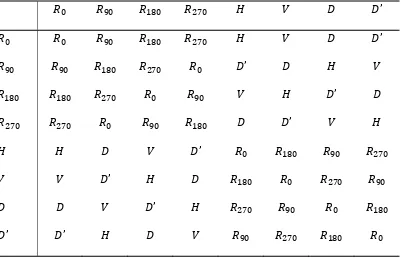
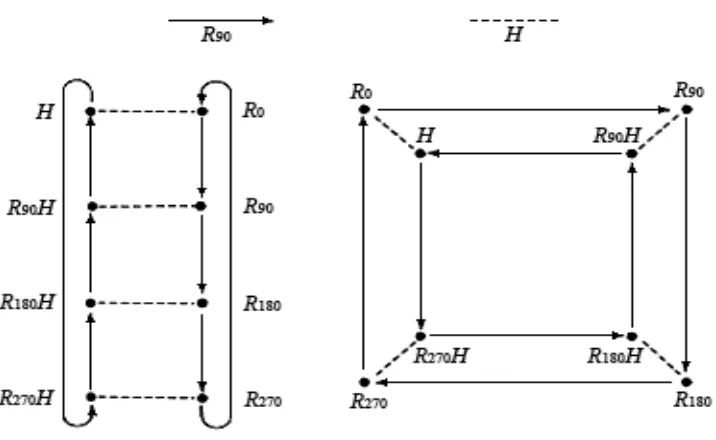
, , , , , , , ’ adalah grup dihedral yang terdiri dari semua
imetri dari suatu bujursangkar atau persegi. (Keterangan: adalah rotasi 0°, adalah rotasi 90°, adalah rotasi 180°, adalah rotasi 270°, adalah
pencerminan terhadap sumbu horisontal atau mendatar, adalah pencerminan
terhadap sumbu vertikal atau tegak, adalah pencerminan terhadap diagonal
tama, ’ adalah pencerminan terhadap diagonal yang lain.) Tabel operasi atau tabel Cayley untuk adalah sebagai berikut.
Tabel 2. 5 Tabel Op s
u
erasi untuk
’
’
’
’
’
’
’
’
’ ’
Grup dihedral dapat dinyatakan dengan | 0, 1;
f adalah pencerminan terhadap garis vertikal untuk n ganjil dan pencerminan
terhadap garis horisontal untuk n genap, dan g adalah rotasi terhadap posisi awal
melalui sudut dengan arah berlawanan jalan jarum jam, untuk n > 2.
orema Lagrange, Subgrup Normal, dan Grup Faktor
Definisi 2. 19
, | ngan .
d
Ha aH| untuk menotasikan
banyaknya elemen dalam himpunan aH, dan |Ha| untuk menotasikan banyaknya
m himpunan Ha.
Contoh 2. 16
Misalkan G = 3 dan H {(1), (13 }. Maka oset-koset kiri dari H di G ah
(1) = {(1)(1), (1)(13)} = {(1), (13)} = {(13)(1), (13)(13)} = (13)H,
(12 = {(12)(1), (12)(13)} = {(12), (132) = {(132 (1), (132 (13)} = 32)H,
(23) = {(23)(1), (23)(13)} = {(23), (123)} = {(123)(1), (123)(13)}= (123)H.
Seda kan kos -koset anan dar H di G adalah
H )= {(1)(1), (13)(1)} = {(1), (13)} = {(1)(13), (13)(13)} = (13)H,
H(12)= {(1)(12), (13)(12)} = {(12), (123)} = {(1)(123), (13)(123)} = (123)H, 7. Koset, Te
Misalkan G adalah grup dan H adalah himpunan bagian dari G. Untuk sebarang
himpunan dinotasikan de aH Secara analogi,
| dan | . Jika H adalah subgrup dari G, maka
himpunan aH disebut koset kiri dari H di G yang memuat a, sedangkan Ha
di-sebut koset kanan ari H di G yang memuat a. Dalam kasus ini, elemen a disebut
perwakilan koset dari aH (atau ). Kita menggunakan |
elemen dala
S = ) k adal
H
)H } ) ) (1
H
ng et k i
31
H 3)= {(1)(23), (13)(23)} = {(23), (132) = {(1)(1 ), (13) 32)}= (1 2)H.
Lemma 2. 1
Misalkan H adalah subgrup dari , dan m a dan b berada di G. Maka,
. a aH,
2. aH
3. aH = bH atau aH bH = ,
= bH jik
,
7. aH adalah subgrup dari G jika dan hanya jika a H.
ukti:
1. a = ae aH.
2. Untuk memeriksa sifat 2, pertama-tama andaikan bahwa aH = H. Maka
. Selanjutnya andaikan bahwa a H dan tunjukkan bahwa
tu enunjukka
a H dan h , dapat diketahui bahwa
, dengan sifat 2.
(2 } 32 (1 3
G isalkan
1
= H jika dan hanya jika a H,
4. aH a dan hanya jika a-1b H,
5. |aH| = |bH|,
6. aH = Ha jika dan hanya jika H = aHa-1
B
aH H dan H aH. Inklusi pertama diperoleh secara langsung dari
ketertu-pan H. Untuk m n bahwa H aH, misalkan h H. Maka, karena
H a-1h H. Sehingga
.
3. Untuk membuktikan sifat 3, andaikan bahwa aH bH ≠ dan buktikan
bahwa aH = bH. Misalkan x aH bH. Maka terdapat h1, h2 di H
sedemi-kian hingga x = ah1 dan x = bh2. Jadi, dan karena
4. Perhatikan bahwa aH = bH jika dan hanya jika a-1aH = a-1bH. Sehingga H =
di H adalah
a-a bh1 = bh2. Jadi, f adalah fungsi
nisi 7. 1,
ter-ka
n bahwa aH = Ha jika dan hanya jika (aH)a-1 = (Ha)a-1, yaitu jika
-1
adalah suatu subgrup, maka aH memuat identitas e. Sehingga, aH
aH = eH = H. Sehingga dari sifat 2,
di-peroleh a H. Sebaliknya, jika a H, maka dengan sifat 2 lagi, aH = H.
Ka-rena H adalah subgrup dari G, maka aH adalah juga subgrup dari G.
■
i G, maka |H| membagi
|G|. Selain itu, banyaknya koset kiri (kanan) berbeda dari H di G adalah |G|/|H|.
Bukti:
Misalkan a H, a H, …, a H menyatakan koset kiri dari H di G yang saling beda.
Maka, untuk setiap a di G, kita mempunyai aH = aiH untuk suatu i. Dengan sifat 1
a-1bH, maka a-1b H, dengan sifat 2.
5. Akan dibuktikan bahwa korespondensi ah → bh untuk semua h
fungsi satu-satu dan pada dari aH ke bH. Misalkan f : aH → bH. Pertam
tama andaikan ah1 = ah2 aH dengan h1, h2 H. Karena G adalah grup, m
ka dengan kanselasi berlaku h1 = h2. Sehingg
satu-satu. Lalu untuk sebarang y, andaikan y bH. Menurut Defi
dapat h H sehingga y = bh. Tetapi h H menentukan ah aH. Ma
. Jadi, f adalah fungsi pada.
6. Perhatika
dan hanya jika aHa = H.
7. Jika aH
eH≠ dan dengan sifat 3, diperoleh
Teorema 2. 7 (Teorema Lagrange)
Jika G adalah grup berhingga dan H adalah subgrup dar
33
dari Lemma 7. 1, a aH. Sehingga setiap anggota dari G berada di salah satu dari
koset aiH. Dengan simbol, G = a1H … arH. Sekarang, sifat 3 dari lemma
me-nunjukkan bahwa gabungan ini adalah saling asing, sehingga |G| = |a1H| + |a2H| +
|H| untuk setiap
… + |arH|. Akhirnya, karena |aiH| = i, diperoleh |G| = r|H|.
■
ormal dari G
semua a di G. Kita menotasikan ini dengan H G.
Untuk sebarang pencerminan f dan
se-Andaikan G adalah grup Abel dan na G adalah grup
erlaku untuk setiap , maka H adalah subgrup
Definisi 2. 20
Suatu subgrup H dari grup G disebut subgrup n jika aH = Ha untuk
Contoh 2. 17
Subgrup rotasi di Dn adalah normal di Dn.
barang rotasi g, diketahui fg = g-1f, sedangkan untuk sebarang rotasi g dan g’,
di-peroleh gg’ = g’g.
Teorema 2. 8
Jika G adalah grup Abel dan H adalah subgrup dari G, maka H adalah subgrup
normal dari G.
Bukti:
H adalah subgrup dari G. Kare
Abel, maka . Akibatnya, |
| . Karena ini b
normal dari G.
Teorema 2. 9
Misalkan G adalah grup dan H suatu subgrup normal dari G. Himpunan G/H =
{aH|a G} adalah grup terhadap operasi (aH)(bH) = abH.
/H
ke G/H adalah benar-benar fungsi. Untuk melakukan ini, andaikan bahwa aH =
a’H dan bH = b’H. Maka a’ = ah dan b’ = bh untuk suatu h , h di H, dan oleh
karena itu ’ ’ . Di sini
digunakan sifat 2 dari Lemma 7. 1 dan kenyataan bahwa H G. Selanjutnya, eH
= H adalah elemen identitas, a-1H adalah invers dari aH, dan
. Ini
membukti-kan bahwa G/H adalah suatu grup.
■
Definisi 2. 21
Jika subgrup H dari G adalah normal, maka himpunan koset kiri (atau kanan) dari
H di G disebut grup faktor dari G oleh H (atau grup hasil bagi dari G oleh H).
Contoh 2. 18
dan H = 6 = {0, 6, 12}. Maka G/H = {0+H, 1+H, 2+H, 3+H,
himpunan G/H. Sehingga (5+H)+(4+H) = 5+4+H = 9+H = Bukti:
Pertama-tama akan ditunjukkan bahwa operasinya terdefinisi dengan baik, yaitu
harus ditunjukkan bahwa korespondensi yang terdefinisi di atas dari G/H × G
1 2 1 2
Misalkan G =
4+H, 5+H}. Untuk menjelaskan bagaimana elemen-elemen grup dioperasikan,
sebagai contoh (5+H)+(4+H). Ini seharusnya menjadi salah satu dari enam elemen
35
3+6+H = 3+H, karena H menyerap semua kelipatan dari 6 dengan sifat 2 dari
omorfisma dan Isomorfisma
G ke grup adalah pemetaan dari
mempertahankan operasi grup, yaitu, ( G.
Definisi 2. 23
Suatu isomorfisma dari grup G ke grup adalah pemetaan satu-satu (atau
pada yang mempertahankan operasi grup, yaitu, (ab) = (a)
.
2. 19
emetakan x ke f dan y ke g. Akan dibuktikan bahwa
m
Misalnya , untuk setiap .
Lemma 7. 1.
8. Hom
Definisi 2. 22
Suatu homomorfisma dari grup G ke yang
ab) = (a) (b) untuk semua a, b di
fungsi) dari G
(b) untuk semua a, b di G. Jika terdapat isomorfisma dari G pada , dapat
dikatakan bahwa G dan adalah isomorfis dan ditulis
Contoh
Misalkan , | , dan | 0, 1;
0, 1, … , 1 . Buktikan bahwa .
Terdapat tiga persamaan yang dipenuhi di G oleh x dan y juga dipenuhi di H jika x
diganti f dan y diganti g, yaitu , . Maka terdapat pemetaan
: yang m adalah
isomorfisma, yaitu pemetaan yang satu-satu, pada, dan memenuhi syarat
: adalah satu-satu jika dan hanya jika , untu
. Misalkan dan . Maka
: adalah pada jika untuk setiap terdapat sedemikian hingga
. Jika H dibangkitkan oleh elemen-elemen dari {f, g}, maka sebarang
hasil kali pangkat bulat dari f dan g adalah bayangan dari hasil kali pangkat bulat
yang bersesuaian dari x dan y. Misalkan dan . Sehingga untuk
setiap terdapat sedemikian hingga .
: adalah homomorfisma jika dan hanya jika ,
untuk setiap , . Maka
.
Jadi, .
k
setiap ,
→ → →
37
B. Teori Graf
1. Graf Berarah Atau Digraf
Definisi 2. 24
Graf terdiri dari himpunan tak kosong simpul V dan himpunan busur
E. Setiap busur mempunyai satu atau dua simpul terhubung dengannya dan simpul
itu disebut titik ujung dari busur tersebut. Suatu busur dikatakan terhubung
dengan titik ujung-titik ujungnya. ,
, , , , ,
, , , , , , , , , , , Definisi 2. 25
Dua simpul u dan v dalam suatu graf G disebut berdampingan di G jika u dan v
adalah titik ujung dari suatu busur di G. Jika e diasosiasikan dengan {u, v}, busur
e disebut menghubungkan simpul u dan v. Simpul u dan v disebut titik ujung dari
suatu busur yang diasosiasikan dengan {u, v}.
Definisi 2. 26
Suatu graf yang setiap busurnya menghubungkan dua simpul berbeda dan tidak
memuat dua busur menghubungkan pasangan simpul yang sama disebut graf
sederhana.
Contoh 2. 20
Graf terdiri dari himpunan simpul dan himpunan
busur . Graf seperti ini dapat
Gambar 2. 1 Graf G
Sebagai contoh, busur {a, b} mempunyai simpul a dan b sebagai titik ujungnya
sehingga busur {a, b} dikatakan terhubung dengan simpul a dan b. Simpul a dan b
berdampingan di G dan misalkan {a, b} = f maka busur f menghubungkan simpul
a dan b. Graf di atas disebut sebagai graf tak berarah karena tidak memuat busur
berarah.
Definisi 2. 27
Graf berarah atau digraf terdiri dari himpunan tak kosong simpul V
dan himpunan busur berarah E. Setiap busur berarah berkaitan dengan pasangan
terurut simpul. Busur berarah yang berkaitan dengan pasangan terurut (u, v)
dikatakan berawal di u dan berakhir di v. ,
Definisi 2. 28
Jika (u, v) adalah suatu busur berarah dari graf G, u dikatakan berdampingan
dengan v dan v dikatakan berdampingan dengan u. Simpul u disebut simpul awal
39
Contoh 2. 21
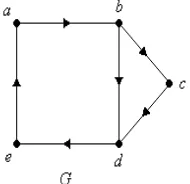
Graf berarah terdiri dari himpunan simpul dan
himpunan busur berarah . Graf
seperti ini dapat digambarkan secara geometris seperti berikut.
, , , , ,
, , , , , , , , , , ,
Gambar 2. 2 Graf Berarah G
Sebagai contoh, busur (a, b) dikatakan berawal di a dan berakhir di b. Simpul a
dikatakan berdampingan dengan b dan b dikatakan berdampingan dengan a.
Simpul a disebut simpul awal dari (a, b) dan b disebut simpul akhir dari (a, b).
2. Lintasan dan Sirkuit Hamilton
Definisi 2. 29
Misalkan n adalah bilangan bulat tak negatif dan G adalah graf tak berarah.
Lintasan dengan panjang n dari u ke v di G adalah barisan dari n busur e1, ..., en
dari G sedemikian hingga e1 diasosiasikan dengan {x0, x1}, e2 diasosiasikan
dengan {x1, x2}, dan seterusnya, dengan en diasosiasikan dengan {xn-1, xn}, di
mana x0 = u dan xn = v. Jika grafnya sederhana, maka lintasan ini dinotasikan
dengan barisan simpul x0, x1, ..., xn. Lintasan adalah sirkuit jika berawal dan
daripada nol. Lintasan atau sirkuit dikatakan melalui simpul x0, x1, ..., xn-1 atau
melintasi busur e1, e2, ..., en. Lintasan atau sirkuit adalah sederhana jika tidak
memuat busur yang sama lebih dari sekali.
Contoh 2. 22
Gambar 2. 3 Graf Sederhana yang Memuat Lintasan dan Sirkuit
Dalam graf sederhana di atas, barisan simpul a, d, c, f, e adalah lintasan sederhana
dengan panjang 4, karena {a, d}, {d, c}, {c, f}, dan {f, e} adalah semua busurnya.
Tetapi barisan simpul d, e, c, a bukan lintasan, karena {e, c} bukan busur. Barisan
simpul b, c, f, e, b adalah sirkuit dengan panjang 4, karena {b, c}, {c, f}, {f, e},
dan {e, b} adalah busur, dan lintasan ini berawal dan berakhir pada simpul b.
Lintasan a, b, e, d, a, b, yang panjangnya 5, bukan lintasan sederhana karena
memuat busur {a, b} dua kali.
Definisi 2. 30
Misalkan n adalah bilangan bulat non negatif dan G adalah graf berarah. Lintasan
dengan panjang n dari u ke v di G adalah barisan busur e1, e2, ..., en dari G
sedemikian hingga e1 diasosiasikan dengan (x0, x1), e2 diasosiasikan dengan (x1,
x2), dan seterusnya, dengan en diasosiasikan dengan (xn-1, xn), di mana x0 = u dan
41
simpulnya x0, x1, ..., xn. Lintasan dengan panjang lebih besar daripada nol yang
berawal dan berakhir pada simpul yang sama disebut sirkuit. Lintasan atau sirkuit
disebut sederhana jika tidak memuat busur yang sama lebih dari sekali.
Definisi 2. 31
Lintasan sederhana di graf G yang melalui setiap simpul tepat sekali disebut
lintasan Hamilton dan sirkuit sederhana di graf G yang melalui setiap simpul tepat
sekali disebut sirkuit Hamilton. Lintasan sederhana x0, x1, ..., xn-1, xn di graf
adalah lintasan Hamilton jika dan
untuk 0 ≤ i < j ≤ n dan sirkuit sederhana x0, x1, ..., xn-1, xn, x0 (dengan n > 0) adalah
sirkuit Hamilton jika x0, x1, ..., xn-1, xn adalah lintasan Hamilton.
, , , . . . , ,
Teka-teki ini dapat diselesaikan dengan menemukan sirkuit pada graf
dalam Gambar 2. 4. Salah satu penyelesaian dari teka-teki tersebut juga
ditunjukkan dalam Gambar 2. 4.
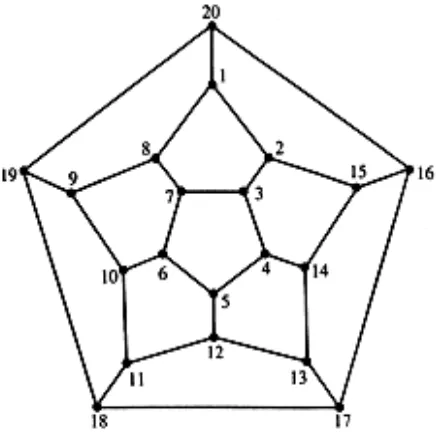
Istilah lintasan dan sirkuit Hamilton muncul dari permainan yang disebut
Icosian puzzle, ditemukan pada tahun 1857 oleh matematikawan Irlandia, Sir
William Rowan Hamilton. Permainan ini terdiri dari dodekahedron kayu, yaitu
segibanyak dengan 12 segilima beraturan sebagai sisi, dengan pasak di setiap
simpul dari dodekahedron dan tali. Dua puluh simpul dari dodekahedron dinamai
dengan nama-nama kota berbeda di dunia. Tujuan dari teka-teki ini adalah dengan
berawal dari suatu kota dan berjalan sepanjang busur dari dodekahedron,
mengunjungi setiap 19 kota lain tepat sekali, dan berakhir dengan kembali pada
kota pertama. Selama perjalanan mengunjungi setiap kota ditandai menggunakan
Gambar 2. 4 Salah Satu Penyelesaian Teka-Teki “Perjalanan Keliling Dunia”
Contoh 2. 23
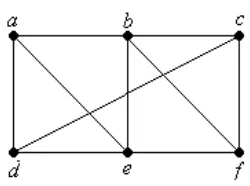
Gambar 2. 5 Graf Sederhana G1, G2, dan G3
Graf G1 mempunyai sirkuit Hamilton, yaitu a, b, c, d, e, a. Graf G2 tidak
mempunyai sirkuit Hamilton, karena sebarang sirkuit yang memuat setiap simpul
harus memuat busur {a, b} dua kali, tetapi graf G2 mempunyai lintasan Hamilton,
yaitu a, b, c, d. Graf G3 tidak mempunyai sirkuit Hamilton ataupun lintasan
Hamilton, karena sebarang lintasan yang memuat semua simpul harus memuat
BAB III
DIGRAF CAYLEY DARI GRUP
Jika seseorang berpikir mengenai aljabar abstrak atau struktur aljabar, maka hal pertama yang hadir dalam pikirannya adalah grup. Terdapat banyak grup berbeda sebanyak cara menggambarkan grup ini. Salah satu cara menunjukkan grup dan elemen pembangkitnya adalah dengan digraf Cayley. Digraf ini merupakan perwakilan berupa gambar dari grup. Dari digraf ini telah hadir penyelidikan tentang lintasan dan sirkuit Hamilton yang terdapat cukup banyak digraf Cayley dengan sifat-sifat khusus di dalamnya.
A. Digraf Cayley dari Grup
Gagasan tentang digraf Cayley dari grup pertama-tama diperkenalkan oleh seorang matematikawan bernama Arthur Cayley pada tahun 1878. Definisi umum menyatakan bahwa digraf Cayley merupakan gambaran grafis dari grup yang diberikan oleh himpunan pembangkit dan relasi. Digraf ini penting untuk dipelajari karena menghubungkan teori graf dengan teori grup dan hubungan ini menghasilkan sebuah metode untuk menggambarkan grup. Secara matematis definisi digraf Cayley dari grup adalah sebagai berikut.
Definisi 3. 1
Misalkan G adalah grup berhingga dan S adalah himpunan pembangkit untuk G. Digraf Cayley dari grup G dengan himpunan pembangkit S, yang dinotasikan
dengan Cay(S:G), dapat didefinisikan sebagai berikut. 1) Setiap elemen dari G adalah simpul dari Cay(S:G).
2) Untuk x dan y di G, terdapat sebuah busur berarah dari x ke y jika dan hanya jika xs = y untuk suatu s S.
Untuk membedakan pembangkit mana yang menghubungkan dua simpul dalam suatu digraf, Cayley mengusulkan agar setiap pembangkit diberikan warna, dan busur berarah yang menghubungkan x ke xs diwarnai dengan warna yang di-berikan pada s. Ia menyebut gambar yang dihasilkan sebagai graf berwarna dari grup tersebut (color graph of the group). Istilah ini kadang-kadang masih diguna-kan. Dalam tulisan ini untuk membedakan pembangkit yang berbeda, akan digu-nakan busur utuh, busur putus-putus, dan busur titik-titik. Secara umum, jika ter-dapat suatu busur berarah dari x ke y, maka tidak perlu terter-dapat busur dari y ke x. Anak panah yang berasal dari x dan menuju ke y menyatakan bahwa terdapat sua-tu busur berarah dari x ke y.
me-45
nyatakan bahwa terdapat suatu busur dari x ke y dan suatu busur dari y ke x. Ini terjadi jika himpunan pembangkit memuat anggota yang inversnya adalah dirinya sendiri dalam grup tersebut. Sebagai contoh, pada Contoh 3. 2, pembangkit (0, 1) inversnya adalah (0,1) dalam grup .
1
0, 1, 2, 3, 4, 5
Gambar 3. 1. Contoh 3. 1
.
adalah grup terhadap operasi penjumlahan dengan pembangkitnya adalah 1. .
Invers dari 1 adalah 5 sehingga busurnya berpanah.
Digraf Cayley dari dengan pembangkit 1 atau Cay({1}: ) diperlihatkan dalam
Gambar 3. 1 Digraf Cay({1}: )
Contoh 3. 2
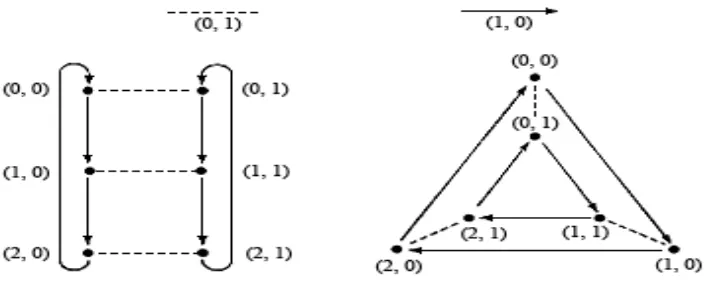
1, 0 , 0, 1 .
0, 1, 2 0, 1
0, 0 , 0, 1 , 1, 0 , 1, 1 , 2, 0 , 2, 1
, ,
.
Invers dari (1, 0) adalah (2, 0) sehingga busurnya berpanah, invers dari (0, 1) ada-lah (1, 0) sehingga busurnya tak berpanah.
Digraf Cayley dari dengan pembangkit (1, 0) dan (0, 1) atau Cay({(1, 0), (0, 1)}: ) diperlihatkan dalam Gambar 3. 2.
Gambar 3. 2 Digraf Cay({(1, 0), (0, 1)}: )
Dengan digraf Cayley dari grup menjadi mudah untuk melihat orde dari beberapa elemen grup, yaitu orde dari elemen identitas dan orde dari pembangkit yang digunakan. Sebagai contoh, orde dari dalam grup yang diberikan dalam Contoh 3. 3 adalah empat karena terdapat empat pemberhentian pada digraf sebelum mencapai sebagai elemen identitas di .
Contoh 3. 3 , .
adalah grup terhadap operasi komposisi dan pembangkitnya adalah dan .
47
Invers dari adalah sehingga busurnya berpanah, invers dari adalah
mbangkit dan atau Cay( , : ) di-am
sehingga busurnya tak berpanah. Digraf Cayley dari dengan pe perlihatkan dalam G bar 3. 3.
Gambar 3. 3 Digraf Cay( , : )
Contoh 3. 4
123 .
adalah grup terhadap operasi komposisi fungsi dan pembangkitnya adalah (12) dan (123).
1 , 12 , 13 , 23 , 123 , 132 .
Invers dari (12) adalah (12) sehingga busurnya tak berpanah, invers dari (123) adalah (132) sehingga busurnya berpanah.
Digraf Cayley dari dengan pembangkit (12) dan (123) atau Cay({(12), (123)}: ) diperlihatkan dalam Gambar 3. 4.
Gambar 3. 4 Digraf Cay({(12), (123)}: )
Contoh 3. 5 12 , 13 .
p terhadap operasi komposisi fungsi dan pembangkitnya adalah (12) dan (13).
Invers dari (12) adalah (12) dan invers dari (13) adalah (13) sehingga busurnya tak berpanah.
Digraf Cayley dari dengan pembangkit (12) dan (13) atau Cay({(12), (13)}: ) diperlihatkan dalam Gambar 3. 5.
adalah gru
1 , 12 , 13 , 23 , 123 , 132 .
49
Contoh 3. 6
12 34 , 123 .
adalah grup terhadap operasi komposisi fungsi dan pembangkitnya adalah (12)(34) dan (123).
Tabel operasi untuk dapat dilihat pada Tabel 2. 2.
Invers dari (12)(34) adalah (12)(34) sehingga busurnya tak berpanah, invers dari (123) adalah (132) s
Digraf Cayley dari dengan pembangkit (12)(34) dan (123) atau Cay({(12)(34), (123)}: ) diperlihatkan dalam Gambar 3. 6.
ehingga busurnya berpanah.
Gambar 3. 6 Digraf Cay({(12)(34), (123)}: )
dari setiap simpul ke simpul selanjutnya seper