PERSAMAAN DIFRENSIAL BIASA
(Buku pegangan mata kuliah Persamaan Difrensial)Oleh
Drs. D a f i k, M.Sc. NIP. 132 052 409
Program Pendikan Matematika
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS JEMBER
Untuk Keluarga Tercinta
Daftar Isi
Daftar Tabel v
Daftar Gambar vi
Kata Pengantar vii
1 Konsep Dasar 1
1.1 Klasifikasi Persamaan Difrensial . . . 1
1.2 Metoda Penyelesaian . . . 3
2 PDP Linier Order Satu 6 2.1 Solusi Analitis PDP Linier Order Satu . . . 6
2.2 Aplikasi Sederhana PDP Order Satu . . . 9
3 PDP Linier Order Dua 11 3.1 Klasifikasi . . . 11
3.2 Persamaan Karakteristik . . . 13
3.3 Bentuk Kanonis . . . 17
3.4 Sarat Bantu . . . 18 4 Identitas Pertama dan Kedua Green 20
5 Aplikasi PDP Order Dua 25
5.1 Vibrasi . . . 25
5.1.1 Vibrasi Pada Senar . . . 25
5.1.2 Vibrasi Pada Membran . . . 28
5.2 Difusi . . . 29
5.3 Aliran Panas . . . 31
5.4 Vibrasi dan Aliran Panas Stasioner . . . 32
6 Deret Fourier 34 6.1 Himpunan Fungsi Ortogonal dan Ortonormal . . . 34
6.2 Deret Fourier Diperumum . . . 36
6.3 Deret Fourier Cosinus dan Sinus . . . 37
Daftar Tabel
6.1 PDP order dua menurut jenisnya. . . 43
Daftar Gambar
2.1 Transformasi sistem koordinat . . . 7
4.1 Luas Permukaan. . . 22
4.2 Fluk medan vektor menembus permukaan. . . 22
5.1 Vibrasi senar dalam sistem koordinat . . . 26
5.2 Vibrasi senar pada daerah terbatas . . . 26
5.3 Vibrasi vertikal membran . . . 28
5.4 Vibrasi vertikal membran . . . 31
Kata Pengantar
Puji syukur kehadirat Allah S.W.T karena atas anugerah dan karuniahNya penulis dapat menyelesaikan buku pegangan kuliah dengan judul ”Persamaan Diferen-sial ParDiferen-sial : Pendekatan Analitik”. Buku pegangan ini dibuat untuk membantu mahasiswa mengikuti mata kuliah Persamaan Difrensial Parsial yang selama ini masih cukup sulit menemukan buku-buku dalam bahasa Indonesia.
Dalam buku pegangan ini dijelaskan konsep Persamaaan difrensial secara umum, PDP linier order satu dan aplikasinya, PDP linier order dua yang dis-ertai penjelasan tentang teknik merubah PDP dalam bentuk kanonis, Identitas pertama dan kedua Green, Aplikasi PDP order dua dalam masalah Difusi, Vibrasi dan aliran panas dan terakhir adalah deret Fourier.
Selanjutnya dalam kesempatan ini penulis tak lupa menyampaikan banyak terima kasih kepada yang terhormat:
1. Rektor Universitas Jember. 2. Dekan FKIP Universitas Jember.
3. Ketua Program Pendidikan Matematika yang telah memberikan motivasi dan rekomendasi penggunaannya dalam perkuliahan.
4. Semua pihak yang terlibat langsung maupun tak langsung dalam penyusunan vii
buku ajar ini.
Semoga bantuan rielnya mendapat balasan yang setimpal dari Allah S.W.T. Akhirnya penulis berharap semoga buku ini memberikan manfaat bagi pembaca, oleh karena itu kritik dan saran masih penulis harapkan untuk penyempurnaan-nya dikemudian hari.
Jember, Januari 2003 Penulis
Daftar Isi
Daftar Tabel
Daftar Gambar
BAB 1
Konsep Dasar
1.1
Klasifikasi Persamaan Difrensial
Pada umumnya dikenal dua jenis persamaan difrensial yaitu Persamaan Difren-sial Biasa (PDB) dan Persamaan DifrenDifren-sial ParDifren-sial (PDP). Untuk mengetahui perbedaan kedua jenis persamaan difrensial itu dapat dilihat dalam definisi berikut. Definisi 1.1.1 Persamaan DifrensialSuatu persamaan yang meliputi turunan fungsi dari satu atau lebih variabel terikat terhadap satu atau lebih variabel bebas disebut Persamaan Difrensial. Selanjutnya jika turunan fungsi itu hanya tergan-tung pada satu variabel bebas maka disebut Persamaan Difrensial Biasa (PDB)
dan bila tergantung pada lebih dari satu variabel bebas disebut Persamaan Difren-sial ParDifren-sial (PDP)
Dalam bahan ajar ini pembahasan persamaan difrensial akan difokuskan pada Persamaan Difrensial Parsial (PDP). Sehingga semua contoh soal dan aplikasinya akan dikaitkan dengan model fenomena persamaan difrensial yang terikat pada
BAB 1. KONSEP DASAR 2 beberapa variabel bebas. Secara simbolik turunan parsial ini dinotasikan dengan ∂, sehingga ∂u ∂x =ux, ∂2u ∂x2 =uxx, ∂ 2u ∂x∂y =uxy =uyx.
Definisi 1.1.2 Order Order suatu PDP adalah order tertinggi dari turunan dalam persamaan sehinggaF(x, y, u, ux, uy, . . . , uxx . . . xx| {z }
n
, . . .) = 0adalah berorder
n, dengan variable bebas x, y.
Definisi 1.1.3 Linieritas dan Homogenitas PDP Order n dikatakan linier bila dapat dinyatakan dalam bentuk
a0(x, y)ux+a1(x, y)uy+· · ·+ak(x, y)uxx . . . xx| {z }
n
, . . .) =F(x, y)
Selanjutnya:
1. Bila tidak dapat dinyatakan dengan bentuk diatas dikatakan tak linier 2. Bila koefisiena0(x), a1(x), . . . , an(x)konstan dikatakan mempunyai koefisien
konstan bila tidak, dikatakan mempunyai koefisien variabel.
3. Bila F(x) = 0 maka PDB tersebut dikatakan homogen bila tidak, disebut nonhomogen.
Definisi 1.1.4 Solusi PDP Solusi dari PDP adalah suatu fungsi u(x, y, . . .)
yang memenuhi persamaan diferensial minimal dari sebarang domain variabel
x, y, . . ..
Contoh 1.1.1 Beberapa contoh fenomena riel dalam PDP adalah sebagai berikut: 1. ux+uy = 0 adalah persamaan transportasi
BAB 1. KONSEP DASAR 3
3. uxx+uyy = 0 adalah persamaan Laplace
4. utt−uxx+u3 = 0 merupakan persamaan gelombang dengan interaksi
5. ut+uux+uxxx = 0 adalah persamaan gelombang despersive
6. utt+uxxx = 0 merupakan persamaan vibrasi pada balok
7. ux+uy = 0 adalah persamaan transportasi
8. ut−iuxx = 0 merupakan persamaan gelombang diskontinyu
1.2
Metoda Penyelesaian
Terdapat tiga jenis metoda yang dapat digunakan untuk menentukan solusi dari suatu PDB yaitu:
1. Metoda Analitik. Metoda ini dapat menghasilkan dua bentuk solusi yaitu bentuk eksplisit dan implisit, yang dicari melalui teknik deduktif analogis dengan menggunakan konsep-konsep matematik. Kelebihannya dapat mengetahui bentuk fungsi solusinya namun tidak cukup fleksibel un-tuk masalah-masalah yang komplek.
2. Metoda kualitatif . Solusi ini hanya dapat memberikan gambaran secara geometris bagaimana visualisasi dari solusi PDB. Dengan mengamati pola grafik gradien ”field” (direction field) maka dapat diestimasi solusi PDB itu. Keunggulannya dapat memahami secara mudah kelakuan solusi suatu PDB namun fungsi asli dari solusinya tidak diketahui, dan juga kurang fleksibel untuk kasus yang komplek.
BAB 1. KONSEP DASAR 4 3. Metoda Numerik. Pada saat sekarang metoda ini merupakan metoda yang sangat fleksibel. Metoda ini berkembangan sesuai dengan perkem-bangan komputer dan dapat menyelesaiakan suatu PDB dari level yang mudah sampai level yang komplek. Walaupun fungsi solusi tidak diketahui secara eksplisit maupun implisit namun data yang diberikan dapat divisu-alisir dalam grafik sehingga dapat dianalisis dengan baik. Namun metoda ini berdasarkan pada prinsip-prinsip aproksimasi sehingga solusi yang di-hasilkan adalah solusi hampiran (pendekatan). Sebagai konsukwensi dari penggunaan metoda ini adalah adanya evaluasi berulang dengan menggu-nakan komputer untuk mendapatkan hasil yang akurat. Salah satu metoda yang poipuler adalah metoda Beda Hingga (Beda Hingga) dan Elemen Hingga (Finite Element).
Suatu contoh diberikan persamaan difrensial uxx = 0 maka solusi analitik
diperoleh dengan mengintegralkan kedua ruas persamaan ini dua kali.
Z
uxx(x, y)dx =
Z
0dx
ux(x, y) = c ganti dengan sebarang fungsi y
= f(y) Z ux(x, y)dx = Z f(y)dx ux(x, y) = f(y)x+g(y)
merupakan solusi umum dari PDP diatas.
Untuk model uxx +u = 0 teknik penyelesaiannya dapat mengadopsi teknik
yang dipakai dalam menyelesaikan PDB order 2 dengan akar-akar komplek pada persamaan karakteristiknya yaitu u =c1eλxcosµx+c2eλxsinµx. Dalam hal ini
BAB 1. KONSEP DASAR 5 r2+ 1 = 0 sehingga akar-akarnya adalah r
12=±i, dengan demikian solusi umum
PDPnya adalah u(x, y) =f(y) cosµx+f(y) sinµx.
Sedang model sederhana lainnya adalah uxy = 0 dimana solusi analitiknya
adalah Z uxy(x, y)dx = Z 0dx uy(x, y) = f(y) Z uy(x, y)dy = Z f(y)dy ux(x, y) = F(y) +g(x)
BAB 2
PDP Linier Order Satu
2.1
Solusi Analitis PDP Linier Order Satu
Bila diberikan fungsi dengan dua variabelu(x, y) maka PDP linier order satu yang paling sederhana adalah ux = ∂u∂x = 0 atau uy = ∂u∂y = 0. Sementara dengan
aturan Chain kedua turunan parsial ini didefinisikan sebagai ∂u ∂x = ∂u ∂x ∂x ∂x + ∂u ∂y ∂y ∂x (2.1) ∂u ∂y = ∂u ∂y ∂y ∂y + ∂u ∂x ∂x ∂y (2.2)
Jumlah kedua PDP yang paling sederhana diatas dengan koefisien konstan dapat disajikan dalam
aux+buy = 0 (2.3)
PDP ini dapat diselesaikan dengan dua cara. 1. Metoda Kualitatif
Kuantitas dariaux+buy adalah turunan berarah dariudalam suatu vektor
BAB 2. PDP LINIER ORDER SATU 7 dengan arah V = [a, b] = ai +bj. Hal ini selalu bernilai nol, dengan kata lain u(x, y) pasti sama dengan konstan dalam arah V. Vektor [b,−a] adalah orthogonal terhadap V. Sedangkan garis yang sejajar dengan V adalahbx−ay=cdan persamaan ini disebut persamaan garis karakteristik. Solusi PDP diatas selalu konstan dalam masing-masing garis karakteristik ini sehingga tergantung hanya pada bx−ay. Dengan demikian solusinya adalah
u(x, y) =f(bx−ay). 2. Metoda Koordinat
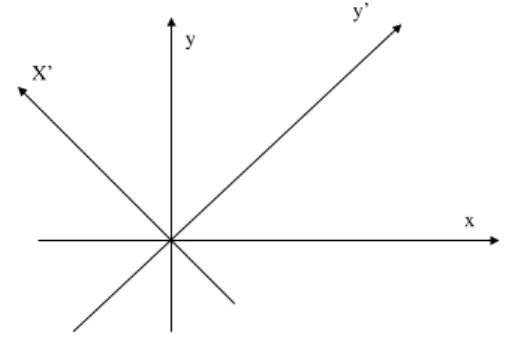
Dalam sistem koordinat x, y dapat kita transformasikan kedalam sistem
y’ y
x X’
Gambar 2.1: Transformasi sistem koordinat
koordinat lainx0, y0 dimanax0 dany0 tetap saling tegak lurus, lihat Gambar
2.1. Misal ditetapkanx0 =ax+by makay0 =bx−ay. Dengan aturan Chain
turunan u(x0, y0) terhadapx dan y adalah:
∂u ∂x = ∂u ∂x0 ∂x0 ∂x + ∂u ∂y0 ∂y0 ∂x = aux0 +buy0 ∂u ∂y = ∂u ∂y0 ∂y0 ∂y + ∂u ∂x0 ∂x0 ∂y = −auy0 +bux0
BAB 2. PDP LINIER ORDER SATU 8 Selanjutnya substitusikan kedalam persamaan aux+buy = 0 didapat
a(aux0+buy0) +b(−auy0+bux0) = 0 a2u
x0 +abuy0 +b2ux0 −abuy0 = 0 (a2+b2)ux0 = 0. Dengan demikian untuk (a2 +b2)6= 0 maka
ux0 = 0 Z ux0 dx0 = Z 0dx0 u(x, y) = f(y0) sehingga u(x, y) =f(bx−ay) (2.4) merupakan solusi umum PDP diatas.
Contoh 2.1.1 Diberikan PDP 4ux −3uy = 0 dengan sarat awal u(0, y) = y3
maka solusi umum PDP ini adalahu(x, y) = f(−3x−4y). Nilai awalu(0, y) =y3
berimplikasi f(−4y) = y3. Misal w = −4y maka y = w
−4 sehingga f(w) = w
3
64,
dengan demikian u(x, y) = f(−3x−4y) = (3x+464y)3.
Selanjutnya bila persamaan 2.3 dikembangkan kedalam koefisien variabel, yakni
aux+byuy = 0 (2.5)
maka vektor arah dapat ditetapkanV= [a, by]. Dalam bidang xy dapat dikatakan bahwa V adalah suatu vektor dengan gradien bya. Sehingga dydx = bya. Solusinya
BAB 2. PDP LINIER ORDER SATU 9 tentu saja adalah y =Ceabx, dan sekaligus menjadi kurva karakteristikdari PDP
jenis ini. Kemudian aturan berantai didefinisikan sebagai berikut: ∂u(x, y) ∂x = ∂u ∂x ∂x ∂x + ∂u ∂y ∂y ∂x =ux+uyyx ∂u(x, y) ∂y = ∂u ∂x ∂x ∂y + ∂u ∂y ∂y ∂y =uxxy+uy
Untuk mendaptkan persamaan aux +byuy = 0 maka pastilah ∂u(x, y) = 0
sehingga solusinya adalah konstan. Sehingga solusi u(x, Cebax) akan memenuhi
bila x = 0. Dengan demikian u(x, Cebax) = u(0, Ceab0) = u(0, C). Karena y =
Cebax maka C = e−abxy sehingga u(x, y) = u(0, e−abxy). Hal ini berarti solusi
umum PDP itu adalah
u(x, y) =f(e−b
axy) (2.6)
Untuk meyakinkan fungsi u(x, y) = f(e−b
axy) benar-benar merupakan solusi
dari PDP 2.5 dapat dilakukan substitusi langsung terhadap persamaan tersebut, yaitu dengan menentukan ux =−abe−
b
axyf(e−baxy) danuy =e−abxf(e−abxy).
Contoh 2.1.2 Suatu PDP ux+yuy = 0 dengan sarat awal u(0, y) = y3 maka
solusi umum PDP ini adalah u(x, y) = f(e−xy). Nilai awal u(0, y) =y3
berimp-likasi f(y) = y3, dengan demikian u(x, y) = f(e−xy) = e−3xy3.
2.2
Aplikasi Sederhana PDP Order Satu
Suatu fluida, katakan zat cair, mengalir dengan laju konstan c sepanjang pipa horisontal dengan arah positip. Sebagai contoh kongkrit amati proses penyebaran polusi air. Bila u(x, t) adalah konsentrasi dalam gram/centimeter dalam waktu
BAB 2. PDP LINIER ORDER SATU 10 t, maka model arus ini dapat dimodel dalam persamaan difrensial parsial order satu sebagai:
ut+cux= 0 (2.7)
Untuk menurunkan rumus ini, asumsikan polusi itu bergerak sepanjang [0, b] maka jumlah polusi itu adalah M =R0bu(x, t)dx dalam gram. Saat selanjutnya, t+h, polusi bergerak kearah positif sepanjang ch centimeter sehingga
M =
Z b+ch
ch
u(x, t+h)dx.
Turunkan hasil pengintegralan persamaan ini terhadap b didapat u(b, t) =u(b+ch, t+h).
Selanjutnya gunakan aturan Chain untuk menurunkannya terhadap h, maka ∂u(b, t) ∂h = ∂u(b+ch, t+h) ∂h = ∂u ∂(b+ch) ∂(b+ch) ∂h + ∂u ∂(t+h) ∂(t+h) ∂h = ∂u ∂(b+ch)c+ ∂u ∂(t+h) 0 = cub+ch(b+ch, t+h) +ut+h(b+ch, t+h).
Gantib+chdengan xdan t+h dengan t, maka dapat disimpulkan cut(b, t) +cux(b, t) = 0,
atau
cut+cux = 0,
BAB 3
PDP Linier Order Dua
3.1
Klasifikasi
Persamaan PDP linier order dua dapat disajikan dalam bentuk
auxx+ 2buxy+cuyy +dux+euy+f u=g. (3.1)
Misaluxx diganti dengan α2uxx,uxy denganαβ,uyy denganβ2,ux denganα,
uy dengan β maka persamaan itu menjadi
aα2+ 2bαβ+cβ2+dα+cβ+f u=g
sehingga fungsi P(α, β) dapat didefinisikan sebagai
P(α, β) =aα2+ 2bαβ+cβ2+dα+cβ+f, dimana fungsi ini akan memenuhi sifat
• Merupakan fungsi hiperbolik bila b2−ac > 0
• Merupakan fungsi parabolik bila b2−ac= 0
BAB 3. PDP LINIER ORDER DUA 12 • Merupakan fungsi eliptik bila b2−ac < 0.
Dengan demikian PDP linier order dua dapat digolongkan dalam tiga klasifikasi tersebut.
Contoh 3.1.1 Tentukan klasifikasi dari PDP berikut
• 3uxx+ 2uxy + 5uyy+xuy = 0
• uxx+yuyy = 0
Secara umum PDP linier order dua disajikan dalam
n X i,j=1 aijuxixj+ n X i=1 biuxi+cu=d. (3.2)
Dipahami bahwauxixj =uxjxi maka koefisien-koefisien PDP itu juga akan berlaku
untuk aij =aji, dan koefisien itu dapat disajikan dalam matrik n×n A = [aij].
Nilai eigen dari matrik ini diperoleh dari menyelesaikan persamaandet(A−λI) = 0 dalam λ. Selanjutnya n merupakan order PDP,r menyatakan banyaknya nilai λyang nol dansmenyatakan banyaknya nilaiλyang positif maka klasifikasi PDP dalam bentuk itu adalah sebagai berikut:
• merupakan PDPhiperbolikbila r= 0 dans= 1 ataur= 0 dans=n−1 • merupakan PDPparabolik bila r >0 (atau jika det(A= 0)
• merupakan PDPeliptik bila r= 0 dan s= 0 atau r = 0 dans=n • merupakan PDPultrahiperbolik bila r= 0 dan 1< s < n−1
BAB 3. PDP LINIER ORDER DUA 13 Penyelesaian 3.1.1 Dengan memahami koefisien-koefisien PDP diatas maka matrik A dapat disajikan dalam:
A=
koef ux1x1 koef ux1x1 koef ux1x1
koef ux1x1 koef ux1x1 koef ux1x1
koef ux1x1 koef ux1x1 koef ux1x1
= 3 0 0 0 1 2 0 2 4
Ingat ux2x3 = ux3x2 dan dibagi 2 sebab permisalan kita 2bαβ.Dengan demikian
det(A−λI) = (3−λ)λ(λ−5) = 0, dimana λ1 = 0, λ1 = 3 dan λ1 = 5. Dapat
disimpulkan bahwa r >0 sehingga persamaan diatas merupakan PDP parabolik.
3.2
Persamaan Karakteristik
Penyelesaian PDP linier order dua secara analitik jauh lebih sulit diband-ingkan PDP linier order satu. Bahkan untuk kasus-kasus tertentu PDP ini tidak dapat diselesaikan dengan cara analitik. Salah satu cara yang paling mungkin adalah mengkaji persamaan karakterirtik dari PDP tersebut.
Untuk keperluan ini akan diperkenalkan variabel bebas baru ξ dan η sebagai koordinat transformasi dari variabel bebasx, y keξ, η, dimana kedua variabel ini saling bebas (lepas) dan dinyatakan sebagai fungsi ξ = φ(x, y) dan η = ψ(x, y) sehingga φxψy −φyψx = 0.
Selanjutnya persamaan 3.1 dapat ditulis dalam
auxx+ 2buxy+cuyy+ suku-suku dengan order lebih rendah, (3.3)
dapat dapat ditransformasikan kedalam bentuk
BAB 3. PDP LINIER ORDER DUA 14 Permasalahan yang muncul sekarang, bagaimana fungsi A, B dan C direpresen-tasikan.
Untuk menentukannya, akan digunakan aturan Chain untuk u(ξ, η) dimana ∂u ∂x = ∂u ∂ξ ∂ξ ∂x + ∂u ∂η ∂η ∂x ux = uξφx+uηψx, (3.5) sedangkan ∂u ∂y = ∂u ∂ξ ∂ξ ∂y + ∂u ∂η ∂η ∂y uy = uξφy +uηψy. (3.6)
Turunkan persamaan 3.5 terhadap x satu kali didapat
uxx =uξφxx+ (uξ)xφx+uηψxx+ (uη)xψx. (3.7)
Sementara
(uξ)x = uξξφx+uξηψx
(uη)x = uηξφx+uηηψx.
Substitusikan dua persamaan terakhir ini kedalam persamaan 3.7 didapat uxx =uξξφ2x+ 2uξηφxψx+uηηψ2x+uξφxx+uηψxx. (3.8)
Selanjutnya turunkan lagi persamaan 3.5 terhadap y dan juga turunkan per-samaan 3.6 terhadap y, dengan cara yang sama didapat
uxy = uξξφxφy+uξη(φxψy+φyψx) +uηηψxψy+uξφxy+uηψxy (3.9)
BAB 3. PDP LINIER ORDER DUA 15 Substitusikan ekspresi uxx, uxy dan uyy kedalam persamaan 3.3 didapat
auxx+ 2buxy +cuyy+R = (aφx2 + 2bφxφy+cφ2y)uξξ +2¡aφxψx+b(φxψy+φyψx) +cφyψy ¢ uξη +(aψ2 x+ 2bψxψy +cψy2)uηη+R.
Dengan demikian fungsi A, B dan C asosiatif dengan A = aφ2 x+ 2bφxφy+cφ2y B = aφxψx+b(φxψy+φyψx) +cφyψy C = aψ2 x+ 2bψxψy+cψ2y, sehingga auxx+ 2buxy+cuyy+R =Auξξ+ 2Buξη+Cuηη+R (3.11)
dimana R = (aφxx + 2bφxy +cφyy)uη + (aψxx+ 2bψxy +cψyy)uη. Bila φ dan ψ
adalah fungsi linier dari x, y maka dapat ditunjukkan bahwa R = 0. Persamaan karakteristik (3.11) dapat dipilih dalam bentuk
az2
x+ 2bzxzy +czy2 = 0. (3.12)
Selanjutnya persamaan karakteristik dari persamaan (3.1) didapat dari menyele-saikan persamaan
ady2 −2bdxdy+cdx2 = 0. (3.13) Teorema 3.2.1 z(x, y) =γ merupakan persamaan karakteristik dari persamaan (3.1) jika dan hanya jika z(x, y) =γ solusi dari (3.13), dimana γ =konstanta.
BAB 3. PDP LINIER ORDER DUA 16 Bukti 3.2.1 Misalz(x, y) =γ memenuhi persamaan dari persamaan (3.12) dan z(x, y) 6= 0. Definisikan suatu fungsi y = f(x, γ) dimana fx = 0 maka dengan
aturan Chain fx = ∂f ∂x ∂x ∂x + ∂f ∂γ ∂γ ∂x = 0 ∂f ∂x = − ∂f ∂γ ∂γ ∂x ∂y ∂x = − zx(x, y) zy(x, y)
Sekarang bagi persamaan (3.12 dengan z2
y didapat a¡zx zy ¢2 + 2bzx zy +c= 0, Dengan demikian a¡∂y ∂x ¢2 −2b∂y ∂x +c= 0 atau a¡dy dx ¢2 −2bdy dx +c= 0. Dengan kata lain z(x, y) =γ solusi dari (3.13).
Contoh 3.2.1 Tentukan jenis persamaan dan kurva karakteristik PDP berikut ini:
1. 2uxx−4uxy −6uyy+ux= 0
2. 4uxx+ 12uxy −9uyy−2ux+u= 0
BAB 3. PDP LINIER ORDER DUA 17 Penyelesaian 3.2.1 No. 1, dipahami bahwa a = 2, b = −2 dan c = −6 dan b2−ac= 16>0 sehingga persamaan ini merupakan PDP hiperbolik. Kemudian
dengan menggunakan koefisien-koefisien ini dihasilkan PDB 2¡dy dx
¢2
+4dy
dx−6 = 0.
Gunakan rumus abc untuk menentukan dy
dx didapat
dy
dx =−1±2.
Dengan demikian kurva karakteristiknya merupakan solusi PDB tersebut, yaitu x−y=γ, atau 3x+y=γ.
Untuk No. 2, dan 3, sebagai latihan individual.
3.3
Bentuk Kanonis
Transformasi dari persamaan difrensial parsial khusus untuk order lebih dari satu dipandang penting. Hal ini berguna dalam proses penyelesaian suatu PDP. Dengan bentuk kanonis suatu PDP dapat disederhanakan sehingga dapat diper-timbangkan apakah persamaan tersebut bisa diselesaikan secara analitik atau tidak. Bila solusi analitik dapat diraih, maka dari bentuk kanonis inilah solusi umum suatu PDP diturunkan.
Untuk keperluan ini dibutuhkan fungsi transformasi ξ = φ(x, y) dan η = ψ(x, y). Kemudian permisalkan kedua fungsi ini dalam persamaan karakteristik suatu PDP, selanjutnya lakukan transformasi. Dalam hal ini penentuan bentuk kanonis tergantung pada sisi prinsipal, artinya
1. Bila PDP itu merupakan persamaan hiperbolik maka sisi prinsipalnya adalah uξη atau uξξ−uηη atau A =C = 0 pada persamaan (3.11).
BAB 3. PDP LINIER ORDER DUA 18 2. Bila PDP itu merupakan persamaan parabolik maka sisi prinsipalnya adalah
uηη atau B =C = 0 pada persamaan (3.11).
3. Bila PDP itu merupakan persamaan eliptik maka sisi prinsipalnya adalah uξξ+uηη atau A=B = 0 pada persamaan (3.11).
Sebagai contoh akan ditentukan bentuk kanonis dari 2uxx−4uxy−6uyy+ux = 0.
PDP ini merupakan persamaan hiperbolik sehingga sisi prinsipalnya adalah uξη
atau A =C = 0 untuk persamaan (3.11). Sementara persamaan karateritiknya adalahx−y=γ dan 3x+y=γ. Tetapkanξ =φ(x, y) =x−ydanξ =ψ(x, y) = 3x+y, sehinggaφx = 1, φxx = 0, φy =−1, φyy = 0, φxy = 0;ψx = 3, φxx = 0, ψy =
1, φyy = 0, φxy = 0. Sekarang persamaan (3.11) menjadi
2(aφxψx+b(φxψy +φyψx) +cφyψy)uξη +uξφx+uηψx = 0
2(2φxψx−2(φxψy+φyψx)−6φyψy)uξη +uξφx+uηψx = 0
2£2(1)(3)−2¡(1)(1) + (−1)(3)¢−6(−1)(1)¤uξη+uξ(1) +uη(3) = 0
Dengan demikian bentuk kanonis PDP ini adalah 32uξη+uξ+ 3uη = 0.
Bandingkan bentuk ini dengan persamaan semula maka jelas diperoleh bentuk yang lebih sederhana. Tidak tertutup kemungkinan bentuk ini dapat diselesaikan secara analitik.
3.4
Sarat Bantu
Ada dua sarat bantu dalam PDP yaitu sarat awal dan sarat batas. Sarat awal adalah kodisi yang dipenuhi suatu PDP dalam domain Ω pada saat awal peristiwa
BAB 3. PDP LINIER ORDER DUA 19 fisika. Misal suatu persamaan dinyatakan dengan uxx−utt = 0 maka sarat awal
yang mungkin adalahu(x,0) =f(x). Sarat batas adalah sarat yang terjadi pada batas-batas domain awal dan akhir sustu PDP. Sarat batas ini dikelompokkan dalam tiga jenis sarat batas, yaitu:
• sarat batas Dirichlet u=g • sarat batas Neuman (flux) ∂u
∂n =g
• sarat batas Campuran αu+β∂u ∂n =g
BAB 4
Identitas Pertama dan Kedua
Green
Identitas Green banyak dipakai dalam pembahasan PDP dengan order lebih tinggi dari satu, dengan demikian informasi ini sangat penting untuk dipahami. Untuk membahas identitas pertama dan kedua Green dibutuhkan konsep dan notasi vektor sehingga dalam bab ini akan didahului dengan definisi dan teorema diferensial vektor ini.
Definisi 4.0.1 Bila f = f(x, y, z) adalah fungsi dalam C1(Ω) dimana Ω ∈ <n
maka gradf =∇f = ∂f ∂xi+ ∂f ∂yj + ∂f ∂zk
adalah gradien darif. Kemudian jikan adalah vektor satuan di<3 maka turunan
berarah dari f dalam arah n didefinisikan sebagai
∂f ∂n =∇f ·n= ∂f ∂xn1+ ∂f ∂yn2+ ∂f ∂zn3 20
BAB 4. IDENTITAS PERTAMA DAN KEDUA GREEN 21 Definisi 4.0.2 Jika w= w(x, y, z) adalah fungsi dalam C1(Ω) dimana Ω∈ <n,
atau w=w1(x, y, z)i+w2(x, y, z)j+w3(x, y, z)k maka divergensi dari w adalah
divw=∇ ·f = ∂w1 ∂x + ∂w2 ∂y + ∂w3 ∂z , sehingga div gradf =4f = ∇ · ∇f = · ∂ ∂x ∂ ∂y ∂ ∂z ¸ · · ∂f ∂x ∂f ∂y ∂f ∂z ¸T = ∇2f = ∂ 2f ∂x + ∂2f ∂y + ∂2f ∂z .
Kemudian disisi lain juga dikenal rotasi f yaitu
rotf =∇ ×f = i j k ∂ ∂x ∂y∂ ∂z∂ f1 f2 f3
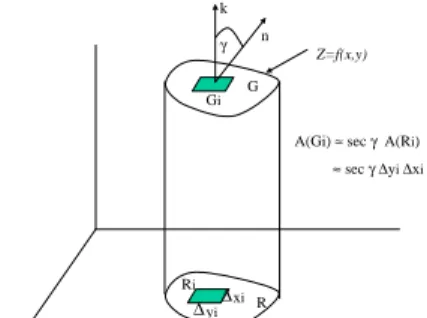
Teorema 4.0.1 (Integral Permukaan)MisalGsuatu permukaan yang diberikan oleh z = f(x, y), dengan (x, y) di R. Jika f ∈ C1(R) dengan g(x, y, z) =
g(x, y, f(x, y)) kontinyu pada R maka Z G Z g(x, y, z)ds = Z R Z g(x, y, f(x, y) secγ dA (4.1) = Z R Z g(x, y, f(x, y) q f2 x +fy2+ 1dydx (4.2)
BAB 4. IDENTITAS PERTAMA DAN KEDUA GREEN 22 k n Gi G Z=f(x,y) Ri R yi xi γ ∆ ∆
A(Gi) ≈ sec γ A(Ri)
≈ sec γ ∆yi ∆xi
Gambar 4.1: Luas Permukaan.
Selanjutnya andaikata G suatu permukaan dua sisi yang sedemikian mulus dan anggap bahwa ia terendam di dalam fluida dengan suatu medan kecepatan kontinyu F(x, y). Jika 4S adalah luas sepotong kecil dari G, maka disana F hampir konstan, dan volume fluida 4V yang melewati potongan ini dalam arah normal satuan n, lihat Gambar 4.2 adalah 4V ≈ F ·n4S. Dengan demikian disimpulkan bahwa
fluk F yang melintasiG=RGR F ·n dS (4.3)
G n F ∆S z y x
Gambar 4.2: Fluk medan vektor menembus permukaan.
Dalam hal ini juga dapat ditunjukkan bahwa rumus fluks F yang melintasi permukaan G dapat dikembangkan melalui beberapa teorema berikut.
BAB 4. IDENTITAS PERTAMA DAN KEDUA GREEN 23 Teorema 4.0.2 (Teorema Gauss) Misal F = Mi+Nj +P k berupa medan vektor dimana M, N, P ∈ C1(S) dan M, N, P ∈ C1(∂S) dan bila n merupakan
vektor normal satuan keluar dari ∂S maka Z ∂S Z F ·n dS= Z Z S Z divF dV. Lihat Kalkulus vektor untuk pembuktian
Teorema 4.0.3 (Teorema Divergensi) Jika Ω adlah daerah terbatas dengan batas berupa permukaan mulus sepotong-sepotong S. Misal terdapat sebarang garis memotong S pada titik tertentu, selanjutnya untuk sebuah vektor normal satuan keluar n =n(x)dari S jugaw adalah vektor kontinyu dimanaw∈C1(Ω)
dan w∈C0( ¯Ω) maka Z Z Ω Z ∇ ·w dΩ = Z S Z w·n dS
Teorema 4.0.4 (Identitas Green) Jika u dan v adalah fungsi skalar pada
C2(Ω) dan C1( ¯Ω), maka teorema divergensi dan teorema identitas diferensial
∇ ·(u∇v) = ∇u· ∇v +u∇2v akan membentuk rumus identitas Green pertama
dan kedua sebagai berikut: Z Ω u∇2v dΩ = Z S u∂v ∂ndS− Z Ω ∇u· ∇v dΩ (4.4) Z Ω (u∇2v−v∇2u)dΩ = Z S (u∂v ∂n−v ∂u ∂n)dS (4.5) dimana ∂v ∂n = ∂v∂xn1+∂v∂yn2+∂v∂zn3 =∇ ·n
BAB 4. IDENTITAS PERTAMA DAN KEDUA GREEN 24 Bukti 4.0.1 Rumus identitas diferensial memberikan
∇ ·(u∇v) = ∇u· ∇v+u∇2v
u∇2v = ∇ ·(u∇v)− ∇u· ∇v
Z Ω u∇2v dΩ = Z Ω ∇ ·(u∇v)dΩ− Z Ω ∇u· ∇v dΩ Lihat teorema divergensi
= Z S u∇v·n dS− Z Ω ∇u· ∇v dΩ = Z S u∂v ∂n dS− Z Ω ∇u· ∇v dΩ
Selanjutnya untuk identitas Green yang kedua dapat dibuktikan sebagai berikut:
Z Ω (u∇2v−v∇2u)dΩ = Z Ω u∇2v dΩ− Z Ω v∇2u dΩ = Z S u∂v ∂n dS− Z Ω ∇u· ∇v dΩ − Z S v∂u ∂n dS+ Z Ω ∇v· ∇v dΩ = Z S u∂v ∂n dS− Z S v∂u ∂n dS = Z S ¡ u∂v ∂n −v ∂u ∂n ¢ dS
BAB 5
Aplikasi PDP Order Dua
5.1
Vibrasi
5.1.1
Vibrasi Pada Senar
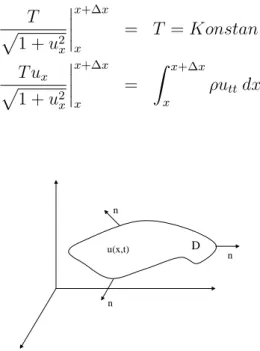
Vibrasi pada senar ini adalah suatu perumpamaan vibrasi pada dimensi satu. Pada aplikasi vibrasi dalam PDB peninjauan vibrasi ini hanya terfokus pada waktu t namun dalam PDP ini selain tergantung pada waktu posisi x juga dibicarakan. Misal y(x,t) adalah perpindahan dari titik setimbang pada saat t dan posisi x. Senar sangat fleksibel dan homogen sehingga tegangan merata disepanjang senar. Misal T(x, t) adalah besar tegangan dan ρ adalah densitas senar persatuan panjang maka dengan homogenitas senar gradien pada x+ ∆x adalah yx(x, t) atau [1yx], lihat Gambar 5.1 dan 5.2.
MisalT1 =T(x, t) danT2 =T(x+∆x, t) masing-masing tegangan kawat yang
terjadi di ujung-ujung P dan Q, maka kondisi dua gelombang, yaitu gelombang longitudinal (horisontal) dan transversal (vertikal) adalah sebagai berikut:
BAB 5. APLIKASI PDP ORDER DUA 26 1. pada gerakan horisontal
T1cosα = T2cosβ =T =Konstan
T1(1) p 1 +y2 x = pT2(1) 1 +y2 x =T =Konstan
2. pada gerakan vertikal
F = ma T2sinβ−T1sinα = ρ∆x∂ 2y ∂x2 T2yx p 1 +y2 x − pT1yx 1 +y2 x = ρ∆x∂2y ∂x2. P Q x x + x l x y 0 α β ∆ T(x,t) T(x+ x,t)∆
Gambar 5.1: Vibrasi senar dalam sistem koordinat
P Q α β 1 y x 1 + yx2
BAB 5. APLIKASI PDP ORDER DUA 27 Bagi kedua ruas dengan T pada gelombang longitudinal maka
T2sinβ T2cosβ − T1sinα T1cosα = ρ∆x T ∂2y ∂x2 1 ∆x[tanβ−tanα] = ρ 1 T ∂2y ∂x2.
Padahal tanβ adalah gradien padax+∆xsehingga tanβ =
µ dy dx ¶ x+∆x , demikian juga tanα adalah gradien pada x sehingga tanα=
µ dy dx ¶ x , sehingga 1 ∆x[ µ dy dx ¶ x+∆x − µ dy dx ¶ x ] = ρ T ∂2y ∂x2. (5.1)
Ingat definisi turunan pertama dari f(x), lim ∆x→0 f(x+ ∆x)−f(x) ∆x =f 0(x) = ∂f(x) ∂x .
Dengan demikian persamaan (5.1) menjadi lim ∆x→0 1 ∆x[ µ dy dx ¶ x+∆x − µ dy dx ¶ x ] = lim ∆x→0 ρ T ∂2y ∂x2 yxx = ρ Tytt
Dengan demikian vibrasi pada senar dalam simpangan u adalah
utt =c2uxx (5.2)
dimana c=
q
T
ρ, dan persamaan ini disebut juga persamaan umum gelombang
Selanjutnya variasi persamaan gelombang ini dinyatakan sebagai berikut: • bila terdapat gaya redaman utt−c2uxx +rut= 0, r >0
• bila terdapat gaya elastisitas transversal utt−c2uxx+ku= 0, k >0
• bila terdapat gaya luar dan bebas dari gaya redaman dan elastisitas transver-salutt−c2uxx =f(x, t)
BAB 5. APLIKASI PDP ORDER DUA 28
5.1.2
Vibrasi Pada Membran
Misalu(x, y, t) adalah gerak vertikal membran dengan domain D dan tegan-gan T, lihat Gambar 5.3. Sebagaimana pada vibrasi senar dibawah ini akan berlaku. T p 1 +u2 x ¯ ¯ ¯ ¯ x+∆x x = T =Konstan T ux p 1 +u2 x ¯ ¯ ¯ ¯ x+∆x x = Z x+∆x x ρuttdx D u(x,t) n n n
Gambar 5.3: Vibrasi vertikal membran
Dalam dimensi dua tidak lain sama dengan turunan berarah ∂u
∂n sehingga
persamaan itu dapat ditransformasikan dalam F = Z s T∂u ∂n ds= Z D Z ρutt dxdy=ma Padahal ∂u
∂n =∇u·n =n· ∇u sehingga
= Z s T(∇u·n)ds= Z D Z ρutt dD = Z D Z ∇ ·(T∇u)dD= Z D Z ρuttdD Sehingga ∇ ·(T∇u) = ρutt,
BAB 5. APLIKASI PDP ORDER DUA 29 dimana T adalah konstanta. Rumus terakhir inilah persamaan vubrasi dalam membran yang dapat ditulis secara umum sebagai berikut:
utt =c2∇ · ∇u (5.3)
dimana c = qT
ρ. Dalam hal ini ∇ · ∇u = div gradu dan dikenal sebagai
per-samaan Laplace yang dapat dikembangkan menjadi: • dalam dimensi dua ∇ · ∇u=uxx+uyy
• dalam dimensi tiga ∇ · ∇u=uxx+uyy +uzz
Penulisan ∇ · ∇u= ∆usehingga bentuk terumum dari vibrasi adalah
utt =c2∆u (5.4)
5.2
Difusi
Fenomena difusi banyak terjadi pada perusahaan perusahaan yang mengeloh bahan baku cairan. Salah satu contoh adalah gerakan zat pewarna dalam zat cair. Gerakan itu terjadi dari konsentrasi yang lebih tinggi ke konsentrasi yang lebih rendah. Tingkat gerakan berbanding lurus dengan arah konsentrasi (gradien berarah konsentrasi ∂u
∂n) yang selanjutnya dikenal dengan hukum difusi ”Fick”.
Misal u(x, t) adalah besar konsentrasi dengan satuan (massa per satuan pan-jang) dari zat pewarna pada posisi x pada pipa dalam waktu t, maka antara posisi x0 dan x1 jumlah massa dinyatakan dalam
M(t) =
Z x1
x0
BAB 5. APLIKASI PDP ORDER DUA 30 sehingga ∂M(t) ∂t = Z x1 x0 ut(x, t)dx. (5.5)
Dipahami juga bahwa perubahan massa tergantung pada perubahan konsentrasi masuk dan perubahan konsentrasi keluar sehingga
∂M(t)
∂t =k(ux(x1, t)−ux(x0, t)), (5.6) dimana k adalah konstanta proporsionalitas. Gabungan persamaan (5.5) dan (5.6) menghasilkan
Z x1
x0
ut(x, t)dx=k(ux(x1, t)−ux(x0, t)), (5.7)
kemudian turunkan terhadap x1
ut(x1,1) =kuxx1(x1, t),
dan ganti x1 =x sehingga ut(x, t) =kuxx(x, t) atau
ut=kuxx (5.8)
merupakan persamaan difusi yang dimaksud. Analog dengan vibrasi, persamaan difusi dapat dikembangkan menjadi
Z D Z utdD= Z s k∂u ∂n ds, lihat persamaan (5.7) Padahal ∂u
∂n =∇u·n =n· ∇u sehingga
Z D Z utdD = Z s k(∇u·n)ds = Z D Z ∇ ·(k∇u)dD = Z D Z k∇ · ∇u dD
BAB 5. APLIKASI PDP ORDER DUA 31 Sehingga ut =k∇ · ∇u yang secara umum ditulis sebagai
ut=k∆u
atau
ut =k(uxx+uyy) dalam dimensi dua (5.9)
ut =k(uxx+uyy +uzz) dalam dimensi tiga (5.10)
5.3
Aliran Panas
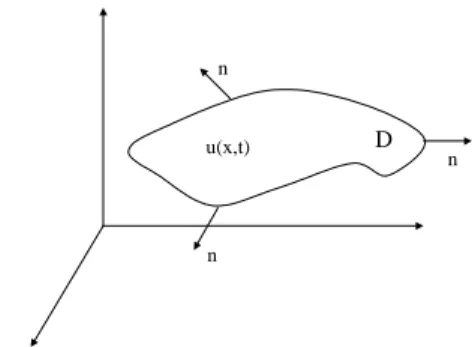
Penurunan rumus ini akan dikembangkan dari dua definisi khusus yang penulis anggap definisi ini dalam peristiwa fisik d=lahir dari beberapa aksioma-aksioma. Definisi 5.3.1 Misal B suatu benda pejal diruang, D sebarang daerah pejal diB
dengan batas permukaan S, lihat Gambar 5.4.
D
u(x,t)
n
n n
Gambar 5.4: Vibrasi vertikal membran
Bila u(x, y, z, t) adalah suhu di titik (x, y, z) pada B dan v kecepatan aliran panas pada B maka kecepatan itu disajikan dalam v = −k∇u dimana k adalah konduktivitas panas pada B. Jumlah panas yang keluar dari daerah D persatuan waktu adalah Hout(t) =
R
S
R
BAB 5. APLIKASI PDP ORDER DUA 32 H(t) = R RDR cρu dD, dimanacadalah kapasitas panas danρadalah rapat massa benda per satuan volum. Selanjutnya perubahan panas pada D adalah
∂H(t) ∂t = Z Z D Z cρutdD (5.11)
Definisi 5.3.2 Hukum Fourier mengatakan bahwa aliran panas dari yang bersuhu tinggi ke yang bersuhu lebih rendah sebanding dengan gradien suhu, dengan asumsi bahwa panas tidak akan lenyap kecuali meninggalkan daerah itu hanya melewati batas-batas permukaan S. Dengan demikian perubahan energi panas dalam D
sama dengan fluk panas melalui batas-batasnya, yaitu:
∂H ∂t = Z S Z k(n· ∇u)dS (5.12)
Dari (5.11) dan (5.12) dapat dikembangakan
Z Z D Z cρutdD = Z S Z k(n· ∇u)dS = Z Z D Z k∇ ·(∇u)dD = Z Z D Z k∇2u dD
atau cρut=k∇2u. Dalam bentuk yang paling umum adalah
ut=s2∆u
adalah persamaan aliran panas yang dimaksud, dimana s =
q
k
cρ sebuah
kon-stanta.
5.4
Vibrasi dan Aliran Panas Stasioner
Bila peristiwa fisika tidak berubah dengan adanya perubahan waktu maka dikatakan ut = utt = 0 sehingga kedua peristiwa ini dapat dinyatakan dalam
BAB 5. APLIKASI PDP ORDER DUA 33 persamaan
∆u= 0 (5.13)
Persamaan ini selanjutnya dinamakan persamaan Laplace dan solusinya dikatakan fungsi harmonik. Sebagai contoh, misal kita menaruh benda panas dalam oven dan ditutup rapat-rapat. Bila tidak ada jumlah panas yang meninggalkan ruang tertutup itu suhunya akan terus konstan dan inilah yang dikatakan sebagai titik setimbang.
BAB 6
Deret Fourier
6.1
Himpunan Fungsi Ortogonal dan
Ortonor-mal
Solusi analitik berdasarkan deret Fourier dikembangkan dari konsep keortog-onalan dan keortonormalan fungsi-fungsi, oleh karena itu akan didahulukan pem-bahasan terhadap konsep ini. Suatu definisi keortogonalan dan keortonornalan yang diungkapkan oleh Powell menyebutkan bahwa
Definisi 6.1.1 Dua fungsi f dan g yang terdefinisi pada interval[a, b] dikatakan ortogonal bila Rabf(x)g(x)dx = 0.
Sebagai contoh Powell menyebutkan
Contoh 6.1.1 f(x) = sinnx, g(x) = sinmx atau f(x) = cosnx, g(x) = cosmx untuk n 6= m dan n, m ∈ bilangan asli, adalah fungsi-fungsi ortogonal pada selang interval [0, π]
BAB 6. DERET FOURIER 35 Definisi 6.1.2 Dua fungsi f dan g yang terdefinisi pada interval[a, b] dikatakan ortonormal bila f dan g ortogonal dan juga memenuhi sifat Rabf2(x)dx = 1 dan
Rb
ag2(x)dx= 1.
sebagai implikasi dari definisi ini maka √Rfb(x)
af2(x)
dan √Rgb(x)
ag2(x)
adalah fungsi-fungsi ortonormal pada selang [a, b], (1981 : 107-123).
Selanjutnya masih meneruskan penjelasan Powell tentang definisi himpunan fungsi ortogonal dan ortonormal
Definisi 6.1.3 Himpunan fungsi-fungsi©φ1, φ2, . . . , φn
ª
yang terdefinisi pada in-terval [a, b] dikatakan himpunan ortogonal pada selang tersebut bila
Z b
a
φn(x)φm(x)dx= 0 ∀n 6=m
dan dikatakan ortonormal bila Z b a φn(x)φm(x)dx= 0 Jikam6=m 1 Jikam=n Dengan demikian bila ©φ1, φ2, . . . , φn
ª
adalah himpunan fungsi-fungsi ortogonal maka untukγn = µ Rb a φ2n(x)dx ¶1/2 >0, himpunan©φ1 γ1, φ2 γ2, . . . , φn γn ª adalah him-punan fungsi-fungsi ortonormal.
Definisi 6.1.4 Himpunan fungsi-fungsi©φ1, φ2, . . . , φn
ª
yang terdefinisi pada in-terval [a, b] dikatakan ortogonal terhadap fungsi bobot w(x) pada selang tersebut bila
Z b
a
w(x)φn(x)φm(x)dx= 0, ∀n6=m
dan dikatakan ortogonal terhadap fungsi bobot w(x) bila Z b a w(x)φn(x)φm(x)dx= 0 Jikam 6=m 1 Jikam =n
BAB 6. DERET FOURIER 36 Dapat dipahami bahwa definisi 6.1.3 adalah kasus khusus dari definisi 6.1.4 di-mana w(x) = 1.
6.2
Deret Fourier Diperumum
Untuk memberikan gambaran bagaimana konsep deret Fourier itu dibangun, diperlukan generalisasi dari beberapa definisi diatas. Beberapa konsep dibawah ini akan mengarahkan pada apa yang disebut dengan deret Fourier.
Definisi 6.2.1 Misal©φn(x)
ª
himpunan fungsi ortogonal pada interval[a, b]dan
f(x) adalah suatu fungsi yang terdefinisi pada selang tersebut, maka bila
cn=
Rb
afR(x)φn(x)dx b
aφ2ndx
, deret dengan ekspresi
∞
X
n=1
cnφn(x), x∈[a, b] (6.1)
merupakan deret Fourier diperumum dari f(x) pada interval [a, b] dimana cn
adalah koefisien Fourier dari f(x) terhadap himpunan ortogonal ©φn(x)
ª untuk
n = 1,2, . . .
Dua hal penting yang terjadi pada deret Fourier diperumum ini, 1. bila©φn(x)
ª
adalah himpunan ortonormal pada [a, b] maka cn menjadi
cn = Z b a f(x)φn(x)dx 2. bila ©φn(x) ª = ©1,cosnπx l sinnπxl ª
pada selang interval [−l, l] maka deret (6.1) menjadi a0 2 + P∞ n=1 µ ancosnπxl +bnsinnπxl ¶ (6.2)
BAB 6. DERET FOURIER 37 dimana a0 = 1 l Z l −l f(x)dx (6.3) an = 1 l Z l −l f(x) cosnπx l dx (6.4) bn = 1 l Z l −l f(x) sinnπx l dx (6.5)
Persamaan (6.2) selanjutnya disebutDeret Fourierdarif(x) pada selang (−l, l) dana0, an, bnadalah koefisien-koefisien Fourier dengan formulasi pada (6.3), (6.4)
dan (6.5).
6.3
Deret Fourier Cosinus dan Sinus
Pada kasus-kasus khusus deret Fourier itu tidak muncul dengan dua suku namun hanya satu suku cosinus atau sinus. Deret Fourier yang seperti ini disebut deret Fourier cosinus atau sinus. Untuk menurunan rumus ini terlebih dahulu dapat diingat kembali fungsi genap dan ganjil. Sebagaimana dijelaskan dalam Seeley
Definisi 6.3.1 Fungsi f(x) dikatakan fungsi genap pada selang interval (−l, l)
apabila f(x) =f(−x) dan dikatakan fungsi ganjil bila f(x) =−f(x) untuk ∀x∈ (−l, l).
Sebagai contoh Seeley memberikan beberapa kategori Contoh 6.3.1 Fungsi-fungsi
1. f(x) = a,|x|, x2, x4, x8, x2n,cosαx,secαx adalah fungsi-fungsi genap pada
BAB 6. DERET FOURIER 38
2. f(x) = x, x3, x5, x7, x2n−1,sinαx, cosec αx,tanαx, ctan αx adalah
fungsi-fungsi ganjil pada selang interval (−l, l) dan (−∞,∞) (1982 :86-95).
Beberapa sifat yang dipenuhi fungsi-fungsi genap dan ganjil diberikan dalam aksioma berikut ini.
Aksioma 6.3.1 Bila fungsi f(x) adalah fungsi 1. fungsi ganjil pada selang interval (−l, l) maka
Z l
−l
f(x)dx= 0
2. fungsi genap pada selang interval (−l, l) maka Z l −l f(x)dx = 2 Z l 0 f(x)dx Aksioma 6.3.2 Bila
1. f dan g adalah fungsi genap pada selang interval (−l, l) maka f±g, αf, f g
dan f /g,(g 6= 0) genap pada (−l, l).
2. f dan g adalah fungsi ganjil pada selang interval (−l, l) maka f ±g, αf
ganjil sedangkan f g dan f /g,(g 6= 0) genap pada (−l, l).
3. f genap dan g ganjil pada selang interval (−l, l) maka f g dan f /g,(g 6= 0)
ganjil pada (−l, l).
Dengan demikian bila f(x) terdefinisi pada (−l, l), maka untuk f(x) genap berdasarkan aksioma 6.3.1 dan 6.3.2 deret Fourier (6.2) dari f(x) menjadi
a0 2 + ∞ X n=1 ancos nπx l (6.6)
BAB 6. DERET FOURIER 39 dimana a0 = 2 l Z l 0 f(x)dx an = 2 l Z l 0 f(x) cosnπx l dx
Deret (6.6) dikenal sebagaideret Fourier cosinus darif(x) pada selang (−l, l). Sementara untuk f(x) ganjil deret Fourier (6.2) darif(x) menjadi
∞ X n=1 bnsin nπx l (6.7) dimana bn = 2 l Z l 0 f(x) sinnπx l dx
Deret (6.7) ini dikenal sebagaideret Fourier sinus darif(x) pada selang (−l, l). Misalf(x) terdefinisi pada selang interval (0, l), maka fungsif(x) dapat diper-luas pada selang (−l, l) sehingga f(x) genap pada selang ini dengan mengambil f(x) = f(−x) untuk (−l,0). Maka deret Fourier dari f(x) adalah
a0 2 + ∞ X n=1 ancos nπx l (6.8) dimana a0 = 2 l Z l 0 f(x)dx an = 2 l Z l 0 f(x) cosnπx l dx
Deret (6.8) merupakan deret Fourier cosinus dari f(x) pada selang (0, l). Dengan cara yang sama, f(x) dapat diperluas sehingga f(x) adalah ganjil pada selang (−l, l) dengan mengambilf(x) = f(−x) untuk (−l,0). Maka deret Fourier dari f(x) adalah ∞ X n=1 bnsin nπx l (6.9)
BAB 6. DERET FOURIER 40 dimana bn = 2 l Z l 0 f(x) sinnπx l dx
Deret (6.7) ini merupakan deret Fourier sinus dari f(x) pada selang (0, l). Sekarang kita tinjau deret Fourier dari f(x) pada selang (a, b). Ambil 2l = b−a sehingga (a, b) = (a, a+ 2l). Dengan mengambil a seagai −l dan b sebagai l maka deret Fourier dari f(x) pada selang (a, b) ditulis sebagai
a0 2 + ∞ X n=1 µ ancos 2nπx b−a +bnsin 2nπx l ¶ (6.10) dimana a0 = 2 b−a Z l −l f(x)dx an = 2 b−a Z l −l f(x) cosnπx l dx bn = 2 b−a Z l −l f(x) sinnπx l dx
Untuk lebih jelasnya dapat dikuti contoh berikut.
Contoh 6.3.2 Tentukan deret Fourier dari f(x) = x pada selang (0,1) Penyelesaian 6.3.1 Disinia= 0, b= 1 dengan demikian l =b−a= 1. Jadi
a0 = 2 1 Z 1 0 f(x)dx= 2 Z 1 0 x dx=x2 ¯ ¯ ¯ ¯ 1 0 = 1
BAB 6. DERET FOURIER 41 an = 2 Z 1 0 f(x) cos 2nπx dx= 2 Z 1 0 xcos 2nπx dx = 2 2nπ Z 1 0 x d(sin 2nπx) = 1 nπ ¡ xsin 2nπx ¯ ¯ ¯ ¯ 1 0 − Z 1 0 sin 2nπx dx¢ = 1 nπ ¡ 0 + 1 2nπ cos 2nπx ¯ ¯ ¯ ¯ 1 0 ¢ = 1 2n2π2 ¡ cos 2nπ−1¢= 0 bn = 2 Z 1 0 f(x) sin 2nπx dx= 2 Z 1 0 xsin 2nπx dx = − 2 2nπ Z 1 0 x d(cos 2nπx) = − 1 nπ ¡ xcos 2nπx ¯ ¯ ¯ ¯ 1 0 − Z 1 0 cos 2nπx dx¢ = − 1 nπ ¡ cos 2nπ− 1 2nπ sin 2nπx ¯ ¯ ¯ ¯ 1 0 ¢ = − 1 nπ cos 2nπ = 1 nπ
Dengan demikian deret Fourier dari f(x) =x pada selang (0,1) adalah 1 2 − 1 π ∞ X n=1 sin 2nπx n
Soal-Soal Latihan
1. Tentukan sifat kelinieran, kehomogenan dan order dari PDP dibawah ini (a) ut−uxx = 0
(b) ut−uxx+xu= 0
(c) utt−uxx+x2 = 0
(d) ux(1 +u2x)−1/2+uy(1 +u2y)−1/2 = 0
2. Bila F = x5y−2yz2 + 4xyz dan w = x2yzi+ 3xyz2j + (x2 −z2)k maka
tentukan hal berikut ini (a) ∇F, ∇ ·w, ∇ ×w (b) ∇ · ∇F,∇ ·(∇ ×w)
(c) ∂w
∂n, dimana n adalah normal vektor satuanw.
3. Selesaikan persamaan partial order pertama berikut ini. (a) 5ut+ 3ux = 0, dengan sarat u(x,0) = sinx
(b) 3uy +uxy = 0, (Petunjuk : permisalkan v =uy)
(c) (1 +x2)u
x+uy = 0, dengan saratu(0, y) =y2
(d) √1−x2u
x+uy = 0, dengan sarat u(0, y) =y
(e) yux+xuy = 0, dengan saratu(0, y) =e−y
2
43 (f) ux+uy =ex+2y, dengan sarat u(x,0) =y
4. Berilah tandaX untuk menentukan jenis PDP order dua berikut.
No Persamaan Eliptik Parabolik Hiperbolik
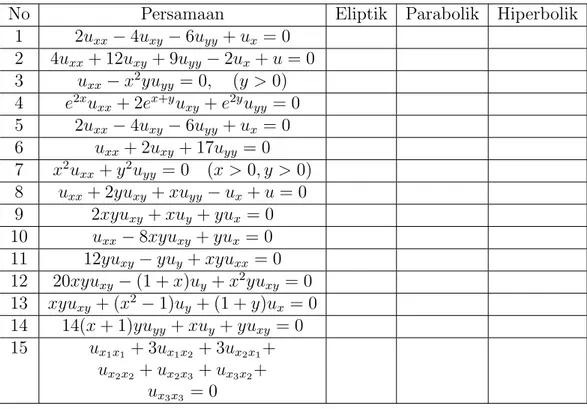
1 2uxx−4uxy −6uyy+ux = 0 2 4uxx+ 12uxy + 9uyy −2ux+u= 0 3 uxx −x2yuyy = 0, (y >0) 4 e2xu xx+ 2ex+yuxy+e2yuyy = 0 5 2uxx−4uxy −6uyy+ux = 0 6 uxx+ 2uxy + 17uyy = 0 7 x2u xx+y2uyy = 0 (x >0, y >0) 8 uxx+ 2yuxy +xuyy−ux+u= 0 9 2xyuxy +xuy+yux = 0 10 uxx−8xyuxy +yux = 0 11 12yuxy −yuy +xyuxx = 0 12 20xyuxy−(1 +x)uy +x2yuxy = 0
13 xyuxy + (x2−1)uy+ (1 +y)ux = 0
14 14(x+ 1)yuyy+xuy +yuxy = 0
15 ux1x1 + 3ux1x2 + 3ux2x1+
ux2x2 +ux2x3 +ux3x2+
ux3x3 = 0
Tabel 6.1: PDP order dua menurut jenisnya.
5. Pada soal nomor 4 diatas, masing-masing tentukan kurva karaketeristiknya. 6. Ulangilah soal nomor 4 untuk menentukan bentuk kanonis dari
masing-masing persamaan.
7. Selesaikan persoalan dibawah ini.
(a) Suatu senar panjangnya 2 m direntangkan dan kedua ujungnya diikat. Kemudian titik tengahnya diangkat (ditarik) setinggih, dan selanjut-nya senar dilepas dengan kecepatan awal nol. Tentukan model PDP getaran senar ini lengkap dengan sarat bantunya.
44 (b) Suatu bola pejal homogen dengan jari-jari R. Misal suhu awal adal f(r), dimana variabel r adalah jarak ke titik pusat bola, dan suhu pada permukaan bola adalah nol, sehingga suhu dalam bola adalah fungsi u(r, t). Tentukan model PDP aliran panas ini.
8. Selesaikan soal-soal berikut ini.
(a) Buktikan bahwa f(x) = sinnx dan g(x) = cosmx untuk n 6= m, dan n, melemen bilangan asli adalah ortogonal
(b) Buktikan bahwaf(x) = √1 lsin nπx l danf(x) = √1lsin mπx l untukn 6=m,
dan n, melemen bilangan asli adalah ortonormal
(c) Buktikan bahwa fn(x) = sinnπx dimana n = 1,2, . . . adalah
him-punan fungsi ortogonal (d) Buktikan bahwa f(x) = √1
lsin nπx
l dimana n = 1,2, . . . adalah
him-punan fungsi ortonormal
(e) Tentukan deret Fourier dari fungsi f(x) =x, −π < x < π (f) Tentukan deret Fourier dari fungsif(x) =x2, −π < x < π
9. Selesaikan soal-soal berikut. (a) L{eat}, L{e−at} (b) L{sinat}, L{cosat} (c) L{sinat}, L{cosat} (d) L−1{1 s}, L−1{e1at} (e) L−1{ 1 s2+a2}, L−1{s2+sa2} (f) sederhanakanL{ay00+by0+cy=0}
45 10. Buktikan bahwa u(x, y) = f(x)g(y) solusi dari PDP uuxy = uxuy untuk
seluruh pasangan berurut fungsi yang terdiferensialkan f dan g pada satu variabel.
11. Tunjukkan bahwa un(x, y) = sinnxsinhny merupakan solusi dari uxx +
uyy = 0 untuk setiap n >0.
12. suatu operator £dikatakn operator linier bila
£(u +v) =£u +£v £(cv) =c£v
dimana c adalah sebarang konstanta. Selanjutnya PDP £u = 0 adalah merupakan persamaan linier bila £ adalah operator yang linier. Untuk beberapa persamaan dibawah ini nyatakan ordernya, kelinierannya dan ke-homogenannya (a) ut−uxx+ 1 = 0 (b) ut−uxx+xu= 0 (c) ut−uxxt+uux = 0 (d) utt−uxx+x2 = 0 (e) iut−uxx+u/x= 0 (f) ux(1 +u2x)−1/2+uy(1 +u2y)−1/2 = 0 (g) ux+eyuy = 0 (h) ut+uxxxx+ √ 1 +u= 0
46 14. Selesaikan PDP 3uy +uxy = 0 (Petunjuk: Permisalkan v =uy).
15. Selesaikan PDP (1 +x2)u
x+uy = 0 denganu(0, y) = y2.
16. Selesaikan PDP yux+xuy = 0 dengan u(0, x) =e−y
2
. 17. Selesaikan PDP aux+buy+cu= 0.
18. Selesaikan PDP ux+uy +u=ex+2y denganu(x,0) = 0.
19. Gunakan metoda koordinat untuk menyelesaikan PDPux+2uy+(2x−y)u=
2x2+ 3xy−2y2.
20. Suatu vektor didefinisikan sebagaif(x, y, z) = x2yzi+ 3xyz2j+ (x2−z2)k.
Tentukan div f dan rotf.
21. Tentukan fluks keatas dari F = −yi+xi+ 9k yang melintasi permukaan bola z=p9−x2−y2; 0≤x2+y2 ≤4.
22. Diberikan w =w(x, y, z) = xi+yj +zk. Misal Ω adalah suatu bola yang berpusat di (0,0,0) dengan jari-jari a maka tunjukkan bahwa kasus ini memenuhi teorema divergensi diatas.
23. Amati persamaan difrensialuxx−4uxy + 4uyy = 0.
(a) Berikan informasi lengkap tentang tipe persamaan ini.
(b) Tunjukkan bahwa u(x, y) = f(y+ 2x) +xg(y+ 2x) untuk sebarang f dan g merupakan solusi persamaan tersebut. (Petunjuk : Gunakan substitusi langsung.)
(c) Untuk sarat bantu u(0, y) = e−3y+4 dan u
x(0, y) = 2y, tentukan solusi
47 24. Sebutkan jenis PDP order dua ini, (1 +x)uxx+ 2xyuxy−y2uyy = 0,
selan-jutnya tentukan kurva karakteristik dan bentuk kanonisnya.
25. (Teorema Divergensi.) Jika Ω adalah daerah sebarang dengan batas permukaan S, sedangkan n adalah vektor normal satuan kearah luar dari S maka untuk sebarang vektorv ∈Ck(Ω), k = 0,1,2 akan berlaku
Z Ω ∇ ·v dΩ = Z S v·n dS.
Selanjutnya buktikan bahwa untuk sebarang u ∈ Ck(Ω) tersebut akan
berlaku (a) RΩu∇2v dΩ =R Su∂n∂v dS− R Ω∇u· ∇v dΩ (b) RΩ¡u∇2v−v∇2u¢dΩ =R S ¡ u∂v ∂n −v∂u∂n ¢ dS
26. Dalam fenomena riel suatu PDP akan muncul bersama-sama dengan sarat bantunya yaitu sarat batas dan sarat awal.
(a) Tentukan tiga jenis sarat batas yang anda ketahui (b) Bila diberikan model PDP
utt = c2uxx+h(x), 0< x < l, t >0
u(0, t) = A, ux(l, t) +αu(l, t) =A
u(x,0) = f(x), ut(x,0) =g(x)
tentukan sarat batas jenis apa yang dimiliki dan sebutkan pula sarat awalnya.
(c) Suatu kawat yang panjangnya l direntangkan dan titik tengahnya di-angkat (ditarik) setinggi h. Kemudian kawat tersebut dilepas den-gan kecepatan awal v(x) sehingga terjadi peristiwa getaran denden-gan
48 model persamaanutt =c2uxx, dimanau(x, t) menunjukkan simpangan
getaran kawat. Tentukan sarat bantu peristiwa getaran ini kemudian susun suatu model PDP lengkap dengan sarat bantunya, lihat point (b). 27. Diketahui f(x) = 1; 0< x < π 2 : π < x <2π f(x+ 2π)
(a) Gambarlah fungsi tersebut.
(b) Tentukan deret Fourier yang sesuai dengan f(x).
(c) Berdasarkan jawaban (b) diatas tentukan f(0), f(π) dan f(2π) (d) Dengan memasukkan nilai x= π
2 pada deret Fourier soal (b), tentukan
deret numerik untuk π
4.
28. f(x) adalah fungsi periodik dengan periode 2π, dan didefinisikan dengan f(x) =x, −π < x < π
(a) Tentukan deret Fourier yang sesuai untuk f(x). (b) Dengan memasukkan nilai x = π
2 pada deret Fourier pada soal (a),
tentukan deret berganti-ganti tanda untuk π
4
(c) Dari deret Fourier (a), hitunglah f(x) untukx=−π dan x=π. 29. HitunglahRπ0exsinnxdx
49 30. Tunjukkan bahwaf(x) yang didefinisikan oleh
f(x) = −k; −π < x <0 k : 0< x < π f(x+ 2π)
adalah fungsi ganjil, dan gambarlah. Kemudian tentukan deret fourier sinus dari f(x).
31. Tunjukkan bahwaf(x) yang didefinisikan oleh
f(x) = x+ 1; 0< x < π −x+ 1 : −π < x <0 f(x+ 2π)
adalah fungsi genap, dan gambarlah. Kemudian tentukan deret fourier cosinus dari f(x).
32. Deret Fourierf(x) pada selang interval (−l, l) adalah a0 2 + ∞ X n=1 ¡ ancos nπ l x+bnsin nπ l x ¢
dimana a0, an dan bn adalah koefisien-koefisien Fourier yang terdefinisi
se-cara khusus. Selanjutnya bila
f(x) = 0; −π 2 < x <0 2 : 0< x < π 2
Tentukan deret Fourier f(x) ini pada selang interval (−π
2,
π