2.1. Analisa Getaran
Analisa getaran merupakan salah satu alat yang sangat bermanfaat sebagai prediksi awal terhadap adanya masalah pada mekanikal, elektrikal dan proses pada peralatan, mesin-mesin dan sistem proses yang kontinu di pabrik. Sehingga analisa getaran saat ini menjadi pilihan teknologi predictive maintenance yang paling sering digunakan [8].
Disamping manfaatnya dalam hal predictive maintenance, teknik analisa getaran juga digunakan sebagai teknik untuk mendiagnosa, yang dapat diaplikasikan antara lain untuk: acceptance testing, pengendalian mutu, mendeteksi bagian yang mengalami kelonggaran, pengendalian kebisingan, mendeteksi adanya kebocoran, desain dan rekayasa mesin, dan optimasi produksi.
2.1.1. Karakteristik Getaran
Getaran secara teknis didefenisikan sebagai gerak osilasi dari suatu objek terhadap posisi objek awal/diam, seperti yang ditunjukkan pada gambar 2.1. Gerakan massa dari posisi awal menuju atas dan bawah lalu kembali ke posisi semula, dan akan melanjutkan geraknya disebut sebagai satu siklus getar. Waktu yang dibutuhkan
untuk satu siklus disebut sebagai periode getaran. Jumlah siklus pada suatu selang waktu tertentu disebut sebagai frekuensi getaran [9].
Gambar 2.1. Sistem getaran sederhana
Frekuensi adalah salah satu karakteristik dasar yang digunakan untuk mengukur dan menggambarkan getaran. Karakteristik lainnya yaitu perpindahan, kecepatan dan percepatan. Setiap karakteristik ini menggambarkan tingkat getaran, hubungan karakteristik ini dapat dilihat pada gambar 2.2.
Perpindahan (displacement) mengindikasikan berapa jauh suatu objek bergetar, kecepatan (velocity) mengindikasikan berapa cepat objek bergetar dan percepatan (acceleration) suatu objek bergetar terkait dengan gaya penyebab getaran. Satuan yang digunakan tiap karakteristik dapat dilihat pada Tabel 2.1. Untuk keperluan program preventive maintenance, kecepatan getar adalah karakteristik yang penting untuk diukur.
Tabel 2.1. Karakteristik dan satuan getaran
Satuan
Karakteristik Getaran Metrik British
Perpindahan microns peak-to-peak (1µm=0.001mm) mils peak-to-peak (0.001 in) Kecepatan Mm/s in/s Percepatan G (1g = 980 cm/s2) G (1g = 5386 in/s2) Frekuensi cpm, cps, Hz cpm, cps, Hz (Sumber: Maintenance Engineering Handbook)
2.1.2. Gerak Harmonik
Getaran dari sebuah mesin merupakan resultan dari sejumlah getaran individu komponen yang muncul oleh gerak ataupun gaya pada komponen mekanikal ataupun proses pada mesin ataupun sistem yang saling terkait. Setiap komponen individu yang bergetar ini memiliki gerak periodik. Gerakan akan berulang pada periode waktu tertentu. Interval atau selang waktu τ , dimana getaran berulang biasanya diukur dalam satuan waktu yaitu detik.
Setiap frekuensi komponen mesin dapat dihitung dengan rumus berikut ini:
τ
1 =
f (2.1)
dan frekuensi lingkaran atau kecepatan sudut dapat dihitung dengan rumus
τ π
ω =2 1 (2.2)
dengan substitusi pers (2.1) terhadap persamaan (2.2), maka
f π
ω =2 (2.3)
Besaran ω biasanya diukur dalam radian per detik.
Bentuk sederhana dari gerak periodik disebut sebagai gerak hamonik, lihat Gambar 2.2. Pada gerak harmonik, hubungan antara perpindahan maksimum dan waktu dapat ditampilkan:
t X
x= sinω (2.4)
Perpindahan adalah ukuran dari jarak aktual yang dilalui komponen mesin yang timbul dari getaran komponen. Nilai maksimum dari perpindahan yaitu X , yang disebut sebagai amplitudo getaran.
Kecepatan dalam gerak harmonik berdasarkan persamaan (2.4) dapat diperoleh dari hasil diferensial perpindahan terhadap waktu, yaitu:
( )
X t x dt dx ω ω cos = = & (2.5)Persamaan (2.5) menunjukkan bahwa kecepatan juga dinyatakan sebagai getaran harmonik dengan nilai maksimum yaitu ω . X
Sedangkan percepatan harmonik dapat diturunkan dari persamaan (2.5) sehingga:
(
X)
t x dt d ω ω sin 2 2 2 − = = && (2.6)Persamaan (2.6) menjelaskan bahwa percepatan juga dinyatakan sebagai getaran harmonik dengan nilai maksimum yaitu ω2X .
2.1.3. Gerak Periodik
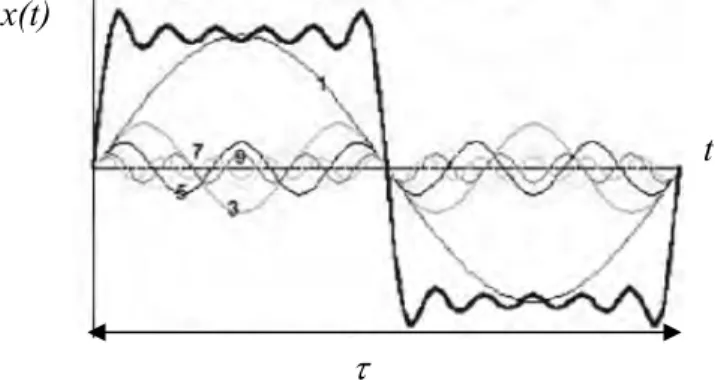
Getaran mesin pada umumnya memiliki beberapa frekuensi yang muncul bersama-sama. Gerak periodik dapat dihasilkan oleh getaran bebas sistem dengan banyak derajat kebebasan, dimana getaran pada tiap frekuensi natural memberi sumbangan. Getaran semacam ini menghasilkan bentuk gelombang kompleks yang diulang secara periodik seperti ditunjukkan pada Gambar 2.3.
Gambar 2.3. Gerak periodik gelombang sinyal segiempat dan gelombang pembentuknya dalam domain waktu
t x(t)
Gerak harmonik pada Gambar 2.3, dapat dinyatakan dalam deretan sinus dan cosinus yang dihubungkan secara harmonik. Jika x(t)adalah fungsi periodik dengan periode τ , maka fungsi ini dapat dinyatakan oleh deret Fourier [10]sebagai:
t a t a t a a t
x( )= 12 0 + 1cosω1 + 2cosω2...+ ncosωn
t b
t b
t
b1sinω1 + 2sinω2 ...+ nsinωn
+ (2.7)
dengan
τ π
ω1 = 2 ; ωn =2ω1
Pada gelombang segiempat berlaku x(t)= ± pada t =0, dan t =X τ, dan seterusnya. Deret ini menunjukkan nilai rata-rata dari fungsi yang diskontinu. Untuk menentukan nilai koefisien a dan n b , kedua ruas persamaan (2.7) dengan cos tn ω dan sin tω , kemudian setiap suku diintegrasi untuk lama perioda τ . Dengan mengingat hubungan berikut, = ≠ =
∫
mt ntdt jikajikamm nn , 2 , 0 cos cos 0 τ ω ω τ = ≠ =∫
mt ntdt jikajikamm nn , 2 , 0 sin sin 0 τ ω ω τ (2.8) = ≠ =∫
mt ntdt jikajika mm nn , 0 , 0 cos sin 0 τ ω ωDari persamaan (2.8), maka untuk m = n, diperoleh hasil
∫
= τ ω τ 20 ( )cos 1 tdt t x an n (2.9)∫
= τ ω τ 20 ( )cos 1 tdt t x bn n (2.10)Persamaan deret Fourier berdasarkan nilai gelombang empat persegi:
X t x( )= untuk 0 < t < τ/2 dan X t x( )=− untuk τ/2 < t < τ Maka koefisien a dan n b dapat dihitung, sebagai berikut: n
0 cos cos 2 1 2 2 0 = − =
∫
∫
τ τ τ ω ω τ X dt X dt an n nkarena, cos cos 0
2 2 0 = =
∫
∫
τ τ τ ω ωndt ndt dan − =∫
∫
τ τ τ ω ω τ 2 2 0 sin sin 2 1 dt X dt X bn n n[
τ]
τ τ ω ω τ 2 0 2 (cos ) ) (cos ) 2 ( 1 n n X X n + =[
(1 cos ) (1 cos )]
) 2 (τ n nτ2 nτ2 X − + − =akan menghasilkan nilai b =0 untuk n bilangan genap, dan n b =n 4X τ2untuk n bilangan ganjil. Sehingga deret Fourier untuk gelombang empat persegi menjadi:
+ + + + = .... 7 7 sin 5 5 sin 3 3 sin sin 8 ) (t X t t t t x τ (2.11)
2.1.4. Getaran Yang Tereksitasi Secara Harmonik
Pada sebuah sistem yang dipengaruhi oleh eksitasi harmonik paksa, maka respon getarannya akan berlangsung pada frekuensi yang sama dengan frekuensi eksitasi/perangsangnya. Salah satu sumber eksitasi harmonik adalah ketidak seimbangan pada mesin-mesin yang berputar. Eksitasi ini mungkin tidak diinginkan oleh mesin karena dapat mengganggu operasinya atau mengganggu keamanan struktur mesin itu bila terjadi amplitudo getaran yang besar.
Gambar 2.4. Gaya pengganggu harmonik dari ketidak seimbangan yang berputar
Perhatikan sistem pegas massa yang dibatasi untuk hanya bergerak dalam arah vertikal dan dirangsang oleh mesin yang berputar yang tidak seimbang, seperti terlihat pada Gambar 2.4. Ketidakseimbangan itu ditunjukkan oleh massa eksentrik
mdengan eksentrisitas eyang berputar dengan kecepatan sudut ω . Dengan mengambil x sebagai simpangan massa yang tak berputar
(
M −m)
dari posisiωt m M 2 k 2 k c x
setimbang statik, maka simpangan m adalah x+esinωt[11]. Jadi persamaan geraknya adalah: x c kx t e x dt d m x m
M − )&&+ ( + sin )=− − &
( 22 ω
yang dapat disusun kembali menjadi:
t me kx x c x M + &+ =( ω2)sinω && (2.12)
Dengan mengganti (meω2)dengan o
F yang disebut gaya harmonik, maka persamaan
(2.12) identik dengan persamaan gerak sistem dengan satu derajat kebebasan yang mengalami redaman karena kekentalan, yaitu:
t F kx x c x
M&&+ &+ = osinω (2.13) Solusi khusus persamaan (2.13) adalah osilasi keadaan tunak (steady state) dengan frekuensi ω yang sama dengan frekuensi eksitasi. Solusi khusus dapat diasumsikan berbentuk
) sin(ω −φ
= X t
x (2.14)
dengan X adalah amplitudo osilasi dan φadalah beda fasa simpangan terhadap gaya eksitasi.
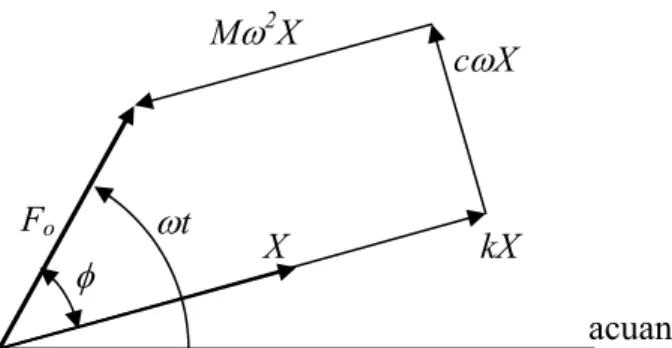
Amplitudo dan fasa pada persamaan (2.16) dapat diperoleh dengan mensubstitusikan persamaan (2.16) ke dalam persamaan diferensial (2.15). Dengan mengingat bahwa dalam gerak harmonik fasa kecepatan dan percepatan masing-masing mendahului fasa simpangan pada 90o dan 180o, maka suku-suku persamaan diferensial tadi juga dapat ditunjukkan secara grafik pada Gambar 2.5.
Gambar 2.5. Hubungan vektor untuk getaran paksa dengan redaman
Dari diagram vektor pada Gambar 2.5, dapat dilihat bahwa:
2 2 2) ( ) (k Mω cω F X o + − = (2.15) dan tan 1 2 ω ω φ M k c − = − (2.16)
2.1.5. Getaran Non Linier
Pada sistem pegas-massa sederhana yang ditunjukkan pada Gambar 2.6, persamaan karakteristik sistem ini dinyatakan sebagai,
0 = + kx
x
m && (2.17)
Persamaan (2.17) ini dikenal sebagai persamaan linier yang didasarkan pada asumsi bahwa pegas elastis mengikuti hukum Hooke, dimana kurva karakteristik dari gaya dan perpindahan berupa garis lurus.
acuan kX cωX Mω2X X ωt φ Fo
Gambar 2.6. Sistem pegas-massa sederhana
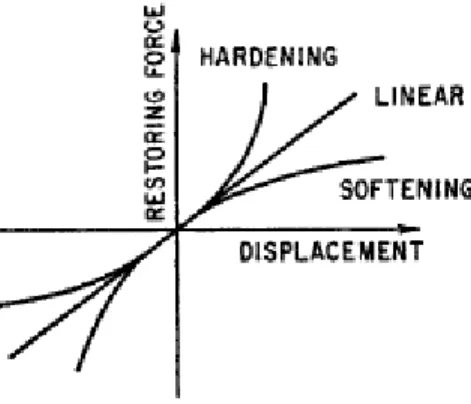
Pada kenyataannya, kebanyakan bahan tidak menunjukkan karakteristik linear. Pada kasus kumparan pegas sederhana, deviasi dari linear timbul ketika mengalami kompresi yang besar dan kumparan hampir menutup, demikian juga sebaliknya ketika mengalami regangan yang sangat besar hingga kumparan kehilangan identitas individunya. Dari kedua kasus tersebut, pegas menampilkan suatu karakteristik bahwa gaya reaksi meningkat pesat dibanding perpindahan. Karakteristik seperti ini disebut juga hardening.
Sama seperti halnya pada sistem pegas massa, sistem pendulum sederhana juga menunjukkan karakteristik yang disebut softening. Kedua tipe karakteristik ini dapat dilihat pada Gambar 2.7. Suatu sistem sederhana dengan gaya restoring berupa
softening dan hardening dapat digambarkan dalam bentuk persamaan,
0 ) ( ± 2 3 = +k x x x m&& µ (2.18)
Yang mana tanda (+) untuk karakteristik hardening dan tanda (-) untuk karakteristik
Gambar 2.7. Kurva karakteristik gaya restoring untuk sistem getaran linier, hardening dan softening
Bentuk lain dari sistem yang non linier dapat dilihat pada amplitudo getaran dawai (string) yang diberi massa terpusat, seperti yang ditampilkan pada Gambar 2.8.
Gambar 2.8. Getaran dari dawai yang dibebani
Persamaan diferensial untuk sistem non linier adalah,
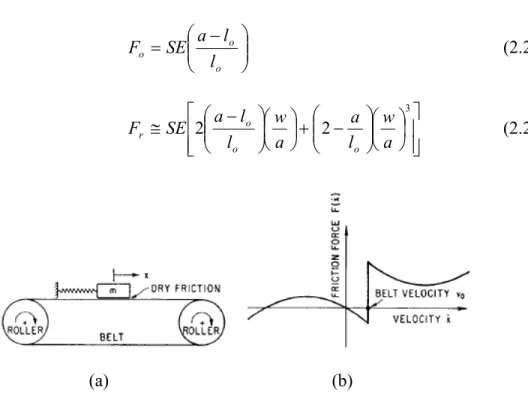
0 2 ) ( 1 3 3 3 3 3 = + − + + w b a b a F SE w ab F w m&& o o (2.19)
Dimana F adalah initial tension, S adalah luas penampang, dan E adalah modulus o
elastisitas dawai. Apabila a = b dan dengan panjang setengah dari panjang dawai l . o
− = o o o l l a SE F (2.20) − + − ≅ 3 2 2 a w l a a w l l a SE F o o o r (2.21) (a) (b)
Gambar 2.9. Sistem friksi sabuk:(a) Getaran tereksitasi sendiri pada sistem friksi sabuk dan (b) Kurva karakteristik gaya redaman pada sistem friksi (a)
Pada sistem friksi sabuk pada Gambar 2.9 (a), kondisi non linier terjadi akibat friksi kering antara massa dan sabuk yang bergerak. Sabuk dengan kecepatan konstan
o
v , dan persamaan geraknya adalah,
0 ) ( + = +F x kx x m&& & (2.22)
dimana gaya friksi F & ditampilkan pada Gambar 2.9 (b). Untuk nilai perpindahan (x) yang besar maka redaman dinyatakan positif, memiliki kemiringan positif, dan menghilangkan energi dari sistem. Sedangkan untuk nilai perpindahan yang kecil, redaman dinyatakan negatif dan, memiliki kemiringan negatif dan menambah energi pada sistem.
2.1.6. Pengukuran Gerakan dan Persamaan Dasar
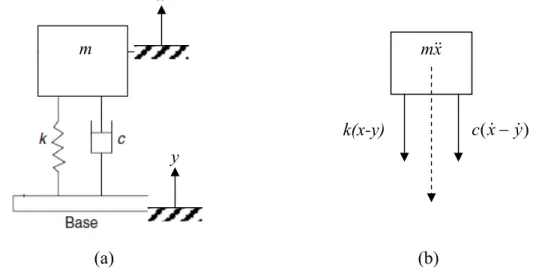
Pada pengukuran getaran struktur/mesin yang bergetar pada Gambar 2.10, alat ukur dipasang pada struktur/mesin yang hendak diukur, mempunyai gerakan absolut
t Y
y= sinωf , yang hanya bergerak dalam arah vertikal. Massa kecil dari struktur pendukung dapat diabaikan karena dapat dianggap sebagai bagian dari mesin.
(a) (b)
Gambar 2.10. Respon alat pengukur gerakan dan diagram benda bebas massa bergetar
Elemen-elemen alat ukur terdiri dari m, k, c. Perpindahan absolut massa m dan base masing-masing adalah x dan y, sehingga perpindahan relatif massa m terhadap base adalah z=x−y. Dan hasil pengukuran alat ini merupakan fungsi dari gerak relatif tadi. Dari diagram benda bebas yang ditunjukkan pada Gambar 2.10.(b), persamaan diferensial yang mengatur gerakan massa m [12], yaitu:
) ( ) (x y c x y k x
m&&=− − − &− & (2.23) Substitusikan z=x−ydan turunannya ke dalam persamaan (2.23), maka diperoleh:
x m &&
m
x
y
z c kz y
z
m(&&− )&& =− − &
y m kz z c z
m&&+ &+ =− &&
mz&&+ &cz+kz =−mωf2Ysinωft (2.24) Sisi kanan persamaan (2.24) adalah gaya paksa akibat getaran struktur yang diukur, sedangkan sisi kiri adalah getaran relatif alat ukur. Penyelesaian steady-state persamaan ini adalah:
2 2 2 ) 2 ( ) 1 ( ) sin( ) / ( r r t k Y m z f f ξ ψ ω ω + − − = ) sin( ) 2 ( ) 1 ( 2 2 2 ψ ω ξ − + − = Y t r r r z f (2.25) dimana: 2 1 2 tan r r − = ξ ψ , ω ωf r = , m k = ω
Persamaan (2.25) adalah persamaan dasar untuk alat ukur getaran. Simbol y dan turunannya terhadap waktu adalah simbol yang menunjukkan getaran struktur yang diukur.
Untuk sinyal getaran yang hanya memiliki komponen satu harmonik tunggal, ada dua pilihan untuk menggambarkan amplitudo getaran yaitu:
a. Amplitudo nilai single-peak (SP) = X b. Amplitudo nilai peak-to-peak (PP) = 2X
Meskipun demikian, sinyal getaran seringkali merupakan sinyal yang bersumber dari lebih dari satu sinyal harmonik, bahkan beberapa, dan oleh sebab itu suatu nilai rata-rata dari amplitudo getaran sering digunakan untuk menyatakan besar sinyal getaran. Dua perjanjian nilai rata-rata dimaksud adalah nilai absolut rata-rata dan nilai RMS, yang merupakan evaluasi dari selang waktu ∆t berikut ini [13],
∫
∆ + ∆ = = t t t dt x t average A 1 (2.26) 2 1 2 1 ∆ = t+ t∫
∆ t dt x t RMSaverage (2.27)Dan untuk sinyal harmonik sederhana pada persamaan (2.25), kedua persamaan nilai rata-rata (2.26) dan (2.27) akan menghasilkan nilai amplitudo sebenarnya, yakni
X
A=0.637 dan RMS =0.707X
Pada analisa dinamika rotor dan pada penentuan tindakan perbaikan (trouble
shooting) dari mesin-mesin berputar, tindakan verifikasi dan hasil prediksinya
dipengaruhi oleh instrumentasi dan teknik pengukuran yang digunakan [13].
2.1.6.1. Pemilihan Parameter dan Transducer
Dalam pemilihan parameter yang akan diukur seringkali ditentukan berdasarkan spesifikasi ataupun standar yang tersedia. Dalam kasus dimana hal ini tidak tersedia maka pertimbangan pada Tabel 2.2. dapat digunakan [14], atau menggunakan flattest spectrum rule.
Tabel 2.2. Panduan pemilihan parameter yang akan diukur
No. Parameter Faktor pemilihan
1. Percepatan a. Digunakan pada frekuensi tinggi dimana pengukuran memberikan
output sinyal paling tinggi
b. Digunakan ketika gaya, beban dan tarikan perlu dianalisa-dimana gaya proporsional terhadap percepatan
c. Digunakan ketika diperlukan transducer yang berukuran kecil dan massa kecil.
2. Kecepatan a. Digunakan ketika pengukuran getaran perlu dikorelasi dengan pengukuran bunyi, karena tekanan bunyi (sound pressure) proporsionl terhadap kecepatan getaran permukaan.
b. Digunakan pada frekuensi sedang dimana batas output pengukuran perpindahan sangat kecil untuk mengukur dengan baik.
c. Digunakan secara ekstensif pada pengukuran mesin dimana spektrum kecepatan lebih seragam dibandingkan dengan spektra perpindahan dan percepatan
d. Digunakan ketika pengukuran pada struktur resonansi dikorelasi dengan
modal stress, karena modal stress proporsional terhadap kecepatan
modal pada frekuensi resonansi
3. Perpindahan a. Digunakan ketika amplitudo dari perpindahan sangat penting–misalnya komponen yang bergetar tidak boleh tersentuh atau dimana perpindahan diatas nilai yang diberikan merusak mesin
b. Digunakan ketika besar perpindahan mengindikasikan stress untuk dianalisa
c. Digunakan pada frekuensi rendah, dimana output accelerometer atau
velocity pick-ups terlalu kecil untuk pengukuran yang baik.
d. Digunakan untuk mengukur gerak relatif antara badan dan struktur dari mesin
4. Strain Digunakan ketika sebagian dari spesimen perlu diuji variasi strain –nya terhadap pengaruh getaran, biasanya dibatasi pada frekuensi rendah
Sumber: Harris’ Shock and Vibration Handbook. 5th ed New York: McGraw Hill.. 2002 p 15.5
2.1.6.2. Pemasangan Transducer Pengukur Sinyal Getaran
Berbagai metode pemasangan transducer pada permukaan yang diuji, antara lain:
1) Transducer dengan ikatan baut pada permukaan uji dengan menggunakan ulir 2) Transducer dengan ikatan semen pada permukaan uji
3) Transducer dengan ikatan lapisan lilin
4) Transducer dengan magnet permanen dilekatkan pada permukaan yang
ferromagnetic
5) Transducer dipasang pada keranjang pada permukaan yang diuji 6) Transducer di pegang langsung dengan tangan terhadap permukaan uji.
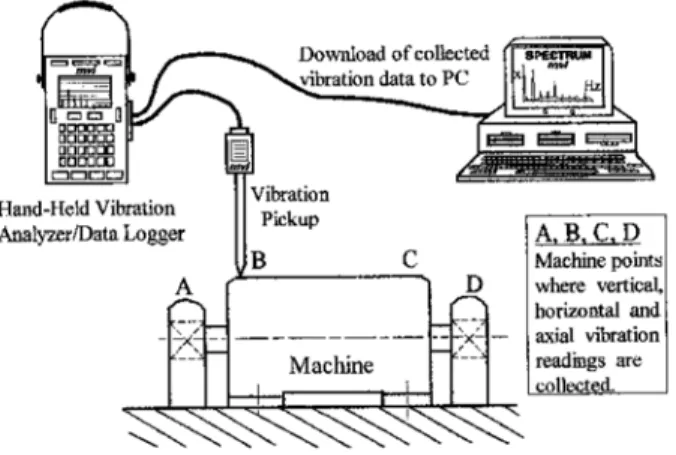
Suatu alternatif dengan biaya yang cukup murah dalam pemantauan secara kontinu sinyal getaran adalah dengan mengambil data getaran dari mesin pada interval waktu rutin melalui alat vibration analyzer genggam yang dapat menampilkan output analisa getaran langsung ditempat seperti (nilai puncak, filter, RMS dan lainnya) dan spektrum FFT. Alat genggam ini dilengkapi dengan sebuah
accelerometer vibration pick-up, sehingga teknisi pemeliharaan dapat secara aman
menyentuh bagian yang akan dipantau pada tiap mesin dalam pemeriksaan rutin seperti ilustrasi pada Gambar 2.11.
2.1.7. Analisa Sinyal Getaran dan Identifikasi Penyebab Getaran
2.1.7.1. Kecenderungan (trend) getaran , nilai acuan (baseline), dan standar
Pada mesin yang beroperasi dalam kondisi paling baik sekalipun, pemantauan sinyal getaran akan memunculkan amplitudo, meskipun berada pada tingkat getaran yang dapat diterima. Suatu perubahan adalah dampak yang wajar dari adanya perubahan kondisi operasi, misalnya: perubahan suhu, perubahan beban, keausan, dan fluktuasi dari lingkungan mesin. Dan pada saat amplitudo berada diatas baseline, maka trend perlu dicermati oleh teknisi agar tetap secara kontinu menguji kebutuhan potensial terhadap:
a. Adanya perubahan kondisi operasi mesin yang sementara b. Penjadwalan dini terhadap tindakan perbaikan
c. Penghentian segera operasi mesin oleh karena adanya kenaikan yang signifikan dari amplitudo getaran mesin.
Ketika tingkat getaran mesin mulai bertambah melampaui tingkat baseline, seperti yang dapat dilihat pada Gambar 2.12, hal ini menandakan masalah pada mesin mulai timbul, dan pertambahan pada tingkat getaran seringkali bukan merupakan gejala dari masalah tersembunyi. Perhatian diberikan pada mesin yang mulai menunjukkan kenaikan pada tingkat getarannya.
Data baseline yang dimaksud adalah sekumpulan data yang diukur atau diobservasi pada saat mesin beroperasi dan dapat diterima dan stabil. Hasil pengukuran dapat dibandingkan dengan nilai baseline untuk mendeteksi adanya perubahan. Data baseline hendaknya secara akurat mendefinisikan kondisi stabil dari mesin, terutama kondisi operasi normalnya. Oleh karena itu pada mesin dengan kondisi operasi berbeda, baseline untuk perbedaan kondisi ini juga berbeda.
Untuk mesin baru atau telah diperbaiki, maka akan ada periode keausan. Sehingga, umumnya akan terlihat perubahan nilai yang diukur selama beberapa hari atau minggu selama beroperasi. Maka, perlu diberikan waktu untuk terjadinya keausan sebelum data baseline diambil.
Sedangkan untuk mesin yang telah beroperasi pada periode waktu yang cukup lama, dan baru pertama kali dipantau, baseline dapat diambil sebagai titik referensi adanya
trend. Untuk mengevaluasi tingkat keparahan (severity) dari sinyal getaran pada
mesin berputar, International Organization for Standardization (ISO) telah menerbitkan suatu standar untuk mengevaluasi berdasarkan kelas dan tipe dari mesin yang disajikan pada Tabel 2.3 [14].
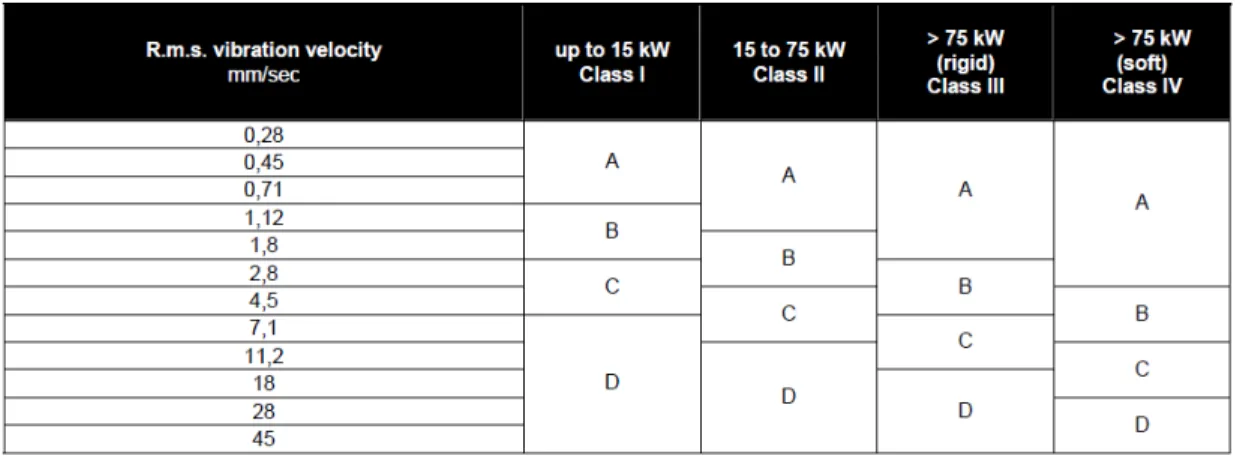
Tabel 2.3 Kriteria zona evaluasi tingkat getaran tipikal
(sumber: Reference Standar for Vibration Monitoring and Analysis)
Pada standar tersebut, parameter yang diukur adalah kecepatan getaran dan dibandingkan nilai RMS kecepatan berdasarkan klasifikasi daya mesin yaitu:
a. Kelas I (Class I) untuk mesin dengan daya dibawah 15 kW b. Kelas II (Class II) untuk mesin dengan data diantara 15 – 75 kW c. Kelas III (Class III), untuk mesin rigid dengan daya diatas 75 kW d. Kelas IV (Clas IV), untuk mesin fleskibel dengan daya diatas 75 kW Sedangkan A, B, C, D pada Tabel 2.3 menunjukkan zona kriteria evaluasi yaitu:
a. Zona A, yaitu getaran pada mesin yang baru dipasang dan akan diserah terimakan
b. Zona B, yaitu getaran pada mesin yang dapat diterima dengan syarat mesin tidak boleh dioperasikan secara terus menerus/lama.
c. Zona C, yaitu getaran pada mesin yang dianggap tidak memuaskan untuk pengoperasian terus menerus untuk waktu yang lama. Umumnya mesin
dioperasikan untuk waktu yang terbatas pada kondisi ini, sampai kesempatan untuk tindakan perbaikan dilakukan.
d. Zona D, yaitu nilai getaran yang dapat mengakibatkan kerusakan pada mesin.
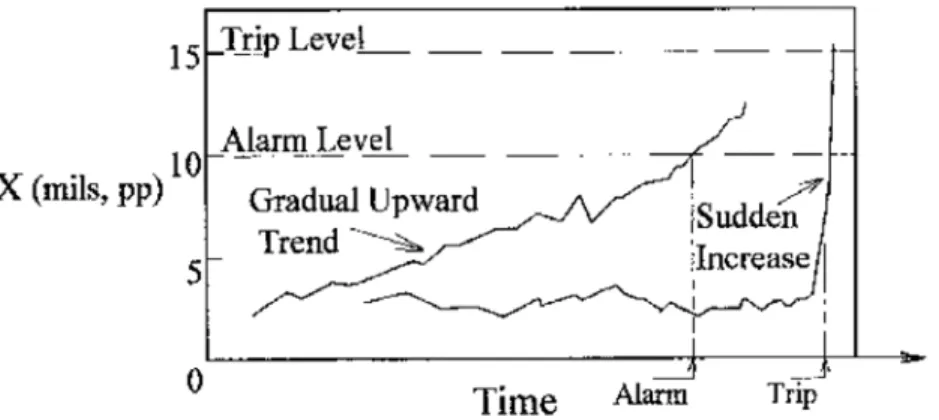
Untuk mesin-mesin yang didesain dengan jam operasi yang panjang/lama maka diberikan secara praktis ISO 10816-3 yang memberikan batasan getaran operasional, yaitu alarms dan trips.
Alarms merupakan nilai batas dari getaran yang ditentukan untuk memberikan
peringatan dini bahwa getaran sudah mencapai ataupun ada perubahan yang signifikan. Apabila batas alarms terjadi, pengoperasian mesin dapat dilanjutkan untuk sementara waktu sambil dilakukan investigasi untuk mengidentifikasi penyebab perubahan getaran dan menentukan tindakan perbaikannya. Nilai batas alarm pada standar adalah 1,25 kali di atas batas zona B.
Trips merupakan batasan getaran mendekati tingkat getaran yang dapat menyebabkan
kerusakan pada mesin. Apabila batasan trip sudah dicapai, maka tindakan perbaikan harus segera dilaksanakan untuk mengurangi getaran dan mesin dihentikan pengoperasiannya. Nilai batas trips pada standar adalah 1,25 kali di atas batas zona C.
2.1.7.2. Spektrum Frekuensi
Ide dasar dari transformasi Fourier adalah fungsi suatu sinyal domain waktu dapat dibangun dari penjumlahan fungsi sinus dengan distibusi berkelanjutan dari
frekuensi, mulai dari nol sampai kepada frekuensi yang diinginkan. Pada sinyal getaran periodik yang berulang atau pada periode tertentu, deret Fourier dapat diaplikasikan dan jumlah komponen sinus hanya pada frekuensi diskrit yang merupakan perkalian integer, n = 1, 2,...dari frekuensi dasar.
Meskipun getaran mesin sering memiliki jumlah komponen harmonik signifikan yang terbatas, frekuensi tersebut sering pula bukan merupakan perkalian integer dari frekuensi dasar, dan oleh karena itu transformasi Fourier, dan bukan deret Fourier, adalah alat yang memadai untuk melacak sinyal getaran mesin dari domain waktu menjadi domain frekuensi [14].
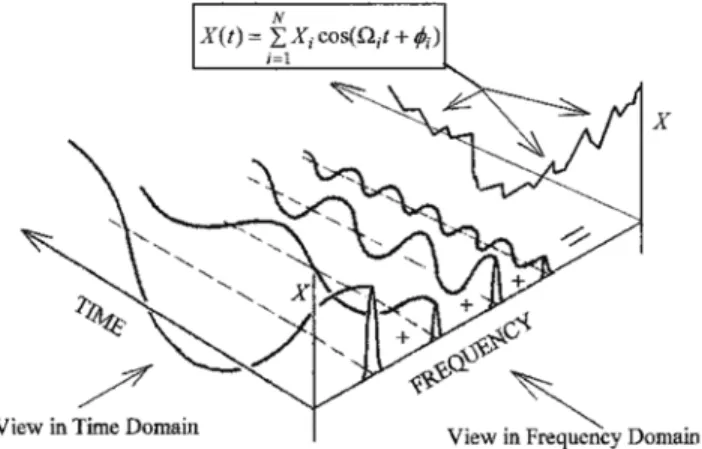
Hubungan antara sinyal fungsi waktu, X(t) dan spektrum frekuensi atau transformasi Fourier, dapat dilihat pada Gambar 2.13. Dengan mentransformasikan sinyal domain waktu menjadi domain frekuensi, komponen yang mempengaruhi sinyal getaran tersebut dapat diidentifikasi.
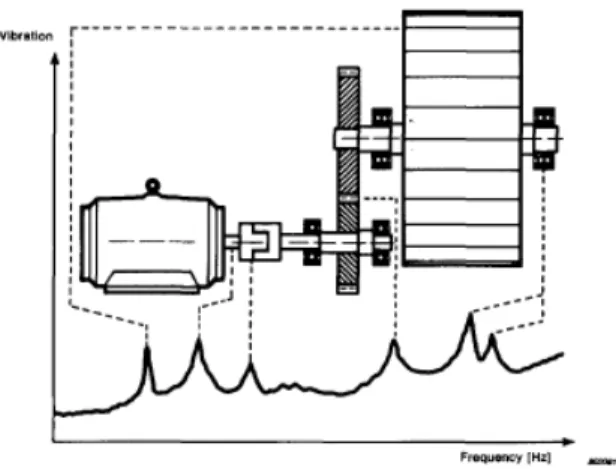
Analisa spektrum sinyal berbasis waktu digunakan untuk kebutuhan berbagai investigasi, terutama untuk mendiagnosa dan menyelesaikan masalah getaran seperti dapat dilihat pada Gambar 2.14.
Spektrum dari sinyal getaran yang diukur dari sebuah mesin berputar dapat dilihat pada Gambar 2.15. Frekuensi komponen 1N (satu per revolusi atau synchronous) seringkali yang paling besar, karena adanya massa unbalance pada bagian rotor. Komponen harmonik dengan perkalian integer dari frekuensi (2N, 3N, ....) dari kecepatan putaran juga muncul, namun amplitudonya relatif lebih kecil.
Gambar 2.14. Kegagalan pada elemen mesin akan memunculkan amplitudo pada frekuensi tertentu
Harmonik pada frekuensi subsynchronous juga sering dijumpai, mulai dari persentase kecil dari kecepatan putaran hingga hampir mendekati komponen 1N. Secara khusus untuk kepentingan penelitian ini, maka frekuensi komponen untuk mengindentifikasi getaran [15] dapat dilihat pada Lampiran 3.
Gambar 2.15. Suatu sinyal getaran dari mesin berputar dalam spektrum frekuensi
2.1.7.3. Rotor Orbit Trajectories
Rotor orbit trajectories secara khusus digunakan untuk analisa pada lateral rotor vibration (LRV), yang memberikan tambahan informasi diagnosa komponen
mesin yang bermanfaat untuk analisa trouble shooting. Hal ini terutama untuk mengindentifikasi penyebab natural dari masalah getaran pada mesin-mesin berputar. LRV, juga disebut transverse rotor vibration adalah gerak orbit pada bidang radial terhadap sumbu putar rotor.
Model sederhana dari LRV yaitu gerakan orbit rotor yang memiliki dua derajat kebebasan (degree of freedom), seperti yang ditampilkan pada Gambar 2.16. Pada model ini, masa rotor m, dapat berubah posisi pada bidang radial x-y. Massa ini terhubung dengan struktur melalui pegas dan peredam yang tereksitasi oleh gaya radial yang berubah terhadap waktu, misalnya gaya akibat massa unbalance
Gambar 2.16. Model LRV sederhana dua derajat kebebasan
Dua persamaan gerak dari model ini yang dipengaruhi oleh gaya eksitasi yang berasal dari F =ma, maka diperoleh,
t F x k x c x
m&&+ &x + x = ocosω (2.28)
t F y k y c y
m&&+ y&+ y = osinω (2.29) Pada kondisi isotropik, yaitu: kx =ky ≡k dan cx =cy ≡c, maka persamaan (2.28) dan (2.29) dapat di tulis dalam bentuk matrix,
= + + ) ( ) ( 0 0 0 0 0 0 t F t F y x k k y x c c y x m m y x & & && && (2.30)
Untuk menggambarkan resultan dari perpindahan sistem pada persamaan (2.30) yang bergetar pada sumbu x dan y dengan frekuensi yang sama ω , maka setiap gerak harmonik dapat disajikan sebagai vektor dan berlaku penjumlahan vektor.
Apabila dianggap bahwa massa m dari kondisi unbalance dianggap berosilasi secara simultan dengan gerak harmonik sederhana yang memiliki frekuensi yang sama menurut sumbu x dan y. Maka perpindahan dari partikel dapat dituliskan:
) sin( t x X x= ω +φ (2.31) ) sin( t y Y y = ω +φ (2.32)
Dengan menghilangkan waktu t pada persamaan (2.31) dan (2.32), maka variabel yang tersisa adalah hanya x dan y, sementara X , Y , φx, dan φy merupakan konstanta. Dengan mengembangkan argumen dari sinus, maka diperoleh:
x x t t X x ω φ ω φ sin cos cos sin + = dan, y y t t Y y ω φ ω φ sin cos cos sin + = maka,
(
x y y x)
x y t Y y X x φ φ ω φ φ φ φ sin cos sin cos sin sin sin − = − (2.33) dan(
x y y x)
y x t X x Y y φ φ ω φ φ φ φ sin cos sin cos cos cos cos − = − (2.34)Dengan melakukan perkalian kuadrat dan penjumlahan terhadap persamaan (2.33) dan (2.34) maka,
(
y x)
(
y x)
XY xy Y y X x φ φ φ φ − = + −2 cos − sin 2 2 2 2 2 (2.35)Biasanya sumbu utama dari elipse akan menanjak terhadap sumbu x dan y, tetapi hal ini akan menjadi sumbu utama ketika ada perbedaan fase φy −φx =π 2, maka persamaan (2.35) menjadi bentuk yang lebih dikenal,
1 2 2 2 2 = + Y y X x (2.36)
Jika X =Y = A, maka persamaan (2.36) menjadi x2 + y2 = A2. Saat
x y φ
φ − = 0, 2π, 4π, dan seterusnya, maka akan diperoleh persamaan
x X Y y=
yang merupakan suatu garis lurus yang memiliki kemiringan Y/X. Kembali lagi untuk φy − = φx π, 3π, 5π, dan seterusnya, akan diperoleh:
x X Y y=−
yang merupakan suatu garis lurus namum dengan kemiringan yang berlawanan. Lintasan jejak partikel ini dapat dilihat pada Gambar 2.17 dan secara mudah dapat digambarkan dengan menggunakan program simulasi matematika Matlab versi 6.1.
Untuk menggambarkan kurva dua dimensi dari fungsi x dan y dengan menggunakan Matlab versi 6.1. digunakan perintah ”ezplot”. Berdasarkan fungsi dasar pada persamaan (2.31 dan 2.32), maka kurva koordinat diketahui:
) sin( ), sin( ) , (x y = t t+δ , dimana: δ π π π π π π π ,2π 4 7 , 2 3 , 4 5 , , 4 3 , 2 , 4 , 0 =
Dengan memberikan perintah kedalam MatLab versi 6.1 untuk tiap φ, yaitu: >> ezplot('sin(t)','sin(t+δ )')
Maka diperoleh kurva untuk masing-masing φ seperti pada Gambar 2.17.
Gambar 2.17 Berbagai lintasan orbit dalam sistem getaran yang simultan pada sumbu yang tegak lurus dimana gerak harmonik sederhana memiliki frekuensi yang sama.
Untuk menggambarkan gerak partikel unbalance dalam ruang tiga dimensi, persamaan fungsi ditambahkan dalam arah sumbu z. sehingga ada persamaan gerak harmonik sederhana ketiga yaitu:
) sin( t z Z
z= ω +φ (2.37)
Apabila X=Y=Z=A, maka kurva koordinat dalam dimensi ruang adalah: ) sin( ), sin( ), sin( ) , , (x y z = t t+δ t , δ=0 δ=π/4 δ=π/2 δ=3π/4 δ=π δ=5π/4 δ=3π/2 δ=7π/4
perintah yang dituliskan kedalam MatLab versi 6.1 untuk φ =π 2, yaitu: >> ezplot3(’sin(t)’,’sin(t+π )’,’sin(t)’) 2
akan menghasilkan lintasan orbit dalam dimensi ruang dengan pada frekuensi yang sama seperti yang ditunjukkan pada Gambar 2.18.
Gambar 2.18. Lintasan orbit perpindahan partikel dalam dimensi ruang
2.2. Model Skala Centrifugal Fan
Secara teknis, fan dan blower merupakan dua alat/mesin yang berbeda namun
memiliki fungsi yang sama yaitu memindahkan sejumlah udara atau gas pada tekanan tertentu. Istilah fan untuk menyatakan mesin yang tekanannya tidak melebihi 2 psig, sedangkan blower untuk menyatakan mesin dengan tekanan discharge antara 2 – 10 psig. Untuk mesin dengan tekanan discharge di atas 10 psig disebut sebagai kompresor. Istilah blower juga digunakan untuk kompresor rotari (positive
2.2.1 Klasifikasi Fan
Fan dapat diklasifikasikan dalam dua klasifikasi yaitu: axial fan dan centrifugal fan. Axial fan beroperasi seperti propeler, yang menghasilkan aliran
udara disepanjang porosnya yang dapat dilihat pada Gambar 2.19.
Gambar 2.19. Tiga jenis blade axial fan
Centrifugal fan menghasilkan aliran udara dengan mempercepat arus udara
secara radial dan mengubah energi kinetik menjadi tekanan. Centrifugal fan dapat menghasilkan tekanan tinggi dengan efisiensi tinggi, dan dapat dibuat dalam berbagai tingkat kondisi operasional. Berbagai jenis centrifugal fan dapat dilihat pada gambar 2.20.,yang memiliki beberapa jenis blade, antara lain:
a) Forward curve fan, memiliki kecepatan putar yang sangat rendah untuk mengalirkan sejumlah udara. Fan jenis ini biasanya diaplikasikan untuk sistem pemanas bertekanan rendah, ventilasi, dan air conditioning
b) Radial blade fan, secara umum yang paling efisien diantara centrifugal fan yang memiliki bentuk blade mengarah titik poros. Fan jenis ini digunakan untuk pemindahan bahan dan industri yang membutuhkan fan dengan tekanan di atas menengah.
Gambar 2.20. Lima jenis blade centrifugal fan
c) Radial tip fan, lebih efisien dibandingkan fan tipe radial blade yang di desain tahan terhadap keausan dan aliran udara yang erosif.
d) Backward-inclined fan memiliki blade yang lurus dengan ketebalan tunggal.
Fan ini diaplikasikan pada sistem pemanas, ventilasi, air conditioning dan
industri dimana blade akan mengalami lingkungan yang korosif dan erosif. e) Air foil fan adalah tipe centrifugal fan yang dikembangkan untuk memperoleh
efisiensi tinggi. Fan ini diaplikasikan pada sistem pemanas, ventilasi, air
conditioning dan udara bersih industri untuk penghematan energi
(a) (b)
2.2.2. Prinsip dan Desain Model Skala
Persyaratan dari suatu model yang diskalakan yaitu memenuhi tiga tujuan berikut ini:
a. Dapat mentranformasikan secara proporsional fitur pada kondisi asli yang sulit untuk ditangani sehingga dapat dikelola, seperti: ukuran yang sangat besar, aliran yang sangat lambat, pelepasan energi yang sangat cepat, dan dimensi yang mikroskopis.
b. Memperpendek waktu eksperimen dengan menyederhanakan sejumlah variabel.
c. Dapat memberikan pemahaman yang mendalam terhadap suatu fenomena.
Berbagai jenis model telah banyak digunakan dengan tujuan berbeda, antara lain: 1) Model subjektif, model ini merupakan model konseptual yang dikembangkan
oleh filsuf atau sosiologis, untuk merefleksikan pandangannya terhadap struktur kemanusiaan dan lingkungan sosial.
2) Model kualitatif, model ini merupakan model yang sesuai dengan spesifikasi, contohnya:
a) Breadboard model, yang memiliki sedikit kemiripan, namun fisiknya dapat membantu dalam memastikan suatu alat baru dapat berfungsi dengan baik. b) Mock-up model, yang menampilkan bagian eksternal dari suatu konsep baru
c) Test bed, pilot plant, dan development model, yang merupakan perangkaian awal elemen yang esensial dari mesin baru, dengan tujuan untuk mengetahui adanya malfuction dan untuk mengarahkan pengembangan selanjutnya.
d) Prototype, merupakan produk akhir dari tahap pengembangan, dapat dilakukan penyesuaian final dan mengawali suatu seri dari produksi awal. 3) Model Analog, model ini dirancang untuk menampilkan hubungan kuantitatif
antar parameter yang dapat diatur, contoh sederhananya: model boneka dari mobil, kapal, pesawat terbang, dan peta geografi.
4) Model Matematis, model ini berkembang dengan adanya komputer dan analisis sistem yang diterapkan mulai ilmu pengetahuan hingga keilmuan yang tidak dapat diukur secara kualitatif seperti, perilaku manusia, proses kejiwaan, fungsi biologis, rencana tata kota, dan management.
5) Model Skala, merupakan suatu model eksperimen/pengujian untuk menampilkan perilaku fisik dari suatu fenomena asli, atau suatu prototype.
Model skala merupakan suatu pengganti yang valid dari suatu sistem yang oleh karena (terlalu besar, terlalu kecil, terlalu pelan, terlalu cepat, terlalu mahal, tidak dapat diakses, dan tidak dapat dikelola), tidak dapat di eksplorasi di tingkat
prototype. Apabila dapat diskalakan dengan benar, maka paramater fisik yang dapat
diukur dan relevan pada model skala dapat memberikan prediksi secara kuantitatif yang berhubungan dengan rancangan prototype.
Perilaku yang homologos dari elemen model dapat dijamin apabila setiap
parameter, variabel dalam skalar, vektor dan tensor dari tiap elemen prototype dapat ditranformasikan melalui perkalian dari suatu konstanta atau faktor skala. Faktor skala adalah suatu konstanta yang merupakan harga pembesaran atau pengecilan dari ukuran sebenarnya.
Faktor model skala secara umum dapat dikelompokkan menjadi dua yaitu: 1) Faktor skala primer
2) Faktor skala sekunder
Tabel 2.4. Faktor skala primer yang disyaratkan pada ilmu fisika
Faktor Skala Primer Bidang Panjang l* Waktu t* Gaya F* Suhu θ* Arus Listrik i* Geometri 9 - - - - Kinematika 9 9 - - - Statika 9 - 9 - - Dinamika 9 9 9 - - Thermodinamika 9 9 9 -
Perpindahan kalor dan
massa 9 9 9 9 -
Elektrostatis 9 - 9 - 9
Elektrodinamis
Elektromagnetis 9 9 9 - 9
Magnethidrodinamik 9 9 9 9 9
sumber: Scale Models in Engineering Fundamental and Application, Pergamon Press, Oxford, 1977,p.33.
Faktor skala primer dalam penerapannya dibidang ilmu fisika dapat dilihat pada Tabel 2.4. yang memperlihatkan bahwa faktor skala primer yang perlu diperhatikan tidak lebih dari lima. Apabila faktor skala primer ini dapat diterapkan, maka seluruh faktor skala sekunder otomatis akan dipenuhi, dan hasilnya adalah model skala.
Sistem yang homologos dalam penelitian ini, adalah sebuah prototype dan sebuah model yang mengalami perubahan skala dimensi geometri poros dan perubahan skala beban impeller yang ditampilkan, pada Gambar 2.21. dengan daftar skala dapat dilihat pada Lampiran 4.
Kuantitas yang esensial dari poros diskalakan secara geometris, yaitu satuan panjang, dihubungkan dengan faktor skala maka:
' ' 3 3 ' 2 2 ' 1 1 ' * L L l l l l l l x x l L L = = = = = (2.38)
yang terkait dengan waktu, dikalikan dengan faktor skala:
1 0 0 ' 1 1 * t t t t t = = (2.39)
dan seluruh yang terkait dengan gaya, dikalikan dengan faktor skala:
' * P P F F F = (2.40)
sehingga bentuk, gaya dan waktu dari model dan prototype akan memiliki kemiripan. Sedangkan kecepatan, momen, tarikan, dan energi kinetik merupakan produk dari skala primer disebut sebagai faktor skala sekunder.
Hanya faktor skala primer yang perlu diperhitungkan oleh karena faktor skala sekunder dapat dengan mudah diturunkan dari faktor skala primer, sebagai contoh dapat dilihat faktor skala sekunder dari kecepatan sebagai berikut:
' ' 3 3 ' 2 2 ' 1 1 * ... n n v v v v v v v v v = = = = =
Kecepatan juga dapat ditampilkan dalam turunan pertama jarak terhadap waktu,
maka: ' ' ' 2 ' 2 2 2 ' 1 ' 1 1 1 * ... n n n n dt dl dt dl dt dl dt dl dt dl dt dl v = = = =
Berdasarkan kesepakatan terhadap geometris dan waktu yang disyaratkan yaitu: ' 1 * 1 l .l l = , ' 2 * 2 l .l
l = , dan seterusnya, dan ' 1 * 1 t .t t = , ' 2 * 2 t .t
t = , dan seterusnya, maka:
* * ' 2 ' 2 2 2 * * ' 1 ' 1 1 1 * * * ... t l dt dl dt dl t l dt dl dt dl t l v = = = = (2.41)
Dengan cara yang sama, maka skala faktor sekunder dapat diturunkan dari dua atau lebih skala faktor primer, seperti dibawah ini:
a. Skala faktor luas : A* =l*2
b. Skala faktor percepatan : * * *2 t l
a =
c. Skala faktor momen : M* =F*.l*
d. Skala faktor daya : *
* * * * * . . t l F v F P = =
2.2.3. Karakteristik Desain Model Centrifugal Fan
Berdasarkan standar AMCA (Air Movement and Control Association) pada Lampiran 4, 5, 6, dan 7, dalam perencanaan terhadap model backward-inclined
centrifugal fan yang digunakan dalam penelitian adalah fan model skala dari depericarper fan dapat dilihat pada Gambar 2.22.
Karakteristik model skala disesuaikan dengan Depericarper fan yang terpasang di PKS, yaitu
a. Arrangement (AMCA 99-2404-03) : 2 SWSI b. Inlet Box Position (AMCA 99-2405-03) : 90o
c. Designation (AMCA 99-2406-03) : Clock wise up blast d. Motor Position (AMCA 99-2407-03) : Z
Gambar 2.22. Model skala centrifugal fan tipe 2 SWSI
2.3. Bantalan Anti Gesek
Bagian yang berputar dari suatu mesin ditahan oleh suatu jenis bearing (bantalan). Bantalan ini dapat diklasifikasikan atas dua group: journal atau sleeve
bearing dan antifriction bearing (bantalan anti gesek).
Journal atau sleeve bearing menawarkan paling sedikit dan paling ekonomis
peralatan penahan bagian bergerak, lihat Gambar 2.23. Tidak ada bagian yang bergerak dan normalnya sepotong metal menutupi (enclosing) sebuah poros. Istilah “journal” artinya bagian penahan (supporting) pada poros.
Gambar 2.23. Bantalan journal atau sleeve
Bantalan jenis bola (ball) atau peluru, rol (roller) dan jarum (needle), pada Gambar 2.24, diklasifikasikan sebagai bantalan anti gesek (antifriction bearing) dimana gesekan telah berkurang pada nilai minimum. Bantalan jenis ini dapat dibagi atas dua group : radial bearing dan thrust bearing.
Gambar 2.24. Berbagai tipe elemen gelinding pada bantalan
Kecuali untuk desain khusus, bantalan peluru/bola dan rol terdiri atas dua buah cincin (ring), satu set elemen gelinding (rolling element) dan rumah bantalan (cage) yang dapat dilihat pada Gambar 2.25.
.
Gambar 2.25. Struktur Bantalan Anti Gesek
2.3.1. Beban pada Bantalan
Beban pada bantalan berasal dari poros yang dipasang pada bantalan [19], seperti yang dapat dilihat pada Gambar 2.26. Beban ini dapat berasal dari, impeller, beban sendiri poros dan lainnya. Secara umum poros diasumsikan kaku, dan
misalignment pada bantalan oleh karena poros bengkok diabaikan. Sehingga gaya
reaksi yang terjadi dapat ditentukan dari persamaan statik.
Sehingga berlaku: 0 = ΣF , F1 +F2 −P=0 0 = ΣM , F1l−P(l−a)=0
Gambar 2.27. Sistem poros pada dua bantalan dengan beban overhung
Untuk beban overhanging seperti pada Gambar 2.27, maka persamaan 2.42 dan 2.43 dapat digunakan dengan asumsi bahwa jarak arah kiri dari tangan kiri dianggap negatif, sehingga persamaan:
± = l a P F1 1 (2.42) l a P F2 =± (2.43)
Apabila sejumlah beban P terdapat pada poros seperti pada Gambar 2.28, k maka gaya reaksi pada bantalan dapat diperoleh dengan prinsip superposisi. Dalam hal ini bentuk persamaannya menjadi:
∑
= = ± =k n k k k l a P F 1 1 1 (2.44)∑
= = ± = k n k k l a P F 1 2 (2.45)Gambar 2.28. Sistem poros pada dua bantalan dengan beban kombinasi
Persamaan 2.44 dan 2.45 adalah valid untuk beban yang berada pada satu bidang. Apabila tiap beban berada pada bidang yang berbeda, maka pembebanan diselesaikan pada tiap sumbu ortogonalnya, sebagai contoh, k
x
P dan k z
P (dengan
asumsi sumbu poros pada arah y). Berdasarkan gaya reaksi bantalan arah radial F1x,
z F1 , F2xdan F2z, maka: 2 1 2 1 2 1 1 (Fx Fz) F = + (2.46) 2 1 2 2 2 2 2 (F x Fz) F = + (2.47) 2.3.2. Nomenklatur Bantalan
Nomenklatur dari bantalan bola unit terpadu FYH mengikuti standar JIS (Japanese Industrial Standards) B 1557, yang mengatur pengkodean terhadap model
bantalan/housing, diameter, diameter bore, asesoris serta kekhususan. Nomenklatur bantalan yang digunakan, yaitu:
2.3.3. Umur Bantalan
Apabila bantalan dapat dipelihara dalam keadaan tetap bersih, dilumasi, dipasang dan terlindungi dari abu dan kotoran, serta dioperasikan pada suhu yang sesuai, maka fatik logam adalah satu-satunya penyebab kegagalannya.
Pengukuran umur yang umum adalah:
a. Jumlah revolusi dari cincin bagian dalam sampai pada kemunculan bukti awal terjadinya fatik
UK F
06
J
Fitting code
Tolerance class of spherical bore of the housing is J7 (not shown on the bearing that the spherical bore diameter exceeds 120 mm) Bore dia. code
(Bore dia. code) × 5 = Nominal bearing bore dia. (mm)
2
Diameter series code For light duty Housing model code Square four-bolt flange type Bearing model code
b. Jumlah jam yang digunakan pada kecepatan sudut standar hingga muncul bukti awal terjadinya fatik
Istilah umum yang digunakan adalah umur bantalan (bearing life), yang digunakan pada kedua pengukuran yang disebutkan di atas, penting untuk diketahui, sebagaimana halnya pada kasus fatik, umur didefinisikan sebagai jumlah revolusi (atau jam pada kecepatan konstan) total dari pengoperasian bantalan sampai kriteria kegagalan berkembang.
Umur efektif (rating life) dari sekumpulan bantalan bola didefinisikan sebagai jumlah revolusi (atau jam pada kecepatan konstan) dimana 90 persen dari sekumpulan bantalan akan mencapai atau melampaui kondisi sebelum berkembangnya kegagalan. Istilah umur minimum (minimum life), umur L , dan 10
umur B juga digunakan sebagai sinonim dari umur efektif. 10
Sedangkan umur median (median life) adalah persen ke limapuluh dari sekumpulan bantalan. Istilah umur rata-rata (average life) digunakan sebagai sinonim dari umur median. Pada sejumlah bantalan yang diuji, umur median diantara 4 – 5 kali dari umur L . 10
Umur bantalan sesuai katalog bantalan FYH dihitung dengan rumus:
3 6 10 60 10 ⋅ = r r th P C n L (2.48)
dimana: n = kecepatan poros (rpm) r
r
P = beban radial dinamik ekivalen (N)
Perhitungan umur bantalan yang digunakan pada penelitian ini dapat di lihat pada Lampiran 8. Beban radial dinamik ekivalen yang merupakan kombinasi dari beban radial dan beban aksial dihitung dengan rumus:
a r
r XF YF
P = + (2.49)
dimana: X = faktor beban radial dari Tabel 2.5. Y = faktor beban aksial dari Tabel 2.5.
r
F =beban radial (N)
a
F =beban aksial (N)
Untuk menggunakan Tabel 2.5 maka diperlukan basic static radial loading, C0r dan faktor,f diperoleh dari spesifikasi bantalan. 0
Tabel 2.5. Faktor beban radial ( X ) dan faktor beban aksial (Y )
Fa / Fr ≤ e Fa / Fr ≤ e r a C F f 0 0 E X Y X Y 0.172 0.19 2.30 0.345 0.22 1.99 0.689 0.26 1.71 1.03 0.28 1.55 1.38 0.30 1.45 2.07 0.34 1.31 3.45 0.38 1.15 5.17 0.42 1.04 6.89 0.44 1 0 0.56 1.00
2.4 Sabuk-V (V-belt)
Transmisi sabuk [22] dapat dibagi atas 3 (tiga) kelompok, yaitu:
1. Sabuk rata (flat belt) dipasang pada puli silinder dan meneruskan momen antara dua poros yang jaraknya dapat mencapai 10 meter dengan perbandingan putaran antara 1:1 sampai dengan 6:1.
2. Sabuk dengan penampang trapesium (v-belt) dipasang pada puli dengan alur dan meneruskan momen antara dua poros yang jaraknya dapat mencapai 5 meter dengan perbandingan putaran antara 1:1 sampai dengan 7:1.
3. Sabuk dengan gigi (timing belt) yang digerakkan dengan sproket pada jarak pusat sampai 2 meter, dan meneruskan putaran secara tepat dengan perbandingan antara 1:1 sampai 6:1.
Sabuk paling umum dijumpai di industri adalah sabuk-V, karena penanganannya mudah serta harga murah. Kecepatan sabuk pada umumnya direncanakan antara 10 – 20 m/s, serta dapat mentransmisikan daya hingga 500 kW. Sabuk-V terbuat dari karet dan mempunyai penampang trapesium. Tenunan tetoron atau semacamnya dipergunakan sebagai inti sabuk untuk membawa tarikan yang besar, hal ini dapat dilihat pada Gambar 2.29.
Gambar 2.29. Penampang sabuk-V klasik
2.4.1. Tipe Dan Ukuran Nominal Sabuk-V
Tiap dimensi sabuk-V telah distandarisasi oleh pabrikan dan pada umumnya dapat dibagi/diklasifikasikan menjadi 2 (dua), yaitu: heavy-duty (industri) dan
light-duty (fractional-horsepower). Sabuk-V untuk industri berdasarkan penampangnya
(Gambar 2.30) terdiri dari 2 tipe dasar, yaitu: penampang konvensional/klasik (A, B, C, D, dan E) dan penampang sempit (3V, 5V, dan 8V).
Gambar 2.30. Penampang sabuk-V industri: (a) Penampang konvensional, dan (b) Penampang sempit
(a) (b)
Terpal
2.4.2. Panjang Sabuk-V
Untuk menyatakan panjang dari sabuk-V ada tiga nomenklatur yang umum digunakan sesuai cara pengukurannya, yaitu: panjang bagian luar (OC: outside
circumference), panjang efektif (Le: effective length), dan panjang pitch (Lp: pitch length).
Panjang bagian luar (OC) biasanya diukur secara sederhana dengan pita ukur yang diletakkan dibagian luar sabuk-V. Cara ini merupakan metode yang baik untuk memperoleh panjang nominal, namun sulit untuk mendapatkan nilai yang akurat dan konsisten oleh karena sabuk-V diukur pada saat tidak diberi tarikan (tension), sehingga tidak dapat menyatakan panjang sabuk saat dioperasikan.
Panjang efektif (Le) diukur langsung saat terpasang yang ditentukan berdasarkan penjumlahan dari dua kali jarak poros ditambah dengan panjang keliling bagian luar dari sebuah puli, ukuran ini yang biasa digunakan dilapangan.
Panjang pitch (Lp) merupakan panjang dari aksis netral dari sabuk, yaitu panjang dari kabel (tension cord line). Oleh karena kabel berada di dalam sabuk, sehingga sulit untuk diukur namun dapat dihitung dengan rumus [21],
(
) (
)
C d D d D C Lp 4 2 2 2 − + + + = π (2.50)dimana: C = jarak antar poros D = diameter puli besar d = diameter puli kecil
Pemilihan terhadap penampang dan panjang efektif sabuk-V dapat dilihat pada Lampiran 9.
2.4.3. Tarikan Statik dan Gaya Defleksi Sabuk-V.
Sabuk-V dapat mentransmisikan daya dengan baik pada rentang tarikan yang cukup lebar. Untuk mengoptimalkan umur dan performa sabuk serta menghindari tarikan pada poros dan bantalan yang tidak diinginkan, perlu dihitung dan diukur tarikan yang diberikan berdasarkan beban yang akan bekerja. Cara untuk menghitung yaitu metode defleksi gaya (force deflection) sesuai rekomendasi Mechanical Power
Transmission Association (MPTA), hal ini dapat dilihat pada Gambar 2.31.
Gambar 2.31. Pengukuran defleksi sabuk-V
Metode ini menerjemahkan tarikan statik menjadi gaya defleksi yang diberikan pada sabuk dan menghasilkan defleksi dengan norma defleksi q, sebesar 1/64” tiap 1 inci panjang span (Ls) atau 1,6 mm tiap 100 mm span. Defleksi sabuk
diukur ditengah span dalam arah tegak lurus span (Ls). Jarak defleksi q, dalam satuan
inci yang disyaratkan dihitung dengan rumus:
64 s L
q= (2.51)
dimana panjang span (Ls) dapat dihitung dengan rumus:
2 2 2 − − = C D d Ls (2.51.a)
dimana : Ls = panjang rentangan (inci)
C = Jarak antar poros (inci)
D,d = Diameter puli (inci)
Besarnya tarikan pada sabuk-V idealnya adalah tarikan terendah dimana sabuk tidak akan slip pada kondisi beban tertinggi, lihat Gambar 2.32. Hal ini akan menghasilkan umur sabuk yang paling baik dan beban pada poros yang rendah.
Gambar 2.32. Vektor tarikan statik sabuk
Metode praktis untuk menghitung dan mengukur tarikan statik (static tension) sabuk berdasarkan beban/daya rencana dihitung dengan rumus:
+ − = c b d st g V W V N P K K T 1 60 9 . 0 10 5 . 2 15 2 3 θ θ (2.52)
dimana T =Tarikan statik sabuk (lb), st
Kθ = Faktor koreksi busur kontak
Pd = Daya rencana (hp)
W = Berat sabuk tiap kaki satuan panjang (lb), lihat Tabel 2. 6 V = Kecepatan sabuk (fpm)
gc = konstanta gravitasi : 32.2 ft/sec2
Nb = Jumlah sabuk yang digunakan
Tabel 2.6. Berat sabuk (W) dan faktor modulus sabuk(Ky)
Penampang Sabuk Berat Sabuk W (lb/ft) Faktor Modulus sabuk
3L 4L 5L A AX B BX C CX D, DX 3V, 3VX 5V 5VX 8V, 8VX 0.04 0.06 0.09 0.07 0.06 0.13 0.11 0.23 0.21 0.42 0.05 0.14 0.12 0.37 5 6 9 6 7 9 10 16 18 30 4 12 13 22
Faktor koreksi busur Kθ, dapat dihitung dengan rumus: − = R R Kθ 1.25 1 (2.52.a)
dimana R adalah rasio tarikan yang dihitung dengan rumus:
(0.008941)( )θ e
R= (2.52.b)
dan θ = sudut busur kontak dari diameter puli terkecil dalam satuan derajat:
− = − C d D 2 cos 2 1 θ (2.52.c)
Daya rencana dihitung dengan rumus:
P
Pd =1.15 (2.52.d)
yang mana P adalah daya motor terpasang (hp), sedangkan rumus kecepatan sabuk :
12
Dn
V =π (2.52.e)
Rentang gaya minimum dan maksimum yang direkomendasikan untuk mesin dengan sabuk-V berjumlah satu dapat dihitung dengan rumus:
1) Gaya minimum yang direkomendasikan
16 min y y s st L K L T P + = (2.53.a)
2) Gaya maksimum yang direkomendasikan
16 5 . 1 max y y s st L K L T P + = (2.53.b)
Sesuai rekomendasi MPTA, untuk keperluan analisa tarikan statis sabuk-V berjumlah satu, akibat gaya defleksi Pa, dengan defleksi berjarak q, dapat dihitung
dengan rumus: y p s a st K L L P T − = 16 (2.54)
Dimana : Pa = Gaya defleksi yang aktual diukur (lb)
Ky = Faktor Modulus sabuk (lihat Tabel 2.13)
Ls = Panjang span (inci)
Lp = Panjang pitch sabuk (inci)
2.4.4. Beban Statis pada Poros Akibat Tarikan Sabuk-V
Beban statis pada poros Fs, didefinisikan sebagai resultan dari tarikan akibat
tarikan statis sabuk Ts disepanjang garis sumbu penggerak (drive center line) pada
saat diam, lihat Gambar 2.33.
Besar beban statis poros Fst, adalah sama untuk puli penggerak dan yang
digerakkan, yang dihitung dengan rumus:
= 2 sin 2 b st θ st N T F (2.55)
2.4.5. Tarikan Operasi dan Beban Dinamis Sabuk-V
Tarikan sabuk-V pada saat mesin beroperasi menimbulkan dua tarikan yaitu
tight –side tension TT, dan slack-side tension TS, yang dihasilkan oleh adanya torsi Q
dan tarikan statis Tst, hal ini dapat dilihat pada Gambar 2.34.
Gambar 2.34. Vektor tarikan operasi dan beban dinamis poros sabuk-V
Torsi merupakan fungsi dari daya nyata yang ditransmisikan Pr dan
kecepatan sabuk-V. Untuk menentukan daya nyata dapat digunakan pengukuran sehingga perhitungan lebih akurat, namun apabila tidak tersedia, dapat menggunakan daya motor. Sehingga tarikan efektif Te (lb) untuk tiap sabuk dapat dihitung dengan
rumus:
( )
b S T e VN d Q T T T = − =2 =33000 Pr (2.56)Tight side tension TT (lb) dapat dihitung dengan rumus: 2 1 60 9 . 0 9 . 0 2 e c st T T g V W T T + − = (2.57)
maka slack side tension TS dapat dihitung dengan rumus:
e T
S T T
T = − (2.58)
Sama seperti beban statis poros, maka beban dinamis poros Fdy juga
merupakan resultan dari tarikan yang terdapat pada sabuk. Beban dinamis poros akibat tarikan sabuk merupakan penjumlahan vektor dari TT dan TS. dengan rumus:
(
2 cosθ)
2 2 S T S T b dy N T T T T F = + − (2.59) 2.5. Kerangka KonsepHasil yang diperoleh dalam suatu penelitian dipengaruhi oleh variabel-variabel penelitian itu sendiri. Kerangka konsep dalam penelitian ini digambarkan seperti Gambar 2.35.
Permasalahan adalah perbedaan respon getaran yang diakibatkan oleh perubahan tarikan sabuk-V, yang menjadi variabel bebas dan input alat pengukur getaran, sedangkan variabel terikat yaitu amplitudo getaran yang timbulkan. Hasil yang diperoleh dari pengukuran meliputi respon getaran dari bantalan yaitu kecepatan getaran (RMS) dalam mm/s, spektrum frekuensi beserta respon getarannya. Setelah dilakukan analisa trend getaran, spektrum frekuensi dan rotor orbit trajectories, maka
akan diambil kesimpulan dari hasil penelitian sesuai tujuan khusus. Tahapan
pelaksanaan penelitian dapat dilihat pada diagram alur proses penelitian Lampiran 10.
Gambar 2.35. Kerangka Konsep Penelitian
Permasalahan:
Getaran pada bantalan model skala centrifugal fan akibat perubahan tarikan sabuk-V sebagai parameter untuk memantau tingkat keadaan mesin dalam teknik pemeliharaan yang bersifat prediktif
Bantalan Model Centrifugal Fan:
• Model skala centrifugal fan • Titik pengukuran getaran • Kecepatan putaran poros • Amplitudo kecepatan getaran
keseluruhan (rms)
• Spektrum frekuensi sistem
Hasil yang diperoleh :
• Frekuensi eksitasi sistem • Trend getaran bantalan • Spektrum frekuensi getaran
bantalan
• Orbit perpindahan getaran
Variabel Bebas
• Beban dinamis akibat tarikan sabuk-V