Materi Teknik Optimasi

Masalah separable programming adalah

masalah nonlinear programming dengan

bentuk seperti berikut : Max (atau min) z =

s.t (i = 1, 2, …, m)

Separable programming dapat diselesaikan

dengan pendekatan piece wise linear

function untuk setiap f_j(x_j )dan g_ij(x_j)

2 Eni Sumarminingsih, SSi, MM

 





n

j

j j x

f

1





 n

j

i

ij b

g

Sebelum melakukan pendekatan piece wise linear

function untuk fj(xj ) dan gij(xj) perlu ditentukan aj

dan bj (untuk j = 1, 2, …, n) sedemikian hingga nilai

pada solusi optimal akan memenuhi aj ≤ xj ≤ bj

Berikutnya pilih titik grid p_j,1 , p_j,2, …p_j,k dengan

aj = pj,1 ≤ pj,2 ≤ … ≤ pj,k = bj

(untuk kesederhanaan, untuk setiap variabel dapat digunakan banyak grid yang sama ).

Konsep dasar dari metode separable programming

adalah mendekati setiap fungsi fj(xj ) dan gij(xj)

Secara formal, misalkan

maka untuk 0 _{  } 1

Secara umum, untuk pendekatan masalah

separable programming xj dapat dinyatakan

sebagai

(j = 1, 2, …, n) dengan (j = 1, 2, …, n)

(j = 1, 2, …, n ; r = 1, 2, …, k)

4 Eni Sumarminingsih, SSi, MM

1 , ,r  j  j r

j x p

p





_{, 1}

,



1







_{j r j r}

j

p

p

x





k j k j j j j j

j

p

p

p

x





_{,1 ,1}





_{,2 ,2}









_{, ,}

1

, 2

, 1

,  j   j k 

j  

 

0

,r  j

Sehingga f_j(x_j ) dapat didekati dengan

Untuk memastikan keakuratan pendekatan

ini, maka harus dipastikan bahwa untuk setiap j (j = 1, 2, …, n), maksimum hanya ada dua _j,r yang positif

Untuk j tertentu misalkan _j,k positif maka

_{j,k - 1} atau _j,k+1 harus positif dan bukan _j,r yang lain

_j,k dikatakan adjacent dengan _{j,k - 1} dan

_j,k+1

Secara lengkap, pendekatan masalah

separable programming dapat dinyatakan sebagai berikut:

max (atau min) s.t

(i= 1, 2, ..., m)

(j = 1, 2, …, n)

(j = 1, 2, …, n ; r = 1, 2, …, k)

asumsi adjacency

















      n

j j j j j j k j k

p f p f p f z

1 ,1 ,1 ,2 ,2 , ,

 

 

















_i

n

j j ij j j ij j j k ij j k

b p g p g p

g    



1 ,1 ,1 ,2 ,2 , ,

    1 , 2 , 1

,  j   j k 

j  

 

0

,r  j

_{Dapat dilihat bahwa pendekatan separable programming} adalah masalah linear programming sehingga dapat

diselesaikan dengan metode simplek.

Namun demikian, penyelesaian dengan metode simplek memungkinkan asumsi adjacency terlanggar atau tidak terpenuhi.

Untuk menghindari hal tersebut, metode simplek perlu

dimodifikasi, yaitu dengan menambah aturan sebagai berikut :

1. Jika untuk j tertentu, semua j,k = 0, maka setiap j,k boleh

masuk sebagai basis.

2. Jika untuk j tertentu, j,k positif maka hanya j,k-1 atau j,k+1

yang boleh masuk sebagai basis

3. Jika untuk j tertentu, terdapat dua j,k yang positif, maka tidak

boleh ada j,k lain yang dapat masuk sebagai basis

Terdapat dua kasus di mana metode

simplek biasa dapat digunakan untuk menyelesaikan pendekatan terhadap

separable programming dan menghasilkan solusi yang secara otomatis memenuhi

asumsi adjacency, yaitu

1. Jika separable programming adalah

masalah maksimisasi, setiap f_j(x_j)

concave dan setiap g_ij(x_j) adalah convex

2. Jika separable programming adalah

masalah minimisasi, setiap adalah f_j(x_j)

Contoh permasalahan

Misalkan ingin dicari solusi optimal dari

masalah berikut :

Max

S.t

Permasalahan ini adalah masalah separable

programming dengan

10 Eni Sumarminingsih, SSi, MM









2

2 2 1 2 2 1

1 30 x x 35 x x 2x

x

z      

2 2 2

1 2

1 35 2 3

30x x x x

z    

250 2 ₂2

2

1  x 

x

20

2 1  x 

x

0

, ₂

1 x 

x

 

2

1 1

1

1 x 30x 2x

f   f₂

 

x₂ 35x₂  3x₂2

 

2

1 1

11 x x

g  g12

 

x2 2x22

 

_{1 1}

21 x x

dan dapat ditetapkan a₁ = a₂ = 0 dan b₁=b₂=20 (karena

x₁, x₂ ≥ 0 dan ada kendala ).

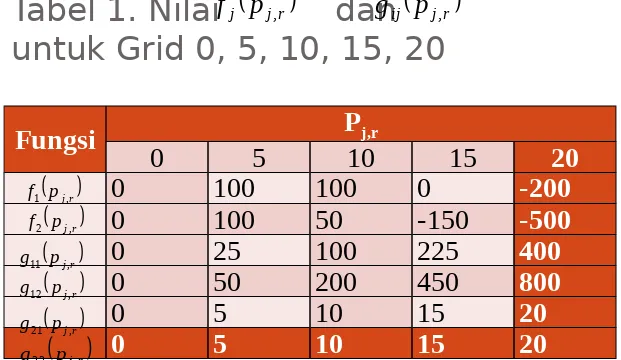
Misalkan dipilih 5 grid ( semakin banyak grid akan semakin baik) untuk setiap variabel

dengan grid p₁₁= p₂₁=0 ,p₁₂=p₂₂= 5, p₁₃=p₂₃=10 , p₁₄=p₂₄=15, p₁₅=p₂₅=20 .

Sehingga didapat nilai dan nilai untuk grid tersebut adalah sebagai

berikut:

20

2 1  x 

x



_{j r}



j p

Tabel 1. Nilai dan

untuk Grid 0, 5, 10, 15, 20

12

Fungsi

P

j,r

0

5

10

15

20

0

100

100

0

-200

0

100

50

-150

-500

0

25

100

225

400

0

50

200

450

800

0

5

10

15

20

0

5

10

15

20

Eni Sumarminingsih, SSi, MM



pj r



f_{1 ,}



pj r



f_{2 ,}



pj r



g_{11 ,}



pj r



g_{12 ,}



pj r



g_{21 ,}



pj r



g_{22 ,}



_{j r}



j p

Dari Tabel 1. dapat dituliskan pendekatan

masalah separable programming untuk contoh

permasalahan adalah sebagai berikut: Max

s.t

Asumsi adjacency

25 24 23 22 15 13

12 100 200 100 50 150 500

100 ˆ               z 250 800 450 200 50 400 225 100

25₁₂  ₁₃  ₁₄  ₁₅  ₂₂  ₂₃  ₂₄  ₂₅ 

20 20 15 10 5 20 15 10

5₁₂  ₁₃  ₁₄  ₁₅  ₂₂  ₂₃  ₂₄  ₂₅ 

1

15 14

13 12

11       1 25 24 23 22

21     



0

,r  j

14

Permasalahan ini adalah permasalahan linear

programming sehingga dapat diselesaikan dengan metode simpleks biasa karena untuk contoh permasalahan ini, setiap f_j(x_j) adalah

concave dan setiap g_ij(x_j) adalah convex. Solusi optimal dari permasalahn ini adalah Hal ini berarti dan sedang .

Jika dibandingkan dengan solusi optimal sebenarnya yaitu

dan dengan z = 214.5, solusi

dengan pendekatan separable programming cukup dekat.

Eni Sumarminingsih, SSi, MM

1

22 12  



5 ) 5 ( 1

1  

x x₂ 1(5) 5 zˆ _200

5 . 7

1 

x

83 . 5

2 