Pembahasan Soal UN SMP 2012 10 Paket

(1)

Pembahasan Soal

TAHUN PELAJARAN 2011/2012

((((10

10

10 10 P

P

Paket

P

aket

aket Soal

Soal

Soal))))

A13, A17, B25, B29, C32, A13, A17, B25, B29, C32, A13, A17, B25, B29, C32,

A13, A17, B25, B29, C32, C37, D45, D49, E52, E57C37, D45, D49, E52, E57C37, D45, D49, E52, E57C37, D45, D49, E52, E57

Disusun Oleh :

Alfa Kristanti

SMPN 3 Kalibagor

Distributed by :

(2)

1 | Pembahasan UN 2012 A13 by Alfa Kristanti

Urutan pengerjaan operasi hitung

Operasi hitung Urutan pengerjaan

Dalam kurung 1

1. Urutan pengerjaan operasi hitung Operasi hitung Urutan pengerjaan

Dalam kurung 1 Jumlah kelereng mereka adalah ....

A. 44

2.100.000,00 dengan suku bunga tunggal 8% setahun. Saat diambil. Tabungan ayah menjadi Rp 2.282.000,00. Lama ayah

Ingat!

1. Bunga = Jumlah tabungan – Modal

2. Bunga =

12 × 100 ×

(3)

menabung adalah .... A. 13 bulan B. 14 bulan C. 15 bulan D. 16 bulan

Bunga = 2.282.000 – 2.100.000 = 182.000

Lama = 12 × 100 ×182.000 8 × 2.100.000 = 13

Jawab : A 7 Dua suku berikutnya dari barisan 3, 4, 6, 9,

... adalah .... A. 13, 18 B. 13, 17 C. 12, 26 D. 12, 15

3, 4, 6, 9, 13, 18

1 2 3 4 5

Jawab : A 8 Dari barisan aritmetika diketahui suku ke-7

= 22 dan suku ke-11 = 34. Jumlah 18 suku pertama adalah ....

A. 531

B. 666

C. 1062 D. 1332

Ingat!

Pada Barisan Aritmetika 1. Un = a + (n-1)b

2. Sn =

2 2 + −1

U7 = a + 6b = 22

U11 = a + 10b = 34 

 4b =  12 b = 3

a + 6b = 22  a + 6(3) = 22 a + 18 = 22 a = 22 – 18 a = 4

S18 =

18

2 2 4 + 18−1 3 = 9 (8 + (17)3) = 9 (8 + 51) = 9 (59) = 531

Jawab : A 9 Amuba akan membelah diri menjadi dua

setiap 15 menit. Jika mula-mula ada 30 amuba, maka banyak amuba selama 2 jam adalah ....

A. 900

B. 1.800 C. 3.840 D. 7.680

Ingat!

Pada barisan geometri Un = a × rn-1

a = 30, r = 2 2 jam = 120 menit n = 120

15 + 1 = 8 + 1 = 9

U9 = 30 × 29 – 1 = 30 × 28 = 30 × 256 = 7.680 Jawab : D 10 Faktor dari 49p2 – 64q2 adalah ....

A. (7p – 8q)(7p – 8q) B. (7p + 16q)(7p – 4q) C. (7p + 8q)(7p – 8q) D. (7p + 4q)(7p – 16q)

Ingat!

a2 – b2 = (a + b)(a – b)

49p2 – 64q2 = (7p)2 – (8q)2 = (7p + 8q)(7p – 8q) Jawab : C

11 Himpunan penyelesaian dari  7p + 8 < 3p – 22, untuk p bilangan bulat adalah ....

A. {...,  6,  5,  4} B. {..., 0, 1, 2} C. { 2,  1, 0, ...} D. {4, 5, 6, ...}

 7p + 8 < 3p – 22  7p + 8 – 3p < – 22  10p + 8 < – 22  10p < – 22 – 8  10p < – 30 p > − 30

− 10

p > 3  Hp = { 4, 5, 6, ...}

Jawab : D

(4)

12 Jumlah tiga bilangan ganjil berurutan adalah 75. Jumlah bilangan terkecil dan terbesar bilangan tersebut adalah ....

A. 48 B. 50

C. 140

D. 142

Misalkan bilangan pertama = p Maka bilangan kedua = p + 2 Bilangan ketiga = p + 4

p + p + 2 + p + 4 = 75 3p + 6 = 75 3p = 75 – 6 3p = 69 p = 23 sehingga :

bilangan pertama = 23 bilangan kedua = 23 + 2 = 25 bilangan ketiga = 23 + 4 = 27

Jumlah bil. terkecil dan terbesar = 23 + 27 = 50 Jawab : B 13 Dikelas 9A terdapat 36 orang siswa, setelah

didata terdapat 7 orang gemar IPA, 9 orang gemar matematika, dan 5 orang siswa gemar keduanya. Banyak siswa yang tidak gemar keduanya adalah ....

A. 28 orang B. 27 orang C. 26 orang

D. 25 orang 2 + 5 + 4 + x = 36

11 + x = 36

x = 36 – 11 x = 25

Jawab : D 14 Diketahui f(x) = px + q, f(1) =  5, dan

f(4) = 5. Nilai f( 6) adalah .... A.  15

B.  9 C. 7 D. 10

f(1) =  p + q =  5 f(4) = 4p + q = 5   5p =  10 p = 2

4p + q = 5  4(2) + q = 5 8 + q = 5 q = 5 – 8 q =  3

f( 6) = 2( 6) + ( 3) =  12  3 =  15

Jawab : A 15 Diketahui rumus fungsi f(x) =  2x + 5.

Nilai f ( 4) adalah .... A.  13

B.  3 C. 3 D. 13

f(x) =  2x + 5

f( 4) =  2( 4) + 5 = 8 + 5 = 13

Jawab : D 16 Gradien garis  3x– 2y = 7 adalah ....

A. 3 2

B. − 2

3

C. − 3

2

D. − 7

3

Ingat!

ax + by + c = 0  m = −

 3x – 2y = 7  a =  3, b = – 2

m = − = − − 3 − 2 =

3 − 2= −

3 2

Jawab : C

IPA MTK

5 7 – 5

= 2 9 – 5 _{= 4}

x

x = tdk keduanya

(5)

17 Keliling suatu persegipanjang 28 cm. Jika panjangnya 2 cm lebih dari lebarnya, luas persegipanjang tersebut adalah ....

A. 28 cm2 18 Diketahui keliling belahketupat 100 cm dan

panjang salah satu diagonalnya 48 cm. Luas belahketupat tersebut adalah ....

A. 336 cm2 B. 600 cm2 C. 672 cm2 D. 1.008 cm2

Ingat!

Panjang sisi belah ketupat = s Kbelahketupat = 4 × s

Pada segitiga siku-siku yg diarsir berlaku :

x2 = 252– 242 = 625 – 576 = 49 x = 49 = 7 cm

persegipanjang EFGH! Jika luas daerah yang tidak diarsir 68 cm2, luas daerah yang diarsir adalah ....

Bagian bangun yang diarsir merupakan hasil dari tumpukan dua bangun bukan potongan dari dua bangun, sehingga hasil penjumlahan luas dua bangun dikurangi dengan bagian bangun yang tidak diasir harus dibagi 2.

Ltdk diarsir = 68 cm 20 Sebidang tanah berbentuk trapesium sama

kaki. Panjang sisi sejajarnya 24 m dan 14 m, dan jarak sisi sejajar 12 m. Jika sekeliling tanah tersebut dibuat pagar, panjang pagar seluruhnya adalah ....

A. 50 m

(6)

B. 51 m

C. 62 m

D. 64 m

Pada segitiga siku-siku yang diarsir berlaku : AD2 = 122 + 52 = 144 + 25 = 169  AD = 169 = 13 m

BC = AD = 13 m

Ktrapesium = AB + BC + CD + AD

= 24 + 13 + 14 + 13 = 64 m

Jawab : D 21 Perhatikan gambar berikut!

Besar sudut nomor 1 adalah 95o dan besar sudut nomor 2 adalah 110o. Besar sudut nomor 3 adalah ....

A. 5o B. 15o C. 25o D. 35o

Ingat !

1. Sudut bertolak belakang besarnya sama, 2. Sudut sehadap besarnya sama,

3. Jumlah sudut saling berpelurus = 180o, 4. Jumlah sudut dalam segitiga = 180o.

1 = 4 = 95o (bertolak belakang) 5 = 4 = 95o (sehadap)

2 + 6 = 180o (berpelurus) 110 o + 6 = 180o

6 = 180 o - 110 o 6 = 70 o

3 + 5 + 6 =180 o (dalil jumlah sudut ∆) 3 + 95 o + 70o = 180 o

3 + 165 o =180 o 3 = 180 o 165 o 3 = 15 o

Jawab : B 22 Perhatikan gambar!

Garis LN adalah …. A. Garis bagi

B. Garis tinggi C. Garis berat D. Garis sumbu

Ingat!

(7)

Jawab : A 23 Perhatikan gambar!

P adalah titik pusat lingkaran dan luas juring PLM = 24 cm2. Luas juring PKN adalah ….

A. 27 cm2 B. 30 cm2 C. 32 cm2 D. 39 cm2

Ingat!

� 1

� 2=

� 1

� 2

�� =

� � ��

24 = 60 45

L juring PKN = 60 × 24 45 =

1.440

45 = 32 cm

2

Jawab : C

24 Dua buah lingkaran berpusat di A dan B dengan jarak AB = 20 cm. Panjang garis singgung persekutuan dalam 16 cm dan panjang jari-jari lingkarang dengan pusat A = 5 cm. Panjang jari-jari lingkaran dengan pusat B adalah ….

A. 7 cm B. 10 cm C. 12 cm

D. 17 cm

Ingat!

Jika Gd = Garis singgung persekutuan dalam

j = Jarak pusat 2 lingkaran

r1 dan r2 = Jari-jari lingkaran 1dan 2

Gd = 2− 1+ 2 2Gd 2

= j2 – (r1 + r2) 2

162 = 202 – (5 + r2) 2

 (5 + r2) 2

= 202 162 (5 + r2)

2

= 400  256 (5 + r2)

2

= 144 5 + r2 = 144

5 + r2 = 12

r2 = 12 – 5

r2 = 7

Jawab : A 25 Persamaan garis melalui titik (–2, 5) dan

sejajar garis x–3y + 2 = 0 adalah …. A. 3x– y = 17

B. 3x + y = 17 C. x– 3y = –17 D. x + 3y = –17

Ingat!

1. ax + by + c = 0  m = −

2. Persamaan garis melalui titik (x1,y1)

dengan gradien m adalah y – y1 = m (x–

x1)

(8)

3. Jika dua garis sejajar, maka m2 = m1

x– 3y + 2 = 0  a = 1 dan b = – 3

m1 = − = −

1 − 3=

1 3

kedua garis sejajar, maka m2 = m1 =

1 3 melalui titik (–2, 5) x1 =  2 dan y1 = 5

y – y1 = m (x – x1)

y – 5 = 1

3 (x– ( 2))

y – 5 = 1

3 (x + 2) 3y – 15 = x + 2

3y – x = 2 + 15 x + 3y = 17

x 3y =  17

Jawab : C 26 Perhatikan gambar!

Segitiga ABC kongruen dengan segitiga POT. Pasangan sudut yang sama besar adalah ….

A. BAC = POT B. BAC = PTO C. ABC = POT

D. ABC = PTO

ABC = POT

Jawab : C

27 Perhatikan gambar!

Jika DE : DA = 2 : 5, maka panjang EF adalah ...

A. 10,4 cm B. 36,4 cm C. 64,4 cm D. 69,4 cm

EF = × + × + =

2 × 80 + 3 × 54 2 + 3

= 160 + 162 5 =

322

5 = 64,4 cm

Jawab : C 28 Sebuah tiang tingginya 2 m memiliki

bayangan 250 cm. Pada saat yang sama bayangan sebuah gedung 40 m.

Tinggi gedung tersebut adalah …. A. 30 m

B. 32 m C. 35 m

D. 50 m

t. tiang = 2 m  bayangan tiang = 250 cm

t. gedung =... m  bayangan gedung = 40 m = 4.000 cm

��

�� =

� � �

� � � �

2

5 – 2 = 3

(9)

2

�� = 250 4.000

Tinggi gedung = 2 × 4.000 250 =

8.000

250 = 32 m

Jawab : B 29 Perhatikan gambar kerucut!

Garis PQ adalah .... A. Jari-jari B. Diameter C. Garis pelukis D. Garis tinggi

Garis PQ = garis pelukis

Jawab : C

30 Perhatikan gambar di bawah!

Yang merupakan jaring-jaring balok adalah ….

A. I dan II B. II dan III C. III dan IV D. I dan IV

Yang merupakan jaring-jaring balok adalah I dan IV

Jawab : D

31 Volume kerucut yang panjang diameter alasnya 20 cm dan tinggi 12 cm adalah .... (π = 3,14)

A. 1.256 cm3 B. 1.884 cm3 C. 5.024 cm3 D. 7.536 cm3

Ingat! Vkerucut =

1 3 �

2

d = 20 cm  r = 10 cm t = 12 cm

Vkerucut =

1

3 × 3,14 × 10

2_{× 12 = 3,14 × 100 × 4}

= 314 × 4 = 1.256 cm3

Jawab : A

32 Volume bola terbesar yang dapat

dimasukkan ke dalam dus berbentuk kubus dengan panjang rusuk 12 cm adalah ….

A. 144 π cm3 B. 288 π cm3 C. 432 π cm3 D. 576 π cm3

Ingat! Vbola =

4 3 �

3

Perhatikan !

Bola terbesar yang dapat masuk dalam kubus adalah bola dengan diameter = rusuk

Rusuk kubus = diameter = 12 cm  r = 6 cm Vbola =

4 3 �

3₌4

3 ×� × 6 × 6 × 6 = 4 ×� × 2 × 6 × 6

= 288π cm3

Jawab : B

(10)

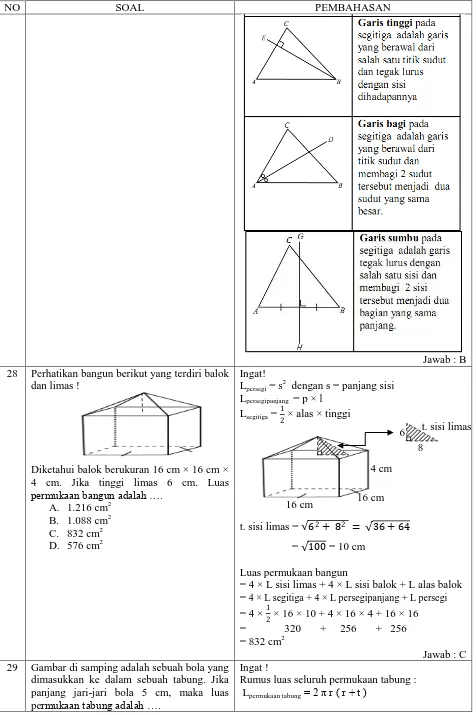
33 Perhatikan bangun berikut yang terdiri balok dan limas !

Diketahui balok berukuran 8 cm x 8 cm x 11 cm. Jika tinggi limas 3 cm. Luas permukaan bangun adalah ….

A. 592 cm2 B. 560 cm2 C. 496 cm2 D. 432 cm2

Ingat! Lpersegi = s

2

dengan s = panjang sisi Lpersegipanjang = p × l

Lsegitiga =

1

2 × alas × tinggi

t. sisi limas = 32_{+ 4}2₌ _{9 + 16 =} _{25 = 5} cm

Luas permukaan bangun

= 4 × L sisi limas + 4 × L sisi balok + L alas balok = 4 × L segitiga + 4 × L persegipanjang + L persegi = 4 × 1

2 × 8 × 5 + 4 × 11 × 8 + 8 × 8 = 80 + 352 + 64 = 496 cm2

Jawab : C 34 Perhatikan gambar!

Jika jari-jari bola 12 cm, maka luas seluruh permukaan tabung adalah ….

Ingat !

Rumus luas seluruh permukaan tabung : Lpermukaan tabung= 2 π r ( r + t )

Perhatikan !

Karena ukuran bola adalah yang terbesar dapat masuk ke dalam tabung maka jari-jari tabung = jari-jari bola dan tinggi tabung = diameter bola

Jari-jari tabung = jari-jari bola = 12 cm

Tinggi tabung = diameter bola = 2 × 12 = 24 cm

Lpermukaan tabung= 2 π r ( r + t ) = 2 × π × 12 (12 + 24)

= 24 π (36) = 864 π cm2

Jawab : B 35 Data ulangan matematika beberapa siswa

sebagai berikut: 64, 67, 55, 71, 62, 67, 71, 67, 55. Modus dari data tersebut adalah ….

A. 62 B. 64 C. 67 D. 71

Ingat !

Modus = data yang sering muncul

Data : 55, 55, 62, 64, 67, 67, 67, 71, 71 Maka modus = 67 (muncul 3 kali)

Jawab : C

36 Berat rata-rata 14 orang siswa putra 55 kg, sedangkan berat rata-rata 6 orang siswa putri 48 kg. Berat rata-rata seluruh siswa tersebut adalah ….

A. 51,9 kg B. 52,9 kg C. 53,2 kg D. 53,8 kg

Jumlah berat siswa putra = 14 × 55 = 770 Jumlah berat siswa putri = 6 × 48 = 288 + Jumlah berat semua siswa = 1.058

Jumlah seluruh siswa = 14 + 6 = 20

Berat rata-rata keseluruhan = 1.058

20 = 52,9 kg Jawab : B 8 cm

8 cm 3

4

3 t. sisi limas

11 cm

(11)

37 Hasil tes matematika kelas VII B sebagai berikut :

Banyaknya siswa yang mendapatkan nilai lebih dari 7 adalah ….

A. 8 orang B. 11 orang C. 17 orang D. 27 orang

Banyaknya siswa yang nilainya lebih dari 7 = 7 + 3 + 1

= 11 orang

Jawab : B

38 Diagram lingkaran menyatakan kegiatan yang diikuti oleh siswa dalam satu sekolah.

Jika banyak siswa yang ikut kegiatan renang 48 orang, maka banyak siswa yang ikut kegiatan drama adalah ….

Sudut suka drama = 360o (90o+ 60o + 80o + 100o) = 360o 330o = 30o

Maka

banyak anak yg ikut drama = 30

80 × 48 = 18 orang

Jawab : A

39 Sebuah dadu dilambungkan satu kali. Peluang muncul mata dadu faktor dari 6 adalah ….

A. 1

6

B. 1

2

C. 2

3

D. 5

6

Banyaknya mata dadu = 6

Banyaknya faktor dari 6 = 4 (yaitu : 1, 2, 3,6) Maka

P (faktor dari 6) = 4 6 =

2 3

Jawab : C

40 Virama mempunyai 20 kelereng berwarna putih, 35 kelereng berwarna kuning, dn 45 kelereng berwarna hijau yang ditempatkan pada sebuah kaleng. Jika diambil sebuah kelereng dari kaleng tersebut, maka peluang kelereng yang terambil berwarna putih adalah ….

A. 1

20

B. 1

5

C. 1

4

D. 1

2

Kelereng putih = 20 Kelereng kuning = 35 Kelereng hijau = 45 + Jumlah Kelereng = 100 Maka

P ( 1 kelereng putih) = 20 100 =

1 5

Jawab : B Paskibra

Drama

100o Pramuka

Musik

60o 80o Renang

(12)

Dalam kurung 1

Dalam kurung 1 barisan tersebut adalah ....

A. 896

(13)

S16 =

16

2 2 3 + 16−1 3 = 8 (6 + (15)3) = 8 (6 + 45) = 8 (51) = 408

Jawab : D 6 Amuba membelah diri menjadi dua setiap 20

menit. Jika mula-mula terdapat 15 amuba, maka selama 2 jam banyak amuba adalah ....

A. 2120 B. 1920

C. 960

D. 480

Ingat!

a = 15, r = 2 2 jam = 120 menit n = 120

20 + 1 = 6 + 1 = 7

U7 = 15 × 27 – 1 = 15 × 26 = 15 × 64 = 960

Jawab : C 7 Dua suku berikutnya dari barisan 3, 4, 6, 9,

... adalah .... A. 13, 18 B. 13, 17 C. 12, 26 D. 12, 15

3, 4, 6, 9, 13, 18

1 2 3 4 5

Jawab : A 8 Uang adik berbanding uang kakak 3 : 5. Jika

selisih uang keduanya Rp.180.000,00, maka jumlah uang mereka adalah ….

A. Rp.288.000,00 B. Rp.300.000,00 C. Rp.480.000,00 D. Rp.720.000,00

adik = 3 bagian dan kakak = 5 bagian Selisihnya = 180.000

5 bagian – 3 bagian = 180.000 2 bagian = 180.000 1 bagian = 180 .000

2 1 bagian = 90.000

Jumlah = 5 bagian + 3 bagian = 8 bagian = 8 × 90.000 = 720.000

Jawab : D

9 Rudi menabung di bank sebesar Rp

1.400.000,00. Bank memberi suku bunga tunggal sebesar 15% setahun. Saat diambil tabungan Rudisebesar Rp 1.522.500,00, maka lama Rudi menabung adalah ....

A. 6 bulan B. 7 bulan C. 8 bulan D. 9 bulan

Ingat!

2. Bunga =

12 × 100 ×

Bunga = 1.522.500 – 1.400.000 = 122.500

Lama = 12 × 100 ×122.500 15 × 1.400.000 = 7

Jawab : B 10 Warga kelurahan Damai mengadakan kerja

bakti, 90 orang membawa cangkul, dan 48 orang membawa cangkul dan sapu lidi. Jika banyak warga kelurahan Damai 120 orang, maka banyak warga yang hanya membawa sapu lidi adalah ….

42 + 48 + x = 120 90 + x = 120

x = 120 – 90 x = 30

Jawab : A 11 Gradien garis x– 3y =  6 adalah ....

A.  3

Ingat!

ax + by + c = 0  m = −

x = hanya sapu lidi

cangkul Sapu lidi

48 90 – 48 = 42

x

(14)

B. − 1

3

C. 1 3

D. 3

x– 3y =  6  a = 1, b = – 3

m = − = − 1 − 3 =

1 3

Jawab : C 12 Persamaan garis melalui titik (2, –1) dan

tegak lurus garis y = 2x+ 5 adalah …. A. 2x + y = 0

B. 2x– y = 0 C. x + 2y = 0 D. x– 2y = 0

Ingat!

1. Y = mx+ c  gradien = m

x1)

3. Jika dua garis tegaklurus, maka m2 × m1 =  1 atau m2 = −

1

y = 2x + 5  m1 = 2

kedua garis tegaklurus, maka m2 = −

1

= −1 2

melalui titik (2, –1) x1 = 2 dan y1 = 1

y – y1 = m (x–x1)

y – (1) = −1

2 (x– 2)

y + 1 = −1

2 (x – 2) 2y + 2 =  1( x 2)

2y + 2 = x + 2

2y + x = 2 – 2

x + 2y = 0

Jawab : C 13 Faktor dari 4x2– 36y2 adalah ....

A. (2x+6y)(2x– 6y) B. (2x– 6y)(2x– 6y) C. (4x– 6y)(x + 6y) D. (4x + 6y)(x + 6y)

Ingat!

a2– b2 = (a + b)(a – b)

4x2– 36y2= (2x)2– (6y)2 = (2x + 6y)(2x– 6y)

Jawab : A 14 Persegipanjang mempunyai panjang 2 kali

lebarnya. Jika keliling persegipanjang 54 cm, maka luas persegipanjang adalah ….

A. 108 cm2 B. 128 cm2 C. 162 cm2 D. 171 cm2

Ingat!

Kpersegipanjang = 2 (p + l )

Lpersegipanjang = p × l

Panjang 2 kali lebarnya  p = 2l Kpersegipanjang = 2 (p + l ) = 54

2 (2l + l ) = 54 2 (3l ) = 54 6l = 54 l = 54

6

l = 9 cm  p = 2l = 2(9) = 18 cm

Lpersegipanjang = p × l = 18 × 9 = 162 cm 2

Jawab : C 15 Diketahui rumus fungsi f(x) =  2x + 5.

Nilai f ( 4) adalah .... A.  13

B.  3

f(x) =  2x + 5

f( 4) =  2( 4) + 5 = 8 + 5 = 13

Jawab : D

(15)

C. 3 D. 13

16 Fungsi f didefinisikan dengan rumus f(x) = px + q, f(3) =  10, dan f( 2) = 0, maka nilai f( 7) adalah ....

A.  18 B.  10 C. 10 D. 18

f(3) = 3p + q =  10 f( 2) =  2p + q = 0  5p =  10 p =  2

3p + q =  10  3( 2) + q =  10  6 + q =  10 q =  10 + 6 q =  4

f( 7) =  2( 7) + ( 4) = 14  4 = 10

Jawab : C 17 Himpunan penyelesaian dari 2x+ 3 ≤ x  2,

untuk x bilangan bulat adalah .... A. {...,  8, 7,  6,  5} B. {...,  3,  2,  1, 0} C. { 5,  4,  3,  2, ...} D. {...,  1, 0, 1, 2}

2x+ 3 ≤ x  2 2xx+ 3 ≤  2 x ≤  2 – 3

x ≤  5  Hp = { 5,  4,  3,  2, ...} Jawab : C

18 Jumlah tiga bilangan ganjil berurutan adalah 39. Jumlah bilangan terkecil dan terbesar dari bilangan tersebut adalah ….

A. 22 B. 24 C. 26 D. 28

Jumlah bil. terkecil dan terbesar = 11 + 15 = 26 Jawab : C 19 Perhatikan gambar!

Titik O adalah pusat lingkaran dan luas juring OLM = 12 cm2. Luas juring OKL adalah ….

A. 14 cm2 B. 15 cm2 C. 16 cm2 D. 18 cm2

Ingat!

� 1

� 2=

� 1

� 2

�� =

� � ��

12 = 80 60

L juring OKL = 12 × 80 60 =

960

60 = 16 cm

2

Jawab : C

20 Diketahui jarak antara dua titik pusat lingkaran 26 cm. panjang jari-jari lingkaran yang kecil 4 cm dan panjang garis singgung persekutuan luar 24 cm. panjang jari-jari lingkaran yang besar adalah ….

Ingat! Jika Gl = Garis singgung persekutuan luar j = Jarak pusat 2 lingkaran

r1 dan r2 = Jari-jari lingkaran 1dan 2

Gl = 2₋

1− 2 2 Gl2 = j2– (r1 r2) 2

(16)

5 | Pembahasan UN 2012 A17 by Alfa Kristanti 21 Perhatikan gambar berikut!

Besar sudut nomor 1 adalah 95o dan besar

3. Jumlah sudut saling berpelurus = 180o, dengan panjang rusuk 18 cm adalah ….

A. 1296 π cm3

Rusuk kubus = diameter = 18 cm  r = 9 cm

(17)

Jika DP : PA = 1 : 2, maka panjang PQ adalah ...

A. 12 cm B. 10 cm C. 9 cm D. 8 cm

PQ = � × + � × � + � =

1 × 18 + 2 × 6 1 + 2

= 18 + 12 3 =

30

3 =10 cm

Jawab : B

25 Ali yang tingginya 150 cm mempunyai bayangan 2 m. Pada saat yang sama bayangan sebuah gedung 24 m. Tinggi gedung adalah ….

A. 16 m B. 18 m C. 30 m

D. 32 m

t. Ali = 150 cm  bayangan Ali = 2 m

t. gedung =... cm  bayangan gedung = 24 m

��

�� =

� �

� � � �

150

�� = 2 24

Tinggi gedung = 24 × 150

2 =

3.600

2 = 1.800 cm

= 18 m

D. ABC = PTO

ABC = POT

Jawab : C

Garis BD adalah …. A. Garis berat

B. Garis tinggi C. Garis bagi D. Garis sumbu

Ingat! 6 cm

18 cm

P Q

1

2

6 cm

18 cm

P Q

(18)

Jawab : B 28 Perhatikan bangun berikut yang terdiri balok

dan limas !

Diketahui balok berukuran 16 cm × 16 cm × 4 cm. Jika tinggi limas 6 cm. Luas permukaan bangun adalah ….

A. 1.216 cm2 B. 1.088 cm2 C. 832 cm2 D. 576 cm2

Ingat! Lpersegi = s

2

Lsegitiga =

1

2 × alas × tinggi

t. sisi limas = 62_{+ 8}2₌ _{36 + 64}

= 100 = 10 cm

= 4 × L sisi limas + 4 × L sisi balok + L alas balok = 4 × L segitiga + 4 × L persegipanjang + L persegi

= 4 × 1

2 × 16 × 10 + 4 × 16 × 4 + 16 × 16 = 320 + 256 + 256 = 832 cm2

Jawab : C 29 Gambar di samping adalah sebuah bola yang

dimasukkan ke dalam sebuah tabung. Jika panjang jari-jari bola 5 cm, maka luas permukaan tabung adalah ….

Ingat !

16 cm 16 cm

6 8

t. sisi limas

4 cm

(19)

Perhatikan !

Karena ukuran bola adalah yangterbesar dapat masuk ke dalam tabung maka jari-jari tabung = jari-jari bola dan tinggi tabung = diameter bola

= 10 π (15) = 150 π cm2

Jawab : B 30 Perhatikan gambar di bawah!

Jawab : D

31 Luas belahketupat yang panjang salah satu diagonalnya 10 cm dan kelilingnya 52 cm adalah ….

A. 120 cm2 B. 130 cm2 C. 240 cm2 D. 260 cm2

Ingat!

Lbelahketupat =

1

2 × d1 × d2 d1 = 10 cm

Kbelahketupat = 4 × s = 52

S = 13 cm

x2 = 132 – 52 = 196 – 25 = 144 x = 144 = 12 cm

maka d2 = 2 × x = 2 × 12 = 24 cm

Lbelahketupat =

1

2 × d1 × d2 = 1

2 × 10 × 24 = 120 cm

2

Jawab : A 32 Perhatikan gambar persegi PQRS dengan

panjang PQ = 12 cm dan persegi panjang ABCD dengan DC = 15 cm, AD = 6 cm. Luas daerah yang tidak diarsir 198 cm2. Luas daerah yang diarsir adalah ....

A. 18 cm2 B. 36 cm2 C. 54 cm2 D. 72 cm2

Ingat! Lpersegi = s

2

Perhatikan !

Ltdk diarsir = 198 cm 2

Lpersegi = 12

2

= 144 cm2 Lpersegipanjang = 15 × 6 = 90cm

2

5

5 x 13

(20)

Ldiarsir = �

+ _� _� −

2

Ldiarsir =

144 + 90 − 198

2 =

36

2 = 18 cm

2

Jawab : A

33 Di atas sebidang tanah berbentuk

persegipanjang dengan ukuran 15 m × 6 m akan dibuat pagar di sekelilingnya. Untuk kekuatan pagar, setiap jarak 3 m ditanam tiang pancang. Banyak tiang pancang yang ditanam adalah ….

A. 12 B. 13 C. 14 D. 15

Ingat!

Banyak tiang pancang = �

Kpersegipanjang = 2 (p + l ) = 2 (15 + 6) = 2(21) = 42 m

Banyak tiang pancang = � = 42 3 = 14

Jawab : C 34 Perhatikan gambar kerucut!

Garis AC adalah .... A. Diameter B. Jari-jari C. Garis pelukis D. Garis tinggi

Garis AC = garis pelukis

Jawab : C

35 Perhatikan tabel nilai ulangan matematika dari sekelompok siswa:

Banyaknya siswa yang mendapat nilai kurang dari 7 adalah ….

A. 6 siswa B. 8 siswa C. 17 siswa D. 18 siswa

Banyaknya siswa yang nilainya kurang dari 7 = 1 + 3 + 5 + 8

= 17 orang

Jawab : C

36 Diagram lingkaran berikut menunjukkan kegemaran 200 siswa dalam mengikuti ekstrakurikuler di suatu sekolah. Banyak siswa yang gemar robotik adalah ….

% gemar robotik

= 100%  (12% + 20% + 30% + 10% + 13%) = 100%  85% = 15%

Maka

banyak anak yg gemar robotik = 15% × 200 = 15

100 × 200 = 30 orang

Jawab : D

(21)

37 Tinggi sekelompok siswa sebagai berikut: 141 cm, 160 cm, 150 cm, 154 cm, 148 cm, 150 cm, 154 cm, 153 cm, 150 cm, 148 cm. Modus dari data tersebut adalah ….

A. 148 B. 149 C. 150

D. 160

Ingat !

Data : 141, 148, 148, 150, 150, 150, 153, 154, 154, 160

Maka modus = 150 (muncul 3 kali)

Jawab : C 38 Berat badan rata-rata 15 siswa pria 52 kg,

sedangkan beerat badan rata-rata 25 siswa wanita 48 kg. Berat badan rata-rata seluruh siswa adalah ….

A. 50,5 kg B. 50 kg C. 49,5 kg D. 49 kg

Jml berat siswa pria = 15 × 52 = 780 Jml berat siswa wanita = 25 × 48 = 1.200 + Jumlah berat semua siswa = 1.980

Berat rata-rata keseluruhan = 1.980

40 = 49,5 kg Jawab : C 39 Di atas sebuah rak buku terdapat:

10 buku ekonomi 50 buku sejarah 20 buku bahasa 70 buku biogafi

Jika diambil sebuah buku secara acak, peluang yang terambil buku sejarah adalah ….

A. 1

150

B. 1

50

C. 1

3

D. 1

2

Buku ekonomi = 10 Buku sejarah = 50 Buku bahasa = 20

Buku biografi = 70 + Jumlah buku = 150

Maka

P ( 1 buku sejarah) = 50 150 =

1 3

Jawab : C

40 Sebuah dadu dilambungkan satu kali. Peluang muncul mata dadu kurang dari 4 adalah ….

A. 1

6

B. 1

3

C. 1

2

D. 2

3

Banyaknya mata dadu kurang dari 4 = 3

(yaitu : 1, 2, 3) Maka

P (mata dadu kurang dari 4) = 3 6 =

1 2

Jawab : C

(22)

1 | Pembahasan UN 2012 B25 by Alfa Kristanti

Dalam kurung 1

Jika selisih uang keduanya Rp.180.000,00, maka jumlah uang mereka adalah ….

A. Rp.288.000,00

(23)

6 Rudi menabung di bank sebesar Rp

1.400.000,00. Bank memberi suku bunga tunggal sebesar 15% setahun. Saat diambil tabungan Rudisebesar Rp 1.522.500,00, maka lama Rudi menabung adalah ....

Ingat!

2. Bunga =

12 × 100 ×

Bunga = 1.522.500 – 1.400.000 = 122.500

Lama = 12 × 100 ×122.500 15 × 1.400.000 = 7

Jawab : B 7 Dua suku berikutnya dari barisan 3, 4, 6,

9, ... adalah .... A. 13, 18 B. 13, 17 C. 12, 26 D. 12, 15

3, 4, 6, 9, 13, 18

1 2 3 4 5

Jawab : A 8 Suatu barisan aritmetika diketahui U6 =

18 dan U10 = 30. Jumlah 16 suku pertama adalah ....

A. 896

B. 512

C. 448

D. 408

Ingat!

Pada Barisan Aritmetika 1. Un = a + (n-1)b

2. Sn = ₂ 2 + −1

U6 = a + 5b = 18

U10 = a + 9b = 34 

 4b =  16 b = 4

a + 5b = 18 a + 5(4) = 18 a + 20 = 18 a = 18 – 20 a = – 2

S16 =

16

2 2 −2 + 16−1 4 = 8 (4 + (15)4) = 8 (4 + 60) = 8 (56) = 448

Jawab : C 9 Dalam setiap 20 menit amuba membelah

diri menjadi dua. Jika mula-mula ada 50 amuba, selama 2 jam banyaknya amuba adalah ....

A. 1.600 B. 2.000 C. 3.200 D. 6.400

Ingat!

a = 50, r = 2 2 jam = 120 menit

n = 120

20 + 1 = 6 + 1 = 7

U7 = 50 × 27 – 1 = 50 × 26 = 50 × 64 = 3.200

Jawab : C 10 Faktor dari 4x2 – 36y2 adalah ....

A. (2x+6y)(2x – 6y) B. (2x– 6y)(2x– 6y) C. (4x – 6y)(x + 6y) D. (4x + 6y)(x + 6y)

Ingat!

a2 – b2 = (a + b)(a – b)

4x2 – 36y2= (2x)2 – (6y)2 = (2x + 6y)(2x – 6y)

Jawab : A 11 Himpunan penyelesaian dari 2x– 3 ≥–

5x+ 9, untuk x bilangan bulat adalah .... A. {3, 2, 1, 0, ...}

B. { 1, 0, 1, 2, ...}

 2x – 3 ≥ –5x + 9  2x + 5x – 3 ≥ 9 3x ≥ 9 + 3 3x ≥ 12

(24)

C. {2, 3, 4, ...}

D. {4, 5, 6, 7, ...} x≥

12 3

x≥ 4  Hp = { 4, 5, 6, 7, ...}

Jawab : D 12 Jumlah tiga bilangan ganjil berurutan

adalah 45. Jumlah bilangan terbesar dan terkecil bilangan tersebut adalah ....

A. 26 B. 30 C. 34 D. 38

Jumlah bilangan terkecil dan terbesar = 13 + 17 = 30

Jawab : B 13 Perhimpunan pengrajin beranggota 73

orang, 42 orang memproduksi anyaman rotan dan 37 orang memproduksi anyaman rotan dan anyaman bambu. Banyak orang yang hanya memproduksi anyaman bambu adalah ....

D. 68 orang 5 + 37 + x = 73

42 + x = 73

x = 73 – 42x = 31

Jawab : A 14 Suatu fungsi didefinisikan dengan rumus

f(x) = mx + n, f(0) = 4, dan f( 1) = 1,maka nilai f(3) adalah ....

A.  13 B. 5 C. 5 D. 13

f(0) = 0 + n = 4  n = 4 f( 1) =  m + n = 1

 m + n = 1  m + 4 = 1  m = 1 – 4  m = – 3 m = 3

f(3) = 3(3) + 4 = 9+4 =  5

Jawab : B 15 Diketahui rumus fungsi f(x) =  2x + 5.

Nilai f ( 4) adalah .... A.  13

B.  3 C. 3 D. 13

f(x) =  2x + 5

f( 4) =  2( 4) + 5 = 8 + 5 = 13

Jawab : D 16 Gradien garis 4x – 6y = 24 adalah ....

A. 3 2

B. 2 3

Ingat!

ax + by + c = 0  m = −

4x – 6y = 24  a = 4, b = – 6

Rotan Bambu

37 42 – 37 = 5

x x = hanya bambu

(25)

A. 28 cm2 18 Diketahui keliling belahketupat 100 cm

dan panjang salah satu diagonalnya 48 cm. Luas belahketupat tersebut adalah ....

A. 336 cm2 B. 600 cm2 C. 672 cm2 D. 1.008 cm2

Ingat!

x2 = 252 – 242 = 625 – 576 = 49  x = 49 = 7 cm

persegipanjang EFGH! Jika luas daerah yang tidak diarsir 68 cm2, luas daerah yang diarsir adalah ....

A. 24 cm2

(26)

20 Sebidang tanah berbentuk trapesium sama kaki. Panjang sisi sejajarnya 24 m dan 14 m, dan jarak sisi sejajar 12 m. Jika sekeliling tanah tersebut dibuat pagar, panjang pagar seluruhnya adalah ....

A. 50 m

B. 51 m

C. 62 m

D. 64 m

Pada segitiga siku-siku yang diarsir berlaku :

AD2 = 122 + 52 = 144 + 25 = 169  AD = 169 = 13 m

BC = AD = 13 m

Ktrapesium = AB + BC + CD + AD = 24 + 13 + 14 + 13

= 64 m

Jawab : D 21 Perhatikan gambar berikut!

Besar sudut nomor 1 adalah 95o dan besar sudut nomor 2 adalah 110o. Besar sudut nomor 3 adalah ....

A. 5o B. 15o C. 25o D. 35o

Ingat !

3. Jumlah sudut saling berpelurus = 180o, 4. Jumlah sudut dalam segitiga = 180o. 1 = 4 = 95o (bertolak belakang) 5 = 4 = 95o (sehadap)

2 + 6 = 180o (berpelurus) 110 o + 6 = 180o

6 = 180 o - 110 o 6 = 70 o

3 + 5 + 6 =180 o (dalil jumlah sudut ∆) 3 + 95 o + 70o = 180 o

3 + 165 o =180 o

3 = 180 o 165 o 3 = 15 o

Garis LN adalah …. A. Garis bagi

B. Garis tinggi C. Garis berat D. Garis sumbu

Ingat!

14

14 24

5 5

12

A B

C D

(27)

Diketahui sudut AOB = 120o, sudut BOC = 150o dan luas juring OAB = 84 cm2. Luas juring BOC adalah ….

A. 110 cm2 B. 105 cm2 C. 100 cm2 D. 95 cm2

Ingat!

� 1

� 2=

� 1

� 2

�� =

� �

84

� � =

120 150

L juring BOC = 150 × 84 120 =

12.500

120 = 105cm

2

Jawab : B

24 Diketahui panjang garis singgung

persekutuan luar dua lingkaran dengan pusat P dan Q 15 cm, jarak PQ = 17 cm, dan jari lingkaran P = 2 cm. Jika jari-jari lingkaran P kurang dari jari-jari-jari-jari lingkaran Q, maka panjang jari-jari lingkaran Q adalah ….

A. 30 cm B. 16 cm C. 10 cm D. 6 cm

Ingat!

Jika Gl = Garis singgung persekutuan luar j = Jarak pusat 2 lingkaran

r1 dan r2 = Jari-jari lingkaran1dan 2

Gl = 2− 1− 2 2 Gl

2

= j2 – (r1 r2) 2

152 = 172 – (rQ2) 2

 (rQ 2) 2

= 172 152 (rQ 2)2 = 289 225

(rQ 2) 2

= 64 rQ 2 = 64

rQ 2 = 8

rQ = 8 + 2

rQ = 10

Jawab : C 25 Persamaan garis melalui titik (2, – 3) dan

sejajar garis 2x– 3y + 5 = 0 adalah …. A. 3x+2y = 13

B. 3x– 2y = 13 C. 2x+ 3y = 13 D. 2x– 3y = 13

Ingat!

1. ax + by + c = 0  m = −

2. Persamaan garis melalui titik (x1,y1) dengan

gradien m adalah y – y1 = m (x–x1)

(28)

2x– 3y + 5 = 0 a = 2 dan b = – 3

m1 = − = −

2 − 3=

2 3

2 3 melalui titik (2, –3)x1 = 2 dan y1 = – 3

y – y1 = m (x – x1)

y – (– 3) = 2 3(x–2)

y +3 = 2 3(x– 2)

3y +9 = 2(x– 2)

3y + 9 = 2x– 4

3y – 2x = – 4–92x + 3y = – 13

2x 3y = 13

Jawab : D 26 Perhatikan gambar!

D. ABC = PTO

ABC = POT

Jawab : C

Jika DP : PA = 1 : 2, maka panjang PQ adalah ...

A. 12 cm B. 10 cm C. 9 cm D. 8 cm

PQ = � × + � × � + � =

1 × 18 + 2 × 6 1 + 2

= 18 + 12 3 =

30

3 =10 cm

Jawab : B

28 Sebuah tiangyang tingginya 2 m memiliki bayangan 150 cm. Pada saat yang sama bayangan sebuah pohon12 m.Tinggi pohon tersebut adalah ….

A. 8 m B. 9 m

t. tiang = 2 mbay. tiang = 150 cm

t. pohon =... m bay.pohon = 12 m = 1.200 cm

��

�� ℎ =

� � �

� � ℎ

1

2 6 cm

18 cm

6 cm

18 cm

P Q P

Q

(29)

C. 15 m

D. 16 m 2

�� ℎ =

150 1.200

Tinggi gedung = 2 × 1.200 150 =

2.400

150 = 16 m

Jawab : D 29 Perhatikan gambar kerucut!

Garis AC adalah .... A. Diameter B. Jari-jari C. Garis pelukis D. Garis tinggi

Garis AC = garis pelukis

Jawab : C

30 Perhatikan gambar di bawah!

Jawab : D

31 Tinggi sebuah kerucut 30 cm dan diameter alasnya 21 cm, dengan π = 22

7. Volume kerucut itu adalah ....

A. 16.860 cm3 B. 10.395 cm3 C. 6.930 cm3 D. 3.465 cm3

Ingat! Vkerucut =

1 3 �

2

d = 21 cm  r = 21 2 cm t = 30 cm

Vkerucut =

1 3 ×

22 7 ×

21 2 ×

21

2 × 30 = 1 × 11 × 21 × 15 = 3.465 cm3

Jawab : D

32 Volume bola terbesar yang dapat

dimasukkan ke dalam dus berbentuk kubus dengan panjang rusuk 18 cm adalah ….

Ingat! Vbola =

4 3 �

3

Perhatikan !

Rusuk kubus = diameter = 18 cm  r = 9 cm Vbola =

4 3 �

3₌4

3 ×� × 9 × 9 × 9 = 4 ×� × 3 × 9 × 9

= 972π cm3

Jawab : B

(30)

33 Perhatikan bangun berikut yang terdiri balok dan limas !

A. 368 cm2 B. 384 cm2 C. 438 cm2 D. 440 cm2

Ingat! Lpersegi = s

2

Lsegitiga =

1

2 × alas × tinggi

t. sisi limas = 42_{+ 3}2₌ _{16 + 9 =} ₂₅ = 5 cm

= 4 × L sisi limas + 4 × L sisi balok + L alas balok = 4 × Lsegitiga + 4 × L persegipanjang + Lpersegi = 4 × 1

2 × 6 × 5+ 4 × 12 × 6 + 6 × 6 = 60 + 288 + 36 = 384 cm2

Jawab : B 34 Gambar di samping adalah sebuah bola

yang dimasukkan ke dalam sebuah tabung. Jika panjang jari-jari bola 5 cm, maka luas permukaan tabung adalah ….

Ingat !

Perhatikan !

Karena ukuran bola adalah yangterbesar dapat masuk ke dalam tabung maka jari-jari tabung = jari-jari bola dan tinggi tabung = diameter bola

= 10 π (15) = 150 π cm2

Jawab : B 35 Dari dua belas kali ulangan matematika

pada satu semester, Dania mendapat nilai : 60, 55, 70, 65, 75, 70, 80, 70, 55, 75, 80, 85. Modus dari data tersebut adalah ….

A. 70 B. 75 C. 80 D. 85

Ingat !

Data : 55, 55, 60, 65, 70, 70, 70, 75, 75, 80, 80, 85 Maka modus = 70 (muncul 3 kali)

Jawab : A

36 Nilai rata-rata 24 siswa wanita 70, sedangkan rata-rata nilai 16 siswa pria 80. Nilai rata-rata keseluruhan siswa tersebut adalah ….

A. 74 B. 75 C. 76

Jumlah nilai siswa wanita = 24 × 70 = 1.680 Jumlah nilai siswa pria = 16 × 80 = 1.280 + Jumlah nilai semua siswa = 2.960

Jumlah seluruh siswa = 24 + 16 = 40 6 cm

6 cm 4

3

4 t. sisi limas

12 cm

(31)

D. 78 _{Nilai rata-rata keseluruhan =}2.960

40 = 74

Jawab : A 37 Tabel di bawah adalah hasil ulangan

matematika kelas 9A.

Nilai 4 5 6 7 8 9 10

Frekuensi 3 7 8 4 5 0 2 Banyak siswa yang mendapatkan nilai kurang dari 7 adalah ….

Banyak siswa yang nilainya kurang dari 7 = 3 + 7 + 8

= 18 orang

Jawab : D

38 Diagram lingkaran berikut menunjukkan data mata pelajaran yang digemari siswa kelas IX.

Jika banyak siswa 140 orang, maka banyak siswa yang gemar matematika adalah ….

% gemar matemtk = 100%  (14% +14%+24%+13%)

= 100%  65% = 35%

Maka

banyak anak yg gemar matematika = 35% × 140 = 35

100 × 140 = 49 orang

Jawab : C

39 Sebuah dadu dilambungkan satu kali. Peluang muncul mata dadu faktor dari 6 adalah ….

A. 1 6

B. 1 2

C. 2 3

D. 5 6

Banyaknya faktor dari 6 = 4 (yaitu : 1, 2, 3,6) Maka

P (faktor dari 6) = 4 6 =

2 3

Jawab : C

40 Dalam sebuah kotak terdapat 4 bola kuning, 14 bola merah, dan 6 bola hijau. Sebuah bola diambil secara acak, maka peluang terambil bola berwarna kuning adalah ….

A. 1

14

B. 1 6

C. 1 5

D. 1 4

Bola kuning = 4 Bola merah = 14 Bola hijau = 6 + Jumlah bola = 24 Maka

P ( 1 bola kuning) = 4 24 =

1 6

Jawab : B

(32)

Dalam kurung 1

(33)

a = 8

S18 =

18

2 2 8 + 18−1 3 = 9 (16 + (17)3) = 9 (16 + 51) = 9 (67) = 603

Jawab : B 6 Dalam setiap 20 menit amuba membelah diri

menjadi dua. Jika mula-mula ada 50 amuba, selama 2 jam banyaknya amuba adalah ....

A. 1.600 B. 2.000 C. 3.200 D. 6.400

Ingat!

a = 50, r = 2 2 jam = 120 menit

n = 120

20 + 1 = 6 + 1 = 7

U7 = 50 × 27 – 1 = 50 × 26 = 50 × 64 = 3.200 Jawab : C 7 Dua suku berikutnya dari barisan 3, 4, 6, 9,

... adalah .... A. 13, 18 B. 13, 17 C. 12, 26 D. 12, 15

3, 4, 6, 9, 13, 18

1 2 3 4 5

Jawab : A 8 Uang Wati berbanding uang Dini 1 : 3. Jika

selisih uang wati dan Dini Rp.120.000,00, jumlah uang mereka adalah ….

A. Rp.160.000,00 B. Rp.180.000,00 C. Rp.240.000,00 D. Rp.360.000,00

Wati = 1 bagian dan Dini = 3 bagian Selisihnya = 120.000

3 bagian – 1 bagian = 120.000 2 bagian = 120.000 1 bagian = 120 .000

2 1 bagian = 60.000

Jumlah = 1 bagian + 3 bagian = 4 bagian = 4 × 60.000 = 240.000

Jawab : C

9 Ali menabung di bank sebesar

Rp.2.000.000,00 dengan suku bunga tunggal 6% pertahun. Pada saat diambil uang Ali

menjadi Rp.2.080.000,00. Lama Ali

menabung adalah …. A. 6 bulan B. 7 bulan C. 8 bulan D. 9 bulan

Ingat!

2. Bunga =

12 × 100 ×

Bunga = 2.080.000 – 2.000.000 = 80.000

Lama = 12 × 100 × 80.000

6 × 2.000.000 = 8 bulan

Jawab : C

10 Perhimpunan pengrajin beranggota 73

orang, 42 orang memproduksi anyaman rotan dan 37 orang memproduksi anyaman rotan dan anyaman bambu. Banyak orang yang hanya memproduksi anyaman bambu adalah ....

5 + 37 + x = 73 42 + x = 73

x = 73 – 42x = 31

Jawab : A

Rotan Bambu

37 42 – 37 = 5

x _x_{= hanya bambu}

(34)

11 Gradien garis 4x– 6y = 24 adalah .... A. 3

2

B. 2 3

C. − 2

3

D. − 3

2

Ingat!

ax + by + c = 0  m = −

4x – 6y = 24  a = 4, b = – 6

m = − = − 4 − 6 =

4 6=

2 3

Jawab : B

12 Persamaan garis melalui titik (–2, 5) dan sejajar garis x – 3y + 2 = 0 adalah ….

A. 3x – y = 17 B. 3x + y = 17 C. x – 3y = –17 D. x + 3y = –17

Ingat!

1. ax + by + c = 0  m = −

x1)

x– 3y + 2 = 0  a = 1 dan b = – 3

m1 = − = −

1 − 3 =

1 3

1 3 melalui titik (–2, 5) x1 =  2 dan y1 = 5

y – y1 = m (x – x1)

y – 5 = 1

3 (x– ( 2))

y – 5 = 1

3 (x + 2) 3y – 15 = x + 2

3y – x = 2 + 15 x + 3y = 17

x 3y =  17

Jawab : C 13 Faktor dari 81a2 – 16b2 adalah ....

A. (3a – 4b)(27a + 4q) B. (3a + 4b)(27a – 4b) C. (9a  4b)(9a + 4b) D. (9a  4b)(9a  4b)

Ingat!

x2 – y2 = (x + b)(x – b)

81a2 – 16b2 = (9a)2 – (4b)2 = (9a + 4b)(9a – 4b) Jawab : C 14 Sebuah persegipanjang memiliki panjang

sama dengan 2 kali lebarnya, sedangkan kelilingnya 42 cm. Luas persegipanjang tersebut adalah ….

A. 392 cm2 B. 294 cm2 C. 196 cm2 D. 98 cm2

Ingat!

Panjang 2 kali lebarnya  p = 2l Kpersegipanjang = 2 (p + l ) = 42

2 (2l + l ) = 42 2 (3l ) = 42 6l = 42 l = 42

6

l = 7 cm  p = 2l = 2(7) = 14 cm

Jawab : D 15 Diketahui rumus fungsi f(x) =  2x + 5.

Nilai f ( 4) adalah .... A.  13

f(x) =  2x + 5

f( 4) =  2( 4) + 5 = 8 + 5 = 13

(35)

B.  3 C. 3 D. 13

Jawab : D

16 Suatu fungsi didefinisikan dengan rumus f(x) = mx + n, f(0) = 4, dan f( 1) = 1,maka nilai f(3) adalah ....

A.  13 B. 5 C. 5 D. 13

f(0) = 0 + n = 4  n = 4 f( 1) =  m + n = 1

 m + n = 1  m + 4 = 1  m = 1 – 4  m = – 3 m = 3

f(3) = 3(3) + 4 = 9+4 =  5

Jawab : B 17 Himpunan penyelesaian dari 2x –3 ≥–5x +

9, untuk x bilangan bulat adalah .... A. {3, 2, 1, 0, ...}

B. { 1, 0, 1, 2, ...} C. {2, 3, 4, ...} D. {4, 5, 6, 7, ...}

 2x–3 ≥ –5x + 9  2x + 5x – 3 ≥ 9 3x ≥ 9 + 3 3x ≥ 12 x≥12

3

x≥ 4  Hp = { 4, 5, 6, 7, ...}

Jawab : D 18 Jumlah tiga bilangan ganjil berurutan adalah

45. Jumlah bilangan terbesar dan terkecil bilangan tersebut adalah ....

A. 26 B. 30 C. 34 D. 38

Jumlah bilangan terkecil dan terbesar = 13 + 17 = 30

Diketahui O adalah titik pusat lingkaran dan luas juring OPQ = 24 cm2. Luas juring OQR adalah ….

A. 26 cm2 B. 30 cm2 C. 32 cm2 D. 36 cm2

Ingat!

� 1

� 2=

� 1

� 2

�� =

� ��

24 = 60 40

L juring OQR = 60 × 24 40 =

1.440

40 = 36 cm

2

Jawab : D

(36)

20 Jarak titik pusat dua lingkaran berpusat di titik P dan Q adalah 25 cm. Panjang garis singgung persekutuan luarnya 20 cm dan panjang jari-jari lingkaran dengan pusat P adalah 3 cm. Jika panjang jari-jari lingkaran P lebih pendek dari jari-jari lingkaran Q, maka panjang jari-jari lingkaran dengan pusat Q adalah ….

Jika Gl = Garis singgung persekutuan luar j = Jarak pusat 2 lingkaran 21 Perhatikan gambar berikut!

Besar sudut nomor 1 adalah 95o dan besar

3. Jumlah sudut saling berpelurus = 180o, dengan panjang rusuk 18 cm adalah ….

A. 1296 π cm3

Rusuk kubus = diameter = 18 cm  r = 9 cm

(37)

= 4 ×� × 3 × 9 × 9 = 972π cm3

Jika CY : YB = 2 : 3, maka panjang XY adalah ...

A. 9,0 cm B. 11,5 cm C. 13,0 cm D. 14,5 cm

XY = � × + � × � + � =

2 × 22 + 3 × 7 2 + 3

= 44 + 21 5 =

65

5 = 13 cm

Jawab : C

25 Sebuah tongkat panjangnya 2 m mempunyai panjang bayangan 75 cm. Pada saat yang sama panjang bayangan sebuah menara TV 15 m. Tinggi menara TV tersebut adalah ….

A. 40 m B. 45 m C. 48 m

D. 60 m

t. tongkat = 2 m  bay. tongkat = 75 cm

t. menara =... m  bay. menara = 15 m = 1.500 cm

��

�� =

� � �

� �

2

�� =

75 1.500

Tinggi menara = 2 × 1.500 75 =

3.000

75 = 40 m

D. ABC = PTO

ABC = POT

Jawab : C

Garis RS adalah …. A. Garis berat

B. Garis sumbu

Ingat!

2

3

(38)

C. Garis tinggi D. Garis bagi

Jawab : A 28 Perhatikan bangun berikut yang terdiri balok

dan limas !

A. 368 cm2 B. 384 cm2 C. 438 cm2 D. 440 cm2

Ingat! Lpersegi = s

2

Lsegitiga =

1

2 × alas × tinggi

t. sisi limas = 42_{+ 3}2₌ _{16 + 9 =} ₂₅ = 5 cm

= 4 × L sisi limas + 4 × L sisi balok + L alas balok = 4 × Lsegitiga + 4 × L persegipanjang + Lpersegi = 4 × 1

2 × 6 × 5+ 4 × 12 × 6 + 6 × 6 = 60 + 288 + 36 = 384 cm2

Jawab : B 29 Pada gambar di samping adalah bola di

dalam tabung. Jika jari-jari bola 7 cm, maka luas seluruh permukaan tabung adalah ….

Ingat !

6 cm

6 cm 4

3

4 t. sisi limas

12 cm

(39)

Perhatikan !

Karena ukuran bola adalah yang terbesar dapat masuk ke dalam tabung maka jari-jari tabung = jari-jari bola dan tinggi tabung = diameter bola

= 14 π (21) = 294 π cm2

Jawab : B 30 Perhatikan gambar di bawah!

Jawab : D

31 Diketahui keliling belahketupat 52 cm dan panjang salah satu diagonalnya 24 cm. Luas belahketupat ABCD adalah ....

A. 312 cm2 B. 274 cm2 C. 240 cm2 D. 120 cm2

Ingat!

Lbelahketupat =

1

2 × d1 × d2 d1 = 24 cm

Kbelahketupat = 4 × s = 52

S = 13 cm

x2 = 132– 122 = 169 – 144 = 25 x = 25 = 5 cm maka d2 = 2 × x = 2 × 5 = 10 cm

Lbelahketupat =

1

2 × d1 × d2 = 1

2 × 24 × 10 = 120 cm

2

Jawab : D 32 Perhatikan gambar persegipanjang ABCD

dan persegi PQRS !. Luas daerah yang tidak diarsir 529 cm2. Luas daerah yang diarsir adalah ….

A. 60 cm2 B. 71 cm2 C. 120 cm2 D. 240 cm2

Ingat!

Lpersegi = s2 dengan s = panjang sisi

Perhatikan !

Ltdk diarsir = 529 cm 2

Lpersegi = 17

2

= 289 cm2 Lpersegipanjang = 20 × 18 = 360cm

2

12

12 x 13

(40)

Ldiarsir = �

+ _� _� −

2

Ldiarsir =

289 + 360 − 529

2 =

120

2 = 60 cm

2

Jawab : A

33 Pak Rahman mempunyai sebidang tanah berbentuk persegipanjang dengan ukuran 30 m × 25 m. Tanah tersebut dipagari kawat sebanyak tiga kali lilitan. Panjang minimal kawat yang dibutuhkan adalah ….

A. 110 m B. 330 m C. 440 m

D. 240 m

Ingat!

Ktanah = Kpersegipanjang = 2 (p + l ) = 2 (30 + 25)

= 2 (55) = 110 m

Panjang kawat minimal = 3 × Kpersegipanjang

= 3 × 110 = 330 m

Jawab : B 34 Perhatikan gambar kerucut!

Garis AB adalah .... A. Jari-jari B. Garis pelukis C. Garis tinggi D. Diameter

Garis AB = garis pelukis

Jawab : B

35 Tabel di bawah adalah hasil ulangan matematika kelas 9A.

Nilai 4 5 6 7 8 9 10

Frekuensi 3 7 8 4 5 0 2

Banyak siswa yang mendapatkan nilai kurang dari 7 adalah ….

Banyak siswa yang nilainya kurang dari 7 = 3 + 7 + 8

= 18 orang

Jawab : D

36 Diagram lingkaran berikut menunjukkan data mata pelajaran yang digemari siswa kelas IX.

Jika banyak siswa 140 orang, maka banyak siswa yang gemar matematika adalah ….

A. 35 orang

% gemar matemtk = 100%  (14% +14%+24%+13%)

= 100%  65% = 35%

Maka

banyak anak yg gemar matematika = 35% × 140 = 35

100 × 140 = 49 orang

Jawab : C

18 cm

(41)

B. 42 orang C. 49 orang D. 65 orang

37 Dari dua belas kali ulangan matematika pada satu semester, Dania mendapat nilai : 60, 55, 70, 65, 75, 70, 80, 70, 55, 75, 80, 85. Modus dari data tersebut adalah ….

A. 70 B. 75 C. 80 D. 85

Ingat !

Data : 55, 55, 60, 65, 70, 70, 70, 75, 75, 80, 80, 85 Maka modus = 70 (muncul 3 kali)

Jawab : A

38 Nilai rata-rata 24 siswa wanita 70, sedangkan rata-rata nilai 16 siswa pria 80. Nilai rata-rata keseluruhan siswa tersebut adalah ….

A. 74 B. 75 C. 76 D. 78

Jumlah nilai siswa wanita = 24 × 70 = 1.680 Jumlah nilai siswa pria = 16 × 80 = 1.280 + Jumlah nilai semua siswa = 2.960

Nilai rata-rata keseluruhan = 2.960 40 = 74

Jawab : A 39 Dalam sebuah kotak terdapat 4 bola kuning,

14 bola merah, dan 6 bola hijau. Sebuah bola diambil secara acak, maka peluang terambil bola berwarna kuning adalah ….

A. 1

14

B. 1 6

C. 1 5

D. 1 4

Bola kuning = 4 Bola merah = 14 Bola hijau = 6 + Jumlah bola = 24 Maka

P ( 1 bola kuning) = 4 24 =

1 6

Jawab : B

40 Sebuah dadu dilambungkan satu kali. Peluang muncul mata dadu lebih dari 4 adalah ….

A. 1

6

B. 1

4

C. 1

3

D. 2

3

Banyaknya mata dadu lebih dari 4 = 2 (yaitu :5, 6) Maka

P (mata dadu lebih dari 4) = 2 6 =

1 3

Jawab : C

(42)

1 | Pembahasan UN 2012 C32 by Alfa Kristanti

Dalam kurung 1

(43)

S18 =

18

2 2 4 + 18−1 3 = 9 (8 + (17)3) = 9 (8 + 51) = 9 (59) = 531

Jawab : A 6 Amuba akan membelah diri menjadi dua

setiap 15 menit. Jika mula-mula ada 30 amuba, maka banyak amuba selama 2 jam adalah ....

A. 900

B. 1.800 C. 3.840 D. 7.680

Ingat!

a = 30, r = 2 2 jam = 120 menit n = 120

15 + 1 = 8 + 1 = 9

U9 = 30 × 29 – 1 = 30 × 28 = 30 × 256 = 7.680 Jawab : D 7 Dua suku berikutnya dari barisan 3, 4, 6, 9,

... adalah .... A. 13, 18 B. 13, 17 C. 12, 26 D. 12, 15

3, 4, 6, 9, 13, 18

1 2 3 4 5

Jawab : A 8 Perbandingan kelereng Dito dan Adul

adalah 9 : 5. Sedangkan selisihnya 28. Jumlah kelereng mereka adalah ....

A. 44 B. 50 C. 78 D. 98

Dito = 9 bagian dan Adul = 5 bagian Selisihnya = 28

9 bagian – 5 bagian = 28 4 bagian = 28 1 bagian = 28

4 1 bagian = 7

Jumlah = 9 bagian + 5 bagian = 14 bagian = 14 × 7 = 98

Jawab : D

9 Ayah menabung di bank sebesar Rp

2.100.000,00 dengan suku bunga tunggal 8% setahun. Saat diambil. Tabungan ayah menjadi Rp 2.282.000,00. Lama ayah menabung adalah ....

Ingat!

2. Bunga =

12 × 100 ×

Bunga = 2.282.000 – 2.100.000 = 182.000

Lama = 12 × 100 ×182.000 8 × 2.100.000 = 13

Jawab : A 10 Dikelas 9A terdapat 36 orang siswa, setelah

didata terdapat 7 orang gemar IPA, 9 orang gemar matematika, dan 5 orang siswa gemar keduanya. Banyak siswa yang tidak gemar keduanya adalah ....

D. 25 orang 2 + 5 + 4 + x = 36

11 + x = 36 x = 36 – 11 x = 25

Jawab : D 11 Gradien garis  3x – 2y = 7 adalah ....

A. 3 2

Ingat!

ax + by + c = 0  m = −

IPA MTK

5 7 – 5 = 2

9 – 5 = 4

x

x = tdk keduanya

(44)

B. − 2

3

C. − 3

2

D. − 7

3

 3x– 2y = 7  a =  3, b = – 2

m = − = − − 3 − 2 =

3 − 2= −

3 2

Jawab : C

12 Persamaan garis melalui titik (–2, 5) dan sejajar garis x–3y + 2 = 0 adalah ….

A. 3x– y = 17 B. 3x + y = 17 C. x– 3y = –17 D. x + 3y = –17

Ingat!

1. ax + by + c = 0  m = −

x1)

x – 3y + 2 = 0 a = 1 dan b = – 3

m1 =

−

= − 1 − 3 =

1 3

1 3 melalui titik (–2, 5)x1 =  2 dan y1 = 5

y – y1 = m (x – x1)

y – 5 = 1

3(x– ( 2))

y – 5 = 1 3(x + 2) 3y – 15 = x + 2

3y – x = 2 + 15 x + 3y = 17

x 3y =  17

Jawab : C 13 Faktor dari 49p2– 64q2adalah ....

A. (7p – 8q)(7p – 8q) B. (7p + 16q)(7p – 4q) C. (7p + 8q)(7p – 8q) D. (7p + 4q)(7p – 16q)

Ingat!

a2– b2 = (a + b)(a – b)

49p2– 64q2 = (7p)2– (8q)2 = (7p + 8q)(7p – 8q) Jawab : C

A. 28 cm2 B. 30 cm2 C. 48 cm2 D. 56 cm2

Ingat!

panjangnya 2 cm lebih dari lebarnya  p = l + 2 Kpersegipanjang = 2 (p + l ) = 28

2 (l + 2 + l ) = 28 2 (2l + 2) = 28 4l + 4 = 28 4l = 28 – 4 4l = 24

l = 6 cm  p = l + 2 = 6 + 2 = 8 cm

Jawab : C 15 Diketahui rumus fungsi f(x) =  2x + 5.

Nilai f ( 4) adalah .... A.  13

B.  3

f(x) =  2x + 5

f( 4) =  2( 4) + 5 = 8 + 5 = 13

(45)

C. 3 D. 13

Jawab : D

16 Diketahui f(x) = px + q, f(1) =  5, dan f(4) = 5. Nilai f( 6) adalah ....

A.  15 B.  9 C. 7 D. 10

f(1) =  p + q =  5 f(4) = 4p + q = 5   5p =  10

p = 2

4p + q = 5  4(2) + q = 5 8 + q = 5 q = 5 – 8 q =  3

f( 6) = 2( 6) + ( 3) =  12  3 =  15

Jawab : A 17 Himpunan penyelesaian dari  7p + 8 < 3p –

22, untuk p bilangan bulat adalah .... A. {...,  6,  5,  4}

B. {..., 0, 1, 2} C. { 2,  1, 0, ...} D. {4, 5, 6, ...}

 7p + 8 < 3p – 22  7p + 8 – 3p < – 22  10p + 8 < – 22  10p < – 22 – 8  10p < – 30 p >− 30

− 10

p > 3  Hp = { 4, 5, 6, ...}

Jawab : D 18 Jumlah tiga bilangan ganjil berurutan adalah

75. Jumlah bilangan terkecil dan terbesar bilangan tersebut adalah ....

A. 48 B. 50

C. 140

D. 142

Jumlah bil. terkecil dan terbesar = 23 + 27 = 50 Jawab : B 19 Perhatikan gambar!

P adalah titik pusat lingkaran dan luas juring PLM = 24 cm2. Luas juring PKN adalah ….

A. 27 cm2 B. 30 cm2 C. 32 cm2 D. 39 cm2

Ingat!

� 1

� 2=

� 1

� 2

�� =

� � ��

24 = 60 45

L juring PKN = 60 × 24 45 =

1.440

45 = 32 cm

2

Jawab : C

20 Dua buah lingkaran berpusat di A dan B dengan jarak AB = 20 cm. Panjang garis singgung persekutuan dalam 16 cm dan

Ingat!

Jika Gd = Garis singgung persekutuan dalam

j = Jarak pusat 2 lingkaran