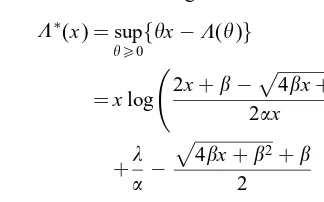www.elsevier.com/locate/dsw
Analysis of the M
=
D
=
1-type queue based on an integer-valued
rst-order autoregressive process
(
Soohan Ahn
a;∗, Gyemin Lee
b, Jongwoo Jeon
a aDepartment of Statistics, Seoul National University, Seoul 151-742, South Korea bDepartment of Statistics, Gyeongsang National University, 660-701, South KoreaReceived 1 November 1999; received in revised form 1 April 2000
Abstract
In this paper, we propose a queueing model based on an integer-valued rst-order autoregressive(INAR(1)) process. We derive the queue length distribution and its asymptotic decay rate of the proposed model. Also, our numerical study shows that the new model can be considered as an alternative approach to the well-known MMPP=D=1 queue in terms of performance and amount of computational work. c2000 Elsevier Science B.V. All rights reserved.
Keywords:INAR(1) process; MMPP=D=1 queue; Asymptotic decay rate
1. Introduction
Integrated service communication systems usually have very complicated input streams which are the superposition of a number of several tracs. A typical example is a statistical multiplexer, whose input con-sists of a superposition of packetized voice sources together with data trac [7]. These input streams have an important distinction that the number of packet arrivals in adjacent time intervals can be highly correlated, which signicantly aects queueing per-formance of the system. Thus, a great interest has recently risen in the modeling of these complicated
(
This research was supported by KOSEF through Statistical Re-search Center for Complex Systems at Seoul National University.
∗Corresponding author. Fax: +82-2-873-1146.
E-mail address:[email protected] (S. Ahn).
input streams and in the analysis of the resulting queueing model.
Within this framework, various input processes have been studied. A particularly interesting process is the Markov modulated Poisson process(MMPP), which is an extended Poisson process. It possesses important properties which make it suitable for mod-eling complicated arrival processes. By using the MMPP as an arrival process, various computer and communication systems have been analyzed. How-ever, the amount of computational work to analyze the queueing model based on the MMPP, explodes as the number of the aggregated input streams increases [3]. Hence, we are interested in an integer-valued rst order autoregressive (INAR(1)) process introduced by Al-Osh and Alzaid [1]. This process not only enables us to appropriately model the correlation of trac streams but also is analytically tractable. In this paper,
we shall provide a computational algorithm for the queue length distribution of the INAR(1)=D=1 queue, and derive its asymptotic decay rate using the results of Chang [2], Glynn and Whitt [4].
This paper is organized as follows. In Section 2, we review the procedure of computing the stationary queue length distribution of the MMPP=D=1 queue for the comparison to the INAR(1)=D=1 queue. In Section 3.1, we review the INAR(1) process and its properties. Section 3.2 provides a recursive algorithm for comput-ing the queue length distribution of the INAR(1)=D=1 queue. In Section 4, we obtain the asymptotic de-cay rate of the queue length distribution. Finally, we present several numerical studies in order to com-pare the INAR(1)=D=1 queue with the MMPP=D=1 queue.
2. Review: MMPP/D/1 queue
In this section, we introduce, based on Lucantoni [8], how to compute the stationary queue length distri-bution of the MMPP=D=1 queue where the determin-istic service time is 1 and the number of the states of the phase of the MMPP arrival process ism.
Let Q(n) and J(n), respectively, denote the num-ber in the system and the phase of the MMPP arrival process immediately after the nth departure from the queue. Then, (Q(n); J(n)) is a Markov chain and has a transition probability matrixP∗
of the following form.
P∗ =
B0 B1 B2 B3 · · ·
A0 A1 A2 A3 · · ·
0 A0 A1 A2 · · ·
0 0 A0 A1 · · ·
· · · ·
: (1)
Note thatAn’s andBn’s arem×msquare matrices. Let
alsox=(x0;x1; : : :) be the stationary probability vector ofP∗
, wherexi; i¿0, arem-vectors andxP∗ =x.
For computing the stationary probability vector x
ofP∗
, the stochastic matrixGwhich satises the fol-lowing nonlinear matrix equation (2), is needed.
G= ∞ X
n=0
AnGn: (2)
Given the matrix G and the vector x0, the vectors xn; n= 1;2; : : : ; are recursively obtained from the
formula
xn= x0B˜n+
n−1 X
k=1
xkA˜n+1−k
!
(I−A1˜ )−1
; (3)
where,
˜
An=An+An+1G+An+2G2+: : : ; ˜
Bn=Bn+Bn+1G+Bn+2G2+: : : :
(4)
Lucantoni [8] also provides the procedure of obtaining the vectorx0. The stationary queue length distribution
(0); (1); : : :can be easily obtained by
(n) =e′
xn;
whereeis the column vector of 1’s.
From Eqs. (2) – (4) and Lucantoni [8], the com-putation of the stationary queue length distribution of the MMPP=D=1 queue, requires approximations of An; Bn;A˜n;B˜nandGand truncations of the innite
ma-trix sequence {Ai} and{Bi} depending on a certain
accuracy. Hence, there are two problems in computa-tion, i.e., the rst is that the computational work ex-plodes as the number of states of the phase of the MMPP increases [3], and the second is that the speed of convergence becomes seriously slow under heavy trac conditions [6].
3. Analysis of INAR(1)/D/1 queue
3.1. INAR(1) process
In this section, we introduce the denition of the INAR(1) process and describe its properties based on Al-Osh and Alzaid [1]. We shall rst present the de-nition of the operator◦based on Steutel and Van Harn [9]. LetX be a non-negative integer-valued random variable and then for any ∈[0;1] the operator ◦is dened by
◦X =
X
X
i=1
Zi (5)
where Zi is independent of X and is a sequence of
i.i.d. random variables such that
From the denition of the operator ◦, it is clear that 0◦X = 0; 1◦X =X; E(◦X) =E(X) and for any ∈[0;1]; ◦(◦X) = ()◦X.
The stationary INAR(1) process{An: n= 1;2; : : :}
is dened by
An=◦An−1+n; (6)
where{n}is a sequence of i.i.d. Poisson random
vari-ables with meanandnis independent ofAn−1. From now on, we shall call andn correlation factor and
innovation factor, respectively.
The mean ofAn is simplyE[An] =E[An−1] +. Since the process{An}is stationary, it should be that
E[An] =
1−:
For any non-negative integerk, the covariance at lag k; (k), is given by
(k) =Cov(An−k; An) =k(0) (7)
where(0) =Var(An) ==(1−). Eq. (7) shows that
the autocorrelation decays exponentially with lag k and has the same form as the Yule–Walker equation in the AR(1) process.
Al-Osh and Alzaid [1] describe four techniques for estimating and for a given realizationa0; : : : ; an.
These are Yule–Walker estimation, conditional least squares estimation, maximum likelihood estimation conditional on the initial observation, and the uncon-ditional maximum likelihood estimation.
3.2. Queue-length distribution of the INAR(1)=D=1
queue
In this section, based on the INAR(1) process, we propose a new queueing system and derive the queue length distribution of the proposed queueing model.
Let {n; n¿0} be a sequence of times when
ser-vices occur. We assume that the number of arrivals which can be served at each time n is 1. And we
shall deneAnandQnas number of packets arrived at
the system during the (n−1; n] and the queue length in the system at time +
n, respectively. Then, a new
queueing model, called the INAR(1)=D=1 queue, can be dened as follows.
(i) 1−0; 2−1; : : :are constant 1 and0= 0.
(ii) Anis the INAR(1) process.
(iii) Qn= (Qn−1+An−1)+, where (x)+= max{0; x}.
The INAR(1) process dened in (6) can be inter-preted as follows: the rst term◦An−1is the num-ber of packets induced by the trac streams at time n−1 and the second termnis the number of packets
arriving from outside at time n. Since the INAR(1) process includes the Poisson process as a special case, the INAR(1)=D=1 queue can be considered as an ex-tended M=D=1 queue.
From the denition of An and Qn, we can easily
see that (An; Qn) is a two-dimensional discrete-time
Markov chain, whose state space is{(i; j): 06i6j+ 1; 06j ¡∞}. Let us denote
i; j= lim
n→∞P(An=i; Qn=j)
for all possible states and dene
ai; j=P(An=j|An−1=i)
= min(i; j)
X
k=0
i k
k(1−)i−kp
j−k; (8)
where pk =P(1 =k); k = 0;1; : : : : Then we
ob-tain the following balance equation for 06i6j+ 1; 06j ¡∞,
i; j= (0;0a0;0+1;0a1;0)1(i=j=0)
+
j−i+2 X
k=0
k; j−i+1ak; i; (9)
where 1(·) is an indicator function. LetQ denote the stationary queue length random variable and
(j)≡P(Q=j) =
j+1 X
i=0 i; j:
We also dene forr; s ¿0
ai(s) =
X
j
ai; jsj; (r; s) =
X
i; j
i; jrisj (10)
and (s) =E[s1]. Then, we obtain
and we derive the following theorem which is necessary for computing the stationary queue-length distribution of the INAR(1)=D=1 queue. Let the trac intensity ≡E[A1] ==(1−).
Theorem 1. Under the condition ¡1;
B= 1−: (12)
This theorem says that when the queue is empty after the service is completed, the probability that there is no arrival before the next service, equals 1 – trac intensity.
Proof. From Eq. (11), we have
s(r; s) = (s−1)B+(1−+rs; s) (rs):
Dierentiating both sides of the above equation with respect tos, we obtain
(r; s) +s @
It is easily shown that
@
Thus, we can obtain the following equation:
1 =B+E[1] +E[A1]:
SinceE[A1] ==(1−) in Section 3.1, we derive Eq. (12). So the theorem is completely proved.
Now, we shall obtain a recursive algorithm which provides the exact stationary queue length distribution
of the INAR(1)=D=1 queue. Let
where0n is then-dimensional column vector of 0’s
anda∗
m; n; 06m6n−1; n¿1;are (m+2)-dimensional
row vectors dened by
a∗
Note thatAn’s andBn’s are known matrices depending
only onai; j’s dened in Eq. (8). Computation ofx0:
From Eq. (9) and Theorem 1, we obtain
Solving this equation, it can be easily seen that
x0= (0;0; 1;0) ′
= (1−)×B0: (17)
Computation ofx1:
From Eq. (9), it can be easily seen that
x(2)
1 =2;1=A1x0: (18)
Also, Eq. (9) and Theorem 1 yield the following equa-tion:
0;0= 1−+p0;1a0;0+1;1a1;0+2;1a2;0; 1;1=0;1a0;1+1;1a1;1+2;1a2;1:
Solving this equation, we obtain
x(1)
Hence, it can be easily seen that
x(2)n =An(x
Now, we consider x(1)n . Using the equations of
0; n−1 and 1; n in (9), we can get the following
Solving Eq. (23), it follows that
0; n=C
From Eqs. (22) and (25), we can obtain
xn=Bn
Thus, we can recursively obtain the exact stationary queue length distribution of the INAR(1)=D=1 queue. From the result of this section and properties of the INAR(1) process, the INAR(1)=D=1 queue has some advantages that the INAR(1) process can model the correlation of trac streams as the MMPP, that the stationary queue length distribution can be com-puted exactly and that the computational work of ob-taining the stationary queue length distribution of the INAR(1)=D=1 queue is very small, and does not in-crease as the trac intensity becomes high. Further-more, we shall show by numerical studies in Section 5, that the INAR(1)=D=1 queue can be a good substi-tute for the MMPP=D=1 queue.
4. Asymptotic decay rate
In this section, we obtain the asymptotic decay rate of the stationary queue length distribution of the INAR(1)=D=1 queueing model. By the results of Chang [2], and Glynn and Whitt [4], the asymptotic decay rate can be obtained if the INAR(1) process satises the large deviation principle(LDP).
Let{An}; n= 1;2; : : :denote the INAR(1) process
dened in Section 2 and() denote the asymptotic logarithmic moment generating function dened by
() = lim
Theorem 2. The asymptotic logarithmic moment generating function;can be represented by
() =
and the sequence of random variables {Pn
i=1Ai=n} satises the LDP with the rate function∗
which is the Legendre transformation of ;that is; ∗
(x) = sup[x−()].
Proof. From the property of the INAR(1) process, we can show that fors ¿0,
Since the INAR(1) process has a Poisson marginal distribution with mean=(1−), for ¡−log(), Gartner–Ellis theorem,{Pn
i=1Ai=n}satises the LDP
with the following rate function
∗
From Chang [2], and Glynn and Whitt [4], the sta-tionary queue-length distribution of the INAR(1)=D=1 has the following asymptotic decay rate:
lim
is the unique positive solution of the equa-tion() =.
5. Numerical studies
In this section, we present several numerical studies in order to compare the stationary queue length dis-tribution of the INAR(1)=D=1 queue with that of the MMPP=D=1 queue.
For the numerical studies, we consider the MMPP=D=1 queue whose arrival process is the su-perposition of several homogeneous 2-state MMPP’s with the following parameters:
R=
We compute the queue length distributions of the MMPP=D=1 queues for 10 cases where the number of superpositions of the 2-state MMPP’s varies from 1 to 10.
For the INAR(1)=D=1 queue, we determine the cor-relation factorand the innovation factorsuch that both the MMPP=D=1 queue and the INAR(1)=D=1 queue have the same trac intensity and asymptotic decay rate. To do so, we use results of Kesidis et al. [5] and Section 4.
Fig. 1. Comparison of log-tail queue-length distributions of MMPP=D=1 and INAR(1)=D=1.
MMPP=D=1 queue when the number of superposi-tions is large. Consequently, the INAR(1)=D=1 queue can be considered as an alternative approach to the MMPP=D=1 queue when a number of homogeneous 2-state MMPP’s are superposed.
Acknowledgement
The authors thank the referee for careful reading of the manuscript and the indications leading to the improved representations of the recursive algorithm in Section 3.1.
References
[1] M.A. Al-Osh, A.A. Alzaid, First-order integer-valued autoregressive(INAR(1)) process, J. Time Ser. Anal. 3 (1987) 261–275.
[2] C.S. Chang, Stability, queue length and delay of deterministic and stochastic queueing networks, IEEE Trans. Automat. Control 39 (1994) 913–931.
[3] A.I. Elwalid, Markov modulated rate processes for modeling, analysis and control of communication networks, Ph.D. Thesis, Graduate School of Arts and Science, Columbia University, 1991.
[4] P.W. Glynn, W. Whitt, Logarithmic asymptotics for steady state tail probabilities in a single server queue, J. Appl. Probab. 31A (1993) 131–159.
[5] G. Kesidis, J. Walrand, C.S. Chang, Eective bandwidths for multiclass Markov uids and other ATM Sources, IEEE=ACM Trans. Networking 1 (1993) 424–428.
[6] J. Ye, S.Q. Li, Folding algorithm: a computational method for nite QBD processes with level-dependent transitions, IEEE Trans. Comm. 42 (1994) 662–671.
[7] D.M. Lucantoni, V. Ramaswami, Ecient algorithms for solving the non linear matrix equation arising in phase type queues,Comm.Statist.-Stochastic Models 1 (1985) 29–52. [8] D.M. Lucantoni, New results on the single server service with
Batch Markovian arrival process, Comm. Statist.-Stochastic Models 7 (1991) 1–46.