PENYELESAIAN PERSAMAAN DIFERENSIAL LANE-EMDEN DENGAN MENGGUNAKAN METODE EULER DAN
METODE DEKOMPOSISI ADOMIAN Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Maria Benedikta Kurnia NIM: 163114031
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
SOLUTION TO THE LANE-EMDEN DIFFERENTIAL EQUATION BASED ON THE EULER METHOD AND ADOMIAN
DECOMPOSITION METHOD Final Project
Presented as a Partial Fulfillment of Requirements To Obtain the Degree of Sarjana Matematika
In Mathematics
By:
Maria Benedikta Kurnia Student ID: 163114031
MATHEMATICS STUDY PROGRAM, DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v MOTTO
“Jadikanlah diri sebagai
vi
HALAMAN PERSEMBAHAN
Karya ini ku persembahkan untuk Tuhan Yesus, Bapa, Mama, Mulyani serta keluargaku dan almamaterku.
ix ABSTRAK
Tugas akhir ini membahas tentang penyelesaian persamaan diferensial Lane-Emden dengan menggunakan dua metode penyelesaian di dalam matemat-ika. Persamaan diferensial Lane-Emden lebih dikenal di bidang Astrofisika terkhusus pada masalah pemodelan struktur bintang.
Metode yang digunakan adalah metode Euler yang pendekatannya dasarkan pendekatan numeris dan metode dekomposisi Adomian dengan ber-dasarkan pendekatan analitis. Metode Euler merupakan metode numeris yang dapat digunakan untuk menyelesaikan persamaan diferensial, baik tingkat satu maupun tingkat yang lebih tinggi, dengan nilai awal diberikan. Metode dekompo-sisi Adomian adalah salah satu metode analitis yang dapat digunakan juga dalam menyelesaikan persamaan diferensial, dalam penyelesaiannya menghasilkan fungsi pendekatan berdasarkan polinomial Adomian.
Dengan demikian, hasil yang diperoleh dalam tugas akhir ini dapat digunakan untuk memeriksa metode yang akurat untuk menyelesaikan persamaan diferensial Lane-Emden berdasarkan kecilnya galat yang dihasilkan.
Kata kunci: Persamaan diferensial, persamaan diferensial Lane-Emden, metode
x ABSTRACT
This final project is discuss about the solving of Lane-Emden differential equation using by two solutions methods in mathematics. Lane-Emden differen-tial equations is well known in astrophysics sector, particularly in the stellar structure.
The method used in the final project is Euler method which approach based on numerical and Adomian decomposition with an analytical approach-ment. Euler method is a numerical method which could be use to solve the dif-ferential equations problem at the level 1 and higher, with the initial values given. Adomian decomposition method is one of the analytical method that could be use as well to solve the differential equations, it’s solution resulting the functional approach which based on polynomial Adomian.
Therefore, the results obtained from the thesis is able to to examine the accurate method to solve the Lane-Emden differential equations based on the small error generated.
Keywords: differential equation, Lane-Emden differential equation, Euler
xiii DAFTAR ISI
HALAMAN JUDUL……...………i
HALAMAN JUDUL DALAM BAHASA INGGRIS………ii
LEMBAR PERSETUJUAN ... iii
LEMBAR PENGESAHAN ... iv
MOTTO ... v
HALAMAN PERSEMBAHAN ... vi
PERNYATAAN KEASLIAN KARYA ... vii
LEMBAR PERNYATAAN PERSETUJUAN ... viii
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... viii
ABSTRAK ... ix ABSTRACT ... x KATA PENGANTAR ... xi BAB I ... 1 PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 3 C. Batasan Masalah ... 3 D. Tujuan Penulisan ... 3 E. Manfaat Penulisan ... 4 F. Metode Penulisan ... 4 G. Sistematika Penulisan ... 4 BAB II ... 6
PERSAMAAN DIFERENSIAL DAN TOPIK TERKAIT ... 6
A. Turunan ... 6
1. Turunan Pertama ... 9
2. Turunan Kedua ... 11
B. Persamaan Diferensial ... 14
xiv
PERSAMAAN DIFERENSIAL LANE-EMDEN DAN METODE
PENYELESAIANNYA ... 18
A. Pemodelan untuk Mendapatkan Persamaan Diferensial Lane-Emden ... 18
B. Metode Euler untuk Menyelesaikan Persamaan Diferensial Lane-Emden22 C. Metode Dekomposisi Adomian untuk Menyelesaikan Persamaan Diferensial Lane-Emden ... 30
BAB IV ... 37
PENYELESAIAN PERSAMAAN DIFERENSIAL LANE-EMDEN ... 37
A. Simulasi Numeris dengan Menggunakan Metode Euler ... 37
B. Simulasi Analitis dengan Menggunakan Metode Dekomposisi Adomian 55 C. Diskusi Hasil ... 72 BAB V ... 75 PENUTUP... 75 A. Kesimpulan ... 75 B. Saran ... 76 DAFTAR PUSTAKA ... 77 LAMPIRAN ... 79
xv
DAFTAR GAMBAR
Gambar 2.1. Grafik ilustrasi pendekatan turunan orde satu dengan beda maju . 11
Gambar 4.1. Grafik solusi eksak contoh 4. 1. ... 42
Gambar 4.2. Grafik solusi eksak contoh 4.1 dibandingkan terhadap fungsi 𝑧𝑛 dengan menggunakan metode Euler. ... 42
Gambar 4.3. Grafik menunjukkan fungsi 𝑤𝑛 ... 43
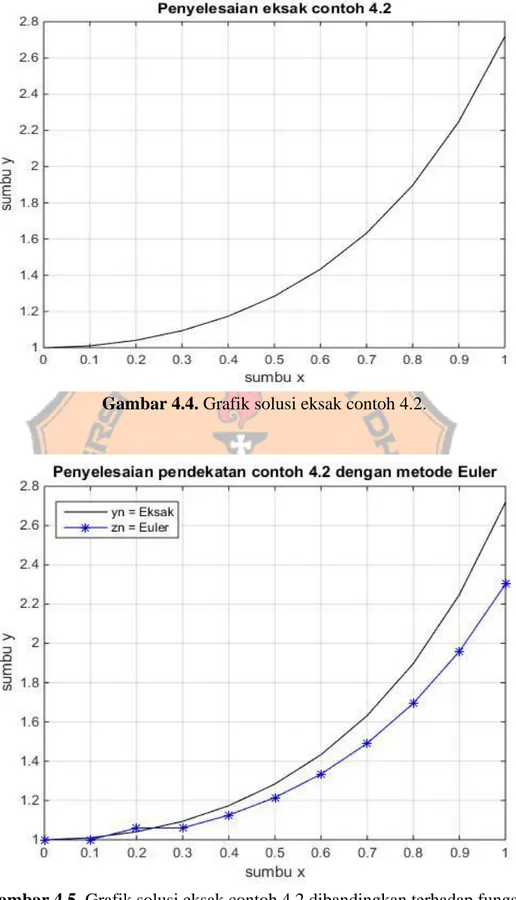
Gambar 4.4. Grafik solusi eksak contoh 4.2 ... 48
Gambar 4.5. Grafik solusi eksak contoh 4.2 dibandingkan terhadap fungsi 𝑧𝑛 dengan menggunakan metode Euler. ... 48
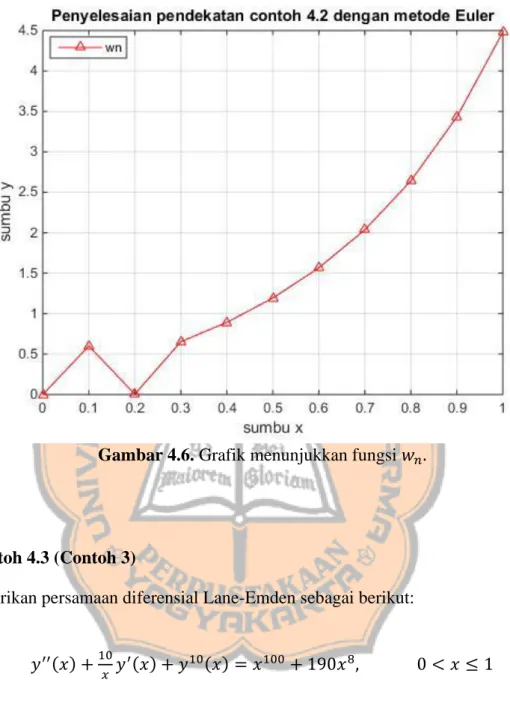
Gambar 4.6. Grafik menunjukkan fungsi 𝑤𝑛 ... 49
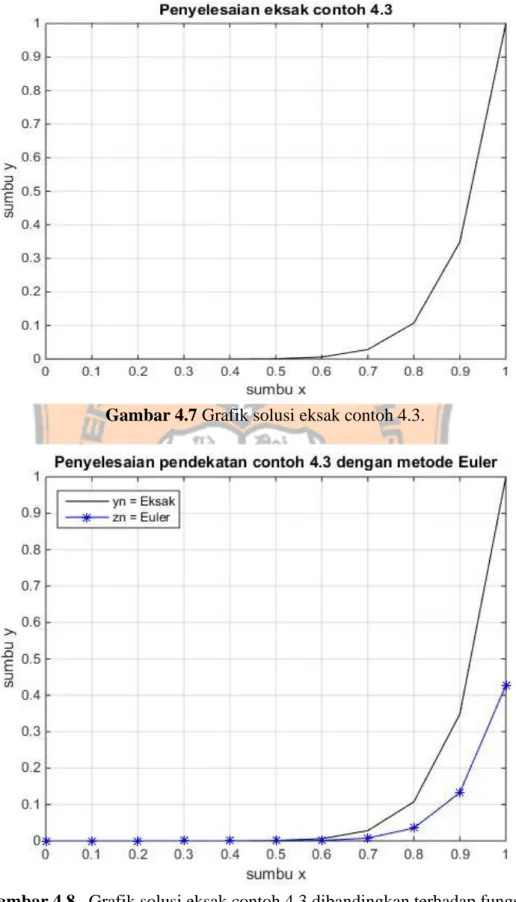
Gambar 4.7. Grafik solusi eksak contoh 4. 3. ... 42
Gambar 4.8. Grafik solusi eksak contoh 4.3 dibandingkan terhadap fungsi 𝑧𝑛 dengan menggunakan metode Euler. ... 42
Gambar 4.9. Grafik menunjukkan fungsi 𝑤𝑛 ... 55
Gambar 4.10. Grafik penyelesaian eksak contoh 4.4. ... 67
Gambar 4.11. Grafik pendekatan contoh 4.4 dengan metode dekomposisi Adomian ... 61
Gambar 4.12. Grafik penyelesaian eksak contoh 4.5. ... 67
Gambar 4.13. Grafik penyelesaian pendekatan contoh 4.5 dengan metode dekomposisi Adomian. ... 67
Gambar 4.14. Grafik penyelesaian eksak contoh 4.6. ... 67
Gambar 4.15. Grafik penyelesaian pendekatan contoh 4.6 dengan metode dekomposisi Adomian ... 71
Gambar 4.16. Grafik ilustrasi pendekatan contoh 1. ... 72
Gambar 4.17. Grafik ilustrasi pendekatan contoh 2. ... 73
xvi
DAFTAR TABEL
Tabel 3.1. Hasil perhitungan untuk soal 3.2 dengan metode Euler ... 27
Tabel 4.1. Hasil perhitungan untuk soal 4.1 dengan metode Euler ... 41
Tabel 4.2. Hasil perhitungan untuk soal 4.2 dengan metode Euler ... 47
Tabel 4.3. Hasil perhitungan untuk soal 4.3 dengan metode Euler ... 53
Tabel 4.4. Hasil perhitungan untuk soal 4.4 dengan metode dekomposisi Adomian ... 60
Tabel 4.5. Hasil perhitungan untuk soal 4.5 dengan menggunakan metode dekomposisi Adomian ... 66
Tabel 4.6. Hasil perhitungan untuk soal 4.6 dengan menggunakan metode dekomposisi Adomian ... 70
1 BAB I
PENDAHULUAN A. Latar Belakang
Matematika merupakan salah satu ilmu pengetahuan yang banyak diterapkan dalam kehidupan sehari-hari dan juga diterapkan dalam berbagai bidang ilmu pengetahuan. Salah satu kegunaan ilmu matematika adalah untuk membuat model matematis dari masalah-masalah nyata. Model ini dapat membantu kita untuk menyelesaikan masalah-masalah tersebut dengan menggunakan berbagai metode penyelesaian yang ada di dalam matematika.
Matematika mempelajari persamaan diferensial yang merupakan persamaan yang menyatakan hubungan antara suatu fungsi dengan turunan-turunannya. Persamaan diferensial dapat dibedakan menjadi dua berdasarkan banyak variabel bebasnya, yaitu persamaan diferensial biasa dan persamaan diferensial parsial.
Persamaan diferensial biasa adalah persamaan diferensial yang hanya memuat satu variabel bebas sedangkan persamaan diferensial parsial memuat lebih dari satu variabel bebas. Salah satu contoh persamaan diferensial biasa adalah persamaan diferensial Lane-Emden yang banyak ditemukan di bidang fisika dan astrofisika.
Persamaan diferensial Lane-Emden merupakan jenis persamaan diferensial biasa nonlinear yang berorde dua. Contoh penggunaannya meliputi pemodelan struktur bintang, dan lain-lain. Persamaan diferensial Lane-Emden pertama kali dipelajari oleh ahli fisika bernama Robert Emden pada tahun 1907 dengan bentuk sebagai berikut:
𝑦′′+2 𝑥𝑦
′+ 𝑓(𝑦) = 0,
2
Model dari persamaan diferensial Lane-Emden merupakan persamaan diferensial nonlinear yang cukup sulit untuk diselesaikan secara analitis. Mes-kipun demikian, persamaan diferensial Lane-Emden dapat diselesaikan dengan menggunakan metode hampiran. Metode hampiran yang dapat digunakan adalah metode Euler dan metode dekomposisi Adomian. Metode tersebut akan menghasilkan nilai pendekatan dengan galat tertentu berdasarkan nilai awal yang diberikan dan banyaknya iterasi dalam penghitungan.
Metode Euler merupakan salah satu metode numeris yang dapat digunakan untuk menyelesaikan persamaan diferensial tingkat satu dengan nilai awal yang diketahui.
Dipandang persamaan:
𝑑𝑦
𝑑𝑡 = 𝑓(𝑡, 𝑦)
dengan nilai awal 𝑦(𝑡0) = 𝑦0 dan t menyatakan waktu. Secara umum metode
Euler dapat ditulis sebagai berikut:
𝑦𝑛+1 = 𝑦𝑛+ 𝑓(𝑡𝑛, 𝑦𝑛)(𝑡𝑛+1− 𝑡𝑛), 𝑛 = 0, 1, 2, 3, …
dimana, n adalah banyaknya iterasi dalam penghitungan, dan tn menyatakan waktu pada langkah ke-n (Boyce & DiPrima, 2013). Di sini, y adalah fungsi terhadap t. Dengan kata lain, yn adalahfungsi terhadap tn .
Selain metode Euler yang disebutkan di atas, ada pula metode dekompo-sisi Adomian yang akan digunakan. Metode dekompodekompo-sisi Adomian pertama kali ditemukan oleh George Adomian. Metode ini telah terbukti dapat diterapkan dengan mudah untuk menyelesaikan persamaan diferensial biasa atau parsial, lin-ear ataupun non-linlin-ear.
3
Pada metode dekomposisi Adomian ini, tidak perlu melakukan linearisasi. Solusi yang dihasilkan merupakan solusi pendekatan. Solusi yang didapatkan kemudian diilustrasikan dengan grafik menggunakan komputer sehingga dapat menggambarkan pendekatan dari solusi eksak dari persamaan diferensial Lane-Emden.
B. Rumusan Masalah
Rumusan masalah dalam tugas akhir ini adalah:
1. Bagaimana model dari persamaan diferensial Lane-Emden?
2. Bagaimana menyelesaikan persamaan diferensial Lane-Emden secara numeris dengan menggunakan metode Euler?
3. Bagaimana menyelesaikan persamaan diferensial Lane-Emden secara analitis dengan menggunakan metode dekomposisi Adomian?
C. Batasan Masalah
Dalam tugas akhir ini akan dibahas mengenai bagaimana memperoleh model persamaan diferensial Lane-Emden dan penyelesaian hampirannya. Metode yang digunakan adalah metode Euler dan metode dekomposisi Adomian.
D. Tujuan Penulisan
Tujuan penulisan tugas akhir ini adalah:
1. Menjabarkan bentuk dari persamaan diferensial Lane-Emden.
2. Mencari penyelesaian numeris persamaan diferensial Lane-Emden dengan menggunakan metode Euler.
3. Mencari penyelesaian analitis persamaan diferensial Lane-Emden dengan menggunakan metode dekomposisi Adomian.
4 E. Manfaat Penulisan
Manfaat yang diperoleh dari tugas akhir ini adalah mengetahui penyelesaian persamaan diferensial Lane-Emden dengan menggunakan kedua metode tersebut.
F. Metode Penulisan
Tugas akhir ini ditulis berdasarkan kajian pustaka, seperti jurnal-jurnal matematika dan buku-buku matematika, serta praktik pemograman MATLAB.
G. Sistematika Penulisan
Tugas akhir ini disusun dengan sistematika sebagai berikut: BAB I: PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penelitian G. Sistematika Penulisan
BAB II: PERSAMAAN DIFERENSIAL DAN TOPIK TERKAIT A. Turunan
1. Turunan Pertama 2. Turunan Kedua
B. Persamaan Diferensial Biasa
BAB III: PERSAMAAN DIFERENSIAL LANE-EMDEN DAN METODE PENYELESAIANNYA
A. Menjabarkan Model dari Persamaan Diferensial Lane-Emden
5
C. Metode Dekomposisi Adomian untuk Menyelesaikan Persamaan Diferensial Lane-Emden
BAB IV: PENYELESAIAN PERSAMAAN DIFERENSIAL LANE-EMDEN A. Simulasi Numeris dengan Metode Euler
B. Simulasi Analitis dengan Metode Dekomposisi Adomian C. Diskusi Hasil BAB V: PENUTUP A. Kesimpulan B. Saran DAFTAR PUSTAKA LAMPIRAN
6 BAB II
PERSAMAAN DIFERENSIAL DAN TOPIK TERKAIT
Pada bab ini, penulis menjelaskan teori-teori yang akan digunakan dalam menyelesaikan persamaan diferensial Lane-Emden antara lain, turunan yang meliputi turunan pertama dan turunan kedua, serta persamaan diferensial biasa.
A. Turunan
Subbab ini akan membahas turunan berdasarkan referensi dari Thomas (2010).
Definisi 2.1
Turunan dari suatu fungsi 𝑓 pada titik 𝑥 , yang dinotasikan sebagai 𝑓′(𝑥) didefinisikan sebagai berikut:
𝑓′(𝑥) = lim ℎ→0
𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ
dengan syarat limitnya ada.
Contoh 2.2
Contoh ini diambil dari buku Thomas (2010). Andaikan 𝑓(𝑡) = 16𝑡2. Carilah 𝑓′(1). Penyelesaian: 𝑓′(1) = lim ℎ→0 𝑓(1 + ℎ) − 𝑓(1) ℎ = lim ℎ→0 [16(1 + ℎ)2] − [16(1)2] ℎ = lim ℎ→0 [16 + 32ℎ + 16ℎ2] − [16] ℎ = limℎ→0 16(ℎ + ℎ2) ℎ = lim ℎ→016(2 + ℎ) = limℎ→016(2 + 0) = 32.
7 Contoh 2.3
Contoh ini diambil dari buku Thomas (2010). diberikan 𝑓(𝑥) = 𝑥 𝑥−1. Tentukanlah 𝑓 ′(𝑥). Penyelesaian: diperoleh 𝑓(𝑥) = 𝑥 𝑥−1 dan 𝑓(𝑥 + ℎ) = 𝑥+ℎ (𝑥+ℎ)−1 , sehingga: 𝑓′(𝑥) = lim ℎ→0 𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ = lim ℎ→0 𝑥 + ℎ (𝑥 + ℎ) − 1− 𝑥 𝑥 − 1 ℎ = lim ℎ→0 1 ℎ. (𝑥 + ℎ)(𝑥 − 1) − 𝑥(𝑥 + ℎ − 1) (𝑥 + ℎ − 1)(𝑥 − 1) = lim ℎ→0 1 ℎ. −ℎ (𝑥 + ℎ − 1)(𝑥 − 1) = lim ℎ→0 −1 (𝑥 + ℎ − 1)(𝑥 − 1) = −1 (𝑥 − 1)2, 𝑥 ≠ 1. Definisi 2.4
Definisi turunan (derivatif) di atas dapat ditulis ulang sebagai berikut (Thomas, 2010):
Diberikan fungsi 𝑓: 𝐷𝑓 ⊆ ℝ → ℝ maka turunan (derivatif) dari fungsi 𝑓 pada titik 𝑥 adalah
𝑓′(𝑥) = lim ℎ→0
𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ
atau misalkan 𝑧 = 𝑥 + ℎ, sehingga ℎ = 𝑧 − 𝑥 dan ℎ mendekati 0 jika dan hanya jika 𝑧 mendekati 𝑥. Jadi dapat ditulis,
𝑓′(𝑥) = lim 𝑧→𝑥
𝑓(𝑧) − 𝑓(𝑥) 𝑧 − 𝑥 dengan syarat nilai limitnya ada.
8 Contoh 2.5
Contoh ini diambil dari buku Thomas (2010).
Gunakan defenisi 2.4 untuk mencari nilai 𝑓′(𝑥) jika diberikan 𝑓(𝑥) = √𝑥, untuk 𝑥 > 0. Penyelesaian: 𝑓′(𝑥) = lim 𝑧→𝑥 𝑓(𝑧) − 𝑓(𝑥) 𝑧 − 𝑥 = lim 𝑧→𝑥 √𝑧 − √𝑥 𝑧 − 𝑥 = lim 𝑧→𝑥 √𝑧 − √𝑥 (√𝑧 − √𝑥)(√𝑧 + √𝑥) = lim 𝑧→𝑥 1 (√𝑧 + √𝑥) = lim 𝑧→𝑥 1 (√𝑥 + √𝑥) = 1 2√𝑥. Teorema 2.6
Jika 𝑓 memiliki turunan pada 𝑥 = 𝑐, maka 𝑓 kontinu di 𝑥 = 𝑐 (Thomas, 2010). Bukti dapat dilihat pada buku karangan Thomas (2010) yang berjudul Thomas’
Calculus Early Transcendentals.
Banyak notasi yang dapat digunakan untuk menyatakan turunan dari fungsi 𝑦 = 𝑓(𝑥), dimana 𝑥 adalah variabel bebas, dan 𝑦 adalah variabel terikat (Thomas, 2010) sebagai berikut:
𝑓′(𝑥) = 𝑦′=𝑑𝑦 𝑑𝑥 = 𝑑𝑓 𝑑𝑥 = 𝑑 𝑑𝑥𝑓(𝑥) = 𝐷(𝑓)(𝑥) = 𝐷𝑥𝑓(𝑥) simbol 𝑑
𝑑𝑥 dan 𝐷 menunjukkan operasi diferensiasi. Notasi 𝑑𝑦
𝑑𝑥 dibaca “turunan
dari 𝑦 terhadap 𝑥 dan 𝐷(𝑓)(𝑥) dibaca “turunan dari 𝑓 terhadap 𝑥 . Sedangkan 𝑓′(𝑥) dan 𝑦′ berasal dari notasi yang digunakan Newton untuk menyatakan
9
Selanjutnya, akan membahas turunan pertama dan turunan kedua beserta contohnya dengan menggunakan pendekatan metode Euler, berdasarkan referensi dari Thomas (2010), Ross (1989), Burden & Faires (2011).
Sebelumnya akan dibahas mengenai ekspansi deret Taylor terlebih dahulu.
Teorema 2.7
Misalkan 𝑓 adalah sebuah fungsi yang diturunkan ke 𝑛 + 1, yaitu 𝑓(𝑛+1) pada interval [𝑎, 𝑏], dan 𝑥0 𝜖 [𝑎, 𝑏]. Untuk setiap 𝑥 𝜖 [𝑎, 𝑏] ada 𝜉(𝑥) diantara 𝑥0 dan 𝑥 dengan 𝑓(𝑥) = 𝑃𝑛(𝑥) + 𝑅𝑛(𝑥) (2.1) dimana 𝑃𝑛(𝑥) = 𝑓(𝑥0) + 𝑓′(𝑥0)(𝑥 − 𝑥0) + 𝑓′′(𝑥0) 2! (𝑥 − 𝑥0) 2+ ⋯ +𝑓 (𝑛)(𝑥 0) 𝑛! (𝑥 − 𝑥0) 𝑛 dan 𝑅𝑛(𝑥) =𝑓 (𝑛+1)(𝜉(𝑥)) (𝑛 + 1)! (𝑥 − 𝑥0) 𝑛+1.
Persamaan (2.1) di atas dapat ditulis lagi sebagai berikut:
𝑓(𝑥𝑖+1) = 𝑓(𝑥𝑖) + 𝑓′(𝑥𝑖)(𝑥 − 𝑥𝑖) + 𝑓′′(𝑥𝑖) 2! (𝑥 − 𝑥𝑖) 2+ ⋯ +𝑓(𝑛)(𝑥𝑖) 𝑛! (𝑥 − 𝑥𝑖) 𝑛 + 𝑅 𝑛(𝑥)
atau dalam bentuk lain, dapat ditulis lagi dengan Δ𝑥 = 𝑥 − 𝑥𝑖.
𝑓(𝑥𝑖+1) = 𝑓(𝑥𝑖) + 𝑓′(𝑥𝑖)(Δ𝑥) + 𝑓′′(𝑥𝑖) 2! (Δ𝑥) 2+ ⋯ +𝑓(𝑛)(𝑥𝑖) 𝑛! (Δ𝑥) 𝑛+ 𝑅 𝑛(𝑥) (2.2) 1. Turunan Pertama
Turunan dari sebuah fungsi biasanya dinyatakan sebagai:
𝑓′(𝑥) = lim ℎ→0
𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ .
10
Pada kasus-kasus tertentu seringkali fungsi 𝑓(𝑥) tidak diketahui secara eksplisit, tetapi hanya diberikan beberapa titik data saja. Hal ini mengakibatkan tidak dapat ditentukan turunan secara analitis. Sebaliknya, pada kasus lain, meskipun 𝑓(𝑥) diketahui secara eksplisit tetapi bentuknya rumit dan sulit diselesaikan untuk memperoleh nilai turunannya, seperti contoh berikut ini:
a. 𝑓(𝑥) = 𝑥+1 √𝑥2−𝑥+1+ 1 √3tan −1 2𝑥−1 √3 b. 𝑓(𝑥) = 𝑥3cos−1 𝑎 𝑥− 𝑎√𝑥 2 − 𝑎2 c. 𝑓(𝑥) =1 2tan −1𝑥 +1 4𝑙𝑛 (𝑥+1)2 𝑥2+1.
Untuk tiga contoh kasus di atas, dalam memperoleh nilai turunannya dapat dikerjakan secara numeris, dimana nilai yang diperoleh merupakan nilai hampirannya. Salah satu metode numeris yang dapat dipakai untuk menyelesaikannya adalah hampiran beda maju.
Jika deret Taylor pada persamaan (2.2), di potong sampai pada dua suku pertama, diperoleh: 𝑓(𝑥𝑖+1) = 𝑓(𝑥𝑖) + 𝑓′(𝑥𝑖)(Δ𝑥) + 𝑅1 (2.3) dimana, 𝑅1 =𝑓′′(𝜉) 2! (Δ𝑥) 2 atau 𝑅1 Δ𝑥 = 𝑓′′(𝜉) 2 Δ𝑥. Di sini 𝜉 ∈ (𝑥𝑖, 𝑥𝑖+1).
Kedua ruas persamaan (2.3) dibagi dengan Δ𝑥, akan menghasilkan: 𝑓(𝑥𝑖+1) Δ𝑥 = 𝑓(𝑥𝑖) Δ𝑥 + 𝑓′(𝑥𝑖)(Δ𝑥) Δ𝑥 + 𝑅1 Δ𝑥 atau 𝑓′(𝑥𝑖) ≈𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖) Δ𝑥 − 𝑅1 ∆𝑥.
11
Jadi, kita memperoleh nilai hampiran untuk turunan pertama dari 𝑦 = 𝑓(𝑥) sebagai berikut: 𝑓′(𝑥𝑖) ≈ 𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖) Δ𝑥 + 𝑂(∆𝑥) (2.4) dengan memisalkan 𝑂(∆𝑥) = −𝑅1 ∆𝑥.
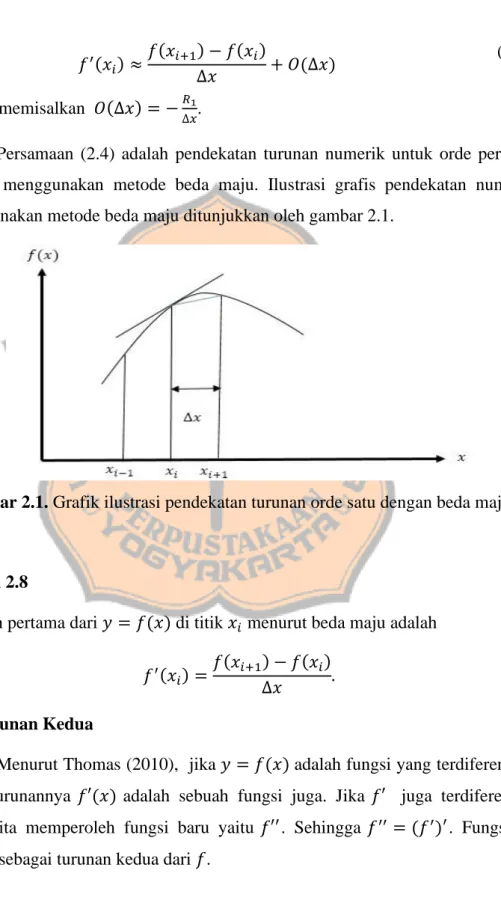
Persamaan (2.4) adalah pendekatan turunan numerik untuk orde pertama dengan menggunakan metode beda maju. Ilustrasi grafis pendekatan numerik menggunakan metode beda maju ditunjukkan oleh gambar 2.1.
Gambar 2.1. Grafik ilustrasi pendekatan turunan orde satu dengan beda maju.
Definisi 2.8
Turunan pertama dari 𝑦 = 𝑓(𝑥) di titik 𝑥𝑖 menurut beda maju adalah
𝑓′(𝑥 𝑖) =
𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖)
∆𝑥 .
2. Turunan Kedua
Menurut Thomas (2010), jika 𝑦 = 𝑓(𝑥) adalah fungsi yang terdiferensial, maka turunannya 𝑓′(𝑥) adalah sebuah fungsi juga. Jika 𝑓′ juga terdiferensial maka kita memperoleh fungsi baru yaitu 𝑓′′. Sehingga 𝑓′′ = (𝑓′)′. Fungsi 𝑓′′ disebut sebagai turunan kedua dari 𝑓.
12
Beberapa simbol yang dapat digunakan untuk menunjukan turunan dari suatu fungsi terhadap 𝑥, sebagai berikut:
𝑓′′(𝑥) =𝑑 2𝑦 𝑑𝑥2 = 𝑑 𝑑𝑥( 𝑑𝑦 𝑑𝑥) = 𝑑𝑦′ 𝑑𝑥 = 𝑦 ′′= 𝐷2(𝑓)(𝑥) = 𝐷 𝑥2𝑓(𝑥).
Simbol 𝐷2 berarti operasi diferensiasi dilakukan dua kali.
Sifat- Sifat Turunan
a) Jika 𝑓(𝑥) = 𝑘, maka 𝑓′(𝑥) = 0. 𝑘 adalah konstanta.
b) Jika 𝑓(𝑥) = 𝑥𝑛, maka 𝑓′(𝑥) = 𝑛𝑥𝑛−1. c) Jika 𝑓(𝑥) = 𝑘𝑥𝑛, maka 𝑓′(𝑥) = 𝑘𝑛𝑥𝑛−1. d) Jika 𝑓(𝑥) = 𝑢𝑣, maka 𝑓′(𝑥) = 𝑢′𝑣 + 𝑢𝑣′. e) Jika 𝑓(𝑥) =𝑢 𝑣, maka 𝑓 ′(𝑥) =𝑢′𝑣−𝑢𝑣′ 𝑣2 . Contoh 2.9
Contoh ini diambil dari buku Thomas (2010). Jika 𝑦 = 𝑥6, maka 𝑦′= 6𝑥5. Tentukanlah 𝑦′′. Penyelesaian: 𝑦′′ =𝑑𝑦′ 𝑑𝑥 = 𝑑 𝑑𝑥(6𝑥 5) = 30𝑥4. Jadi, 𝐷2(𝑥6) = 30𝑥4. Contoh 2.10
Contoh ini diambil dari buku Thomas (2010).
Jika diberikan 𝑦 = 𝑥3 − 3𝑥2+ 2, maka tentukanlah 𝑦′′.
Penyelesaian:
Mencari turunan pertama terlebih dahulu.
𝑦′= 𝑑 𝑑𝑥(𝑥
3− 3𝑥2+ 2) = 3𝑥2 − 6𝑥.
13 𝑦′′ = 𝑑
𝑑𝑥(3𝑥
2− 6𝑥) = 6𝑥 − 6.
Beberapa kasus khusus, nilai dari turunan kedua dari fungsi 𝑦 = 𝑓(𝑥), tidak dapat ditentukan secara analitis. Hal tersebut bisa saja karena fungsinya rumit atau pada titik tertentu nilai fungsinya tidak ada. Oleh karena itu, kita dapat menggunakan turunan numeris dalam penyelesaiannya. Salah satu metode numeris yang dapat digunakan adalah hampiran beda-pusat.
Selanjutnya akan dibentuk skema beda hingga untuk turunan kedua fungsi 𝑓(𝑥).
Jika deret Taylor pada persamaan (2.2) dipotong sampai empat suku pertama, akan diperoleh: 𝑓(𝑥𝑖+1) = 𝑓(𝑥𝑖) + 𝑓′(𝑥𝑖)(Δ𝑥) + 𝑓′′(𝑥𝑖) 2! (Δ𝑥) 2+𝑓 (3)(𝑥 𝑖) 3! (Δ𝑥) 3+ 𝑅 3(∆𝑥) (2.5) 𝑓(𝑥𝑖−1) = 𝑓(𝑥𝑖) − 𝑓′(𝑥 𝑖)(Δ𝑥) + 𝑓′′(𝑥 𝑖) 2! (Δ𝑥) 2−𝑓(3)(𝑥𝑖) 3! (Δ𝑥) 3+ 𝑅 3(∆𝑥) (2.6) dimana 𝑅3(𝑥) =𝑓(3+1)(𝜉(𝑥)) (3+1)! (𝑥 − 𝑥0) 3+1 atau 𝑅 3(𝑥) = 𝑓(4)(𝜉(𝑥)) 24 (∆𝑥) 4.
Menjumlahkan persamaan (2.5) dan (2.6), sehingga diperoleh:
𝑓(𝑥𝑖+1) + 𝑓(𝑥𝑖−1) = 2𝑓(𝑥𝑖) + 2
𝑓′′(𝑥𝑖) 2! (Δ𝑥)
2 + 2𝑅 3(∆𝑥)
dapat ditulis lagi sebagai berikut:
𝑓(𝑥𝑖+1) + 𝑓(𝑥𝑖−1) = 2𝑓(𝑥𝑖) + 𝑓′′(𝑥
𝑖)(Δ𝑥)2+
𝑓(4)(𝜉(𝑥)) 12 (∆𝑥)
4
14
𝑓′′(𝑥𝑖)(∆𝑥)2 = 𝑓(𝑥𝑖+1) − 2𝑓(𝑥𝑖) + 𝑓(𝑥𝑖−1) −
𝑓(4)(𝜉(𝑥)) 12 (∆𝑥)
4
kedua ruas pada persamaan di atas, dioperasikan dengan 1
(∆𝑥)2, sehingga diperoleh: 𝑓′′(𝑥𝑖)(Δ𝑥)2 (Δ𝑥)2 = 𝑓(𝑥𝑖+1) (Δ𝑥)2 − 2𝑓(𝑥𝑖) (Δ𝑥)2 + 𝑓(𝑥𝑖−1) (Δ𝑥)2 − 𝑓(4)(𝜉(𝑥)) 12 (∆𝑥)4 (Δ𝑥)2 atau 𝑓′′(𝑥𝑖) =𝑓(𝑥𝑖+1) (Δ𝑥)2 − 2𝑓(𝑥𝑖) (Δ𝑥)2 + 𝑓(𝑥𝑖−1) (Δ𝑥)2 − 𝑓(4)(𝜉(𝑥)) 12 (Δ𝑥) 2
diperoleh hampiran beda pusat untuk turunan kedua dari 𝑓(𝑥) adalah sebagai berikut: 𝑓′′(𝑥𝑖) =𝑓(𝑥𝑖+1) − 2𝑓(𝑥𝑖) + 𝑓(𝑥𝑖−1) (Δ𝑥)2 + 𝑂(Δ𝑥) 2 (2.7) dengan 𝑂(Δ𝑥)2 = −𝑓(4)(𝜉(𝑥)) 12 (Δ𝑥) 2. B. Persamaan Diferensial
Dalam subbab ini akan dibahas persamaan diferensial berdasarkan acuan dari Boyce & DiPrima (2012) dan Ross (1989). Persamaan diferensial yang akan dibahas antara lain definisi serta contoh persamaan diferensial, persamaan diferensial biasa, persamaan diferensial parsial, orde dari persamaan diferensial, dan persamaan diferensial linear atau tak linear.
Defenisi 2.11 (Persamaan diferensial)
Menurut Boyce & DiPrima (2012), persamaan diferensial adalah persamaan yang mengandung turunan di dalamnya.
15 Contoh 2.12
Persamaan berikut ini merupakan contoh persamaan diferensial: 𝑑𝑦 𝑑𝑥= −2𝑥 + 5 (2.8) 𝑑2𝑦 𝑑𝑡2 + 𝑑𝑦 𝑑𝑡 = −20𝑡 (2.9) 𝜕4𝑢 𝜕𝑦4 = 𝜕𝑢 𝜕𝑡 (2.10) 𝜕2𝑢 𝜕𝑥2+ 𝑑2𝑢 𝑑𝑦2 = 𝑑2𝑢 𝑑𝑧2 (2.11)
Definisi 2.13 (Persamaan diferensial biasa)
Persamaan diferensial biasa adalah persamaan diferensial yang hanya memuat satu variabel bebas di dalamnya.
Contoh 2.14
Persamaan (2.8) di atas merupakan persamaan diferensial biasa dengan variabel bebasnya adalah 𝑥 dan variabel terikatnya adalah 𝑦. Persamaan (2.9) juga merupakan persamaan diferensial biasa, yang mana variabel bebasnya adalah 𝑡 dan variabel terikatnya adalah 𝑦.
Definisi 2.15 (Persamaan diferensial parsial)
Persamaan diferensial parsial adalah persamaan diferensial yang memuat lebih dari satu variabel bebas di dalamnya.
Contoh 2.16
Persamaan (2.10) merupakan persamaan diferensial dimana 𝑢 merupakan variabel terikat dan 𝑦, 𝑡 adalah variabel bebasnya. Persamaan (2.11) juga merupakan persamaan diferensial parsial, dengan 𝑢 adalah variabel terikat dan 𝑥, 𝑦, 𝑧 adalah variabel bebasnya.
16 Definisi 2.17 (Orde dari persamaan diferensial)
Menurut Ross (1989), orde dari suatu persamaan diferensial adalah tingkat tertinggi dari turunan yang muncul dalam persamaan diferensial terkait. Bentuk umum dari persamaan diferensial adalah:
𝐹(𝑥, 𝑦, 𝑦′, … , 𝑦(𝑛)) = 0 (2.12) disebut sebagai persamaan diferensial biasa orde 𝑛.
Contoh 2.18
Persamaan (2.8) merupakan persamaan diferensial biasa berorde satu dan persamaan (2.9) merupakan persamaan diferensial biasa berorde 2. Sedangkan, persamaan (2.10) merupakan persamaan diferensial parsial berorde empat dan persamaan (2.11) adalah persamaan diferensial parsial berorde dua.
Definisi 2.19 (Persamaan diferensial biasa yang linear)
Berdasarkan Ross (1989), suatu persamaan (2.12) disebut linear jika fungsi 𝐹 adalah suatu fungsi linear dari variabel 𝑦, 𝑦′, … , 𝑦(𝑛). Persamaan diferensial biasa berorde 𝑛, berbentuk sebagai berikut:
𝑎0(𝑥)𝑑 𝑛𝑦 𝑑𝑥𝑛+ 𝑎1(𝑥) 𝑑𝑛−1𝑦 𝑑𝑥𝑛−1+ ⋯ + 𝑎𝑛−1(𝑥) 𝑑𝑦 𝑑𝑥+ 𝑎𝑛(𝑥)𝑦 = 𝑏(𝑥) (2.13)
dengan 𝑎0 tidak sama dengan nol.
Contoh 2.20
Persamaan (2.8) dan (2.9) merupakan persamaan diferensial biasa, dapat ditinjau bahwa dua persamaan tersebut memiliki variabel bebas dan turunan-turunannya berpangkat satu, tidak ada perkalian antara turunan dan varibel terikatnya, serta tidak ada bentuk nonlinear dari turunan dan variabel terikatnya.
Definisi 2.21 (Persamaan diferensial biasa yang nonlinear)
Suatu persamaan diferensial biasa, bisa dikatakan nonlinear jika persamaan diferensial biasa tersebut tidak linear.
17 Contoh 2.22.
Berikut ini adalah beberapa contoh persamaan diferensial biasa yang taklinear:
10𝑑𝑥 𝑑𝑦− 25𝑥 2 = 0 (2.14) 𝑑3𝑢 𝑑𝑣3 + ( 𝑑𝑢 𝑑𝑣) 2 − 10𝑢 = 0 (2.15) 𝑑3𝑢 𝑑𝑡3 + ( 𝑑2𝑢 𝑑𝑡2) ( 𝑑𝑢 𝑑𝑡) − 2𝑢 = 0 (2.16)
18 BAB III
PERSAMAAN DIFERENSIAL LANE-EMDEN DAN METODE PENYELESAIANNYA
Pada bagian ini, penulis akan menjabarkan bagaimana cara memperoleh bentuk dari persamaan diferensial Lane-Emden. Penulis juga akan mejabarkan metode Euler dan metode dekomposisi Adomian, beserta skema tiap metode ter-sebut yang akan diterapkan dalam menyelesaikan persamaan diferensial Lane-Emden.
A. Pemodelan untuk Mendapatkan Persamaan Diferensial Lane-Emden Dalam subab ini akan dibahas mengenai bagaimana persamaan diferensial Lane-Emden diperoleh berdasarkan referensi dari Ravi dan Donal (2007).
Misalkan ada sebuah awan gas yang berbentuk bola, yang mana 𝑟 jari-jari dan 𝑝 adalah pusat. Tekanan total pada jarak 𝑟 dari pusat 𝑝 dinotasikan sebagai 𝑝(𝑟). Jumlah seluruh tekanannya diperoleh dari tekanan gas biasa dan radiasi. Sehingga dapat ditulis sebagai:
𝑝(𝑟) =1 3𝑎𝑇
4+𝑅𝑇
𝑣
(3.1)
dimana, 𝑎 adalah konstanta radiasi, 𝑇 adalah suhu total, 𝑅 adalah konstanta gas, dan 𝑣 adalah volume. Tekanan dan kepadatan 𝜌 = 𝑣−1 berbeda dengan 𝑟 dan 𝑝 =
𝐾𝜌𝛾 dengan, 𝐾 adalah konstanta politropik dan 𝛾 merupakan konstanta politropik eksponen. Andaikan 𝑚 adalah massa dari bola gas yang berjari-jari 𝑟 dan 𝐺 merupakan konstanta gravitasi. Sehingga dapat ditulis persamaan setimbangnya sebagai berikut: 𝑑𝑝 𝑑𝑟 = − 𝐺𝑚𝜌 𝑟2 (3.2)
19 𝑑𝑚
𝑑𝑟 = 4𝜋𝑟
2𝜌 (3.3)
dengan mengalikan 𝑟2
𝜌 pada kedua ruas persamaan (3.2), diperoleh:
𝑟2 𝜌
𝑑𝑝
𝑑𝑟 = −𝐺𝑚
(3.4)
kedua ruas pada persamaan (3.4), dioperasikan dengan 𝑑
𝑑𝑟 akan menghasilkan: 𝑑 𝑑𝑟( 𝑟2 𝜌 𝑑𝑝 𝑑𝑟) = −𝐺 𝑑𝑚 𝑑𝑟 (3.5)
substitusi persamaan (3.3) ke dalam persamaan (3.5), sebagai berikut:
𝑑 𝑑𝑟( 𝑟2 𝜌 𝑑𝑝 𝑑𝑟) = −𝐺(4𝜋𝑟 2𝜌) (3.6)
kedua ruas pada persamaan (3.6) dikali dengan 1
𝑟2, sehingga: 1 𝑟2 𝑑 𝑑𝑟( 𝑟2 𝜌 𝑑𝑝 𝑑𝑟) = −𝐺4𝜋𝜌 (3.7)
kedua ruas pada persamaan (3.7) ditambah dengan 𝐺4𝜋𝜌, diperoleh:
1 𝑟2 𝑑 𝑑𝑟( 𝑟2 𝜌 𝑑𝑝 𝑑𝑟) + 𝐺4𝜋𝜌 = 0 (3.8)
20 misalkan 𝛾 = 1 + 𝜇−1=𝜇+1
𝜇 dan 𝜌 = 𝜆𝜙
𝜇 , maka 𝑝 = 𝐾𝜌1+𝜇−1 =
𝐾𝜆1+𝜇−1𝜙𝜇+1.
Substitusi 𝑝 = 𝐾𝜆1+𝜇−1𝜙𝜇+1 dan 𝜌 = 𝜆𝜙𝜇 ke persamaan (3.8) sehingga
diperoleh: 1 𝑟2 𝑑 𝑑𝑟( 𝑟2 𝜆𝜙𝜇 𝑑 𝑑𝑟(𝐾𝜆 1+𝜇−1𝜙𝜇+1)) = −𝐺4𝜋𝜆𝜙𝜇 1 𝑟2 𝑑 𝑑𝑟( 𝑟2 𝜆𝜙𝜇(𝐾𝜆1+𝜇 −1 (𝜇 + 1)𝜙𝜇)𝑑𝜙 𝑑𝑟) = −𝐺4𝜋𝜆𝜙 𝜇 1 𝑟2 𝑑 𝑑𝑟(𝑟 2(𝐾𝜆1𝜇(𝜇 + 1))𝑑𝜙 𝑑𝑟) = −𝐺4𝜋𝜆𝜙 𝜇
kedua ruas dioperasikan dengan 1
𝐾𝜆 1 𝜇(𝜇+1) , sehingga diperoleh: 1 𝑟2 𝑑 𝑑𝑟(𝑟 2𝑑𝜙 𝑑𝑟) = − 𝐺4𝜋𝜆𝜙𝜇 𝐾𝜆 1 𝜇(𝜇 + 1) 1 𝑟2 𝑑 𝑑𝑟(𝑟 2𝑑𝜙 𝑑𝑟) = − 𝐺4𝜋𝜆1− 1 𝜇𝜙𝜇 𝐾(𝜇 + 1) . Misalkan 𝑘2 =𝐺4𝜋𝜆 1−𝜇1
𝐾(𝜇+1), sehingga dapat ditulis:
1 𝑟2 𝑑 𝑑𝑟(𝑟 2𝑑𝜙 𝑑𝑟) = −𝑘 2𝜙𝜇
21 1 𝑟2 𝑑 𝑑𝑟(𝑟 2𝑑𝜙 𝑑𝑟) + 𝑘 2𝜙𝜇 = 0 (3.9)
dimana, 𝜙 menyatakan potensial gravitasi, 𝜆 adalah densitas dan 𝜇 merupakan berat molekul awan gas.
Misalkan 𝑥 = 𝑘𝑟, dan diambil 𝑘 = 1, persamaan (3.9) di atas dapat diubah menjadi: 𝑑2𝜙 𝑑𝑥2 + 2 𝑥 𝑑𝜙 𝑑𝑥 + 𝜙 𝜇 = 0. (3.10)
Persamaan (3.10) merupakan persamaan diferensial Lane-Emden, (Rudolf, dkk., 2012). Persamaan diferensial Lane-Emden yang akan diselesaikan dalam tugas akhir ini berbentuk:
𝑦′′(𝑥) +𝛼
𝑥𝑦
′(𝑥) + 𝑓(𝑥, 𝑦) = 𝑔(𝑥).
Karena persamaan diferensial Lane-Emden mengandung fungsi 𝑔(𝑥) ∈ (0,1] , maka ada beberapa fungsi yang menyebabkan suatu persamaan diferensial bukan merupakan persamaan diferensial Lane-Emden, contohnya sebagai berikut:
a) 𝑔(𝑥) =𝑥 3− 1 𝑥 − 1, tidak kontinu di 𝑥 = 1. b) 𝑔(𝑥) =𝑥 2+ 5𝑥3 4𝑥 − 2 , tidak kontinu di 𝑥 = 0.5. c) 𝑔(𝑥) = sin (𝑥) 0.5𝑥 − 0.5, tidak kontinu di 𝑥 = 1.
22
B. Metode Euler untuk Menyelesaikan Persamaan Diferensial Lane-Emden Metode Euler merupakan suatu metode yang dapat digunakan untuk menyelesaikan persamaan diferensial. Dalam penulisan ini, metode Euler digunakan untuk menyelesaikan persamaan diferensial Lane-Emden.
Masalah nilai awal persamaan diferensial dapat dinyatakan sebagai berikut:
𝑑𝑦
𝑑𝑡 = 𝑓(𝑡, 𝑦), 𝑎 ≤ 𝑡 ≤ 𝑏, 𝑦(𝑎) = 𝛼
(3.11)
Suatu persamaan diferensial dapat dicoba diselesaikan secara numeris apabila tidak dapat diselesailkan secara analitis. Salah satu metode numeris yang dapat digunakan sadalah metode Euler.
Tahap awal solusi pendekatan numerik adalah dengan menentukan titik-titik dalam jarak yang sama di dalam interval [𝑎, 𝑏], dapat dicari sebagai berikut:
𝑡𝑛 = 𝑎 + 𝑛ℎ, 𝑛 = 0,1,2,3, … , 𝑁 (3.12)
dimana n merupakan banyaknya langkah dalam penghitungan dan h merupakan jarak tetap antar titik yang dapat dirumuskan dengan:
ℎ =𝑏 − 𝑎
𝑁 = 𝑡𝑖+1− 𝑡𝑖
(3.13)
Metode Euler diturunkan dari deret Taylor. Misalkan fungsi 𝑦(𝑡) adalah fungsi kontinu dan memiliki turunan dalam interval [𝑎, 𝑏]. Maka deret Taylor dinyatakan sebagai:
23 𝑦(𝑛+1) = 𝑦𝑛+ (𝑡𝑛+1− 𝑡𝑛)𝑦′(𝑡𝑛) +(𝑡𝑛+1− 𝑡𝑛) 2 2 𝑦′′(𝜀𝑛) (3.14) dengan 𝜉𝑛 ∈ (𝑡𝑛, 𝑡𝑛+1).
Karena ℎ = 𝑡𝑛+1− 𝑡𝑛 maka persamaan (3.14) dapat ditulis menjadi:
dan 𝑦(𝑡) memenuhi persamaan diferensial (3.11), sehingga:
𝑦(𝑛+1)= 𝑦𝑛+ ℎ𝑦′(𝑡𝑛) +ℎ
2
2 𝑦′′(𝜀𝑛).
(3. 16)
Metode Euler dibangun berdasarkan pendekatan 𝑦𝑛 = 𝑦(𝑡𝑛) dengan
mengabaikan suku terakhir pada persamaan (3.16). Jadi, metode Euler dapat dinyatakan sebagai berikut (Burden dan Faires, 2011):
𝑦0 = 𝛼 (3.17)
𝑦𝑛+ℎ = 𝑦𝑛 + ℎ𝑓(𝑡𝑛, 𝑦𝑛) (3.18)
dimana 𝑛 = 0,1,2,3, … , 𝑁 − 1.
Contoh 3.1
Selesaikan persamaan diferensial berikut dengan menggunakan metode Euler. Diberikan persamaan diferensial sebagai berikut:
𝑦(𝑛+1) = 𝑦𝑛+ ℎ𝑦′(𝑡𝑛) +ℎ
2
2 𝑦′′(𝜀𝑛)
24
𝑦′= 𝑦 − 𝑡2+ 1, 0 ≤ 𝑡 ≤ 2, 𝑦
0 = 0.5,
dengan ℎ = 0.5.
Penyelesaian:
Menentukan banyaknya iterasi dalam perhitungan;
𝑁 =𝑏 − 𝑎 ℎ = 2 − 0 0.5 = 4 dan 𝑡𝑛 = 𝑎 + 𝑛ℎ = 0 + 𝑛(0.5) = 0.5𝑛; 𝑛 = 0,1,2,3.
sehingga persamaan Eulernya dapat ditulis sebagai;
𝑦𝑛+1 = 𝑦𝑛+ ℎ(𝑦𝑛− 𝑡𝑛2+ 1)
= 𝑦𝑛 + 0.5(𝑦𝑛− (0.5𝑛)2+ 1).
Iterasi ke-1 (substitusi 𝑛 = 0 pada 𝑦𝑛+1) dengan syarat awal diberikan 𝑦0 = 0.5, sehingga diperoleh:
𝑦0+1= 𝑦0+ 0.5(𝑦0− (0.5(0))2+ 1)
𝑦1 = 0.5 + 0.5(0.5 − (0.5(0))2+ 1) = 1.25.
Iterasi ke-2 (substitusi 𝑛 = 1 pada 𝑦𝑛+1) dengan 𝑦1 = 1.25, sehingga diperoleh: 𝑦1+1 = 𝑦1+ 0.5(𝑦1− (0.5(1))2+ 1)
𝑦2 = 1.25 + 0.5(1.25 − (0.5(1))2+ 1)
= 2.25.
Iterasi ke-3 (substitusi 𝑛 = 2 pada 𝑦𝑛+1) dengan 𝑦2 = 2.25, sehingga diperoleh:
𝑦2+1= 𝑦2+ 0.5(𝑦2− (0.5(2))2+ 1)
𝑦3 = 2.25 + 0.5(2.25 − (0.5(2))2+ 1)
25 = 3.375.
Iterasi ke-4 (substitusi 𝑛 = 3 pada 𝑦𝑛+1) dengan 𝑦3 = 3.375, sehingga diperoleh: 𝑦3+1= 𝑦2+ 0.5(𝑦3− (0.5(3))2+ 1)
𝑦4 = 3.375 + 0.5(3.375 − (0.5(3))2+ 1)
= 4.4375.
Dalam penjelasan persamaan (3.18) di atas, metode Euler hanya digunakan untuk menyelesaikan satu persamaan diferensial. Penjelasan selanjutnya, metode Euler digunakan untuk menyelesaikan sistem persamaan diferensial yang berbentuk: 𝑑𝑥 𝑑𝑡= 𝑓(𝑡, 𝑥, 𝑦), (3.19) 𝑑𝑦 𝑑𝑡 = 𝑔(𝑡, 𝑥, 𝑦), (3.20)
dengan nilai awal 𝑥(𝑡0) = 𝑥0, 𝑦(𝑡0) = 𝑦0, dan dari persamaan (3.13) diperoleh ℎ = 𝑡1 − 𝑡0 sehingga
𝑥1 = 𝑥0+ ℎ[𝑓(𝑡0, 𝑥0, 𝑦0)] (3.21)
𝑦1 = 𝑦0+ ℎ[𝑔(𝑡0, 𝑥0, 𝑦0)] (3.22) secara umum, dengan ℎ = 𝑡𝑛+1− 𝑡𝑛 diperoleh (Ross, 1989)
𝑥𝑛+1 = 𝑥𝑛+ ℎ[𝑓(𝑡𝑛, 𝑥𝑛, 𝑦𝑛)] (3.23)
𝑦𝑛+1 = 𝑦𝑛+ ℎ[𝑔(𝑡𝑛, 𝑥𝑛, 𝑦𝑛)]
26
Contoh 3.2
Selesaikan sistem persamaan diferensial berikut:
𝑑𝑥
𝑑𝑡 = 5𝑥 − 2𝑦, 𝑑𝑦
𝑑𝑡 = 3𝑥,
𝑥(0) = 1, 𝑦(0) = 2.
Lakukan perhitungan pada 𝑡 = 0.1 dan 𝑡 = 0.4, dengan ℎ = 0.1.
Penyelesaian:
Misalkan 𝑓(𝑡, 𝑥, 𝑦) = 5𝑥 − 2𝑦, 𝑔(𝑡, 𝑥, 𝑦) = 3𝑥, 𝑥0 = 1, 𝑦0 = 2. Akan dicari
nilai 𝑡0 = ℎ − 𝑡1 = 0.1 − 0.1 = 0. Persamaan (3.23) diperoleh:
𝑥𝑛+1 = 𝑥𝑛 + ℎ𝑓(𝑡𝑛, 𝑥𝑛, 𝑦𝑛) = 𝑥𝑛 + ℎ(5𝑥𝑛− 2𝑦𝑛) 𝑦𝑛+1 = 𝑦𝑛+ ℎ𝑔(𝑡𝑛, 𝑥𝑛, 𝑦𝑛) = 𝑦𝑛+ ℎ(3𝑥𝑛).
Iterasi ke-1 (substitusi 𝑛 = 0 pada 𝑥𝑛+1 dan 𝑦𝑛+1), dengan syarat awal diberikan 𝑥0 = 1, 𝑦0 = 2, 𝑡1 = 0.1. 𝑥0+1= 𝑥0+ ℎ𝑓(𝑡0, 𝑥0, 𝑦0) 𝑥1 = 1 + (0.1)𝑓(0,1,2) = 1 + (0.1)(1) = 1.1 𝑦0+1= 𝑦0 + ℎ𝑔(𝑡0, 𝑥0, 𝑦0) 𝑦1 = 2 + (0.1)𝑔(0,1,2) = 2 + (0.1)(3) = 2.3.
Iterasi ke-2 (substitusi 𝑛 = 1 pada 𝑥𝑛+1 dan 𝑦𝑛+1), dengan 𝑥1 = 1.1, 𝑦1 = 2.3,
𝑡2 = 𝑡1+ ℎ = 0.1 + 0.1 = 0.2.
𝑥1+1= 𝑥1+ ℎ𝑓(𝑡1, 𝑥1, 𝑦1) 𝑥2 = 1.1 + (0.1)𝑓(0.1,1.1,2.3)
= 1.1 + (0.1)(0.9) = 1.19
27
𝑦2 = 2.3 + (0.1)𝑔(0.1,1.1,2.3) = 2.3 + (0.1)(3.3) = 2.63.
Iterasi ke-3 (substitusi 𝑛 = 2 pada 𝑥𝑛+1 dan 𝑦𝑛+1), dengan 𝑥2 = 1.19, 𝑦2 =
2.63, 𝑡3 = 𝑡2+ ℎ = 0.2 + 0.1 = 0.3. 𝑥2+1= 𝑥2+ ℎ𝑓(𝑡2, 𝑥2, 𝑦2) 𝑥3 = 1.19 + (0.1)𝑓(0.2,1.19,2.63) = 1.19 + (0.1)(0.69) = 1.259 𝑦2+1 = 𝑦2+ ℎ𝑔(𝑡2, 𝑥2, 𝑦2) 𝑦3 = 2.63 + (0.1)𝑔(0.2,1.19,2.63) = 2.3 + (0.1)(3.57) = 2.987.
Iterasi ke-4 (substitusi 𝑛 = 3 pada 𝑥𝑛+1 dan 𝑦𝑛+1), dengan 𝑥3 = 1.259, 𝑦3 = 2.987, 𝑡4 = 𝑡3+ ℎ = 0.3 + 0.1 = 0.4. 𝑥3+1= 𝑥3+ ℎ𝑓(𝑡3, 𝑥3, 𝑦3) 𝑥4 = 1.259 + (0.1)𝑓(0.3,1.259,2.987) = 1.259 + (0.1)(0.321) = 1.2911 𝑦3+1 = 𝑦3+ ℎ𝑔(𝑡3, 𝑥3, 𝑦3) 𝑦4 = 2.987 + (0.1)𝑔(0.3,1.259,2.987) = 2.987 + (0.1)(3.777) = 3.3647.
Tabel 3.1. Hasil perhitungan untuk soal contoh 3.2 dengan metode Euler.
𝑛 𝑡𝑛 Euler 0 0.1 𝑥1 = 1.1 𝑦1 = 2.3 1 0.2 𝑥2 = 1,19 𝑦2 = 2.63 2 0.3 𝑥3 = 1.259 𝑦3 = 2.987 3 0.4 𝑥4 = 1.2911 𝑦4 = 3.3647
28
Karena persamaan diferensial Lane-Emden berorde 2, pertama-tama mengubah bentuk persamaan diferensial Lane-Emden tersebut menjadi sistem persamaan diferensial biasa. Persamaan baru yang didapat terdiri dari 2 persamaan diferensial nonlinear dan berorde satu.
Bentuk dari persamaan diferensial Lane-Emden adalah :
𝑦′′(𝑥) +𝛼
𝑥𝑦
′(𝑥) + 𝑓(𝑥, 𝑦) = 𝑔(𝑥), 0 < 𝑥 ≤ 1, 𝛼 ≥ 0. (3.24)
Persamaan (3.24) di atas, dapat ditulis dalam bentuk lain, yaitu:
𝑑2𝑦 𝑑𝑥2+ 𝛼 𝑥 𝑑𝑦 𝑑𝑥+ 𝑓(𝑥, 𝑦) = 𝑔(𝑥), 0 < 𝑥 ≤ 1, (3.25)
dengan kondisi awal :
𝑦(0) = 𝐴, 𝑦′(0) = 𝐵, (3.26)
dimana A dan B adalah kostanta, 𝑓(𝑥, 𝑦)adalah fungsi real kontinu dan 𝑔(𝑥) ∈ 𝐶[0,1]. Penyelesaian: Misalkan: 𝑧(𝑥) = 𝑦(𝑥) ⇒𝑑𝑧 𝑑𝑥 = 𝑑𝑦 𝑑𝑥 = 𝑤(𝑥) 𝑑𝑧 𝑑𝑥 = 𝑤(𝑥) ⟺ 𝑧 ′(𝑥) = 𝑤(𝑥) (3.27)
29 𝑤(𝑥) = 𝑑𝑧 𝑑𝑥= 𝑑𝑦 𝑑𝑥 ⇒ 𝑑𝑤 𝑑𝑥 = 𝑑2𝑦 𝑑𝑥2 = 𝑔(𝑥) − ( 𝛼 𝑥 𝑑𝑦 𝑑𝑥) − 𝑓(𝑥, 𝑦) 𝑑𝑤 𝑑𝑥 = 𝑔(𝑥) − 𝛼 𝑥𝑤(𝑥) − 𝑓(𝑥, 𝑦). (3.28) Sehingga persamaan (3.24) dapat diubah menjadi:
{ 𝑑𝑧 𝑑𝑥 = 𝑤(𝑥) 𝑑𝑤 𝑑𝑥 = 𝑔(𝑥) − 𝛼 𝑥𝑤(𝑥) − 𝑓(𝑥, 𝑧). (3.29)
Menurut (Ross, 1989), hal ini dilakukan agar persamaan diferensial Lane-Emden dapat diselesaikan menggunakan metode Euler, dengan nilai awal yang diberikan pada persamaan (3.26).
Selanjutnya, persamaan (3.29) diselesaikan menggunakan metode Euler. Sesuai persamaan (3.23), dengan nilai awal yang diberikan pada persamaan (3.26), dan memilih ukuran h yang tetap yaitu ℎ = 𝑡𝑛+1− 𝑡𝑛, maka penyelesaian
persamaan (3.29) dengan nilai pendekatan pada 𝑥𝑛+1 = 𝑥𝑛+ ℎ, adalah: 𝑧𝑛+1 = 𝑧𝑛+ ℎ(𝑤𝑛)
𝑤𝑛+1 = 𝑤𝑛+ ℎ(𝑔(𝑥𝑛) − 𝛼
𝑥𝑛𝑤(𝑥𝑛) − 𝑓(𝑥𝑛, 𝑧𝑛)
(3.30)
30
C. Metode Dekomposisi Adomian untuk Menyelesaikan Persamaan Diferensial Lane-Emden
Dalam subbab ini akan dibahas mengenai metode dekomposisi Adomian (MDA) dan penyelesaian persamaan diferensial biasa linear maupun nonlinear dengan menggunakan metode dekomposisi Adomian. Salah satu contohnya ada-lah persamaan diferensial Lane-Emden.
Menurut Adomian (1998), metode dekomposisi Adomian pertama kali dikenalkan dan dikembangkan oleh George Adomian. Metode ini terbukti mem-iliki keunggulan, akurat dalam menyelesaikan masalah-masalah linear maupun non-linear, persamaan diferensial biasa ataupun persamanaan diferensial parsial. Metode dekomposisi Adomian ini menyelesaikan permasalahan secara langsung tanpa melakukan linearisasi terlebih dahulu.
Diberikan persamaan diferensial berikut:
𝐿𝑦 + 𝑅𝑦 = 𝑔, (3.31)
di mana 𝐿 merupakan operator turunan pada tingkat terendah yang diasumsikan mempunyai invers. 𝑅 adalah operator diferensial linear lainnya dan 𝑔 adalah nilai awal.
Substitusikan fungsi invers dari 𝐿 yaitu 𝐿−1 pada kedua sisi persamaan (3.31),
se-hingga diperoleh:
𝐿−1(𝐿𝑦 + 𝑅𝑦) = 𝐿−1𝑔
atau
𝐿−1(𝐿𝑦) + 𝐿−1(𝑅𝑦) = 𝐿−1𝑔
31
𝑦 + 𝐿−1(𝑅𝑦) = 𝐿−1𝑔.
Kedua ruas pada persamaan di atas ditambah dengan −𝐿−1(𝑅𝑦), diperoleh:
𝑦 = 𝐿−1𝑔 − 𝐿−1(𝑅𝑦)
atau
𝑦 = 𝑓 − 𝐿−1(𝑅𝑦) (3.32)
dengan 𝑓 merupakan fungsi hasil dari pengintegrasian 𝑔 dan dari nilai awal yang diberikan dan diasumsikan untuk ditentukan.
Metode dekomposisi Adomian (Adomian, 1998) mengandung dekompo-sisi dari fungsi 𝑦 yang tidak diketahui dari beberapa persamaan dalam bentuk jumlah dari bilangan tak hingga dari komponen terdefinisi dengan deret kompo-sisi:
𝑦 = ∑ 𝑦𝑛, 𝑛 = 0, 1, 2, ⋯ .
∞
𝑛=0
(3.33)
Selanjutnya, substitusi persamaan (3.33) ke persamaan (3.32) menjadi:
∑ 𝑦𝑛 = 𝑓 − 𝐿−1(𝑅 (∑ 𝑦𝑛 ∞ 𝑛=0 )) ∞ 𝑛=0
atau dapat ditulis dalam bentuk lain:
𝑦0+ 𝑦1+ 𝑦2+ ⋯ = 𝑓 − 𝐿−1(𝑅(𝑦
0+ 𝑦1+ 𝑦2 + ⋯ )).
Sehingga diperoleh skema sebagai berikut: 𝑦0 = 𝑓,
32 𝑦𝑘+1 = −𝐿−1(𝑅(𝑦𝑘)), 𝑘 = 0,1 ,2, ⋯, (3.34) atau 𝑦0 = 𝑓, 𝑦1 = −𝐿−1(𝑅(𝑦0)), 𝑦2 = −𝐿−1(𝑅(𝑦1)), 𝑦3 = −𝐿−1(𝑅(𝑦2)), ⋮ 𝑦𝑘+1= −𝐿−1(𝑅(𝑦 𝑘)), 𝑘 = 0, 1, 2, ⋯.
Setelah memperoleh 𝑦0, 𝑦1, 𝑦2, 𝑦3, ⋯ , 𝑦𝑘+1 substitusikan ke persamaan
(3.33) untuk memperoleh solusi dalam bentuk deret.
Karena pembahasan di atas hanya membahas penyelesaian persamaan diferensial linear orde pertama menggunakan metode dekomposisi Adomian, se-lanjutnya akan dibahas mengenai penyelesaian persamaan diferensial orde tinggi dengan menggunakan metode dekomposisi Adomian.
Pada persamaan (3.33) telah dipaparkan bahwa metode dekomposisi Adomian mengandung dekomposisi dari fungsi 𝑦 yang tidak diketahui dari be-berapa persamaan dalam bentuk jumlah dari bilangan tak hingga dari komponen terdefinisi dengan deret komposisi:
𝑦 = ∑ 𝑦𝑛, 𝑛 = 0, 1, 2, ⋯ ,
∞
𝑛=0
33
Namun pada kasus lain, suku nonlinear yang ordenya lebih tinggi. Misal-nya fungsi 𝑓(𝑥, 𝑦) seperti 𝑦2, 𝑦𝑦
𝑥, 𝑦𝑥2 dan lain-lain dapat dinyatakan dalam deret
tak berhingga yang disebut sebagai polinomial Adomian dan berbentuk:
𝑓(𝑥, 𝑦) = ∑ 𝐴𝑛(𝑦0, 𝑦1, 𝑦2, ⋯ , 𝑦𝑛), ∞
𝑛=0
dengan polinomial Adomian 𝐴𝑛 dapat dihitung untuk semua bentuk nonlinear.
Polinomial Adomian 𝐴𝑛 dapat ditentukan dengan rumus sebagai berikut (Adomian dan Rach, 1983):
𝐴𝑛 = 1 𝑛! 𝑑𝑛 𝑑𝜆𝑛 [𝑓 (∑ 𝜆𝑖𝑦𝑖 𝑛 𝑖=0 )] 𝜆=0 , 𝑛 = 0,1,2,3, ⋯, (3.35)
dengan 𝜆 adalah suatu parameter.
Setelah 𝐴𝑛 diperoleh substitusikan ke persamaan (3.34) untuk mendapat-kan penyelesaian dari fungsi 𝑓(𝑥, 𝑦) dengan metode dekomposisi Adomian.
Selanjutnya, akan dibahas mengenai metode dekomposisi Adomian untuk menyelesaikan persamaan diferensial Lane-Emden.
Bentuk dari persamaan diferensial Lane-Emden adalah sebagai berikut:
𝑦(0) = 𝐴, 𝑦′(0) = 𝐵.
Pada permasalahan ini dapat dipilih 𝐿 sebagai operator dari turunan tingkat dua. 𝑦′′(𝑥) +𝛼
𝑥𝑦
′(𝑥) ditulis dalam bentuk lain, sebagai berikut
𝑦′′(𝑥) +𝛼
𝑥𝑦
34
𝐿𝑦 = −𝑓(𝑥, 𝑦) + 𝑔(𝑥) (3.36) dimana operator turunan 𝐿 dapat ditentukan dengan:
𝐿 = 𝑥−𝛼 𝑑
𝑑𝑥(𝑥
𝛼 𝑑
𝑑𝑥).
𝐿 memiliki invers, yaitu 𝐿−1 dan ditentukan dengan:
𝐿−1(∙) = ∫ 𝑥−𝛼∫ 𝑥𝛼 (∙)𝑑𝑥 𝑑𝑥. 𝑥 0 𝑥 0 (3.37)
Operasikan 𝐿−1 pada kedua ruas persamaan (3.36),
𝐿−1(𝐿𝑦) = −𝐿−1(𝑓(𝑥, 𝑦)) + 𝐿−1(𝑔(𝑥)).
Operasikan 𝐿−1(𝐿𝑦) sehinga diperoleh:
𝑦(𝑥) = 𝐿−1(𝑔(𝑥)) − 𝐿−1(𝑓(𝑥, 𝑦)).
Berdasarkan persamaan (3.33), persamaan di atas dapat ditulis sebagai:
𝑦(𝑥) = 𝐴 + 𝐵𝑥 + 𝐿−1(𝑔(𝑥)) − 𝐿−1(𝑓(𝑥, 𝑦)). (3.38) Menurut Wazwaz, dkk (2014), untuk solusi dari 𝑦(𝑥), metode dekompo-sisi Adomian memberikan deret tak terbatas sebagai berikut:
𝑦(𝑥) = ∑ 𝑦𝑛(𝑥)
∞ 𝑛=0
,
dengan deret suku banyak yang tak terbatas didefenisikan oleh
𝑓(𝑦) = 𝑓 (∑ 𝑦𝑛(𝑥) ∞ 𝑛=0 ) = ∑ 𝐴𝑛(𝑦0, 𝑦1, ⋯ , 𝑦𝑛) ∞ 𝑛=0 .
35
Untuk bentuk tak linear dari 𝑓(𝑦), dimana 𝐴𝑛 adalah suku banyak Adomian dide-fenisikan dengan: 𝐴𝑛 = 1 𝑛! 𝑑𝑛 𝑑𝜆𝑛 [𝑓 (∑ 𝜆𝑖𝑦𝑖 𝑛 𝑖=0 )] 𝜆=0 , 𝑛 = 0,1,2,3, ⋯.
Dimana, 𝜆 adalah suatu parameter.
𝐴𝑛 dapat dijabarkan dalam bentuk yang sederhana menjadi (Mutaish dan Hasan, 2018): 𝐴0 = 1 0! 𝑑0 𝑑𝜆0 [𝑓 (∑ 𝜆𝑖𝑦𝑖 0 𝑖=0 )] 𝜆=0 = 𝑓(𝑦0), 𝐴1 = 1 1! 𝑑1 𝑑𝜆1 [𝑓 (∑ 𝜆 𝑖𝑦 𝑖 1 𝑖=0 )] 𝜆=0 = 𝑦1𝑓′(𝑦0), 𝐴2 = 1 2! 𝑑2 𝑑𝜆2 [𝑓 (∑ 𝜆 𝑖𝑦 𝑖 2 𝑖=0 )] 𝜆=0 = 𝑦2𝑓′(𝑦0) +𝑦1 2 2!𝑓 ′′(𝑦 0), ⋮
dengan mensubstitusikan persamaan (3.34) dan (3.35) pada persamaan (3.38), di-peroleh: ∑ 𝑦𝑛(𝑥) = 𝐴 + 𝐵𝑥 + 𝐿−1𝑔(𝑥) − 𝐿−1(∑ 𝐴 𝑛 ∞ 𝑛=0 ) ∞ 𝑛=0 (3.39)
atau secara rekursif dapat ditulis sebagai:
𝑦0(𝑥) = 𝐴 + 𝐵𝑥 + 𝐿−1(𝑔(𝑥))
𝑦𝑘+1(𝑥) = −𝐿−1(𝐴
𝑘), 𝑘 = 0, 1, 2, ⋯,
(3.40)
36 𝑦0(𝑥) = 𝐴 + 𝐵𝑥 + 𝐿−1(𝑔(𝑥)) = 𝐴 + 𝐵𝑥 + ∫ 𝑡𝑥 −𝛼 0 (∫ 𝑠𝛼𝑔(𝑠)𝑑𝑠 𝑡 0 ) 𝑑𝑡, 𝑦1(𝑥) = −𝐿−1(𝐴 0) = − ∫ 𝑡−𝛼 𝑥 0 (∫ 𝑠𝛼(𝐴 0) 𝑡 0 (𝑠) 𝑑𝑠) 𝑑𝑡, 𝑦2(𝑥) = −𝐿−𝛼(𝐴1) = − ∫ 𝑡−𝛼 𝑥 0 (∫ 𝑠𝛼(𝐴1) 𝑡 0 (𝑠) 𝑑𝑠) 𝑑𝑡, 𝑦𝑘+1(𝑥) = −𝐿−1(𝐴 𝑘) = − ∫ 𝑡−𝛼 𝑥 0 (∫ 𝑠𝛼(𝐴𝑘) 𝑡 0 (𝑠) 𝑑𝑠) 𝑑𝑡. (3.41)
Jadi, penyelesaian dari persamaan (3.38) adalah sebagai berikut:
𝑦(𝑥) = 𝑦0(𝑥) + 𝑦1(𝑥) + 𝑦2(𝑥) + ⋯
untuk 𝑛 pendekatan dapat dinyatakan sebagai berikut (Hosseini dan Abbasbandy, 2015):
𝜙𝑛(𝑥) = ∑ 𝑦𝑖(𝑥), 𝑛 = 1, 2, 3, ⋯ , 𝑛−1
𝑖=0
37 BAB IV
PENYELESAIAN PERSAMAAN DIFERENSIAL LANE-EMDEN
Pada bagian ini, penulis akan melakukan simulasi penyelesaian untuk persamaan diferensial Lane-Emden dengan menggunakan metode Euler dan metode dekomposisi Adomian, serta mendiskusikan hasil dari simulasi tersebut. Contoh soal berdasarkan Vanani dan Aminatei (2010).
A. Simulasi Numeris dengan Menggunakan Metode Euler
Contoh 4.1 (Contoh 1)
Diberikan persamaan diferensial Lane-Emden sebagai berikut:
𝑦′′(𝑥) +2 𝑥𝑦
′(𝑥) + 𝑦(𝑥) = 6 + 12𝑥 + 𝑥2+ 𝑥3, 0 < 𝑥 ≤ 1.
dengan solusi eksak diberikan oleh 𝑦(𝑥) = 𝑥2+ 𝑥3.
a) Buatlah sistem PDB orde satu dari persamaan di atas.
b) Buatlah skema metode Euler untuk menyelesaikan bagian (a)
c) Diketahui 𝑥 = 10−9, 𝑦(10−9) = 𝑦′(10−9) = 0, selesaikan persamaan
tersebut berdasarkan bagian (b) dengan ℎ = 0.1, hitunglah nilai 𝑦 ketika 0 < 𝑥 ≤ 1.
Penyelesaian
a) Buatlah sistem PDB orde satu dari persamaan di atas. Menggunakan persamaan (3.27) dan (3.28), misalkan:
𝑧(𝑥) = 𝑦(𝑥) ⟹ 𝑧′(𝑥) = 𝑦′(𝑥) = 𝑤(𝑥)
𝑤(𝑥) = 𝑧′(𝑥) = 𝑦′(𝑥) ⟹ 𝑤′(𝑥) = 𝑦′′(𝑥) = 𝑔(𝑥) −2
𝑥𝑤(𝑥) − 𝑧(𝑥) dengan 𝑔(𝑥) = 6 + 12𝑥 + 𝑥2+ 𝑥3.
38 {
𝑧′(𝑥) = 𝑤(𝑥) 𝑤′(𝑥) = 𝑔(𝑥) −2
𝑥𝑤(𝑥) − 𝑧(𝑥).
b) Buatlah skema metode Euler untuk menyelesaikan bagian (a)
dengan memilih 𝑥𝑛+1 = 𝑥𝑛+ ℎ, sehingga nilai pendekataanya sesuai
persamaan (3.30) diberikan oleh: misal: 𝐹(𝑥, 𝑧, 𝑤) = 𝑤(𝑥) ⟹ 𝐹(𝑥𝑛, 𝑧𝑛, 𝑤𝑛) = 𝑤𝑛 𝐺(𝑥, 𝑧, 𝑤) = 𝑔(𝑥) −2 𝑥𝑤(𝑥) − 𝑧(𝑥) ⟹ 𝐺(𝑥𝑛, 𝑧𝑛, 𝑤𝑛) = 𝑔(𝑥𝑛) − 2 𝑥𝑛 𝑤𝑛 − 𝑧𝑛.
Sehingga dapat ditulis:
𝑧𝑛+1 = 𝑧𝑛+ ℎ𝐹(𝑥𝑛,𝑧𝑛, 𝑤𝑛) = 𝑧𝑛+ ℎ(𝑤𝑛)
𝑤𝑛+1= 𝑤𝑛+ ℎ𝐺(𝑥𝑛, 𝑧𝑛, 𝑤𝑛) = 𝑤𝑛 + ℎ (𝑔(𝑥𝑛) − 2
𝑥𝑛𝑤𝑛− 𝑧𝑛) dimana 𝑛 = 1, 2, 3, ….
c) Diketahui 𝑥 = 10−9, 𝑦(10−9) = 𝑦′(10−9) = 0 , selesaikan persamaan
tersebut berdasarkan bagian (b) dengan ℎ = 0.1, hitunglah nilai 𝑦 ketika
0 < 𝑥 ≤ 1.
Penyelesaian:
dengan syarat awal diberikan 𝑧0 = 𝑦(10−9) = 0, 𝑤0 = 𝑦′(10−9) = 0, dan
ℎ = 0.1.
Iterasi ke-1, (substitusi 𝑛 = 0 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ), 𝑥1 = 0.1. 𝑧0+1 = 𝑧1 = 𝑧0+ 0.1(𝑤0) = 0 + 0.1(0) = 0 + 0 = 0
𝑤0+1 = 𝑤1 = 0 + 0.1 [(6 + 12𝑥0+ 𝑥02+ 𝑥03) − 2
𝑥0𝑤0− 𝑧0] = 0 + 0.1[(6.000000012 − 0 − 0)] = 0.6000000012.
Iterasi ke-2 (substitusi 𝑛 = 1 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ), dengan 𝑧1 = 0, 𝑤1= 0.6000000012, dan 𝑥2 = 0.2
39 𝑧1+1 = 𝑧2 = 𝑧1 + 0.1(𝑤1) = 0 + 0.1[0.6000000012] = 0 + 0.06000000012 = 0.06000000012. 𝑤1+1 = 𝑤2 = 𝑤1+ 0.1 [(6 + 12𝑥1+ 𝑥12+ 𝑥13) − 2 𝑥1𝑤1 − 𝑧1] = 0.6000000012 − 0.478899989177 = 0.121100012023
Iterasi ke-3 (substitusi 𝑛 = 2 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛 + ℎ), dengan 𝑧2 = 0.06000000012, 𝑤2 = 0.121100012023, ℎ = 0.1 dan 𝑥3 = 0.3. 𝑧2+1 = 𝑧3 = 𝑧2+ 0.1(𝑤2) = 0.06000000012 + 0.1(0.121100012023) = 0.06000000012 + 0.012110001202300 = 0.07211000132 𝑤2+1 = 𝑤3 = 𝑤2+ 0.1 [(6 + 12𝑥2+ 𝑥22+ 𝑥23) − 2 𝑥2𝑤2− 𝑧2] = 0.121100012023 + 0.7176999898 = 0.8388000018.
Iterasi ke-4 (substitusi 𝑛 = 3 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛 + ℎ), dengan 𝑧3 = 0.07211000132, 𝑤3 = 0.8388000018, ℎ = 0.1 dan 𝑥4 = 0.4. 𝑧3+1 = 𝑧4 = 𝑧3+ 0.1(𝑤3) = 0.07211000132 + 0.1(0.8388000018 = 0.07211000132 + 0.08388000018 = 0.15599000150 𝑤3+1 = 𝑤4 = 𝑤3+ 0.1 [(6 + 12𝑥3+ 𝑥32+ 𝑥33) − 2 𝑥3𝑤3 − 𝑧3] = 0.8388000018 + 0.4052890017 = 1.2440890036.
Iterasi ke-5 (substitusi 𝑛 = 4 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ ), dengan 𝑧4 = 0.15599000150, 𝑤4 = 1.2440890036, ℎ = 0.1 dan 𝑥5 = 0.5. 𝑧4+1 = 𝑧5 = 𝑧4+ 0.1(𝑤4) = 0.15599000150 + 0.1(1.2440890036) = 0.15599000150 + 0.12440890036 = 0.2803989018 𝑤4+1 = 𝑤5 = 𝑤4+ 0.1 [(6 + 12𝑥4+ 𝑥42+ 𝑥 43) − 2 𝑥4𝑤4− 𝑧4] = 1.2440890036 + 0.4647565009 = 1.7088455045.
40
Iterasi ke-6 (substitusi 𝑛 = 5 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ ), dengan 𝑧5 = 0.28039890187, 𝑤5 = 1.7088455045, ℎ = 0.1 dan 𝑥6 = 0.6. 𝑧5+1 = 𝑧6 = 𝑧5+ 0.1(𝑤5) = 0.28039890187 + 0.1(1.7088455045) = 0.28039890187 + 0.17088455045 = 0.45128345232 𝑤5+1 = 𝑤6 = 𝑤5+ 0.1 [(6 + 12𝑥5+ 𝑥52+ 𝑥53) − 2 𝑥5𝑤5− 𝑧5] = 1.7088455045 + 0.5259219107 = 2.2347674152.
Iterasi ke-7 (substitusi 𝑛 = 6 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ ), dengan 𝑧6 = 0.45128345232, 𝑤6 = 2.2347674152, ℎ = 0.1 dan 𝑥7 = 0.7. 𝑧6+1 = 𝑧7 = 𝑧6+ 0.1(𝑤6) = 0.45128345232 + 0.1(2.2347674152) = 0.45128345232 + 0.22347674152 = 0.67476019385 𝑤6+1= 𝑤7 = 𝑤6+ 0.1 [(6 + 12𝑥6+ 𝑥62+ 𝑥63) − 2 𝑥6𝑤6− 𝑧6] = 2.2347674152 + 0.5875491856 = 2.8223166009.
Iterasi ke-8 (substitusi 𝑛 = 7 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ ), dengan 𝑧7 = 0.67476019385, 𝑤7 = 2.8223166009, ℎ = 0.1 dan 𝑥8 = 0.8 𝑧7+1 = 𝑧8 = 𝑧7+ 0.1(𝑤7) = 0.67476019385 + 0.1(2.8223166009) = 0.67476019385 + 0.28223166009 = 0.95699185394 𝑤7+1= 𝑤8 = 𝑤7+ 0.1 [(6 + 12𝑥7+ 𝑥72 + 𝑥 73) − 2 𝑥7𝑤7− 𝑧7] = 2.8223166009 + 0.64944781155 = 3.4717644125.
Iterasi ke-9 (substitusi 𝑛 = 8 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ ), dengan
𝑧8 = 0.95699185394, 𝑤8 = 3.4717644125, ℎ = 0.1 dan 𝑥9 = 0.9. 𝑧8+1 = 𝑧9= 𝑧8+ 0.1(𝑤8) = 0.95699185394 + 0.1(3.4717644125) = 0.95699185394 + 0.34717644125 = 1.30416829520 𝑤8+1= 𝑤9= 𝑤8+ 0.1 [(6 + 12𝑥8+ 𝑥82+ 𝑥 83) − 2 𝑥8𝑤8− 𝑧8] = 3.4717644125 + 0.71155971411 = 4.18332412662.
41
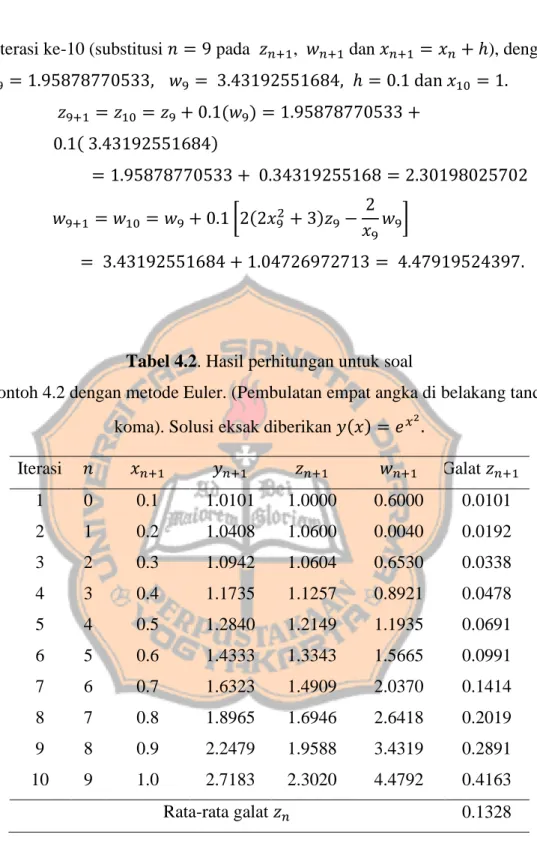
Iterasi ke-10 (substitusi 𝑛 = 9 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛 + ℎ), dengan 𝑧9 = 1.30416829520, 𝑤9 = 4.18332412662, ℎ = 0.1 dan 𝑥10= 1. 𝑧9+1 = 𝑧10 = 𝑧9+ 0.1(𝑤9) = 1.30416829520 + 0.1(4.18332412662) = 1.3320000002 + 0.41833241266 = 1.72250070786 𝑤9+1 = 𝑤10= 𝑤9+ 0.1 [(6 + 12𝑥9+ 𝑥92+ 𝑥93) − 2 𝑥9𝑤9− 𝑧9] = 4.18332412662 + 0.77385558944 = 4.95717971606.
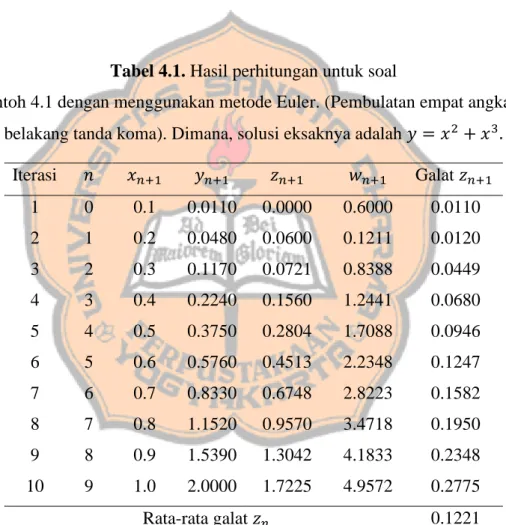
Tabel 4.1. Hasil perhitungan untuk soal
contoh 4.1 dengan menggunakan metode Euler. (Pembulatan empat angka di belakang tanda koma). Dimana, solusi eksaknya adalah 𝑦 = 𝑥2+ 𝑥3.
Iterasi 𝑛 𝑥𝑛+1 𝑦𝑛+1 𝑧𝑛+1 𝑤𝑛+1 Galat 𝑧𝑛+1 1 0 0.1 0.0110 0.0000 0.6000 0.0110 2 1 0.2 0.0480 0.0600 0.1211 0.0120 3 2 0.3 0.1170 0.0721 0.8388 0.0449 4 3 0.4 0.2240 0.1560 1.2441 0.0680 5 4 0.5 0.3750 0.2804 1.7088 0.0946 6 5 0.6 0.5760 0.4513 2.2348 0.1247 7 6 0.7 0.8330 0.6748 2.8223 0.1582 8 7 0.8 1.1520 0.9570 3.4718 0.1950 9 8 0.9 1.5390 1.3042 4.1833 0.2348 10 9 1.0 2.0000 1.7225 4.9572 0.2775 Rata-rata galat 𝑧𝑛 0.1221
42
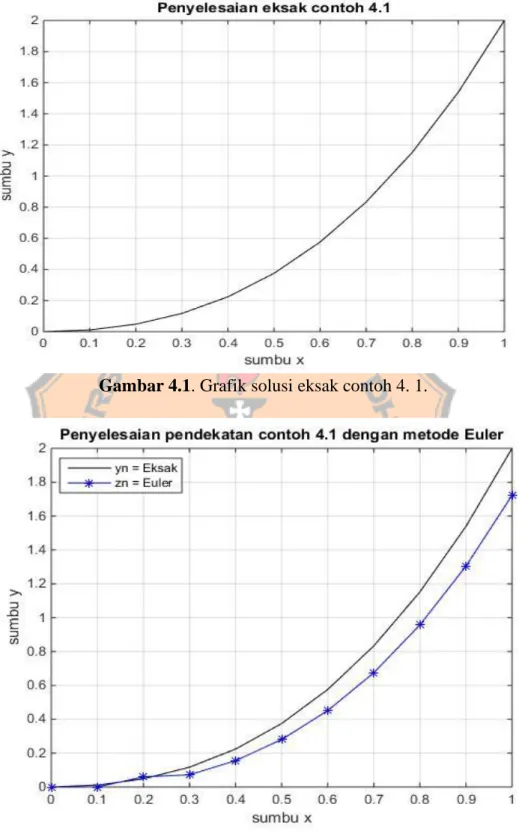
Gambar 4.1. Grafik solusi eksak contoh 4. 1.
Gambar 4.2. Grafik solusi eksak contoh 4.1 dibandingkan terhadap fungsi 𝑧𝑛 dengan menggunakan metode Euler.
43
Gambar 4.3. Grafik menunjukkan fungsi 𝑤𝑛.
Contoh 4.2 (Contoh 2)
Diberikan persamaan diferensial Lane-Emden sebagai berikut:
𝑦′′(𝑥) +2
𝑥𝑦
′(𝑥) = 2(2𝑥2+ 3)𝑦(𝑥), 0 < 𝑥 ≤ 1.
dengan solusi eksak diberikan oleh 𝑦(𝑥) = 𝑒𝑥2.
a) Buatlah sistem PDB orde satu dari persamaan tersebut. b) Buatlah skema metode Euler untuk menyelesaikan bagian (a)
c) Misalkan diketahui 𝑦(10−9) = 1, 𝑦′(10−9) = 0, selesaikan persamaan
tersebut berdasarkan bagian (b) dengan ℎ = 0.1, hitunglah nilai 𝑦 ketika 0 < 𝑥 ≤ 1.
Penyelesaian:
a) Buatlah sistem PDB orde satu dari persamaan tersebut. Menggunakan persamaan (3.27) dan (3.28), misalkan:
44
𝑧(𝑥) = 𝑦(𝑥) ⟹ 𝑧′(𝑥) = 𝑦′(𝑥) = 𝑤(𝑥)
𝑤(𝑥) = 𝑧′(𝑥) = 𝑦′(𝑥) ⟹ 𝑤′(𝑥) = 𝑦′′(𝑥) = 𝑔(𝑥) −2
𝑥𝑤(𝑥) dengan 𝑔(𝑥) = 2(2𝑥2+ 3)𝑦(𝑥) = 2(2𝑥2+ 3)𝑧(𝑥).
Jadi, persamaan di atas dapat diubah menjadi:
{
𝑧′(𝑥) = 𝑤(𝑥)
𝑤′(𝑥) = 2(2𝑥2+ 3)𝑧(𝑥) −2
𝑥𝑤(𝑥).
b) Buatlah skema metode Euler untuk menyelesaikan bagian (a)
dengan memilih 𝑥𝑛+1 = 𝑥𝑛+ ℎ, sehingga nilai pendekataanya sesuai persamaan (3.30) diberikan oleh:
misal: 𝐹(𝑥, 𝑧, 𝑤) = 𝑤(𝑥) ⟹ 𝐹(𝑥𝑛, 𝑧𝑛, 𝑤𝑛) = 𝑤𝑛 𝐺(𝑥, 𝑧, 𝑤) = 2(2𝑥2+ 3)𝑧(𝑥) −2 𝑥𝑤(𝑥) ⟹ 𝐺(𝑥𝑛, 𝑧𝑛, 𝑤𝑛) = 2(2𝑥𝑛2+ 3)𝑧𝑛− 2 𝑥𝑛𝑤𝑛. Sehingga dapat ditulis:
𝑧𝑛+1 = 𝑧𝑛+ ℎ[𝐹(𝑥𝑛, 𝑧𝑛, 𝑤𝑛)] = 𝑧𝑛 + ℎ𝑤𝑛
𝑤𝑛+1 = 𝑤𝑛+ ℎ𝐺(𝑥𝑛, 𝑧𝑛, 𝑤𝑛) = 𝑤𝑛+ ℎ [2(2𝑥𝑛2+ 3)𝑧𝑛− 2
𝑥𝑛𝑤𝑛] dimana 𝑛 = 1, 2, 3, …,
c) Misalkan diketahui 𝑦(10−9) = 1, 𝑦′(10−9) = 0, selesaikan persamaan
tersebut berdasarkan bagian (b) dengan ℎ = 0.1, hitunglah nilai 𝑦 ketika 0 < 𝑥 ≤ 1.
Jawab:
dengan syarat awal diberikan 𝑧0 = 𝑦(10−9) = 1, 𝑤
0 = 𝑦′(10−9) = 0, ℎ = 0.1.
Iterasi ke-1 (substitusi 𝑛 = 0 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ), 𝑥1 = 0.1. 𝑧0+1= 𝑧1 = 𝑧0+ 0.1(𝑤0) = 1 + 0.1(0) = 1 + 0 = 1
45 𝑤0+1 = 𝑤1 = 𝑤0+ 0.1 [2(2𝑥02+ 3)𝑧0 − 2 𝑥0 𝑤0] = 0 + 0.60000000000 = 0.60000000000. Iterasi ke-2 (substitusi 𝑛 = 1 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ),
dengan 𝑧1 = 1, 𝑤1 = 0.6000000000, ℎ = 0.1 dan 𝑥2 = 0.2. 𝑧1+1 = 𝑧2 = 𝑧1+ 0.1(𝑤1) = 1 + 0.1(0.6000000000) = 1 + 0.06000000000 = 1.06000000000 𝑤1+1 = 𝑤2 = 𝑤1+ 0.1 [2(2𝑥12+ 3)𝑧1− 2 𝑥1 𝑤1] = 0.6000000000 − 0.59599998792 = 0.00400001208. Iterasi ke-3 (substitusi 𝑛 = 2 pada 𝑧𝑛+1 , 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ ),
dengan 𝑧2 = 1.06000000000, 𝑤2 = 0.00400001208, ℎ = 0.1 dan 𝑥3 = 0.3. 𝑧2+1 = 𝑧3 = 𝑧2+ 0.1(𝑤2) = 1.06000000000 + 0.1(0.00400001208) = 1.0202010035 + 0.0416324311 = 1.06040000120 𝑤2+1= 𝑤3 = 𝑤2+ 0.1 [2(𝑥22+ 3)𝑧2− 2 𝑥2 𝑤2] = 0.00400001208 + 0.64895998810 = 0.65296000018. Iterasi ke-4 (substitusi 𝑛 = 3 pada 𝑧𝑛+1, 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ), dengan 𝑧3 =
1.06040000120, 𝑤3 = 0.65296000018, ℎ = 0.1 dan 𝑥4 = 0.4. 𝑧3+1 = 𝑧4 = 𝑧3+ 0.1(𝑤3) = 1.06040000120 + 0.1(0.65296000018) = 1.06040000120 + 0.06529600001 = 1.12569600122 𝑤3+1 = 𝑤4 = 𝑤3+ 0.1 [2(2𝑥32+ 3)𝑧3− 2 𝑥3 𝑤3] = 0.65296000018 + 0.23910773568 = 0.89206773587.
Iterasi ke-5 (substitusi 𝑛 = 4 pada 𝑧𝑛+1 , 𝑤𝑛+1 dan 𝑥𝑛+1 = 𝑥𝑛+ ℎ ),
dengan 𝑧4 = 1.12569600122, 𝑤4 = 0.89206773587, ℎ = 0.1 dan 𝑥5 = 0.5.
𝑧4+1= 𝑤5 = 𝑧4+ 0.1(𝑤4)
= 1.12569600122 + 0.1(0.89206773587)