i
PENYELESAIAN PERSAMAAN DIFERENSIAL PARSIAL
NONLINEAR DENGAN MENGGUNAKAN METODE
DEKOMPOSISI ADOMIAN
TUGAS AKHIR
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Disusun Oleh :
Maria Febronia Sedho Dheno NIM: 123114008
PROGRAM STUDI MATEMATIKA, JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
SOLUTIONS TO NONLINEAR PARTIAL DIFFERENTIAL
EQUATIONS BY THE ADOMIAN DECOMPOSITION
METHOD
A THESIS
Presented as Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Sains Mathematics Study Program
Written by :
Maria Febronia Sedho Dheno Student ID: 123114008
MATHEMATICS STUDY PROGRAM, DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v
HALAMAN PERSEMBAHAN
Tugas akhir saya persembahkan untuk orang-orang terkasih:
vi
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya, bahwa tugas akhir yang saya tulis ini tidak memuat karya atau bagian karya orang lain kecuali yang disebutkan dalam daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 25 Januari 2017
vii ABSTRAK
Persamaan diferensial parsial terdiri dari persamaan diferensial parsial linear dan nonlinear. Beberapa model persamaan diferensial parsial nonlinear antara lain adalah persamaan Burger, persamaan gelombang air dangkal (PGAD), persamaan gelombang gravitasi, dan persamaan gelombang kinematik. Agar perhitungan menjadi lebih cepat dan sederhana, PGAD kemudian disederhanakan ke dalam model lain yang salah satunya adalah persamaan gelombang gravitasi dan persamaan gelombang kinematik.
Dalam tugas akhir ini, keempat model persamaan diferensial parsial nonlinear di atas diselesaikan dengan menggunakan metode dekomposisi Adomian (MDA). Dengan menggunakan MDA, solusi persamaan diferensial diasumsikan sebagai jumlahan fungsi atau deret tak hingga fungsi dengan bantuan polinomial Adomian. Polinomial Adomian digunakan untuk menyelesaikan suku nonlinear dalam persamaan diferensial tersebut. Persamaan diferensial harus disertai dengan kondisi awal agar persamaan diferensial tersebut dapat diselesaikan. Kondisi awal yang diberikan tersebut sangat berpengaruh terhadap solusi yang didapatkan.
Sebagai tindak lanjut dari penggunaan konsep MDA dalam keempat persamaan diferensial parsial nonlinear di atas adalah jika terdapat solusi eksak eksplisit dari masalah yang dicari maka deret yang diperoleh konvergen sangat cepat ke solusi tersebut. Solusi pendekatan MDA merupakan solusi yang berasal dari deret terpotong yaitu yang biasanya melibatkan beberapa suku saja. Secara eksplisit, solusi pendekatan tersebut bergantung pada variabel ruang dan waktu.
viii ABSTRACT
Partial differential equations are of linear and nonlinear. Some models of nonlinear partial differential equations, are Burger equation, Shallow Water Equation (SWE), gravity wave equation, and kinematic wave equation. In order to make the calculation becomes faster and simpler, SWE is simplified into other models, which are gravity wave equation and kinematic wave equation.
In this thesis, the four models of nonlinear partial differential equations are solved by using Adomian Decomposition Method (ADM). By using this method, the solution of differential equation is assumed as the sum of functions or infinite series of functions with the help of Adomian polynomials. Adomian polynomial is used for solving the nonlinear term in the differential equation. The differential problem, the series converges quickly into the solution. The approximate solution is the solution derived from a truncated series which is usually involving only several terms. Explicitly, the approximate solution depends on the space and time variables.
ix
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma:
Nama : Maria Febronia Sedho Dheno
NIM : 123114008
Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:
Penyelesaian Persamaan Diferensial Parsial Nonlinear dengan Menggunakan Metode Dekomposisi Adomian
beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Sanata Dharma untuk menyimpan, mengalihkan ke dalam bentuk media lain, mengelolanya dalam pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun memberikan royalti kepada saya selama tetap menyantumkan nama saya sebagai penulis.
Demikian pernyataan ini saya buat dengan sebenarnya. Dibuat di Yogyakarta
Pada tangggal 25 Januari 2017 Yang menyatakan
x
KATA PENGANTAR
Puji dan syukur kepada Tuhan Yang Maha Esa, atas berkat dan rahmat yang diberikan sehingga penulis dapat menyelesaikan tugas akhir ini.
Makalah ini dibuat sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Matematika, Universitas Sanata Dharma. Banyak tantangan dalam proses penulisan tugas akhir ini, namun dengan penyertaan Tuhan serta dukungan dari berbagai pihak akhirnya skripsi ini dapat diselesaikan. Untuk itu penulis ingin mengucapkan terima kasih kepada:
1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D. selaku Dekan Fakultas Sains dan Teknologi, sekaligus selaku dosen pembimbing yang dengan sabar dan penuh antusias dalam membimbing selama proses penulisan tugas akhir ini.
2. Bapak Y. G. Hartono, S.Si., M.Sc. selaku Kepala Program Studi Matematika.
3. Bapak dan Ibu Dosen Program Studi Matematika yang telah memberikan ilmu yang sangat bermanfaat bagi penulis.
4. Kedua orang tuaku, Melkhior Dheno dan Rosalina Bate, serta kedua adikku Maria Theresia Wua Dheno dan Gregorius Hermanus Resi Dheno yang selalu mendukungku dengan penuh kasih dan memberikan masukkan positif kepadaku.
xi
6. Teman-teman seperjuangan prodi Matematika yaitu Ilga, Happy, Ajeng, Bobi, Rian, Budi, Ega, Amanda, Anggun, Dewi, Lia, Arum, Noni, Putri, Sila, Juli, Risma, Tika, dan Auxi yang selalu membantuku saat aku kesulitan dalam belajar dan dalam penyusunan tugas akhir ini.
7. Teman-teman dan kakak-kakak kece personil Wisma Goreti yaitu, kak Oppy, kak Orry, kak Cici, ka Lenny, Yanzher, dan Elsa yang selalu mendukung dan membantu dalam penyusunan tugas akhir ini.
Penulis juga mengucapkan terima kasih kepada semua pihak yang telah membantu dalam penyusunan tugas akhir ini.
Yogyakarta, 25 Januari 2017 Penulis,
xii
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
HALAMAN PERNYATAAN KEASLIAN KARYA ... vi
ABSTRAK ... vii
ABSTRACT ... viii
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
BAB I PENDAHULUAN ... 1
A. Latar Belakang ... 1
B. Rumusan Masalah ... 6
C. Pembatasan Masalah ... 6
D. Tujuan Penulisan ... 6
E. Metode Penulisan ... 7
F. Manfaat Penulisan ... 7
xiii
BAB II PERSAMAAN DIFERENSIAL ... 9
A. Turunan Fungsi ... 9
B. Klasifikasi Persamaan Diferensial ... 13
C. Integral ... 16
D. Barisan... 20
E. Deret ... 20
F. Deret Taylor dan Deret Maclaurin ... 22
G. Konvergensi Deret Taylor ... 23
BAB III METODE DEKOMPOSISI ADOMIAN ... 29
A. Metode Dekomposisi Adomian untuk Persamaan Diferensial Nonlinear ... 29
B. Metode Dekomposisi Adomian untuk Persamaan Burger ... 39
C. Metode Dekomposisi Adomian untuk Persamaan Gelombang Air Dangkal ... 43
D. Metode Dekomposisi Adomian untuk Persamaan Gelombang Gravitasi ... 54
E. Metode Dekomposisi Adomian untuk Persamaan Gelombang KInematik ... 62
BAB IV KONVERGENSI METODE DEKOMPOSISI ADOMIAN ... 66
A. Perumuman dan Hipotesis Metode Dekomposisi Adomian ... 66
B. Teorema Konvergensi ... 67
xiv
BAB V PENUTUP ... 71
A. Kesimpulan ... 71
B. Saran ... 72
DAFTAR PUSTAKA ... 73
1 BAB I PENDAHULUAN
Dalam bab ini akan dibahas mengenai latar belakang, rumusan masalah, batasan masalah, tujuan penulisan, manfaaat penulisan, dan sistematika penulisan.
A. Latar Belakang
Persamaan diferensial adalah suatu persamaan yang melibatkan turunan dari satu atau lebih variabel terikat yang berhubungan dengan satu atau lebih variabel bebas (Ross, 1984). Permasalahan yang berhubungan dengan persamaan diferensial sering kita jumpai dalam kehidupan sehari-hari. Permasalahan tersebut seperti dalam bidang sains dan teknik. Klasifikasi persamaan diferensial bisa di dasarkan pada: banyaknya variabel yang terlibat, derajat persamaan diferensial, linear atau nonlinear, dan homogen atau nonhomogen. Beberapa model dalam bentuk persamaan diferensial yaitu persamaan diferensial biasa dan persamaan diferensial parsial.
Model-model lain dari persamaan diferensial parsial yaitu seperti persamaan Burger, persamaan gelombang air dangkal, persamaan gelombang gravitasi, dan persamaan gelombang kinematik. Persamaan Burger, persamaan gelombang gravitasi, dan persamaan gelombang kinematik merupakan model khusus dari persamaan gelombang air dangkal. Dalam tugas akhir ini dipandang empat model di atas dalam menyelesaikan persamaan diferensial parsial dengan menggunakan metode dekomposisi Adomian (MDA).
Menurut Wazwaz (2009), persamaan Burger adalah persamaan diferensial parsial fundamental dalam mekanika fluida. Persamaan ini pertama kali dikenalkan oleh Johannes Martinus Burger (1895-1981). Persamaan Burger dapat dirumuskan sebagai berikut:
(1.1)
dengan adalah kecepatan aliran dan variabel independen dan secara berturut-turut menyatakan jarak sepanjang arah aliran dan waktu
Secara matematis, seperti ditulis oleh Al-Khaled dan Allan (2004) persamaan gelombang air dangkal (PGAD) dapat dirumuskan sebagai berikut
(
) ( )
(1.2)
dengan , dan memenuhi kondisi awal sebagai berikut:
( ) ( ) (1.3)
dengan adalah kedalaman air dari permukaan air hingga dasar tanah, adalah kecepatan fluida, dan adalah kedalaman air dari permukaan
air hingga dasar tanah saat air dalam keadaan diam. Variabel independen dan secara berturut-turut menyatakan jarak sepanjang arah aliran dan waktu. Ilustrasi aliran air dinyatakan dalam Gambar 1.1.
R. Martins, J. Leandro, dan S. Djordjević memperkenalkan persamaan
Saint-Venant (PSV), sebagai bentuk lain dari PGAD. Persamaan ini sering disederhanakan sehingga menjadi sangat praktis, menjadikan perhitungan yang sangat cepat, atau untuk representasi fisis. Untuk mengurangi waktu perhitungan atau meningkatkan stabilitas, PSV sering disederhanakan ke dalam model lain seperti persamaan gelombang kinematik, persamaan gelombang difusif, dan persamaan gelombang gravitasi. Model persamaan gelombang gravitasi adalah sebagai berikut:
(1.4)
dengan adalah kedalaman air, adalah debit air dan adalah percepatan gravitasi. Dan model persamaan gelombang kinematik adalah sebagai berikut:
(1.5)
dengan adalah ketinggian air dan variabel independen dan secara berturut-turut menyatakan jarak sepanjang arah aliran dan waktu.
persamaan diferensial parsial yang diselesaikan dengan MDA. Dalam MDA, solusi persamaan diferensial diasumsikan sebagai jumlahan fungsi atau deret tak hingga fungsi dengan bantuan polinomial Adomian. Polinomial Adomian digunakan untuk menyelesaikan suku nonlinear dalam persamaan diferensial tersebut. Polinomial Adomian dibentuk menggunakan ekspansi deret Taylor pada fungsi tertentu, yang diasumsikan sebagai fungsi analitik. Persamaan diferensial harus disertai dengan kondisi awal agar persamaan diferensial dapat diselesaikan. Kondisi awal yang diberikan tersebut sangat berpengaruh terhadap solusi yang didapatkan (Adomian,1994).
Banyak peneliti mengungkapkan bahwa jika terdapat solusi eksak dari masalah yang dicari maka deret yang diperoleh konvergen sangat cepat ke solusi tersebut. Konsep konvergensi dari deret dekomposisi telah didiskusikan oleh banyak peneliti untuk menjelaskan konvergensi yang cepat dari deret yang dihasilkan tersebut. Cherruault telah memperkenalkan mengenai konsep konvergensi metode Adomian dalam makalahnya. Selain itu, Cherruault dan Adomian juga menyajikan bukti konvergensi baru dari metode Adomian tersebut. Bukti konvergensi inilah yang digunakan penulis dalam menyelidiki konvergensi dari MDA.
B.
Rumusan Masalah
Tugas akhir ini terdiri dari beberapan rumusan-rumusan masalah yang terlihat seperti di bawah ini:
1. Bagaimana menyelesaikan suatu persamaan diferensial parsial dengan MDA?
2. Bagaimana menyelesaikan persamaan Burger dengan MDA? 3. Bagaimana menyelesaikan PGAD dengan MDA?
4. Bagaimana menyelesaikan persamaan gelombang gravitasi dengan MDA?
5. Bagaimana menyelesaikan persamaan gelombang kinematik dengan MDA?
6. Bagaimana konvergensi dari MDA ?
C.
Batasan Masalah
Pembahasan masalah dalam tugas akhir ini akan dibatasi pada menyelesaikan suatu persamaan diferensial parsial dengan MDA, yang meliputi: persamaan Burger, PGAD, persamaan gelombang gravitasi, persamaan gelombang kinematik. Selain itu, akan dibahas juga tentang konvergensi dari MDA.
D.
Tujuan Penulisan
1. Menerapkan MDA untuk memperoleh solusi eksplisit pendekatan untuk persamaan diferensial parsial dengan suku sumber.
2. Menggambarkan bagaimana metode dekomposisi dapat membantu untuk memperoleh solusi yang akurat dan konvergensi yang cepat mengenai hukum konservasi dengan suku sumber.
E.
Metode Penulisan
Metode penulisan yang digunakan adalah studi pustaka dari buku-buku dan jurnal serta praktek simulasi dengan bantuan komputer.
F.
Manfaat Penulisan
Dengan menerapkan MDA pada persamaan diferensial, diperoleh suatu penyelesaian yang merupakan suatu fungsi eksplisit terhadap variabel bebas. Dengan demikian, jika diberikan sebarang nilai variabel bebas, maka penyelesaian di titik variabel bebas itu dapat dihitung dengan cepat. Perhitungan ini dilakukan tanpa diskretisasi numeris dari domain.
G.
Sistematika Penulisan
Sistematika penulisan tugas akhir ini terdiri dari lima bab yaitu sebagai berikut:
C.Batasan Masalah D.Metode Penulisan E. Tujuan Penulisan F. Manfaat Penulisan
BAB II PERSAMAAN DIFERENSIAL A.Turunan Fungsi
B.Klasifikasi Persamaan Diferensial C.Integral
D.Deret Taylor dan Deret Maclaurin E. Konvergensi Deret Taylor
BAB III METODE DEKOMPOSISI ADOMIAN
A.Metode Dekomposisi Adomian untuk Persamaan Diferensial Parsial Nonlinear
B.Metode Dekomposisi Adomian untuk Persamaan Burger
C.Metode Dekomposisi Adomian untuk Persamaan Gelombang Air Dangkal.
D.Metode Dekomposisi Adomian untuk Persamaan Gelombang Gravitasi.
E. Metode Dekomposisi Adomian untuk Persamaan Gelombang Kinematik
BAB IV KONVERGENSI METODE DEKOMPOSISI ADOMIAN A.Teorema Konvergensi
B.Kecepatan Konvergensi BAB V PENUTUP
9 BAB II
PERSAMAAN DIFERENSIAL
Dalam bab ini akan ditulis mengenai konsep-konsep dasar atau teori-teori dasar dalam penyelesaian tugas akhir ini. Teori-teori dasar tersebut meliputi: turunan fungsi, klasifikasi persamaan diferensial, integral, barisan, deret, deret Taylor, deret Maclaurin dan konvergensi deret Taylor.
A.Turunan Fungsi
Pada subbab ini akan dibahas mengenai turunan fungsi yang meliputi turunan fungsi satu variabel dan turunan fungsi dua variabel. Berikut akan dijelaskan definisi untuk turunan fungsi.
Definisi 2.1
Turunan fungsi didefinisikan sebagai:
di setiap titik sehingga limit di atas ada dan hingga. Dan jika ada maka fungsi dikatakan terdiferensial atau mempunyai turunan di .
Penyelesaian:
Fungsi di atas bukan merupakan fungsi linear, maka dengan menggunakan definisi 2.1, penyelesaiannya adalah sebagai berikut:
Turunan Fungsi Implisit
Fungsi dikatakan fungsi implisit sebab hubungan antara variabel bebas dan variabel takbebas diberikan secara tidak eksplisit. Dalam mencari turunan untuk fungsi implisit, maka dapat dilakukan dengan 2 cara yaitu dengan mengubah fungsi tersebut menjadi fungsi ekplisit dan dengan menggunakan metode penurunan implisit.
Contoh 2.2 Tentukan
Cara 1 Penurunan Eksplisit Dengan mengubah menjadi fungsi eksplisit, yaitu
Dengan menggunakan Definisi 2.1, kita peroleh:
Cara 2 Penurunan Implisit Dengan menurunan kedua ruas terhadap , maka:
Solusi yang dihasilkan oleh kedua cara di atas terlihat berbeda. Solusi yang diberikan oleh Cara 1 hanya melibatkan , sedangkan solusi yang diberikan oleh Cara 2 melibatkan dan . Namun, ingat bahwa dalam Cara 1 telah diubah fungsi semula ke dalam fungsi eksplisit yaitu dengan mengubah fungsi dalam bentuk dan diperoleh . Lalu dengan mensubsitusikan ke
dalam bentuk
pada solusi yang dihasilkan oleh Cara 2, maka diperoleh:
B. Klasifikasi Persamaan Diferensial
Pada bagian ini akan dibahas klasifikasi persamaan diferensial yang meliputi contoh dan definisi persamaan diferensial, persamaan diferensial biasa, persamaan diferensial parsial, orde persamaan diferensial, dan kelinearan persamaan diferensial.
Definisi 2.2
Persamaan diferensial adalah suatu persamaan yang melibatkan turunan dari satu atau lebih variabel terikat yang berhubungan dengan satu atau lebih variabel bebas.
Contoh 2.2
Contoh persamaan diferensial adalah sebagai berikut:
(
Contoh 2.3
Pada Contoh 2.2 dapat dilihat bahwa persamaan (2.1) dan (2.2) adalah persamaan diferensial biasa. Dalam persamaan (2.1) variabel adalah satu-satunya variabel bebas, dan adalah variabel terikat. Dan dalam persamaan (2.2) variabel bebasnya adalah , dengan adalah variabel terikat.
Definisi 2.4
Persamaan diferensial parsial adalah persamaan diferensial yang melibatkan turunan parsial dari satu atau lebih variabel terikat yang berhubungan dengan lebih dari satu variabel bebas.
Contoh 2.4
Pada Contoh 2.2 dapat dilihat bahwa persamaan (2.3) dan (2.4) adalah persamaan diferensial parsial. Dalam persamaan (2.3) variabel dan adalah variabel bebas dan adalah variabel terikat. Dan dalam persamaan (2.4) terdapat tiga variabel bebas yaitu , , dan sedangkan adalah variabel terikat.
Definisi 2.5
Orde atau derajat dari persamaan diferensial adalah orde atau tingkat tertinggi dari turunan yang terlibat dalam suatu persamaan diferensial.
Contoh 2.5
(2.3) dan (2.4) secara berturut-turut adalah persamaan diferensial orde pertama dan kedua.
Definisi 2.6
Suatu persamaan diferensial biasa linear orde , dengan variabel terikat dan variabel bebas , dapat dinyatakan dalam bentuk
Kedua persamaan diferensial biasa berikut adalah persamaan diferensial biasa linear. Pada kedua persamaan tersebut, variabel adalah variabel terikat. Perhatikan bahwa dan turunan-turunannya terjadi dengan pangkat pertama saja dan tidak ada perkalian dari dan/atau turunan dari .
Persamaan diferensial biasa nonlinear adalah suatu persamaan diferensial biasa yang tidak linear. Persamaan diferensial biasa yang tidak berbentuk seperti persamaaan (2.6) dikatakan persamaan diferensial biasa nonlinear.
Contoh 2.8
Persamaan (2.9) adalah persamaan diferensial biasa nonlinear karena variabel terikat terdapat pada derajat kedua dalam bentuk . Persamaan (2.10) juga merupakan persamaan diferensial biasa nonlinear karena terdapat bentuk
yang melibatkan pangkat tiga pada turunan pertamanya. Persamaan (2.11) juga nonlinear karena pada bentuk
melibatkan perkalian terhadap variabel terikat dan turunan pertamanya.
C.Integral
Pada bagian ini akan dibahas mengenai definisi integral dan contoh-contohnya dari integral tentu.
Nilai anti turunan dari fungsi di atas bukan sebab turunannya
disebut integral tentu (atau integral Riemann) dari sampai diberikan oleh:
Gambar 2.1 Ilustrasi fungsi satu variabel.
maka akan dibuat titik-titik dengan dan . Ini menunjukan bahwa interval tertutup tersebut akan dipartisi menjadi subinterval yaitu Dari setiap subinterval akan diambil sembarang titik ̅ dan yang merupakan panjang interval dengan . Disini . Seperti contoh .
Cara lain untuk menghitung adalah dengan menggunakan rumus sebagai berikut:
Rumus integral tentu pada Definisi 2.10 diperoleh dengan terlebih dahulu menentukan nilai Jumlahan Riemann atau jumlah luas persegi panjang. Nilai hampiran luas persegi panjang diperoleh dari definisi dasar luas persegi panjang yaitu dengan ketentuan panjangnya merupakan ̅ dan lebarnya merupakan . Sehingga untuk menghitung hampiran luas
Luas daerah di bawah kurva diaproksimasikan dengan total hampiran luas persegi panjang masing-masing subinterval yang dibentuk tersebut, sehingga aproksimasi luas di bawah kurva adalah Hal ini berarti bahwa total pula aproksimasi luasan dan semakin dekat dengan luasan yang sebenarnya. Dengan demikian,
∑ ̅
D.Barisan
Pada subbab mengenai konsep barisan ini, hanya dibatasi pada konsep barisan konvergen dan divergen beserta contohnya.
Definisi 2.11
Suatu barisan dikatakan kovergen ke suatu bilangan jika untuk setiap bilang posistif terdapat suatu bilang bulat sedemikian sehingga untuk semua
Jika tidak terdapat bilang , maka barisan tersebut dikatakan barisan divergen.
Jika konvergen ke , maka , atau secara sederhana . Dan merupakan limit dari barisan.
Contoh 2.10
Tunjukkan bahwa .
Penyelesaian
Misalkan Akan ditunjukkan bahwa terdapat bilangan bulat sedemikian hingga untuk semua ,
| |
Bentuk implikasi di atas terpenuhi jika atau . Jika adalah sebarang
bilangan bulat yang lebih besar dari , maka bentuk implikasi di atas terpenuhi
untuk semua . Sehingga terbukti bahwa
E.Deret
Pada subbab ini hanya dibatasi pada konsep deret konvergen dan divergen beserta contohnya.
Definisi 2.12
Diberikan suatu barisan bilangan , suatu ekspresi dalam bentuk
∑
adalah barisan jumlah parsial dari deret, dengan adalah jumlah parsial ke- . Jika barisan jumlah parsial konvergen ke limit , maka deret tersebut konvergen dan jumlahannya adalah . Dalam kasus ini, akan dituliskan sebagai berikut:
∑
Jika barisan jumlah parsial dari suatu deret tidak konvergen, maka deret tersebut dikatakan deret divergen.
Contoh 2.11
Selidiki kekonvergenan dari deret dibawah ini:
Penyelesaian
Jika diperhatikan
( )
sehingga diperoleh jumlah parsial ke- nya adalah:
( )
dan Jadi, karena barisan jumlah-jumlah
parsialnya konvergen ke 1, maka deret di atas juga konvergen. F. Deret Taylor dan Deret Maclaurin
Pada subbab ini akan dibahas mengenai definisi dan contoh-contoh deret Taylor dan deret Maclaurin.
Definisi 2.13
Misalkan adalah sebuah fungsi yang memiliki turunan-turunan dari semua tingkat pada interval tertentu dengan adalah titik interior. Maka deret Taylor
Deret Maclaurin yang diberikan oleh adalah
Akan dicari . Dengan turunan maka diperoleh konvergen ke fungsi itu sendiri. Hal ini dapat dilihat dengan teorema berikut. Teorema 2.1 Teorema Taylor
Jika dan turunan-turunan pertama hingga ke- kontinu pada interval tertutup antara dan , dan terdiferensial pada interval terbuka antara dan , maka terdapat bilangan antara dan sedemikian sehingga:
Bukti
dengan turunan pertama -nya masih sesuai dengan fungsi dan turunan pertama -nya pada .
Sekarang akan dipilih suatu nilai tertentu dari yang membuat kurva sesuai dengan kurva asli pada , yaitu:
(2.13) dengan didefinisikan oleh persamaan (2.13), maka fungsi:
Terlihat bahwa teorema Rolle berhasil diaplikasikan pada yaitu:
sedemikian sehingga
sedemikian sehingga
sedemikian sehingga
Karena kontinu pada dan terdiferensial pada , dan , bahwa teorema Rolle mengimplikasikan bahwa terdapat suatu
bilangan pada sedemikian sehingga
(2.14)
Jika diturunkan total dari kali, maka diperoleh:
(2.15)
Berdasarkan persamaan (2.14) dan (2.15), diperoleh:
(2.16)
Dan berdasarkan persamaan (2.13) dan (2.16), diperoleh:
Maka terbukti.
Ketika menggunakan teorema Taylor, maka akan diasumsikan tetap dan adalah variabel bebas. Rumus Taylor mudah digunakan saat mengganti dengan
Rumus Taylor
Jika mempunyai turunan-turunan dari semua tingkat pada interval terbuka yang memuat , maka untuk setiap bilangan bulat positif dan untuk setiap di ,
(2.17)
dengan
(2.18)
untuk antara dan .
Ketika teorema Taylor dinyatakan seperti di atas, hal ini mengatakan bahwa untuk setiap , maka:
Fungsi ditentukan oleh nilai dari turunan ke di titik yang bergantung pada kedua dan , dan terletak di antara mereka.
Persamaan (2.12) disebut rumus Taylor. Fungsi disebut suku error untuk aproksimasi oleh terhadap interval .
Definisi 2.14
∑
dapat diperkirakan dengan tanpa mengetahui nilai , untuk mengetahuinya
untuk setiap ,
dan deret konvergen untuk setiap , maka:
∑
29 BAB III
METODE DEKOMPOSISI ADOMIAN
Dalam bab ini akan dibahas mengenai metode dekomposisi Adomian (MDA) dan penyelesaian beberapa persamaan diferensial parsial baik linear maupun nonlinear dengan menggunakan metode dekomposisi Adomian. Beberapa persamaan diferensial parsial tersebut adalah persamaan Burger, persamaan gelombang air dangkal, persamaan gelombang gravitasi, dan persamaan gelombang kinematik.
A.Metode Dekomposisi Adomian untuk Persamaan Diferensial Parsial Nonlinear
Dalam bagian ini akan dibahas mengenai penerapan metode dekomposisi Adomian dalam menyelesaikan persamaan diferensial parsial nonlinear yang akan diawali dengan penyelesaian persamaan diferensial parsial orde pertama dengan menggunakan MDA.
a. MDA untuk Menyelesaikan Persamaan Diferensial Parsial Linear Orde Pertama
Untuk memberikan gambaran mengenai metode dekomposisi Adomian, maka perhatikan persamaan diferensial linear berikut:
dengan adalah suatu fungsi yang diasumsikan mempunyai invers, adalah fungsi diferensial linear dan adalah suku sumber. Dengan mensubsitusikan fungsi invers pada kedua sisi persamaan (3.1), maka diperoleh:
dengan adalah suku yang dihasilkan dari proses pengintegralan terhadap suku sumber .
Metode Adomian mendefinisikan solusi berdasarkan suatu deret takhingga seperti yang dituliskan berikut, yaitu:
∑
(3.3)
Atau
( ) (3.4)
Sehingga diperoleh skema di bawah ini: (3.3) untuk memperoleh solusi dalam bentuk deret.
Untuk mempermudah dalam memahami konsep metode ini, maka akan diperhatikan persamaan diferensial parsial orde pertama nonhomogen berikut, yaitu:
(3.7)
dengan nilai awal sebagai berikut:
(3.8)
dan
(3.9)
(3.10) dan
(3.11)
Dalam bentuk operator, maka persamaan (3.7) dapat ditulis sebagai berikut:
(3.12)
dengan setiap operator di atas diasumsikan dapat diinverskan dan opeator dan dimisalkan sebagai berikut:
∫ (3.13)
dan
∫ (3.14)
Ini berarti bahwa:
(3.15)
Dengan mensubsitusikan pada kedua sisi persamaan (3.12) maka diperoleh:
dengan mengoperasikan , diperoleh:
( )
atau
( )
atau
Hasil pada persamaan (3.16) di atas diperoleh dengan menggunakan persamaan (3.15) dan dengan nilai awal . Berdasarkan penjelasan sebelumnya bahwa deret himpunan metode dekomposisi adalah sebagai berikut:
∑
(3.17)
Subsitusikan persamaan (3.17) pada kedua sisi persamaan (3.16), sehingga menghasilkan:
∑
(∑
) (3.18)
Atau dapat dituliskan sebagai berikut:
(3.19)
Adomian mengatakan bahwa suku diidentifikasikan sebagai kondisi awal atau nilai awal dan ditambah hasil dari untuk kasus ini, dengan keduanya diasumsikan diketahui.
(3.20)
Hal ini jelas terlihat bahwa keakuratan pendekatan dapat ditingkatkan secara signifikan hanya dengan melakukan iterasi berkali-kali. Sehingga pendekatan suku ke- untuk dapat ditulis sebagai berikut:
∑
(3.21)
Untuk masalah konkret, dimana solusi eksak tidak dapat diperoleh dengan mudah maka akan menggunakan deret terpotong (3.21) untuk memperoleh solusi pendekatan.
b. MDA untuk Menyelesaikan Persamaan Diferensial Parsial Nonlinear Orde Tinggi
Dalam penjelasan sebelumnya terlihat bahwa MDA diterapkan dalam persamaan diferensial linear orde pertama. Metode ini diterapkan secara langsung dan secara mudah untuk masalah nonhomogen. Subbab ini akan menerapkan MDA untuk menyelesaikan persamaan diferensial parsial nonlinear. Hal ini sangat penting karena dalam menyelesaikan persamaan diferensial parsial tidak hanya terdapat suku linear saja namun terdapat suku nonlinear juga seperti , dan lain sebagainya.
Berikut ini akan dijelaskan secara rinci mengenai skema Adomian dalam menghitung suku nonlinear. Untuk memudahkan, maka penjelasan mengenai persamaan diferensial parsial nonlinear akan didukung dengan beberapa contoh ilustratif yang mencakup berbagai bentuk nonlinear.
Telah diketahui bahwa metode dekomposisi Adomian menunjukkan bahwa fungsi yang tak diketahui dapat diwakili oleh deret dekomposisi berikut:
∑
(3.22)
dengan dapat dihitung dengan cara rekursif. Namun demikian, suku nonlinear seperti , dan lain-lain bisa dinyatakan dalam deret terbatas yang
disebut polinomial Adomian yang dituliskan sebagai berikut:
∑
(3.23)
Untuk menyelesaikan persamaan diferensial parsial nonlinear dengan menggunakan MDA terdapat beberapa cara. Salah satunya adalah polinomial Adomian untuk suku nonlinear dapat didefinisikan dengan menggunakan formula sebagai berikut:
[ (∑ )]
Namun, dalam tugas akhir ini penulis tidak menggunakan cara di atas, sebab memerlukan perhitungan yang lebih rumit. Sehingga dalam tugas akhir ini penulis menggunakan cara lain.
Cara yang akan diperkenalkan selanjutnya ini merupakan cara sederhana dan dapat mempermudah dalam menghitung polinomial Adomian. Cara ini didasarkan pada aljabar dan identitas trigonometri serta deret Taylor. Cara ini menggunakan operasi dasar dan tidak memerlukan formula tertentu, yang diambil dari buku karangan Wazwaz (2009).
Seperti yang didefinisikan oleh metode dekomposisi yaitu cara ini menunjukkan bahwa mensubsitusi sebagai jumlahan dari dengan . Hal ini jelas bahwa selalu ditentukan independen dari polinomial lainnya dengan , dan didefinisikan sebagai berikut:
(3.24)
Cara ini mengasumsikan bahwa pertama memisahkan
untuk setiap suku nonlinear . Dengan melakukan pemisahan ini
ekspansi yang dihasilkan sedemikian sehingga jumlah subskrip dari komponen dalam setiap suku adalah sama. Setelah melakukan pengumpulan suku-suku tersebut maka perhitungan polinomial Adomian dengan demikian selesai.
Untuk meningkatkan pemahaman mengenai cara ini maka akan diperkenalkan beberapa contoh berikut.
i. Kasus Polinomial Nonlinear Misalkan .
Akan dimisalkan sebagai berikut, yaitu:
∑
Hasil ekspansi dari persamaan (3.26) dapat disusun kembali dengan mengelompokan semua suku dengan jumlah dari subskrip adalah sama. Ini berarti bahwa persamaan (3.26) dapat ditulis sebagai berikut:
(3.27)
Maka polinomial Adomian secara lengkap adalah sebagai berikut:
dan seterusnya.
ii. Turunan Nonlinear Misalkan .
Akan dimisalkan sebagai berikut, yaitu :
∑
(3.28)
Dengan mensubsitusikan persamaan (3.28) kedalam maka diperoleh:
( )
(3.29)
Dengan mengumpulkan suku-suku seperti yang sudah dijelaskan sebelumnya, maka diperoleh:
(3.30)
Sehingga polinomial Adomiannya adalah sebagai berikut:
dan seterusnya.
B. Metode Dekomposisi Adomian untuk Persamaan Burger Dipandang persamaan Burger sebagai berikut:
(3.31)
dengan nilai awal,
Persamaan (3.31) di atas akan ditulis dalam bentuk:
(3.32)
Misalkan
dan . Maka persamaan (3.31) di atas ditulis dalam bentuk sebagai berikut:
(3.33)
Dengan mensubsitusikan pada kedua sisi persamaan (3.33), diperoleh:
Oleh sebab itu diperoleh solusi sebagai berikut:
Dengan menggunakan pendekatan suku ke- , maka dapat ditulis dalam bentuk sebagai berikut,yaitu: dipandang nilai awal sebagai berikut:
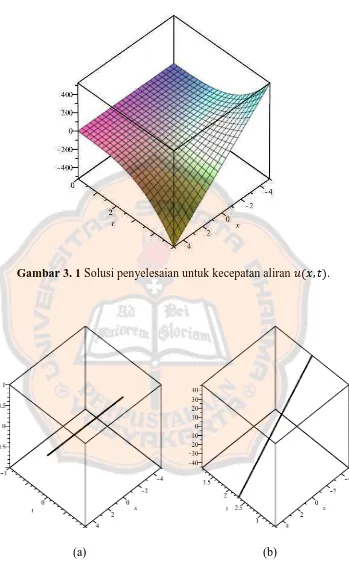
Gambar 3. 1 Solusi penyelesaian untuk kecepatan aliran .
(a) (b)
Gambar 3.2 Solusi untuk kecepatan aliran saat (a) dan saat
Jadi, setiap iterasi pada persamaan (3.39) diatas jika dijumlahkan akan
Akibatnya, diperoleh solusi eksak sebagai berikut:
(3.41)
dengan | | atau jaminan kekonvergenan solusi eksak tersebut yaitu .
C. Metode Dekomposisi Adomian untuk Persamaan Gelombang Air Dangkal
air hingga dasar tanah saat air dalam keadaan diam. Variabel independen dan secara berturut-turut menyatakan jarak sepanjang arah aliran dan waktu.
Persamaan (2.1) dapat ditulis ke bentuk yang lebih sederhana, yaitu:
(3.44)
dengan
( ) ( ) (3.45)
Untuk menyelesaikan PGAD dengan menggunakan MDA, maka persamaan di atas akan ditulis sebagai berikut:
untuk memudahkan perhitungan, maka bentuk pada persamaan diatas akan diubah menjadi:
[ ]
Misalkan , maka:
[ ] (3.51)
Berdasarkan hasil penurunan persamaan (3.46) dan (3.47) dengan MDA ,maka diperoleh:
[ ] (3.52)
dan
[ ] (3.53)
dengan:
Misalkan ∑ , ∑ dan
∑
∑
dengan , , dan adalah bentuk polinomial Adomian. Ketiga permisalan diatas akan disubsitusikan ke dalam persamaan (3.52) dan (3.53) untuk memperoleh solusi dan .
Untuk mencari solusi , maka akan disubsitusikan ketiga permisalan di atas, sehingga di peroleh:
[∑
Karena diketahui ∑ , maka:
( )
Sehingga diperoleh:
Dan karena diketahui ∑ , maka:
( )
Berdasarkan hasil dari penggunaan MDA ke dalam PGAD, maka diperoleh penyelesaian sebagai berikut:
dan
[ ]
dengan kondisi awal:
dan
Sehingga solusi penyelesaian untuk dan adalah sebagai berikut:
dan
∑
dan
∑
Untuk lebih memahami mengenai penerapan MDA dalam PGAD maka akan diperlihatkan sebuah contoh. Dengan mengacu pada persamaan (3.44) dan (3.45) maka dipandang
dengan ketinggian awal dan kecepatan awal dari air secara berurut-urut ditentukan oleh:
dan
Dengan menggunakan program MAPLE, maka solusi untuk ketinggian air
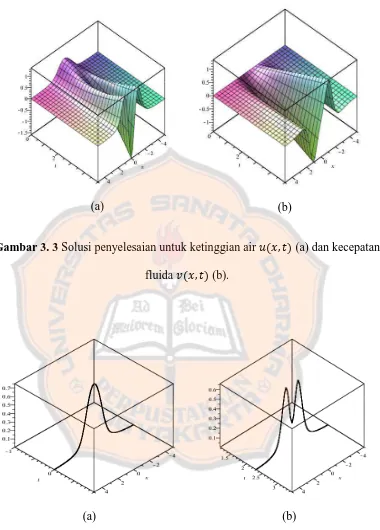
dan kecepatan fluida dapat dihitung. Solusi untuk ketinggian air
(a) (b)
Gambar 3. 3 Solusi penyelesaian untuk ketinggian air (a) dan kecepatan fluida (b).
(a) (b)
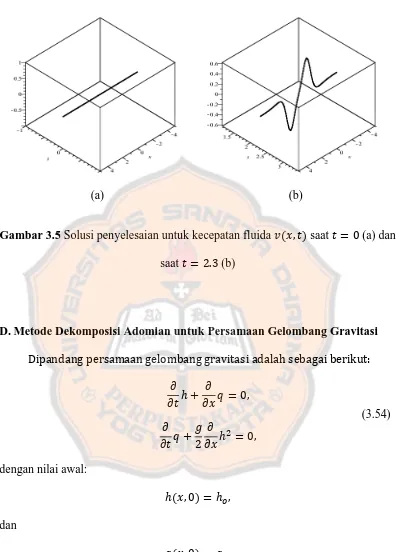
(a) (b)
Gambar 3.5 Solusi penyelesaian untuk kecepatan fluida saat (a) dan saat (b)
D.Metode Dekomposisi Adomian untuk Persamaan Gelombang Gravitasi Dipandang persamaan gelombang gravitasi adalah sebagai berikut:
(3.54)
dengan nilai awal:
dan
Untuk menyelesaikan persamaan gelombang gravitasi dengan menggunakan MDA, maka persamaan (3.54) akan ditulis sebagai berikut:
Dengan langkah yang sama yaitu menggunakan operasi ∫ pada
Sehingga diperoleh persamaan baru yaitu sebagai berikut:
atau
karena ∑ , sehingga diperoleh:
Selanjutnya dengan mensubsitusikan dan ke dalam persamaan (3.62), diperoleh:
(∑
)
karena ∑ maka diperoleh:
atau
karena ∑ maka diperoleh:
Maka dapat dihitung sebagai berikut:
Berdasarkan hasil dari penggunaan MDA ke dalam persamaan gelombang gravitasi, maka diperoleh penyelesaian sebagai berikut:
(3.63)
Dipandang nilai awal untuk kedalaman air dan debit air secara berturut-turut adalah sebagai berikut:
dan
Dengan adanya nilai awal, maka pendekatan suku ke- dari kedalaman air dan debit air dapat ditentukan dengan menggunakan skema persamaan (3.63).
Lalu dengan menggunakan program MAPLE, maka solusi untuk kedalaman air adalah sebagai berikut:
( ) ( )
(
)
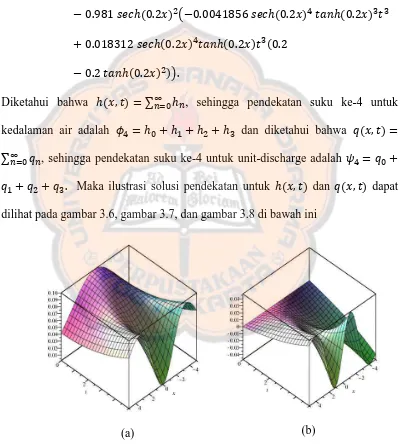
Diketahui bahwa ∑ , sehingga pendekatan suku ke-4 untuk kedalaman air adalah dan diketahui bahwa ∑ , sehingga pendekatan suku ke-4 untuk unit-discharge adalah
Maka ilustrasi solusi pendekatan untuk dan dapat
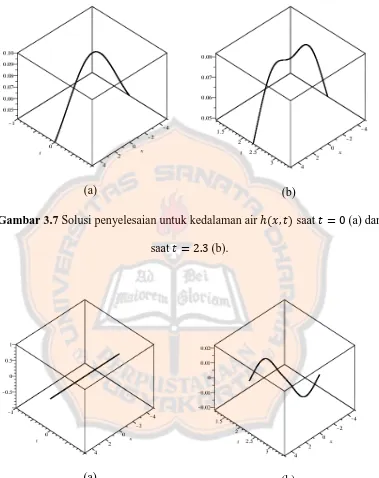
dilihat pada gambar 3.6, gambar 3.7, dan gambar 3.8 di bawah ini
(a) (b)
(a) (b)
Gambar 3.7 Solusi penyelesaian untuk kedalaman air saat (a) dan saat (b).
(a) (b)
Gambar 3.8 Solusi penyelesaian untuk debit air saat (a) dan saat
E.Metode Dekomposisi Adomian untuk Persamaan Gelombang Kinematik Di pandang persamaan gelombang kinematik adalah sebagai berikut:
(3.64)
dengan nilai awalnya:
Persamaan diatas merupakan persamaan diferensial parsial nonlinear, dengan
menyatakan ketinggian air dan variabel dan secara berturut-turut
menyatakan jarak sepanjang arah aliran dan waktu. Dengan mengaplikasikan
karena , maka persamaan di atas menjadi:
Misalkan ∑ dan ∑ , lalu akan disubsitusikan ke persamaan di atas sehingga diperoleh:
sehingga dapat dihitung sebagai berikut:
(3.65)
Dengan menggunakan pendekatan suku ke- , maka dapat ditulis dalam bentuk sebagai berikut,yaitu:
∑
(3.66)
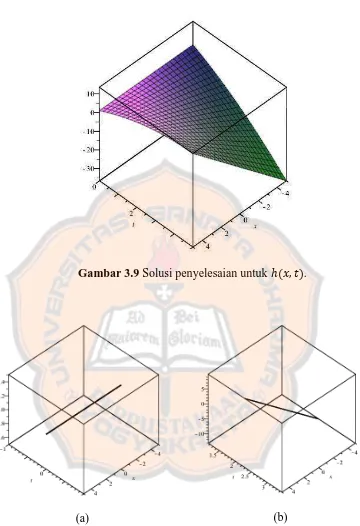
Dengan menggunakan program MAPLE, diperoleh:
Gambar 3.9 Solusi penyelesaian untuk .
(a) (b)
66 BAB IV
KONVERGENSI METODE DEKOMPOSISI ADOMIAN
Pada bagian ini akan dibahas mengenai konvergensi metode dekomposisi Adomian. Yang akan dibahas yaitu mengenai bukti konvergensi baru dari metode Adomian yang didasarkan pada sifat-sifat deret konvergen. Dan pada akhirnya akan disimpulkan beberapa hasil kecepatan konvergensi dari metode ini yang memungkinkan dapat menyelesaikan persamaan nonlinear.
A.Perumuman dan Hipotesis Metode Dekomposisi Adomian
Pertama, akan diingatkan kembali mengenai prinsip utama metode Adomian yaitu dipandang persamaan fungsional nonlinear umum berikut:
(4.1)
dengan dan secara berturut-turut adalah operator nonlinear dan suatu fungsi yang diberikan.
Metode Adomian memungkinkan untuk memperoleh solusi dari persamaan (4.1) sebagai deret berhingga ∑ dengan menggunakan skema berulang seperti yang ditulis dibawah ini:
dengan adalah polinomial Adomian.
Untuk menentukan konvergensi dari metode dekomposisi Adomian adalah dengan melihat 2 hipotesis berikut, yaitu:
1. Solusi untuk ditentukan sebagai deret fungsi yaitu ∑ . Selain itu, deret konvergen mutlak yaitu ∑| | .
2. Fungsi nonlinear terdapat dalam setiap deret dengan radius konvergensi sama dengan infinity. Dengan kata lain:
∑
| | (4.3)
Hipotesis ini hampir selalu memenuhi dalam masalah fisis yang konkret.
B.Teorema Konvergensi
Pada bagian ini akan dibahas mengenai teorema konvergensi dan pembuktiannya.
Teorema 4.1
Berdasarkan hipotesis 1 dan 2, deret Adomian ∑ merupakan solusi untuk persamaan (4.1) dan memenuhi persamaan (4.2).
Karena ∑ | | berkonvergensi mutlak, maka dapat ditulis
Deret pada persamaan (4.4) adalah konvergen mutlak karena:
∑ [ ∑ ( ) dan dengan demikian deret pada persamaan (4.5) dapat dibentuk kembali.
Hal ini dapat dengan mudah dibuktikan bahwa:
∑ ∑
(4.6)
yang membuktikan bahwa deret Adomian ∑ merupakan perumuman dari deret Taylor. Hal ini membuktikan bahwa memenuhi persamaan (4.2) diatas.
∑ ∑
(4.7)
Persamaan (4.7) di atas dipenuhi jika . Hal ini mengakibatkan adanya hubungan Adomian dalam persamaan (4.2). Teorema terbukti.
C.Kecepatan Konvergensi
Untuk menunjukkan kecepatan konvergensi dari MDA adalah dengan menggunakan lemma beserta buktinya di bawah ini.
Lemma 4.1
‖ ‖ dan ‖ ‖ dengan suatu variabel bebas, maka ∑
merupakan suatu solusi pendekatan persamaan fungsional. Jika deret lengkap diganti dengan deret terpotong yang melibatkan suku , maka galatnya sama dengan .
Bukti
Metode Adomian memberikan hasil yang sangat baik bahkan jika diambil deret terpotong dengan banyaknya suku yang sedikit. Hasil tersebut diperoleh dari analogi deret Adomian dan deret Taylor. Sehingga, diperoleh:
|∑ variabel bebas , dan bahwa juga dibatasi dalam norm oleh suatu , maka galat yang diberikan dibatasi oleh:
(4.10)
71 BAB V PENUTUP
Pada bab ini diberikan kesimpulan mengenai pembahasan pada bab-bab sebelumnya serta saran untuk penelitian selanjutnya.
A. Kesimpulan
Telah dilihat bahwa metode dekomposisi yang ditulis oleh G. Adomian dapat menyelesaikan persamaan nonlinear. Dalam tugas akhir ini penulis menyelesaikan persamaan diferensial parsial nonlinear dengan menggunakan MDA tersebut. Penyelesaian dengan menggunakan MDA ini didukung dengan teori-teori dasar seperti persamaan diferensial, turunan, integral, deret Taylor dan deret Maclaurin serta konsep konvergensi deret Taylor.
Terlihat bahwa penggunaan MDA pada keempat persamaan di atas memperoleh solusi eksak sehingga deret yang diperoleh konvergen sangat cepat ke solusi eksak tersebut dan galat pemotongannya dapat dihitung. Sehingga, deret terpotong yang biasanya melibatkan beberapa suku merupakan solusi pendekatan. Solusi pendekatan ini secara eksplisit bergantung pada variabel ruang dan waktu.
B.Saran
73 DAFTAR PUSTAKA
Adomian, G. (1988). A review of the decomposition method in applied mathematics. Journal of Mathematical Analysis and Applications, 135 (2): 501-544.
Adomian, G. (1998). Solution of nonlinear partial diferential equations. Applied Mathematics Letters, 11 (3): 121-123.
Al-Khaled, K. dan Allan, F. (2004). Construction of solutions for the shallow water equations by the decomposition method. Mathematics and Computers in Simulation, 66 (6): 479-486.
Bermudes, A. Dan Vasquez, E.M. (1994). Upwind methods for hyperbolic conservation laws with source terms. Computation Fluids, 23 (8): 1049-1071.
Cherruault, Y. and Adomian, G. (1993). Decomposition methods: a new proof of convergence, Mathl. Comput. Modelling, 18 (12): 103-106.
Dawson, C. dan Mirabito, M.C. (2008). “The Shallow Water Equations”. http://users.ices.utexas.edu/~arbogast/cam397/dawson_v2.pdf/ Diakses tanggal 28 September 2015.
Dispini, M. and Mungkasi, S. (2016). Adomian decomposition method used to solve the shallow water equations, AIP Conference Proceedings, 1746: 020055.
Martins, R., Leandro, J. and Djordjevic, S. (2016). Analytical solution of the classical dam-break problem for the gravity wave-model equations, Journal of Hydraulic Engineering, 142 (4): 06016003.
Mungkasi, S dan Dheno, M. F. S. (2016). Adomian decomposition method used to solve the gravity wave equations. International Conference on Engineering, Science and Nanotechnology. To appear in AIP Conference Proceeding. Ross, S.L. (1984). Differential Equations. New Delhi: John Wiley and Sons, Inc.
Thomas, G. B. (2010). Thomas’ Calculus Early Transcendentals. Boston: Person Education.
74
Lampiran
Berikut ini adalah code program MAPLE untuk perhitungan persamaan gelombang gravitasi dan persamaan gelombang kinematik dengan menggunakan MDA.
1. Perhitungan untuk persamaan Burger
2. Perhitungan untuk persamaan gelombang air dangkal (PGAD)
>
3. Perhitungan untuk persamaan gelombang gravitasi
4. Perhitungan untuk persamaan gelombang kinematik
>
ABSTRAK
Persamaan diferensial parsial terdiri dari persamaan diferensial parsial linear dan nonlinear. Beberapa model persamaan diferensial parsial nonlinear antara lain adalah persamaan Burger, persamaan gelombang air dangkal (PGAD), persamaan gelombang gravitasi, dan persamaan gelombang kinematik. Agar perhitungan menjadi lebih cepat dan sederhana, PGAD kemudian disederhanakan ke dalam model lain yang salah satunya adalah persamaan gelombang gravitasi dan persamaan gelombang kinematik.
Dalam tugas akhir ini, keempat model persamaan diferensial parsial nonlinear di atas diselesaikan dengan menggunakan metode dekomposisi Adomian (MDA). Dengan menggunakan MDA, solusi persamaan diferensial diasumsikan sebagai jumlahan fungsi atau deret tak hingga fungsi dengan bantuan polinomial Adomian. Polinomial Adomian digunakan untuk menyelesaikan suku nonlinear dalam persamaan diferensial tersebut. Persamaan diferensial harus disertai dengan kondisi awal agar persamaan diferensial tersebut dapat diselesaikan. Kondisi awal yang diberikan tersebut sangat berpengaruh terhadap solusi yang didapatkan.
Sebagai tindak lanjut dari penggunaan konsep MDA dalam keempat persamaan diferensial parsial nonlinear di atas adalah jika terdapat solusi eksak eksplisit dari masalah yang dicari maka deret yang diperoleh konvergen sangat cepat ke solusi tersebut. Solusi pendekatan MDA merupakan solusi yang berasal dari deret terpotong yaitu yang biasanya melibatkan beberapa suku saja. Secara eksplisit, solusi pendekatan tersebut bergantung pada variabel ruang dan waktu.
ABSTRACT
Partial differential equations are of linear and nonlinear. Some models of nonlinear partial differential equations, are Burger equation, Shallow Water Equation (SWE), gravity wave equation, and kinematic wave equation. In order to make the calculation becomes faster and simpler, SWE is simplified into other models, which are gravity wave equation and kinematic wave equation.
In this thesis, the four models of nonlinear partial differential equations are solved by using Adomian Decomposition Method (ADM). By using this method, the solution of differential equation is assumed as the sum of functions or infinite series of functions with the help of Adomian polynomials. Adomian polynomial is used for solving the nonlinear term in the differential equation. The differential equation must be accompanied by an initial condition so that the differential equation can be solved. The initial condition which is given greatly affects the obtained solution.
As the follow-up of the use of the ADM in the four nonlinear partial differential equations above is that if there is an explicit exact solution of the problem, the series converges quickly into the solution. The approximate solution is the solution derived from a truncated series which is usually involving only several terms. Explicitly, the approximate solution depends on the space and time variables.