S
ISTEMP
ERSAMAANL
INIER DANM
ATRIKS1. SISTEM PERSAMAAN LINIER
Secara umum, persamaan linier dengan n variabel (x x1, ,...,2 xn) didefinisikan sebagai persamaan yang dapat dinyatakan dalam bentuk:
1 1 2 2 ... n n a x a x a x b
dengan a a1, ,...,2 an dan b merupakan konstanta riil. Variabel-variabel dalam persamaan linier seringkali disebut sebagai faktor-faktor yang tidak diketahui.
Perlu diperhatikan bahwa persamaan linier tidak mengandung hasil kali atau akar dari variabel. Seluruh variabel yang ada hanya dalam bentuk pangkat pertama dan bukan merupakan argumen dari fungsi-fungsi trigonometri, logaritma, ataupun eksponensial.
Solusi dari persamaan linier a x1 1a x2 2 ... a xn n b adalah suatu urutan bilangan dari bilangan s s1, ,...,2 sn sedemikian sehingga persamaan tersebut akan terpenuhi jika menyubstitusikan x1s x1, 2 s2,...,xn sn. Kumpulan semua solusi dari persamaan itu disebut himpunan penyelesaian (himpunan solusi).
Sistem persamaan linier merupakan sejumlah tertentu persamaan linier dalam variabel
1, ,...,2 n
x x x . Sebarang sistem m persamaan linier dengan n variabel dituliskan sebagai berikut:
11 1 12 2 1 1
21 1 22 2 2 2
1 1 2 2
... ...
... n n
n n
m m mn n m
a x a x a x b
a x a x a x b
a x a x a x b
dengan x x1, ,...,2 xn adalah faktor yang belum diketahui serta a dan b dengan subskrip merupakan konstanta.
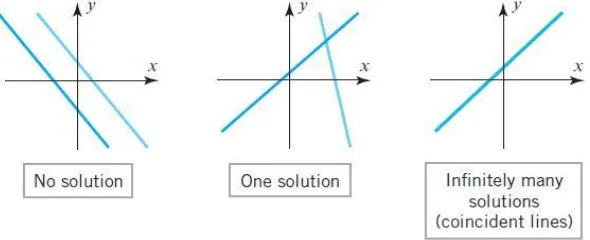
Suatu sistem persamaan linier yang tidak memiliki solusi disebut tidak konsisten, sedangkan jika terdapat paling tidak satu solusi dalam sistem disebut konsisten. Suatu sistem persamaan linier yang konsisten dapat memiliki tepat satu solusi atau memiliki takterhingga banyaknya solusi.
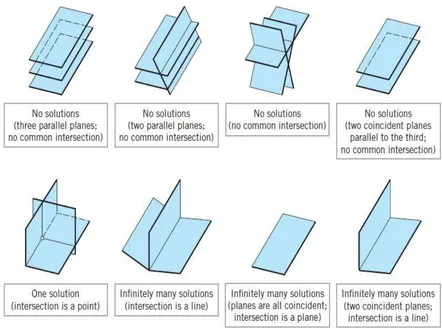
Interpretasi mengenai solusi dari suatu sistem persamaan linier dapat dilihat pada gambar-gambar berikut ini.
Gambar 1.2 Interpretasi geometri suatu sistem persamaan linier dengan tiga variabel
>> SISTEM PERSAMAAN LINIER HOMOGEN
Suatu sistem persamaan linier disebut homogen jika semua bentuk konstantanya adalah 0, yaitu sistem ini memiliki bentuk:
11 1 12 2 1
21 1 22 2 2
1 1 2 2
... 0
... 0
... 0
n n
n n
m m mn n
a x a x a x
a x a x a x
a x a x a x
Setiap sistem persamaan linier homogen adalah konsisten karena semua sistem semacam ini memiliki solusi x10, x2 0, ..., xn 0. Solusi ini disebut solusi trivial. Jika terdapat
solusi lain, maka solusi-solusi tersebut disebut solusi nontrivial.
Karena sistem linier homogen selalu memiliki solusi trivial, maka hanya terdapat dua kemungkinan untuk solusi-solusinya:
sistem tersebut hanya memiliki solusi trivial,
2. MATRIKS
Matriks adalah kelompok bilangan yang disusun dalam suatu jajaran berbentuk persegi atau persegi panjang yang terdiri dari baris-baris dan kolom-kolom. Nama dari suatu matriks biasanya dilambangkan dengan huruf kapital. Beberapa istilah dasar berkaitan dengan matriks yaitu:
a. Baris suatu matriks adalah bagian susunan bilangan yang dituliskan mendatar atau
horisontal dalam matriks.
b. Kolom suatu matriks adalah bagian yang dituliskan tegak atau vertikal dalam
matriks.
c. Elemen / unsur / entri suatu matriks adalah bilangan-bilangan (riil atau kompleks)
yang menyusun matriks itu.
d. Ordo adalah ukuran suatu matriks yang ditentukan oleh banyaknya baris kali
banyaknya kolom. Contoh: matriks A memiliki 2 baris dan 3 kolom, maka ordo matriks itu adalah 2 3 , dan dinotasikan A2 3 .
Secara umum, suatu matriks A dapat ditulis sebagai berikut:
aij menyatakan entri matriks dengan:
i = 1, 2, 3, ..., m j = 1, 2, 3, ..., n
Jika menginginkan notasi yang singkat, maka matriks di atas dapat ditulis sebagai:
a mn. Entri pada baris ke-i dan kolom ke-j pada matriks A juga biasa dinyatakan dengan simbol
A ij sehingga
A ij = aij .Suatu matriks yang hanya terdiri dari satu kolom disebut matriks kolom (vektor kolom), sementara suatu matriks yang hanya terdiri dari satu baris disebut matriks baris (vektor baris).
Dua matriks dikatakan sama (setara) jika kedua matriks memiliki ordo yang sama dan entri-entri yang seletak (bersesuaian) mempunyai nilai yang sama. Dalam notasi matriks, jika A = [aij] dan B = [bij] memiliki ordo yang sama, maka A = B jika dan hanya jika aij = bij untuk
semua nilai i dan j.
>> OPERASI PADA MATRIKS
Jika A dan B adalah matriks-matriks dengan ordo yang sama, maka:
A B
ij A ij B ij aijbij- (A – B) adalah adalah matriks yang diperoleh dengan mengurangkan entri-entri pada A dengan entri-entri yang bersesuaian pada B.
A B
ij A ij B ij aij bijPerkalian skalar dengan matriks yaitu: jika bilangan skalar k dikalikan dengan matriks A, maka kalikan bilangan k dengan semua entri pada A. Jika A = [aij], maka:
ij ij ij k A kA kaPerkalian matriks dengan matriks yaitu: jika matriks A berordo m q dan matriks B berordo q n , maka (A B ) adalah suatu matriks C = [cij] berordo m n yang entri-entrinya
diperoleh dari penjumlahan hasil kali entri-entri pada baris ke-i matriks A dengan entri-entri pada kolom ke-j matriks B yang bersesuian, dengan i1, 2, 3, ...,m dan j1, 2, 3, ...,n. Pernyataan ini dapat ditulis sebagai berikut:
1 1 2 2
1
...
n
ij ik kj i j i j in nj k
c a b a b a b a b
>> SIFAT-SIFAT ARITMETIKA MATRIKS
Dengan mengasumsikan bahwa ordo matriks sedemikian rupa sehingga operasi-operasi tersebut yang disebutkan dapat dilakukan, aturan-aturan aritmetika matriks berikut ini berlaku. Misalkan pula a dan b merupakan suatu skalar/konstanta.
(a) A B B A (Hukum komutatif dalam penjumlahan matriks)
(b) A(B C ) ( A B )C (Hukum asosiatif dalam penjumlahan matriks) (c) A BC( ) ( AB C) (Hukum asosiatif dalam perkalian matriks) (d) A B C( )ABAC (Hukum distributif kiri)
(e) (B C A ) BA CA (Hukum distributif kanan) (f) A B C( ) ABAC
(g) (B C A ) BA CA (h) a B C( )aBaC (i) a B C( )aB aC (j) (a b C ) aCbC (k) (a b C ) aCbC (l) a bC( )(ab C)
(m) a BC( ) ( aB C) B aC( )
>> TRANSPOS MATRIKS
Jika A adalah matriks berordo m n , maka transpos dari A, dinyatakan dengan AT, didefinisikan sebagai matriks n m yang didapatkan dengan mempertukarkan baris-baris dan kolom-kolom dari A, sehingga kolom pertama dari AT adalah baris pertama dari A, kolom kedua dari AT adalah baris kedua dari A, dan seterusnya.
T
ji ij
Jika ordo matriks sedemikian rupa sehingga operasi-operasi berikut dapat dilakukan, dan k merupakan skalar sebarang, maka sifat-sifat transpos ini berlaku.
(a) ( T T)
kA kA dengan k adalah suatu konstanta (e) ( )T T T
AB B A
>> TRACE SUATU MATRIKS
Jika A merupakan suatu matriks persegi, maka trace dari A yang dinyatakan dengan tr(A), didefinisikan sebagai jumlah entri-entri pada diagonal utama A. Trace dari matriks A tidak dapat didefinisikan jika A bukanlah matriks persegi.
Contoh:
>> MATRIKS YANG DIPERBESAR
Jika lokasi-lokasi dari +, x, dan = dapat diingat, maka sistem persamaan linier yang terdiri dari m persamaan linier dengan n variabel
11 1 12 2 1 1
>> ELIMINASI GAUSS-JORDAN
Eliminasi Gauss-Jordan ini lebih dikenal dengan operasi baris elementer (OBE). Langkah-langkah eliminasi Gauss-Jordan dalam suatu sistem persamaan linier adalah:
1. perhatikan kolom paling kiri yang tidak seluruhnya nol,
2. jika perlu, pertukarkan baris paling atas dengan baris lain untuk menempatkan entri taknol pada puncak yang diperoleh pada langkah pertama,
3. jika entri yang kini berada pada puncak kolom yang diperoleh pada langkah awal adalah a, kalikan baris pertama dengan 1/a sehingga terbentuk 1 utama,
4. tambahkan kelipatan yang sesuai dari baris paling atas ke baris-baris di bawahnya sehingga semua entri di bawah 1 utama menjadi 0,
5. tutuplah baris paling atas dan mulailah lagi dengan langkah pertama pada submatriks yang tersisa; lanjutkan langkah ini hingga seluruh matriks berada dalam bentuk eselon baris,
6. mulai dengan baris taknol terakhir dan bergerak ke atas, tambahkan kelipatan yang sesuai dari tiap baris ke baris di atasnya untuk memperoleh nol di atas 1 utama.
Contoh:
Tambahkan –2 kali baris pertama ke baris kedua untuk memperoleh:
2 1
Tambahkan –3 kali baris pertama ke baris ketiga untuk memperoleh:
3 1
Kalikan baris kedua dengan 1
2 untuk memperoleh:
Tambahkan –3 kali baris kedua ke baris ketiga untuk memperoleh:
7 17
7 17
2 kali baris ketiga ke baris kedua dan –2 kali baris ketiga ke baris pertama untuk
memperoleh:
Tambahkan –1 kali baris kedua ke baris pertama untuk memperoleh:
1 2
>> JENIS-JENIS MATRIKS
1. Matriks baris
Matriks baris adalah matriks yang hanya terdiri dari dari satu baris. Sebagai contoh:
2 0 ; −1 3 −5 ; 1 4 6 3 5
2. Matriks kolom
Matriks kolom adalah matriks yang hanya terdiri dari satu kolom. Sebagai contoh:
2
Matriks nol adalah matriks yang seluruh entrinya berupa bilangan 0. Sebagai contoh:
0 0
4. Matriks persegi
Matriks persegi adalah matriks yang banyaknya baris sama dengan banyaknya kolom. Sebagai contoh:
5. Matriks identitas
Matriks identitas (𝐼𝑛) adalah matriks persegi sedemikian sehingga aij 0 jika i j dan 1
ij
1 0
0 1 = 𝐼2 ;
1 0 0 0 1 0 0 0 1
=𝐼3
6. Matriks segitiga atas
Suatu matriks persegi A[ ]aij sedemikian sehingga aij 0 jika i j disebut matriks segitiga atas. Atau, dengan kata lain, matriks segitiga atas adalah matriks yang semua entri di bawah diagonal utamanya merupakan bilangan nol. Sebagai contoh:
7. Matriks segitiga bawah
Suatu matriks persegi A[ ]aij sedemikian sehingga aij 0 jika i j disebut matriks segitiga bawah. Atau, dengan kata lain, matriks segitiga bawah adalah matriks yang semua entri di atas diagonal utamanya merupakan bilangan nol. Sebagai contoh:
8. Matriks diagonal (kuasi-skalar)
Matriks diagonal adalah matriks persegi sedemikian sehingga aij 0 jika i j.
2 0 0 0 −1 0 0 0 0
= diag 2,−1, 0
9. Matriks skalar
Matriks skalar adalah matriks persegi sedemikian sehingga aij 0 jika i j dan
ij
a x (x merupakan suatu skalar) jika i j. Sebagai contoh:
2 0 0 0 2 0 0 0 2
= 2 𝐼(3)
10. Matriks idempoten
Suatu matriks persegi disebut sebagai matriks idempotent jika 2
A A. Sebagai contoh:
4 −2 6 −3
2
= 4 −2 6 −3
11. Matriks involutorik
Suatu matriks persegi disebut sebagai matriks involutorik jika 2
A I . Sebagai contoh:
1 0 0 −1
2
= 1 0 0 1
12. Matriks simetrik
Suatu matriks persegi disebut simetrik jika T
1 2 3 2 0 −4 3 −4 −2
13. Matriks simetrik-miring
Suatu matriks persegi disebut simetrik-miring jika T
A A. Sebagai contoh:
0 2 3
−2 0 −4
−3 4 0
>> MATRIKS INVERS
Jika A adalah matriks persegi, dan jika terdapat matriks B yang ordonya sama dengan matriks A sedemikian rupa sehingga AB = BA = I, maka A disebut matriks nonsingular
(dapat dibalik) dan B disebut sebagai matriks invers dari A. Jika matriks B tidak dapat didefinisikan (atau dengan kata lain, matriks A tidak mempunyai invers), maka A dinyatakan sebagai matriks singular.
TEOREMA 1
Jika B dan C kedua-duanya adalah invers dari matriks A, maka B = C.
Teorema 1 menyatakan bahwa matriks yang dapat dibalik hanya memiliki tepat satu invers.
TEOREMA 2
Matriks
𝐴= 𝑎 𝑏
𝑐 𝑑
nonsingular jika ad – bc ≠ 0, dan inversnya dapat dicari menggunakan rumus berikut:
𝐴−1 = 1
𝑎𝑑 − 𝑏𝑐 −𝑐𝑑 −𝑏𝑎 = 𝑑 𝑎𝑑 − 𝑏𝑐
−𝑏 𝑎𝑑 − 𝑏𝑐 −𝑐
𝑎𝑑 − 𝑏𝑐
𝑎 𝑎𝑑 − 𝑏𝑐
TEOREMA 3
Jika A dan B adalah matriks nonsingular dan berordo sama, maka:
a. 1 1
AA A A I; dimana matriks I adalah matriks identitas
b. 1 1 1
(AB) B A
c. 1 1 1
(BA) A B
d. 1 1
(A ) A
TEOREMA 4
Jika A adalah matriks nonsingular, maka T
A juga merupakan matriks nonsinngular dan
1 1
( T) ( )T
Suatu matriks A berordo 𝑚×𝑛 dikatakan memiliki matriks invers kiri L
Matriks invers kiri (kanan) dari suatu matriks tidaklah bersifat tunggal.
Teorema 5 menyatakan bahwa matriks invers kiri (ataupun kanan) dari suatu matriks tidak hanya memiliki tepat satu invers kiri (ataupun invers kanan), melainkan memiliki banyak kemungkinan. Perhatikan contoh berikut.
1 2
Dari contoh di atas, dapat dilihat bahwa matriks B dan C merupakan matriks invers kiri dari matriks A, tetapi matriks A bukanlah matriks invers kanan dari matriks B maupun C. merupakan matriks nonsingular dan L 1
A A . Akibatnya, pastilah R L A A . Jika A adalah suatu matriks persegi dan mempunyai suatu matriks invers kanan R
A , maka A merupakan matriks nonsingular dan R 1
A A . Akibatnya, pastilah L R A A .
>> MATRIKS ELEMENTER
Selanjutnya akan dipelajari definisi dari matriks tipe khusus yang dapat digunakan untuk melakukan operasi baris elementer melalui perkaliann matriks.
Suatu matriks persegi 𝑛×𝑛 disebut matriks elementer jika matriks tersebut dapat diperoleh dari matriks identitas 𝐼𝑛 dengan melakukan operasi baris elementer tunggal.
Berikut ini terdapat empat matriks elementer dan operasi-operasi yang menghasilkannya.
Ketika suatu matriks A dikalikan dengan sisi kirinya matriks elementer pada E, dampaknya adalah dilakukannya operasi baris elementer terhadap A. Ini merupakan isi dari Teorema 7 berikut.
TEOREMA 7
Jika matriks elementer E diperoleh dengan cara melakukan operasi baris elementer tertentu terhadap 𝐼𝑚, dan jika A adalah matriks 𝑚×𝑛, maka hasil kali EA adalah matriks yang dihasilkan jika operasi yang sama dilakukan terhadap A.
Sebagai contoh, perhatikan matriks berikut.
1 0 2 3
Jika baris ketiga matriks tersebut dijumlah dengan 3 kali baris pertama, maka akan diperoleh:
3 1
Matriks elementer dari operasi ‘b33b1’ terhadap matriks A adalah:
3 1
Berdasarkan Teorema 7, diperoleh:
TEOREMA 8
Setiap matriks elementer merupakan matriks nonsingular (dapat dibalik), dan inversnya juga merupakan matriks elementer.
TEOREMA 9
Jika A adalah matriks 𝑛×𝑛, maka persamaan-persamaan berikut adalah ekuivalen. (a) A merupakan matriks nonsingular.
(b) A𝐱= 𝟎 hanya memiliki solusi trivial.
(c) Bentuk eselon baris tereduksi dari A adalah 𝐼𝑛.
(d) A dapat dinyatakan sebagai hasil kali dari matriks-matriks elementer.
Sebagai aplikasi dari Teorema 9, dapat dicari metode untuk menentukan invers dari suatu matriks nonsingular.
3 2 1
Hal yang perlu diingat adalah, untuk mencari invers dari matriks 𝐴 nonsingular, harus dicari suatu urutan operasi baris elementer yang mereduksi 𝐴 menjadi identitas dan melakukan urutan operasi yang sama terhadap 𝐼𝑛 untuk memperoleh 𝐴−1. Metode sederhana
untuk melakukan prosedur ini diberikan pada contoh berikut.
Contoh:
Tentukan invers dari
Jadi, 1
>> MINOR DAN KOFAKTOR
Jika A adalah suatu matriks persegi, maka minor dari entri 𝒂𝒊𝒋 dinyatakan sebagai 𝑀𝑖𝑗 dan didefinisikan sebagai determinan dari submatriks yang tersisa setelah baris ke-i dan kolom ke-j dihilangkan dari A. Bilangan −1 𝑖+𝑗 𝑀
>> MATRIKS KOFAKTOR DAN MATRIKS ADJOIN
disebut matriks kofaktor dari A dan dinyatakan sebagai cofac(A). Transpos dari matriks ini
disebut matriks adjoin dari A dan dinyatakan sebagai adj(A).
Contoh:
. Tentukan matriks kofaktor dan matriks adjoin dari matriks A !
Kofaktor-kofaktor dari matriks A adalah
11 Jadi, matriks kofaktor dari A adalah
dan matriks adjoin A adalah
L A T I H A N S O A L
1. Manakah dari persamaan berikut yang merupakan persamaan linier? a) x3y7 d) x13 x2 5
b) 1
2 3 1
b x c e) 3a2b c ac 5 c) p12p23p3p4 0 f) ylogx
2. Tentukanlah solusi untuk sistem persamaan linier berikut dengan menggunakan operasi baris elementer.
3. Misalkan A, B, C, D, dan E adalah matriks-matriks dengan ordo berikut:
4 5
A , B4 5 , C5 2 , D4 2 , E5 4
Tentukan apakah pernyataan-pernyataan berikut ini dapat didefinisikan. Bagi yang dapat didefinisikan, berikan ordo matriks hasilnya.
a. BA d. E AC( ) g. ABB
b. E A( B) e. AEB h. ( T )
A E D
c. ACD f. T
E A
4. Selesaikanlah a, b, c, dan d pada persamaan matriks berikut.
8 1
5. Misalkan matriks M dan N diberikan sebagai berikut:
1 2
6. Perhatikan sistem persamaan linier berikut
2
Untuk nilai a berapakah sistem ini: a. tidak memiliki solusi
b. tepat satu solusi
7. Untuk nilai n berapakah, sistem persamaan linier homogen berikut:
memiliki solusi nontrivial?
8. Perhatikan matriks-matriks berikut ini.
1 2
9. Perhatikan matriks-matriks di bawah ini.
3 4 1
10. Tentukan invers dari
0 1 5
11. Tentukanlah matriks kofaktor dan matriks adjoin dari matriks P berikut.