Fakultas Ilmu Komputer
Universitas Brawijaya
3332
Support Vector Regression Untuk Peramalan Permintaan Darah: Studi
Kasus Unit Transfusi Darah Cabang
–
PMI Kota Malang
M. Raabith Rifqi1, Budi Darma Setiawan2, Fitra A. Bacthiar3
Program Studi Teknik Informatika, Fakultas Ilmu Komputer, Universitas Brawijaya Email: 1[email protected], 2[email protected], 3[email protected]
Abstrak
PMI bertanggung jawab untuk memenuhi permintaan darah dari rumah sakit. Pengelola pusat penyimpanan darah memiliki tugas yang sangat penting, yaitu memprediksi sebuah kebutuhan komponen darah untuk meminimalisir penuhnya maupun kekurangan pasokan darah. Darah hanya memiliki masa hidup 35 hari sejak didonorkan. Jika sudah melewati waktu tersebut maka sudah tidak bisa digunakan lagi. Berlebihnya ataupun kekurangan pasokan darah di tempat penyimpaan seharusnya tidak terjadi, karena dapat berdampak pada tingginya angka jumlah pasien meninggal. Demi mengurangi kerugian yang jika terjadi, maka perlu dilakukan penelitian yang menggunakan metode prediksi permintaan darah yang diimplementasikan ke dalam sistem. Salah satunya dengan metode Support Vector Regression yang cocok untuk peramalan permintaan darah. Dalam impelementasikan SVR menggunakan normalisasi data min – max dan menggunakan fungsi kernel RBF. Berdasarkan hasil pengujian untuk metode SVR yang telah dilakukan, hasil nilai MAPE yang paling minimum yakni 3.899% dengan nilai parameter lambda = 10, sigma = 0,5, cLR = 0,01, C =0,1, epsilon = 0,01, jumlah fitur data = 4 dan jumlah iterasi sebanyak 5000, dari 12 data uji yang digunakan. Hasil Nilai MAPE yang dihasilkan <10% dan dapat dikategorikan baik untuk memprediksi jumlah permintaan darah.
Kata kunci: peramalan, permintaan darah, support vector regression, SVR
Abstract
PMI is responsible for meeting blood demand from hospitals. The management of the blood storage center has a very important task, to predict the requirement of blood components to minimize the ex less and the lack of blood supply. Blood has only a life span of 35 days since donated. If it is past the time then it can not be used anymore. Excess or lack of blood supply at the site should not occur, because it can affect the number of patients death. In order to reduce the losses that if it occurs, it is necessary to do research that uses the prediction method of blood predict that is implemented in a system. One of them with Support Vector Regression method that is suitable for blood demand forecasting. Implement SVR using normalized min - max data and use RBF kernel function. Based on the test results for the SVR method that has been done, the result of the minimum MAPE value is 3.899% with the parameter value lambda = 10, sigma = 0.5, cLR = 0.01, C = 0.1, epsilon = 0.01, number of data features = 4 and number of iterations of 5000, of the 12 test data used. The resulting MAPE value is <10% and can be categorized as good for predicting the amount of blood demand.
Keywords: forecasting, blood demand, support vector regression, SVR
1. PENDAHULUAN
Cairan yang terpenting yang ada di dalam tubuh manusia adalah darah. Darah merupakan cairan yang diproduksi dalam tubuh manusia dan berfungsi untuk mengedarkan sari-sari makanan, oksigen serta zat-zat lain yang dibutuhkan, transportasi bahan-bahan kimia yang dihasilkan oleh metabolisme dalam tubuh,
darah yang hilang supaya nyawa seorang tersebut terselamatkan (Rifandi, Setiawan, & Tibyani, 2017).
Dalam waktu berkala, rumah sakit membutuhkan sejumlah komponen darah yang berada dan disediakan oleh PMI untuk memenuhi kebutuhan pasien rumah sakit yang datang dalam kondisi apapun. Pusat penyimpanan darah bertanggung jawab untuk memenuhi permintaan darah dari rumah sakit tersebut. Semua informasi untuk penggunakan terakhir komponen darah oleh sebuah rumah sakit sangatlah penting untuk mengembangkan pengelolaan dan strategi keputusan untuk meningkatkan pemanfaatan sumberdaya tersebut. Strategi keputusan tersebut tidak mudah karena darah serta komponen darah merupakan sumberdaya penting yang mudah rusak (Lang dalam Filho, Cezarino & Salviano, 2012). Dalam darah terdapat sel darah merah atau eritrosit yang hanya memiliki masa hidup 35 hari sejak didonorkan, jika sudah melewati waktu tersebut maka sudah tidak bisa digunakan untuk melakukan transfusi darah ke manusia (Rutherford, Cheng, & Bailie, 2016). Pada dasarnya Palang Merah Indonesia (PMI) sebagai pengelola pusat penyimpanan darah memiliki tugas yang sangat penting, yaitu memprediksi atau memperkirakan kebutuhan komponen darah untuk meminimalisir penuhnya maupun kerugian dikarenakan darah yang terbuang dan rusak (Lang dalam Filho, Cezarino & Salviano, 2012).
Berlebihnya suatu pasokan darah di tempat penyimpanan itu tidak seharusnya terjadi dan kekurangnya pasokan dapat berdampak pada tingginya angka jumlah pasien yang meninggal. Karena pendonor darah merupakan aset langka yang dibatasi waktu untuk mendonorkan darahnya (Belien & Force, 2012). Untuk mengurangi kerugian yang jika terjadi kelebihan dan kekurangan pasokan darah maka perlu dilakukan penelitian yang menggunakan metode untuk membantu menyesuaikan pasokan darah dengan meramalkan permintaan darah.
Ada beberapa metode peramalan dengan model peramalan kuantitatif, salah satunya dengan metode Support Vector Regression. Metode Support Vector Regression yang di terapkan oleh Sethu Vijayakumar dan Si Wu (1999) untuk menyelesaikan permasalahan peramalan yang bentuk regresi (Vijayakumar & Wu, 1999). Metode Support
Vector Regression telah banyak digunakan untuk membantu peneliti di bagian prediksi atau peramalan dan terbukti menghasilkan peramalan dengan tingkat kesalahan cukup rendah. Serta pada algoritme SVR cocok menggunakan data yang nilainya acak atau data yang bermodel data non-linear.
Sebagai rujukan utama dalam penelitian ini yang telah dilakukan oleh (Rifandi, Setiawan, & Tibyani, 2017) dengan topik yang sama yaitu peramalan permintaan darah dengan metode fuzzy time series dan dioptimasikan dengan particle swarm optimization berhasil. Berdasarkan pengujian yang dilakuan menghasilkan optimum bernilai cost (MSE) sebesar 60435,685 serta tingkat akurasi dari kesalahan sistem ini (MAPE) sebesar 7,76457% dari 12 data uji yang digunakan (Rifandi, Setiawan, & Tibyani, 2017). Pada penelitian yang menggunakan Support Vector Regression dalam prediksi harga saham PT. XL Axiata (Yasin, Prahutama, & Utami, 2014) di dapatkan hasil bahwa SVR mempunyai tingkat akurasi 92,47% untuk data training dan 83,39% untuk data testing. Kemudian pada penelitian berikutnya, metode SVR digunakan untuk prediksi harga emas di Pert Mint, Australia dengan cara melihat data sebelumnya untuk membentuk fungsi regresi. Melalui penelitiannya, Dubey membuktikan bahwa peramalan harga emas menggunakan SVR memberikan nilai MAPE terbaik dibandingkan menggunakan metode ANFIS yaitu sebesar 0.0063055 (Dubey, 2016). Berdasarkan permasalahan dan referensi penelitian yang telah dipaparkan, penulis mengusulkan sebuah penelitian dengan judul
“Peramalan Permintaan Darah: Studi Kasus Unit Transfusi Darah Cabang – PMI Kota Malang”. Metode Support Vector Regression digunakan untuk melakukan peramalan permintaan darah. Hasil penelitian ini diharapkan dapat membantu pihak Unit Transfusi Darah dalam menyesuaikan stok darah berdasarkan peramalan yang dilakukan.
2. SUPPORT VECTOR REGRESSION
Jordi, & Saepudin, 2015). Overfitting merupakan perilaku data yang pada saat fase training menghasilkan nilai akurasi peramalan yang hampir sempurna yang sama dengan nilai aktual data (Yasin, Prahutama, & Utami, 2014).Tujuan algoritme SVR yaitu menemukan suatu garis pemisah atau yang disebut Hyperplane terbaik. Hyperplane terbaik dapat ditemukan dari mengukur margin dari hyperplane tersebut. Margin merupakan jarak antara hyperplane dengan data terdekat. Data yang terdekat dari margin disebut dengan support. Setelah memperpanjang SVM menjadi Non-linear ditunjukan dengan persamaan beriku
t:
𝑓(𝑥) = ∑ ( 𝛼𝑙𝑖=1 𝑗∗− 𝛼𝑗) ( 𝐾(𝑥𝑖,𝑥) + 𝜆2) (1)
Seperti kasus klasifikasi, hanya beberapa koefisien ( 𝛼𝑗∗− 𝛼𝑗) yang hasilnya tidak bernilai nol, dan titik data yang sesuai disebut Support Vector (Vijayakumar, & Wu, 1999).
3. ALGORITME SEQUENTIAL LEARNING
Proses sequential learning adalah proses yang terdapat dalam setiap perhitungan fungsi SVR. Salah satu metode yang digunakan untuk mendapatkan garis pemisah/hyperplane yang optimal dalam metode SVR adalah metode sequential yang dikembangkan oleh Vijayakumar. Berikut adalah langkah- langkahnya (Vijayakumar & Wu, 1999):
1. Inisialisasi 𝛼𝑖 = 0, 𝛼𝑖∗= 0, Hitung matrik 𝑅𝑖𝑗 dengan Persamaan 2.
𝑅𝑖𝑗 = (𝐾(𝑥𝑖, 𝑥𝑗) + 𝜆2) 𝑢𝑛𝑡𝑢𝑘 𝑖, 𝑗 = 1, … (2)
Dimana
𝑅𝑖𝑗 = matriks 𝐻𝑒𝑠𝑠𝑖𝑎𝑛, 𝑥𝑖 = data ke − i , 𝑥𝑗 = data ke − j, 𝜆 =Variabel Skalar
Parameter lambda (𝜆) atau variabel skalar adalah menunjukan ukuran skalar untuk pemetaan ruang pada kernel SVR. (Vijayakumar & S. Wu, Si, 1999).
2. Untuk setiap data training , 𝑖 = 1 sampai n dihitung:
3. Menghitung nilai error dengan Persamaan 3, kemudian menghitung nilai delta Alpha star dan delta alpha dengan Persamaan 4, dan menghitung alpha star dan alpha dengan Persamaan 5.
1. 𝐸𝑖 = 𝑦𝑖− ∑ (𝛼𝑛𝑗=1 𝑗∗− 𝛼𝑗) 𝑅𝑖𝑗 (3)
2. 𝛿𝛼𝑖∗= 𝑚𝑖𝑛{𝑚𝑎𝑥[𝛾 (𝐸𝑖− 𝜀), −𝛼𝑖∗], 𝐶 − 𝛼𝑖∗}
𝛿𝛼𝑖 = 𝑚𝑖𝑛{𝑚𝑎𝑥[𝛾 (−𝐸𝑖− 𝜀), −𝛼𝑖],
𝐶 − 𝛼𝑖} (4)
3. 𝛼𝑖∗= 𝛼𝑖∗+𝛿𝛼𝑖∗
𝛼𝑖 = 𝛼𝑖+ 𝛿𝛼𝑖 (5)
Dimana 𝐸𝑖 = nilai error, 𝑦𝑖 = nilai aktual data latih, 𝛼𝑖∗ = lagrange multiplier, 𝛼𝑖 = lagrange multiplier, 𝑅𝑖𝑗 = matriks 𝐻𝑒𝑠𝑠𝑖𝑎𝑛, 𝛿𝛼𝑖∗ = variable tunggal, bukan bentuk dari
perkalian 𝛿 dengan 𝛼𝑖∗, 𝛿𝛼𝑖 = variable tunggal, bukan bentuk dari perkalian 𝛿 dengan𝛼𝑖, 𝛾 = Nilia 𝐿𝑒𝑎𝑟𝑛𝑖𝑛𝑔 𝑅𝑎𝑡𝑒, 𝜀 = parameter epsilon, 𝐶 = parameter kompleksitas. Cara menghitung parameter gama 𝛾 ditunjukan dalam Persamaan 6.
𝛾 =𝑀𝑎𝑥 (𝑀𝑎𝑡𝑟𝑖𝑘 𝐻𝑒𝑠𝑠𝑖𝑎𝑛 )𝑐𝐿𝑅 (6)
Parameter untuk menghitung nilai 𝛿𝛼𝑖∗ dan 𝛿𝛼𝑖 menggunkan 3 parameter yaikni nilai
parameter gama (𝛾), epsilon (𝜀), dan Complexcity (C). Parameter gama (𝛾) merupakan nilai learning rate, untuk mendapatkan nilai gama harus memakai nilai parameter cLR (coefisien Learning Rate). Parameter cLR merupakan konstanta laju pembelajaran. (Vijayakumar & S. Wu, Si, 1999). Selajutnya untuk parameter yang digunakan untuk menghitung nilai 𝛿𝛼𝑖∗ dan 𝛿𝛼𝑖 yakni parameter epsilon (𝜀). Parameter epsilon (𝜀) digunakan dalam mengatur batas kesalahan fungsi f(x), nilai tersebut menyelubungi nilai dari fungsi f(x) sehingga akan menbentuk yang disebut daerah error - zone. Dan jika nilai f(x) melebihi error – zone yang tebentuk makan akan dikenai penalti sebesar dari parameter C yang telah diatur (Furi, Jordi, & Saepudin, 2015). Dan yang terakhir nilai parameter C yakni mempersentasikan batas penalti toleransi terhadap kesalahan peramalan, semakin besar nilai parameter C menjadikan model peramalan semakin tidak mentoleransi kesalahan sehingga memberikan nilai peramlan yang baik(Furi, Jordi, & Saepudin, 2015).
4. Kembali ke langkah ketiga sampai kondisi iterasi maksimum atau max (|𝛿𝛼𝑖|) < 𝜀 𝑑𝑎𝑛 max (|𝛿𝛼𝑖∗| < 𝜀
5. Fungsi regresinya yaitu dengan Persamaan 15.
Dimana
𝛼𝑖∗ = lagrange multiplier, 𝛼𝑖 = lagrange multiplier, 𝑥𝑖 = data ke −i , 𝑥𝑗 = data ke − j,𝜆 = Variabel Skalar.
6. Menghitung nilai evaluasi kerja sistem dengan cara menentukan ukuran kesalahan, pada penelitian ini menggunakan salah satu cara menentukan ukuran kesalahan yakni Mean Absolute Percentage Error (MAPE). Pengukuran nilai MAPE dipilih untuk menguji akurasi karena memberikaan hasil yang relatife lebih akurat (Nugroho & Purqon, 2015). Persamaan MAPE ditunjukan persamaan sebagai berikut (Setiyoutami, Anggraeni, & Kusumawardani, 2012)
:
𝑀𝐴𝑃𝐸 = 1𝑛∑ |𝑦′𝑖−𝑦𝑖𝑦𝑖 |
𝑙
𝑖=1 × 100 (8)
Dimana n = jumlah data uji, 𝑦′𝑖 = Hasil prediksi atau hasil data peramalan pada indeks ke – i =1, 2, 3, …, l,𝑦𝑖 = data sebenarnya (data aktual) pada indeks ke –i =1, 2, 3, …, l,l = nilai banyaknya dimensi data.
4. KERNEL RADIAL BASIS FUNCTION
(RBF)
Untuk mendukung menyelesaikan
permasalahakn non – linear dengan algoritme SVR, maka digunakan fungsi kernel. Untuk memecahkan masalah linear dalam ruang dimensi tinggi, yang harus dilakukan adalah mengganti inner product (𝑥𝑖 dan 𝑥𝑗) dengan fungsi kernel. Keunggulan dari penggunaan fungsi kernel ini yaitu mampu dapat berhubungan dengan ruang fitur berdimensi lebih tinggi tanpa perlu menghitung pemetaan dari secara eksplisit (Furi, Jordi, & Saepudin, 2015). Kinerja dari algoritme SVR ditentukan oleh jenis fungsi kernel yang akan digunakan dan pengaturan parameter kernel (Che, & Wang, 2014). Fungsi yang sering digunakan yakni fungsi kernel Radial Basis Function (RBF) Kernel dengan Persamaan berikut (Furi, Jordi, & Saepudin, 2015):
- Radial Basis Function (RBF) Kernel
𝐾 (𝑥𝑖, 𝑥𝑗) = exp (−2𝜎12) ( 𝑥𝑖− 𝑥𝑗) (9)
Dimana 𝑥𝑖= data ke − i, 𝑥𝑗 = data ke − j,𝜎 = parameter 𝑠𝑖𝑔𝑚𝑎.
Parameter sigma (𝜎) merupakan konstanta dari fungsi kernel Gaussian RBF untuk mengatur persebaran data kedalam dimensi fitur yang lebih tinggi (Furi, Jordi, & Saepudin, 2015).
5. METODOLOGI
5.1 DATA PENELITIAN
Data yang digunakan pada peneletian ini yaitu data permintaan darah dalam bentuk perbulan diperoleh dari Badan Pusat Statistik Kota Malang, yang telah di himpunnya dari Unit Tranfusi Darah Cabang – PMI Kota Malang
terdapat dalam buku “Kota Malang dalam
Angka”. Data yang digunakan Mulai tahun 2010 sampai Tahun 2015. Sebanyak 60 data, yang merupakan jumlah permintaan darah dan komponen darah dalam perbulan mulai dari tahun 2010 hingga tahun 2014. Data tersebut akan dipergunakan untuk data latih dalam penelitian ini yang akan ditunjuukan pada Tabel 1. Kemudian untuk data uji sebanyak 12 data, yang merupakan permintaan darah dan komponen darah dalam bentuk perbulan pada tahun 2015.
diberikan nilai range antara 0 sampai 1 (Saranya, 2013). Rumus normalisasi min - max dijabarkan dalam Persamaan 2.1 berikut: (Fattahi, 2016)
𝑥𝑀==𝑥𝑥− 𝑥𝑚𝑎𝑥− 𝑥𝑚𝑖𝑛𝑚𝑖𝑛 (8)
Dimana 𝑥𝑀 = Hasil normaliasi data yang bernilai range, X = data asli atau dataset, 𝑥𝑚𝑖𝑛 = data minimum dari data asli atau data
set, 𝑥𝑚𝑎𝑥 = data maksimum dari data asli atau data set.
Setelah data dinormalisasi pada hasil akhir data hanya dalam range 0 sampai 1, untuk mengatahui data sebenarnya pada hasil akhir makan di perlukan denormaliasi. Denormaliasi yaitu proses mengembalikan data nilai hasil akhir normalisai ke data asli. Denormalisasi dalam Persamaan 9 berikut:
Denormalisasi = (𝑥𝑀( 𝑥𝑚𝑎𝑥− 𝑥𝑚𝑖𝑛)) + 𝑥𝑚𝑖𝑛 (9)
Dimana 𝑥𝑀 = Hasil normaliasi data yang bernilai range, X = data asli atau data set, 𝑥𝑚𝑖𝑛 = data minimum dari data asli atau data
set, 𝑥𝑚𝑎𝑥 = data maksimum dari data asli atau dataset.
5.2 SUPPORT VECTOR REGRESSION YANG
DIIMPLEMENTASIKAN
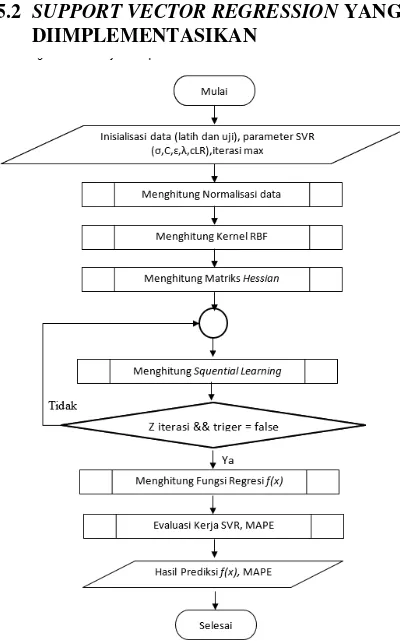
Gambar 1 Diagram Alir Algoritme SVR
Pada parameter di algoritme ini peneliti yang menenetukan parameter- parameter tersebut
yakni lambda, epsilon, cLR (coefiseien Learning Rate), C (complexity), sigma, jumlah fitur data dan jumlah iterasi. Pada implementasi algoritme Support Vector Regression data diambil semua dan di sususn sesuai fitur yang di inputkan. Fitur data disini merupakan data pada bulan sebelumnya. Setelah itu akan diproses
normalisasi menggunakan min – max
Normalization. Setelah perhitungan normalisai kemudian ini sialisai alpha star dan alpha dengan bernilai nol. Kemudian menghitung kernel RBF, didalam kernel RBF terlebih dahulu menghitung jarak dengan cara membandingakan data yang sudah tersusun oleh fitur data yang telah diinputkan, setelahmenghitung jarak menghitung kernel dengan Persamaan 9. Setelah menghitung kernel selanjutnya matrik 𝑅𝑖𝑗 (matriks Hessian) menggunakan Persamaan 2. Selanjutnya setelah mengitung matriks Hessian yakni menghitung nilai error, delta alpha star, delta alpha, serta menghitung update alpha star dan alpha yang termasuk dalam proses Sequetial Learning berulang sampai kondisi terpenuhi. Selnjutnya setalah mendapatkan nilai update alpha star dan alpha makan menghitung fungsi regresi f(x) dengan Persamaan 1. Kemudian setalah mendapatkan nilai fungsi regresinya maka sealnjutnya menghitung denormalisai, dan berikutnya menghitung nilai error rate dengan menggunakan Mean AbsoultePercentage Error (MAPE).
5.3 PENGUJIAN
Perancangan ini dilakukan untuk menguji dan mengevaluasi hasil parameter untuk prekdisi permintaan darah dengan Algoritme support vector regression Adapun beberapa uji coba yang akan dilakukan untuk mengevaluasi sistem yang dibuat, yaitu: 1. Pengujian nilai parameter λ (lambda) SVR. 2. Pengujian nilai parameter σ (sigma) SVR. 3. Pengujian nilai parameter cLR (coefisien
learning rate) SVR.
4. Pengujian nilai parameter C (Complexity) SVR.
5. Pengujian nilai parameter ɛ (epsilon) SVR. 6. Pengujian nilai fitur data pada SVR. 7. Pengujian jumlah iterasi SVR.
tahun 2010 hingga 2014, dan untuk data uji sebanyak 12 diambil dari data permintaan dan komponen darah pada tahun 2015. Serta parameter untuk pengujian selanjutnya akan dilakukan parameter yang terbaik dari pengujian sebelumnya.
6. HASIL DAN PEBAHASAN
6.1 Pengujian Pengujian Nilai Parameter 𝝀
(Lambda)
Pengujian parameter algoritme SVR dilakukan untuk menetukan nilai parameter lambda (λ), terbaik sehingga bisa meghasil solusi atau prediksi yang bagus dan tepat dalam kasus permasalahan ini. Nilai parameter lambda (λ) yang diujikan sesusai dengan perancang sebelumnya. Nilai parameter lain yang dimasukan dalam pengujian ini peneliti terlebih dahulu menentukan nilai yang akan dimasukan, dan nilai parameter lambda (λ) yang akan di masukan dalam pengujian ini sebagai berikut nilai parameter sigma = 0.5, nilai parameter epsilon = 0.00001, nilai parameter C = 10, nilai parameter cLR = 0.01, jumlah iterasi = 5000, jumlah fitur = 4.
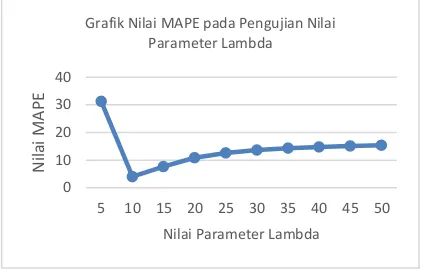
Parameter lambda (𝜆) atau variable skalar adalah menunjukan ukuran skalar untuk pemetaan ruang pada kernel SVR. Nilai parameter lambda semakin tinggi maka semakin baik nilai evaluasi yang diberikan, tetapi beresiko memiliki waktu komputasi yang lama. Karena disebabkan konvergensi yang melambat sering dengan proses learning yang kurang stabil (Vijayakumar, & Wu, 1999). Serta nilai parameter lambda akan menyesuaikan nilai sigma, nilai sigma merupakan parameter dari nilai konstanta kernel RBF Gaussian. Berdasarkan hasil pengujian, diperoleh nilai MAPE yang minimum adalah 4.04 dinyatakan dalam nilai parameter lambda yakni 10. Berdasarkan kriteria nilai MAPE 4.04 dapat dinyatakan nilai MAPE sangat baik. Hal ini menunjukan bahwa nilai parameter lambda dengan nilai parameter kecil bisa menyebabkan nilai penskalaan ruang pemetaan kernel kurang sesuai sehingga nilai error rate meningkat. Sebaliknya jika nilai parameter tinggi maka nilai penskalan ruang pemetaan kernel sesuai, sehingga nilai error rate bisa menurun dapat dilihat pada Gambar 2 pada nilai parameter lambda 10. Namun jika nilai parameter lambda terlalu besar akan menyebabkan proses learning tidak stabil sehingga nilai error ratenya
meningkat. Dapat dilihat pada Gambar 2 seperti nilai parameter 15 sampai 50 proses learning tidak stabil sehingga nilai erro rate
meningkat
.Gambar 2 Grafik Hasil Pengujian Parameter Lambda
6.2 Pengujian Nilai Parameter 𝝈(Sigma)
Pengujian parameter algoritme SVR dilakukan untuk menetukan nilai parameter sigma (σ), terbaik sehingga menghasil solusi atau nilai prediksi yang bagus dan tepat dalam kasus permasalahan ini. Nilai parameter sigma (σ) yang diujikan sesusai dengan perancang sebelumnya. Data yang digunakan pada pengujian ini menggunakan data yang sama serta mengambil nilai parameter yang terbaik dari pengujian selanjutnya.
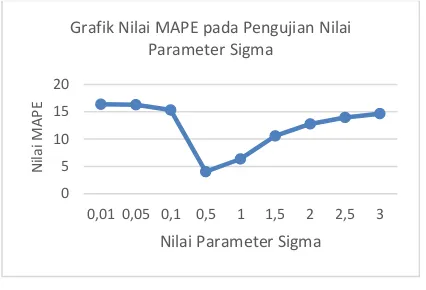
Parameter sigma (𝜎) merupakan konstanta dari fungsi kernel Gaussian RBF untuk mengatur penyebaran data kedalam dimensi fitur yang lebih tinggi (Furi, Jordi, & Saepudin, 2015). Jika sigma bernilai terlalu kecil maka kurva peramalan yang dihasilkan menjadi sangat halus dikurva peramalan yang terbentuk, namun jika terlalu besar maka kurva peramalanya dihasilkan sangat kasar (Kurniasih, Mariani, & Sugiman, 2013). Berdasarkan hasil pengujian yang telah dilakukan, diperoleh nilai MAPE yang minimum yakni 4.04 dinyatakan dalam nilai parameter sigma yakni 0.5. Berdasarkan kriterian nilai MAPE yang terdapat pada nilai MAPE 4.04 dapat dinyatakan nilai MAPE sangat baik. Hal ini menujukkan bahwasanya nilai parameter sigma bernilai lebih kecil menyebabkan memberikan nilai persebaran datanya tidak sesuai dan berakibat nilai error rate meningkat. Sebaliknya nilai parameter sigma sesuai dengan variasi data bisa mengakibatkan nilai prediksi cukup bagus. Tetapi jika nilai parameter sigma terlalu besar menyebakan persebaran data semakin tidak seimbang sehingga nilai prediksi yang dihasilkan tidak sesuai dan nilai pada error rate akan meningkat. Seperti pada nilai Grafik Nilai MAPE pada Pengujian Nilai
penigkatan cukup tinggi sampai sampai nilai parameter sigma bernlai 3.
Gambar 3 Grafik Hasil Pengujian Paramater Sigma
6.3 Pengujian Nilai Parameter cLR
Pengujian parameter algoritme SVR dilakukan untuk menetukan nilai parameter coefisien Learning Rate (cLR), terbaik sehingga akan meghasil solusi atau prediksi yang bagus dan tepat dalam kasus permasalahan ini.Nilai parameter cLR yang diujikan sesusai dengan perancang sebelumnya. Data yang digunakan pada pengujian ini menggunakan data yang sama serta mengambil nilai parameter yang terbaik dari pengujian selanjutnya. Nilai parameter lain yang dimasukan dalam pengujian nilai parameter cLR sebagai berikut, nilai parameter sigma = 0.5, nilai parameter epsilon = 0.00001, nilai parameter C = 10, nilai parameter lambda = 10, jumlah iterasi = 5000, jumlah fitur = 4.
Parameter cLR marupakan konstanta laju pembelajaran, semakin kecil nilai cLR maka proses learning semakin lambat, tetapi nilai yang dihasilkan untuk peramalan lebih baik dan sebaliknya (Vijayakumar, & Wu, 1999). Berdasarkan pada pengujian yang telah dilakukan yang telah digambarkan pada Gambar 4, diperoleh nilai parameter cLR yang minimum dinyatakan pada parameter yang bernilai 0.01, nilia MAPE nilai parameter cLR 0.01 bernilai 4.04. Berdasarkan kriteria nilai MAPE 4.04 dapat dinyatakan nilai MAPE sangat baik. Hal ini menunjukan bahwasanya nilai parameter cLR dengan nilai minimum menghasilkan nilai prediksi yang cukup baik, namun apabila nilai cLR terlalu besar menghasilkan nilai error rate yang meningkat dan hasil prediksi yang buruk. Dikarena bahwa nilai regresi di pengaruhi oleh nilai alpha star dan alpha, sedangkan nilai alpha star dan alpha dipengaruhi oleh nilai gama. Apabila nilai gama keluar dari batas solusi maka, nilai gama tidak akan mendapatkan nilai
alpha star dan alpha yang pas sehingga nilai
akurasinya meninggkat.
Gambar 4 Grafik Hasil Pengujian Parameter cLR
6.4 Pengujian NIlai Paramter C (Complexcity)
Pengujian parameter algoritme SVR dilakukan untuk menetukan nilai parameter complexity (C), terbaik sehingga akan meghasil solusi atau prediksi yang bagus dan tepat dalam kasus permasalahan ini. Nilai parameter Complexity yang diujikan sesusai dengan perancang sebelumnya. Data yang digunakan pada pengujian ini menggunakan data yang sama, serta mengambil nilai parameter yang terbaik dari pengujian selanjutnya. Nilai parameter lain yang dimasukan dalam pengujian nilai parameter complexity (C) sebagai berikut nilai parameter sigma = 0,5, nilai parameter epsilon = 0,00001, nilai parameter cLR = 0,01, nilai parameter lambda = 10, jumlah iterasi = 5000, jumlah fitur = 4.
Parameter C adalah batas penalti toleransi terhadap kesalahan peramalan, semakin besar nilai parameter C menjadikan model peramalan semakin tidak mentoleransi kesalahan sehingga memberikan nilai peramlan yang baik (Furi, Jordi, & Saepudin, 2015). Berdasarkan grafik pengujian pada Gambar 5 nilai MAPE terendah didapatkan pada parameter sigma bernilai 0.1. Hal ini menujukan bahwa nilai parameter C dengan nilai parameter yang besar mendapatkan nilai prediksi yang cukup baik. Penyataan tentang, semakin besar nilai parameter C menjadikan model peramalan semakin tidak mentoleransi kesalahan sehingga memberikan nilai peramlan yang baik (Furi, Jordi, & Saepudin, 2015), terbukti pada hasil pengujian dalam Gambar 5 dimana nilai parameter C mulai nilai parameter C bernilai 0.1 sampai nilai parameter C bernilai 200 memilki nilai error rate terkecil dan konstan. Pada Gambar 5 menunjukan nilai error rate menurun
0 Grafik Nilai MAPE pada Pengujian Nilai
Parameter Sigma
drastis ketika nilai C = 0,05 lalu mendapatkan nilai konstan saat nilai parameter C bernilai 0.1 hingga bernilai 200. .
Gambar 5 Grafik Hasil Pengujian Parameter C
6.5 Pengujian Nilai Parameter Ɛ (Epsilon)
Pengujian parameter algoritme SVR dilakukan untuk menetukan nilai parameter epsilon (Ɛ), terbaik sehingga akan meghasil solusi atau prediksi yang bagus dan tepat dalam kasus permasalahan ini. Nilai parameter epsilon (Ɛ) yang diujikan sesusai dengan perancang sebelumnya. Data yang digunakan pada pengujian ini menggunakan data yang sama, serta mengambil nilai parameter yang terbaik dari pengujian selanjutnya. Nilai parameter lain yang dimasukan dalam pengujian nilai parameter epsilon (Ɛ) sebagai berikut nilai parameter sigma = 0,5, nilai parameter cLR = 0,01, nilai parameter C = 1, nilai parameter lambda = 10, jumlah iterasi = 5000, jumlah fitur = 4.
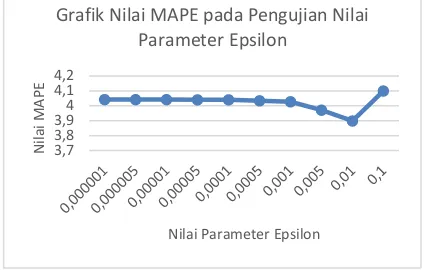
Parameter epsilon (𝜀) digunakan dalam mengatur batas kesalahan fungsi f(x), nilai tersebut menyelubungi nilai dari fugsi f(x) sehingga akan membentuk yang disebut daerah error - zone. Dan jika nilai f(x) melebihi error – zone yang tebentuk makan akan dikenai penalti sebesar dari parameter C yang telah diatur (Furi, Jordi, & Saepudin, 2015). Berdasarkan grafik pengujian pada Gambar 6 nilai MAPE terendah didapatkan pada parameter sigma bernilai 0,01. Hal ini menunjukan bahwasanya nilai epsilon dengan nilai parameter kecil belum tentu memberikan nilai prediksi yang cukup baik. Hal ini akan bergantung pada nilai parameter – parameter yang lain. Nilai parameter epsilon bernilai kecil akan menyebabkan semakin banyak melakukan proses pembelajaran (learning training) serta lama menemukan solusi. Sedangkan nilai epsilon semakin besar nilai toleransi kesalahan mengakibatkan proses pembelajaran (learning training) akan menjadi
singkat dan menyebabkan nilai error rate meningkat. Tetapi jika nilai epsilon terlalu besar menyebabkan pencarian solusinya keluar dari batas seperti nilai parameter epsilon 0,1.
Gambar 6 Grafik Hasil Pengujian Parameter Epsilon
6.6 Pengujian Nilai Fitur Data
Gambar 7 Garfik Pengujian Jumlah Fitur
Pengujian parameter algoritme SVR dilakukan untuk menetukan nilai fitur data (prediksi di mulai pada bulan sebelumnya), terbaik sehingga akan meghasil solusi atau prediksi yang bagus dan tepat dalam kasus permasalahan ini. Nilai parameter fitur data yang diujikan sesusai dengan perancang sebelumnya yakni pada Bab 3. Untuk nilai rentang pada nilai parameter fitur data ini peneliti mengambil nilai rentang 2 – 11 yang diurutkan serta akan diujikan pada pengujian fitur data. Dalam penelitian ini dilakukan sebanyak 6 kali dalam setiap kali pengujian dilakukan maka menggunakan data pengujian yang berbeda tetapi menggunkan nilai parameter yang sama. Nilai parameter lain yang dimasukan dalam fitur datasebagai berikut nilai parameter sigma = 0,5, nilai parameter epsilon = 0,01, nilai parameter cLR = 0,01, nilai parameter lambda = 10, jumlah iterasi = 5000, jumlah Nilai C = 40.
Hasil pengujian nilai MAPE semakin banyak untuk jumlah fitur yang digunakan belum tentu menjamin semakin kecil nilai error rate bernilai
0
Grafik Nilai MAPE pada Pengujian Parameter C
Grafik Nilai MAPE pada Pengujian Nilai Parameter Epsilon
Nilai jumlah Paramter Fitur Data
kecil. Hal tersebut terjadi dapat terpengaruh nilai paramter algoritme SVR dalam memelajari jumlah fitur yang digunakan. Nilai parameter ang lebih sesuai dengan jumlah fitur 4 sehingga menghasilkan nilai prediksi yakni 3,899%. Berdasarkan kriteria nilai MAPE yang terdapat pada Tabel 2.2 nilai MAPE 3,899% dapat dinyatakan nilai MAPE sangat baik. Karena pada pola data pada saat fitur dat bernilai 4 pola data yang diambil secara umum tetap, tetapi jika nilai fitur data kurang atau lebih bernilai maka pola data yang diambil secara umu tidak tetap ataupun berbeda.
6.7 Pengujian Jumlah Iterasi
Gambar 8 Garfik Pengujian Jumlah Iterasi
Pengujian parameter algoritme SVR dilakukan untuk menetukan jumlah iterasi terbaik sehingga, akan meghasil solusi atau prediksi yang bagus dan tepat dalam kasus permasalahan ini. Nilai iterasi yang diujikan sesusai dengan perancang sebelumnya yakni pada Bab 3. Untuk nilai variasi pada nilai jumlah iterasi ini peneliti mengambil nilai dari 10, 50, 100, 500, 1000, 1500, 5000, 5500, dan 10000 yang ditentukan oleh peneliti. Nilai parameter lain yang dimasukan dalam pengujian jumlah iterasi sebagai berikut: nilai parameter sigma = 0,5 , nilai parameter epsilon = 0.01, nilai parameter cLR = 0,01, nilai parameter lambda = 10, jumlah fitur = 4, jumlah Nilai C =1.
Berdasarkan grafik pengujian pada Gambar 8 nilai MAPE terendah didapatkan pada jumlah iterasi 5000. Serta semakin besar jumlah iterasi maka kemampuan observasi pola data pada algoritme SVR akan semakin bagus, namun jika jumlah iterasi terlalu besar maka kemampuan observasi pada pola datapun menjadi tidak stabil dan akirnya error rate akan meningkat. Terlihat pada Gambar 8 bahwa jumlah semakin besar semakin bagus nilai error rate, namun pada iterasi berjumlah 10000 mengalami penanjakan cukup signifikan dikarena jumlah iterasi terlalu
besar dan observasi pada pola data menjadi tidak stabil pada akhirnya nilai error rate meningkat.
6.8 Hasil Penerapan Parameter Optimum
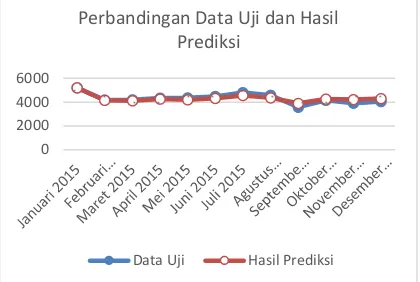
Berdasarkan pengujian yang dilakukan terhadap 12 data uji yang telah ditentukan sebelumnya, tingkat kesalahan peramalan (MAPE) yang dihasilkan oleh sistem yakni 3.899%. Pada Gambar 9 ditunjukkan grafik perbandingan antara data uji dengan hasil peramalannya.
Gambar 9 Grafik Hasil Parameter optimum
7. KESIMPULAN
Berdasarkan hasil pengujian dan analisis yang telah di laksanakan dalam melakakukan penelitian prediksi permintaan darah menggunakan algoritme Support Vector RegressionI (SVR), beberapa kesimpulan yang didapatkan Pengaruh masing – masing parameter terhadap data peramalan permintaan darah menggunakan algoritme Support Vector Regression (SVR) sangat bervariasi. Nilai parameter lambda dan sigma yang bernilai kecil cenderung menghasilkan nilai prediksi yang baik, sedangkan nilai parameter complexity, epsilon dan cLR cenderung besar menghasilkan nilai error rate yang cederung baik. Namun untuk parameter sigma dan lambda jika bernilai terlalu besar rawan menghasilkan nilai MAPE yang tinggi.
Hasil evaluasi kinerja pada algoritme Support Vector Regression untuk peramalan permintaan darah ini menggunakan Mean Absolute Percentage Error (MAPE). Berdasarkan hasil pengujian yang telah dilakukan hasil nilai MAPE yang paling minimum yakni 3,899% dengan nilai parameter lambda = 10, sigma = 0,5, cLR = 0,01, C =0,1, epsilon = 0,01, jumlah fitur data = 4 dan jumlah iterasi sebanyak 5000 yang menggunakan data testing sebanyak 12 data. Hasil Nilai MAPE yang telah di hasil <10% dan dapat
0 2000 4000 6000
Perbandingan Data Uji dan Hasil Prediksi
dikategorikan baik untuk memprediksi jumlah permintaan darah.
Berdasarkan penelitian
prediksi permintaan darah menggunkan
algoritme
Support Vector RegressionI (SVR) yang telah dilakukakan, beberapa saran yang diberikan untuk penelitian selanjutnya antara lain, Menambahkan data untuk data latih dan data uji sehingga mendapatkan prediksi yang sesuai. Menambahkan metode lain yang cocok untuk prediksi serta menambahkan metode optimasi, sehingga dapat meningkatkan hasil prediksi dan menurunkan hasil error yang di hasilkan oleh sistem.8. DAFTAR PUSTAKA
Badan Pusat Statistika Kota Malang. 2011 MALANG DALAM ANGKA: Malang City In figures 2011. Malang: Badan Pusat Statistika Kota Malang.
Badan Pusat Statistika Kota Malang. 2012 MALANG DALAM ANGKA: Malang City In figures 2012. Malang: Badan Pusat Statistika Kota Malang.
Badan Pusat Statistika Kota Malang. 2013 MALANG DALAM ANGKA: Malang City In figures 2013. Malang: Badan Pusat Statistika Kota Malang.
Badan Pusat Statistika Kota Malang. 2014 MALANG DALAM ANGKA: Malang City In figures 2014. Malang: Badan Pusat Statistika Kota Malang.
Badan Pusat Statistika Kota Malang. 2015 MALANG DALAM ANGKA: Malang City In figures 2015. Malang: Badan Pusat Statistika Kota Malang.
Badan Pusat Statistika Kota Malang. 2016 MALANG DALAM ANGKA: Malang City In figures 2016. Malang: Badan Pusat Statistika Kota Malang.
Dubey, A. D., 2016. Gold Price Prediction Using Support Vector Regression and ANFIS Models. International Conference on Computer Communication and Informatics.
Febriana, W. E. & Widodo, D. A., 2012. Analisis Peramalan Kombinasi terhadap Jumlah Permintaan Darah di Surabaya (Studi Kasus: UDD PMI Kota Surabaya). JURNAL SAINS DAN SENI ITS, Volume 1, pp. 20-24.
Fattahi, H., 2016. A Hybrid Support Vector Regression with Ant Colony Optimization
Algorithm In Estimation of Safety Factor For Circular Failure Slope. International Journal of Optimization in Civil Engineering, pp.63-75.
Filho, O. S., Carvalho, M. A., Cezarino, W., Silva, R., & Salviano, G.2013. DemandForecasting for Blood Components Distribution of a Blood Supply Chain. 6th IFAC Conference on management and Control of Production andLogistics (pp. 565-571). Fortaleza: ScienceDirect.
Furi, R. P., Jordi & Saepudin, D., 2015. Prediksi Financial Time Series Menggunakan Independent Component Analysis dan Support Vector Regression Studi Kasus : IHSG dan JII. e-proceding of engineering, Volume 2 , p. 3610.
Nugroho, N. A. & Purqon, A., 2015. PROSIDINGSKF201516-17 Desember 2015Analisis 9 Saham Sektor Industri di Indonesia Menggunakan Metode SVR. PROSIDING SKF , pp. 295 - 300.
Rifandi, A. D. A., Setiawan, B. D. & Tibyani, 2017. Optimasi Interval Fuzzy Time Series Menggunakan Particle Swarm-Optimization Pada PeramalanPermintaan Darah: Studi Kasus unit Tranfusi Daerah Cabang- PMI Kota Malang. Jurnal pengembangan Teknologi Informasi dan Ilmu Komputer, Volume 2 No 7, p. 2770.
Rutherford, C., Cheng, S. Y. & Bailie, K., 2016. Evidence of Bullwhip in the Blood Supply Chain. ResearchGate, p. 1.
Saranya, C., Manikandan, G., 2013. A Study on Normalization Techniques for Privacy Preserving Data Mining. International Journal of Engineering and Technology. Vol. 5 No. 3, Juni-July 2013