Bank Soal Seleksi PTN

(1)

SELEKSI MASUK PERGURUAN TINGGI NEGERI

(UMPTN, SPMB, UM-UGM, SIMAK UI, SNMPTN, SBMPTN)

1992 - 2014

http://m4th-lab.blogspot.com

1.167 BUTIR SOAL

DENIH HANDAYANI, S.Pd

MATH-LAB

http://m4th-lab.blogspot.com

denih_handayani@yahoo.com

Line@ : @llj1225w

▸ Baca selengkapnya: soal seleksi ppih

(2)

PERSAMAAN KUADRAT 1. UMPTN 1992 Rayon A

Jika dan merupakan akar-akar persamaan

, maka

( ) berlaku untuk sama dengan ....

A. 0 atau 12 D. 42 atau 56 B. 2 atau 12 E. 72 atau 90 C. 20 atau 30

2. UMPTN 1992 Rayon B

Akar-akar persamaan kuadrat adalah dan . Persamaan kuadrat dengan akar-akar dan adalah ....

A. B. C. ( ) D. ( ) E. ( ) 3. UMPTN 1992 Rayon C

Akar-akar persamaan kuadrat ( ) adalah dan , jika , maka sama dengan ....

A. 4 D. 1

B. 3 E. 0

C. 2

4. UMPTN 1992 Rayon C

Kedua persamaan dan mempunyai akar-akar real untuk ....

A. D.

B. E.

C.

( ) akan

mempunyai akar-akar yang real jika nilai memenuhi ....

A. D.

B. E.

C.

6. UMPTN 1993 Rayon C

Nilai-nilai agar persamaan kuadrat (

) ( ) mempunyai

akar-akar positif adalah ....

A. D.

B. atau E.

C.

7. UMPTN 1994 Rayon A

Jika dan akar-akar persamaan kuadrat

adalah dan maka

....

A. 2 D. 5

B. 3 E. 6

C. 4

dan adalah akar-akar persamaan kuadrat . Jika , maka nilai yang memenuhi adalah ....

A. 1 D. 7

B. 3 E. 6

C. 4

dan akan

mempunyai satu akar persekutuan jika nilai sama dengan ....

A. D. 1

B. E. 3

C.

Persamaan kuadrat yang akar-akarnya dua kali dari akar-akar persamaan kuadrat adalah .... A. B. C. D. E. 11. UMPTN 1996 Rayon B

Jika persamaan mempunyai akar kembar, maka banyak himpunan bagian dari himpunan penyelesaian adalah ....

A. 0 D. 3

B. 1 E. 4

(3)

dan adalah akar-akar persamaan kuadrat . Jika , maka nikai adalah .... A. D. 12 B. E. 13 C. 13. UMPTN 1996 Rayon C

Jika jumlah kedua akar persamaan ( ) sama dengan nol, maka akar-akar itu adalah ….

A. dan D. 4 dan

B. dan E. 5 dan

C. 3 dan

Akar-akar persamaan yaitu dan . Jika , maka nilai

adalah ….

A. 2 D. 8

B. 4 E. 10

C. 6

15. UMPTN 1997 (Rayon A)

Agar kedua akar persamaan real dan yang satu kebalikan yang lain, maka ….

A. B. atau C. atau D. E. 16. UMPTN 1997 (Rayon B)

Salah satu akar persamaan adalah lima lebih besar dari akar yang lain. Nilai adalah ….

A. atau 1 D. atau 4 B. atau 2 E. atau 5 C. atau 3

17. UMPTN 1997 (Rayon B)

Persamaan kuadrat yang akar-akarnya dua lebih besar dari akar-akar persamaan

adalah …. A. B. C. D. E. 18. UMPTN 1997 Rayon C

Diketahui dan adalah akar-akar persamaan . Persamaan kuadrat yang akar-akarnya dan adalah ….

A. B. C. D. E. 19. UMPTN 1997 Rayon C

dan merupakan akar-akar persamaan kuadrat

. Maka ….

A. 1 D. 3

B. E. 4

C.

20. UMPTN 1997 (Rayon C)

Diketahui persamaan dengan bilangan real. Supaya di dapat dua akar berlainan yang positif, maka harus di penuhi ….

A. D.

B. E.

C.

Jika dan akar-akar persamaan , maka persamaan kuadrat yang akar-akarnya

dan adalah …. A. B. C. D. E. 22. UMPTN 1998 (Rayon A)

Jika dan merupakan akar-akar real persamaan

, maka nilai adalah ….

A. 2 atau D.

B. atau 1 E. C. atau

Selisih kuadrat akar-akar persamaan adalah 6. Nilai adalah ….

(4)

A. D.

B. E.

C.

Persamaan kuadrat mempunyai akar-akar dan dengan dan . Persamaan kuadrat yang akar-akarnya dan adalah …. A. B. C. D. E. 25. UMPTN 1998 (Rayon C) Jika persamaan

mempunyai dua akar yang sama untuk dan , maka ….

A. D. 2

B. E. 7

C.

Jika dalam persamaan diketahui , maka kedua akar persamaan ini….

A. Positif dan berlainan B. Negatif dan berlainan C. Berlawanan

D. Berlainan tanda E. Tidak real

Akar-akar persamaan ( ) ( ) adalah dan . Jika , maka ….

A. atau D. atau B. atau E. atau C. atau

Jika dan akar persamaan kuadrat ( ) , dan √ maka nilai

sama dengan ….

A. 2 atau D. atau 7

B. atau 3 E. 3 atau 7 C. atau 7

Jika jumlah kuadrat akar-akar persamaan sama dengan jumlah pangkat tiga akar-akar persamaan , maka nilai adalah ….

A. 8 D.

B. 6 E.

C.

Jika dan adalah akar-akar persamaan

, maka ( ) ….

A. ( ) D. ( )

B. ( ) E. ( )

C.

Akar-akar persamaan adalam dan . Persamaan kuadrat yang akar-akarnya dan adalah …. A. B. C. D. E. 32. UMPTN 2001 (Rayon A)

Persamaan kuadrat mempunyai akar-akar dan . Persamaan kuadrat yang akar-akarnya dan adalah ….

A. B. C. D. E. 33. UMPTN 2001 (Rayon A) Persamaan kuadrat ( ) mempunyai akar-akar dan , sedangkan persamaan kuadrat yang akar-akarnya dan adalah ( ) Nilai ….

(5)

C. 9

Jika jumlah kuadrat akar-akar real persamaan sama dengan jumlah kebalikan akar-akar persamaan ( ) , maka nilai sama dengan ....

A. 2 D.

B. E. 3

C.

Akar-akar persamaan kuadrat adalah satu lebih kecil dari tiga kali akar-akar persamaan kuadrat . Persamaan kuadrat yang akar-akarnya dan adalah ....

A. B. C. D. E. 36. UMPTN 2001 (Rayon B)

Jika dan akar-akar persamaan maka persamaan yang akar-akarnya adalah ( ) dan ( ) adalah …. A. B. C. D. E. 37. UMPTN 2001 (Rayon B)

Jika dan merupakan akar-akar persamaan kuadrat maka persamaan kuadrat yang akar-akarnya dan adalah …. A. B. C. D. E. 38. UMPTN 2001 (Rayon B)

Jika salah satu akar persamaan kuadrat ( ) ( ) adalah dua kali akar lainnya, maka nilai adalah ....

A. 5 atau D. atau B. 5 atau E. atau

C. 5 atau

Persamaan kuadrat yang masing-masing akarnya tiga kali akar persamaan kuadrat adalah .... A. B. C. D. E. 40. UMPTN 2001 (Rayon B)

Akar-akar persamaan kuadrat adalah dan . Jika , maka nilai adalah ....

A. atau D. 7 atau 2

B. atau E. 7 atau

C. atau

Jika dan merupakan akar-akar persamaan dan ( ) maka nilai .... A. D. 2 B. E. 4 C. 42. UMPTN 2001 (Rayon C)

Jika dan akar-akar dari persamaan | | dan , maka .... A. 4 D. 34 B. 14 E. 49 C. 24 43. SPMB 2002 (Regional I)

Jika persamaan kuadrat ( ) ( ) mempunyai dua akar real yang sama, maka konstanta ....

A. dan D. 2 dan

B. dan 3 E. 3 dan

C. dan 3

44. SPMB 2003 (Regional I)

Jumlah dua bilangan positif adalah 32. Jika jumlah dari kebalikan setiap bilangan tersebut adalah

(6)

maka selisih dari bilangan terbesar dan terkecil adalah …. A. 16 D. 8 B. 12 E. 6 C. 10 45. SPMB 2003 (Regional I)

Jika salah satu akar persamaan kuadrat tiga lebih besar dari salah satu akar

, maka bilangan asli sama dengan ....

A. 1 D. 4

B. 2 E. 5

C. 8

46. SPMB 2003 (Regional II)

Jika dan adalah akar-akar persamaan kuadrat , maka persamaan kuadrat yang akar-akarnya dan adalah ....

A. B. C. D. E. 47. SPMB 2003 (Regional III)

Selisih dua bilangan adalah 10. Pada saat hasil kali kuadrat kedua bilangan itu maksimum, jumlah kedua bilangan tersebut adalah ....

A. D. 0

B. E. 2

C.

48. UM UGM 2003

Jika √ dan √ , maka ….

A. 36 D. 30

B. 34 E. 28

C. 32

Jika dan adalah akar-akar persamaan kuadrat , maka persamaan kuadrat yang akar-akarnya dan adalah ....

A. B. C. D. E. 50. SPMB 2004 (Regional II)

Jika dan dengan adalah akar-akar suatu persamaan kuadrat dan , maka persamaan kuadrat tersebut adalah ....

A. ( ) B. ( ) C. ( ) D. ( ) E. ( ) 51. SPMB 2004 (Regional III)

Akar-akar persamaan kuadrat adalah dan . Jika ( ), maka ....

A. 5 D. 9

B. 7 E. 13

C. 8

52. UM-UGM 2004

Jika dan adalah akar-akar persaman maka persamaan dengan akar-akar

dan dapat difaktorkan menjadi ....

A. ( )( ) B. ( )( ) C. ( )( ) D. ( )( ) E. ( )( ) 53. SPMB 2005 (Regional II)

Fungsi memenuhi persamaan . Agar persamaan ini mempunyai tepat satu akar real, maka konstanta ....

A. 0 D.

B. E. 2

C. 3

54. SPMB 2005 (Regional III)

Akar-akar persamaan kuadrat adalah dan . Jika , maka ....

A. D. 12

B. E. 24

C.

Akar-akar persamaan kuadrat adalah dan . Persamaan kuadrat yang akar-akarnya dan adalah ….

(7)

A. B. C. D. E. 56. UM UGM 2006 Kode 382

Nilai agar persamaan kuadrat mempunyai dua akar berlainan dan positif adalah ….

A. D.

B. E.

C.

Persamaan kuadrat mempunyai akar dan dengan . Persamaan kuadrat yang akar-akarnya ( ) dan ( ) adalah …. A. B. C. D. E. 58. UM UGM 2007

Diberikan dan merupakan akar dari persamaan ( ) . Nilai

minimum bila nilai sama dengan ….

A. D. 1

B. E. 2

C.

59. SNMPTN 2008

Persamaan kuadrat mempunyai akar dan . Jika persamaan kuadrat mempunyai akar dan , maka …. A. D. B. E. C.

60. SNMPTN 2008

Persamaan kuadrat mempunyai akar-akar dan . Jika , maka . . . .

A. atau 1 D. atau B. atau E. atau C. atau

61. SBMPTN 2008

Persamaan kuadrat mempunyai akar dan . Jika dan adalah tiga suku pertama deret aritmatika maka konstanta ....

A. 2 D. 8

B. 4 E. 10

C. 6

62. SNMPTN 2009 Kode 383

Jika kedua akar persamaan

saling berlawanan tanda, tetapi mempunyai nilai mutlak yang sama, maka nilai sama dengan . . . . A. D. B. E. 1 C. 63. SIMAK UI 2009 Kode 921

Misalkan selsih kuadrat akar-akar persamaan

( ) sama dengan 20, maka nilai .... A. D. 5 B. E. 9 C. 64. SIMAK UI 2009 Kode 931

Jika dan adalah akar-akar persamaan kuadrat , maka persamaan kuadrat yang mempunyai akar-akar ( ) dan ( ) adalah …. A. B. C. D. E. 65. SIMAK UI 2009 Kode 951

Misalkan selisih akar-akar dan selisih akar-akar ( ) bernilai sama maka perkalian seluruh akar-akar persamaan kuadrat tersebut adalah ....

A. D. 56

B. E. 72

C.

Persamaan ( ) mempunyai akar-akar dan untuk ....

(8)

B. E.

C.

67. SIMAK UI 2009 Kode 911

Akar-akar persamaan adalah dan . Jika maka nilai .... A. D. 4 B. E. 8 C. 68. SIMAK UI 2010 Kode 203 Persamaan kuadrat ( ) mempunyai akar-akar dan . Jika nilai dari

√ √ , maka hasil kali dari nilai-nilai yang memenuhi adalah ….

A. D. 4

B. √ E. 5

C. √

69. SBMPTN 2013 kode 124

Jika selisih akar-akar ( ) adalah 2, maka nilai adalah ....

A. D. 10

B. E. 20

C.

70. SBMPTN 2013 Kode 221

Persamaan kuadrat ( ) mempunyai akar-akar dan . Jika ( ) maka nilai adalah ….

A. 4 D.

B. 3 E.

C. 2

Persamaan kuadrat dengan , mempunyai akar-akar dan . Jika

mempunyai akar-akar dan maka ....

A. D. 1

B. E. 2

C.

Diketahui dan akar-akar persamaan . Jika dan akar-akar persamaan kuadrat , maka . . . . A. B. C. D. E. 73. SBMPTN 2014 Kode 663

Jika dan akar-akar persamaan kuadrat , maka . . . .

A. 10 D. 6

B. 9 E. 4

C. 7

Jika selisih akar-akar ( ) adalah 2, maka nilai adalah . . . .

A. D. 10

B. E. 20

(9)

FUNGSI KUADRAT

Supaya garis memotong parabola di dua titik, maka nilai harus .... A. atau B. atau C. atau D. E. 2. UMPTN 1992 (Rayon A)

Jika grafik mempunyai titik puncak ( ), maka nilai dan adalah ....

A. D. B. E. C. 3. UMPTN 1994 (Rayon A)

Supaya garis memotong grafik fungsi ( ) , maka haruslah ....

A. D.

B. E.

C.

Jika garis lurus menyinggung parabola ( ) , maka nilai sama dengan ....

A. 1 D. 1 atau 49

B. 49 E. 1 atau

C. atau 49

Jumlah absis titik-titik potong antara grafik fungsi ( ) dan grafik fungsi ( )

adalah ....

A. 1 D. 4

B. 2 E. 5

C. 3

Grafik di bawah ini adalah grafik dari....

A. B. C. D. E. 7. UMPTN 1995 (Rayon B)

Jika suatu fungsi kuadrat ( ) diketahui bahwa ( ) ( ) dan mempunyai nilai maksimum 1, maka ( )adalah ....

A. D.

B. E.

C.

8. Jika grafik fungsi di atas grafik fungsi maka ....

A. D.

B. E.

C.

9. Jarak kedua titik potong parabola dengan sumbu adalah 5 satuan panjang, maka ....

A. D.

B. E.

C.

Supaya grafik fungsi seluruhnya di atas grafik fungsi , maka nilai harus memenuhi ....

A. D.

B. E.

C.

Fungsi kuadrat yang mempunyai nilai minimum 2 untuk dan mempunyai nilai 3 untuk adalah .... A. B. C. D. 1 3 3 2

(10)

E.

12. Parabola dan berpotongan di titik ( ) dan ( ). Jika , maka nilai sama dengan....

A. 2 aatau D. 1 atau B. 2 atau E. 1 atau C. 1 atau

Garis diketahui memotong parabola di titik ( ) dan ( ) Jika

dan , maka nilai dan adalah .... A. dan B. dan C. dan D. dan E. dan 14. UMPTN 1997 (Rayon B)

Garis akan menyinggung parabola jika sama dengan ....

A. 4,5 D.

B. E.

C. 5,5

Garis melalui titik ( ) dan memiliki gradien . Agar memotong grafik pada dua titik yang berbeda, maka haruslah ....

A. B. C. D. atau E. atau 16. UMPTN 1998 (Rayon A)

Jika fungsi ( ) ( ) mencapai nilai tertinggi untuk , maka nilai ....

A. D.

B. E. 1

C.

Nilai tertinggi fungsi ( ) ialah 3, sumbu simetrinya adalah ....

A. D. 2

B. E. 4

C.

Garis memotong kurva di titik puncak . Koordinat titik adalah ....

A. ( ) D. ( )

B. ( ) E. ( )

C. ( )

Nilai minimum fungsi yang ditentukan oleh rumus ( ) adalah 20. Nilai ( ) adalah ....

A. D. 20

B. E. 28

C.

20. Fungsi kuadrat ( ) yang grafiknya melalui titik ( ) dan ( ) serta mempunyai sumbu simetri , mempunyai nilai ekstrim .... A. Minimum 2 D. Maksimum 3 B. Minimum 3 E. Maksimum 4 C. Minimum 4

21. Jika garis menyinggung parabola , maka sama dengan ....

A. D. 2

B. E. 3

C.

Jika fungsi kuadrat mempunyai nilai maksimum 3, maka ....

A. 2 D. 15

B. 6 E. 30

C. 9

Jika fungsi kuadrat mempunyai nilai maksimum , maka ....

A. D. 10

B. E. 20

(11)

24. Jika fungsi ( ) ( ) mempunyai nilai maksimum 8, maka nilai ....

A. 3 D. 3 atau

B. E. 3 atau 21

C.

Garis menyinggung parabola

. Absis puncak parabola

adalah ....

A. D. 1

B. E. 2

C. 1

Fungsi kuadrat yang grafiknya melalui titik ( ) dan titik terendahnya sama dengan puncak dari grafik ( ) adalah ....

A. B. C. D. E. 27. UMPTN 2000 (Rayon A)

Grafik fungsi memotong sumbu di titik-titik ( ) dan ( ). Fungsi ini mempunyai nilai ekstrim ....

A. Maksimum D. Minimum

B. Minimum E. Maksimum

C. Maksimum

28. Fungsi ( ) mempunyai nilai minimum 21 dan memotong sumbu di titik yang berordinat 25. Nilai adalah ....

A. 8 atau D. atau B. 8 atau 6 E. 6 atau C. atau 6

Grafik fungsi kuadrat dan fungsi linear berpotongan pada titik jika .... A. B. C. atau D. E. atau

30. Jika fungsi kuadrat ( ) mempunyai sumbu simetri maka nilai ekstrim fungsi itu adalah ....

A. Maksimum 1 D. Maksimum 9 B. Minimum 3 E. Maksimum 18 C. Maksimum 5

31. Diketahui parabola ( ) dan garis lurus . Jika parabola dan garis lurus itu saling bersinggungan, maka nilai sama dengan ....

A. atau 8 D. atau B. atau 4 E. 2 atau 8 C. 2 atau

32. Fungsi ( ) ( ) ( ) mempunyai nilai maksimum 4. Untuk maka nilai ....

A. D. 64

B. E. 92

C.

Suatu garis lurus mempunyai gradien dan memotong parabola di titik ( ). Titik potong lainnya mempunyai koordinat ....

A. ( ) D. ( )

B. ( ) E. ( )

C. ( )

34. Supaya garis lurus menyinggung parabola , maka nilai adalah ....

A. atau D. 6 atau 2 B. atau E. 12 atau 4 C. atau

Sayrat agar grafik fungsi linear ( ) menyinggung grafik fungsi kuadrat ( ) adalah .... A. B. C. atau D. atau E. atau

(12)

Grafik fungsi ( ) menyinggung sumbu di titik dan memotong sumbu di titik . Panjang ruas garis adalah ....

A. √ D. √

B. √ E. √

C. √

37. SPMB 2005 Regional I Nilai untuk grafik fungsi pada gambar d samping adalah . . . . A. B. C. D. E. 38. SPMB 2005 (Regional I)

Jika fungsi kuadrat ( ) mencapai minimum di titik ( ) dan ( ) maka ( ) ....

A. D.

B. E.

C.

Jika fungsi ( ) ( ) mempunyai nilai maksimum dan nilai minimum , maka .... A. 0 D. 16 B. 4 E. 128 C. √ 40. SPMB 2007 (Regional I) Parabola ( ) ( ) terletak di atas sumbu untuk nilai yang memenuhi ….

A. √ D. √

B. √ E. √

C. √

41. UM UGM 2007

Jika fungsi ( ) mencapai minimum di dan grafik fungsi melalui titik ( ) dan ( ), maka nilai ….

A. 6 D. 12

B. 8 E. 16

C. 10

42. SNMPTN 2008

Parabola memotong sumbu di titik A. jika garis singgung titik A pada parabola memotong sumbu x di titik ( ), maka ….

A. D.

B. E.

C.

Grafik fungsi ( ) dapat diperoleh dengan cara menggeser grafik fungsi ( ) ke arah . . . .

A. Kanan sumbu sejauh 2 satuan dan kearah bawah sumbu sejauh 3 satuan

B. Kiri sumbu sejauh 3 satuan dan kearah atas sumbu sejauh 2 satuan

C. Kanan sumbu sejauh 3 satuan dan kearah bawah sumbu sejauh 2 satuan

D. Kanan sumbu sejauh 6 satuan dan kearah bawah sumbu sejauh 7 satuan

E. Kanan sumbu sejauh 2 satuan dan kearah atas sumbu sejauh 3 satuan

Jika fungsi kuadrat ( ) melalui titik ( ) dan mecapai minimum di titik ( ) maka sama dengan ....

A. D.

B. E.

C.

45. SBMPTN 2013 kode 124

Jika grafik fungsi kuadrat ( ) mempunyai titik puncak ( ) dan memotong sumbu negatif, maka ....

A. dan B. dan C. dan

(13)

D. dan E. dan 46. SBMPTN 2013 Kode 124

Parabola mempunyai titik puncak ( ) Jika dan dua suku pertama

deret geometri tak hingga dengan jumlah tak hingga adalah 9, maka nilai adalah ….

A. D. 3

B. E. 4

(14)

Bagi Anda yang membutuhkan Bank Soal Matematika dalam Format Office Word (dapat diedit) bisa hubungi saya via email denih_handayani@yahoo.com

EKSPONEN

1. UMPTN 1992 (Rayon C) Diketahui ( ) _{. Jika}₍ ₎ ( ) maka .... A. 6 D. B. 5 E. C. 4 2. UMPTN 1993 (Rayon A)

Nilai yang memenuhi persamaan ( ) √ _{adalah ....}

A. D.

B. E.

C.

Jumlah nilai-nilai yang memenuhi dan adalah .... A. D. 15 B. 17 E. 1 C. 4. UMPTN 1994 (Rayon A)

Nilai-nilai yang memenuhi persamaan ( )( )_{adalah ....} A. B. C. D. E. 5. UMPTN 1994 (Rayon A) Jika √ ₍ ) ( ) maka nilai adalah .... A. 7 D. 16 B. 12 E. 33 C. 15 6. UMPTN 1995 (Rayon C) _{nilai dari} _.... A. atau 8 D. atau √ B. atau 4 E. √ atau √ C. atau 4 7. UMPTN 1995 (Rayon C) Jika ( ) _{, maka ....} A. B. atau C. atau D. atau E. 8. UMPTN 1995 (Rayon C) Penyelesaian persamaan ( ) adalah .... A. D. B. E. C. 9. UMPTN 1996 (Rayon A)

Untuk dan yang memenuhi sistem persamaan _dan _{, maka} nilai .... A. 6 D. 15 B. 8 E. 20 C. 10 10. UMPTN 1996 (Rayon B) Bentuk

dapat dituliskan tanpa eksponen

negatif menjadi .... A. ( ) ( ) D. ( ) ( ) B. ( ) ( ) E. ( ) ( ) C. ( ) ( ) 11. UMPTN 1996 (Rayon C)

Nilai yang memenuhi adalah { adalah .... A. D. 1 B. E. C. 12. UMPTN 1998 (Rayon A) ( ) ( ) ....

(15)

A. √ D. √

B. √ E.

C.

Jumlah akar-akar persamaan adalah ....

A. 6 D.

B. 5 E.

C. 0

Bentuk ( ) dapat disederhanakan menjadi ....

A. √ D. √

B. √ E. √

C. √

Jika dan , maka nilai √ .... A. D. 100 B. E. 2.000 C. 16. UMPTN 1999 (Rayon A) ( ) ( ) ( ) …. A. D. B. E. C. 17. UMPTN 1999 (Rayon B)

Nilai yang memenuhi √ (√ ) adalah …. A. atau B. C. D. E. 18. UMPTN 1999 (Rayon C) ( ) ₍ ) ( ) …. A. D. ( ) B. E. C. 19. UMPTN 1999 (Rayon C)

Nilai maksimum nilai mutlak dan minimum nilai mutlak dari pada selang adalah .... A. dan 0 D. dan 0 B. dan 0 E. 9 dan 0 C. dan 0 20. UMPTN 2000 (Rayon A) Diberikan persamaan ( √ ) ( ) √

Jika memenuhi persamaan, maka nilai …. A. D. B. E. C. 21. UMPTN 2000 (Rayon B)

Jika dan adalah akar-akar persamaan _{, maka nilai} …. A. 0 D. B. 2 E. C. 22. UMPTN 2000 (Rayon C)

Jumlah semua nilai yang memenuhi persamaan ₍ ₎_{adalah ….}

A. 0 D. 3

B. 1 E. 4

C. 2

23. UMPTN 2001 (Rayon B) Nilai yang memenuhi

( )( ) adalah .... A. atau B. atau C. D. E.

(16)

Nilai yang memenuhi _{adalah ….}

A. D. B. E. C. 25. SPMB 2003 (Regional I) Jika maka ( ) ( ) ( ) .... A. D. B. E. C. 26. SPMB 2003 (Regional I)

Nilai yang memenuhi persamaan √ _{adalah ....} A. D. 1 B. 1 E. 2 C. 27. SPMB 2003 (Regional II) Nilai dari (√ √ √ )( √ √ √ )(√ √ ) …. A. D. 2 B. E. 4 C. 28. UM-UGM 2003

Nilai yang memenuhi persamaan ( ) √ adalah .... A. D. 3 B. E. 5 C. 2 29. SPMB 2004 (Regional I)

Jika , maka dinyatakan dalam dan adalah ....

A. D.

B. E.

C.

Jika dan memenuhi sistem persamaan ; _{maka nilai} adalah .... A. 0 D. 4 B. 2 E. 5 C. 3 31. SPMB 2004 (Regional I)

Nilai yang memenuhi persamaan _{adalah ....}

A. D.

B. E.

C.

Nilai yang memenuhi persamaan (√ ) adalah ....

A. 4 D.

B. 2 E.

C. 0

Nyatakan bentuk berikut dalam pangkat positif dan bentuk akar, .... A. √ √ D. (√ √ ) B. √ √ E. (√ √ ) C. √ √ 34. SPMB 2004 (Regional II)

Nilai yang memenuhi persamaan (√ ) ( ) adalah ....

A. D. 2

B. E. 4

C. 1

Jika bilangan bulat, maka nilai dari

.... A. D. B. E. C. 36. SPMB 2004 (Regional II)

Nilai yang memenuhi persamaan

( )

(17)

A. D. 1

B. E. 2

C.

Penyelesaian dari persamaan √ adalah .... A. D. 4 B. 2 E. 5 C. 38. SPMB 2004 (Regional III) Penyelesaian √ adalah .... A. D. 1 B. 1 E. 2 C. 39. SPMB 2004 (Regional III) Penyelesaian persamaan √ adalah .... A. D. 1 B. 1 E. 2 C. 40. SPMB 2004 (Regional III) Penyelesaian persamaan adalah .... A. * + D. * + B. * + E. * + C. * + 41. UM-UGM 2004

Jika memenuhi persamaan ( √ ) √ ( ) , maka .... A. D. B. E. C. 42. UM-UGM 2004

Bila dan maka nilai √ √ .... A. D. 16 B. 6 E. 20 C. 43. UM-UGM 2004 Jika ( √ √ ) ( ) (_√) ( ) maka sama dengan .... A. 0 D. B. E. 1 C. √ 44. UM-UGM 2004 ( √ )( √ ) √ .... A. √ D. 15 B. 19 E. √ C. √ 45. UM-UGM 2004

Jika memenuhi persamaan ₍ ₎ _, maka sama dengan ....

A. D.

B. E. 0

C. 46. UM-UGM 2004

Jika dan memenuhi sistem persamaan { Maka .... A. D. 1 B. 1 E. 2 C. 47. SPMB 2005 (Regional II)

Nilai yang memenuhi persamaan ( ₎ ₍ ₎ _{adalah ....}

A. D.

B. E.

C.

Nilai yang memenuhi persamaan √ adalah .... A. D. 5 B. E. 6 C.

(18)

Nilai yang memenuhi persamaan √( ) ( ) adalah .... A. D. 0 B. E. 1 C. 50. SPMB 2005 (Regional III) Jika √ , maka .... A. 0 D. √ B. E. √ C. 3 51. SPMB 2005 (Regional I) Jika ( ) _dan_{( )} _, maka ( ) ( ) ... A. D. B. E. C. 52. SMPB 2006 Regional I Jika ( √ ) dan ( √ ) , maka ( ) _{( )} _…. A. 1 D. 6 B. 2 E. 8 C. 4 53. SMPB 2006 Regional I Jika ( ) ( ) dan ( ) ( ) maka …. A. √ D. √ B. √ E. √ C. 54. UM UGM 2006 Kode 382

Bentuk sederhana dari √ √ adalah ….

A. √ √ D. √ √

B. √ √ E. √ √

C. √

55. UM UGM 2006 Kode 382

Diberikan dan bilangan real dengan dan . Jika dan . Maka nilai adalah ….

A. 0 D. 4

B. 1 E. 5

C. 3

56. UM UGM 2006 Kode 382 Bentuk sederhana dari: ( ) ( ) ( ) ( ₎ adalah …. A. D. B. E. C. 57. SMPB 2006 (Regional I)

Nilai yang memenuhi ( √ ) ( √ ) adalah …. A. atau D. atau B. atau E. atau C. atau 58. SMPB 2007 (Regional I) Solusi persamaan ( ) √ adalah …. A. D. B. E. C. 59. SNMPTN 2008

Dalam bentuk pangkat rasional √ √ √ . . . . A. D. B. E. C. 60. SNMPTN 2008

Dalam bentuk positif , ( ) …. A. ( )( ) B. ( )( ) C. ( ) D. ( ) E. ( ) 61. SNMPTN 2008

Nilai x yang memenuhi persamaan √ adalah ….

(19)

A. D. B. E. 2 C. 62. SNMPTN 2008 Jika √ √ √ , maka …. A. 1 D. 4 B. 2 E. 5 C. 3 63. SIMAK UI 2009 Kode 911 √ √ √ .... A. √ D. 1 B. √ E. 0 C. √ 64. SIMAK UI 2009 Kode 911

Jika dan merupakan akar-akar persamaan _maka _.... A. D. -1 B. E. -3 C. 1 65. SIMAK UI 2009 Kode 911 Nilai dari: √ √ √ √ √ √ √ .... A. 10 D. 7 B. 9 E. 6 C. 8 66. SIMAK UI 2009 Kode 921 Jika √ √ dan √ √ maka .... A. 0 D. 10 B. 1 E. 14 C. 8 67. SIMAK UI 2009 Kode 931 ( ) _{adalah ….} A. B. atau C. D. atau E. 68. SIMAK UI 2009 Kode 941 Himpunan penyelesaian dari ( ) ( ) adalah …. A. * + D. * + B. * + E. * + C. * + 69. SIMAK UI 2010 Kode 203

Bilangan bulat terkecil yang memenuhi pertidaksamaan (√ ) ( ) √ adalah …. A. D. 6 B. E. 7 C. 70. SBMPTN 2013 kode 124 Jika maka .... A. √ D. 3 B. √ E. 6 C. √ 71. SBMPTN 2014 Kode 663 Jika , dengan maka . . . . A. 0 D. 3 B. 1 E. 4 C. 2

(20)

LOGARITMA

Jika memenuhi persamaan Dengan demikian sama dengan .... A. atau 3 D. atau 1 B. atau 3 E. atau C. atau 2

Jika memenuhi persamaan maka sama dengan ....

A. 4 D.

B. 2 E.

C. 1

jika dan memenuhi persamaan : maka .... A. 5 D. 110 B. 6 E. 1.100 C. 60 4. UMPTN 1993 (Rayon A) Jika

, maka ( | |) dapat ditentukan untuk .... A. B. C. D. atau E. atau 5. UMPTN 1993 (Rayon B) Penyelesaian persamaan:

( ) adalah dan . Maka ....

A. D.

B. E.

C.

Jika ( ) ( ) maka nilai maksimum ( ) sama dengan .... A. 302 D. 318 B. 306 E. 324 C. 212 7. UMPTN 1994 (Rayon A) Untuk dan . .... A. D. B. E. C. ( ) 8. UMPTN 1994 (Rayon A)

Hasil kali semua nilai yang memenuhi persamaan . √ ( )_/_{adalah ....}

A. 144 D. 5

B. 100 E. 6

C. 72

9. UMPTN 1944 (Rayon B) Hasil kali akar-akar persamaan :

( )_{adalah ....}

A. D. 3

B. E. 9

C. 1

Jika dan maka .... A. D. B. E. C. 11. UMPTN 1994 (Rayon B)

Nilai yang memenuhi persamaan

( ) ( ) adalah .... A. D. 3 B. 3 E. 2 C. 2 12. UMPTN 1994 (Rayon C)

Jika dan adalah akar-akar persamaan ( )_{, maka}_{sama dengan ....}

A. _{D. 10}

B. _{E. 100}

(21)

Jika dan adalah akar-akar persamaan ( ( )) ( ) maka nilai dari | | adalah ....

A. D. B. E. C. 14. UMPTN 1994 (Rayon C) . / . / . / .... A. D. B. E. 1 C. 15. UMPTN 1995 (Rayon A)

Semua nilai yang memenuhi pertidaksamaan ( ) adalah .... A. D. B. E. C. 16. UMPTN 1995 (Rayon A) Jika , nilai .... A. D. B. E. C. 17. UMPTN 1995 (Rayon A)

Nilai yang memenuhi persamaan :

( ) ( ) adalah .... A. √ D. B. 3 E. C. √ 18. UMPTN 1995 (Rayon A) Diketahui deret A. Deret hitung dengan beda B. Deret hitung dengan beda C. Deret ukur dengan perbandingan D. Deret ukur dengan perbandingan E. Bukan deret hitung maupun deret ukur

19. UMPTN 1995 (Rayon A) Jika ( ) _{, maka ....} A. B. atau C. D. atau E. 20. UMPTN 1995 (Rayon B) Jika ( ) ( ) ( ) maka .... A. ( √ ) atau ( √ ) B. ( √ ) atau ( √ ) C. ( √ ) atau ( √ ) D. ( √ ) atau E. ( √ ) atau 21. UMPTN 1995 (Rayon B)

Himpunan jawab pertidaksamaan ( ) adalah .... A. * | + B. * | + * | + C. * | + D. * | + * | + E. * | + * | + 22. UMPTN 1995 (Rayon B) Jika ( ) maka ( ) . / sama dengan .... A. D. B. 9 E. C. 7 23. UMPTN 1995 (Rayon A)

Diketahui sistem persamaan dan . Nilai dan yang memenuhi persamaan itu mempunyai jumlah ....

A. 225 D. 75

B. 150 E. 50

(22)

Jika dan adalah akar-akar persamaan :

( ) , maka ( ) adalah .... A. 39 D. 19 B. 29 E. 9 C. 20 25. UMPTN 1996 (Rayon A)

Himpunan penyelesaian pertidaksmaan ( ) adalah .... A. * | + B. * | + C. * | + D. * | + E. * | + 26. UMPTN 1996 (Rayon B) Jika .

/ , maka nilai yang memenuhi adalah ....

A. D. 3

B. E. 4

C. 2

Nilai-nilai yang memenuhi ( ) adalah .... A. D. B. E. atau C. 28. UMPTN 1996 (Rayon C) Jika ( ) maka .... A. D. 1 B. E. 2 C. 29. UMPTN 1996 (Rayon C) Nilai yang memenuhi

adalah .... A. atau B. C. D. atau E. atau 30. UMPTN 1997 (Rayon A) Jika dan maka .... A. 144 D. 1.024 B. 272 E. 1.040 C. 528 31. UMPTN 1997 (Rayon A)

jika , dan positif, maka adalah .... A. 0 D. B. 1 E. C. 2 32. UMPTN 1997 (Rayon A) dipenuhi untuk sama dengan .... A. 8 D. 2 B. 6 E. 1 C. 4 33. UMPTN 1997 (Rayon B) Jika ( ) , maka .... A. D. B. E. C. 34. UMPTN 1997 (Rayon B)

Jika , maka sama dengan .... A. D. B. E. C. 35. UMPTN 1997 (Rayon B)

Jumlah dari penyelesaian persamaan : sama dengan ....

A. D.

B. E.

(23)

36. UMPTN 1997 (Rayon C) Jika ( ) maka .... A. D. ( ) B. E. ( ) C. ( ) 37. UMPTN 1997 (Rayon C) Jika maka sama dengan .... A. 3 D. B. E. atau C. atau 38. UMPTN 1997 (Rayon C) Jika _{, maka}_.... A. D. B. E. C. 6 39. UMPTN 1998 (Rayon A) .... A. D. B. E. C. 40. UMPTN 1998 (Rayon A) Jika dan ( ) , maka .... A. 28 D. 16 B. 22 E. 12 C. 20 41. UMPTN 1998 (Rayon A)

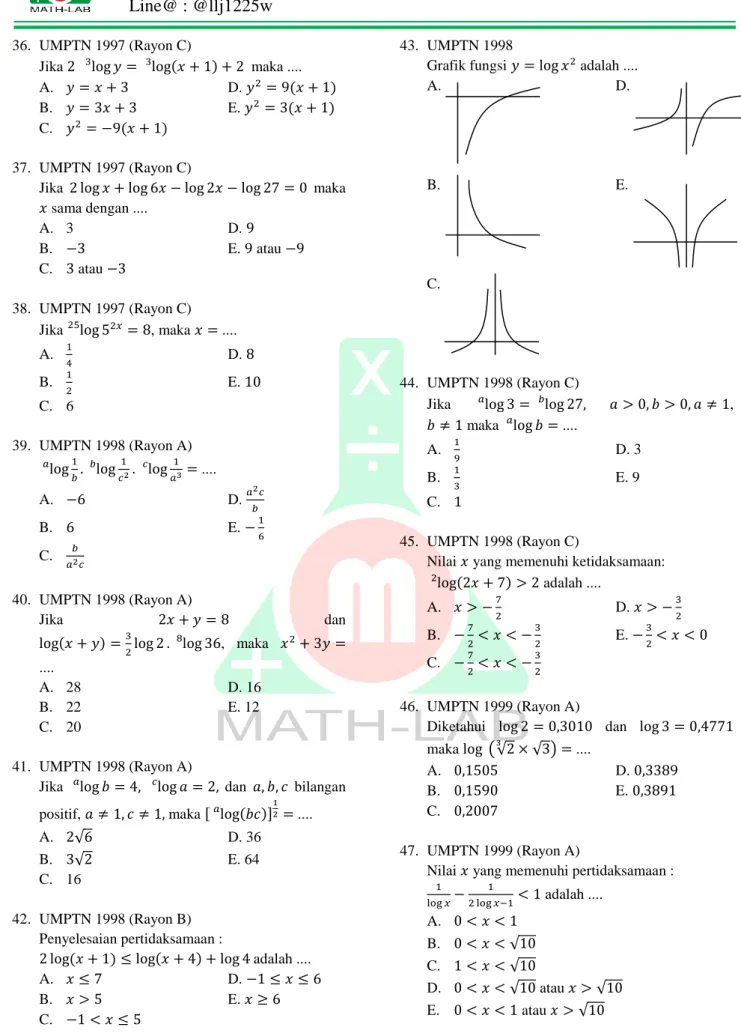
Jika dan bilangan positif, maka , ( )- .... A. √ D. 36 B. √ E. 64 C. 16 42. UMPTN 1998 (Rayon B) Penyelesaian pertidaksamaan : ( ) ( ) adalah .... A. D. B. E. C. 43. UMPTN 1998

Grafik fungsi adalah ....

A. D. B. E. C. 44. UMPTN 1998 (Rayon C) Jika , maka .... A. D. 3 B. E. 9 C. 45. UMPTN 1998 (Rayon C)

Nilai yang memenuhi ketidaksamaan: ( ) adalah .... A. D. B. E. C. 46. UMPTN 1999 (Rayon A) Diketahui dan maka ( √ √ ) .... A. D. B. E. C. 47. UMPTN 1999 (Rayon A)

Nilai yang memenuhi pertidaksamaan : adalah .... A. B. √ C. √ D. √ atau √ E. atau √

(24)

Jika dan bilangan-bilangan positif dengan

dan ; , maka ( ) adalah .... A. ( ) . / B. ( ) . / C. ( ) . / D. ( ) . / E. ( ) . / 49. UMPTN 1999 (Rayon B)

Nilai yang memenuhi persamaan: { adalah .... A. B. ( ) C. D. E. 50. UMPTN 1999 (Rayon B) Nilai-nilai yang memenuhi

( ) adalah .... A. √ √ B. C. √ atau √ D. atau E. atau √ 51. UMPTN 1999 (Rayon B)

Nilai-nilai yang memenuhi adalah .... A. B. C. atau D. atau E. 52. UMPTN 1999 (Rayon C)

Nilai yang memenuhi persamaan : ( ) _{adalah ....} A. 42 D. B. 41 E. C. 39 53. UMPTN 2000 (Rayon B)

Jika dan memenuhi persamaan: ( ) maka .... A. √ D. √ B. √ E. √ C. √ 54. UMPTN 2000 (Rayon B) Nilai yang memenuhi:

( ) ( ) ( ) adalah .... A. ( ) D. 10 B. ( ) E. 1 C. ( ) 55. UMPTN 2000

Nilai yang memenuhi persamaan:

( ₎_{adalah ....}

A. D. atau

B. E. atau

C.

Jika dan maka .... A. D. B. E. C. 57. UMPTN 2000 (Rayon C)

Jika dan memenuhi persamaan:

( )_{, maka nilai} _....

A. D.

B. E.

C.

Nailai maksimum dari ( ) ( ) ( ) adalah ....

(25)

B. 4 E. 16 C. 6

Jumlah akar-akar persamaan sama dengan ....

A. 10 D. 0

B. 6 E.

C. 2

Jika dan maka ....

A. 40 D.

B. E.

C.

Nilai yang memenuhi ( ) dengan adalah .... A. B. atau C. D. atau E. 62. UMPTN 2001 (Rayon A) Jika , maka ... A. D. B. E. ( ) C. 63. UMPTN 2001 (Rayon A) Jika dan , dan maka .... A. D. ( ) B. E. ( ) C. 64. UMPTN 2001 (Rayon B)

Jika dan , maka ( )_{( )} A. 2 D. B. 4 E. C. 65. UMPTN 2001 (Rayon B) Jika dan , maka .... A. D. 5 B. 3 E. 6 C. 4 66. UMPTN 2001 (Rayon B) Jika , maka .... A. ( ) D. B. ( ) E. C. 67. UMPTN 2001 (Rayon B)

Jika maka nilai ....

A. D. 4

B. E. 5

C.

Pertidaksamaan ( ) mempunyai penyelesaian untuk ....

A. B. C. 5 atau D. atau E. 69. UMPTN 2001 (Rayon B) Nilai yang memenuhi :

| ( ) ( ) | adalah .... A. D. B. E. C. 70. UMPTN 2001 (Rayon C) Jika √ , maka .... A. D. B. E. C.

(26)

Nilai yang memenuhi dengan adalah .... A. B. C. atau D. E. 72. SPMB 2002 (Regional I)

Jika , dan maka √ √ .... A. D. 2 B. E. 3 C. 1 73. SPMB 2002 (Regional III) Jika . / maka .... A. D. B. E. C. . / 74. SPMB 2003 (Regional I) Jika , maka .... A. D. B. E. C. 75. SPMB 2003 (Regional II)

Nilai yang memenuhi persamaan ( ) √ adalah .... A. 16 atau 4 D. 8 atau B. 16 atau E. 8 atau 4 C. 8 atau 2 76. UM-UGM 2003 (Regional I) Jika , maka .... A. D. B. E. C. 77. SPMB 2004 (Regional III) Jika maka penyelesaian

( ( ))( √ ) adalah ....

A. 1 D. 4

B. 2 E. 5

C. 3

Jika dan memenuhi persamaan ( ) ( ) ( ) , maka .... A. 81 D. 120 B. 96 E. 144 C. 108 79. SPMB 2004 (Regional I)

Jika dan , maka .... A. D. B. E. C. 80. SPMB 2004 (Regional II) Jika , maka .... A. D. ( ) B. E. ( ) C. ( ) 81. SPMB 2004 (Regional II) ( ) ( ) √ .... A. D. 4 B. 1 E. 5 C. 2 82. SPMB 2004 (Regional II)

Jika dan ( ) maka nilai adalah ....

A. 25 D. 28

B. 26 E. 30

C. 27

83. UM-UGM 2004

Jika dan dengan memenuhi persamaan , dan maka ....

(27)

A. 12 D. 8

B. 10 E. 6

C. 9

Nilai yang memenuhi persamaan ( ) _{adalah ....}

A. 1 D. 1 atau 4

B. 4 E. 2 atau 4

C. 1 atau 2

Jika dan maka .... A. D. ( ) B. E. ( ) C. ( ) 86. SMPB 2006 Regional I Jika , maka …. A. D. B. E. C. 87. SMPB 2006 Regional I Jika ( ) , maka ∑ ( ) …. A. 46 D. 52 B. 48 E. 54 C. 50 88. UM UGM 2006 Kode 382

Jika memenuhi ( ) dan memenuhi ( ( ))( ) maka nilai adalah …. A. 16 D. 9 B. 13 E. 4 C. 10 89. SMPB 2007 (Regional I)

Jika dan adalah akar-akar persamaan: ( ) maka …. A. 0 D. 1000 B. 10 E. 1100 C. 100 90. SNMPTN 2008

Jika ( √ ) dan . / maka . . . . A. D. B. E. C. 91. SNMPTN 2008 ( ) ( ) mempunyai akar-akar dan dengan maka . . . .

A. 0 D. 3

B. 1 E. 4

C. 2

92. SNMPTN 2008

Deret geometri tak hingga

( ( )) ( ( )) ( ( )) ...

Mempunyai jumlah untuk x yang memenuhi

A. D.

B. E.

C.

93. SNMPTN 2008

Jika dan maka …. A. D. B. E. ( ) C. ( ) 94. SIMAK UI 2009 Kode 921 Misalkan ( ) dan ( )

_{untuk semua} _dalam domain, maka nilai adalah ....

A. D. B. E. 2 C. 95. SIMAK UI 2009 Kode 951 ( )( ) ( )( ) ( )( ) ... A. D. 2 B. E. 3

(28)

C.

Jika ( ) merupakan penyelesaian dari sistem berikut: ( ) ( ) Maka nilai …. A. 2 D. 9 B. 4 E. 13 C. 5 97. SIMAK UI 2010 Kode 203 Nilai …. A. 0 D. 5 B. 1 E. 6 C. 2 98. SIMAK UI 2010 Kode 204 Jika ( ) ( ) , maka √ √ …. A. 1 D. 5 B. 2 E. 16 C. 4 99. SBMPTN 2013 kode 124 Jika dan , maka nilai adalah .... A. 8 D. 2 B. 6 E. 1 C. 4 100.SIMAK UI 2010 Kode 205

Jika memenuhi persamaan , maka

…. A. atau D. atau B. 4 atau E. 2 atau C. 1 atau 101.SBMPTN 2013 Kode 427 Jika dan , maka nilai adalah . . . . A. 8 D. 2 B. 6 E. 1 C. 4 102.SBMPTN 2014 Kode 652

Jika dan , maka .... A. D. B. E. C. 103.SBMPTN 2014 Kode 652

Jika dan adalah penyelesaian persamaan ( ) maka .... A. 2 D. B. E. C. 104.SBMPTN 2014 Kode 663 Diketahui ( ) . Jika dan penyelesaian persamaan ( ) ( ) ( ) ( ) ( ), maka . . . .

A. D.

B. E.

(29)

TURUNAN (DIFERENSIAL)

Diketahui fungsi ( )

. Garis singgung grafiknya pada memotong sumbu di titik ( ). Nilai adalah . . . .

A. 2 D.

B. E.

C.

Untuk memproduksi unit barang per hari diperlukan biaya ( ) rupiah. Jika barang itu harus harus diproduksikan, maka biaya produksi per unit yang paling rendah tercapai bila per hari diproduksi . . . .

A. 1.000 unit D. 3.000 unit B. 1.500 unit E. 4.000 unit C. 2.000 unit

Koordinat titik-titik singgung pada kurva ( ) yang garis singgungnya sejajar dengan garis adalah . . . . A. ( ) dan ( ) B. ( ) dan ( ) C. ( ) dan ( ) D. ( ) dan ( ) E. ( ) dan ( ) 4. UMPTN 1992 Rayon B Fungsi ( ) mempunyai . . . . A. Maksimum di dan minimum di B. Minimum di dan maksimum di C. Maksimum di dan minimum di D. Minimum di dan maksimum di

E. Maksimum di dan minimum di 5. UMPTN 1993 Rayon A

Jika garis singgung pada sejajajr dengan garis singgung pada , maka koefisien arah garis singgung tersebut adalah . . . A. 2 D. 16 B. 12 E. 20 C. 14 6. UMPTN 1993 Rayon B Jika , maka . . . . A. B. C. D. E. 7. UMPTN 1993 Rayon C Jika , maka . . . . A. B. C. D. E. 8. UMPTN 1993 Rayon A

Dua kandang berdampingan masing-masing dengan ukuran m , m, dan luasnya 12 m2. Agar panjang pagar yang diperlukan sesedikit mungkin maka panjang dan berturut-turut adalah . . . . A. 2 m dan 6 m D. 3 m dan 4 m B. 6 m dan 2 m E. 23 m dan 23 m C. 4 m dan 3 m 9. UMPTN 1993 Rayon A Jika ( ) ( ) maka ( ) adalah . . . . A. ( ) D. B. ( ) E. C. 10. UMPTN 1994 Rayon C

Nilai ekstrim fungsi ( ) ( )( ) dicapai pada . . . . A. dan B. dan C. dan D. dan E. dan 11. UMPTN 1995 Rayon A Diketahui ( ) . Jika ( ) , maka nilai haruslah . . . .

(30)

B.

C.

D. atau E. atau 12. UMPTN 1995 Rayon A

Jika dan akar-akar persamaan maka mencapai nilai minimum untuk sama dengan . . . .

A. D. 2

B. E. 1

C.

Persamaan garis singgung di titik ( ), pada kurva adalah . . . . A. B. C. D. E. 14. UMPTN 1995 Rayon A Fungsi mencapai maksimum untuk nilai . . . .

A. D.

B. E. 3

C.

Fungsi turun untuk nilai-nilai . . . .

A. D.

B. E.

C.

Kurva ( ) naik untuk nilai-nilai . . . . A. B. C. D. 3 atau E. 17. UMPTN 1996 Rayon B

Persamaan garis yang menyinggung kurva di titik ( ) adalah . . . .

A. D.

B. E.

C.

Persamaan garis yang tegak lurus garis singgung kurva di titik ( ) adalah . . . .

A. B. C. D. E. 19. UMPTN 1996 Rayon A

Seekor semut merayap pada bidang . Pada saat ia berada di titik ( ( ) ( )) dengan ( ) dan ( ) . Semut itu akan berjarak minimum ke sumbu pada saat jarak semut itu dari sumbu sama dengan . . . .

A. 2 D. 5

B. 3 E. 6

C. 4

Sebuah roda berputar mengelilingi titik pusatnya. Sudut simpangan setiap titik pada roda tersebut pada waktu dirumuskan sebagai berikut:

( )

Besar sudut pada waktu kecepatan sudutnya sama dengan nol adalah . . . .

A. 198 D. 75 B. 195 E. 50 C. 190 21. UMPTN 1997 Rayon A Jika ( ) , maka turunan _{( )}_{adalah . . .} . A. ( ) D. ( ) B. ( ) E. ( ) C. ( ) 22. UMPTN 1997 Rayon A

Titik belok dari fungsi adalah . . . .

(31)

B. ( ) E. ( ) C. ( ) 23. UMPTN 1997 Rayon A Diketahui ( ) dan ( ) jika ( ) ( ) ( ), maka ( ) adalah . . . . A. D. B. E. C. 24. UMPTN 1997 Rayon A Sebuah pintu berbentuk seperti gambar. Keliling pintu sama dengan . Agar luas pintu maksimum, maka sama dengan . . . . A. D. B. E. C. 25. UMPTN 1997 Rayon C Jika ( ) ( √ ) , maka ( ) . . . . A. √ B. √ C. √ D. √ E. √ 26. UMPTN 1997 Rayon B

Grafik dari mempunyai garis singgung mendatar pada titik singgung . . . .

A. ( ) D. ( ) dan

( )

B. ( ) E. ( ) dan ( ) C. ( ) dan ( )

Jika fungsi ( ) ( ) mencapai nilai tertinggi untuk , maka nilai . . . .

A. D.

B. E. 1

C.

Persamaan garis yang menyinggung kurva pada titik dengan absis adalah . . . . A. D. B. E. C. 29. UMPTN 1998 Rayon A Jika ( ) dan ( ) , ( ) , maka . . . . A. 0 D. 2 B. 1 E. C. 30. UMPTN 1998 Rayon B

Persamaan garis lurus yang menyinggung grafik ( ) di titik ( ) adalah . . . . A. D. B. E. C. 31. UMPTN 1999 Rayon A Jika ( ) , dan ( ) adalah turunan ( ), maka ( ) . . . . A. D. 1 B. E. 2 C. 32. UMPTN 1999 Rayon A

Diberikan kurva dengan persamaan . Kurva turun pada . . . .

A. atau B. atau C. D. E. 𝑥 𝑥 𝑥

(32)

Diberikan suatu kurva dengan persamaan ( ) dengan ( ) untuk . Nilai maksimum dari ( ) adalah . . . .

A. 4 D. 7

B. 5 E. 8

C. 6

Persamaan garis yang melalui titik ( ) dan membentuk segitiga di kuadran pertama dengan luas terkecil adalah . . . .

A. ( ) B. ( ) C. ( ) D. ( ) E. ( ) 35. UMPTN 1999 Rayon C

Jika nilai stasioner dari ( ) adalah , maka . . . .

A. 0 atau 1 D. 1

B. 0 atau E.

C. 0 atau

Jarak yang ditempuh sebuah mobil dalam waktu diberikan oleh fungsi ( ) . Kecepatan tertinggi mobil itu dicapai pada waktu . . . .

A. 5 D. 2

B. 4 E. 1

C. 3

Jika nilai maksimum fungsi √ adalah 4, maka . . . .

A. 3 D. 7

B. 4 E. 8

C. 5

Garis singgung di titik ( ) pada kurva ( ) √ memotong sumbu dan sumbu di titik ( ) dan ( ). Nilai . . . .

A. D. B. E. C. 39. UMPTN 2000 Rayon C

Sebuah benda berputar pada sumbunya. Pada waktu setiap jari-jari roda itu sudah menjalani sudut sebesar . Kelajuan perubahan kecepatan sudutnya . . . .

A. Selalu semakin tinggi B. Selalu makin rendah

C. Makin tinggi hanya pada D. Makin rendah hanya pada E. Paling tinggi pada 40. UMPTN 2001 Rayon A

Turunan dari ( ) ( ) adalah . . . .

A. ( )( ) B. ( )( ) C. ( )( ) D. ( )( ) E. ( )( ) 41. UMPTN 2001 Rayon A

Jarak terpendek titik ( ) ke titik pada parabola adalah . . . .

A. √ D. √

B. √ E. √

C. √

Turunan fungsi √( ) adalah . . . . A. √ D. √ B. √ E. √ C. √ 43. UMPTN 2001 Rayon B

Suatu proyek pembangunan gedung sekolah dapat diselesaikan dalam hari dengan biaya proyek per hari ( ) ratus ribu rupiah. Agar biaya proyek minimum maka proyek tersebut diselesaiakn dalam waktu . . . .

A. 40 hari D. 120 hari B. 60 hari E. 150 hari C. 90 hari

(33)

Jika fungsi ( ) pada selang mempunyai nilai maksimum dan nilai minimum , maka nilai . . . .

A. 78 D. 108

B. 88 E. 118

C. 98

Rusuk suatu kubus bertambah panjang dengan kelajuan 7 cm per detik. Kelajuan bertambahnya volume pada saat rusuk panjangnya 15 cm adalah . . . . . A. B. C. D. E. 46. UMPTN 2001 Rayon B

Jika ( ) √ , maka nilai ( ) . . . .

A. D.

B. E.

C.

Persamaan garis singgung di titik dengan pada kurva √ adalah . . . . A. B. C. D. E. 48. UMPTN 2001 Rayon C

Jika ( ) merupakan invers dari fungsi

( )

dan ( ) adalah turunan dari _{( )}_{, maka}_{( )}_{. . . .} A. D. B. E. C. 49. UMPTN 2001 Rayon C

Jika ( ) merupakan turunan ( ) √ maka nilai ( ) . . . . A. D. B. E. C. 50. SPMB 2002 Regional I

Turunan pertama dari adalah . . . .

A. D. B. E. C. 51. SPMB 2002 Regional II Bila maka . . . . A. D. B. E. C. 52. SPMB 2002 Regional II

Grafik fungsi ( ) untuk yang memenuhi . . . . A. atau B. C. D. atau E. 53. SPMB 2002 Regional III

Suatu perusahaan menghasilkan produk dengan biaya total sebesar rupiah. Jika semua produk perusahaan tersebut terjual dengan harga Rp40,00 untuk setiap produknya, maka laba maksimum yang diperoleh adalah . . . .

A. Rp3.535,00 D. Rp3.550,00 B. Rp3.540,00 E. Rp3.555,00 C. Rp3.545,00

54. SPMB 2003 Regional I

Grafik fungsi ( ) √ naik untuk nilai yang memenuhi . . . .

A. D.

B. E.

C.

Dari karton berbentuk persegi dengan sisi cm akan dibuat sebuah kotak tanpa tutup dengan cara

(34)

menggunting empat persegi di pojoknya sebesar cm. volume kotak maksimum untuk . . . .

A. atau D.

B. E.

C.

56. UM-UGM 2003

Jika fungsi ( ) hanya didefinisikan untuk nilai-nilai yang memenuhi dan mencapai nilai maksimum pada saat , maka nilai adalah . . . .

A. 6 D.

B. E. 3

C.

Turunan pertama dari fungsi ( ) ( ) ( ) adalah ( ) . . . .

A. D.

B. E.

C.

Nilai maksimum dari fungsi ( ) ( ) adalah . . . .

A. 8 D. 24

B. 12 E. 32

C. 16

Jumlah dari bilangan pertama dan kuadrat bilangan kedua adalah 75. Nilai terbesar dari hasil kali kedua bilangan tersebut adalah . . . .

A. 50 D. 250

B. 75 E. 350

C. 175

Fungsi ( ) turun untuk nilai yang memenuhi . . . . A. D. B. E. atau C. 61. SPMB 2004 Regional I Funsi ( )

turun untuk nilai yang memenuhi . . . . A. B. atau C. atau D. atau E. atau 62. SPMB 2004 Regional II

Fungsi ( ) turun untuk semua nilai yang memenuhi . . . .

A. D. B. E. C. 63. SPMB 2004 Regional II Fungsi ( ) mencapai . . . . A. Maksimum di ( ) B. Maksimum di ( ) C. Minimum di ( ) D. Minimum di ( ) E. Minimum di ( ) 64. SPMB 2004 Regional II

Kurva naik untuk nilai yang memenuhi . . . . A. atau B. atau C. D. E. 65. SPMB 2004 Regional II

Jika kurva mencapai nilai minimum di titik ( ) maka . . . .

A. D. 2

B. E. 3

C.

66. SPMB 2004 Regional II

Jika garis menyinggung kurva √ di titik yang berabsis 1, maka garis akan memotong sumbu di titik . . . .

A. ( ) D. ( )

B. ( ) E. ( )

C. ( )

67. SPMB 2004 Regional III

Fungsi ( ) turun untuk nilai yang memenuhi . . . .

(35)

A. D.

B. E.

C.

Grafik fungsi ( ) naik untuk nilai yang memenuhi . . . . A. B. C. D. atau E. atau 69. SPMB 2004 Regional III

Persegi panjang terletak pada segitiga siku-siku , dan , maka maka luas minimum adalah . . . . A. 16 B. 18 C. 20 D. 22 E. 24 70. SPMB 2004 Regional I

Sika siku-siku sama kaki, dan , maka luas minimum dari segi empat adalah . . . . A. 50 B. 100 C. 125 D. 150 E. 200 71. SPMB 2004 Regional II

Jika siku-siku sama kaki, dan , maka luas minimum dari segi empat adalah . . . . A. 3,75 B. 4,00 C. 6,00 D. 6,75 E. 8,00 72. UM-UGM 2004

Nilai maksimum dari fungsi trigonometri ( ) ( ) adalah . . . .

A. D. 5

B. 1 E.

C. 0

Pada selang , fungsi mempunyai nilai maksimum . . . .

A. D.

B. E. 8

C.

Pada selang , jarak terjauh dari kurva ( ) dengan sumbu adalah . . . . A. 1 D. 8 B. 2 E. 16 C. 4 75. SPMB 2005 Regional I Jika ( ) , maka ( ) . . . . A. D. B. E. 2 C. 76. SPMB 2005 Regional II

Turunan pertama dari fungsi ( ) adalah ( ) . . . . A. D. B. E. C. 77. SMPB 2006 Regional I

Nilai minimum dari fungsi adalah ….

A. D.

B. 13 E.

C. 12

78. SMPB 2006 Regional I

Grafik melalui titik ( ). Jika grafik turunannya ( ) melalui titik ( ) maka konstanta dan adalah …. A. dan B. dan C. dan 𝑆 𝑃 𝑄 𝑇 𝑅 𝑈

(36)

D. dan E. dan 79. UM UGM 2006 Kode 382 Jika ( ) dengan maka ( ) …. A. ( ( )) B. ( ( )) C. ( ( ( )) ) D. ( ( )) E. ( ( )) 80. UM UGM 2006 Kode 382 Jika ( ) . Maka adalah …. A. B. √ C. √ D. √ √ E. √ √ 81. UM UGM 2006 Kode 382

Jika fungsi didefinisikan pada , maka nilai terbesar dari adalah ….

A. 3 D.

B. E.

C. 5

82. SPMB 2007 (Regional I) Jika ( )

, maka turunan fungsi di 0 adalah ( ) ….

A. D. 1

B. E.

C.

Suatu proyek dapat dikerjakan selama hari , dengan biaya setiap harinya ( ) juta rupiah. Jika biaya minimum proyek tersebut adalah R juta rupiah, maka ….

A. 750 D. 14000

B. 940 E. 1750

C. 1170 84. SNMPTN 2008

Jika ( ) , maka fungsi turun untuk semua yang memenuhi . . . . A. atau B. atau C. atau D. atau E. 85. SNMPTN 2008

Nilai minimum dari fungsi ( )√ adalah ….

A. -2 D. 1

B. -1 E. 2

C. 0

86. SNMPTN 2008

Turunan pertama dari fungsi adalah …. A. ( ) B. ( ) C. ( ) D. E. 87. SIMAK UI 2009 Kode 911, 931

Jika kurva ( )( ) turun pada interval maka nilai ....

A. D. 2

B. E. 3

C.

88. SIMAK UI 2009 Kode 911, 921 Gunakan petunjuk C

Diberikangrafik fungsi ( ) , maka ....

(1) ( ) tidak ada

(2) Fungsi naik di selang ( ) (3) Fungsi turun di selang ( )

(37)

Luas persegi panjang terbesar yang dapat dibuat dalam daerah yang dibatasi kurva dan adalah …. A. 20 satuan luas B. 16 satuan luas C. √ satuan luas D. satuan luas E. √ satuan luas 90. SIMAK UI 2009 Kode 931 Jika ( )( )( )( ), maka untuk adalah …. A. D. 2 B. E. 8 C. 91. SIMAK UI 2010 Kode 204

Sebuah tempat air terbuat dari plat baja yang berbentuk separuh tabung (sesuai gambar). Bagian atas terbuka dan kapasitasnya liter. Agar

bahan pembuatnya sehemat mungkin, nilai …. meter.

A. 1 D. 50

B. 5 E. 100

C. 10

92. IMAK UI 2010 Kode 205

Jika diketahui ( ) | |, maka laju perubahan ( ) pada saat , di mana

akan sama dengan ….

A. ( ) D. _{( )} B. ( ) E. ( ) C. _{( )} 93. SIMAK UI 2010 Kode 205 Diketahui ( ) ( ) , nilai maksimum dari fungsi tersebut adalah ….

A. 2 D. 5

B. 3 E. 6

C.

Diketahui ( ) dan ( ) . Jika ( ) ( ( ) ) , maka ( ) ....

A. D. 8

B. E. 12

(38)

LIMIT FUNGSI

1. UMPTN 1992 Rayon A ( ) √ A. 0 D. B. E. C. 2. UMPTN 1992 Rayon B _{√ √} A. 0 D. √ B. E. C. 1 3. UMPTN 1992 Rayon C √ √ A. D. B. E. 1 C. 4. UMPTN 1993 Rayon A Jika √

maka sama dengan . . . . A. 3 D. B. 2 E. C. 1 5. UMPTN 1994 Rayon A ( ) ( ) A. ( ) D. ( ) B. ( ) E. ( ) C. ( ) 6. UMPTN 1994 Rayon A (√( )( ) ) A. D. B. E. C. 0 7. UMPTN 1994 Rayon B ( √ ) A. D. B. 0 E. 2 C. 8. UMPTN 1994 Rayon C

Nilai dari √ adalah . . . .

A. D. B. E. C. 0 9. UMPTN 1995 Rayon A ( ) ( ) ( ) A. D. B. E. C. 0 10. UMPTN 1995 Rayon B ( ) A. D. 3 B. E. 5 C. 11. UMPTN 1995 Rayon C ( ) A. 0 D. B. E. 4 C. 12. UMPTN 1996 Rayon C √ √ A. 0 D. √ B. E. C. √ 13. UMPTN 1996 Rayon A ( ) A. 5 D. 9 B. 6 E. C. 8

(39)

14. UMPTN 1996 Rayon B √ √ √ √ A. 0 D. B. E. C. √ 15. UMPTN 1997 Rayon A A. 2 D. B. 1 E. C. 0 16. UMPTN 1997 Rayon A √ A. 1 D. B. E. C. 17. UMPTN 1997 Rayon B A. D. B. E. 2 C. 18. UMPTN 1997 Rayon B √ √ A. √ D. √ B. √ E. √ C. √ 19. UMPTN 1997 Rayon C √ √ A. √ D. √ B. √ E. C. 20. UMPTN 1997 Rayon A √ √ A. 0 D. B. E. 2 C. 21. UMPTN 1997 Rayon C √ A. D. B. E. C. 0 22. UMPTN 1997 Rayon C √ A. D. B. E. C. 23. UMPTN 1998 Rayon A ( ) A. D. B. E. C. 24. UMPTN 1998 Rayon B Nilai ( ) adalah . . . . A. 1 D. B. E. C. 25. UMPTN 1998 ( )( ) ( )( ) A. D. 5 B. E. C. 2 26. UMPTN 1998 Rayon C A. D. 3 B. E. 6 C. 2

(40)

27. UMPTN 1998 Rayon C Nilai adalah . . . . A. 0 D. 6 B. 2 E. C. 4 28. UMPTN 1998 Rayon A √ √ ( ) A. D. B. E. C. 29. UMPTN 1998 Rayon B √ A. 30 D. B. 1 E. C. 0 30. UMPTN 1998 Rayon C A. D. B. E. C. 31. UMPTN 1999 Rayon A ( ) A. D. B. E. C. 32. UMPTN 1999 Rayon B √ A. D. 1 B. 0 E. 4 C. 33. UMPTN 1999 Rayon B ( ) A. D. B. E. C. 34. UMPTN 1999 Rayon C √ √ A. 0 D. 1 B. √ E. C. 35. UMPTN 1999 Rayon C A. 32 D. 8 B. 24 E. 4 C. 16 36. UMPTN 2000 Rayon A √ √ A. √ D. √ B. √ E. √ C. 37. UMPTN 2000 Rayon A A. D. B. 1 E. C. 38. UMPTN 2000 Rayon B A. 0 D. 1 B. E. 2 C. √ 39. UMPTN 2000 Rayon B Jika ( ) , maka ( ) ( ) A. D. 6 B. 0 E. 9 C. 3 40. UMPTN 2000 Rayon B √ √