MODEL MATEMATIKA PENYEBARAN PENYAKIT DEMAM
BERDARAH DENGUE
JUMADI
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
BOGOR
2008
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis Model Matematika Penyebaran Penyakit Demam Berdarah Dengue adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Agustus 2008
J u m a d i NIM 060051
ABSTRACT
JUMADI. Mathematical Model of Dengue Disease Transmission. Under direction of PAIAN SIANTURI and N. K. KUTHA ARDANA
Dengue disease was transmitted to human through infected mosquito Aedes Aegypti. It was found widely in the tropical regions of the world. Infection of dengue virus could be grouped into two mechanisms. The first mechanism was vertical transmission in mosquito body, where virus could be transmitted by female mosquito into her eggs. The second mechanism was transmission from mosquito into human body and conversely. In this study, mathematical models were used to study the behavior of the transmission of dengue disease. The mathematical model of the disease with assumption of healthy mosquito eggs was compared to the modified mathematical model of dengue disease assuming that some of mosquito eggs were infected by dengue virus. The seasonal influence, especially temperature, was considered in the analysis. The standard dynamical analysis was applied to both mathematical models. Numerical results showed that infected mosquito eggs influenced the spreading of dengue disease. There were bigger oscillation in the susceptible and infected human population, as well as in the infected mosquito, as a result of stronger seasonal influence during extrinsic incubation.
RINGKASAN
JUMADI. Model Matematika Penyebaran Penyakit Demam Berdarah Dengue. Dibimbing oleh PAIAN SIANTURI, dan N. K. KUTHA ARDANA.
DBD adalah penyakit yang disebabkan oleh virus dengue. Penyebaran virus demam berdarah dengue ditularkan oleh nyamuk. Nyamuk Aedes aegypti merupakan nyamuk utama penyebar virus dengue, namun spesies lain seperti
Aedes albopictus, Aedes polynesiensis, berperan sebagai nyamuk sekunder.
Peningkatan penyebaran demam berdarah dengue yang mencolok terjadi pada awal dan akhir musim hujan hal ini karena tempat perindukan nyamuk terbentuk dengan tertampungnya air hujan.
Penularan virus ini dapat dikelompokkan menjadi dua mekanisme. Mekanisme pertama, transmisi vertikal dalam tubuh nyamuk. Pada mekanisme ini virus dapat ditularkan oleh nyamuk betina pada telurnya dan juga dapat ditularkan dari nyamuk jantan ke nyamuk betina melalui kontak seksual, tetapi tidak berlaku sebaliknya (Malavige et al. 2004). Mekanisme kedua, transmisi dari nyamuk ke dalam tubuh manusia dan sebaliknya. Pemodelan penyebaran penyakit demam berdarah dengue akan mempermudah dalam memahami dinamika penyebaran penyakit dalam suatu populasi.
Beberapa penelitian tentang model matematika untuk mengkaji penyebaran DBD antara lain telah dilakukan oleh Esteva (1998) yaitu memodelkan penyebaran penyakit DBD dengan dua jenis virus dengue berbeda yang menyerang manusia. Derouich (2003 ) membuat model pada kasus dua epidemik dengan dua virus yang berbeda. Nuraini et al. (2007) meneliti model penyebaran virus dengue dalam aliran darah manusia. Pongsumpun (2006) memodelkan penyebaran DBD dengan melihat pengaruh musim pada masa inkubasi virus di dalam nyamuk.
Modifikasi model ini dilakukan karena pada umumnya pemodelan penyebaran demam berdarah dengue masih berasumsi bahwa semua kelahiran nyamuk dalam keadaan bebas dari virus.. Selanjutnya model yang telah dimodifikasi dilakukan analisis kestabilan dan simulasi numerik. Simulasi dilakukan dengan pemrograman berbasis fungsional menggunakan software
Mathematica 6.0 untuk membandingkan kedua model penyebaran DBD tersebut.
Pengaruh musim terutama suhu dipertimbangkan dalam analisis ini karena masa inkubasi ekstrinsik di dalam suhu rendah itu adalah lebih lama, padahal rata-rata masa hidup nyamuk 14 hari.
Hasil analisis yang telah dilakukan terhadap model modifikasi penyebaran penyakit DBD diperoleh 2 titik tetap yaitu
dan dengan proporsi manusia peka, proporsi manusia terinfeksi dan proporsi nyamuk terinfeksi. Pada titik tetap , populasi hanya terdiri dari proporsi manusia peka saja. Sedangkan pada titik tetap , populasi terdiri dari ketiga kelas. Analisis kestabilan titik tetap tersebut bergantung pada nilai , dengan adalah bilangan reproduksi dasar. Jika <1, maka titik tetap bersifat stabil. Pada titik tetap bersifat stabil jika >1.
Selanjutnya dari hasil simulasi, diperoleh informasi, semakin kecil rata-rata gigitan nyamuk per hari maka proporsi manusia peka semakin besar,
sedangkan proporsi manusia terinfeksi dan nyamuk terinfeksi semakin kecil serta bersifat tak linear. Semakin kecil rata-rata gigitan nyamuk per hari mengakibatkan waktu untuk mencapai stabil semakin lama. Semakin besar peluang telur nyamuk terinfeksi maka proporsi manusia peka semakin kecil, proporsi manusia terinfeksi semakin besar dan bersifat linear , sedangkan proporsi nyamuk terinfeksi semakin besar serta bersifat tak linear. Semakin besar peluang telur nyamuk terinfeksi mengakibatkan waktu untuk mencapai stabil semakin cepat. Waktu untuk mencapai stabil pada model modifikasi lebih cepat dari model asli. Perilaku osilasi akan berubah lebih besar pada proporsi populasi manusia peka, manusia terinfeksi dan nyamuk terinfeksi, selagi pengaruh keragaman musim pada masa inkubasi ekstrinsik menjadi lebih besar.
© Hak cipta milik Institut Pertanian Bogor, tahun 2008 Hak cipta dilindungi Undang-undang
1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber
a Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik
atau tinjauan suatu masalah.
b Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor.
2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk apapun tanpa izin Institut Pertanian Bogor.
MODEL MATEMATIKA PENYEBARAN PENYAKIT DEMAM
BERDARAH DENGUE
JUMADI
Tesis
sebagai salah satu syarat untuk memperoleh gelar
Magister Sains pada
Departemen Matematika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
BOGOR
2008
Judul Tesis : Model Matematika Penyebaran Penyakit Demam Berdarah Dengue Nama : Jumadi NIM : G551060051 Disetujui Komisi Pembimbing Dr. Paian Sianturi
Ir. N.K. Kutha Ardana, M.Sc. Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan
Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Nopember 2007 ini ialah masalah penyebaran penyakit demam berdarah dengue, dengan judul Model Matematika Penyebaran Penyakit Demam Berdarah Dengue.
Terima kasih penulis ucapkan kepada Bapak Dr. Paian Sianturi dan Bapak Ir. N. K. Kutha Ardana, M.Sc selaku pembimbing, atas segala saran dan bimbingannya. Terima kasih juga disampaikan kepada Bapak Drs. Ali Kusnanto, M.Si. yang telah banyak memberikan saran selaku penguji luar komisi. Ucapan terima kasih penulis disampaikan pada Departemen Agama Republik Indonesia yang telah memberikan beasiswa. Ungkapan terima kasih juga disampaikan kepada istri dan anak serta seluruh keluarga, atas segala doa dan kasih sayangnya.
Semoga karya ilmiah ini bermanfaat.
Bogor, Agustus 2008
RIWAYAT HIDUP
Penulis dilahirkan di Klaten pada tanggal 28 Agustus 1970 dari ayah Mardi Utomo dan ibu Samijem. Penulis merupakan putra Pertama dari tiga bersaudara.
Tahun 1989 penulis lulus dari SMA Negeri Prambanan Klaten dan pada tahun yang sama lulus seleksi IKIP Yogyakarta. Penulis memilih Jurusan Pendidikan Matematika pada Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam Program D3 dan selesai pada tahun 1992. Tahun 1995 melanjutkan kuliah di IKIP Medan lulus tahun 1997.
Tahun 1993 penulis menjadi staf pengajar di SMP Muhammadiyah 19 Pematangsiantar dan SMA Muhammadiyah 7 Serbalawan. Pada tahun 1994 masuk PNS dan mengajar di MTs Negeri Pematangsiantar. Pada tahun 2006 penulis lulus seleksi masuk Program Magister Program Studi Matematika Terapan Institut Pertanian Bogor melalui jalur Beasiswa Utusan Daerah Departemen Agama Republik Indonesia.
DAFTAR ISI
Halaman
DAFTAR TABEL ………..xi
DAFTAR GAMBAR ………xii
DAFTAR LAMPIRAN ………xiv
I PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Tujuan Penelitian ... 2
II LANDASAN TEORI ... 3
2.1 Sistem Persamaan Diferensial ... 3
2.2 Titik Tetap ... 3
2.3 Pelinieran ... 4
2.4 Komunitas Multi-Spesies dan Kriteria Routh-Hurwitz ... 5
2.5 Solusi Numerik Sistem Persamaan Diferensial ... 7
II MODEL MATEMATIKA PENYEBARAN PENYAKIT DBD ... 8
3.1 Penyebaran Virus DBD ... 8
3.2 Model Matematika ... 9
3.3 Modifikasi Model ... 11
3.4 Model dengan Pengaruh Musim ... 13
IV HASIL DAN PEMBAHASAN ... 15
4.1 Penentuan Titik Tetap ... 15
4.2 Analisis Kestabilan ... 15
4.2.1 Perilaku di Sekitar Titik Tetap
... 16
4.2.2 Perilaku di Sekitar Titik Tetap
... 17
4.3 Simulasi Model ... 18
4.3.1 Nilai-nilai Parameter ... 18
4.3.2 Hasil Simulasi Model ... 19
V KESIMPULAN DAN SARAN ... 30
5.1 Kesimpulan ... 30
5.2 Saran ... 30
DAFTAR PUSTAKA ... 31
LAMPIRAN ... 32
DAFTAR TABEL
Halaman 1 Nilai-nilai Parameter Model Asli dan Model Modifikasi ……….. 19 2 Hubungan antara , , dan b………. 40
3 Hubungan antara , , dan ……….... 41
DAFTAR GAMBAR
Halaman 1 Skema penyebaran DBD dengan asumsi semua telur nyamuk sehat... 9 2 Skema penyebaran DBD dengan asumsi sebagian telur nyamuk
terinfeksi. ………. 12 3 Proporsi manusia peka , proporsi manusia terinfeksi dan
proporsi nyamuk terinfeksi dengan =5.29 ……….. 20 4 Proporsi ketiga kelompok yakni , , dan pada Gambar 3,
ditampilkan dalam 3 dimensi ……….. 20 5 Proporsi manusia peka
dengan nilai rata-rata gigitan nyamuk (b) berbeda dan nilai parameter yang lain tetap ……… 21 6 Proporsi manusia terinfeksi
dengan nilai rata-rata gigitan nyamuk (b) berbeda dan nilai parameter yang lain tetap ……….. 21 7 Proporsi nyamuk terinfeksi dengan nilai rata-rata gigitan nyamuk (b)
berbeda dan nilai parameter yang lain tetap ……… 21 8 Proporsi manusia peka , proporsi manusia terinfeksi ,
proporsi nyamuk terinfeksi dan = 5.34 ……… 22 9 Proporsi ketiga kelompok yakni , , dan pada Gambar 8,
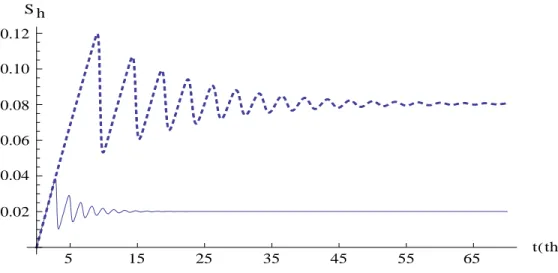
ditampilkan dalam 3 dimensi ……….. 22 10 Proporsi manusia peka nilai peluang telur nyamuk terinfeksi
berbeda ……… 23 11 Proporsi manusia terinfeksi dengan nilai peluang telur nyamuk
terinfeksi berbeda ……… 23
12 Proporsi nyamuk terinfeksi dengan nilai peluang telur nyamuk
terinfeksi berbeda ……… 24
13 Hubungan antara proporsi manusia peka , manusia terinfeksi , dan nyamuk terinfeksi , dengan rata-rata gigitan nyamuk per hari disimulasikan pada [0.1, 2] step 0.1 (lihat lampiran 6) ………... 24 14 Hubungan proporsi manusia peka , manusia terinfeksi
dan nyamuk terinfeksi dengan peluang transmisi virus dari nyamuk kepada telurnya disimulasikan pada [0, 1] step 0.1 (lihat lampiran 7) 25
15 Proporsi manusia peka pada model asli dan model modifikasi …….. 26 16 Proporsi manusia terinfeksi
pada model asli dan model modifikasi 26 17 Proporsi nyamuk terinfeksi
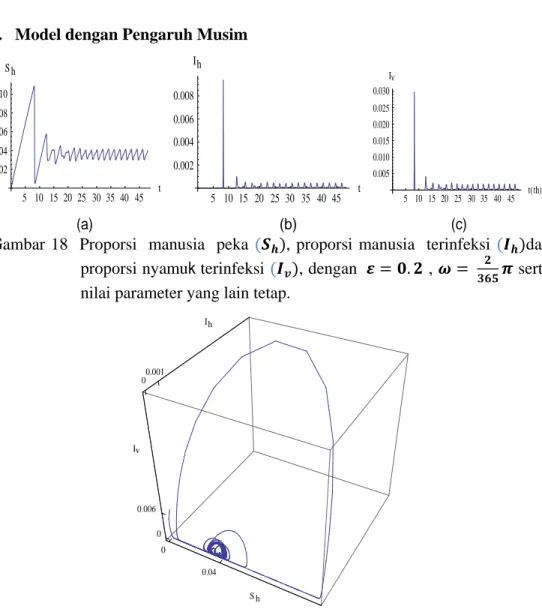
pada model asli dan model modifikasi ... 26 18 Proporsi manusia peka , proporsi manusia terinfeksi dan
proporsi nyamuk terinfeksi , dengan , serta nilai parameter yang lain tetap ……… 27 19 Proporsi ketiga kelompok yakni , , dan pada Gambar 18,
ditampilkan dalam 3 dimensi ……….. 27 20 Proporsi manusia peka , proporsi manusia terinfeksi dan
proporsi nyamuk terinfeksi (Iv) dengan , ………. 28 21 Proporsi ketiga kelompok yakni , , dan pada Gambar 20,
ditampilkandalam 3 dimensi ………... 28 22 Proporsi manusia peka , proporsi manusia terinfeksi dan
proporsi nyamuk terinfeksi (Iv) dengan , serta nilai
parameter yang lain tetap ……… 29
DAFTAR LAMPIRAN
Halaman
1 Bukti teorema 2 kriteria Routh Hurwitz ……….. 33
2 Program mencari titik tetap model modifikasi ……… 34
3 Mencari nilai , , dan ………. 35
4 Program untuk simulasi model ………... 37
5 Program Plot hubungan , , dengan b dan ………. 38
6 Tabel 2 Hubungan antara , , dan b……… 40
7 Tabel 3 Hubungan antara , , dan ……….. 41
I PENDAHULUAN
1.1 Latar BelakangPenyakit Demam Berdarah Dengue (DBD) telah ada di Australia, Eropa, Asia, Amerika Selatan dan Afrika sejak abad 19. Di Indonesia DBD timbul sebagai wabah untuk pertama kalinya di Surabaya pada tahun 1968 (Indra, 2003). Penyebab penyakit ini ialah virus Dengue dan ditularkan melalui gigitan nyamuk
Aedes Aegypti sebagai faktor utama. Pemodelan penyebaran penyakit DBD akan
mempermudah dalam memahami dinamika penyebaran penyakit dalam suatu populasi.
Beberapa penelitian tentang model matematika untuk mengkaji penyebaran DBD antara lain telah dilakukan oleh Esteva (1998) yaitu memodelkan penyebaran penyakit DBD dengan dua jenis virus dengue berbeda yang menyerang manusia. Derouich (2003 ) membuat model pada kasus dua epidemik dengan dua virus yang berbeda. Nuraini et al. (2007) meneliti model penyebaran virus dengue dalam aliran darah manusia. Pongsumpun (2006) memodelkan penyebaran DBD dengan melihat pengaruh musim pada masa inkubasi virus di dalam nyamuk. Dalam tesis ini akan dibahas modifikasi model dari model terakhir yang dibuat oleh Pongsumpun.
Modifikasi model ini dilakukan karena pada umumnya pemodelan penyebaran demam berdarah dengue masih berasumsi bahwa semua kelahiran nyamuk dalam keadaan bebas dari virus. Berdasarkan penelitian, nyamuk betina yang terinfeksi dapat menurunkan virus kepada telurnya (Malavige et al. 2004). Dengan demikian sebagian nyamuk yang lahir akan tertular virus. Berdasarkan ini dilakukan modifikasi model.
Selanjutnya model yang telah dimodifikasi dilakukan analisis kestabilan dan simulasi numerik. Simulasi dilakukan dengan pemrograman berbasis fungsional menggunakan software Mathematica 6.0 untuk membandingkan kedua model penyebaran DBD tersebut. Pengaruh musim terutama suhu dipertimbangkan dalam analisis ini.
2
1.2 Tujuan Penelitian
1 Mengkaji model penyebaran penyakit demam berdarah dengue.
2 Melakukan modifikasi model penyebaran penyakit demam berdarah dengue.
3 Melakukan analisis kestabilan.
4 Mengimplementasikan model ke dalam pemrograman berbasis fungsional.
II LANDASAN TEORI
2.1 Sistem Persamaan DiferensialDefinisi 1 [Sistem Persamaan Diferensial Linear (SPDL)]
Suatu sistem persamaan diferensial dinyatakan sebagai berikut:
dengan A adalah matriks koefisien konstan berukuran dan b vektor konstan. Sistem tersebut dinamakan SPDL orde 1 dengan kondisi awal . Jika
b=0 sistem dikatakan homogen dan dikatakan tak homogen jika .
[Tu, 1994] Definisi 2 [Sistem Persamaan Diferensial Tak Linear (SPDTL)]
Suatu sistem persamaan diferensial dinyatakan sebagai berikut:
(1.2) dengan
dan diasumsikan fungsi tak linear
pada .
Sistem (1.2) disebut sistem persamaan diferensial tak linear.
[Braun, 1983] Definisi 3 [Sistem Persamaan Diferensial Mandiri ]
Misalkan suatu sistem persamaan diferensial (SPD) dinyatakan sebagai berikut
(1.3) dengan f merupakan fungsi kontinu bernilai riil dari x dan mempunyai turunan parsial kontinu. Persamaan (1.3) disebut persamaan diferensial mandiri (autonomous) karena tidak memuat t secara eksplisit di dalamnya.
[Tu, 1994]
2.2 Titik Tetap
Definisi 4 [Titik Tetap]
4
Titik disebut titik tetap atau titik kritis atau disebut juga titik kesetimbangan jika
[Tu, 1994] Titik Tetap Stabil
Misalkan
adalah titik tetap sebuah persamaan diferensial dan x(t) adalah solusi dengan kondisi awal x(0)=x0, dimana x0 . Titik dikatakan titik tetap stabil, jika untuk setiap > 0, terdapat r > 0, sedemikian sehingga x0 x r
,maka x t( ) x untuk t > 0.
[Vershult, 1990] Analisis Kestabilan Titik Tetap
Analisa kestabilan untuk setiap titik tetap yang berbeda untuk setiap nilai eigen yakni:
1 Sistem adalah stabil jika dan hanya jika setiap nilai eigen dari
bernilai negatif.
2 Sistem adalah tidak stabil jika dan hanya jika minimal satu nilai eigen dari
bernilai positif.
[Borrelli dan Coleman, 1998] 2.3 Pelinieran
Analisis kestabilan SPDTL dilakukan melalui pelinieran.Misalkan diberikan SPDTL sebagai berikut:
1.4 Dengan menggunakan ekspansi Taylor untuk suatu titik tetap , maka persamaan
(1.4) dapat ditulis senagai berikut:
1.5 Persamaan tersebut merupakan SPDTL dengan adalah matriks Jacobi,
5
dan suku berorde tinggi yang bersifat . Selanjutnya pada persamaan (1.5) disebut pelinearan dari sistem tak linear persamaan (1.4) yang didapat dalam bentuk .
Untuk suatu sistem yang berada dalam bidang
akan diperoleh dengan , , dengan
, , ,
dan
. Nilai dan kecil sekali sehingga dapat diabaikan.
[Tu, 1994] 2.4 Komunitas Multi-Spesies dan Kriteria Routh-Hurwitz
Suatu model populasi dengan k spesies yang berinteraksi dalam komunitas dapat dituliskandalam bentuk persamaan
atau dapat ditulis dalam notasi vektor
dengan fungsi tak linear pada .
Kestabilan sistem tersebut dapat ditentukan dengan urutan sebagai berikut: 1. Menentukan titik tetap ) yang memenuhi .
2. Pelinearan dengan menentukan matriks Jacobi pada titik tetap, yakni:
6
3. Menentukan nilai eigen , dengan menyelesaikan . Nilai eigen ini akan memenuhi persamaan karakteristik berikut:
Jika nilai eigen semua riil negatif, maka titik tetap adalah stabil. Jika nilai eigen tidak dapat ditentukan dengan mudah, maka kestabilan untuk
, dapat ditentukan dengan Kriteria Routh-Hurwitz, berikut: Kriteria Routh-Hurwitz
Teorema 1:
Diberikan persamaan karakteristik
Selanjutnya didefinisikan matriks Hurwitz sebagai berikut:
dengan dan
Semua nilai eigen dari persamaan karakteristik mempunyai bagian riil yang negatif (titik tetap stabil) jika dan hanya jika determinan dari semua matriks Hurwitz positif, yaitu:
, untuk j= 1, 2, …, k.
Berdasarkan kriteria Routh-Hurwitz untuk k = 2, 3, 4 disebutkan bahwa titik tetap stabil jika dan hanya jika
k = 2, , k = 3, , ,
k = 4, , , ,
[Edelstein-Keshet,1988]
7
Untuk kasus k = 3, kriteria Routh-Hurwitz disajikan dalam Teorema 2 berikut.
Teorema 2
Misalkan , , bilangan riil. Bagian riil dari setiap nilai eigen persamaan karakteristik
adalah negatif jika dan hanya jika , dan . Bukti: di lampiran 1.
2.5 Solusi Numerik Sistem Persamaan Diferensial
Suatu sistem persamaan diferensial mempunyai bentuk umum ,
, dimana nilai awal pada waktu , t variabel riil, y: R Rn vektor nilai fungsi pada t, f:Rn+1 Rn, dan notasi turunan terhadap t, yaitu :
.
Sistem persamaan diferensial tersebut dapat juga ditulis dalam bentuk sebagai berikut:
Dalam tesis ini solusi numerik dari sistem persamaan diferensial akan diselesaikan dengan menggunakan software Mathematica 6.0.
8
II MODEL MATEMATIKA PENYEBARAN PENYAKIT DBD
3.1 Penyebaran Virus DBD
DBD adalah penyakit yang disebabkan oleh virus dengue. Penyebaran virus demam berdarah dengue ditularkan oleh nyamuk. Nyamuk Aedes aegypti merupakan nyamuk utama penyebar virus dengue, namun spesies lain seperti
Aedes albopictus, Aedes polynesiensis, berperan sebagai nyamuk sekunder.
Peningkatan penyebaran demam berdarah dengue yang mencolok terjadi pada awal dan akhir musim hujan hal ini karena tempat perindukan nyamuk terbentuk dengan tertampungnya air hujan.
Pada suhu lingkungan 300 C, virus DBD memerlukan waktu 8 -10 hari untuk menyelesaikan masa inkubasi ekstrinsik dari lambung sampai ke kelenjar ludah nyamuk (Indra, 2003). Di daerah-daerah di mana terjadi perubahan temperatur di dalam setiap musim, transmisi virus demam berdarah selalu berkurang pada suhu rendah. Contoh mewabahnya virus demam berdarah di daerah dingin berhenti pada temperatur yang turun ke 14-15 0 C pada awal musim dingin. Hal ini disebabkan masa inkubasi ekstrinsik di dalam suhu rendah itu adalah lebih lama dari masa inkubasi ekstrinsik di dalam suhu yang tinggi, pada hal rata-rata masa hidup nyamuk 14 hari. Nyamuk-nyamuk itu tidak pernah sembuh dari infeksi karena terinfektif mereka berakhir dengan kematian (Gubler,1998). Pada suhu di bawah 200 C sebelum menyebarkan virus, nyamuk sudah mati.
Penularan virus ini dapat dikelompokkan menjadi dua mekanisme. Mekanisme pertama, transmisi vertikal dalam tubuh nyamuk. Dimana virus dapat ditularkan oleh nyamuk betina pada telurnya dan juga dapat ditularkan dari nyamuk jantan ke nyamuk betina melalui kontak seksual, tetapi tidak berlaku sebaliknya (Malavige et al. 2004). Mekanisme kedua, transmisi dari nyamuk ke dalam tubuh manusia dan sebaliknya. Penularan dari manusia kepada nyamuk hanya dapat terjadi bila nyamuk mengigit manusia yang sedang mengalami viremia, yaitu 2 hari sebelum panas sampai 5 hari setelah demam timbul. Setelah virus berada dalam tubuh nyamuk, virus yang sampai ke dalam lambung nyamuk akan berkembangbiak, kemudian akan migrasi yang akhirnya akan sampai di
9
kelenjar ludah memerlukan waktu 8-10 hari untuk menyelesaikan masa inkubasi ekstrinsik. Virus yang berada pada lokasi ini setiap saat sudah dapat ditularkan kembali kepada manusia.
3.2 Model Matematika
Populasi manusia dibagi menjadi tiga kelas, yaitu manusia yang peka ( ), manusia yang terkena infeksi ( ), dan manusia yang sembuh ( ). Manusia yang peka adalah manusia yang bukan imun dan tidak terkena infeksi. Manusia yang terkena infeksi adalah manusia yang terkena virus DBD dan dapat menularkan kepada individu lain dengan perantara nyamuk. Manusia sembuh adalah manusia yang sembuh dari penyakit dan tidak dapat tertular lagi.
Populasi nyamuk dibedakan menjadi dua kelas yaitu nyamuk yang peka ( ), nyamuk yang terkena infeksi ( ). Nyamuk yang peka adalah nyamuk yang rentan terhadap penyakit demam berdarah dengue. Sedangkan nyamuk terinfeksi adalah nyamuk yang terkena infeksi dan dapat menularkan kepada individu lain.
Asumsi-asumsi yang berlaku adalah :
1. Ukuran populasi manusia dan nyamuk konstan sehingga laju kelahiran sama dengan laju kematian.
2. Rata-rata gigitan individu nyamuk pada manusia per hari adalah konstan. 3. Nyamuk tidak pernah sembuh setelah terinfeksi penyakit.
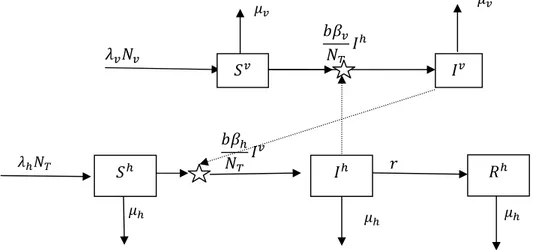
Secara skematis, pola penyebaran penyakit demam berdarah dengue dapat digambarkan dalam diagram kompartemen berikut:
Gambar 1 Skema penyebaran DBD dengan asumsi semua telur nyamuk sehat
10
Dari asumsi-asumsi tersebut, proporsi penginfeksian manusia peka ( ) oleh nyamuk terinfeksi ( ) per hari adalah perbandingan antara peluang transmisi virus demam berdarah dari nyamuk ke manusia dengan banyaknya inang yang menjadi sumber makanan nyamuk dikalikan dengan rata-rata gigitan nyamuk pada manusia per hari dan banyaknya nyamuk yang terinfeksi ( ), dinyatakan sebagai berikut: Manusia peka ( ) tersebut berpindah menjadi manusia terinfeksi ( ). Manusia terinfeksi setiap hari yang meninggal secara alami sebanyak .
Proporsi penginfeksian nyamuk peka ( ) akibat menggigit manusia terinfeksi ( ) per hari adalah perbandingan antara peluang transmisi virus demam berdarah dari manusia ke nyamuk dengan banyaknya inang yang menjadi sumber makanan nyamuk dikalikan dengan rata-rata gigitan nyamuk pada manusia per hari dan banyaknya manusia yang terinfeksi ( ), diekspresikan sebagai berikut:
Selanjutnya nyamuk peka tersebut berpindah menjadi nyamuk terinfeksi ( ). Nyamuk peka mati secara alami sebanyak per hari.
Berdasarkan skema Gambar 1, dapat dimodelkan menggunakan sistem persamaan diferensial berikut :
dengan (2)
dan adalah populasi manusia, adalah populasi nyamuk,
11
b adalah rata-rata gigitan individu nyamuk pada manusia (per hari), adalah peluang transmisi virus demam berdarah dari nyamuk ke
manusia,
adalah peluang transmisi virus demam berdarah dari manusia ke nyamuk,
adalah laju kematian alami manusia (per hari), r adalah laju kesembuhan manusia terinfeksi (per hari),
adalah laju kematian alami dari nyamuk (per hari).
Sistem persamaan (1) disederhanakan dengan pemisalan , , , , dan , maka diperoleh sistem persamaan (2) sebagai berikut :
dengan ,
dan
(4)
dengan ketiga kondisi dan (5)
3.3 Modifikasi Model
Model penyebaran virus DBD sebelumnya menggunakan asumsi semua telur nyamuk sehat. Berdasarkan penelitian, nyamuk yang terinfeksi dapat menularkan virus pada telurnya, maka modifikasi model diperlukan untuk mendapatkan model yang lebih baik. Model yang baru menggunakan asumsi sebagian telur nyamuk terinfeksi. Parameter baru yaitu menyatakan peluang transmisi virus dari nyamuk pada telurnya dan parameter yang lain tetap.
Kondisi populasi manusia pada model dengan asumsi sebagian telur nyamuk terinfeksi sama dengan model awal. Keadaan populasi nyamuk mengalami perubahan karena asumsi sebagian telur nyamuk terinfeksi. Jumlah nyamuk yang peka ( ) akan meningkat karena bertambahnya kelahiran nyamuk
12
r
sehat dan akan berkurang karena gigitan nyamuk kepada populasi manusia terinfeksi serta karena kematian alami. Populasi nyamuk yang terkena infeksi ( ) akan meningkat karena kelahiran nyamuk terinfeksi, gigitan nyamuk kepada populasi manusia terinfeksi dan berkurang karena kematian alami.
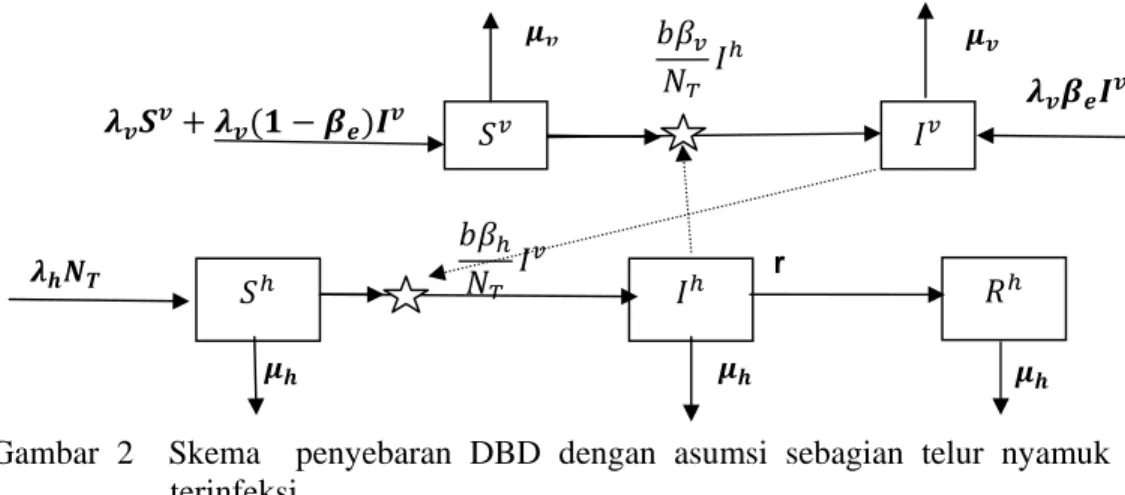
Secara skematis, pola penyebaran virus DBD dengan asumsi sebagian telur nyamuk terinfeksi dapat digambarkan dalam diagram kompartemen berikut:
Gambar 2 Skema penyebaran DBD dengan asumsi sebagian telur nyamuk terinfeksi
Model matematika penyebaran penyakit demam berdarah dengue dengan asumsi sebagian telur nyamuk terinfeksi, dapat dinyatakan dengan persamaan-persamaan berikut :
dengan kondisi (7)
dan adalah populasi manusia, adalah populasi nyamuk,
adalah laju kelahiran manusia (per hari), adalah laju kelahiran nyamuk (per hari),
13
b adalah rata-rata gigitan individu nyamuk pada manusia (per hari),
adalah peluang transmisi virus demam berdarah dari nyamuk ke telurnya,
adalah peluang transmisi virus demam berdarah dari nyamuk ke manusia,
adalah peluang transmisi virus demam berdarah dari manusia ke nyamuk,
adalah laju kematian alami manusia (per hari),
r adalah laju kesembuhan manusia terinfeksi (per hari), adalah laju kematian alami nyamuk (per hari).
Sistem persamaan (6) disederhanakan dengan pemisalan , , , , dan , maka diperoleh sistem persamaan berikut:
dengan , dan n=
(9) dengan ketiga kondisi + + =1 dan S v + Iv = 1 (10) 3.4 Model dengan Pengaruh Musim
Perubahan musim membuat perubahan suhu, sehingga pola musiman mempengaruhi di dalam penyebaran penyakit demam berdarah. Variasi di dalam masa inkubasi ekstinsik disebabkan oleh perubahan-perubahan suhu, semakin rendah suhu masa inkubasi semakin lama. Periode laten masa inkubasi virus di dalam nyamuk bergantung pada suhu (T), dengan asumsi perubahan suhu bersifat periodik mengikuti perubahan musim. Ketergantungan masa inkubasi pada suhu dapat diperhatikan pada variasi berikut, pada T= 310C, hari dan pada T= 210C, hari (Pongsumpun, 2006). Variasi ini dapat dinyatakan sebagai suatu variasi sinusoidal sedemikian bahwa
14
(11)
di mana adalah suatu ukuran dari pengaruh pola musiman pada proses transmisi. Dengan demikian model matematika dari model modifikasi karena pengaruh perubahan musim dapat dinyatakan oleh persamaan diferensial berikut:
dengan kondisi (13)
Selanjutnya sistem persamaan (12) disederhanakan, dengan pemisalan , , , , dan , maka sistem persamaan diferensialnya menjadi
dengan , dan n=
dengan ketiga kondisi dan
(15) Selanjutnya dilakukan analisis kestabilan model penularan penyakit demam berdarah dengue yang menghasilkan beberapa titik tetap. Analisis titik tetap tersebut nantinya akan dihasilkan syarat kestabilan untuk masing-masing titik tetap.
IV HASIL DAN PEMBAHASAN
4.1 Penentuan Titik TetapAnalisis titik tetap pada sistem persamaan diferensial sering digunakan untuk menentukan suatu solusi yang tidak berubah menurut waktu, yaitu pada saat dan . Titik tetap dari sistem persamaan diferensial (8) akan diperoleh dengan menentukan dan . Dari hasil analisis akan diperoleh dua jenis titik tetap, yaitu titik tetap bebas penyakit (Disease-free equilibrium-DFE) dan titik tetap endemik. Titik tetap bebas penyakit adalah titik tetap yang memuat nilai =0 dan . Titik tetap endemik adalah titik tetap yang memuat nilai atau .
Titik tetap dari sistem persamaan diferensial (8) dengan menggunakan
software Mathematica, diperoleh titik tetap bebas penyakit
dan titik tetap endemik dengan
untuk penyedehanaan, dituliskan
4.2 Analisis Kestabilan
Analisis kestabilan di sekitar titik tetap dapat ditentukan dengan prosedur sebagai berikut:
1 Menentukan matriks Jacobi dari sistem persamaan. 2 Menentukan matriks Jacobi pada titik tetap.
3 Menentukan nilai eigen , dengan menyelesaikan . Jika nilai eigen semua riil negatif maka titik tetap tersebut stabil. Kestabilan untuk sistem persamaan yang terdiri dari lebih dari 2 persamaan. Jika nilai eigen tidak dapat ditentukan dengan mudah, maka digunakan kriteria Routh-Hurwitz.
16
4.2.1 Perilaku di Sekitar Titik Tetap
Misalkan sistem persamaan (8) ditulis sebagai berikut:
(18)
h
Dengan melakukan pelinearan persamaan (18) maka diperoleh matriks Jacobi:
Kestabilan sistem persamaan diperoleh dengan menganalisis nilai eigen pada titik tetapnya.
Pelinearan pada titik tetap diperoleh matriks Jacobi sebagai berikut:
Sistem akan stabil jika nilai eigen matriks Jacobi negatif. Nilai eigen matriks Jacobi dapat ditentukan dengan menyelesaikan , yaitu:
( (
dengan
17
Perhatikan bahwa bagian riil nilai eigen semua akan negatif jika . Jadi jika , maka titik tetap pada adalah stabil.
4.2.2 Perilaku di Sekitar Titik Tetap
Pelinearan persamaan (8) pada titik tetap diperoleh matriks Jacobi sebagai berikut:
Jika semua nilai eigen yang diperoleh oleh diagonal matriks Jacobi mempunyai bagian riil negatif maka solusi titik tetap adalah stabil. Nilai eigen matriks Jacobi dapat ditentukan dengan menghitung , dengan adalah Matriks Jacobi untuk titik tetap , adalah nilai eigen dan I adalah matriks identitas. Jadi dengan demikian, diperoleh persamaan karakteristik dari
, yaitu (20) dengan ; dan atau
.
Nilai eigen dari persamaan (20) sulit ditentukan, maka kestabilan di sekitar titik tetap
akan diselidiki dengan menggunakan kriteria Routh-Hurwitz. Berdasarkan kriteria Routh-Hurwitz kondisi kestabilan persamaan (8) pada titik tetap akan stabil jika dan hanya jika memenuhi syarat-syarat berikut: , , (21) . (22)
18
Perhatikan bahwa untuk , koefisien-koefisien pada persamaan (20) bernilai positif ( , , dan ), sehingga kondisi (21) terpenuhi. Sementara kondisi (22) juga terpenuhi, karena
karena 0 , maka
dari persamaan ( 17 ) dinyatakan bahwa ,
sehingga
Kesimpulan .
Kriteria kestabilan Routh-Hurwitz terpenuhi jika , dengan kata lain titik tetap adalah stabil. adalah bilangan reproduksi dasar pada penyebaran penyakit DBD.
4.3 Simulasi Model
Sebagaimana yang telah disebutkan di awal tulisan ini, salah satu tujuan penelitian ini untuk mengimplementasikan model ke dalam pemrograman berbasis fungsional. Penelitian ini juga bertujuan membandingkan perilaku model penyebaran penyakit DBD, yaitu model dengan asumsi semua telur nyamuk sehat dan model dengan asumsi sebagian telur nyamuk terinfeksi. Pada kedua model dilakukan simulasi komputer dengan melakukan perubahan rata-rata gigitan nyamuk per hari. Secara khusus, untuk model dengan asumsi sebagian telur nyamuk terinfeksi dilakukan simulasi dengan melakukan perubahan nilai peluang telur nyamuk terinfeksi.
4.3.1 Nilai-nilai Parameter
Parameter merupakan laju kematian populasi manusia, yakni per hari sesuai dengan harapan hidup pada manusia 70 tahun. Nilai laju kelahiran populasi manusia
19
sama dengan laju kematian populasi manusia. Rata-rata masa hidup nyamuk adalah 14 hari (Pongsumpun 2006), maka laju kematian nyamuk ( = 0,071) per hari. Laju kelahiran sama dengan laju kematian ( . Nilai parameter seluruhnya ditunjukkan pada tabel 1.
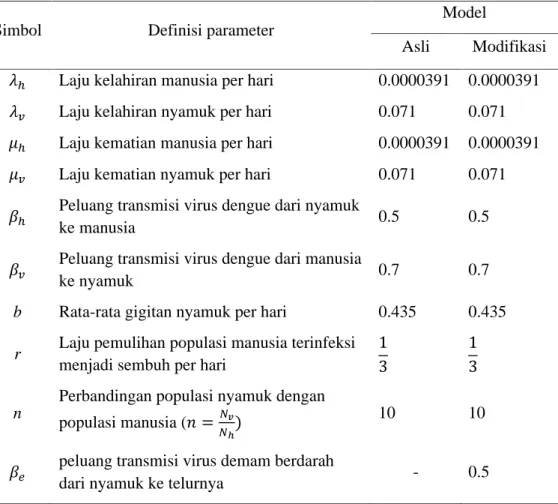
Tabel 1 Nilai-nilai Parameter Model Asli dan Model Modifikasi Simbol Definisi parameter
Model
Asli Modifikasi Laju kelahiran manusia per hari 0.0000391 0.0000391 Laju kelahiran nyamuk per hari 0.071 0.071 Laju kematian manusia per hari 0.0000391 0.0000391 Laju kematian nyamuk per hari 0.071 0.071 Peluang transmisi virus dengue dari nyamuk
ke manusia 0.5 0.5
Peluang transmisi virus dengue dari manusia
ke nyamuk 0.7 0.7
b Rata-rata gigitan nyamuk per hari 0.435 0.435
r Laju pemulihan populasi manusia terinfeksi
menjadi sembuh per hari
n
Perbandingan populasi nyamuk dengan
populasi manusia ( 10 10
peluang transmisi virus demam berdarah
dari nyamuk ke telurnya - 0.5
4.3.2 Hasil Simulasi Model
Pada simulasi ini akan dilakukan untuk kasus dengan >1 dengan syarat awal bahwa terdapat sejumlah populasi manusia dan nyamuk yang sudah terinfeksi. Proporsi awal populasi manusia sehat [S(0)]= 0, manusia terinfeksi [I(0)]=0.0025 dan nyamuk terinfeksi [Iv(0)]=0.006.
20
a. Model Asli (a)
(b)
(c)
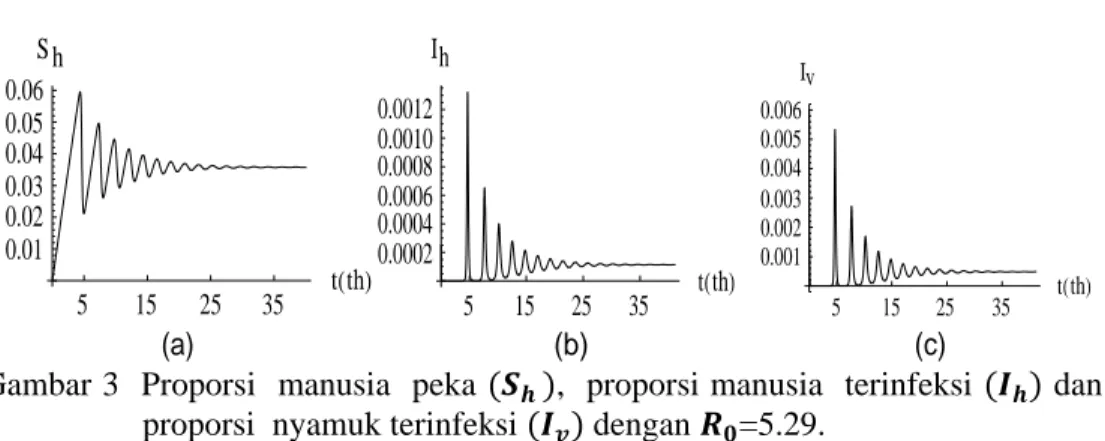
Gambar 3 Proporsi manusia peka , proporsi manusia terinfeksi dan proporsi nyamuk terinfeksi dengan =5.29.
Gambar 4 Proporsi ketiga kelompok yakni , , dan pada Gambar 3, ditampilkan dalam 3 dimensi.
Berdasarkan Gambar 3, proporsi awal manusia peka berosilasi menuju nilai stabil yakni 0.03576. Proporsi manusia terinfeksi berosilasi yang akhirnya menuju nilai stabil yakni 0.00011. Proporsi nyamuk terinfeksi berosilasi yang akhirnya menuju nilai stabil yakni 0.00048 . Dari Gambar 3 menunjukkan bahwa solusi tersebut stabil dengan titik tetap endemik (0.03576,0.00011,0.00048). Tipe kestabilan titik tetap tersebut ditampilkan dalam 3 dimensi pada Gambar 4 berbentuk spiral.
5 15 25 35 t th 0.01 0.02 0.03 0.04 0.05 0.06 S h 5 15 25 35 t th 0.0002 0.0004 0.0006 0.0008 0.0010 0.0012 Ih 5 15 25 35 t th 0.001 0.002 0.003 0.004 0.005 0.006 Iv
0
0.03
0.06
S h
0
0.00011
0.001
Ih
0
0.00048
0.006
Iv
21
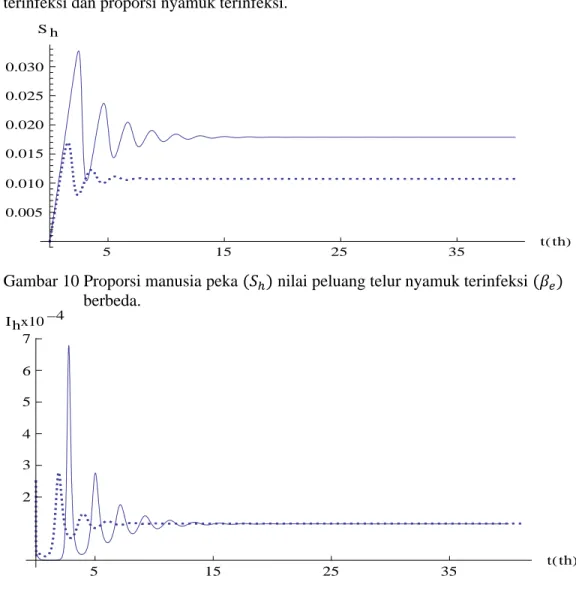
Pada Gambar 5, 6, dan 7 ditunjukkan pengaruh penurunan rata-rata gigitan terhadap proporsi manusia sehat, manusia terinfeksi dan nyamuk terinfeksi.
Gambar 5 Proporsi manusia peka
dengan nilai rata-rata gigitan nyamuk (b) berbeda dan nilai parameter yang lain tetap.
Gambar 6 Proporsi manusia terinfeksi
dengan nilai rata-rata gigitan nyamuk (b) berbeda dan nilai parameter yang lain tetap.
Gambar 7 Proporsi nyamuk terinfeksi dengan nilai rata-rata gigitan nyamuk (b) berbeda dan nilai parameter yang lain tetap.
b=0.58, =7.05 b= 0.29, = 3.53 b=0.58, =7.05 b= 0.29, = 3.53 b=0.58, =7.05 b= 0.29, = 3.53 5 15 25 35 45 55 65 t th 0.02 0.04 0.06 0.08 0.10 0.12 S h 5 15 25 35 45 55 65 t th 0.0005 0.0010 0.0015 I h 5 15 25 35 45 55 65 t th 0.001 0.002 0.003 0.004 0.005 0.006 0.007 Iv
22
Berdasarkan Gambar 5, 6, dan 7 ditunjukkan bahwa penurunan rata-rata gigitan nyamuk meningkatkan proporsi manusia peka, menurunkan proporsi manusia terinfeksi dan nyamuk terinfeksi. Penurunan rata-rata gigitan nyamuk menyebabkan waktu untuk mencapai stabil lebih lama dan nilai A semakin kecil. Hal ini menunjukkan penyebaran penyakit DBD semakin menurun.
b. Model Modifikasi
(a) (b) (c)
Gambar 8 Proporsi manusia peka , proporsi manusia terinfeksi , proporsi nyamuk terinfeksi dan = 5.34.
Gambar 9 Proporsi ketiga kelompok yakni , , dan pada Gambar 8, ditampilkan dalam 3 dimensi.
Berdasarkan Gambar 8, proporsi manusia peka berosilasi menuju nilai yang stabil yakni 0.017887 . Proporsi manusia terinfeksi dan proporsi nyamuk terinfeksi berosilasi yang akhirnya menuju nilai yang stabil yakni 0.000115 dan 0.000987. Dari Gambar 8 ditunjukkan bahwa solusi tersebut stabil dengan titik
tetap endemik (0.017887, 0.000115, 0.000987). Tipe kestabilan titik tetap tersebut ditampilkan dalam 3 dimensi pada Gambar 9 berbentuk spiral.
5 15 25 35 t th 0.005 0.010 0.015 0.020 0.025 0.030 S h 5 15 25 35 t th 2 4 6 Ihx10 4 5 15 25 35 t th 0.001 0.002 0.003 0.004 0.005 0.006 Iv 0 0.0179 S h 0 0.00011 Ih 0 0.00098 0.006 Iv
23
Pada Gambar 10, 11 dan 12, ditunjukkan pengaruh peningkatan peluang telur nyamuk terinfeksi
terhadap proporsi manusia sehat, proporsi manusia terinfeksi dan proporsi nyamuk terinfeksi.
Gambar 10 Proporsi manusia peka nilai peluang telur nyamuk terinfeksi berbeda.
Gambar 11 Proporsi manusia terinfeksi dengan nilai peluang telur nyamuk terinfeksi berbeda. =0.5, =5.34 = 0.7, =5.36 =0.5, =5.34 = 0.7, =5.36 5 15 25 35 t th 0.005 0.010 0.015 0.020 0.025 0.030 S h 5 15 25 35 t th 2 3 4 5 6 7 Ihx10 4
24
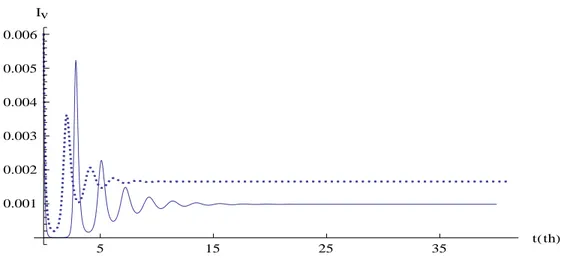
Gambar 12 Proporsi nyamuk terinfeksi dengan nilai peluang telur nyamuk terinfeksi berbeda.
Dari Gambar 10, 11 dan 12, ditunjukkan bahwa peningkatan peluang telur nyamuk terinfeksi mengakibatkan waktu untuk mencapai stabil lebih cepat dan nilai A semakin besar. Hal ini menunjukkan penyebaran penyakit DBD semakin mewabah. Peningkatan peluang telur nyamuk terinfeksi mengakibatkan proporsi manusia peka semakin kecil. Selanjutnya pengaruh perubahan rata-rata gigitan dan peluang telur nyamuk terinfeksi terhadap proporsi manusia peka, manusia terinfeksi, dan nyamuk terinfeksi pada kondisi stabil dapat dilihat pada Gambar 13 dan 14.
(a) (b) (c)
Gambar 13 Hubungan antara proporsi manusia peka , manusia terinfeksi , dan nyamuk terinfeksi , dengan rata-rata gigitan nyamuk per hari disimulasikan pada [0.1, 2] step 0.1 (lihat lampiran 6). Berdasarkan Gambar 13 peningkatan rata-rata gigitan nyamuk, akan berakibat pada penurunan proporsi manusia peka , peningkatan proporsi manusia terinfeksi dan peningkatan proporsi nyamuk terinfeksi . Secara umum hubungan dengan b dilihat dari persamaan (16) bersifat tak linear. Proporsi manusia peka meningkat seiring dengan menurunnya proporsi populasi
=0.5, =5.34 = 0.7, =5.36 5 15 25 35 t th 0.001 0.002 0.003 0.004 0.005 0.006 Iv 1 3 5 b 0.1 0.2 0.33 S h 1 3 5 b 77 90 100 110 117 Ihx10 6 1 3 5 b 0.003 0.005 0.007 0.009 0.011 Iv
25
manusia terinfeksi dan populasi nyamuk terinfeksi. Peningkatan rata-rata gigitan nyamuk menyebabkan meningkatnya proporsi manusia terinfeksi dan nyamuk terinfeksi. Peningkatan proporsi manusia terinfeksi sangat kecil (hampir tidak mengalami perubahan), sedangkan peningkatan proporsi nyamuk terinfeksi bersifat linier.
(a) (b) (c) Gambar 14 Hubungan proporsi manusia peka , manusia terinfeksi
dan nyamuk terinfeksi dengan peluang transmisi virus dari nyamuk kepada telurnya disimulasikan pada [0, 1] step 0.1 (lihat lampiran 7).
Dari Gambar 14, ditunjukkan hubungan antara proporsi manusia peka dan peluang telur nyamuk terinfeksi pada kondisi stabil, diperoleh informasi semakin besar peluang telur nyamuk terinfeksi maka proporsi manusia peka semakin kecil. Peningkatan nilai akan meningkatkan proprosi manusia terinfeksi yang sangat kecil (hampir tidak mengalami perubahan). Peningkatan nilai akan meningkatkan proprosi nyamuk terinfeksi, pada nilai proporsi nyamuk terinfeksi dapat dilihat pada Lampiran 7.
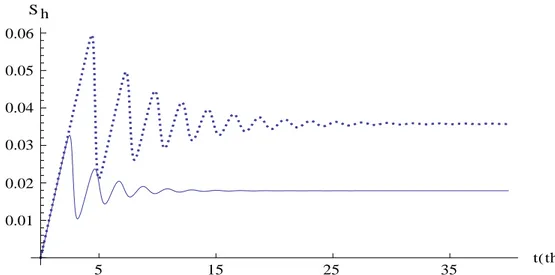
Pada Gambar 15, 16, dan 17 ditunjukkan perbandingan model asli dan model modifikasi. Model asli adalah model penyebaran penyakit DBD dengan asumsi semua telur nyamuk sehat, sedangkan model modifikasi dengan asumsi sebagian telur nyamuk terinfeksi.
0.5 1 e 0.005 0.010 0.015 0.020 0.025 0.030 0.035 S h 0.6 1 e 114 115 117 116 Ihx10 6 0.6 0.9 1 e 0.2 0.4 0.6 0.8 1.0 Iv
26
Gambar 15 Proporsi manusia peka pada model asli dan model modifikasi.
Gambar 16 Proporsi manusia terinfeksi
pada model asli dan model modifikasi.
Gambar 17 Proporsi nyamuk terinfeksi
pada model asli dan model modifikasi. Model Asli, =5.29 Model Modifikasi, =5.34 Model Asli, =5.29 Model Modifikasi, =5.34 Model Asli, =5.29 Model Modifikasi, =5.34 5 15 25 35 t th 0.01 0.02 0.03 0.04 0.05 0.06 S h 5 15 25 35 t th 2 4 6 8 10 12 I hx10 4 5 15 25 35 t th 0.001 0.002 0.003 0.004 0.005 0.006 Iv
27
Berdasarkan Gambar 15, proporsi manusia peka model asli lebih besar dari model modifikasi. Pada saat proporsi manusia sehat model asli 0.035756 , sedangkan untuk model modifikasi 0.017887. Gambar 16 menunjukkan proporsi manusia terinfeksi pada model asli lebih kecil dari model modifikasi,yaitu 0.000113 dan 0.000115. Gambar 17 menunjukkan bahwa proporsi nyamuk terinfeksi model modifikasi dua kali lebih besar dari model asli, yaitu 0.000987 dan 0.000485. Waktu untuk mencapai stabil model modifikasi lebih cepat dari model asli. Nilai A model modifikasi lebih besar dari model asli. Jadi asumsi sebagian telur nyamuk terinfeksi berpengaruh pada penyebaran penyakit DBD.
c. Model dengan Pengaruh Musim
(a)
(b)
(c)
Gambar 18 Proporsi manusia peka , proporsi manusia terinfeksi dan proporsi nyamuk terinfeksi , dengan , serta nilai parameter yang lain tetap.
Gambar 19 Proporsi ketiga kelompok yakni , , dan pada Gambar 18, ditampilkan dalam 3 dimensi.
5 10 15 20 25 30 35 40 45 t 0.02 0.04 0.06 0.08 0.10 S h 5 10 15 20 25 30 35 40 45 t 0.002 0.004 0.006 0.008 Ih 5 10 15 20 25 30 35 40 45 t th 0.005 0.010 0.015 0.020 0.025 0.030 Iv 0 0.04 S h 0 0.001 Ih 0 0.006 Iv
28
(a)
(b)
(c)
Gambar 20 Proporsi manusia peka , proporsi manusia terinfeksi dan proporsi nyamuk terinfeksi (Iv) dengan , .
Gambar 21 Proporsi ketiga kelompok yakni , , dan pada Gambar 20, ditampilkandalam 3 dimensi.
Dari Gambar 18 dan 20 proporsi populasi manusia peka
berosilasi terus menuju pada nilai yang periodik. Proporsi manusia terinfeksi dan nyamuk terinfeksi turun selanjutnya naik berosilasi menuju pada nilai yang periodik. Semakin besar ukuran pengaruh keragaman musim pada masa inkubasi ekstrinsik , perilaku osilasi akan berubah lebih besar. Gambar 19 dan 21 merupakan tampilan 3 dimensi dari Gambar 18 dan 20 yang menunjukkan bahwa pengaruh musim membuat perilaku model bersifat periodik.
Pada Gambar 22 ditunjukkan perbandingan perilaku model modifikasi dan model dengan pengaruh musim.
5 15 25 35 t th 0.005 0.010 0.015 0.020 0.025 0.030 Sh 5 15 25 35 t th 2 4 6 8 10 12 Ihx10 4 5 15 25 35 t th 0.002 0.004 0.006 0.008 Iv 0 S h 0 0.001 Ih 0 0.006 Iv
29
(a)
(b)
(c)
Gambar 22 Proporsi manusia peka , proporsi manusia terinfeksi dan proporsi nyamuk terinfeksi (Iv) dengan , serta nilai parameter yang lain tetap.
Gambar 22 menunjukkan perbedaan perilaku model modifikasi dengan model dengan pengaruh musim. Model modifikasi setelah berosilasi akhirnya menuju stabil, sedangkan pada model dengan pengaruh musim tetap berosilasi yang bersifat periodik.
Dari seluruh hasil simulasi dapat dilihat perbedaan dinamik yang terjadi pada model. Nilai yang tidak berubah menurut waktu dengan asumsi sebagian telur nyamuk terinfeksi lebih kecil dari nilai dengan asumsi semua telur nyamuk sehat dan nilai hampir sama, sedangkan nilai lebih besar. Penurunan rata-rata gigitan nyamuk perhari mengakibatkan periode osilasi dan waktu untuk mencapai stabil lebih lama. Peluang telur nyamuk terinfeksi yang semakin besar menyebabkan turunnya proporsi manusia sehat, meningkatnya proporsi manusia terinfeksi dan nyamuk terinfeksi. Pengaruh perubahan musim membuat perilaku model bersifat periodik.
Model musim Model modifikasi 5 15 25 35 t th 0.005 0.010 0.015 0.020 0.025 0.030 S h 5 15 25 35 t th 2 4 6 8 10 12 Ihx10 4
5
15 25 35
t th
0.002
0.004
0.006
0.008
Iv
30
V KESIMPULAN DAN SARAN
5.1 KesimpulanBerdasarkan hasil pembahasan, dapat disimpulkan bahwa hasil analisis yang telah dilakukan terhadap model modifikasi penyebaran penyakit DBD diperoleh 2 titik tetap yaitu
dan dengan
proporsi manusia peka, proporsi manusia terinfeksi dan proporsi nyamuk terinfeksi. Pada titik tetap , populasi hanya terdiri dari proporsi manusia peka saja. Sedangkan pada titik tetap , populasi terdiri dari ketiga kelas. Analisis kestabilan titik tetap tersebut bergantung pada nilai , dengan adalah bilangan reproduksi dasar. Jika <1, maka titik tetap bersifat stabil. Pada titik tetap bersifat stabil jika >1.
Selanjutnya dari hasil simulasi untuk kasus >1, diperoleh informasi tentang pengaruh perubahan rata-rata gigitan (b) per hari, peluang telur nyamuk terinfeksi dan perubahan musim terhadap perilaku model penyebaran DBD sebagai berikut:
1 Semakin kecil rata-rata gigitan nyamuk per hari maka proporsi manusia peka semakin besar, sedangkan proporsi manusia terinfeksi dan nyamuk terinfeksi semakin kecil serta bersifat tak linear.
2 Semakin besar rata-rata gigitan nyamuk per hari atau peluang telur nyamuk terinfeksi mengakibatkan waktu untuk mencapai stabil semakin cepat .
3 Semakin besar peluang telur nyamuk terinfeksi maka proporsi manusia peka semakin kecil, proporsi manusia terinfeksi semakin besar dan bersifat linear, sedangkan proporsi nyamuk terinfeksi semakin besar serta bersifat tak linear. 4 Waktu untuk mencapai stabil model modifikasi lebih cepat dari model asli. 5 Perilaku osilasi akan berubah lebih besar selagi pengaruh keragaman musim
pada masa inkubasi ekstrinsik menjadi lebih besar. 5.2 Saran
Penelitian ini perlu dilanjutkan khususnya pada model dengan pengaruh musim dengan melibatkan masa inkubasi virus pada nyamuk dan manusia .
31
DAFTAR PUSTAKA
Brawn M. 1983. Differential Equations and Their Applications. New York : Springer-Verlag.
Borrelli RL, Coleman CS. 1998. Differential Equations. John Wiley and Sons, Inc. USA.
Derouich M, Boutayeb A and Twizell EH. 2003. A Model of Dengue Fever. BioMedical Engineering OnLine 4: 1-10.
Esteva L. 1998. Dynamics of Dengue Disease. Mexico :Cinvestav-Ipv.
Gubler DJ. 1998. Dengue and Dengue Hemorhagic Fever. Clinical Microbiology Review 11: 450-496.
Heath TM. 1997. Scientific Computing. New York: The Mcgraw-Hill Companies Indra C. 2003. Pemberantasan Vektor Demam Berdarah Dengue. Medan: Bagian
Kesehatan Lingkungan Fakultas Kesehatan Masyarakat Universitas Sumatera Utara.
Edelstein-Keshet L, 1988. Mathematical Models in Biology, New York : Random House.
Malavige GN., Fernando S., Fernando DJ., Seneviratne SL. 2004. Dengeu Viral
Infections, Postgrad Med Journal 80: 588-601.
Nuraini N, Soewono E, dan Sidarto KA. 2007. A Mathematical Model of Dengue
Internal Transmission Process. J. Indones. Math. Soc. (MIHMI) 13:
123-132.
Pongsumpun P. 2006. Transmission Model For Dengue Disease With and
Without the Effect of Extinsic Incubation Period. KMITL Sci. Tech. J. 6 :
74- 82
Tu PNV. 1994. Dynamical System, An Introduction with Applications in
Economics and Biology. New York : Springer-Verlag.
Verhulst F. 1990. Nonlinear Differential Equations and Dynamical Systems. Springer-Verlag, Berlin.
32
33
Lampiran 1 Bukti teorema 2 kriteria Routh Hurwitz Teorema 2
Misalkan , , bilangan riil. Bagian riil dari setiap nilai eigen persamaan karakteristik
adalah negatif jika dan hanya jika , dan . Bukti:
Dari persamaan , maka ,
dan . Berdasarkan Teorema 1, bagian riil dari setiap akar persamaan karakteristik adalah negatif jika dan hanya jika
, untuk j= 1, 2,3, dengan (1) (2)
(3) Dari (1), diperoleh Dari (2), diperoleh
Dari (3), diperoleh , karena
sehingga diperoleh .
Dengan demikian diperoleh bahwa bagian riil dari semua akar persamaan karakteristik adalah negatif jika dan hanya jika
, , dan .
34
Lampiran 2
Program mencari titik tetap model modifikasi Dengan mathematica 6.0
Solve[{ h- h*S*iv- h*S==0, h*S*iv-( h+r) i==0, v (1-iv)
i+ v* e*iv- v*iv==0},{S,i,iv}]
{{S 1,i 0,iv 0},{S ( v h-(-1+ e) (r+ h) v)/( v ( h+ h)),i ( h ( h v+(-1+ e) (r+ h) v))/( v (r+ h) ( h+ h)),iv ( h ( h v+(-1+ e) (r+ h) v))/( h ( v h-(-1+ e) (r+ h) v))}} dan
35
Lampiran 3
Mencari nilai , , dan .
; dan
36
37
dengan
Lampiran 4
Program untuk simulasi model
h=0.0000391 v=0.071 h=0.5 v=0.7 n=10 Manipulate[Plot[Evaluate[S[t]/.First[NDSolve[{S'[t] h-b* h *n* S[t] *Iv[t]- h* S[t],II'[t] b* h* n*S[t]
*Iv[t]-( h+r)*II[t],Iv'[t] b * v*(1-Iv[t])*II[t]- v *Iv[t]+ v * e *Iv[t],S[0] 0,II[0] 0.00025,Iv[0] 0.006},{S,II,Iv},{t,0,175 00}]]],{t,0,365*50},PlotRange All, AxesLabel {"t(tahun)", "Sh"} ,Ticks {{{365*5,5}, {3650,10},{365*15,15},{365*20,20},{365*25,25},{365*30,30},{3 65*35,35},{365*40,40},{365*45,45},{365*50,50},{365*55,55},{3 65*60,60},{365*65,65},{365*70,70}},Automatic} ],{b,0,3}, { e,0,1}] Manipulate[Plot[Evaluate[II[t]/.First[NDSolve[{S'[t] h-b* h *n* S[t] *Iv[t]- h* S[t],II'[t] b* h* n*S[t] *Iv[t]-( h+r)*II[t],Iv'[t] b * v*(1-Iv[t])*II[t]- v *Iv[t]+ v * e *Iv[t],S[0] 0,II[0] 0.00025,Iv[0] 0.006},{S,II,Iv},{t,0,175 00}]]],{t,0,365*50},PlotRange All,, AxesLabel {"t(tahun)", "Ih"},Ticks {{{365*5,5},
38
{3650,10},{365*15,15},{7300,20},{365*25,25},{10950,30},{365* 35,35},{14600,40},{365*45,45},{17500,50},{365*55,55},{21150, 60},{365*65,65},{24800,70}},Automatic}],{b,0,3},{ e,0,1}] Manipulate[Plot[Evaluate[Iv[t]/.First[NDSolve[{S'[t] h-b* h *n* S[t] *Iv[t]- h* S[t],II'[t] b* h* n*S[t] *Iv[t]-( h+r)*II[t],Iv'[t] b * v*(1-Iv[t])*II[t]- v *Iv[t]+ v * e *Iv[t],S[0] 0,II[0] 0.00025,Iv[0] 0.006},{S,II,Iv},{t,0,175 00}]]],{t,0,365*50},PlotRange All, AxesLabel {"t(tahun)", "I"},Ticks {{{365*5,5}, {3650,10},{365*15,15},{7300,20},{365*25,25},{10950,30},{365* 35,35},{14600,40},{365*45,45},{17500,50},{365*55,55},{21150, 60},{365*65,65},{24800,70}},Automatic}],{b,0,3},{ e,0,1}] Manipulate[ParametricPlot3D[Evaluate[{S[t],II[t],Iv[t]}/.Fir st[NDSolve[{S'[t] h-b* h *n* S[t] *Iv[t]- h*
S[t],II'[t] b* h* n*S[t] *Iv[t]-( h+r)*II[t],Iv'[t] b * v*(1-Iv[t])*II[t]- v *Iv[t]+ v * e *Iv[t],S[0] 0,II[0] 0. 00025,Iv[0] 0.006},{S,II,Iv},{t,0,70000}]]],{t,0,70000},Plo tRange All,Axes True,AxesLabel {"Sh","Ih",
"Iv"},Ticks {{0,0.03,0.06},{0,0.00011,0.0012},
{0,0.00036,0.007}},BoxRatios {1,1,1 }],{b,0,1},{ e,0,1}] Lampiran 5
Program Plot hubungan , , dengan b dan
h=0.0000391; v=0.071; e=0.5; h=0.5; v=0.7;n=10;r=1/3; Sh[b_]:=(b v h+(r + h )(1- e) v)/(b2n h v+b v h) Ih[b_]:=(b2 n h v h- h (r+ h)(1- e) v)/(b v(r+ h) (b n h+ h)) Iv[b_]:=(b2n h v h- h(r+ h)(1- e) v)/(bn h(b v h+(r+ h) (1- e) v))
39
Plot[{Sh[b]},{b,0.1,5},PlotRange All,Ticks {{0,1,3,5},{0,0.1
0,0.20,0.33}},AxesLabel {"b","Sh"},PlotStyle {Thick},
AxesOrigin {0,0.00002},AspectRatio 1]
Plot[{Ih[b]},{b,0.1,5},Ticks {{0,0.1,0.5,1,3,5},{{0.000077,7
7},{0.000090,90},{0.000100,100},{0.000110,110},{0.000117,117 }}},AxesLabel {"b","Ihx10-6"},PlotStyle {Thick},
AxesOrigin {0,0.00007},AspectRatio 1]
Plot[{Iv[b]},{b,0.1,5},Ticks {{0,1,3,5},{0,0.001,0.003,0.005
,0.007,0.009,0.011}},PlotRange All,PlotStyle {Thick},AxesOr igin {0,0.0001},AxesLabel {"b", "Iv"},AspectRatio 1]
Gigitan=Table[{b,Sh[b],Ih[b],Iv[b]},{b,0.1,5,0.1}];
data=TableForm[Gigitan,TableHeadings {Automatic,{"b","Sh","I h","Iv"}}] h=0.0000391; v=0.071;b=0.435; h=0.5; v=0.7;n=10;r=1/3; S[ e_]:=(b v h+(r + h )(1- e) v)/(b2 n h v+b v h) II[ e_]:=(b2 n h v h- h (r+ h)(1- e) v)/(b v(r+ h) (b n h+ h)) Iv[ e_]:=(b2 n h v h- h (r+ h) (1- e) v)/(b n h (b v h+(r+ h) (1- e) v))
Plot[{S[ e]},{ e,0,1},PlotRange All,Ticks {{0,0.5,1},A
utomatic},AxesLabel {" e","Sh"},AxesOrigin {0,0},
AspectRatio 1,PlotStyle {Thick}]
Plot[{II[ e]},{ e,0,1},Ticks {{0,0.6,1},{{114*10-6,114}, {115*10-6,115},{117*10-6,117},{116*10-6,116}}},PlotRange All,
AxesLabel {" e","Ihx10 -6
"},AxesOrigin {0,269*10-6}, AspectRatio 1,PlotStyle {Thick}]}]
Plot[{Iv[ e]},{ e,0,1},Ticks {{0,0.6,0.9,1},Automatic}
,PlotRange All,AxesLabel {" e","Iv"},AspectRatio 1,
PlotStyle {Thick}]
telur=Table[{ e,S[ e] ,II[ e],Iv[ e]},{ e,0,1,0.1}];
TableForm[telur,TableHeadings {Automatic,{" e","Sh","Ih", "Iv"}}]
40
Lampiran 6
Tabel 2 Hubungan antara , , dan b
No
1 0.1 0.338187 7.76E-05 0.000153 2 0.2 0.08457 0.000107 0.000423 3 0.3 0.037596 0.000113 0.000667 4 0.4 0.021153 0.000115 0.000905 5 0.5 0.013541 0.000116 0.001139 6 0.6 0.009406 0.000116 0.001373 7 0.7 0.006912 0.000116 0.001605 8 0.8 0.005293 0.000117 0.001837 9 0.9 0.004183 0.000117 0.002068 10 1 0.003389 0.000117 0.0023 11 1.1 0.002802 0.000117 0.00253 12 1.2 0.002355 0.000117 0.002761 13 1.3 0.002007 0.000117 0.002991 14 1.4 0.001731 0.000117 0.003222 15 1.5 0.001508 0.000117 0.003452 16 1.6 0.001326 0.000117 0.003682 17 1.7 0.001175 0.000117 0.003912 18 1.8 0.001048 0.000117 0.004141 19 1.9 0.000941 0.000117 0.004371 20 2 0.000849 0.000117 0.0046 21 2.1 0.00077 0.000117 0.004829 22 2.2 0.000702 0.000117 0.005059 23 2.3 0.000643 0.000117 0.005288 24 2.4 0.00059 0.000117 0.005517 25 2.5 0.000544 0.000117 0.005745 26 2.6 0.000503 0.000117 0.005974 27 2.7 0.000467 0.000117 0.006203 28 2.8 0.000434 0.000117 0.006431 29 2.9 0.000405 0.000117 0.006659 30 3 0.000378 0.000117 0.006888 31 3.1 0.000354 0.000117 0.007116 32 3.2 0.000333 0.000117 0.007344 33 3.3 0.000313 0.000117 0.007572 34 3.4 0.000295 0.000117 0.0078 35 3.5 0.000278 0.000117 0.008027 36 3.6 0.000263 0.000117 0.008255 37 3.7 0.000249 0.000117 0.008482 38 3.8 0.000236 0.000117 0.00871
41
39 3.9 0.000224 0.000117 0.008937 40 4 0.000213 0.000117 0.009164 41 4.1 0.000203 0.000117 0.009391 42 4.2 0.000194 0.000117 0.009618 43 4.3 0.000185 0.000117 0.009845 44 4.4 0.000176 0.000117 0.010072 45 4.5 0.000169 0.000117 0.010298 46 4.6 0.000161 0.000117 0.010525 47 4.7 0.000155 0.000117 0.010751 48 4.8 0.000148 0.000117 0.010977 49 4.9 0.000142 0.000117 0.011204 50 5 0.000137 0.000117 0.01143 Lampiran 7.
Tabel 3 Hubungan antara , , dan
No