Analisis Model Kinematik Peluru Kendali Pada Penembakan Target Menggunakan Metode Kendali Optimal

Abstrak— Peluru kendali merupakan salah satu wahana nir awak (WANA) yang dapat dikendalikan atau memiliki sistem pengendali otomatis untuk mencari target atau menyesuaikan arah. Masalah pengendali dengan kendala sudut dan waktu akhir dikaji dalam Tugas Akhir ini. Variabel bebas pada model kinematik tak-linear peluru kendali ke target diubah dari waktu terbang ke sudut hadap peluru kendali. Kemudian pengendali diperoleh pada transformasi model kinematik tersebut dengan prinsip minimum Pontryagin. Tujuan pengendali adalah menepatkan arah gerak peluru kendali ke target dengan memenuhi kendala sudut dan waktu akhir. Selanjutnya, daerah range pada beberapa parameter kendala dianalisis untuk memeriksa kelayakan pengendali. Dalam Tugas Akhir ini, simulasi numerik diberikan untuk menunjukkan keefektifan metode kendali optimal pada performansi sistem.

Kata Kunci— daerah range, sudut hadap, wahana nir awak (WANA), waktu akhir.

1. PENDAHULUAN

ASALAH kendali optimal adalah untuk menentukan pengendali yang memenuhi suatu sistem dinamik dan beberapa kendala dengan meminimumkan atau memaksimumkan suatu fungsi tujuan [1]. Kendali itu sendiri mempunyai makna besarnya input yang diberikan untuk membawa suatu keadaan awal ke keadaan akhir yang sesuai dengan fungsi tujuan.

Optimasi dilakukan untuk mendapatkan satu penyelesaian masalah yang membutuhkan informasi sebelumnya sehingga dapat menentukan langkah selanjutnya dalam menyelesaikan masalah tersebut. Pada beberapa masalah optimasi juga digunakan karena tidak adanya data pengukuran secara langsung atau sulit untuk diamati secara langsung. Salah satu metode optimasi yang telah dikenal adalah pengendalian optimal. Metode ini untuk mengoptimasi variabel keadaan dari sistem dinamik [2].

Model yang digunakan pada Tugas Akhir ini adalah model kinematik peluru kendali pada penembakan target diam. Model kinematik ini pada awalnya adalah fungsi turunan terhadap waktu. Oleh karena model dari sistem dikendalikan terhadap sudut hadap, maka model kinematik peluru kendali ditransformasi menjadi model kinematik dengan variabel bebasnya adalah sudut hadap peluru kendali sebagai pengganti waktu terbang. Kemudian dilakukan pengendalian optimal pada model kinematik peluru kendali dengan fungsi tujuannya adalah meminimumkan sudut hadap penembakan dan energi yang dibutuhkan. Kendali optimal diselesaikan dengan prinsip minimum Pontryagin dan

variabel-variabel yang mempengaruhi kendali optimal untuk peluru kendali dioptimasi dengan menggunakan metode kendali optimal. Hasil optimasi tersebut digunakan untuk mengimplementasikan kendali optimal pada panduan peluru kendali. Kemudian, kelayakan pengendali diselidiki dengan menganalisis daerah range pada beberapa parameter kendala. Dalam hal ini, dipilih parameter yang tepat pada daerah range agar dapat menghasilkan performansi sistem yang diinginkan. Selanjutnya, hasil analisis disimulasi untuk menunjukkan keefektifan metode kendali optimal terhadap performansi sistem.

2. MODEL KINEMATIK PELURU KENDALI

Kinematik peluru kendali merupakan gerakan peluru kendali ke target dengan mengabaikan gaya penyebab gerakannya dalam menempuh suatu lintasan tertentu. Secara matematis, peluru kendali dan target diasumsikan sebagai partikel yang diperlakukan sebagai titik. Arah gerak peluru kendali menuju target adalah menyamping dengan sudut hadap awal adalah berlawanan arah jarum jam.

Gambar 1. Geometri Lintasan [3]

Berdasarkan geometri lintasan pada Gambar 1, model kinematik dari peluru kendali ke target yang bergerak vertikal 2 dimensi diberikan sebagai berikut [3]:

θ cos V dt dX = θ sin V dt dY = V a dt d = θ

Analisis Model Kinematik Peluru Kendali

Pada Penembakan Target Menggunakan Metode

Kendali Optimal

Restu Tri Astuti, Subchan

[1]

, dan Kamiran

[2]

Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Teknologi Sepuluh Nopember (ITS)

Jl. Arief Rahman Hakim, Surabaya 60111

Email: subchan@matematika.its.ac.id

[1]

; kamiran@matematika.its.ac.id

[2]

M

(i)

(ii)

(iii)

dengan syarat batas: , 0 ) (t₀ = X X(t_f)= X_f , 0 ) (t₀ = Y Y(t_f)=Y_f , ) (₀ θ₀ θ t = θ(t_f)=θ_f

V adalah kecepatan, t adalah waktu terbang, (X,Y) adalah posisi dan θ adalah sudut hadap peluru kendali. Posisi awal peluru kendali diasumsikan menjadi sistem koordinat awal, dengan axis-X positif adalah panjang LOS. Indeks bawah 0 dan f menunjukkan nilai pada kondisi awal dan akhir. Percepatan a tegak lurus terhadap vektor kecepatan peluru kendali.

3. PENGENDALIAN OPTIMAL

Prinsip minimum Pontryagin digunakan untuk memperoleh kendali terbaik pada model kinematik dari keadaan awal hingga keadaan akhir, yaitu meminimalkan fungsi tujuan dengan kendali u(θ) terbatas. Berikut ini diberikan satu cara dalam menyelesaikan masalah kendali optimal yang diformulasikan sebelumnya. Cara ini menggunakan persamaan Hamiltonian. Langkah penyelesaiannya adalah sebagai berikut [4]:

1. Bentuk Hamiltonian, yaitu:

) , , ( ' ) , , ( ) , , , (x u λ θ = L x u θ +λf x u θ H .

2. Selesaikan persamaan kendali, minimumkan bentuk persamaan Hamiltonian H terhadap u . =0

∂ ∂ u H

untuk memperoleh kondisi stasioner pengendaliu *.

3. Dapatkan Hamiltonian saat kondisi stasioner untuk variabel kendali, yaitu: H*(x,u,λ,θ)=H(x,u*,λ,θ). 4. Selesaikan persamaan co-state:

λ(θ) *(x,u,λ,θ) x H ∂ ∂ − =

 _{dengan syarat batas diberikan}

oleh state awal dan state akhir.

5. Substitusikan hasil-hasil dari langkah (4) ke dalam persamaan u* pada langkah (2) untuk memperoleh kendali optimal yang dicari.

4. ANALISIS MODEL KINEMATIK PELURU KENDALI

Kondisi akhir t_f dan θ_f pada Persamaan (2) ditentukan dengan transformasi: , V X x= , V Y y= dan V a = ω sehingga Persamaan (1) dapat ditulis sebagai berikut:

θ cos = dt dx θ sin = dt dy V a dt d = θ

dengan syarat batas: , 0 ) (t0 = x x(t_f)= x_f = X_f

/

V , 0 ) (t₀ = y y(t_f)= y_f =Y_f

/

V , ) (₀ θ₀ θ t = θ(t_f)=θ_f

Persamaan ( i dan 4) ( ii4 ) dibagi oleh ( iii4 ) dengan dimisalkan ω≠0 dan u(θ)=1/ω, sehingga diperoleh:

θ θ θ u( )cos ddx = θ θ θ u( )sin ddy = ) (θ θ u ddt =

dengan syarat batas: , 0 ) (θ0 = x x(θ_f)=x_f , 0 ) (θ₀ = y y(θ_f)= y_f , 0 ) (θ₀ = t t(θ_f)=t_f

Permasalahan dalam Tugas Akhir ini adalah mendapatkan lintasan peluru kendali dari kondisi awal hingga akhir dengan meminimumkan sudut hadap penembakan dan energi yang digunakan pada sistem, yaitu dengan menggunakan sudut yang optimum dari pergerakan peluru kendali ke target sehingga fungsi tujuan dapat diformulasikan sebagai berikut:

θ θ θ θ d u J f ) ( 2 1 min 0 2 ∫ =

dengan: θ =sudut hadap, θ₀ ≤θ≤θ_f. θ₀ =sudut hadap awal.

θ_f =sudut hadap akhir.

Pengendalian optimal diperoleh dengan meminimumkan persamaan state terhadap pengendali dalam daerah pengendali. Sehingga kondisi perlu yang dibentuk oleh prinsip minimum Pontryagin adalah persamaan co-state dan kondisi stasioner dari persamaan Hamiltonian.

1. Persamaan Hamiltonian f' λ + = L H ) ( ) sin cos ( ) ( 2 1 2 _{θ λ θ λ θ λ θ} u u + _x + _y + _t = 2. Kondisi stasioner 0 = ∂ ∂ u H ) sin cos ( ) ( _{x y t} uθ =− λ θ+λ θ+λ 3. Persamaan co-state

































































= ∂ ∂ − ∂ ∂ − ∂ ∂ − = 0 0 0 t H y H x H t y x λ λ λ   

4. Subsitusi persamaan (10) ke Persamaan (5), diperoleh: ) cos cos sin cos (λ 2θ λ θ θ λ θ θ x y t d dx + + − = (i) (ii) (iii) (i) (ii) (iii) (i) (ii) (iii) (i) (ii) (iii) (ii) (iii) (i) (2) (3) (4) (5) (6) (7) (8) (9) (10)

) sin sin cos sin (λ θ θ λ 2θ λ θ θ x y t d dy + + − = ) sin cos ( _{x y t} d dt λ θ λ θ λ θ =− + +

5. Integral Persamaan (11) dengan syarat batas (6), diperoleh nilai pengali Lagrange sebagai berikut:

) )(sin( sin (sin 2 1 [ det 0 0 θ θ θ θ λ = − f _f − _f − x A t 2 0 0 ( ) 2 1 [ det ))] (θ θ θ −θ − + − − f _f f A x ) 2 sin 2 )(sin ( 4 1 0 0 θ θ θ θ − − − _{f f} ] ) cos (cosθ − θ0 2 − _f ) )(sin( cos (cos 2 1 [ det 0 0 θ θ θ θ λ = f _f − _f − y A t ) ( 4 1 [ det ))] (θ −θ₀ + − θ −θ₀ − f _f f A x ) cos (cos ) 2 cos 2 (cos θ_f − θ₀ + θ_f − θ₀ )] sin (sinθ_f − θ₀ ))] ( sin ) (( 4 1 [ det 0 2 2 0 θ θ θ θ λ = − f _f − − _f − t A t ) sin (sin 2 1 [ det 0 θ θ − − + f _f A x ))] ( ) (sin(θ_f −θ₀ − θ_f −θ₀ dengan )] sin( ) [( detA= θ_f −θ₀ − θ_f −θ₀ ) ( 4 1 ) ( 4 1 [ θ −θ₀ 2 + θ −θ₀ × _{f f} ] 1 ) cos( ) ( _{0 0}

sin

θ_f −θ + θ_f −θ −

Berdasarkan Persamaan (5), yaitu u(θ)=1/ω dan V

a / =

ω , maka penyelesaian analitik pada masalah kendali dengan kendala waktu dan sudut yaitu:

t y x V a λ θ λ θ λ + + − = sin cos

Untuk mendapatkan waktu tempuh, maka persamaan (13) disubsitusikan ke persamaan (1iii), kemudian diintegralkan dengan syarat batas (2iii).

1. Subsitusi persamaan (13) ke (1iii), diperoleh:

t y x dt d λ θ λ θ λ θ + + − = sin cos 1

2. Integral persamaan (14) dengan syarat batas (2iii), diperoleh: + − − = λ_x

(

sinθ_f sinθ₀

)

go T ) ( ) cos (cosθ θ₀ λ θ θ₀ λ_{y f} − − _{t f} −

Pengendali dikatakan fisibel jika kendala akhir terpenuhi. Berdasarkan persamaan (13) dapat dinyatakan bahwa

persamaan percepatan akan berlaku jika dan hanya jika persamaan penyebut (denumenator) tidak bernilai nol selama peluru kendali bergerak.

Teorema 1[3]:

Dengan kondisi batas xf,θ0,θf,dan tf , pengendali akan

fisibel jika dan hanya jika 0 sin cos + _y + _t ≠ x θ λ θ λ λ ] , [θ₀ θ_f θ∈ ∀ atau

[

θ_f,θ₀] Akibat 1:

Dengan kondisi batas x_f,θ₀,θ_f,dan t , pengendali akan _f fisibel jika dan hanya jika

0 2 2 2 _{− − >} y x t λ λ λ

Untuk mencapai target dengan waktu yang tepat, maka perlu untuk menentukan daerah range waktu akhir pada pengendali. Penentuan daerah range ini dapat menghasilkan performansi sistem yang diinginkan. Berikut diberikan definisi dari daerah range waktu akhir, yaitu:

Definisi 1[3]:

Dengan kondisi batas x_f,θ₀,θ_f,himpunan waktu akhir t _f yang memenuhi persamaan (16)-(17) disebut daerah range waktu akhir t_f dan dinotasikan sebagai Φ(t_f).

Selanjutnya, untuk mendapatkan daerah range waktu akhir t , yaitu dengan menggunakan Persamaan (17) dapat _f ditulis sebagai berikut:

+ − − = − − 2 2 2 2 1 2 3 2 2 2 ) ( _f y x t λ λ c c c t λ + − −cd c d t_f d c ) ( 2 _{3 3 1 1 2 2} 0 2 2 2 1 2 3 −d −d > d dengan: 2 / )] ( ) )[sin( sin (sin _{0 0 0} 1 =− θf − θ θf −θ − θf −θ c 2 / )] ( ) )[sin( cos (cos _{0 0 0} 2 = θf − θ θf −θ − θf −θ c 4 / )] ( ) )][sin( ( ) [sin( _{0 0 0 0} 3 = θf −θ + θf −θ θf −θ − θf −θ c − − − − − − = ( )(sin2 sin2 ) 4 1 ) ( 2 1 [ ₀ 2 _{0 0} 1 xf θf θ θf θ θf θ d ] ) cos (cosθ −_f θ₀ 2 + − − − = ( )(cos2 cos2 ) 4 1 [ _{0 0} 2 xf θf θ θf θ d ] sin sin cos cos

)(

)

(

θ_f − θ₀ θ_f − θ₀ 2 / sin( sin sin

)[

)

(

)]

(

0 0 0 3 =−xf θf − θ θf −θ

−

θf −θ d

sehingga dari Persamaan (17), diperoleh: Akibat 2:

Dengan kondisi batas x_f,θ₀,θ_f,dan t , pengendali _f dikatakan fisibel jika:

+ − − = 2 2 2 2 1 2 3 ) ( ) (t_f c c c t_f h + − −cd c d t_f d c ) ( 2 _{3 3 1 1 2 2} 0 2 2 2 1 2 3 −d −d > d (11) (12) (13) (14) (15) (16) (17) (18) (19)

dengan memperhatikan Persamaan (18)-(19), diperoleh: 4 ) (sin 2 2 2 2 1 2 3 θ θ ∆− ∆ = − −c c c

















− ∆ + ∆ + ∆ ∆ + ∆ × 2cos 2 4 2 sin 4 sin2 θ θ θ θ2 _θ

dengan ∆θ =θ_f −θ₀, sehingga dapat ditulis: 0 2 2 2 1 2 3 −c −c < c ⇔∆θ∈

(

−4.28,4.28

)

dan ∆θ ≠0.

5. SIMULASI DAN ANALISIS

Hasil analisis parameter kendala sudut hadap dan waktu akhir pada model kinematik peluru kendali selanjutnya diimplementasikan untuk proses simulasi. Simulasi ini diberikan untuk menunjukkan keefektifan metode kendali optimal terhadap performansi sistem. Untuk nilai parameter dari kinematik peluru kendali dapat digunakan nilai data pada Tabel 1-3.

Tabel 1. Data Parameter Kinematik Misil I

Parameter Nilai V _{(250 /} 2₎ s m ) , (x₀ y₀ (0,0) ) , (x_f y_f (40,0) ) , (θ₀ θ_{f (−60}0_,900₎

Berikut ini adalah grafik lintasan peluru kendali. Berdasarkan nilai parameter pada Tabel 1, maka dari Persamaan (19) diperoleh daerah range waktu akhir

) 6 . 70 , 8 . 50 ( ) (t_f = s s

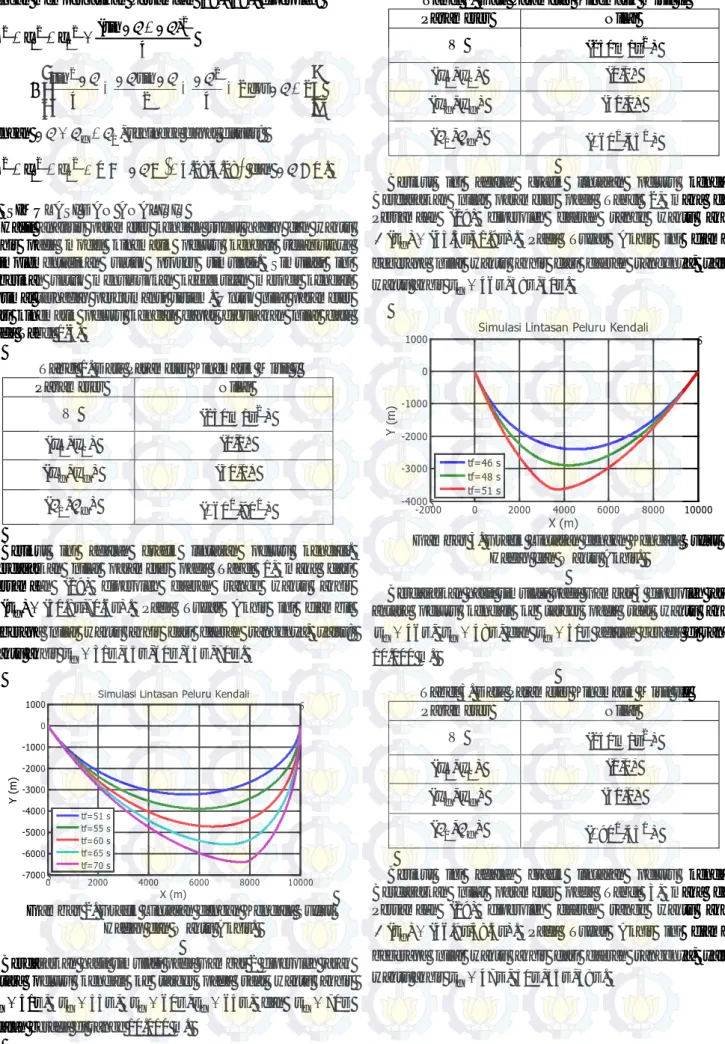
Φ . Pada Tugas Akhir ini diambil beberapa nilai waktu akhir dari daerah rangenya, yaitu: waktu akhir t_f =51s,55s,60s,65s,70s. 0 2000 4000 6000 8000 10000 -7000 -6000 -5000 -4000 -3000 -2000 -1000 0 1000 X (m) Y ( m )

Simulasi Lintasan Peluru Kendali

tf=51 s tf=55 s tf=60 s tf=65 s tf=70 s

Gambar 2. Grafik Lintasan dengan Kendala Sudut

Hadap dan Waktu Akhir.

Berdasarkan hasil simulasi pada Gambar 2 diperoleh jarak antara peluru kendali ke target pada saat waktu akhir

s

t_f =51 , t_f =55s, t_f =60s,t_f =65s, dan t_f =70s adalah berada di range 10.000 m.

Tabel 2. Data Parameter Kinematik Misil II

Parameter Nilai V _{(250 /} 2₎ s m ) , (x0 y0 (0,0) ) , (x_f y_f (40,0) ) , (θ₀ θ_{f (−60}0_,450₎

Berikut ini adalah grafik lintasan peluru kendali. Berdasarkan nilai parameter pada Tabel 2, maka dari Persamaan (19) diperoleh daerah range waktu akhir

) 9 . 51 , 5 . 45 ( ) (t_f = s s

Φ . Pada Tugas Akhir ini diambil beberapa nilai waktu akhir dari daerah rangenya, yaitu: waktu akhir t_f =46s,48s,51s. -2000 0 2000 4000 6000 8000 10000 -4000 -3000 -2000 -1000 0 1000 X (m) Y ( m )

Simulasi Lintasan Peluru Kendali

tf=46 s tf=48 s tf=51 s

Gambar 3. Grafik Lintasan dengan Kendala Sudut

Hadap dan Waktu Akhir.

Berdasarkan hasil simulasi pada Gambar 3 diperoleh jarak antara peluru kendali ke target pada saat waktu akhir

s

t_f =46 , t_f =48s, dan t_f =51s adalah berada di range 10.000 m.

Tabel 3. Data Parameter Kinematik Misil III

Parameter Nilai V _{(250 /} 2₎ s m ) , (x₀ y₀ (0,0) ) , (x_f y_f (40,0) ) , (θ₀ θ_{f (−90}0_,450₎

Berikut ini adalah grafik lintasan peluru kendali. Berdasarkan nilai parameter pada Tabel 3, maka dari Persamaan (19) diperoleh daerah range waktu akhir

) 4 . 58 , 9 . 46 ( ) (t_f = s s

Φ . Pada Tugas Akhir ini diambil

beberapa nilai waktu akhir dari daerah rangenya, yaitu: waktu akhir t_f =47s, 50s,55s,58s.

-2000 0 2000 4000 6000 8000 10000 -5000 -4000 -3000 -2000 -1000 0

1000 Simulasi Lintasan Peluru Kendali

X (m) Y ( m ) tf=47 s tf=50 s tf=55 s tf=58 s

Gambar 4. Grafik Lintasan dengan Kendala Sudut

Hadap dan Waktu Akhir.

Berdasarkan hasil simulasi pada Gambar 4 diperoleh jarak antara peluru kendali ke target pada saat waktu akhir

s

t_f =47 , t_f =50s, t_f =55s dan t_f =58s adalah berada di range 10.000 m.

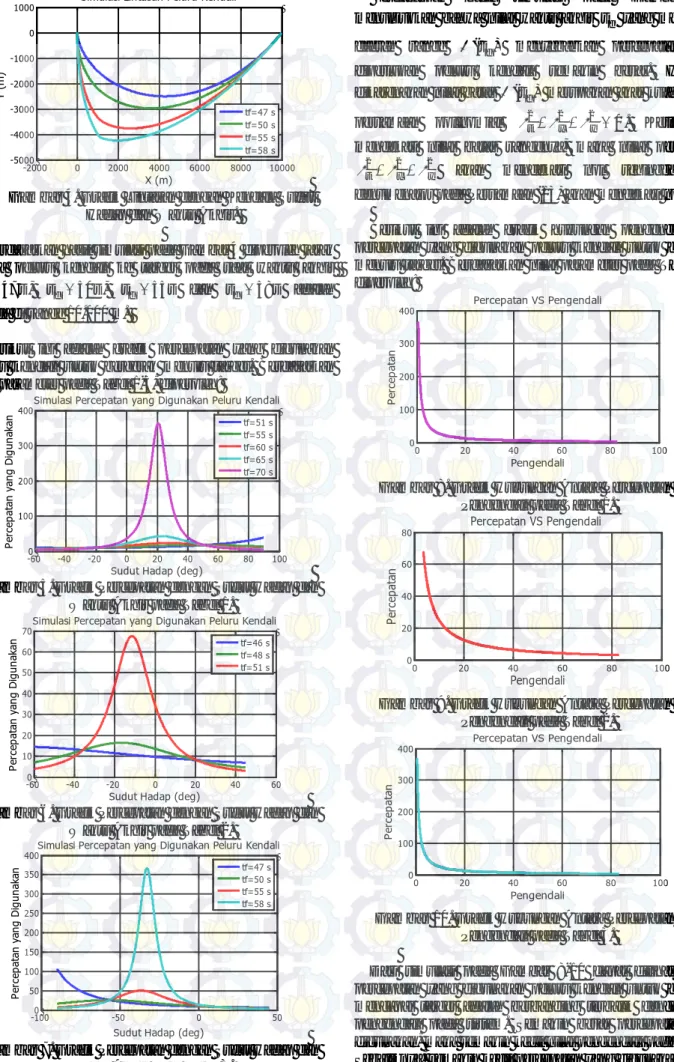
Berikut ini adalah grafik percepatan yang digunakan peluru kendali untuk bergerak menuju target. Berdasarkan nilai parameter pada Tabel 1-3, diperoleh:

-600 -40 -20 0 20 40 60 80 100 100

200 300

400Simulasi Percepatan yang Digunakan Peluru Kendali

Sudut Hadap (deg)

Pe rc ep at an y an g D ig un ak an tf=51 s tf=55 s tf=60 s tf=65 s tf=70 s

Gambar 5. Grafik Percepatan dengan Sudut Hadap dan

Waktu Akhir pada Tabel 1.

-600 -40 -20 0 20 40 60 10 20 30 40 50 60 70

Sudut Hadap (deg)

Pe rc ep at an y an g D ig un ak an

Simulasi Percepatan yang Digunakan Peluru Kendali tf=46 s tf=48 s tf=51 s

Gambar 6. Grafik Percepatan dengan Sudut Hadap dan

Waktu Akhir pada Tabel 2.

-1000 -50 0 50 50 100 150 200 250 300 350 400

Sudut Hadap (deg)

Pe rc ep at an y an g D ig un ak an

Simulasi Percepatan yang Digunakan Peluru Kendali tf=47 s tf=50 s tf=55 s tf=58 s

Gambar 7. Grafik Percepatan dengan Sudut Hadap dan

Waktu Akhir pada Tabel 3.

Berdasarkan hasil simulasi pada Gambar 5-7 menunjukkan bahwa nilai waktu akhir t yang mendekati _f daerah range Φ(t_f) menyebabkan percepatan yang diperlukan peluru kendali semakin besar. Hal ini dikarenakan nilai batas Φ(t_f) merupakan akar kuadrat dari persamaan polinomial λ2t −λ2x−λ2y =0. Ketika t f

mendekati nilai batas rangenya, maka nilai persamaan

2 2 2 y x t λ λ

λ − − akan mendekati nol sehingga nilai denumenator pada Persamaan (13) akan mendekati nol pula. Berikut ini adalah grafik hubungan pengendali dan percepatan yang digunakan peluru kendali untuk bergerak menuju target. Berdasarkan nilai parameter pada Tabel 1-3 diperoleh: 0 20 40 60 80 100 0 100 200 300 400 Pengendali Per cep at an Percepatan VS Pengendali

Gambar 8. Grafik Hubungan Antara Percepatan dan

Pengendali pada Tabel 1.

0 20 40 60 80 100 0 20 40 60 80 Percepatan VS Pengendali Pengendali Per cep at an Gambar 9. Grafik Hubungan Antara Percepatan dan

Pengendali pada Tabel 2.

0 20 40 60 80 100 0 100 200 300 400 Percepatan VS Pengendali Pengendali Per cep at an Gambar 10. Grafik Hubungan Antara Percepatan dan

Pengendali pada Tabel 3.

Dari simulasi pada Gambar 8-10 dapat dilihat bahwa percepatan yang digunakan peluru kendali untuk bergerak mencapai target adalah berbanding terbalik dengan nilai pengendali pada sistem. Semakin besar percepatan yang digunakan, maka semakin kecil nilai pengendali pada sistem. Sebaliknya, semakin kecil percepatan yang digunakan, maka

semakin besar nilai pengendali pada sistem. Hal ini sesuai dengan Persamaan (13).

6. KESIMPULAN

Berdasarkan hasil simulasi dari analisis dan pembahasan yang telah dilakukan mengenai analisis model kinematik peluru kendali dengan menggunakan metode kendali optimal, diperoleh kesimpulan bahwa :

a) Jarak antara peluru kendali ke target pada saat waktu akhir t adalah berada di range 10.000 m. Semakin besar _f nilai waktu akhir t , maka lintasan peluru kendali semakin _f panjang. Sehingga lintasan yang paling optimal adalah pada saat nilai waktu akhir t_f mendekati daerah range waktu akhir Φ(t_f) .

b) Nilai waktu akhir t yang mendekati daerah range waktu _f akhir Φ(t_f) menyebabkan percepatan yang diperlukan peluru kendali semakin besar sehingga semakin besar percepatan yang digunakan peluru kendali untuk bergerak menuju target, maka semakin kecil nilai pengendali pada sistem. Sebaliknya, semakin kecil percepatan yang digunakan peluru kendali untuk bergerak menuju target, maka semakin besar nilai pengendali pada sistem.

DAFTARPUSTAKA

[1] Siouris, G. (2003). Missile Guidance and Control Systems.

USA:Springer.

[2] Tahiyatul, A., Subchan. (2011). “Control Estimation with

EKF-UI-WDF Method of The Missile-Target Interception Model”. Proceedings of The IceMath. Topics, pp. xx-xx.

[3] Zhao, S., Zhou, R., dan Wei, C. (2009). “Design and Feasibility

Analysis of a Closed-Form Guidance Law with both Impact Angle and Time Constraints”. Journal of Astronautics. Vol.30, Hal. 1000-1328.