BAB 2. Landasan Teori

BAB 2

Landasan Teori

2.1. Teori Himpunan Fuzzy

Definisi : Andaikan X titik-titik ruang (objek), dengan elemen umum dari X yang dinotasikan dengan x, X = { x } [16].

Himpunan fuzzy adalah himpunan yang unsur-unsurnya memiliki derajat keanggotaan. Himpunan fuzzy diperkenalkan oleh Lutfih A. Zadeh (1965) sebagai perluasan dari pengertian himpunan klasik. Pada teori himpunan klasik, keanggotaan dari unsur-unsur dalam himpunan dinilai dalam hal biner menurut kondisi bivalen-elemen baik termasuk atau tidak termasuk dalam himpunan. Sebaliknya, teori himpunan fuzzy memungkinkan penilaian bertahap dari keanggotaan elemen dalam himpunan, ini digambarkan dengan bantuan sebuah fungsi keanggotaan yang dinilai dalam unit nyata interval [0,1].

Dalam teori himpunan fuzzy, himpunan A dikatakan crisp jika sebarang anggota-anggota yang ada pada himpunan A tersebut dikenakan fungsi yang akan bernilai 1 yakni jika 𝑎 ∈ 𝐴 maka fungsi 𝑎 = 1. Namun jika 𝑎 ∈ 𝐴, maka nilai fungsi

yang dikenakan pada 𝑎 adalah 0. Nilai fungsi yang dikenakan pada sebarang anggota himpunan A dikatakan sebagai nilai keanggotaan. Jadi pada himpunan crisp, hanya mempunyai 2 nilai keanggotaan yaitu 0 atau 1. Tetapi pada himpunan fuzzy, nilai keanggotaan dari anggota-anggotanya tidak hanya 0 dan 1 saja. Tapi berada pada interval tertutup [0,1]. Dengan kata lain himpunan A dikatakan fuzzy selama fungsi

𝜇 ∶ 𝐴 → 0,1 .

Himpunan Fuzzy didasarkan pada gagasan untuk memperluas jangkauan fungsi karakteristik sedemikian hingga fungsi tersebut akan mencakup bilangan real pada interval [0,1]. Nilai keanggotaannya menunjukkan bahwa suatu item dalam semesta pembicaraan tidak hanya berada pada 0 atau 1, namun juga nilai yang terletak diantaranya. Dengan kata lain, nilai kebenaran suatu item tidak hanya bernilai benar atau salah. Nilai 0 menunjukkan salah, nilai 1 menunjukkan benar, dan masih ada nilai-nilai yang terletak antara benar dan salah [8].

Misalkan diketahui klasifikasi sebagai berikut :

MUDA umur < 35 tahun

SETENGAH BAYA 35 umur 55 tahun

TUA umur > 55 tahun

Dengan menggunakan pendekatan crisp, amatlah tidak adil untuk menetapkan nilai SETENGAH BAYA. Pendekatan ini bisa saja dilakukan untuk hal-hal yang bersifat diskontinu. Misalkan klasifikasi untuk umur 55 dan 56 sangat jauh berbeda, umur 55 tahun termasuk SETENGAH BAYA, sedangkan umur 56 tahun sudah tidak termasuk tua. Demikian pula kategori MUDA dan TUA. Orang yang berumur 34 tahun dikatakan MUDA, sedangkan orang yang berumur 35 tahun sudah TIDAK MUDA lagi. Orang yang berumur 55 tahun termasuk SETENGAH BAYA, orang yang berumur 55 tahun lebih 1 hari sudah TIDAK SETENGAH BAYA lagi. Dengan

demikian pendekatan crisp ini sangat tidak cocok untuk diterapkan pada hal-hal yang bersifat kontinu, seperti umur.

Selain itu, untuk menunjukkan suatu umur pasti termasuk SETENGAH BAYA, atau tidak termasuk SETENGAH BAYA, dan menunjukkan suatu nilai kebenaran 0 atau 1, dapat digunakan nilai pecahan dan menunjuk 1 atau nilai yang dekat dengan 1 untuk umur 45 tahun, kemudian perlahan menurun menuju ke 0 untuk umur dibawah 35 tahun dan diatas 55 tahun.

Pusat dari fungsi keanggotaan untuk beberapa himpunan fuzzy A didefinisikan sebagai daerah dari universe yang dicirikan oleh keanggotaan lengkap dan penuh dalam himpunan A yaitu pusat terdiri dari elemen-elemen x dari universe sehingga 𝜇_𝐴 𝑥 = 1.

Penyokong dari fungsi tujuan untuk beberapa himpunan fuzzy A didefinisikan sebagai daerah dari universe yang dicirikan oleh keanggotaan tak nol dalam himpunan A yaitu penyokong terdiri dari elemen-elemen x dari universe sehingga 𝜇_𝐴 𝑥 > 0. Suatu himpunan fuzzy yang pendukungnya merupakan satu titik di dalam universe disebut fuzzy singleton.

Batas dari fungsi tujuan untuk beberapa himpunan fuzzy A didefinisikan sebagai daerah dari universe berisi elemen-elemen yang memiliki keanggotaan tak nol tetapi juga keanggotaan tidak lengkap yaitu batas terdiri dari elemen-elemen x dari universe sehingga 0 < 𝜇_𝐴 𝑥 < 1.

Himpunan fuzzy convex dilukiskan oleh fungsi keanggotaan yang nilai keanggotaan merupakan penambahan tepat secara monoton atau nilai keanggotaan merupakan pengurangan tepat secara monoton atau nilai keanggotaan merupakan penambahan tepat secara monoton kemudian nilai keanggotaan merupakan pengurangan tepat secara monoton dengan menambahkan nilai untuk elemen dalam universe. Dengan kata lain, jika untuk beberapa nilai elemen x, y, z dalam himpunan fuzzy A, relasi 𝑥 < 𝑦 < 𝑧 yang mengandung arti bahwa

𝜇𝐴 𝑦 ≥ min [𝜇𝐴 𝑥 , 𝜇𝐴 𝑧 ] (2.1)

2.1.1. Fungsi Keanggotaan

Fungsi keanggotaan (membership function) adalah suatu kurva yang menunjukkan pemetaan titik-titik input data ke dalam nilai keanggotaannya (sering juga disebut dengan derajat keanggotaan) yang memiliki interval antara 0 sampai 1 [8].

Sebuah himpunan fuzzy A dari bilangan riil  didefinisikan oleh fungsi keanggotaannya (dinotasikan oleh A)

𝜇𝐴 ∶  → 0,1 (2.2)

Jika 𝑥 ∈  maka 𝜇_𝐴 𝑥 dikatakan sebagai derajat keanggotaan x dalam A. Himpunan fuzzy dalam disebut normal jika terdapat 𝑥 ∈  sehingga 𝜇_𝐴 𝑥 = 1 .

2.1.2. Bilangan Fuzzy Triangular

Sebuah himpunan fuzzy A disebut bilangan fuzzy triangular dengan nilai tengah a, sebelah kiri 𝛼 > 0 , dalam disebut convex jika A adalah unimodal (sebagai sebuah fungsi). Bilangan fuzzy dan sebelah kanan 𝛽 > 0. Fungsi keanggotaannya adalah sebagai berikut : 𝜇𝐴 𝑥 = 1 − 𝑎−𝑥 _𝛼 𝑎 − 𝛼 ≤ 𝑥 ≤ 𝑎 1 − 𝑥−𝑎 _𝛽 𝑎 ≤ 𝑥 ≤ 𝑎 + 𝛽 0 𝑙𝑎𝑖𝑛𝑛𝑦𝑎 (2.3)

Penyokong A adalah (𝑎 − 𝛼, 𝑎 + 𝛽). Bilangan fuzzy triangular dengan nilai tengah a dilihat sebagai nilai kwantitas fuzzy. “ x dekat terhadap a “atau” x hampir sama dengan a”.

𝜇 𝑥 1

𝑎 − 𝛼 𝑎 𝑎 + 𝛽 x Gambar 2.1 Bilangan Fuzzy Triangular

2.1.3. Bilangan Fuzzy Trapezoidal

Sebuah himpunan fuzzy A disebut bilangan fuzzy trapezoidal dengan interval toleransi [a,b], sebelah kiri 𝛼 dan kanan 𝛽. Fungsi keanggotaannya adalah sebagai berikut :

𝜇𝐴 𝑥 = 1 − 𝑎−𝑥 𝛼 𝑎 − 𝛼 ≤ 𝑥 ≤ 𝑎 1 𝑎 ≤ 𝑥 ≤ 𝑏 1 − 𝑥−𝑎 _𝛽 𝑎 ≤ 𝑥 ≤ 𝑏 + 𝛽 0 𝑙𝑎𝑖𝑛𝑛𝑦𝑎 (2.4)

Penyokong A adalah (𝑎 − 𝛼, 𝑎 + 𝛽). Bilangan fuzzy trapezoidal dapat dilihat sebagai nilai kwantitas fuzzy. “ x mendekati pada interval [a,b] ”.

𝜇 𝑥 1

x

𝑎 − 𝛼 a b 𝑏 + 𝛽

Gambar 2.2 Bilangan Fuzzy Trapezoidal

2.2 Goal Programming

2.2.1 Konsep Dasar dari Goal Programming

Dalam bukunya [9], Linier goal programming (LGP) merupakan pengembangan Linier Programming (LP). LGP diperkenalkan oleh Charnes dan Cooper pada awal tahun 60-an. Perbedaan utama dari LGP dan LP terletak pada struktur dan penggunaan fungsi tujuan. Dalam LP fungsi tujuannya hanya mengandung satu tujuan, sementara dalam LGP semua tujuan apakah satu atau beberapa digabungkan dalam sebuah fungsi tujuan. Ini dapat dilakukan dengan mengekspresikan tujuan itu dalam bentuk kendala (goal constraint), memasukkan suatu variabel simpangan (deviational variable) dalam kendala itu untuk mencerminkan seberapa jauh tujuan itu dicapai, dan menggabungkan variabel simpangan dalam fungsi tujuan. Dalam LP tujuannya bisa

maksimasi atau minimisasi, sementara dalam LGP tujuannya adalah meminimumkan penyimpangan-penyimpangan dari tujuan-tujuan tertentu. Ini berarti semua masalah LGP adalah masalah minimisasi.

a. Berikut ini adalah definisi dari beberapa istilah dan lambang yang biasa digunakan dalam LGP.

 Decision variable (Variabel keputusan) : seperangkat variabel yang tidak diketahui (dalam model LGP dilambangkan dengan x_j, dimana j = 1,2,…,n) yang akan dicari nilainya

 Right hand side values (RHS) : nilai – nilai yang biasanya menunjukkan ketersediaan sumber daya (dilambangkan dengan b_i) yang akan ditentukan kekurangan atau kelebihan penggunaannya.

 Goal (Tujuan) : keinginan untuk meminimumkan angka penyimpangan dari suatu nilai RHS pada suatu goal constraint / kendala tujuan tertentu.

 Goal Constraint (Kendala Tujuan): sinonim dari istilah goal equation, yaitu suatu tujuan yang diekspresikan dalam persamaan matematik dengan memasukkan variabel simpangan.

 Preemptive priority factor : suatu system urutan (yang dilambangkan dengan P_k, dimana k = 1,2,…,K dan K menunjukkan banyaknya tujuan dalam model) yang memungkinkan tujuan-tujuan disusun secara ordinal dalam model LGP. Sistem urutan itu menempatkan tujuan-tujuan dalam susunan dengan hubungan seperti berikut :

𝑃₁ > 𝑃₂ > ⋯ > 𝑃_𝑘

1

P merupakan tujuan yang paling penting

2

P merupakan tujuan yang kurang penting dan seterusnya.

 Deviational vearible (Variabel simpangan) : variabel-variabel yang menunjukkan kemungkinan penyimpangan negatif dari suatu nilai RHS kendala tujuan (dalam

model LGP dilambangkan dengan d_i, dimana i = 1,2,…,m dan m adalah banyaknya kendala tujuan dalam model) atau penyimpangan positif dari suatu nilai RHS (dilambangkan dengan d_i). Variabel-variabel ini serupa dengan slack variabel dalam LP.

 Differential weight (bobot) : timbangan matematik yang diekspresikan dengan angka kardinal (dilambangkan dengan w_kidimana k =1,2,…, K: i =1,2,…m) dan digunakan untuk membedakan variabel simpangan i di dalam suatu tingkatan prioritas k.

 Technological coeffient (koefisien teknologi) : nilai-nilai numerik (dilambangkan dengan a_ij) yang menunjukkan penggunaan nilai b_iper unit untuk menciptakan

j x .

b. Unsur-unsur Linear Goal Programming (LGP)

Setiap model LGP paling sedikit terdiri dari tiga komponen yaitu, sebuah fungsi tujuan, kendala tujuan dan kendala non-negatif.

 Fungsi Tujuan

Ada tiga jenis fungsi tujuan dalam LGP, yaitu :

Minimumkan Z =



  _ m i i i d d 1

Fungsi tujuan diatas digunakan jika variabel simpangan dalam suatu masalah tidak dibedakan menurut prioritas atau bobot.

Minimumkan Z =



   _ m i i i k d d P 1 ) ( untuk k = 1,2,…,K

Fungsi tujuan diatas digunakan dalam suatu masalah dimana urutan tujuan-tujuan diperlukan, tetapi variabel simpangan di dalam setiap tingkat prioritas memiliki kepentingan yang sama.

Minimumkan Z =



   _ m i i i k kiP d d w 1 ) ( untuk k = 1,2,…,K

Fungsi tujuan diatas digunakan dalam suatu masalah dimana tujuan-tujuan diurutkan dan variabel simpangan pada setiap tingkat prioritas dibedakan dengan menggunakan bobot yang berlainan w_ki[8].

) (x

Fi merupakan bentuk matematika yang mewakili tujuan dan biadalah nilai sisi kanan/ level aspirasi.

Ada tiga kemungkinan tujuan yaitu: i i x b f ( ) i i x b f ( ) i i x b f ( )  Kendala Tujuan

Ada enam jenis kendala tujuan yang berlainan yang maksud setiap jenis kendala itu ditentukan oleh hubungannya dengan fungsi tujuan.pada tabel berikut:

Kendala Tujuan Variabel simpangan dalam fungsi tujuan Kemungkinan Simpangan Penggunaan Nilai RHS yang diinginkan i i j ijx d b a    d_i Negatif = b_i i i j ijx d b a    d_i Positif = b_i i i i j ijx d d b a       i

d Negatif dan positif bi atau lebih

i i i j ijx d d b a       i

Kendala Tujuan Variabel simpangan dalam fungsi tujuan Kemungkinan Simpangan Penggunaan Nilai RHS yang diinginkan i i i j ijx d d b a       i

d dan d_i Negatif dan positif = b_i

i i j

ijx d b

a    d_i (artf.) Tidak ada pas = b_i

Setiap jenis kendala tujuan harus punya satu atau dua variabel simpangan yang ditempatkan pada fungsi tujuan. Dimungkinkan adanya kendala-kendala persamaan linier. Persamaan pertama maknanya serupa dengan kendala pertidaksamaan  dalam masalah program linier maksimisasi. Persamaan kedua maknanya serupa dengan kendala pertidaksamaan  pada masalah program linier minimisasi. Persamaan ketiga, keempat dan kelima semuanya memperbolehkan penyimpangan dua arah, tetapi persamaan kelima mencari penggunaan sumber daya yang diingginkan sama dengan b_i. Ini serupa dengan kendala persamaan dalam linier programming, tetapi tidak menempel pada solusi karena dimungkinkan adanya penyimpangan negatif dan positif. Jika kendala persamaan dianggap perlu dalam perumusan model linear goal programming (LGP), ia dapat dimasukkan dengan menempatkan sebuah variabel artifial d_i, seperti pada persamaan keenam. Persamaan ketiga dan keempat memperbolehkan adanya penyimpangan positif dan negatif dari nilai RHSnya.

 Kendala Non-Negatif

Seperti dalam liear programming, variabel-variabel model LGP biasanya bernilai lebih besar atau sama dengan nol. Semua model LGP terdiri dari variabel simpangan dan variabel keputusan, sehingga pernyataan non-negatif dilambangkan sebagai :

0 ,

,d  d   x

 Kendala Struktural

Disamping ketiga komponen yang telah disebutkan itu, dalam model LGP kadang-kadang terdapat komponen yang lain, yaitu kendala struktural artinya kendala-kendala lingkungan yang tidak berhubungan langsung dengan tujuan-tujuan masalah yang dipelajari. Variabel simpangan tidak dimasukkan dalam kendala ini, karena itu, kendala ini tidak diikutsertakan dalam fungsi tujuan.

2.3. Model Fuzzy Goal Programming

Pemaparan teori himpunan fuzzy untuk masalah goal programming pertama kali dikemukakan oleh Hannan(1981) juga Ignizio (1982). Secara komprehensif berbagai aspek teori keputusan dengan menggunakan pendekatan fuzzy goal programming didiskusikan oleh Rubin dan Narasimhan (1984) juga Tiwarki dkk (1986). Aplikasinya untuk pemodelan keputusan untuk berbagai aspek yang luas, misalnya untuk persoalan manajemen lingkungan diungkapkan oleh Tiwari dkk (1985).

Ada sedikit perbedaan antara Goal Programming dan Fuzzy Goal Programming yaitu goal programming membutuhkan pengambil keputusan untuk menetapkan dengan pasti nilai-nilai aspirasi untuk setiap tujuan yang ingin dia capai, sedangkan kemudian ditetapkan dalam cara yang tidak teliti. Tujuan fuzzy di sini dianggap sebagai tujuan dengan tingkat aspirasi tidak tepat. Pertimbangan kepentingan relatif berbeda dan tujuan prioritas dalam tujuan fuzzy layak daripada yang lain. Narasimhan telah menggunakan linguistik variabel, seperti "sangat penting", "kurang penting" dan "agak penting", untuk menggambarkan bobot fuzzy tujuan, dan didefinisikan keanggotaan sesuai fungsi dengan menentukan interval derajat keanggotaan yang diinginkan untuk mencerminkan pentingnya.

Model formulasi fuzzy goal programming adalah sbb: Cari nilai

𝑋 𝑥₁, 𝑥₂, … , 𝑥_𝑛 ∈ 𝑅𝑛 _(2.5) Sehingga memenuhi 𝑍_𝑘 𝑋 ≲ ≅ ≳ 𝑔_𝑘, 𝑘 = 1,2, … , 𝐾 S.t 𝐴𝑋 ≲ ≅ ≳ 𝑏_𝑖, 𝑋 ≥ 0, 𝑏𝑖 ∈ 𝑅𝑚 (2.6)

Dimana X adalah vektor variabel-variabel keputusan, 𝑔_𝑘 adalah ketidakjelasan level aspirasi ke- k tujuan 𝑍𝑘 𝑋 (𝑘 = 1,2, … , 𝐾), A adalah koefisien matriks, b adalah

vektor nilai kanan (sumber)

𝐴𝑋 ≲≅ ≳

𝑏_𝑖 mewakili kendala fuzzy, dimana ≳ dan ≲ menunjukkan pada versi fuzzy dari dan .

Sekarang dalam situasi pengambilan keputusan fuzzy, fuzzy goal dicirikan oleh fungsi keanggotaannya secara beturut-turut.

2.4 Bilevel programming

Masalah pemrograman bilevel merupakan masalah optimisasi hirarki dimana himpunan bagian dari variabel kendala menjadi sebuah solusi dari masalah optimisasi parameter yang diberikan melalui variabel sisa. Masalah pemrograman bilevel merupakan masalah pemrograman multilevel dengan dua level. Pemrograman bilevel termasuk dua masalah optimisasi dimana daerah kendala dari masalah level pertama secara implicit merupakan penentuan oleh masalah optimisasi yang lain. Struktur optimisasi hirarki muncul secara natural dalam banyak aplikasi ketika aksi level kedua tergantung keputusan level pertama. Aplikasi dari pemrograman bilevel dan multilevel temasuk transportasi (pemungutan pajak, perencanaan jaringan, perkiraan permintaaan perjalanan), manajemen (distribusi piutang, lokasi jaringan fasilitas), dll. Masalah pemrograman bilevel diformulasikan untuk masalah dimana dua pengambil keputusan membuat keputusan secara sukses. Sebagai contoh dalam perusahaan desentralisasi manajemen atasan membuat keputusan sebagai budget dari perusahaan dan kemudian

setiap divisi menentukan perencanaan produksi dalam pengetahuan yang baik dari budget.

Penelitian dalam pemrograman matematika multi-level yang menyelesaikan rencana organisasi dan masalah mengambil keputusan telah tersebar secara luas. Penelitian dan aplikasi telah dipusatkan secara utama dalam pemrograman bilevel. Dalam masalah Bilevel Programming (BLP), setiap pengambil keputusan mencoba mengoptimalkan fungsi tujuannya sendiri tanpa mengikuti tujuan-tujuan dari bagian lain, tetapi keputusan dari setiap bagian mempengaruhi nilai-nilai tujuan dari bagian lain.

Pengambil keputusan tingkat pertama atau disebut leader bergerak pertama dengan memilih sebuah x dalam usaha meminimumkan fungsi tujuannya 𝐹 (𝑥, 𝑦) dengan syarat ikatan kendala pasti. Kemudian pengambil keputusan tingkat kedua atau disebut follower mengamati aksi leader dan bereaksi dengan memilih y untuk meminimumkan fungsi tujuannya 𝑓 (𝑥, 𝑦) dibawah beberapa kendala.

Masalah bilevel dapat diformulasikan sebagai berikut: min𝑥𝐹 (𝑥, 𝑦) s.t 𝐺 𝑥, 𝑦 ≤ 0 (2.7) min𝑦𝑓 𝑥, 𝑦 s.t 𝑔 𝑥, 𝑦 ≤ 0 dimana 𝐹 ∶ 𝑅𝑛1 𝑥 𝑅𝑛2 → 𝑅, 𝐺 ∶ 𝑅𝑛1 𝑥 𝑅𝑛2 → 𝑅𝑚1 , 𝑓 ∶ 𝑅𝑛1 𝑥 𝑅𝑛2 → 𝑅, 𝑔 ∶ 𝑅𝑛1 𝑥 𝑅𝑛2 → 𝑅𝑚2 2.5 Optimisasi Multi-Objektif

Sesuai dengan namanya, Multi-Objective Optimization Problem (MOOP) berhubungan dengan lebih dari satu fungsi tujuan. Masalah mengambil keputusan dalam praktik kebanyakan , multiple objektive atau multiple criteria adalah jelas. Oleh

karena kekurangan metode penyelesaian yang sesuai, MOOP telah banyak dikelompokkan dan diselesaikan sebagai masalah optimasi single-objective di masa yang lalu. Akan tetapi, ada sejumlah perbedaan pokok antara prinsip-prinsip pengerjaaan dari algoritma optimasi single dan multi-objective. Dalam masalah optimasi single-objective, tugasnya adalah mencari satu solusi yang mengoptimalkan fungsi tujuan tunggal. Kemudian ide tersebut diperluas pada optimasi multi-objective yaitu menemukan satu solusi optimal yang berkorespondensi pada setiap fungsi tujuan.

2.5.1. Masalah Optimasi Multi-Objective

Masalah optimasi multi-objective memiliki sejumlah fungsi tujuan yang akan diminimumkan atau dimaksimumkan. Sebagaimana di dalam masalah optimasi single-objective, biasanya masalah juga memiliki sejumlah kendala di mana solusi fisibel (termasuk solusi optimal) harus terpenuhi. Berikut ini, menyatakan masalah optimasi multi-objective (MOOP) dalam bentuk umumnya:

Min/Maks 𝑓_𝑚 (𝑋), 𝑚 = 1, 2, … , 𝑀

Kendala 𝑔_𝑗 𝑋 ≥ 0, 𝑗 = 1, 2, … , 𝐽 (2.8) 𝑕_𝑘 𝑋 = 0, 𝑘 = 1, 2, … , 𝐾

𝑥_𝑖(𝐿) ≤ 𝑥_𝑖 ≤ 𝑥_𝑖(𝑈), 𝑖 = 1, 2, … , 𝑛

Solusi 𝑥 adalah sebuah vektor 𝑛 variabel keputusan : 𝑥₁, 𝑥₂, … , 𝑥_𝑛 𝑇. Himpunan akhir kendala disebut batas variabel, membatasi setiap variabel keputusan

𝑥𝑖 untuk mengambil sebuah nilai dengan batas bawah 𝑥_𝑖(𝐿) dan batas atas 𝑥_𝑖(𝑈).

Batas-batas ini merupakan sebuah ruang variabel keputusan 𝒟, atau menyatakan ruang keputusan.

Berhubungan dengan masalah tersebut, terdapat 𝐽 persamaan dan 𝐾 persamaan kendala. Istilah 𝑔_𝑗 𝑋 dan 𝑕_𝑘 𝑋 disebut fungsi kendala.

Ketidaksamaan kendala dinyatakan sebagai jenis „ ≥, =‟, walaupun jenis persamaan kendala „ ≤. =‟ juga dinyatakan dalam formula di atas. Sebuah solusi 𝑥 yang tidak memenuhi semua kendala 𝐽 + 𝐾 dan semua batas variabel 2𝑁 yang dinyatakan di atas disebut solusi infisibel. Dengan kata lain, jika beberapa solusi 𝑥 memenuhi semua kendala dan batas variabel, disebut sebagai solusi fisibel. Dengan demikian, disadari bahwa dalam kehadiran kendala, keseluruhan ruang variabel keputusan 𝒟 tidak harus fisibel. Himpunan semua solusi fisibel disebut daerah fisibel atau 𝒮.

Walaupun ada perbedaan yang signifikan dalam cara bahwa sebuah fungsi kriteria dan sebuah fungsi tujuan didefinisikan, dalam pandangan yang luas dinyatakan identik. Salah satu perbedaan menonjol antara single-objective dengan multi-objective adalah bahwa dalam optimasi multi-objective fungsi tujuan merupakan sebuah ruang multi-dimensional, dalam tambahan pada ruang variabel keputusan biasa. Ruang tambahan ini disebut ruang tujuan, 𝒵. Untuk setiap solusi 𝑥 dalam ruang variabel keputusan, ada sebuah titik di dalam ruang tujuan dinyatakan dengan 𝑓 𝑥 = 𝑧 = 𝑧₁, 𝑧₂, … , 𝑧_𝑀 𝑇. Pemetaan terjadi antara 𝑛 – dimensi vektor solusi dan sebuah 𝑀 − dimensi vektor tujuan.

Optimasi multi-objektive kadang-kadang mengacu pada optimasi vektor, karena sebuah vektor tujuan, sebagai ganti tujuan tunggal, dioptimalkan.

2.5.1.1 Masalah Optimasi Multi-Objective Linier dan Nonlinier

Jika semua fungsi tujuan dan fungsi kendala linier, hasil MOOP disebut program linier objective. Seperti masalah pemrograman linier, program linier multi-objective juga memiliki banyak sifat. Akan tetapi, jika beberapa fungsi tujuan atau fungsi kendala adalah nonlinier, hasil masalah itu disebut masalah nonlinier

multi-objective. Sayangnya, untuk teknik penyelesaian masalah nonlinier sering tidak memiliki bukti yang konvergen. Karena kebanyakan kenyataanya masalah optimasi multi-objective merupakan nonlinier pada dasarnya, tidak diasumsikan beberapa struktur khusus tujuan dan fungsi kendala di sini.

𝑥3 𝑓2

𝑥₂

𝑓₁

𝑥₁

Gambar 2.3 Perwakilan hubungan dari ruang variabel keputusan dan ruang tujuan

2.5.1.2 Masalah Optimasi Konvex dan Nonkonvex

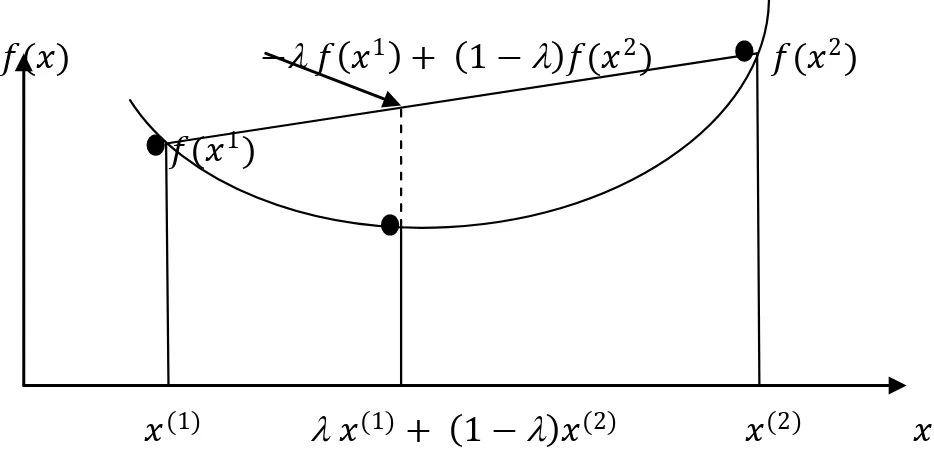
Definisi 2.1 Sebuah fungsi 𝑓 ∶ ℝ𝑛 ⟶ ℝ merupakan fungsi konveks jika ada dua pasangan solusi 𝑥(1), 𝑥(2) 𝜖 ℝ𝑛 , maka kondisi berikut adalah benar:

𝑓 𝜆𝑥(1)_{+ 1 − 𝜆 𝑥}(2) _{≤ 𝜆 𝑓 𝑥}(1) _{+ 1 − 𝜆 𝑓 𝑥}(2) _(2.9)

untuk semua 0 ≤ 𝜆 ≤ 1.

Definisi di atas menimbulkan sifat fungsi konveks sebagai berikut:

1. Aproksimasi linier 𝑓 𝑥 pada suatu titik dalam interval 𝑥(1), 𝑥(2) selalu menaksir terlalu rendah nilai fungsi sebenarnya.

2. Matriks hessian 𝑓 𝑥 adalah definit positif untuk semua 𝑥.

3. Untuk sebuah fungsi konveks, minimum lokal selalu merupakan minimum global.

Gambar 2.3 mengilustrasikan sebuah fungsi konveks. Sebuah fungsi yang menyatakan persamaan yang ditunjukkan dalam persamaan (2.2) dengan tanda „ ‟

fungsi adalah konveks dengan suatu interval, matriks hessian ∇2 𝑓 dihitung dan diperiksa kedefinitan positif pada semua titik di dalam interval tersebut. Salah satu cara memeriksa kedefinitan positif suatu matriks adalah menghitung nilai eigen matriks dan diperiksa untuk melihat apakah semua nilai eigen positif untuk menguji apakah sebuah fungsi 𝑓 adalah nonkonveks dalam sebuah interval, matriks hessian

−∇2 _{𝑓 diperiksa untuk mengetahui kedefinitan positif-nya. Jika matriks tersebut}

definit positif, fungsi 𝑓 adalah non-konveks.

Adalah sangat menyenangkan menyadari bahwa jika sebuah fungsi 𝑔 𝑥 adalah nonkonveks, himpunan solusi memenuhi 𝑔 𝑥 ≥ 0 mewakili himpunan konveks. Jadi, ruang pencarian fisibel yang dibentuk dengan fungsi kendala nonkonveks akan melampirkan daerah konveks.

𝑓(𝑥) − 𝑓 𝑥1 + 1 − 𝑓(𝑥2) 𝑓(𝑥2) 𝑓(𝑥1)

𝑥(1)  𝑥(1)+ 1 − 𝑥(2) 𝑥(2) 𝑥 Gambar 2.4 Ilustrasi fungsi convex

Definisi 2.1.2 Sebuah masalah optimasi multi-objective adalah konveks jika semua fungsi tujuan konveks dan daerah fisibel konveks (atau semua persamaan kendala adalah nonkonveks dan kesamaan kendala adalah linier).

Berdasarkan definisi ini, sebuah pemrograman linier multi-objective adalah masalah konveks.

Bidang dari Linear Fractional Programming (LFP), secara luas dikembangkan oleh seorang matematisi Hungaria B.Martos dan asosiasinya di tahun 1960an dengan memusatkan pada masalah optimisasi. Beberapa metode penyelesaian masalah ini disarankan tahun (1962), Charnes dan Cooper telah menyarankan metode mereka dengan bergantung pada transformasi ini (LFP) kepada ekivalen program linier. Metode yang lain disebut metode fungsi tujuan yang diperoleh dari Bitran dan Novaes (1973) digunakan menyelesaikan LFP dengan menyelesaikan barisan program linier dengan hanya menghitung kembali gradien lokal dari fungsi tujuan.

Bentuk umum dari masalah LFP dapat dibuat sbb : Optimalkan 𝑓 𝑥 = 𝑐

𝑇_{𝑥+ 𝛼}

𝑑𝑇 _{𝑥+ 𝛽} (2.10)

Kendala 𝐴𝑥 = 𝑏

𝑥 ≥ 0, dimana 𝑥, 𝑐𝑇, 𝑑𝑇, ∈ 𝑅𝑛, 𝑏 ∈ 𝑅𝑚, 𝛼, 𝛽 ∈ 𝑅.

Untuk beberapa nilai dari x, 𝑑𝑇 𝑥 + 𝛽 mungkin akan sama pada nol tetapi disini kita mengambil hanya kasus 𝑑𝑇 𝑥 + 𝛽 > 0. Jika mengambil lebih dari satu tujuan dalam masalah linear fractional programming yang umum, maka masalah dikenal sebagai masalah linear fractional programming multiobjektif. Secara matematika itu dapat ditulis sebagai Optimalkan 𝐹 𝑥 = 𝐹₁ 𝑥 , 𝐹₂ 𝑥 , 𝐹₃ 𝑥 , … , 𝐹_𝑘 𝑥 , (2.11) Dimana 𝐹_𝑖 𝑥 = _𝑚𝑓𝑖 𝑥 𝑖 𝑥 = 𝑐_𝑖𝑇 𝑥+ 𝛼𝑖 𝑑_𝑖𝑇 𝑥+ 𝛽𝑖 .

Juga, 𝑓_𝑖 𝑥 = 𝑐_𝑖𝑇 𝑥 + 𝛼_𝑖, 𝑚_𝑖 𝑥 = 𝑑_𝑖𝑇 𝑥 + 𝛽_𝑖 adalah nilai fungsi real dalam X, dimana 𝑋 = {𝑥 ∶ 𝐴_𝑥 ≤, =, ≥ 𝑏, 𝑥 ≥ 0, 𝑥 ∈ 𝑅𝑛, 𝑏 ∈ 𝑅𝑚, 𝐴 = 𝑎_{𝑖𝑗 𝑚𝑥𝑛}, 𝛼_𝑖, 𝛽_𝑖 ∈

𝑅} diasumsikan merupakan himpunan tak kosong-konvex terbatas dalam 𝑅𝑛, dan

𝑑_𝑖𝑇 _{𝑥 + 𝛽}

𝑖 > 0 𝑖 = 1,2, … , 𝑘 , ∀ 𝑥 ∈ 𝑋.

Masalah Pemrograman bi-level dimana setiap pengambil keputusan mempunyai fungsi multiobjektif yang dapat memaximumkan dan dua pengambil keputusan dapat menentukan keputusan mereka secara bekerja sama. Sehingga masalah pemrograman bi-level linear multi-objektif diformulasikan sebagai berikut:

max𝑙𝑒𝑣𝑒𝑙 𝑎𝑡𝑎𝑠 𝑍11 𝑥1𝑥2 = 𝑐111 𝑥1+ 𝑐211 𝑥2… max_{𝑙𝑒𝑣𝑒𝑙 𝑎𝑡𝑎𝑠} 𝑍_𝑘1 _𝑥 1𝑥2 = 𝑐1𝑘1 𝑥1+ 𝑐2𝑘1 𝑥2 max_{𝑙𝑒𝑣𝑒𝑙 𝑏𝑎𝑤𝑎 𝑕} 𝑍₁2 _𝑥 1𝑥2 = 𝑐112 𝑥1+ 𝑐212 𝑥2… max_{𝑙𝑒𝑣𝑒𝑙 𝑏𝑎𝑤𝑎 𝑕} 𝑍_𝑘2 _𝑥 1𝑥2 = 𝑐1𝑘2 𝑥1+ 𝑐2𝑘2 𝑥2 (2.11) Subject to 𝐴₁𝑥₁+ 𝐴₂𝑥₂ ≤ 𝑏, 𝑥₁, 𝑥₂ ≥ 0

Dimana 𝑥₁ 𝑑𝑎𝑛 𝑥₂ adalah dimensi 𝑛₁ dan 𝑛₂, dimensi variabel vektor keputusan dari pengambil keputusan pada level atas dan level bawah secara berurutan, 𝑍_𝑖1 𝑥₁𝑥₂ ,

𝑖 = 1,2, … 𝑘₁ dan 𝑍_𝑖2 𝑥₁𝑥₂ , 𝑖 = 1,2, … 𝑘₂ adalah fungsi tujuan ke-i dari pengambil keputusan pada level atas dan level bawah berturut-turut. 𝑐_𝑖𝑗1 dan 𝑐_𝑖𝑗2 merupakan dimensi 𝑛𝑖 konstanta baris vektor.

Diasumsikan bahwa ada dua tingkatan dalam struktur hirarki dengan pengambil keputusan tingkat pertama (FLDM) dan pengambil keputusan tingkat kedua (SLDM). Andaikan vektor variabel keputusan 𝑥 = 𝑥₁, 𝑥₂ ∈ 𝑅𝑛 dipartisi antar kedua perencana. Pengambil keputusan tingkat pertama memiliki kontrol atas vektor

𝑥₁ ∈ 𝑅𝑛1 _{dan pengambil keputusan tingkat kedua} 𝑥

2 ∈ 𝑅𝑛2 , dimana 𝑛 = 𝑛1+ 𝑛2.

Selanjutnya, asumsikan bahwa

𝐹_𝑖 𝑥₁, 𝑥₂ ∶ 𝑅𝑛1 𝑥 𝑅𝑛2 → 𝑅𝑚1, 𝑖 = 1,2 _(1.1) adalah masing-masing vektor fungsi tujuan tingkat pertama dan tingkat kedua. Jadi masalah BL- MOLFP tipe minimisasi dapat dirumuskan sebagai berikut :

Tingkat1

min_𝑥1𝐹₁ 𝑥₁, 𝑥₂ = min_𝑥1(𝑓₁₁ 𝑥₁, 𝑥₂ , 𝑓₁₂ 𝑥₁, 𝑥₂ , … , 𝑓_{1𝑚 1}(𝑥₁, 𝑥₂)), (1.2) dimana 𝑥₂ menyelesaikan

min_𝑥2𝐹₂ 𝑥₁, 𝑥₂ = min_𝑥2(𝑓₂₁ 𝑥₁, 𝑥₂ , 𝑓₂₂ 𝑥₁, 𝑥₂ , … , 𝑓_{2𝑚 1}(𝑥₁, 𝑥₂)) (1.3) subject to 𝑥 ∈ 𝐺 = 𝑥 = 𝑥₁, 𝑥₂ ∈ 𝑅𝑛 _𝐴 1𝑥1+ 𝐴2𝑥2 ≤ = ≥ 𝑏, 𝑥 ≥ 0, 𝑏 ∈ 𝑅 𝑚 _{≠ ∅ (1.4)} dimana 𝑓_𝑖𝑗 𝑥₁𝑥₂ = 𝑐𝑖𝑗𝑥+ 𝛼𝑖𝑗 𝑑𝑖𝑗𝑥+𝛽𝑖𝑗 (1.5)

𝑗 = 1,2, … , 𝑚₁, 𝑖 = 1 untuk fungsi tujuan pengambil keputusan tingkat pertama

𝑗 = 1,2, … , 𝑚₂, 𝑖 = 2 untuk fungsi tujuan pengambil keputusan tingkat kedua Dan dimana

i. 𝑥1 = 𝑥11, 𝑥12, 𝑥13, … , 𝑥1𝑛1 , 𝑥2 = 𝑥21, 𝑥22, 𝑥23, … , 𝑥2𝑛2

ii. G adalah serangkaian pilihan kendala layak convex bilevel iii. 𝑚₁adalah jumlah fungsi tujuan tingkat pertama,

iv. 𝑚₂ adalah jumlah fungsi tujuan tingkat kedua, v. m adalah jumlah kendala,

vi. 𝐴_𝑖 ∶ 𝑚 × 𝑛₁ matriks, i = 1, 2,

vii. 𝑐_𝑖𝑗, 𝑑_𝑖𝑗 ∈ 𝑅𝑛, 𝑑_𝑖𝑗𝑥 + 𝛽_𝑖𝑗 ≥ 0 untuk semua 𝑥 ∈ 𝐺 viii. 𝛽_𝑖𝑗 , 𝛼_𝑖𝑗 adalah konstanta