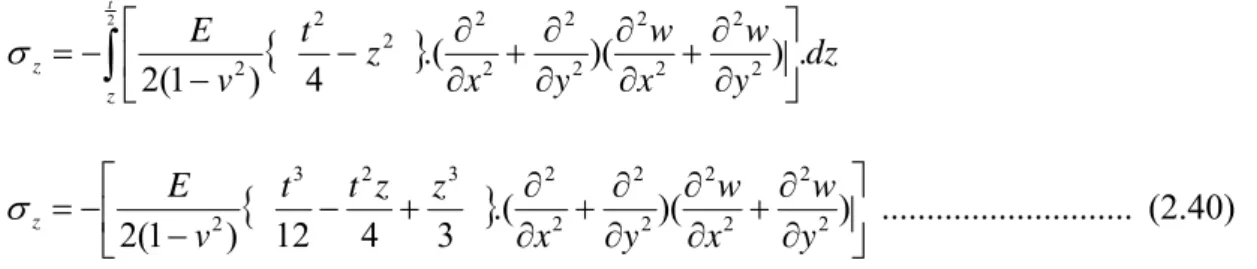BAB II TEORI DASAR PELAT

BAB II

TEORI DASAR PELAT

II.1 Teori Dasar Elastisitas Linier

Teori elastisitas merupakan cabang yang sangat penting dari fisika statis, yang mengkaji hubungan antara gaya, perpindahan, tegangan dan regangan dalam benda elastis. Bila suatu benda pejal dibebani oleh gaya luar, benda tersebut akan berubah bentuk atau

akan mengalami deformasi, sehingga timbul tegangan dan regangan. Perubahan bentuk ini

tergantung pada konfigurasigeometris dari benda tersebut dan pada sifat mekanis bahannya. Dalam teori elastisitas kita batasi pembahasannya hanya pada bahan yang elastis linier, yaitu keadaan dimana hubungan antara regangan dan tegangan bersifat linier dan perubahan bentuk serta tegangan akan hilang bila gaya luar dihilangkan. Selain itu, teori elastisitas menganggap bahan bersifat homogen dan isotropik, dengan demikian sifat mekanis bahan sama dalam segala arah.

Dalam statika benda tegar (rigid body), kita hanya mengkaji gaya luar (external forse) yang bekerja pada suatu benda dan tidak meninjau perubahan bentuk yang timbul. Sebaliknya, dalam teori elastisitas kita meninjau perubahan bentuk akibat gaya luar. Melalui perubahan bentuk pada benda tersebut, gaya-gaya luar dikonversi menjadi gaya dalam (internal force).

II.2 Komponen Tegangan

Pn

P1

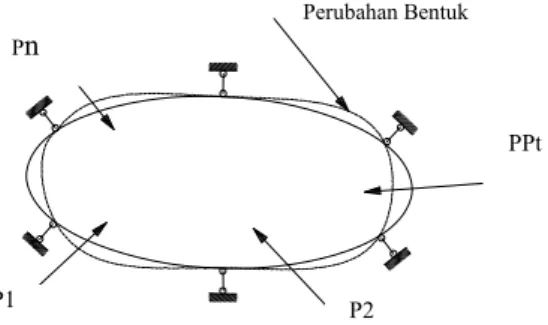
Gambar 2.1 Respon suatu benda elastis terhadap gaya luar Sumber : Teori dan analisis pelat ( Szilard,1989)

P2 Perubahan Bentuk

PPt

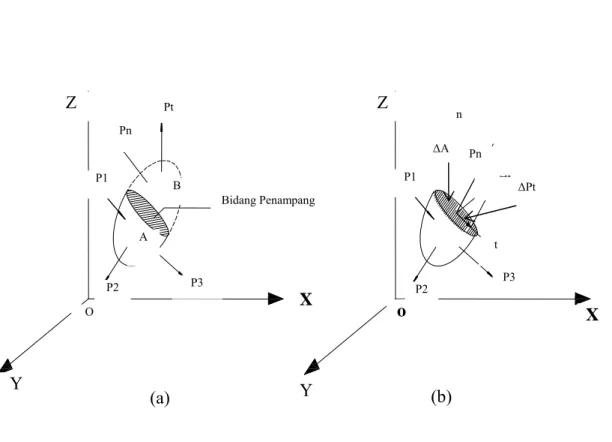
setimbang. Untuk menentukan gaya dalam yang timbul diantara partikel-partikel benda tersebut, bayangkanlah benda tersebut dipenggal menjadi dua bagian oleh suatu bidang, seperti Gambar 2.2.a..jika sekarang kita bayangkan bahwa bagian B dihilangkan,

keseimbangan benda tersebut harus dipertahankan oleh gaya-gaya luar yang bekerja pada

permukaan penampangnya. Kemudian kita ambil suatu luas ∆A yang kecil pada

penampang tersebut dan kita nyatakan gaya dalam yang bekerja pada luasan ini sebagai ∆P (Gambar 2.2 b).Perbandingan ∆P/∆A adalah tegangan rata-rata yang didefenisikan sebagai limit dari perbandingan, jadi Tegangan adalah :

σ = A P Lim n  

( gaya persatuan luas )...(2.1)

P3 o P2 X Z Z Y t P3 Bidang Penampang A Pt _n ΔA ΔP P1 B Pn ΔPt P1 Pn O P2 X Y _(b) (a)

Karena ∆P pada umumnya tidak tegak lurus penampang, kita lebih mudah

menggunakan komponen normal (tegak lurus) dan tangensial (sebidang). Dengan

demikian, defenisi tegangan normal σ dan tegangan geser τ ( Gambar 2.2b) adalah :

Gambar 2.2 Metode Irisan

Sumber : Teori dan analisis pelat (Szilard, 1989)

σ

= A P Lim n   dan

τ

= A P Lim n   ……….……(2.2) Dimana tegangan pada suatu bidang adalah vektor suatu tegangan. Resultante

tegangan dengan mudah dapat dicari dengan penjumlahan vektor dari

komponen-komponennya.Keadaan tegangan pada benda elastis biasanya bervariasi dari satu titik ke titik lainnya, jadi dapat dituliskan σ (x,y,z) dan τ ( x,y,z).

Untuk menggambarkan keadaan tegangan tiga dimensi , ambillah suatu elemen yang

sangat kecil dalam bentuk kotak yang sisinya , yang mukanya sejajar dengan

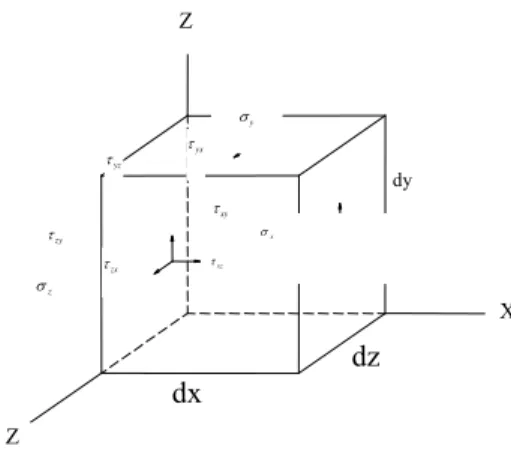
bidang koordinat (Gambar 2.3). Komponen tegangan normal X, Y, dan Z, masing-masing diberi notasi σx, σy, dan σz . Subkripnya (huruf bawah) menunjukkan garis normal (tegak lurus) permukaan tempat vektor tegangan tersebut bekerja.

z y x d d

d , ,

Gambar 2.3 Elemen tiga dimensi Sumber : Teori dan analisis pelat (Szilard, 1989)

Tegangan geser τ biasanya memiliki dua subkrip. Subkrip pertama menunjukkan arah garis normal permukaan, sedangkan subkrip kedua menunjukkan arah vektor tegangan geser τ. Karena tegangan merupakan fungsi dari letaknya terhadap suatu benda,

intensitasnya akan berubah bila bidang rujukannya digerakkan sejauh .

Pertambahan yang timbul dinyatakan oleh dua suku pertama dari deret Taylor (Gambar

2.3). z y x d d d , , Z dx dy dz X Z yx  y  yz  xy  x  z  zy  zx  xz

Perjanjian tanda berikut akan digunakan , yaitu pada bidang dekat suatu elemen (dipandang dari ujung sumbu koordinat positif), semua tegangan yang bekerja dalam arah sumbu koordinat positif dianggap positif. Pada bidang jauh suatu elemen, semua tegangan yang bekerja pada arah sumbu koordinat negatif dianggap positif.perjanjian tanda ini mengikuti aturan umum dalam praktek bidang teknik, yakni tarikan bertanda positif dan tekanan bertanda negatif.

Keadaan tegangan tiga dimensi disembarang titik benda elastis ditentukan oleh sembilan komponen tegangan dengan matrik sebagai beikut :

[ σ ] = ... ... ( 2.3 )           z zy zx yz y yx xz xy x         

yang simetris terhadap diagonal utama. Karena sifat simetris ini , maka :

, yx xy 

  xz zx, dan yzzy.... ... ...( 2.4 )

Persamaan 2.3 disebut Hukum Timbal Balik Tegangan Geser. Dengan demikian enam besaran

σ

x ,

σ

y

,

σ

z , _xy _yx, _xz _zx, dan _yz_zy cukup untuk

menjelaskan tegangan yang bekerja pada koordinat bidang melalui sebuah titik, besaran inilah yang disebut Komponen Tegangan pada sebuah titik.

Untuk kasus dua dimensi, maka

σ

z, _xz, dan _yz, sama dengan nol. Dengan

demikian keadaaan tegangan bidang ( plane stress ) yang besarnya tidak tergantung kepada z yang tidak berubah sepanjang tebalnya. Berarti komponen ini hanya merupakan fungsi x dan y saja.

II.3 Komponen Regangan

Benda elastis yang diperlihatkan pada Gambar 2.1 ditumpu sedemikian rupa sehingga perpindahan benda tegar / rigid body ( tranlasi dan rotasi ) tidak terjadi. Karena benda elastis tersebut berubah bentuk akibat gaya luar, setiap titik padanya mengalami

perpindahan elastis yang kecil. Dengan menyatakan komponen perpindahan tranlasi dalam arah X, Y, Z, sebagai u, v, w dapat kita tuliskan :

u = f1 ( x, y, z ) v = f2 ( x, y, z ) w = f3 ( x, y, z ) ... ( 2.5 )

yang menunjukkan bahwa komponen perpindahan merupakan fungsi dari letaknya.

Untuk menghubungkan perpindahan dan perubahan bentuk, tinjaulah kembali kotak

yang sangat kecil dengan sisi , , pada suatu benda elastis (Gambar2.3). Karena

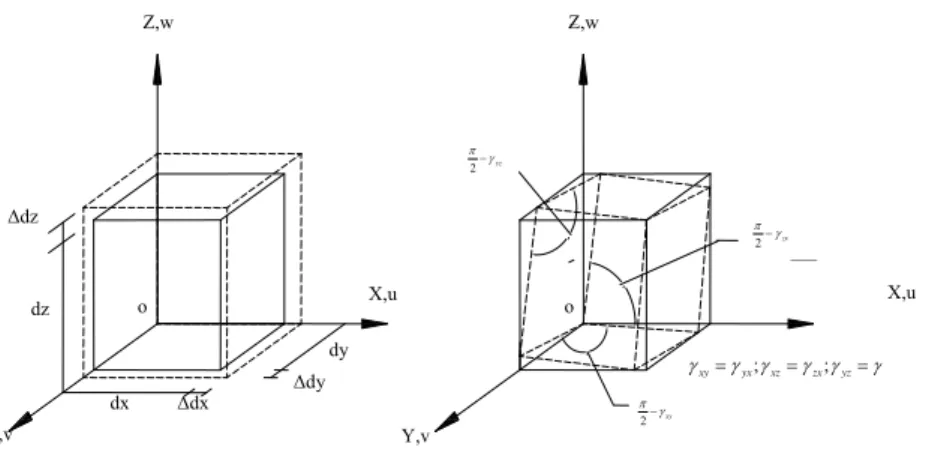
keseluruhan benda elasis itu berubah bentuk, elemen yang sangat kecil tersebut juga akan berubah bentuk, yakni sepanjang sisinya dan sudut antara permukaannya yang semula siku - siku juga akan berubah. (Gambar 2.4).

x

d d_y dz

Z,w Z,w

Gambar 2.4 Deformasi suatu elemen

Sumber : Teori dan analisis pelat (Szilard, 1989)

Dengan membatasi pembahasan pada perubahan bentuk yang sangat kecil, kita defenisikan regangan normal

ε

, perubahan satuan panjang satuan. Misalnya regangan normal dalam arah X adalah :

ε

x =

dx dx 

...2.6 )

di mana pertambahan dxdapat dinyatakan dengan suku kedua deret Taylor dx

x u dx ( )     , jadi untuk ketiga arah dapat dituliskan :

X,u Y,v dz dx dy Δdx Δdy o Y,v o Δdz yz  _ 2 zx  _ 2 X,u xy  _ 2 yz zx xz yx xy       ;  ; 

ε

x = x u   ;

ε

y = y v   ;

ε

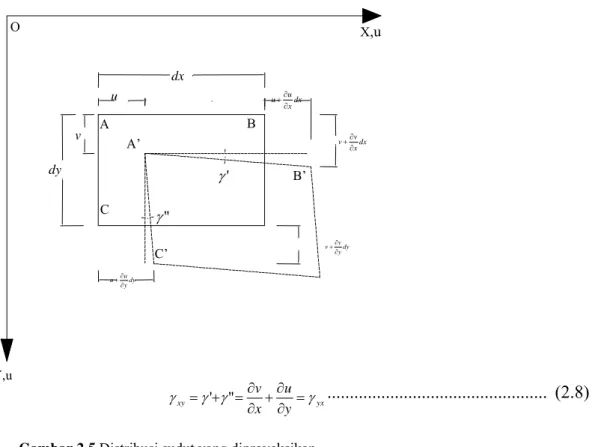
x = z w   ...2.7 )

Akibat pengaruh regangan geser , permukaan elemen tersebut akan berputar (Gambar 2.4b). Sebagai contoh, dengan mengambil proyeksi elemen tersebut pada bidang XY,( Gambar 2.5 ), kita defenisikan regangan geser sebagai distorsi sudut.

O _X,u dx u dx x u u    B A v _dx x v v    A’ dy _{' B’} C _" dy y v v    C’ dy y u u    Y,u yx xy y u x v _             ' " ... (2.8)

Gambar 2.5 Distribusi sudut yang diproyeksikan Sumber : Teori dan analisis pelat (Szilard, 1989)

Dengan cara yang sama kita peroleh :

zx yz x w z u _         ; yz zy y w z v _         ... (2.9) Sama halnya dengan tensor tegangan (persamaan 2.2) disuatu titik , regangan tensor dapat didefenisikan :

 

              z zy zx yz y yx xz xy x        ... (2.10)

Selanjutnya dapat dilihat bahwa dengan memiliki tiga satuan perpanjangan dalam tiga arah yang saling tegak lurus dan tiga regangan geser dengan arah yang sama, sehingga perpanjangan dalam arah sembarang dan pelentingan sudut antara dua arah sembarang dapat dihitung. Keenam besaran

ε

x ,

ε

y,

ε

z,

γ

xy ,

γ

xz ,

γ

yz disebut Komponen Regangan ( Component of Strain ).Untuk kasus dua dimensi, perpindahan memanjang sepanjang w sama dengan nol, maka dari persamaan 2.6 dan 2.8 didapat

0        x w z u xz  ; 0       y w z v yz  ;

ε

z = 0 ... (2.11)

II.4. Hubungan Tegangan - Regangan ( Hukum Hooke )

Hubungan linier antara komponen regangan dan komponen tegangan umumnya dikenal sebagai Hukum Hooke. Untuk bahan struktur yang menunjukkan batas elastis linier

yang jelas, Hukum Hooke suatu dimensi menghubungkan tegangan dan regangan normal

sebagai :

σ

=

ε

.

E

...(

2.12) dengan E adalah Modulus Elastisitas.

Jika tegangan normal bekerja dalam arah X, perpanjangan

ε

x, diikuti oleh

perpendekan lateral, maka regangan dalam arah X ,Y, Z adalah :

ε

x = E x  ;

ε

y = E vy  ;

ε

z = E vz  ... (2.13) dimana v suatu konstanta yang disebut dengan Poisson Ratio yang berkisar antara 0,15 – 0,35 untuk kebanyakan bahan struktur.

Persamaan 2.12 dapat juga digunakan untuk kasus penekanan sederhana dimana modulus elastis dan Poisson Ratio pada keadaan tekan sama dengan keadaan tarik.

Untuk kasus struktur linier yang mengikuti hukum Hooke, prinsip superposisi dapat diterapkan, dengan demikian jika

σ

x ,

σ

y,dan

σ

z bekerja secara bersamaan pada elemen

yang kecil tersebut, hukum Hooke dapat diperluas menjadi :

ε

x = 1[ _x v( _{y z})] E    

ε

y = 1[ _y v( _{z x})] E     ... (2.14)

ε

z = 1[ _z v( _{x y})] E    

Dengan cara yang sama , hubungan tegangan geser dan regangan geser adalah :

γ

=

G



... (2.15) Dimana G adalah Modulus Geser yang mempunyai hubungan dengan Modulus Elastisitas dan Poisson Ratio yakni : G =

) 1 ( 2 v E  ... (2.16)

Jika regangan geser bekerja pada semua permukaan elemen, persamaan 2.14 menjadi :

G xy xy    , G yz yz    , G zx zx    ... (2.17) Persamaan 2.13 dan persamaan 2.16 menghasilkan komponen regangan sebagai fungsi komponen tegangan.

Kadangkala komponen tegangan dinyatakan sebagai komponen regangan. Komponen ini dapat diperoleh sebagai berikut :

Tambahkan persamaan 2.13 bersama sama dengan notasi

e =

ε

x +

ε

y +

ε

z , θ =

σ

x +

σ

y +

σ

z ... (2.18)

Kita dapatkan hubungan antara pengembangan volume e dengan jumlah tegangan normal θ,yaitu :

e =  E v) 2 1 (  ...2.19) Persamaan diatas dapat disederhanakan menjadi :

σ

y+

σ

z = _x v Ee _ 2 ) 1 ( ... (2.20) Gunakan notasi persamaan 2.17 dan selesaikan persamaan 2.13 untuk

memperoleh

σ

x

,

σ

y, dan

σ

z sehingga didapat :

x x v E e v v vE _  ) 1 ( ) 2 1 )( 1 (      y y v E e v v vE _  ) 1 ( ) 2 1 )( 1 (      ... ………(2.21) z z v E e v v vE _  ) 1 ( ) 2 1 )( 1 (      Dan gunakan e v v vE ) 2 1 )( 1 (    

Dan persamaan 2.20 ini menjadi :

x x e G   2 y y e G   2 . ... (2.22) z z e G   2

II.5 Perilaku Umum Pelat Terlentur

Pelat dan shell pada mulanya adalah suatu Elemen struktur bidang rata maupun lengkung Dimana ketebalannya lebih kecil dibandingkan dimensi lainnya. Ketebalan suatu pelat biasanya diukur pada arah normal sumbu ( garis berat ) pelat. Dilihat dari segi

ketebalannya pelat dapat dikategorikan dalam tiga jenis yaitu :

1. Pelat tipis dengan lendutan kecil ( thin plate with small deflection )

3. Plat tebal ( thick plate )

dan dilihat dari segi cara transper gaya dari pelat ke kolom,pelat dibagi atas tiga jenis yaitu :

1. Pelat dengan balok ( Slab with beam )

2. Pelat tanpa balok dan drop panel disekitar kolom (Flat Slab) 3. Pelat tanpa balok,drop panel ( Flat Plate)

Gambar 2.6a. Flat slab Gambar 2.6b. Plate with beam

Kolom Pelat Kolom Balok Pelat kolom Pelat Drop panel

Gambar 2.6c Flat Plate

Sumber : Teori dan analisis pelat (Szilard, 1989)

Melihat kategori tersebut sering digunakan dan diaplikasikan untuk mendefenisikan pelat tipis sebagai perbandingan tebal dengan bentang terpendek pelat lebih kecil dari 1/20 (untuk material beton). Dengan hanya mempertimbangkan lendutan kecil pada pelat tipis ,

terdapat suatu penyederhanaan yang konsisten dengan besarnya lendutan yang biasanya ditemukan pada struktur pelat.

Asumsi yang mendasar didalam teori lendutan kecil pada pelat terlentur atau disebut teori klasik untuk material isotropik, homogen, dan elastis didasarkan pada geometri lendutan ( deformasi ) antara lain :

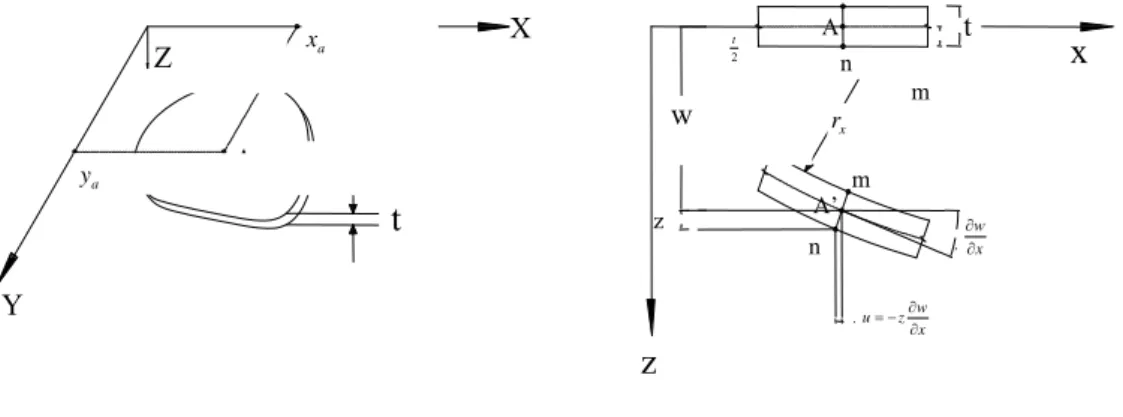
Gambar 2.7 Geometri Elemen Pelat

Sumber : Teori dan analisis pelat (Szilard, 1989)

1. Lendutan di tengah bentang pelat lebih kecil dibanding ketebalan pelat itu sendiri dan kemiringan kelengkungan pelat sangat kecil sehingga dapat diabaikan .

2. Penampang pada bidang sistim pelat tidak berobah pada saat terjadi lenturan

3. Bidang tegak lurus pada bidang sistem pelat akan tetap tegak lurus setelah pelenturan

sehingga regangan geser vertical γxz dan γyz dapat diabaikan.

4. Tegangan normal di tengah bentang σ z sangat kecil dibanding komponen lainnya

sehingga dapat diabaikan . Pada pelat tebal, regangan geser sangat penting seperti balok pada umumnya.

II.6 Hubungan Regangan – Kelengkungan

Beranjak dari anggapan yang tersebut diatas, regangan – perpindahan dapat digambarkan sebagai berikut :

ε

x = x u  

ε

z = z w   = 0 X Y Z A t a y t A a x _x 2 t n m w rx m A’ z z n x w   x w z u    

ε

y = y v   xz= z u x w      =0... (2.23) xy  = x v y u      _yz = z v y w      =0 Melalui persamaan : xz  = 0      z u x w z u x w       x z u w       ) , (x y u x w u  _o     dan v(x,y) y w z v     

akan didapatkan fungsi w dalam parameter x,y atau w = (x,y), dengan kata lain

perpindahan lateral tidak dipengaruhi fungsi komponen z ( tebal pelat ).dengan asumsi kedua diatas didapatkan harga uo(x,y) = 0 dan vo(x,y) = 0.

Sehingga didapat : x w z u    dan y w z v     ... (2.24) subtitusi persamaan 2.24 ke persamaan 2.23 dan menghasilkan :

ε

x = 2 2 ) ( x w z x w z x          ,

ε

y = 2 2 y w z    , xy= y x w z     . 2 2 ... ( 2.25) Persamaan ini memberikan nilai regangan di setiap titik. Kelengkungan dari pelat terlentur didefenisikan sebagai laju perubahan kemiringan sudut sepanjang pelat.dengan asumsi pertama dan persamaan 2.24, luasan kemiringan pelat diabaikan dan diferensial parsial pada persamaan 2.25 mewakili kelengkungan pelat.

Sehingga kelengkungan k ( kappa ) pada tengah bentang yang parallel dengan bidang xz, yz, dan xy dapat digambarkan sebagai berikut :

y y y k w y r       ( ) 1

xy y xy k w x r       ( ) 1 _{………(2.26)}

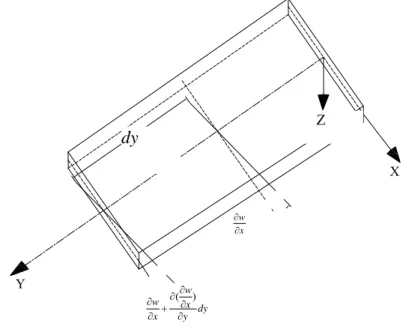
Gambar 2.8 Sumbu Lokal Puntir Elemen Pelat

Sumber : Teori dan analisis pelat (Szilard, 1989)

Sehingga hubungan regangan dan kelengkungan adalah superposisi persamaan 2.25

dengan persamaan 2.26 sebagai :

ε

x = zk_x ,

ε

y = zk_y

,

γ

xy = zk_xy... (2.27)

II.7 Tegangan dan Resultan Tegangan

Pada kasus tegangan dan regangan tiga dimensi yang mengikuti Hukum Hook untuk

benda isotropis, homogen dan elastis, hubungan tegangan – regangan adalah sebagai berikut :

ε

x =1[ _X v( _{y z})] E     G xy xy   

ε

y =1[ _y v( _{x z})] E     G xz xz    ………...(2.28)

ε

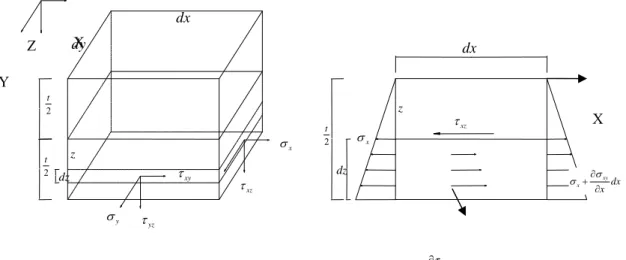
z = 1[ _z v( _{x y})] E     G yz yz    Z dy X x w   Y dy y x w x w       ( )

Gambar 2.9 Komponen - komponen Tegangan pelat Sumber : Teori dan analisis pelat (Szilard, 1989)

dimana :

E = Modulus elestis bahan V = Poisson ratio

G = Modulus geser [ G = E/2.(1+V) ]

Notasi untuk tegangan normal digunakan lambing

σ

(sigma) dan tegangan geser

digunakan lambang

τ

(tau). Subcript pertama menunjukkan arah normal terhadap bidang

yang ditinjaudan huruf kedua menunjukkan arah tegangan itu sendiri.

Tegangan normal bernilai positif bila tegangan tersebut menghasilkan tegangan tarik dan sebaliknya.arah positif tegangan geserpada sisi sembarang dari elemen kubus diambil sebagai arah positif sumbu koordinat, apabila tegangan tarik pada sisi yang sama

mempunyai arah positifdari sumbu yang bersangkutan.Apabila arah tegangan tarik berlawanan dengan arah positif, maka arah positif komponen tegangan geser dibalik. Dengan memasukkan : 0    _{yz xz} x    Diperoleh : dx dy X Z dx Y 2 t 2 t dz 2 t xy z  y  yz  dz z xz  x  x xz  X dx x xy x _     dy y xy xy _    

) ( 1 2 x y x v v E _{ }     ) ( 1 2 y x y v v E _{ }     ………...(2.29) xy xy G   .

Untuk pelat lengkung persamaan menjadi : ) ( 1 . ) ( 1 . 2 2 2 2 2 2 y w v x w v z E vk k v z E y x x              ………(2.30) y x xy xy w v z E k v z E          . . 1 . ) ( 1 . 2 2 2  ...………. (2.31)

Dari persamaan – persamaan diatas dapat diketahui bahwa tegangan tidak terjadi pada sumbu pelat dan akan berubah secara linier sepanjang tebal pelat yang diakibatkan oleh momen lentur Mx, My, dan Mxy.

Dengan mengambil integral pada Gambar 2.5 :

2 . . . . . 2 2 2





    t t t t y x z x y z y xd d d z d M d z  ... (2.32)

Dengan cara yang sama tegangan yang lain akan diperoleh dan dibuat dalam bentukmatrik hubungan momen lentur dan tegangan :



 _                    2 2 . . t t z xy y x xy y x d z M M M    . ... (2.33) Dimana : M_xy M_yx

Hubungan gaya geser dengan tegangan geser adalah :



 _                    2 2 . t t z yz xz y x d Q Q   ………..(2.34)

z t t x x zd M . . 2 2



  



         2 2 2 2 2 2 2₎.( ). . 1 ( . t t Z X zd y w x w v z E M



         2 2 2 2 2 2 2 2₎.( ). . 1 ( t t z X z d y w x w v E M ) ( ) 1 ( 12 . 2 2 2 2 2 3 y w x w v t E MX        ………...(2.35) Faktor -) 1 .( 12 . 2 3 v t E

 disebut faktor kekakuan lentur pelat.

Dari persamaan – persamaan tersebut diatas diperoleh :

3 . 12 t z Mx x   12. ₃ . t z M_y y   12. ₃ . t z M_xy xy   ………. (2.36)

Untuk menentukan komponen – komponen tegangan arah z yaitu : _z, _xz, dan _yz Digunakan persamaan differensial kesetimbangan untuk elemen pelat dalam suatu bentuk tegangan umum :

0         z xz y xy x x    0         z x yz xy y y    ... (2.37) x z xz z       + 0   z yz 

Dari persamaan 2.37 diperoleh : ) ( y x z xz x xz           



 _     2( ). t z xy x xz dz y x   









dz y x w v z E y y w v x w v z E x t z xz ) . 1 . ( ) 1 . ( 2 2 2 2 2 2 2



                         









dz y x w v z E y w v x w v z E t z xz . . 1 . 1 ( . 2 2 3 3 3 3 3 2



                  



_                     2 . . 1 . . 1 . . 1 . 2 3 2 3 2 3 3 2 t z xz dz y x w v z E y x w v v z E x w v z E 







                 2 . 1 1 1 . . 1 . 2 2 3 3 3 2 t z xz dz v v v y x w z E x w v z E 



_       2 ( ). 1 . 2 2 2 2 2 t z xz dz y w x w x v z E 



( )



4 ) 1 ( 2 2 2 2 2 2 2 2 y w x w x z t v E xz                  ……….(2.38)

Dengan cara yang sama diperoleh :



( )



4 ) 1 ( 2 2 2 2 2 2 2 2 y w x w y z t v E yz _                 ... (2.39)

melalui persamaan diatas dapat dilihat distribusi komponen tegangan xzdan yz

sepanjang ketebalan pelat merupakan persamaan parabola. Sedangkan komponen tegangan normal _zdapat ditentukan melalui persamaan ketiga pada persamaan 2.37

dengan mensubstitusi komponen tegangan yang telah diperoleh pada persamaan 2.38 dan

2.39 sebagai berikut : ) ( y x z yz xz z           



_     2( ). t z yz xz dz y x   











                                     2 . ( . 4 ) 1 ( 2 ) ( . 4 ) 1 ( 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 t z z dz y w x w y z t v E x y w x w x z t v E x 











                                 2 . ( . 4 ) 1 ( 2 ) ( . 4 ) 1 ( 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 t z x dz y w x w y w z t v E y w x w x z t v E 





dz y w x w y x z t v E t z z .( )( ) . 4 ) 1 ( 2 2 2 2 2 2 2 2 2 2 2 2 2



                    





_                     .( )( ) 3 4 12 ) 1 ( 2 2 2 2 2 2 2 2 2 3 2 3 2 y w x w y x z z t t v E z  ... (2.40)

komponen tegangan arah z selalu kecil dibandingkan dengan tegangan – pada arah lain (plane stress) dan ini sesuai dengan asumsi ke empat di atas, dimana tegangan arah z pada bidang tengah pelat sangat kecil dan dapat diabaikan.

II.8 Variasi Tegangan di dalam Pelat

Komponen tegangan pda umumnya berubah dari titik ke titik lainnya pada suatu pelat yang diberi beban. Perubahan atau variasi ini disebabkan oleh pengaruh

kesetimbangan statis antara komponen - komponen tegangan. Untuk memenuhi keadaan ini perlu dibuat suatu hubungan seperti persamaan kesetimbangan.

Perhatikan suatu elemen pelat kecil dx dy yang memikul beban terbagi merata per satuan luas p ( Gambar 2.7 ). Untuk penyederhanaan, diasumsikan gaya dan momen yang bekerja pada sisi penampang terdistribusi merata sepanjang sisi elemen.

Dengan adanya perubahan tempat, misalnya dari sudut kiri atas ke sudut kanan bawah elemen pelat, maka salah satu komponen gaya misalkan Mx yang beraksi pada sisi elemen negatif akan berubah relatif terhadap elemen positif.

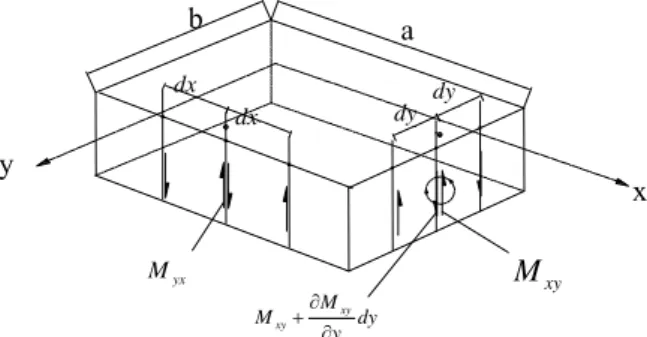
Gambar 2.10 Komponen gaya dan momen elemen pelat Sumber : Teori dan analisis pelat (Szilard, 1989)

y Q x z p Mxy My Mx Mxy dy dx dx x Q Q x x _   dx x M M xy xy _   y dy y M M y y _   dy y Q Q y y _   dy y M M xy xy _   dx x M M x x _  

Turunan parsial dipergunakan karena Mx adalah fungsi dari x dan y. dari Gambar 2.7, pelat dalam kondisi setimbang bilamana jumlah gaya yang bekerja pada arah z sama dengan nol. 0 . . . . . .        dy dx p dy dx y Q dy dx x Qx y Sehingga diperoleh : 0 . . _{ }      p y Q x Qx y ... (2.41)

Kesetimbangan momen pada sumbu x :

0 . . . . . . . .        dy dx Q dy dx y M dy dx x M y y xy sehingga diperoleh : 0 . .        y y xy Q y M x M ... (2.42) Begitu juga dengan kesetimbangan momen pada sumbu y :

0 . .        x x xy Q x M y M ... (2.43) Substusikan persamaan 2.42 dan 2.43 ke persamaan 2.41 sehingga diperoleh

p y M y x M x M_x xy y _          2 2 2 2 2 . 2 ... (2.44) Persamaaan 2.44 merupakan persamaan differensial kesetimbangan lentur pelat tipis. Gaya geser vertikal dinyatakan dalam fungsi x dan y adalah turunan pertama dari

persamaan kesetimbangan momen pada persamaan 2.14 menjadi :

 

w x D y w x w x D Q_{x 2} 2 2 2 2                    



w y D y w x w y D Qy 2 2 2 2 2                    



... (2.45)

Dimana ₂ 2 2 2 2 y x       

II.9 Persamaan Lendutan Pelat

Persamaan differensial dasar lendutan pelat diambil dari persamaan 2.14 dan 2.45 menjadi : D p y K y x K x Kx xy y           2 2 2 2 2 . 2 ... (2.46) Dengan mengganti persamaan kelengkungan diatas menjadi persamaan

lendutandengan memasukkan persamaan 2.26 diperoleh :

D p y w y x w x w           4 4 2 2 4 4 4 . 2 ... (2.47) Persamaan ini merupakan persamaan differensial lendutan pelat yang yang dibebani beban merata sebesar p. Persamaan lendutan w didapat dengan mengintegrasikan

persamaan persamaan tersebut pada syarat batas yang ada. Jika persamaan 2.45 dan persamaan 2.47 dimasukkan kedalam persamaaan tegangan pada (2.37), (2.38) dan (2.39) akan diperoleh :       _{1 (}2 ₎2 2 3 t z t Qx xz   _ _{1 (}2 ₎2_ 2 3 t z t Qy yz 



₍2 ₎3



3 1 2 4 3 t z t z p z     ... (2.48)

II.10 Beberapa Syarat Batas

Distribusi tegangan yang terjadi pada pelat tidak terlepas dari syarat batas (boundary condition), antara lain gaya dan perpindahan. Pada persamaan differensial kesetimbangan pelat dibutuhkan dua syarat batas utama pada masing – masing tepi yaitu lendutan dan rotasi atau gaya dan momen atau kombinasi antara keduanya.

Perbedaan yang mendasar antara syarat batas pelat dan balok adalah momen puntir (torsi) disepanjang tepi pelat.

Beberapa kondisi batas untuk suatu pelat persegi panjang, dimana sumbu x dan y diambil sejajar dengan sisi-sisi pelat yaitu :

a. Tepi terjepit

Jika pada tepi pelat x = a terjepit, lendutan dan kemiringan sepanjang tepi ini adalah nol. 0 ) (w x_a   0        a x x w

b. Tepi yang ditumpu sederhana

Jika pada tepi pelat x= a ditumpu sederhana, maka lendutan sepanjang tepi ini adalah nol. Namun tepi ini dapat berputar bebas terhadap garis tepi, sehingga tidak terdapat Momen lentur Mx sepanjang tepi ini.

 

w _xa 0

 

₂ 0 2 2 2                 a x a x y w v x w D Mx c. Tepi bebas

Jika tepi pelat bebas pada x = a, maka pada tepi ini tidak terdapat momen lentur Mx dan momen puntir Mxy dan gaya geser Qx, sehingga :





0 ) ( ₂ 2 2 2         _ a x a x y w v x w D Mx





0 . ) 1 ( ) ( 2        _ a x a x xy y x w v D M





0 ) ( 2₂ 2₂           _ a x a x x y w x w x D Q                    y x w v y w D x M Q Vy y xy 2 3 3 3 ) 2 (

b _a dx _dy dy dx y x xy M yx M

Gambar 2.11. Transpormasi puntir Mxy Sumber : Teori dan analisis pelat (Szilard, 1989)

Oleh Kelvin dan Tait dua kondisi batas Mxy dan Qx ini dapat dijadikan satu, Karena momen puntir Mxy dy yang bekerja pada suatu elemen sepanjang dy pada tepi x = a dapat digantikan dengan dua buah gaya vertical sebesar Mxy dan terpisah dengan jarak sebesar dy.

Dari gambar terlihat bahwa :

a x xy x y M Q            . '

Oleh karena persyaratan gabungan antara momen puntir Mxy dan gaya geser Qx sepanjang tepi batas x = a menjadi :

0 ) ( ) ' (        x_a xy x x x x y M Q Q Q v atau 0 ) 2 ( ₂ 3 3 3                 a x x y x w v x w D v

Dengan mentranspormasikan momen puntir seperti yang terlihat pada Gambar 2.7 selain diperoleh gaya geser Q’x sepanjang tepi x = a, juga diperoleh dua buah gaya

terpusat pada sudut tepi tersebut. Dengan cara yang sama, transpormasi momen puntir Myx sepanjang tepi y = b juga akan menghasilkan gaya geser sepanjang tepi dan gaya terpusat pada sudutnya. Sehingga besarnya reaksi pada sudut R untuk x = a dan y ialah :

dy y M M xy xy _  

b y a x b y a x xy y x w v D M R _{   }       _, 2 ) _, . )( 1 ( 2 ) .( 2