ANALYSIS
Seeing the trees as a forest: what counts in green accounting
Robert D. Cairns *
Department of Economics,McGill Uni6ersity,855Sherbrooke St.W.,Montreal,Canada H3A2T7 Received 14 October 1999; received in revised form 3 May 2000; accepted 1 June 2000
Abstract
Applying ‘green’ accounting to value the commercial contribution and depletion of a forest is only a short-run variation of the traditional approach to net national product (NNP) and arguably provides less information. Green adjustments can make a vital difference, however, by introducing nonmarketed values. Since optimal NNP is the linearized Hamiltonian, values are taken at the margin and exclude consumers’ surpluses, unlike in cost – benefit analysis. Green NNP may also require imputation of unmarketed exports and imports. © 2001 Elsevier Science B.V. All rights reserved.
Keywords:Environmental accounting; Forests; Depletion; Non-priced amenities; Inter-national externality
www.elsevier.com/locate/ecolecon
1. Introduction
A widely held perception is that the value added from commercial harvesting of a natural resource is recognized in the national accounts as part of the net earnings of firms and payments to factors, but that the depletion of the resource is neglected. Furthermore, vital, non-priced ‘ameni-ties’ of environmental resources depleted by com-mercial activity are also neglected. A premise of ‘green’ national accounting is that all contribu-tions of natural resources and the environment should be accounted similarly to consumption or investment, and all types of depletion similarly to
the depreciation of produced capital. A forest can be viewed as a prototypical resource for green accounting because of its depletion as a commer-cial asset and because of its many non-commer-cial, non-priced benefits to society.
The present study argues that correct green accounting for the commercial aspects of a forest would be different from most proposals which are current in the economic literature. We follow that literature by assuming that market prices are cor-rect social shadow values, as would be found in a model of maximizing aggregate social welfare. Therefore, a decentralized, microeconomic ap-proach to valuing an individual forest, using mar-ket prices, is appropriate. Unlike the literature, however, our analysis is based on that pioneered by Martin Faustmann in the 19th century. We * Tel.: +1-514-3983660; fax:+1-514-3984938.
E-mail address:[email protected] (R.D. Cairns).
apply the approach consistently with the value-added method of summing the contributions of individual economic units to obtain traditional net national product (NNP).
Appropriate economic and accounting method-ology raises a further issue, however, of whether it is worthwhile to implement green accounting: the practices of the traditional national accounts and green accounting are, in a sense to be elaborated, equivalent. For the commercial aspects of forestry, traditional NNP is arguably superior to green NNP.
For non-priced amenities, on the other hand, green accounting would be a giant step forward. Because market prices do not exist, we revert to an aggregate model to obtain expressions for the shadow prices of the amenities. We argue that the interpretation by Weitzman (1976) of NNP as an index of welfare requires that valuation be done at the margin, excluding consumers’ surpluses. If there are international environmental externali-ties, green NNP may not capture all flows in the balance of trade unless adjustments are made in the external accounts.
2. The forest as a purely commercial resource
2.1. A re6iew of Faustmann’s analysis
Suppose that the best use of a parcel of land for the foreseeable future is as forest land, the opti-mal choice of species being replanted after each harvest. Also suppose that the prices in all mar-kets are shadow values for the economy, so that maximizing the value of the forest using these prices leads to socially optimal decisions. Let the quantity of useful wood in a forest of aget\0 be
q(t), and have price p(t) and harvest cost H(t). Let the cost of planting a new rotation beP, the appropriate interest rate be r, and variable profit bep(t)=p(t)q(t)−H(t). A commercial forester’s problem is to choose the optimal rotation period (time between planting and felling), T, so as to
max
T
−P+ %
n=1
[p(T)−P]e−rnT
n
=L.In the solution, the value of the land in sup-porting forestry is L, and
p;(T)=rp(T)+rL. (1)
At the temporal margin, the rate of increase in profit from holding the trees an instant longer, p;(T), is equal to the interest on the capital tied up in the forest in the form of trees (rp(T)) and forest land (rL).
At time t=0, just after a harvest, a forestry firm is holding only bare land, and the value of the forest, V(t), is given byV(0)=L. Moreover, if capital markets are in equilibrium (so that there is no further opportunity for arbitrage), then an instant after planting the value of the forest (land with seedlings) is given byV(0+)
=L+P. This is the net present value, on the assumptions (1) that the trees are left to grow until exactly time Tand (2) that the rotation is repeated forever thereafter. At time T, the value has grown to V(T)=V(0+
)erT=(L+P)erT.
We can also express the value at time T as the net contribution of the forest products plus the value of bare land:
(L+P)erT=V(T)=p(T)+L. (2)
It is worth observing that, while the forest can be imagined to be an even-aged stand on a given area, it could as easily be a stand with multiple ages, with selective cutting of trees of age T, possibly on a sustained basis. In this case, the same type of analysis would be used to derive the optimal value of T. Presumably there would be higher costs of planting P and cuttingH(T); for example, economies of scale might not be fully exploited. Ceteris paribus, this would imply a smaller value ofL. The use of selective harvesting would presumably be chosen in order to reap other amenities from the forest. Such practice would increase the social value of bare land, as compared with considering only its commercial values (see Section 3 below).
2.2. Green accounting
increase in social consumption opportunities of
p(T)q(T). A part of this value, H(T), is a pay-ment to factors, and is treated in well-understood ways. The remainder, [(L+P)erT−L], is the
de-cline in value of the forest, or depreciation, at time T.
The variable profit of the firm, p(T)q(T)−
H(T), is called the rent of the forest. Therefore, depreciation atTexactly offsets the rent obtained at T. It would appear that, properly measured, the net income should be exactly offset in the national accounts by an entry for depletion of the forest. An implication is that the net contribution of the forest to national income is nil, for the resources making up the harvest costH(T) could have been used elsewhere in a fully employed economy, producing a value of H(T) at the mar-gin. This is the widely held perception mentioned above, and would imply that NNP is not so large as measured by the national accounts.
But this is not a complete view of the contribu-tion of the forest. At timeT+, there is an
invest-ment of P in planting the next rotation. Depreciation net of this investment is (L+
P)(erT−1). The portion P(erT−1) is the
depreci-ation of the accumulated value of the investment made at time 0 in the producing stand.1
This component of the rent, then, is a quasi rent to the investment (to the human contribution). The re-maining portion, L(erT
−1), is the depletion of natural capital:
L(erT−1)=p(T)q(T)−H(T)−PerT. (3)
Some have argued that depletion is less than the total rent; our analysis indicates that the reason is the appropriate accounting for invest-ments made in planting. Depletion is also less than the net cash flow, [p(T)q(T)−H(T)−P].
Some have viewed the problem of forestry ac-counting as being analogous to acac-counting for a nonrenewable resource, except that the forest can grow as well as be extracted. Analysis based on this view yields a relationship for rent at the
marginwhich is analogous to Hotelling’s rule. The distinction between marginal and average rent becomes an issue. This formulation is inconsistent with the point-output nature of the problem. Eq. (3) indicates that the relevant magnitudes are
incremental, not marginal.2
An intuitive way to perceive the distinction being made here is to note that, at the chosen harvest time, all trees of the relevant cohort are harvested. The forester adjusts the timing of the harvest at the margin, not production (one tree more or less to be harvested now or left for the future). There is no analogy to Hotelling’s rule for a nonrenewable resource, and it is not germane to distinguish between marginal and average magni-tudes. Eq. (1) resembles Hotelling’s rule. But it holds only at T, not through time.
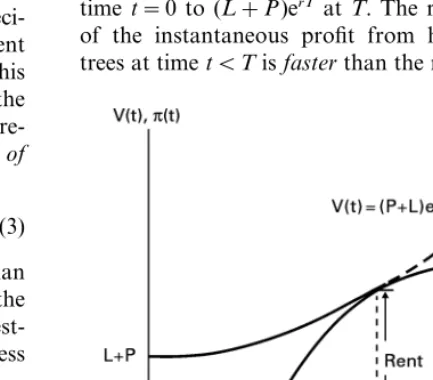
At any timet(0,T], the value is what the land with trees of agetwould fetch in a perfect capital market, or
V(t)=(L+P)ert.
In Fig. 1, the value V(t) rises from L+P at time t=0 to (L+P)erT at T. The rate of growth
of the instantaneous profit from harvesting the trees at timetBTisfasterthan the rate of growth
Fig. 1. The solution to Faustman’s Problem. 1At timeT, there is a reinvestment ofP, and hence there is
an explicit expectation that an investment ofPforTperiods in this forest will have a return ofr. A similar point holds for the reinvestment ofL.
of capital value until T, when the two are equal. As there is no thought of harvesting before or after timeT, either of which would result in a loss of value, the rate of growth of the trees for tBT is not pertinent to the valuation of the resource. Rather, at time t, there is an appreciation of the
6alue of the forest,
V: (t)=r(L+P)ert=rV(t). (4)
In the green accounts, this appreciation would be accounted as an investment.3 Also, at times
t=nT, n=0, 1, 2, 3, …, planting costs P would be accounted as an investment. As is necessary for correct accounting, the undiscounted sum of the investments in the forest is equal to the net value at any time, in particular, at timeT:
(L+P)+
&
T
0
r(L+P)erTdt=(L+P)erT.
2.3. Comparison of traditional and green accounting
The differences of traditional national account-ing from the green method above are that
there is no attribution of an increase in social
welfare resulting from growth in value for
t(0,T), asV: (t) is not recognized as an invest-ment; and
there is no accounting for depletion of the
forest at the time of harvest, T.
At timeT, the addition to (traditional) NNP is 1. an addition to consumption of p(T)q(T) (on the income side, income to harvesters, H(T), and variable profit p(T)), plus
2. an addition to investment of P (with corre-sponding entries on the income side), minus 3. depreciation of the original investment (att=
0) ofP,
a net total (at timeT) of p(T)q(T).
Green net national expenditure recognizes an investment at t=0 of P. At times t(0,T), it recognizes further investments of V: (t)=r(L+
P)ert, having undiscounted sum (L+P)(erT−1).
At time T, there are investment P, depreciation [L(erT−1)+PerT], and consumption p(T)q(T).
The undiscounted net total over the interval (0,T] is p(T)q(T).
In both methods, the contribution of a national forest is the sum over its component stands, as reported by economic units such as firms. In both methods, at time t=0 the contribution to NNP,
P, is the same. Fort\0 there is the same (undis-counted) total,p(T)q(T).4
Therefore,for the com
-mercial aspects of forestry, green and traditional NNP are equi6alent, in the sense that they give the
same total NNP over the harvest cycle. The equiv-alence arises because in this model it is assumed that there is no feature of the forest which is not captured in market prices.
Green NNP explicitly recognizes the growth of a forest’s value through time, and hence contribu-tions in the form of ‘investments’ (through forgo-ing the harvest until time T) to intertemporal social well-being. Manipulation of Eqs. (2) – (4) shows that the growth of value can be expressed as V: =r[p(T)−P]ert
/(erT
−1). In terms of dis-crete, annual measurements, with (1+i)=er, the
change in value in year t is
Vt+1−Vt=
i[p(T)−P](1+i)t
[(1+i)T−1] .
Since value is increasing at rate (1+i ), most of the attributed investment occurs toward time T, the point at which traditional NNP attributes the full rent as net income. Suppose that T=50. For typical interest rates, the investment even in year 40 represents less that 4% of the net cash flow,
4It could also be that the firm leases the land from a landowner. In this case, the amountrLwould be accounted as rental income to the landowner at each instantt. If the firm had other sources of profit, this amount would reduce the firm’s profit at that instant. In that case, the net effect on traditional net national income would be nil. If the firm had no other source of income, rental payments would be deducted at time T from p(T)q(T)−H(T). Green accounting would have no effect on total (undiscounted) NNP over the cycle. 3This is consistent with the formula of Weitzman (1976),
which is a special case of the asset – market equilibrium equa-tion,C=rV−V:: the instantaneous payment is equal to the sum of interest on the capital value and depreciation. Con-sumption of the forest at timet(0,T) is nil. Any allocation at
timet(0,T) between land and planting (between nature and
p(50)−P. The proportion of investment at-the national forest includes oat-ther ages, at-the total effect of a change to green accounting will be attenuated, even if the ages are not evenly dis-tributed.
In sum, green accounting has a purely short-run effect on the national accounts, and does not capture the long-run concerns which motivate the perceived need to do green accounting. In prac-tice, the changes may not be significant.
Moreover, the changes in value, (Vt+1−Vt), in
the green method are not observed in a market, but are imputed.5 An advantage of traditional NNP is that the accountant does not have to impute values, but uses only observed transac-tions in markets. In effect, in traditional NNP, the appreciation of the forest is realized at the same time as its depreciation, with a net effect of zero. Also, timber and pulp prices fluctuate in practice, and the rate of growth of trees is not deterministic but dependent on climatic factors. These stochas-tic features could affect the path of p(t)q(t) through time, and hence the realized value of T
through the stochastic analog of Eq. (1). By deal-ing with realized values of variables, traditional practice obviates the need to make complicated imputations of option value. Furthermore, the traditional accounts measure directly the level of human economic activity in an industry, which is what they were devised to measure, and the mon-itoring of which remains central to macroeco-nomic policy.
In this point-input, point-output problem with prices equal to social shadow values, there would seem to be information lost in using green NNP rather than traditional NNP, despite the addi-tional effort required for making imputations.
2.4. Non-optimality, old growth and deforestation
While we have made reference to Faustmann’s analysis as a motivator of the present one, there is no need to assume that the chosen rotation period is the optimal one, for the current or any future rotation. If the chosen harvest time is not optimal, then the main other change is that the value of the land is lower than the optimal value,L. Under the assumption that market prices are equal to social shadow values, traditional NNP correctly values the (lower) contribution of the forest to social well-being. For example, if the rotation period is longer than optimal, green NNP attributes spuri-ous capital gains for times t(0,T) if Faust-mann’s formula is used, and must impute capital losses for t\T, up to the chosen harvest time. Therefore, traditional NNP is more practical than green NNP if the actual rotation period is not the optimal one.
Consider the harvest of a forest primeval. It is easiest first to assume that the forest is cut all at once. (Below we allow harvesting to occur through time.) If L is the market value of bare land, and other variables are as above, then the value of the forest at the time of harvest, T0, is
V(T0)=p(T0)q(T0)−H(T0)+L.
After harvest but before planting, the value of the land isL. (This would be the value determined as above for the forest assuming new rotations, or else in some other use.) Whatever that value may be, the depletion at time T0 is equal to the full rent, p(T0)q(T0)−H(T0), and depreciation is this magnitude less the planting costPor other ready-ing of the land. We are attributready-ing the original ‘investment in planting’ the forest to nature.
The option to leave the trees growing past age
T0would give rise to changes in the value because of changes in price and possibly harvest cost. In keeping with our discussion, it would seem futile to estimate these changes in the national accounts. Rather, economists would point to the losses in national income and welfare resulting from sub-optimal policy.
If, on the other hand, the forester’s plan is to harvest the forest at rateq(t) from timet=T0 to
t=T0+S, then the present value at T0 is 5In practice, both T and [p(T)−P] would have to be
projected. In some countries there are markets for forests. But there are not transactions for each piece of land at each date, as would be required actually to observe each valueVtand
V(T0)= %
T0+S t=T0
p(t)q(t)−H(q(t)) (1+i)t−T0 .
Some have observed that this forest has analo-gies to a mine, especially if it is not to be re-planted. Even so, we do not have recourse to Hotelling’s rule, nor find any use for what some have called ‘Hotelling rent’ (for details see Cairns, 2000a). Consider the part of the stand to be cut at time t\T
0. It has present value
6
t(T0)=
p(t)q(t)−H(q(t)) (1+i)t−T0 .
During time sBt, there is an appreciation of the value of this part of the stand, equal to
6t(s+1)−6t(s)=ip(t)q(t)−H(q(t))
(1+i)t−s .
This could be imputed as an appreciation. The total (undiscounted) appreciation of the value of this part of the stand to time t is then
A= %
T0+t−1 s=T0
[6t(s+1)−6t(s)]=6t(T0+t)−6t(T0).
In this case, the depreciation of this part of the stand is
D=p(t)q(t)−H(q(t))=6
t(T0+t).
Therefore, the total net depreciation of the stand is
D−A=6
t(T0),
and the total over all stands isV(T0), the value at the time it is decided to cut the forest. Alterna-tively, the value V(T0) could be recorded at time
T0, and be depreciated over time. Ideally, the depreciation would be 6 The net gain,Nt, is the total of the appreciation
above; it arises because interest increases the value of this part of the stand from6
t(T0) at timeT0to
6
t(T0+t) at time T0+t. In practice, an account-ing formula could be used for the depletion of the full value V(T0).
An environmentalist might react to this analysis by remarking that the preference for traditional over green NNP arises because Faustmann’s forest is a sustained forest, and that a major environmental concern is deforestation. Suppose that a forest is taken into another use, and in this use has a different value from that in forestry. Some have argued that a special treatment of this change in value should be made in the accounts. But, so long as the 6alues in question are all
commercial, the appropriate treatment of the change in value is conceptually not different from that applied to other assets which change their uses, such as buildings or rezoned urban land. Indeed, the source of environmentalists’ concern about deforestation is loss of non-commercial
value.
Therefore, as far as the purely commercial as-pects of forestry are concerned, there is no com-pelling reason to change the current practice of accounting for forests. Even if the forest is ex-ploited suboptimally, the economic and account-ing implications are comparable with those in non-resource industries. The equivalency we have noted arises because accounting methods have been designed over the centuries to provide the maximal obtainable information about the effi-ciency of commercial activities.
The only exception is the harvesting of a forest directly from its pristine state. In this case, as we have observed above, depletion should be at-tributed. The reason is that the original planting, by nature, is not ‘priced’. Non-priced features constitute a systematic problem.
3. Non-priced amenities
For values which are not priced in markets, shadow prices can be determined using a macroe-conomic model. Let there be a stock R of an environmental asset producing amenitiesA(R) and let social utilityUbe given by a function of current consumption C and amenities. The aim of the planner is to maximize
t U[C,A(R)]e−r(s−t)ds.
Let the produced capital stock be K and evolve through time through investment I and physical deterioration dK according to the equa-tionK: =I−dK. Let total output be a function of the produced capital stock,F(K). Let the environ-mental asset evolve according to the equation
R: =M−aF(K)−gR, with M being the level of improvements or maintenance; aF(K) being degradation due to economic activity; and gR
being degradation from natural causes. Finally, let the cost of the different types of expenditures in terms of consumption be given by f(I) and c(M), so that C=F(K)−f(I)−c(M).
The current-value Hamiltonian of this problem is
H=U(C,A)+6(I−dK)+u[M−aF(K)−gR].
If the problem has no exogenous source of time dependence, then Weitzman shows that the Hamiltonian at any time is equal to interest on the present value of the discounted utility (the objective) at that time. Therefore, the Hamilto-nian is a form of generalized income from the generalized wealth of the economy. If there is time dependence, such as the natural fluctuations in the climate that have been observed by climatologists studying the history of the earth before the indus-trial revolution, then to retain this interpretation, a term measuring the ‘drift’ of the system should be added to the Hamiltonian (Cairns, 2000b). Interpreting the Hamiltonian as a measure of current contributions to the objective amounts to making the reasonable assumption that the drift from year to year is negligible.
The Hamiltonian can be written analogously to an affine function:
This ‘affine Hamiltonian’ isequal tothe Hamil-tonian, and not an approximation from a Taylor’s series expansion. It consists of
1. a term S(C,A), which we identify as the total consumers’ surplus over goods and amenities in utility terms, plus
2. terms involving quantities times prices of goods or amenities which enter the utility function, C(U/(C+A(U/(A, plus
3. the net investment terms 6(I−dK)+u[M−
aF(K)−gR].
The welfare functionUcan be scaled such that
(U/(C=p(t), the (money) price of consumption
goods. The first-order, necessary conditions for a maximum are that 6=f%(I)(U/(C=pf%(I)=p
I,
the market price of investment goods, and that
u=pc%(M)=p
M, the market price of
mainte-nance expenditures. Thus, we can write the affine Hamiltonian as
H=S(C,A)+pC+A(U
(A +pI(I−dK)
+pM[M−aF(K)−gR].
We define green NNP by evaluating consump-tion and amenities at the margin. That is to say, we linearizethe ‘affine Hamiltonian’ by purging it of its intercept, the consumers’ surplus, which depends non-linearly on Cand A:
NNP=pC+A(U
(A +pI(I−dK)
+pM[M−aF(K)−gR].
Purging the non-linearities permits aggregating results from small economic units at the econo-my’s shadow prices, as is done in traditional NNP using market prices as proxies for shadow prices.6 Consistently, with our analysis of the commercial forest, traditional NNP, pC+pII+pMM,
cor-rectly attributes commercial values if the market prices actually are shadow prices. Traditional NNP, however, neglects the terms, A(U/(A and
pM[aF(K)+gR], which are to be included in
green NNP. Contrary to the intuition of some, maintenance (or defensive) expenditures M con-tinue to be included. But green NNP also im-putes, as a form of depletion, any environmental costs, including natural ones gR.
Some have reasoned that ‘greening’ the na-tional accounts could utilize cost – benefit analysis to obtain the non-commercial values. Our discus-sion points up a subtle difference between cost – benefit analysis and both the environmental and traditional accounts. Consumers’ surpluses (more properly, compensating or equivalent variations) are a part of the social values of particular assets and are estimated in a cost – benefit analysis. But NNP abstracts from consumers’ surpluses by valuing consumption at the margin (at market prices, where they exist). The part of consumers’ surplus which is attributable to amenities, should not be part of green NNP, just as the part which is attributable to marketed goods is not a part of traditional NNP. In general, consumers’ surplus may not easily be divided among marketed and environmental goods. For example, both food and some amenities are essential to life.
Some changes in forest use may not, however, be subject to internalization by even this type of imputation of shadow values. For example, forests may be burnt without regard to interna-tional transmission of pollutants in air or water, or cut without regard to global warming. Reduc-ing international pollution is a public good; the global shadow value of reducing it is the sum of the marginal values over all inhabitants of the globe.
The sum of the marginal values over the citi-zens of even a large industrial country is much smaller than this global shadow value. Therefore, evaluating preservation at the global shadow value overstates the value to a home country of control, and entering it into green NNP overval-ues the contribution to welfare of the given na-tion. But imposing the sum of national marginal values as a mandated price within a country would imply an internationally suboptimal ratio of prices.
What can be done in this case is to impute the difference between the shadow value and the
do-mestic willingness to pay as an export to other countries. This shadow export of real value would have to be compensated by a shadow transfer of, say, some service abroad.7 By the same token, imports would have to be imputed for the results of other countries’ efforts which benefit the nationals of the country under discus-sion, as well as an offsetting shadow transfer of a service from the country. In the real expenditure accounts, though, such imports could otherwise go unnoticed; they would not affect the country’s green NNP, as they would offset additions to imputed consumption that they engendered. But they would be needed to account correctly for trade flows.
4. Conclusion
The compelling reason for ‘greening’ the forest accounts is the one which many ecologists have raised, namely, recognizing the non-commercial
(or non-priced) features of a forest. Value added in the traditional accounts is a superior measure of the commercial aspects of forest value and depletion, be the forest optimally utilized or not. If non-priced amenities are local then tradi-tional NNP should be increased by imputing the values of their flows in green satellite accounts. If the amenities are global, imputations need to be made of trade flows based on sums of marginal valuations over the relevant groups.
Imputing values of non-priced amenities or costs is subtle and difficult. Because valuation of benefits should be made at the margin, cost – benefit analysis may need to be modified to be used as a tool of valuation. Despite the subtlety and difficulty, advances would be obtained from a greater focus on such issues.
Acknowledgements
I thank Joseph Doucet and two referees for helpful comments, and FCAR and SSHRC for financial support.
References
Ahmad, Y., El Serafy, S., Lutz, E., 1989. Environmental Accounting for Sustainable Development. The World Bank, Washington, DC.
Cairns, R., 2000a. Accounting for resource depletion: a microeconomic approach. Rev. Income Wealth 46 (1), 21 – 31.
Cairns, R., 2000b. Sustainability accounting and green ac-counting. Environ. Dev. Econ. 5, 49 – 51.
Dasgupta, P., 1982. The Control of Resources. Oxford Univer-sity Press, Oxford.
Pearce, D., 1994. Assessing the social rate of return from investment in temperate-zone forestry. In: Layard, R., Glaister, S. (Eds.), Cost – Benefit Analysis, second ed. Cam-bridge University Press, CamCam-bridge.
Weitzman, M., 1976. On the welfare significance of national product in a dynamic economy. Q. J. Econ. 90, 156 – 162.