MODUL PENGANTAR STATISTIK PENDIDIKAN

PENGANTAR STATISTIK PENDIDIKAN

1. PENDAHULUAN

1.1. Pengertian statistik dan statistika

Statistik adalah kumpulan data, bilangan maupun non bilangan yang disusun dalam table dan atau diagram yang melukiskan suatu persoalan

Statistika adalah pengetahuan yang berhubungan dengan cara-cara pengumpulan data, pengolahan atau penganalisaannya dan penarikan kesimpulan berdasarkan kumpulan data dan penganalisaan yang dilakukan.

1.2. Data Statistik

Menurut sumbernya kita mengenal data intern dan data ekstern. Data intern adalah data yang diperoleh dari perusahaan atau instansi yang bersangkutan. Sedangkan data ekstern diperoleh dari luar instansi atau perusahaan tersebut. Data ekstern dibedakan menjadi data primer dan data sekunder. Data primer adalah data yang diusahakan/didapatkan sendiri, misalnya dengan melakukan wawancara, pengukuran atau penelitian langsung. Sedangkan data sekunder adalah data yang diperoleh dari referensi/instansi/lembaga lain misalnya data diperoleh dari LIPI, BPS, dsb.. Semua data-data yang baru dikumpulkan dan belum pernah diolah disebut sebagai data mentah.

1.3. Populasi dan sampel

Populasi adalah keseluruhan pengamatan yang menjadi perhatian kita baik yang berhingga maupun tak berhingga jumlahnya. Seringkali tidak praktis mengambil data dari keseluruhan populasi untuk menarik suatu kesimpulan. Untuk itu dilakukan pengambilan sampel yaitu sebagian atau himpinan bagian dari populasi. Sampel yang diambil haris dapat merepresentasikan populasi yang ada. Prosedur pengambialan sampel yang menghasilkan kesimpulan yang konsisten terlalu tinggi atau terlalu rendah mengenai suatu ciri populasi dikatakan berbias. Untuk menghindari kemungkinan bias ini perlu dilakukan pengambian contoh acak atau contoh acak sederhana. Contoh acak sederhana didefinisikan sebagai contoh yang dipilih sedemikian rupa sehingga setiap himpunan bagian yang berukuran n dari populasi mempunyai peluang terpilih yang sama.

1.4. Pembulatan angka

Dalam perhitungan dan analisis data statistik seringkali diperlukan pembulatan angka-angka. Berikut ini adalah beberapa aturan tentang pembulatan angka-angka. 1. Jika angka yang harus dihilangkan adalah 4 atau kurang, maka angka terkanan

yang mendahuluinya tetap.

Contoh: Rp. 59.376,- dibulatkan menjadi Rp. 59 ribu.

2. Jika angka yang haarus dihilangkan adalah lebih dari 5 atau angka 5 diikuti angka bukan nol maka angka yang mendahuluinya ditambah dengan 1.

Contoh: 176,51 kg dibulatkan menjadi 177 kg.

3. Jika angka yang harus dihilangkan hanya angka 5 atau angka 5 diikuti nol, maka angka yang mendahuluinya tetap jika genap dan ditambah 1 jika ganjil.

2. PENYAJIAN DATA

Secara garis besar ada dua macam cara penyajian data dalam statistika yaitu: 11. Tabel atau daftar yang dapat berbentuk:

0 a. Daftar baris kolom

1 b. Daftar distribusi frekuensi

22. Grafik atau diagram yang terbagi menjadi: 3a. Diagram batang atau balok

4b. Diagram garis atau grafik 5c. Diagram lingkaran

Daftar distribusi frekuensi dan grafiknya

Dalam distribusi frekuensi data dikelompokkan dalam beberapa kelas interval misalnya a–b, c-d dan seterusnya. Ada beberapa istilah yang digunakan dalam distribusi frekuensi yaitu:

11. Limit kelas atau ujung kelas yaitu nilai-nilai terkecil dan terbesar dalam setiap kelas interval. Nilai terbesar disebut sebagai limit atas kelas dan nilai terkecil disebut sebagai limit bawah kelas.

22. Batas kelas yaitu limit kelas ± setengah nilai skala terkecil. Nilai yang besar disebut batas atas kelas dan nilai yang kecil disebut sebagai batas bawah kelas.

33. Titik tengah kelas atau tanda kelas yaitu nilai yang terletak pada engah setiap kelas interval. Aturan umum yang digunakan untuk menentukan titik tengah kelas atau tanda kelas adalah:

Tanda kelas = ± ½ (limit bawah + limit atas) Macam-macam distribusi frekuensi

11. Distribusi frekuensi

22. Distribusi frekuensi. Relative (%)

33. Distribusi frekuensi kumulatif kurang dari 44. Distribusi frekuensi kumulatif lebih dari Cara membuat Tabel Distribusi Frekwensi

Jumlah data : n

Rentang : max – min

Banyak interval : 13,3log n  Aturan Sturges

Panjang interval : _banyakren_{_}tan_intg_erval

awal interval : min + panjang interval – satuan terkecil data tepi : batas satuan_terkecil_data

2 1

Dengan menggunakan aturan pembuatan distribusi frekuensi tersebut di atas dapat dibuat sebuah distribusi frekuensi dengan 7 kelas sebagai berikut:

3. MACAM-MACAM UKURAN

UKURAN PEMUSATAN

Ukuran pemusatan dibagi dalam dua kelompok 11. Ukuran gejala pusat, meliputi

 Rata-rata hitung (mean)  Rata-rata ukur

 Rata-rata harmonic  Rata-rata gabungan  Modus

Rata-rata Hitung (Mean)

Diperoleh dengan membagi jumlah seluruh data dengan banyak data

n x

M



i



Jika masing-masing mempunyai frekuensi maka rata-ratanya disebut sebagai rata-rata terboboti.







i i i

f x f M

Jika kita mempunyai data n1, n2, n3, … dengan nilai rata-rata masing-masing .. maka rata-rata gabungan data di atas dinyatakan dengan

Untuk data-data yang tersusun dalam distribusi frekuensi rata-ratanya dihitung dengan

atau dengan cara singkat/sandi (khusus untuk lebar kelas yang sama) yakni sebagai berikut

Median (Me)

Median adalah nilai tengah suatu data jika datanya telah disusun dalam distribusi frekuensi

   

 

   

 

 



f F n c L

Me 2 k

1

Modus (Mo)

Modus adalah nilai atau fenomena yang paling sering muncul jika datanya telah disusun dalam distribusi frekuensi

    

  

  

2 1

1 d d

d c L Mo

2. Ukuran letak, meliputi :

 Kuartil  Desil  Persentil

KUARTIL

Letak  ; 1,2,3 4

1

  datakei n i Ki

Untuk data yang disusun dalam distribusi frekuensi

3 , 2 , 1 , 4 _             _   i f F n i c L

Ki k

L = tepi bawah kelas c = panjang kelas

k

F _{= frekwensi kumulatif sebelum kelas}

f = frekwensi kelas DESIL

Jika sekumpulan data dibagi menjadi sepuluh bagian yang sama setelah di urutkan maka nilai yang membaginya disebut desil.

Letak  ; 1,2,3,...,9 10

1

  datakei n i Di

Untuk data yang disusun dalam distribusi frekuensi

9 ,..., 3 , 2 , 1 , 10 _             _   i f F n i c L

Di k

L = tepi bawah kelas c = panjang kelas

k

F _{= frekwensi kumulatif sebelum kelas}

f = frekwensi kelas PERSENTIL

Jika sekumpulan data dibagi menjadi seratus bagian yang sama setelah di urutkan maka nilai yang membaginya disebut persentil.

Letak  ; 1,2,3,...,99 100

1

  datakei n i Pi

Untuk data yang disusun dalam distribusi frekuensi

99 ,..., 3 , 2 , 1 , 100 _                i f F n i c L

Pi k

L = tepi bawah kelas c = panjang kelas

k

F _{= frekwensi kumulatif sebelum kelas}

f = frekwensi kelas UKURAN SIMPANGAN

Ukuran simpangan digunakan sebagai gambaran bagaimana berpencarnya suatu data kuantitatif. Ukuran-ukuran tersebut yaitu:

Rentang = data terbesar – data terkecil Rentang antar kuartil (RAK)

1 3 K

K

RAK  

Simpangan kuartil (SK)

Simpangan baku

 untuk sampel disimbolkan dengan s  untuk populasi disimbolkan dengan 

Kuadrat simpangan baku disebut varians

Varians sampel dihitung dengan





1

2 2

 





n x x

s i

atau







1



2 2

2

 







n n

x x

n

s i i

Jika datanya dalam distribusi frekuensi :





1

2 2

 





n x x f

s i i

atau







1



2 2

2

 







n n

x f x

f n

s i i i i

Bilangan baku/ Nilai Z

Bilangan baku/nilai z didefinisikan sebagai :

Atau lengkapnya

Ukuran-ukuran simpangan diatas merupakan ukuran absolut. Jika dari simpangan absolut diambil simpangan bakunya, maka kita dapat koefisien Variasi

Selain ukuran simpangan/ disperse absolut, dikenal pula dispersi relatif yang dinyatakan :

UKURAN KEMIRINGAN Pengertian

Model lengkungan

Rumus koefisien kemiringan menurut Pearson

s Mo x Kp1  

 

s Me x Kp2 3 

1 3

3 2 1 3

2 K K

K K K Kp

   

10 90

90 50 10 4

2 P P

P P P Kp

   

Kriteria :

Menurut Pearson koefisien kemiringan diatas ada tiga kriteria untuk mengetahui model distribusi dari sekumpulan data, yaitu :

Normal

Kp0

Positip

Kp 0

Negatip Kp0

UKURAN KERUNCINGAN Pengertian

Ukuran keruncingan (kurtosis) adalah derajat kepuncakan dari suatu distribusi, biasanya diambil relatif terhadap distribusi normal.

Model lengkungan

KEMIRINGAN

Mean Median

Modus

Mean

Median Modus

Simetris Negatip Positip

Rumus koefisien keruncingan :

 

10 90

1 3 2 1

P P

K K K

  

Kriteria :

Dari hasil koefisien kurtosis diatas, ada tiga kriteria untuk mengetahui model distribusi dari sekumpulan data, yaitu :

Mesokurtik K 0,263

k Leptokurti K 0,263

k Platikurti K 0,263

4. PENGGUNAAN BEBERAPA DAFTAR

Pengertian dari daftar distribusi

Pada bagian ini akan dibahas tentang kurva-kurva normal yang berasal dari distribusi dengan peubah acak kontinu, oleh karena lebih banyak digunakan dalam kehidupan sehari-hari terutama dalam dunia pendidikan.

Distribusi normal baku z (gauss)

Distribusi Gauss merupakan distribusi yang paling sering digunakan. Fungsi distribusi Gauss diberikan dengan persamaan :

Distr. Platikurtik (datar dan menyebar)

Distr. Mesokurtik (normal)

Distr. Leptokurtik (tinggi dan tipis)

2 2 1 2 1 ) (             x e x

f (1)

dimana :  = konstanta yang nilainya 3,1416... e = konstanta yang nilainya 2,7183...

 _{= parameter, yaitu rata-rata distribusi populasi}

 = parameter, yaitu simpangan baku distribusi populasi x = peubah kontinu yang nilainya  x

Sifat distribusi normal :

1. grafiknya selalu terletak diatas sumbu x 2. bentuk grafiknya simetris terhadap x

3. modus tercapai pada

   0,3989

4. grafiknya asymtottis terhadap sumbu x

5. luas daerah grafik sama dengan satu satuan persegi

Dalam pemakaiannya rumus diatas tidak lagi digunakan, karena sudah disiapkan daftar distribusi normal baku. Distribusi normal baku adalah distribusi normal dengan nilai rata-rata  _{= 0 dan simpangan baku  = 1. Fungsi densitinya dinyatakan}

dalam peubah acak z seperti :

(2) dengan daerah z adalah interval  x

Dari hubungan (1) dan (2) distribusi normal ini menjadi distribusi normal baku dengan menggunakan transformasi.

    x

z _{(populasi) dan}

s x

z  (sampel)

Contoh 1 :

Nilai rata-rata ujian masuk perguruan tinggi 67,75 dengan simpangan baku 6,25. Jika distribusinya normal dan banyak calon 10.000 orang, tentukan :

a. Berapa % banyak calon yang nilainya lebih dari 70 ? b. Berapa orang calon yang nilainya antara 70 dan 80 ? Penyelesaian :

a. Dengan rumus 0,36

25 , 6 75 , 67 70 70 ;      

 x z

s x x z 2 2 1 2 1 )

(z e z

f  

lihat tabel z0,36 0,1406

luas daerah yang lebih besar dari z0,36 0,50,1406 0,3594

jadi banyak calon yang nilainya lebih besar dari 70 adalah 35,94 %

b. 0,36 0,1406

25 , 6 75 , 67 70 36 , 0

1   



 z

z

persentasi calon yang terletak antara nilai 70 dan 80 adalah 0,4750 – 0,1406 = 0,3344, jadi banyaknya calon adalah 0,3344 x 10.000 = 3.344 orang

Contoh 2 :

15 % dari tamatan SMA merupakan hasil PMDK, Sampel acak yang berukuran 600 tamatan SMA telah digunakan. Tentukan nilai kemungkinan yang akan terdapat : a. Paling sedikit 70 orang dan paling banyak 80 orang sebagai hasil PMDK ? b. Lebih besar atau sama dengan 100 orang yang memperoleh PMDK ? Penyelesaian :

a. x terletak antara : (70 – 0,5) < x < (80 + 0,5) atau 69,5 < x < 80,5 rata-rata :  np 6000,1590

simpangan baku :   np(1p)  6000,1510,158,75

4904 , 0 34 , 2 75 , 8 90 5 , 69 34 , 2

1   



 z

z _dan 1,09 0,3621

75 , 8 90 5 , 80 09 , 1

2   



 z

z

nilai kemungkinan terdapat paling sedikit 70 orang dan paling banyak 80 orang sebagai hasil PMDK adalah 0,4904 – 0,3621 = 0,1283

b. lebih besar atau sama dengan 100 artinya x ≥ (100-0,5) atau x ≥ 99,5 3621 , 0 09 , 1 75 , 8 90 5 , 99 09 , 1      z z

nilai kemungkinan lebih besar atau sama dengan 100 adalah 0,5 – 0,3621 = 0,1379

Distribusi student t

Distribusi peubah acak kontinu lainnya adalah distribusi yang ditemukan oleh seorang mahasiswa yang tidak mau disebut namanya. Untuk menghargai hasil penemuan itu, distribusinya disebut distribusi student atau lebih dikenal dengan distribusi ”t”, bentuk persamaannya adalah :

n n t K t f 2 1 2 1 1 ) (           

berlaku untuk  t dan K merupakan tetapan yang besarnya tergantung dari besar n sedemikian sehingga luas daerah antara kurva fungsi itu dan sumbu t adalah 1.

Bilangan (n-1) disebut derajat kebebasan (dk)

Bentuk kurva distribusi t mirip dengan bentuk kurva normal baku. Contoh 1:

dk = 14 – 1 = 13

α = 5 %, maka p = 100 % - 5 % = 95 % = 0,95 lihat daftar t0,95(13) 1,77

Contoh 2 :

Untuk n = 18, tentukan nilai t sehingga luas daerah kurva yang dicari sama dengan 95 %

Penyelesaian :

1 0,95 0,025 0,95 0,025 0,975 2 1       p

dk = 18 – 1 = 17

lihat daftar t0,975(17)  2,11

Distribusi khi-kuadrat Distribusi 2

 (baca : khi kuadrat) juga merupakan peubah acak kontinu dengan

bentuk persamaan :

u e Ku u f 2 1 1 2 1 ) (   

dengan u = 2

 > 0

dk =  _{sedemikian rupa sehingga luas dibawah kurva sama} dengan 100 % atau 1

Grafiknya mempunyai kemiringan positip Contoh :

Untuk yang berdistribusi _2 _{dengan dk = 17, carilah nilai }2 _{sehingga luas :} a. dari 2

 ke kanan sama dengan 0,05

b. dari 2

 ke kiri sama dengan 0,25

c. dari 2

 dengan luas diarsir 0,1

Penyelesaian :

a. 210,05 17 20,95(17) 27,6 b. 20,25(17) 12,8

c. biasanya digunakan ”fifty-fifty” 0,1 0,05 2

1

 , artinya kekiri = 0,05 dan kekanan =

(1 – 0.05) = 0,95

67 , 8 ) 17 ( 05 , 0 2 

 dan 20,95(17) 27,6

Distribusi F

Fungsi density distribusi F mempunyai persamaan :  

1 2

1 2 1 2 1 2 2 1 1 ) (                F F K F f

1

 adalah dk untuk pembilang, sedangkan 2 merupakan dk penyebut, grafiknya asimetris dengan kemiringan yang positip.

Kalau kita perhatikan setiap pasangan dk yang digunakan tersedia dua bilangan yang dapat dipilih, yaitu bilangan yang letaknya diatas dan bilangan yang letaknya dibawah. Bilangan yang diatas menunjukkan nilai F untuk luas daerah dari nilai F ke kanan sebesar 0,05 ( p = 0,05), sedang bilangan yang dibawha menunjukkan nilai F untuk luas daerah dari nilai F ke kanan sebesar 0,01 ( p = 0,01), simbolnya ditulis

) , ( 05 , 0 12

F _dan F0,01(1,2).

Sedang untuk menghitung (1 – p) digunakan rumus   

1 2

2 1

, ,

1

1

  



p p

F

F  

Contoh :

Dengan dk pembilang 9 dan dk penyebut 21, nilai F sehingga luas daerah dari F ke kanan sama dengan 0,01 adalah ...

Penyelesaian :

9,21 3,40

01 ,

0 

F

Pengujian Persyaratan Analisis

Dalam melakukan analisis data yang menggunakan teknik korelasional dengan dua berntuk perhitungan yaitu korelsi product moment dan regresi diperlukan asumsi – asumsi tertentu agar intrepretasi terhadap hisilnya dapat dipertanggungjawabkan dilihat dari sudut pandang statistika. Dalam hubungan ini, asumsi/persyaratan yang perlu dipenuhi adalah :

 Korelasi product momen/Pearson 1. sampel diambil secara acak 2. ukuran sampel minimum dipenuhi

3. data sampel masing-masing variabel berdidtribusi normal 4. bentuk regresi linier (Santosa Murwani. 2000. h 32)

sementara itu menurut Dennis E. Hinkle menyatakan bahwa analisis menggunakan korelasi Pearson perlu memenuhi dua kondisi yaitu :

1. Variabel yang dikorelasikan harus berpasangan bagi individu atau subjek yang sama.

2. variabel yang dikorelasikan skala pengukurannya harus interval atau rasio, dan hubungannya harus bersifat linier.

3. Homogenitas kelompok

 Regresi (Fred N. KerlingerElazar J. Pedhazur : 1973 : 47)

1. Skor Variabel Y (dependent Variable) harus berdistribusi normal untuk setiap nilai X, sedangkan untuk variabel bebas (X) tidak disyaratkan berdidtribusi normal.

2. Skor variabel dependen (Y) mempunyai varians yang sama (homogenitas variansi) untuk setiap nilai variabel bebas (X).

karena itu uraian berikut akan difokuskan pada pengujian normalitas dan homogenitas.

1. Uji Normalitas Distribusi

Terdapat beberapa cara pengujian normalitas distribusi yaitu menggunakan formula/prosedur Kolmogorov-Smirnov, Liliefors, dan Chi Square (2 )

1.1. Uji Kolmogorov-Smirnov

Untuk perhitungan normalitas distribusi, dimisalkan terdapat sekelompok data dengan skala pengukuran interval dengan dua variabel bebas dan satu variabel terikat sebagai berikut :

Tabel skor Variabel bebas (X) dan variabel terikat (Y)

X1 X2 Y

4 1 7

4 2 12

9 8 17

12 8 20

12 10 21

Dari tabel tersebut misalkan kita ingin menguji normalitas variabel Y , maka untuk memudahkan diperlukan tabel bantu sebagai berikut :

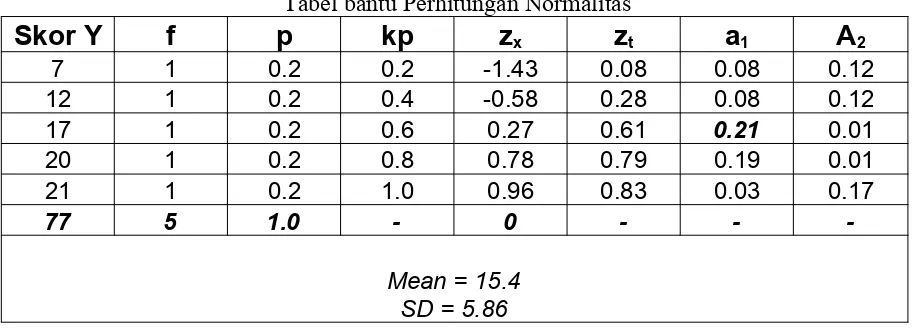
Tabel bantu Perhitungan Normalitas

Skor Y

f

p

kp

z

x

z

t

a

1

A

2

7 1 0.2 0.2 -1.43 0.08 0.08 0.12

12 1 0.2 0.4 -0.58 0.28 0.08 0.12

17 1 0.2 0.6 0.27 0.61 0.21 0.01

20 1 0.2 0.8 0.78 0.79 0.19 0.01

21 1 0.2 1.0 0.96 0.83 0.03 0.17

77 5 1.0 - 0 - -

-Mean = 15.4 SD = 5.86

 Langkah-langkah perhitungan :

Setelah data dimasukan dalam kolom pertama dan dihitung frekuensinya, kemudian dilakukan perhitungan sebagai berikut :

1. Cari prosentasi (p) dengan cara frekuensi (f) dibagi dengan jumlah data. Dalam contoh baris pertama di atas adalah 1 : 5 = 0.2, demikian seterusnya sampai selesai untuk setiap frekuensi.

3. Cari nilai Zx dengan cara Skor Y dikurangi dengan Mean/nilai rata-rata

dibagi nilai Standar Deviasi, sebagai contoh untuk baris pertama adalah (7 – 15.4)/5.86 = - 1.43. untuk baris selanjutnya dihitung dengan cara yang sama. 4. Cari nilai Z tabel (Zt) dengan melihat Tabel Kurva Normal baku (Tabel Z )

berdasarkan nilai Zx –nya, contoh untuk baris pertama. Nilai Z tabel dilihat dalam

baris 1,4 dan kolom 3, diperoleh nilai Z sebesar 0.4236, karena nilai Zx – nya

bernilai minus maka nilai Z tabel yang diisikan adalah 0.5 - 0.4236 = 0.0764 (0.08). bila Zx bernilai positif maka nilai Z tabel yang diisikan adalah ditambah 0.5.

5. Nilai a1 diperoleh dengan cara menyelisihkan nilai Kp dengan nilai Zt di

bawahnya, sedang untuk baris pertama nilai Zt langsung diisikan, contoh untuk

baris kedua nilai 0.08 diperoleh dengan cara 0.2 – 0.28 = -0.08 (yang dipakai nilai mutlaknya).

6. nilai a2 diperoleh dengan menyelisihkan nilai Kp dengan nilai Zt yang

sejajar, contoh untuk baris pertama 0.2 – 0.08 = 0.12.

7. setelah selesai cari nilai a maksimum, diperoleh nilai 0.21, kemudian bandingankan dengan nilai tabel pada baris N = 5, pada tingkat signifikansi 0.05 diperoleh nilai 0.565, karena a maksimum lebih kecil dari nilai D maksimum berarti distribusi normal.

1.2. Uji Lilliefors

Cara lain pengujian normalitas distribusi adalah menggunakan formula Lilliefors, berikut akan diberikan contoh perhitungan dengan menggunaka data pada pengujian Kolmogorof-Smirnov

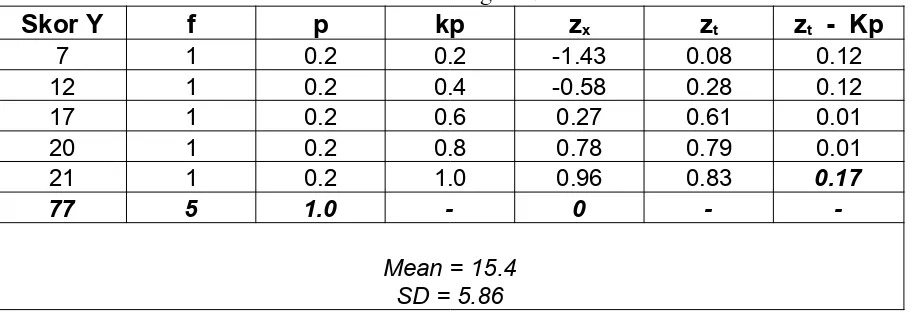
Tabel bantu Perhitungan Normalitas

Skor Y f p kp zx zt zt - Kp

7 1 0.2 0.2 -1.43 0.08 0.12

12 1 0.2 0.4 -0.58 0.28 0.12

17 1 0.2 0.6 0.27 0.61 0.01

20 1 0.2 0.8 0.78 0.79 0.01

21 1 0.2 1.0 0.96 0.83 0.17

77 5 1.0 - 0 -

-Mean = 15.4 SD = 5.86

Dengan melihat tabel di atas nampak bahwa perhitungan dengan menggunakan uji Lilliefors sama dengan perhitungan dengan menggunakan uji Kolmogorov-smirnov dalam penentuan nilai tiap-tiap kolom, sedangkan kolom terakhir dalam pengujian normalitas distribusi ini sama dengan nilai a2 pada uji

Kolmogorov-Smirnov.

Sesudah kolom-kolom lengkap terisi kemudian tentukan L0 maksimum dari

kolom terakhir (zt - Kp), dimana diperoleh Lo = 0.17, bandingkan nilai ini dengan Lt

pada baris N = 5 dengan taraf signifikansi 0.05 yaitu sebesar 0.337, dan karena Lo =

0.17 lebih kecil dari Lt = 0.33, maka distribusi data tersebut Normal.

1.3. Uji Chi-Kuadrat

Pengujian dengan cara ini agak berbeda dengan dua cara sebelumnya, dimana dalam pengujian ini harus dicari selisih antara Zt dengan Zt dibawahnya yang

menggambarkan luas tiap kelas, dan perlunya dicari frekuensi yang diharapkan serta tidak perlunya dicari prosentase. Namun untuk itu sebaiknya data dikelompokan terlebih dahulu agar dapat ditentukan batas kelasnya. Untuk lebih jelas berikut akan dikemukakan cara perhitungan dengan menggunakan data pada pengujian sebelumnya.

 Menentukan distribusi frekuensi : 1. Jumlah Kelas Interval

1 + 3,3 log n  1+ 3.3 log 5 = 3.306 (ditetapkan 3)

2. Range (rentang)

Data terbesar – Data terkecil  21 - 7 = 14 3. Panjang kelas interval ( i )

i = Range (rentang) : Jumlah Kelas Interval  14/3 = 4.6(5)

Tabel bantu Perhitungan Normalitas

Skor Y Batas _Kelas zx zt Lki Fh fo (fo-fh)

2

fh

6.5 -1.52 0.06

7 – 11 11.5 -0.67 0.25 0.19 0.95 1 0.026

12 – 16 16.5 0.19 0.58 0.33 1.65 1 0.256

17 – 21 21.5 1.04 0.85 0.27 1.35 3 2.017

- - - 5 2.299

Mean = 15.4 ; SD = 5.86

 Cara pengisian kolom-kolom

o Untuk pengisian kolom Zx dan Zt caranya sama seperti dalam pengujian

Kolmogorov-Smirnov dan Lilliefors.

o Kolom Lki (Luas tiap kelas interval) dicari dengan menyelisihkan Zt dengan Zt

sebelumnya, contoh nilao 0.19 diperoleh dari 0.25 – 0.06.

o Kolom fh diperoleh dengan cara nilai Lki dikalikan dengan jumlah data. o Kolom fo adalah frekuensi tiap kelompok data Skor Y.

o Sesudah itu kemudian dicari nilai X2 masing-masing kelompok kemudian

dijumlahkan, hasilnya diperoleh nilai 2.299, nilai ini kemudian dibandingkan dengan nilai tabel pada tingkat kepercayaan 95% pada baris 2 (jumlah kelompok dikurangi satu), diperoleh nilai X2 _{tabel sebesar 5.99. karena X}2

hitung lebih kecil dari X2 _{tabel maka distribusi normal.}

2. Pengujian homogenitas Variansi

dokemukakan cara perhitungan dengan menggunakan data-data yang telah dipergunakan dalam uji normalitas.

Tabel skor Variabel bebas (X) dan variabel terikat (Y)

X1 X2 Y

4 1 7

4 2 12

9 8 17

12 8 20

12 10 21

Dengan data tersebut maka perhitungan uji homogenitas dilakukan dua kali terhadap variabel Y, pertama yang dikelompokan berdasarkan X1 dan kedua yang

dikelompokan berdasarkan X2 , pengelompokan dilakukan dengan mengurutkan nilai

X dari kecil ke besar, dan contoh perhitungan hanya akan menggunakan data X1

dengan Y.

 Langkah-langkah perhitungan

o Kelompokan skor nilai Y berdasarkan pengurutan skor nilai X1

X1 Y Kelompok

4 7 1

4 12 1

9 17 2

12 20 3

12 21 3

o Pengelompokan di atas menunjukan terdapat 3 kelompok data yang anggotanya terdiri : untuk kelompok satu adalah 7 dan 12; kelompok dua 17; dan kelompok tiga adalah 20 dan 21.

o Sesudah diketahui kelompoknya, untuk memudahkan perhitungan masukan ketiga kelompok tersebut pada tabel berikut

Sampel/Klp db 1/db si2 log si2 db log si2 db si2

1 1 1.00 12.5 1.097 1.097 12.5

2 0 0 0 0 0 0

3 1 1.00 0.5 -0.301 -0.301 0.5

0.796 13

2 2

o Kolom si2 _{merupakan varians dari tiap kelompok, cara mencarinya dapat}

digunakan rumus (N x ΣX2_{) - (Σ X)}2_{/N(N – 1). Contoh untuk kelompok sati (2}

x 193) – (19)2 _{/ 2(1)  386 – 361/ 3 = 12.5}

o Kemudian cari varian gabungan (s2_{) dengan rumus : Σ db si}2_{/ Σ db, hasilnya}

adalah 13/2 = 6.5.

o Cari nilai B dengan rumus (Σ db) log s2 _{= 2 x 0.813 = 1.626. sesudah}

diketahui nilai B, kemudian hitung nilai Chi-Kuadrat (X2_{) dengan rumus (Ln 10)}

x (B - (Σ db) log s2_{)  2.3026 x (1.626 – 0.796 ) = 1.911}

o Nilai X2 _{tersebut kemudian dibandingan dengan nilai X}2 _{tabel pada tingkat}

o Kesimpulan : karena X2 _{hitung lebih kecil dari X}2 _{tabel maka kelompok data}

tersebut bersifat homogen (1.911 < 3.84).

Pengujian homogenitas bila untuk regresi ganda dengan variabel bebas X1 dan X2 ,

pengujian homogenitas Variansi dilakukan dua kali yaitu untuk regresi Y atas X1 dan

untuk regresi Y atas X2, sehingga harus dilakukan pengelompokan Y berdasarkan X1

dan pengelompokan Y berdasarkan X2, adapun langkah-langkah perhitungannya

UNTUK DIDISKUSIKAN

1. Lakukan pengujian normalitas distribusi terhadap data berkut dengan tiga cara pengujian untuk masing-masing variabel

Tabel skor Variabel bebas (X) dan variabel terikat (Y)

X1 X2 Y

15 32 41

13 33 42

18 32 43

18 35 44

19 33 45

13 35 49

15 38 46

19 38 50

2. Lakukan pengujian Homogenitas Variansi terhadap data berikut dalam konteks regresi ganda

Tabel skor Variabel bebas (X) dan variabel terikat (Y)

X1 X2 Y

25 42 51

23 43 52

28 42 53

28 45 54

29 43 55

23 45 59

25 48 56

29 49 60

29 48 62

4.2.1. Regresi

Istilah regresi pertama kali digunakan oleh Francis Galton pada tahun 1887 ketika mengadakan penelitian tentang hubungan antara tinggi orang tua dengan tinggi anaknya, dan sampai pada kesimpulan bahwa rata-rata tinggi anak yang berasal dari orang tua yang tinggi lebih rendah dibanding rata-rata tinggi orang tuanya, sedangkan anak-anak yang berasal dari orang tua yang rendah, tinggi rata-ratanya lebih tinggi dari tinggi orang tuanya, dengan demikian terjadi regress

(kemunduran) atau tendensi terjadinya penurunan. Selanjutnya istilah Regression

digunakan untuk menggambarkan garis yang menunjukan arah hubungan antar variabel, serta dipergunakan untuk melakukan prediksi, selain istilah tersebut, di kalangan akhli Statistik ada juga yang menggunakan istilah estimating line atau garis taksiran sebagai padanan istilah Regresi.

Sutrisno Hadi dalam bukunya Analisis Regresi menyatakan bahwa analisis

regresi bertujuan untuk :

1. memeriksa apakah garis regresi tersebut bakal efisien dipakai sebagai dasar

2. Menghitung persamaan garis regresi

3. untuk mengetahui sumbangan relatif dan sumbangan efektif bila prodiktornya lebih dari satu variabel.

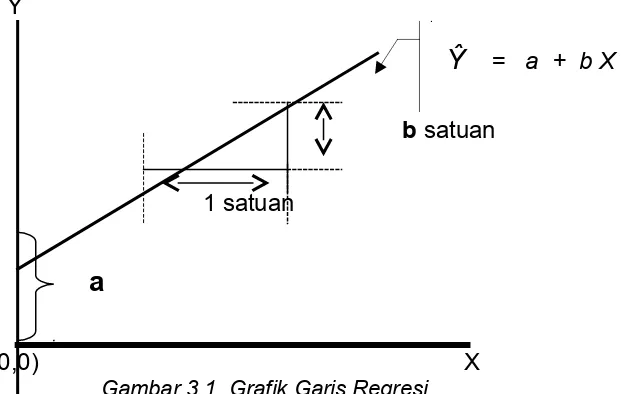
Regresi yang terdiri dari satu variabel bebas (predictor) dan satu variabel terikat (Response/Criterion) disebut regresi linier sederhana (bivariate regression), sedangkan regresi yang variabel bebasnya lebih dari satu disebut regresi jamak (Multiple regression/multivariate regression), yang dapat terdiri dari dua prediktor (regresi ganda) maupun lebih. Dalam persamaan regresi variabel bebas (predictor) biasanya dilambangkan dengan X, dan variabel terikat dilambangkan dengan Y, dalam penulisan persamaan Y perlu diberi topi (Y cap) untuk menunjukan Y yang diprediksi berdasarkan persamaan (Regression equation). Adapun bentuk persamaannya adalah :

1.

Ŷ

= a + b X (Regresi linier sederhana)

2.

Ŷ

= a + b1X1 + b2X2 (Regresi linier Ganda/dua prediktor)

3.

Ŷ

= a + b1X1 + b2X2 + b3X3 (Regresi linier tiga prediktor)

a adalah koefisien konstanta dari persamaan, yang berarti nilai Y pada saat nilai b = nol, dan pada saat ini garis regresi akan memotong garis Y, sehingga a juga biasa disebut intercept. Sementara itu b adalah koefisien regresi atau koefisien arah dari persamaan regresi, yang menunjukan besarnya penambahan Y apabila niai X

Y

b satuan

1 satuan

a

(0,0) X

Gambar 3.1. Grafik Garis Regresi

Gambar di atas dapat memberikan pemahaman tentang konsep analisis regresi dengan melihat posisi masing-masing koefisien, baik koefisien konstan (a) maupun koefisien arah atau koefisien regresi (b). dan untuk lebih mendalami analisisnya berikut ini akan diberikan contoh perhitingan regresi yang dimulai dengan regresi linier sederhana kemudian regresi multiple dengan dua prediktor (regresi ganda) 4.2.1.1. regresi linier sederhana (satu prediktor)

Untuk keperluan perhitungan dalam analisis regresi, contoh variabel yang akan dipergunakan dalam perhitungan adalah variabel Motivasi (X) sebagai variabel bebas, dan variabel Kinerja (Y) sebagai variabel terikat.

Sesuai dengan persyaratan analisis yang mengharuskan skala pengukuran/datanya bersifat interval atau rasio (statistik Parametrik), maka data berikut merupakan data interval hasil konversi dari data ordinal (Skala sikap) dengan menggunakan Method of summated rating.

Tabel 4.2

Data Skor Motivasi dan Kinerja

Variabel X (Motivasi) Variabel Y (Kinerja)

20 60

30 50

50 70

60 80

80 120

90 110

330 490

Tabel 4.3

Mencari Persamaan Regresi menggunakan Skor Kasar

X Y X2 _XY

20 60 400 1200

30 50 900 1500

50 70 2500 3500

60 80 3600 4800

80 120 6400 9600

90 110 8100 9900

330 490 21900 30500

Rumus mencari a dan b menggunakan dua persamaan : Σ Y = Na + bΣX

Σ XY = aΣX + bΣX2

I. 490 = 6a + 330 b (x 110) II. 30500 = 330a + 21900 b (x 2)

I. 53900 = 660 a + 36300 b II. 61000 = 660 a + 43800 b 7100 = 7500 b

b = 7100 : 7500 = 0.946667 (0.95) 490 = 6a + 330 (0.95)

6a = 490 - 313.5 = 176.5 a = 176,5 : 6 = 29.4

Ŷ

= 29,4 + 0.95 X

Cara lain mencari a dan b dengan menggunakan tabel 3.3 b = N (ΣXY) - (ΣX) (ΣX)

N (ΣX2_{) - (ΣX)}2

a = ΣY - b ΣX  Y - bX

N

b = 6 (30500) - (330) (490) 6 (21900) - (330)2

= 21300 22500

= 0,946667 (0.95)

a = 490 - 0.95 (330) 6

= 176.5  Y - bX  81.67 - 55 (0,95) = 29.42 (29.4)

6

= 29.4166 (29,4)

Ŷ

= 29,4 + 0.95 X

Tabel 4.4.

Mencari Persamaan Regresi dengan menggunakan simpangan

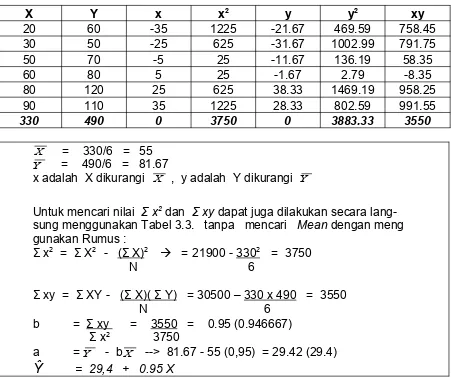
X Y x x2 _{y y}2 _xy

20 60 -35 1225 -21.67 469.59 758.45

30 50 -25 625 -31.67 1002.99 791.75

50 70 -5 25 -11.67 136.19 58.35

60 80 5 25 -1.67 2.79 -8.35

80 120 25 625 38.33 1469.19 958.25

90 110 35 1225 28.33 802.59 991.55

330 490 0 3750 0 3883.33 3550

X = 330/6 = 55 Y = 490/6 = 81.67

x adalah X dikurangi X , y adalah Y dikurangi Y

Untuk mencari nilai Σ x2 _{dan Σ xy dapat juga dilakukan secara}

lang-sung menggunakan Tabel 3.3. tanpa mencari Mean dengan meng gunakan Rumus :

Σ x2 _{= Σ X}2 _{- (Σ X)}2 _{ = 21900 - 330}2 _{= 3750}

N 6

Σ xy = Σ XY - (Σ X)( Σ Y) = 30500 – 330 x 490 = 3550 N 6

b = Σ xy _{= 3550 = 0.95 (0.946667)}

Σ x2 ₃₇₅₀

a = Y - bX --> 81.67 - 55 (0,95) = 29.42 (29.4)

Ŷ

= 29,4 + 0.95 X

Tabel 4.5.

Mencari Persamaan Regresi dengan menggunakan koefisien korelasi

X Y x x2 _{y y}2 _Xy

20 60 -35 1225 -21.67 469.59 758.45

30 50 -25 625 -31.67 1002.99 791.75

50 70 -5 25 -11.67 136.19 58.35

60 80 5 25 -1.67 2.79 -8.35

80 120 25 625 38.33 1469.19 958.25

90 110 35 1225 28.33 802.59 991.55

330 490 0 3750 0 3883.33 3550

Standar Deviasi X (SdX) = 27.39 ; Standar Deviasi Y (SdY) = 27.86

b = r x (SdY : SdX )

b = 0.9302 x ( 27.86 : 27.39 ) = 0.946 (0.95)

a = Y - bX --> 81.67 - 55 (0,95) = 29.42 (29.4)

Ŷ

= 29,4 + 0.95 X

4.2.1.2. Pengujian Signifikansi dan linieritas Garis Regresi

Setelah diperoleh persamaan garis regresi, langkah berikutnya adalah melakukan pengujian apakah persamaan tersebut signifikan serta linier atau tidak. Untuk itu terlebih dahulu perlu dicari Jumlah kuadrat untuk masing-masing sumber Varian sebagai berikut :

Jumlah Kuadrat :

JKT(Jumlah Kuadrat Total) =  Y2

JK (Jumlah Kuadrat) (a) = ( Y) 2

N

JK (R) (Jumlah Kuadrat Total direduksi) = JKT - JK (a)

JK (Jumlah Kuadrat) (b) = b  xy

JKS (Jumlag Kuadtar Sisa) = JKR - JK (b)

JK (G)(Jumlah Kuadrat Galat) =  (yk 2)

JK(TC) (Jumlah Kuadrat Tuna Cocok) = JKS - JKG

Untuk lebih jelasnya akan dilakukan perhitungan dengan mengacu pada Tabel berikut

 xy

r

xy =

(x2) (y2)

3550 3550

r

xy = = = 0.9302

Tabel 4.6.

X Y Y2 _{x X}2 _{y y}2 _xy

20 60 3600 -34 1156 -24 576 816

20 50 2500 -34 1156 -34 1156 1156

50 80 6400 -4 16 -4 16 16

60 80 6400 6 36 -4 16 -24

84 120 14400 30 900 36 1296 1080

90 114 12996 36 1296 30 900 1080

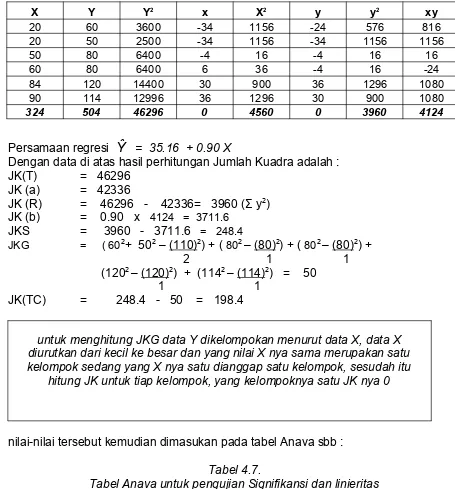
324 504 46296 0 4560 0 3960 4124

Persamaan regresi

Ŷ

= 35.16 + 0.90 X

Dengan data di atas hasil perhitungan Jumlah Kuadra adalah :

JK(T) = 46296

JK (a) = 42336

JK (R) = 46296 - 42336= 3960 (Σ y2₎

JK (b) = 0.90 x 4124 = 3711.6 JKS = 3960 - 3711.6 = 248.4

JKG = ( 602_{+ 50}2 _{– (110)}2_{) + ( 80}2 _{– (80)}2_{) + ( 80}2 _{– (80)}2_{) +}

2 1 1

(1202 _{– (120)}2_{) + (114}2 _{– (114)}2_{) = 50}

1 1 JK(TC) = 248.4 - 50 = 198.4

untuk menghitung JKG data Y dikelompokan menurut data X, data X diurutkan dari kecil ke besar dan yang nilai X nya sama merupakan satu kelompok sedang yang X nya satu dianggap satu kelompok, sesudah itu

hitung JK untuk tiap kelompok, yang kelompoknya satu JK nya 0

nilai-nilai tersebut kemudian dimasukan pada tabel Anava sbb :

Tabel 4.7.

Tabel Anava untuk pengujian Signifikansi dan linieritas Persamaan regresi

Sumber

Varians Db JK RJK Fh Ft0.05 Ft_0.01

Total 6 46296

Regresi a Regresi b Sisa

1 1 4

42336 3711.6 248.4

42336 3711.6 62.1

59.77 7.71 21.20

Tuna Cocok Galat

3 1

198.4 50

66.13

50 1.32 216 5403

1. Persamaan Regresi

Ŷ

= 35.16 + 0.90 X signifikan karena Fh > Ft (59.77 > 21.20 – 7.71) baik pada taraf kepercayaan 95 % (0.05) maupun pada taraf kepercayaan 99 % (0.01)

2. Persamaan Regresi

Ŷ

= 35.16 + 0.90 X linier baik pada taraf kepercayaan 99 % (0.01) Fh < Ft (1.32 < 5.40), maupun pada taraf kepercayaan 95 % (0.05) Fh < Ft (1.32 < 5403).

4.2.2. Korelasi

Korelasi adalah suatu hubungan, Koefisien korelasi adalah indeks arah dan besaran suatu hubungan/relasi, Koefisien korelasi Product Moment ( r ) dapat dihitung dengan beberapa rumus yang ekuivalen. Ada beberapa manfaat dalam mempelajari korelasi yakni :

1. Penentuan adanya hubungan serta besarnya hubungan antara variabel dapat diketahui, sebab koefisien korelasi merupakan ukuran yang dapat menjelaskan besar kecilnya hubungan

2. dengan mengetahui adanya hubungan, maka prediksi terhadap variabel lainnya dapat dilakukan dengan bantuan garis regresi.

Korelasi pada dasarnya hanya menunjukan tentang adanya hubungan antara dua variabel atau lebih serta besarnya hubungan tersebut, ini berarti bahwa korelasi tidak menunjukan hubungan sebab akibat. Apabila dipahami sebagai suatu

hubungan sebab akibat, hal itu bukan karena diketahuinya koefisien korelasi

melainkan karena rujukan teori/logika yang memaknai hasil perhitungan, oleh karena itu analisa korelasional mensyaratkan acuan teori yang mendukung adanya

hubungan sebab akibat dalam variabel-variabel yang dianalisa hubungannya.

Koefisien korelasi dari suatu perhitungan berkisar antara +1 dan –1, koefisien korelasi yang bertanda (+) menunjukan arah korelasi yang positif, sedangkan yang bertanda (-) menunjukan arah hubungan yang negatif. Sementara itu bila koefisien korelasi bernilai 0, berarti tidak ada hubungan antara variabel satu dengan variabel lainnya. Hubungan tersebut bila digambarkan nampak sebagai berikut :

Y Y

Korelasi Positif Korelasi Negatif

0 X 0 X

Y

Tidak berkorelasi

Berikut ini akan dikemukakan beberapa cara perhitungan untuk memperoleh nilai koefisien korelasi .

4.2.2.1. Korelasi Sederhana

korelasi sederhana merupakan korelasi yang mencoba memahami hubungan antara satu variebel bebas (X) dengan satu variabel terikat (Y). dalam

perhitungannya terdapat beberapa cara yang dapat dipergunakan, berikut ini akan dikemukakan beberapa contoh perhitungan, dan jika terdapat sedikit perbedaan hasil untuk masing-masing cara perhitungan,hal itu semata-mata akibat proses

pembulatan

1. Rumus yang menggunakan Standar Skor

Penghitungan nilai koefisien korelasi dengan menggunakan rumus standar skor dapat dilakukan dengan melaksanakan langkah-langkah sebagai berikut :

a. Menghitung nilai rata-rata untuk tiap variabel yang akan dikorelasikan. b. Menghitung nilai Standar deviasi untuk tiap-tiap variabel yang akan

dikorelasikan.

c. Menghitung nilai Z untuk masing-masing variabel yang akan dikorelasikan dengan menyelisihkan masing-masing niali tiap variabel untuk kemudian dibagi dengan nilai Standar deviasinya

d. Mengalikan nilai Z variabel satu dengan yang lainnya, kemudian dijumlahkan

e. Membagi hasil jumlah perkalian nilai Z tersebut dengan jumlah data dikurangi satu

Adapun rumusnya adalah :

 zxzy

rxy =

n – 1 dimana :

r

xy = Koefisien korelasi antara variabel X dengan variabel Y

zx = X – X

Sdx

zy = Y - Y

Sdy

Untuk memudahkan perhitungan dapat dibuat tabel bantu sebagai berikut :

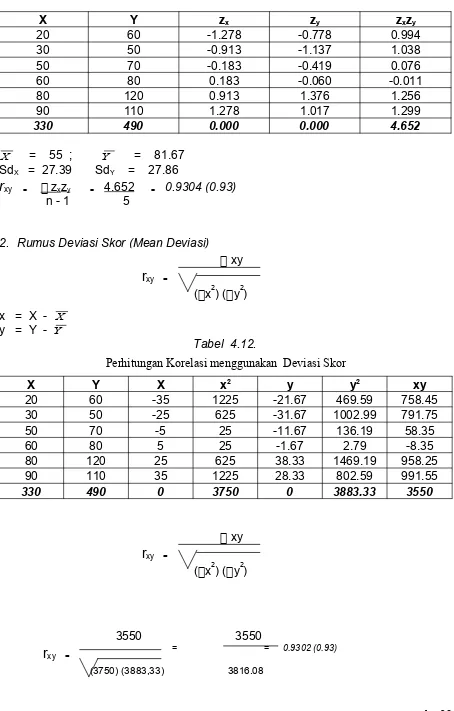
Perhitungan Korelasi menggunakan Standar Skor

X Y zx zy zxzy

20 60 -1.278 -0.778 0.994

30 50 -0.913 -1.137 1.038

50 70 -0.183 -0.419 0.076

60 80 0.183 -0.060 -0.011

80 120 0.913 1.376 1.256

90 110 1.278 1.017 1.299

330 490 0.000 0.000 4.652

X = 55 ; Y = 81.67

SdX = 27.39 SdY = 27.86

r

xy =  z xzy = 4.652 = 0.9304 (0.93)

n - 1 5

2. Rumus Deviasi Skor (Mean Deviasi)

x = X - X

y = Y - Y

Tabel 4.12.

Perhitungan Korelasi menggunakan Deviasi Skor

X Y X x2 _{y y}2 _xy

20 60 -35 1225 -21.67 469.59 758.45

30 50 -25 625 -31.67 1002.99 791.75

50 70 -5 25 -11.67 136.19 58.35

60 80 5 25 -1.67 2.79 -8.35

80 120 25 625 38.33 1469.19 958.25

90 110 35 1225 28.33 802.59 991.55

330 490 0 3750 0 3883.33 3550

 xy

r

xy =

(x2) (y2)

 xy

r

xy =

(x2) (y2)

3550 3550

r

xy = = = 0.9302 (0.93)

3. Rumus dengan metode Product Moment

Momen adalah ukuran yang didasarkan pada deviasi tiap nilai variabel. Momen X adalah x dan momen Y adalah y. Product Moment (Pm) adalah hasil perkalian antara momen X dengan Momen Y, yang dirumuskan :

Pm =  xy

N - 1

selanjutnya Koefisien korelasi dihitung sbb : r = Pm . Sdx . Sdy

Pm = 3550 = 710 5

r = 710 . 27.39 x 27.86

r = 710 . = 0.9304 (0.93)

763.08

4. Rumus Angka Kasar (Raw Score) Karl Pearson Tabel 4.13

X Y X2 _Y2 _XY

20 60 400 3600 1200

30 50 900 2500 1500

50 70 2500 4900 3500

60 80 3600 6400 4800

80 120 6400 14400 9600

90 110 8100 12100 9900

330 490 21900 43900 30500

= 21300 / (150 x 152.64)

r = 0.9302 (0.93)

5. Rumus menggunakan Persamaan dan Koefisien arah regresi Tabel 4.14.

N  XY - ( X) ( Y)

r = N  X2 – ( X)2 N  Y2– ( Y)2

6 x 30500 - 330 x 490

r =

X Y X2 _{XY (Y - Y )}2 _{Ŷ (Y - Ŷ) (Y - Ŷ)}2

20 60 400 1200 469.59 48.4 11.6 134.56

30 50 900 1500 1002.99 57.9 -7.9 62.41

50 70 2500 3500 136.19 76.9 -6.9 47.61

60 80 3600 4800 2.79 86.4 -6.4 40.96

80 120 6400 9600 1469.19 105.4 14.6 213.16

90 110 8100 9900 802.59 114.9 -4.9 24.01

330 490 21900 30500 3883.33 489.9 0.1 522.71

r = 1 - Σ (Y- Ŷ) 2

Σ (Y- Y )2

r _{= 1 - 522.71}

3883.33

r _{= 1 - 0.13460}

r _{= 0.8653}

r = 0.9302 (0.93)

r = b (Sdx : Sdy)

r = 0.946 (0.95) x (27.39 : 27.86 )

r = 0.9300 (0.93)

4.2.2.2. Pengujian signifikansi Korelasi Sederhana

Uji signifikansi :

th

=

r

(N - 2)

( 1 - r ) th > t t = korelasi signifikan

th < t t = korelasi tidak signifikan

Bila diterapkan pada hasil perhitungan korelasi di atas, hasilnya adalah : Uji signifikansi : r = 0.93

th

= 0.93

(6 - 2)

( 1 - 0.93 )

th = 1.86

0.2645

th = 7.032

kemudian t hitung( th ) tersebut dibandingkan dengan t tabel ( tt ), hasilnya

menunjukan bahwa korelasi tersebut signifikan karena

t

h lebih besar dari

t

t

(7.032>2.13) pada taraf kepercayaan 95 % (0,05) dengan derajat kebebasan 4 (nilai t tabel dapat dilihat dalam daftar tabel t)

4.2.4. penafsiran koefisien korelasi

koefisien korelasi pada dasarnya tidak hanya menunjukan hubungan antara variabel satu dengan lainnya, tapi juga menunjukan indeks proporsi perbedaan satu variabel terkait dengan variabel lainnya, dengan demikian koefisien korelasi juga menunjukan berapa besar varians total satu variabel berhubungan denga varians variabel lain. Hal ini berarti bahwa tiap nilai r perlu ditafsirkan posisinya dalam keterkaitan tersebut.

Untuk memberikan tafsiran pada nilai koefisien korelasi, dapat digunakan patokan berikut :

POSITIF NEGATIF PENAFSIRAN

0.90 - 1.00 -0.90 - -1.00 Korelasi sangat tinggi (Very high)

0.70 - 0.90 -0.70 - -0.90 Korelasi tinggi (High)

0.50 - 0.70 -0.50 - -0.70 Korelasi sedang (moderate)

0.30 - 0.50 -0.30 - -0.50 Korelasi rendah (Low)