1.1 Hasil Pembelajaran - MTE3101 PPG Topik 1 Sistem Pernomboran

(1)

Topik 1

Sistem Pernomboran

1.0 Sinopsis

Tajuk ini merangkumi perkembangan sistem pernomboran yang pelbagai bermula dari

sistem pernomboran awal hingga ke sistem pernomboran Hindu-Arab sekarang. Sistem pernomboran awal yang dibincangkan termasuk Sistem pernomboran Gundalan(Tally),

Sistem pernomboran Roman, Sistem pernomboran Mesir, Sistem pernomboran Mayan dan sistem pernomboran Babylonian. Di bawah sistem pernomboran Hindu-Arab, bilangan simbol dan kumpulan dalam pelbagai asas di titikberatkan. Anda juga akan mempelajari

bagaimana untuk menukar dari satu asas kepada asas sepuluh dan sebaliknya.

1.1 Hasil Pembelajaran

1. Membandingkan perkembangan Sistem Pernomboran yang pelbagai. 2. Menukarkan asas b kepada asas 10 dan sebaliknya.

1.2 Kerangka konsep

Sistem pernomboran

Sistem pernomboran Awal Sistem pernomboran Yang lain.

Sistem Pernomboran Hindu-Arab

(2)

1.3 Sistem pernomboran Awal

Pada masa lampau,manusia menggunakan pelbagai cara untuk merekod nombor yang

diperlukan. Sebagai contoh untuk mewakilkan bilangan kambing biri-biri dalam kumpulan, pengembala kambing mengumpul batu-batu kecil. Dengan memadankan batu-batu kecil

dengan kumpulan kambing, pengembala boleh mengetahui jika ada kambingnya yang hilang. Ahli Matematik pada masa ini menamakan cara padanan ini sebagai padanan satu

dengan satu.

Kebelakangan ini , manusia menggunakan cara lain untuk merekod barang kepunyaan mereka. Mereka mengikat tali pada kulit kayu atau melukis tanda gundalan pada batu

untuk memadankan tali dengan tanda gundalan. Sebenarnya, kayu gundalan dan batu-batu kecil adalah perkembangan penting ke arah penciptaan sistem pernomboran.

Kayu Gundalan

Kemudian manusia mula menggunakan simbol untuk mewakili nombor. Sebagai contoh,

gambar “sayap” digunakan untuk mewakili dua objek. Pada kebanyakan sistem

penomboran awal, manusia membentuk nombor dengan cara mengulangi simbol asas

dan menambah nilai untuk mendapat nombor yang mereka kehendaki. Orang-orang Egypt, Greek dan Roman menggunakan sistem pernomboran seperti ini. Gambarajah di

bawah memaparkan Sistem Pernomboran Greek..

(3)

Orang Hindu menggunakan sistem pernomboran yang lebih tinggi dari yang lain. Ia

mengikut prinsip nilai tempat dan menggunakan sepuluh nombor. Sistem ini berkebang secara beransur-ansur ke dalam Sistem Hindu-Arab kita sekarang (juga dikenali sebagai

sistem nombor perpuluhan) dan digunakan sekarang di seluruh dunia.

Perkembangan pelbagai Sistem Pernomboran awal ditunjukkan di bawah.

1.3.1 Sistem Pernomboran Gundalan (The Tally Numeration System)

Sistem pernomboran ini adalah yang paling mudah di antara semua sistem pernomboran. Ia terdiri daripada satu garisan tunggal ,mewakili setiap objek yang dikira. Walau

bagaimanapun terdapat dua kelemahan menggunakan sistem ini iaitu (1) nombor yang besar memerlukan simbol individu yang banyak, (2) sangat sukar untuk membaca nombor yang terdiri daripada nombor yang besar. Contoh; bolehkah anda dengan cepat

memberitahu apakah nombor yang diwakili oleh tanda gundalan di bawah? Tidak mudahkan ?

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

Sistem Gundalan di tambahbaik dengan cara “pengumpulan” , di mana gundalan yang kelima ditandakan dengan dan diletakkan melintang di setiap empat gundalan

supaya menjadi satu kumpulan terdiri daripada lima seperti di bawah:

IIII

Mengumpul adalah cara paling mudah untuk mengenal nombor yang diwakilkan. Dengan menggunakan teknik pengumpulan, bolehkah anda sekarang beritahu apakah nombor

yang di wakilkan oleh gundalan dalam contoh di atas.

1.3.2 Sistem Pernomboran Mesir ( Around 3400 BC)

Sistem hieroglifik Mesir (The Egyptian hieroglyphic system ) adalah contoh Sistem Pengumpulan Pernomboran mudah. Nombor-nombor dibentuk dengan menggabungkan

(4)

Sistem pernomboran ini adalah berasaskan tanda gundalan, iaitu

I II III IIII IIIII IIIIII IIIIIII IIIIIIII IIIIIIIII

1 2 3 4 5 6 7 8 9

Bagaimanapun, selepas 9, mereka memerlukan satu simbol baharu yang memerlukan

“pengumpulan” untuk mewakili set nombor tertentu. Nilai berikutnya ialah ∩ (tulang tumit) yang mewakili 10.

Angka Mesir menggunakan cara untuk merekod kuantiti adalah berdasarkan asas 10

dengan simbol satu,sepuluh dan kuasa sepuluh berturut-turut. Suatu hieroglifik khusus digunakan untuk setiap nombor yang berkuasa sepuluh. Bagaimanapun tidak ada simbol untuk sifar. Oleh itu suatu simbol tertentu dihapuskan di dalam angka bila gandaan

sepuluh bukan sebahagian dari nombor tersebut.

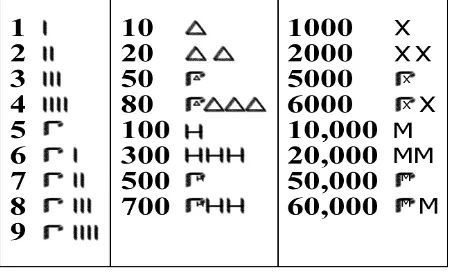
Sebahagian simbol yang digunakan di dalam angka Mesir ditunjukkan di bawah:

Sistem Mesir adalah mengikut sifat penambahan. (additive property); iaitu nilai sesuatu

nombor Sebagai contoh:

Apakah nombor yang diwakili oleh heiroglifik berikut?

Tepat! heiroglifik di atas mewakili nilai 21,346.

Cuba tuliskan 465,123 menggunakan Sistem Pernomboran Mesir. Semoga Berjaya!

1.3.3 Sistem pernomboran Roman (Antara 500 B.C. dan A.D. 100)

Sistem pernomboran Roman adalah lebih canggih berbanding dengan sistem

(5)

“Prinsip penolakan”(“subtractive principle”) yang membolehkan nombor diwakili secara lebih ringkas dan

“Prinsip pendaraban (“multiplicative principle”) yang memudahkan untuk menulis nombor yang bernilai besar.

Jadual berikut menujukkan lapan abjad yang digunakan untuk mewakili nilai berbeza di

dalam sistem Pernomboran Roman dan nilai sepadannya di dalam Sistem Pernomboran Hindu-Arab.

Angka Roman Angka Hindu-Arab

I 1

V 5

X 10

L 50

C 100

D 500

M 1000

Jadual 1

Peraturan tertentu mesti dipatuhi bila menggunakan Sistem Pernomboran Roman, iaitu:

Hanya simbol I, X, C, dan M boleh diulang, tetapi tidak boleh menulis simbol lebih

daripada 3 kali secara berturut-turut. Jika simbol keempat diperlukan, gunakan

prinsip penolakan.

Bila menggunakan prinsip penolakan, kita hanya boleh menolak I, X, C, dan M (tidak V, L, atau D – tanpa dengan “5”)

Kita hanya boleh menolak angka daripada 2 angka bersebelahan yang paling tinggi.

(contoh. kita boleh ada IV dan IX, tetapi kita tidak boleh ada IL, IC, ID, IM)

Gunakan palang di atas simbol atau beberapa simbol untuk menandakan

pendaraban dengan 1000 contoh;

V bermakna 5 x 1000 = 5000; IX bermakna 9 x 1000 = 9000

(6)

Contoh contol lain diberi di bawah:



Jika angka Roman disenaraikan sedemikian hingga setiap angka mempunyai nilai lebih

besar dari angka di sebelah kanannya, maka nilai angka boleh didapati menggunakan sifat penambahan. Setiap angka I, X, C dan M boleh diulang sebanyak tiga kali. Angka-angka

V, L, dan D tidak diulang, contoh: XVI = ? CCCVI = ?

MMCCCLXII = ?



Jika angka yang disenarai sedemikian hingga setiap angka TIDAK mempunyai nilai

yang besar daripada angka disebelah kanannya, maka nilai angka tersebut didapati menggunakan sifat penambahan dan sifat penolakan. Hanya angka I, X, dan C,

yang boleh ditolak daripada angka lain. Contoh:

IV = ? ; IX = ? ; XL = ? ; XC = ?; CD = ?; CM = ?; CXLIV = ?; MCDLXXI = ?



Selanjutnya penolakan nilai dibenarkan jika nilai bagi angka di sebelah kanan berada

pada baris pertama dan kedua selepas angka sebelah kiri seperti dalam jadual 1.

Sebagai contoh:

XL = ? ; XC = ?

tetapi XD tidak sama dengan 490 kerana X terletak pada baris 3 daripada D di dalam Jadual di atas.

Apakah 490 menggunakan simbol Roman?

490 = ___________________

Tahniah! Anda berjaya!



Sistem Roman ialah sistem kedudukan ( positional system) kerana kedudukan suatu

nombor boleh memberi kesan pada nilai nombor yang diwakili. Sebagai contoh: XI ialah sebelas manakala IX ialah sembilan.



Bila menulis nombor besar, Sistem Pernomboran Roman juga menggunakan sifat

pendaraban. Contoh:

IX = 9 x 1000 = 9000 ;

(7)

Cuba ini:

Tulis menggunakan angka Roman:

579 4,709 = ___________________________

304,536 8,070 = ___________________________

1.3.4 Sistem Pernomboran Mayan. ( Antara A.D. 300 dan A.D. 900)

Sistem Pernomboran Mayan berasaskan sistem 20 (vigesimal) yang menggunakan hanya tiga simbol terdiri dari sistem cengkerang, palang dan titik di dalam sistem nilai menegak.Suatu titik mewakili satu, palang mewakili lima dan cengkerang mewakili sifar.

Carta di bawah menunjukkan kitaran pertama yang lengkap bagi nombor Mayan.

Angka Mayan

Seperti sistem nombor sekarang, nilai tempat digunakan untuk mengembangkan sistem Mayan bagi mendapatkan nilai yang besar. Bagaimanapun, sistem ini mempunyai dua

perbezaan yang signifikan berbanding sistem kita gunakan sekarang ; iaitu 1) nilai tempat disusun secara menegak. dan 2) mereka menggunakan asas 20, atau sistem vigesimal.

Baca dan cari maklumat tentang nilai tempat dalam Sistem Mayan berbanding sistem kita yang menggunakan asas 10. Untuk mendapatkan semua nombor yang lain, Mayan hanya

(8)

Bila ditulis sebagai eksponen ia menjadi: 1, 101, 102, 103, d.l.l. Maka, sistem asas 20

mempunyai nilai tempat seperti berikut: 1, 201, 202, 203, d.l.l. Walau bagaimanapun Mayan mempunyai satu penyimpangan daripada asas 20. Nilai tempat adalah:

1, 20, 20∙18, 202∙18, 203∙18 etc.

Oleh kerana orang Mayan lebih berminat dalam mengira hari dan kalendar tahunan

mereka mempunyai 360 hari, maka adalah lebih sesuai untuk nilai digit ketiga terkecil menjadi 20∙18 = 360 dan bukan 20∙20 = 400. Orang Mayan menyusun nombor mereka

untuk menandakan nilai tempat berbeza. Prinsipal berkenaa ditunjukkan di dalam carta di bawah.

Jumlah di bawah, 31,781,148 ialah versi ringkas untuk nilai di dalam sisitem asas 10 kita.

Nombor yang ditulis dengan ringkas di dalam sistem Mayan ialah: 11.0.14.0.17.8 di mana nombor yang ditulis antara masa ialah nombor untuk nilai tempat.

Ada dua kelebihan bila menggunakan sistem ini iaitu: 1) Nombor yang besar lebih senang

untuk dinyatakan dan 2) aritmetik mudah untuk diselesaikan oleh pengguna.

Mayan number chart from: http://en.wikipedia.org/wiki/Maya_numerals

=

11(2,880,000) = 31,680,000

= 0

∙

144,000 = 0

= 14

∙

7200 = 100,800

= 0∙360 = 0

=17∙20 = 340

(9)

Proses penambahan mudah boleh dilakukan dengan hanya menggabungkan dua atau

lebih set simbol ( set yang sama) seperti di bawah:

Untuk aritmetik yang lebih rumit, kita boleh meminjam bila mencapai nilai 20 dan bukan 10.

Seperti yang ditunjukkan di bawah.

Kita lihat contoh di bawah:

Contoh:

Tulis sebagai angka Hindu-Arab. Penyelesaian:

Angka Mayan yang diberi mempunyai empat tempat. dari atas ke bawah, nilai tempatnya ialah 7200, 360, 20, dan 1.

Mula dengan mewakilkan setiap angka pada setiap baris sebagai angka Hindu-Arab seperti di bawah:

Darabkan setiap angka Hindu-Arab dengan nilai tempat yang

berikutnya.

(10)

Sekarang, nyatakan angka Hindu-Arab berikut menggunkan angka Mayan .

489

1813

1.3.5 Sistem Pernomboran Babylonian (Antara 3000 dan 2000 B.C.)

Sistem ini menggunakan dua angka, iaitu satu dan sepuluh seperti ditunjukkan di bawah.

Gambarajah di bawah menunjukkan Sistem Babylonian iaitu sistem kedudukan asas-60 (sexagesimal) system. Perhatikan bahawa dari nombor 1 hingga 59 ,sistem ini adalah

berulang, iaitu sistem ini adalah sistem penambahan ( additive system).

Angka Babylonian

Walaupun sistem pernomboran Babylonian berkembang pada masa yang sama seperti

sistem Mesir, namun Sistem Babylonian dalah lebih canggih dalam penggunaan nilai tempat, di mana simbol digunakan untuk mewakili nilai berbeza bergantung kepada tempat

yang ditulis. Kedudukan setiap angka membrti kesan kepada nilainya.

(11)

contoh dua nilai sepuluh dalam Babylonian yang ditulis bersebelahan boleh ditafsirkan

sebagai 20, atau 610 atau mungkin 3060. Dari tahun 300 B.C. berikutnya suatu simbol berasingan terdiri dari dua segitiga kecil disusun di atas satu sama lain bertindak sebagai

penentu tempat (placeholder) untuk menandakan ruang kosong bagi mengelak kekeliruan. Walaupun penetu tempat bertindak seolah-olah nombor sifar, orang Babylonian tidak

1.4 Sistem Pernomboran Hindu-Arab (Sekitar A.D. 800)

Sistem Pernomboran Hindu-Arab yang digunakan hari ini dikembangkan sekitar tahun A.D. 800. Nama ini diperolehi atas sumbangan dari kedua dua orang Hindu dan Arab kepada

sistem ini. Orang Hindu memperkembangkan abjad dan menggunakan huruf untuk mewakilkan digit dalam sistem pernomboran ini.

7882

2 Wakilkan setiap angka sebagai angka

Hindu-Arab.

Darabkan setiap angka Hindu-Arab dengan nilai tempat yg sepatutnya.

(12)

Ciri penting dalam sistem ini ialah kita boleh menulis angka bagi sebarang nombor, sama ada besar atau kecil,menggunakan hanya sepuluh simbol yang disebut digit,

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Perkataan digit bermaksud “jari tangan” atau “jari kaki”. Disebabkan hanya sepuluh

simbol asas yang digunakan,sistem Pernomboran Hindu-Arab dipanggil Sistem Pernomboran Perpuluhan.

Satu lagi prinsip dalam sistem ini ialah “Pengumpulan sepuluh-sepuluh” (sistem perpuluhan) dimans sepuluh satu di ganti dengan satu sepuluh, dan sepuluh-sepuluh

diganti dengan satu ratus. seratus sepuluh diganti dengan satu ribu dan seterusnya. Bilangan objek yang dikumpulkan sedemikian dipanggil asas bagi sistem itu. Oleh itu, sisitem Hindu-Arab ialah sistem asas sepuluh.

Angka Hindu-Arab boleh ditulis dalam bentuk cerakin ( expanded form), di mana nilai bagi

setiap digit dalam setiap kedudukan adalah jelas. Sebagai contoh, kita menulis 663 dalam bentuk cerakin sebagai:

663 = (6 x 100) + (6 x 10) + (3 x 1)

= (6 x 102) + (6 x 101) + (3 x 1)

Sistem Pernomboran Hindu-Arab ialah sistem nilai kedudukan atau sistem nilai tempat.

Nilai kedudukan dalam sistem ini berasaskan kuasa 10, seperti ditunjukkan di bawah: …, 105, 104, 103, 102, 101, 10

Untuk memahami dan menghargai mengapa sistem Hindu-Arab lebih superior berbanding

yang lain dan digunakan di seluruh dunia, baca lebih mengenai sumbangan berikut kepada

sistem ini:

Digits

Pengumpulan sepuluh-sepuluh

Nilai tempat

(13)

Contoh 1:

Tuliskan 3407 dalam bentuk cerakin. Penyelesaian:

3407 = (3 x 103) + (4 x 102) + (0 x 101) + (7 x 1) , atau = (3 x 1000) + (4 x 100) + (0 x 10) + (7 x 1) Contoh 2:

Nyatakan bentuk cerakin berikut sebagai angka Hindu-Arab.l: (7 x 103) + (5 x 101) + (4 x 1). Penyelesaian:

(7 x 103) + (5 x 101) + (4 x 1) = (7 x 103) + (0 x 102) + (5 x 101) + (4 x 1) = 7054

Cuba ini.

Tuliskan setiap berikut dalam bentu cerakin.

728,407

60,006,060

Untuk membandingkan perkembangan sistem pernomboran awal, anda perlu mencari maklumat tentang sistem pernomboran lain. Baca dengan lebih lanjut dan teroka dalam

sesawang untuk mendapat lebih maklumat tentang ini.

Selamat Membaca! Selamat Meneroka!

1.5 Sistem pernomboran Lain.

Pengumpulan sepuluh-sepuluh adalah ciri penting dalam sistem pernomboran Hindu-Arab dan kita panggil sistem ini sistem asas sepuluh. Asas bagi sitem penomboran mewakili

bilangan simbol yang digunakan dalam pengumpulan. Semua nombor ditulis dalam bentuk kuasa mengikut asasnya.

1.5.1 Bilangan simbol dan kumpulan dalam pelbagai asas

(14)

lima,dua belas-dua belas atau nombor lain. Untuk asas lebih daripada sepuluh, simbol lain

boleh diperkenalkan. Pengumpulan sebelas-sebelas, atau dua belas-dua belas, simbol lain seperti huruf T, E dan U mungkin digunakan untuk mewakili nilai sepuluh, sebelas dan dua

belas. Jadual di bawah menunjukkan beberapa contoh pengumpulan asas lain.

Asas Simbol Cara Pengumpulan Notasi

(15)

Pengumpulan dud-dua,lapan-lapan dan enam belas-enam belas memberi kita gambaran

tentang sistem pernomboran yang di gunakan dalam komputer.

Binary-Quartet/Hexadecimal Conversion

Binary 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 Hexadecimal 0 1 2 3 4 5 6 7 8 9 A B C D E F Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Hubungan antara asas 2, 8 dan 16

Untuk merumuskan sistem pernomboran dengan asas selain daripada sepuluh, kita perlu mempelajari lebih tentang nombor dan jenis simbol yang digunakan selain mengetahui cara menukar daripada satu asas (katakan asas b) ke asas 10 dan sebaliknya.

1.5.2 Menukar asas b kepada asas 10 dan sebaliknya.

Untuk menukar asas b kepada asas sepuluh, kita perlu menulis angka dalam bentuk

cerakin. Nombor yang dihasilkan ialah dalam asas sepuluh. Lihat contoh di bawah.

Contoh :

Tukarkan 1011dua kepada asas sepuluh.

Penyelesaian:

1011dua = (1 x 23 )+ (0 x 22)+ (1 x 21) + (1 x 20) = 8 + 0 + 2 + 1 + 0 = 11

Sekarang cuba buat sendiri.

Tukarkan kepada asas sepuluh.

1110012

12345

307628

54297

(16)

Menukar asas 10 kepada asas b :

Untuk menukar asas 10 kepada sebarang asas, kita perlu lihat pada suatu pola, sebagai contoh:

Untuk menukar asas 10 kepada asas 2, kumpulkan dua-dua.

Untuk menukar asas 10 kepada asas 3, kumpulkan tiga-tiga.

Untuk menukar asas 10 kepada asas 4, kumpulkan empat-empat.

Untuk menukar asas 10 kepada asas 5, kumpulkan lima-lima.

Pengumpulan bagi pola di atas dirumuskan dalam jadual di bawah.

Proses pengumpulan di atas boleh diterjemahkan menggunakan pembahagian mudah. Berikut adalah contoh untuk menjelaskan proses ini.

Contoh: Tukarkan 53 kepada asas 2

Gunakan proses berikut untuk menukar nombor perpuluhan kepada bentuk binari.

Bahagikan nombor perpuluhan dengan 2 dan ambil bakinya.Ulang proses ini

sehingga mendapat hasil 0.

Nombor binari dibentuk dengan mengambil baki dari bawah ke atas.

(17)

Baca dari bawah ke atas ,kita akan dapat 1101012 .

Sekarang, cuba sendiri . Selamat Mencuba!

Tukarkan 678 kepada asas 2

Tukarkan 2345 kepada asas 5

Perkara perlu di buat:

Sub-topik 1.3 dan 1.4

1. Cari maklumat tambahan mengenai tajuk di atas dari sumber berlainan. Anda di

galakkan untuk meneroka sesawang “Numeration Systems”. 2. Tuliskan nota ringkas.

Sub-topik 1.5

1. Rujuk pada „Resource Materials‟ dan baca Smith, K. J. (2001). “The Nature of

Mathematics”. Pacific Grove CA: Brooks and Cole : muka surat. 129 -140

2.

Buat latihan tentang cara menukar asas b kepada asas 10 dan sebaliknya. Anda

(18)

Peringatan : Simpan nota dan bahan yang dicetak termasuk penyelesaiannya

di dalam portfolia masing-masing.

Rujukan

Musser, G. L., et al.(2006). Mathematics for Elementary Teachers. 7th ed. USA: John Wiley

Smith, K.J. (2001). The Nature of Mathematics. 9th ed. Pacific Grove CA: Brooks /Cole Thomson Learning

1. The Development of Ancient Numeration Systems: http://mtl.math.uiuc.edu/projects/2/Wood/frame.htm

2. Mayan Numeration:

http://www.hanksville.org/yucatan/mayamath.html

http://72.40.235.132/search?q=cache:uuG7HTn90kJ:lacosta.cs.txstate.edu/Mmath

lessons/Year3Fall/MayanNumberingsystem.

3. Number bases: