SIMULASI NUMERIK KONVEKSI ALAMI DALAM KOTAK 2-D DENGAN VARIASI KEMIRINGAN DENGAN METODE SKEMA KOMPAK ORDE TINGGI SKRIPSI

(1)

perpustakaan.uns.ac.id digilib.uns.ac.id

commit to user

SIMULASI NUMERIK KONVEKSI ALAMI DALAM KOTAK 2-D DENGAN VARIASI KEMIRINGAN

DENGAN METODE SKEMA KOMPAK ORDE TINGGI

SKRIPSI

Diajukan sebagai salah satu syarat untuk memperoleh gelar

Sarjana Teknik

Oleh :

DANDUN MAHESA PRABOWOPUTRA NIM. I1409013

JURUSAN TEKNIK MESIN

FAKULTAS TEKNIK UNIVERSITAS SEBELAS MARET

SURAKARTA

(2)

commit to user

ii

SIMULASI NUMERIK KONVEKSI ALAMI DALAM KOTAK 2-D DENGAN VARIASI KEMIRINGAN

DENGAN METODE SKEMA KOMPAK ORDE TINGGI

Disusun oleh :

Dandun Mahesa Prabowoputra NIM. I1409013

Dosen Pembimbing I Dosen Pembimbing II

Eko Prasetya Budiana, S.T,M.T. Purwadi Joko Widodo, S.T,M.Kom NIP. 197109261999031002 NIP. 197301261997021001

Telah dipertahankan di hadapan dosen tim penguji pada hari kamis tanggal 26 Juli 2012

1. D.Danardono, S.T,M.T,PhD.

NIP. 196905141999031001 ………..

2. Tri Istanto, S.T,M.T.

NIP. 197308202000121001 ………..

3. Wibawa Endra Juwana, S.T,M.T.

NIP. 197009112000031001 ………..

Mengetahui,

Ketua Jurusan Teknik Mesin Koordinator Tugas Akhir

(3)

commit to user

iii

MOTTO DAN PERSEMBAHAN

Motto

Ilmu itu seperti udara, siapapun bisa mendapatkannya . Asalkan dia mau untuk menghirupnya. (anonym)

Manusia tidak memilih dirinya untuk menjadi luar biasa, melainkan mereka memilih untuk melakukan hal-hal yang luar biasa. (Sir Edmund

Hillary)

Happiness is when what you think, what you say, and what you do are in harmony. ( Mahatma Gandhi)

Persembahan

Tugas Akhir ini saya persembahkan kepada :

Bapak (Alm. Handoyo Cipto) , Ibu (Hariani Pancawati)

Kakak ( Jati Kusuma, Indira Putri Andini, Lindawati)

(4)

commit to user

iv ABSTRAK

DANDUN MAHESA P, Simulasi Numerik Konveksi Alami Dalam Kotak 2-D Dengan Variasi Kemiringan Dengan Metode Skema Kompak Orde Tinggi

Penelitian ini dilakukan untuk mengetahui fenomena yang terjadi, meliputi pola aliran dan distribusi temperatur pada permasalahan Konveksi alami, pada kotak 2D dengan variasi kemiringan. Variasi sudut dilakukan pada kemiringan 00, 300, 450, 900, 1200, 1350, 1500, dan 1800.

Tulisan ini menguraikan metode untuk penyelesaiaan konveksi alami kondisi steady dalam kotak 2D dengan variasi kemiringan. Metode ini didasarkan pada skema Runge–Kutta untuk diskritisasi waktu dan skema kompak beda hingga orde-4 untuk diskritisasi ruang.Penyelesaian permasalahan tekanan dengan menggunakan metode kompresibilitas tiruan. Metode beda hingga dituliskan dengan bahasa Fortran sedangkan distribusi temperatur dan pola aliran divisualisasikan dengan perangkat lunak Matlab.

Visualisasi menunjukan bahwa pola aliran dan mekanisme perpindahan panas dipengaruhi oleh besarnya sudut kemiringan. Perbandingan nilai hasil pada metode ini dengan nilai hasil metode lain seperti MLB, DQ analysis, dan algoritma pseudo–spectral Chebsyev, yang dipublikasikan oleh peneliti lain pada penelitian sebelumnya, menunjukan kedekatan yang membuktikan metode ini dapat diterima. Penelitian ini Metode skema kompak orde-tinggi mampu memberikan hasil yang baik untuk kasus konveksi alami pada kotak 2D dengan bilangan Rayleigh mencapai 107. Program yang telah dibuat telah mampu mencapai persamaan kontinuitas mendekati angka 0 yaitu pada nilai 10-3.2 sampai 10-3,59.

Kata kunci : konveksi alami, skema kompak, skema Runge – Kutta , sudut

(5)

commit to user

v

ABSTRACT

DANDUN MAHESA P, Numerical Simulation of natural convection in 2D cavity with inclination variation by Higher-Order Compact Schemes method

The research was conducted to determine the phenomena, including stramlines and temperature distribution in a natural convection problem, the 2D cavity with inclination variations. Variations of the inclination angle 00, 300, 450, 900, 1200, 1350, 1500, and 1800.

This paper outlines a method for solving steady state natural convection in a 2D cavity with a variation of the inclination. The method is based on the Runge-Kutta scheme for time discretization and compact finite difference scheme order-4 for the discretization of space. The pressure problems were solved by using the artificial compressibility method. The finite difference method was written in Fortran language whereas the temperature and flow patterns were visualized with Matlab software.

The visualization showed that the flow pattern and heat transfer mechanisms are influenced by the magnitude of the inclination. Comparison of the results of this method with the results of other method MLB, DQ analysis, and pseudo–spectral Chebsyev, in previous studies, showes the closeness which proves this method is acceptable. This research method of high-order compact schemes can give good results for the case of natural convection in a 2D cavity with the Rayleigh number reaches 107. The programs that have been made is able to reach the continuity equation close to 0, i.e at 10-3.2 to 10 -3.59.

(6)

commit to user

vi

KATA PENGANTAR

Puji dan syukur Alhamdulillah penulis panjatkan kehadirat Allah SWT,

yang senantiasa melimpahkan rahmat, hidayah serta kekuatan kepada Penulis,

sehingga Penulis dapat melaksanakan penelitian dan menyelesaikan laporan

Tugas Akhir dengan judul “ SIMULASI NUMERIK KONVEKSI ALAMI DALAM KOTAK 2-D DENGAN VARIASI KEMIRINGAN DENGAN METODE SKEMA KOMPAK ORDE TINGGI ”, sebagai salah satu syarat untuk memperoleh gelar Sarjana Teknik di Jurusan Teknik Mesin Fakultas Teknik

Universitas Sebelas Maret Surakarta.

Dalam penyusunan Tugas Akhir ini penulis banyak memperoleh bantuan

dari berbagai pihak yang sangat berarti demi kesempurnaan Tugas Akhir ini. Oleh

sebab tersebut pada kesempatan ini penulis mengucapkan rasa terima kasih

sedalam dalamnya kepada :

1. Didik Djoko Susilo, S.T.,M.T., selaku Ketua Jurusan Teknik Mesin UNS.

2. Bapak Eko Prasetya Budiana, ST.,MT., selaku Pembimbing I tugas akhir,

atas bimbingan, nasehat, kesabaran, motivasi dan ilmu pengetahuan yang

diajarkannya.

3. Bapak Purwadi Joko Widodo, S.T.,M.Kom, selaku Pembimbing II tugas

akhir, atas bimbingan, nasehat, kesabaran dan ilmu pengetahuan yang

diajarkannya.

4. Bapak Heru Sukanto, ST.,MT, selaku Pembimbing Akademik.

5. Bapak–bapak dosen dan staf karyawan di lingkungan Teknik Mesin UNS,

atas didikan, nasehat, ilmu yang diajarkan dan kerjasamanya.

6. Ayah, Ibu, kakak dan adik yang selalu memberikan dorongan semangat dan

doa kepada Penulis terima kasih untuk kasih sayangnya.

7. Teman–teman Teknik Mesin transfer angkatan 2009 dan teman–teman

Teknik Mesin UNS

8. Seluruh pihak yang telah membantu Penulis dalam menyelesaikan skripsi

ini.

Dengan segenap bantuan dan dukungan yang telah diberikan kepada penulis

(7)

commit to user

vii

Penulis menyadari bahwa Tugas Akhir ini masih belum dapat dikatakan

sempurna, untuk itu dengan sangat dan rendah hati penulis menerima kritikan

maupun saran yang membangun demi kesempurnaan Tugas Akhir tersebut. Akhir

kata penulis berharap Tugas Akhir ini dapat bermanfaat bagi para pembaca pada

umumnya dan penulis pada khususnya.

Surakarta, Juli 2012

(8)

commit to user

viii DAFTAR ISI

HALAMAN JUDUL... i

HALAMAN PENGESAHAN ………... ii

MOTTO DAN PERSEMBAHAN……….. ... iii

ABSTRAK………. .. iv

ABSTRACT……… ... v

KATA PENGANTAR……… ... vi

DAFTAR ISI………. ... viii

DAFTAR GAMBAR……… ... x

DAFTAR TABEL ... xii

DAFTAR NOTASI...……….. ... xiii

DAFTAR LAMPIRAN……. ... xv

BAB I PENDAHULUAN ... 1

1.1 Latar Belakang Masalah ... 1

1.2 Perumusan Masalah ... 2

1.3 Batasan Masalah ... 3

1.4 Tujuan Penelitian ... 3

1.5 Manfaat Penelitian ... 3

1.6 Sistematika Penulisan ... 3

BAB II LANDASAN TEORI ... 5

2.1 Tinjauan Pustaka ... 5

2.2 Dasar Teori………. ... 6

2.2.1 Persamaan Atur Konveksi Alami……… ... 7

2.2.2 Diskritisasi Waktu……… .. 8

2.2.3 Diskritisasi Ruang……… .. 8

2.2.4 Metode Kompresibilitas Tiruan ... 11

BAB III PELAKSANAAN PENELITIAN... 12

3.1 Alat dan Bahan ... 12

3.1.1. Alat……… ... 12

(9)

commit to user

ix

3.2 Garis Besar Penelitian ... 12

3.3 Diskritisasi Persamaan Atur ... 14

3.3.1 Diskritisasi Persamaan Momentum ... 14

3.3.2 Diskritisasi Persamaan Energi ... 15

3.3.3 Diskritisasi Metode Kompresibilitas Tiruan ... 16

3.4 Diskritisasi Syarat Batas ... 16

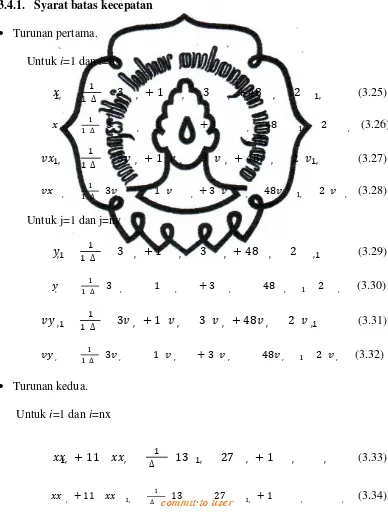
3.4.1 Syarat Batas Kecepatan ... 17

3.4.2 Syarat Batas Tekanan ... 18

3.4.3 Syarat Batas Temperatur ... 18

3.5 Algoritma Pemrograman ... 19

BAB IV HASIL DAN PEMBAHASAN ... 21

4.1 Validasi Program ... 21

4.2 Simulasi Konveksi Alami Dalam Kotak 2D ... 25

BAB V PENUTUP... 40

5.1 Kesimpulan ... 40

5.2 Saran ... 41

DAFTAR PUSTAKA ... 42

(10)

commit to user

x

DAFTAR GAMBAR

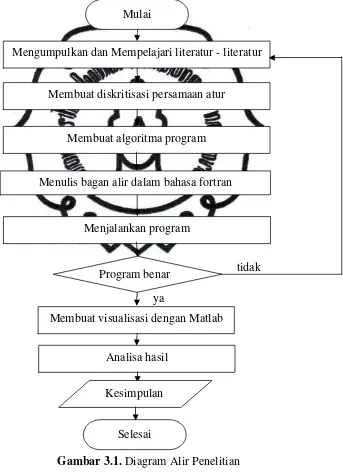
Gambar 3.1 Diagram Alir Penelitian ... 13

Gambar 3.2 Kondisi batas dan syarat batas ... 16

Gambar 3.3 Kotak 2D dengan kemiringan ... 17

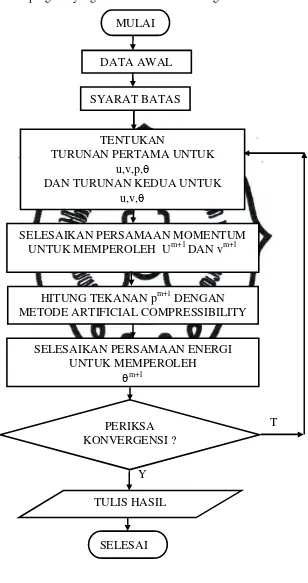
Gambar 3.4 Diagram Alir Program ... 20

Gambar 4.1 Kondisi batas dan syarat batas penelitian ... 21

Gambar 4.2 Perbandingan Isotermal penelitian Munir dengan hasil penelitian pada(a) kemiringan ( ) =400,

Gambar 4.14 Komponen gaya apung dalam kotak miring ... 36

Gambar 4.15 konvergensi untuk Ra=106 dan Sudut Kemiringan 00 ... 37

(11)

commit to user

xi

(12)

commit to user

xii

DAFTAR TABEL

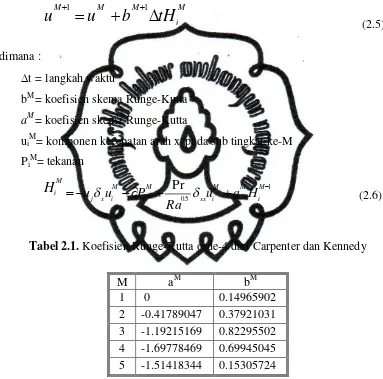
Tabel 2.1 Koefisien Runge-Kutta orde-4 dari Carpenter dan Kennedy ... 8

Tabel 4.1 Hasil Perhitungan dan Perbandingan untuk Ra=106 ... 22

Tabel 4.2 Hasil Perhitungan dan Perbandingan untuk Ra=107 ... 22

Tabel 4.3 Hasil nilai Nu rata-rata dan Perbandingan untuk Ra=105 ... 23

(13)

commit to user

xiii

DAFTAR NOTASI

a : koefisien skema kompak

aM : koefisien skema Runge-Kutta

b : koefisien skema kompak

bM : koefisien skema Runge-Kutta

c : konstanta persamaan konveksi 1-D

g : percepatan gravitasi (m/s2)

H : tinggi kotak

HM : variabel untuk skema Runge-Kutta

i,j : indek nodal

k : numerical wave number

Lr : variabel referensi untuk panjang kotak

nx : jumlah index arah x

Vr : variabel referensi untuk kecepatan

x,y : koordinat

Pr : bilangan Prandtl

Ra : bilangan Rayleigh

t : variabel waktu

tr : variabel reverensi untuk waktu

Huruf Yunani

a : koefisien skema kompak b : koefisien ekspansi volumetri d : operator diferensial

¶ : operator diferensial parsial

(14)

commit to user

xiv F : variabel generik

F’ : variabel turunan pertama F” : variabel turunan kedua r : densitas

q : variabel temperatur Ø : sudut kemiringan

(15)

commit to user

xv

DAFTAR LAMPIRAN

Lampiran 1. Non-Dimensional Persamaan Atur ... 44

Lampiran 2. Skema kompak beda-hingga... 47

Lampiran 3. Program Penyelesaian Konveksi Alami ... 49

Lampiran 4. Program Perhitungan Tambahan ... 55

(16)

commit to user

1 BAB I PENDAHULUAN

1.1Latar Belakang Masalah

Proses perpindahan panas dapat terjadi melalui tiga cara, yaitu secara

konduksi, konveksi, dan radiasi. Perpindahan panas konveksi adalah perpindahan

panas yang terjadi di antara permukaan benda dengan fluida yang bergerak ketika

temperatur keduanya berbeda. Perpindahan panas secara konveksi berdasarkan

jenis penyebab aliran fluida yang terjadi, dikategorikan menjadi dua kategori yaitu

konveksi paksa dan konveksi alami.

Konveksi paksa (forced convection) adalah konveksi yang mana aliran fluida yang terjadi disebabkan adanya alat-alat eksternal, seperti fan, pompa,

aliran udara atmosfer (angin). Sedangkan konveksi alami (natural convection)

adalah perpindahan panas antara suatu permukaan dan fluida yang mengalir

diatasnya, dimana aliran fluida disebabkan oleh adanya perbedaan densitas fluida

yang ditimbulkan oleh pemanasan dan pendinginan. Densitas fluida akan

berkurang jika fluida mendapat pemanasan sehingga fluida akan mengapung dan

daerah yang ditinggalkan akan diisi oleh fluida yang relatif dingin. Fluida yang

relatif panas jika mendekati dinding yang relatif dingin densitasnya akan

meningkat sehingga akan mengalir turun akibat tarikan gaya grafitasi. Dengan

demikian densitas merupakan driving force sirkulasi fluida.

Konveksi alami memegang peranan penting dalam rekayasa industri seperti:

perancangan alat penukar kalor, perancangan ventilasi, pendinginan

transformator, pendinginan kabel bawah tanah dan pendinginan komponen

elektronika. Penelitian mengenai fenomena pada konveksi alami telah banyak

dilakukan baik secara eksperimental maupun secara numerik. Penelitian secara

eksperimen laboratorium untuk mengetahui fenomena yang terjadi pada proses

konveksi alami membutuhkan biaya yang cukup mahal dan proses yang cukup

rumit. Oleh karena itu, dikembangkan penelitian secara numerik yang

membutuhkan biaya yang jauh lebih murah. Berbagai metode pendekatan numerik

(17)

commit to user

2

menggunakan model matematika dari persamaan kontinyuitas, persamaan

Navier-Stokes dan persamaan energi. Penelitian konveksi alami secara numerik

berkembang pesat sejalan dengan perkembangan komputer digital berkecepatan

tinggi yang semakin pesat.

Perkembangan penelitian secara numerik terus berkembang dari tahun ke

tahun. Le Quere (1990) meneliti konveksi alami dalam kotak 2-D dengan

diskritasi pseudo-spectral yang didasarkan pada polinomial Chebyshev, kemudian

Wilson dan Demuren (1998) menggunakan skema kompak untuk mendiskritisasi

turunan ruang dan skema Runge-Kutta untuk mendiskritisasi turunan waktu pada

simulasi aliran fluida tak mampat. Lo (2009) meneliti konveksi alami pada kotak

2D dan 3D dengan DQ analisis menggunakan formulasi velocity-vorticity. Azwadi

(2010) melakukan penelitian pada konveksi alami pada kotak 2D dengan sudut

kemiringan dimana metode yang digunakan adalah metode lattice Boltzmann,

begitu juga Munir dan Sidik (2011) meneliti konveksi alami pada kotak 2D

dengan kemiringan menggunakan metode lattice Boltzmann. Sen (2012) meneliti

persamaan konveksi untuk kondisi unsteady dengan metode skema kompak

orde-4 secara implisit.

1.2Perumusan Masalah

Perumusan masalah dalam penelitian ini adalah :

1. Bagaimana membuat diskritisasi pada permasalahan konveksi alami dalam

kotak 2-D, dengan menggunakan skema kompak beda hingga orde-4 untuk

diskritisasi ruang dan skema Runge-Kutta orde-4 untuk diskritisasi waktu

dengan variasi kemiringan.

2. Bagaimanakah membangun sebuah sistem (program) yang

mengimplementasikan model yang telah dibuat agar dapat dikomputasikan

oleh komputer.

3. Bagaimanakah membuat visualisasi 2-D berdasarkan hasil komputasi

(18)

commit to user

3

1.3Batasan Masalah

Masalah pada penelitian ini dibatasi pada persoalan konveksi alami pada

kotak 2-D dengan variasi kemiringan. Penyelesaian masalah tersebut

menggunakan skema kompak beda hingga orde-4 untuk diskritisasi ruang, dan

skema Runge-Kutta orde-4 untuk diskritisasi waktu, untuk memperoleh vektor

kecepatan dan distribusi temperatur.

1.4Tujuan Penelitian

Tujuan penelitian ini adalah mengekplorasi skema kompak orde-tinggi

untuk menyelesaikan permasalahan dan mengetahui fenomena yang terjadi pada

konveksi alami pada kotak 2-D dengan variasi kemiringan. Hal tersebut meliputi

vektor kecepatan dan distribusi temperatur.

1.5Manfaat Penelitian

Manfaat dari penelitian ini adalah :

1. Untuk mengembangkan ilmu pengetahuan, terutama dalam bidang

komputasi numerik dinamika fluida dan perpindahan panas.

2. Untuk mengetahui penerapan skema kompak orde tinggi pada permasalahan

konveksi alami 2D.

1.6Sistematika Penulisan

Sistematika penulisan yang digunakan :

1. BAB I : PENDAHULUAN

Berisi dasar-dasar dan latar belakang pengambilan tugas akhir dan

penyusunan skripsi.

2. BAB II : LANDASAN TEORI

Berisi tentang tinjauan pustaka, dasar teori konveksi alami, skema kompak

beda hingga orde-4 untuk pendekatan turunan ruang dan skema

Runge-Kutta orde-4 untuk pendekatan turunan waktu serta metode kopresibilitas

(19)

commit to user

4

3. BAB III : PELAKSANAAN PENELITIAN

Berisi tentang alat dan bahan yang digunakan dalam penelitian, cara

penelitian, diskritisasi persamaan atur.

4. BAB IV : HASIL DAN PEMBAHASAN

Berisi data hasil penelitian (simulasi) dan pembahasannya.

5. BAB V : PENUTUP

Berisi kesimpulan yang diperoleh dan saran-saran bagi penelitian

selanjutnya.

6. DAFTAR PUSTAKA

(20)

Prosedur numerik dengan orde akurasi tinggi telah dikembangkan untuk

menyelesaikan persamaan Navier-Stokes pada problem aliran fluida tak mampat

2-D dan 3-D. Metode tersebut didasarkan pada skema Runge-Kutta untuk

diskritisasi waktu dan skema kompak beda hingga untuk diskritisasi ruang.

Persamaan tekanan diselesaikan dengan metode kompresibilitas tiruan.

Le Querre (1990) menggunakan algoritma pseudo–spectral Chebsyev untuk

meneliti konveksi alami pada kotak 2D dengan dinding kiri di panasi, dinding

kanan didinginkan, serta dinding atas dan bawah adiabatik. Dengan metode ini

dapat menghilangkan osilasi numerik dan mencapai hasil yang akurat hingga nilai

Ra 108.

Wilson dan Demuren (1998), menggunakan skema kompak beda hingga

untuk diskritasi ruang dan skema Runge-Kutta untuk diskritasi waktu pada

simulasi aliran fluida tak mampat. Pada penelitian ini skema kompak beda hingga

digunakan untuk diskritisasi turunan ruang dan skema Runge-Kutta orde-empat

untuk diskritasi turunan waktu.

Sulistyono (2006) melakukan penelitian untuk mengetahui fenomena yang

terjadi pada konveksi alami kotak 2D dengan berbagai variasi kemiringan dengan

menggunakan metode beda hingga. Zhao dan Dai (2007) menggunakan metode

skema kompak orde-4 dalam permasalahan perpindahan panas konduksi dengan

kondisi batas Neumann. Laizet (2009) menggunakan skema kompak orde tinggi

untuk meneliti aliran fluida tak mampat . Lo (2009) meneliti konveksi alami

dengan sudut kemiringan pada kotak 2D dan 3D dengan DQ analisis

menggunakan formulasi velocity-vorticity.

Azwadi (2010) melakukan penelitian pada konveksi alami pada kotak 2D

dengan sudut kemiringan 200-1600, dimana metode yang digunakan adalah

metode lattice Boltzmann. Kondisi batas yang digunakan adalah pemanasan dari

samping kiri, dan pendinginan dari samping kanan serta perfectly conducting wall

(21)

commit to user

6

Munir dan Sidik (2011) meneliti konveksi alami pada kotak 2D dengan

kemiringan menggunakan metode lattice Boltzmann. Dimana kondisi batas yang

digunakan adalah pemanasan dari samping kiri, dan pendinginan dari samping

kanan serta perfectly conducting wall pada bagian atas dan bawah pada penelitian

pertama, dan isolasi pada bagian atas dan bawah pada penelitian berikutnya. Sen

(2012) meneliti persamaan konveksi untuk kondisi unsteady dengan metode skema kompak orde-4 secara implisit.

2.2Dasar Teori

Konveksi alami adalah perpindahan panas di antara sebuah permukaan dan

fluida yang bergerak di atasnya dengan gerakan fluida yang disebabkan gaya

apung (buoyancy force) yang timbul karena perbedaan density akibat perbedaan tekanan di dalam aliran (Oosthuizen,1999).

Dewasa ini, berkembang metode Lattice Boltzmann (MLB), dimana MLB

merupakan teknik simulasi yang sangat berguna untuk pemodelan fluida dengan

banyak fase dan komponen. Dinamika fluida umumnya mencakup

partikel-partikel mikroskopik, sehingga kalkulasinya sangat rumit yang tidak bisa

diselesaikan sepenuhnya melalui metode tradisional.MLB berbasis pada model

partikel mikroskopik dan persamaan kinetik, memberikan alternatif numerik untuk

memecahkan masalah ini, namun MLB memiliki tingkat kerumitan boundaries dan beban komputasi yang tinggi.Penghitunga fase yang lebih banyak

memerlukan ketelitian yang tinggi menyebabkan waktu hitung lebih panjang.

Sedangkan untuk skema kompak beda hingga dengan akurasi orde-4 dan orde-6,

ternyata skema tersebut memiliki resolusi yang lebih baik dibanding skema beda

hingga biasa. Skema kompak beda hingga orde-4 memiliki grid stensil yang sama

dengan skema beda hingga orde-dua, hal ini mempermudah penerapan metode ini

pada model matematika, akurasinya tinggi, fleksibel, dan pengoperasianya lebih

mudah.

Persamaan atur konveksi alami terdiri dari persamaan kontinyuitas,

persamaan momentum dan persamaan energi. Model matematika dari persamaan

atur konveksi alami terdiri dari persamaan diferensial parsial orde-1 dan orde-2.

(22)

commit to user

7

maka terlebih dahulu dibuat diskritisasi persamaan atur. Diskritisasi waktu

dilakukan dengan skema Runge-Kutta orde-4 dan diskritisasi ruang dengan skema

kompak beda hingga orde-4.

2.2.1Persamaan atur konveksi alami

Pada konveksi alami dengan perbedaan temperatur yang kecil, maka berlaku

pendekatan Boussenesq, yaitu dalam analisis mengenai aliran pada konveksi

alami, properties fluida diasumsikan konstan kecuali perubahan density terhadap

temperatur yang menyebabkan munculnya gaya apung (buoyancy force) (Oosthuizen, 1999). Sehingga untuk permasalahan 2-D persamaan atur konveksi

alami dalam bentuk variabel tak berdimensi adalah sebagai berikut (Quere,1990):

Pesamaan Kontinuitas :

)  焸



 0 (2.1)

Persamaan Navier Stokes :

)

Persamaan di atas diperoleh dengan membagi variabel berdimensi dengan

variabel referensi. Variabel referensi untuk panjang adalah Lr=H, untuk kecepatan

(23)

commit to user

8

2.2.2Diskritisasi waktu

Diskritisasi waktu untuk persamaan momentum menggunakan skema

Runge-Kutta orde-4 dari Williamson (Wilson dan Demuren,1998) yang didefinisikan

sebagai berikut :

bM = koefisien skema Runge-Kutta

aM = koefisien skema Runge-Kutta

uiM= komponen kecepatan arah xi pada sub tingkat ke-M

PiM= tekanan

Tabel 2.1. Koefisien Runge-Kutta orde-4 dari Carpenter dan Kennedy

M aM bM

1 0 0.14965902 2 -0.41789047 0.37921031 3 -1.19215169 0.82295502 4 -1.69778469 0.69945045 5 -1.51418344 0.15305724

2.2.3Diskritisasi Ruang

Skema beda-hingga orde-2 untuk turunan pertama memiliki galat dispersi

yang besar, sedangkan skema kompak beda hingga memiliki kelebihan yaitu

(24)

commit to user

9

a. Turunan pertama.

Bentuk diskritisai turunan pertama dengan pendekatan skema kompak beda

hingga orde-4 dan orde-6 dirumuskan oleh Wilson dan Demuren (1998). Bentuk

persamaanya adalah : kompak orde-3 dengan persamaan sebagai berikut :

å

Untuk skema orde-6, syarat batas diselesaikan dengan skema ekplisit

(25)

Untuk syarat batas pada i=2 dan i=N-1 juga digunakan skema ekplisit orde-lima

sebagai berikut :

Persamaan skema kompak beda hingga untuk turunan kedua adalah sebagai

berikut :

a = koefisien skema kompak beda hingga turunan kedua

Untuk orde-empat, a=1/10, a=6/5, b=0 dan untuk orde-enam, a=2/11, kompak orde-3 sebagai berikut :

(26)

commit to user

11

2.2.4Metode Kompresibilitas Tiruan (Artificial Compressibility)

Konsep metode kompresibilitas tiruan adalah menambahkan turunan terhadap

waktu pada persamaan kontinyuitas. Bentuk modifikasi persamaan adalah :

0

= Ñ + ¶ ¶

V t

p

e

(2.13)

Dimana e adalah konstanta positif. Persamaan ini tidak mempunyai arti fisik jika

(27)

a. Laptop dengan spesifikasi Intel(R) Pentium(R) Dual CPU T2390 @1.86GHz,

Memori 3062 MB

b. Perangkat lunak Mikrosoft Fortran Power Station 4.0 dan Matlab

c. Printer Canon iP 1980

3.1.2.Bahan

a. Perangkat lunak hasil implementasi penyelesaian numerik persamaan

Navier-Stoke, persamaan kontinuitas, dan persamaan energi dengan skema kompak

beda hingga digunakan untuk diskritisasi turunan ruang dan skema

Runge-Kutta orde-4 untuk diskritasi turunan waktu.

b. Data-data referensi untuk bahan penyusunan kode.

3.2Garis Besar penelitian

Penelitian dilakukan dengan cara membuat implementasi program untuk

menyelesaikan persamaan momentum, persamaan energi dan persamaan

kontinyuitas dengan pendekatan skema kompak orde-4 dan skema Runge-Kutta

orde-4. Langkah-langkah penelitian yang dilakukan adalah seperti berikut :

1. Mengumpulkan literatur

2. Mempelajari literatur

a. Mempelajari penelitan-penelitian yang pernah dilakukan

b. Mempelajari persamaan atur yang berhubungan dengan permasalahan

3. Merencanakan algoritma program

a. Membuat diskritisasi persamaan atur

b. Menyusun bagan alir program

4. Menulis bagan alir dalam bahasa program (Fortran)

5. Menjalankan program

6. Validasi Program

(28)

commit to user

13

ya

tidak a. Kesalahan penulisan

b. Kesalahan algoritma

8. Membuat visualisasi hasil program dengan perangkat lunak Matlab

9. Menyusun laporan penelitian

Garis besar penelitian tersebut dapat dibuat diagram alir sebagai berikut :

Gambar 3.1. Diagram Alir Penelitian Mengumpulkan dan Mempelajari literatur - literatur

Membuat diskritisasi persamaan atur Mulai

Membuat algoritma program

Menulis bagan alir dalam bahasa fortran

Menjalankan program

Program benar

Membuat visualisasi dengan Matlab

Analisa hasil

(29)

commit to user

14

3.3Diskritisasi Persamaan Atur

Persamaan atur konveksi alami terdiri dari persamaan kontinuitas,

persamaan momentum dan persamaan energi. Model matematika dari persamaan

atur konveksi alami terdiri dari persamaan diferensial parsial orde-1 dan orde-2.

Agar persamaan atur konveksi alami dapat diaplikasikan dalam bahasa program

maka terlebih dahulu dibuat diskritisasi persamaan atur. Diskritisasi waktu

dilakukan dengan skema Runge-Kutta orde-4 dan diskritisasi ruang dengan skema

kompak beda hingga orde-4. Matrik yang terbentuk dari diskritisasi turunan ruang

adalah matrik tridiagonal yang bisa diselesaikan dengan algoritma Thomas.

3.3.1 Diskritisasi persamaan momentum

a. Persamaan momentum arah x:

�.

Diskritisasi waktu (Runge-Kutta) :

, � , 㻘 � ∆ , (3.2)

, , A, 鶈, 9, A, 㻘䫠5 AA, 㻘 99,

㻘䫠 cos∅ 㻘 _, _(3.3)

Diskritisasi Ruang ( Skema Kompak orde- 4) :

(30)

b. Persamaan momentum arah y :

�

, � , 㻘 � ∆ , (3.10)

, , 鶈A, 鶈, 鶈9, 9, 㻘䫠5 鶈AA, 㻘鶈99,

㻘䫠 sin∅ 㻘 _, _(3.11)

· _{Turunan pertama}

3.3.2. Diskritisasi persamaan energi

�

(31)

commit to user

16

, , A, 鶈, 9, 㻘 � AA, 㻘 99, 㻘 , (3.19)

3.3.3. Diskritisasi metode kompresibilitas tiruan.

, � , 㻘 � ∆ , (3.24)

, A, 9, 㻘 , (3.25)

3.4Diskritisasi Syarat Batas

Dalam penelitian ini kasus yang dibahas adalah konveksi alami dalam

kotak 2-D dengan dinding bawah di panasi, dinding atas didinginkan, serta

dinding kiri dan kanan adiabatik dengan variasi kemiringan. Untuk kondisi batas

domain adalah pada seluruh dinding kecepatan bernilai nol sedangkan syarat

batas tekanan dan temperatur adalah seperti berikut :

(32)

commit to user

17

Gambar 3.3. Kotak 2D dengan kemiringan ∅

3.4.1. Syarat batas kecepatan

· _{Turunan pertama.}

Untuk i=1 dan i=nx

A�, _{� ∆}� 3 , 㻘 1 , 3 , 㻘 48 , 2 �, (3.25)

A , _{� ∆}� 3 , 1 , 㻘 3 , 48 �, 2 , (3.26)

鶈A�, _{� ∆}� 3鶈 , 㻘 1 鶈 , 3 鶈 , 㻘 48鶈 , 2 鶈�, (3.27)

鶈A , _{� ∆}� 3鶈 , 1 鶈 , 㻘 3 鶈 , 48鶈 �, 2 鶈 , (3.28)

Untuk j=1 dan j=ny

9,� _{� ∆}� 3 , 㻘 1 , 3 , 㻘 48 , 2 ,� (3.29)

9, _{� ∆}� 3 , 1 , 㻘 3 , 48 , � 2 , (3.30)

鶈9,� _{� ∆}� 3鶈, 㻘 1 鶈, 3 鶈, 㻘 48鶈, 2 鶈,� (3.31)

鶈9, _{� ∆}� 3鶈, 1 鶈, 㻘 3 鶈, 48鶈, � 2 鶈, (3.32)

· _{Turunan kedua.}

Untuk i=1 dan i=nx

AA_�, 㻘 11 AA_, _∆� 13 _�, 27 _, 㻘 1 _, _, (3.33)

(33)

commit to user

18

鶈AA�, 㻘 11鶈AA , _∆� 13鶈�, 27鶈 , 㻘 1 鶈 , 鶈 , (3.35)

鶈AA , 㻘 11鶈AA �, _∆� 13鶈 , 27鶈 �, 㻘 1 鶈 , 鶈 , (3.36)

Untuk j=1 dan j=ny

99,�㻘 11 99, _∆� 13 ,� 27 , 㻘 1 , , (3.37)

99, 㻘 11 99, � _∆� 13 , 27 , �㻘 1 , , (3.38)

鶈99,�㻘 11鶈99, _∆� 13鶈,� 27鶈, 㻘 1 鶈, 鶈, (3.39)

鶈99, 㻘 11鶈99, � _∆� 13鶈, 27鶈, �㻘 1 鶈, 鶈, (3.40)

3.4.2. Syarat batas tekanan

Untuk i=1 dan i=nx

A_�, (3.41)

A _, (3.42)

Untuk j=1 dan j=ny

9,� (3.43)

9, (3.44)

3.4.3. Syarat batas temperatur

Untuk i=1 dan i=nx

qA_�, �

� ∆ 3q , 㻘 1 q , 3 q , 㻘 48q , 2 q�, (3.45)

qA _, �

(34)

Algoritma pemrograman tersebut dapat dituliskan sebagai berikut :

1. Tentukan kondisi awal dan kondisi batas untuk semua variabel (u,v,q_,p).

2. Hitung turunan pertama dari kecepatan, temperatur dan tekanan

(ux,uy,vx,vy,q_x,q_y,px,py) _dan _turunan _kedua _dari _kecepatan _dan

temperatur(uxx,uyy,vxx,vyy,q_xx,q_{yy) dengan skema kompak orde-empat.}

3. Hitung kecepatan(u,v) dengan skema Runge-Kutta orde-empat.

4. Hitung tekanan dengan metode artificial compressibility.

5. Hitung temperatur(q_{)dengan skema Runge-Kutta orde-4.}

6. Periksa apakah sudah mencapai batas perhitungan atau belum, jika belum

kembali ke langkah 2, jika sudah ke langkah 7.

7. Tulis hasil

(35)

commit to user

20

Bagan alir program yang akan dibuat adalah sebagai berikut:

Gambar 3.4. Diagram Alir Program MULAI

DATA AWAL

SYARAT BATAS

TENTUKAN

TURUNAN PERTAMA UNTUK u,v,p,q

DAN TURUNAN KEDUA UNTUK u,v,q

SELESAIKAN PERSAMAAN MOMENTUM UNTUK MEMPEROLEH Um+1 DAN vm+1

HITUNG TEKANAN pm+1 DENGAN METODE ARTIFICIAL COMPRESSIBILITY

SELESAIKAN PERSAMAAN ENERGI UNTUK MEMPEROLEH

qm+1

PERIKSA KONVERGENSI ?

TULIS HASIL

SELESAI Y

(36)

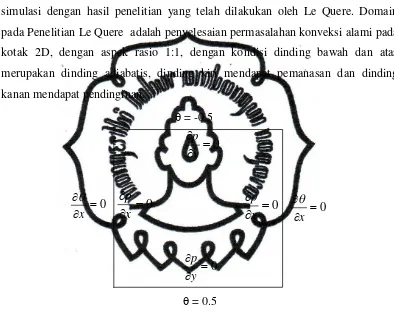
Validasi program dilakukan dengan cara membandingkan hasil dari proses

simulasi dengan hasil penelitian yang telah dilakukan oleh Le Quere. Domain

pada Penelitian Le Quere adalah penyelesaian permasalahan konveksi alami pada

kotak 2D, dengan aspek rasio 1:1, dengan kondisi dinding bawah dan atas

merupakan dinding adiabatis, dinding kiri mendapat pemanasan dan dinding

kanan mendapat pendinginan.

Gambar 4.1. Kondisi batas dan syarat batas Penelitian

Kondisi Batas Le Quere sama dengan kondisi batas pada penelitian pada

sudut kemiringan ( ) = 900 . Hasil Perhitungan akan dibandingkan dengan

penelitian Le Quere pada Ra=106, dan Ra=107. Hasil perhitungan dan

(37)

commit to user

22

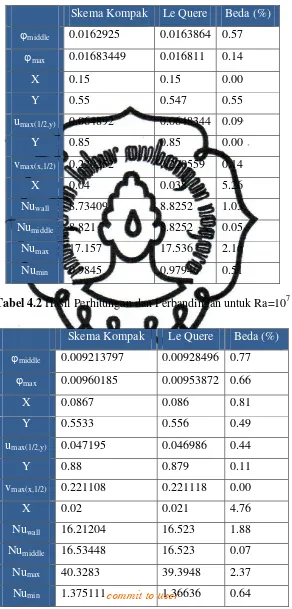
Tabel.4.1 Hasil Perhitungan dan Perbandingan untuk Ra=106

Skema Kompak Le Quere Beda (%)

jmiddle 0.0162925 0.0163864 0.57

jmax 0.01683449 0.016811 0.14

X 0.15 0.15 0.00

Y 0.55 0.547 0.55

umax(1/2,y) 0.064892 0.0648344 0.09

Y 0.85 0.85 0.00

vmax(x,1/2) 0.220252 0.220559 0.14

X 0.04 0.038 5.26

Nuwall 8.73409 8.8252 1.03

Numiddle 8.821 8.8252 0.05

Numax 17.157 17.536 2.16

Numin 0.9845 0.97946 0.51

Tabel 4.2 Hasil Perhitungan dan Perbandingan untuk Ra=107

Skema Kompak Le Quere Beda (%)

jmiddle 0.009213797 0.00928496 0.77

jmax 0.00960185 0.00953872 0.66

X 0.0867 0.086 0.81

Y 0.5533 0.556 0.49

umax(1/2,y) 0.047195 0.046986 0.44

Y 0.88 0.879 0.11

vmax(x,1/2) 0.221108 0.221118 0.00

X 0.02 0.021 4.76

Nuwall 16.21204 16.523 1.88

Numiddle 16.53448 16.523 0.07

Numax 40.3283 39.3948 2.37

(38)

commit to user

23

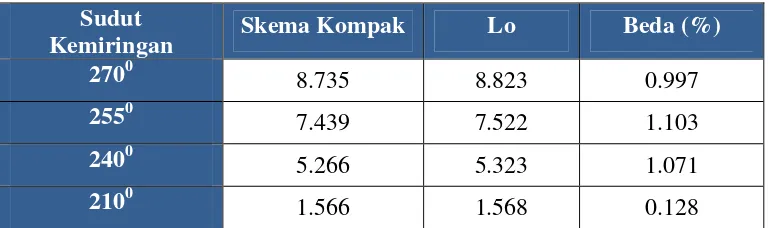
Sudut kemiringan yang lain dilakukan validasi dengan membandingkan

dengan hasil penelitian yang telah dilakukan oleh Lo. Domain untuk penelitian.Lo

pada permasalahan konveksi alami, kotak 2D dengan aspek rasio 1 :1, dengan

kondisi dinding bawah dan atas merupakan dinding adiabatis, dinding kanan

mendapat pemanasan dan dinding kiri mendapat pendinginan.

Kondisi Batas ini sama dengan kondisi batas pada penelitian pada sudut

kemiringan ( ) = 2700. Pada penelitian Lo kotak dimiringkan berlawanan

dengan arah jarum jam. Hasil Perhitungan akan dibandingkan dengan penelitian

Lo pada Ra=105, dan Ra=106. Hasil perhitungan Nusselt rata-rata dan

perbandingan dengan hasil penelitian Lo disajikan dalam tabel 4.3 dan 4.4.

Tabel 4.3 Hasil nilai Nusselt rata-rata dan Perbandingan untuk Ra=105

Sudut

Tabel 4.4 Hasil nilai Nusselt rata-rata dan Perbandingan untuk Ra=106

Sudut

Validasi secara visual dilakukan dengan membandingkan hasil visual

isotermal dengan hasil visual isotermal pada penelitian Munir. Hasil penelitian

Munir menggunakan metode lattice Boltzmann dan kondisi batas yang sama

dengan kondisi batas pada penelitian. Perbandingan ditunjukan dengan gambar

(39)

commit to user

24

(a)

(b)

(c)

Gambar 4.2. perbandingan Isotermal penelitian Munir dengan Hasil penelitian pada (a) kemiringan ( ) =400, (b) kemiringan ( ) = 1200,

(40)

commit to user

25

Hasil perhitungan yang ditunjukan tabel 4.1 sampai 4.4 menunjukkan

kedekatan yang baik antara hasil penelitian dengan hasil penelitian Le Quere

maupun Lo. Secara visual, hasil penelitian menunjukan kemiripan dengan

penelitian yang dilakukan Munir. Sehingga dapat dikatakan hasil penelitian dari

skema kompak orde tinggi memiliki kesesuaian yang baik.

4.2.Simulasi Konveksi Alami dalam kotak 2D

Simulasi kasus konveksi alami dalam kotak 2-D ditampilkan dengan susunan

grid sebesar 101 x 101, bilangan Prandtl (Pr) = 0.71 , langkah waktu dt = 0.005

dan angka Rayleigh yang digunakan adalah Ra = 106 dengan rasio 1:1 . Hasil

simulasi selengkapnya dapat dilihat pada gambar berikut :

· Distribusi temperatur :

Gambar 4.3 Isotermal pada Ra = 106, sudut = 00 Panas

Dingin

Iso

la

si

Isol

(41)

commit to user

26

(a)

(b)

Gambar 4.4 Isotermal pada Ra = 106, (a) sudut = 300 (b) sudut = 450 Dingin

Panas Isolasi

Isolasi

Dingin

Panas Isolasi

(42)

commit to user

27

(a)

(b)

Gambar 4.5 Isotermal pada Ra = 106, (a) sudut = 600 (b) sudut = 900 Dingin

Panas

Isolasi

Isolasi Isolasi

di

ngi

n

P

ana

(43)

commit to user

28

(a)

(b)

Gambar 4.6 Isotermal pada Ra = 106, (a) sudut = 1200 (b) sudut = 1350 Isolasi

Isolasi Panas

Dingin

Isolasi

Isolasi Panas

(44)

commit to user

29

(a)

(b)

Gambar 4.7 Isotermal pada Ra = 106, (a) sudut = 1500 (b) sudut = 1800 Isolasi

Isolasi Isolasi

Isolasi

dingin Panas

Panas

(45)

commit to user

30

· streamlines :

(a)

(b)

(46)

commit to user

31

(a)

(b)

(47)

commit to user

32

(a)

(b)

(48)

commit to user

33

(a)

(b)

(49)

commit to user

34

Simulasi kasus konveksi alami dalam kotak 2-D ditampilkan dengan

susunan grid sebesar 81 x 41, bilangan Prandtl (Pr) = 0.71 , langkah waktu dt =

0.0005, sudut = 00 dan angka Rayleigh yang digunakan adalah Ra = 106 dengan

rasio 2:1. Hasil simulasi selengkapnya dapat dilihat pada gambar berikut :

Gambar 4.12 Streamlines untuk rasio 2:1

Gambar 4.13 Isotermal untuk rasio 2:1 Isolasi

Panas

(50)

commit to user

35

Hasil plot isotermal pada gambar 4.3 sampai dengan gambar 4.7

menunjukan distribusi temperatur secara visual. Gambar 4.3 pada sudut = 00,

terlihat bahwa pergerakan fluida panas bergerak keatas karena adanya gaya apung

(buoyancy force). Hal ini disebabkan karena density yang turun akibat dari temperatur panas, sedangkan fluida dingin bergerak ke bawah karena density lebih

besar serta adanya gaya gravitasi. Temperatur fluida yang dekat dengan dinding

sangat terpengaruh oleh temperatur di dinding. Gambar 4.3 menunjukkan

pengaruh nilai Ra pada distribusi temperatur, dimana bagian yang relatif panas di

bagian kiri bawah semakin condong ke atas dan distribusi temperatur yang relatif

dingin di bagian kanan bawah semakin condong ke bawah, hal ini karena

pengaruh kecepatan gerakan fluida yang membawa panas pada nilai Ra tersebut.

Hal ini pun terjadi pada kemiringan kotak untuk sudut = 300,450,600 , 900 ,

1200, 1350 dan 1500 yang di tunjukan pada gambar 4.4 sampai 4.7. Gambar

isotherm tersebut Di sini terlihat bahwa kecepatan fluida pada dinding kiri dan

kanan relatif cepat dari pada bagian tengah. Pada dinding yang dipanaskan, fluida

mendapat pemanasan sehingga densitas fluida mengecil . Penyusutan densitas

pada dinding yang dipanaskan menyebabkan terjadinya gaya apung sehingga

fluida bergerak ke atas. Aliran fluida setelah mencapai dinding atas bergerak

turun dan selanjutnya membelok ke arah dinding yang didinginkan dan

mengalami pendinginan. Gerakan fluida turun setelah mencapai dinding atas

disebabkan oleh pengaruh inersia. Hal ini terjadi karena nilai Bilangan Prandtl

untuk udara adalah Pr<1 sehingga keseimbangan persamaan aliran dipengaruhi

oleh inersia. Untuk nilai Pr>1 maka pengaruh inersia akan semakin berkurang

sehingga keseimbangan persamaan aliran dipengaruhi oleh friction dan buoyancy.

Setelah mencapai dinding dingin fluida membelok ke bawah, karena temperatur

dinding lebih rendah, sehingga fluida mengalami pendinginan sehingga

densitasnya meningkat, dengan demikian kecepatan aliran bertambah karena

pengaruh gaya gravitasi. Setelah mencapai dinding bawah aliran fluida bergerak

ke atas karena pengaruh inersia kemudian berbelok ke dinding yang dipanaskan

dan mengalami pemanasan pada dinding kiri. . Dimana fenomena ini menjelaskan

(51)

commit to user

36

Gambar 4.14 Komponen gaya apung dalam kotak miring

Gambar 4.7 (b), untuk kemiringan sudut = 1800 menunjukan tidak terjadi

perpindahan panas secara konveksi, melainkan perpindahan panas terjadi secara

konduksi. Hal ini dikarenakan pemanasan terjadi pada bagian atas, dan

pendinginan terjadi pada bagian bawah. Sehingga fluida tidak terjadi pergerakan,

dan efek gaya apung (buoyancy force) tidak terjadi pada sudut ini.

Gambar. 4.8 dan Gambar 4.11 menunjukkan plot dari streamlines untuk sudut kemiringan sudut = 300,450,600 , 900 , 1200, 1350 dan 1500. Simulasi pada

Ra 106 dengan sudut kemiringan ≥ 300,fluida yang dekat dengan dinding panas

dipanaskan dan naik karena pengaruh gaya apung (buoyancy force). Kemudian

fluida yang didinginkan oleh dinding dingin, fluida terjadi peningkatan density

yang kemudian akan turun. Hal ini digambarkan secara sederhana melalui

gambar 4.14. Hasil simulasi untuk sudut kemiringan > 300, pada bagian tengah

muncul sel lebih dari satu karena tingginya gaya tarik gravitasi di sepanjang

dinding vertikal dari kotak. Sedangkan untuk hasil simulasi pada sudut

kemiringan yang lebih rendah ( < 300), hanya sel pusat tunggal muncul karena

kecepatan aliran yang lebih tinggi di sepanjang dinding panas dan dingin.

Hasil simulasi untuk sudut kemiringan =00 yang ditunjukan gambar 4.8

(a) terdapat satu gulungan sel, dimana bila rasio ditingkatkan maka akan terlihat

beberapa gulungan sel. gulungan sel itu biasa disebut benard sell. Hal ini nampak

lebih jelas pada simulasi kasus dengan rasio 2:1. Dimana hal ini ditunjukan pada

plot Streamlines gambar 4.12. Gambar tersebut menunjukan adanya 2 benard sell. TH

TC

(52)

commit to user

37

Gambar 4.15 konvergensi untuk Ra=106 dan Sudut Kemiringan 00

(53)

commit to user

38

(54)

commit to user

39

Gambar kurva konvergensi pada gambar 4.15 sampai gambar 4.22

menunjukan nilai logaritma -3,2 sampai -3,59. Nilai logaritma tersebut

menunjukan bahwa program yang telah dibuat telah mampu mencapai persamaan

kontinuitas mendekati angka 0 yaitu pada nilai 10-3.2 sampai 10-3,59. Sehingga dari

gambar kurva konvergensi menunjukan bahwa skema kompak orde tinggi dapat

(55)

commit to user

40 BAB V PENUTUP

5.1 Kesimpulan

Dari penelitian dan pembahasan yang telah dilakukan, dapat ditarik

beberapa kesimpulan yaitu :

a. Hasil penelitian pada domain kotak 2D pada sudut kemiringan 900

menunjukkan kedekatan nilai yang baik dengan hasil penelitian Querre pada

Ra = 106 dan Ra = 107. Pada sudut kemiringan 2700, 2550, 2400, dan 2100

menunjukan kedekatan nilai yang baik dengan hasil penelitian Lo. Prosentase

perbedaan kurang dari 5% secara keseluruhan.

b. Metode skema kompak orde-tinggi mampu memberikan hasil yang baik untuk

kasus konveksi alami pada kotak 2D dengan bilangan Rayleigh mencapai 107.

c. Konveksi alami pada kotak 2D dengan kemiringan telah dapat disimulasikan

dengan penyelesaian persamaan Navier Stokes menggunakan metode skema

kompak orde-tinggi , dimana ditunjukan dengan gambar pola streamlines, dan

distribusi temperatur.

d. Pada kotak 2D dengan pemanasan dari bawah ( sudut kemiringan 00) terjadi

konveksi alami dengan pola aliran fluida membentuk benard sell.

e. Arah pergerakan fluida pada kotak 2D yang dimiringkan mengikuti arah

bouyancy forcé, dimana pada sisi panas bergerak keatas, dan pada sisi dingin bergerak kebawah.

f. Pada kotak 2D dengan pemanasan dari atas ( sudut kemiringan 1800) tidak

terjadi perpindahan panas konveksi, melainkan perpindahan panas secara

konduksi.

g. program yang telah dibuat telah mampu mencapai persamaan kontinuitas

(56)

commit to user

41

5.2 Saran

Untuk lebih mengembangkan ilmu pengetahuan dibidang simulasi numerik,

penulis memberikan saran :

a. Dilakukan penelitian lebih lanjutmengenai konveksi alami pada bidang 3D

b. Melakukan pengembangan dengan metode yang dapat menghasilkan