1
Abstrak — Terdapat beberapa penyakit yang memiliki
masa inkubasi, semisal penyakit meales (cacar). Dalam model epidemik masa inkubasi biasa disebut periode la-ten (exposed). Model SEIR merupakan model matematika untuk penyakit-penyakit tersebut. Pada penulisan ini dianalisa kestabilan dari model SEIR. Akan ditunjukkan bahwa kestabilan titik ekuilibrium tergantung pada rasio reproduksi dasar (𝑹𝑹𝟎𝟎). Tidak terjadi endemik jika 𝑹𝑹𝟎𝟎< 1 dan terjadi endemik jika 𝑹𝑹𝟎𝟎> 1. Selanjutnya dilakukan penyelesaian numerik untuk model SEIR menggunakan metode Runge-Kutta Orde 4. Metode ini digunakan un-tuk menyelesaikan persamaan diferensial yang menyang-kut nilai awal dengan ukuran langkah waktu yang berva-riasi, sehingga dapat memenuhi stabilitas lokal dari titik kesetimbangan.
Katakunci — Bilangan Reproduksi Dasar, Model
SEIR, Metode Runge-Kutta Orde 4. I. PENDAHULUAN
ODEL matematika adalah salah satu alat yang dapat membantu dalam menyelesaikan masalah dalam kehidupan nyata. Masalah-masalah tersebut dapat dibawa ke dalam model matematis dengan menggunakan asumsi-asumsi tertentu. Selanjutnya akan dicari solusinya baik secara analitis maupun numerik. Salah satu masalah dalam kehidupan adalah mengenai penyebaran penyakit. Dalam dunia kesehatan terdapat penyakit yang bersifat menular (in-fectious diseases) dan tidak menular (non in(in-fectious diseas-es). Pada sebagian kasus, terdapat penyakit yang dapat memasuki kondisi endemik. yaitu kondisi dimana mewabahnya suatu penyakit pada suatu wilayah dalam kurun waktu yang lama. Beberapa penyakit yang mengalami kondisi endemik adalah malaria, measles (cacar) dan poliomyelitis (polio).
Model epidemik mempelajari tentang dinamika penyeba-ran atau penulapenyeba-ran suatu penyakit pada suatu populasi [1]. Model epidemik pertama kali bertipe SIR yang dikemukaa-kan oleh Kermack dan McKendrick (1927) [2]. Pada per-kembangannya model ini terus dimodifikasi dengan asumsi yang berbeda-beda agar bisa menjelaskan berbagai fenomena penyakit yang makin kompleks [1].
Beberapa penyakit seperti measles (campak), malaria, pertusis dan HIV memiliki masa inkubasi, yaitu masa dimana virus sudah masuk pada tubuh manusia namun tubuh tersebut belum menunjukkan adanya infeksi suatu penyakit. Dalam model epidemik masa inkubasi biasa disebut periode laten (exposed). Li dkk (1994) mengkontruksi model epidemic SEIR yang terdiri dari empat kompartemen dengan mempertimbangkan adaya penularan pada periode laten. Selanjutnya Li dkk (1999) mengasumsikan bahwa besar laju rekrutmen dan kematian alami tidak sama. [3]
Prihandoko.B (2009) dalam penelitiannya, Analisis kualitatif dan bifurkasi pada model epidemik tipe SEIR dengan transmisi vertikal. Mengkaji tentang penyebaran penyakit bertipe SEIR dengan transmisi vertikal. Dimana penyakit menyebar melalui transfer transpacental (bersifat turun-menurun) [4]. Dalam tugas akhir ini akan dibahas permodelan SEIR transmisi horizontal, dengan mem-pertimbangkan adanya penularan pada periode laten.
II. METODE PENELITIAN A. Tahap Studi Literatur
Pada tahap ini dilakukan identifikasi permasalahan dengan mencari referensi yang menunjang penelitian semisal jurnal ilmiah, buku-buku Tugas Akhir maupun artikel dari internet.
B. Tahap Mengkaji Model SEIR dengan memperhatikan penularan pada periode laten
Dilakukan kajian model SEIR dengan menyusun asumsi-asumsi tertentu sehingga dapat dibuat model kompartemen dengan 4 kelompok individu, yaitu individu susceptible (individu yang rentan terhadap penyakit), exposed (individu-individu yang tertular penyakit tetapi belum menunjukkan tanda-tanda mengidap penyakit), infected (individu yang terjangkit dan dapat menularkan penyakit), dan recovered (individu yang telah sembuh dari penyakit).
C. Tahap Menganalisa Kestabilan Lokal
Pada model dinamik SEIR akan ditentukan titik kesetimbangan bebas penyakit dan titik kesetimbangan endemik. dari titik setimbang bebas penyakit didapatkan Labibah Rochmatika,Drs. M. Setijo Winarko, M.Si dan Drs. Lukman Hanafi, M.Sc
Jurusan Matematika, Fakultas MIPA, Institut Teknologi Sepuluh Nopember (ITS) Jl. Arief Rahman Hakim, Surabaya 60111
Email: setijo_winarko@yahoo.com
Penyelesaian Numerik dan Analisa Kestabilan
pada Model Epidemik SEIR
dengan Memperhatikan Adanya Penularan
pada Periode Laten
2 bilangan reproduksi dasar (𝑅𝑅0). Kemudian untuk menentukan kestabilan lokal dengan membentuk matriks Jacobian pada titik kesetimbangan bebas penyakit dan titik kesetimbangan endemik yang selanjutnya dapat ditentukan nilai eigen matrik Jacobiannya.
D. Tahap Menyusun Simulasi Numerik Runge-Kutta Orde 4 Pada tahap ini dilakukan penyusunan simulasi numerik skema Runge-Kutta Orde 4 dari model dinamik SEIR. Simulasi menggunakan software pemrograman yaitu MATLAB yang menggambarkan grafik kestabilan dan penyelesaian numerik model dinamik SEIR.
E. Tahap Kesimpulan dan Saran
Setelah dilakukan analisa dan pembahasan maka akan diambil suatu kesimpulan dan saran sebagai masukan untuk pengembangan penelitian lebih lanjut.
III. ANALISIS DAN PEMBAHASAN A. Model Epidemik SEIR
Model epidemik tipe SEIR mempunyai asumsi-asumsi sebagai berikut :
a. Populasi dibagi menjadi 4 kelompok yaitu :
𝑆𝑆 adalah populasi susceptible yaitu individu-individu yang rentan terhadap penyakit pada saat 𝑡𝑡.
𝐸𝐸 adalah populasi exposed yaitu individu-individu yang tertular penyakit tetapi belum menunjukkan tanda-tanda mengidap penyakit pada saat 𝑡𝑡.
𝐼𝐼 adalah populasi infected yaitu individu-individu pengidap penyakit menularkan penyakit pada saat 𝑡𝑡.
𝑅𝑅 adalah populasi individu recovered yaitu individu yang telah sembuh/ bebas penyakit pada saat 𝑡𝑡.
b. 𝛼𝛼10 adalah laju kematian yang disebabkan penyakit pada klas laten, sedangkan 𝛼𝛼20 adalah laju kematian yang disebabkan penyakit pada klas terinfeksi.
c. 𝛽𝛽10 adalah laju kontak klas laten, 𝛽𝛽20 adalah laju kontak pada klas terinfeksi, dan 𝛽𝛽30 adalah laju kontak pada klas sembuh,
d. 𝑘𝑘0 adalah laju kesembuhan, 𝛾𝛾0 adalah laju antara terekspose dan terinfeksi.
Dari asumsi-asumsi tersebut diperoleh model epidemik tipe SEIR sebagai berikut:
𝑑𝑑𝑆𝑆 𝑑𝑑𝑡𝑡 = 𝐴𝐴 − 𝛽𝛽10𝑆𝑆𝐸𝐸 − 𝛽𝛽20𝑆𝑆𝐼𝐼 − 𝛽𝛽30𝑆𝑆𝑅𝑅 − 𝜇𝜇𝑆𝑆 𝑑𝑑𝐸𝐸 𝑑𝑑𝑡𝑡 = 𝛽𝛽10𝑆𝑆𝐸𝐸 + 𝛽𝛽20𝑆𝑆𝐼𝐼 + 𝛽𝛽30𝑆𝑆𝑅𝑅 − 𝛾𝛾0𝐸𝐸 − (𝜇𝜇 + 𝛼𝛼10)𝐸𝐸 𝑑𝑑𝐼𝐼 𝑑𝑑𝑡𝑡 = 𝛾𝛾0𝐸𝐸 − 𝑘𝑘0𝐼𝐼 − (𝜇𝜇 + 𝛼𝛼20)𝐼𝐼 𝑑𝑑𝑅𝑅 𝑑𝑑𝑡𝑡 = 𝑘𝑘0𝐼𝐼 − 𝜇𝜇𝑅𝑅 B. Domain Penyelesaian
Dalam melakukan perhitungan, nilai input yang dimasukkan harus memenuhi keterbatasan penyelesaian, hal
ini dilakukan untuk memudahkan pada saat simulasi. Kriteria kestabilan dari sistem persamaan diferensial tergantung pada perilaku sistem. Jika 𝑁𝑁 adalah proporsi jumlah populasi total maka, 𝑁𝑁 = 𝑆𝑆 + 𝐸𝐸 + 𝐼𝐼 + 𝑅𝑅, sehingga 𝑑𝑑𝑁𝑁 𝑑𝑑𝑡𝑡 = 𝑑𝑑𝑆𝑆 𝑑𝑑𝑡𝑡+ 𝑑𝑑𝐸𝐸 𝑑𝑑𝑡𝑡+ 𝑑𝑑𝐼𝐼 𝑑𝑑𝑡𝑡+ 𝑑𝑑𝑅𝑅 𝑑𝑑𝑡𝑡 = 𝐴𝐴 − 𝜇𝜇(𝑆𝑆 + 𝐸𝐸 + 𝐼𝐼 + 𝑅𝑅) − 𝛼𝛼10𝐸𝐸 − 𝛼𝛼20𝐼𝐼 = 𝐴𝐴 − 𝜇𝜇𝑁𝑁 − 𝛼𝛼10𝐸𝐸 − 𝛼𝛼20𝐼𝐼 dimisalkan 𝜇𝜇 𝑑𝑑𝑡𝑡 = 𝑑𝑑𝑑𝑑; 𝛼𝛼1=𝛼𝛼10 𝜇𝜇 dan 𝛼𝛼2= 𝛼𝛼20 𝜇𝜇 maka persamaan diatas menjadi:
𝑑𝑑𝑁𝑁 𝑑𝑑𝑑𝑑 =
𝐴𝐴
𝜇𝜇− 𝑁𝑁 − 𝛼𝛼1𝐸𝐸 − 𝛼𝛼2𝐼𝐼 (1.1) persamaan (1.1) dapat diselesaikan dengan menggunakan pemisahan variabel. Asumsikan individu pada klas laten dan terinfeksi sama dengan nol. Maka persamaan (1.1) menjadi:
𝑑𝑑𝑁𝑁 𝑑𝑑𝑑𝑑 =
𝐴𝐴 𝜇𝜇− 𝑁𝑁
dengan menggunakan metode pemisahan variabel didapatkan persamaan sebagai berikut:
𝑁𝑁(𝑑𝑑) = −1𝜇𝜇�1𝐶𝐶𝑒𝑒−𝑑𝑑− 𝐴𝐴�
lim𝑑𝑑→∞𝑁𝑁(𝑑𝑑) = lim𝑑𝑑→∞−1𝜇𝜇�1𝐶𝐶𝑒𝑒−𝑑𝑑− 𝐴𝐴�
= 𝐴𝐴
𝜇𝜇
Hal ini menunjukkan bahwa jumlah populasi tidak konstan, tetapi memiliki batas atas yaitu 𝐴𝐴
𝜇𝜇. Dari daerah penyelesaian diatas, didapatkan daerah keterbatasan penyelesaian dari sistem yaitu,
Ω = �(𝐸𝐸, 𝐼𝐼, 𝑅𝑅, 𝑁𝑁)|0 ≤ 𝐸𝐸 + 𝐼𝐼 + 𝑅𝑅 ≤ 𝑁𝑁 ≤𝐴𝐴𝜇𝜇� C. Titik Kesetimbangan Bebas Penyakit
Titik setimbang bebas penyakit merupakan suatu titik setimbang dimana jumlah populasi yang terjangkit penyakit bernilai nol. Hal ini berarti tidak terjadi penyebaran pada populasi atau 𝐼𝐼 = 0. Titik kesetimbangan model dapat diperoleh dengan menjadikan ruas kanan dari system model epidemic SEIR sama dengan nol. Sebelumnya dimisalkan terlebih dahulu 𝑑𝑑𝑡𝑡 = 𝑑𝑑𝑑𝑑; 𝛽𝛽1=𝛽𝛽𝜇𝜇10; 𝛽𝛽2 =𝛽𝛽𝜇𝜇20; 𝛽𝛽3=𝛽𝛽𝜇𝜇30; 𝑘𝑘 =𝑘𝑘𝜇𝜇0; 𝛾𝛾 =𝛾𝛾𝜇𝜇0; 𝛼𝛼1=𝛼𝛼𝜇𝜇10 dan 𝛼𝛼2=𝛼𝛼𝜇𝜇20 Sehingga didapat: 𝐴𝐴 𝜇𝜇− 𝛽𝛽1𝑆𝑆𝐸𝐸 − 𝛽𝛽2𝑆𝑆𝐼𝐼 − 𝛽𝛽3𝑆𝑆𝑅𝑅 − 𝑆𝑆 = 0 (1.2) 𝛽𝛽1𝑆𝑆𝐸𝐸 + 𝛽𝛽2𝑆𝑆𝐼𝐼 + 𝛽𝛽3𝑆𝑆𝑅𝑅 − 𝛿𝛿𝐸𝐸 = 0 (1.3) 𝛾𝛾𝐸𝐸 − 𝜔𝜔𝐼𝐼 = 0 (1.4) 𝑘𝑘𝐼𝐼 − 𝑅𝑅 = 0 (1.5) pada saat 𝐼𝐼 = 0. Maka dari persamaan (1.4) didapatkan 𝐸𝐸 = 0, dan dari persamaan (1.5) didapatkan 𝑅𝑅 = 0, hal ini menyebabkan nilai 𝑆𝑆 =𝐴𝐴
𝜇𝜇 pada persamaan (1.2). Jadi diperoleh titik ekuilibrium bebas penyakit 𝐸𝐸0= �𝐴𝐴
3 D. Titik Kesetimbangan Endemik
Titik setimbang endemik merupakan suatu titik setimbang yang menunjukkan masih adanya kemungkinan penyebaran penyakit pada populasi. Syarat untuk mendapatkan titik setimbang endemik berbeda dari sebelumnya. jumlah populasi yang terjangkit penyakit tidak bernilai nol.
Dari persamaan (1.4) dapat dituliskan 𝐼𝐼 =𝛾𝛾𝐸𝐸
𝜔𝜔, selanjutnya nilai 𝐼𝐼 disubtitusikan ke persamaan (1.1) sehingga didapatkan:
𝐸𝐸∗=𝜔𝜔 𝜇𝜇�
𝐴𝐴−𝜇𝜇𝑁𝑁
𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾� (1.6) Dari persamaan (1.4) dapat dituliskan 𝐼𝐼 =𝜔𝜔𝐼𝐼
𝛾𝛾, selanjutnya nilai 𝐸𝐸 disubtitusikan ke persamaan (1.1) sehingga diperoleh persamaan sebagai berikut:
𝐼𝐼∗=𝛾𝛾 𝜇𝜇�
𝐴𝐴−𝜇𝜇𝑁𝑁
𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾� (1.7) Subtitusikan nilai 𝐼𝐼∗ pada persamaan (1.5) didapatkan: 𝑅𝑅∗= 𝑘𝑘𝛾𝛾
𝜇𝜇� 𝐴𝐴−𝜇𝜇𝑁𝑁
𝛼𝛼1𝜔𝜔+ 𝛼𝛼2𝛾𝛾� (1.8) Persamaan (1.2) dapat disederhanakan menjadi
𝐴𝐴
𝜇𝜇− 𝑆𝑆(𝛽𝛽1𝐸𝐸 + 𝛽𝛽2𝐼𝐼 + 𝛽𝛽3𝑅𝑅 + 1) = 0 ⇔ 𝑆𝑆 =𝜇𝜇 (𝛽𝛽 𝐴𝐴
1𝐸𝐸+𝛽𝛽2𝐼𝐼+𝛽𝛽3𝑅𝑅+1)
Subtitusikan nilai 𝐸𝐸∗, 𝐼𝐼∗, 𝑅𝑅∗ pada persamaan diatas, didapatkan:
𝑆𝑆∗ = 𝐴𝐴( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾)
𝐴𝐴−𝜇𝜇𝑁𝑁 (𝛽𝛽1𝜔𝜔+𝛽𝛽2𝛾𝛾+𝛽𝛽3𝑘𝑘𝛾𝛾)+𝜇𝜇( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) (1.9) Dari langkah-langkah diatas didapat titik setimbang endemik
𝐸𝐸1= (𝑆𝑆∗, 𝐸𝐸∗, 𝐼𝐼∗, 𝑅𝑅∗) Dengan 𝑆𝑆∗= 𝐴𝐴( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) 𝐴𝐴−𝜇𝜇𝑁𝑁 (𝛽𝛽1𝜔𝜔+𝛽𝛽2𝛾𝛾+𝛽𝛽3𝑘𝑘𝛾𝛾)+𝜇𝜇 ( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) 𝐸𝐸∗=𝜔𝜔 𝜇𝜇� 𝐴𝐴−𝜇𝜇𝑁𝑁 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾� 𝐼𝐼∗=𝛾𝛾 𝜇𝜇� 𝐴𝐴−𝜇𝜇𝑁𝑁 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾� 𝑅𝑅∗= 𝑘𝑘𝛾𝛾 𝜇𝜇� 𝐴𝐴−𝜇𝜇𝑁𝑁 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾� F. Bilangan Reproduksi
Bilangan reproduksi dasar (basic reproduction number) merupakan parameter yang digunakan untuk mengetahui tingkat penyebaran suatu penyakit. Bilangan
reproduksi dasar 𝑅𝑅0 dari model dapat dicari dengan langkah-langkah sebagai berikut,
Subtitusikan nilai 𝑆𝑆∗, 𝐸𝐸∗, 𝐼𝐼∗ dan 𝑅𝑅∗ pada persamaan (1.3) menjadi: 𝐴𝐴( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) 𝜇𝜇 �(𝐴𝐴−𝜇𝜇𝑁𝑁 )(𝛽𝛽1𝜔𝜔+𝛽𝛽2𝛾𝛾+𝛽𝛽3𝑘𝑘𝛾𝛾)+𝜇𝜇( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾)�� 𝐴𝐴−𝜇𝜇𝑁𝑁 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾� × (𝛽𝛽1𝜔𝜔 + 𝛽𝛽2𝛾𝛾 + 𝛽𝛽3𝑘𝑘𝛾𝛾) − 𝛿𝛿𝜔𝜔𝜇𝜇� 𝛼𝛼1𝐴𝐴−𝜇𝜇𝑁𝑁𝜔𝜔 + 𝛼𝛼2𝛾𝛾� = 0 ⇔ (𝐴𝐴 − 𝜇𝜇𝑁𝑁)��𝛿𝛿𝜔𝜔𝜇𝜇𝑁𝑁 − 𝐴𝐴(𝛿𝛿𝜔𝜔 − 𝛼𝛼1𝜔𝜔− 𝛼𝛼2𝛾𝛾)�(𝛽𝛽1𝜔𝜔 + 𝛽𝛽2𝛾𝛾 + 𝛽𝛽3𝑘𝑘𝛾𝛾) − 𝛿𝛿𝜔𝜔𝜇𝜇( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾)� = 0 (1.10) Persamaa n (4.10) dapat dituliskan secara sederhana menjadi
𝐹𝐹(𝑁𝑁)(𝐴𝐴 − 𝜇𝜇𝑁𝑁) = 0 Dengan
𝐹𝐹(𝑁𝑁) = �𝛿𝛿𝜔𝜔𝜇𝜇𝑁𝑁 − 𝐴𝐴(𝛿𝛿𝜔𝜔 − 𝛼𝛼1𝜔𝜔− 𝛼𝛼2𝛾𝛾)�(𝛽𝛽1𝜔𝜔 + 𝛽𝛽2𝛾𝛾 + 𝛽𝛽3𝑘𝑘𝛾𝛾) − 𝛿𝛿𝜔𝜔𝜇𝜇( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾)
System berada pada titik kesetimbangan bebas penyakit 𝑃𝑃0= �𝐴𝐴𝜇𝜇, 0,0,0� pada interval �𝐴𝐴𝜇𝜇, 0� 𝐹𝐹 �𝐴𝐴𝜇𝜇� = �𝛿𝛿𝜔𝜔𝜇𝜇𝐴𝐴𝜇𝜇− 𝐴𝐴(𝛿𝛿𝜔𝜔 − 𝛼𝛼1𝜔𝜔− 𝛼𝛼2𝛾𝛾)� (𝛽𝛽1𝜔𝜔 + 𝛽𝛽2𝛾𝛾 + 𝛽𝛽3𝑘𝑘𝛾𝛾) − 𝛿𝛿𝜔𝜔𝜇𝜇( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) = �𝐴𝐴𝛿𝛿𝜔𝜔 − 𝐴𝐴(𝛿𝛿𝜔𝜔 − 𝛼𝛼1𝜔𝜔− 𝛼𝛼2𝛾𝛾)�(𝛽𝛽1𝜔𝜔 + 𝛽𝛽2𝛾𝛾 + 𝛽𝛽3𝑘𝑘𝛾𝛾) − 𝛿𝛿𝜔𝜔𝜇𝜇( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) = 𝐴𝐴( 𝛼𝛼1𝜔𝜔+𝛼𝛼2𝛾𝛾)(𝛽𝛽1𝜔𝜔 + 𝛽𝛽2𝛾𝛾 + 𝛽𝛽3𝑘𝑘𝛾𝛾) − 𝛿𝛿𝜔𝜔𝜇𝜇( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) = 𝛿𝛿𝜔𝜔𝜇𝜇( 𝛼𝛼1𝜔𝜔+𝛼𝛼2𝛾𝛾) �𝐴𝐴(𝛽𝛽1𝜔𝜔 +𝛽𝛽𝛿𝛿𝜔𝜔 𝜇𝜇2𝛾𝛾 +𝛽𝛽3𝑘𝑘𝛾𝛾)− 1� = 𝛿𝛿𝜔𝜔𝜇𝜇( 𝛼𝛼1𝜔𝜔+𝛼𝛼2𝛾𝛾)[𝑅𝑅0− 1]
Sehingga didapatkan nilai 𝑅𝑅0=𝐴𝐴(𝛽𝛽1𝜔𝜔 +𝛽𝛽𝛿𝛿𝜔𝜔 𝜇𝜇2𝛾𝛾 +𝛽𝛽3𝑘𝑘𝛾𝛾)
G. Kestabilan Lokal Titik Kesetimbangan Bebas Penyakit Kestabilan model ditentukan oleh nilai eigen matriks Jacobian dari persamaan (1.2) sampai (1.5) pada titik kesetimbangan bebas penyakit 𝐸𝐸0= �𝐴𝐴
𝜇𝜇, 0,0,0� Misal: 𝑓𝑓(𝑆𝑆, 𝐸𝐸, 𝐼𝐼, 𝑅𝑅) =𝑑𝑑𝑆𝑆𝑑𝑑𝑑𝑑 = 𝐴𝐴𝜇𝜇− 𝛽𝛽1𝑆𝑆𝐸𝐸 − 𝛽𝛽2𝑆𝑆𝐼𝐼 − 𝛽𝛽3𝑆𝑆𝑅𝑅 − 𝑆𝑆 𝑔𝑔(𝑆𝑆, 𝐸𝐸, 𝐼𝐼, 𝑅𝑅) =𝑑𝑑𝐸𝐸𝑑𝑑𝑑𝑑 = 𝛽𝛽1𝑆𝑆𝐸𝐸 + 𝛽𝛽2𝑆𝑆𝐼𝐼 + 𝛽𝛽3𝑆𝑆𝑅𝑅 − 𝛿𝛿𝐸𝐸 ℎ(𝑆𝑆, 𝐸𝐸, 𝐼𝐼, 𝑅𝑅) =𝑑𝑑𝑑𝑑𝑑𝑑𝐼𝐼 = 𝛾𝛾𝐸𝐸 − 𝜔𝜔𝐼𝐼 𝑖𝑖(𝑆𝑆, 𝐸𝐸, 𝐼𝐼, 𝑅𝑅) =𝑑𝑑𝑅𝑅𝑑𝑑𝑑𝑑 = 𝑘𝑘𝐼𝐼 − 𝑅𝑅
Sehingga didapat matriks Jacobian pada titik kesetimbangan bebas penyakit adalah :
4 𝐽𝐽 = ⎝ ⎜ ⎜ ⎛−1 −𝛽𝛽1 𝐴𝐴 𝜇𝜇 −𝛽𝛽2𝐴𝐴𝜇𝜇 −𝛽𝛽3𝐴𝐴𝜇𝜇 0 𝛽𝛽1𝐴𝐴𝜇𝜇 − 𝛿𝛿 𝛽𝛽2𝐴𝐴𝜇𝜇 𝛽𝛽3𝐴𝐴𝜇𝜇 0 0 𝛾𝛾0 −𝜔𝜔𝑘𝑘 0−1 ⎠ ⎟ ⎟ ⎞
Nilai eigen diperoleh dari
|𝐽𝐽 − 𝜆𝜆𝐼𝐼| = 0 maka � �−1 − 𝜆𝜆 −𝛽𝛽1 𝐴𝐴 𝜇𝜇 −𝛽𝛽2 𝐴𝐴 𝜇𝜇 −𝛽𝛽3 𝐴𝐴 𝜇𝜇 0 𝛽𝛽1𝐴𝐴𝜇𝜇 − 𝛿𝛿 − 𝜆𝜆 𝛽𝛽2𝐴𝐴𝜇𝜇 𝛽𝛽3𝐴𝐴𝜇𝜇 0 0 𝛾𝛾0 −𝜔𝜔 − 𝜆𝜆𝑘𝑘 −1 − 𝜆𝜆 0 � � = 0
didapatkan persamaan sebagai berikut: (1 + 𝜆𝜆) �𝜆𝜆3− �𝛽𝛽
1𝐴𝐴𝜇𝜇− 𝛿𝛿 − 𝜔𝜔 − 1� 𝜆𝜆2− ��𝛽𝛽1𝐴𝐴𝜇𝜇− 𝛿𝛿� (1 + 𝜔𝜔) − 𝜔𝜔 + 𝛽𝛽2𝐴𝐴𝜇𝜇𝛾𝛾� 𝜆𝜆 − 𝛾𝛾𝐴𝐴𝜇𝜇( 𝛽𝛽3𝑘𝑘 + 𝛽𝛽2) − �𝛽𝛽1𝐴𝐴𝜇𝜇− 𝛿𝛿� 𝜔𝜔� = 0 (1.11) Salah satu nilai eigen dari persamaan (1.11) adalah -1, nilai eigen yang lain merupakan akar-akar polynomial berikut:
𝜆𝜆3+ 𝐴𝐴𝜆𝜆2+ 𝐵𝐵𝜆𝜆 + 𝐶𝐶 = 0 (1.12)
dengan
𝐴𝐴 = −𝛽𝛽1𝐴𝐴𝜇𝜇+ 𝛿𝛿 + 𝜔𝜔 + 1 > 0
𝐵𝐵 =𝜔𝜔 −�𝛽𝛽1𝐴𝐴𝜇𝜇− 𝛿𝛿� (1 + 𝜔𝜔)− 𝛽𝛽2𝐴𝐴𝜇𝜇𝛾𝛾 > 0 𝐶𝐶 =−𝛾𝛾𝐴𝐴𝜇𝜇� 𝛽𝛽3𝑘𝑘 + 𝛽𝛽2�−�𝛽𝛽1𝐴𝐴𝜇𝜇− 𝛿𝛿�𝜔𝜔 > 0
Untuk mencari nilai eigen yang lain dapat digunakan metode Routh Huwitz. Dengan menentukan tanda pada bagian real dari nilai eigen dapat diketahui kestabilan system. Berikut tabel Routh huwiz
Tabel 1
Persamaan Karakteristik Routh-Hurwitz 𝑎𝑎0= 1 𝑎𝑎2= 𝐵𝐵 𝑎𝑎1= 𝐴𝐴 𝑎𝑎3= 𝐶𝐶 𝑏𝑏1=𝑎𝑎1𝑎𝑎2𝑎𝑎− 𝑎𝑎0𝑎𝑎3
1
Didapatkan 𝑎𝑎1𝑎𝑎2> 𝑎𝑎0𝑎𝑎3, karena elemen pada kolom pertama table Routh Huwitz memiliki tanda yang sama yaitu positif maka system titik kesetimbangan bebas penyakit 𝐸𝐸0= �𝐴𝐴𝜇𝜇, 0,0,0� stabil asimtotik lokal.
H. Kestabilan Lokal Titik Kesetimbangan Endemik
Pada titik kesetimbangan endemic 𝐸𝐸1(𝑆𝑆∗, 𝐸𝐸∗, 𝐼𝐼∗, 𝑅𝑅∗)atau dapat pula diganti dengan 𝐸𝐸1(𝐸𝐸∗, 𝐼𝐼∗, 𝑅𝑅∗, 𝑁𝑁∗)matriks Jacobiannya adalah 𝐽𝐽∗= � 𝑚𝑚𝛽𝛽1− 𝑛𝑛 − 𝛿𝛿 𝛾𝛾 0 − 𝛼𝛼1 𝑚𝑚𝛽𝛽2− 𝑛𝑛 −𝜔𝜔 𝑘𝑘 − 𝛼𝛼2 𝑚𝑚𝛽𝛽3− 𝑛𝑛 0 −1 0 𝑛𝑛 0 0 −1 � (1.13)
Nilai eigen diperoleh dari
|𝐽𝐽 − 𝜆𝜆𝐼𝐼| = 0
dengan misalkan 𝑛𝑛 = (𝛽𝛽1𝐸𝐸 + 𝛽𝛽2𝐼𝐼 + 𝛽𝛽3𝑅𝑅) dan 𝑚𝑚 = 𝛿𝛿𝜔𝜔
𝜔𝜔 𝛽𝛽1+𝛾𝛾𝛽𝛽2+𝑘𝑘𝛾𝛾𝛽𝛽3 Sehingga didapat persaman sebagai berikut: (1 + 𝜆𝜆)�𝜆𝜆3+ �(1 + 𝜔𝜔) + (𝑛𝑛 + 𝛿𝛿 − 𝑚𝑚𝛽𝛽
1)�𝜆𝜆2+ �𝛾𝛾(𝑛𝑛 − 𝑚𝑚𝛽𝛽2) + 𝛼𝛼1𝑛𝑛 + 𝜔𝜔 + (𝑛𝑛 + 𝛿𝛿 − 𝑚𝑚𝛽𝛽1)(1 + 𝜔𝜔)�𝜆𝜆 + 𝜔𝜔 (𝑛𝑛 + 𝛿𝛿 − 𝑚𝑚𝛽𝛽1) +
𝛾𝛾(𝑛𝑛 − 𝑚𝑚𝛽𝛽2) + 𝛾𝛾𝑘𝑘(𝑛𝑛 − 𝑚𝑚𝛽𝛽3) + 𝑛𝑛(𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾)� = 0 (1.14)
Salah satu nilai eigen dari persamaan (1.14) adalah -1, nilai eigen yang lain merupakan akar-akar polynomial berikut: 𝜆𝜆3+ 𝐷𝐷𝜆𝜆2+ 𝐸𝐸𝜆𝜆 + 𝐹𝐹 = 0 (1.15) dengan 𝐷𝐷 = (1 + 𝜔𝜔)+�𝑛𝑛 + 𝛿𝛿 − 𝑚𝑚𝛽𝛽1�> 0 𝐸𝐸 = 𝛾𝛾(𝑛𝑛 − 𝑚𝑚𝛽𝛽2) + 𝛼𝛼1𝑛𝑛 + �𝜔𝜔 − (𝑚𝑚𝛽𝛽1− 𝑛𝑛 − 𝛿𝛿) × (1 + 𝜔𝜔)� > 0 𝐹𝐹 = 𝜔𝜔 (𝑛𝑛 + 𝛿𝛿 − 𝑚𝑚𝛽𝛽1) + 𝛾𝛾(𝑛𝑛 − 𝑚𝑚𝛽𝛽2) + 𝛾𝛾𝑘𝑘(𝑛𝑛 − 𝑚𝑚𝛽𝛽3) + 𝑛𝑛(𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) > 0
Untuk mencari nilai eigen yang lain dapat digunakan metode Routh Huwitz sebagaimana pada matriks jacobian titik kesetimbangan bebas penyakit.
Karena elemen pada kolom pertama table Routh Huwitz memiliki tanda yang sama yaitu positif maka system titik kesetimbangan endemic 𝐸𝐸1(𝐸𝐸∗, 𝐼𝐼∗, 𝑅𝑅∗, 𝑁𝑁∗) stabil asimtotik lokal.
I. Penyelesaian Numerik
Penyelesaian numerik yang didapatkan digunakan untuk memeriksa hasil analitis yang telah didapatkan pada sub bab sebelumnya. Metode Runge-Kutta orde empat adalah salah satu metode numerik yang dapat digunakan untuk menyelesaikan persamaan diferensial yang menyangkut nilai awal dengan ukuran langkah waktu ℓ yang bervariasi. dengan membuat simulasi numeriknya menggunakan software MATLAB dengan memberikan nilai awal 𝑆𝑆(0) = 40, 𝐸𝐸(0) = 15, 𝐼𝐼(0) = 25 dan 𝑅𝑅(0) = 20. dengan parameter 𝐴𝐴 = 0.5, 𝜇𝜇 = 0.2, 𝛾𝛾 = 1.2, 𝑘𝑘 = 0.4, 𝛼𝛼1= 0.1, 𝛼𝛼2= 0.2, 𝛽𝛽1= 0.001, 𝛽𝛽2= 0.1, dan 𝛽𝛽3= 0.002 [3].
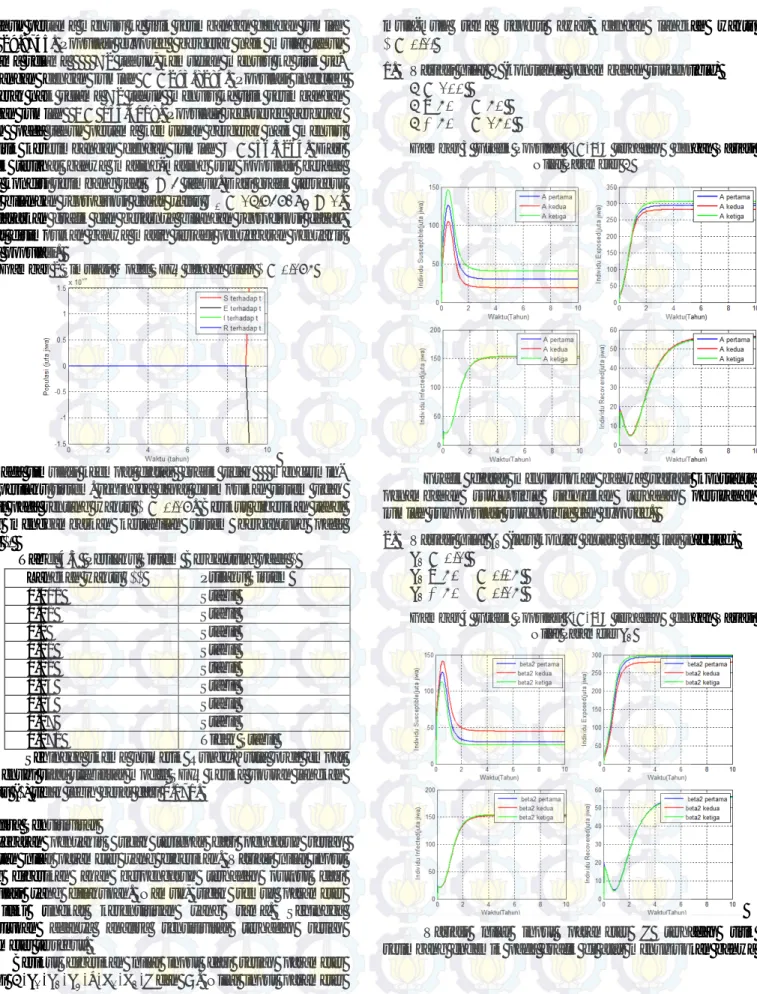
Gambar 1 Simulasi Model SEIR dengan nilai ℓ = 0.001
Pada gambar di atas menunjukkan bahwa populasi susceptible bergerak naik ±8 bulan, kemudian menurun
pa-5 da tahun pertama menuju ke titik setimbangan dengan jumlah 𝑆𝑆 = 29.8745. Populasi exposed bergerak naik mulai tahun pertama selama ±2 tahun, kemudian menuju ke titik se-timbangan dengan jumlah 𝐸𝐸 =293.8284. Populasi infected bergerak naik selama ±2 tahun menuju ke titik setimbangan dengan jumlah 𝐼𝐼 = 153.3018. Populasi recovered bergerak turun pada tahun pertama kemudian bergerak naik menuju ke titik kesetimbangan dengan jumlah 𝑅𝑅 = 56.3264. Dari grafik terlihat bahwa masing-masing sub populasi berada pada kondisi setimbang saat 𝑡𝑡 > 4 tahun. Dari grafik tersebut nilai bilangan reproduksi dasar yaitu 𝑅𝑅0= 16.747283 > 1. Berdasarkan grafik dan besarnya bilangan reproduksi dasar, dapat disimpulkan bahwa masih terjadi penyebaran penyakit pada populasi.
Gambar 2 Simulasi Model SEIR dengan nilai ℓ = 0.175
Pada simulasi keempat diatas grafik tidak mencermin-kan perilaku sistem. sehingga dapat disimpulmencermin-kan sistem tidak stabil pada rentang waktu ℓ = 0.17. Berikut diberikan tabel yang menggambarkan kestabilan sistem bergantung pada nilai ℓ.
Tabel 4.5 Perilaku Sistem Bergantung pada ℓ Langkah waktu (ℓ) Prilaku Sistem
0.001 Stabil 0.01 Stabil 0.1 Stabil 0.11 Stabil 0.12 Stabil 0.15 Stabil 0.16 Stabil 0.17 Stabil 0.171 Tidak Stabil
Sehingga skema numerik Runge-Kutta orde empat memenuhi sifat stabilitas model SEIR ketika ukuran langkah waktu (ℓ) tidak lebih besar dari 0.171.
Analisa Sensitivitas
Penyebaran penyakit tidak terlepas dari pengaruh setiap inputan nilai parameter yang diberikan. Variasi nilai input yang diberikan akan berpengaruh terhadap output dari simulasi yang dilakukan. Namun, tidak semua parameter memiliki tingkat kesensitivan yang sama. Sehingga diperlukan adanya analisa sensitivitas terhadap setiap parameter tersebut.
Berikut diberikan nilai input dari setiap parameter yakni 𝐴𝐴, 𝛽𝛽1, 𝛽𝛽2, 𝛽𝛽3, 𝜇𝜇, 𝛼𝛼1, 𝛼𝛼2, 𝛾𝛾 dan 𝐾𝐾. Nilai input parameter
mula-mula sama seperti awal, dengan langkah waktu ℓ = 0.1.
1. Variasi nilai 𝐴𝐴 (konstanta penambahan susceptible) 𝐴𝐴 = 100
𝐴𝐴 − 50% = 50 𝐴𝐴 + 50% = 150
Gambar 3 Grafik Populasi 𝑆𝑆, 𝐸𝐸, 𝐼𝐼, 𝑅𝑅 terhadap 𝑡𝑡 dengan Variasi
Nilai Parameter 𝐴𝐴
Grafik diatas menunjukkan bahwa variasi konstanta penambahan susceptible signifikan terhadap perubahan jumlah subpopulasi susceptible dan exposed.
2. Variasi nilai 𝛽𝛽2 (laju kontak antara pada klas infected) 𝛽𝛽2= 0.1
𝛽𝛽2− 50% = 0.05 𝛽𝛽2+ 50% = 0.15
Gambar 4 Grafik Populasi 𝑆𝑆, 𝐸𝐸, 𝐼𝐼, 𝑅𝑅 terhadap 𝑡𝑡 dengan Variasi
Nilai Parameter 𝛽𝛽2
Variasi nilai input parameter 𝛾𝛾 terhadap titik setimbang endemik pada grafik di atas menunjukkan bahwa
6 variasi laju antara terexposed dan infected hanya signifikan terhadap perubahan subpopulasi infected.
3. Variasi nilai 𝐾𝐾 (laju kesembuhan) 𝐾𝐾 = 0.4
𝐾𝐾 − 50% = 0.2 𝐾𝐾 + 50% = 0.6
Gambar 5 Grafik Populasi 𝑆𝑆, 𝐸𝐸, 𝐼𝐼, 𝑅𝑅 terhadap 𝑡𝑡 dengan Variasi
Nilai Parameter 𝐾𝐾
Variasi nilai input parameter 𝐾𝐾 terhadap titik setimbang endemik pada grafik populasi terhadap waktu menunjukkan bahwa variasi laju kesembuhan hanya signifikan terhadap perubahan subpopulasi recovery.
Sesuai dengan analisa sensitivitas yang telah dilakukan, didapatkan beberapa parameter yang sensitif terhadap arah penyebaran penyakit yaitu 𝐴𝐴, 𝜇𝜇, 𝛽𝛽2, 𝛾𝛾 dan 𝐾𝐾.
IV. KESIMPULAN
Berdasarkan hasil analisa yang telah dilakukan, dapat diperoleh kesimpulan sebagai berikut :
1. Bilangan reproduksi dasar dari model SEIR dengan memperhatikan penularan pada peiode laten adalah 𝑅𝑅0=𝐴𝐴(𝛽𝛽1𝜔𝜔 +𝛽𝛽𝛿𝛿𝜔𝜔 𝜇𝜇2𝛾𝛾 +𝛽𝛽3𝑘𝑘𝛾𝛾) Titik setimbang bebas penyakit stabil asimtotik jika 𝑅𝑅0< 1, ini menunjukkan bahwa tidak terjadi penularan penyakit. Sedangkan titik kesetimbangan endemik adalah stabil asimtotik jika 𝑅𝑅0> 1, sehingga menunjukkan bahwa terjadi penularan penyakit ketika 𝑅𝑅0 lebih dari 1.
2. Didapatkan titik setimbang dari model epidemic SEIR yaitu
a. titik setimbang bebas penyakit 𝐸𝐸0�0,0,0,𝐴𝐴 𝜇𝜇� b. titik setimbang endemik 𝐸𝐸1(𝑆𝑆∗, 𝐸𝐸∗, 𝐼𝐼∗, 𝑅𝑅∗)
dengan 𝑆𝑆∗= 𝐴𝐴( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) 𝐴𝐴−𝜇𝜇𝑁𝑁(𝛽𝛽1𝜔𝜔+𝛽𝛽2𝛾𝛾+𝛽𝛽3𝑘𝑘𝛾𝛾 )+𝜇𝜇( 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾) 𝐸𝐸∗=𝜔𝜔 𝜇𝜇� 𝐴𝐴−𝜇𝜇𝑁𝑁 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾� 𝐼𝐼∗=𝛾𝛾 𝜇𝜇� 𝐴𝐴−𝜇𝜇𝑁𝑁 𝛼𝛼1𝜔𝜔 + 𝛼𝛼2𝛾𝛾� 𝑅𝑅∗= 𝑘𝑘𝛾𝛾 𝜇𝜇� 𝐴𝐴−𝜇𝜇𝑁𝑁 𝛼𝛼1𝜔𝜔+ 𝛼𝛼2𝛾𝛾�
3. Hasil penyelesaian numerik model SEIR dengan metode Runge-Kutta orde empat memenuhi sifat stabilitas model SEIR ketika ukuran langkah waktu ℓ tidak lebih besar dari 0.171
4. Dengan melakukan variasi nilai input dari masing-masing parameter maka didapatkan parameter sensitif, yaitu yang memberikan pengaruh yang cukup besar terhadap arah penyebaran penyakit pada populasi.
Parameter-parameter sensitif tersebut ialah 𝐴𝐴, 𝜇𝜇, 𝛽𝛽2, 𝛾𝛾 dan 𝐾𝐾.
V. DAFTARPUSTAKA
[1] Guihua Li, Zhen Jin.(2005). “Global Stability of SEIR epidemic model with infectious forse in latent, infected and immune period”.Chaos, Solitons and Fractals. Hal 1177-1184
[2] Hethcote HW, van den Drissche P.(1991). “Some epidemiological models with nonlinear incidence”. J Math BiolVol 29.Hal 271.
[3] Rusdi Wahyudi,dkk.(2012).”Kestabilan Model Epidemik SEIR dengan Waktu Tunda”.Tugas Akhir jurusan Matematika Universitas Hasanuddin.
[4] Priyandoko Bagus.(2009).”Analisis kualitatif dan bifurkasi pada model epidemik tipe SEIR dengan transmisi vertikal”.Tugas akhir jurusan matematika ITS.
[5] Gao LQ, Hethcote HW.(1992).”Disease transmission models with density-depent demographics”. J Math Biol. 30:717.
[6] Hethcote HW, van den Drissche P.(1991). “Some epi-demiological models with nonlinear incidence”. J Math Biol. 29:271.
[7] Derrick WR, van den Drissche P.(1993).” A disease transmition model in a non constant population”. J Math Biol. 31: 495.
[8] Nedelman J. (1985).”Introductory review. Some new thoughts about some old malaria models”. Math Biosci. Hal. 15-32.