BAB III m BAHASAN KONSTRUKSI GF(3 ) dalam penelitian ini dapat dilakukan dengan mengacu pada konsep perluasan filed pada Bab II bagian 2.8.

(1)

Untuk mengonstruksi GF(3 )m dalam penelitian ini dapat dilakukan dengan mengacu pada konsep perluasan filed pada Bab II bagian 2.8.

Karena 3 adalah bilangan prima, maka berdasarkan Teorema 2.22  adalah field₃ berhingga yang himpunan elemennya {0, 1, 2} dengan operasi penjumlahan dan operasi perkalian dilakukan dalam modulo 3 dan merupakan ring komutatif. Karena  adalah₃ ring komutatif, maka berdasarkan Teorema 2.34 3[ ]x adalah himpunan dari semua

polinomial dalam x atas  dengan operasi penjumlahan dan perkalian polinomial₃

merupakan ring komutatif yang dinyatakan sebagai

1

3[ ] { 0 1 ... 1 3}

m m

m m i

x  a a x a _x  a x a 

  . Operasi penjumlahan pada 3[ ]x

bersifat asosiatif, terdapat elemen identitas yaitu polinomial nol, setiap polinomial

3

( ) [ ]

a x  x terdapat polinomial a x( ) sebagai elemen invers, dan merupakan grup komutatif. Di lain pihak, operasi perkalian pada ₃[ ]x bersifat asosiatif, distributif terhadap operasi penjumlahan.

Misalkan p x( )₃[ ]x adalah polinomial irreducible berderajat m , jika ada akar c sehingga p c( )0, maka himpunan semua polinomial yang dibangun oleh p x( ) merupakan ideal utama p x( ) dan dapat dibentuk ring faktor 3[ ]x p x( ) . Karena

( )

p x adalah polinomial irreducible berderajat m , maka berdasarkan Teorema 2.42

( )

p x merupakan ideal maksimal. Dengan mengacu pada Teorema 2.32, maka

3[ ]x p x( )

 adalah field. Berdasarkan Teorema 2.47, ₃[ ]x p x( ) ₃[ ]c merupakan perluasan dari field  . Selanjutnya berdasarkan Teorema 2.50, elemen-elemen₃ ₃[ ]c dapat dinyatakan secara unik dalam bentuk {b₀b c₁ 1 ... b_m_₁cm1 b_i . Di lain₃} pihak, berdasarkan Teorema 2.51, 3[ ]c merupakan ruang vektor berdimensi-m atas  .3

Untuk kepentingan komputasi, maka elemen ₃[ ]c dapat direpresentasikan sebagai vektor terner dari derajat terkecil ke derajat terbesar dalam bentuk [a₀, a₁, . . . , a_m_₁].

(2)

Berdasarkan Teorema 2.52, setiap field berhingga GF(3 )m mempunyai elemen sebanyak pangkat dari bilangan prima berorder 3m. Akibatnya, berdasarkan Teorema 2.53 maka GF(3 )m ₃[ ]x p x( ) . Dari proses di atas, maka GF(3 )m merupakan himpunan dari semua polinomial berderajat kurang dari m yang dinyatakan dalam teorema berikut.

Teorema 3.1 Misalkan p x( ) adalah polinomial irredusible berderajat m atas  , maka₃

1

0 1 1 3

(3 )m { ... _m m _i }

GF  a a x a _x  a  adalah field berhingga.

Bukti :

Diketahui p x( ) adalah polinomial irredusibel berderajat m atas  .3

Misalkan : 3[ ] (3 )

m

f  x GF adalah fungsi yang didefinisikan ( ( )) ( )(mod ( ))

f g x g x p x .

Misalkan g x₁( ), g x₂( )  ₃[ ]x maka f merupakan homomorfisma, karena

1 2 1 2 ( ( ) ( )) ( ( ) ( ))(mod ( )) f g x g x  g x g x p x 1 2 (g x( ))(mod ( )) (p x g x( ))(mod ( ))p x   1 2 ( ( )) ( ( )) f g x f g x   1 2 1 2 ( ( ) ( )) ( ( ) ( ))(mod ( )) f g x g x  g x g x p x 1 2 (g x( ))(mod ( ))(p x g x( ))(mod ( ))p x  1 2 ( ( )) ( ( )) f g x f g x 

Fungsi f juga surjektif, karena untuk setiap ( )(mod ( )) (3 )m

g x p x GF maka terdapat

3

( ) [ ]

g x  x sedemikian sehingga f g x( ( ))g x( )(mod ( ))p x .

Kernel dari f adalah ker( )f { ( )g x 3[ ]x f g x( ( ))0} 3 { ( )g x [ ]x g x( )(mod ( ))p x 0}  _  ( ) p x 

(3)

Karena fungsi f homomorfisma yang surjektif maka f merupakan epimorfisma dengan ker( )f  p x( ) . Berdasarkan Teorema Dasar Homomorfisma (Teorema 2.30), maka 3[ ] ( ) 3[ ] (3 )

m x p x  c GF

  . Akibatnya, GF(3 )m adalah field yang elemen-elemennya merupakan himpunan semua polinomial-polinomial berderajat paling banyak

1

m yang dinyatakan secara unik sebagai GF(3 )m {a₀a x₁  ... a_m_₁xm1 a_i . ■₃}

Dari keisomorfikan GF(3 )m dengan ₃[ ]x p x( ) ₃[ ]c , maka operasi dan representasi elemen-elemennya dapat dijelaskan sebagai berikut.

Misalkan, diberikan fungsi polinomial ( ) { 0 1 ... 1 1 3}

m m i a x  a a x a _ x  a  dan 1 0 1 1 3 ( ) { ... _m m _i }

b x  b b x b _x  b  . Operasi penjumlahan dalam GF(3 )m didefinisikan sebagai c x( )a x( )b x( )  c₀ c x₁  ... c_m_₁xm1 dengan

0 ( 0 0) mod 3

c  a b , c₁(a₁b₁) mod 3, . . . , c_m_₁ (a_m_₁b_m_₁) mod 3. Operasi perkalian dalam (3 )m

GF didefinisikan sebagai perkalian polinomial modulo p x( ), yaitu mengambil sisa dari perkalian a x( ) dan b x( ) setelah dibagi dengan p x( ) dinotasikan

( ) ( ) ( ) mod ( )

c x a x b x p x .

Elemen GF(3 )m dapat direpresentasikan sebagai bentuk polinomial

1

0 1 1 3

{ ... m }

m i

a a x a _ x  a  , bentuk basis baku 2 1

{1, ,c c , . . . , cm}, bentuk koordinat vektor [a₀, a₁, . . . , a_m_₁].

Karena GF(3 )m adalah field berhingga, maka himpunan elemen-elemen tak-nol dari GF(3 )m membentuk grup siklik terhadap operasi perkalian, dinotasikan GF(3 )m *. Hal ini disajikan dalam teorema berikut ini.

Teorema 3.2 Grup GF(3 )m * merupakan grup siklik terhadap operasi perkalian berorder 3m1.

Bukti :

(4)

Karena GF(3 )m * berorder 3m1, maka  paling banyak merupakani 3m1 elemen berbeda sehingga terdapat r , dimana 1 r 3m1 berlaku

r i i   _ _{ ( . ).} . r i i i i    _  _ ( . ) 1 r i i    _

sehingga diperoleh r 1. Jadi r minimum sehingga O( ) r.

Selanjutnya, misalkan r adalah order maksimal dari elemen GF(3 )m * terhadap operasi perkalian, maka akan berlaku r 1 0, untuk setiap (3 )m

GF

_ 

. Karena setiap elemen dari GF(3 )m merupakan akar dari polinomial r 1, akibatnya polinomial berderajat r dapat mempunyai paling banyak r akar.

Karena GF(3 )m * grup siklik terhadap operasi perkalian maka terdapat GF(3 )m  , dan r3m1 tetapi r3m1, hal ini menunjukkan bahwa r3m1. Dengan demikian, GF(3 )m *   {1, , 2,...,3m2} dan berorder 3m1.

Terbukti GF(3 )m * siklik. ■

Definisi 3.3 Suatu elemen  dalam finite field GF(3 )m * disebut elemen primitif atau generator dari GF(3 )m , jika GF(3 )m * {1, , 2,...,3m2} (Ling 2004).

Definisi 3.4 Polinomial irreducible f x( )GF(3)[ ]x berderajat m disebut polinomial primitif dengan akar  , jika  adalah generator dari GF(3 )m  (Menezes 1997).

Berdasarkan sifat dari grup siklik bahwa setiap elemen (3 )m

GF  memenuhi

polinomial 3m1 1 0 dan selalu mempunyai akar  primitif sebagai pembangun (3 )m

GF . Untuk membangun algoritme aritmetik GF(3 )m dalam penelitian ini dilakukan dengan mengambil polinomial primitif berderajat m atas  yang merupakan₃ polinomial minimum m x( )a₀a x₁  ... a x_m m dimana  merupakan akar primitifnya sedemikian sehingga m( ) 0. Selanjutnya tentukan basisnya di GF(3 )m sebagai ruang vektor atas  . Misalkan₃ GF(3 )m adalah field berhingga dan  adalah elemen primitif dalam GF(3 )m , maka bentuk basis standar dari polinomial primitifnya adalah

(5)

2 3 2

{1,  , , ...,  m } dan setiap elemen  j GF(3 )m dapat dinyatakan secara unik sebagai j a₀a x₁  ... a_m_₁xm1 dimana a_i . Untuk kepentingan komputasi,₃ maka bentuk basis  dapat direpresentasikan sebagai koordinat vektor terner darij derajat terkecil ke derajat terbesar dalam bentuk j [a₀, a₁, . . . , a_m_₁].

Pengambilan polinomial primitif dalam penelitian ini dapat dilakukan secara komputasi menggunakan Software Maple 11 dengan langkah-langkah sebagai berikut. Pertama-tama tes apakah polinomial irreducible atau tidak. Selanjutnya, tes polinomial irreducible primitif atau tidak. Adapun Algoritme 3.1 dan Algoritme 3.2 merupakan algoritme rutin yang akan digunakan pada Algoritme 3.3 dan Algoritme 3.4.

Algoritme 3.1

Deskripsi : Prosedur untuk menghitung Axmod B

Input : Vektor A[ ,a₀ a₁, . . . , a_s], vektor B[ ,b₀ b₁, . . . , b ]_t , dan integer x Output : H AxmodB

1. Ubah x dalam basis 2 2. Isi G = H, H = [1] 3. Jika X1= 1, maka H = G

4. Untuk i mulai 2 sampai panjang vektor X, lakukan 4.1 Hitung K = perkalian G dengan G

4.2 Hitung G = sisa hasil bagi K dengan B 4.3 Jika Xi= 1, maka lakukan

4.3.1 Hitung L = perkalian H dengan G 4.3.2 Hitung H = sisa hasil bagi L dengan B 5. Return(H)

Algoritme 3.2

Deskripsi : Prosedur untuk menghitung Gcd dari vektor A dan vektor B Input : Vektor A[ ,a₀ a₁, . . . , a_s], vektor B[ ,b₀ b₁, . . . , b ]_t Output : RAGcd A B( , )

1. Hitung a = panjang vektor A dan b = panjang vektor B 2. Isi RA = A, RB = B

3. Jika a < b, maka RA = B dan RB = A 4. Jika RB = [0], maka return(RA)

5. Hitung L = sisa hasil bagi RA dengan RB 6. Isi RA = RB dan RB = L

7. Untuk i selama RB ≠ [0], maka lakukan berulang-ulang 7.1 Hitung L = sisa hasil bagi RA dengan RB

(6)

7.2 Isi RA = RB dan RB = L 8. Return(RA)

Vektor terner yang dibangkitkan, cek apakah irreducible atau tidak menggunakan Algoritme 3.3. Algoritme ini didasarkan pada Teorema 2.55.

. Algoritme 3.3

Deskripsi : Prosedur untuk memeriksa polinomial irreducible atau tidak Input : Vektor A[ ,a₀ a₁, . . . , a_s]

Output : Apakah irreducible ?

1. Hitung a = panjang vektor A - 1 2. Hitung m = 2 m       3. Isi W [0,1]

4. Untuk i dari 1 sampai m, lakukan

4.1 Hitung W  AxmodB menggunakan Algoritme 3.1 4.2 Hitung U = jumlah vektor W dengan [0, 2]

4.3 Hitung H = Gcd(A,B) menggunakan Algoritme 3.2 4.4 Hitung h = panjang vektor H

4.4.1 Jika h > 1, maka return(false) 5. Return(true)

Selanjutnya, cek apakah primitif atau tidak dengan menggunakan Algoritme 3.4. Algoritme ini didasarkan pada Teorema 2.56.

Algoritme 3.4

Deskripsi : Prosedur untuk memeriksa polinomial irreducible adalah primitif Input : Vektor A[ ,a₀ a₁, . . . , a_s]

Output : Apakah polinomial primitif ?

1. Hitung m = panjang vektor A – 1 2. Hitung h3m1

3. Hitung F = faktor prima dari h 4. Hitung a = panjang vektor F 5. Untuk i dari 1 sampai a , lakukan

5.1 Hitung kh F/ _i

5.2 Hitung H = [0, 1]kmod A menggunakan Algoritme 3.1 5.3 Jika H = [1], maka return(false)

(7)

Pembangkitan vektor terner yang primitif dalam penelitian ini dapat dilakukan dengan memilih vektor yang bersuku kecil, yaitu vektor bersuku dua dengan menggunakan Algoritme 3.5, vektor bersuku tiga dengan menggunakan Algoritme 3.6, vektor bersuku empat dengan menggunakan Algoritme 3.7.

Algoritme 3.5

Deskripsi : Prosedur untuk membangkitkan polinomial primitif bersuku dua Input : Bilangan bulat positif m

Output : Vektor primitif bersuku dua Y 1. Untuk i dari 1 sampai 4, lakukan

1.1 Jika (i mod 3)  0, maka

1.1 Ubah X = dari desimal ke vektor terner 1.2 Hitung x = panjang elemen X

1.3 Isi vektor Y = [X, 0...(m - x), 1]

1.4 T = Test irreducible Y menggunakan Algoritme 3.3 1.4 Jika T = true, maka

1.4.1 U = Test Primitif Y menggunakan Algoritme 3.4 1.4.2 Jika U = true, maka

2. Return(Y)

Jika vektor primitif bersuku dua tidak ada maka vektor primitifnya dapat dipilih dari vektor primitif bersuku tiga dengan menggunakan Algoritme 3.6.

Algoritme 3.6

Deskripsi : Prosedur untuk membangkitkan polinomial primitif bersuku tiga Input : Bilangan bulat positif m dan floor((m+1)/2)

Output : Vektor primitif bersuku tiga Y 1. Untuk i dari 1 sampai 2, lakukan

1.1 Untuk j dari 1 sampai 2, lakukan

1.1.1 T = Test irreducible menggunakan Algoritme 3.3 1.1.2 Jika T = true, maka

U = Test Primitif menggunakan Algoritme 3.4 1.1.3 Jika U = true, maka Return(Y)

1.2 Untuk k dari 1 sampai (m-2), lakukan

1.1.1 T = Test irreducible menggunakan Algoritme 3.3 1.1.2 Jika T = true, maka

U = Test Primitif menggunakan Algoritme 3.4 1.1.3 Jika U = true, maka Return(Y)

(8)

Jika vektor primitif bersuku tiga tidak ada maka vektor primitifnya dapat dipilih dari vektor primitif bersuku empat atau lebih dengan menggunakan Algoritme 3.7.

Algoritme 3.7

Deskripsi : Prosedur untuk membangkitkan polinomial primitif bersuku tiga Input : Bilangan bulat positif m dan floor((m+1)/2)

Output : Vektor primitif bersuku tiga Y 1. Untuk i dari 1 sampai 2, lakukan

1.1 Untuk j dari 1 sampai 2, lakukan 1.1.1 Untuk k dari 1 sampai 2, lakukan

1.1.1.1 T = Test irreducible menggunakan Algoritme 3.3 1.1.1.2 Jika T = true, maka

U = Test Primitif menggunakan Algoritme 3.4 1.1.1.3 Jika U = true, maka Return(Y)

1.1.2 Untuk l dari 1 sampai (m-3), lakukan

2. Return(Y)

Pemilihan polinomial primitif bersuku kecil dimaksudkan agar dapat mempercepat proses kalkulasi aritmetik field (3 )m

GF . Polinomial primitif bersuku kecil yang digunakan dalam penelitian ini dapat dilihat pada Lampiran II. Selanjutnya, untuk kepentingan komputasi polinomial primitif yang dipilih direpresentasikan sebagai vektor terner yang dipilih akan disimpan dalam basis data. Untuk menggunakan basis data tersebut cukup dipanggil derajat tertinggi.

Sebagai contoh, misalkan pilih m3. Untuk membangun field GF(3 )3 dapat dikerjakan dari  , karena₃  merupakan subfield dari₃ GF(3 )3 . Ambil polinomial primitif m x( )x32x 1 ₃[ ]x yang merupakan polinomial minimum berderajat 3 dimana  adalah akar primitifnya. Periksa apakah akar  merupakan algebraic atau tidak.

(9)

Ambil GF(3) sedemikian sehingga m( ) 0.

Untuk  0, maka m(0)032.0 1 1  . Jadi  0 bukan akar dari m x( ). 1

  , maka m(1) 1 3 2.1 1 1  . Jadi  1 bukan akar dari m x( ). 2

  , maka m(2)232.2 1 1  . Jadi  2 bukan akar dari m x( ).

Karena untuk  0,  1, dan  2 bukan akar dari polinomial m x( ), ini menunjukkan bahwa  merupakan algebraic. Pilih akar  pada perluasan field ₃ sedemikian sehingga m( ) 0 mengakibatkan m( ) 32  1 0  3   . 2 Dengan 3   2 dapat digunakan untuk membangun perluasan field yang memuat semua akar-akar dari polinomial m x( )₃[ ]x , sehingga diperoleh

4 3 2 2     , 5 4 22  2, 6 5 2  1, 7 6 2 2 2 2       , 8 7 222, 9 8   1, 10 9 2    , . . . , 25 24 221, 26 25 0 1. Selanjutnya, karena polinomial m x( ) berderajat 3 maka 2

{1,  , } bebas linear atas ₃( ) . Artinya {1,  , 2} merupakan basis dari ₃( ) , sehingga ₃( ) merupakan ruang vektor berdimensi 3 atas  . Selanjutnya, subfield dari₃ GF(3 )3 terdiri dari  dan₃ 3

(3 )

GF dengan masing-masing ordernya adalah 3 dan 27. Elemen-elemen

dari subfield yang berorder 3 adalah {0, 1, 2}, sedangkan elemen-elemen subfield yang berorder 27 adalah field itu sendiri yaitu {0, 1, , ..., 25} dengan basisnya

25

{1, , ...,  }. Jadi GF(3 )3 27{0, 1, , ..., 25} dengan basisnya adalah

25

{0, 1, , ...,  } dan jika elemen nol dikeluarkan maka GF(3 )3 akan membentuk grup siklik yang dibangkitkan oleh  , dinotasikan GF(3 )3    . Jadi

3 25

(3 ) 26 {1, , ..., }

GF      dengan basisnya adalah{1, , ..., 25}.

Dengan demikian, himpunan semua polinomial-polinomial berderajat kurang dari 3 atas  yang dibangun oleh polinomial primitif₃ 3

3

( ) 2 1 [ ]

(10)

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 {0, 1, 2, , 1, 2, 2 , 2 1, 2 2, , 1, 2, , 2 , 1, 2, 2 1, 2 2, 2 , 2 1, 2 2, 2 , 2 1, 2 2, 2 2 , 2 2 1, 2 2 2}                                                                

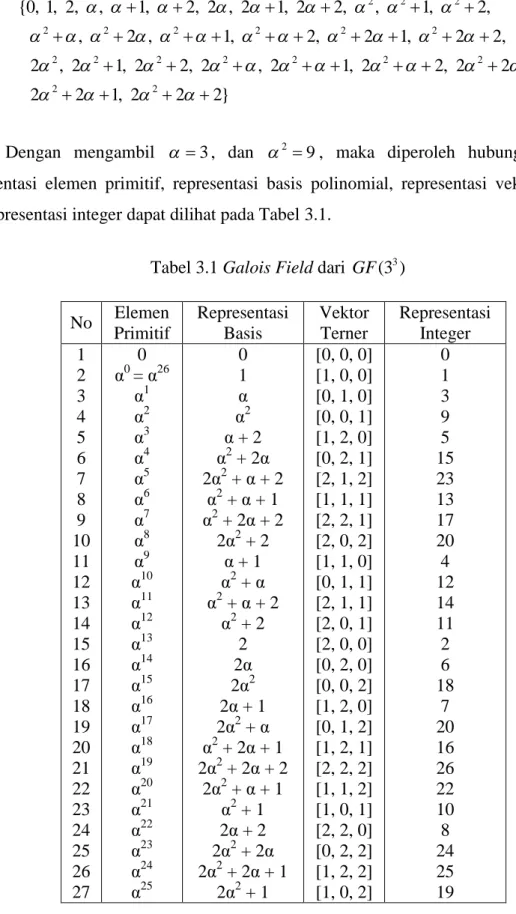
Dengan mengambil  3, dan 2 9, maka diperoleh hubungan antara representasi elemen primitif, representasi basis polinomial, representasi vektor terner, dan representasi integer dapat dilihat pada Tabel 3.1.

Tabel 3.1 Galois Field dari GF(3 )3

No Elemen Primitif Representasi Basis Vektor Terner Representasi Integer 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 0 α0 = α26 α1 α2 α3 α4 α5 α6 α7 α8 α9 α10 α11 α12 α13 α14 α15 α16 α17 α18 α19 α20 α21 α22 α23 α24 α25 0 1 α α2 α + 2 α2 + 2α 2α2+ α + 2 α2 + α + 1 α2 + 2α + 2 2α2+ 2 α + 1 α2 + α α2 + α + 2 α2 + 2 2 2α 2α2 2α + 1 2α2+ α α2 + 2α + 1 2α2+ 2α + 2 2α2+ α + 1 α2 + 1 2α + 2 2α2+ 2α 2α2+ 2α + 1 2α2+ 1 [0, 0, 0] [1, 0, 0] [0, 1, 0] [0, 0, 1] [1, 2, 0] [0, 2, 1] [2, 1, 2] [1, 1, 1] [2, 2, 1] [2, 0, 2] [1, 1, 0] [0, 1, 1] [2, 1, 1] [2, 0, 1] [2, 0, 0] [0, 2, 0] [0, 0, 2] [1, 2, 0] [0, 1, 2] [1, 2, 1] [2, 2, 2] [1, 1, 2] [1, 0, 1] [2, 2, 0] [0, 2, 2] [1, 2, 2] [1, 0, 2] 0 1 3 9 5 15 23 13 17 20 4 12 14 11 2 6 18 7 20 16 26 22 10 8 24 25 19