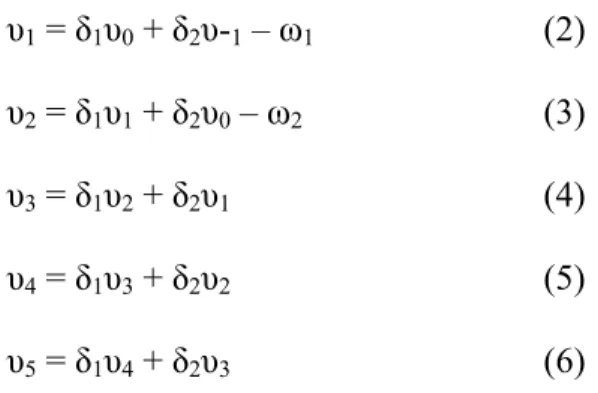HASIL DAN PEMBAHASAN 5.1 Penyajian Data
Berikut dibawah ini adalah data yang didapat dari GK AUTO.
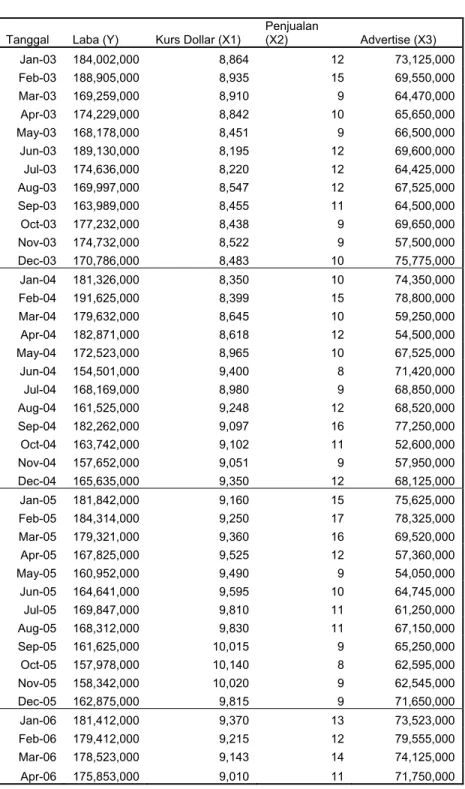
Tabel 5.1 Data Variabel
Tanggal Laba (Y) Kurs Dollar (X1) Penjualan (X2) Advertise (X3) Jan-03 184,002,000 8,864 12 73,125,000 Feb-03 188,905,000 8,935 15 69,550,000 Mar-03 169,259,000 8,910 9 64,470,000 Apr-03 174,229,000 8,842 10 65,650,000 May-03 168,178,000 8,451 9 66,500,000 Jun-03 189,130,000 8,195 12 69,600,000 Jul-03 174,636,000 8,220 12 64,425,000 Aug-03 169,997,000 8,547 12 67,525,000 Sep-03 163,989,000 8,455 11 64,500,000 Oct-03 177,232,000 8,438 9 69,650,000 Nov-03 174,732,000 8,522 9 57,500,000 Dec-03 170,786,000 8,483 10 75,775,000 Jan-04 181,326,000 8,350 10 74,350,000 Feb-04 191,625,000 8,399 15 78,800,000 Mar-04 179,632,000 8,645 10 59,250,000 Apr-04 182,871,000 8,618 12 54,500,000 May-04 172,523,000 8,965 10 67,525,000 Jun-04 154,501,000 9,400 8 71,420,000 Jul-04 168,169,000 8,980 9 68,850,000 Aug-04 161,525,000 9,248 12 68,520,000 Sep-04 182,262,000 9,097 16 77,250,000 Oct-04 163,742,000 9,102 11 52,600,000 Nov-04 157,652,000 9,051 9 57,950,000 Dec-04 165,635,000 9,350 12 68,125,000 Jan-05 181,842,000 9,160 15 75,625,000 Feb-05 184,314,000 9,250 17 78,325,000 Mar-05 179,321,000 9,360 16 69,520,000 Apr-05 167,825,000 9,525 12 57,360,000 May-05 160,952,000 9,490 9 54,050,000 Jun-05 164,641,000 9,595 10 64,745,000 Jul-05 169,847,000 9,810 11 61,250,000 Aug-05 168,312,000 9,830 11 67,150,000 Sep-05 161,625,000 10,015 9 65,250,000 Oct-05 157,978,000 10,140 8 62,595,000 Nov-05 158,342,000 10,020 9 62,545,000 Dec-05 162,875,000 9,815 9 71,650,000 Jan-06 181,412,000 9,370 13 73,523,000 Feb-06 179,412,000 9,215 12 79,555,000 Mar-06 178,523,000 9,143 14 74,125,000 Apr-06 175,853,000 9,010 11 71,750,000
Dan data dibawah ini merupakan data dari GK AUTO yang akan dijadikan sebagai patokan dalam membandingkan dengan hasil peramalan.
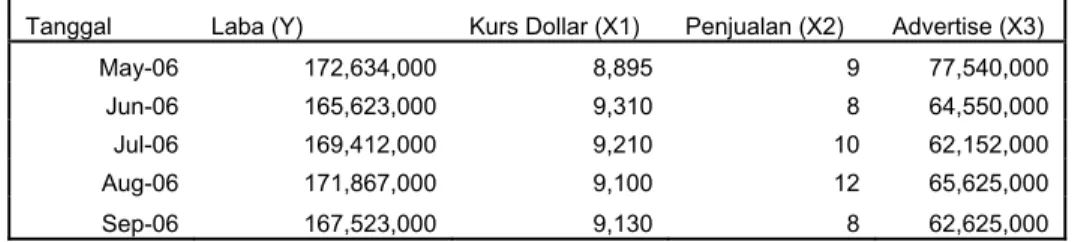
Tabel 5.2 Data untuk perbandingan
Tanggal Laba (Y) Kurs Dollar (X1) Penjualan (X2) Advertise (X3)
May-06 172,634,000 8,895 9 77,540,000 Jun-06 165,623,000 9,310 8 64,550,000 Jul-06 169,412,000 9,210 10 62,152,000 Aug-06 171,867,000 9,100 12 65,625,000 Sep-06 167,523,000 9,130 8 62,625,000
Variabel-variabel yang digunakan adalah tiga variabel bebas yang mempengaruhi variabel tidak bebas (variabel keuntungan atau laba). Penjelasan variabel dari tabel di atas dijelaskan sebagai berikut :
¾ Kurs Dollar (Rp) : Variabel bebas ini dirasa cukup mempengaruhi karena jika dilihat Gambar2.1 yaitu proses sistem bisnis GK Auto, maka terlihat sering sekali terjadi pengimportan barang dari luar negeri.
¾ Penjualan (Kuantitas) : Variabel bebas ini sudah jelas pengaruhnya dalam mempengaruhi keuntungan, semakin banyak penjualan untung semakin besar, disini penjualan yang dimaksud adalah penjualan mobil saja dan spare part tidak, hal ini dilakukan karena besarnya penjualan spare part tidak dibarengi dengan besarnya jumlah keuntungan yang diterima jika dibandingkan dengan keuntungan dari penjualan mobil.
¾ Biaya Pemasaran (Advertise) (Rp) : Variabel bebas ini jika dilihat dari Gambar 2.1 maka cukup mempengaruhi hasil minat pelanggan untuk membeli barang mereka.
¾ Keuntungan (Rp) : Variabel tidak bebas ini merupakan keuntungan dari penjualan mobil dan spare part.
Hasil Korelasi dari data Tabel 5.1 dan Tabel 5.2 (Jan 2003 – Sept 2006):
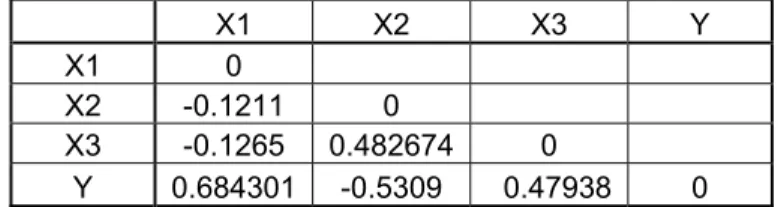
Tabel 5.3 Korelasi antar variabel
X1 X2 X3 Y
X1 0
X2 -0.1211 0
X3 -0.1265 0.482674 0
Y 0.684301 -0.5309 0.47938 0
5.2 Pengolahan Data Analisis 5.2.1 Multiple Regression
Dalam peramalan menggunakan metode Regresi Berganda ini, menggunakan semua variabel yang terdapat di Tabel 5.1 yaitu 3 variabel bebas dan 1 variabel bebas data diambil sampai April 2006, dan sisa datanya digunakan untuk pengecekan galat menggunakan MSE atau MAPE. Dimana tiga variabel bebas yaitu Kurs Dollar (X1),
Penjualan (X2) dan Biaya Advertise (X3), dan variabel tidak bebasnya yaitu data laba
atau keuntungan (Y) yang juga sebagai data yang akan diramal melalui metode Regresi Berganda ini.
5.2.1.1 Pengecekan Multikolinearitas
Yang harus dilakukan pertama kali di dalam pengolahan data menggunakan metode Regeresi Berganda adalah harus dilakukannya pengecekan Multikolinearitas terlebih dahulu untuk tidak menghasilkan kekacauan model untuk data linear.
Disajikan pada Tabel 5.3 jika melihat dari data dari tabel tersebut maka akan terlihat korelasi-korelasi antar variabel , baik antara variabel bebas dengan variabel tidak bebas , ataupun dengan sesama variabel bebas .
Kolinearitas jelas akan terjadi jika salah satu kolerasi antara variabel bebas tidak lebih dari 0.75. jika kolerasi antar variabel bebas ada yang melebihi 0.75 maka akan terjadi kesalahan model seperti yang dijelaskan di Bab 3.4.1.1. Tetapi untuk meyakinkan bahwa tidak adanya multikolineritas yang terjadi maka akan digunakan garis batas Z untuk perbandingan. Dan jika melihat dari tabel 5.2 maka akan terlihat seperti berikut :
¾ Kolerasi X1 & X2 = -0.1211 ¾ Kolerasi X1 & X3 = -0.1265 ¾ Kolerasi X1 & X3 = 0.482674
Dan dengan menggunakan persamaan 3-4-20 maka menghasilkan garis batas Z sebagai berikut dengan tingkat kepercayaan 95% dan n = 45
-0.292 < r(n) < 0.292
Jika membandingkan korelasi antar variabel dengan garis batas Z, maka akan terlihat korelasi antar X1 dan X3 melebihi garis batas Z, dan hal ini dapat menyebabkan multikolinearitas. Namun jika melihat lebih lanjut maka korelasi antar variabel bebas tersebut tidak ada yang melebihi 0.75. Dalam hal ini multikolinearitas mungkin terjadi karena melebih garis batas Z, tetapi tidak pasti terjadi karena masih belom melebihi 0.75.
Naum metode Regresi Berganda tetap menggunakan data Tabel 5.1 untuk digunakan dengan alasan, yaitu : nilai korelasi X1 dan X3 = 0.482 yang ternyata tidak terlalu jauh dari garis batas Z dan nilai korelasinya cukup jauh dari terjadinya
multikolinearitas yaitu 0.75, sehingga kecil kemungkinannya untuk terjadi multikolinearitas.
5.2.1.2 Pengecekan Significant menggunakan F-test
Setelah melakukan pengecekan multikolinearitas, maka diperlukan pengecekan significance test, yaitu dengan menggunakan F-test untuk mengecek apakah tepat jika digunakan garis regresi. Dengan menggunakan persamaan 3-2-1 maka nilai F-test didapat sebagai berikut :
F-test = 26.51505853
Dan dengan menggunakan tabel F dengan tingkat kepercayaan 95% dan v1 = 3 dan v2 = 40 maka menghasilkan nilai F tabel = 2.84.
Dan karena F-test lebih besar dari F tabel maka statistik koefesien variabel bebas adalah tidak significance berbeda dengan 0, Oleh karena itu adalah benar dan tepat untuk menggunakan persamaan regresi model linier atau regresi model Y = a + b1X1 +
b2X2 + b3X3.
5.2.1.3 Mengolah Data
Di dalam pengolahan data dengan menggunakan metode Regresi Berganda, perlu adanya pembagian matrix untuk variabel bebas dan variabel tidak bebas. Dimana variabel matrix variabel bebas ditulis dalam X, dan matrix variabel tidak bebas ditulis dalam Y. Hal pertama yang harus dilakukan adalah melakukan standarisasi dari setiap nilai variabel bebas menggunakan persamaan 3-1-13, 3-1-14 dan 3-1-15.
Tabel 5.4 Tabel nilai υ dan σ
x1 x2 x3
υ 9070.375 11.25 67410700
σ 95.23852 3.354101966 8210.402
Yang kemudian menggunakan persamaan 3-1-13 untuk membakukan nilai, yang kemudian dijadikan matrix X seperti yang terlihat dibawah ini.
1 -0.39673521 4.827185944 0.432986807 1 -0.260244841 24.13592972 0.162100113 1 -0.30830483 -14.48155783 -0.222824196 1 -0.439028001 -8.045309907 -0.133412644 1 -1.190686231 -14.48155783 -0.069006017 1 -1.68282052 4.827185944 0.165888738 1 -1.634760531 4.827185944 -0.226233959 1 -1.006135873 4.827185944 0.008660797 1 -1.182996633 -1.609061981 -0.220551021 1 -1.215677425 -14.48155783 0.169677363 1 -1.054195862 -14.48155783 -0.750958534 1 -1.129169445 -8.045309907 0.633783937 1 -1.384848587 -8.045309907 0.525808122 1 -1.290651009 24.13592972 0.862995755 1 -0.817740715 -8.045309907 -0.618356656 1 -0.869645504 4.827185944 -0.978276039 1 -0.202572854 -8.045309907 0.008660797 1 0.633670957 -20.91780576 0.303794692 X= 1 -0.173736861 -14.48155783 0.109059362 1 0.341466223 4.827185944 0.084054436 1 0.051183888 30.57217765 0.745548377 1 0.060795886 -1.609061981 -1.122243793 1 -0.037246492 -14.48155783 -0.716860908 1 0.537550979 4.827185944 0.054124298 1 0.172295061 24.13592972 0.622418062 1 0.345311022 37.00842557 0.827003817 1 0.556774974 30.57217765 0.159826938 1 0.873970903 4.827185944 -0.761566684 1 0.806686918 -14.48155783 -1.012373665 1 1.008538872 -8.045309907 -0.201986758 1 1.421854779 -1.609061981 -0.466811652 1 1.46030277 -1.609061981 -0.019753891 1 1.81594669 -14.48155783 -0.163721645 1 2.056246636 -20.91780576 -0.364897637 1 1.825558688 -14.48155783 -0.368686262 1 1.431466777 -14.48155783 0.321222367 1 0.57599897 11.26343387 0.463144263 1 0.278027037 4.827185944 0.920203994 1 0.139614268 17.69968179 0.508759309 1 -0.116064874 -1.609061981 0.328799617
Dibentuk pula matrix Y tanpa standarisasi nilai, seperti yang terlihat dibawah ini 184,002,000 188,905,000 169,259,000 174,229,000 168,178,000 189,130,000 174,636,000 169,997,000 163,989,000 177,232,000 174,732,000 170,786,000 181,326,000 191,625,000 179,632,000 182,871,000 172,523,000 Y= 154,501,000 168,169,000 161,525,000 182,262,000 163,742,000 157,652,000 165,635,000 181,842,000 184,314,000 179,321,000 167,825,000 160,952,000 164,641,000 169,847,000 168,312,000 161,625,000 157,978,000 158,342,000 162,875,000 181,412,000 179,412,000 178,523,000 175,853,000
Setelah Terbentuk Matrix X dan Y kemudian dilanjutkan perhitungan dengan mencari X’X dan X’Y 40 -3.63598E-15 2.02061E-14 0 X'X= -3.63598E-15 40 -72.70089106 -2.653412312 2.02061E-14 -72.70089106 9010 151.9541519 0 -2.653412312 151.9541519 11 6,899,612,000.00 X'Y= -201,294,855.52 3,946,732,972.80 96,403,937.33
Kemudian dilanjutkan dengan mencari (X’X)-1, sampai disini diperlukan invers. disini digunakanlah metode Gauss Jordan untuk pencarian Matrix Invers dengan rumus [ A | I ]
-> [ I | A-1 ] (W.Johnsonn, 2002, p92-102). Berikut di bawah ini adalah langkah
pengubahan Matrix (X’X) menjadi (X’X)-1
40 -3.64E-15 2.02E-14 0 1 0 0 0 -3.6E-15 40 -72.70089 -2.653412 0 1 0 0 2E-14 -72.70089 9010 151.9542 0 0 1 0 0 -2.653412 151.9542 11 0 0 0 1 1 -9.09E-17 5.05E-16 0 0.025 0 0 0 /40 -3.6E-15 40 -72.70089 -2.653412 0 1 0 0 2E-14 -72.70089 9010 151.9542 0 0 1 0 0 -2.653412 151.9542 11 0 0 0 1 1 -9.09E-17 5.05E-16 0 0.025 0 0 0 0 40 -72.70089 -2.653412 9.09E-17 1 0 0 R2+3.63598E-15R1 0 -72.70089 9010 151.9542 -5.1E-16 0 1 0 R3-2.02060E-14R1 0 -2.653412 151.9542 11 0 0 0 1 1 -9.09E-17 5.05E-16 0 0.025 0 0 0 0 1 -1.817522 -0.066335 2.27E-18 0.025 0 0 /40 0 -72.70089 9010 151.9542 -5.1E-16 0 1 0 0 -2.653412 151.9542 11 0 0 0 1
1 0 3.4E-16 -6.03E-18 0.025 2.27E-18 0 0 R1+9.08995E-17R2 0 1 -1.817522 -0.066335 2.27E-18 0.025 0 0
0 0 8877.865 147.1315 -3.4E-16 1.817522 1 0 R3+72.70089R2 0 0 147.1315 10.82399 6.03E-18 0.066335 0 1 R4+2.65341R2
1 0 3.4E-16 -6.03E-18 0.025 2.27E-18 0 0 0 1 -1.817522 -0.066335 2.27E-18 0.025 0 0
0 0 1 0.016573 -3.8E-20 0.000205 0.00011 0 /8877.8645109864 0 0 147.1315 10.82399 6.03E-18 0.066335 0 1
1 0 0 -1.17E-17 0.025 2.2E-18 -3.8E-20 0 R1-3.399395E-16R3 0 1 0 -0.036214 2.2E-18 0.025372 0.0002 0 R2+1.81752R3 0 0 1 0.016573 -3.8E-20 0.000205 0.00011 0
0 0 0 8.385597 1.17E-17 0.036214 -0.01657 1 R4-147.131515R3
1 0 0 -1.17E-17 0.025 2.2E-18 -3.8E-20 0 0 1 0 -0.036214 2.2E-18 0.025372 0.0002 0 0 0 1 0.016573 -3.8E-20 0.000205 0.00011 0
0 0 0 1 1.39E-18 0.004319 -0.00198 0.1192521 /8.3855965
1 0 0 0 0.025 2.25E-18 -6.1E-20 1.391E-18 R1+1.1663614E-17R4 0 1 0 0 2.25E-18 0.025528 0.00013 0.0043186 R1+0.03621378R4 0 0 1 0 -6.1E-20 0.000133 0.00015 -0.001976 R1-0.016572849R4 0 0 0 1 1.39E-18 0.004319 -0.00198 0.1192521
2.50E-02 2.25E-18 -6.13E-20 1.39E-18
(X’X)-1 = 2.25326E-18 0.025528484 0.000133154 0.00431857 -6.1342E-20 0.000133154 0.000145393 -0.001976347
1.39E-18 4.32E-03 -1.98E-03 1.19E-01
Langkah selanjutnya yaitu dengan mencari (X’X)-1X’Y yaitu dengan cara mengkalikan (X’X)-1 dengan X’Y
172,490,300.00 (X’X)-1X’Y = -4,196,901.53 356,498.05 2,826,951.63
Setelah Mendapatkan (X’X)-1X’Y maka dapat diketahui nilai a , b1 , b2 ,b3 dalam model
Y = a + b1X1 + b2X2 + b3X3 . Dari Matrix (X’X)-1X’Y maka didapat model Regresi
Berganda sebagai berikut.
Y = 172,490,300.00– 4,196,901.53 X1 + 356,498.05X2 + 2,826,951.63X3
Yang Kemudian Model ini digunakan untuk mendapatkan data Bulan Mei sampai Sept 2006 melalui data variabel bebas yang telah dibakukan. Hasil peramalan disajikan di Tabel 5.5 di bawah ini.
Tabel 5.5 Hasil Peramalan Regresi Berganda 2006 May 170,912,348.38
2006 June 162,487,042.52 2006 July 167,369,210.32 2006 Aug 173,589,658.06 2006 Sept 163,526,959.41
5.2.2 Transfer Function / MARIMA
Peramalan menggunakan metode Fungsi Transfer atau MARIMA menggunakan dua variabel atau bivariate data, satu sebagai variabel tidak bebas, dan yang satunya lagi variabel bebas yang mempengaruhi variabel tidak bebas tersebut. Dimana variabel bebas (Y dan juga sebagai data Deret Output) yaitu data biaya advertise (X dan juga sebagai data Deret Input) dan variabel tidak bebasnya yaitu biaya keuntungan dan juga sekaligus sebagai data yang akan diramalkan oleh metode MARIMA.
Seperti halnya Regresi Berganda, data yang digunakan hanya sampai April 2006, dan sisa data digunakan untuk pengecekan galat menggunakan MSE atau MAPE.
5.2.2.1 Identifikasi Bentuk Model
Langkah yang harus dilakukan pertama kali dalam tahap pertama ini adalah dengan melakukan pengecekan data mentah nilai Y, dengan cara melakukan perhitungan autokorelasi untuk mengecek apakah data mentah Y tersebut stationer atau tidak dengan melihat apakah ada data dari tabel 5.4 mulai dari time lag ke 3 di bawah ini terdapat nilai yang di luar garis Z .
Tabel 5.6 Autokorelasi nilai Yt
rYY(1) rYY(2) rYY(3) rYY(4) rYY(5) rYY(6) rYY(7) rYY(8) rYY(9) rYY(10)
0.412 0.062 -0.214 -0.042 0.076 -0.007 -0.198 -0.262 -0.165 0.126
Dan dengan menggunakan persamaan 3-4-20 maka menghasilkan garis batas Z sebagai berikut dengan tingkat kepercayaan 95% dan k = 40
-0.31 < rYY(k) < 0.31
Jika dilihat maka mulai time lag ke 3 sampai ke 10 tidak terdapat nilai korelasi yang diluar garis batas Z, maka kestationeran atau kestatisan terjadi di data ini. Yang kemudian dilanjutkan dengan membuat pembedaan data terhadap X dan Y melalui persamaan 3-4-1A dan 3-4-1B, maka akan menghasilkan data sebagai berikut :
Tabel 5.7 Pembeda Pertama Deret Input (Biaya Advertise)
dan Deret Output (Laba)
t xt yt t xt yt 0 0 0 20 8,730,000 20,737,000 1 -3,575,000 4,903,000 21 -24,650,000 -18,520,000 2 -5,080,000 -19,646,000 22 5,350,000 -6,090,000 3 1,180,000 4,970,000 23 10,175,000 7,983,000 4 850,000 -6,051,000 24 7,500,000 16,207,000 5 3,100,000 20,952,000 25 2,700,000 2,472,000 6 -5,175,000 -14,494,000 26 -8,805,000 -4,993,000 7 3,100,000 -4,639,000 27 -12,160,000 -11,496,000 8 -3,025,000 -6,008,000 28 -3,310,000 -6,873,000 9 5,150,000 13,243,000 29 10,695,000 3,689,000 10 -12,150,000 -2,500,000 30 -3,495,000 5,206,000 11 18,275,000 -3,946,000 31 5,900,000 -1,535,000 12 -1,425,000 10,540,000 32 -1,900,000 -6,687,000 13 4,450,000 10,299,000 33 -2,655,000 -3,647,000 14 -19,550,000 -11,993,000 34 -50,000 364,000 15 -4,750,000 3,239,000 35 9,105,000 4,533,000 16 13,025,000 -10,348,000 36 1,873,000 18,537,000 17 3,895,000 -18,022,000 37 6,032,000 -2,000,000 18 -2,570,000 13,668,000 38 -5,430,000 -889,000 19 -330,000 -6,644,000 39 -2,375,000 -2,670,000
Setelah mendapatkan nilai pembeda xt dan yt, maka diperlukan perhitungan autokorelasi
dari nilai xt untuk menentukan model ARIMA dari data xt tersebut.
Tabel 5.8 Autokorelasi nilai xt
rxx (1) rxx (2) rxx (3) rxx (4)
-0.202 -0.121 -0.348 0.063
Dan dengan menggunakan persamaan 3-4-20 maka menghasilkan garis batas Z sebagai berikut dengan tingkat kepercayaan 95% dan k = 40
Dengan melihat Tabel 5.6 time lag ke 1 dan ke 2 ternyata tidak terdapat nilai yang melebihi garis batas nilai Z , sehingga menghasilkan q = 0 atau MA(0). Untuk Pencarian nilai AR maka diperlukan perhitungan Partial Autokorelasi menggunakan persamaan 3-4-22 dan 3-4-23A. Berikut adalah hasil Partial Autokorelasi untuk timelag 1 dan 2.
θ1 = partial rxx(1) = -0.202 θ2 = partial rxx(2) = 0.085326
Jika melihat dari data partial Autokorelasi maka terlihat pula AR yang dihasilkan adalah p = 0 atau AR(0) karena nilai θ1 lebih kecil dari garis batas Z Pencarian differential (d)
tidak diperlukan di dalam pencarian model ini, sehingga d = 0. Sehingga akhirnya model ARIMA (p, d, q) yang dicari menghasilkan model ARIMA (0, 0, 0) atau ARMA (0, 0).
Karena model yang didapat adalah ARIMA (0,0) maka persamaan untuk mencari pemutihan dapat diuraikan sebagai berikut :
t t x x x B B α θ φ = ) ( ) (
karena AR(0) dan MA(0) maka persamaan berubah menjadi
t t x =α 1 1
Yang kemudian jika dikalikan silang maka akan menjadi persamaan
t t x =α atau t t =x α
Tetapkanlah αt = 0 dan lanjutkan, maka akan diperoleh :
α2 = x2
perhitungan α3 sampai α39 dilanjutkan untuk melengkap deret pemutihan untuk deret
input.
Setelah pemutihan deret Input dilakukan, maka dilakukan juga pemutihan deret output dari yt menjadi βt, dapat digunakan mempergunakan persamaan :
t t
x =β
1 1
yang kemudian jika dikalikan maka menghasilkan persamaan : βt = yt
Tetapkanlah βt = 0 dan lanjutkan, maka akan diperoleh :
β2 = y2
= -19,646,000
perhitungan β3 sampai β39 dilanjutkan untuk melengkap deret pemutihan untuk deret
Tabel 5.9 Deret Input dan Deret Output Setelah diputihkan t αt βt t αt βt 1 0 0 21 -24,650,000 -18,520,000 2 -5,080,000 -19,646,000 22 5,350,000 -6,090,000 3 1,180,000 4,970,000 23 10,175,000 7,983,000 4 850,000 -6,051,000 24 7,500,000 16,207,000 5 3,100,000 20,952,000 25 2,700,000 2,472,000 6 -5,175,000 -14,494,000 26 -8,805,000 -4,993,000 7 3,100,000 -4,639,000 27 -12,160,000 -11,496,000 8 -3,025,000 -6,008,000 28 -3,310,000 -6,873,000 9 5,150,000 13,243,000 29 10,695,000 3,689,000 10 -12,150,000 -2,500,000 30 -3,495,000 5,206,000 11 18,275,000 -3,946,000 31 5,900,000 -1,535,000 12 -1,425,000 10,540,000 32 -1,900,000 -6,687,000 13 4,450,000 10,299,000 33 -2,655,000 -3,647,000 14 -19,550,000 -11,993,000 34 -50,000 364,000 15 -4,750,000 3,239,000 35 9,105,000 4,533,000 16 13,025,000 -10,348,000 36 1,873,000 18,537,000 17 3,895,000 -18,022,000 37 6,032,000 -2,000,000 18 -2,570,000 13,668,000 38 -5,430,000 -889,000 19 -330,000 -6,644,000 39 -2,375,000 -2,670,000 20 8,730,000 20,737,000
Tahap selanjutnya yaitu dengan mengecek deret αt terjadi stationer atau tidak ,
dengan cara perhitungan autokorelasi.
Tabel 5.10 Autokorelasi nilai αt
rαα(1) rαα(2) rαα(3) rαα(4) rαα(5) rαα(6) rαα(7) rαα(8) rαα(9) rαα(10)
-0.210 -0.121 -0.348 0.067 -0.069 0.225 0.209 -0.107 -0.036 -0.492
Dan dengan menggunakan persamaan 3-4-20 maka menghasilkan garis batas Z sebagai berikut dengan tingkat kepercayaan 95% dan k = 39
Korelasi dari α dari time lag ke 1 sampai ke 10 hampir tidak ada yang melebihi batas garis Z, hanya di timelag ke 3 dan 10 tetapi hanya melebihi sedikit dari garis batas Z, sehingga deret α dapat dikategorikan sebagai stationer atau statis, sehingga metode fungsi transfer dapat dilanjutkan ke tahap berikutnya .
Dalam tahap penaksiran bobot impuls perhitungan untuk menghitung nilai dari bobot impuls dapat menggunakan persamaan 3-4-10 dan dengan bantuan Tabel 5.11 dan tabel 5.12 .
Tabel 5.11 Rata-rata dan ragam dari αt dan βt
αt βt
Rata2 56,410.256 -334,666.667
Ragam 68,078,722,447,074.30 107,829,284,017,094.00
Tabel 5.12 Korelasi nilai αt dan βt
rαβ(0) rαβ(1) rαβ(2) rαβ(3) rαβ(4) rαβ(5) rαβ(6) rαβ(7) rαβ(8) rαβ(9) rαβ(10)
0.423 -0.273 -0.032 -0.354 0.305 -0.058 0.131 0.001 0.003 -0.371 0.005
υ0 = (0.423) 68,078,722,447,074.30107,829,284,017,094.00 = 0.532584
dan penaksiran bobot dilanjutkan sampai ke υ6. Hasil keseluruhan nilai bobot dapat
dilihat di tabel 5.13.
Tabel 5.13 Taksiran bobot impuls υ0 0.532584 υ1 -0.34295 υ2 -0.04043 υ3 -0.44514 υ4 0.383251 υ5 -0.07316 υ6 0.164901
Pengidentifikasian (r, s, b) untuk model fungsi transfer merupakan hal yang susah untuk ditentukan, nilai r dan s tidak dapat dilihat secara pasti oleh model fungsi transfer ini. tetapi hal ini dapat diargumenkan sebagai 4 (r + s = 4) karena pada tabel 5.11 terlihat untuk k = 0 , 1 , 2 dan 9 (terdapat 4 korelasi) secara signifikan lebih besar dari 0 . karena itu dapat dikatan bahwa r = 2 dan s = 2 .
Untuk nilai b dapat ditentukan dengan melihat mulai time lag atau k keberapakah deret input yang telah diputihkan (advertise) mulai mempengaruhi deret output yang telah diputihkan (keuntungan) . Hal ini terlihat di tabel 5.11 bahwa di dalam bulan itu juga (timelag = 0) deret input mulai mempengaruhi deret output . karena itu nilai parameter b langsung dapat ditentukan sebagai 0. Setelah mendapatkan 3 nilai r, s dan b maka dapat ditentukan bahwa model fungsi transfer dengan (r, s ,b) = (2, 2, 0).
Pembentukan data deret noise (nt) dapat digunakan dengan menggunakan
persamaan 3-4-11 dan menggunakan data bobot impuls dari tabel 5.12. Jika melihat tabel bobot impuls maka akan terlihat adanya 6 time lag (disini menggunakan 6 karena di timelag ke 7 deret input sudah hampir tidak mempengaruhi deret output sama sekali) karena itu bobot impuls dicari sampai pada υ6. Perhitungan menggunakan persamaan 3-4-11 dan nilai n akan dimulai dari n7 (karena terdapat 6 bobot yang dipakai), Tetapi pada
akhirnya nilai n7 akan diubah menjadi nilai yang pertama atau n1.
n7 = y7 – (0.532584)x7 – (-0.342954)x6 - . . . – (0.164901)x1
= -4,639,000 – (0.537794)3,100,000 – (0.257637)-5,175,000 – . . . – (-0.08164)-3,575,000
Hasil keseluruhan disajikan di tabel 5.14 berikut ini :
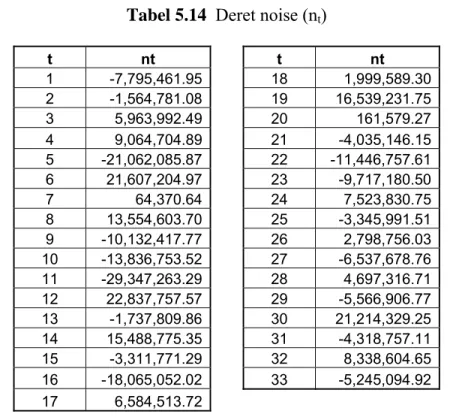
Tabel 5.14 Deret noise (nt)
t nt t nt 1 -7,795,461.95 18 1,999,589.30 2 -1,564,781.08 19 16,539,231.75 3 5,963,992.49 20 161,579.27 4 9,064,704.89 21 -4,035,146.15 5 -21,062,085.87 22 -11,446,757.61 6 21,607,204.97 23 -9,717,180.50 7 64,370.64 24 7,523,830.75 8 13,554,603.70 25 -3,345,991.51 9 -10,132,417.77 26 2,798,756.03 10 -13,836,753.52 27 -6,537,678.76 11 -29,347,263.29 28 4,697,316.71 12 22,837,757.57 29 -5,566,906.77 13 -1,737,809.86 30 21,214,329.25 14 15,488,775.35 31 -4,318,757.11 15 -3,311,771.29 32 8,338,604.65 16 -18,065,052.02 33 -5,245,094.92 17 6,584,513.72
Penentuan model ARMA untuk deret noise dapat diperiksa dengan perhitungan autokorelasi .
Tabel 5.15 Autokorelasi nt
rnn(1) rnn(2) rnn(3) rnn(4) rnn(5) rnn(6) rnn(7) rnn(8) rnn(9) rnn(10)
-0.270 0.128 -0.494 -0.007 0.048 0.402 -0.149 -0.215 -0.147 -0.092
Dan dengan menggunakan persamaan 3-4-20 maka menghasilkan garis batas Z sebagai berikut dengan tingkat kepercayaan 95% dan k = 33
Jika membandingkan nilai autokorelasi di atas dengan garis batas Z , maka terlihat di time lag ke 1 dan ke 2 tidak terdapat nilai yang melebihi nilai batas Z, sehingga nilai MA dapat diketahui sebagai 0 atau MA(0). Untuk Pencarian nilai AR maka diperlukan perhitungan Partial Autokorelasi menggunakan persamaan 3-4-22 dan 3-4-23A. Berikut adalah hasil Partial Autokorelasi untuk timelag 1 dan 2.
θ1= partial rnn(1) = -0.270
θ2= partial rnn(2) = 0.430034
Jika melihat dari data partial Autokorelasi maka terlihat pula AR yang dihasilkan adalah p = 0 atau AR(0) karena nilai θ1 lebih kecil dari garis batas Z Pencarian differential (d)
tidak diperlukan di dalam pencarian model ini, sehingga ditetapkan d = 0. Dan akhirnya deret noise yang dimodelkan menghasilkan model ARIMA (0, 0, 0) atau ARMA (0, 0).
5.2.2.2 Penaksiran Parameter-Parameter Model
Setelah mendapatkan model fungsi transfer atau MARIMA (r, s, b) dan model ARIMA pada deret noise (p, d, q) maka akhirnya model keseluruhan fungsi transfer dapat dibentuk yaitu, fungsi transfer (2, 2, 0) + deret noise (0, 0) yang akhirnya model fungsi transfer dapat dibentuk sebagai berikut :
t t t x a B B B B y + − − + − = ) 1 ( ) ( 2 2 1 2 2 1 0 δ δ ω ω ω
Tahap selanjutnya yaitu dengan melakukan taksiran parameter-parameter penduga yang akan digunakan oleh model fungsi transfer di atas. Penaksiran parameter-parameter dapat dilakukan dengan substitusi melalui persamaan 3-4-13 yang akhirnya melalui model fungsi transfer(2, 2, 0)(0, 0) membentuk persamaan
υ1 = δ1υ0 + δ2υ-1 – ω1 (2)
υ2 = δ1υ1 + δ2υ0 – ω2 (3)
υ3 = δ1υ2 + δ2υ1 (4) (4-1-1)
υ4 = δ1υ3 + δ2υ2 (5)
υ5 = δ1υ4 + δ2υ3 (6)
untuk keterangan nilai υ dengan subskrip negatif contoh υ -1, maka nilai υ = 0.
Pada akhirnya melalui persamaan di atas maka nilai-nilai parameter dapat dicari dan disajikan di Tabel 5.16 sebagai berikut :
Tabel 5.16 Taksiran paramater untuk model fungsi transfer δ1 = -0.81237
δ2 = -0.53507
ω0 = 0.53258
ω1 = -0.0897
ω2 = 0.03406
5.2.2.3 Pemeriksaan Diagnostik pada Model
Model fungsi transfer atau MARIMA di bagian 5.2.2.2 dapat lebih dipersingkat prosedurnya seperti : t b t t a B B x B B y ) ( ) ( ) ( ) ( φ θ δ ω + = −
bila dikalikan dengan δ(B)φ(B)kita peroleh
t b t t B B x B B a y B B) ( ) ( ) ( ) ( ) ( ) ( φ δ φ δ φ δ = − +
Dengan model MARIMA (2, 2, 0) (0, 0) maka diperoleh persamaan :
t t t x a B B B B y + − − − − = ) 1 ( ) ( 2 2 1 2 2 1 0 δ δ ω ω ω
yang lanjutkan dengan mengkalikan tiap parameternya menjadi (1 – δ1B – δ2B2) yt = (ω0 – ω1B - ω2B2) xt + (1 – δ1B – δ2B2) at
kemudian dengan melakukan pengaturan perkalian maka menjadi yt = (δ1)yt-1 + (δ2)yt-2
+ (ω0)xt – (ω1)x t-1 – (ω2)xt-2 (4-1-2)
+ at – (δ1)a t-1 – (δ2)a t-2
Persamaan juga dapat diubah untuk mendapatkan nilai at
at = yt – (δ1)yt-1 – (δ2)yt-2
– (ω0)xt + (ω1)x t-1 + (ω2)x t-2 (4-1-3)
+ (δ1)a t-1 + (δ2)a t-2
Dan dengan menggunakan bantuan Tabel 5.16 maka perhitungan nilai at menjadi dapat
dilakukan. a7 = y7 – (δ1)y6 – (δ2)y5 – (ω0)x5 + (ω1)x4 + (ω2)x3 + (δ1)a6 + (δ2)a5 = (-4,639,000) – (-0.81237)(-14,494,000) – (-0.53507)(20,952,000) – (0.53258)( 3,100,000) + (-0.0897)(850,000) + (0.03406)( 1,180,000) + (-0.81237)( 0) + (-0.53507)(0) = -6,283,918.64
perhitungan at dilanjutkan terus sampai a40, yang kemudian a7 dianggap sebagai t ke 1
dan hal ini berlangsung trus sampai ke t33. berikut adalah hasil lengkap perhitungan at
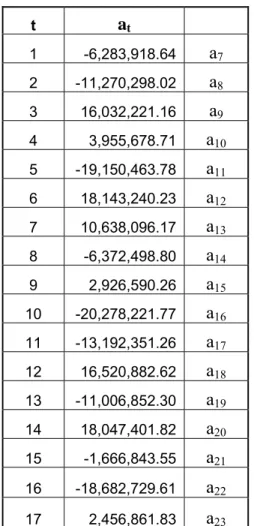
Tabel 5.17 Nilai akhir pelengkap (at) t at t at 1 -6,283,918.64 a7 18 22,709,434.20 a24 2 -11,270,298.02 a8 19 -1,617,667.22 a25 3 16,032,221.16 a9 20 -447,307.61 a26 4 3,955,678.71 a10 21 -5,642,582.59 a27 5 -19,150,463.78 a11 22 -11,506,710.83 a28 6 18,143,240.23 a12 23 -1,491,906.09 a29 7 10,638,096.17 a13 24 12,683,459.33 a30 8 -6,372,498.80 a14 25 -7,301,765.02 a31 9 2,926,590.26 a15 26 -5,639,584.97 a32 10 -20,278,221.77 a16 27 373,118.31 a33 11 -13,192,351.26 a17 28 -3,262,195.37 a34 12 16,520,882.62 a18 29 392,682.43 a35 13 -11,006,852.30 a19 30 22,024,794.30 a36 14 18,047,401.82 a20 31 -5,688,434.09 a37 15 -1,666,843.55 a21 32 2,655,792.49 a38 16 -18,682,729.61 a22 33 -1,618,714.22 a39 17 2,456,861.83 a23
Pengecekan kestationeran atau korelasi yang pada dasarnya telah nol dapat dilakukan dengan 2 cara yaitu dengan cara yang dijelaskan di bagian 3.4.2.4 atau dengan cara X2 dalam persamaan 3-4-17. tetapi karena akan lebih sulit menggunakan cara X2, karena diperlukan pengetahuan tentang seberapa maksimum lag yang akan dijadikan acuan, maka digunakanlah cara di bagian 3.4.2.4 dengan hanya mengambil 10 time lag untuk dibandingkan dengan garis batas Z .
Tabel 5.18 Aukokorelasi at
raa(1) raa(2) raa(3) raa(4) raa(5) raa(6) raa(7) raa(8) raa(9) raa(10)
-0.205 -0.324 0.178 -0.319 0.0312 0.526 -0.399 -0.134 0.014 -0.145
Dan dengan menggunakan persamaan 3-4-20 maka menghasilkan garis batas Z sebagai berikut dengan tingkat kepercayaan 95% dan n = 33
-0.341 < rnn (k) < 0.341
Jika melihat dimulai time lag ke 3 sampe ke 10, maka terlihat di timelag ke 6 dan ke 7 berada di luar garis batas Z, namun karena berhenti hanya sampai ke timelag 7 dan tidak berlanjut ke timelag 8 maka, nilai at dapat dikatakan statis atau stationer.
Hal ini berlaku juga untuk pengecekan kestatisan antara α dan a, penggunaan cara X2 akan menyulitkan, karena itu digunakan cara yang dijelaskan di bagian 3.4.2.4 dengan hanya mengambil 10 time lag untuk dibandingkan dengan garis batas Z.
Tabel 5.19 Korelasi αt dan at
rαa(1) rαa(2) rαa(3) rαa(4) rαa(5) rαa(6) rαa(7) rαa(8) rαa(9) rαa(10)
-0.017 0.040 -0.323 0.144 0.468 -0.071 -0.288 0.011 -0.190 0.202
Dan dengan menggunakan persamaan 3-4-20 maka menghasilkan garis batas Z sebagai berikut dengan tingkat kepercayaan 95% dan n = 33
-0.341 < rnn (k) < 0.341
Kembali terlihat bahwa di timelag ke 5 menyebabkan ketidakstatisan, tetapi karena tidak berlanjut ke timelag berikutnya, maka hal korelasi αt dan at masih dapat dianggap
5.2.2.4 Penggunaan Model Fungsi Transfer / MARIMA untuk peramalan
Setelah semua pengecekan telah memenuhi, maka akan masuk ke tahap peramalan menggunakan model MARIMA yang telah dibuat dan parameter-parameter yang telah didapat. Dengan menggunakan persamaan 4-1-2 yang telah maka peramalan dihitung. Peramalan data Y yang ingin diramal adalah data bulan Mei 2006 atau data ke 40, (karena data Yt dan yt dimulai dari indeks ke 0 bukan ke 1) sehingga perhitungan
dimulai dari index ke y40 dapat dilihat sebagai berikut, dengan bantuan Tabel 5.6, Tabel
5.15 dan Tabel 5.16: Y40 = (δ1)y39+ (δ2)y38 + (ω0)x40 – (ω1)x39– (ω2)x38 + a40 – (δ1)a39 – (δ2)a38 = (-0.81237)(-2,670,000) – (-0.53507)(-889,000) + (0.53258) (5,790,000) – (-0.0897) (-2,375,000) – (0.03406) (-5,430,000) + (0) – (-0.81237) (-4,372,435.51) – (-0.53507) (-421,070.44) = 793,347
Dan peramalan Y40 (Mei 2006) menghasilkan nilai sebagai berikut : Y40 = Y39 + y40
= 175,853,000 + (793,347)
= 176,646,346.72
Begitu juga untuk peramalan Y41 dan yang seterusnya .
Perhatikan bahwa bila kita ingin meramal Y40 , maka akan terlihat persamaan
(ω0)x40, dimana x40 tidak tersedia, karena itu diperkuakn suatu penanganan nilai xt
data Xt yang diberikan oleh perusahaan tidak sampai berhenti di April 2006, maka dapat dengan mudah mengambil data May 2006 dan seterusnya untuk digunakan dalam pencarian xt lebih lanjut, tanpa harus menggunakan penangan lebih lanjut seperti
peramalan untuk xt dan lain sebagainya. Berikut adalah hasil lengkap hasil peramalan
yang disajikan di tabel berikut ini :
Tabel 5.20 Hasil peramalan MARIMA 2006 May 181,659,291.64 2006 June 171,186,987.28 2006 July 173,948,063.47 2006 Aug 179,385,453.04 2006 Sept 172,286,375.82
5.3 Analisis Data Hasil dan Error
Peramalan tetaplah peramalan, hal yang tidak dapat dilepaskan dari galat. Melalui penghitungan galat menggunakan MSE (persamaan 3-5-1) dan MAPE (persamaan 3-5-2) maka akan terlihat peramalan yang lebih baik antara metode Regresi Berganda dan MARIMA.
Tabel 5.21 Data Laba Pengamatan dan Peramalan
Tanggal Pengamatan Regresi Berganda MARIMA 2006 May 172,634,000 170,912,348 181,659,292 2006 June 165,623,000 162,487,042 171,186,987 2006 July 169,412,000 167,369,210 173,948,063 2006 Aug 171,867,000 173,589,658 179,385,453 2006 Sept 167,523,000 163,526,959 172,286,376
Gambar 5.1 Grafik Hasil Pengamatan dan Peramalan
Grafik Hasil Pengamatan dan Peramalan
150,000,000 155,000,000 160,000,000 165,000,000 170,000,000 175,000,000 180,000,000 185,000,000 2006 May 2006 June 2006 July 2006 Aug 2006 Sept Tanggal R upi ah Pengamatan Regresi Berganda Fungsi Transfer
Tabel 5.22 Hasil galat MAPE dan MSE
MAPE MSE
MARIMA 3.69% 42,441,320,161,766.00
Regresi Berganda 1.49% 7,181,476,807,624
Melalui Hasil Perhitungan galat dapet terlihat bahwa melalui perhitungan galat baik melalui MSE dan MAPE metode Regresi Berganda menghasilkan peramalan yang lebih baik dari peramalan MARIMA, bahkan jika melihat melalui grafik peramalan Regresi Berganda bahkan sangat mendekati data pengamatan. Hal ini terjadi karena variabel Regresi Berganda yang mempengaruhi variabel tidak bebas (data laba) lebih banyak dari MARIMA, dengan perbandingan tiga variabel bebas untuk Regresi Berganda dan satu variabel bebas untuk MARIMA.
Tetapi peramalan multivariate melalui Metode Regresi dan MARIMA memperlihatkan peramalan yang sangat baik, hal ini bisa dilihat melalui galat MAPE yang hanya 3,69% untuk Fungsi Transfer dan 1.49% untuk Regresi Berganda. Dan jika
melihat kembali melalui grafik tampak pola Regresi Berganda dan MARIMA mengikuti pola pengamatan.
Melalui Data yang disajikan Tabel 5.21 dan Tabel 5.22, maka Hipotesis dapat dijawab sebagai berikut :
¾ Metode Regresi Berganda menghasilkan peramalan yang lebih baik dari metode Fungsi Transfer atau MARIMA dengan menggunakan ukuran MSE.
¾ Metode Regresi Berganda menghasilkan peramalan yang lebih baik dari metode Fungsi Transfer atau MARIMA dengan menggunakan ukuran MAPE.
Peramalan menggunakan data multivariate menggunakan metode Regresi Berganda dan MARIMA mempunyai kelemahan yang mendasar di dalam peramalan. Kedua metode ini memerlukan data variabel bebas di waktu yang sama untuk meramalkan variabel tidak bebasnya. Karena itu memerlukan penanganan secara terpisah seperti peramalan untuk melengkapi variabel bebas tersebut.
5.4 Implementasi
5.4.1 Spesifikasi Kebutuhan Sarana
Untuk dapat menjalankan program aplikasi peramalan ini dibutuhkan perangkat keras dan lunak yang spesifikasinya sebagai berikut :
5.4.1.1 Spesifikasi Perangkat Keras yang Dibutuhkan
Spesifikasi dari perangkat keras yang digunakan dalam pengembangan dan pengujian program aplikasi peramalan ini adalah sebagai berikut :
¾ CPU AMD Athlon XP 1700+ ¾ Memory 512 MB DDRAM ¾ Hard Disk 80 GB
¾ Resolusi monitor 1024 x 768 pixels
5.4.1.2 Spesifikasi Perangkat Lunak yang Dibutuhkan
Selain spesifikasi kebutuhan perangkat keras seperti yang telah disebutkan diatas, dibutuhkan pula spesifikasi piranti lunak sebagai berikut:
¾ Operating System: Microsoft Windows XP/2000/NT ¾ Java 2 SDK, SE v1.4.0
¾ Class JfreeChart ¾ Microsoft Access
5.4.2 Persiapan Data
Pada awal proses pengoperasian program aplikasi peramalan ini, data yang harus disisapkan adalah data peramalan yang akan diramal, serta variabel-variabel bebasnya. Yang data tersebut dapat dimasukan ke dalam database melalui dua cara yaitu pengisian database secara manual, atau import menggunakan Excel. Penggunaan software ini harus memiliki kriteria-kriteria sebagai berikut :
¾ User Harus mengetahui secara umum variabel yang mempengaruhi di dalam peramalan dan dapat mengisi variabel bebas dan variabel tidak bebas tersebut secara benar ke dalam database.
¾ Di dalam pengimportan melalui Excel, tidak diperbolehkan ada data-data lain yang tidak berhubungan dengan data peramalan, karena jika user melakukan
proses pengimportan ke dalam database, maka database akan berisi data lain yang tidak ada hubungannya dengan data peramalan.
5.4.3 Pengujian Aplikasi
Pada saat aplikasi dijalankan, akan tampil menu utama. Pada saat ini user dapat memilih antara load data (dapat dilihat di Gambar5.4) yang dilanjutkan dengan mengklik process atau masuk ke halaman view/search dengan memilih menu
File>Search Data. Pengujian Program secara lengkap dapat dilihat di LAMPIRAN I.
Di halaman process ini, seluruh perhitungan peramalan melalui metode Regresi Berganda dan Fungsi Transfer atau MARIMA dapat dilihat hasilnya baik dalam tabel maupun dalam bentuk grafik. Untuk perhitungan galat hanya ditampilkan dalam tampilan seperti tabel.
Di halaman view atau search data, dapat dilakukan dengan mencari data yang sudah di save ke dalam database dan dapat ditampilkan kembali.
Gambar 5.4 Tampilan Menu Search
5.4.4 Hasil Peramalan pada Aplikasi dan Feedback GK AUTO
Hasil Peramalan pada program atau aplikasi software memberikan hasil yang sedikit berbeda dengan perhitungan secara manual. Hal ini disebabkan adanya perbedaan perhitungan angka di belakang koma yang lebih detail dilakukan oleh aplikasi program.
Tabel 5.23 Hasil Perbandingan Peramalan Regresi Berganda dengan Aplikasi Regresi Berganda
Manual Regresi Berganda Software 170,912,339 170,912,348 162,487,032 162,487,043 167,369,200 167,369,210 173,589,648 173,589,658 163,526,949 163,526,959
Tabel 5.24 Hasil Perbandingan Peramalan MARIMA dengan Aplikasi
MARIMA Manual MARIMA Software
181,659,292 181,657,565 171,186,987 171,186,073 173,948,063 173,947,990 179,385,453 179,383,481 172,286,376 172,287,275
Melalui Tabel 5.23 dan 5.24 maka terlihat bahwa perbedaan peramalan yang dihasilkan sangatlah kecil, sehingga kesalahan ini hampir dapat disebut tidak ada.
GK AUTO memberikan evaluasi yang baik untuk aplikasi ini, hal ini dikarenakan aplikasi yang dibuat memberikan peramalan yang cukup baik, sehingga memudahkan GK AUTO untuk mengatur keuangan yang terdapat didalam sistem mereka.
5.4.5 Open Problem
Tujuan aplikasi ini sudah berhasil dicapai, tetapi masih beberapa aspek yang tidak dapat dipenuhi atau tidak terdapat di dalam aplikasi ini. Beberapa aspek tersebut adalah:
¾ Variabel data jumlah variabel bebas yang bisa diterima oleh aplikasi ini hanya terbatas sampai tiga variabel bebas.
¾ Pengimportan data langsung dari Excel tidak dapat dilakukan, karena ketidaksediaannya open server untuk menjalankan aplikasi pengimportan dari Excel.
¾ Mencari cara mengurangi ketergantungan program aplikasi penggunaan java terhadapat spesifikasi RAM yang tinggi.